Positive-unlabeled convolutional neural networks for particle picking in cryo-electron micrographs

Abstract

Cryo-electron microscopy is a popular method for protein structure determination. Identifying a sufficient number of particles for analysis can take months of manual effort. Current computational approaches find many false positives and require significant ad hoc post-processing, especially for unusually-shaped particles. To address these shortcomings, we develop Topaz, an efficient and accurate particle picking pipeline using neural networks trained with a general-purpose positive-unlabeled (PU) learning method. This framework enables particle detection models to be trained with few, sparsely labeled particles and no labeled negatives. Topaz retrieves many more real particles than conventional picking methods while maintaining low false positive rates, is capable of picking challenging unusually-shaped proteins (e.g. small, non-globular, and asymmetric), produces more representative particle sets, and does not require post hoc curation. We demonstrate the performance of Topaz on two difficult datasets and three conventional datasets. Topaz is modular, standalone, free, and open source (http://topaz.csail.mit.edu)

Introduction

Single particle cryo-electron microscopy (cryoEM) is a method capable of resolving high-resolution structures of proteins in near-native states. CryoEM projection images (micrographs) can contain hundreds or thousands of individual protein projections (particles). Given a sufficient number of particles, the 3D structure of the protein can be determined¹. However, due to the low signal-to-noise ratio (SNR) of cryoEM images, large numbers of observations are required for accurate reconstruction. Studies show a log-linear relationship between the number of particles included and the inverse resolution of the reconstruction^2,3. The concentration of protein on EM grids, efficiency of data collection, and completeness and accuracy of particle identification are factors determining the total number of particles available for downstream reconstruction and hence the achievable resolution. In particular, particle identification (particle picking) is a major bottleneck, often taking weeks or even months with current workflows for small or non-globular particles, due to variability in particle shapes and structured noise in micrographs.

A variety of methods have been developed for particle picking automation. The most common are Difference of Gaussians (DoG) and template-based approaches^4–8. However, these methods are unable to detect unusually shaped particles and suffer from high false positive rates causing them to require significant post-picking curation. Most commonly, researchers use iterative 2D/3D classification and discard poor subsets by eye. These picking methods and downstream curation introduce significant bias into the final particle set, potentially removing rare particle views and conformations^9–11. Newer methods based on convolutional neural networks (CNNs) have been proposed^12–14, which use positive and negative labeled micrograph regions to train CNN classifiers which then predict labels for the remaining regions. However, due to factors like low SNR, structured background, and the distribution of particle morphologies, researchers must label a large number of regions for training — a non-trivial and time-consuming task. Moreover, the diverse characteristics of negative data make it difficult to manually label a representative set of negative examples, and hence the number of labeled negatives must be an order of magnitude larger than the number of positives to achieve acceptable performance¹⁵. This has limited adoption by the cryoEM community and hand-labeling remains the gold standard.

To overcome the challenges inherent in current automatic particle picking methods, we newly frame particle picking as a positive-unlabeled (PU) learning problem. We seek to learn a classifier of positives and negatives given a small number of labeled positive regions and the remaining unlabeled regions. PU learning has proved to be an effective paradigm when working with partially labeled data in other domains (e.g. document classification¹⁶, time series classification¹⁷, and anomaly detection¹⁸). Recent work has explored general purpose PU learning for neural network models based on estimating the true positive-negative risk, but overfitting remains a challenge for PU learning¹⁹. Therefore, we instead approach PU learning as a constrained optimization problem in which we wish to find classifier parameters to minimize classification errors on the labeled data subject to a constraint on the expectation over the unlabeled data. By imposing this constraint softly with a novel generalized expectation (GE) criteria²⁰, we are able to mitigate overfitting and train high accuracy particle classifiers using very few labeled data points. Furthermore, by combining our PU learning method with autoencoder-based regularization, we can further reduce the amount of labeled data required for high performance.

Here, we present Topaz, a pipeline for particle picking using convolutional neural networks with PU learning. Topaz retrieves many more particles than alternative methods while maintaining a low false positive rate. It substantially reduces the need for particle curation, removes systematic bias in particle picking introduced by conventional pickers and 2D/3D classification procedures, and allows for robust and representative particle analysis and classification. Furthermore, Topaz is capable of reliably picking previously challenging particles (e.g. small, non-globular, asymmetric) while avoiding aggregation, grid substrate, and other background objects, all while requiring minimal example particles.

We first demonstrate Topaz’s capabilities on a novel protein dataset for the Toll receptor — a ~105 kDa, non-globular, asymmetric particle. Despite aggregation and sparse labeling in the dataset, Topaz enables a 3.7 Å reconstruction and resolves secondary structures not possible with other methods. Topaz also decreases anisotropy by better detecting conventionally difficult particle views. Additionally, on three publicly available datasets, we find that by using Topaz with only 1,000 labeled training examples, we are able to retrieve many more real particles than were included in the published particle sets. In addition, we are able to solve 3D structures of equal or greater quality to those found using the published particles, despite the published particles having been taken through significant manual curation. Remarkably, the Topaz results do not require any ad hoc post-processing typically required for high-resolution structures; we feed Topaz particles directly into alignment and reconstruction. Finally, we compare our GE-based PU learning method against other off-the-shelf PU learning approaches and find that our method improves over the current state-of-the-art in application to training particle detection models. Topaz was a critical component in determining the single particle behavior of an elongated clustered protocadherin²¹.

Topaz source code is freely available (https://github.com/tbepler/topaz) and can be installed through Anaconda, Pip, Docker, Singularity, and SBGrid²². Topaz is designed to be modular, has been integrated into Appion²³, is being integrated into Relion²⁴, CryoSparc²⁵, EMAN2⁵, Scipion²⁶, and Focus²⁷, and can easily be integrated into other cryoEM software suites in the future. Topaz runs efficiently on a single GPU computer and includes a standalone GUI²⁸ to assist with particle labeling.

Results

1. The Topaz Pipeline

The Topaz particle picking pipeline is composed of three main steps (Figure 1): (1) whole micrograph preprocessing, optionally with a mixture model newly designed to capture micrograph statistics (Online Methods, Supplementary Figures 1, 2 & 3), (2) neural network classifier training with our PU learning framework, and (3) sliding window classification of micrographs and particle coordinate extraction by non-maximum suppression.

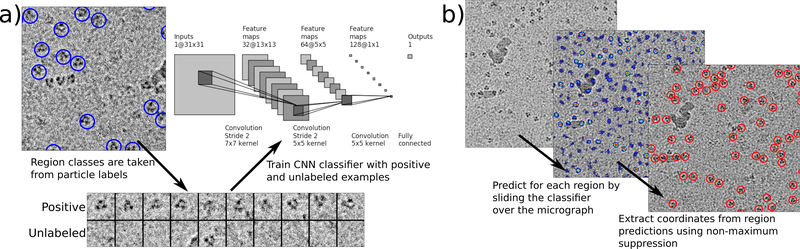
Figure 1 |.

Topaz particle picking pipeline using CNNs trained with positive and unlabeled data. (a) Given a set of labeled particles, a CNN is trained to classify positive and negative regions using particle locations as positive regions and all other regions as unlabeled. Labeled particles from EMPIAR-10096 are indicated by blue circles and a few positive and unlabeled regions are depicted. (b) Once the CNN classifier is trained, particles are predicted in two steps. First, the classifier is applied to each micrograph region to give per region predictions. Second, coordinates are extracted from the region predictions using non-maximum suppression. The left image shows a raw micrograph from EMPIAR-10096. The middle image depicts the micrograph with overlaid region predictions [blue = low confidence, red = high confidence]. The right image indicates predicted particles after using non-maximum suppression on the region predictions.

Classifier training from positive and unlabeled data

We frame particle picking as a PU learning problem in which we seek to learn a classifier that discriminates between particle and non-particle micrograph regions given a small number of labeled particles and many unlabeled micrograph regions. CNN classifiers are trained using minibatched stochastic gradient descent with a novel objective function, GE-binomial (Online Methods), which explicitly models the sampling statistics of minibatch training to regularize the classifier’s posterior over the unlabeled data. Combining this with an optional autoencoder module allows high-accuracy classifiers to be trained despite using very few positive examples. This approach allows us to overcome overfitting problems associated with recent PU learning methods developed for neural networks in domains other than cryoEM analysis and to effectively pick particles in challenging cryoEM datasets.

Micrograph region classification and particle extraction

Given a trained CNN particle classifier, we extract predicted particle coordinates and their associated predicted probabilities. First, we calculate the per pixel predicted probabilities by applying the classifier to each micrograph region as a sliding window. Then, to extract coordinates from these dense predictions, we use the well-known non-maximum suppression algorithm to greedily select high scoring pixels and remove their neighbors from consideration as particle centers. This yields a list of predicted particle coordinates and their associated model scores for each micrograph.

2. Topaz picks challenging particles and orientations

We explore the ability of Topaz to detect challenging particles on a small, asymmetric, non-globular, and aggregated protein, a Toll receptor. To this end, we compare particles picked by Topaz (trained with 686 labeled particles) with particles picked using several other methods: DoG⁷ and template picking followed by 2D class averaging and manual filtering and CNN-based methods crYOLO²⁹ and DeepPicker¹² (Online Methods). The CNN-based methods were all trained following the software instructions with default settings and identical labeled particles.

After four rounds of 2D classification and filtering, DoG finds 770,263 good particles from an initial stack of 1,599,638 and template picking finds 627,533 good particles from an initial stack of 1,265,564. Using Topaz, after one round of 2D classification, we are left with 1,006,089 of an initial 1,010,937 particles, indicating that Topaz gives a remarkably low false positive rate of only 0.5% on this data. We then compare the quality of the picked particles by taking each particle set through reconstruction (Figure 2a,b,c). We find that particles picked using Topaz yield a structure with 0.731 sphericity at FSC_0.143 = 3.70 Å resolution, compared to 0.706 sphericity at 3.92 Å for template picked particles and 0.652 sphericity at 3.86 Å for particles picked using DoG. Furthermore, only the Topaz particle based density map is of high enough quality to reliably resolve secondary structure (beta-strands) and allow for model building. Other CNN-based picking methods, crYOLO and DeepPicker, are unable to find sufficient numbers of good particles for high-resolution reconstruction. crYOLO finds 131,300 particles resulting in a 6.8 Å structure while DeepPicker fails to find any meaningful particles in this dataset (Supplementary Figures 4 – 7).

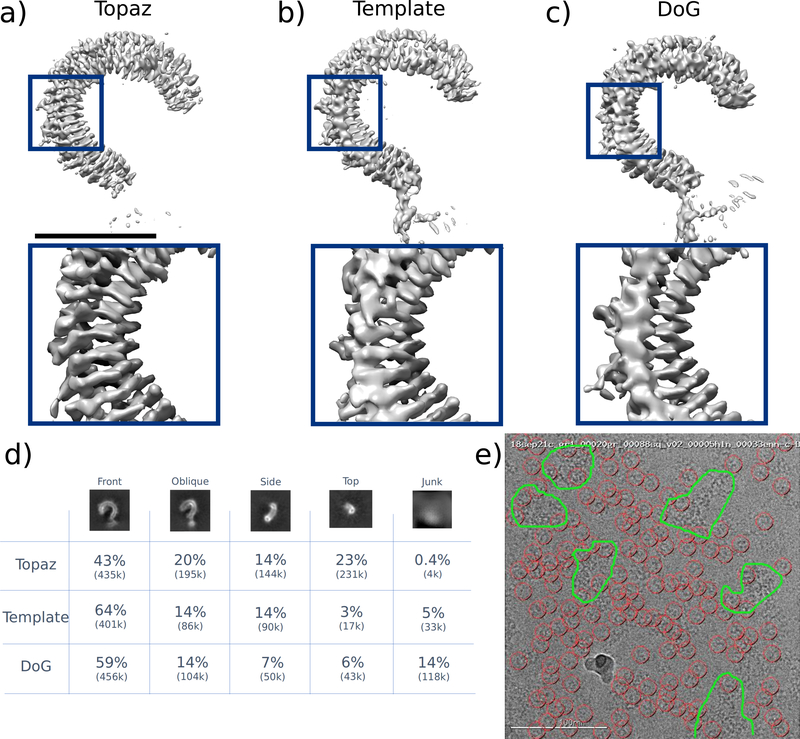
Figure 2 |.

Reconstructions of the Toll receptor using particles picked by Topaz, template-based (Template), and DoG methods. Template and DoG particles were filtered through multiple rounds of 2D classification before analysis. Topaz particles were not filtered. (a) Density map using particles picked with Topaz. The global resolution is 3.70 Å at FSC_0.143 with a sphericity of 0.731. (b) Density map using particles picked using template picking. The global resolution is 3.92 Å at FSC_0.143 with a sphericity of 0.706. (c) Density map using particles picked using difference of Gaussians (DoG). The global resolution is 3.86 Å at FSC_0.143 with a sphericity of 0.652. (d) Quantification of picked particles for each protein view based on 2D classification. (e) Example micrograph (representative of >100 micrographs examined) showing Topaz picks (red circles) and protein aggregation (outlined in green). Scale bar for the top of (a) is 5 nm.

We next quantify the ability of these methods to detect different particle views. This particle is strongly asymmetric and non-globular, thus it is important for picking methods to retrieve the full spectrum of view angles. By counting the number of particles assigned to each view in 2D class averages, we find that Topaz retrieves a much larger fraction of oblique, side, and top views of the Toll receptor than do DoG and template methods (Figure 2d). In addition, we note that these micrographs are challenging - containing junk and significant protein aggregation, yet Topaz is uniquely able to avoid these micrograph regions while picking only good particles (Figure 2e, Supplemental Figure 4).

3. Topaz enables high-resolution reconstruction with no post-processing

We next evaluate the full Topaz particle picking pipeline by generating reconstructions for three cryoEM datasets containing T20S proteasome (EMPIAR-10025), 80S ribosome (EMPIAR-10028), and rabbit muscle aldolase (EMPIAR-10215). Each of these datasets already has a curated set of particles yielding high quality reconstructions which we compare with particles predicted by Topaz, trained with 1,000 positives, based on reconstruction quality (Online Methods). We standardize the reconstruction procedure by using cryoSPARC homogeneous refinement on the raw Topaz particle sets (i.e. no post-processing was applied) and published particle sets with identical settings for each dataset. By considering the reconstruction resolution at decreasing probability thresholds (increasing numbers of particles) predicted by Topaz, we select the particle set that optimizes the resolution for each dataset.

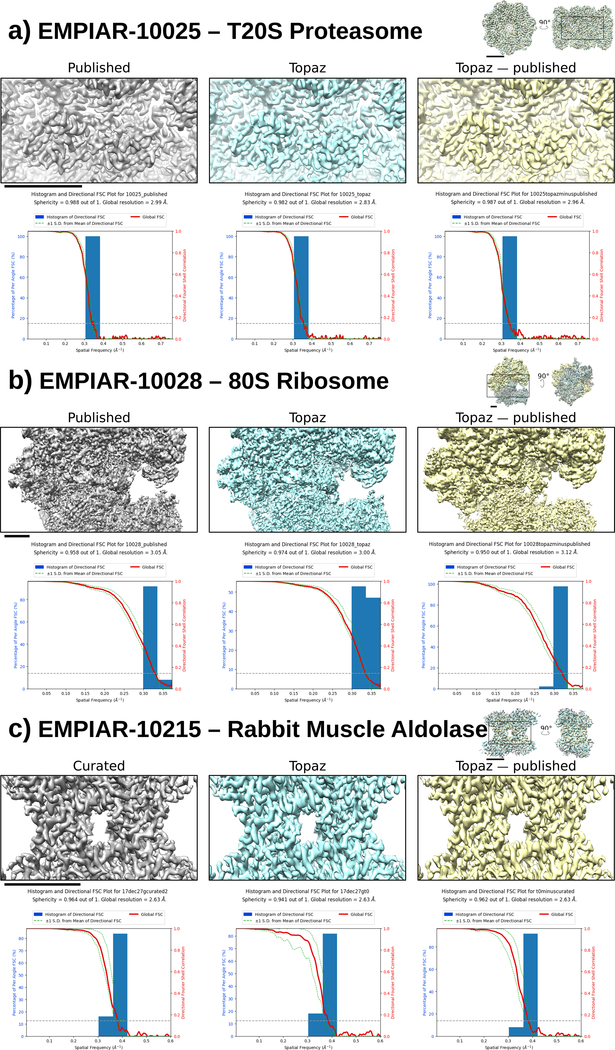
We find that Topaz is able to retrieve substantially more good particles than were present in the curated particle sets, finding 3.22, 1.72, and 3.68 times more particles in EMPIAR-10025, EMPIAR-10028, and EMPIAR-10215 respectively. Furthermore, reconstructions from the Topaz particle sets are of equal or higher quality to those given by the curated particles (Figure 3). Topaz maps reach roughly equivalent resolution to the published structures for 80S ribosome and rabbit muscle aldolase while improving the resolution by ~0.15 Å over the published structures for the T20S proteasome. Remarkably, this was achieved using only 1,000 labeled examples and no filtering of the particle set (e.g. particle filtering with 2D or 3D class averaging or iterative reconstructions removing poor particles). We note that even though these labeled training particles are extremely sparse, PU learning enables Topaz to pick with high precision as seen in example micrographs (Supplementary Figures 8, 9, and 10). We verify that the additional particles found by Topaz are good particles by performing reconstructions using only the newly picked particles and find nearly identical structures (Figure 3). For aldolase, although Topaz finds many more particles than were in the published dataset, the Topaz, curated, and the Topaz minus curated particle sets achieve the same reconstruction resolution (2.63 Å at FSC_0.143), suggesting that the ~200k particles in the published set is already sufficient to reach the resolution limit of the data given standard reconstruction methods.

Figure 3 |.

Single particle reconstructions from published particles, Topaz particles, and Topaz particles with published particles removed (left to right). Below each reconstruction is the corresponding 3DFSC plot. (a) T20S proteasome (EMPIAR-10025) using the provided aligned, dose-weighted micrographs. (b) 80S ribosome (EMPIAR-10028). (c) Rabbit muscle aldolase (EMPIAR-10215). Scale bars: 3 nm

4. Topaz particle predictions are well-ranked and contain few false positives

We next quantify the quality of the particles predicted by Topaz over varying predicted probability thresholds by calculating the reconstruction resolution and estimating the number of false positive particles based on 2D class averaging. For each dataset, reconstructions are calculated using particles predicted by Topaz at decreasing probability cutoffs (Figure 4a). The resolution of Topaz structures increases as we include more good particles and then drops once the threshold becomes small and too many false positives are included as demonstrated by the dip in resolution for the last threshold of EMPIAR-10025. Furthermore, we compare these curves with those obtained by randomly subsampling the published particle sets and find that Topaz particles quickly match the resolution of the published particles for the proteasome and ribosome datasets. For the aldolase dataset, we see that more Topaz particles are required to match and then exceed the resolution of the curated particle set. This could be because Topaz does not find enough side views of the particle until the probability is sufficiently lowered whereas the curated dataset has been filtered to be enriched for these views (Supplementary Figure 11).

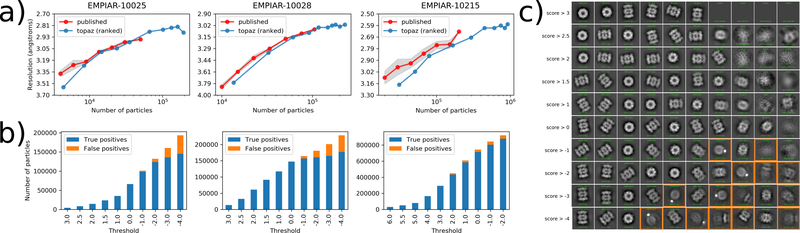
Figure 4 |.

Reconstruction resolution and 2D class averages for Topaz particles at decreasing log-likelihood ratio thresholds. (a) Number of particles vs. reconstruction resolution for Topaz particles (increasing number of particles corresponds to decreasing log-likelihood threshold) and randomly sampled subsets of the published particle set. Resolution is as reported by cryoSPARC. For the published particle sets the mean of three replicates is marked with standard deviation shaded in grey. (b) Stacked bar plots show the quantification of the number of true and false positives at each threshold based on 2D class averages. Decreasing threshold corresponds to increasing number of predicted particles. True positives are colored in blue and false positives in orange. (c) 2D class averages obtained at each score threshold for the T20S proteasome (EMPIAR-10025). Number of particles (ptcls) and effective sample size (ess) for each class are reported by cryoSPARC. NaN is reported for classes without any particles assigned. Classes determined to be false positives are marked with orange boxes. Several classes which appear to be false positives at high score thresholds do not contain any particles and, therefore, are not highlighted.

We also classified the particle sets at each threshold into ten classes and manually examined the class averages to determine whether each class represented true particles or false positives. As expected, we find that as the probability threshold is decreased, the fraction of false positives increases (Figure 4b), yet remains remarkably low even at relaxed thresholds. Furthermore, particles appear to be well-ranked in that noisy or unusual particle classes only start to appear at low thresholds. For example, the T20S proteasome dataset is contaminated with gold particles which appear as dark spots in the micrographs. Particles in close proximity to gold are only selected as the probability threshold is decreased (Figure 4). Similar trends can be observed in the ribosome (Supplementary Figure 12) and aldolase (Supplementary Figure 11) class averages. This can also be seen in the precision-recall curves for these datasets (Supplementary Figures 13) where Topaz maintains remarkably high precision even at high recall levels.

5. Our GE criteria based PU learning method outperforms other general-purpose PU learning approaches

Comparison of PU learning methods

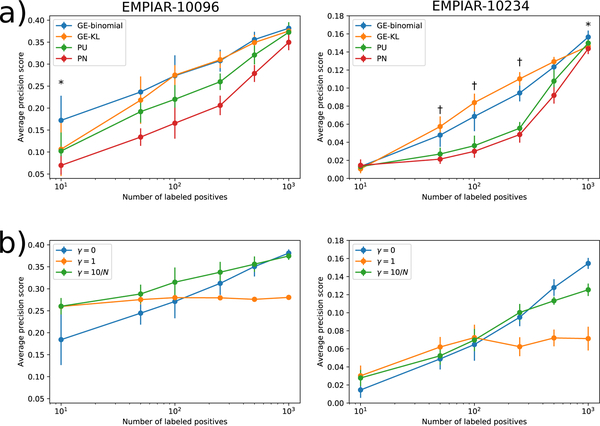
We consider two generalized expectation-based approaches to PU learning, GE-KL and GE-binomial (Online Methods), and evaluate their effectiveness by benchmark against the recent non-negative risk estimator approach of Kiryu et al.¹⁹ (NNPU) and the naive approach in which unlabeled data are considered as negative for classifier training (PN) on two additional cryoEM datasets. This is important to keep our PU learning methods development separate from the full Topaz evaluation above. The first dataset, EMPIAR-10096, is a publicly available dataset containing influenza hemagglutinin trimer particles and the second, EMPIAR-10234 (clustered protocadherin), is a challenging dataset provided by the Shapiro lab containing a stick-like particle with low SNR (Supplementary Figure 14). For purposes of comparison, we simulated positively labeled datasets of varying sizes by randomly subsampling the set of all positive examples within the training set of each dataset.

We find that across all experiments, classifiers trained with our GE criteria-based objective functions dramatically outperform those trained with the NNPU or PN methods. Generally, GE-binomial and GE-KL classifiers display similar performance with a few important exceptions where GE-binomial gives better results. For the dataset with more compact particles, EMPIAR-10096, GE-binomial gives significantly (p<0.05 by Student’s paired t-test) better test set average-precision scores than GE-KL when the number of data points is tiny (10 positive examples; Figure 5a). At larger numbers of positives, both methods are statistically equivalent. On the challenging EMPIAR-10234 dataset, GE-binomial significantly outperforms GE-KL at 1,000 labeled examples (p<0.05) whereas GE-KL gives better results (p<0.05) within the 50–250 range of labeled examples. These results indicate that our GE-based PU learning approaches dramatically outperform previous PU learning methods, enabling particle picking despite few labeled positives on the challenging EMPIAR-10234 dataset and substantially improving picking quality on the easier EMPIAR-10096. Although GE-binomial and GE-KL perform similarly in this experiment, we do find that GE-binomial outperforms GE-KL in the two important cases of 10 easy particles and 1,000 difficult particles.

Figure 5 |.

Comparison of models trained using different objective functions with varying numbers of labeled positives on the EMPIAR-10096 and EMPIAR-10234 datasets. (a) Plots show the mean and standard deviation of the average-precision score for predicting positive regions in the EMPIAR-10096 and EMPIAR-10234 test set micrographs for models trained using either the naive PN, Kiryo et al.’s non-negative risk estimator (PU), our GE-KL, or our GE-binomial objective function. Each number of labeled positives was sampled 10 times independently. (*) indicates experiments in which GE-binomial achieved higher average-precision than GE-KL with p < 0.05. (†) indicates experiments in which GE-KL achieved higher average-precision than GE-binomial with p < 0.05 according to a two-sided dependent t-test. (b) Plots show the mean and standard deviation of the average-precision score for models trained jointly with autoencoders with different reconstruction loss weights (γ). γ=0 corresponds to training the classifier without the autoencoder. γ=10/N means the reconstruction loss is weighted by 10 divided by the number of labeled positives used to train the model.

Augmentation with autoencoder

We next consider whether classifier performance can be improved when few labeled data points are available by introducing a generator network with corresponding reconstruction error term in the objective to form a hybrid classifier+autoencoder network (Online Methods). We hypothesized that including this reconstruction component would improve the generalizability of the classifier when few labeled data points are available by requiring that the feature vectors given by the encoder network be descriptive of the input – acting as a sort of machine learning technique known as regularization.

We evaluate this hypothesis by training classifiers with different settings of the autoencoder weight, γ, and varying numbers of labeled data points, N, on the EMPIAR-10096 and EMPIAR-10234 datasets (Online Methods). We find that including the decoder network with reconstruction error term in the objective (γ = 1 and $\gamma =\frac{10}{N}$) improves classifier performance in the few labeled data points regime (Figure 5b). As the number of data points increases, the benefit of using the autoencoder decreases and then hurts classifier performance due to over-regularization. Our results from both datasets suggest that using the autoencoder with $\gamma =\frac{10}{N}$ gives best results when N ≤ 250 and that not using the autoencoder is best for N > 250. Combined with PU learning, autoencoder-based regularization is an effective method to further improve classifier performance when few labeled positives are available.

Discussion

Since our work originally appeared in RECOMB 2018³⁰ and as an arXiv preprint, other works have followed on bioRxiv that propose alternative CNN-based particle picking methods^29,31. However, these methods follow the supervised learning paradigm (i.e. some variant of PN learning) and are limited by the associated assumptions. In the future, it may also be possible to provide particle detection models pretrained on many publicly available datasets; however, we note that fully-labeled, ground-truth datasets are presently unavailable and that these models are unlikely to generalize to new datasets with conventionally difficult particles, which we focus on here. While it may seem difficult to provide labeled data upfront, in practice we find that explicitly relaxing the requirement to completely label micrographs significantly eases this burden and is a major advantage of Topaz over other CNN-based methods. Users may also “bootstrap” the labeling procedure using existing picking and curation methods, while remaining cautious against reintroducing bias. We note that there may be some difference between randomly sampling from a curated particle set and particles that would be labeled by a user. However, the Toll receptor and clustered protocadherin training sets were both provided by hand-labeling and demonstrate that labeling a small, representative set of particles is easily achievable even for conventionally difficult datasets.

Although we use a simple CNN architecture with reasonable default hyperparameters and show that it performs well on these datasets, any model architecture that can be trained with gradient descent can use our GE-criteria objective functions to learn from positive and unlabeled data. Furthermore, additional hyperparameter tuning, such as L2 or dropout regularization, can improve model performance. The only hyperparameters introduced by our objective function is the unknown positive class prior, π, and the constraint strength, λ. Although the positive class prior could also be chosen by cross validation, we observed that our results were relatively insensitive to its choice (Supplementary Figure 15). Furthermore, we do not find that λ needs to be changed from the default setting. Our proposed GE-binomial PU learning method could also have widespread utility for object detection in other domains, for example in light microscopy or medical imaging, where positive labels are frequently incomplete. Additionally, although we proposed GE-binomial for positive-unlabeled learning, it is straightforward to extend to the typical semi-supervised case (where some labeled negative regions are provided) by taking the expectation of the loss over all labeled data in the first term.

Topaz particle probability thresholding allows particles to be included iteratively until the reconstruction resolution stops improving. It is possible for reconstruction algorithms to explicitly take these probabilities into account when determining 3D structures in the future.

Topaz requires researchers to label very few particles to achieve high quality predictions. It performs well independently of particle shape, opening automated picking to a wide selection of proteins previously too difficult to locate computationally. In addition, our pipeline is computationally efficient – training in a few hours on a single GPU and producing predictions for hundreds of micrographs in only minutes. Furthermore, once a model is trained for a specific particle, it can be applied to new imaging runs of the same particle. Topaz greatly expedites structure determination by cryoEM, enabling particle picking for previously difficult datasets, reducing the manual effort required to achieve high-resolution structures, and thus increasing the efficiency of cryoEM workflows and the completeness of particle analytics.

Online Methods

1. Dataset description

Aligned and summed micrographs and star files containing published particle sets were retrieved from EMPIAR for datasets EMPIAR-10025³², EMPIAR-10028³³, and EMPIAR-10096³⁴. Aligned and summed micrographs and hand-labeled particle coordinates were provided by the Shapiro lab for the EMPIAR-10234 dataset. Aligned and summed micrographs and curated in-house particle set were provided by the New York Structural Biology Center for the EMPIAR-10215 dataset. Micrographs for each dataset were downsampled to the resolution specified in Table 1 and normalized as described in the following section. Each dataset was then split into training and test sets at the micrograph level. The number of micrographs and labeled particles in each split are also reported in Table 1. To demonstrate the utility of our GMM normalization method, we also retrieved micrographs for EMPIAR-10261³⁵ from EMPIAR.

Table 1|.

Summary of cryoEM datasets and hyperparameters used for classifier training on each. Each dataset was downsampled and split into train and test sets at the whole micrograph level.

							Train		Test
Dataset	Protein	Original (ang/pix)	Down-sampled (ang/pix)	Particle radius (pix)	Training radius (pix)	π	Number of micro-graphs	Number of particles	Number of micro-graphs	Number of particles
EMPIAR-10025	T20S proteasome	0.98	15.7	7	3	0.035	156	39653	40	10301
EMPIAR-10028	80S ribosome	1.34	10.7	12	3	0.012	831	80701	250	24546
EMPIAR-10096	Hemagglu-tinin trimer	1.31	5.24	10	4	0.035	347	100465	100	29535
EMPIAR-10215	Rabbit muscle aldolase	0.832	6.64	10	3	0.1	865	163758	200	39347
EMPIAR-10234	Clustered protocad-herin	1.061	8.49	15	4	0.015	67	1167	20	373
Toll receptor	Toll receptor	0.832	3.328	25	5	0.035	30	686	14	362

2. Micrograph normalization

Images are normalized using a per-image scaled two component Gaussian mixture model. Given K images, each pixel is modeled as being drawn from a two component Gaussian mixture model, parameterized by ρ, the mixing parameter, μ₀,σ₀,μ₁, and σ₁, the means and standard deviations of the Gaussian distributions, with a scalar multiplier for each image, α_1...K. Let x_i,j,k be the value of the pixel at position i,j in image k, it is distributed according to

$$z_{i,j,k}\sim \text{Bernoulli}\left(\rho \right)$$

$$x_{i,j,k}\vee z_{i,j,k}\sim \text{Gaussian}\left({\alpha }_k{\mu }_{z_{i,j,k}},{\left({\alpha }_k{\sigma }_{z_{i,j,k}}\right)}^2\right)$$

where z_i,j,k is a random variable denoting the component membership of the pixel. The maximum likelihood values of the parameters ρ,μ₀,μ₁,σ₀,σ₁ and α_1...K are found by expectation-maximization for each data set. Then, the pixels are normalized by first dividing by the image scaling factor and then standardizing to the dominant mixture component. Let μ′, σ′ be μ₀,σ₀ if ρ < 0.5 and μ₁,σ₁ otherwise, then the normalized pixel values x′_i,j,k are given by

$$x{\mathrm{\prime }}_{i,j,k}=\frac{\left(\frac{x_{i,j,k}}{{\alpha }_k}-\mu \mathrm{\prime }\right)}{\sigma }.$$

We positively contrast this normalization with standard affine normalization of micrographs (Supplementary Figures 1, 2, & 3). In affine normalization, micrographs are transformed by subtracting the mean and dividing by the standard deviation of all pixel values in each micrograph.

3. PU learning baselines

Let P be the set of labeled positive micrograph regions (centered on a particle), and U be the set of unlabeled micrograph regions where π is the fraction of positive examples within U. Then, the task is to learn a classifier (g) that discriminates between positive and negative regions given P and U. When π is small, treating the unlabeled examples as negatives for the purposes of classifier training with the following standard loss minimization objective, for suitable cost function L, can be effective

$$\pi E_{x\sim P}\left[L\left(g\left(x\right),1\right)\right]+\left(1-\pi \right)E_{x\sim U}\left[L\left(g\left(x\right),0\right)\right]$$ (PN)

However, in general, this approach suffers from overfitting due to poor specification of the classification objective - it is minimized when positives are perfectly separated from unlabeled data points. To address this, Kiryo et al.¹⁹ recently proposed an unbiased estimator of the true positive-negative classification objective for positive and unlabeled data with known π and a non-negative estimator (PU) which is shown to reduce overfitting still present in the unbiased estimator.

4. PU learning with generalized expectation criteria

Here, we adopt an alternative approach to positive-unlabeled learning not based on estimating the PN misclassification risk. Instead, we observe that the unlabeled data with known π can be used to constrain a classifier such that it minimizes the classification loss on the labeled data and matches the expectation (π) over the unlabeled data. In other words, we wish to find the classifier, g, that minimizes E_x∼P[L(g(x),1)] subject to the constraint E_x∼U[g(x)] = π. This constraint can be imposed “softly” through a regularization term in the objective function with weight λ:

$$E_{x\sim P}\left[L\left(g\left(x\right),1\right)\right]+\lambda KL\left(E_{x\sim U}\left[g\left(x\right)\right]\vee \pi \right)$$ (GE-KL)

In this objective function, we impose the constraint through the KL-divergence between the expectation of the classifier over the unlabeled data and the known fraction of positives which is minimized when these terms are equal. This approach is an instance of a general class of posterior regularization called generalized expectation (GE) criteria, as specifically proposed by Mann and McCallum²⁰. However, because we wish for our classifier to be a neural network and to optimize the objective using minibatched stochastic gradient descent, the gradient of the objective must be approximating using samples from the data. Estimates of the gradient of the GE-KL objective from samples are biased, which could cause SGD to find a suboptimal solution.

To address this issue, we propose an alternative GE criteria, GE-binomial, defined so as to minimize the difference between the distribution over the number of positives in the minibatch and the binomial distribution parameterized by π. The number of positive data points, k, in a minibatch of N samples from U follows the binomial distribution with parameter π. Furthermore, the classifier g also describes a distribution over the number of positives in the minibatch as

$$q(k)=\sum _{y\in Y\left(k\right)}\prod _{i=1}^{N}g{\left(x_i\right)}^{y_i}\left(1-g{\left(x_i\right)}^{\left(1-y_i\right)}\right)$$

where x is a micrograph region, y is an indicator vector (y_i ∈ {0,1}) denoting which data points are positive (y_i = 1) and negative (y_i = 0) and Y(k) is the set of all such vectors summing to k. This allows us to define the new GE criteria as the cross entropy between these two distributions ${\sum }_{k=1}^{N}q\left(k\right)\text{logp}\left(k\right)$ giving the full GE-binomial objective function

$$E_{x\sim P}[L\left(g\left(x\right),1\right)]+\lambda {\sum }_{k=1}^{N}q\left(k\right)\text{logp}\left(k\right)$$ (GE-binomial)

In practice, because computing exact q(k) is slow, we make a Gaussian approximation with mean ${\sum }_{i=1}^{N}g\left(x_i\right)$ and variance ${\sum }_{i=1}^{N}g\left(x_i\right)\left(1-g\left(x_i\right)\right)$ and substitute the Gaussian PDF with these parameters for q in the above equation.

5. Autoencoder-based classifier regularization

When including the autoencoder component, we break our classifier network into two components: an encoder network composed of all layers except the final linear layer and the linear classifier layer. We denote these networks as f and c, respectively, with the full network, g, being given by g(x) = c(f(x)). Furthermore, we introduce a deconvolutional (also called transposed convolutional, see next section) decoder network, d, which takes the output of the feature extractor network and returns a reconstruction of the input image, x′ = d(f(x)). The objective function is then modified to include a term penalizing the expected reconstruction error over all images in the dataset, D, with weight γ

$$E_{x\sim P}[L\left(c\left(f\left(x\right)\right),1\right)]+\lambda \sum _{k=1}^{N}q\left(k\right)\text{logp}\left(k\right)+\gamma E_{x\sim D}[{\vee x-d\left(f\left(x\right)\right)\vee }_2^2]$$

This forms the full GE-binomial objective function with autoencoder component used in Topaz.

6. Classifier and autoencoder architectures and hyperparameters

We use a simple three-layer convolutional neural network with striding, batch normalization³⁶, and parametric rectified linear units (PReLU) as the classifier in this work. The model is organized as 32 conv7×7 filters with batch normalization and PReLU, stride by 2, 64 conv5×5 filters with batch normalization and PReLU, stride by 2, 128 conv5×5 filters with batch normalization and PReLU, and a final fully connected layer with a single output. We use sigmoid activation on this output to convert it into the predicted probability of a region being from the positive class (i.e. the output is interpreted as the log-likelihood ratio between positive and negative classes).

When augmenting with an autoencoder, we use a decoder structure similar to that of DCGAN³⁷. The d-dimensional representation output by the final convolutional layer of the classifier network is projected to a small spatial dimension but large feature dimension representation. This is repeatedly projected into larger spatial dimension and smaller feature dimension representations until the final output is of the original input image size. Specifically, this model is structured as repeated transpose convolutions with batch normalization and leaky ReLU activations. Let z be the representation output by the final convolutional layer of the classifier and X’ be the image reconstruction given by the decoder, the decoder structure is z -> transpose conv4×4 128-d, batch normalization, leaky ReLU -> transpose conv4×4 64-d, stride 2, batch normalization, leaky ReLU -> transpose conv4×4 32-d, stride 2, batch normalization, leaky ReLU -> transpose conv3×3 1-d, stride 2 -> X’.

7. PU learning benchmarking

To compare classifiers trained with the different objective functions, we simulate hand-labeling with various amounts of effort by randomly sampling varying numbers of particles from the training sets to treat as the positive examples. All other particles are considered unlabeled. We use cross entropy loss for the labeled particles. The values of π used for training are specified in Table 1. For GE-KL we set the GE criteria weight, λ, to 10 as recommended by Mann and McCallum²⁰. For GE-binomial, we set this parameter to 1. The classifier is then trained with those positives and evaluated by average-precision score (see next section for description of classifier evaluation) on the test set micrographs. This is repeated with 10 independent samples of particles for each number of positives. Statistical significance of performance differences between methods at each number of labeled positive examples is assessed using a two-sided t-test.

We also evaluate classifiers trained with autoencoder components and input reconstruction weight, γ, and varying numbers of labeled data points, N. We compare models trained with γ = 0 (no autoencoder), γ = 1, and $\gamma =\frac{10}{N}$. For each setting of γ and N, we train 10 models with different sets of N randomly sampled positives and calculate the average-precision score for each model on the test split of each dataset.

8. Classifier evaluation

Classifiers were evaluating by average-precision score. This score is a measure of how well ranked the micrograph regions were when ordered by the predicted probability of containing a particle and corresponds to the area under the precision-recall curve. It is calculated as the sum over the ranked micrograph regions of the precision at k elements times the change in recall

$$\sum _{k=1}^n\text{Pr}\left(k\right)\left(\text{Re}\left(k\right)-\text{Re}\left(k-1\right)\right)$$

where precision (Pr) is the fraction of predictions that are correct and recall (Re) is the fraction of labeled particles that are retrieved in the top k predictions. Let TP(k) be the number of true positives in the top k predictions, then Pr and Re are given by

$$\text{TP}(k)=\sum _{i=1}^k{y}_i$$

$$\text{Pr}(k)=\frac{\text{TP}(k)}{k}$$

$$\text{Re}(k)=\frac{\text{TP}(k)}{{\sum }_{i=1}^n{y}_i}$$

This measure is commonly used in information retrieval.

9. Non-maximum suppression algorithm for extracting particle coordinates

Non-maximum suppression chooses coordinates and their corresponding predicted probabilities of being a particle greedily starting from the highest scoring region. In order to prevent nearby pixels from also being considered particle candidates, all pixels within a second user-defined radius are excluded when a coordinate is selected. We set this radius to be the half major-axis length of the particle, however, smaller radii may give better results for closely packed, irregularly shaped particles.

10. Micrograph pre-processing

For EMPIAR-10025 and EMPIAR-10096, the aligned and summed micrographs along with CTF estimates were taken directly from the public data release on EMPIAR. For EMPIAR-10028 and EMPIAR-10261, frames were aligned and summed without dose compensation using MotionCor2³⁸. Whole micrograph CTF estimates provided with the public release were used for this dataset.

For the clustered protocadherin dataset (EMPIAR-10234), single particle micrographs were collected on a Titan Krios (Thermo Fisher Scientific) equipped with a K2 counting camera (Gatan, Inc.); the microscope was operated at 300 kV with a calibrated pixel size of 1.061 Å. 10 secs exposures were collected (40 frames/micrograph), for a total dose of 68 e^–/Ų with a defocus range of 1 to 4 μm. A total of 896 micrographs were collected using Leginon³⁹. Frames were aligned using MotionCor2³⁸. 1,540 particles were picked manually using Appion Manual Picker²³ from 87 micrographs and used as a training dataset for Topaz.

The rabbit muscle aldolase dataset (EMPIAR-10215) was collected on a Titan Krios (Thermo Fisher Scientific) equipped with a K2 counting camera (Gatan, Inc.) in super-resolution mode; the microscope was operated at 300 kV with a calibrated super-resolution pixel size of 0.416 Å. 6 secs exposures were collected (30 frames/micrograph), for a total dose of 70.32 e^–/Ų with a defocus range of 1 to 2 μm. A total of 1,052 micrographs were collected using Leginon³⁹. Frames were aligned, Fourier binned by a factor of 2, and dose compensated using MotionCor2³⁸. Whole-image CTF estimation was performed using CTFFIND4⁴⁰.

The Toll receptor dataset was collected on a Titan Krios (Thermo Fisher Scientific) equipped with a K2 counting camera (Gatan, Inc.); the microscope was operated at 300 kV with a calibrated pixel size of 0.832 Å. 6 secs exposures were collected (40 frames/micrograph), for a total dose of 73.48 e^-/Ų with a defocus range of 1.5 to 2.0 μm. A total of 9,323 micrographs were collected using Leginon. Frames were aligned using MotionCor2³⁸. Whole-image CTF estimation was performed using CTFFIND4⁴⁰.

11. 3D reconstruction procedure

Reconstruction was performed using cryoSPARC²⁵. For each particle set, we first generated an ab initio structure with a single class. These structures were then refined using cryoSPARC’s “homogenous refinement” option with symmetry specified depending on the dataset (T20S proteasome: D7, 80S ribosome: C1, aldolase: D2). For the aldolase dataset, we used C2 symmetry for ab initio structure determination. Otherwise, all other parameters were left in the default setting. When evaluating the quality of Topaz particle sets for decreasing score thresholds, each particle set was selected by taking all particles predicted by the Topaz model with scores greater than or equal to the given threshold. Reconstructions were calculated for each of these sets independently as described above.

12. Removal of overlapping particles

In order to evaluate the quality of the extra particles predicted by Topaz, we remove particles from the Topaz particle set that are also included in the published particle set. This was done by removing all Topaz particles with centers within the particle radius of a particle center in the published particle set.

13. 2D class averages (EMPIAR-10025, EMPIAR-10028, EMPIAR-10215)

Class averages were calculated using the cryoSPARC “2D Classification” option. All settings were left as default except the number of 2D classes which was set to 10 for every particle set.

14. 3D structure analysis (EMPIAR-10025, EMPIAR-10028, EMPIAR-10215)

The final 3D reconstructions were analyzed visually in UCSF Chimera⁴¹ and with 3DFSC³⁴. In Chimera, the published/previous 3D reconstruction was first loaded (with the fit PDB structure, if available) to which the newly-processed 3D reconstruction was then aligned. The structures were visually compared and representative areas were chosen for display in Figure 4. The 3DFSCs were calculated using the public server, https://3dfsc.salk.edu, which compares Fourier shell components for several solid angles to determine the range of resolutions and the amount of anisotropy in the reconstruction.

15. Toll receptor particle picking

1,599,638 particles were picked using DoG Picker 2⁷ from 8,974 micrographs and imported into cryoSPARC for all subsequent processing. After particle curation using 2D Classification described below, the particle picks from 44 micrographs were visually inspected. Picks in areas of obvious particle aggregation were removed, and lower SNR particles corresponding to views typically missed by DoG Picker were selected. The resulting 1,048 particles were split into 686 training and 362 testing particles at the micrograph level. Topaz was then trained on the training particles and applied with the default score threshold of 0 for particle prediction. The “oblique,” “side,” and “top” 2D classes (Figure 3d) were lowpass filtered to 15 Å and used for template correlation with FindEM⁴² implemented in the Appion²³ software package.

The crYOLO²⁹ network was trained on the complete set of 1,048 labeled particles with 20% held out for validation by default. Micrographs were filtered and training was performed as described in the crYOLO tutorial. Picking was performed at the default threshold of 0.3.

The DeepPicker¹² network was also trained on the complete set of 1,048 particles. Though no micrograph processing is required in the DeepPicker tutorial, micrographs were binned in Fourier space and lowpass filtered to 10 Å using EMAN2⁵. Even with a threshold of 0, no particles were predicted by DeepPicker.

16. Toll receptor 3D reconstruction

All reconstructions were performed using cryoSPARC²⁵. For all particle picking approaches, we performed 2D Classification with default parameters and 100 2D classes, then removed obvious non-particles. For the DoG dataset, four rounds of 2D Classification yielded 770,263 particles from an initial stack of 1,599,638. For the template dataset, four rounds of 2D Classification yielded 627,533 particles from an initial stack of 1,265,564. For the Topaz dataset, one round of 2D Classification yielded 1,006,089 particles from an initial stack of 1,010,937. For the crYOLO dataset, one round of 2D Classification yielded 131,300 particles from an initial stack of 133,644. For all datasets, ab initio reconstruction was used to generate an initial model, and the structures were further refined using homogeneous refinement with C1 symmetry, followed by non-uniform refinement. All parameters were left in their default setting. Unfiltered half-maps and masks were used to calculate 3DFSCs using the public server, https://3dfsc.salk.edu.

Data availability statement

Single particle half maps, full sharpened maps, and masks for T20S proteasome, 80S ribosome, rabbit muscle aldolase, and the Toll receptor (DoG, template, and Topaz picks) have been deposited to the Electron Microscopy Data Bank (EMDB) with accession codes EMD-9194, EMD-9201, EMD-9202, EMD-9206, EMD-9207, EMD-9208, EMD-9209, EMD-9210, EMD-9211, EMD-20529, EMD-20531, and EMD-20532. The full rabbit muscle aldolase dataset has been deposited to the Electron Microscopy Pilot Image Archive (EMPIAR) with accession code EMPIAR-10215.

Code availability statement

Source code for Topaz is publicly available via Code Ocean⁴³ and on GitHub at https://github.com/tbepler/topaz. Updates to Topaz will be posted at http://topaz.csail.mit.edu. Topaz is licensed under the GNU General Public License v3.0.