Long-range temporal coordination of gene expression in synthetic microbial consortia

Abstract

Synthetic microbial consortia have an advantage over isogenic synthetic microbes because they can apportion biochemical and regulatory tasks among the strains. However, it is difficult to coordinate gene expression in spatially extended consortia because the range of signaling molecules is limited by diffusion. Here, we show that spatiotemporal coordination of gene expression can be achieved even when the spatial extent of the consortium is much greater than the diffusion distance of the signaling molecules. To do this, we examined the dynamics of a two-strain synthetic microbial consortium that generates coherent oscillations in small colonies. In large colonies, we find that temporally coordinated oscillations across the population depend on the presence of an intrinsic positive feedback loop that amplifies and propagates intercellular signals. These results demonstrate that synthetic multi-cellular systems can be engineered to exhibit coordinated gene expression using only transient, short-range coupling among constituent cells.

Introduction

Synthetic biologists are now adept at engineering transcriptional gene circuits to create novel phenotypes within microbes. To date, a large variety of synthetic genetic devices have been developed, including toggle switches^1,2, oscillators^3–5, and logic gates^6,7. In each of these, transcription factors and their cognate promoters are rearranged in order to regulate gene transcription within single cells. Intercellular signaling pathways have also been engineered to regulate gene expression in populations of cells⁸. To do this, synthetic biologists have generally used quorum sensing systems taken from Gram-negative bacteria that utilize N-acyl homoserine lactones (HSLs)⁹. Synthetic versions of rewired intercellular pathways have allowed synthetic biologists to generate multicellular systems that mediate intercellular communication¹⁰, mimic predator-prey systems¹¹, display population-level oscillations^12,13, and create spatial patterns^14,15. Such coordination of gene expression across time and space through intercellular signaling pathways will be important if we are to use synthetic multicellular systems in complex environments such as soils or the gut microbiome, or interface with materials and bioelectronics.

Existing multicellular synthetic microbial systems have been constructed to operate in either well-mixed^13,16, or resource-limited environments^15,17. Intercellular signaling is simplified in these environments, as either coupling between cells is uniform (in well-mixed environments), or cells quickly go to stationary phase (in resource-limited environments). However, as the size of synthetic multicellular systems increases it becomes important to consider environments that are not well mixed, i.e. those in which intercellular signaling via small molecules has a limited range within the population. Such considerations are important because large multicellular synthetic systems will need to coordinate their behaviors across both space and time.

Some efforts have been made to coordinate gene expression in large synthetic colonies. For instance, Prindle et al. showed that oscillations between colonies of synthetic bacteria could be synchronized through engineered cell-cell communication mediated by hydrogen peroxide gas exchange¹⁸. However, gas exchange is not always the best option for cell-cell communication, as non-vaporous chemical means (especially HSLs) are more commonly accessible, and do not trigger native redox signaling pathways. Therefore, we need to better understand how to temporally coordinate gene expression in spatially extended bacterial communities using intercellular chemical signals.

Here, we show that gene expression within a spatially extended synthetic bacterial consortium can be temporally coordinated through chemically mediated intercellular communication. We examine the dynamics of a two-strain synthetic bacterial consortium in which the two strains emit two orthogonal quorum sensing molecules to generate a regulatory network with linked positive and negative feedback. When co-cultured in a small (~100μm) microfluidic device, the two strains exhibit emergent transcriptional oscillations of genes within the synthetic network. We find that when these two strains are co-cultured in a spatially extended microfluidic trap (~2mm), synchronization of the entire population is possible even though the diffusion of the signaling molecules provides only short-range interactions among the cells. Through a combination of experimental perturbations and computational simulations, we find that the temporal coordination of gene expression in our system depends on the regulatory structure (i.e. the presence or absence of various transcriptional feedback loops) of the network controlling intercellular signaling. In particular, a key positive feedback loop allows cells in an oscillating consortium to amplify signals locally. This amplification can reduce the phase difference between neighboring bacterial subpopulations, and is thus critical for synchronization across a spatially extended system. This is in contrast to smaller, well-mixed populations, which can exhibit synchronous oscillations for a variety of regulatory structures, including those without intrinsic positive feedback. We thus show how molecular interactions within individual cells are crucial for synchronization of spatially extended populations.

Our findings represent a major step towards the creation of large, synthetic, multicellular systems. To be useful, such systems need to quickly coordinate their activity through a distributed network of local interactions. The mechanisms we describe show how to design communities of synthetic microbes to achieve this goal, and suggest how their counterparts in the wild have evolved to do so.

Results

Microbial consortia in spatially extended chambers

To examine gene regulation and cell-cell signaling in spatially extended synthetic microbial consortia, we turned to a two-strain synthetic consortium we developed previously¹³. When co-cultured, intercellular signaling pathways between the two cell types create a coupled positive and negative feedback regulatory architecture that produces oscillations (see Fig. 1a). Briefly, one strain acts as an “activator” and the other as a “repressor.” When the synthetic circuit within the activator strain is ON (i.e. its promoters are active), it produces a cell-cell signaling molecule (C4-homoserine lactone, C4HSL) that up-regulates the synthetic circuits in both strains. Similarly, when the circuit within the repressor strain is ON, it produces an orthogonal cell-cell signaling molecule (3-OHC14-HSL) that down-regulates the circuits in both strains. We refer to C4HSL and 3-OHC14-HSL as the activating and repressing signals, respectively. When the two strains are co-cultured, coupling between these positive and negative feedback loops leads to oscillations in compact microfluidic chambers¹³.

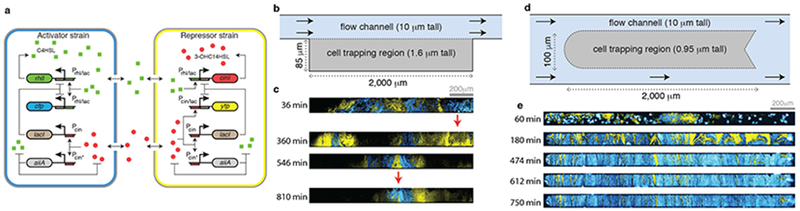
Figure 1.

Dynamics of the two-strain oscillator in large microfluidic devices. (a) Circuit diagram of the two-strain oscillator. (b) Simplified schematic of an extended “hallway” microfluidic device (Supplementary Fig. 10b). This device is similar to the compact chamber used by Chen et al, 2015¹³, with the width of the chamber extended to 2000μm. (c) Representative fluorescence images of cells growing in the extended hallway device (n=3 independent experiments). The spatial arrangement of the two strains keeps fluctuating (red arrows point to two areas of high fluctuation). (d) Simplified schematic of the extended “open” microfluidic device 2000μm in width (Supplementary Fig. 10a). The trap is open on all sides, allowing cells to align vertically, and thus minimizing fluctuations in spatial arrangement of the two cell strains. (e) Representative fluorescence images of cells growing in the open device (n=18 independent experiments). The spatial arrangement of the cells eventually stabilizes, simplifying the spatio-temporal dynamics of the two-strain oscillator. The images show times at which fluorescence is high.

In the compact chamber we used in our previous study the diffusion time is much shorter than the oscillatory period of the consortium¹³. It takes approximately one minute for the HSLs to diffuse through the compact chamber^12,13, whereas the oscillation period is 2hrs. Hence, the signaling delay between strains is negligible and the consortium exhibits synchronous chamber-wide oscillations.

Bacteria in their native environments, however, are not always confined to microscopic spaces. A chemical signal emitted at one point may reach only a small portion of a spatially extended population, and even then with considerable delay. We therefore asked whether one could engineer spatially extended microbial consortia to exhibit coherent dynamics despite these obstacles. To address this question we designed and constructed a microfluidic device with a growth chamber 20 times longer than the compact chamber we used previously (2,000μm vs 100μm) (Fig. 1b) ¹³. We found that in this hallway chamber, which had walls on three sides, the spatial arrangement of the two strains kept fluctuating, making it difficult to analyze the resulting dynamics of the microbial consortia (Fig. 1c and Supplementary Fig. 1). Thus, we constructed and used another microfluidic device in which the trapping region was open to media flow on all sides, and hence cells and signaling molecules could exit the chamber in any direction (Fig. 1d). As shown in previous theoretical work^19–21 and confirmed in a more extensive accompanying experimental study²², this design supports a stable distribution of strains once the trap was filled.

Since diffusion time scales with the square of the distance, we expected that the HSL signal would take roughly 20²=400 times longer to diffuse through this chamber than through the smaller chamber used in our previous study. Thus a chemical signal emitted at one end of the chamber would take several hours to reach the other end. Moreover, at steady state the magnitude of a signal emanating from one position decays exponentially as a function of distance from the source since extracellular HSL can diffuse out of the chamber. Thus, we expected coupling between cells to be primarily local, making globally coherent oscillations unlikely. However, we observed spatially synchronous oscillations in the extended chamber (Supplementary Video 1; Fig. 1e and Supplementary Fig. 2). We next asked how and when such synchrony is maintained despite the presence of steep gradients and delays in the chemical signals coupling the strains.

Positive feedback is essential for global synchrony

Our observation of coherent oscillations in the consortium implied that cells could amplify a signal received at the right time, translating local entrainment into global synchrony. How a received signal is relayed, however, depends on the architecture of the synthetic circuits within each cell. We therefore asked what features of the genetic circuits that drive the oscillations are also responsible for the emergence of coherent spatio-temporal dynamics. To answer this question, we examined consortia with four different circuit architectures obtained by removing either or both of the intrinsic feedback loops (Fig. 2a–d). Specifically, we examined consortia in which the positive feedback loop in the activator strain and/or the negative feedback loop in the repressor strain were removed¹³. We denote the four circuits as P_iN_j where the indices, i,j = 1,2, refer to the number of positive and negative regulatory links in the circuit graph, respectively.

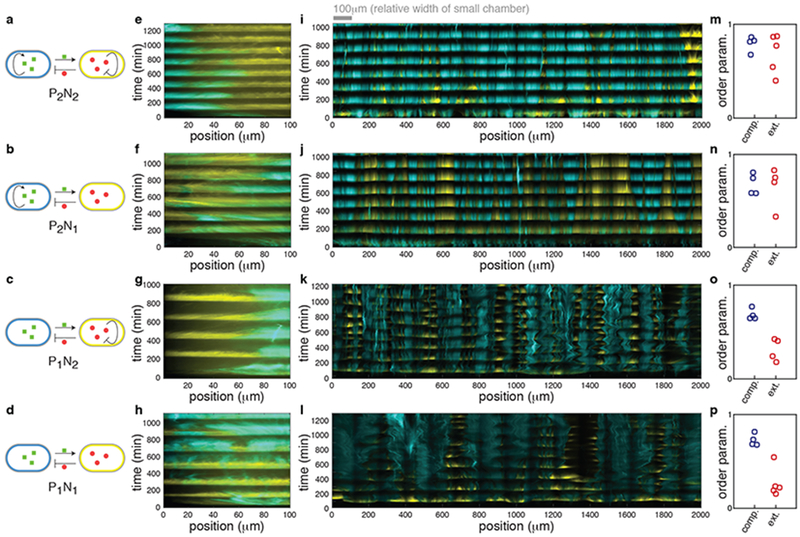
Figure 2.

Comparison of the dynamics of different circuit topologies in the compact and extended microfluidic devices. (a-d) Simplified circuit diagram of the P₂N₂, P₂N₁, P₁N₂ and P₁N₁ architectures. (e-l) Representative kymographs of four architectures in the compact hallway chamber (e-h) and in the extended open chamber (i-l) (n=4 independent experiments for each of these except (i) and (l) for which n=5). The kymographs of (e-h) were obtained by reanalyzing data from our previous work³ where the compact hallway chamber was used¹³. We observed similar behavior in a compact open chamber (Supplementary Fig. 3m). See Supplementary Fig. 2 for an explanation of kymograph construction. (m-p) Experimentally measured order parameters for each experiment in the compact (blue circles) and extended (red circles) chambers. The mean order parameter does not differ between architectures with and without positive feedback in the compact chamber (mean order parameters are 0.70 and 0.75 with and without positive feedback respectively, p=0.33, two-sided Welch’s t-test, n=8 independent experiments). However, in the extended chamber the mean order parameters are 0.29 and 0.69 for architectures with and without positive feedback, and this difference is significant (p = 2.3x10⁻⁴, two-sided Welch’s t-test, n=9 independent experiments).

As we reported previously¹³, all four architectures exhibit robust, synchronous oscillations in the compact chamber (Fig. 2e–h and Supplementary Fig. 3a–d). However, only the P₂N₂ and P₂N₁ architectures supported oscillations that were spatially coherent across the extended chamber (Fig. 2i, j and Supplementary Fig. 3e, f). Consortia with the P₁N₂ and P₁N₁ architectures broke into smaller, locally synchronous, oscillating subpopulations (Fig. 2k, l and Supplementary Fig. 3g, h).

We quantified the degree of spatial synchrony in the space–time diagrams (kymographs), using an order parameter, Ω (Fig. 2m–p; see Methods for details): Ω ~ 1 indicates spatially coherent oscillations, and Ω ~ 0 disorganized behavior^23,24. By reanalyzing the data from our previous study, we found that all four architectures supported spatially coherent oscillations (high order parameters) in the compact hallway chamber. In contrast, only architectures with intrinsic positive feedback (i.e. P₂N₂ and P₂N₁) exhibited a high order parameter in the spatially extended open chamber (Fig. 2m, n, similar results were obtained with other methods Supplementary Fig. 3i–l; see Methods). We therefore concluded that the intrinsic positive feedback loop in the activator strain was essential for spatial synchrony in spatially extended populations.

A mathematical model captures consortium dynamics

We next developed a mathematical model to better understand the circuit mechanisms that mediate coherent oscillations in spatially extended consortia. We built on a previously developed model that successfully captured the transcriptional dynamics of consortia in the compact chamber¹³. To describe the spatio-temporal dynamics of consortia in the extended chamber we included a single spatial dimension corresponding to the long axis of the extended trap. The resulting equations captured the dynamics of the genetic circuits, fluctuations in local strain ratios, as well as the diffusion of extra-cellular signaling molecules that mediate interactions between the strains (parameters were constrained by experimental observations, see Methods and Supplementary Tables 1 and 2).

We used our model to examine how the four architectures influence the evolution of initial phase differences. To do so, we initialized each of four sets of simulations (corresponding to the four architectures) with the same set of 10³ randomly generated initial phases with spatial phase variance estimated from experimental data (Fig. 2i–l and Supplementary Fig. 3e–h) (see Methods). Our model successfully captured experimentally observed features of the spatio-temporal dynamics in the extended chamber (Fig. 2i–l): Consortia without intrinsic positive feedback exhibited spatially asynchronous oscillations (Ω = 0.19±0.04 for P₁N₂ and Ω = 0.18±0.04 for P₁N₁), while spatially coherent oscillations emerged in consortia with the positive feedback (Ω =0.73±0.2 for P₂N₂, and Ω =0.74±0.15 for P₂N₁) (Fig. 3a).

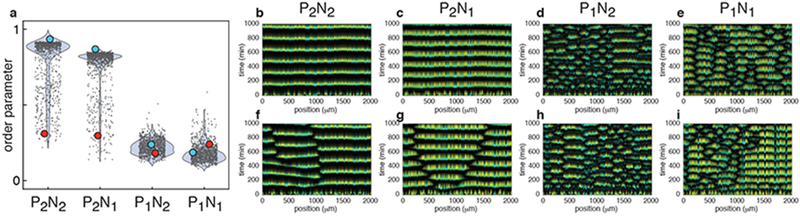
Figure 3.

The mathematical model reproduces the experimentally observed spatio-temporal dynamics exhibited by the four regulatory architectures. (a) Calculated order parameters for different initial conditions. The width of the shaded blue regions represents the empirical probability density of the distribution of the individual results (dots). The same set of 10³ random initial phases and ratios between two strains were used in simulations of all four architectures (n=10³ independent simulations for each). The order parameters for the P₂N₁ and P₂N₁ architectures were much higher than those for the P₁N₂ and P₁N₁ architectures. (b-e) Representative simulations using the same initial conditions (blue dots in (a)) that resulted in high order parameters in the P₂N₂ and P₂N₁ architectures, but not in the P₁N₂ and P₁N₁ architectures (n=10³ independent simulations for each). (f-i) Representative simulations using the same initial conditions (red dots in (a)) that resulted in low order parameters in each regulatory architecture (n=10³ independent simulations for each). Low order parameters in simulations with P₂N₁ and P₂N₁ architectures reflected the emergence of 2-3 subpopulations oscillating in anti-phase (f, g). In contrast, low order parameters reflected spatially disorganized behavior in P₁N₂ and P₁N₁ architectures (h, i).

Note that even in the same chamber, depending on the initial phase differences among strains, the level of synchrony (i.e. the order parameter) varies considerably. The green circles in Fig. 3a highlight illustrative examples of high order parameters in the P₂N₂ and P₂N₁ architectures, with corresponding kymographs shown in Fig. 3b–e. Small order parameters corresponded to qualitatively different spatio-temporal patterns in consortia with and without the positive feedback (e.g. red circles in Fig. 3a): In consortia of type P₂N₂ and P₂N₁ a low order parameter reflected the emergence of two to three large, synchronized subpopulations oscillating in anti-phase (Fig. 3f, g). In contrast, a low order parameter generally indicated the fracturing of P₁N₂ and P₁N₁ type consortia into small subpopulations with shifting phase relationships (Fig. 3h, i). These dynamics were consistent with those we observed experimentally in consortia with corresponding architectures (Fig. 2i–l and Supplementary Fig. 3e–h).

Positive feedback increases sensitivity to activator

We next used our model to probe the mechanisms by which intrinsic positive feedback mediates global coherence of gene expression in spatially extended populations. As concentrations of the signaling molecules decay quickly with distance from the source (Supplementary Fig. 4), distant subpopulations in the chamber communicate only indirectly. Thus we conjectured that the positive feedback is essential for effective long-range coupling.

To test our hypothesis, we first examined the effect of unidirectional coupling on two oscillating, spatially localized subpopulations. To do this, we tracked the concentration of the extracellular signals (i.e. both C14HSL and C4HSL) emitted by a receiving (driven) subpopulation 50μm (Fig. 4a; dashed box) from a sender (driving) subpopulation (Fig. 4a; solid box). We then probed the effect of signals expressed by the sender subpopulation (Fig. 4b) on the oscillation phase (ϕ) of a receiving consortium (Fig. 4c and Supplementary Fig. 5a–f). The receiving subpopulation’s constitutive strains were perturbed in response to the received signal. This resulted in deviations in the oscillatory trajectory, and thus the phases, of the driven consortium. By calculating the magnitude of the phase shift (Δϕ) as a function of the phase (ϕ) when the input signal was received, we obtained the phase response curve (PRC) (Supplementary Fig. 5g) ^25,26; The PRC has positive values when the phase is advanced by the input signal and negative values when the phase is delayed by the input signal (Fig. 4d, e; see Methods for details). We defined phase ϕ = 0 as the point in the oscillatory cycle where the activator promoter is fully activated and thus the released activator signal is at its maximum (Fig. 4c).

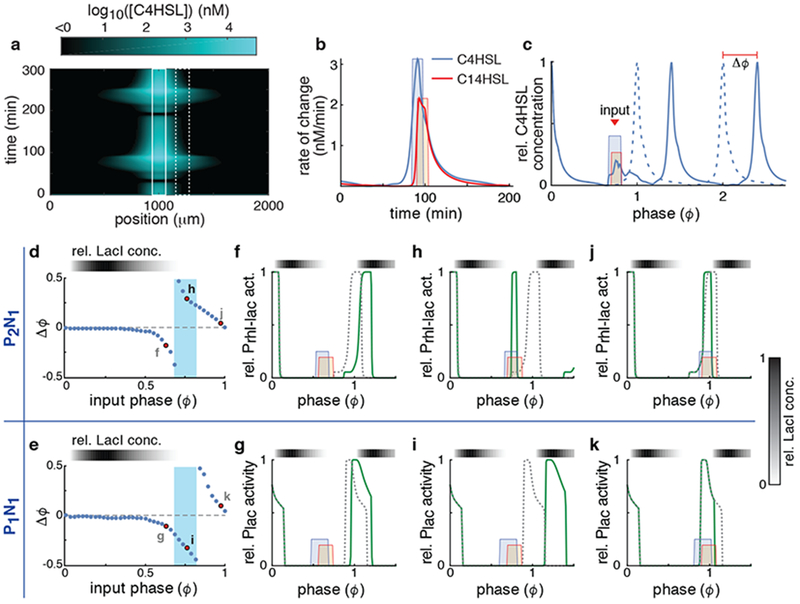
Figure 4.

Positive feedback changes the response to incoming signals. (a) Simulated concentration of C4HSL emitted from a single source in the middle of a trap (solid box) as a function of space and time (See Supplementary Fig. 4b for C14HSL). (b) Simulated rate of change of the two HSLs in a receiving population at 50 μm from their source (dashed box in (a)). Also shown are the square pulses we used as approximations of these incoming signals for further simulations. Shown are simulations obtained using the P₂N₂ architecture. Results are similar for other architectures (Supplementary Fig. 4). (c) Relative C4HSL concentration produced by the receiving population (dashed box in (a)) in the presence (solid curve) and absence (dashed curve) of the incoming signal (colored boxes). From these we estimated the phase shift (Δϕ) of the receiving population. Here ϕ=0 is defined as the phase at which the C4HSL concentration of the receiving population is at its maximum. (d-e) The change in the phase (Δϕ) of the receiving population as a function of the phase (ϕ) at which the driving signal pulse is received for the P₂N₁ (d) and P₁N₁ (e) architectures. The highlighted points refer to subsequent panels. (f-k) Relative transcriptional activity (solid green curve) of the P_rhl-lac promoter of the P₂N₁ (top) and P_lac of the P₁N₁ (bottom) architectures in response to signals received at three different phases (red dots in (d) and (e)). The dashed line is the activity of the promoter in the absence of the signal.

We can relate the shape of the computed PRC directly to the underlying molecular mechanisms by examining the response of the system to perturbations at different phases (Fig. 4f–k). The response of the receiving consortium is roughly independent of the presence or absence of the intrinsic positive feedback loop, except when 0.7<ϕ<0.8 (Fig. 4d, e; blue zones), and has several stages. When 0<ϕ<0.5 LacI is high (Fig. 4d and e; gray scale bars), the promoter is repressed (Supplementary Fig. 5a and b), and the phase of the responding consortium is not affected by an incoming signal (Fig. 4d, e). When 0.5<ϕ<0.7 LacI begins to deplete and the promoter is ready to be de-repressed (Supplementary Fig. 5a and b). Hence the repressor signal prevents de-repression and delays the phase (Fig. 4f, g). When 0.7<ϕ<0.8 LacI is depleted and both promoters begin to turn on (Supplementary Fig. 5a and b). In the absence of positive feedback (P₁N₁ architecture), the incoming repressor signal prevents the activation of the promoters and delays the oscillation phase (Fig. 4i). In contrast, positive feedback (P₂N₁ architecture) amplifies the impact of the incoming activator signal (Supplementary Fig. 6), accelerating the activation of the promoter (e.g. P_rhl/lac) and advancing the phase of the oscillator (Fig. 4h). When 0.8<ϕ<1 the promoter is active (Supplementary Fig. 5a and b). The incoming repressor signal accelerates the deactivation of the promoter and advances the phase (Fig. 4j, k). The qualitative shapes of the PRCs for both the P₂N₂ and P₁N₂ architectures are similar to those of the P₂N₁ and P₁N₁ architectures, respectively (Supplementary Fig. 7). In sum, the addition of a positive feedback loop makes a consortium more sensitive to the activator signal by increasing the range of phases at which the activator signal accelerates promoter activation. This in turn extends the range over which an activator signal advances the phase of the responding subpopulation.

To understand the impact of the feedback-mediated increase in sensitivity on the spatial coherence of oscillations we next examined the evolution of phase differences between coupled subpopulations^25,26. We used the previously obtained PRCs to define a mapping from the phase difference between two interacting subpopulations on one cycle, Δϕ, to the phase difference during the next cycle, Δϕ_new (Fig. 5a, b and Supplementary Fig. 8a, b; see Methods for details).

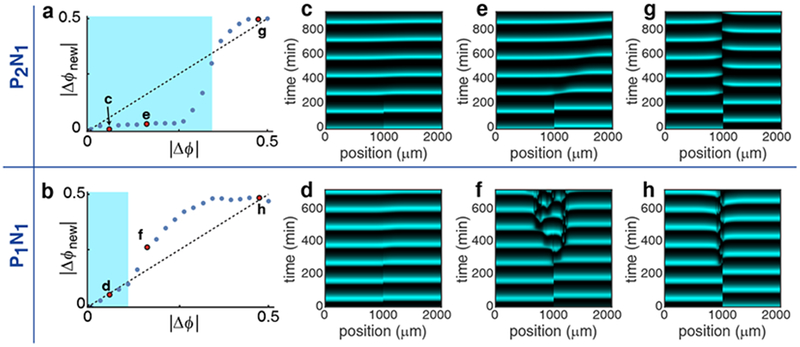
Figure 5.

Intracellular positive feedback promotes synchronization between reciprocally coupled consortia. (a and b) The mapping from Δϕ to Δϕ_new for the P₂N₁ (a) and P₁N₁ (b) architectures. In both cases the map has two stable fixed points: Δϕ=0 (synchrony) and Δϕ=0.5 (anti-phase). For initial phase differences (Δϕ) that satisfy |Δϕ_new |<|Δϕ| (the blue region), this map predicts eventual synchrony. On the other hand, for initial phase differences that do not satisfy this inequality (outside the blue region), the map predicts anti-phase oscillations. (c-h) We simulated a spatially extended consortium in an extended trap with different initial phase differences between the two consortium halves. We show results for the three initial values corresponding to the red points in panels (a) and (b). The behavior of the extended population agrees with predictions from the analysis of two coupled localized populations (a, b).

The region for which phase differences between two coupled populations shrink from one cycle to the next is larger for the P₂N₁ architecture than the P₁N₁ architecture (the range in which |Δϕ_new|<|Δϕ| is highlighted in blue in Fig. 5a, b). To confirm this prediction, we simulated a spatially extended, oscillating population separating it into two equal halves that are initially out of phase (Fig. 5c–h). In agreement with the behavior of two spatially localized coupled subpopulations (Fig. 5a, b), the P₂N₁ (Fig. 5c, e) architecture reached global synchrony for a wider range of initial phase differences between the population halves than the P₁N₁ architecture (Fig. 5d). Specifically, when the two halves of the consortium start with a phase difference of |Δϕ|=0.1 they reach approximate synchrony after one oscillatory cycle for both the P₂N₁ (Fig. 5c) and P₁N₁ (Fig. 5d) architectures. An initial phase difference (Fig. 5a, b; |Δϕ|=0.3) predicted to lead to synchrony for P₂N₁, but not the P₁N₁ architecture, lead to synchrony in the P₂N₁ consortium (Fig. 5e), but resulted in a breakdown in spatiotemporal order in the P₁N₁ consortium (Fig. 5f). Furthermore, initial phase differences outside the blue (synchronization) regions in Fig. 5a and b tended to approach a phase difference of |Δϕ|=0.5 over subsequent oscillations, leading to anti-phase oscillations between the two population halves (Fig. 5f, g, h).

Our model suggests the biochemical mechanisms driving synchrony: When the leading subpopulation releases a signal (i.e. HSL), the promoter of the trailing subpopulation must not be repressed to allow its phase to be shifted. If this signal arrives before the promoter in the trailing subpopulation is activated, then the positive feedback allows the signal to accelerate promoter activation. This advances the trailing phase, and reduces the phase difference between the populations (Fig. 5e). The opposite occurs in the absence of the positive feedback: Here the repressor signal dominates and delays the activation of the promoter of the trailing subpopulation (the wide phase delay zone in Fig. 4e), increasing the phase difference between the subpopulations (Fig. 5f).

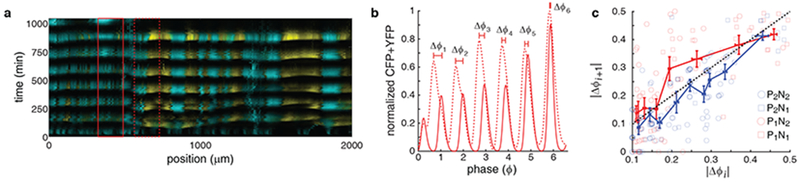
We observed the behavior predicted by this modeling approach when we reanalyzed our data (Fig. 2i–l and Supplementary Fig. 3e–h) to compare the evolution of phase differences in each of the four architectures. Specifically, we tracked the evolution of phases of pairs of subpopulations in the chamber from cycle to cycle. We defined a subpopulation as the part of the consortium within a 167 μm wide region of the trap. We examined the evolution of phases for subpopulations that were 67μm apart (Fig. 6a), close to the distance we used to obtain PRCs (Fig 4a, b). By sliding the two 167μm windows across the extent of the trap, we obtained 25 pairs of subpopulations for each experiment (see Method for details). We next computed the phase difference between the two subpopulations within each pair of windows across multiple oscillations (Fig. 6b). This allowed us to determine how the phase difference between each pair of neighboring subpopulations evolved from one cycle (Δϕ_i) to the next (Δϕ_i+1). We approximated the phase difference maps by relating the phase difference at the beginning and the end of the same cycle (Fig. 6c). Our analysis of the experimental data agrees with our theoretical prediction (Fig. 5a, b): a reduction in the phase difference occurs, on average, for a much wider range of input phase differences in consortia with a positive feedback loop (blue curve) than those without (red curve) (Fig. 6c).

Figure 6.

Experimental estimation of the phase difference maps. (a) Kymograph of a P₂N₂ consortium with windows indicating the relative positions of two example subpopulations used to calculate phase difference maps (n=5 independent experiments). The paired subpopulation windows are 167μm wide, and 67μm apart. (b) Average total fluorescence as a function of phase for the two subpopulations in the windows shown in (a). Here Δϕ_i represents the phase difference at the peak of the i^th cycle. The phase differences are decreasing and the two subpopulations reach synchrony at the 6^th cycle. (c) The mapping of phase differences (|Δϕ_i+1| as a function of |Δϕ_i |) for different architectures (light symbols) was computed using the data presented in Fig. 2i–l and Supplementary Fig. 3e–h. We obtained mean phase difference maps for each consortium type by averaging groups of 10 phase differences sequentially, separately for consortia with (blue curve) and without (red curve) a positive feedback loop. On average, phase differences shrink for consortia with the positive feedback, as the blue curve lies below the diagonal. In contrast, phase differences grow for consortia without the positive feedback, as the red curve is mostly above the diagonal. Error bars represent standard error.

Our model suggests that positive feedback increases a consortium’s sensitivity to the activator signal by increasing the range of phases at which the activator signal accelerates promoter activation. This extends the range over which an activator signal advances the phase of the responding subpopulation, pulling interacting populations closer to synchrony (see Supplementary Fig. 8 for further details about the mechanisms and extensions to multiple populations). Interestingly, amplification via a positive feedback loop can also help coordination in spatial trigger waves, despite slow diffusion²⁷. However, we note that the dynamics of spatial oscillators and trigger waves are distinct, and details of the molecular mechanisms supporting each are different.

Discussion

We demonstrated that local coupling in synthetic bacterial communities can synchronize oscillations in a spatially extended population. Interestingly, in our system positive feedback within an activator strain of the population was necessary to achieve this. Without such feedback, the intercellular signals that couple the constituent cells are not amplified, and the limited spatial range of diffusion hinders the emergence of globally synchronous oscillations.

Positive feedback plays a critical role in generating robust oscillations in synthetic oscillators constructed in single, isogenic cellular populations^4,28. However, in a previous study we found that, in a small chamber, the addition of a negative feedback loop was needed to maintain robust oscillations in the face of fluctuating population ratios between activator and repressor strains of a consortium¹³. We have designed the spatially extended chamber to minimize such fluctuations in population ratios, and observed robust oscillations even in the absence of the negative feedback (Figs. 1 and 2). Therefore, different features of the gene circuit architecture may be responsible for supporting robust local dynamics, and globally coherent dynamics on the population level.

Various natural systems also achieve spatially coherent oscillations using only local coupling²⁹. Interestingly, many of them appear to use intracellular positive feedback loops to achieve such synchrony, in accord with our findings. For instance, after starvation, a population of Dictyostelium is driven to aggregate via synchronous oscillations in cAMP signaling³⁰. The spatial scales of the chemical gradients of cAMP are small compared to the size of the population, and thus distant cells communicate only indirectly. Dictyostelium has been shown to use a local positive feedback loop to amplify local signals: the extracellular cAMP inhibits the degradation of intracellular cAMP, which triggers local excitation (i.e. amplification)^30–32 allowing for the signal to propagate more effectively. A second example is provided by the interlinked positive and double-negative feedback loops among Cdk1/Wee1A/Cdc25C that lead to the spatially coordinated mitosis in the large, fertilized X. laevis egg³³. Finally, the master circadian clock located in the suprachiasmatic nucleus consists of ~20,000 individual oscillators coupled via various excitatory and inhibitory neurotransmitters. The circadian clock generates synchronized oscillations and functions as a timekeeper of our body^34–36. Interestingly, each individual circadian oscillator has an intracellular transcriptional positive feedback loop mediated by Rors³⁷, although its role in achieving globally coherent rhythms has not been investigated. These examples suggest that signal amplification through local positive feedback is used by a variety of biological systems to drive emergent behaviors in spatially extended systems. We have shown that a similar mechanism can be used to engineer spatially extended synthetic microbes that exhibit collective behavior even when they interact only locally.

Online Methods

Calculation of the Order parameter

To quantify the synchrony of CFP and YFP oscillations across the chamber, we used the order parameter (Ω) introduced by Shinomoto and Kuramoto^23,24. First, we partitioned the image of the chamber horizontally into 600 rectangular compartments, each approximately 3.33μm in width. We then computed the average CFP and YFP intensities in each compartment. We denote by $X_k^C(t_i)$ and $X_k^Y(t_i)$ the CFP and YFP intensity, respectively in the k^th compartment (k=1, 2, … ,600) at time t_i (i=1, 2, … ,T) where T is the number of times at which measurements were taken at 6 min intervals. After centering the data by defining

$${\widehat{X}}_k^j(t_i)=X_k^j(t_i)-<X_k^j>,$$

where j = C or Y and < $X_k^j$ > is the average of $X_k^j$ over time, we estimated the phase ${\varphi }_k^j$ of ${\widehat{X}}_k^j$ by using the Hilbert Transform. The phase ${\varphi }_k^j$ lies between 0 and 1 and is 0 at the time at which ${\widehat{X}}_k^j$ achieves its peak value.

The phases, ${\varphi }_k^C$, of compartments that do not contain the activator strain and phases, ${\varphi }_k^Y$, in compartments with no repressor strain should not be used in determining the order parameter. Thus, we tracked the density of activator and repressor strains in each compartment: We denote by $N_t^C$ and $N_t^Y$ the numbers of compartments (among 600 total compartments) that contained activator and repressor strains, respectively, at time t. We denoted the l^th compartment of each of the $N_t^C$ and $N_t^Y$ compartments of the two types by $k_t^C(l)$ and $k_t^Y(l)$, respectively. We then calculated the order parameter of CFP and YFP oscillations using

$$\langle \mid \frac{1}{N_t^C}\sum _{l=1}^{N_t^C}{e}^{2\pi i{\varphi }_{k_t^c(l)}^c(t)}+\frac{1}{N_t^Y}\sum _{l=1}^{N_t^Y}{e}^{2\pi i{\varphi }_{k_t^Y(l)}^Y(t)}-\langle \frac{1}{N_t^C}\sum _{l=1}^{N_t^C}{e}^{2\pi i{\varphi }_{k_t^c(l)}^c(t)}+\frac{1}{N_t^Y}\sum _{l=1}^{N_t^Y}{e}^{2\pi i{\varphi }_{k_t^Y(l)}^Y(t)}\rangle \mid \rangle ,$$

where angle brackets indicate an average over time.

The order parameter is close to 0 when different portions of the chamber or different strains are out of phase with each other, or in the absence of oscillations^23,24. The parameter is close to 1 when the oscillations of both CFP and YFP across the chamber are synchronous and in-phase. While we lumped the order parameters of both CFP and YFP together for simplicity (Fig. 2m–p of the main text), they can be calculated individually by separating CFP and YFP terms in the order parameter equation. The individually computed order parameters behave similarly to the combined order parameter: the absence of the positive feedback loop leads to low values. Specifically, Ω of YFP is 0.33 ± 0.21, 0.36 ± 0.17, 0.71 ± 0.24, and 0.76 ± 0.18 for P₁N₁, P₁N₂, P₂N₁, and P₂N₂, respectively, and Ω of CFP is 0.45 ± 0.14, 0.42 ± 0.15, 0.64 ± 0.17, and 0.65 ± 0.2 for P₁N₁, P₁N₂, P₂N₁, and P₂N₂, respectively.

Correlation matrix analysis

We also used correlation matrix analysis³⁸ to quantify the synchrony of CFP and YFP oscillations across the chamber (Fig. 2 and Supplementary Fig. 3). We first centered and normalized $X_k^C(t_i)$ and $X_k^Y(t_i)$ as follows:

$${\widehat{X}}_k^j(t_i)=\frac{X_k^j(t_i)-<X_k^j>}{{\sigma }_k^j},$$

where j = C or Y and < $X_k^j$ >, and ${\sigma }_k^j$ are the mean and standard deviation of $X_k^j$ over time, respectively. Using the normalized timeseries, we defined the equal-time correlation matrix C as:

$$C_{\mathit{mn}}={\sum }_{i=1}^T({\widehat{X}}_m^C(t_i)+{\widehat{X}}_m^Y(t_i))({\widehat{X}}_n^C(t_i)+{\widehat{X}}_n^Y(t_i)),$$

where m, n=1, 2, … 600. The eigenvalues of the correlation matrix are real and their sum is equal to the dimension of the matrix (i.e. 600)³⁸. If the oscillations are independent across the chamber and between the strains then C has small off-diagonal elements, and is thus be close to the identity matrix. In this case its eigenvalues are clustered around 1. On the other hand, if oscillations are synchronous between the strains and across the chamber, then all entries in C all equal 1. The maximal eigenvalue thus equals the dimension of the matrix (600 in this case). Thus, the value of the maximal eigenvalue divided by 600 (Λ_max) is close to 0 when strains in different portions of the chamber are out of phase, and close to 1 when they are synchronous. For the compact chamber, m, n=1, 2, … 100 and thus the maximal eigenvalue is divided by 100 (Supplementary Fig. 3i–l).

Description of the mathematical model

Previously, we proposed a system of 16 delay differential equations, which successfully captured the dynamics of the intra-cellular genetic networks, and extra-cellular molecular signals of bacterial consortia grown in the compact microfluidic chamber (see Chen et al. for details)¹³:

$$\begin{gathered} \frac{{\mathit{dR}}_a}{\mathit{dt}}=\frac{{\eta }_{R0}+{\eta }_{R1}{(H_a^{\tau }∕K_H)}^{n_H}}{1+{(H_a^{\tau }∕K_H)}^{n_H}+{(L_a^{\tau }∕K_L)}^{n_L}}-\frac{d_C{R}_a}{K_C+R_a+A_a+L_a+F_a+M_a}-{\mathit{dR}}_a \\ \frac{{\mathit{dL}}_a}{\mathit{dt}}=\frac{{\eta }_{L0}+{\eta }_{L1}{(I_a^{\tau }∕K_I)}^{n_I}}{1+{(I_a^{\tau }∕K_I)}^{n_I}}-\frac{d_C{L}_a}{K_C+R_a+A_a+L_a+F_a+M_a}-{\mathit{dL}}_a \\ \frac{{\mathit{dA}}_a}{\mathit{dt}}=\frac{{\eta }_{A0}+{\eta }_{A1}{(I_a^{\tau }∕K_I)}^{n_I}}{1+{(I_a^{\tau }∕K_I)}^{n_I}}-\frac{d_C{A}_a}{K_C+R_a+A_a+L_a+F_a+M_a}-{\mathit{dA}}_a \\ \frac{{\mathit{dC}}_r}{\mathit{dt}}=\frac{{\eta }_{C0}+{\eta }_{C1}{(H_r^{\tau }∕K_H)}^{n_H}}{1+{(H_r^{\tau }∕K_H)}^{n_H}+{(L_r^{\tau }∕K_L)}^{n_L}}-\frac{d_C{C}_r}{K_C+C_r+A_r+L_r+Y_r+M_r}-{\mathit{dC}}_r \\ \frac{{\mathit{dL}}_r}{\mathit{dt}}=\frac{{\eta }_{L0}+{\eta }_{L1}{(I_r^{\tau }∕K_I)}^{n_I}}{1+{(I_r^{\tau }∕K_I)}^{n_I}}-\frac{d_C{L}_r}{K_C+C_r+A_r+L_r+Y_r+M_r}-{\mathit{dL}}_r \\ \frac{{\mathit{dA}}_r}{\mathit{dt}}=\frac{{\eta }_{A0}+{\eta }_{A1}{(I_r^{\tau }∕K_I)}^{n_I}}{1+{(I_r^{\tau }∕K_I)}^{n_I}}-\frac{d_C{A}_r}{K_C+C_r+A_r+L_r+Y_r+M_r}-{\mathit{dA}}_r \\ \frac{{\mathit{dF}}_a}{\mathit{dt}}=\frac{{\eta }_{F0}+{\eta }_{F1}{(H_a^{\tau }∕K_H)}^{n_H}}{1+{(H_a^{\tau }∕K_H)}^{n_H}+{(L_a^{\tau }∕K_L)}^{n_L}}-\frac{d_C{F}_a}{K_C+R_a+A_a+L_a+F_a+M_a}-{\mathit{dF}}_a-{\mathit{mF}}_a \\ \frac{{\mathit{dM}}_a}{\mathit{dt}}={\mathit{mF}}_a-\frac{d_C{M}_a}{K_C+R_a+A_a+L_a+F_a+M_a}-{\mathit{dM}}_a \\ \frac{{\mathit{dY}}_r}{\mathit{dt}}=\frac{{\eta }_{Y0}+{\eta }_{Y1}{(I_r^{\tau }∕K_I)}^{n_I}}{1+{(I_r^{\tau }∕K_I)}^{n_I}+{(L_r^{\tau }∕K_L)}^{n_L}}-\frac{d_C{Y}_r}{K_C+C_r+A_r+L_r+Y_r+M_r}-{\mathit{dY}}_r-{\mathit{mY}}_r \\ \frac{{\mathit{dM}}_r}{\mathit{dt}}={\mathit{mY}}_r-\frac{d_C{M}_r}{K_C+C_r+A_r+L_r+Y_r+M_r}-{\mathit{dM}}_r \end{gathered}$$ (1)

See Supplementary Tables 1 and 2 for the description of variables and parameters. To describe the spatio-temporal dynamics of consortia in the extended chamber we extended this model by adding a spatial dimension. In particular, we modeled how different quantities vary across the horizontal direction of the chamber. We did not include a vertical dimension because signals diffused virtually instantaneously in the vertical direction, and thus variations in concentration are negligible in this direction. As noted in the main text, in the extended open chamber after a transient period cells formed vertical strips (Fig. 1d, e). As a result, there was little variation in strain ratio in the vertical direction.

To model the diffusion of the extra-cellular signaling molecules (H and I in Eq. (1)), we extended the delay differential equations defining our earlier model to the following set of partial delay differential equations,

$$\begin{gathered} \frac{\partial H_e(x,t)}{\partial t}=D_H{\nabla }^2{H}_e(x,t)+\frac{d_a(x,t)}{d_e(x,t)}{\pi }_H(H_a(x,t)-H_e(x,t)) \\ +\frac{d_r(x,t)}{d_e(x,t)}{\pi }_H(H_r(x,t)-H_e(x,t))-{\mu }_e{H}_e(x,t) \\ \frac{\partial I_e(x,t)}{\partial t}=D_I{\nabla }^2{I}_e(x,t)+\frac{d_a(x,t)}{d_e(x,t)}{\pi }_I(I_a(x,t)-I_e(x,t)) \\ +\frac{d_r(x,t)}{d_e(x,t)}{\pi }_I(I_r(x,t)-I_e(x,t))-{\mu }_e{I}_e(x,t) \end{gathered}$$ (2)

Here, x indicates the horizontal location along the chamber. The subscripts of H_j(x,t) and I_j(x,t) indicate whether a variable represents concentration within a strain or in extracellular space: For instance, H_a(x, t), H_r(x, t), and H_e(x, t) are the concentrations of C4HSL in the activator strain, the repressor strain, and the extracellular space at location x in the chamber at time t, respectively.

In addition, D_i is the diffusion coefficient in the chamber, π_i is the transport rate through cell membranes, and μ_e is the extracellular dilution rate due to flow (i=H or I) (Supplementary Table 2). The functions d_a(x, t), d_r(x, t), and d_e(x, t) respectively describe the fraction of repressor strain density, activator strain density, and extracellular density, respectively. Following previous experimental measurement ¹⁹, we set d_e(x, t)=0.2 and d_a(x, t)+d_r(x, t)=0.8. We determined the values of d_a(x, t) and d_r(x, t) from the spatio-temporal dynamics of bacterial populations in the experiment (see below for details).

To simulate this system, we discretized space using Δx=20μm² to define a spatial mesh with N_x=100 elements (Supplementary Fig. 9). We then converted the partial delay-differential equations into a system of N_x coupled delay differential equations each of which described the local dynamics within a section along the chamber. The individual equations within the system of delay differential equations were coupled via a discrete diffusion operator, D_H(H_e(x − Δx, t)+H_e(x + Δx, t) − 2H_e(x, t))/Δx² and D_I(I_e(x − Δx, t) + I_e(x + Δx, t) − 2I_e(x, t))/Δx². Reflecting boundary conditions at x=0 and x=2000μm were used, consistent with the design of the chamber (Fig. 1d). All simulations were performed using Mathematica 11.0 (Wolfram Research, Champaign, IL) running on a cluster of 16×8-Ghz CPUs.

We generated initial spatial distributions (i.e. {d_a(0, 0), d_a(Δx, 0), d_a(2Δx, 0), … d_a(N_x Δx, 0)} and {d_r(0, 0), d_r(Δx, 0), d_r(2Δx, 0), … d_r(N_xΔx, 0)}) and initial phase distributions randomly by sampling from a normal distribution, N(0.4, 0.145) and N(0, 0.15), respectively, using the standard deviation of initial spatial distributions and initial phase distributions across the chamber obtained from experimental data (Fig. 2i–l and Supplementary Fig. 3e–h). For simplicity, spatial correlations of initial phase distributions were not considered. Furthermore, to capture the temporal fluctuation of strain distributions observed in the experiment (Fig. 2i–l and Supplementary Fig. 3e–h), we assumed that the fraction of repressor and activator strain density evolved according to a diffusion process:

$${\mathrm{d}}_{\mathrm{i}}(\mathrm{x},\mathrm{t}+\tau )={\mathrm{d}}_{\mathrm{i}}(\mathrm{x},\mathrm{t})+\sqrt{\tau }\mathrm{N}(0,0.01),$$

where τ = 1 min and i = a or r. Strain ratio fluctuations are relatively low in the open chamber, as noted above.

In our original model, we obtained 32 of the 39 parameters either from our own experiments, or from previously published results. We kept these values in the present study (Supplementary Table 2). In our previous study, we sampled the seven unknown parameters randomly, and observed that the behavior of model was overall robust over a large region of the parameter space¹³. We therefore selected one set of these seven parameters for simplicity: We set the concentration of ClpXP is 1820 nM and S_R, S_C, S_L, S_A, S_F, and S_Y (which determining the basal production rates of RhlI, CinI, LacI, AiiA, CFP, and YFP) are 3.06, 37.23, 4.52, 9.54, 113, and 6.8, respectively (Supplementary Table 2). Finally, D_H=4800μm²/min was obtained from a previous study¹² and by comparing the molecular weights of C4HSL (159g/mol) and C14HSL (326g/mol)³⁹, we estimated $D_I=\sqrt{159∕326}\times 4800\mu {\mathrm{m}}^2∕\min \approx 3360\mu {\mathrm{m}}^2∕\min$.

Phase response curve (PRC)

In our simulations the population was partitioned into subpopulations which communicated via HSL signals through the diffusion term, D_H∇²H_e(x,t) and D_I∇²I_e(x,t) in Eq. (2) (Supplementary Fig. 9). Therefore, by simulating the input signal, which consists of both activator and repressor signal from the neighboring populations, we could investigate the impact of signals from a neighboring population on the phase of an observed population. Specifically, we calculated how much the diffusion rate of activator and repressor signals (i.e. D_H∇²H_e(x,t) and D_I∇²I_e(x,t) in the model Eq. (2)) are increased by a signal from a neighboring population 50μm away (Fig. 4a, b) (we present results for 50μm, but the qualitative results are similar provided the distance is small enough for the driving signal to be sufficiently strong).

To understand the effect of the input signal in simulations we increased the diffusion rate of both repressor and activators in a similar way, and subsequently measured the resulting phase shift in the receiver population (Fig. 4c and Supplementary Fig. 5a–g). Specifically, to obtain the phase response curve (PRC) (Fig. 4d, e), we rescaled time so that the period of simulated oscillations is normalized to 1 and thus every point on the oscillation could be assigned a phase (0≤ϕ<1). We chose the reference phase (ϕ = 0) as the point at which the activator promoter is fully activated and the released activator signal (C4HSL) is at its maximum (Fig. 4b, c). Thus the point with phase ϕ corresponds to the point on the oscillation at a time t=Tϕ in the cycle, where T is the oscillation period. When the input signal is given at a specific phase ϕ, the oscillatory trajectory is perturbed and thus the phase is shifted (Fig. 4c and Supplementary Figs. 5a–f). Comparing the perturbed (solid line in Fig. 4c and Supplementary Figs. 5e-j) and unperturbed trajectories (dashed line in Fig. 4c and Supplementary Figs. 5a–f) allowed us to measure the phase shift. This allowed us to plot the effect of the input signal on the phase as a function of the phase at which the signal was delivered (Supplementary Fig. 5g). If coupling is not too strong, the evolution of the phase difference between such populations can be approximated using PRCs obtained from unidirectional interactions^25,26. Denoting the PRC by H, and the phase difference between the two populations by Δϕ, after one cycle of oscillation the phase of each of the two coupled subpopulation changes by H(Δϕ) and H(−Δϕ), respectively. Thus the phase difference between the two populations after one cycle equals H(Δϕ)−H(−Δϕ). The mapping of the phase difference, Δϕ, from one cycle, to the phase difference, Δϕ_new, at the next cycle can thus be written as Δϕ_new=Δϕ+ H(Δϕ)−H(−Δϕ) (Fig. 5a, b).

Experimental estimation of phase difference maps

We first partitioned the image of the chamber horizontally into 600 rectangular compartments each 3.33μm in width (see Calculation of the Order parameter section for details). Using this partition we constructed two sliding windows: Each window consisted of 50 partition compartments (~3.33μm*50≈167 μm) and each pair was separated by 20 compartments (~3.33μm*20≈67μm apart) (Fig. 6a). By sliding the two windows across the extent of the trap, we obtained 25 window pairs: The first window encompassed the region from 67k μm to 67k+167 μm, and the second from 67(k+1) +167μm to 67(k+1)+334 μm for k=0, 1, 2, … 24 (note that 67×25+334μm is approximately 2000μm) (Fig. 6a). In each window, we averaged the CFP and YFP intensities, and computed the times at which they peaked (Fig. 6b). We estimated the phase differences by dividing the differences of the peak times between two windows by the average period of oscillation in the two windows (Fig. 6b).

Construction of microfluidic devices

Microfluidic devices (Supplementary Fig. 10) were manufactured as previously described⁴⁰. Briefly, the molds for the devices were created with a 4” silicon wafer (Silicon Quest, San Jose, CA) that was first cleaned with acetone and isopropyl alcohol, and then dried with compressed nitrogen. Next, for each layer of the device, we coated the wafer with SU-8 series photoresist (MicroChem, Newton, MA), and then evenly distributed the resist by spinning the wafer for 30 seconds in a spin coater (Brewer Instruments, Roala, MO). We baked the wafer at 95°C. After letting the wafer cool to room temperature, we mounted it and a photomask (CAD/Art Services, Bandon, OR) to a mask aligner (SUSS, Germany). We exposed the resist to UV light for cross-linking and then baked the wafer at 95°C to finalize cross-linking. Next, we used SU-8 developer (MicroChem, Newton, MA) to remove Uncross-linked. After all layers were on the wafer, we hard-baked the wafer at 150°C to solidify the resist. Finally, to ensure PDMS liftoff, we coated wafer with release agent (((tridecafluoro-1,1,2,2-tetrahydrooctyl)-1-trichlorosilane), Pfaltz & Bauer, Waterbury, CT) for 5 minutes under vacuum.

To create the devices from the molds, we first mixed polydimethylsiloxane (PDMS) polymer base and curing agent (Sylgaard 184, Dow Corning, Midland, MI) at a 10:1 ratio until completely mixed (~5 min) and removed all bubbles by degassing under vacuum. We next poured the mixed PDMS onto the mold (wrapped in aluminum foil to contain the PDMS) and again degassed the PDMS mixture before baking at 80°C for 2 hours. We removed the cured PDMS monolith and punched ports for fluidic connections with a 0.5mm biopsy punch (GE Healthcare, Pittsburgh, PA) before cutting individual chips from the monolith. We next sonicated the individual chips in methanol for 8 minutes twice (using fresh methanol the second time) and baked the chips at 80°C for 30 minutes to remove methanol. Before attaching the monoliths to glass coverslips we first cleaned the monoliths with tape with tape (3M, St. Paul, MN) and rinsed #1.5 coverslips (VWR, Radnor, PA) with isopropyl alcohol and dried them with compressed nitrogen. We further cleaned the monoliths and coverslips in an UV/ozone oven (Jelight Co., Irvine, CA) for 3 minutes and immediately placed inverted monoliths onto the coverslips to bind. We finally baked the completed devices at 80°C overnight to finalize binding.

Strain and plasmid preparation

The strain and plasmids used for this study are fully described in Chen et al.¹³, and the plasmids are listed in Supplementary Table 3. Briefly, for each consortium, an activator plasmid (pC247 for P₂ or pC165 for P₁) and the inverter plasmid pC239 were co-transformed into the E. coli strain CY027 (BW25113 ΔlacI ΔaraC ΔsdiA P_trc*-cinR P_trc*-rhlR) to create the activator strains. A repressor plasmid pC365 and an inverter plasmid (pC239 for N₂ or pC235 N₁) were transformed into E. coli strain CY027 to create the repressor strains. After overnight culture in LB media (supplemented with 50 μg/ml kanamycin and 100 μg/ml spectinomycin), each strain was inoculated 1:200 into 5 ml fresh media. When the OD600 of each strain reached 0.4, cells were spun down and mixed into 5 ml fresh LB media with antibiotics and 0.1% Tween 20 and loaded into the microfluidic device. After the cells were loaded across the full chamber, fresh media with antibiotics and 1 mM IPTG was added to the channel with a final flow velocity of 50 μm/s through the widest part of the channel (a higher rate on just outside of the trapping chamber, ~150μm/s). Phase contrast and fluorescence images were acquired at 14 positions along the length of the trap every 6 minutes at 60X magnification.