Quantifying the axonal pathways directly stimulated in therapeutic subcallosal cingulate deep brain stimulation

Abstract

Deep brain stimulation (DBS) of the subcallosal cingulate (SCC) is an emerging experimental therapy for treatment‐resistant depression. New developments in SCC DBS surgical targeting are focused on identifying specific axonal pathways for stimulation that are estimated from patient‐specific computational models. This connectomic‐based biophysical modeling strategy has proven successful in improving the clinical response to SCC DBS therapy, but the DBS models used to date have been relatively simplistic, limiting the precision of the pathway activation estimates. Therefore, we used the most detailed patient‐specific foundation for DBS modeling currently available (i.e., field‐cable modeling) to evaluate SCC DBS in our most recent cohort of six subjects, all of which were responders to the therapy. We quantified activation of four major pathways in the SCC region: forceps minor (FM), cingulum bundle (CB), uncinate fasciculus (UF), and subcortical connections between the frontal pole and the thalamus or ventral striatum (FP). We then used the percentage of activated axons in each pathway as regressors in a linear model to predict the time it took patients to reach a stable response, or TSR. Our analysis suggests that stimulation of the left and right CBs, as well as FM are the most likely therapeutic targets for SCC DBS. In addition, the right CB alone predicted 84% of the variation in the TSR, and the correlation was positive, suggesting that activation of the right CB beyond a critical percentage may actually protract the recovery process.

1. INTRODUCTION

Major depressive disorder (MDD) is a lifelong episodic illness (Mueller & Leon, 1996). Approximately 33% of patients with MDD do not respond to four consecutive antidepressant strategies (Rush et al., 2006), and of the nonresponders, approximately 52% do not respond to subsequent electroconvulsive therapy (Heijnen et al., 2010). For individuals with chronic unremitting MDD (i.e., treatment‐resistant depression, or TRD), deep brain stimulation (DBS) represents an evolving experimental therapy.

Various anatomical targets are currently under investigation for treating depression with DBS including the medial forebrain bundle (Schlaepfer et al., 2014), nucleus accumbens (Bewernick et al., 2012), ventral capsule/ventral striatum (Bergfeld et al., 2016), and the subcallosal cingulate (SCC) (Mayberg et al., 2005). Of these targets, the SCC region is the most studied (Crowell et al., 2014), with published reports spanning 167 patients at 21 separate centers. SCC DBS evaluations include various open‐label studies, a single‐blinded discontinuation study (Holtzheimer et al., 2012), and most recently, an industry‐sponsored double‐blinded study, BROADEN, which was halted after a futility analysis (Holtzheimer et al., 2017). Limitations in the understanding of the underlying neural target for SCC DBS and clinical trial design are thought to be key contributors to the recent setbacks in development of the therapy.

Subsequent to initiation of the BROADEN clinical trial, substantial scientific advances have been made toward identifying possible therapeutic stimulation targets for SCC DBS (Mayberg et al., 2016). Axonal pathways residing within the white matter adjacent to the SCC region are the current focus of investigation (Lujan et al., 2013; Riva‐Posse et al., 2014), and with advances in patient‐specific imaging of axonal pathways, new surgical targeting strategies are being explored (Riva‐Posse et al., 2018). As such, the most recent SCC DBS research practices rely on a combination of image guidance and model‐based connectomic analyses to identify a patient‐specific “connectomic blueprint” for prospective surgical targeting (Noecker et al., 2018). Although this connectomic DBS targeting strategy has been successful in preliminary clinical studies (Riva‐Posse et al., 2018), the model‐based predictor used in our previous SCC DBS analyses was highly simplified and known to suffer from substantial limitations in estimating the axonal response to stimulation (Gunalan et al., 2018).

The goal of this work was to identify the axonal pathways that were directly stimulated in our most recent cohort of SCC DBS patients using the most advanced DBS models currently available. These advanced DBS models are referred to as field‐cable pathway‐activation models (FC PAMs), and they incorporate far more technical detail than simple DBS models that rely on volume of tissue activated (VTA) estimates (Gunalan et al., 2017). However, given that most previous analyses of SCC DBS have relied on VTA models, we also compared our new results to those previous methods. We evaluated the responses of four white matter pathways in the SCC region to DBS in six TRD patients, all of which were responders to the therapy. The results help to refine the understanding of which axonal pathways are necessary and sufficient for eliciting an antidepressant effect in SCC DBS.

2. MATERIALS AND METHODS

We evaluated six patients with severe, chronic depression that were enrolled in a research protocol at Emory University (http://clinicaltrials.gov NCT01984710) (Table 1). Each subject was implanted with the Activa PC+S DBS system (Medtronic PLC, Minneapolis, MN) using a protocol approved by the Emory University Institutional Review Board and the US Food and Drug Administration under an Investigational Device Exemption (FDA IDE G130107). This protocol included a connectomic surgical targeting strategy that relied on a patient‐specific DBS model developed in StimVision (Noecker et al., 2018). A summary of the inclusion and exclusion criteria as well as more information on the clinical protocol can be found in the work by Riva‐Posse et al. (2018). All six patients met the requirements for SCC DBS therapeutic response at 24 weeks after surgery. Response to treatment was defined as a 50% reduction in the 17‐item Hamilton depression rating scale (HDRS‐17), and remission was defined as seven points or less on the HDRS‐17.

Table 1.

Patient informationa

Patient	Sex	Age at surgery (years)	Age of MDD onset (years)	Duration of current MDE (months)	Lifetime number of MDEs	Current number of medications	Baseline HDRS‐17
1	M	60	28	132	2	3	19.25
2	M	53	25	24	3	4	20.50
3	F	58	20	12	3	7	22.75
4	F	43	30	60	2	2	20.25
5	F	66	36	36	4	5	23.25
6	F	45	16	24	5	3	23.50

MDD = major depressive disorder; MDE = major depressive episode; F = female; M = male; HDRS = Hamilton depression rating scale; SCC = subcallosal cingulate; DBS = deep brain stimulation.

^aAll patients had a melancholic MDD‐subtype and consented to SCC‐DBS treatment.

2.1. Acquisition of imaging data

All preoperative magnetic resonance imaging (MRI) data were collected using a Siemens 3‐Tesla Trio Tim scanner (Siemens Medical Solutions, Malvern, PA) with maximum gradient strength of 40 mT/m. High‐resolution 3D T1‐weighted (T1W) data were acquired using a magnetization‐prepared rapid gradient echo imaging sequence: 176 slices, 1 × 1 × 1 mm³, TR/TE = 2,600 ms/3.02 ms, flip angle = 8°. Diffusion‐weighted images (DWI) were collected using high‐angular resolution imaging sequence with a 32‐channel coil: 128 noncollinear directions with 11 non‐diffusion weighted images (b = 0); b value = 1,000 s/mm²; 2 × 2 × 2 mm³; 64 slices; TR/TE = 3292 ms/96 ms; multi‐band acceleration factor = 3 (Xu et al., 2013). Acquisition times were reduced using a multi‐band echo planar imaging acceleration (Hutter et al., 2018). To correct the susceptibility‐induced distortion artifact, all diffusion data were acquired twice with two opposite phase encoding directions: anterior to posterior and posterior to anterior (Holland et al., 2010). Postoperative computed tomography (CT) images were collected 3 weeks after surgery to identify contact locations on the DBS lead using a LightSpeed 16 scanner (GE Medical System, 0.46 × 0.46 × 0.65 mm³ voxel size).

2.2. Preprocessing of imaging data

T1W images were corrected for RF/B1 inhomogeneities using the FMRIB Software Library (FSL, https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) script, fsl_anat (Smith et al., 2004). DWI data were corrected for distortions using FSL's topup and eddy tools, respectively (Andersson & Sotiropoulos, 2016). Postoperative CT images were thresholded, and intensities were inverted for aligning to preoperative T1W images using the Analysis of Functional NeuroImages toolbox (AFNI, https://afni.nimh.nih.gov/) (Cox, 1996).

All images were registered to the patient's respective T1W space using FSL's image registration tool, flirt (Jenkinson et al., 2002; Jenkinson & Smith, 2001), with 12 degrees of freedom. The CT was registered to the T1W images using AFNI's align_epi_anat with 9 degrees of freedom. We also used FSL's nonlinear registration tool, fnirt (Anderson et al., 2010), to register the standard Montreal Neurological Institute (MNI) 152 (1 mm) brain to the patient's T1W brain.

2.3. Segmentation

We used FSL's brain extraction tool, bet (Smith, 2002), to isolate the brain from the T1W image, and then, we used FSL's automated segmentation tool, fast (Zhang et al., 2001), to subdivide the brain image into gray matter, white matter, and cerebrospinal fluid (CSF). The patient's parenchyma and CSF were registered to the same structures in a single‐patient atlas named multimodal imaging‐based detailed anatomical (MIDA) model (Iacono et al., 2015) using FSL's flirt with 12 degrees of freedom. The bones and other soft tissues outside the brain were approximated by mapping structures from MIDA to T1W space (Gunalan et al., 2017; Figure 1a). The location of various nuclei within the patient brain was approximated by mapping structures from MNI152 standard space to the patient's T1W space. The MNI brain was also parsed into cortical regions using Freesurfer's recon tool (Fischl, 2012), and all subcortical nuclei, except for the ventral striatum, were defined using the Harvard‐Oxford Structural Atlases (Desikan et al., 2006; Eickhoff et al., 2005; Mazziotta et al., 2001). We defined a ventral striatal region (see Section 2.5) by constructing a sphere that circumscribed streamlines terminating in the confluence of the amygdala, caudate, and striatum.

Figure 1.

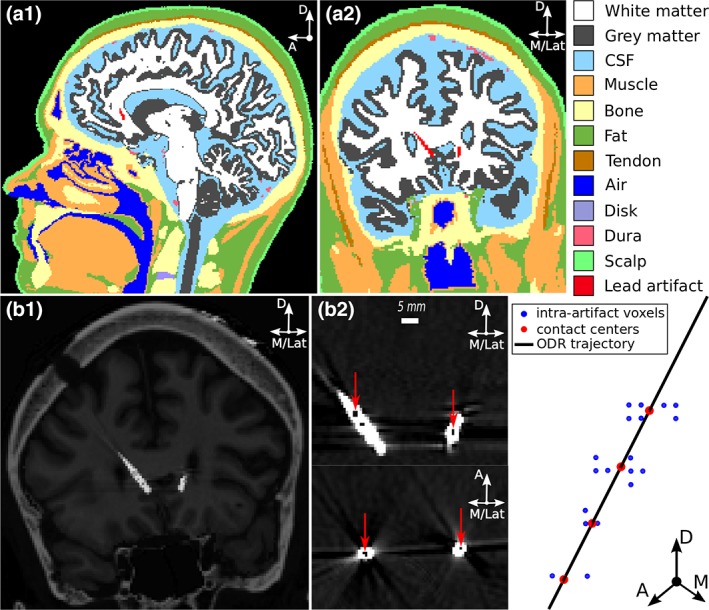
Image‐based volume conductor model of Patient 2. (a1) Sagittal and (a2) coronal views of patient's head segmented into 12 different regions. Knowledge of the locations and electrical properties of the different head regions was used to construct a volume conductor model of the patient's head. (b1) Artifacts produced by the Medtronic 3387 leads in the postoperative computed tomography image were identified using regions of minimal intensity within the artifacts and (b2) orthogonal distance regression was used to fit a straight trajectory to the intra‐artifact regions (red arrows). The 3387 leads were modeled as surfaces within the volume conductor model. D = dorsal; A = anterior; M = medial; Lat = lateral

2.4. Electrode contact localization

Regions of local minimal intensity within the artifact of the DBS lead in the CT images were collinear with the dark streak artifacts emanating from the presumed location of the electrodes, consistent with previous observations (Hemm et al., 2009). Across all patients, the distance between the centroids of adjacent regions had a mean and standard deviation of 3.0 mm and 0.3 mm, respectively, consistent with the design of the Medtronic 3387 leads. These minimal intensity regions were then used to determine the contact centers (Figure 1b) using the connected components tool in Seg3D (http://www.sci.utah.edu/cibc-software/seg3d.html). The coordinates of the voxels constituting the masks were mapped into T1W space using ANFI's Vecwarp. The trajectory of the electrode shaft was straight along the four contacts; therefore, we used orthogonal distance regression to define a best‐fit trajectory through the point clouds in T1W space. A rigid‐body model of the 3387 lead was then moved along the best‐fit trajectory. The best‐fit trajectory was the principal eigenvector of the covariance matrix of the set of points. The 3387 lead was positioned so that it minimized the group sum of square distances.

2.5. Tractography

We used streamlines from tractography to approximate the trajectories and locations of axons within white matter pathways of interest surrounding the SCC region. Probabilistic tractography was conducted using the diffusion MRI toolkit, Camino (Cook et al., 2006). First, we estimated diffusion parameters from the DWI data using FSL's bedpostx toolbox, and then, we used Camino's FACT algorithm (Mori et al., 1999) to conduct the Monte Carlo‐based tracking with a ball‐and‐stick algorithm.

We chose a ball‐and‐stick algorithm because it provides a good compromise between sensitivity (i.e., detecting true connections) and specificity (i.e., avoiding false connections) (Thomas et al., 2014). Tracts were seeded from a patient‐specific region of interest, which was the union of eight 30‐mm spheres whose centers were coincident with the centers of the eight electrode contacts (Table 2). One hundred streamlines were seeded from each voxel within the seed region, yielding between 2.8 and 3.9 million streamlines, depending on the patient (additional details are available in the Supporting Information Supplementary Material). We kept only those streamlines whose curvature was <60° over 5 mm of arc length and had a total arc length of >40 mm. A curvature threshold of 60° is predicted to provide the best tradeoff between sensitivity and specificity for ball‐and‐stick algorithms (Thomas et al., 2014). Setting a total arc length threshold of 40 mm removed spurious interhemispheric streamlines that connected the frontal pole masks. The sampled distribution of electrode‐to‐axons distances did not significantly change with a doubling of the number of streamlines generated per voxel. However, it is important to note that the number of axons used in our DBS simulations was defined to approximate how axons would be spatially distributed within the pathway but was not intended to be representative of the true number of axons in the pathway.

Table 2.

Seed‐to‐target probabilistic tractography

Constrainta/pathway	FM	CB	UF	FP
Seed regionb	30 mm ROI	30 mm ROI	30 mm ROI	30 mm ROI
Target 1	Left PFC + FP	N/A	Ipsi. FP	Ipsi. FP
Target 2	Right PFC + FP	N/A	Ipsi. temporal cortex + amygdala	Ipsi. thalamus + ventral striatum
Waypointb	10 mm ROI	10 mm ROI + MCC	10 mm ROI	10 mm ROI
Exclusion	CSF	CSF + Cont. hemisphere	CSF + Cont. hemisphere	CSF + Cont. hemisphere

FM = forceps minor; CB = cingulum bundle; UF = uncinate fasciculus; FP = frontal pole; CSF = cerebral spinal fluid; MCC = midcingulate cortex; ROI = region of interest; ipsi. = ipsilateral; cont. = contralateral; N/A = not applicable.

^aAdditional curvature and length constraints were imposed.

^bROI were the union of eight 30‐mm spheres centered about the eight contacts. Another ROI constructed with 10‐mm spheres was used to reduce the number of streamlines.

We identified seven pathways from the probabilistic streamlines: one interhemispheric pathway and six intrahemispheric pathways (Figure 2). Streamlines that connected the two prefrontal cortices or frontal poles were defined as forceps minor (FM). In a given hemisphere, pathways were defined as follows: the cingulum bundle (CB) passed through the midcingulate cortex while avoiding the contralateral hemisphere; the uncinate fasciculus (UF) connected the frontal pole to the temporal cortex or amygdala; and subcortical projections connected the frontal pole to the thalamus or ventral striatum (FP). Finally, we mapped the streamlines from the patient's DW space to their T1W space to enable their integration into the anatomical model of the patient.

Figure 2.

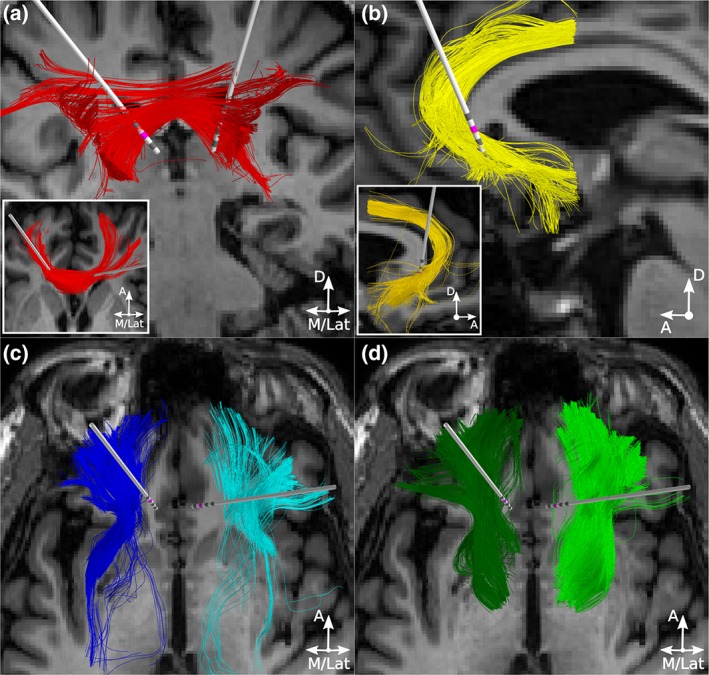
Candidate therapeutic pathways in Patient 2. Probabilistic tractography was used to define (a) one interhemispheric pathway, forceps minor (red streamlines) and three intrahemispheric pathways per hemisphere: (b) cingulum bundle (yellow streamlines), (c) uncinate fasciculus (blue streamlines), and (d) subcortical projections from the frontal pole to the thalamus and ventral striatum (green streamlines). Active contacts are in pink. D = dorsal; A = anterior; M = medial; Lat = lateral [Color figure can be viewed at http://wileyonlinelibrary.com]

Preliminary simulations revealed that axons with electrode‐to‐axon distances of greater than 10 mm were not activated at the stimulation parameters considered herein. Therefore, we ignored axons whose minimum distant was more than 10 mm beyond any of the four contacts, thereby removing axons with activation thresholds greater than 10 V. The resultant number of streamlines for each pathway of each patient are provided in the Supporting Information Supplemental Material (Table S1). If the number of axons in a given pathway was still greater than 1,000 after all the constraints were applied, we sampled 1,000 axons in a pseudo‐random manner so that the distributions of electrode‐to‐axons distances for the subpopulations and full populations were not statistically different (2‐Sample Kolmogorov–Smirnov test, α = 0.05). These steps were taken to reduce the number of simulations, thereby making the analyses more computationally tractable.

2.6. Field‐cable models

The FC PAMs constructed in this study incorporate realistic head geometries, lead locations, electrical properties, and axonal trajectories derived from patient‐specific imaging data. The detailed methodology for constructing image‐based patient‐specific FC PAMs has been presented previously (Gunalan et al., 2017; Howell & McIntyre, 2016, 2017) and is briefly summarized below.

The first major component of an FC PAM is the volume conductor. The head was parsed into three domains: (a) an encapsulation domain defined as the two 0.5 mm thick layers surrounding the two 3387 leads (Medtronic Inc., Minneapolis, MN), (b) a brain domain delineated by the outer boundaries of the brain volume and the encapsulation domain, and (c) a non‐brain domain delineated by the outer boundaries of brain domain and the scalp. We used FSL's dtifit tool to fit a single tensor to each voxel of the patient‐specific DWI data, and subsequently, we used the load preservation approach (Howell & McIntyre, 2016) to define a conductivity tensor, Σ, for each voxel within that patient's head. Because DWI data were only used within the boundaries of the patient's brain, Σ within Domain 2 were anisotropic, whereas Σ within Domains 1 and 3 were isotropic and defined using only an effective isotropic conductivity, σ (Gunalan et al., 2017).

We used COMSOL (version 5.1) to construct a tetrahedral mesh for each patient head, which was subsequently refined within a 20 mm × 20 mm × 30 mm rectangular prism surrounding the eight contacts of the two bilateral leads. Elements in Domain 1, the encapsulation domain, were assigned conductivities between 0.05 and 0.2 S/m so that for each patient, the predicted dynamic resistances of each electrode matched that measured by the Medtronic programming device (Section 2.7 and Supporting Information Figure S1). Elements in Domains 2 and 3, the brain and non‐brain domains, respectively, were assigned conductivity tensors based on their proximity to the nearest neighbor in the tensor field defined by the structured rectangular grid in the patient's T1W space.

We modeled monopolar electrode configurations by defining Dirichlet boundary conditions at the active contact and 0 V at the neck region of the model. Inactive contacts were treated as ideal conductors subject to an additional constraint and integral boundary condition, per contact; all electric potentials within the contact were equal in value, and the net current flow through the surface of the contact was 0 A. Neumann boundary conditions of 0 A/mm² were used to model the electrode shaft and scalp surface (minus the neck) as perfect insulators. We used the finite element method in COMSOL to solve Laplace's equation for the electric potentials (Φ) within the head.

$$\nabla ·\left(\Sigma ·\mathrm{\nabla \Phi }\right)=0$$ (1)

The variation of the potentials over time was approximated by multiplying the solution at time = 0 (Equation (1)) with a time‐varying waveform derived from an equivalent circuit model of the stimulus generated by the implanted pulse generator (Lempka et al., 2018).

The second major component of the FC PAM is the cable model of the axon. Multi‐compartment cable models were constructed and solved in the NEURON simulation environment (version 7.3). We started with the MRG axon model (McIntyre et al., 2002) and modified some of the geometric parameters to better reflect axons of the central nervous system (Howell & McIntyre, 2016). Each streamline was modeled as a myelinated fiber of passage. Each axon model was categorized into one of the four pathways based on the connectivity described in Section 2.5. All axons were stimulated with a scaled version of the extracellular potentials calculated from Equation (1) (Figure 3a), and during stimulation, we recorded the transmembrane potential of the axon. The threshold stimulus amplitude for generation of an action potential (AP) was determined using a binary search algorithm (precision = 0.01 V). We considered the axon active when there was one propagating action potential recorded for each pulse in the 130 Hz train of pulses (Figure 3b). Cable models of axons were solved in parallel using a high‐performance compute cluster.

Figure 3.

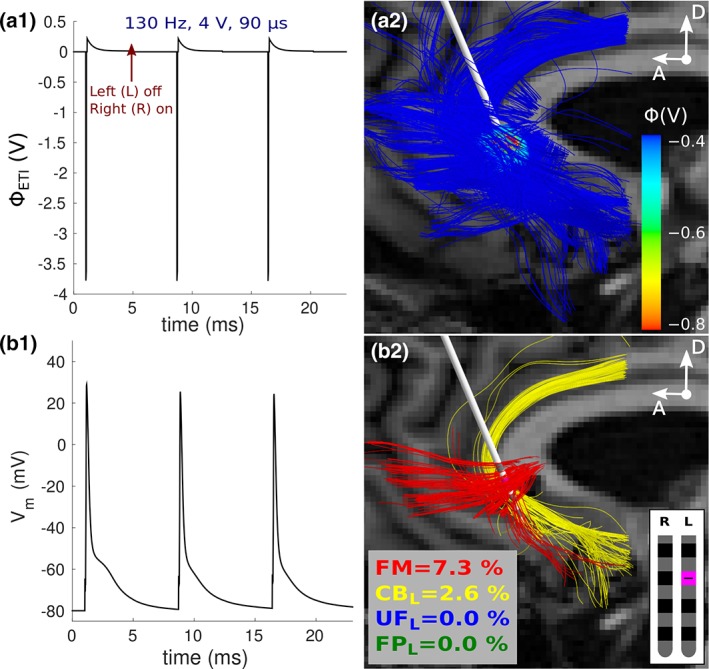
Quantifying responses of cable models to SCC DBS in Patient 2. (a1) Temporal variation in the potentials at the electrode–tissue interface. (a2) Spatial variation in the potentials over forceps minor and cingulum bundle. Only a subset of axons is displayed for visualization purposes. (b1) Active axons were those that responded one‐to‐one to the applied stimulus pulses during interleaved stimulation. (b2) The axons directly activated at the clinical settings. SCC = subcallosal cingulate; DBS = deep brain stimulation [Color figure can be viewed at http://wileyonlinelibrary.com]

Very few (<1%) of the axons in the genu of the corpus callosum and pathways of the frontal cortex have fiber diameters greater than 2 μm (Aboitiz et al., 1992; Liewald et al., 2014). Therefore, we chose to model axons with a 2‐μm fiber diameter because they represent the most excitable but non‐negligible constituents of these pathways. Although fiber diameters greater than 4 μm are rare in the aforementioned regions, we also modeled the response of 5.7‐μm diameter axons to achieve parity with previous modeling works.

2.7. Dynamic resistances

The Medtronic implantable pulse generator measures the dynamic resistance of the load 70 μs after the onset of the stimulus pulse (Lempka et al., 2018). We refer to this dynamic resistance as R ₇₀, which was monitored weekly for the first year and every 2 months thereafter. R ₇₀ fluctuated by hundreds of ohms before 50 days post‐surgery, and in two subjects, R ₇₀ began to drift by hundreds of ohms approximately 200 days post‐surgery, presumably because of depletion of the battery. Our FC PAMs were constructed to represent chronic stimulation, after pneumocephalus has subsided and the glial scar has formed; therefore, the electrical properties of the scar in our model were chosen so that the predicted R ₇₀ (i.e., for each contact) matched the average R ₇₀, between 50 and 200 days post‐surgery.

2.8. Volumes of tissue activated

Most previous models of SCC DBS have estimated axonal responses using a VTA (Chaturvedi et al., 2013). The specific implementation of a VTA PAM implemented in StimVision (Noecker et al., 2018), the surgical targeting tool used in Riva‐Posse et al. (2018), was derived by using a series of ellipsoids to approximate planar regions of activation from a simplified FC PAM. Two artificial neural networks (ANNs) were used to approximate the relationship between combinations of stimulation parameters (the input) and the center and radii of the ellipsoids (the output). Each ANN consisted of 12 inputs, 1 hidden layer, and a linear output layer, and both networks were trained using the Levenberg–Marquardt algorithm (Chaturvedi et al., 2013). This VTA model was also used to create the PAM results presented in our previous analyses of clinical SCC DBS (Choi et al., 2015; Riva‐Posse et al., 2014; Riva‐Posse et al., 2018).

To ascertain the relative accuracy of this simplified algorithm, we compared the results obtained with VTAs to that of the patient's FC PAM. Given an electrode configuration, an electrode resistance (R ₇₀), stimulus pulse width, and fiber diameter, we generated an ellipsoid‐based VTA to estimate which axons were activated. We defined the stimulation threshold for direct activation of an axon as the minimum voltage amplitude needed to generate a VTA that intersected the respective streamline for a given stimulation setting.

2.9. Analyses

Axonal responses in each FC PAM were evaluated at the patient's therapeutic DBS setting (Table 3). Subsequently, we used each patient's FC PAM to quantify how axonal responses varied when stimulation was delivered through one of the other three electrodes on a lead. We did not model how activation of presynaptic inputs and/or antidromic invasion of the APs affected the underlying network dynamics of brain circuits. As such, our analyses only estimated which pathways were directly entrained by the DBS electric field. The Medtronic PC+S system delivers interleaved stimulation; therefore in total, we evaluated eight monopolar cathodic configurations per patient. The results of each patient's FC PAM were then compared to that of their VTA PAM.

Table 3.

Clinical stimulus parameters and outcome metricsa

Patient	Active contact (left/right)b	TSR (days)	Baseline HDRS‐17	One‐year HDRS‐17a
1	C2/C2	133	19.25	6
2	C2/C1	84	20.50	7
3	C1/C1	142	22.75	10
4	C2/C2	189	20.25	11
5	C2/C1	8	23.25	2
6	C2/C1	36	23.50	3

HDRS‐17 = 17‐item Hamilton depression rating scale; TSR = time to a stable response.

^aTime to well is the time it took the patient's baseline HDRS‐17 to drop by >50% and remain for at least four consecutive weeks. The 1‐year HDRS‐17 is taken at 1‐year, post‐surgery.

^bStimulation parameters: frequency = 130 Hz, pulse width = 90 μs, amplitude = 4 V, polarity = cathodic. C = contact/electrode, with C0 being most proximal to the tip.

Activation of the putative therapeutic targets is believed to exert an antidepressant effect, and a greater antidepressant effect may potentially reduce the time it takes for a patient to respond to DBS therapy. To test this assumption, we used the percentage of activated axons in each pathway as regressors in a linear model to predict the patient's time to a stable response (TSR) (Table 3). The dependent variable in the regression model was the patient's TSR, which is the time it takes a patient to respond and maintain a response for at least 4 weeks. The independent variables, or regressors, were the percentages of axons activated in each pathway for a given fiber diameter, 2 or 5.7 μm, separately. Lasso regression in MATLAB (R2014b) was used to find the set of regressors that maximized the adjusted coefficient of determination (R ²), and subsequently, incremental/partial F‐tests (α = 0.05) were conducted to determine if nested subsets of the regressors had coefficients that were not statistically different than zero. Because of our small sample size, we also used a permutation test to estimate the false positive rates of the regression coefficients.

3. RESULTS

We constructed bilateral FC PAMs for six patients (Table 1) that had undergone SCC DBS for chronic unremitting depression. These models incorporated the latest advances in biophysical modeling of DBS (Gunalan et al., 2017) and were used to predict the axonal response at each patient's therapeutic DBS settings, as well as other monopolar cathodic electrode configurations. Subsequently, we compared the results of the patient‐specific FC PAMs, the gold standard in this study, to the results generated via VTA PAMs.

3.1. Matching the dynamic resistances

Across all patients and contacts, R ₇₀ ranged between 0.123 and 1.50 kΩ, with a total mean and standard deviation of 1.13 kΩ and 0.280 kΩ, respectively (Figure 4). We also observed that R ₇₀ increased with increasing distance from the tip of the lead. The patient‐specific volume conductor head models could account for most of these observed trends, and we were able to match the average R ₇₀ to within 1% accuracy in all but two contacts, which had errors of 1.2% and 2.5%, respectively. A more detailed analysis of the dynamic resistances is included in the Supporting Information Supplemental Material (Section S.2).

Figure 4.

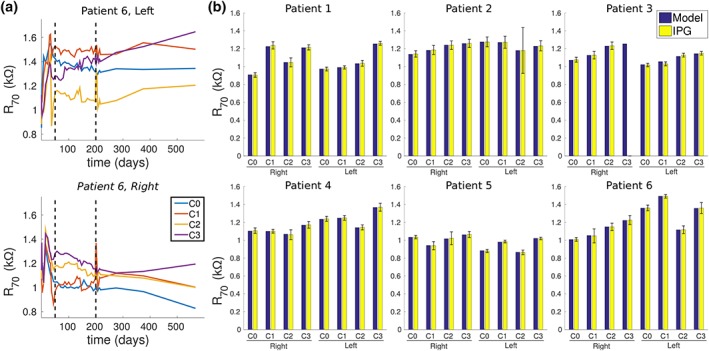
Predicted and measured dynamic resistances. (a) Dynamic resistances measured by the implantable pulse generator 70 μs after the onset of the stimulus pulse (i.e., R ₇₀) in Patient 6. Contact 0 (C0) is closest to the tip. Although R ₇₀ were monitored weekly for the first year and every 2 months thereafter, we only analyzed R ₇₀ between 50 and 200 days after surgery (dashed lines), when the measurements were relatively stable. (b) The predicted R ₇₀ versus the average R ₇₀ that was measured 50–200 days post‐surgery in all six patients; the bars for the IPG data denote ±1 standard deviation. Because the fourth contact (C3) on the right lead was broken in Patient 3, no measured values for this contact are shown [Color figure can be viewed at http://wileyonlinelibrary.com]

3.2. Axonal responses

We began by quantifying the response of axons in each FC PAM using a fiber diameter of 2 μm for each modeled axon (Figure 5). SCC DBS at the therapeutic clinical settings directly activated both CBs in every subject expect Patient 4, where only the right CB was activated. FM was also activated in most patients, but only in Patients 1–3 was the percent activation greater than 1% of the total population of axons. Compared to FM and CB, the two other pathways were activated to a much lesser degree. For example, activation of either UF or FP was less than 0.2% in all but one patient.

Figure 5.

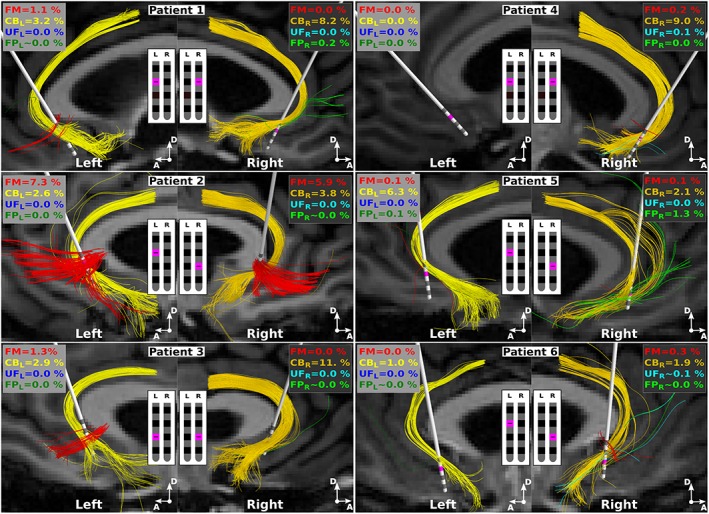
Axons directly activated by SCC DBS. Streamlines indicate the axon models directly activated by the extracellular stimulus at each patient's clinical setting: 130 Hz, 4 V, 90 μs, monopolar cathodic configuration (pink). All axons had a fiber diameter of 2 μm, and right and left denotes the responses when either the right or left lead is active. Percentages denote the percentage of each pathway that is activated. FM = forceps minor; CB = cingulum bundle; UF = uncinate fasciculus; FP = subcortical connections from frontal pole to thalamus and ventral striatum; L = left; R = right [Color figure can be viewed at http://wileyonlinelibrary.com]

We then used the FC PAMs to quantify the axonal responses as we changed the active contact used for stimulation. In general, the percentage of axons activated in FM and CB steadily increased as the active contact moved distal to the electrode tip (Supporting Information Figure S2). We observed the same trends when using a fiber diameter of 5.7 μm for the axons, except that more axons in each pathway were activated (Supporting Information Figure S2). Despite using a larger fiber diameter, there was still very little activation (<1%) of UF and FP compared to that of CB and FM.

The axons that were directly activated in the CBs had some of their termini in Brodmann area (BA) 25 and passed adjacent to BA 24 and 33 (Figure 5). Axons activated in FM terminated in the medial prefrontal cortex (mPFC), more specifically, in the medial aspects of BA 10 and superior aspects of BA 11. Although there was very little activation of UF and FP, the axons that were activated were the medial most aspects of those respective pathways.

3.3. Correlations of axonal responses with clinical outcomes

Four regressors (FM, left CB, right CB, and right FP) explained 99% of the variation in the patient's TSR (Figure 6a). Activation of the right CB, alone, explained 84% of the variance in TSR, and the addition of FM, left CB, and right FP did not contribute significant information to the linear model (incremental F‐test, p > .05). Therefore, increases in predictive power from the inclusion of FM, left CB, and right FP in the linear model was likely because of overfitting. The same trends were observed when we substituted the TSR with the 1‐year HDRS‐17 (Table 3). Considering the 720 different ways of permuting the six TSRs, the false positive rate of regression coefficient for the right CB was ~0.0083.

Figure 6.

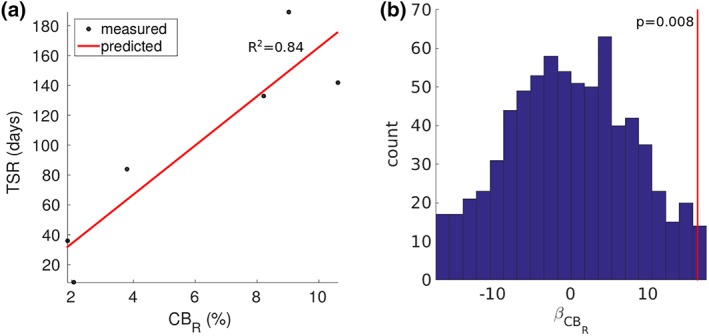
Predicting the time to a stable response (TSR). (a) TSR as a function of the percentage of axons activation in the right cingulum bundle (CB_R). R ² = coefficient of determination. (b) Regression coefficients for CB_R across all 720 permutations of TSR in the six patients. The red line denotes the value for the regression coefficient when TSR is not permuted [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4. FC PAM versus VTA PAM

We conducted a head‐to‐head comparison of predictions between the VTA PAM and the respective FC PAM for each patient (Figure 7). Compared to the FC PAM, VTA PAMs markedly overestimated the activation thresholds of the 5.7 μm axons, leading to a pronounced underestimation in the total percent activation of each pathway for most of the stimulation range (0–10 V) (Figure 7b). Errors in activation thresholds were on the order of volts, with the median error across patients ranging between 0.6 and 1.6 V (Figure 7c). As a result of these errors, the extent of activation, as predicted by using the intersection of streamlines with the VTA, was underestimated by several millimeters (Figure 7d).

Figure 7.

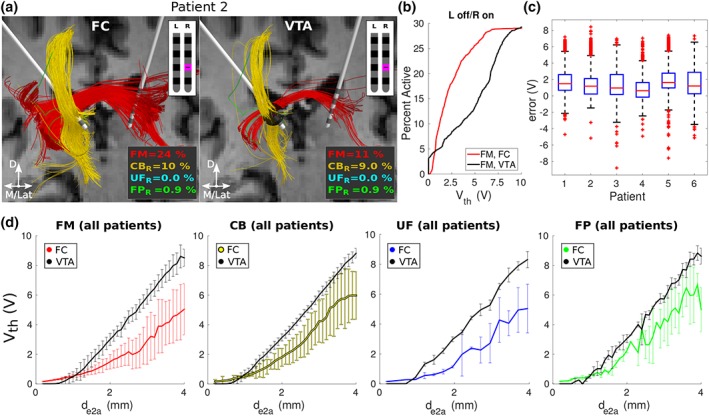
Estimating responses of 5.7 μm‐diameter axons with FC PAM versus VTA PAM. (a) Axons activated in the right hemisphere of Patient 2 at their clinical setting: 4 V, 90 μs, 130 Hz, electrode 1 (pink). For the VTA PAM, axons were considered active when they intersected the VTA (black ellipsoid). D = dorsal; M = medial; Lat = lateral; L = left; R = right. (b) Percentage of FM activated by the right lead in Patient 2 at various amplitudes. (c) Errors in voltage stimulation thresholds (V _th) between the FC and VTA PAMs of each patient. Errors are aggregated across contacts two and three (C1 and C2, respectively) and all pathways. (d) V _th (mean ± 1 standard deviation) versus the electrode‐to‐axon distance (d _e2a) for each pathway. d _e2a is the minimum distance from the axon to the surface of the active electrode. Values were averaged across both leads/hemispheres and all patients. FM = forceps minor; CB = cingulum bundle; UF = uncinate fasciculus; FP = connections from the frontal pole to the thalamus and ventral striatum; FC = field‐cable; VTA = volume of tissue‐activated; PAM = pathway activation model [Color figure can be viewed at http://wileyonlinelibrary.com]

Previous VTA‐based analyses of SCC DBS likely generated differing estimates of the spatial extent of activation for a number of reasons. First, earlier VTA PAMs assumed an unrealistically large fiber diameter of 5.7 μm. Second, these analyses typically assessed activation at 8 mA with an assumed electrode impedance of 1 kΩ. Increasing the fiber diameter to 5.7 μm and stimulation amplitude to 8 V in the current cohort of subjects resulted in activation of markedly more axons in UF and FP (Figures 7 and 8, and Supporting Information Figure S2). As such, these model parameter details can explain many of the general differences in activated pathway findings between studies.

Figure 8.

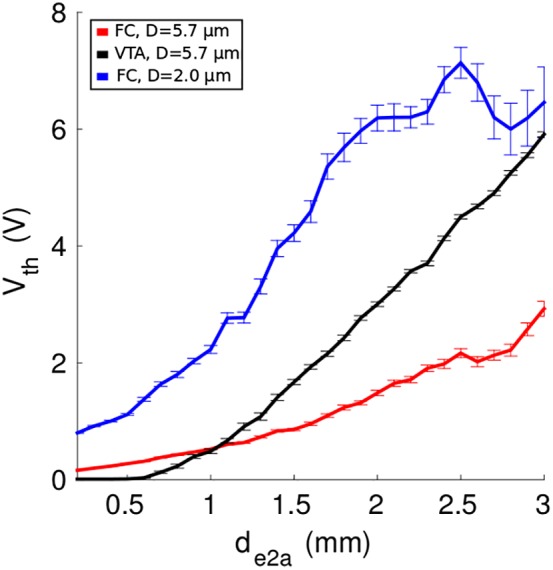
Role of axon diameter in models of SCC DBS. Previous FC‐ and VTA‐based analyses assumed a fiber diameter (D) of 5.7 μm (black and red), whereas the patient‐specific FC PAMs in this work used 2.0 μm (blue). Thresholds (±1 standard error of the mean) and distances are averaged across all patients, hemispheres, and pathways. V _th = activation threshold for stimulation; d _e2a = minimum electrode‐to‐axon distance; SCC = subcallosal cingulate; DBS = deep brain stimulation; FC = field‐cable; VTA = volume of tissue‐activated; PAM = pathway activation model [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

Computational characterization of the neural response to DBS holds promise for guiding clinical decisions on electrode placement and stimulation parameter settings, particularly in psychiatric applications where behavioral responses can take days or weeks to manifest. We used the most anatomically and electrically accurate bioelectric field models of DBS currently available to quantify the neural response to therapeutic SCC DBS. We found that the right CB was activated in all patients and the left CB was activated in all but one patient. FM was activated in half of the patients, and there was very little (≤0.2%) or no activation of UF or FP in all but one patient. The percent activation of the right CB could explain 84% of the variance in the TSR, with greater percentages predicting longer recovery. Given that all of the patients we analyzed met the criteria for a response at 1 year, we conclude that the right CB, left CB, and FM are all likely therapeutic targets for SCC DBS. However, activation of the right CB, beyond a critical percentage, may actually protract the time it takes to reach a stable therapeutic response.

4.1. Therapeutic targets for SCC DBS

The subgenual (anterior) cingulate cortex, or SCC, is a critical hub with extensive connections to both cortical and subcortical areas. Tracing studies in nonhuman primates reveal that the SCC has reciprocal connections with the orbitofrontal, prefrontal, and dorsal cingulate cortices (Carmichael & Price, 1995; Heilbronner & Haber, 2014; Vogt & Pandya, 1987), as well as subcortical connections to or from the amygdala, ventral striatum, thalamus, and brainstem (Freedman et al., 2000; Heilbronner & Haber, 2014; Kunishio & Haber, 1994). In addition, in humans, various positron emission tomography (PET) (Mayberg et al., 1999; Videbech et al., 2001) and functional MRI (fMRI) (Smith et al., 2011) studies implicate the SCC as an important region for emotional processing and dysfunction in MDD. Furthermore, increased functional connectivity within the SCC may serve as a biomarker for identifying treatment resistance in MDD (Greicius et al., 2007).

Scientific understanding of how high‐frequency electrical stimulation of the SCC directly or indirectly normalizes cortical activity in chronic depression is very limited (Mayberg et al., 2005). Nonetheless, given that the primary effects of electrical stimulation are believed to be because of the direct activation of axons (Ranck, 1975), we posit that the therapeutic targets in SCC DBS primarily reside within the white matter adjacent to the SCC. The first modeling study to estimate the neural response to chronic SCC DBS was a retrospective analysis of a single responder. Lujan et al. (2013) used an FC PAM to estimate axonal activation using either the patient's therapeutic or nontherapeutic contacts. That analysis predicted activation of UF and FP at both the therapeutic or nontherapeutic contact. However, FM and CB were only activated with the therapeutic contact. Riva‐Posse et al. (2014) extended that analysis to a larger cohort of responders and nonresponders using the more simplistic VTA‐based PAMs. In that work, all responders shared a common activation pattern containing FM, CB, UF, and FP. Given these results, in combination with PAM results from anterior limb of internal capsule DBS studies (Gutman et al., 2009; Lujan et al., 2012), a common linkage between DBS for depression targets was hypothesized to be activation of axonal connections to the ventral medial prefrontal cortex. However, counter to the previous findings, the SCC DBS FC PAMs analyzed in this study predicted very little or no activation of UF and FP (Figure 5). This suggests that direct activation of these two pathways may not be necessary for eliciting an antidepressant response in SCC DBS and that CB activation is a uniquely important aspect of the therapy.

The evolving hypothesis from this work is that some combination of activating the two CBs and FM is sufficient for a response in most, but not all SCC DBS patients (Supporting Information Figure S3). Paired with the finding that transient best responses evoked by stimulation of the left SCC region during surgery are a prognostic indicator of effective SCC DBS (Choi et al., 2015), and it is possible that co‐activation of the left CB and FM generates a greater antidepressant effect than activation of the right CB. However, unilateral testing of whether left‐ or right‐sided chronic stimulation alone is adequate for a therapeutic response remains to be evaluated.

Although the results of this study provide more detailed insight into the specific pathways that are necessary and sufficient for generating a therapeutic response to SCC DBS, we do not believe that the available data can justify abandoning the current surgical targeting paradigm (Noecker et al., 2018; Riva‐Posse et al., 2018). That protocol has been very successful, and the “confluence point” of CB, FM, UF, and FP streamlines represents a unique location in the patient brain that can be algorithmically defined. The same cannot be said for targeting a single pathway alone, which represent more ambiguous targeting goals, as the pathway can be stimulated at a larger range of points along its trajectory. Therefore, we believe the current SCC DBS “connectomic blueprint” approach (Riva‐Posse et al., 2018) represents the simplest strategy to reduce surgical variance in the clinical investigation of the therapy.

4.2. Therapeutic mechanisms of SCC DBS

Intraoperative behavioral assessments and corresponding tractographic analysis suggest that direct activation of the CB facilitates changes in interoception (Choi et al., 2015). This implicates modulation of the rostral anterior cingulate cortex (ACC) and anterior insular cortex (Medford & Critchley, 2010), which send and receive projections via the subgenual CB (Bush et al., 2000). The subgenual CB also connects to the dorsal ACC (Jones et al., 2013; Wu et al., 2016), which is a lesion target for treating chronic depression (Steele et al., 2008) and a stimulation target for treating chronic neuropathic pain (Boccard et al., 2017; Spooner et al., 2007). As such, these various interventions may act by disrupting pathological communication patterns between the SCC and ACC.

Unfortunately, clearly identifying the gray matter territories that are directly modulated by DBS represents a difficult problem. Electrical stimulation generates action potentials that propagate both orthodromically and antidromically from the site of initiation in the axon (McNeal, 1976). Given that most neurons make synaptic connections in both the local region of their cell body, as well as distant regions, electrically stimulating the axon generates synaptic action in many places. However, models capable of quantifying such things are only beginning to be developed (Anderson et al., 2018), and the long‐term goal is to link those predictions with things like fMRI measurements (Bernal‐Casas et al., 2017).

A unique finding from the SCC DBS FC PAMs was the positive correlation between the patient's TSR and the percentage of right CB activated at the therapeutic settings (Figure 6). Previous DBS modeling studies in both movement disorders (Frankemolle et al., 2010) and psychiatric disorders (Hartmann et al., 2016) have suggested that unintentional “overstimulation” of an initially therapeutic region can act to limit outcomes. If we assume that chronic high frequency DBS of the CB induces some degree of disconnection with its synaptic targets (McIntyre & Anderson, 2016), then possibly disconnecting too much of the CB with SCC DBS has detrimental effects. For example, alterations in the integrity of the CB have been implicated as a possible reason for depressive symptoms. The severity of lesions in the left CB is a prognostic indicator for poor outcomes in treating late‐life depression (Taylor et al., 2014). Reductions in fractional anisotropy in the right CB are associated with depressive symptoms in astherosclerotic vascular disease (Bijanki et al., 2013), and fractional anisotropy in both CBs is negatively correlated with a familial history of depression (Bracht et al., 2015). Given these observations, it appears that although high frequency driving of the subgenual CB projections is therapeutic to a point, overstimulation of the pathway may actually be detrimental (Figure 6).

4.3. Study limitations

The principal limitation of this study is the lack of a “ground‐truth” to verify the model predictions. The patient‐specific FC PAMs constructed in this study used the most detailed and advanced methods for modeling DBS currently available (Gunalan et al., 2017). The individual components of these models, namely the volume‐conductor and cable models, can be validated and constrained by experimental data (McIntyre et al., 2002; Miocinovic et al., 2009), and we used measurements from each patient's implantable stimulator to constrain our models even further (Figure 4). However, there are currently no experimental techniques for directly measuring the percentage of white matter pathways activated by DBS. Nonetheless, indirect methods are possible. Electroencephalograms of cortical responses generated by the applied stimulus in DBS (Kibleur et al., 2017; Waters et al., 2018), and local field potentials recorded with the inactive electrodes (Smart et al., 2018), represent excellent opportunities for DBS biophysicists and electrophysiologists to begin to converge upon analyses that would be mutually beneficial.

Our results are also limited by errors associated with estimating of the location, volume, and trajectory of the pathways of interest. We chose to use a tractographic algorithm that is expected to have the best tradeoff between specificity and sensitivity (see Section 2.5), but tractography algorithms have issues, albeit to different degrees, with pathways that kiss or overlap (Maier‐Hein et al., 2017). For example, FP may have overextended the medial aspects of UF, and UF may have overextended the lateral aspects of FP, and the anterior thalamic radiations may have overextended the lateral aspects of FM. As such, the pathways constructed in the work likely present a liberal estimate of the true volume occupied by these pathways. Moreover, we did not parse the nominal pathways into their respective subdivisions. For example, we neither distinguished between subgenual and retrosplenial subdivisions of CB (Jones et al., 2013; Wu et al., 2016), nor the three subdivisions of the UF (Bhatia et al., 2018). Future attempts at identifying subdivisions within pathways may help improve the specificity of tractographic analysis and help delineate which gray matter areas are directly affected by DBS.

This study also suffered from a small sample size. To date, 34 patients have been implanted in three cohorts at Emory University: (a) 17 in Holtzheimer et al. (2012), (b) 11 in Riva‐Posse et al. (2018), and (c) the 6 patients in this study. Patient selection has remained relatively constant across all the cohorts (Crowell et al., 2015), with Cohorts 2 and 3 being the most homogeneous, clinically. In terms of targeting, the therapeutic contacts in Cohorts 2 and 3 were selected using a connectomic blueprint (Riva‐Posse et al., 2018) and intraoperative behavioral responses (Choi et al., 2015). However, only in Cohort 3 was the DBS electrode targeting process standardized with StimVision (Noecker et al., 2018). Cohort 3 also received voltage‐regulated stimulation with the Activa PC+S DBS system, whereas Cohorts 1 and 2 received current‐regulated stimulation with the Libra DBS system (Abbott Laboratories, Chicago, IL). Therefore, Cohort 3 defined a distinct group, which was a key reason why we focused our analysis on those six patients.

Finally, when modeling DBS, there are significant errors that can arise from image co‐registration (Klein et al., 2009) and imprecise localization of the DBS electrode in a postoperative CT (Hemm et al., 2009). To alleviate these concerns, processed images were inspected by three separate raters (i.e., KSC, JR, and BH), and we localized the electrode array using beam‐hardening artifacts that agreed with the expected geometry of the lead (Figure 1). Then we parameterized the FC PAMs so that they recapitulated impedance measurements from the implanted device (Figure 4).

5. CONCLUSIONS

Medical imaging and tractography continue to evolve and improve in concert with the field of connectomic brain stimulation modeling. These advances are paving the way for more detailed analyses that refine our predictions of the therapeutic targets underlying DBS. Whereas previous modeling efforts identified four candidate therapeutic axonal pathway targets in SCC DBS, our anatomically and electrically detailed patient‐specific models suggest the focus should be narrowed to the left and right CB, as well as FM. As such, the result of this study help guide an ongoing effort to identify the necessary and sufficient effects of stimulation for eliciting an antidepressant effect in SCC DBS.

CONFLICT OF INTERESTS

CCM is a shareholder in Surgical Information Sciences, as well as a paid consultant to Boston Scientific Neuromodulation and Kernel. HSM is a paid consultant with licensed intellectual property to Abbott Neuromodulation. All other authors reported no biomedical financial interests or potential conflicts of interests.

Supporting information

Appendix S1: Supporting Information

Howell B, Choi KS, Gunalan K, Rajendra J, Mayberg HS, McIntyre CC. Quantifying the axonal pathways directly stimulated in therapeutic subcallosal cingulate deep brain stimulation. Hum Brain Mapp. 2019;40:889–903. 10.1002/hbm.24419