On the Effectiveness of Deep Representation Learning: the Atrial Fibrillation Case

Abstract

The automatic and unsupervised analysis of biomedical time series is of primary importance for diagnostic and preventive medicine, enabling fast and reliable data processing to reveal clinical insights without the need for human intervention. Representation learning (RL) methods perform an automatic extraction of meaningful features that can be used, e.g., for a subsequent classification of the measured data. The goal of this study is to explore and quantify the benefits of RL techniques of varying degrees of complexity, focusing on modern deep learning (DL) architectures. We focus on the automatic classification of atrial fibrillation (AF) events from noisy single-lead electrocardiographic signals (ECG) obtained from wireless sensors. This is an important task as it allows the detection of sub-clinical AF which is hard to diagnose with a short in-clinic 12-lead ECG. The effectiveness of the considered architectures is quantified and discussed in terms of classification performance, memory/data efficiency and computational complexity.

1. INTRODUCTION

Deep learning (DL) has amply demonstrated its knowledge extraction capabilities in the identification of features for the classification of clinical images [1]. For example, DL has been shown to possess classification skills on par with board-certified ophthalmologists for detecting diabetic retinopathy and macular edema from retinal fundus images [2]. In [3], it reached a level of accuracy on a par with dermatologists in the identification and classification of skin cancers. Likewise, DL is a promising approach to the analysis of biomedical time series. In fact, the small receptive field of the first neural network layers allows for the assessment of local and small-scale signal characteristics, such as localizing specific patterns or performing ECG intra-beat morphology analysis. Instead, deeper layers consider low-level features jointly, obtaining a meaningful (high-level) representation of the underlying (raw) information, which facilitates a subsequent classification task. Innovative DL architectural designs have been recently proposed, but a clear evaluation of these methods in terms of performance, complexity and efficiency when utilized with biomedical time series is still lacking. The purpose of the present study is to fill this gap, by carrying out a comprehensive analysis of advanced representation learning (RL) methods for the classification of one-dimensional (1D) biomedical signals. We focus on an important clinical problem, the detection of atrial fibrillation (AF). AF is the most common significant heart arrhythmia, associated with a 5-fold increase in the risk of a stroke and a 2-fold risk of mortality [4]. It is also especially well suited for screening, as there are preventive anticoagulant therapies available that have been shown to decrease the risk of these complications by 65% [5]. In addition, a gold-standard for diagnosis exists in the form of an ECG. In the past, ECG monitoring was limited to only 10 seconds of screening (12-lead ECG) during an annual check-up, often missing intermittent AF events [6] and potentially delaying AF diagnosis by years. Nowadays, thanks to commercial wireless devices, it is possible for individuals to obtain their ECG at any time without the need for a clinical visit, making the need for a precise and automated detection of AF from individually-obtained ECG traces uniquely important. The challenge for the AI algorithm is to interpret a single-lead ECG signal obtained in free-living conditions, which is much noisier than the corresponding clinical 12-lead ECG signal.

In general, two broad categories of processing methods can be identified when analyzing biomedical data. The first one relies on the selection of a set of clinical features, which are usually suggested by clinical studies, and on the subsequent detection of such features into the signal [7]. These approaches, referred to in the following as feature engineering methods, require a specific domain knowledge to transform raw (unprocessed) data into a suitable representation that is able to generalize on unseen data, and that can be used, for example, to train a classifier. An alternative approach embraces the concept of representation learning (RL). It encompasses methods that automatically discover useful data representations to carry out classification, detection or regression tasks, without the need for feature engineering. This approach is particularly effective in the presence of non-clinical signals, such as the photoplethysmography (PPG) signal [8], or in the presence of short and noisy ECG signals, as those considered in this paper.

In the present work, we investigate both approaches, with particular focus on RL techniques exploiting advanced DL architectures. Our main goal is to explore and quantify the benefits of architectural designs with varying degree of complexity, providing a clear and comprehensive overview. Each of the presented architectures implements a specific technique, including residual connections, inception modules and depthwise separable convolutions, whose effectiveness is here quantified and discussed in terms of classification performance, memory/data efficiency and computational complexity.

Quantitative results are provided for the AF detection problem from short and noisy ECG traces, but most of our considerations and findings can be generalized to other biomedical time series, and should be taken into account when dealing with any modern RL based design.

2. METHODS

The proposed analysis of ECG signals is organized into three phases: 1) signal pre-processing, 2) feature extraction, and 3) classification. Next, we describe these phases and present two approaches for feature extraction: 2.a) a classical feature engineering approach, and 2.b) a novel representation learning approach. For both, several solutions are investigated and compared.

2.1. Single-lead ECG dataset

The data used in this study has been made publicly available as part of the 2017 PhysioNet and Computing in Cardiology Challenge. All the traces have been acquired using AliveCor’s single-channel ECG wireless sensors, which can record short ECG signals by touching two electrodes with the fingertips. To use such device, the subject should hold one electrode in each hand, creating a single-lead equivalent ECG. Some of the ECGs were inverted, since the device does not have a preferred orientation [9].

This dataset is divided into a public set with 8, 528 ECG records and a hidden set of 3, 628 records (not publicly available and used by us only once to test our algorithm), sampled at f_s = 300 Hz with different duration (from 9 to 61 seconds). Each record has been classified using ten different algorithms and a set of at least three experts [9] into one of these four classes: normal sinus rhythm (5, 154 samples in the public dataset), AF (771 samples), other type of arrhythmias (2, 557 samples) and noisy data (46 samples).

2.2. Signal pre-processing

The ECG signal intervals are usually affected by many sources of noise (electrode contact noise, baseline drift, motion artifacts, instrumentation noise, power line and electromyography interference), and other unpredictable factors due to the subject’s position or the electrodes’ coupling. Before the feature extraction phase, they need to be pre-processed to improve the performance of the classifier.

First, a high-pass filter based on wavelet transformation is used to reduce the baseline wander, a low frequency artifact present in most ECG traces, which can be the result of movement and breathing. Wavelet-based filters have been proved to excel in the preservation of the signal’s morphological traits [10]. In detail, the acquired ECG signal is decomposed using a discrete wavelet transform (DWT) at a predefined decomposition level L. Then, the approximation coefficients associated with the last level L (corresponding to the lowest frequency) are set to zero, and the inverse DWT is used to obtain the filtered signal. L corresponds to a cut-off frequency f_c, obtained as

$$L={\text{log}}_2\left(f_s/f_c\right)-1,$$ (1)

where f_s is the sampling frequency. The frequency of the baseline wander for ECG signals is usually between 0.1 Hz (in the absence of movement) and 0.65 Hz (during a stress test) [11]. In this study, we consider f_c = 0.3 Hz, which leads to L = 9 for f_s = 300 Hz. The wavelet used is Daubechies 9.

Amplitude normalization typically consists of a linear rescaling leading to unbiased unit norm signals. Since this normalization is independently applied to each trace, we refer to it as element-wise normalization, to distinguish it from the batch normalization used in the DL architectures. To analyze the effect of the normalization on the classification performance, we also tested the DL models without including this process.

Finally, all the considered DL architectures are optimized for a fixed size input. If the ECG signal happens to be longer, a 30 seconds interval is randomly selected from it and used as input for the trained classifiers.

2.3. Feature extraction: feature engineering approach

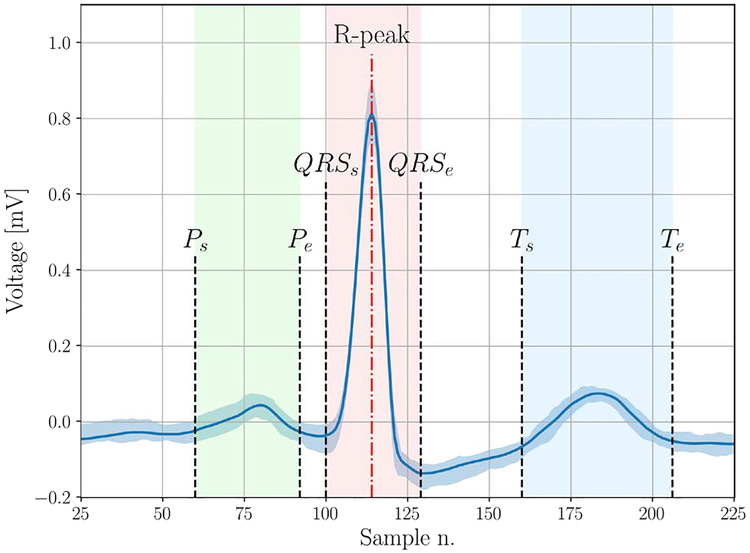
In this section, we detail the process to extract expert features from the ECG signal. During this process, we develop automatic algorithms with the aim to mimic a human expert trying to manually classify the ECG traces. A first group of features is related to the heart-rate analysis. This category includes some statistical metrics, such as the average, variability and entropy, obtained by analyzing the sequence of RR intervals, i.e., the time between two consecutive R peaks. Although of primary importance, the sole use of RR interval features is not sufficient for a comprehensive characterization of the ECG signal. Further processing is required to extract more precise timing information. To cope with the noise present in ECG recordings, a classical approach consists in using the wavelet transform and analyzing the signal in the time-frequency domain. We verified that carrying out a wavelet-based analysis on the raw signal sometimes produces inaccurate localization of the points of interest (start and end points of ECG waves). Thus, we adopted the signal averaged ECG approach (SAECG), a denoising method that has already shown its effectiveness in ECG signal processing [12]. Briefly, given an ECG signal x with N samples, we split the ECG trace $x=[x(1),\dots ,x(N)]\in {ℝ}^N$ into R intervals, where each interval contains a single QRS complex. Hence, the intervals are aligned (based on the location of the R peaks) and averaged to obtain a single characteristic ECG shape s. Following this, we implemented a wavelet-based ECG delineator to identify the start and end of the P-wave, the T-wave and the QRS complex (see Fig. 1).

Fig. 1.

SAECG example where the points extracted by the ECG delineator are indicated in the figure and the vertical shaded area represents the interquartile range of the aligned beats.

At the end of this phase an accurate estimation of informative intervals can be performed, including the PR, QRS, QT and ST segments, and also the amplitude of the P and T waves. The main issue with the evaluation of the SAECG is the loss of information on the inter-beat morphology variability, which represents an important factor to consider for arrhythmia detection. To overcome this limitation, the amplitude dispersion index (ADI) [13] has been also estimated during the evaluation of the SAECG, both for the P-wave and the T-wave.

Finally, a 2-layer multilayer perceptron (MLP) classifier has been trained using the above expert features to classify the ECG traces into the four classes: normal rhythm, AF, other arrhythmias and noise. In Sec. 4, the expert feature performance is compared against that of DL architectures.

2.4. Feature extraction: representation learning approach

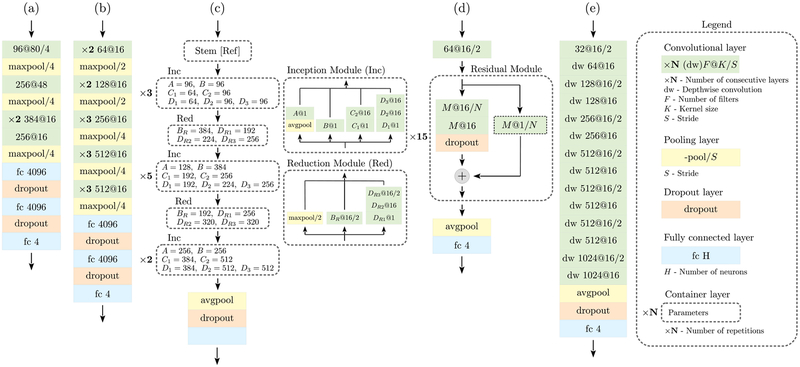
One of the main purposes of this study is to analyze the benefits and disadvantages of modern RL approaches when applied to 1D signals. In the following, we delve into the proposed architectures, whose details are shown in Fig. 2.

Fig. 2.

Network schemes for all the considered architectures. The notation used is detailed in the legend on the right.

(a) The architecture in Fig. 2-(a) was the first convolutional network to be successfully trained on a very large dataset (several millions of images) for the classification of a thousand different classes [14]. It consists of five convolutional layers, followed by two fully-connected ones, where the non-linear activation functions at the output of each layer are ReLU. Max-pooling is used as a dimensionality reduction method and to increase the spatial invariance of features. Dropout is applied at the output of the fully-connected layers during training as regularization technique. Typical implementations use 11×11, 5×5 and 3×3 convolution kernels, which have been respectively replaced by 1×80, 1×48 and 1×16 kernels in our mono-dimensional version. After an exploratory phase, we found that a 1D kernel of size 1×16 is a good compromise between number of parameters and computational power, and we adopt it to replace the bi-dimensional 3×3 kernel used in the vast majority of implementations. In Fig. 2-(a), we observe that the convolutional kernel size K decreases layer after layer. At the same time, the number of filters increases, and the data dimensionality is consistently reduced to obtain a more abstract and compact representation of the data after each layer.

(b) The architecture in Fig. 2-(b) increases the depth of the network while keeping the same basic structure of the previous model. In our implementation, we consider a total of 13 convolutional layers with constant kernel size K. It has been shown that stacking several smaller convolutions the receptive field considerably increases with the depth, leading to better performance than with a single large convolution [15]. The drawback is a significant increase in complexity (i.e., in the number of network parameters, the weights), with a higher risk of overfitting. Substantial dimensionality reduction is performed using max pooling.

(c) The architecture in Fig. 2-(c) is designed to deal with two of the issues encountered with deeper networks. (I1) Overfitting, due to the increased number of parameters. (I2) Sparsification, since the training of large convolutions can led to sparse parameter matrices, making the computation inefficient. It has been observed that part of these computations may not be required. The Inception network is an attempt to approximate sparse convolutions through more efficient and dense blocks. In particular, the computation is split into different parts, each one with its specific purpose. In our implementation, we consider four parallel branches for each layer, the outputs of which are concatenated to form the input of the next layer, as detailed in Fig. 2. A key task is performed by 1×1 convolutions, which are used to efficiently map the local relations among the filters onto a reduced space. This procedure can be intuitively represented as a compression, and the key point is to approximate sparse operations in the original space with dense operations in the compressed space. Each of the four branches performs a different computation. In the inception module (Inc), the network entails an average pooling to increase the spatial invariance, a pure 1×1 convolution, a single and a two-layer convolution to process local correlations. Even though a 1×1 convolution is used in each branch, it is worth noting that, after the final concatenation, the input and output dimensionality are exactly matched, having chosen appropriately the parameters of the inception module. The dimensionality reduction task is indeed carried out by a separate reduction module, which reduces the input dimension while increasing the number of filters, following the typical behavior of a deep network. Our implementation is based on [16]. Finally, an average pooling along the feature maps before the last classification block is included.

(d) The architecture in Fig. 2-(d) is designed to address the following issues of very deep models: (I1) The gradient becames exponentially small with the network (backpropagation) depth, preventing the parameters to be effectively updated (vanishing gradients). (I2) The model has too many parameters, so the network becomes harder to train, leading to sub-optimal results or lack of convergence (degradation problem). Residual layers have been introduced to mitigate these problems by adding an identity mapping on each layer. In this way, instead of learning the direct relation between input and output, these modules learn the residual representation, hence the name. If a layer, for any reason, is not able to be effectively trained, the identity mapping allows for the propagation of the previously processed information, making it possible to optimize extremely deep architectures without suffering from the degradation problem. Furthermore, these modules also address the issue of vanishing gradients. The presence of shortcut connections allows the gradients to easily propagate back through the network. Our implementation is inspired by [17], where the authors obtained promising results for ECG analysis.

(e) Two final issues are addressed by the architecture in Fig. 2-(e). (I1) The large number of parameters, and (I2) the high computation demand. This network exploits depthwise separable convolutions to address them [18]. For a standard convolution with F_I input channels, F_O output channels, and K kernel parameters, the total number of parameters required is F_I × F_O × K. Here, this computation is split into two steps. (S1) A depthwise convolution is applied to the input data, which performs a spatial convolution independently over each channel, entailing F_I × K weights. (S2) A pointwise convolution, i.e., a 1×1 convolution, is used to project the output into the new channel space, considering also the relations among the channels, with F_I×F_O weights. The total number of parameters is F_I(K + F_O), with a reduction in computation by a factor 1/F_O + 1/L, where L represents the dimensionality of the input feature maps [18]. As for the residual network implementation, no pooling is used between the layers; instead, a stride operation is used to reduce the dimensionality, which further decreases the computational requirements.

2.5. Training procedure

A stochastic gradient descent optimization method is used to minimize a weighted cross-entropy loss function. Given an input ECG sequence x, each classifier acts as a function mapping x into a stochastic vector y(x, w) = (y₁, y₂, …, y_C), whose j-th entry y_j(x, w) represents the estimated probability that the input x belongs to class j, with j = 1, …, C, where C is the number of classes. Since the dataset is labeled, each input example x has an associated (ground truth) class label c, which has been set as described in Sec. 2.1. The loss function for a given generic sample x of class c, is

$$f(x,c,w)={\alpha }_c\left[-\text{log}\left(\frac{e^{y_c(x,w)}}{{\sum }_j{e}^{y_j(x,w)}}\right)\right],$$ (2)

where α_c is the class weight, used to cope with imbalanced datasets and computed as the fraction of samples of class c over the total number of samples in the training set. If $\mathcal{X}$ is the set of all training examples, we define the batch set as $\mathcal{B}\subset \mathcal{X}$, with cardinality $B=\left|\mathcal{B}\right|$. The optimization method minimizes a further loss function, obtained averaging f(x, c, w) over the batch set $\mathcal{B}$, and adding a weight regularization term ∥w∥²

$$F(\mathcal{B},w)=\frac{1}{B}\sum _{(x,c)\in \mathcal{B}}f(x,c,w)+\beta \Vert w{\Vert }^2,$$ (3)

where the regularization parameter β is implemented as a weight decay during the updates. Batch normalization has been implemented after each convolution and before the ReLU activation function, as it increases the training stability and also acts as a regularizer [19].

3. PERFORMANCE MEASURES

A 5-fold cross validation approach has been used for the presented numerical results: the public dataset has been randomly split into 5 subsets, maintaining for each the original distribution between the classes. One subset is used as a test set (subset $\mathcal{T}$), while the remaining ones constitute the training and validation subsets.

Each test sample $\mathit{x}\in \mathcal{T}$ is associated with a ground truth label $c(x)\in \mathcal{C}=\left\{C_S,C_A,C_O,C_N\right\}$, corresponding to normal sinus rhythm, AF, other arrhythmias, or noise, respectively. The output of the classifier is another label $c_p(x)\in \mathcal{C}$, which represents the predicted class.

Precision and recall have been considered as the performance metrics. The precision estimates the fraction of examples correctly predicted as a specific class c_p (true positives) among all the examples predicted as c_p, and it can be interpreted as the probability that a new example with predicted class c_p, actually belongs to that class, i.e.,

$$\text{precision}(\rho )=\frac{{\sum }_{x\in \mathcal{T}}1(c(x)=\rho )\cdot 1\left(c_p(x)=\rho \right)}{{\sum }_{x\in \mathcal{T}}1\left(c_p(x)=\rho \right)},$$ (4)

where ρ ∈ {C_S, C_A, C_O, C_N }, and $1(\cdot )$ is the indicator function, with $1(Z)=1$ if Z is true, and $1(Z)=0$ otherwise.

The recall estimates the fraction of samples belonging to a specific class that are correctly classified (sensitivity). It can be seen as the probability that a new example of class c will be correctly classified. It is defined as

$$\text{recall}(\rho )=\frac{{\sum }_{x\in \mathcal{T}}1\left(c(x)=\rho \right)\cdot 1\left(c_p(x)=\rho \right)}{{\sum }_{x\in \mathcal{T}}1\left(c(x)=\rho \right)}.$$ (5)

The F1-measure combines precision and recall through an harmonic mean, providing a good way to compare different algorithms:

$$\text{F}1(\rho )=\frac{2{\sum }_{x\in \mathcal{T}}1\left(c(x)=\rho \right)\cdot 1\left(c_p(x)=\rho \right)}{{\sum }_{x\in \mathcal{T}}\left[1\left(c_p(x)=\rho \right)+1(c(x)=\rho )\right]}.$$ (6)

In order to have a global performance assessment metric, we also define a score, which is evaluated by averaging the given metric m ∈ {precision, recall, F1} among the normal sinus rhythm, AF and other arrhythmias classes, i.e.,

$$\text{score}(m)=\frac{{\sum }_{\rho \in \{\mathcal{S},\mathcal{A},\mathcal{O}\}}m(\rho )}{3}.$$ (7)

4. RESULTS AND DISCUSSION

4.1. Representation learning

In Tab. 1, we use the validation subsets to compare the performance of the classification for the five DL architectures (Sec. 2.3) and the MLP classifier with expert features (EF, Sec. 2.4). Each neural network has been trained for a total of 200 epochs, with a step-based learning rate annealing policy, starting from λ = 0.1, and reducing this value by a factor of 3 every 25 epochs. In a preliminary analysis we determined that starting with a high learning rate drives to better performance in this case. Gradient clipping has been applied to have a more stable training. By observing the precision and recall for each class, we see that the performance of the feature engineering approach is significantly lower than that of all the considered DL architectures. Focusing on the AF class, we notice a lower precision and a higher recall, corresponding to a higher misclassification rate. These findings cannot be generalized, as new expert features can be derived and added to the MLP framework, but they provide a benchmark of the advantages of DL architectures. In particular, they suggest that predefined features may not be appropriate to extract information in a realistic environment and in free-living conditions, e.g., in the presence of time-varying noise and artifacts due to the movement of the sensor. Data-driven techniques, instead, excel in such complex scenarios, where the diversity of the acquired signals could heavily affect the classification performance, being able to automatically learn the best way to fit the training data. We note that the dataset is imbalanced, and the performance of the classifiers is influenced by the amount of data available for each class, since the neural networks effectiveness is highly affected by the training data dimensionality. As expected, considering the limited data available, the learned features are not able to accurately classify noisy signals. Some improvements may be obtained using data augmentation techniques, and these improvements are left for future work.

TABLE 1.

Performance metrics for all of the presented architectures and for the expert features (EF) approach. Results are quantified in terms of precision and recall for each class, global average score, training time and number of parameters. Standard deviation is also reported.

		(a)	(b)	(c)	(d)	(e)	EF
Precision	Normal rhythm	0.873 ± 0.011	0.889 ± 0.007	0.887 ± 0.012	0.892 ± 0.005	0.879 ± 0.009	0.865 ± 0.005
	Atrial fibrillation	0.786 ± 0.032	0.808 ± 0.044	0.827 ± 0.021	0.834 ± 0.017	0.849 ± 0.027	0.672 ± 0.033
	Other arrhythmias	0.744 ± 0.013	0.747 ± 0.007	0.789 ± 0.031	0.757 ± 0.012	0.787 ± 0.014	0.617 ± 0.012
	Noisy traces	0.685 ± 0.046	0.650 ± 0.068	0.643 ± 0.066	0.721 ± 0.084	0.722 ± 0.094	0.679 ± 0.087
Recall	Normal rhythm	0.907 ± 0.005	0.903 ± 0.007	0.921 ± 0.015	0.910 ± 0.007	0.928 ± 0.008	0.826 ± 0.010
	Atrial fibrillation	0.739 ± 0.036	0.767 ± 0.052	0.802 ± 0.046	0.780 ± 0.017	0.788 ± 0.038	0.831 ± 0.031
	Other arrhythmias	0.701 ± 0.026	0.739 ± 0.011	0.733 ± 0.040	0.761 ± 0.013	0.735 ± 0.020	0.640 ± 0.018
	Noisy traces	0.636 ± 0.048	0.622 ± 0.063	0.613 ± 0.080	0.529 ± 0.055	0.520 ± 0.064	0.556 ± 0.044
Score		0.791 ± 0.014	0.808 ± 0.012	0.825 ± 0.009	0.822 ± 0.009	0.827 ± 0.008	0.739 ± 0.013
Training Time [s]		35.1 ± 3.3	93.3 ± 12.5	227.8 ± 28.8	97.3 ± 32.4	58.4 ± 14.1	-
Num. of parameters [Millions]		60	116	54	43	4	-

By analyzing the score values, we also observe that the classification performance increases using deeper architectures, as noticed by comparing network (a) and (b), or with more advanced structures, like (c) and (d), with the inclusion of inception modules and residual connections. On the downside, deeper architectures entail a higher number of parameters and an increase in computational complexity. A remarkable result is achieved by depth-wise separable convolutions in network (e), which performs on par with more complex architectures in terms of accuracy, while leading to substantial reductions in training time and number of parameters, as shown in Tab. 1.

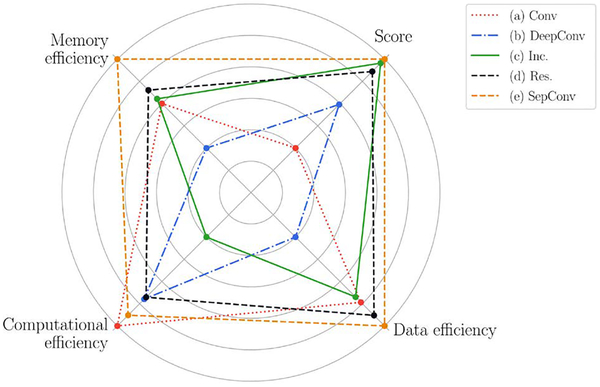
The effectiveness of each architecture in extracting relevant information from the underlying data, here defined as data efficiency, is also an important factor to take into account. It can be quantified by analyzing the amount of data required to converge to the optimal performance (not affected by training time). This information, along with the classification performance (score), memory efficiency (number of parameters) and computational efficiency (training time), is summarized in Fig. 3 for each of the five DL techniques. The results are normalized such that for each dimension the worst technique has a point in the inner circle, while the best one has a point in the outer circle. This provides a useful overview for analyzing the effect of the techniques used in the considered architectures. First, we notice that network (a), composed by just a few convolutional layers, has the lowest computational complexity, but it does not perform well along the other dimensions. The deeper version (b) allows for a slightly better classification performance, but at the expense of a serious degradation of data, memory and computational efficiency. Hence, the simple stacking of convolutional layers, without any adjustment, is not generally recommended. The use of inception modules in network (c) brings a great benefit to all the considered metrics, except for the computational requirement, mainly due to their complex structure. This network has the capability to learn very complex representation of data, but this is sometimes unnecessary, especially for 1D signal analysis, as in this case study. The residual connections of network (d) effectively mitigate the vanishing gradients and the degradation problem discussed in Sec. 2.4-d, without any evident downside. They should be considered in most of the modern RL implementations. The great performance of network (e) demonstrates the effectiveness of depthwise separable convolution to approximate the full convolutional operation, which generally leads to inefficient (sparse) parameter matrices. Although this result cannot be generalized, it frequently occurs, in particular when the data dynamics are not very complex and for low data availability. To prove the reliability of the presented results, an additional test has been carried out using the hidden test set, not publicly available and not included in the public dataset (see Sec. 2.1). According to the discussed results, we have chosen the network (e) as the representative DL architecture, which has been trained following the same guidelines described in Sec. 2, but considering a higher number of epochs (2, 000), and with a more relaxed learning rate annealing (halved every 150 epochs). Our algorithm achieves a score(F1) = 0.80 (defined in Sec. 3). State-of-the-art results, which entail the combined analysis of clinical and RL based features or very specific domain knowledge [20], can achieve a score of 0.83, very close to our implementation. Although the performance of the presented method may be further improved, this would require a tuning targeted to the specific case study and more time consuming optimization methods, leading to less general results. These problem-dependent and highly specialized optimizations are not deemed interesting in view of understanding pros and cons of DL and feature engineering techniques, which is the main scope of this paper.

Fig. 3.

Overall graphical comparison among the DL architectures.

4.2. Deep network vs expert features

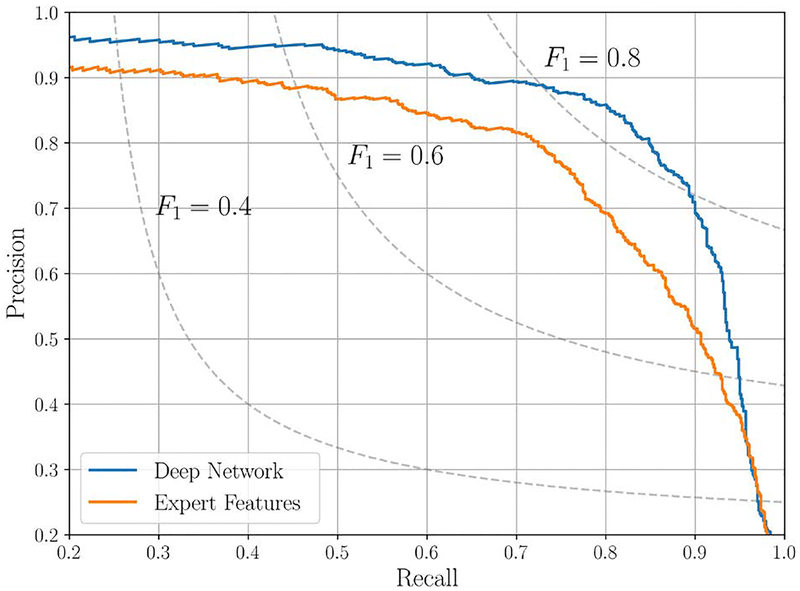
In this analysis, a cross-validation is used to perform the test on all the samples in the dataset, leading to a greater reliability of the results, while keeping a strict separation between training and testing samples. Focusing on the AF detection problem, in this section we reduce the problem to a binary classification task, where the goal is to determine whether the input ECG signal x presents AF or not. Under this assumption, each sample in the testing set is classified as AF if the corresponding estimated probability is greater than a threshold τ. By varying τ, we can measure distinct value pairs for precision and recall. This procedure generates a curve in a precision-recall plane (PRC), shown in Fig. 4 for both the representative RL model and the expert features based classifier, making it possible to choose an operational point for the classifiers. The benefits of data-driven RL are clear, as it achieves a higher precision for any value of the recall. These kind of results are characteristic for signals acquired in free-living conditions or noisy environments, where expert based algorithms may be unreliable. On the contrary, a data-driven approach excels under these conditions, proving to be a robust data processing approach. Nevertheless, a significant downside associated to most of the RL methods is related to the human interpretability of the results (which morphological features in the signal were triggering the decision). This is fundamental for the proper integration of these technique into clinical practice, allowing clinicians to interpret the outcome of the DL algorithm and subsequently inform the individual [21].

Fig. 4.

Precision-recall curve (aFib class) for the final deep network implementation and the expert feature approach. The isocurves for some levels of F1-measure are also shown for increased readability.

In this scenario, however, the usability of learning approaches can still be very valuable. First, RL methods can be used to improve the accuracy and reliability of clinically accepted features, especially in noisy environment (e.g. for continuous monitoring in free-living conditions). Moreover, transfer learning techniques can be used to leverage both AI and a more classical approach for improved results, thereby allowing the coexistence of interpretable clinical knowledge along with RL based features. For example, this can be achieved by injecting manually engineered features in one of the last layers of a RL architecture, typically in a later stage of the conventional RL training. This remains an open point at the center of current research.

5. CONCLUSIONS

In this study, we perform a comprehensive analysis of the benefits and downsides of several representation learning (RL) techniques of varying degrees of complexity, focusing on modern deep learning (DL) architectures applied to biomedical signals. The obtained results show how the design of the network architecture may considerably affect the classification performance in terms of accuracy, memory/data efficiency and computational complexity. Of particular interest is the mitigation of the vanishing gradients and degradation problems by residual connections, and the high efficiency of depthwise separable convolutions, which overcome the sparsification issue of classic DL implementations. As a case study, the detection of atrial fibrillation from short and noisy ECG traces is considered. We show that an approach purely based on representation learning outperforms classifiers based on expert features, which require specific domain knowledge. This underlines the great capability of RL to learn meaningful representations of data without requiring human expertise. This is an encouraging result especially for the analysis of less investigated physiological signals, for which a limited number of expert based features have been recognized. The presented RL methods are particularly appealing for screening purposes, where a large amount of complex data is acquired by large populations of subjects over extended periods of time, typically entailing noisy and unsupervised measures from wearables in free living conditions. The use of RL is not meant to replace the more deterministic approach based on manual feature extraction, which remains of primary importance to facilitate the human interpretation of the results, but provides a significant support for improving modern decision making processes. The increasing availability of large datasets, and the possibility of automatic labeling when the wearable is worn together with a clinical sensor, will allow the validation of these techniques for a future use inside and outside the clinic.