Handheld Adaptive Optics Scanning Laser Ophthalmoscope

Abstract

Adaptive optics scanning laser ophthalmoscopy (AOSLO) has enabled in vivo visualization and enhanced understanding of retinal structure and function. Current generation AOSLOs have a large footprint and are mainly limited to imaging cooperative adult subjects. To extend the application of AOSLO to new patient populations, we have designed the first portable handheld AOSLO (HAOSLO) system. By incorporating a novel computational wavefront sensorless AO algorithm and custom optics, we have miniaturized our HAOSLO to weigh less than 200 grams. HAOSLO imaged the cones closest to the fovea with a handheld probe in adults and captured the first AO-enhanced image of cones in infants.

1. INTRODUCTION

The utilization of adaptive optics (AO) to reduce the effect of aberrations in ophthalmic imaging systems has enabled in vivo visualization of retinal neurons [1–4] and has revolutionized the understanding of the structure, function, and neurophysiology of the visual system [5, 6]. In traditional AO ophthalmic imaging, a wavefront sensor detects and a deformable mirror (DM) compensates for the aberrations of the eye. The AO scanning light ophthalmoscope (AOSLO) is the most common imaging system for in vivo visualization of individual photoreceptor cells in adults [7, 8]. AOSLO’s ability to image and count individual cells presents the potential for improvements in the diagnosis and prognosis of retinal diseases and a new benchmark to measure the efficacy of therapies [9]. Among a multitude of applications, the utility of AOSLO has been demonstrated for a number of retinal diseases including Stargardt disease [10], retinitis pigmentosa [11], congenital achromatopsia [12], diabetic retinopathy [13, 14], age-related macular degeneration [15], and acute macular neuroretinopathy [16].

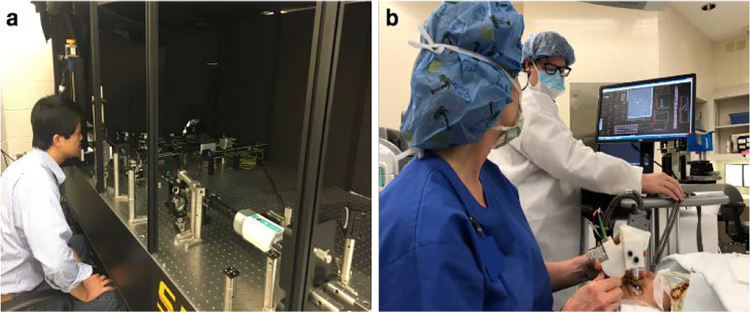
At present, the size and complexity of AOSLO systems limit imaging to patients that are able to sit in an upright position and fixate for several minutes, as shown in Fig. 1(a). Portable handheld AO systems would be useful in acquiring high-resolution images of photoreceptors in adults and children that are supine, under anesthesia, semi-recumbent, or otherwise unable to maintain the required posture, as shown in Fig. 1(b). Unfortunately, integrating wavefront sensing and correcting AO components into SLO results in systems too large and heavy for handheld use. As a compromise, handheld SLO (without AO) was first demonstrated by Kelly et al. [17] and was found to be helpful in imaging children with nystagmus, photophobia, eccentric fixation, cone dystrophy, and mild papilledema. However, due to low resolution, this system was unable to visualize individual photoreceptors. Previously, we demonstrated the first combined SLO and optical coherence tomography (OCT) handheld probes, capable of resolving parafoveal cones without AO within approximately 4° of the fovea [18–20].

Figure 1.

(a) Photograph of an adult subject being imaged by a typical large-footprint AOSLO imaging system. (b) Photograph of an infant patient being imaged by our HAOSLO probe prior to retinal surgery.

A key technology for reducing the footprint and weight of AO-based imagers is the wavefront sensorless (WS) AO technique. WS-AO utilizes iterative and multi-shot computational techniques to estimate the wavefront, eliminating the need for a physical wavefront sensor. Broadly, WS-AO algorithms can be classified into two categories: model-free and model-based. In the model-free approach, the state space of the adaptive element is searched to find the optimum configuration using one or some combination of image quality metrics [21–27]. In the model-based approach, a priori knowledge of the optimized function is used to design an algorithm that exhibits superior convergence [28–30]. WS-AO techniques have been applied to laser systems [31, 32], fiber coupling [33], quantum optics [34], optical tweezers [35], and microscopy [27, 36–42]. WS-AO was first applied to SLO by Hofer et al. to visualize individual cone photoreceptors [43]. Later, WS-AO was applied to enhance the resolution of other ophthalmic imaging technologies, including OCT [44–47].

In this paper, we describe the design and implementation of the first handheld adaptive optics scanning laser ophthalmoscope (HAOSLO). To overcome the weight and size restrictions in integrating AOSLO into handheld form, we used recent advancements in the miniaturization of DM technology and 2D microelectromechanical systems (MEMS) scanning together with a novel, fast WS-AO algorithm and a custom optical and mechanical design. The low weight and small form factor rendered the AOSLO probe suitable for handheld operation, and the fast WS-AO algorithm made HAOSLO well suited for clinical use. We exhibit the utility of this new tool by imaging supine adult patients in the laboratory and young children in a clinical setting. Our probe design and computational algorithms, directly or with minor alteration, are expected to be useful for a variety of applications in ophthalmic imaging of adults, infants, and animal models. Thus, we have made our optical and mechanical designs and computational algorithms open source.

2. METHODS

The HAOSLO probe was designed to meet the following performance specifications: 1) provide AO-corrected SLO images of the retina, 2) span a ≥ 1° field-of-view (FOV) with diffraction-limited resolution at an entrance pupil size achievable by a majority of the infant and adult population under pharmacological dilation, 3) operate at a minimum of 6 frames per second (fps) at a Nyquist sampling rate or higher, 4) have a working distance of approximately 15 mm from the eye, and 5) weigh less than 200 grams with a minimal device form factor. The following subsections describe how we addressed these goals through the optical and mechanical design of the HAOSLO engine and the handheld probe.

A. System Design

The HAOSLO light source was a superluminescent diode (SLD) operating at 774 ± 5 nm (Inphenix, Livermore, CA). A variable optical attenuator (VOA780PM-APC, Thorlabs, Newton, NJ) was used to control the system output power. Polarization-maintaining single mode fiber (PM630-HP, Thorlabs, Newton, NJ) was used to deliver the illumination to the probe, and multimode fiber (M14L02. Thorlabs, Newton, NJ) was used to collect backscattered light from the sample. Polarization optics were used to separate optical pathways for illumination and collection. The detector for the SLO was an avalanche photodiode (APD) (C12703, Hamamatsu, Shizuoka-ken, Japan) with adjustable gain set to 30× and digitized at 5 MS/s using the NI PCI 6115 card (12-bit) (National Instruments, Austin, TX). The SLO signal was low-pass filtered with a cutoff frequency of 2.5 MHz (half the sampling frequency) to avoid aliasing artifacts in the SLO image. The hardware components were controlled using LabVIEW (National Instruments, Austin, TX) software.

B. Optical Design

The system schematic and optical design of the HAOSLO probe are shown in Fig. 2. The optics were optimized in Zemax optical design software (Radiant ZEMAX, Redmond, WA) using an eye model with a gradient index lens [48]. The eye model was modified as described in [19] with glass types adjusted to match human ocular dispersion [49]. A gimbal-less two-axis scanning MEMS micromirror (13L2.3, Mirrorcle Technologies, Richmond, CA) with a 4.2 mm diameter mirror was used to control the position of the beam on the subject’s eye. The vertical or fast axis operated at 1.7 kHz, and the forward sweep of the scanner was utilized for imaging. During the backward sweep of the scanner, the laser was turned off to minimize light exposure. The horizontal or slow scanner of the SLO operated at a rate of 6.8 Hz to record frames at 6.8 fps. Each image of the SLO consisted of 250 × 1464 pixels. A compact DM (DM69, ALPAO, Rue Lavoisier, France) with 69 actuators, a 10.5 mm pupil diameter, a 1.5 mm pitch, and a settling time of 800 μs was used as the adaptive element to correct for wavefront distortions.

Figure 2.

HAOSLO probe system schematic and optical design: red and blue rays depict the illumination and collection paths, respectively. APD: avalanche photodiode, DM: deformable mirror, FM: fold mirror, L1–10: lenses, LP: linear polarizer, MMF: multimode fiber, PBS: polarizing beam splitter, PM: polarization-maintaining, QWP: quarter wave plate, SLD: superluminescent diode, SMF: single mode fiber, and VOA: variable optical attenuator.

We designed custom optical elements to minimize the size of the probe. During the optical design process the SLD source was found to be sufficiently broadband to warrant utilization of achromatic lenses. In total, we designed nine custom achromatic lenses with a consideration for manufacturability by using test plates and common Ohara (Ohara Corp., Branchburg, NJ) glasses available at Optimax (Optimax Systems Inc., Ontario, NY). We performed a tolerance stack analysis to ensure that the optical design was sufficiently resilient to meet the specifications given the tolerances of our optomechanics (see section 2.C). Prescription data for all custom lenses in the system is shown in Table I.

Table I.

Diameter and effective focal length (EFL) of all custom lenses in the HAOSLO probe.

Lens	Diameter (mm)	EFL (mm)
L1	10.00	20.0
L2	6.35	11.0
L3	6.35	46.1
L4	12.70	40.8
L5	12.70	41.2
L6	12.00	95.2
L7	12.00	30.0
L8	10.00	−56.2
L9	10.00	16.4

The light from the illumination fiber input was collimated with lens L1, producing a Gaussian beam with a 1/e² diameter of 3.84 mm. Mechanical constraints of the MEMS scanner limited the beam size at the scanner to 3.3 mm. To improve the resolution of the system given this limited aperture, a 3.3 mm iris was used to truncate the Gaussian beam prior to the MEMS scanner such that the transmittance of the iris was 0.77. Simulations in MATLAB indicated that this truncation factor enabled a resolution improvement of ~15% relative to the use of a narrower Gaussian beam with 99% iris transmittance.

The selection of the entrance beam diameter at the eye was driven by two conflicting motives. A larger entrance beam diameter corresponds to an improvement in resolution but comes at the cost of reduced throughput for patients with smaller dilated pupils such as young children and the elderly. To balance this tradeoff, we performed a meta-analysis of pharmacologically dilated pupil diameter in patients ranging in age from 2 days to 70 years using references [50–55] to determine the optimum entrance beam diameter. We selected a 6.11 mm entrance beam diameter, corresponding to a transmittance of >0.87 in 95% of the newborn population and a transmittance near unity in >90% of the age 50+ population.

Polarization gating was used to mitigate the effect of back-reflections at the lens surfaces and to maximize collection efficiency. The collimated laser output traverses a linear polarizer followed by a polarizing beam splitter (PBS). Before entering the eye, the light traverses a quarter wave plate (QWP) oriented at 45° with respect to the input linear polarization state so that the eye is illuminated with circularly polarized light. The backscattered light from the retina traverses the QWP again, resulting in a linear polarization state that is perpendicular to the initial linear polarization state (neglecting birefringence and depolarization of the eye). The backscattered light is then reflected by the PBS and coupled into a multimode collection fiber by a commercial lens (45–786, Edmund Optics, Barrington, NJ). The effective focal length of the collection lens (20 mm) and multimode fiber core diameter (25 μm) produced an effective pinhole size that was 2.18 times the Airy disk diameter.

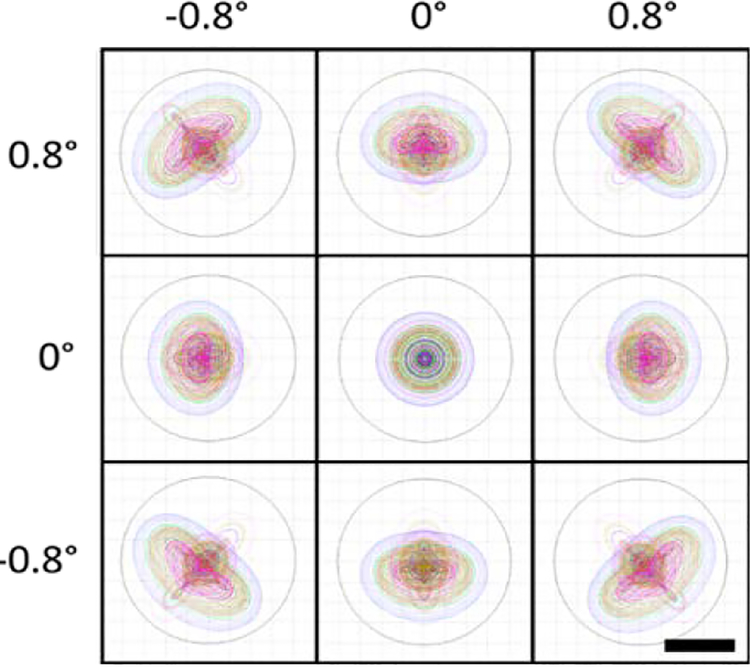
The optical design performance of the HAOSLO system is shown in Fig. 3. The system has a working distance of 15.0 mm (corneal apex to QWP surface). Our optical design achieved diffraction-limited performance over a square FOV of 1.6° × 1.6°, giving a predicted full-width-at-half-maximum (FWHM) spot size diameter of 2.3 μm in the adult eye.

Figure 3.

Spot diagrams for the HAOSLO probe on the retina spanning a 1.6 × 1.6° FOV. HAOSLO is diffraction-limited at 2.3 μm (spot FWHM). Spot diagrams are color coded by wavelength across the source bandwidth. Airy disks are shown by black circles. Scale bar, 2 μm.

C. Mechanical Design

The optical design for the probe was used to specify component locations in the mechanical design. The mechanical design for the system was developed in Solidworks (Dassault Systèmes, Solidworks Corp., Waltham, MA) and is shown with and without the outer casing in Fig. 4. Custom lens tubes and spacers were designed and fabricated to accommodate the closely spaced optics of the system and to maintain a small footprint. The internal skeleton and other structural components were made of aluminum to simplify fabrication and to maintain a low weight. The use of undersized dowel pins along with a tightly toleranced skeleton provided accurate component positioning, while the use of tangential and toroidal interfaces at lens surfaces minimized stress-induced aberration of the optical wavefront.

Figure 4.

(a-b) Renderings of the handheld probe’s optomechanical design. Dimensions: 10.3 × 5.3 × 14.4 cm. (a) Left cross-section of the probe’s internal skeleton. (b) Isometric view of the probe’s internal skeleton. (c) Photograph of the fabricated probe in hand.

We performed a mechanical tolerance stack analysis to ensure that the optical design constraints were satisfied given the specified fabrication tolerances. The enclosure was 3D printed (Objet350 Connex, Stratasys, Edina, MN) from a rigid opaque photopolymer (VeroWhitePlus RGD835, Stratasys, Edina, MN) and consisted of two halves that were joined during assembly and fastened by plastic flat head screws and corresponding tapped holes. The enclosure was mated to the skeleton of the probe with two socket head cap screws. Tightly fit shoulders on the inside of the enclosure prevented movement of the enclosure with respect to the skeleton. Fig. 4(c) shows a photograph of the fabricated probe and enclosure in handheld operation. The handheld probe, without the DM cables, weighed 199 g and was 10.3 cm long × 5.3 cm wide × 14.4 cm tall.

D. Wavefront Sensorless Control

In practical use, a handheld probe has the potential for substantial motion relative to the subject’s pupil. This motion changes which part of the eye’s optics the probe’s light passes through, necessitating a change in DM shape to maintain diffraction-limited performance. While wavefront sensor-based AO control can result in high-speed correction[1], a sensorless approach was utilized to minimize weight and optomechanical complexity and thus facilitate handheld operation. Existing WS-AO algorithms assume a static optimal DM shape [43, 45] and thus are unsuitable for handheld probes. Therefore, we developed a novel stochastic Zernike gradient descent (SZGD) algorithm based on the stochastic parallel gradient descent (SPGD) method [43]. In SZGD, the DM is primarily perturbed with a randomly selected low-order Zernike mode and only occasionally with a random shape as in reference [43], while maximizing the average intensity of the collected image. A flow chart of the algorithm is shown in Fig. 5. The relative frequencies with which each mode was chosen are shown in Table II.

Figure 5.

Flow diagram of the SZGD algorithm. First, images are 5× subsampled to increase the algorithm’s iteration speed. Next, the perturbing shape δ is determined by randomly selecting one of 8 Zernike modes or a uniformly random shape in the actuator basis. All subsequent steps follow the SPGD technique laid out previously in reference [43]. Prior to ending the optimization, the subsampling is removed and the image acquisition speed is restored to its pre-optimization state.

Table II.

Modal perturbation frequencies (MPFs) of the SZGD algorithm for 4.8 mm and 6.0 mm input beam sizes in percent.

Mode	MPF, 4.8 mm (%)	MPF, 6.0 mm (%)
Defocus	50	20
Vertical Astigmatism	10	15
Oblique Astigmatism	10	15
Horizontal Coma	5	5
Vertical Coma	5	5
Vertical Trefoil	5	5
Oblique Trefoil	5	5
Primary Spherical	0	20
Random Shape	10	10

The novelty of this algorithm comes from stochastically iterating over Zernike modes, rather than using a naïve basis [43] or a deterministic iteration [45]. Because the aberrations of the eye are concentrated in the low-order Zernike modes [47], a modal perturbation should correct more of the residual wavefront error than a random perturbation. The stochastic nature of the algorithm allows for dynamic correction, which is necessary to correct for hand motion.

Additionally, we subsampled our FOV by a factor of 5 to improve the iteration speed of the algorithm, which increased the algorithm’s iteration rate from 3.4 Hz to 17 Hz. The algorithm’s iteration rate is half the frame rate of the imaging system because two images need to be acquired for each iteration of the algorithm. The optimization procedure was manually terminated after no observable improvement of the image metric occurred for 20 seconds while imaging adults and 5 seconds while imaging children. Finally, the intensity was optimized over a user-selectable region. For clinical imaging, we selected the central 1° × 1° region of the FOV as a conservative estimation of the isoplanatic patch size [56].

E. Model Eye Imaging Experiment Setup

We evaluated the speed and correction quality of the SZGD algorithm in comparison with an algorithm optimizing only defocus and the SPGD algorithm [43]. In both tests, a model eye consisting of a 75 mm EFL achromatic lens and a diffuse imaging target were first coupled to the system. The system was then allowed to converge using the SPGD method with small perturbations (RMS actuator voltage, 1.2 mV) for five minutes to correct for any inherent system aberrations. The small perturbations enable highly accurate correction at the expense of slow convergence. When assessing the SPGD algorithm, we used larger perturbations (RMS actuator voltage, 5.8 mV) to produce practical convergence times required in clinical imaging. The DM state was saved and considered the base shape. Then, a 1 D spherical trial lens and a 1 D cylindrical trial lens were placed in the model eye path.

For the evaluation of algorithm speed, we measured the mean intensity of the image while each algorithm converged. After convergence, the system was reset to the base shape to test a different algorithm with the same initial condition. For the evaluation of algorithm correction quality, we allowed each algorithm to converge on the diffuse target for five minutes before replacing the diffuse target with a reflective USAF 1951 test chart. The test chart’s angle was adjusted to produce maximum intensity, then 14–35 high resolution frames of the test chart were recorded with 3x oversampling. The diffuse target was then replaced, the DM was reset to the base shape, and the test was repeated for the next algorithm.

F. Human Imaging Experiment Setup and Implementation Details

The system was used to image the retina of seven healthy, undilated adult volunteers, five healthy, dilated adult volunteers, and two young children under anesthesia. Dilation was performed by administration of a solution of 0.5% tropicamide and 5% phenylephrine in adults and a solution of 1% cyclopentolate and 2.5% phenylephrine in children. The use of the experimental setup for in vivo measurements in humans was approved by the Duke University Health System Institutional Review Board and adhered to the tenets of the Declaration of Helsinki. Informed consent was obtained from each subject or guardian. Our protocols allotted up to an hour of imaging on healthy adults and 15 minutes of imaging on young children during examination under anesthesia.

Before each human imaging session, the linear polarizer was rotated to maximize throughput in the illumination channel, and the quarter wave plate was rotated to minimize the lens reflections. Then, the VOA was adjusted to keep the optical power of the probe below the safety limits as measured by a calibrated power meter. The optical power incident on the subject cornea was 0.54 mW or less, which is within the most conservative limits of the ANSI Z136.1 standard [57] for the 774 ± 5 nm source used.

When imaging non-dilated subjects, we reduced the HAOSLO output pupil diameter from 6.11 mm to 4.6 mm by replacing the 3.3 mm iris prior to the MEMS scanner with a 2.5 mm iris. This was done to reliably obtain optimized images without the confounding effects of pupil vignetting on the optimization procedure. The smaller output pupil diameter worsened the theoretical diffraction-limited FWHM resolution from 2.3 to 3.0 μm.

All subjects were imaged with the maximum FOV from HAOSLO, which was 1.4° × 4.0°, at a frame rate of 6.8 Hz and image dimensions of 250 × 1464 pixels. Although this entire FOV is not expected to have diffraction limited performance, the suboptimally aberration-corrected regions were still useful for registration and landmark identification. Additionally, the ability to only use a subregion of the image for WS-AO optimization (see Section 2.D) mitigates possible deleterious effects of anisoplanaticism on the WS-AO algorithm’s performance. Due to a combination of MEMS scanner deformation, intrinsic aberrations of the system, and anisoplanaticism of the eye [56, 58–60], the central region of the FOV up to 1.4° × 1.4° was expected to be best corrected for aberrations. Thus, all zoomed insets visualizing photoreceptors were acquired from this region. All images were dewarped by the method described in reference [18]. HAOSLO images were motion-corrected using StackReg plugin of the ImageJ image processing program (National Institutes of Health, Bethesda, MD) [61].

G. Reproducible Research

We have made the Zemax optical design, Solidworks mechanical design, and LabView software, controlling the hardware, which includes our novel SZGD algorithm, open source and freely available online at http://people.duke.edu/~sf59/HAOSLO.htm.

3. RESULTS

A. Model Eye Imaging

We measured the convergence time of three WS-AO algorithms as described in Section 2. The recorded time courses of mean intensity for each algorithm are shown in Fig. 6(a). The convergence times and final mean intensities, given in arbitrary units (AU), were: 3.6 s and 5.31 AU, 120.6 s and 7.7 AU, and 20.6 s and 7.7 AU for defocus only, SPGD, and SZGD, respectively.

Figure 6.

Quantitative comparison of WS-AO algorithms’ speed and correction quality on a model eye. (a) Time course of WS-AO optimization. Mean intensity across the central 1.4° × 1.4° FOV is shown as a function of iteration number when optimizing in three different optimization modes. (b) Results from imaging a USAF 1951 test target in a model eye with the HAOSLO probe. (c-e) Images obtained after inserting trial lenses and optimizing for five minutes using defocus only correction, SPGD, and SZGD, respectively. (f-i) Insets from (b-e) on Group 5 Elements 2–6. (j-m) Insets from (b-e) on the Group 3 Square with sections of the horizontal and vertical edges indicated. (n-q) and (r-u) Plots of edge-derived PSFs with Gaussian fit and calculated FWHMs indicated for horizontal and vertical directions, respectively. Error bars indicate standard deviation in intensity across the edge.

We then tested the overall aberration correction ability of the three algorithms as described in Section 2.E. An image of the USAF 1951 test chart without aberration is shown in Fig. 6(b). Images after aberration and WS-AO correction are shown in Fig. 6(c–e). Detailed views of Group 5 Elements 2–6 are shown in Fig. 6(f–i). We quantified image quality by first numerically differentiating the horizontal and vertical averaged edge profiles s of the Group 3 square indicated by the red and blue boxes in Fig. 6(j–m). Each differentiated averaged profile of the horizontal or vertical edge, respectively, represents a measurement of the corresponding point spread function (PSF). The PSFs were averaged and fit to a Gaussian function. The averaged PSFs and fits, along with calculated FWHMs, are shown in Fig. 6(n–u).

B. Human Imaging

In our first set of human experiments, we used the HAOSLO probe in handheld mode to image seven healthy, non-dilated adults positioned semi-reclined on a tilted chair. Results from three of these subjects are shown in Fig. 7. The retinal image mosaics shown in Fig. 7 (a–c) were created by merging three cropped (1.2° × 3.4°) HAOSLO frames obtained in a location superior to the fovea, which is indicated at the location of the asterisk. Subject S1 was a 24-year-old male emmetrope, subject S2 was a 29-year-old male emmetrope, and subject S3 was a 27-year-old male with −4.0 D spherical and 0.25 D cylinder refractive error. Zoomed insets from approximately 2.0° eccentricity from the fovea are shown in Fig. 7 (d–f). We also calculated the radial power spectra of two 0.25° FOV regions of the mosaic from each subject and compared the spectra to the cone spacing predicted from histological data for the corresponding eccentricities in reference [62].

Figure 7.

HAOSLO images acquired in handheld operation on three adult volunteers after natural dark adaptation using SZGD correction. (a) Retinal mosaic from subject 1 centered at a location slightly superior to the fovea. Inset (red) is located 2° from the fovea. (b) Retinal mosaic from subject 2 centered at a location slightly inferior to the fovea. Inset (green) is located 2.1° from the fovea. (c) Retinal mosaic from subject 3 centered at a location slightly inferior to the fovea. Inset (blue) is located 1.9° from the fovea. All insets have a 0.75° FOV. Scale bar, 0.25°. (d-f) 0.75° FOV excerpts from the three subjects encoded by the bounding box color. (g-l) Radial power spectra of 0.25° FOV excerpts and comparison to the average histological cone spacing predicted for the corresponding eccentricities in [58]. (g) S1 at 1.75°. (h) S1 at 2.1°. (i) S2 at 1.8°. (j) S2 at 2.5°. (k) S3 at 1.4°. (l) S3 at 1.7°.

Additionally, we imaged five pharmacologically dilated, supine adults to establish the practicality of using this probe to image a subject who cannot sit upright. An image from S2 after pharmacological dilation and while supine is shown in Fig. 8(a).

Figure 8.

HAOSLO images acquired in handheld operation on dilated, supine subjects. Scale bars, 0.25°. (a) Single cropped frame from subject S2 (emmetropic adult) at 2.1° eccentricity. (b) Single cropped frame from fellow eye of SI1 (31-month-old) during examination under anesthesia. (c) Cropped composite of 5 frames from fellow eye of SI2 (22-month-old) during examination under anesthesia.

Finally, we imaged two pharmacologically dilated young children (ages 22 and 31 mos.) under anesthesia. In Fig. 8(b), we show a single frame from the fellow eye of SI1 dilated to a 7 mm pupil, a 31-month-old emmetropic male patient with unilateral persistent fetal vasculature syndrome that included congenital cataract, aphakia, and tractional/rhegmatogenous retinal detachment. In Fig. 8(c), we show an image taken from the fellow eye of SI2 dilated to a 7 mm pupil, a 22-month-old male with unilateral Coats’ disease. The image is a composite of 5 individual registered and merged frames.

5. DISCUSSION

The WS-AO speed comparisons, shown in Fig. 6(a), demonstrate that our novel SZGD algorithm achieved the same correction quality as SPGD but in approximately 1/6th of the time. As expected, the defocus only correction converged very quickly but had a maximum mean intensity less than half that of the other two algorithms. This is most likely due to the aberration caused by the 1 D astigmatic trials lens, which the defocus only algorithm cannot correct. The SPGD [43] and SZGD algorithms both reached the same maximum mean intensity, but SZGD converged 5.9 times faster, which supports claims from prior studies on the superior convergence times of model-based optimization strategies [28–30].

The WS-AO correction quality comparisons, shown in Fig. 6(b–u), also show that SZGD provided nearly identical qualitative image correction to SPGD and corrects more than just defocus. This is indicated qualitatively by the relatively low contrast of Group 5 Elements 2–6 (Fig. 6(f–i)) in the defocus only image as compared to the SPGD- and SZGD-corrected images. Neither SPGD nor SZGD achieved the same level of contrast as the unaberrated test chart, which is likely due to the fixed perturbation magnitude of the algorithms. The fixed perturbation magnitude was chosen to provide the system with agility in the conditions of eye and hand motion; the downside to this is an inability to perfectly converge on a local minimum. SZGD has similar results to SPGD, except in SPGD the horizontal and vertical bars of Group 5 Element 6 had higher and lower contrast, respectively.

The qualitative results also demonstrate near-identical correction by SZGD and SPGD. One caveat must be noted regarding the fits, namely that the PSFs were not perfectly Gaussian. Some PSFs were broader at the base than expected and the defocus horizontal PSF demonstrates ringing. These effects were likely due to the interaction of uncorrected aberrations and the reflective test target and are only observed with the application of trial lenses. Nevertheless, the FWHM of the Gaussian fit serves as a useful comparison. Again, the defocus only correction was quite poor, especially in the horizontal direction. The differences in the PSFs of the SPGD and SZGD-corrected images were minimal despite the almost 6× faster convergence speed. Thus, SZGD based optimization is more practical for in vivo HAOSLO imaging than SPGD.

The image mosaics from the healthy adults (Fig. 7), including the zoomed inserts, show that we are successful in imaging cone photoreceptor mosaics. The radial power spectra show a clear peak in each spectrum at or near the values predicted by histological measurements of cone spacing [62], as close as 1.4° eccentric to the fovea. Without AO, the previous state-of-the-art handheld SLO was only able to quantitatively measure cone density at 3.9° eccentricity in normal adults [18]. Thus, the HAOSLO has resulted in reliable imaging of the cones closest to the fovea (apparently within or at the edge of the foveal avascular zone) ever imaged with a handheld probe.

We also observed cones in each of the supine, dilated subjects. Fig. 8(a) clearly shows the cone mosaic in subject S2 at 2.1° eccentricity, indicating that the probe is suitable for handheld operation on supine subjects. The images in Fig. 8(b–c) mark the first use of adaptive optics to image the cone photoreceptors in young children. Unfortunately, the combination of <2° FOV and limited (≤15 minutes) imaging time in the OR hampered our ability to accurately state the eccentricity at which these images were recorded. If the images were from adults, an inference could be made from histological cone spacing data, but statistically validated age-matched cone densities do not yet exist for young children. In a future design, we will integrate a wide-field camera in our handheld probe to enable knowledge and targeting of the imaging location.

Each of the several hardware and software innovations in this work, individually or together, may be useful in a range of other applications. Our probe and computational algorithms directly or with minor alterations are expected to be useful in a variety of applications for optical engineers, vision scientists, and clinicians for the study of ophthalmic disorders in adults and children, such as for the assessment of progression of hereditary retinal diseases before and after interventions such as gene therapy [59]. Although our intensity-based SZGD algorithm has worked well in the eyes of young children and healthy young adults, it has not been quantitatively evaluated in diseased eyes or the eyes of older subjects. In such eyes, scattering may necessitate incorporation of other image metrics, such as sharpness or contrast, in algorithm design[63, 64]. Additionally, we envision our probe and its design as a starting point to which many modalities may be added, including split detector AOSLO and fluorescence imaging. In addition to impact on research involving human subjects, this robust and portable HAOSLO system has the potential to be an invaluable imaging tool for researchers using large animal models such as dogs for the in vivo study of ophthalmic disorders such as retinal dystrophies [65] and other inherited macular degenerations [66]. To this end, we have made our optical and mechanical designs and computational algorithms open source.

6. CONCLUSIONS

We have demonstrated the first AO retinal imaging probe with a weight and form factor suitable for handheld operation. Our MEMS-based HAOSLO system weighing less than 200 g enables cellular level imaging near the fovea of the human retina. Optical aberrations were corrected without a wavefront sensor using our novel, fast SZGD WS-AO algorithm. Adults were imaged with the probe in handheld operation demonstrating robust imaging performance of photoreceptors near the fovea. Finally, we demonstrated successful imaging of the cone photoreceptors in dilated supine young children and adult subjects. To facilitate reproducibility of our research, we have made the optical and mechanical designs, computational algorithms, and control software for our HAOSLO system freely available online.