Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Apr 25;48(10):5726–5736. doi: 10.1021/es500548h

Multimedia Modeling of Engineered Nanoparticles with SimpleBox4nano: Model Definition and Evaluation

Johannes A J Meesters †,*, Albert A Koelmans ‡,§, Joris T K Quik ‡, A Jan Hendriks †, Dik van de Meent †
PMCID: PMC6863596  PMID: 24766433

Abstract

graphic file with name es500548h_0002.jpg

Screening level models for environmental assessment of engineered nanoparticles (ENP) are not generally available. Here, we present SimpleBox4Nano (SB4N) as the first model of this type, assess its validity, and evaluate it by comparisons with a known material flow model. SB4N expresses ENP transport and concentrations in and across air, rain, surface waters, soil, and sediment, accounting for nanospecific processes such as aggregation, attachment, and dissolution. The model solves simultaneous mass balance equations (MBE) using simple matrix algebra. The MBEs link all concentrations and transfer processes using first-order rate constants for all processes known to be relevant for ENPs. The first-order rate constants are obtained from the literature. The output of SB4N is mass concentrations of ENPs as free dispersive species, heteroaggregates with natural colloids, and larger natural particles in each compartment in time and at steady state. Known scenario studies for Switzerland were used to demonstrate the impact of the transport processes included in SB4N on the prediction of environmental concentrations. We argue that SB4N-predicted environmental concentrations are useful as background concentrations in environmental risk assessment.

Introduction

The nanotechnology industry is rapidly developing engineered nanoparticles (ENPs) that are applied in a great variety of consumer and industrial products.1 ENPs are designed to be nanoscaled (<100 nm) in at least two dimensions, so that nanospecific physicochemical properties emerge from the highly interfacial nature of the chemical material.2 This enables novel and unique applications in a wide spectrum of fields, such as electronics engineering, energy production, biomedical applications, food, agriculture, and many more.3 However, the specific properties of ENPs also raise concern about unforeseen environmental and toxicological consequences.4 There is thus a great need to evaluate the potential environmental risk of ENPs because release to the environment is considered to be inevitable.5

Current environmental risk management policies on chemical substances (e.g., the European Union’s chemical regulation REACH: Registration Evaluation Authorization and Restriction of Chemicals) have been designed for use with so-called “conventional” chemicals, i.e., chemical substances in atomic/ionic or molecular forms, dissolved in water or in the gas phase. However, regulatory procedures urgently need adjustment to become fit for application to the new nanochemicals that generally occur in solid forms, like micro- or nanocolloids.6 Making such adjustments is challenging because of the fundamental differences in transport- and transformation mechanisms between colloids and solutions.6−8 A major difficulty in making models for “conventional” chemicals fit for (nano)colloids is that hardly any field data are available to test the validity of nanoadjusted models.8,9 The adjustment is also an urgent task, since products containing ENPs are already on the market. Previous attempts to model the environmental fate of nanoparticles were meant to provide a first step in environmental exposure estimation of ENPs10,11 and are still too complex for direct implementation in chemical safety assessment frameworks.12 It has therefore been proposed to develop environmental risk assessment strategies with a pragmatic approach and using scientifically justified simplifications.7

This paper is an attempt to aid in this approach by presenting a relatively simple environmental fate model that uses first-order kinetics to estimate environmental background concentrations for nanocolloids in an environmental system that is composed of the compartments air, soil, water, and sediment that are represented as boxes: SimpleBox4nano (SB4N). A similar approach in modeling the fate of nanomaterials in air, water, and soil was recently published by Liu and Cohen.13 Unlike SB4N, Liu and Cohen’s MendNano model assumes fixed (time independent) partitioning ratios for the processes of aggregation and attachment, which control the environmental fate of colloidal systems.8 In SB4N, these processes are modeled mechanistically using first-order rate constants as will be explained in detail below.

SB4N is a modified version of the SimpleBox model, which has served as a regional distribution module in the European Union System for Evaluation of Substances (EUSES) model, used for exposure assessment in REACH.14−16 SB4N adds first-order rate constants for transport- and transformation processes of colloids, where the original SimpleBox model does so only for molecular processes of chemical substances dissolved in water.12 It has been identified that three major adaptations are necessary to make SimpleBox fit for ENPs:6 (1) transformation processes (e.g., from one colloidal form into another by homo- or heteroaggregation) should not be interpreted as removal processes; rather transformation products should be treated as altered species of the same ENP; (2) dissolution should be implemented as a removal mechanism and (3) thermodynamic equilibrium is not expected to be representative for the actual concentrations in the environment, since ENPs generally form unstable colloidal systems.17 The latter implies that concentration ratios of colloidal species cannot be calculated from equilibrium partitioning coefficients but must be modeled dynamically, as the result of forward and backward process rates.6

The aim of the present paper is to provide process formulations for modeling behavior of ENP and to evaluate its potential for use in environmental risk assessment. We explain how environmental concentrations can be calculated as a function of ENP emissions and ENP substance properties using colloidal and ultrafine particle theory. As existing theory cannot exactly describe and predict environmental behavior of colloidal material under field conditions, we have formulated the model to be flexible, so that theoretically derived parameter values can be replaced with experimentally determined ones in case this is preferred. We have implemented the proposed model formulations in the spreadsheet model SimpleBox15 and used them to rework a previously published scenario-analysis of nanomaterials in Switzerland.18The previously published scenario analysis did not consider the impact of removal and transport processes on environmental concentrations, but SB4N does. We have tested SB4N by analyzing differences and commonalities between the outputs. The goal of this exercise is to demonstrate the impact of SB4N’s simulated removal and transport processes on environmental concentrations.

Methods

Model Concept

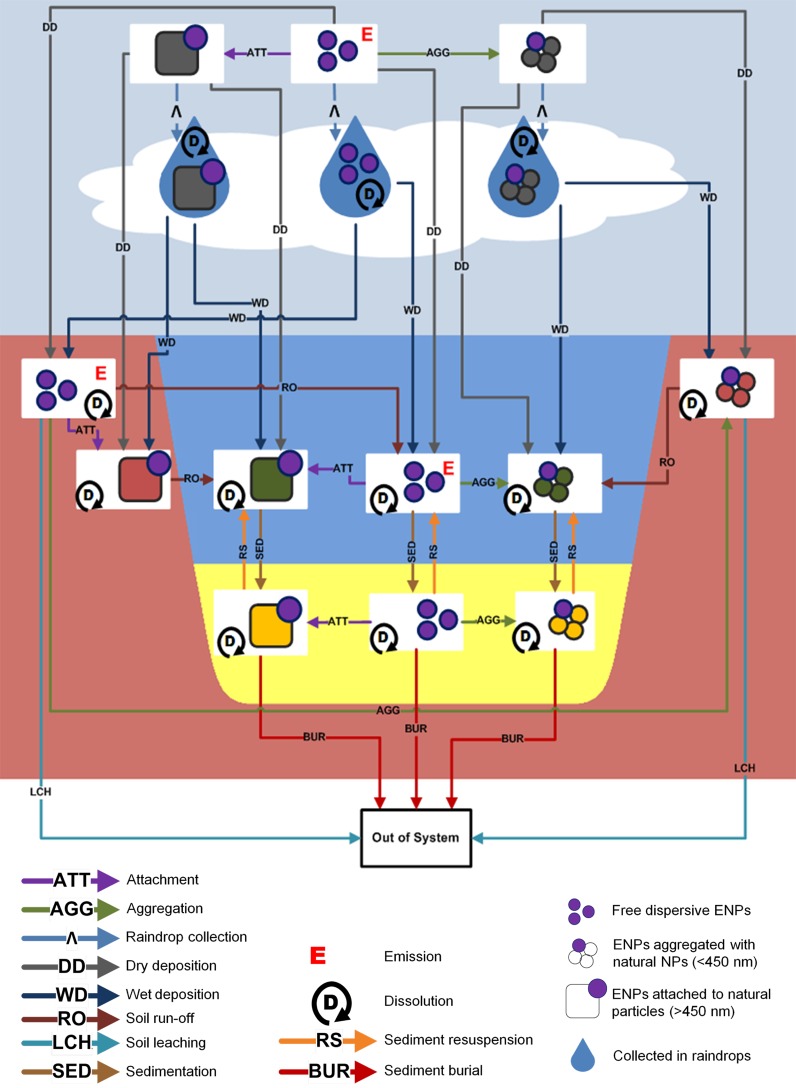
Like the earlier SimpleBox versions, SB4N considers emissions into an environment composed of the compartments atmosphere, surface water, soil, and sediment (Figure 1). Unlike SimpleBox, SB4N treats partitioning between dissolved and particulate forms of the chemical not as equilibrium speciation but as nonequilibrium colloidal behavior.19,20 Therefore, within each compartment ENPs can occur in different physical–chemical forms (species): (1) freely dispersed, (2) heteroaggregated with natural colloidal particles (<450 nm), or (3) attached to larger natural particles (>450 nm) that are prone to gravitational forces in aqueous media. Characterization of the properties (e.g., size distribution (r)) and number concentrations (N) of the natural particles that reside in different environmental compartments are provided as parameter values within the glossary of the Supporting Information (SI Table1).

Figure 1.

Figure 1

Open in a new tab

Overview of model concept SimpleBox4nano.

The fate of airborne ENPs is also influenced by the rain drops that reside in the atmosphere. Therefore, the atmospheric compartment is divided into the subcompartments “rain” and “dry air” to account for the specific rates at which atmospheric particles are taken up in rain drops.21

The SimpleBox model is a classical multimedia mass balance modeling system (“box model”),22,23 in which the masses, m (kg) of ENP in the various environmental compartments (air, water, soil, etc.) are obtained as the steady-state solutions of the mass balance equations for all compartments:

graphic file with name es500548h_m001.jpg 1

A represents the system matrix of rate constants (s–1), and e (kg·s–1) is the vector of emission rates of (pristine) ENP into the environment. The system matrix A holds (pseudo) first-order rate constants for (1) transport between compartments, (2) removal by transport to outside the system, (3) the rates at which ENPs are taken up in aggregates or attach to the surfaces of larger particles, and (4) the rates at which ENPs may be subjected to removal processes such as degradation and dissolution. The first-order rate constants are derived from formulations from the literature and are explained below (Supporting Information, eq 1 and Table 2).

SB4N models the mass concentrations (mi/V = Ci) as state variables, using the same first-order rate constants (ki), written here for a one-compartment system, for which the time-dependent concentrations Ci(t) can be expressed analytically as the total mass mi present in an environmental compartment of volume V at time t at constant emission Ei and removal ki for ENP species i:23

graphic file with name es500548h_m002.jpg 2

These types of calculations are usually performed on one-compartment systems because they become complicated if multiple environmental compartments are involved. If there is transport between compartments in both directions, it is not possible to analytically formulate how the mass of the substance will change over time.23 Obtaining time-dependent solutions of more complex systems of multiple compartments and species, such as SB4N, requires full dynamic, numerical modeling. However, for the special case of nonequilibrium colloidal interactions in SB4N, in which backward processes usually can be neglected, time-dependent solutions can be approximated using an extension and rearrangement of eq 2 wherein the concentration Cj is expressed in terms of removal rate constants kr and incoming transports from other compartments ∑miki,j:

graphic file with name es500548h_m003.jpg 3

This kinetic functionality of SB4N was used to calculate the environmental concentrations of nano-TiO2 in Switzerland after one year of emission. Steady-state calculations (including the sediment compartment) have been calculated with the matrix multiplication (eq 1, Supporting Information, eq 1).

The formulations presented in the model concept have been implemented in a spreadsheet in order to demonstrate the performance of the SB4N model. The spreadsheet model requires the parameters described in the Supporting Information (Table 21) as input for calculating mass concentrations in the compartments atmosphere, soil, surface water, and sediment for free dispersive, aggregated, and attached species of ENPs with one click of the button.

Aggregation and Attachment

Once ENPs have been released into environmental media they may attach to natural particles, such as the aerosol particles in the atmosphere,24 the suspended particles in surface and pore waters,19,20,25 and the solid grains in soil and sediments.26 Natural particles occur in a continuous distribution of sizes, split in SB4N by the often used operationally defined value of 450 nm, meant to separate the “colloidal” from “particulate” material.27 Freely dispersed nanoparticles, small homoaggregates of nanoparticles, and heteroaggregates of nanoparticles with natural colloids (<450 nm) are considered to behave as colloids, whereas heteroaggregates with natural particulates (>450 nm) behave as particulate matter. Size is of crucial importance not only because it directly controls gravitational versus thermal motion28 but also because it controls frequencies and impacts of collision events and high surface areas and high energies enhance colloid aggregation.29

In this paper, heteroaggregation of ENPs with colloidal particles is referred to as “aggregation”, whereas association of ENPs with larger particles is referred to as “attachment”.

Atmosphere: Aerosol Coagulation as Predictor for “Aggregation” and “Attachment”

The mechanism of coagulating ultrafine particles (<100 nm) described in aerosol sciences can be applied to predict the “aggregation” and “attachment” behavior of ENPs in air.18,30

Coagulation is the process wherein aerosol particles collide with one another due to their relative motion and then stick to each other. Diffusion through Brownian motion is the dominant mechanism for collision of ultrafine aerosol particles.31 The rate of coagulation is the product of particle size and diffusion coefficient and is most effective for particles of different sizes (i.e., polydisperse particles). Large particles provide a large absorbing surface area, whereas the smaller particles feature a rapid diffusion.31 The rate of the polydisperse coagulation coefficient is expressed as a function of particle size (r) and diffusivity in air (Dair). Next, the Fuchs transitional correction coefficient (αi,j) is required to express the coagulation coefficient (fcoag) as a first-order rate constant for “aggregation” (kaggA) and “attachment” (kattA) in air.31 The Fuchs correction coefficient increases with particle size approaching the value of 1 for large particles (>1 μm),32 and since it always has a value between 0 and 1 it is applied in SB4N as an efficiency (α) for “aggregation” and “attachment” for ENPs colliding with natural aerosol particles. Both the coagulation rate and the correction coefficient are eventually derived from the particle’s size and mass (Supporting Information, Table 4).31,33

Finally, a characterization of the number concentration, size distribution, and densities of the natural aerosol particles is required. A common characterization that is applied in aerosol sciences is a classification of “nucleation mode aerosols <0.01 μm”, “Aitken accumulation mode aerosols (0.01–0.1 μm)”, and “coarse mode aerosols >0.1 μm”.21,32 The nucleation (∼20 nm) and Aitken accumulation (∼116 nm) mode aerosol are treated by SB4N as colloidal particles because they are both smaller than 450 nm.27,32 Hence, the rate for aggregation in air is expressed as the sum of the coagulation rate for ENPs with nucleation mode and that for Aitken accumulation mode aerosols, whereas coagulation with coarse mode aerosols (∼1800 nm) represents “attachment” in air (Supporting Information, Table 3).32 A characterization of the natural aerosols’ size distribution, number concentration, and the density of the aerosols themselves is presented in the Supporting Information (Table 5).

Surface Water: Aggregation and Attachment Rates

The concepts of colloid science have been applied to estimate the rates for aggregation and attachment of ENPs to the natural particles in aquatic environments. Aggregation (kaggW) and attachment rates (kattW) are commonly obtained by multiplying the number concentrations of natural particles (N) with a collision rate (fcol) and the probability that two particles will actually remain attached after the collision event: the aggregation (αagg) or attachment efficiency (αatt).29 Colloid science describes two types of aggregation:29 (1) fast aggregation, where there is no repulsive interaction between the particles at a collision event, and (2) slow aggregation, where the particles repel each other so that aggregation and attachment efficiencies are very small.

Surface Water: Collision Frequencies

The rate at which particles collide in the aquatic environment is described as a function of the particle size (r), particle density (ρ), the number concentrations of the particles present (N), and characteristics of the surrounding water.34 There are three types of mechanisms that contribute to the collision frequency: (1) Brownian motion (fBrown), where collisions result from random diffusive movement of particles; (2) interception (fintercept), where particles are transported by the motion of the surrounding fluid and collide; and (3) differential settling (fgrav), where a difference in gravitational settling velocities causes the particles to deposit on top of each other.29,34 The sum of the contributions of these mechanisms is referred to as the collision frequency coefficient (fcol). The collision rate (kcol) is derived by multiplying this collision frequency coefficient with the number concentration of the natural counterparticles (Supporting Information, Table 6).34

Surface Water: Aggregation and Attachment Efficiencies

The tendency of colloidal systems to aggregate is well understood and described in the classical Derjaguin Landau35 Verwey Overbeek36 (DLVO) theory of colloid stability. The DLVO theory is presently being modified to add corrective terms for various complications, such as the effects of uncharged polymeric coating, polyelectric coating, and elastic steric stabilization on the van der Waals and electric double-layer interaction energies.37 Unfortunately, to our knowledge, the DLVO theory has not been applied successfully to predict aggregation efficiencies between ENPs and natural colloids under real, complex, and environmental conditions that are not ideal for extrapolations from laboratory conditions.29 Aggregation efficiencies can be reasoned from the repulsive and attractive interaction energies between the two colliding colloids. However, the repulsive energy between ENPs and natural colloid particles in the environment cannot be determined easily and accurately with the DLVO theory,38 without adding corrective terms to describe situation specific conditions (morphology, surface structure, etc.). Instead, it is preferred to obtain aggregation efficiencies from experimental work.12 Apparent efficiencies can be experimentally derived by adding a known number concentration of ENPs to a water sample for which the number concentration and size distribution of the natural particles it contains is measured.39 Observing a decrease in the number concentration of natural particles (e.g., in L–1) provides the opportunity for calculating the efficiencies for aggregation and attachment with first-order kinetics:39

graphic file with name es500548h_m004.jpg 4

Examples of experimentally obtained aggregation and attachment efficiencies are provided in the Supporting Information (Tables 7 and 8 and Figure 1).39,40 When experimental observations of actual attachment efficiencies are not available, the DLVO theory provides the concepts necessary for making estimations.29 Thus, in the case of absent experimental data, we use the DLVO theory by default to derive aggregation efficiencies for SB4N as “order of magnitude estimates”. ENP attachment to the larger natural particles can be approached as an interaction between a nanoparticle and a surface because of their relatively large difference in size (<100 nm versus >450 nm). This type of interaction can also be expressed with the DLVO theory.29 Further explanation on the use of the DLVO theory for the calculation of α can be found in the Supporting Information (Tables 9 and 11).

Soil and Sediments: Attachment and Aggregation Rates

The rates to which ENPs may attach to the solid grains in soil (kattS) and sediments (kattSE) are predicted with the particle filtration theory.26,41 The theory describes colloid (nano)particles in pore waters that deposit to solid grains as a function of filtration (λfilter), collection efficiency (ηo), and an attachment efficiency for porous media (αatt(PM)).41 The collection efficiency (ηo) is determined by the collection mechanisms of Brownian motion (ηBrown), interception (ηintercept), and gravitational settling (ηgrav). The contributions of these mechanisms are predicted with semiempirical relations between the properties of the nanoparticle and the porous medium.41 Filtration is regarded as a characteristic of the porous medium, which can be derived from the diameters of the solid grain collectors (dgrain), the porosity of the medium (f), and the Darcy velocity (UDarcy); see the Supporting Information (Table 12).41

The attachment efficiencies are more difficult to predict but can be derived from packed-bed column experiments.26,42 The collection efficiency and filtration velocity can be estimated with the particle filtration theory, so that an apparent attachment efficiency (αattS,SE) can be derived from the ENPs’ concentration in time (C0 /C(t)):41

graphic file with name es500548h_m005.jpg 5

For some types of ENPs, experimentally determined attachment efficiencies are available in the scientific literature (Supporting Information, Table13).26,42 In case experimental work is not available, the attachment efficiency can be derived with the interaction force boundary layer (IFBL) approximation (Supporting Information, Table 14).43,44

The rates for the aggregation of ENPs with natural colloids appearing in the pore water of soil or sediment are derived with the same approach as for aggregation in surface waters (Supporting Information, Table 3).

Characterization of Altered ENP Species after Attachment or Aggregation

Once an ENP has been attached or aggregated with natural particles the SB4N model treats the ENP as an altered species. The mass of the aggregated or attaches species is characterized as the sum of the mass of the ENP and the mass off the natural particle it sticks to. The same principle is applied to characterize the volume of the aggregated and attached species (Supporting Information, Table 15).

Deposition

Deposition is a transport mechanism that affects the environmental fate of ENPs in various compartments. Atmospheric ENPs will ultimately deposit to soil or surface waters,24 while aquatic ENPs deposit to the sediment compartments at the bottom of surface waters.17 Transport by deposition is included in the SB4N model by deriving first-order rate constants (kdep) from deposition velocities (vdep) of free, aggregated, and attached ENP species

graphic file with name es500548h_m006.jpg 6

in which kdep(i,1,2) is the first-order rate constant for deposition of ENP species i from compartment 1 to 2.

Atmospheric Deposition

Airborne ENPs are likely to deposit from the atmosphere to land or water by Brownian diffusion, interception by a rough surface, or gravitational settling (dry deposition) or through collection by rain (wet deposition).24,30 Wet deposition is included in SB4N by separating the atmosphere into the subcompartments “dry air” and “rain”, each possessing their own mass balance equations for the free, aggregated, and attached ENP species. Raindrop collection is therefore included in the model as the transport of ENPs from “dry air” to “rain”. Specific scavenging coefficients (Λ) express the rates in which the different atmospheric ENPs species are collected. The ENPs collected by raindrops will deposit to land or surface waters by precipitation, whereas the ENPs remaining in dry air will deposit with specific dry deposition velocities.

Wet Deposition

The scavenging coefficients (Λ) for free dispersive, aggregated, and attached species are applied in SB4N as first-order rate constants (kΛ) for the transport from “dry air” to “rain”. They are estimated from the diameter of the raindrops (drain), the precipitation rate (p0), and a collection efficiency coefficient (EΛ).45 The collection efficiency coefficient (EΛ) is based on the mechanisms of below-cloud scavenging, which are Brownian motion (EΛBrown), interception (EΛintercept), and gravitational impaction (EΛgrav). The contribution of these collection mechanisms can be derived from the particle radius (r) and density (ρ) (Supporting Information, Table 16).21

The raindrops are characterized by assuming a monodisperse spectrum of raindrop size.45 This enables the opportunity to derive a raindrop diameter (drain) from a semiempirical relation with precipitation rate (p0):46,47

graphic file with name es500548h_m007.jpg 7

SB4N uses a default precipitation rate of 700 mm·y–1,15 which is also used to derive the removal of ENPs from rain by wet deposition as was expressed in eq 5

graphic file with name es500548h_m008.jpg 8

in which kdep(i,rain,2) is the first-order rate constant for wet deposition of ENP species i from compartment rain to a secondary compartment 2 (soil or surface water).

Since raindrops are aqueous media, it is also possible that ENPs can dissolve inside the raindrop (Supporting Information eq 1 and Table 2).

Dry Deposition

The dry deposition of ENPs s can be expressed as an aerosol particle passing through a series of aerodynamic and surface resistances.30,48 The aerodynamic resistance (RA) is caused by the drag above the surface, which can be characterized as RA = 33 s·m–1 for land and RA = 333 s·m–1 for water surfaces.49 The surface resistance (RS) is determined by the collection efficiencies for Brownian motion (EdBrown), interception (Edintercept), and gravitational impaction (Edgrav). The contributions of these mechanisms are empirically derived from the particle’s radius (r), Schmidt number (Sc), and Stokes number (St), which are ultimately a function of the particle’s radius and mass and some characteristics of the surface the particle deposits to (Supporting Information, Table 17).49

Deposition Velocity of Aquatic ENPs to Sediments

The deposition of aquatic particles to the sediment layers at the bottom of surface waters—also referred to as sedimentation—is determinant for both the concentrations in the water compartment and in the sediment compartment. SB4N employs a sedimentation velocity derived from Stokes’ Law for gravitational settling of particles:28,50

graphic file with name es500548h_m009.jpg 9

The acquired sedimentation velocity (vset) is applied in eq 5, so that the first-order rate constant for deposition (kdep(i,water,sed)) from water bodies (VOLUMEwater) to the surface area of sediment(AREAsediment) is expressed as

graphic file with name es500548h_m010.jpg 10

Dissolution

Although ENPs are often sparingly soluble substances, they may eventually dissolve at some rate to some extent in the excess volumes of water in the environment.17 Once an ENP has been dissolved it no longer applies to the definition of an ENP:6 a solid material that is nanoscaled in at least two dimensions owning specific properties due to its nanoscale.51 SB4N therefore treats the dissolution of ENPs as a removal process in all (sub) compartments that are aqueous media (rain, surface water, pore water).

The mechanism of dissolution depends on the surface chemistry of the ENP and the surrounding water.17 SB4N considers four types of dissolution mechanisms (Supporting Information, Table 18): (1) the Noyes–Whitney equation for dissolution of readily soluble particles, (2) practically insoluble ENP , so that its dissolution rate is zero, e.g., for nano-TiO2, nano-CeO, nano-C,17 (3) dissolution mechanisms that are too complex to predict theoretically and thus require input from experiments,7,12 and (4) dissolution rates that are derived from thermodynamics expressed with an Arrhenius equation.52

Advection

Aggregation, attachment, nanospecific deposition velocities, and dissolution are introduced as new features in the SB4N model that are to be specifically derived per type of ENP. However, ENPs are also subjected to transport processes that only depend on the advective mass flows within the environment, e.g., resuspension of sediment, sediment burial, soil runoff, erosion of soil grains, and leaching of pore water. The first-order rate constants for these processes (krs, krun, kbur, kleach, kerosion., Supporting Information, Table 15) were already derived in the earlier versions of SimpleBox.15In SB4N, the contribution of the nanoindependent advective transports is included by expressing their first-order rate constants in matrix A (Supporting Information, eq 1).

Evaluation

The model functionality was tested by reworking the case of TiO2 in Switzerland published by Mueller and Nowack.18 SB4N was parametrized to match their flow analysis as close as possible, and the same emission scenario was used. The system dimensions and input parameter values for this scenario are presented in Supporting Information (Tables 20 and 21). The model outcomes were compared to reveal and analyze effects of the added process formulations (Supporting Information, Table 22). This evaluation is to demonstrate the SB4N model formulations’ capability to perform environmental exposure estimations of ENPs.

Results and Discussion

Impact of SB4N Transport Processes in a Realistic Emission Scenario

Here we compare outputs of SB4N using a scenario that previously has been presented by Mueller and Nowack based on their material flow analysis model.18 Quantitative estimates for nano-TiO2 emissions in Switzerland have been obtained from this study of Mueller and Nowack who performed a substance flow analysis from products to air, water, and soil. The study also provided rough estimates for predicted environmental concentrations (PECs) reached after 1 year of emission (1-year-PECs) by dividing the annual emissions with the volume of the respective compartments. Environmental removal and transport processes are not included in the PECs reported by Mueller and Nowack.16,18 These PECs are compared with the total concentrations that SB4N calculates for each compartment at the same emission scenario (Table 1). Differences between the PECs estimated by SB4N and Mueller and Nowack are explained by the transport and removal processes that are introduced in the SB4N model. Major differences indicate effective transport and removal processes, whereas minor differences are a consequence of relatively slow rates for these processes (Supporting Information, Table 22).

Table 1. Comparison of Environmental Concentrations Calculated with SimpleBox for Nano (SB4N) and Estimated by PECs Reported by Mueller and Nowack for a Realistic Scenario of Nano-TiO2 Emission in Switzerland18.

compartment emission tons·y–1a PEC after 1 year estimated by Mueller and Nowack, 2008a removal processes introduced in SB4Nb transport inflow introduced in SB4N   PEC after 1 year estimated with SB4N) PEC at steady state estimated with SB4N)
atmosphere 0.06 1.5 × 10–3 μg.m–3 dry deposition wet deposition none total 8.76 × 10–6  (μg·m–3 8.76 × 10–6  (μg·m–3
free in dry air 4.99 × 10–6  (μg·m–3 4.99 × 10–6  (μg·m–3
agg in air 3.76 × 10–6  (μg·m–3 3.76 × 10–6  (μg·m–3
att in dry air 1.22 × 10–8  (μg·m–3 1.22 × 10–8  (μg·m–3
free in rain 1.22 × 10–8  (μg·m–3 1.22 × 10–8  (μg·m–3
agg in rain 2.75 × 10–9  (μg·m–3 2.75 × 10–9  (μg·m–3
att in rain 2.20 × 10–11  (μg·m–3 2.20 × 10–11  (μg·m–3
water 2.78 0.7 μg·L–1 sedimentation atmospheric deposition soil run-off soil erosion sediment resuspensionc total 0.61 μg·L–1 1.51 μg·L–1
free in water 2.81 × 10–2 μg·L–1 2.81 × 10–2 μg·L–1
agg. with natural colloids 0.59 μg·L–1 1.49 μg·L–1
att. to suspended matter 1.15 × 10–6 μg·L–1 9.10 × 10–4μg·L–1
soil 2.19 0.4 μg·kg–1 leaching
run-off
erosion		 atmospheric deposition total 0.403 μg·kg–1 7.63 × 102 μg·kg–1
free in pore water 3.51 × 10–6 μg·kg–1 3.51 × 10–6 μg·kg–1
agg in pore water 1.01 × 10–4 μg·kg–1 1.01 × 10–4μg·kg–1
att to soil solids 0.403 μg·kg–1 7.63 × 102 μg·kg–1
Open in a new tab
a

Original data from ref (18).

b

Dissolution is not included as a removal mechanism for this case study as nano-TiO2 is practically insoluble.

c

Sediment resuspension is formulated as “a resistance to settle” in calculations of the 1-year-PECs estimated by SB4N (Supporting Information, Table 22).

Since nano-TiO2 is assumed to be practically insoluble, all removal processes introduced in SB4N are related to transport from one compartment another or to outside the system (Figure 1). For atmospheric ENPs all removal is related to deposition to water and soil. For the atmospheric compartment SB4N calculated a 1-year-PEC that is a factor 170 smaller than the PEC Mueller and Nowack reported. This implies that atmospheric deposition is a relatively effective removal process as it reduces total concentrations with 2 orders of magnitude (Supporting Information, Table 22). Furthermore, all atmospheric 1-year-PECs that SB4N calculated for the different species of atmospheric ENPs are equal to their respective steady state concentrations. This indicates that in the atmosphere steady state is reached within one year.

The 1-year-PEC that SB4N calculated for ENPs in soil shows little difference with the PEC reported by Mueller and Nowack. A slight increase can be observed after the introduction of atmospheric deposition and removal from soil by leaching, runoff, and erosion. This implies that after 1 year the amount of ENPs entering the soil compartment by atmospheric deposition is slightly larger than the amount of ENPs leaving the soil by removal. Furthermore, it is notable that almost all of the ENPs in soil are calculated to be attached to the solid grains. According to the particle filtration theory ENPs are quite effectively removed from the soil’s pore water by attachment to the soil’s solid grains. However, once the ENPs are attached, erosion is the only removal process, which proceeds very slowly (0.03 mm y–1). This allows the ENPs to accumulate and hence the steady state concentration for ENPs attached to solids in soil is very high (the steady state PEC is reached after >1000 years and is a factor 1900 larger than the 1-year-PEC calculated with SB4N).

In water, the removal of ENPs by sedimentation has not led to a notable difference between the 1-year-PEC calculated with SB4N and the PEC Mueller and Nowack reported for the water compartment. The 1-year-PEC provided by SB4N and the PEC at steady state are also within the same order of magnitude. Most of the ENPs in the water compartment are aggregated with natural colloids for both the 1-year-PECs and the steady-state PECs that are derived with SB4N. Settling of aggregated ENPs is the dominant removal mechanism for ENPs in water20 which rate is calculated to be in the order of magnitude of 1 y–1 (1.64 × 10–8 s–1 ≈ 1 y–1, Supporting Information, Table 22). This explains why the 1-year-PEC calculated by SB4N is about the same as the steady-state PEC.

Uncertainty and Justification of Simplifications

Like in all multimedia fate predictions, the SB4N modeling results are uncertain. This uncertainty is due to a lack of knowledge about some influential parameters: (1) emission rates, (2) physicochemical properties (e.g., size distribution, surface reactivity, state of purity), and (3) interactions with the environment (e.g., dissolution, aggregation and attachment behavior).11 Facing such complexity, SB4N employs scientifically justified simplifications in order to express the mechanisms of the environmental fate of ENPs, e.g., by using default, assumed, or experimentally determined parameter values.

SB4N fits in the pragmatic approach that is required for the environmental risk assessment of ENPs.7 In this approach, simplifications are inevitable but acceptable if they can be justified scientifically.

Release: Emission Patterns

The amount and form of the released ENPs determine their environmental fate.53 Quantitative data on the environmental release of ENPs is limited.54 Therefore, release needs to be estimated from information on the magnitude of ENP production and use, but this information is limited as well.55 Furthermore, emission patterns that characterize the extent to which ENPs are aggregated, attached, or free to disperse at the moment of release are yet to be derived.7 As a consequence of this limited knowledge, emission estimation of ENPs remains speculative.6 In the absence of such knowledge, SB4N assumes that the ENPs are released in their pristine (i.e., freely dispersed) form and are therefore free to disperse. We therefore also assume that the ENPs are released only into the environmental media in which they actually are free to disperse (dry air in the atmosphere, pore water in soil, and the aqueous medium of surface waters).

Air: Treating Atmospheric ENPs as Ultrafine Aerosol Particles

SB4N assumes that the behavior of atmospheric ENPs is similar to the behavior of ultrafine aerosol particles (<100 nm) because the transformation, loss, and dispersion processes that affect natural aerosol particles are also applicable to the dispersion of ENPs.18 This is reasonable, as a comparison between ENPs and other airborne nanoparticles has demonstrated that there are only modest differences in their characteristics and behavior.30 Moreover, such differences become evident only at high local ENP concentrations,30 whereas SB4N considers (low) background concentrations.

Water: Applying Kinetics from Colloid Science

Aggregation, attachment, settling, and dissolution are the dominant nanospecific processes determining the fate of ENPs in water.8,17 SB4N simulates this by using first-order constants for the rates of these processes by applying kinetic equations from colloid science, which is an approach that has been recommended for the aquatic exposure assessment of ENPs.17 A similar approach has been applied successfully in box models predicting the fate of ENPs in rivers;50 the approach has proven useful for a large range of realistic cases. These models dealt with lack of experimental data by applying a range of aggregation and attachment efficiencies, yielding ranges of model outcomes,50 whereas environmental exposure estimation for risk assessment purposes requires most likely outcomes. SB4N prefers estimates of the aggregation and attachment efficiencies obtained from experimental work,12 if these are not available SB4N uses predictions from the DLVO theory when observations under environmental conditions are not available, e.g., when theory cannot adequately account for the complex interactions with natural organic matter or steric interaction forces.29

Soil and Sediments: Applying Particle Filtration Theory on ENPs

SB4N uses the kinetics and semiempirical relations of the particle filtration theory41 to predict the environmental fate in porous media such as soil and sediments. Column experiments investigating the fate and transport of ENPs in porous media show good agreement with the theory.26 However, it is not preferred to predict attachment rates between ENPs and the solid grains with DLVO because it needs verification.56 The DLVO theory does not account for particle effects, charge heterogeneity, or surface roughness,57 while the attachment efficiencies are very sensitive to these type of heterogeneities.29 Therefore, it is preferred to apply attachment efficiencies derived from experimental work. If these are not available, rough estimations for attachment efficiencies can still be derived with the DLVO theory, taking into account that they may not be accurate for a wide set of ENPs and collector surfaces.29

All Compartments: Removal Due to Heteroaggregation Is Assumed To Dominate Compared to Removal Due to Homoaggregation

In SB4N, “aggregation” refers to the process of ENPs sticking to natural colloids. However, ENPs are also able to aggregate with themselves: homoaggregation. At least two ENPs are needed to form one homoaggregate, so that homoaggregation rates are expressed with second-order kinetics. Since homoaggregation obviously does not obey first-order kinetics, it cannot be directly incorporated in SB4N. This problem is overcome in SB4N by disregarding homoaggregation at all. This is justified from experimental observations in which heteroaggregation between ENPs and natural colloids was found to dominate over homoaggregation.20,58 The number concentration of natural colloids is much higher than that of ENPs, given the current and anticipated levels of ENP emission.53 Disregarding the homoaggregation process is an acceptable simplification if the natural colloid concentration is expected to be abundant over the ENP concentration.7,17 This is the case for SB4N, because it assumes a complete dispersion of ENPs within the media over a regional scale. However, this is not the case for local concentrations of ENPs directly after release.50 Where homoaggregation is assumed to be a negligible environmental fate process on a background scale,7 this is not necessarily the case for homoaggregates that are formed at a local scale and then persist at a background scale.58 If the local formation of homoaggregates can be translated into an emission to the regional scale, SB4N is able to predict ENP concentrations using homoaggregate concentrations as input. After all, at a background scale just like ENPs, homoaggregates obey first-order kinetics. Thus, if it is desired, SB4N can be used to predict environmental background concentrations for homoaggregates, but it requires an “emission rate” and the properties of the aggregate as input.

All Aqueous Media: First-Order Dissolution Kinetics

Theoretically, it is not expected that the dissolution of an individual ENP obeys first-order kinetics because the particle will shrink as dissolution proceeds and dissolution is proportional to the particles’ specific surface area that increases.59 However, environmental risk assessment is performed on the total of ENP concentrations. A statistical comparison has shown that differences between the first-order kinetic and the shrinking particle model approach are too small to prefer one for statistical reasons alone.60 For practical reasons, however, the first-order kinetic approach is preferred as it is easier to incorporate in integrated systems such as SB4N.60 In the absence of adequate data, we argue that it is acceptable to use first-order dissolution kinetics for the purpose of environmental risk assessment.17

Perspectives

An implementation of the SB4N model was provided as proof of concept for modeling nanomaterials in SimpleBox version 4 (to be published). SB4N is not the first model that is able to estimate ENP concentrations for an entire environmental system,11 but it may be the first multimedia fate model for ENPs that fits in the current frameworks of chemical safety assessment.12 Existing fate models for ENPs are stochastic models that have been designed to provide a basis for a first environmental exposure estimation of ENPs. They require quantitative data in order to provide a range of probable environmental concentrations by performing a probabilistic material flow analysis (PMFA) that builds on Monte Carlo simulations for air, soil, water, and sediments.9,10,61 The MendNano model developed by Liu and Cohen13 is similar to SB4N, but based on empirical partitioning data, rather than on mechanistic formulations of the key processes. MendNano models the extent to which ENPs are associated with natural particles by means of an attachment weighting factor. SB4N reaches the same by using first-order rate constants for aggregation and attachment, for which theoretical, mechanistic estimations can be used in the absence of empirical data. In this respect, SB4N and MendNano are fundamentally different.

Current chemical safety assessment frameworks prefer model predictions as single values for environmental concentrations derived from chemical substance properties and emissions to the environment.12 SB4N is a mechanistic model designed to perform environmental exposure estimations for this purpose, and hence, it requires physical and chemical properties of the engineered (nano) colloid particle and emission as inputs. When SB4N is applied to estimate environmental exposure to ENPs, it is preferred to apply experimentally derived values for the parametrizations that are not fully covered by existing colloid theory (e.g., aggregation and attachment efficiencies). Experimental data is available for all the parametrizations for which it is preferred26,39,40,42,52 but not for all the different types of ENPs. This indicates that the required experiments can be performed successfully but also stresses the need for more experimental investigation both in general and for the application of the SB4N model. In case experimental data is unavailable, it is still acceptable to use theoretically derived parameter values as long as the resulting uncertainty is accounted for. SB4N’s ability to calculate ENP concentrations in air, soil, water, and sediment makes the model fit for implementation in chemical safety assessment. Furthermore, SB4N is able to predict the extent to which ENPs are associated with natural particles, which becomes useful in for further safety assessment of ENPs.62 Moreover, SB4N covers the adjustments that are required to adapt earlier versions of SimpleBox fit for environmental exposure estimation of ENPs:6 (1) transformation is not interpreted as a removal mechanism because the environmental fate of the transformation products from heteroaggregation and attachment are simulated as a different species of the same ENP, (2) dissolution is included as a mechanism of removal through degradation, and (3) complete and instantaneously reached thermodynamic equilibrium is not assumed; rather, the rates at which the ENPs go toward thermodynamic equilibrium are represented by dissolution, aggregation, and attachment rates. With all the required adjustments accounted for, we believe that SB4N can be implemented in environmental risk assessment frameworks for nanomaterials in the same way as the original SimpleBox15 is used in the environmental risk assessment of traditional chemicals: a multimedia fate model that provides background concentrations for the purpose of environmental exposure estimation.12

Acknowledgments

This work is supported by NanoNextNL, a micro- and nanotechnology consortium of the Government of The Netherlands and 130 partners.

Supporting Information Available

Detailed information and equations for the formulations of the model concept of SB4N. This material is available free of charge via the Internet at http://pubs.acs.org

The authors declare no competing financial interest.

Supplementary Material

es500548h_si_001.pdf (515.3KB, pdf)

References

  1. Abott L. C.; Maynard A. D. Exposure assessment approaches for engineered nanomaterials. Risk. Anal. 2010, 30, 1634–1644. [DOI] [PubMed] [Google Scholar]
  2. Wigginton N. S.; Haus K. L.; Hochella M. F. Jr. Aquatic environmental nanoparticles. J. Environ. Monitor. 2007, 9, 1306–1316. [DOI] [PubMed] [Google Scholar]
  3. Aschberger K.; Micheletti C.; Sokull-Klüttgen B.; Christensen F. M. Analysis of currently available data for characterising the risk of engineered nanomaterials to the environment and human health: Lessons learned from four case studies. Environ. Int. 2011, 37, 1143–1156. [DOI] [PubMed] [Google Scholar]
  4. Pettitt M. E.; Lead J. R. Minimum physicochemical characterisation requirements for nanomaterial regulation. Environ. Int. 2013, 52, 41–50. [DOI] [PubMed] [Google Scholar]
  5. Boxall A. B. A.; Chaudry Q.; Sinclair C.; Jones A.; Aitken R.; Jefferson B.; Watts C. D.. Current and Future Predicted Environmental Exposure to Engineered Nanoparticles; Central Science Library York for the Department of the Environment and Rural Affairs: Sand Hutton, U.K., 2007. [Google Scholar]
  6. Meesters J. A. J.; Veltman K.; Hendriks A. J.; van de Meent D. Environmental Exposure Assessment of Engineered Nanoparticles: Why REACH Needs Adjustment. Integ. Environ. Assess. Man. 2013, 9, e15–e26. [DOI] [PubMed] [Google Scholar]
  7. Praetorius A.; Arvidsson R.; Molander S.; Scheringer M. Facing complexity through informed simplifications: A research agenda for aquatic exposure assessment of nanoparticles. Environ. Sci. Proc. Imp. 2013, 15, 161–168. 2013. [DOI] [PubMed] [Google Scholar]
  8. Hendren C. O.; Lowry M.; Grieger K. D.; Money E. S.; Johnston J. M.; Wiesner M. R.; Beaulieu S. M. Modeling approaches for characterizing and evaluating environmental exposure to engineered nanomaterials in support of risk-based decision making. Environ. Sci. Technol. 2013, 47, 1190–2105. [DOI] [PubMed] [Google Scholar]
  9. Gottschalk F.; Sonderer T.; Scholz R. W.; Nowack B. Possibilities and limitations of modeling environmental exposure to engineered nanomaterials by probabilistic material flow analysis. Environ. Toxicol. Chem. 2010, 29, 1036–1048. [DOI] [PubMed] [Google Scholar]
  10. Gottschalk F.; Scholz R. W.; Nowack B. Probabilistic material flow modeling for assessing the environmental exposure to compounds: methodology and an application to engineered nano-TiO2 particles. J. Environ. Modell. Software 2010, 25, 320–332. [Google Scholar]
  11. Gottschalk F.; Sun T.-Y.; Nowack B. Environmental concentrations of engineered nanomaterials: Review of modelling and analytical studies. Environ. Pollut. 2013, 181, 287–300. [DOI] [PubMed] [Google Scholar]
  12. European Chemical Agency [ECHA]. Guidance on Information Requirements and Chemical Safety Assessment Chapter R.16: Environmental Exposure Estimation; ECHA-10-G-06-EN; ECHA, Helsinki, Finland, 2012.
  13. Liu H. H.; Cohen Y. Multimedia environmental distribution of engineered nanomaterials. Environ. Sci. Technol. 2014, 48, 3281–3292. [DOI] [PubMed] [Google Scholar]
  14. Van de Meent D.SimpleBox: a generic multimedia fate evaluation model; RIVM Report No. 222501002; National Institute of Public Health and the Environment (RIVM): Bilthoven, The Netherlands, 1993.
  15. Brandes L. J.; den Hollander H.; van de Meent D.. SimpleBox 2.0: a nested multimedia fat model for evaluating the environmental fat of chemicals; RIVM Report No. 670208001; National Institute of Public Health and the Environment: Bilthoven, The Netherlands, 1996.
  16. Den Hollander H.; van de Meent D.. Model parameters and equations used in SimpleBox 3.0; RIVM Report No. 601200 003; National Institute of Public Health and the Environment (RIVM): Bilthoven, The Netherlands, 2004.
  17. Quik J. T. K.; Vonk J. A.; Hansen S. F.; Baun A.; van de Meent D. How to assess exposure of aquatic organisms to manufactured nanoparticles. Environ. Int. 2011, 37, 1068–1077. [DOI] [PubMed] [Google Scholar]
  18. Mueller N. C.; Nowack B. Exposure Modeling of Engineered Nanoparticles in the Environment. Environ. Sci. Technol. 2008, 42, 4447–4453. [DOI] [PubMed] [Google Scholar]
  19. Hotze E. M.; Tanapon P.; Lowry G. V. Nanoparticle aggregation: challenges to understanding transport and reactivity in the environment. J. Environ. Qual. 2010, 39, 1909–1924. [DOI] [PubMed] [Google Scholar]
  20. Quik J. T. K.; Stuart M. C.; Wouterse M.; Peijnenburg W.; Hendriks A. J.; van de Meent D. Natural colloids are the dominant factor in the sedimentation of nanoparticles. Environ. Toxicol. Chem. 2012, 31, 1019–1022. [DOI] [PubMed] [Google Scholar]
  21. Seinfeld J. H.; Pandis S. N.. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change; John Wiley & Sons: New York, 2006. [Google Scholar]
  22. Mackay D.Multimedia Environmental Models The Fugacity Approach; Lewis Publishers: London, U.K., 2003. [Google Scholar]
  23. Van de Meent D.; Hollander A.; Peijnenburg; Breure T.. Fate and transport of contaminants. In Ecological Impacts of Toxic Chemicals; Sanchez-Bayo F., van den Brink P. J., Mann R. M., Eds.; Bentham Science Publishers: Oak Park, IL, 2011; pp 13–42. [Google Scholar]
  24. Tiwari A. J.; Marr L. C. The role of atmospheric transformations in determining environmental impacts of carbonaceous nanoparticles. J. Environ. Qual. 2010, 39, 1883–1895. [DOI] [PubMed] [Google Scholar]
  25. Batley G. E.; Kirby J. K.; McLaughlin M. J. Fate and risks of nanomaterials in aquatic and terrestrial environments. Acc. Chem. Res. 2013, 46, 854–862. [DOI] [PubMed] [Google Scholar]
  26. Jones E. H.; Su C. Fate and transport of elemental copper (Cu0) nanoparticles through saturated porous media in the presence of organic materials. Water. Res. 2012, 46, 2445–2456. [DOI] [PubMed] [Google Scholar]
  27. Lead J. R.; Davison W.; Hamilton-Taylor J.; Buffle J. Characterizing colloidal material in natural waters. Aquatic Geochem. 1997, 3, 213–232. [Google Scholar]
  28. Stokes G. G.On the effect of internal friction of fluids on the motion of pendulums. Trans. Cambridge Phil. Soc. IX 1850, 8. [Google Scholar]
  29. Petosa A. R.; Jaisi D. P.; Quevedo I. R.; Elimelech M.; Tufenkji N. Aggregation and deposition of engineered nanomaterials in aquatic environments: Role of physicochemical interactions. Environ. Sci. Technol. 2010, 44, 6532–6549. [DOI] [PubMed] [Google Scholar]
  30. Kumar P.; Fennell P.; Robins A. Comparison of the behaviour of manufactured and other airborne nanoparticles and the consequences for prioritising research and regulation activities. J. Nanopart. Res. 2010, 12, 1523–1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ketzel M.; Berkowicz R. Modelling the fate of ultrafine particles from exhaust pipe to rural background: an analysis of time scales for dilution, coagulation and deposition. Atmos. Environ. 2004, 38, 2639–2652. [Google Scholar]
  32. Jaenicke R.Aerosol Cloud-Climate Interactions; Academic Press, Inc.: San Diego, 1993. [Google Scholar]
  33. Kulmala M.; Dal Maso J.; Makela J. M.; Pirjola J.; Vakeva M.; Aalto P.; Miikulainen P.; Hameri K.; O’Dowd C. D. On the formation, growth and composition of nucleation mode particles. Tellus 2001, 53B, 479–490. [Google Scholar]
  34. Lyklema H.Fundamentals of Interface and Colloid Science; Elsevier Academic Press: Amsterdam, 2005. [Google Scholar]
  35. Derjaguin B. V.; Landau L. D. Theory of stability of strongly charged lyophobic sols and the adhesion of strongly charged particles in solutions of electrolytes. Acta. Physicochim. U.R.S.S. 1941, 14, 633–662. [Google Scholar]
  36. Verwey E. J. W.; Overbeek J. T. G.. Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, 1948. [Google Scholar]
  37. Lin S.; Wiesner M. R. Theoretical investigation on the interaction between a soft particle and a rigid surface. Chem. Eng. J. 2012, 191, 297–305. [Google Scholar]
  38. Arvidsson R.; Molander S.; Sandén B. A.; Hassellov M. Challenges in exposure modeling of nanoparticles in aquatic environments. Hum. Ecol. Risk. Assess. 2011, 17, 245–262. [Google Scholar]
  39. Quik J. T. K.Fate of nanoparticles in the aquatic environment, removal of engineered nanomaterials from the water phase under environmental conditions. Ph.D. Dissertation, Radboud University Nijmegen, The Netherlands, 2013. [Google Scholar]
  40. Keller A. A.; Wang H.; Zhou D.; Lenihan H. S.; Cherr G.; Cardinale B. J.; Miller R.; Ji Z. Stability and aggregation of metal oxide nanoparticles in natural aqueous matrices. Environ. Sci. Technol. 2010, 44, 1962–1967. [DOI] [PubMed] [Google Scholar]
  41. Tufenkji N.; Elimelech M. Correlation equation for predicting single-collector efficiency in physicochemical filtration in saturated porous media. Environ. Sci. Technol. 2004, 38, 529–536. [DOI] [PubMed] [Google Scholar]
  42. Godinez I. G.; Darnault C. J. G. Aggregation and transport of nano-TiO2 in saturated porous media: Effects of pH, surfactants and flow velocity. Water. Res. 2011, 45, 839–851. [DOI] [PubMed] [Google Scholar]
  43. Ruckenstein E.; Prieve D. C. Rate of deposition of Brownian particles under the action of London and double-layer forces. J. Chem. Soc., Faraday Trans. 2 1973, 69, 1522–1536. [Google Scholar]
  44. Spielman L. A.; Friedlander S. K. Role of the electrical double layer in particle deposition by convective diffusion. J. Colloid Interface Sci. 1974, 46, 22–31. 1974. [Google Scholar]
  45. Wang X.; Zhang L.; Moran M. D. Uncertainty assessment of current size-resolved parameterizations for below-cloud particle scavenging by rain. Atmos. Chem. Phys. Discuss. 2010, 10, 2503–2548. [Google Scholar]
  46. Gong S. L.; Barrie L. A.; Blanchet J.-P.; von Salzen K.; Lohmann U.; Lesins G.; Spacek L.; Zhang L. M.; Girard E.; Lin H.; Leaitch R.; Leighton H.; Chylek P.; Huang P. Canadian aerosol module: a size-segregated simulation of atmospheric aerosol processes for climate and air quality models: 1. module development. J. Geophys. Res. 2003, 108 (D1), 3–16. [Google Scholar]
  47. Gong W.; Dastoor A. P.; Bouchet V. S.; Gong S. L.; Makar P. A.; Moran M. D.; Pabla B.; Ḿenard S.; Crevier L.-P.; Cousineau S.; Venkatesh S. Cloud processing of gases and aerosols in a regional air quality model (AURAMS). Atmos. Res. 2006, 82, 248–275. [Google Scholar]
  48. Slinn W. G. N. Predictions for particle deposition to vegetative surfaces. Atmos. Environ. 1982, 16, 1785–1794. [Google Scholar]
  49. Nho-Kim E.-Y.; Michou M.; Peuch V.-H. Parameterization of size-dependent particle dry deposition velocities for global modeling. Atmos. Environ. 2004, 38, 1933–1942. [Google Scholar]
  50. Praetorius A.; Scheringer M.; Hungerbuhler K. Development of environmental fate models for engineered nanoparticles: A case study of TiO2 nanoparticles in the Rhine River. Environ. Sci. Technol. 2012, 46, 6705–6713. [DOI] [PubMed] [Google Scholar]
  51. Bleeker E. A. J.; de Jong W. H.; Geertsma R. E.; Groenewold M.; Heugens E. H. W.; Koers-Jacquemijns M.; van de Meent D.; Popma J. R.; Rietveld A. G.; Wijnhoven S. W. P. Considerations on the EU definition of a nanomaterial: Science to support policy making. Regul. Toxicol. Pharmacol. 2013, 65, 119–125. [DOI] [PubMed] [Google Scholar]
  52. Liu J.; Hurt R. H. Ion release kinetics and particle persistence in aqueous nano-silver colloids. Environ. Sci. Technol. 2010, 44, 2169–2175. [DOI] [PubMed] [Google Scholar]
  53. Gottschalk F.; Nowack B. The release of engineered nanomaterials to the environment. J. Environ. Monitor. 2011, 13, 1145–1155. [DOI] [PubMed] [Google Scholar]
  54. Nowack B.; Ranville J. F.; Diamond S.; Gallego-Urrea J. A.; Metcalfe C.; Rose J.; Horne N.; Koelmans A. A.; Klaine S. J. Potential scenarios for nanomaterial release and subsequent alteration in the environment. Environ. Toxicol. Chem. 2012, 31, 50–59. [DOI] [PubMed] [Google Scholar]
  55. Hendren C. O.; Mesnard X.; Droge J.; Wiesner M. R. Estimating production data for five engineered nanomaterials as a basis for exposure assessment. Environ. Sci. Technol. 2011, 45, 2562–2569. [DOI] [PubMed] [Google Scholar]
  56. Pan B.; Xing B. Applications and implications of manufactured nanoparticles in soils: A review. Eur. J. Soil. Sci. 2012, 63, 437–456. [Google Scholar]
  57. Lerner R. N.; Lu Q.; Zeng H.; Liu Y. The effects of biofilm on the transport of stabilized zerovalent iron nanoparticles in saturated porous media. Water Res. 2012, 46, 975–985. [DOI] [PubMed] [Google Scholar]
  58. Quik J. T. K.; Velzeboer I.; Wouterse M.; Koelmans A. A.; van de Meent D. Heteroaggregation and sedimentation rates for nanomaterials in natural waters. Water Res. 2014, 48, 269–279. [DOI] [PubMed] [Google Scholar]
  59. David C. A.; Galceran J.; Rey-Castro C.; Puy J.; Companys E.; Salvador J.; Monné J.; Wallace R.; Vakourov A. Dissolution kinetics and solubility of ZnO nanoparticles followed by AGNES. J. Phys. Chem. C 2012, 116, 11758–11767. [Google Scholar]
  60. Poot A.; Meerman E.; Gillissen F.; Koelmans A. A. A kinetic approach to evaluate the association of acid volatile sulfide and simultaneously extracted metals in aquatic sediments. Environ. Toxicol. Chem. 2009, 28, 711–717. [DOI] [PubMed] [Google Scholar]
  61. Gottschalk F.; Sonderer T.; Scholz R. W.; Nowack B. Modeled environmental concentrations of engineered nanomaterials (TiO2, ZnO, Ag, CNT, fullerenes) for different regions. Environ. Sci. Technol. 2009, 43, 9216–9222. [DOI] [PubMed] [Google Scholar]
  62. Borm P.; Klaessig F. C.; Landry T. D.; Moudgil B.; Pauluhn J.; Thomas K.; Trottier R.; Wood S. Research strategies for safety evaluation of nanomaterials, part V: Role of dissolution in biological fate and effects of nanoscale particles. Toxicol. Sci. 2006, 90, 23–32. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

es500548h_si_001.pdf (515.3KB, pdf)

Articles from Environmental Science & Technology are provided here courtesy of American Chemical Society

RESOURCES