Relaxation Dispersion NMR to Reveal Fast Dynamics in Brønsted Acid Catalysis: Influence of Sterics and H-Bond Strength on Conformations and Substrate Hopping

Abstract

NMR provides both structural and dynamic information, which is key to connecting intermediates and to understanding reaction pathways. However, fast exchanging catalytic intermediates are often inaccessible by conventional NMR due its limited time resolution. Here, we show the combined application of the ¹H off-resonance R_1ρ NMR method and low temperature (185–175 K) to resolve intermediates exchanging on a μs time scale (ns at room temperature). The potential of the approach is demonstrated on chiral phosphoric acid (CPA) catalysts in their complexes with imines. The otherwise inaccessible exchange kinetics of the E-I ⇌ E-II imine conformations and thermodynamic E-I:E-II imine ratios inside the catalyst pocket are experimentally determined and corroborated by calculations. The E-I ⇌ E-II exchange rate constants (k_ex^185 K) for different catalyst–substrate binary complexes varied between 2500 and 19 000 s^–1 (τ_ex = 500–50 μs). Theoretical analysis of these exchange rate constants revealed the involvement of an intermediary tilted conformation E-III, which structurally resembles the hydride transfer transition state. The main E-I and E-II exchange pathway is a hydrogen bond strength dependent tilting–switching–tilting mechanism via a bifurcated hydrogen bond as a transition state. The reduction in the sterics of the catalyst showed an accelerated switching process by at least an order of magnitude and enabled an additional rotational pathway. Hence, the exchange process is mainly a function of the intrinsic properties of the 3,3′-substituents of the catalyst. Overall, we believe that the present study opens a new dimension in catalysis via experimental access to structures, populations, and kinetics of catalyst–substrate complexes on the μs time scale by the ¹H off-resonance R_1ρ method.

Introduction

In the past decade, ion pair catalysis has witnessed an enormous growth in synthetic applications.¹ Especially, Brønsted acid catalysis is a well-explored class for various enantioselective syntheses.²⁻⁷ However, experiment-based structural and mechanistic studies are very rare, and often the mechanistic insights are obtained by theoretical calculations.⁸⁻¹¹ As a result, the absence of experimental constraints may lead to an underdetermination of the assumed theoretical models. Therefore, experimental detection and characterization of key intermediates and their interactions are pivotal in the elucidation of the plausible pathways of a catalytic reaction and to validate the theoretical models. Often, structural insights of intermediates and their spatial arrangement are obtained from X-ray crystal structures, which provide highly valuable structural information at the atomic level. However, these crystal structures reveal often only a single point of the whole conformational space and thus can conceal the existing dynamics of substrate catalyst complexes (e.g., in the case of chiral phosphoric acids in their binary complexes with imines only one⁵ out of four¹² main conformations was found with X-ray). In addition, solid-state effects may induce thermodynamic preferences differing from those in solution (e.g., dimers versus monomers in ion pair catalysts¹³) and thus complicate the interpretation. In addition, the obtained intermediate structures are generally disconnected points on the reaction profile, which have to be interpolated to connect the points and later extrapolated to interpret the reaction outcome.

In solution, the formed substrate–catalyst complexes exist as Boltzmann-distributed conformers. These intermediates differ in their interaction patterns, e.g., hydrogen bonds, Coulombic interactions, and covalent and noncovalent interactions,^12,14,15 which are vital and might be deterministic for the reaction outcome.¹⁶⁻¹⁹ In this regard, solution NMR spectroscopy provides both structural and dynamic information about multiple Boltzmann-distributed intermediate states of a catalytic reaction. Especially the dynamic information allows connections between the intermediates on the reaction profile and thus reveals rich insights into the reaction mechanism.²⁰ Indeed, NMR, e.g., has been successfully applied to detect intermediates and elucidate reaction mechanisms in photo-,²¹ organo-,^18,22 and transition-metal catalysis,²³⁻²⁸ to study weak intermolecular interactions,^29,30 to reveal aggregations of organic,^15,31 inorganic, and organometallic molecules,^32,33 and to extract kinetic isotope effects.^34,35 Despite this great success, the inherent low sensitivity and low time resolution of NMR make the detection of exchanging and low populated intermediates challenging. In terms of detection of transient low populated key intermediates in the slow exchange regime (∼ms time scale), we successfully demonstrated the application of chemical exchange saturation transfer (CEST)³⁶ in organocatalysis,³⁷ photocatalysis,³⁸ and silicide Zintl ion chemistry.³⁹ However, for investigating fast exchanging intermediates, not only the sensitivity but also the time resolution has to be extended. In this context, NMR relaxation dispersion experiments can play a significant role to quantify the populations and dynamics in the fast exchange regime (ms−μs time scale).⁴⁰⁻⁴² This approach works based on a systematic deciphering of chemical exchange contribution to the relaxation via systematic incrementation of the RF field (B₁), which reveals chemical exchange rates, populations, and chemical shift information. In the past decades, the relaxation dispersion NMR experiments CPMG and R_1ρ methods were successfully applied to study fast dynamics and structures of low populated⁴³ biomolecular conformations (proteins and RNA), which are key to enzymatic functions.^40,41 Both CPMG and R_1ρ reveal the same information.⁴⁴ However, to access faster dynamics the CPMG method is restricted by the number of repeatable π-pulses in a given time period and further requires experimental data at multiple magnetic fields.^40,45 In contrast, the R_1ρ methods apply a continuous RF pulse (spin-lock), and its field (B₁) is systematically varied to access dynamics and hence is not limited by the number of repeatable pulses and suitable for measurement of faster dynamics in terms of NMR.⁴² The 2D analogous CPMG and R_1ρ relaxation dispersion experiments with ¹⁵N and ¹³C nuclei as probes were preferred in biomolecular NMR due to their well-resolved chemical shifts in the spectra and the reduced dipolar and scalar interactions.^40−42,44 However, this approach can only disclose dynamics down to the ≈40 μs time scale.⁴⁶ Additionally, selective labeling of catalyst and substrates in organic reactions is challenging. On the other hand, protons are more sensitive both toward the magnetic field and toward changes in the chemical environment. Thus, it reveals better structural information and relatively faster exchange processes.^45,47 Furthermore, due to the natural abundance of protons in organic molecules, protons are the preferred choice for studying catalytic reactions. However, protons as relaxation dispersion probes suffer from extensive scalar and dipolar interactions, which complicate the analysis and hence limit the applications of proton-based R_1ρ methods. The recent advancement in selective labeling techniques and NMR pulse sequences has partially addressed these problems. One significant advancement was the development of an off-resonance R_1ρ method, in which the spin lock field (B₁) and its offset were simultaneously varied to modulate the effective field, while still maintaining the constant angle (35.30°) of the spin-locked magnetization.^48,49 This enables higher effective fields than the on-resonance R_1ρ method and also improves the accuracy by reducing the coherent evolution due to scalar couplings and minimizing the cross-relaxation contributions to the measured rates. Currently, with the recently reported high-power spin-locking field facilitated by cryogenically cooled probes, it is possible to push the off-resonance R_1ρ method to access <40 μs time scale dynamics as well.^46,47 These improvements have also enabled the application of relaxation dispersion NMR methods in recent ligand binding studies.^45,47 Despite these recent developments and extended applications of relaxation dispersion NMR experiments, so far to the best of our knowledge the relaxation dispersion NMR methods were not applied in mechanistic or structural studies in chemical catalysis.

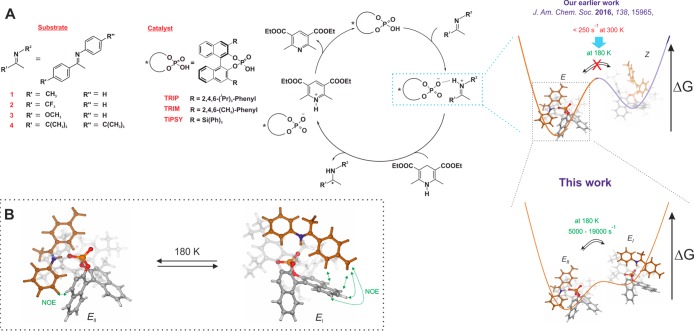
Recently, in the field of chiral phosphoric acid (CPA) catalysis, we achieved significant progress in structural investigations¹² and H-bond characterization¹⁴ of catalyst–imine binary complexes by application of NMR spectroscopy and computational chemistry. For the first time, we showed the coexistence of E- and Z-imine binary complexes by NMR (Figure 1A). In-depth NOE analysis and computational results revealed four major core structures: two correspond to the E-imine (E-I and E-II, Figure 1B), and the other two correspond to the Z-imine (Z-I and Z-II). These four core structures (E-I/II and Z-I/II) possess zwitterionic character and are anchored by a strong hydrogen bond with a highly covalent character. Surprisingly, despite the strong hydrogen bond, we observed a fast exchange (on the NMR time scale) between the substructures (E-I ⇌ E-II; Z-I ⇌ Z-II) even at very low temperature (130 K). Additionally, for binary complexes of various CPAs and imines, we established an internal acidity scale⁵⁰ and confirmed the E-I/II and Z-I/II complexes as four core structures in all of these systems.⁵¹ As demonstrated later in this work, the internal acidity (H-bond strength) and the steric properties of the CPA and/or imine play a significant role in the exchange of E-I and E-II.

Figure 1.

(A) Investigated systems and catalytic cycle of the transfer hydrogenation of ketimines with chiral phosphoric acids: Our earlier work showed the existence of the E- and Z-imine/catalyst binary complex and two fast exchanging conformations for each configuration based on NOE analysis.^12,15 In the present work, we resolved the fast exchanging E-conformations and quantified the rate by R_1ρ experiments and corroborated by calculations for the given catalyst/substrate combinations. (B) Structures of the two E-conformations of TRIP/imine complexes (Type I and Type II), which are in fast exchange even at 180 K.

Despite this enormous progress, due to the fast exchange between E-I ⇌ E-II and Z-I ⇌ Z-II conformers (Figure 1), the quantification of their population and dynamics in the catalyst pocket has remained inaccessible so far and could only be accessed by theoretical calculations. However, the theoretical calculations can have a significant offset to the experimental values, i.e., E/Z-ratio in the CPA/imine complexes.¹⁵ Thus, the validation of theoretical methods applied is highly desirable if possible. The experimental and theoretical determination of the kinetic and thermodynamic properties of these conformers can reveal delicate information such as noncovalent interactions (H-bond, dispersion, electrostatic), active pathways, or possible structures of the transition states. This in turn provides an in-depth understanding of the behavior of the catalyst–substrate complex at the molecular level, i.e., flexibility of the system,⁵² and serves as a basis for further rational development. Additionally, it enables validation and refinement of theoretical models.

Despite our best efforts, i.e., NMR measurements down to 130 K in freonic solvent mixtures, so far it has not been possible to access experimentally the populations and exchange rates of E-I/E-II or Z-I/Z-II. One approach to solve this problem is further reduction of the temperature to slow down the exchange rate. However, the practicability is limited due to the freezing of the solvent. Moreover, it is also difficult to achieve very low temperatures in standard NMR spectrometers.

To access fast dynamics on a molecular level in chemical catalysis, in this work for the first time the combination of low temperature (185–175 K) and ¹H off-resonance R_1ρ was successfully applied to a real catalytic system. Furthermore, fast conformational exchanges (on the NMR time scale and in the absence of the reductant) in CPA/E-imine complexes were experimentally resolved. The rate constants or free energy barriers for the exchange processes were quantified and corroborated by theoretical calculations. Furthermore, by merging NMR spectroscopic and theoretical results, we identified the exact exchange mechanism between E-I and E-II. We could elucidate the influence of the hydrogen bond strength and 3,3′-substituents on the exchange rates and the operative exchange pathways. This was the first time to the best of our knowledge that microsecond dynamics (τ_ex = 500–50 μs) in a catalytic complex were observed in such depths that even a fast hydrogen bond switching/substrate hopping in catalysis was quantified by NMR spectroscopy.

Results and Discussion

System Selection

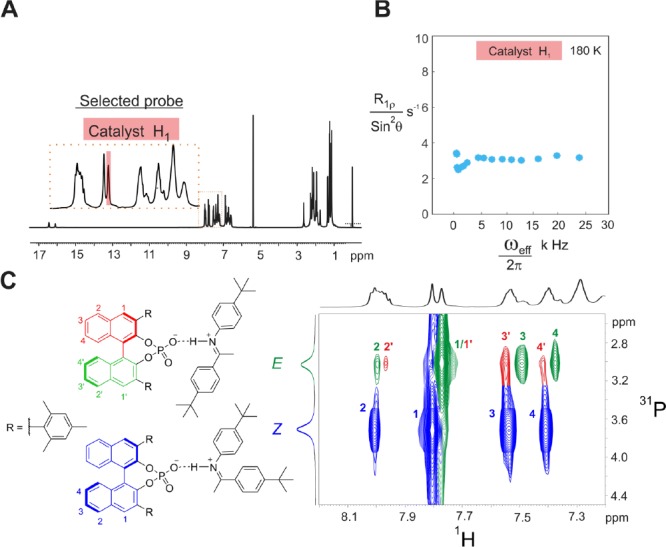
For establishing the method, initially we selected the binary TRIP/1-imine complex due to our detailed knowledge about structures and behavior at low-temperature conditions. The presence of the binary complex is proven by the large trans hydrogen bond scalar coupling (2–3 Hz) traversing between ³¹P and ¹⁵N nuclei.¹⁴ In 1:1 CPA/imine mixtures, the binary complex is formed in a sufficient amount (typically >70% in 1:1 mixtures) which is adequate for the current investigation.⁵⁰ At 180 K, based on our previous solvent screening, we found that dichloromethane (CD₂Cl₂) provides the best chemical shift dispersion and narrow line widths.

The low-temperature condition is crucial to freeze the exchange between the E- and Z-complex, which allows individual analysis of the two configurational complexes by simplifying the exchange matrix. From our previous structural investigation, the presence of E-I and E-II as well as Z-I and Z-II is predicted by DFT calculations and experimentally proven by NOE contacts and hydrogen bond analysis.^12,14 In the E-I conformation, NOE contacts between the ketone moiety of the imine and the BINOL backbone of the catalyst were observed, while the E-II conformation was confirmed by NOE contacts between the aniline moiety and the BINOL backbone (Figure 1B). For TRIP/E-imine complexes, we observed different signal sets for the two naphthyl fragments of the BINOL backbone in the proton spectrum. In contrast, only one set of signals for the backbone of the Z-imine was assigned, which indicates a different fast exchange process between Type I and Type II, leading to backbone averaging.

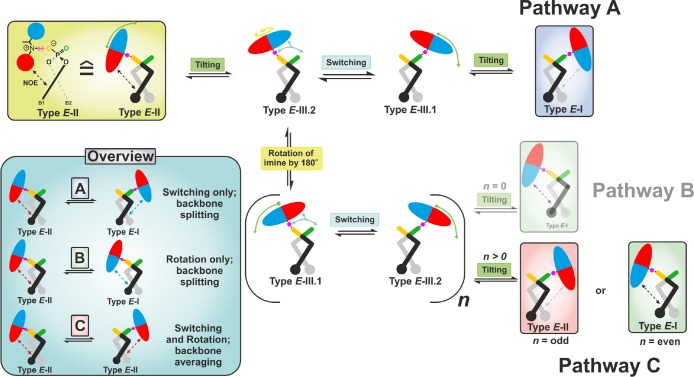
Possible Exchange Pathways

In principal, the fast exchange between Types I and II can be realized by three different pathways (Figure 2). In all pathways, first the imine tilts to an intermediate position denoted as Type III.1/2 (see SI for structure). These structures adopt a similar hydrogen bond geometry as in the ground-state E-I/II. However, the E-imine in Type III.1/2 is found in the middle of the catalyst’s binding pocket, similar to its position in the hydride transfer step or in dimers of the binary complex.¹⁵ Thus, the interaction between the imine and BINOL backbone is lost in the intermediate E-III.1/2. Subsequently after the tilting, the imine either switches the hydrogen bond donor atom (pathway A) or rotates inside the binding pocket without switching the H-bond (pathway B). Afterward, additional tilting leads to the Type I structures. For both pathways (A and B), the two different naphthyl fragments B1 and B2 of the BINOL backbone experience a different chemical environment and thus show different signals in the proton spectra. According to our previous NOE and chemical shift analysis, the exchange between E-I and E-II via rotation only (pathway B: n = 0) is excluded in TRIP, TRIM, and TiPSY binary complexes.^12,15

Figure 2.

Possible fast exchange pathways between E-I and E-II. In pathway A, the interconversion between E-II and E-I occurs inside the complex by tilting, switching, and tilting via the intermediate E-III.2/E-III.1. In contrast, in pathway B (n = 0; H-bond switching off), the exchange occurs via rotation only. In pathway C (n > 0; H-bond switching on), rotation and switching are coupled, yielding either the same conformation (n = odd) or different conformation (n = even). n is the number of occurring switching events prior to tilting.

The pathway C is an intervention of pathway A by the rotation or pathway B by the switching of the imine. This process can lead to the same conformation (Figure 2 pathway C: n = odd; Type E-II → E-II) or to a different conformation (Figure 2 pathway C: n = even; Type E-II → E-I). The first scenario with n is an odd number; the aniline part of the imine (red colored half ellipsoid) at the beginning of this process is placed above the naphthyl moiety B1 (black naphthyl fragment); and at the end the aniline part is located above B2 (gray naphthyl fragment). As both structures are C₂ related, the two naphthyl fragments B1 and B2 experience an identical chemical environment. In a similar way, for the second scenario (n = even), exchange between Type I and Type II occurs. Both scenarios can occur with equal probability. Thus, for the system in equilibrium, pathway C will lead to an exchange between Types I and II as well as to one averaged set of backbone signals with the combined information on Type I and Type II.

In our previous work,¹² pathway A was assumed to be operative for binary TRIP/E-imine complexes based on steric considerations; i.e., the E-imine cannot rotate inside the binding pocket, and in accordance with that backbone splitting was observed.⁵³ However, so far these dynamic exchange pathways were only deduced from NOE contacts and backbone splitting.

To analyze and quantify these fast exchange processes, we applied the recently reported 1D ¹H off-resonance R_1ρ method.⁴⁷ The application of the method mainly involves two parts, selection of proton sites and optimization of the method. The complete details of the method optimization are given in the SI. The selection of proton sites is discussed below.

Probe Selection (Proton Site Selection)

In order to maximize the accuracy of the method, the selected proton or protons must satisfy the following conditions: it should (i) exhibit a significant change in chemical environment (chemical shift) during the E-I ⇌ E-II exchange and (ii) be free from ¹H–¹H scalar couplings, (iii) and the selected proton peak should be free from signal overlap. Based on these criteria, we selected two probes for the TRIP/1 complex, i.e., the protons of the para-methyl group of the imine (Figure 3, green shaded, imine-pMe) and the H₁ proton (Figure 3, red shaded) from the catalyst backbone. Both undergo significant chemical shift changes during the E-I ⇌ E-II process and are free from significant ¹H–¹H scalar couplings. The respective singlet peaks from these two probes of TRIP/1 are depicted in the 1D ¹H spectrum (Figure 3). If both probes are sensing the same chemical exchange process, then both should show similar exchange rates.

Figure 3.

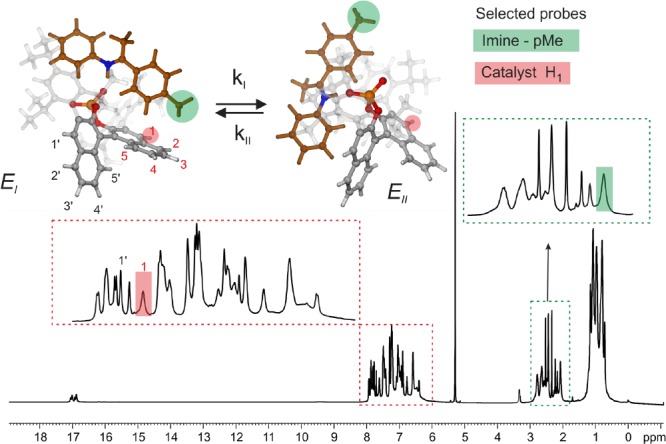
Selection criteria of probes (proton sites) for R_1ρ: (1) significant change in the chemical environment; (2) free from significant scalar coupling; and (3) free from signal overlap. The selected protons and the corresponding peaks in the 1D ¹H spectrum at 600 MHz and 180 K in CD₂Cl₂ are marked in red (catalyst site) and green (imine site).

R_1ρ Measurements

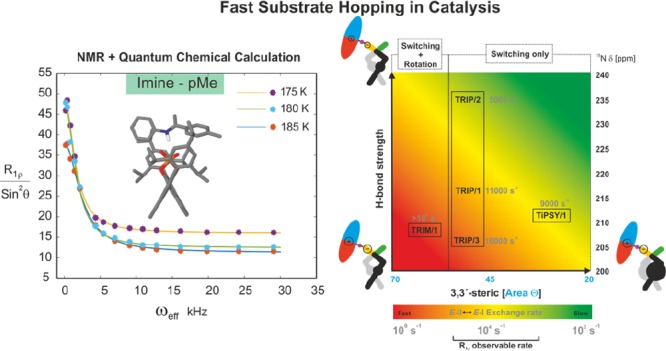
Initially, the R_1ρ relaxation was measured for both the proton sites at 180 K by using optimized constant spinlock duration and varying the effective field (B_eff, see SI). The experimental results for both protons showed an offset-Lorentzian decay of R_1ρ (obtained as R_1ρ/sin² θ, θ is 35°) with increasing effective field (Figure 4), which indicates that the proton sites experience a fast chemical exchange process. The exchange rate (k_ex) of this fast chemical exchange process was extracted by curve fitting (for a fit equation see SI eq 1).⁵⁴ Similar k_ex values for both probes were observed (at 180 K, for imine-pMe k_ex ≈ 12 000 s^–1, and for H₁ of catalyst k_ex ≈ 11 000 s^–1), which reveals that both the proton sites are experiencing the same fast E-I ⇌ E-II process.

Figure 4.

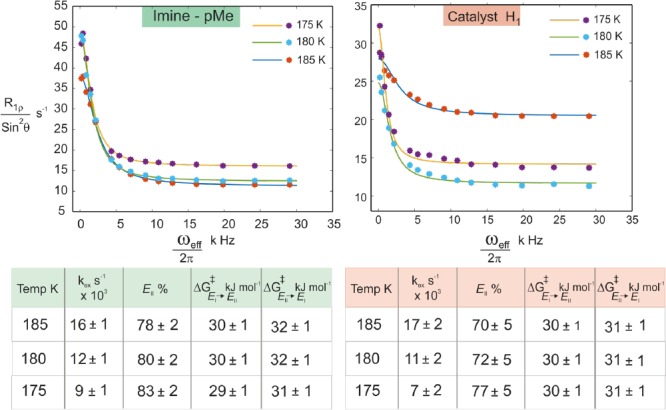
Offset-Lorentzian decay curves from the R_1ρ measurements for both probes (pMe-proton from imine and H₁ from the catalyst) indicate the presence of a fast E-I ⇌ E-II process. The k_ex values of both probes (extracted by curve fitting) show similar values, which confirms that both probes experience the same exchange process. R_1ρ measurements at three different temperatures (175–185 K) allow the extraction of population and the individual exchange rates of both directions.⁵⁵

After this initial establishment of the protocol, we extended the measurement of R_1ρ for both probes at two other temperatures (185 and 175 K, Figure 4) to extract the population ratio E-II:E-I, which facilitates the determination of the free energy barrier ΔG^⧧. At all three temperatures, we observed comparable exchange rates for both probes, which again confirms that both experience the same process. Further analysis (see SI) revealed a population ratio of E-II:E-I of 75:25 on average and an activation barrier for E-I → E-II of 30 kJ/mol at 180 K (Figure 4). The theoretically predicted ratio at 180 K between E-II and E-I of 61:39 corroborates further the experimental results. This good agreement is at first glance surprising since the offset of the predicted E:Z ratio to the experiment was shown in the previous work to be significantly large (calcd E:Z = 99.9:0.1 vs exptl E:Z = 80:20).¹⁵ This can be explained by the similarity in their interactions and geometries between the Type E I and Type E II. The better agreement between theory and experiment validates the theoretical model at least within E-conformations. Furthermore, due to this agreement between theory and experiment a reliable analysis of the exchange process in terms of interactions (H-bonds and steric) is possible by theory.

In conclusion, we successfully applied the R_1ρ method to measure exchange rates on the μs time scale in a real catalytic system, which is the prerequisite to systematically address the influence of steric and H-bond strength on the exchange process.

TRIP/1–3E Imine Complexes: H-Bond-Dependent Exchange Pathway A

Next, we attempted to assign the measured exchange rate in TRIP/1E to the possible pathways. In our systems, exchange proceeding via dissociation–reassociation is slow on the NMR time scale (<50 s^–1, see SI for details) and does not match with the measured experimental rates (10³–10⁴ s^–1). Hence, dissociation can be excluded. The steric bulk of the 3,3′- and imine-substituents hinders the rotation inside the binding pocket, which excludes pathway B (see Figure 2 for exchange pathways). This is validated further in the presented work by the semiempirical molecular dynamics (xtb-MD⁵⁶) showing that rotation does not occur in TRIP/1E even at highly elevated temperatures (300–370 K; see SI).⁵⁷ In pathway A (tilting, switching, tilting), the imine relocates from E-I/II toward E-III.1/2, and subsequently the hydrogen bond switches from one oxygen atom to the other (Figure 2). For the tilting step, theoretical calculations predicted complex multievents involving torsions of the aromatic moieties of the imine and simultaneous translation toward E-III.1/2. Due to the complexity of the tilting process and the number of involved transition states between E-I/II and E-III.1/2, no barrier could be estimated. Structural analysis showed that the hydrogen bond in the tilting step and the resulting intermediates E-III.1/2 are only slightly modulated. Hence, we can assume in a first approximation that the barrier for the tilting is affected by the interaction loss between the BINOL backbone and imine as well as the slight weakening of the hydrogen bond. For the switching step, the corresponding transition state revealed a bifurcated hydrogen bond type and an elongation of the hydrogen bond as well as a drastic change in the POH angle compared to E-I/II and E-III.1/2 (see Figure 5B). Therefore, a significant weakening of the hydrogen bond in the transition state is anticipated.⁵⁸ Together with the interaction loss with the BINOL backbone, a large enthalpic penalty is expected for this switching step. Thus, compared to the tilting step, the H-bond switching is postulated to be rate determining and be largely dependent on the hydrogen bond strength. Indeed, the calculated free energy barrier relative to E-II for the switching (ΔG^⧧_calc(II → I)) equals +31.4 kJ/mol, which adequately fits to the experimental value (ΔG^⧧_exp(II → I)= +31.3 kJ/mol) and suggests that the R_1ρ determined k_ex corresponds to the rate-determining switching process.

Figure 5.

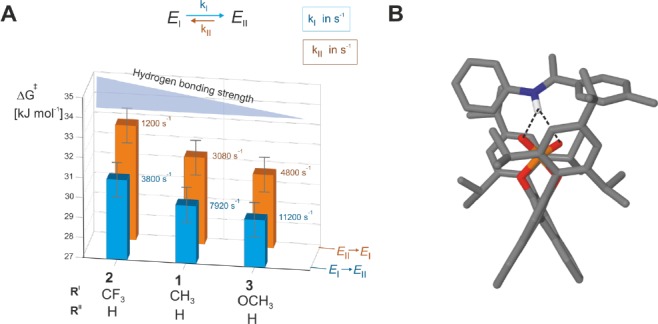
TRIP/imine complexes show a H-bond strength dependent exchange rate (measured at 180 K). (A) Upon decrease of the H-bond strength (via different substituents at the para-position of the ketimine) the free activation barrier of the E-I ⇌ E-II process for pathway A (H-bond switching) is reduced. (B) Theoretical calculations of the transition state of the H-bond switching show a bifurcated H-bond corroborating the experimental observation of a H-bond strength dependent process.

To further confirm this experimentally, we selected a series of imines with similar steric bulk but varying basicity to modulate the hydrogen bond strength (Figure 5). The highest exchange rate is determined for the TRIP complex with imine 3, followed by 1 and 2. Next, the order of hydrogen bond strengths was established according to our previous investigations.^14,50 According to this, the least basic imine 2 possesses the strongest hydrogen bond and the most basic imine 3 the weakest, while 1 is in between.¹⁴ This shows an inverse correlation between the hydrogen bond strength and the exchange rate or a direct correlation to the free energy barrier. The increased barrier due to the stronger H-bond was also computed for imines 1 and 2 (for the process II → I: ΔΔG^⧧_exp (2-1) = +1.4 kJ/mol; ΔΔG^⧧_calc (2-1) = +3.1 kJ/mol), which corroborates the experimental results. Thus, within the investigated TRIP/imine complexes, i.e., similar steric environment, the exchange between E-I and E-II is strongly dependent on the H-bond strength. This is congruent with our previous assumption that hydrogen bond switching (pathway A) is the operative exchange pathway. In summary, both experimental and theoretical results clearly proved that the H-bond switching step is the measured process and rate determining in pathway A.

TRIM/1–3E Imine Complexes: Reduced Sterics Allow for Rotations

To understand the effect of the 3,3′-substituents on the exchange process, which are key to reactivities and selectivities in these catalytic reactions,^59,60 we selected TRIM (see Figure 1A for structure) as the CPA due to its structural similarity to TRIP. In our previous investigations on binary TRIM/imine complexes, we could identify the same four core structures E-I, E-II, Z-I, and Z-II but also observed several alterations compared to the TRIP systems.¹⁵ With identical imines, TRIM forms weaker hydrogen bonds compared to TRIP, which should result in a faster hydrogen bond switching process. Furthermore, in TRIM, neither E- nor Z-imine complexes showed a signal splitting of the BINOL backbone (Figure 6C: averaged BINOL backbone), which suggests pathway C as an exchange pathway between E-I and E-II. Moreover, dimers of the binary complex [TRIM/E-imine]₂ were also identified, which are in slow exchange with the respective monomeric complexes and the free imine.

Figure 6.

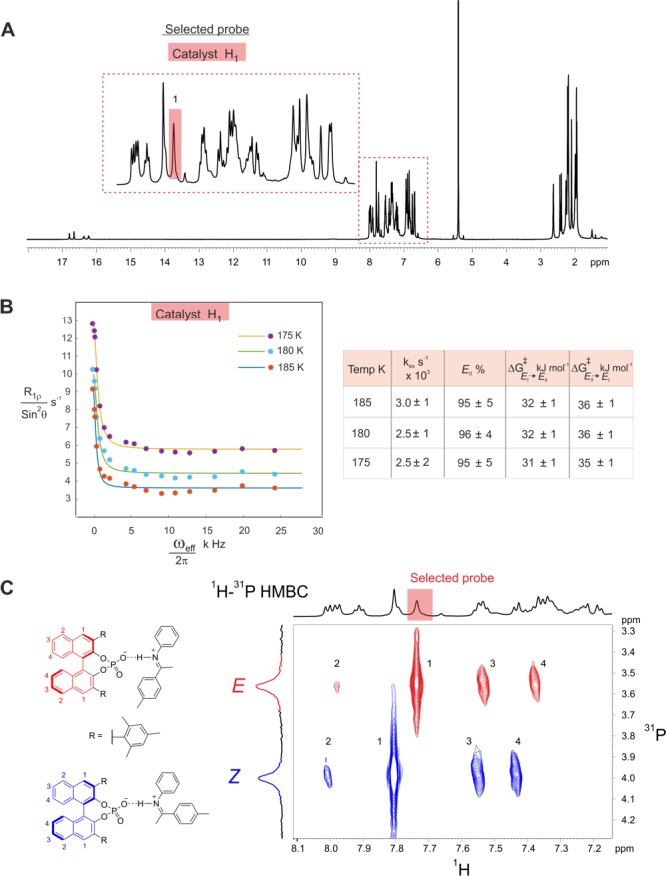
R_1ρ measurements and ¹H–³¹P HMBC spectra of TRIM/1-3E complexes reveal an additional rotational process. (A) Selected H₁-proton signal of the catalyst to observe and quantify the E-II/E-I exchange process by R_1ρ experiments for complex TRIM/1E (¹H spectrum at 180 K and 600 MHz in CD₂Cl₂). (B) Despite calculations indicating a faster switching process for TRIM/1E compared to TRIP/1E (for TRIM/1E: ΔG^⧧_calc(II → I) = +26.4 kJ/mol; ΔG^⧧_calc(I → II) = +22.9 kJ/mol; calculated k_ex = k_I–II + k_II–I = 0.9 × 10⁶ s^–1; not observable by R_1ρ), the R_1ρ decay curves and their analysis showed a slower exchange process, suggesting the presence of an additional pathway (rotation). (C) The absence of backbone splitting confirmed the activated rotation in the exchange process.

Similar to the investigated TRIP systems, the catalyst signal H₁ was used as probe because the corresponding peak is well separated (Figure 6A). In addition, a significant chemical shift difference between E-I and E-II was expected for the H₁ proton. Unlike in TRIP/1, the imine signal of the para-CH₃ substituent of 1 (Figure 6A) was not suitable, as it partially overlapped with the CH₃ signals of the 3,3′-substituent. The same optimized parameters as for TRIP were used in the TRIM systems (for details see SI). Surprisingly, the determined exchange rate of 3 × 10³ s^–1 for TRIM/1 was significantly lower than that for TRIP (11 × 10³ s^–1 see Figure 6B), although a faster exchange was expected due to the weaker hydrogen bond. Hence, we further modulated the hydrogen bond strength in TRIM/imine complexes by varying the imine. However, the TRIM complexes with E-imines 1, 2, and 3 gave similar exchange rates of 2–3 × 10³ s^–1 despite the alteration in H-bond strength (see SI for details on TRIM/2 and TRIM/3). This lack of dependency for TRIM/E-complexes demonstrates that either a different exchange pathway is operative compared to the respective TRIP systems or a shift of the rate-determining step occurs, which is then independent of the H-bond strength. Furthermore, the observed averaging of the BINOL backbone indicates also an alteration in the exchange mechanism. This is validated by theoretical calculations, which predicted a much lower switching barrier for TRIM/1 than those experimentally observed (ΔG^⧧_calc(II → I) = +26.4 kJ/mol; ΔG^⧧_exp(II → I) = +36.0 kJ/mol).

As in TRIP systems, the exchange between TRIM/1E and free imine as well as with the dimer [TRIM/1E]₂ is slow on the NMR time scale, and separated sets of signals were identified for these species. Hence, exchange pathways via association/dissociation or any process including the dimer do not contribute significantly to the measured exchange rates. For pathway A, we expected a backbone splitting as in TRIP, which is not in agreement with the observed signal averaging.⁶¹ On the other hand, the reduced steric bulk of TRIM compared to TRIP⁹ could potentially enable rotation of the E-imine in the binding pocket. Thus, pathway C could be operative, and the two naphthyl fragments of the BINOL backbone will be symmetrized by the exchange. To corroborate the participation of rotation in the exchange pathway, VT-MD simulations from 300 to 350 K were performed. Indeed, the trajectory analysis of the MD at 340 K (Figure 7) revealed that in contrast to TRIP rotation of the E-imine in the binary TRIM/1 complex is possible. From the MD simulation of TRIM/1, the fast switching and tilting of the imine (pathway A) occur over the defined time frame of 4000 ps (Figure 7: red and green shaded binary complexes), which allows the exchange between Type I and Type II. The intervention of tilting and switching by the imine rotation event takes place after ca. 3000 ps (dotted line) and converts the red shaded binary complex to the green shaded binary complex. This leads to an averaging of BINOL backbone peaks observed in NMR.

Figure 7.

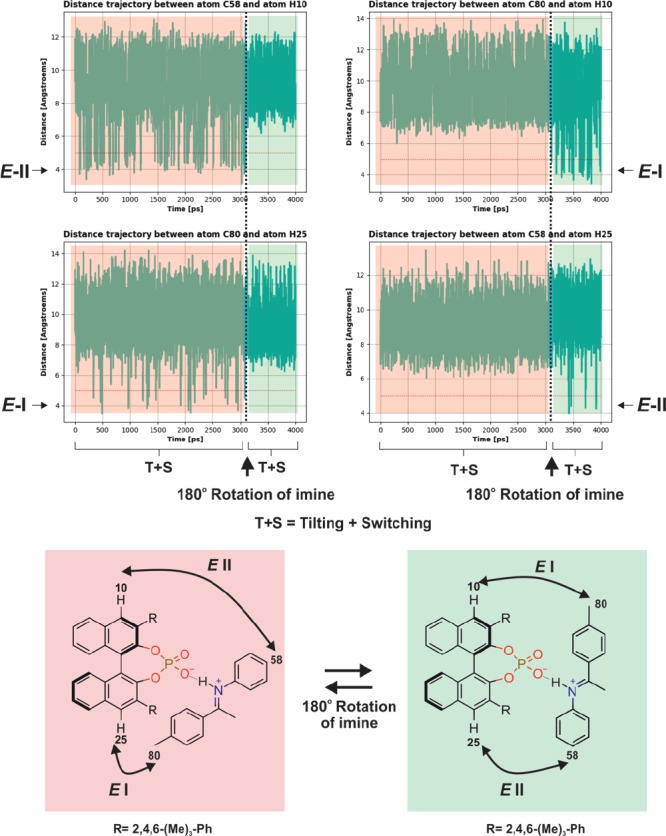
xtb-MD simulations corroborate a rotational exchange process in TRIM/1E. Distance trajectory between selected atoms from semiempirical MD at 340 K for a TRIM/1E complex in CD₂Cl₂. From 0 to 3000 ps (red shaded box), tilting and switching of imine inside the complex occur (similar to the exchange between Type E-I and E-II in TRIP). Then a rotation occurs after 3000 ps (dotted line) with continued switching and tilting (green shaded box) leading to an averaged BINOL backbone signal observed in NMR. The red shaded binary complex is related to the green shaded binary complex by a 180° rotation of the imine. In the red shaded binary complex E-II conformation is marked by a short distance between C58 and H10, while in the E-I conformation C80 is in proximity with H25. The green shaded binary complex showed the alternation of the contact matrix after the rotation of the imine.

TRIM/4E Imine Complex: Disabling of Rotation by Steric Hindrance

To hinder the rotation of the E-imine inside the complex and thus to validate indirectly the previous results, we increased the steric bulk of the imine by introducing two t-butyl groups, one on each side (see Figure 8 for imine 4). The structural analysis of TRIM/4 (see SI for details) revealed the presence of the four core structures by NOE analysis. As in all other investigated TRIP and TRIM systems, two sets of signals were obtained, one featuring an E-imine and the other a Z-imine. This implies that the exchange between Type I and Type II is present and fast on the NMR time scale. Interestingly, in contrast to all other investigated TRIM/imine complexes, no dimers [TRIM/4]₂ were detected, which indicates that the steric repulsion overrides the attractive interactions in the dimer. Additionally, signal splitting of the BINOL backbone is now observed indicating that the rotation process is now disabled as intended (Figure 8C). In terms of H-bond strength, TRIM/4E is positioned between TRIM/1E and TRIM/3E (for details see SI).

Figure 8.

R_1ρ measurements for the TRIM/4E complex showing disabled rotation by the increased steric of the imine 4. (A) Selected peak in the spectra to observe and quantify the E-II/E-I exchange process. (B) No offset-Lorentzian decay was detected by the R_1ρ experiment, indicating both no rotation and a too fast switching. (C) The backbone splitting is restored in the ¹H–³¹P HMBC spectrum due to disabled rotation.

The application of the R_1ρ method with the identical pulse program parameters as before on the catalyst backbone signal H₁ shows no signal decay on increased ω_eff (Figure 8B). This means that the fast exchange process between E-I and E-II (see above) is not in the time scale accessible by R_1ρ (10³–10⁵ s^–1). The computationally estimated exchange rate of TRIM/1E for the switching step is in the order of 10⁶ s^–1. For TRIM/4E an even higher exchange rate is expected due to the weaker hydrogen bond, assuming that the increased sterics of imine 4E does not interfere with the switching process. Hence, the absence of decay in the R_1ρ for TRIM/4E is due to the absence of the rotation. In other words, the decay we observed in TRIM/1-3E is the rotation in pathway C. Thus, we demonstrated that the modification of 3,3′-substituents can alter the operative exchange pathways, i.e., enabling rotation due to reduced steric hindrance. In addition, acceleration of the H-bond switching rate is possible due to the modulations of H-bond strength and the catalyst’s steric properties.

TiPSY/1E Imine Complex: Influence of 3,3′-Substituents on the H-Bond Switching Rate

To qualitatively determine the influence of the catalyst’s sterics on the rate of the switching process, we selected TiPSY/1E. Due to the increased steric property of TiPSY,⁹ the rotation of the E-imine (pathway B and C) inside the catalyst pocket is disabled similar to the situation in TRIP and was confirmed by the backbone splitting in ¹H spectra (see SI). NOE analysis showed a fast exchange between Type E-I and E-II as in other binary complexes, leaving the exchange pathway A being the only operative mechanism.¹⁵

According to the ¹⁵N chemical shift^14,15 (see Figure 9), TiPSY/1E possesses a H-bond strength between TRIP/1E and TRIP/3E. Thus, if the switching process is solely dependent on the H-bond strength, we expect an exchange rate between the ones of TRIP/1E and TRIP/3E. However, if also the steric requirement of the 3,3′-substituent of the catalyst has an influence, then a deviating exchange rate is expected.

Figure 9.

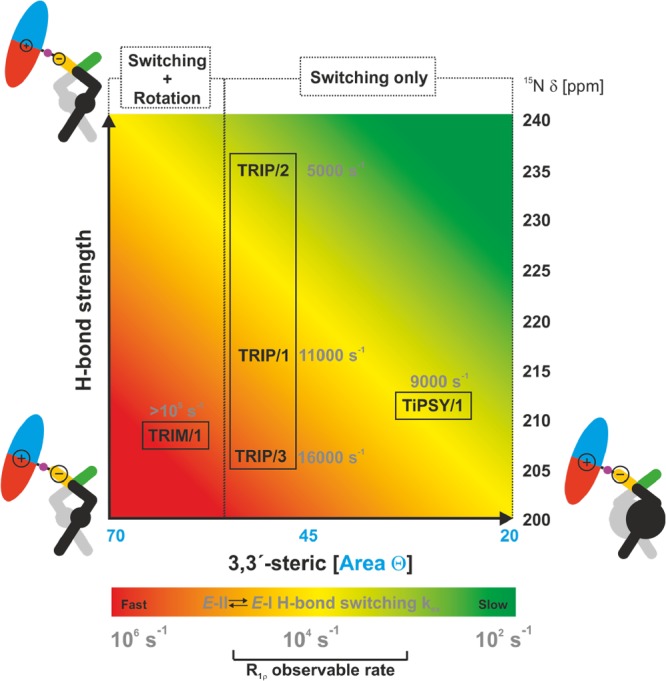
Overview of the present work showing the influence of the size of the 3,3′-substituents (according to the cone size of the binding pocket)⁹ and the H-bond strength (expressed by δ(¹⁵N))^50,63,64 on the exchange pathway and rate. Variation of the imine basicity in TRIP complexes modulates the switching rate proving a H-bond strength dependent process. Reduced sterics and weakening of the H-bond as in TRIM/imine complexes accelerate the H-bond switching process beyond detection in R_1ρ measurements and allow for the rotation of the imine. An increase of 3,3′-steric bulk in a TiPSY imine complex disables the rotation and decelerates the switching process significantly. The newly applied R_1ρ method in catalysis extends the measurable exchange rate from 10³ to 10⁵ s^–1.

The obtained plot from the R_1ρ measurement showed a decay and an exchange rate of 9000 s^–1 at 180 K (see SI and Figure 9). Hence, the operative tilting–switching process is detectable, and its rate is lower than expected from its H-bond strengths. This result confirms the trend already indicated by the switching rates of the TRIP and TRIM/imine complexes:⁶² the switching process is a function of two variables, H-bond strength and steric properties of the 3,3′-substituents (Figure 9).

Conclusion

This study illustrates the potential of relaxation dispersion NMR in chemical catalysis. In contrast to biomolecules, in our system low-temperature applications are possible, which extend the time resolution again by three orders of magnitude (e.g., 300 to 180 K results in a factor of 5000). As a result, processes on the ns time scale at room temperature can be resolved with NMR at low temperature.

As a result, the application of R_1ρ measurements at low temperatures even allowed us to analyze the kinetics of a single hydrogen bond switch, which to our knowledge is so far unprecedented in chemical catalysis. By combining these R_1ρ measurements and theoretical calculations we succeeded to quantify the dynamics and visualize different possible pathways (switching, switching-rotation combined) for E-I ⇌ E-II imine exchange inside the CPA catalyst cavity in ion pair catalysis. These observed mechanistic pathways at the molecular level were dependent on both sterics and H-bond strengths (Figure 9). Alteration at either catalyst or substrate affected the dynamics in terms of both magnitude and mechanism. The rate of the tilting–switching process increased with the decrease of H-bond strength under comparable sterics, indicating H-bond switching as the rate-determining step, which was corroborated by theoretical calculations. On the other hand, reduced sterics significantly accelerated (at least by an order of magnitude) the switching process and in addition enabled a rotational pathway.

We believe that this conformational resolution of the catalyst–substrate complex structures and their dynamics (in the absence of the reductant) by experiment opens a new era in mechanistic investigations of catalytic reactions, toward designing and understanding the catalytic reactions in terms of conformational space (flexibility) and weak interactions (H-bond strength and sterics).

Supporting Information Available

The Supporting Information is available free of charge. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.9b07841.

• Procedure for the imine synthesis and sample preparation. Pulse sequence, parameter optimization, curve fitting, and analysis of the R_1ρ experiments. Additional R_1ρ plots. Structural analysis of binary CPA/imine complexes. Computational details (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.