Exposing the Underlying Relationship of Cancer Metastasis to Metabolism and Epithelial-Mesenchymal Transitions

Summary

Cancer is a disease governed by the underlying gene regulatory networks. The hallmarks of cancer have been proposed to characterize the cancerization, e.g., abnormal metabolism, epithelial to mesenchymal transition (EMT), and cancer metastasis. We constructed a metabolism-EMT-metastasis regulatory network and quantified its underlying landscape. We identified four attractors, characterizing epithelial, abnormal metabolic, mesenchymal, and metastatic cell states, respectively. Importantly, we identified an abnormal metabolic state. Based on the transition path theory, we quantified the kinetic transition paths among these different cell states. Our results for landscape and paths indicate that metastasis is a sequential process: cells tend to first change their metabolism, then activate the EMT and eventually reach the metastatic state. This demonstrates the importance of the temporal order for different gene circuits switching on or off during metastatic progression of cancer cells and underlines the cascading regulation of metastasis through an abnormal metabolic intermediate state.

Graphical Abstract

Highlights

• •We develop an approach to quantify the interplay among metabolism, EMT, and metastasis
• •An intermediate abnormal metabolic state exists in metastatic progression
• •Landscape and path indicate that the metastasis is a sequential process
• •Landscape suggests a potential therapeutic strategy by targeting BACH1 and metabolism

Biological Sciences; Cancer; Cancer Systems Biology; Molecular Network

Introduction

Cancer is a disease involving the changes in underlying gene regulatory networks. Lately, some hallmarks of cancer have been proposed to characterize the cancerization (Hanahan and Weinberg, 2000, Hanahan and Weinberg, 2011). For example, abnormal metabolism is a hallmark of cancer, which has been explored in recent studies (Hanahan and Weinberg, 2011, Boroughs and Deberardinis, 2015). Metastasis has been suggested to account for the great majority of cancer-related deaths, although its underlying mechanism remains elusive (Lambert et al., 2017). Epithelial to mesenchymal transition (EMT) has long been shown to be related to the acquisition of malignant cell traits, such as motility, invasiveness, and tumor-initiating potential, and therefore being associated with the progression of cancer metastasis (Brabletz et al., 2018, Lambert et al., 2017, Gibbons et al., 2009, Thiery et al., 2009). A critical question arises as to what the connections among these hallmarks of cancers are. For example, what is the relationship between EMT and cancer metabolism? And how do they contribute to the cancer metastasis, the most fatal stage of tumors?

Cancer cells have abnormal metabolism compared with normal cells. In the low oxygen and oxygen-free conditions, metabolisms of cells are mainly in glycolysis form that produces less ATP. However, under normoxic conditions, the metabolisms for cancer cells and normal cells are different. Cancer cells often use glycolysis to generate energy, whereas normal cells use glucose for oxidative phosphorylation (OXPHOS). This phenomenon is called Warburg effect (Munozpinedo et al., 2012). Recently, Yu et al. proposed a mathematical model to study the regulations for genes and metabolites on cancer metabolism (Yu et al., 2017), which has been extended to a more complete model in the following work (Jia et al., 2019). However, the global stability and stochastic dynamics of cancer metabolism remain to be elucidated. More importantly, the connection between metabolism and metastasis remains unclear. These issues are critical to the mechanistic understanding of tumorigenesis and have not been fully clarified from previous studies.

Here, we aim to apply the landscape approach to address the above-mentioned issues by investigating the stochastic dynamics of underlying gene regulatory networks for cancer metastasis. The classic Waddington landscape has been proposed as a metaphor to explain the development and differentiation of cells (Waddington, 1957). Recently, the epigenetic landscapes for biological networks have been quantified from various approaches (Wang et al., 2011, Liao and Lu, 2013, Lv et al., 2015, Li and Wang, 2014a, Lu et al., 2014b, Ge and Qian, 2012, Ge and Qian, 2016, Zhang and Wolynes, 2014, Huang et al., 2005) and employed to investigate the stochastic dynamics of embryonic development and cancer (Wang, 2015, Wang et al., 2011, Li and Wang, 2013, Li and Wang, 2014b, Chen et al., 2014, Li and Wang, 2015, Huang, 2013, Li, 2017). From the landscape perspective, different cell types are described as the basins of attraction on a potential surface.

To uncover the mechanisms of the interplay among metabolism, EMT, and cancer metastasis, we constructed a metabolism-EMT-metastasis network by mining the experimental literature and combining these three gene regulatory circuits (Yu et al., 2017, Li and Wang, 2015, Lu et al., 2014a, Jolly et al., 2015b, Lee et al., 2014). The landscape for the metabolism-EMT-metastasis network displays four stable cell types quantified by attractors, characterizing epithelial cell state (E), abnormal metabolic cell state (A), mesenchymal cell state (M), and metastatic cell state (Met), respectively. Importantly, we identified an abnormal metabolic state. We also calculated the minimum action paths (MAPs) to quantify the most probable transition paths for cell fate decision processes in metastatic progression. The MAPs among the four cell states quantify the dynamical processes for how cells switch from the epithelial state to the metastatic state: cells need to first change their metabolism, then finish the EMT and finally enter the metastatic state. This demonstrates the importance of the temporal order for different gene circuits switching on or off in cell fate decision process. We found that the transition path for metastatic process and the transition path for anti-metastatic process are irreversible. The transition actions among attractors are correlated with the potential barriers for basins but provide more accurate descriptions for kinetic switching. By the global sensitivity analysis for the metabolism-EMT-metastasis network based on the transition actions, we identified some critical network elements governing the dynamics of cellular metabolism and metastasis.

To further shed light on the interplay specifically between metabolism and EMT, we explored a subnetwork of the whole network, i.e., an EMT-metabolism regulatory network (blue and green boxes in Figure 1), by neglecting the metastasis circuit (yellow box in Figure 1) and further quantified its potential landscape. The landscape for the EMT-metabolism network displays three stable states (attractors) including epithelial (E) state, mesenchymal (M) state and abnormal metabolic (A) state. To further verify our modeling results, we compared the gene expression data of three types of cancers (one for single-cell RNA sequencing [RNA-seq] data and two for population data) and the landscape, which supports the consistency between the gene expression data and the landscape results (Pastushenko et al., 2018, Cancer Genome Atlas Research Network et al., 2013, Agrawal et al., 2014).

Figure 1.

The Regulatory Network for the Interplay among EMT, Metabolism, and Cancer Metastasis including 16 Gene or Metabolite Nodes and 51 Regulation Links (22 Activations and 29 Inhibitions)

The network from left to right corresponds to the core circuit of metabolism, EMT, and cancer metastasis, respectively. The orange nodes, yellow nodes, and pink nodes represent metabolites, microRNAs, and genes, respectively. The arrows represent activations, and the short bars represent inhibitions.

Previously we have developed a partial self-consistent approximation (PSCA) approach to calculate the potential landscape for high-dimensional gene regulatory systems (Li and Wang, 2013, Li and Wang, 2014a). One limitation of the PSCA approach is that it assumes weak correlations among gene variables (gene expression levels). This approach may not be accurate for the cases in which variables have strong correlations. Here, to resolve this issue, we developed a truncated moment equations (TME) approach. This approach does not rely on assumptions of weak correlations between variables. By comparing the results of both the TME method and PSCA method with the simulation results, we showed that the TME approach provides a more precise description for the probability distribution of the system than that of the PSCA approach. In summary, the TME approach offers a new method to quantify the potential landscape for a high-dimensional gene regulatory system, and the results of landscape and kinetic paths provide new insights into the mechanistic understanding of the interplay among metabolism, EMT, and cancer metastasis in the process of cancer progression.

Results

Regulatory Network Models for Metabolism, EMT, and Cancer Metastasis

Recently, Yu et al. constructed a computational model for cancer metabolism using ordinary differential equations (ODEs), which includes two genes (AMPK and HIF-1) and two metabolites (noxROS and mtROS) (Yu et al., 2017). The EMT has been suggested to be related to metastatic progression (Brabletz et al., 2018, Lambert et al., 2017, Gibbons et al., 2009). So, a critical question would be, are there any connections among EMT, metabolism, and cancer metastasis? To uncover the mechanisms underlying the interplay between EMT, metabolism, and metastasis, we established a metabolism-EMT-metastasis gene regulatory network by incorporating the core components for each process through mining the experimental literature (Figure 1). The metabolism-EMT-metastasis network involves 16 components, including ten genes, two metabolites, and four microRNAs. AMPK, HIF-1, mtROS, and noxROS are the core components controlling cellular metabolism (Figure 1, blue box). SNAIL, ZEB, OCT4, MDM2, miR-145, miR-200, miR-34, and P53 are the core components governing the EMT (Figure 1, green box). RKIP, BACH1, LIN28, and Let7 are the core components governing the metastasis (Figure 1, yellow box) (Lee et al., 2014). The experimental evidences for the interactions among different components are shown in Table S1.

Based on the network structure, we wrote down the ODEs describing the time evolution of relative expression levels for each of the 16 genes or metabolites. The ODEs depicting the dynamic evolution of the metabolism-EMT-metastasis system are shown in Equation 1:

$$\frac{dX}{dt}=g_X\cdot G-k_X\cdot K\cdot X$$ (Equation 1)

Here, X represents the level of the gene expression or the metabolite. $g_X$ and $k_X$ denote the basal synthesis rate and degradation rate of X, respectively. G and K denote the regulation of other genes or metabolites on the synthesis and the degradation of X, respectively. The activation or inhibition regulations among different components are described by the product of the shifted Hill function $H^s\left(Y,S,\lambda ,n\right)=1+\left(\lambda -1\right)\frac{Y^n}{S^n+Y^n}$ (representing the regulation of component Y on component X). Here, λ represents the fold change for the regulations ($\lambda >1$ for activation and $0<\lambda <1$ for inhibition). S represents the threshold of the sigmoidal function, and n is the Hill coefficient, which determines the steepness of the sigmoidal function (Li and Wang, 2013, Li, 2017) (see Supplemental Information Section S1 for more details on how to determine the parameters). The specific ODEs of the metabolism-EMT-metastasis model are shown in Supplemental Information Section S2 and corresponding parameter values are shown in Tables S2 and S3.

Landscape Reveals the Cascade for Metabolism, EMT, and Metastasis

Yu's work provides a basis for understanding the cancer metabolism from a deterministic ODE model (Yu et al., 2017). However, the stochastic dynamics and global properties of cancer metabolism remain to be elucidated, as the fluctuations have been suggested to play critical roles in biological systems, including intrinsic fluctuations from a finite number of molecules and external fluctuations from highly inhomogeneous environments (Swain et al., 2002, Kaern et al., 2005, Thattai and Van, 2001). Also, it is crucial to uncover the dynamical mechanisms for the interplay among metabolism, EMT, and cancer metastasis.

Previously, we have developed a partial self-consistent approximation approach to study the stochastic dynamics for high-dimensional systems by the potential landscape theory (Li and Wang, 2013, Li and Wang, 2014a). One limitation of the PSCA approach is that it assumes the weak correlation between variables, which in some cases may not be accurate. Here, we improved previous methods and developed a Truncated Moment Equations (TME) approach (see Supplemental Information Section S3 and Section S4) to calculate the probability distribution of gene expression levels and obtain the potential landscape. By comparing the two approaches, we showed that the TME approach provides a more precise description for calculating the probability distribution of the systems (see Supplemental Information Section S5, Section S6, Figures S1 and S2 for details).

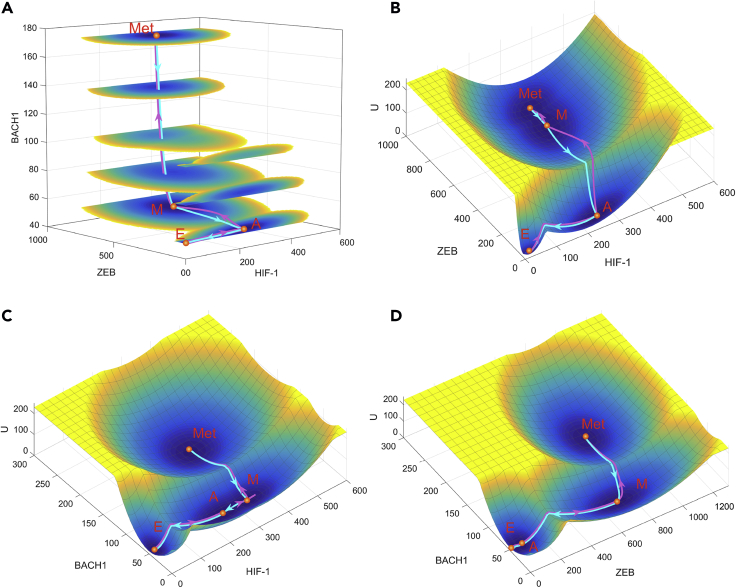
Based on the metabolism-EMT-metastasis regulatory network model (Figure 1), we calculated the steady state probability distribution of the system employing the TME approach and acquired the potential landscape by $U=-\ln P_{ss}$ (Wang et al., 2008, Wang et al., 2011, Li, 2017, Li and Wang, 2014a). Here $P_{ss}$ represents the steady state probability distribution and U represents the dimensionless potential. Because we are dealing with a 16-dimensional potential landscape, it is hard for visualization. Here we pick three representative marker genes, HIF-1, ZEB, and BACH1, as three coordinates and project the 16-dimensional landscape into the three dimensional space (see Figure S3 and Section S7 for another way to show landscape). In this way, we have a four-dimensional landscape, as displayed in Figure 2A. It is worth noting that our major conclusions do not depend on the specific choice of the coordinates (see Figure S4 for landscapes with other pairs of variables as coordinates) because we also calculated the transition actions among different attractors, based on the 16-dimensional state space. On the landscape the blue region represents high probability or low potential and the yellow region represents low probability or high potential. We identified four stable states on the landscape, which characterize epithelial (E), abnormal metabolism (A), mesenchymal (M), and metastatic (Met) cell states, respectively (Figure 2, see Table S4 for stable state gene expression levels for the quadrastable landscape). Importantly, we identified a new intermediate state, which we defined as the abnormal metabolism (A) state, since it has an increased expression of the glycolysis marker gene HIF-1.

Figure 2.

Landscape and Path for the Metabolism-EMT-Metastasis Model Shown in ZEB, HIF-1, and BACH1 Coordinates

(A) Landscape is shown in a four-dimensional picture. The blue regions represent higher probability or lower potential, and the yellow regions indicate lower probability or higher potential. Solid magenta lines represent transition paths from the E to A, M, and Met states. Solid cyan lines represent transition paths from the Met to M, A, and E states.

(B) Two-dimensional landscape and kinetic paths are displayed in HIF-1/ZEB coordinates.

(C) Two-dimensional landscape and kinetic paths are displayed in HIF-1/BACH1 coordinates.

(D) Two-dimensional landscape and kinetic paths are displayed in ZEB/BACH1 coordinates. E, epithelial state; A, abnormal metabolic state; M, mesenchymal state; Met, metastasis state.

See also Figure S4 and Table S4.

From the network structure of our metabolism-EMT-metastasis regulatory network, each of these three circuits studied here can be multistable, e.g., three states in EMT, three states in metabolism, and two states in metastatic circuit. Therefore, if there is no coupling between these three circuits, there are a total of $3\times 3\times 2=18$ possible states. However, the coupling among these circuits can introduce correlations and thus lead to a much smaller number of stable states, as discussed in previous work (Jolly et al., 2015b, Bocci et al., 2018). We need to stress that, although we identified four stable states in our model, it is possible to discover more cell states (e.g., partial EMT state) by fine-tuning parameters, owing to the complexity involved in EMT and cancer metastasis.

Here, the E state has a low HIF-1, low ZEB, and low BACH1 expression. So, the marker genes for the abnormal metabolism, the EMT, and the metastasis are all off. The A state has a high HIF-1, low ZEB, and low BACH1 expression and therefore corresponds to an abnormal aggressive metabolic phenotype (i.e., aerobic glycolysis state) whereby cancer cells change their metabolism to produce energy more quickly. Besides, we have a mesenchymal state with a high HIF-1, high ZEB, and low BACH1 expression and a metastatic state with a high HIF-1, high ZEB, and high BACH1 expression. Previous work has shown experimentally that the metastatic state has high expression level of BACH1, low expression level of RKIP, and Let7 for breast cancer (Lee et al., 2014). Our metastatic attractor from the model is consistent with this experimental observation (see Table S4). To quantify the kinetic transitions among these states, we calculate the kinetic transition paths among different cell states by minimizing the transition actions $\mathcal{S}$, which are also called minimum action paths (MAPs) (see Table S5 for results of transition actions among four states and Supplemental Information Section S8 for how to obtain the transition paths). Figures 2A and 2B show the landscape and transition paths for the quadrastable system in four-dimensional and three-dimensional space, respectively. The magenta paths denote the transitions from the epithelial state to the metastatic state (metastatic progression process), whereas the cyan paths denote the transitions from the metastatic state to epithelial state (de-metastasis process). The transition paths for the E to metastasis state transition and the backward transition paths from metastasis to the E state are not identical, reflected by the disparity between the forward and backward kinetic transition paths. This irreversibility of MAPs is a consequence of non-gradient force, i.e., curl flux (Wang et al., 2008, Li and Wang, 2014a).

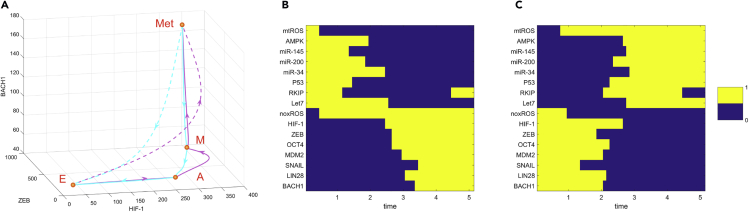
To see the transition path more clearly, we showed both the direct transition path (from E to Met attractor, dashed lines) and indirect transition path (for nearby attractors, solid lines) from minimizing corresponding transition actions (Figure 3A). We found that, for the E to Met transition, the direct transition path (dashed magenta line) is inclined to follow the similar mode as the indirect transition path is (solid magenta line), i.e., the E to Met transition is inclined to go through the attractor states in the middle of the transition. Here, the landscape and the transition paths are both from three-dimensional projection for the whole system (Figures 2 and 3A). To see the paths for more components, we visualized the 16-dimensional transition paths between the E and the Met states by discretizing the gene expression levels of all 16 genes or metabolites (Figures 3B and 3C). For the metastatic progression process, different genes switch on or off in different orders. For example, microRNAs and tumor repressor P53 are first down-regulated. Then the HIF-1 level is increased, indicating a transition to the abnormal metabolic state, which is followed by the ZEB activation indicating the EMT occurs. Finally, the BACH1 is activated, indicating that cells enter the metastatic state. Therefore, both the continuous and discrete kinetic paths suggest that metastasis is a sequential process, i.e., abnormal metabolism precedes EMT, which precedes metastasis. Interestingly, we found that for both metastatic progression and de-metastasis process (Figures 3B and 3C), both mtROS and noxROS switch in the very early stage in the whole cell fate transition process. This suggests that reactive oxygen species (ROS) plays critical roles in regulating cancer metastasis (Ishikawa et al., 2008), presumably because of its prominent influence on the cellular metabolism.

Figure 3.

Transition Paths among Different Cell States

(A) Fixed points and kinetic transition paths between different cell states. Solid magenta lines represent transition paths between nearby states (from E to A, A to M, and M to Met state) in metastatic progression direction. Solid cyan lines represent transition paths between nearby states (from Met to M, M to A, and A to E state) in de-metastasis direction. The dashed lines represent the direct transition path from E to Met state and from Met to E state, respectively.

(B and C) Discrete transition paths from E state to Met state (B) and from Met state to E state (C) in terms of expression levels of 16 genes and metabolites. Relative gene expression levels are discretized to 0 or 1; 1 represents that the corresponding genes are in the activated state and 0 represents that the corresponding genes are in the repressed state. X axis shows the time points along the transition path. E, epithelial state; A, abnormal metabolic state; M, mesenchymal state; Met, metastasis state.

See also Table S4.

The quadrastable landscape for metastasis and the kinetic transition paths between attractors demonstrate that the transitions from epithelial state to metastatic state follow a specific order, i.e., first increasing the expression level of HIF-1, then increasing the expression level of ZEB, and finally increasing the expression level of BACH1. These results suggest that the temporal order for different genes switching on or off is critical for the process of metastatic progression in cancer cells. In the first stage, the cells change their metabolism to an abnormal aggressive form (e.g., aerobic glycolysis). In the second stage, cells finish the EMT process where cells obtain mesenchymal features in numerous different settings (Kalluri, 2009). In the last stage, cells improve their metastatic ability by activating metastasis marker genes, such as BACH1. These results agree well with the observations that EMT induction in cancer cells results in the acquisition of invasive and metastatic properties (Singh and Settleman, 2010).

Global Sensitivity Analysis Identifies the Key Players for the Interplay among Metabolism, EMT, and Metastasis

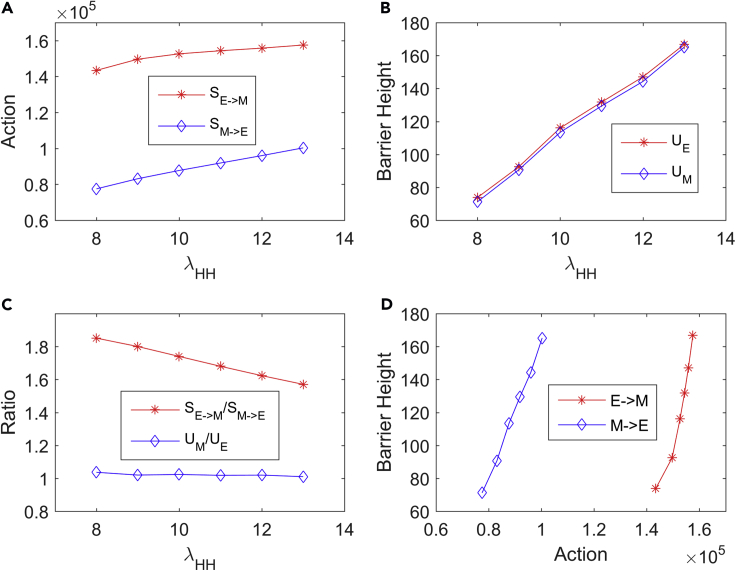
To quantify the topography of landscape, we define the barrier height as the potential difference between the local minimum and the corresponding saddle point. To evaluate the relationship between the transition action and the barrier height, we change the ${\lambda }_{hh}$ (the fold change for the self-activation of HIF-1) to see how the transition action changes with the potential barrier. For simplicity, we use the metabolism-EMT-metastasis network but constrain the parameter choices within the bistable regime (the E state and M state coexist) to calculate both barrier heights and transition actions. From the results (Figure 4), the barrier height and the corresponding transition action both increase as ${\lambda }_{hh}$ increases (Figures 4A and 4B). However, the transition action from the M to E state increases faster than the transition action from the E to M state (Figure 4C, red line). This is because ${\lambda }_{hh}$ quantifies the self-activation of HIF-1, which promotes the glycolysis state and M state. A faster increase of transition action from the M to E state means a more stable M state, which is consistent with the role of ${\lambda }_{hh}$ for promoting HIF-1. This result is not reflected by the barrier height results (Figure 4C, blue line), although there is a statistical correlation between barrier height and transition action (Figure 4D). This suggests that the transition action provides a more precise description for the dynamics of the system than the barrier height, since the barrier heights are calculated from two-dimensional approximation, whereas the transition actions are calculated directly from the high-dimensional system.

Figure 4.

The Relation between Transition Action and Barrier Height Based on the Bistable Landscape of the Metabolism-EMT-Metastasis Model as ${\lambda }_{hh}$ Increases (the Fold Change for the Self-Activation of HIF-1)

(A) The relation between ${\lambda }_{hh}$ and the transition action (S).

(B) The relation between ${\lambda }_{hh}$ and the barrier height (U).

(C) Relative changes for the transition action S (red line) and barrier heights U (blue line) as ${\lambda }_{hh}$ increases.

(D) The barrier height changes as the transition action changes.

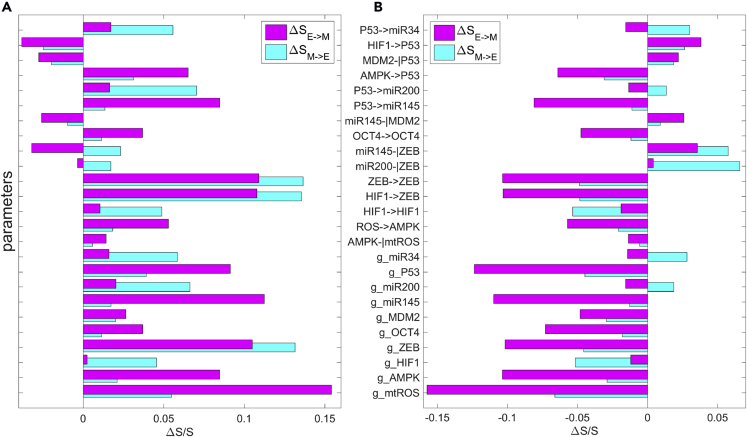
To further study the effects of parameters on the dynamics of the whole network, we performed a global sensitivity analysis on parameters for the metabolism-EMT-metastasis model. For simplicity, we constrained the parameter values in the bistable regime (the E state and M state coexist). We calculated the transition actions between the E state and M state to quantify the feasibility in transitions for EMT and mesenchymal to epithelial transition (MET). We assume that the transition actions for EMT and MET should be critical to metastasis or de-metastasis progress because the EMT is a critical step for metastasis progression. We increase or decrease each parameter (here we focus on the parameters for the synthesis rate and regulatory strengths) individually by $10\text{\%}$ to modulate the situations for gene over-expression or knockdown and for the change of regulatory strengths among genes or metabolites. Then we calculate how the transition actions between the E state and M state change after these perturbations. We also performed a global sensitivity analysis for the metabolic model to uncover the critical factors specifically for the metabolic model (see Supplemental Information Section S9 and Section S10).

From the results of sensitivity analysis, we picked top 25 parameters based on their sensitivity for detailed analysis (see Figure S5 for the complete sensitivity analysis of 61 parameters), which are shown in Figure 5. Among these top 25 paramount parameters, a few of the regulations are related with P53, for example, the activation of AMPK on P53 and the activation of P53 on miR-145. The increase of regulatory strengths for either of these two links will increase the transition actions from the E to M state (or the transition barrier from the E to M state), making the E state more stable. This embodies the critical roles of P53 in preventing cancer metastasis (Powell et al., 2014). This is consistent with our expectations from the network diagram because P53 activates multiple miRNAs and inhibits EMT-promoting factor OCT4, therefore playing a critical role in preventing cancer metastasis. Another prominent factor is the synthesis rate of mtROS, whose increase will greatly enhance the transition action from the E to M state, making the E state more stable. This indicates that mtROS could be a useful target for the cancer therapeutic strategy, probably because of its key influence on metabolism.

Figure 5.

Global Sensitivity Analysis for Parameters Based on the Transition Action for the Metabolism-EMT-Metastasis Model

Y axis represents the 25 parameters. X axis represents the percentage of the change of the transition action ($\mathcal{S}$) relative to $\mathcal{S}$ with default parameters. Here, $S_{E\to M}$ represents the transition action from attractor E to attractor M (magenta bars) and $S_{M\to E}$ represents the transition action from attractor M to attractor E (cyan bars). The top 25 parameters are picked, in which the first 15 parameters represent the regulatory strength (λ) and the last 10 parameters represent the synthesis rate (g) for 10 proteins or metabolites. See Supplemental Information for the complete sensitivity analysis of 61 parameters.

(A) Each parameter is increased by 10%, individually.

(B) Each parameter is decreased by 10%, individually.

Additionally, increasing the fold change of inhibitory regulation of miR-145 on MDM2 (as well as on ZEB), i.e., reducing the inhibitory effects, results in the decrease of transition action from the E state to M state, promoting EMT (Figure 5A). This is because MDM2 inhibits P53 by promoting its degradation. Reducing the inhibition on MDM2 will promote MDM2 and inactivate P53, which will promote EMT owing to the inhibitory roles of P53 on EMT. Similarly, reducing the inhibition of miR-145 on ZEB will promote ZEB and further promote EMT. These predictions from our modeling are consistent with the experimental observations showing that miR-145 blocks the EMT (Zhao et al., 2016).

Another prediction from the sensitivity analysis is that the increase of the strength of the self-activation of ZEB ${\lambda }_{ZZ}$ (or the increase of the synthesis rate of ZEB $g_Z$ or the increase of the fold change for the activation regulation of HIF-1 on ZEB ${\lambda }_{hZ}$) can enhance the transition action from the M state to E state $S_{M\to E}$, making the transition from the M to E state less probable and the M state more stable (Figure 5A). This prediction is consistent with previous finding, showing that ZEB1 levels drive the dynamics of EMT (Jolly et al., 2018). Recently, Jia et al. demonstrated that miR-200/ZEB1 behaves as a three-way decision-making switch enabling transitions among the E, intermediate E/M, and M cell states by theoretical and experimental studies (Jia et al., 2017). Our prediction here is consistent with this previous work (Jia et al., 2017), by emphasizing the role of ZEB as a mesenchymal state promoter. From the network diagram, this is because the increase of the synthesis rate of ZEB or the activation strength of HIF-1 on ZEB will make ZEB activated, which further promotes EMT or the stability of M state. This also agrees with previous studies showing that the ZEB family of transcription factors are inducers of EMT, and P53, miR-200, and miR-139 affect the EMT through ZEB transcription factors (Ohashi et al., 2010, Korpal et al., 2008, Qiu et al., 2015, Sánchez-Tilló et al., 2011).

We also found that the over-expression of HIF-1 will increase the stability of the M state, reflected by the increase of transition action from the M to E state (Figure 5A). From the network topology, the over-expression of HIF-1 will promote ZEB and therefore make the M state more stable. This is consistent with the experimental study showing that the HIF-1 is a significant positive factor for regulating tumor progression and metastatic potential (Liao et al., 2007). Additionally, the inhibition of AMPK will promote EMT and metastasis, indicated by the decrease of transition action from the E to M state (Figure 5B). This is because AMPK promotes the expression of P53, which plays a critical role in inhibiting EMT. Therefore, the inhibition of AMPK will down-regulate P53 and promote EMT. This is also consistent with previous investigations showing that the loss of AMPK activation promotes the invasion and metastasis of pancreatic cancer (Chen et al., 2017).

Model Predictions Based on Landscape and Paths for Cancer Metastasis

Our computational results provide some guidance for experimental studies on the relationships among EMT, metabolism, and cancer metastasis. We summarized the experimental evidences that are consistent with our modeling results, as well as some predictions that could be tested from experimental studies (Table 1). First, we proposed a quadrastable landscape for the interplay among EMT, metabolism, and metastasis. Among the four stable states on the landscape, the epithelial state and mesenchymal state have been suggested from previous studies (Zhang et al., 2014, Lu et al., 2013, Hong et al., 2015). The metastatic state with high BACH1 expression was consistent with a previous study (Lee et al., 2014). Also, a recent work suggested that a combination therapy by targeting BACH1 and mitochondrial metabolism suppressed tumor growth and metastasis in triple-negative breast cancer (Lee et al., 2019), which provides another support that BACH1 could be a marker gene for cancer metastasis. However, the intermediate abnormal metabolic state we identified here has not been explicitly reported from experiments. Therefore, detailed molecular experiments and steady state measurements on cancer metastasis systems might be needed to test if this abnormal metabolic state, along with the multistability, exists.

Table 1.

Major Model Predictions and Experimental Supports

Model Predictions	Supporting References
In metastatic progression, there exists an abnormal metabolic state.	Prediction
Forward and reverse paths for EMT and metastasis are not identical.	(Zhang et al., 2014)
Metastasis is a stepwise progress, i.e., abnormal metabolism, EMT, and metastasis should be activated in a cascade.	Prediction
ROS changes the levels in the very early stage of the cell fate decision process toward EMT or metastasis.	Prediction
Over-expression of P53 attenuates EMT and metastasis progression.	(Powell et al., 2014)
Over-expression of ZEB promotes EMT.	(Sánchez-Tilló et al., 2011, Korpal et al., 2008)
Over-expression of miR-145 attenuates EMT.	(Wang et al., 2017)
Over-expression of HIF-1 promotes EMT and metastasis.	(Liao et al., 2007)
Inhibition of ROS promotes EMT and metastasis.	(Piskounova et al., 2015, Gill et al., 2016)
Inhibition of AMPK promotes EMT and metastasis.	(Chen et al., 2017)

Second, our results for kinetic transition path suggest that cancer metastatic progression is an irreversible process, which is indicated by the fact that the forward transition paths and the backward transition paths are not identical. We also found that the cancer metastatic progression is a sequential progress, i.e., the HIF-1 is first activated, and then the ZEB (characterizing EMT marker genes) is switched on followed by the activation of BACH1 (characterizing metastatic marker genes). These predictions can be tested experimentally.

Third, the discrete path results suggest that ROS changes the levels in the very early stage of the cell fate decision process toward metastasis (Figures 3B and 3C). Our results for the sensitivity analysis show that ROS significantly influences the transition actions for the E to M transition (Figure 5). This suggests that ROS might be a critical factor in the cancer metastatic progression by regulating metabolism. This is consistent with previous findings showing that antioxidants promote metastasis in melanoma (Piskounova et al., 2015, Gill et al., 2016). Previous studies showed that mtROS can also promote metastasis (Ishikawa et al., 2008, Porporato et al., 2014). These controversial conclusions might be related with the fact that cancer cells can use different ways of metabolism, e.g., use glycolysis or OXPHOS metabolism to activate metastasis (Yu et al., 2017).

Of note, the metastatic state identified in our model should represent a state with high expression level of HIF-1 (representing abnormal metabolism), high expression level of ZEB and other EMT marker genes (representing that EMT is activated), and high expression level of BACH1 (representing certain metastatic markers activated). This notion is consistent with the idea of hallmarks of cancer (Hanahan and Weinberg, 2000, Hanahan and Weinberg, 2011), i.e., the cancer metastasis should be a state in which cells have acquired different hallmarks of cancer. To test this type of cells experimentally, one should measure the expression level of relevant genes in the regulatory network and look for the states, for example, with a high level of HIF-1, ZEB, and SNAIL; low level of miR145, RKIP, and Let7; and high level of LIN28 and BACH1 (Table S4). We need to stress that, in our work, we focus on the interplay between metabolism, EMT, and metastasis, and have not explicitly considered the tristability properties of LIN28/Let7 circuit or the interplay between metabolism and stemness. As proposed in previous work (Jolly et al., 2015b), the stemness and EMT can be coupled in a flexible way. So, our metastatic state with high expression level of LIN28 and low expression level of Let7 might be corresponding to the state with stemness and the ability for the tumor initiation (Jolly et al., 2015b). Future work can study how ROS influences the coupling among metabolism, EMT, metastasis, and stemness, which might help to resolve the controversial conclusions for the roles of ROS in metastasis.

Finally, from our sensitivity analysis, the over-expression of P53 will significantly increase the transition action for the transition from the E to M state. This is consistent with the key roles of P53 as a tumor repressor (Powell et al., 2014). However, we found that the over-expression of P53 will also increase the transition action for the transition from the M to E state, which means that it is not very effective to make an M cell switched back to an E cell. This indicates that P53 alone might not be enough to induce the transition of an M state cell back to an E state cell, whereas a better strategy could be targeting multiple genes simultaneously. Of note, recent studies have suggested a computational approach to identify the optimal combination of multiple anti-cancer targets (Li, 2017, Li and Balazsi, 2018).

Landscape and Kinetic Paths for EMT and Cancer Metabolism

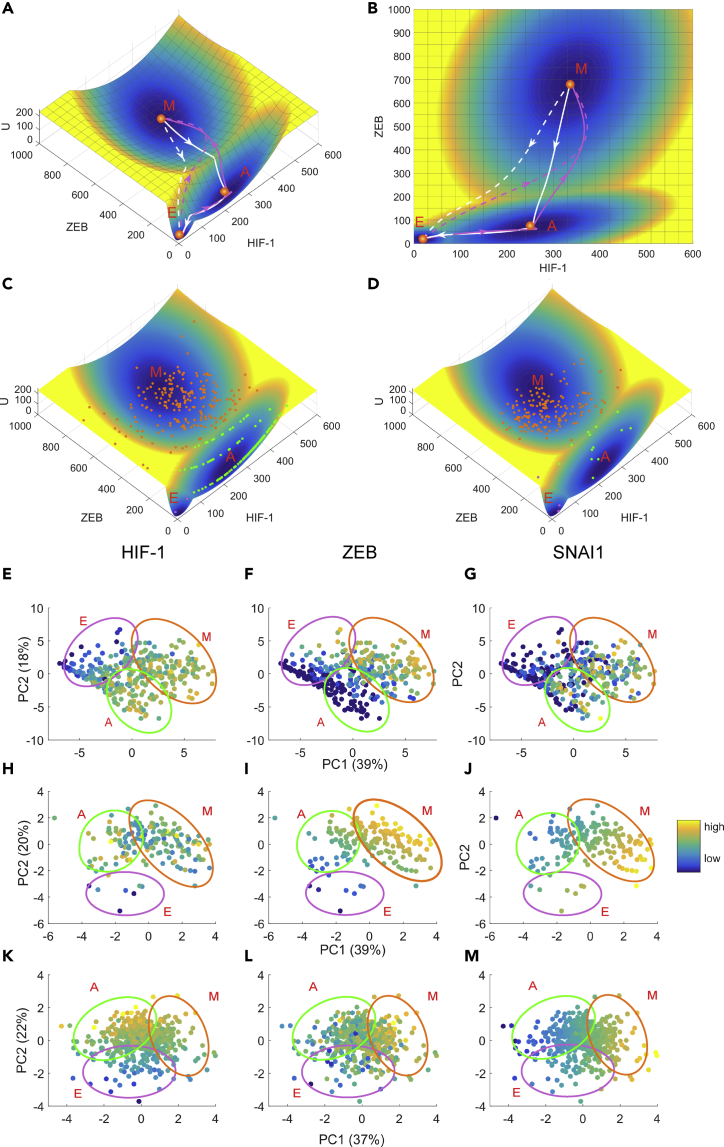
To further reveal the relationship specifically between EMT and metabolism, we quantified the potential landscape of a subnetwork of the whole network by neglecting the metastasis circuit (yellow box in Figure 1), i.e., we consider only the coupling between EMT and metabolism (see Figures S6–S8 and Table S6 for the landscape analysis specifically for the metabolic model). Here we picked ZEB and HIF-1 as the marker genes of EMT and metabolism, respectively, and obtained the potential landscape (Figures 6A and 6B). On the landscape, the blue region denotes lower potential or higher probability and the yellow region denotes higher potential or lower probability. From the landscape of EMT-metabolism, we identified three attractors (cell states), which characterize the epithelial (E), the mesenchymal (M), and an intermediate abnormal metabolic (A) state, respectively. The multistability and the existence of intermediate states of EMT have been suggested from previous work (Lu et al., 2013, Zhang et al., 2014, Li et al., 2016). However, these previous works focus on small circuits and have not considered the influence of cellular metabolism on the EMT. By coupling the EMT circuit and metabolism circuit, here we are able to study the dynamics of the interplay between EMT and metabolism.

Figure 6.

The Tristable Landscape for EMT-metabolism Model and Comparisons with Experimental Data

The EMT-metabolism model corresponds to the subnetwork of the whole network without consideration of metastasis circuit in Figure 1.

(A) Three dimensional landscape and transition paths. Solid magenta lines represent transition paths from the E to A, and M state. Solid white lines represent transition paths from the M to A and to E state. The dashed lines represent the direct transition path from E to M state and from M to E state, respectively.

(B) Two dimensional landscape and transition paths.

(C and D) Landscapes are compared with the gene expression data of single-cell RNA-seq data for a genetic mouse model of skin squamous cell carcinoma (SCC) undergoing EMT including 383 single cells (C) and clinically annotated adult cases of de novo AML from TCGA including 173 samples (D). The gene expression data have been rescaled to fit the landscape. Each point represents a gene expression pattern in ZEB and HIF-1 coordinates for one sample from experiments.

(E-G) PCA plots for the SCC data with respect to HIF-1 (E), ZEB (F), and SNAI1 (G).

(H-J) PCA plots for the AML data with respect to HIF-1 (H), ZEB (I), and SNAI1 (J).

(K-M) PCA plots for the PTC data with respect to HIF-1 (K), ZEB (L), and SNAI1 (M). Three clusters have been marked in the PCA coordinates, which correspond to E state (purple ovals, with low HIF-1/low ZEB expression), A state (green ovals, with high HIF-1/low ZEB expression), and M state (orange ovals, with high HIF-1/high ZEB expression), respectively. The colors in the PCA plots represent the expression levels of key marker genes (e.g., HIF-1, ZEB, and SNAIL) for E, A, and M phenotypes. E, epithelial state; M, mesenchymal state; A, abnormal metabolic state.

To investigate the transition dynamics for the EMT-metabolism system, we calculated the MAPs among different attractors by minimizing the transition actions $\mathcal{S}$. The MAPs for different transitions are shown on the landscape (Figures 6A and 6B). The MAPs from the epithelial state to the mesenchymal state are shown in magenta lines, and the reverse paths are shown in white lines.

The landscape and transition path results indicate that the transition process from the epithelial state to the mesenchymal state can be divided into two steps: the epithelial cells first switch to the intermediate state (or abnormal metabolic state A) with the increase of HIF-1 level and then are transformed to mesenchymal cells with the increase of ZEB level. These results demonstrate that, before cells are transformed to the mesenchymal state, they need to first change their metabolism. Of note, the intermediate abnormal metabolic state we identified here is different from the hybrid state suggested in EMT modeling (Lu et al., 2013) or the hybrid state proposed on cancer metabolism (Yu et al., 2017). The hybrid or intermediate state in EMT models (Lu et al., 2013) was defined as a state with half-epithelial and half-mesenchymal cell properties, and the hybrid or intermediate state in cancer metabolism model (Yu et al., 2017) was defined as a cell state that can use both glycolysis and OXPHOS metabolism. Neither of these two previous models has discussed the interplay between EMT and metabolism. Differently, our intermediate state suggested here corresponds to a state with abnormal metabolism (increased HIF-1 expression) but is still similar to an epithelial cell state (with the similar expression levels of epithelial marker genes as the epithelial cells). Therefore, this builds a connection between EMT and cancer metabolism. As a matter of fact, different studies have suggested that aberrant metabolism plays a key role in developing EMT and cancer metastasis (Huang and Zong, 2017, Sciacovelli and Frezza, 2017; Jiang et al., 2015). We need to stress that our intermediate metabolic state identified here is not in conflict with the previous hybrid state in EMT (Lu et al., 2013, Pastushenko et al., 2018). This difference is due to the disparate resolution of the two models because our models here focus on the interplay between metabolism, EMT, and metastasis, which is more complicated and inclusive than previous models only focusing on EMT. In principle, it is possible to discover both the hybrid EMT state and the abnormal metabolic state by fine-tuning parameters in our models.

Landscape Results Are Supported by Experimental Data

To further validate our modeling results, we compare our EMT-metabolism model with the experimental data (see Supplemental Information Section S11 for a detailed approach of data analysis). Since our model can be considered as a representative EMT-metabolism network (not for some specific types of cancer), we collected three different types of gene expression data from experiments. The first dataset we acquired is the single-cell RNA-seq data for a genetic mouse model of skin squamous cell carcinoma (SCC) undergoing EMT (383 single cells, available from the NCBI Gene Expression Omnibus under accession number GSE110357) (Pastushenko et al., 2018). We also collected another dataset of gene expression data (acute myeloid leukemia [AML]) from The Cancer Genome Atlas (TCGA) (173 samples for clinically annotated adult cases of de novo AML) (Cancer Genome Atlas Research Network et al., 2013). AML is the second most common leukemia diagnosed in both adults and children, and it has been proposed that leukemia cells are inherently metastatic compared with solid tumors (Trendowski, 2015). The regulation of EMT has been suggested to play critical roles in AML development (Meyer, 2017, Carmichael et al., 2016, Stavropoulou et al., 2016). The third dataset we collected is for papillary thyroid carcinoma (PTC) from TCGA including 496 PTC samples (Agrawal et al., 2014). All of these three types of data are time independent and therefore should correspond to the steady-state data. We extracted the expression data for the relevant genes that appear in our network (Figure 1) from these datasets and neglected the miRNAs and metabolites that are not available from the data.

To see if our modeling results agree with these data, we rescaled the expression data to the range of the basins obtained from our models by linearly transforming the expression values, so that they match the landscape basins approximately. We believe that this normalization of the data is reasonable because some corresponding gene expression values from different datasets differ from each other by many folds and they represent different types of cancer in different conditions. By mapping these gene expression data (the gene expression data of HIF-1 and ZEB after normalization) on the landscape (Figures 6C and 6D), we found reasonable consistency between experimental data and our landscape results, i.e., the experimental data also display some clusters, which could correspond to the three stable states (cell types) on the landscape. Here, each point represents a gene expression pattern in the ZEB and HIF-1 coordinates for one sample from experiments (Figures 6C and 6D). The experimental data points can be classified into three different cell states (the E state represented by magenta points, the M state represented by orange points, and the A state represented by green points), which is consistent with our modeling results.

We also compared our modeling results with the experimental data in another way. We performed the principal component analysis (PCA) of the three types of experimental data, which are shown in Figures 6E–6G (SCC data), Figures 6H–6J (AML data), and Figures 6K–6M (PTC data), respectively. In the PCA plots of the SCC data, we can identify three clusters, which are consistent with our landscape results. These three clusters have been marked in the PCA coordinates that correspond to the E state (purple ovals, with low HIF-1/low ZEB expression), A state (green ovals, with high HIF-1/low ZEB expression), and M state (orange ovals, with high HIF-1/high ZEB expression). Here, the colors in the PCA plots represent the expression levels of key marker genes (e.g., HIF-1, ZEB, and SNAIL) for the E, A, and M phenotypes. Importantly, we found that, from the cluster E to cluster A, the HIF1 expression increases (from blue to yellow), whereas the ZEB (and SNAIL) expression does not increase (keeping blue) (Figures 6E–6G). Also, from the cluster A to cluster M, the ZEB (and SNAIL) expression increases significantly (from blue to yellow) (Figures 6E–6G). These experimental data provide a support to the landscape attractors we identified, which is that the E, A, and M states coexist. For the PCA plots of AML and PTC data, we also find similar modes for the three attractor states (E, A, and M) in terms of HIF-1 and ZEB (Figures 6H–6M). Both these ways of validations show good consistency between modeling results and experimental data. It is worth noting that our metabolism-EMT regulatory network is constructed purely by mining the experimental literature and the gene expression data are obtained from a different database, separately. So, the consistency between our modeling results and the experimental data is inspiring, which also confirms the predictive power of our models.

Here, for metabolism and EMT circuit, we found certain consistency between experimental data and our models. But we have not found significant consistency for the metastatic circuit in the SCC dataset we used. This is probably because our metastatic circuit is only a simplified module to represent metastasis (e.g., only one metastasis marker gene BACH1 is involved). To resolve this issue, a more inclusive metastasis model involving more genes is needed. Nevertheless, for the cascading regulation of EMT and metastasis, our previous work by combining modeling and single cell data provides support for this conclusion (Li and Balazsi, 2018).

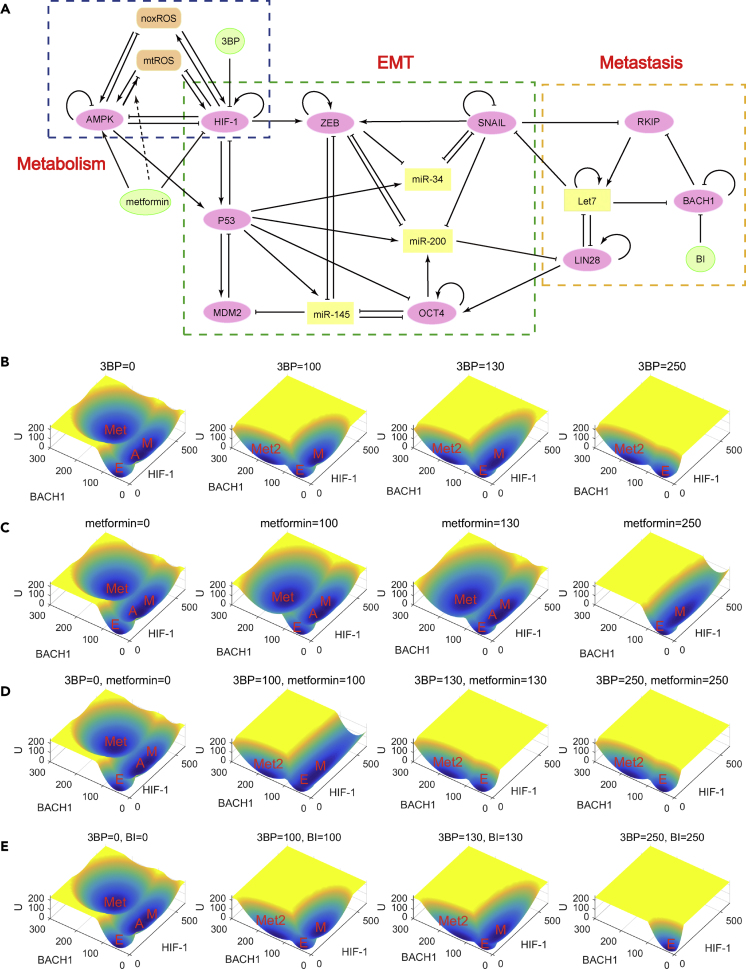
Modeling Anti-Cancer Therapeutic Strategies

Targeting cellular metabolism has been shown to be a promising route against cancer. Several metabolic drugs have been uncovered and shown to be effective against cancers in certain cases, e.g., 3-bromopyruvate (3BP) (Ganapathy-Kanniappan et al., 2010) and metformin (Dowling et al., 2011). It has also been suggested that the combined drugs may be more effective than single drugs (Cheong et al., 2011). However, the underlying mechanisms for why the designed drugs work in certain cases but not in others have yet to be clarified. Here, we propose that these drugs take effects by changing the underlying landscape topography of the metabolism-EMT-metastasis gene regulatory network. We model the drug effects by making perturbations to the key nodes in the network and trace the changes on the landscape shape. Here, the green nodes (Figure 7A) represent the hypothetical drugs, and by changing the levels of drugs we can study how the landscape is influenced (see Supplemental Information Section S12 for detailed ODEs describing the drug influences and Table S7 for parameter values). In Figures 7B–7D, we showed how the landscape shape changes as the drug doses increase for 3BP (Figure 7B), metformin (Figure 7C), and the combined 3BP and metformin therapy (Figure 7D), respectively. We can see that all three therapies are effective on destabilizing the metastatic state, as indicated by the changes in the landscape topograph where the metastatic attractor gradually disappears as the drug doses increase. We found that the combined 3BP and metformin therapy is more effective than either of 3BP or metformin acting alone. This is because, when the drug doses increase to certain level, the combined 3BP and metformin therapy will lead to the disappearance of the A, M, and Met attractors. This does not happen for the single 3BP or metformin therapy (Figures 7B–7D). Therefore, these results are consistent with the experimental studies showing that the combinations of metformin and 2DG (whose effect is similar to 3BP) are more effective than each drug in action alone (Cheong et al., 2011).

Figure 7.

Landscape in Terms of HIF-1 and BACH1 in Response to Different Drugs in Different Levels

(A–E) (A) The metabolism-EMT-metastasis network with new added green nodes representing the hypothetical drugs. The simulated drugs include 3BP (B), metformin (C), combined 3BP and metformin therapy (D), and combined 3BP and BACH1-inhibitor therapy (E). In B–E, the hypothetical drug levels increase from left to right, which represent the drug level of 0, 100, 130, and 250, respectively. E, epithelial state; M, mesenchymal state; A, abnormal metabolic state; Met, metastasis state; Met2, metastasis-like state; BI, BACH1 inhibitor.

We also found that even very large doses of any of these drugs (last column in Figures 7B–7D) alone cannot induce the cells to the E state completely because there are always other abnormal cell states present (Met2 in Figures 7B and 7D, M in Figure 7C). The Met2 state here corresponds to a state with low HIF-1, low ZEB, and high BACH1 expression level, which should be thought of as a metastasis-like state. This can explain why designed drugs work in certain cases but not in the others. It is because cells after drug treatments can still transform to the M state (Figure 7C) or the Met2 state (Figures 7B and 7D), which should preserve certain features of metastasis cells. Therefore, based on these changes in landscape topography, we suggest another therapeutic strategy, which is the combination of 3BP (or metformin) and certain types of BACH1 inhibitor (Figure 7E). The purpose of adding BACH1 inhibitor is to destabilize the Met2 state, so that the cells will be more prone to switch to the E state. As indicated in Figure 7E, the new combination of drugs suggested here can induce the change in landscape topography from four states coexistence to monostable E state alone. The new combination strategy suggests a better treatment for cancer metastasis. In fact, the BACH1 as one of the new targets for suggested combination drugs mentioned earlier has been suggested as a novel individual candidate target for cancer therapy (Davudian et al., 2016). More interestingly, a recent work suggested that a combination therapy by targeting BACH1 and mitochondrial metabolism suppressed tumor growth and metastasis in triple-negative breast cancer (TNBC) (Lee et al., 2019). These experiments provide a strong support for our predictions on the combination drugs.

Recently, an integrated computational and experimental approach was designed to identify effective therapeutic strategies based on temporal sequencing of multiple drugs from deterministic models (Goldman et al., 2015, Goldman et al., 2019). Of note, our current landscape approach is based on the steady-state distribution, where we explored multiple initial conditions from the ODEs. From the landscape perspective, drugs play roles by reshaping the landscape (steady states) and changing the relative stability of different cell states. To see the effects of temporal sequencing of multiple drugs, an approach for calculating temporal landscape (landscape at different time points) has yet to be developed.

Discussion

Abnormal metabolism, EMT, and cancer metastasis are three important processes in the progression of cancer. These processes have been extensively explored individually both from experiments and modeling. However, the underlying mechanisms connecting these processes remain elusive. In this work, we aim to establish a theoretical framework for modeling the interplay among metabolism, EMT, and metastasis to reveal the possible principles for cancer metastasis. We develop a TME approach to quantify the potential landscape. We constructed a metabolism-EMT-metastasis regulatory network and identified four stable states from the landscape: epithelial (E), abnormal metabolic (A), mesenchymal (M), and metastatic (Met) cell states. Importantly, we identified a new abnormal metabolic cell state. We further calculate the MAPs to quantify the most probable transition paths for cell fate decision processes in metastatic progression. The results of landscape and MAPs indicate that the epithelial cells prefer to first change their metabolism, then finish EMT, and eventually enter the metastatic state. By performing a global sensitivity analysis from the transition actions, we identified some key parameters for the metastatic progression, which agree well with experimental observations.

Our landscape results have a few indications for cancer metastasis. First, for metastatic progression, cells prefer to follow a specific sequential order: change their metabolism, finish EMT, and proceed into the metastatic state. This feature indicates that there are interplays among these three processes to generate a temporal order. Second, the intermediate states identified from our models may account for the heterogeneity observed in experiments for tumors. Third, the landscape view considers metastasis state as an attractor. This means that, in principle, metastatic cancer cells can be destroyed by altering the underlying landscape such that the metastasis state is no longer a stable state. To achieve this, a possible effective way should be either intervening genes or regulatory interactions among genes in cancer gene regulatory networks. In fact, recent experimental work showed that EMT-derived breast cancer cells can be induced to differentiate into post-mitotic adipocytes through a combination therapy (Ishay-Ronen et al., 2019). Also, the reverse transitions from M cells to E cells or from hybrid E/M cells to E cells have been observed in experiments (Zhang et al., 2014, Hong et al., 2015). These experiments indicate the possibility for inducing the conversion of metastatic cancer cells to non-invasive cells (e.g., E cells or intermediate state cells) in vivo. On the contrary, the traditional strategy for killing metastatic cells does not change the stability of metastasis attractor. This might be one reason why we often see clinically that after the chemotherapy or radiotherapy the cancer relapses.

Recent studies have identified intermediate hybrid phenotypes both at the single-cell level and population levels across different cancer types (Pastushenko et al., 2018, Jolly et al., 2015a). Our models for the interplay among metabolism, EMT, and metastasis give rise to a quadrastable landscape. This supports the existence of intermediate states in EMT. Additionally, a critical prediction from our model is that the cancer metastatic progression might be a sequential process. Specifically, cancer cells tend to first change their metabolism. Then, with the abnormal metabolism (possibly providing energy more quickly), the EMT circuit is activated. This further leads to the cancer metastasis. This conclusion is partially supported by multiple types of gene expression data (Figures 6C–6H), although gene expression data with dynamical information are needed to further test this prediction. This sequential procedure resembles previous studies suggesting that metastasis appears mainly by a sequential, multi-step process that can be viewed as a cascade of the invasion-metastasis (Lambert et al., 2017). These results indicate that the temporal order is critical for different genes (characterizing different functions or hallmarks of cancer) switching on or off in metastatic progression process and different hallmarks of cancer can interact with each other and cooperate. Our landscape results also indicate that the multistable landscape and the existence of intermediate states play critical roles in metastatic progression. For example, the existence of intermediate states or sequential progression can increase cellular plasticity. As a matter of fact, the epigenetic landscape governing the stability of epithelial-mesenchymal plasticity has been proposed as an illustration (Tam and Weinberg, 2013). Our results offer quantitative supports for the epigenetic landscape of EMT and metastasis.

Our work has certain implications on the origins of cancer. Genetic mutations, metabolic dysfunction, and environmental factors are commonly considered to play distinct roles in the development of tumors. Our work suggests that these factors may be connected to each other intimately, and the debate on which one is dominant can be reconciled in a quantitative way. In fact, different circuits are intertwined with feedbacks to each other, as shown in Figure 1. First, the metabolic disorder undoubtedly plays critical roles in tumor development because from our models the E to A state transition (Figure 2) is a crucial step for tumor development. The metabolic disorder can be caused by the environmental stress (e.g., hypoxia) or the genetic mutations (e.g., oncogene RAS, MYC) (Hanahan and Weinberg, 2011), or combinations of both.

However, the abnormal metabolic state does not necessarily lead to cancer, if the system stays at the A state stably. To become tumor cells or obtain the invasive ability, the cells need to activate other circuits (such as EMT circuit) to induce the A to M state transition (Figure 2). In a similar way, the genetic mutations (inherited or acquired) and the environmental stress (such as UV radiation) can contribute to this step. In fact, this can be considered as a process of accumulations of mutations (e.g., the mutations related to EMT marker genes ZEB and SNAIL). Finally, even in the M state, the cells still have the opportunity of not becoming malignant tumor cells if no M to metastasis state transition is induced. In principle, an M cell can transform back to an A or E cell in certain conditions. However, with the further accumulations of mutations (related with metastasis circuit), the M state cells can be further transformed to metastatic cells. This completes the journey of the cascade for the progression of cancer metastasis. Therefore, the quantitative landscape models offer a possible explanation for the origin of cancer, which supports the notion that cancer originates from the combined effects of accumulated mutations and environmental stress.

The sequential cascade in metastatic progression also suggests that a more effective therapeutic strategy might be targeting multiple circuits (representing different functions) of the cancer network, e.g., targeting metabolism, EMT, and metastasis simultaneously. In fact, many studies have suggested that EMT activation can cause tumor relapse and enhanced tumorigenesis in different human cancer cell lines (Moody et al., 2005, Creighton et al., 2010, Ye and Weinberg, 2015). By modeling the landscape changes with several designed drugs (such as 3BP and metformin), we found that these drugs can weaken the metastatic state in certain circumstances, but they also induce new metastasis-like states. This can explain why some drugs can work in certain cases against cancer but not in others. Our results suggest that the combinations of different drugs should be more effective than single drugs (Cheong et al., 2011). Based on the changes of landscape topography upon drug treatment, we suggest a new therapeutic strategy (combining 3BP/metformin and BACH1 inhibitor), which can lead to a better treatment. Remarkably, our predictions on the combination drugs are partially supported by a recent work showing that a combination therapy by targeting BACH1 and mitochondrial metabolism suppressed tumor growth and metastasis in TNBC (Lee et al., 2019).

Yu et al. proposed that cancer cells use both glycolysis and OXPHOS for metabolism (Yu et al., 2017). In our work, the abnormal metabolic state is more related to glycolysis state marked by higher expression of HIF-1. Our modeling results indicate that the abnormal metabolism (such as aerobic glycolysis) is critical for activating metastasis. This is supported by previous work, e.g., cancer metastasis has long been related to the switch from OXPHOS to glycolysis metabolism, i.e., the Warburg effects (Han et al., 2013, Gatenby and Gillies, 2004, Kamarajugadda et al., 2012). Additionally, both our modeling results and gene expression data from experiments show that HIF-1 is activated in metastatic cancer cells (Figure 6). In fact, previous work has suggested that HIF-1 activation is critical for EMT and HIF-1 activation by acidic microenvironment contributes to tumorigenesis and metastasis (Han et al., 2013). This is consistent with our conclusion that glycolysis metabolism (HIF-1 activation) promotes EMT and then activates metastasis. However, we cannot rule out the possibility that cancer cells could also use OXPHOS metabolism to activate metastasis, which warrants further computational and experimental explorations.

In summary, the TME approach developed in this work provides an effective approach to quantify the stochastic dynamics of high-dimensional gene regulatory systems, and our results provide new insights into the mechanistic understanding of the interplay among metabolism, EMT, and cancer metastasis in the progression of cancer. The landscape and path approach can be used to explore the interplay among other hallmarks of cancer and to study the stochastic dynamics of other biological networks.

Limitations of the Study

One limitation of the current work is that we compare our modeling results only with a few types of cancer data. These data partially support the existence of an abnormal metabolic state. To our best knowledge, it remains challenging to integrate “model driven” approach (such as our gene network models) and “data driven” approach (such as single cell data analysis) in systems biology (Cho et al., 2017). Therefore, we still lack effective ways to compare modeling results and single cell data of cancer, especially for different types of cancer owing to the heterogeneity in many tumors. In this work, we performed some initial attempts for this task. Another limitation is that we considered only certain genes, microRNAs, and metabolites that are important for the processes of metabolism, EMT, and cancer metastasis. In reality, other gene circuits or metabolites can also be important to the whole-cell fate decision processes in cancer metastasis. Third, cancer is a complex disease, which involves many hallmarks (Hanahan and Weinberg, 2000, Hanahan and Weinberg, 2011). Owing to the complexity, in this work we modeled a few hallmarks of cancer, including abnormal metabolism, EMT, and metastasis. Future work can incorporate other critical genes or metabolic circuits (and/or other hallmarks of cancer) into the models of underlying cancer gene regulatory networks, which may lead to the larger complexity but will provide more insights into underlying regulatory mechanisms for cancer metastasis.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: November 22, 2019