Abstract
3-photon excitation enables in vivo fluorescence microscopy deep in densely labeled and highly scattering samples. To date, 3-photon excitation has been restricted to scanning a single focus, limiting the speed of volume acquisition. Here, for the first time to our knowledge, we implemented and characterized dual-plane 3-photon microscopy with temporal multiplexing and remote focusing, and performed simultaneous in vivo calcium imaging of two planes beyond 600 µm deep in the cortex of a pan-excitatory GCaMP6s transgenic mouse with a per-plane framerate of 7 Hz and an effective 2 MHz laser repetition rate. This method is a straightforward and generalizable modification to single-focus 3PE systems, doubling the rate of volume (column) imaging with off-the-shelf components and minimal technical constraints.
1. Introduction
Multiphoton laser-scanning fluorescence microscopy has enabled numerous studies of the structure and function of neural circuits in vivo. To date, the majority of these studies have been performed with two-photon excitation (2PE) in which the energy of two near-infrared photons is simultaneously absorbed to generate fluorescence at visible wavelengths [1,2]. The quadratic dependence of excitation on intensity provides optical sectioning and background reduction in the presence of dense fluorescent staining and volume scattering of excitation light. If scattering is sufficiently strong, however, such as when attempting to image directly through intact bone [3] or at many scattering lengths deep in brain tissue [4,5], the second-order nonlinearity becomes insufficient to suppress fluorescence generated by out-of-focus excitation light, inevitably obscuring the in-focus signal. In such cases, three-photon excitation (3PE) microscopy has been shown to penetrate further and enable high-resolution fluorescence imaging beyond the depth limit of 2PE, enabling for example imaging directly through the skull [6] and into subcortical layers [7]. The longer, short-wave IR wavelengths typically used and third-order nonlinearity in 3PE extend the scattering length and further reduce out-of-focus excitation, respectively.
A significant limitation of 3PE microscopy is the slow acquisition speed which can be over an order of magnitude slower than 2PE imaging. State-of-the-art multiplane and multi-region 2PE methods can acquire up to 10 standard raster-scanned planes at 10 Hz volume rate [8–10]. At present, state-of-the-art 3PE imaging has been demonstrated with an acquisition rate of 106 pixels/sec which is equivalent to imaging a single 2PE plane (512 × 512 pixels) at ≤ 4 Hz [11–13]. Two factors contributing to the comparatively slow acquisition of 3PE are first, the low laser repetition rates used thus far for 3PE imaging, and second, the early stage of technical development. At present, the pulse repetition rates used in 3PE microscopy have been typically ≤ 1 MHz, far below the standard 80 MHz repetition rate in 2PE, limiting the acquisition speed to 15 Hz for 256 × 256 images sampled with 1 pulse per pixel. Recent work, however, indicates 3PE at repetition rates above 1 MHz is practical and might be leveraged for faster imaging. Namely, experiments with a tunable repetition rate source for 2PE determined an ideal range of 1 to 10 MHz for deep 2PE imaging [14], and a recent study by Yildirim et al. [12] postulated a maximum safe repetition rate of 10 MHz for 3PE which, if implemented, could dramatically increase the acquisition speed. Though theoretically promising, whether 3PE at pulse rates above 1 MHz is beneficial for imaging and how to leverage additional pulses toward increasing acquisition speed still remain to be investigated.
To address the challenge of utilizing higher repetition rates, adapting volume imaging techniques from 2PE microscopy to 3PE is clearly sensible. A recent success has been demonstrating extended depth-of-focus scanning with Bessel beam 3PE [15,16], but 2PE methods for imaging multiple planes simultaneously [9,17–19] have not yet been adopted. Here, our goal was to implement 3PE multiplane imaging to accelerate volume acquisition without reducing the per plane frame rate, as well as to minimize the necessary increase in excitation power and sample heating by optimizing excitation efficiency.
2. Multiplane imaging
Compared with 2PE multiplane imaging methods, there are important considerations for implementing multiplane imaging with 3PE. Pulses generated by commercial OPA’s for 3PE are generally shorter than those typically used in 2PE imaging (∼50 fs vs. ∼200 fs transform-limit). Because of the larger spectral bandwidth, focus-shifting methods based on varying refractive elements such as commonly used electro-optic and acousto-optic lenses, as well as liquid crystal spatial light modulators, are complicated by the need to characterize and limit chromatic aberration. Thus, recent work in correcting and shifting the 3PE focus with adaptive optics and remote focusing have relied on mirror-based approaches [20,21]. Moreover, because of the higher-order nonlinearity, signal generation by 3PE is more sensitive to the size of the focal volume. For 3PE, the rate of fluorescence emission at focus can be calculated to increase proportionally with the NA2, therefore benefitting from maintaining high-NA, diffraction-limited focusing more than 2PE which in sufficiently thick samples is independent of the excitation NA [7]. Efficient excitation is particularly important in multiplexing 3PE because water absorption and tissue heating by 1300 nm light places limits on the average power in the sample and therefore the pixel rate and number of planes that can be imaged at a given depth. With these factors in mind, we resolved to avoid chromatic effects while maintaining a high NA of ∼0.9 by shifting the excitation focus with a commercial, plan-achromat air objective in a remote-focusing configuration.
Here, we describe simultaneous 3P imaging of two planes displaced by up to ± 50 µm axially each at 7 Hz frame rate with a 2 MHz effective repetition rate. We designed and constructed a dual-plane 3PE laser-scanning microscope using principles of temporal (time-division) multiplexing [17] and remote focusing [22,23] to separate the spatiotemporal intensity distributions of the two excitation foci. We took advantage of a recently demonstrated demultiplexing circuit developed for multiplane 2PE microscopy [19] to separate analog signals from the two planes into individual channels. To maintain optimal 3PE imaging and minimize tissue heating, we characterized and minimized pulse dispersion and degradation of the remote focus. Finally, we validated dual-plane 3PE in vivo calcium imaging deep in the cortex of an awake, headfixed transgenic mouse. To our knowledge, the description of dual-plane, multiplexed 3PE microscopy is novel. We also note that this method is a straightforward and generalizable modification to single-plane 3PE systems, doubling the rate of volume acquisition with only off-the-shelf components and with minimal software and hardware constraints beyond the availability of an additional DAQ channel.
3. Experimental setup and procedures
3.1. Optical setup
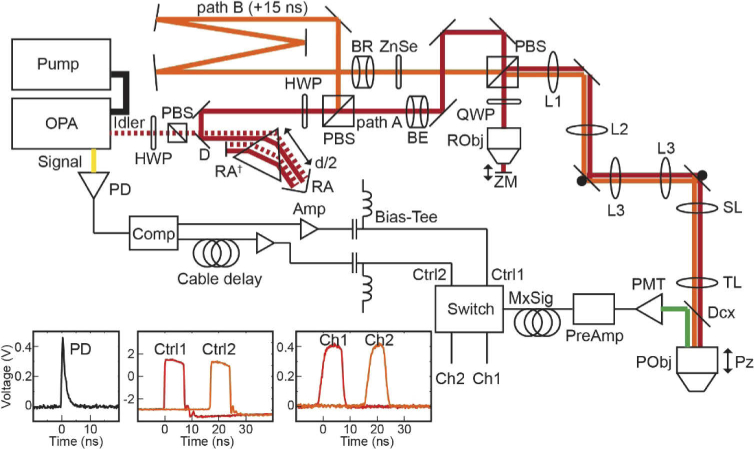
A schematic of the dual-plane remote focusing 3P microscope is shown in Fig. 1. Excitation laser pulses were generated by a commercial non-collinear OPA (Opera-F, Coherent) operating at 1300 nm (idler beam) pumped by a 40 W fiber laser (Monaco, Coherent) operating at 1040 nm. Excitation pulses at the output of the laser were measured to be nominally 2 µJ with a 50 fs pulse duration (PulseCheck, APE). The beam was attenuated by a half-wave plate (AHWP-1600, Thorlabs) and polarizing beam splitter (PBS104, Thorlabs), then directed into a single-prism (N-SF11, PS855, Thorlabs) pulse compressor for dispersion compensation [24]. In this design, the pre-chirp propagation distance, d, is twice the physical distance between the prism and the right-angle mirror. The beam exited the compressor at a lowered height and was picked off by a D-mirror. A second half-wave plate and polarizing beam splitter was used to divide the pre-chirped beam into two paths for either remote focusing or temporal delay. The transmitted beam path (remote focusing; path A) was expanded by a 1.5x beam expander (AC254-100-C; AC254-150-C, Thorlabs) then entered the microscope platform (MIMMS, Sutter Instruments) via a periscope. The reflected beam path (temporal delay; path B) was reflected by a series of mirrors over ∼5 m to delay the pulses by roughly 15 ns relative to path A, then demagnified 2x by a beam reducer (BE-02-05-C, Thorlabs) to compensate for the long propagation distance before entering the microscope via a separate periscope, in the process becoming p-polarized, and recombining with the path A beam at another polarizing beam splitter.
Fig. 1.
System schematic of dual plane 3PE microscope with analog demultiplexing electronics. Dashed red line – idler beam path exiting the laser and sent through pulse compressor. Solid red line – idler beam path exiting the compressor at lowered height and sent through remote focusing. Orange line – idler beam path split from the remote focusing path and sent through temporal delay line. Yellow line – signal beam synchronous with idler pulses. Abbreviations: OPA – optical parametric amplifier, HWP – half-wave plate, PBS – polarizing beam splitter, RA – right-angle mirror, RA† – vertical right-angle mirror, d/2 – distance between prism and right-angle mirror (see main text), D – “D”-shaped pick-off mirror, BE – beam expander (1.5x), BR – beam reducer (0.5x), QWP – quarter-wave plate, RObj – remote focus objective, ZM – z-translation mirror, L1 – doublet lens (f = 150 mm), L2 – doublet lens (f = 100 mm), L3 – Plössl lens (f = 50 mm), SL – scan lens (f = 50 mm), TL – Plössl tube lens (f = 200 mm), Dcx – dichroic beam splitter, PObj – primary objective, Pz – piezo scanner, PMT – photomultiplier tube, PreAmp – pre-amplifer, MxSig – multiplexed signal, Amp – amplifier, Comp – comparator circuit, PD – photodiode. Inset: Oscilloscope traces of photodiode output (left), gate control pulses (center), and demultiplexed channel detection windows exhibited by switching a 0.5 VDC signal input (right).
Initially, the p-polarized path A beam passed through the recombining beam splitter. The linearly polarized beam was circularly polarized by a quarter-wave plate (AQWP-1600, Thorlabs), then entered the remote objective (LCPLN50XIR, 0.65 NA, Olympus). Fully illuminating the remote objective pupil allowed a maximum excitation NA through the primary objective of , where NA1 and NA2, and n1 and n2, are the effective excitation NA’s and immersion indices of the remote and primary objectives, respectively. This was achieved by imaging the remote pupil onto the primary objective pupil at a magnification of , where M1 and M2 are the magnifications of the remote and primary objectives [23]. The focused beam was reflected back through the objective by a mirror mounted on a manual translation stage, and became s-polarized by reverse passage through the quarter-wave plate. The combined beams then entered a 4f-relay (AC254-150-C; AC254-100-C, Thorlabs) configured to image the back pupil of the remote objective onto the scanning galvanometers (6215H, Cambridge Technologies). The x- and y- galvos were also imaged onto each other by a pair of Plössl scanning lenses (paired AC300-100-C, Thorlabs), then imaged onto the pupil of the primary objective (XLPLN25XWMP2, Olympus) by a scan lens (SL50-3P, Thorlabs) and Plössl tube lens (paired AC254-400-C, Thorlabs). The primary objective was mounted on a piezo objective scanner (nPFocus400, nPoint) for fast axial translation. Emitted green fluorescence was separated from incoming excitation light by a dichroic beam splitter (FF735-Di02, Semrock), then filtered by a bandpass filter (ET525-70m-2p, Chroma), and detected by a GaAsP photomultiplier tube (H10770PA, Hamamatsu). Photocurrents from the PMT were amplified by a high-speed pre-amplifier (DHPCA-100, Femto, 200 MHz BW, 103 V/A) and sent into the demultiplexing electronics.
3.2. Demultiplexing electronics
Analog demultiplexing was implemented with an approach based on [19] with modifications appropriate to the 3PE laser. In [19], the control signals for the RF switch are complementary 80 MHz square-wave trains isolated with an 80 MHz bandpass filter from a drifting periodic signal driven by the laser oscillator. Here the control signals are single square waves driven by the relatively infrequent pulses from the 1 MHz amplifier, and thus, precise timing in the coincident arrival of the control and signal pulses is critical, whereas isolating the oscillator frequency is no longer necessary. The signal beam at 855 nm was attenuated by a beamsplitter and neutral density filters, then sampled by an amplified photodiode (DET10A, Thorlabs) with a ∼1 ns rise time. The photodiode pulse was sent into a comparator (LTC6957-HMS3, Analog Devices) which converted the input pulse waveform into two square pulse outputs of ∼8 ns duration, one of which was delayed by 15 ns with cabling. The square pulses were scaled to a peak-to-peak amplitude of 5 V with an amplifier (GVA-83+, MiniCircuits) and shifted to a common mode of -1 V by a bias tee (ZFBT-4R2GW+, MiniCircuits). The conditioned pulses were used to gate an RF switch (CMD196C3, Custom MMIC) whose input signal was switched between two output terminals connected to channels 1 and 2 of the digitizer (see Fig. 1 inset). The analog voltage signal from the pre-amplifier was delayed with cabling to temporally align with the channel windows before being input into the switch. Analog-to-digital conversion of the DAQ channels was also gated by 1 MHz pulses from the TTL sync output from the pump laser.
3.3. Third-order interferometric autocorrelation
The autocorrelator was constructed from a 50:50 non-polarizing beam splitter (BS015, Thorlabs) and a pair of mirrors, one of which was mounted on a piezo translator (nPFocus400, nPoint). Piezo movement was controlled in ScanImage (ScanImage Premium, Vidrio LLC) as a fast Z-axis scanner and synchronized with imaging of fluorescence from 50 µM fluorescein solution. Signal detected from fluorescein was averaged line-by-line and plotted against relative pulse delay calculated from the piezo scan position. Interferometric autocorrelation traces were numerically simulated in MATLAB (Mathworks) for Gaussian pulses of specified bandwidth and group dispersion delay (GDD) as chirp applied in the Fourier domain.
4. Results
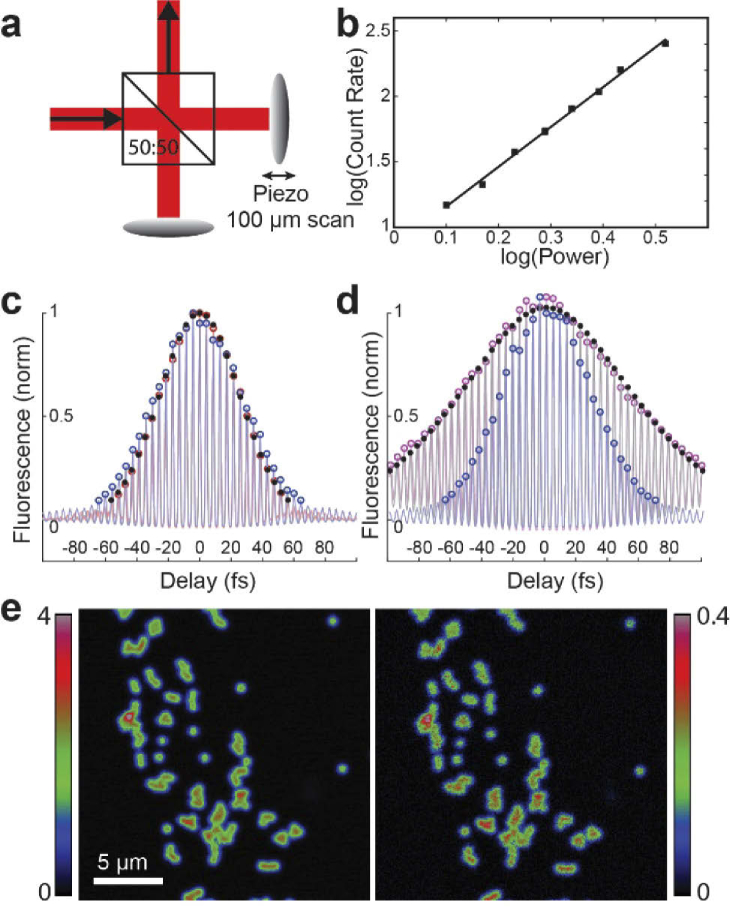
Of significant concern with using remote focusing in 3PE is the additional pulse dispersion introduced by the remote focusing unit, particularly by the double pass through the remote objective. To compensate dispersion, the idler beam was passed through a single-prism compressor which allowed substantial pre-chirp with robust tunability and a compact footprint. Because this pre-chirp was applied to both the remote focusing and temporal delay paths, it was critical to ensure the pulses in the two paths encountered identical GDD and could be ideally compensated at the microscope focus by the same compressor configuration. To characterize the pulse at the microscope focus, we constructed a Michelson interferometer in the beam path and measured 3PE-generated fluorescence in fluorescein while modulating the path length of one interferometer arm with a piezo-actuated mirror (Fig. 2(a)). In our setup, we used a commercial piezo scanner optimized for millisecond displacements of a microscope objective over travel distances of up to half a millimeter, but identical measurements could be obtained with a less specialized actuator and implemented at low cost compared with a commercial autocorrelator. Green fluorescence detected from 50 µM fluorescein excited at 1300 nm displayed a power dependence consistent with a cubic nonlinearity (n = 3.04 ± 0.07; Fig. 2(b)). Delaying one interferometer arm resulted in fringes in the fluorescence level reflecting the third-order interferometric autocorrelation (TIAC) [25,26] of the excitation pulse. We numerically generated TIAC traces for pulses of varying widths and chirps, and determined the best fit of the empirical data by the least-squares error. To cross-validate our measurement of the pulse width, we measured the pulse profile with minimal optics in the path, removing all but the prism compressor, beam expander, and objective, and tuned the compressor length to minimize the width of the TIAC. With the compressor set to a distance d = 44 cm prism separation (-4500 fs2 GDD), the measured trace was best fit by the simulated TIAC of a Gaussian pulse with intensity full-width at half-maximum (FWHM) of 48 fs. This was consistent with estimates of the transform-limited FWHM of the pulse obtained from both measurements of the spectral bandwidth by spectrometer and of the autocorrelation of the undispersed, free-space beam with a commercial autocorrelator (PulseCheck, APE). We similarly optimized the pulse through the full remote focusing path (path A) and obtained a minimal pulse width of 53 fs with 92 cm prism separation, corresponding to ∼11000 fs2 GDD (Fig. 2(c)). Subsequently, measuring the temporally delayed path (path B) with 92 cm prism separation, the FWHM of the chirped pulse was ∼140 fs at focus with a relative negative GDD of -2400 fs2 which we compensated by inserting a disk of ZnSe of 5 mm thickness (Fig. 2(d)). To validate these measurements and examine the effect on excitation efficiency, we removed the interferometer and imaged a fluorescent bead sample with and without the ZnSe disc. We observed nearly a 10-fold difference in fluorescence for equal excitation energy (Fig. 2(e)), demonstrating the importance of proper dispersion compensation for limiting excitation power and tissue heating.
Fig. 2.
Pulse dispersion characterization and compensation. (a), illustration of interferometric autocorrelator setup inserted into the beam path. A 50:50 beam splitter splits incoming pulses between two arms of nearly equal length which are reflected back by mirrors, one of which is mounted on a piezo-actuated translation stage. The pulses are recombined leading to interference and amplitude modulation of the excitation focus. (b), log-log plot of fluorescence vs. excitation power in 50 µM fluorescein with a linear fit of slope n = 3.04. (c), plot of peak-normalized fluorescence detected in fluorescein vs. inter-pulse delay calculated from position of interferometer mirror for minimal optics (d = 44 cm; red circles) and path A (d = 92 cm; blue circles) compared with the minimal best-fit from simulation (FWHM = 48 fs; black dots). (d), plot of peak-normalized fluorescence for path B without the ZnSe disc (d = 92 cm; purple circles) and with the ZnSe disc (5 mm ZnSe, d = 92 cm; blue circles) compared with the best-fit from simulation with negative chirp (GDD = -2400 fs2; black dots). (e), images of 500 nm fluorescent beads in water imaged with (left panel) and without (right panel) the ZnSe disc. Color scale: mean photon rate of 0–4 counts/pixel (left) and 0–0.4 counts/pixel (right, 10x gain).
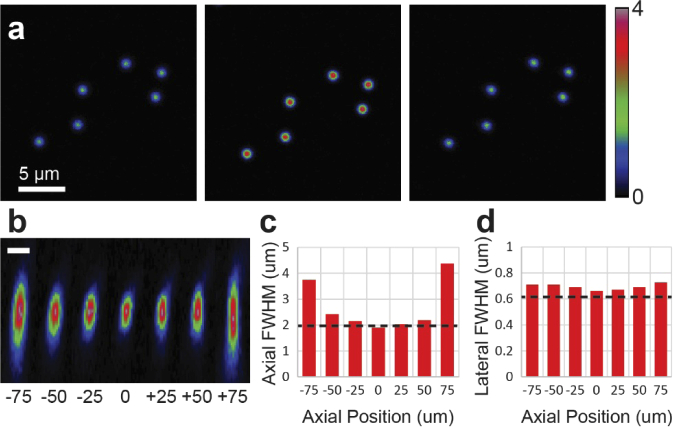
We next examined the range of diffraction-limited remote focusing. Principles of remote focusing can be found detailed in the literature [23,27], and here we provide only a summary description. Briefly, our aim was to modulate the wavefront in the primary objective back pupil to cause axial repositioning of the focus without distorting its shape, i.e. while maintaining the resolution in the native focal plane. In the remote focusing approach, the modulated wavefront is produced in the back pupil of the remote objective and imaged onto the pupil of the primary objective, and so the range of diffraction-limited refocusing is constrained by the axial range over which the wavefront generated remotely corresponds to the ideal wavefront required for proper focusing. One consequence of this correspondence requirement is that the axial range typically shrinks with increasing NA, as the contribution of higher-order spherical terms, which are more difficult to correct precisely, grows with both the NA and magnitude of axial displacement. Thus, the axial range of high NA refocusing may be determined not only by the specifications of the remote and primary objectives, but also their optical quality and tolerances. Given these considerations, we began by measuring the axial range of our remote focusing system empirically.
The PSF measured with 500 nm beads at the native focal plane, i.e. with the remote mirror positioned at the remote focal plane, exhibited a FWHM of 0.67 µm laterally and 1.9 µm axially. By translating the remote mirror, we observed axial displacement of the imaging plane up to ± 50 µm while maintaining near diffraction-limited resolution (Fig. 3(a)). Beyond 50 µm, the focal volume progressively enlarged with significantly reduced resolution (Fig. 3(b)). The cubic nonlinearity implies that even the common definition of a Strehl ratio threshold of 0.8 for diffraction-limited performance (Maréchal criterion) will lead to a 50% reduction in fluorescence from a point emitter, approximately the signal reduction we observed at ± 50 µm displacement. Indeed, the PSF measured at ± 50 µm was only slightly enlarged relative to its size at the native imaging plane, closely matching theoretical predictions for the size of a diffraction-limited focus for an NA of 0.9 (Figs. 3(c) and 3(d)). Based on these measurements, we prescribed the range of the remote-focusing plane to within ± 50 µm.
Fig. 3.
Characterization of PSF with remote focusing. (a), images of 500 nm fluorescent beads taken in the remote focusing plane for axial displacements of -50 µm (left), 0 µm (center), and + 50 µm (right) with equal average power. Color scale: Mean photon rate 0–4 counts/pixel. (b), xz-projection of bead images. Scale bar: 1 µm. (c), graph of measured axial PSF FWHM for different remote focused plane positions. Dashed line denotes theoretical FWHM for NA = 0.9. (d), graph of measured lateral PSF FWHM for plane positions as in (c). Dashed line denotes theoretical FWHM for NA = 0.9 convolved with a 0.5 µm spherical shell representing the bead sample (see Appendix for details).
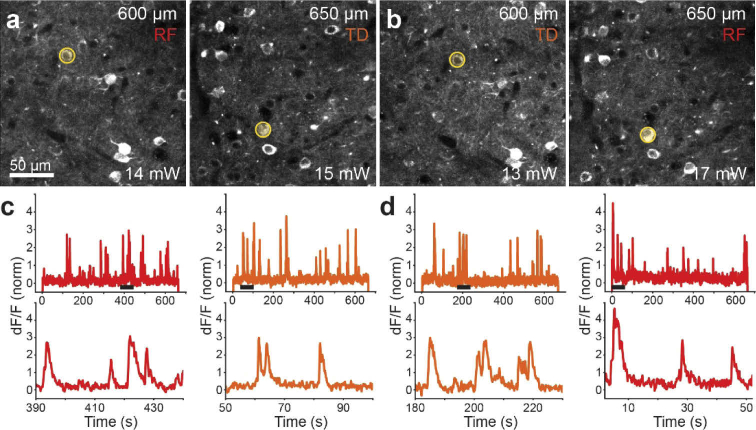
Next, we performed dual-plane calcium imaging of neurons deep in the cortex of a transgenic mouse expressing the genetically encoded calcium indicator GCaMP6s [28] in excitatory neurons throughout cortex (Slc17a7-IRES-Cre;Ai94). We simultaneously imaged two planes located at 600 and 650 µm deep, beyond the 2PE depth limit in these transgenic mice [5], in two 10 minute sessions. Between sessions, we exchanged the planes between path A and path B excitation to demonstrate simultaneous remote focusing at both ± 50 µm planes with conventional focusing at the native imaging plane (Figs. 4(a) and 4(b)).
Fig. 4.
Dual plane calcium imaging of neurons deep in cortex. (a), maximum intensity projections of motion corrected movies from simultaneously acquired planes located at z = 600 µm (left) and z = 650 µm (right) below the cortical surface imaged with the remote focus (RF, path A) and temporally delayed conventional focus (TD, path B), respectively. (b), maximum intensity projections of motion corrected, simultaneously acquired movies from planes in A with the remote focus and conventional focus exchanged. (c), dF/F normalized fluorescence traces extracted from neurons highlighted in A from movies acquired 50 µm above (red) and at (orange) the native imaging plane. Top panel: dF/F trace over the entire movie. Bottom panel: underlined section of full trace. (d), dF/F normalized fluorescence traces extracted from neurons highlighted in B from movies acquired at (orange) and 50 µm below (red) the native imaging plane. Top panel: dF/F trace over the entire movie. Bottom panel: underlined section of full trace.
Consistent with our measurements of the PSF, signal reduction in the planes imaged at ± 50 µm were compensated by modest changes in illumination power (15 mW path B vs. 17 mW path A at 650 µm). Image quality appeared identical between remote and normal focusing with similar features appearing in both movies, including transient activity in small puncta and dendrites. We compared fluorescence traces from spontaneously active neurons after motion correction and segmentation with Suite2p [29] and observed calcium transients of similar amplitude, frequency, and time course in extracted fluorescence traces (Figs. 4(c) and 4(d)).
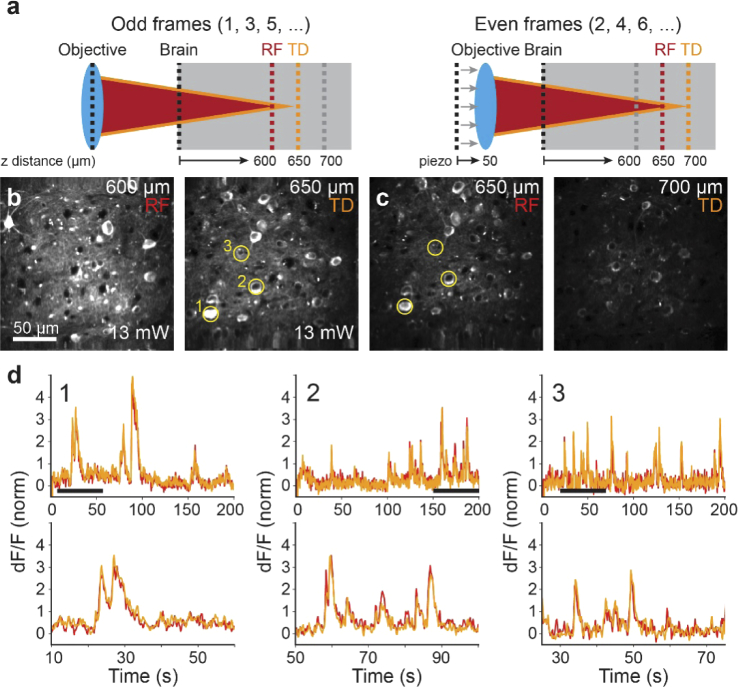
Finally, to sample from additional planes we combined dual-plane acquisition with piezo-controlled movement of the primary objective. We simultaneously imaged two planes located at 600 µm and 650 µm with the remote focus and native focus, respectively, then axially translated the primary objective with a piezo actuator by + 50 µm, thereby moving both foci 50 µm deeper to 650 µm and 700 µm (Figs. 5(a)–5(c)). By alternating the position of the objective between frames, we intentionally imaged the same plane located at 650 µm deep with the native and remote focus in alternating frames to directly compare imaging with conventional and remote focusing. To maintain a sufficient frame rate for imaging GCaMP6s, we halved the number of lines per frame from 256 to 128. This reduced the scan time per frame to 70 ms and resulted in rectangular pixels (0.78 µm x 1.56 µm). The piezo actuator required around 30 ms to step and settle the primary objective over 50 µm, resulting in an overall period of 100 ms per step and a volume rate of 5 Hz for the two objective positions used here. This volume rate was sufficiently fast to track calcium transients in the same neurons between frames and produced identical traces after motion correction and segmentation with Suite2p (Fig. 5(d)).
Fig. 5.
Multi-plane calcium imaging with dual-plane acquisition and objective scanning. (a), illustration of acquisition scheme in which the objective is position-cycled by 50 µm with a piezo scanner between successive frames. (b), maximum intensity projections of motion corrected movies of odd frames from simultaneously acquired planes imaged at 600 µm (left, remote focus) and 650 µm (right, native focus) deep. (c), maximum intensity projections of motion corrected movies from simultaneously acquired planes of even frames imaged at 650 µm (left, remote focus) and 700 µm (right, native focus) deep. (d), dF/F normalized fluorescence traces extracted from identical neurons highlighted in (a) and (b) imaged by the native focus (orange) and the remote focus (red) from alternating frames. Top panel: dF/F trace over the entire movie. Bottom panel: underlined section of full trace.
5. Discussion
The use of 3PE microscopy in neuroscience has grown considerably in recent years, driven by applications requiring high-resolution imaging through strongly scattering and densely fluorescent samples. However, data acquisition speeds with 3PE at present are an order of magnitude slower than comparable acquisition with 2PE, generally increasing the experimental burden and therefore constraining the practicality of using 3PE in situations where it is technically needed. In this work, we performed 3PE imaging in deep cortex at 2 MHz with total average power (30 mW) well below estimates of the thermal limit [6] and with estimated pulse energies at focus (<2 nJ) within the safe range determined in [12] indicating the possibility of further increasing both the pulse repetition rate and imaging speed. The low average power required per plane was made possible by controlling the spatiotemporal profile of excitation light to minimize the pulse width and size of the focal volume, so that they remained close to their physical limits. We implemented dual plane imaging using techniques taken directly from 2PE microscopy with consideration given to the different characteristics of 3PE and anticipate further leveraging of established methods to be helpful, as has also been demonstrated with focus shaping and adaptive optics.
Several improvements to this work are foreseeable. The first challenge is to extend the number and range of imaging planes. Here, we did not move the remote mirror during the acquisition as is typically done in multiplane 2PE systems. The current frame rate of ∼7 Hz is borderline for sequential plane repositioning, but increasing the pulse repetition rate and frame rate with beam multiplexed and/or resonant scanning should permit fast translations of the remote focusing planes with a reasonable overall volume acquisition rate. The range of remote focusing is currently limited by the remote objective. We selected the remote objective used here with the goal of maintaining high-NA, diffraction-limited focus quality and high transmission at 1300 nm with an off-the-shelf part, albeit with an acceptable limit on the range of refocusing. The ± 50 µm axial range measured here is narrower than predicted by theoretical calculations for refocusing with idealized objectives (see Appendix). In theory, diffraction-limited, high-resolution imaging over hundreds of microns axially should be possible if a more ideal remote-focusing objective (e.g. 20X, 0.8 NA, IR air objective) were acquired or designed. However, the empirically determined ± 50 µm range of the current method is sufficient for imaging well-separated planes at depth, as demonstrated in vivo, and is already practical for accelerating 3PE imaging in experiments in which a single focus is currently used.
Another critical challenge is to limit the average power and sample heating as the number of planes is increased. Here, gains from more efficient excitation with adaptive optics [20,30], brighter indicators [31], and adaptive illumination [32] would contribute to reducing the average illumination power per plane. We would also expect ongoing developments in laser technology, such as multi-color 3PE sources [33], will continue to provide further optimization and new opportunities to increase both the speed and flexibility of 3PE volume imaging methods.
6. Conclusion
We have described the implementation and characterization of a dual-plane 3PE laser-scanning microscope with temporal multiplexing and remote focusing, the first description of such to our knowledge. The method is a straightforward and low-cost modification of single-focus 3PE microscopes, and is readily applicable to in vivo imaging.
Acknowledgments
We wish to thank Daniel Flickinger and Natalia Orlova for their expertise and helpful discussions. We wish to thank the founder of the Allen Institute for Brain Science, Paul G. Allen, for his vision, encouragement, and support.
Appendix
Theoretical modeling and estimation of diffraction-limited focus size
We numerically calculated the peri-focal intensity distribution from theory using a vectorial model of diffraction from focusing with a high NA objective [34]. The diffraction-limited excitation volume is modeled as the cube of this intensity distribution which should be proportional to the rate of excitation and fluorescence, and thus defines the size of the 3PE focus. These calculations predict the lateral FWHM of the diffraction-limited 3PE focus to be 0.43 µm which is smaller than the beads used here. Consequently, the lateral FWHM of the measured PSF, i.e. the bead image, reflects a convolution of the 3PE focus with the bead fluorophore distribution, which we numerically performed as a 1-D convolution of the theoretical focal excitation profile and a 500 nm diameter circle. The FWHM of the convolution product is the theoretical limit shown in Fig. 4(d), which is larger than the width of the diffraction-limited focus. At the same time, we expect degradation of the remote focus to be primarily caused by uncorrected spherical modes producing substantial axial elongation with a smaller effect on the width of the focus, and we reasoned that measurement of the axial FWHM would be the more sensitive indicator of focus degradation, consistent with the data in Fig. 4(c). For direct measurement of the axial FWHM, 500 nm beads fully suffice and provide practical advantages of substantially higher signal and photostability, and therefore measurement precision and accuracy, compared with smaller diameter beads.
Theoretical range of diffraction-limited refocusing and objective performance
We follow the theory presented by Botcherby et al. [35] for the range of remote focusing with identical remote and primary objectives. We begin by writing down an expression for the general pupil function produced in the objective back pupil plane by a point source displaced a distance z along the optical axis from the native focus. For z = 0, the optical path length for all rays from the focus to the principal sphere is f, and thus, the optical path difference (OPD) is 0 over the entire pupil, and the light exiting the pupil is collimated. For a source displaced from the native focus at distance z along the axis, the OPD is given by
| (1) |
where is the normalized pupil radius and is the semi-aperture acceptance angle of the lens. Converting Eq. (1) to a phase function, , for the wavefront in the pupil, we find
| (2) |
where n is the refractive index of the lens immersion medium and is the wavenumber of the excitation light. Approximating the outer binomial and expanding to second-order in z, we find
| (3) |
We now consider the case where the pupil wavefront is imaged onto the back pupil of a second objective with a different focal length, aperture angle, and immersion medium. The total phase accumulated for rays traveling from the principle sphere to a position on the optical axis of the second objective is then given by
| (4) |
It is clear in Eq. (4) that substituting the standard remote focusing relations and achieved with proper relay magnification causes cancellation of the first-order terms leaving a residual quadratic term that can be expressed in terms of the primary objective’s coordinates as
| (5) |
If the lenses are identical, i.e. if and , then Eq. (5) reduces to Eq. (18) in [35]. Here, the effect of having asymmetrical lenses is to rescale the total phase by a factor of . The Strehl ratio, S, as calculated in [1] then becomes
| (6) |
where the subscript 2 has been dropped and is assumed to be air and therefore equal to 1. From Eq. (6), we observe that for all other parameters being equal, the axial range delimited by any threshold on S appears to generally increase with the focal length and decrease with the magnification of the objectives. Plotting the Strehl ratio for our objective configuration, the diffraction-limited range where extends to slightly over ± 250 µm (Fig. 6). This is substantially larger than the measured range, but we note two caveats to the theoretical result.
Fig. 6.
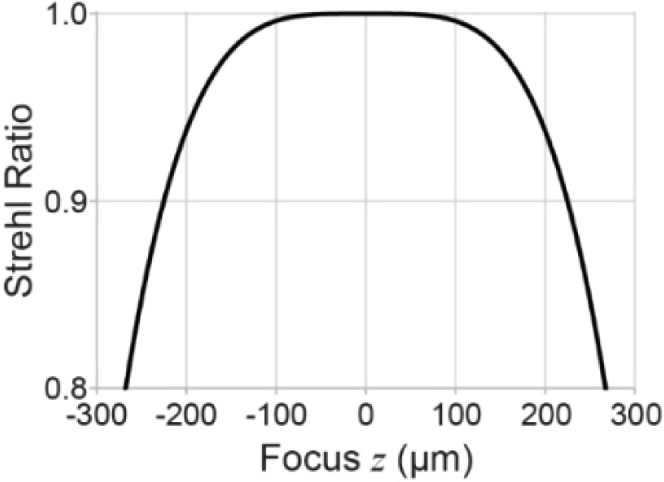
Theoretical range of diffraction-limited refocusing based on Eq. (6).
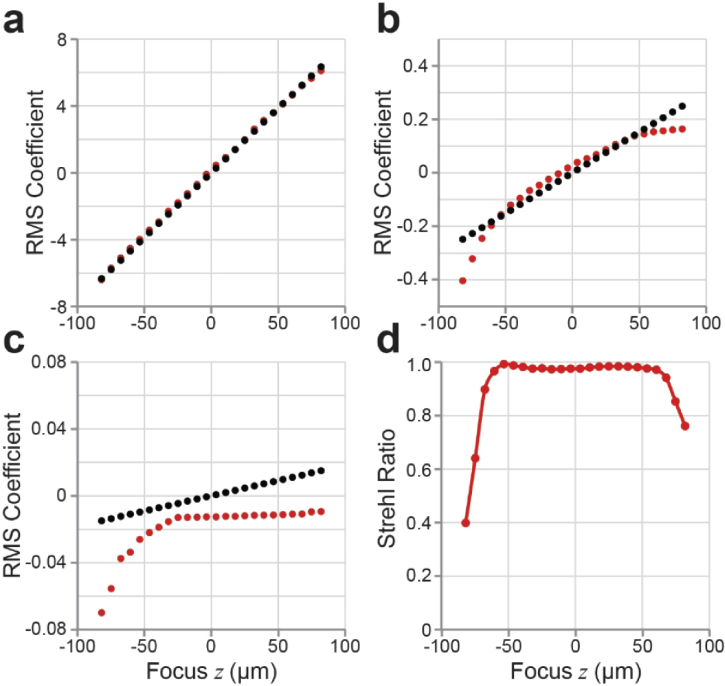
First, the general pupil function in Eq. (1) is idealized and does not account for optical design performance and constraints of real lenses. Second, the theory ignores higher-order terms in the accumulated phase which would also be expected to further limit the range of refocusing. To better determine the actual performance of the remote objective, we imaged the wavefront generated in the remote pupil onto a Shack-Hartmann wavefront sensor (HASO4, Imagine Optic) and recorded the coefficients of defocus, primary spherical, and secondary spherical modes, while translating the remote mirror. We compared the measured values against theoretical values required for ideal focusing and found the closest agreement over an axial range of ± 50 µm (Figs. 7(a)–7(c)).
Fig. 7.
Estimation of diffraction-limited refocusing range from pupil wavefront measurements. (a), Theoretical (black markers) and measured (red markers) values for the rms coefficient of defocus (j = 4, Noll ordering) plotted against axial position of the primary focus. (b), rms coefficient of primary spherical aberration (j = 11, Noll ordering). (c), rms coefficient of secondary spherical aberration (j = 22, Noll ordering). (d), Strehl ratio numerically calculated from simulating the focus generated by the composite wavefront from mode amplitudes in (a)-(c).
Evaluating the Strehl ratio from numerical calculations of the intensity at the focus [36] using the measured coefficients predicted a diffraction-limited range of about ± 70 µm (Fig. 6d), slightly larger than the range measured with beads, but also significantly narrower than the ± 250 µm predicted by the theory given above. Based on these measurements, we believe the performance of the remote objective to be the major factor limiting the axial range. These results suggest further examination and exploration of the design of the remote objective would be beneficial.
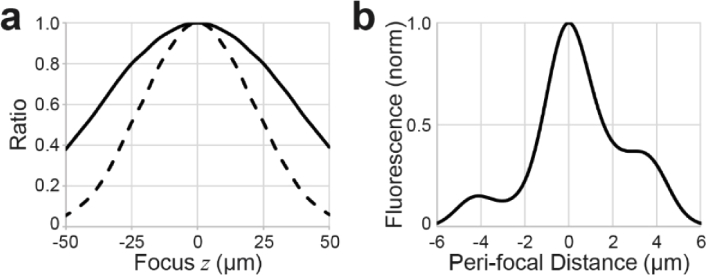
Finally, we note that the measured axial range of the off-the-shelf design at present still outperforms low-NA refocusing methods which control only the defocus term in the objective pupil. In this case, simulations predict an axial range of ± 25 µm and at ± 50 µm display a substantially aberrated focus with a Strehl ratio of 0.4 leading to an overall loss of over 90% in excitation efficiency (Fig. 8).
Fig. 8.
Theoretical performance of defocus-only refocusing for excitation NA of 0.9. (a), Strehl ratio, S, (solid line) and 3PE efficiency (dashed line) calculated as S3 plotted against the axial position of the focus. (b), axial 3PE PSF for 50 µm defocus showing significant aberration.
We conclude that our setup correctly modulates the pupil wavefront over a range of about ± 50 µm. Wider axial ranges should be possible with improved remote lens design or selection, but the current, off-the-shelf objective is still advantageous for implementing high-NA remote focusing compared with technically simpler approaches.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Denk W., Strickler J. H., Webb W. W., “Two-photon laser scanning fluorescence microscopy,” Science 248(4951), 73–76 (1990). 10.1126/science.2321027 [DOI] [PubMed] [Google Scholar]
- 2.Helmchen F., Denk W., “Deep tissue two-photon microscopy,” Nat. Methods 2(12), 932–940 (2005). 10.1038/nmeth818 [DOI] [PubMed] [Google Scholar]
- 3.Park J., Sun W., Cui M., “High-resolution in vivo imaging of mouse brain through the intact skull,” Proc. Natl. Acad. Sci. U. S. A. 112(30), 9236–9241 (2015). 10.1073/pnas.1505939112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Theer P., Denk W., “On the fundamental imaging-depth limit in two-photon microscopy,” J. Opt. Soc. Am. A 23(12), 3139–3149 (2006). 10.1364/JOSAA.23.003139 [DOI] [PubMed] [Google Scholar]
- 5.Takasaki K., Abbasi-Asl R., Waters J., “Superficial bound of the depth limit of 2-photon imaging in mouse brain,” bioRxiv618454 (2019). [DOI] [PMC free article] [PubMed]
- 6.Wang T., Ouzounov D. G., Wu C., Horton N. G., Zhang B., Wu C., Zhang Y., Schnitzer M. J., Xu C., “Three-photon imaging of mouse brain structure and function through the intact skull,” Nat. Methods 15(10), 789–792 (2018). 10.1038/s41592-018-0115-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Horton N. G., Wang K., Kobat D., Clark C. G., Wise F. W., Schaffer C. B., Xu C., “In vivo three-photon microscopy of subcortical structures within an intact mouse brain,” Nat. Photonics 7(3), 205–209 (2013). 10.1038/nphoton.2012.336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sofroniew N. J., Flickinger D., King J., Svoboda K., “A large field of view two-photon mesoscope with subcellular resolution for in vivo imaging,” eLife 5, e14472 (2016). 10.7554/eLife.14472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Stirman J. N., Smith I. T., Kudenov M. W., Smith S. L., “Wide field-of-view, multi-region, two-photon imaging of neuronal activity in the mammalian brain,” Nat. Biotechnol. 34(8), 857–862 (2016). 10.1038/nbt.3594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Han S., Yang W., Yuste R., “Two-Color Volumetric Imaging of Neuronal Activity of Cortical Columns,” Cell Rep. 27(7), 2229–2240.e4 (2019). 10.1016/j.celrep.2019.04.075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ouzounov D. G., Wang T., Wang M., Feng D. D., Horton N. G., Cruz-Hernández J. C., Cheng Y., Reimer J., Tolias A. S., Nishimura N., Xu C., “In vivo three-photon imaging of activity of GCaMP6-labeled neurons deep in intact mouse brain,” Nat. Methods 14(4), 388–390 (2017). 10.1038/nmeth.4183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yildirim M., Sugihara H., So P. T. C., Sur M., “Functional imaging of visual cortical layers and subplate in awake mice with optimized three-photon microscopy,” Nat. Commun. 10(1), 177 (2019). 10.1038/s41467-018-08179-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weisenburger S., Tejera F., Demas J., Chen B., Manley J., Sparks F. T., Martínez Traub F., Daigle T., Zeng H., Losonczy A., Vaziri A., “Volumetric Ca2+ Imaging in the Mouse Brain Using Hybrid Multiplexed Sculpted Light Microscopy,” Cell 177(4), 1050–1066.e14 (2019). 10.1016/j.cell.2019.03.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Charan K., Li B., Wang M., Lin C. P., Xu C., “Fiber-based tunable repetition rate source for deep tissue two-photon fluorescence microscopy,” Biomed. Opt. Express 9(5), 2304 (2018). 10.1364/BOE.9.002304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen B., Huang X., Gou D., Zeng J., Chen G., Pang M., Hu Y., Zhao Z., Zhang Y., Zhou Z., Wu H., Cheng H., Zhang Z., Xu C., Li Y., Chen L., Wang A., “Rapid volumetric imaging with Bessel-Beam three-photon microscopy,” Biomed. Opt. Express 9(4), 1992 (2018). 10.1364/BOE.9.001992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rodríguez C., Liang Y., Lu R., Ji N., “Three-photon fluorescence microscopy with an axially elongated Bessel focus,” Opt. Lett. 43(8), 1914–1917 (2018). 10.1364/OL.43.001914 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cheng A., Gonçalves J. T., Golshani P., Arisaka K., Portera-Cailliau C., “Simultaneous 2-photon calcium imaging at different cortical depths in vivo with spatiotemporal multiplexing,” Nat. Methods 8(2), 139–142 (2011). 10.1038/nmeth.1552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yang W., Miller J. K., Carrillo-Reid L., Pnevmatikakis E., Paninski L., Yuste R., Peterka D. S., “Simultaneous Multi-plane Imaging of Neural Circuits,” Neuron 89(2), 269–284 (2016). 10.1016/j.neuron.2015.12.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tsyboulski D., Orlova N., Griffin F., Seid S., Lecoq J., Saggau P., “Remote focusing system for simultaneous dual-plane mesoscopic multiphoton imaging,” bioRxiv503052 (2018).
- 20.Sinefeld D., Paudel H. P., Ouzounov D. G., Bifano T. G., Xu C., “Adaptive optics in multiphoton microscopy: comparison of two, three and four photon fluorescence,” Opt. Express 23(24), 31472–31483 (2015). 10.1364/OE.23.031472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mok A. T., Wang T., Xia F., Wu C., Xu C., “Simultaneous Two- and Three-photon Imaging of Multilayer Neural Activities with Remote Focusing,” in Conference on Lasers and Electro-Optics (Optical Society of America, 2019), paper AM1I.5. [Google Scholar]
- 22.Botcherby E. J., Juskaitis R., Booth M. J., Wilson T., “Aberration-free optical refocusing in high numerical aperture microscopy,” Opt. Lett. 32(14), 2007–2009 (2007). 10.1364/OL.32.002007 [DOI] [PubMed] [Google Scholar]
- 23.Botcherby E. J., Smith C. W., Kohl M. M., Débarre D., Booth M. J., Juskaitis R., Paulsen O., Wilson T., “Aberration-free three-dimensional multiphoton imaging of neuronal activity at kHz rates,” Proc. Natl. Acad. Sci. U. S. A. 109(8), 2919–2924 (2012). 10.1073/pnas.1111662109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Akturk S., Gu X., Kimmel M., Trebino R., “Extremely simple single-prism ultrashort- pulse compressor,” Opt. Express 14(21), 10101–10108 (2006). 10.1364/OE.14.010101 [DOI] [PubMed] [Google Scholar]
- 25.Diels J. M., Fontaine J. J., McMichael I. C., Simoni F., “Control and measurement of ultrashort pulse shapes (in amplitude and phase) with femtosecond accuracy,” Appl. Opt. 24(9), 1270 (1985). 10.1364/AO.24.001270 [DOI] [PubMed] [Google Scholar]
- 26.Langlois P., Ippen E. P., “Measurement of pulse asymmetry by three-photon-absorption autocorrelation in a GaAsP photodiode,” Opt. Lett. 24(24), 1868 (1999). 10.1364/OL.24.001868 [DOI] [PubMed] [Google Scholar]
- 27.Anselmi F., Ventalon C., Bègue A., Ogden D., Emiliani V., “Three-dimensional imaging and photostimulation by remote-focusing and holographic light patterning,” Proc. Natl. Acad. Sci. U. S. A. 108(49), 19504–19509 (2011). 10.1073/pnas.1109111108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chen T., Wardill T. J., Sun Y., Pulver S. R., Renninger S. L., Baohan A., Schreiter E. R., Kerr R. A., Orger M. B., Jayaraman V., Looger L. L., Svoboda K., Kim D. S., “Ultrasensitive fluorescent proteins for imaging neuronal activity,” Nature 499(7458), 295–300 (2013). 10.1038/nature12354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pachitariu M., Stringer C., Dipoppa M., Schröder S., Rossi L. F., Dalgleish H., Carandini M., Harris K. D., “Suite2p: beyond 10,000 neurons with standard two-photon microscopy,” bioRxiv061507 (2017).
- 30.Ji N., Milkie D. E., Betzig E., “Adaptive optics via pupil segmentation for high-resolution imaging in biological tissues,” Nat. Methods 7(2), 141–147 (2010). 10.1038/nmeth.1411 [DOI] [PubMed] [Google Scholar]
- 31.Dana H., Sun Y., Mohar B., Hulse B. K., Kerlin A. M., Hasseman J. P., Tsegaye G., Tsang A., Wong A., Patel R., Macklin J. J., Chen Y., Konnerth A., Jayaraman V., Looger L. L., Schreiter E. R., Svoboda K., Kim D. S., “High-performance calcium sensors for imaging activity in neuronal populations and microcompartments,” Nat. Methods 16(7), 649–657 (2019). 10.1038/s41592-019-0435-6 [DOI] [PubMed] [Google Scholar]
- 32.Li B., Wang M., Wu C., Charan K., Xu C., “An adaptive excitation source for multiphoton imaging,” in Conference on Lasers and Electro-Optics (Optical Society of America, 2018), paper JTh5C.5. [Google Scholar]
- 33.Guesmi K., Abdeladim L., Tozer S., Mahou P., Kumamoto T., Jurkus K., Rigaud P., Loulier K., Dray N., Georges P., Hanna M., Livet J., Supatto W., Beaurepaire E., Druon F., “Dual-color deep-tissue three-photon microscopy with a multiband infrared laser,” Light: Sci. Appl. 7(1), 12 (2018). 10.1038/s41377-018-0012-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Richards B., Wolf E., “Electromagnetic Diffraction in Optical Systems. II. Structure of the Image Field in an Aplanatic System,” Proc. Royal Soc. Lond. A 253(1274), 358–379 (1959). 10.1098/rspa.1959.0200 [DOI] [Google Scholar]
- 35.Botcherby E. J., Juškaitis R., Booth M. J., Wilson T., “An optical technique for remote focusing in microscopy,” Opt. Commun. 281(4), 880–887 (2008). 10.1016/j.optcom.2007.10.007 [DOI] [Google Scholar]
- 36.Born M., Wolf E., Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (Cambridge University Press, 1999). [Google Scholar]