Abstract
Resting-state functional connectivity analysis using optical neuroimaging holds the potential to be a powerful bridge between mouse models of disease and clinical neurologic monitoring. However, analysis techniques specific to optical methods are rudimentary, and algorithms from magnetic resonance imaging are not always applicable to optics. We have developed visual processing tools to increase data quality, improve brain segmentation, and average across sessions with better field-of-view. We demonstrate improved performance using resting-state optical intrinsic signal from normal mice. The proposed methods increase the amount of usable data from neuroimaging studies, improve image fidelity, and should be translatable to human optical neuroimaging systems.
1. Introduction
Optical functional neuroimaging holds promise to link mouse models of neurological disease to the insights about human neuroscience gained from functional magnetic resonance imaging (fMRI). A major analysis tool in this field is resting-state functional connectivity, which enables mapping of distributed brain networks using correlated hemodynamics in the absence of tasks [1]. The ability to assess brain functional integrity without task- or stimulus-paradigms is well-suited for both clinical populations [2] and preclinical mouse models [3]. Recently, resting-state functional connectivity analysis has been adapted for use with optical intrinsic signal (OIS) imaging [4,5] and for fluorescence imaging using voltage-sensitive dyes [6] and genetically-encoded calcium indicators [7–9]. These techniques, in turn, are stimulating development of new imaging biomarkers of neurologic disease in preclinical models [10–13].
While resting-state optical imaging algorithms are informed by fMRI, direct translation of the entire fMRI processing stream is not possible. For example, concurrent anatomic imaging and whole-brain coverage in MRI enables advanced brain segmentation techniques [14–17]. Furthermore, in MRI, once the cortical surface is identified and the data transformed to an atlas, then analysis across subjects is relatively simple. Since every location in the brain is sampled in every subject, the data can be averaged or concatenated. Conversely, no reliable structural data exists in optical imaging with which to segment the data. For optical neuroimaging in mice, the images consist of the dorsal surface of the brain as well as surrounding tissue (e.g., skull, overlying veins, skin, and hair). In the existing literature, to segment the brain from these other tissue types, a single imaging frame is viewed, and the region corresponding to brain is traced manually [4,5,8,18]. Analysis of functional signals is then performed on pixels judged to be within the brain mask. One important limitation of this method is that it relies significantly on operator judgement which, we hypothesize, causes unintended variability in border selection. Additionally, this approach is limiting because it does not offer flexibility to remove individual pixels within the larger field-of-view, for example to mask regions of low signal-to-noise due to overlying venous sinuses or optical defects in the cranial window.
Lack of whole-brain coverage further complicates the process of combining data across multiple scans. Since the imaged region may vary between subjects, or even sessions from the same subject, an individual pixel might correspond to brain in one mouse but not in another. The most common method to account for variation has been to perform the final analysis only on the intersection of masks from all sessions (i.e., only on those brain areas that were imaged in every session) [10,11,18,19]. The only advantage of this method is simplicity. If there is only slight variation between sessions, then the number of pixels lost by taking the intersection may be minimal, but for studies that include a large number of subjects, even with an ideal field-of-view, the number of pixels lost can become substantial. Similarly, any session with a small field-of-view must be excluded, or else it would corrupt the global analysis for the entire population.
In this contribution, we improve on existing methods by developing semi-automated optical brain image segmentation techniques and averaging methods that tolerate heterogeneity in the field-of-view between scans. Briefly, we first created automated pixel-wise quality control metrics to exclude low quality pixels from the data analysis. Previously, systematic quality control has been used to exclude entire imaging sessions [10,11], but to our knowledge it has never been used on a pixel-wise basis. The initial mask created by this automated process is then used as an initial condition for manual brain segmentation, which we show improves unintended variation in segmentation. Secondly, we developed methods to combine these data across imaging sessions and across subjects in a censored fashion. The new averaging approach accounts for varying fields-of-view and brain masks, with the understanding that data in any pixel may only be partially known. The success of these visual image processing algorithms are demonstrated with resting-state OIS data from mice, but the same fundamental approach should be applicable to task-based paradigms and for other optical modalities such as diffuse optical tomography. Broadly, these techniques should permit an easier, standardized, and more thorough analysis in functional studies that employ optical imaging techniques to study the brain and have large sample size. Thus, they will improve study fidelity and aid the development of imaging biomarkers.
2. Methods
Definitions of the variables used herein are supplied in Table 1 , as well as at first use.
Table 1. Definitions of variables.
| Raw images of light intensity over time as captured by the camera. | |
| Detrended images of light intensity over time. | |
| Mean value of each pixel’s time course. | |
| Standard deviation of each pixel’s time course (after detrending). | |
| Boolean pixel mask for saturation, | |
| where included pixels have a value of 1 and saturated pixels 0. | |
| Boolean pixel mask for signal-to-noise, | |
| where included pixels have a value of 1 and low SNR pixels 0. | |
| Boolean pixel mask for local correlation, | |
| where included pixels have a value of 1 and low local correlation pixels 0. | |
| Combination Boolean mask using the three masks: | |
| , , and . | |
| Manual segmentation. | |
| Guided segmentation. | |
| Masking parameter for SNR mask. | |
| Masking parameter for correlation mask. | |
| Images of changes in the absorption coefficient over time. | |
| Optical pathlength. | |
| Spatial Gaussian smoothing kernel. | |
| Spatially-smoothed images of changes in the absorption coefficient over time.a | |
| Number of pixels included in each pixel’s interpolation after smoothing. | |
| Guided segmentation interpolated by smoothing. | |
| Global signal averaged over the segmented brain.a | |
| Regression coefficient at each pixel for the global signal.a | |
| Images of changes in the absorption coefficient over time | |
| after spatial smoothing and global signal regression.a | |
| Matrix of correlation coefficients. | |
| Boolean mask for correlation coefficient matrix. | |
| Matrix of Fisher-transformed correlation coefficients. |
The subscript i denotes the segmentation method.
2.1. Optical intrinsic signal imaging system
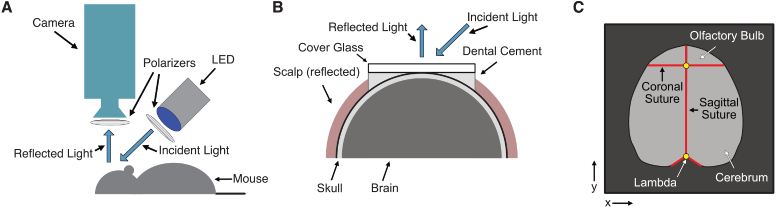
The optical intrinsic signal (OIS) imaging system is similar to that described previously [4] (Fig. 1(A) ). Briefly, illumination is derived from a 470 nm LED (Thorlabs M470L3-C1). Sequential images were acquired with a cooled, CCD camera (iXon 887, Andor Technologies). Crossed polarizers were used to eliminate light signal from specular reflection. The system was controlled with custom-written software using Matlab and the Andor software development kit.
Fig. 1.
Schematic of the optical intrinsic signal (OIS) imaging system. (A) Diagram of system components and light path. (B) Cross-section of the mouse head during imaging. (C) Schematic of the field-of-view demonstrating the goal of segmentation. The exposed brain is shown in light gray, with surrounding hair and skin in dark gray. Major suture landmarks are shown in red. Points used for the atlasing affine transformation are in yellow.
2.2. Animal preparation and imaging
All procedures were approved by the institutional animal care and use committee (IACUC) at the Children’s Hospital of Philadelphia. Male C57bl/6 mice (ages 8 to 13 weeks) were anesthetized with a mixture of ketamine (100 mg/kg) and xylazine (10 mg/kg) through intraperitoneal injection. After adequate anesthesia was achieved (usually after approximately 10 minutes), the animal was held in place with ear bars and kept warm with a heating pad. The hair on the dorsal surface of the head was removed with a depilatory cream, and the scalp was cleaned with iodine and ethyl alcohol. The scalp was incised and reflected to expose the skull from the olfactory bulb (anteriorly) to the superior colliculus (posteriorly) with as much lateral exposure as possible. Either the exposed skull was coated with a thin layer of mineral oil to create a smooth optical interface, or a glass through-skull cranial window was placed using transparent dental cement [20] (Fig. 1(B)). This procedure usually took about 10-15 minutes, and imaging began about 20-30 minutes after anesthetic injection.
Resting-state time series were acquired in 5 minute imaging runs. Three to six runs were obtained sequentially in each mouse (15 to 30 minutes of total imaging time). Data from the camera consists of a series of images of light intensity over time, . The two-dimensional images cover the dorsal surface of the mouse brain and surrounding tissue (Fig. 1(C)), with the direction indicating right-to-left and the direction posterior-to-anterior. The field-of-view of the camera was about 1.5 cm (sampled by 128 pixels for a pixel size of approximately 100 μm × 100 μm) along both the and directions. Each 5-minute run consisted of 8928 frames sampled at 29.76 Hz. To highlight the utility of our statistical methods for wide variations in field-of-view, we also utilized runs that were suboptimal for analysis; errors associated with suboptimal runs include camera saturation and limited dental cement application.
2.3. Masking
Rather than performing a quality-control procedure to keep or eliminate entire runs, we developed a pixel-wise masking procedure to remove pixels likely to contain data unrelated to neural hemodynamics. This procedure was designed to ensure high data quality and to serve as a guide for later brain segmentation. Masks were created to remove (1) saturated pixels, (2) low signal-to-noise pixels, and (3) pixels whose data are uncorrelated with their neighbors. In each case, the mask consists of a Boolean matrix of pixels, , where a value of one indicates a pixel to be kept for analysis, and zero indicates a pixel to be excluded.
First, if at any time, a pixel in the camera was saturated (bit depth ), then the entire time course for that pixel was excluded:
| (1) |
In order to remove temporal drift, a linear trend was removed from every pixel (maintaining the same mean). Specifically, let the mean value of each pixel be:
| (2) |
Then, each pixel’s data was fit to linear trend:
| (3) |
The trend was then removed:
| (4) |
For future use, we define the temporal standard deviation for each pixel:
| (5) |
To remove pixels with low signal-to-noise, we hypothesized that system noise should follow a Poisson process with the standard deviation of each pixel increasing linearly roughly with the square root of the mean intensity of each pixel. This expectation was borne out by visual inspection of the data (see Results). So, the standard deviation data across each session was fit to a linear relationship:
| (6) |
Pixels were considered to have good signal-to-noise if their standard deviation was within a tolerance of this function; otherwise they were excluded:
| (7) |
For the present data, we employed a value of equal to , which was found to be a good discriminator. This value was chosen based on visual inspection of the resulting masks.
Finally, we performed a correlation analysis of each pixel with each of its four neighboring pixels: , , , and . For a pixel to be included, these correlation values had to meet a minimum threshold ():
| (8) |
Note that this method is similar to the fMRI metric regional homogeneity (ReHo) [21], although it relies on correlation coefficients rather than Kendall’s coefficient of concordance. Our expectation was two-fold. First, in pixels corresponding to regions in space where few photons entered tissue and diffused (e.g., due to hair or overlying large vasculature), there would little correlation between neighboring pixels. Secondly, along interfaces (e.g., brain-skin at the edge of the cranial exposure), there would be less correlation between adjacent pixels. Note also, with the system’s field-of-view, the pixel size of the camera is well above the speckle size for the incident light. For our data, we found that of 0.1 was a good discriminator; again this value was chosen based on visual inspection of the data and resulting masks.
2.4. Brain segmentation
Two methods were used for brain segmentation and then compared. The first method was what has been used in prior literature. A false-color image of the mouse brain acquired by the camera was viewed, and the brain was manually segmented from its non-neural surroundings by drawing a border around the brain:
| (9) |
For the remainder of the manuscript, we refer to this method as manual segmentation.
For the new, second method, the three brain masks created above were combined to create one mask per imaging session:
| (10) |
This combined mask was then applied to the same false-color image of the mouse brain. In this way, the person performing the segmentation could see which pixels had been automatically excluded. Using these masked pixels as a guide to where the brain/surrounding-tissue interface should be, further regions were excluded from the brain segmentation manually. Pixels eligible for further processing needed to be within this segmentation and to pass the combined quality metrics:
| (11) |
For the remainder of the manuscript, we refer to this method as guided segmentation.
Our hypothesis was that the guided segmentation would create more consistent brain segmentations than the manual segmentation. To test this hypothesis, for each run, manual segmentation and guided segmentation were both performed twice by one rater (BRW) and once by a second rater (JPC). Both intra- and inter-rater agreement were quantified using three metrics. One metric, the Dice coefficient is a common metric for measuring segmentation overlap; however, it is relatively insensitive to error in settings of high overlap. We also employed the Jaccard coefficient, which is similar to the Dice coefficient, but is more sensitive to error. Finally, since the segmentation errors are entirely errors in the border, for a third metric we used the boundary F1 score (Matlab function bfscore), which compares agreement between the segmentation border contours. For all of these metrics, the possible values range between zero (no agreement) to one (perfect agreement). Values for the metrics for both intra- and inter-rater comparisons are presented as medians and interquartile ranges (IQRs). To judge improvement with the new methodology, the value of each metric for manual segmentation was compared against that for guided segmentation using paired t-tests.
2.5. Image processing
Further analysis beyond the raw images was performed separately with both segmentation methods, with procedures similar to those in prior reports [4]. Intensity measures were converted to relative absorption changes using the modified Beer-Lambert law:
| (12) |
where L is the optical path-length in tissue. Pixel time traces were then filtered to select frequencies from 0.008 to 0.09 Hz (i.e., the low-frequency hemodynamic fluctuations responsible for functional connectivity [1]). Data were then down-sampled to 1 Hz.
2.5.1. Spatial smoothing.
Each image of absorption change was then smoothed with a Gaussian kernel, ( pixel box, 1.3 pixel standard deviation, normalized to total value 1) [4]. In prior publications, which is also the approach we adopt for our analysis of manually segmented data, this smoothing was not affected by the segmentation:
| (13) |
By contrast, for guided segmentation images processed with pixel-wise quality metrics, only the masked pixels were included in the Gaussian smoothing:
| (14) |
With this method, the number of pixels whose values are included in each smoothed pixel is:
| (15) |
A pixel was included in the final analysis if either: (1) it had itself passed the quality metrics, or (2) its value could be interpolated through the smoothing algorithm by using at least ten pixels (out of 24 neighboring pixels within the pixel smoothing box) that had passed the quality metrics:
| (16) |
Thus, after Gaussian filtering, we effectively had a new composite image mask with some of the gaps from masking filled in by interpolation.
2.5.2. Affine transform.
From a representative image for each session, two landmarks were manually located: the lambda (at the midline sagittal junction of the cerebrum and superior colliculus) and the midline sagittal junction of the cerebrum and the olfactory bulb (Fig. 1(C)). Using these references, all sessions were affine transformed without shear (i.e., translation, rotation, and one stretch parameter were allowed to vary) to a common atlas space. Both brain masks (manual and guided) for each mouse were correspondingly transformed.
2.5.3. Global signal regression.
A global signal was then created by averaging over all pixels within the brain segmentation:
| (17) |
and
| (18) |
The global signal was regressed from all pixels before further analysis:
| (19) |
| (20) |
where the subscript, , corresponds to either manual, , or guided, , segmented data.
2.6. Functional connectivity analysis and statistics
For simplicity of analysis, the data series is reshaped to be a -by- matrix, , wherein there are pixels and time-points. Additionally, for simplicity we drop the prime superscripts (as all data forward will have undergone spatial smoothing and global signal regression) and the subscript denoting the segmentation method (since the methods below apply to either segmentation). Without loss of generality, each pixel’s time series was scaled to zero-mean and unit-variance.
2.6.1. Correlation matrix and masking.
With this procedure, we created the matrix of correlation coefficients:
| (21) |
Since correlation coefficients between pixels are of interest only if both are in the brain mask, we constructed a mask for this matrix:
| (22) |
is unity if is a correlation coefficient between two pixels within the brain mask, and it is zero otherwise.
For seed-based functional connectivity analysis, a pixel of interest (the seed) is chosen, and the corresponding row from the connectivity matrix, , selected. These correlation coefficients are then reshaped to pixels and are displayed as a map of correlation coefficients on the surface of the mouse brain (with the equivalent row of providing the brain segmentation). Seeds were selected based on the expected locations of canonical cortical regions from histological mouse brain atlases.
2.6.2. Averaging.
The correlation coefficients are not normally-distributed (they are bounded by −1 and 1). Therefore, for statistical analysis, they are converted using Fisher’s transform to an approximate normal distribution: . This statistic has the advantage that values can be more accurately averaged compared to averaging raw correlation coefficients [22,23].
If the viewed area was the same for every session and for every mouse, then it would be straight-forward to create an averaged correlation (transformed) matrix, because could simply be averaged across sessions. However, since and are different for each session, we must account for this variation. In previous work, analysis was performed on the intersection of all brain masks; we will refer to this procedure in this manuscript as the intersect method. Let the number of sessions for a given mouse be , and let the subscript denote the relevant matrix from each session. Further, let the subscript denote overall data averaged with the intersect method. Then:
| (23) |
| (24) |
We propose to explore the alternative averaging method which treats the data as censored, that is, the data are only partially known. For the purpose of this manuscript, we call this procedure the censored method. Let the subscript denote overall data averaged with the intersect method. Then:
| (25) |
| (26) |
We can also keep track of the number of pixels included in each component of :
| (27) |
For display, the averaged is converted back to a correlation coefficient: . Seed-based correlation analysis is performed as before with a seed pixel being chosen and the corresponding row of displayed with the brain mask being the same row of .
For the intersect method, as one might expect, the final brain segmentation is the intersection of the component brain segmentations. That is, every non-zero row of is equal. On the other hand, with the censored method, the brain segmentation for each seed-based map depends on the seed pixel. For example, consider the case of two sessions with overlapping but non-identical segmentations. Then, pixels with data only from session 1 would have no correlation coefficients with pixels that have data only from sessions 2. Thus, it is important to keep track of so as to be able to construct the appropriate field-of-view for any given seed pixel.
Now, that we have averaged over mice, an equivalent averaging procedure can be used to average across mice, by replacing the products and sums over sessions with products or sums across mice.
3. Results
Seven mice were scanned using our custom-built OIS imaging system. The mice were imaged in 5 minute scans with 3 to 6 scans per mouse. To highlight the ability and value for combining different fields-of-view, mice with suboptimal sessions were included in the data set. Two of the mice were scanned with exposed skulls covered by a thin layer of mineral oil. Five mice were scanned with through-skull cranial windows secured with dental cement; in three of these mice, insufficient dental cement was used, and thus the field-of-view was restricted to the medial cortex. Additionally, there are sporadic other artifacts in the images including camera saturation and bubbles in the dental cement, which will be identified and processed by the pixel-wise quality control metrics.
3.1. Brain segmentation
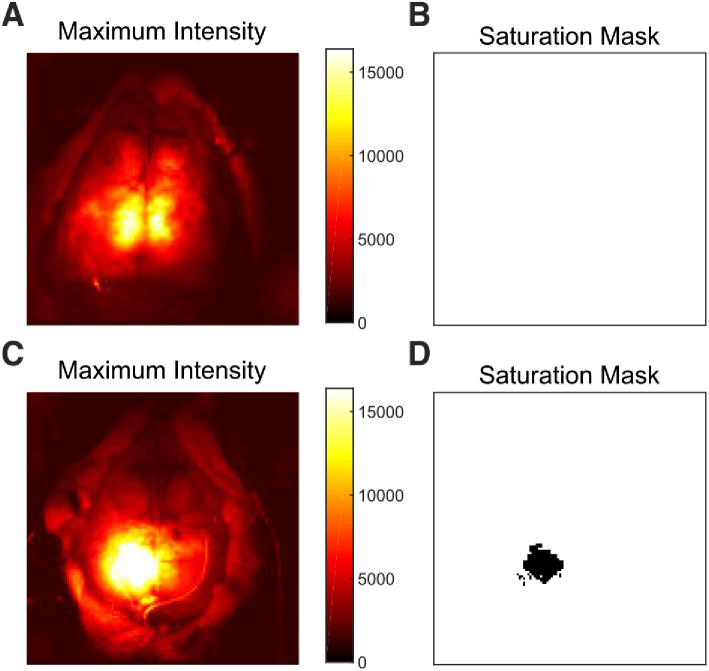
The first step in data processing is quality assessment performed on a pixel-wise basis. Saturation of the CCD camera was rare, but it occurred in some sessions, and in one run it resulted in the exclusion of a relatively large number of pixels in the center of the field-of-view (Fig. 2 ). The median number of pixels excluded by this metric across all sessions was 0 (IQR: 0-0; range: 0-226, 0-1.4%). Note, that there are 16,384 () total pixels in the image.
Fig. 2.
Examples of the saturation masking procedure. Data is shown prior to affine transformation. (A) Image of the maximum light intensity measured over time in mouse 2, session 5. (B) for this session. In this case, no pixels were excluded, and all pixels have a value of 1 (shown in white). (C) Similar image to A for mouse 3, session 3. In this case, the LED was accidentally set to be too bright, resulting in saturation over the left retrosplenial and parietal cortex. (D) The saturation mask, similar to B, for this session demonstrating exclusion of the saturated pixels (marked in black).
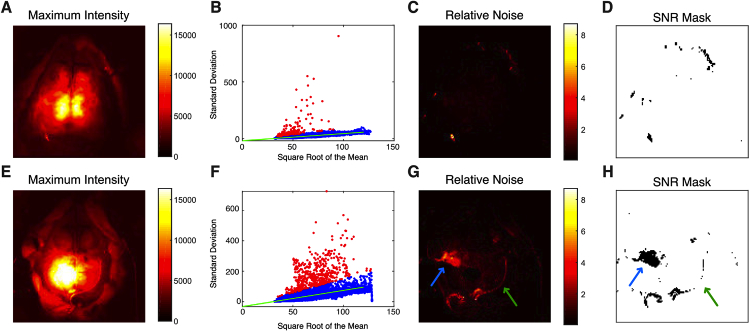
We next masked pixels based on signal-to-noise (Fig. 3 ). For each session, each pixel’s standard deviation over time was plotted against the square root of its mean value. We expected this plot to follow a linear relationship (see Methods). By visual inspection, this expectation was true, with the majority of scans having a tight linear distribution (Fig. 3(B)). The majority of pixels that failed this signal-to-noise threshold fell along the brain-skin interface, but a number of pixels were also excluded from the central area of brain indicating that not all central pixels should be assumed to be of equal quality, as would occur with fully manual segmentation (Fig. 3(C-D)). For other scans, more noisy pixels were present (Fig. 3(F-H)), but again the linear relationship with the square-root of mean pixel counts held, and pixels that were excluded helped to outline the brain interface. The median number of pixels excluded by this metric across all sessions was 208 (1.3%; IQR: 148-300, 0.9-1.8%; range: 19-565, 0.1-3.5%).
Fig. 3.
Example data demonstrating the signal-to-noise pixel quality metric. Data is shown prior to affine transformation. (A) Maximum intensity image (same as Fig. 2(A)) shown as an anatomic reference. (B) The standard deviation of each pixel over time is plotted against the square root of the intensity. Data is from mouse 2, session 5. The linear regression line of best fit is shown in green. Pixels meeting the SNR threshold are colored blue while pixels that failed and will be excluded from analysis are shown in red. (C) Image of the standard deviation for each pixel divided by the square root of the mean intensity for the same data. (D) SNR mask created from the data in C. In this session, only a few pixels were excluded based on this metric (shown in black). (E-H) The same analysis as A-D, now for mouse 3, session 3. Here, while the data is noisier, the same linear relationship holds. Pixels at the border of the dental cement (green arrows) show lower SNR and are excluded (black pixels in H). Additionally, there is a small region in the left sensorimotor cortex (blue arrows) that has low signal-to-noise, which upon examination of the data seems to be due to instability in the camera read-out. Individual low quality pixels can be excluded, and the entire run need not be discarded.
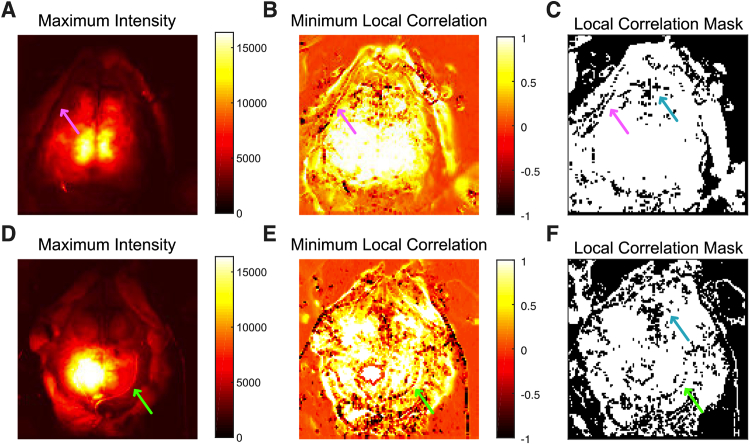
The third quality metric is based on the local correlation between adjacent pixels (Fig. 4 ). Across the visualized cerebral cortex, local correlations are high (near one). Note that these local correlations will not be equal to the correlation coefficients between adjacent pixels in later functional connectivity analysis because, during the current masking step, the data has not undergone temporal filtering and spatial smoothing, which increase local correlation coefficients. As expected, local correlations are very low (near zero) in the regions covered with fur (the upper right and upper left corners of Fig. 4(B, E)); in these cases, the photons do not enter tissue. Local correlation is also low at the border regions (either brain-skin or at the edge of the dental cement, arrows in Fig. 4). The mask thus created is also helpful delineating the brain region and for guiding manual segmentation. Overlying venous sinuses (seen along the midline, for example) also result in lower local correlation. This metric removed the largest number of pixels (due to the large areas of hair in the full images) with a median number of pixels across all sessions excluded of 8193 (50%; IQR: 6661-10011, 41-61%; range: 2687-11048, 16-67%).
Fig. 4.
Example data demonstrating the local correlation quality metric. Data is shown prior to affine transformation. (A) Maximum intensity image (same as Fig. 2(A)) shown as an anatomic reference. (B) Image of the minimum value of the correlation coefficients from each pixel’s surrounding four pixels. Areas covered with hair (in the four corners of the image) have values around zero; boundary regions (e.g., brain-skin) have low correlations as well. Data is from mouse 2, session 5. (C) Mask created from the data in B (excluded pixels in black). Note that the mask highlights boundary areas where the brain region meets the reflected skin flaps (pink arrows). (D-F) The same as A-C for mouse 3, session 3. As with other metrics, the data from this mouse is shown to be noisier, but the mask highlights the edge of the dental cemented region (green arrows). In all sessions, pixels are often removed from the region of the confluence of venous sinuses where the cerebrum meets the olfactory bulb with this mask (cyan arrows).
The structure of the masks using these metrics was generally similar across runs during the same imaging session (Fig. 5 ). In all cases, the masks outlined the interface between brain and surrounding tissue. Additionally, the venous sinuses that run along the sagittal and coronal sutures were frequently removed by masking. However, the masks also captured sources of noise specific to each run: either large areas of spurious signal (Figs. 2(D) and 3(H)) or single pixels unique to each run (Fig. 5).
Fig. 5.
Variation in the masks created by the pixel-wise quality metric across multiple runs in the same mouse (mouse 1, sessions 1-5, prior to affine transformation). In this mouse, camera saturation was never present; so, that mask is not shown. Note also, that the mouse was repositioned after Run 1; so that run is slightly shifted relative to the others. For the SNR mask (upper row), an area at the posterior edge of the left visual cortex (red arrow) is masked in most runs, possibly due to pooling mineral oil (used in this mouse) at that location. Additionally, scattered pixels in the center of the field-of-view are excluded in each run. For the local correlation mask (lower row), the masks area are very similar across runs. Common areas excluded were the areas of fur in the upper right and upper left corners, the venous sagittal sinus (blue arrows), and along the brain-skin interface (green arrows).
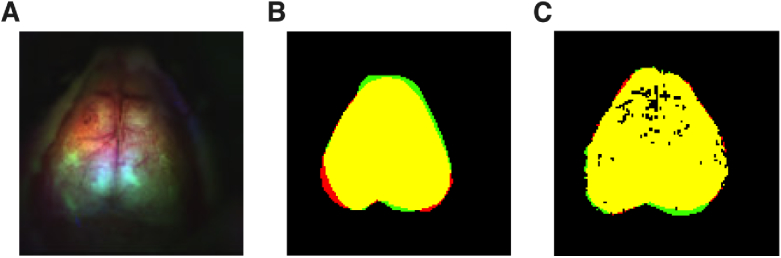
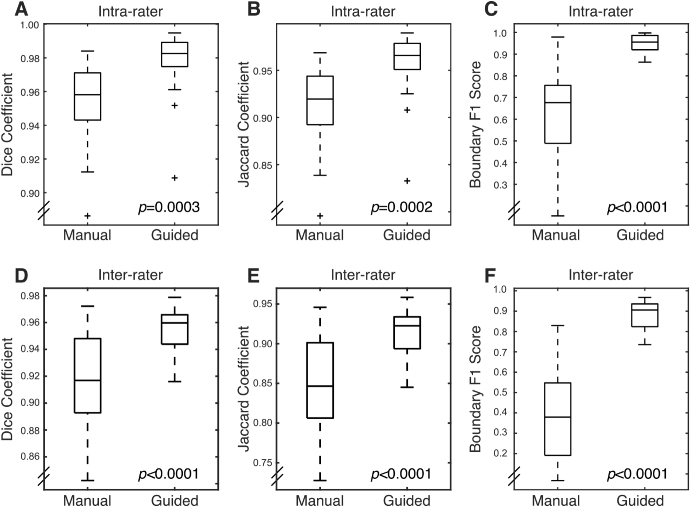
When combined, the three masks form a basis for the guided segmentation. While manual segmentation resulted in errors at the borders of the brain, the semi-automated segmentation resulted in improved intra-rater reliability (Fig. 6 ). This improvement was quantified. Guided segmentation resulted in an increase in all measures of agreement (Fig. 7 and Table 2 ). The Dice coefficient, although relatively insensitive to small variations in overlap, was high for both methods and did exhibit a significant increase with guided segmentation. The Jaccard coefficient, which is more sensitive to small differences, also significantly increased with guided segmentation. The boundary F1 score, which is most sensitive to small differences in the boundary position was highly variable with manual segmentation, but was consistently high with guided segmentation (Fig. 7 and Table 2). As expected, inter-rater agreement was lower than intra-rater agreement, but inter-rater agreement was much improved by using guided segmentation. With manual segmentation, the boundary F1 score, in particular, was very low. Interestingly, with guided segmentation, all measures of agreement were nearly as good as intra-rater agreement (Fig. 7 and Table 2).
Fig. 6.
Demonstration of unintended intra-rater variation in brain segmentation. Data is shown prior to affine transformation. (A) Example false color image from a single imaging frame from the OIS system as used for brain segmentation (mouse 2, session 5). (B) Variation in manual segmentation between two sessions by the same reader. Pixels within the first segmentation are colored red while those in the second segmentation are colored green. The overlap between the two segmentations is shown in yellow. (C) Reduced variation (greater overlap) is seen between two segmentations when using guided segmentation.
Fig. 7.
Box plots for measures of segmentation reliability. For all metrics, guided segmentation decreased variation for both intra- and inter-rater segmentation. (A) Dice coefficient for intra-rater segmentation. (B) Jaccard coefficient for intra-rater segmentation. (C) Boundary F1 score for intra-rater segmentation. (D-F) Same as A-C for inter-rater segmentation.
Table 2. Metrics for intra- and inter-rater agreement using manual and guided segmentation. All values are presented as the median and interquartile range.
| Intra-rater | |||
|---|---|---|---|
| Manual | Guided | P-value | |
| Dice Coefficient | 0.96 (0.94–0.97) | 0.98 (0.97–0.99) | 0.0003 |
| Jaccard Coefficient | 0.92 (0.89–0.94) | 0.97 (0.95–0.98) | 0.0002 |
| Boundary F1 Score | 0.68 (0.49–0.76) | 0.96 (0.92–0.99) | |
| Inter-rater | |||
| Manual | Guided | P-value | |
| Dice Coefficient | 0.92 (0.89–0.95) | 0.96 (0.94–0.97) | |
| Jaccard Coefficient | 0.84 (0.81–0.90) | 0.92 (0.89–0.93) | |
| Boundary F1 Score | 0.37 (0.19–0.55) | 0.91 (0.82–0.94) | |
3.2. Single-session functional connectivity
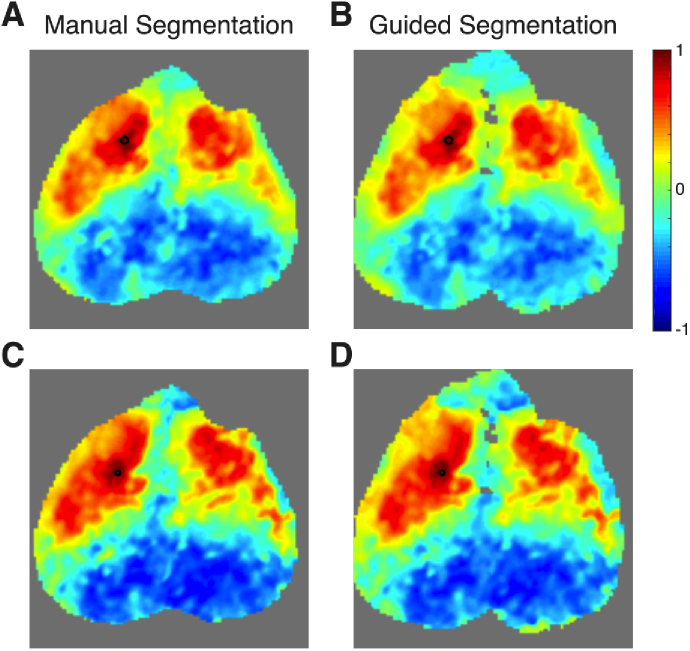
In addition to serving as a guide for segmentation, masked pixels were removed from further analysis, including smoothing and global signal regression. One might hypothesize that this masking should result in cleaner hemodynamic signals and less noise in the correlation maps. We have examined this question for a variety of scenarios and summarize some of these findings below. Generally, when a seed was chosen from a pixel that passed all the quality metrics, there was not an appreciable difference between the maps using either segmentation method (Fig. 8(A-B) ). Similarly, if a seed was chosen from a pixel that failed a quality metric, but was surrounded by good pixels, then there was not a large effect (Fig. 8(C-D)). Thus, for this basic level of functional connectivity analysis, spatial smoothing did a reasonable job of removing the effects of noisy pixels even in the absence of masking.
Fig. 8.
The effects of the pixel-wise quality metrics on the results of seed-based functional connectivity analysis in single sessions. Data is shown from mouse 1, session 1 after affine transformation. First a seed was chosen from the left motor cortex (black circle) that had passed all quality metrics. Functional connectivity maps are shown using both manual (A) and guided segmentation (B). The two maps are similar; thus the presence of low quality pixels at distant locations has little effect on the overall map. Then, a nearby pixel also in the left motor cortex was chosen as a seed (black circle). This seed failed the local correlation mask, but was filled in by interpolation during spatial smoothing and thus is present in both segmentations. Maps from manual segmentation (C) are similar to that from guided segmentation (D). Thus, in this basic analysis, the Gaussian spatial smoothing is able to ameliorate the effects of isolated low quality pixels even without masking.
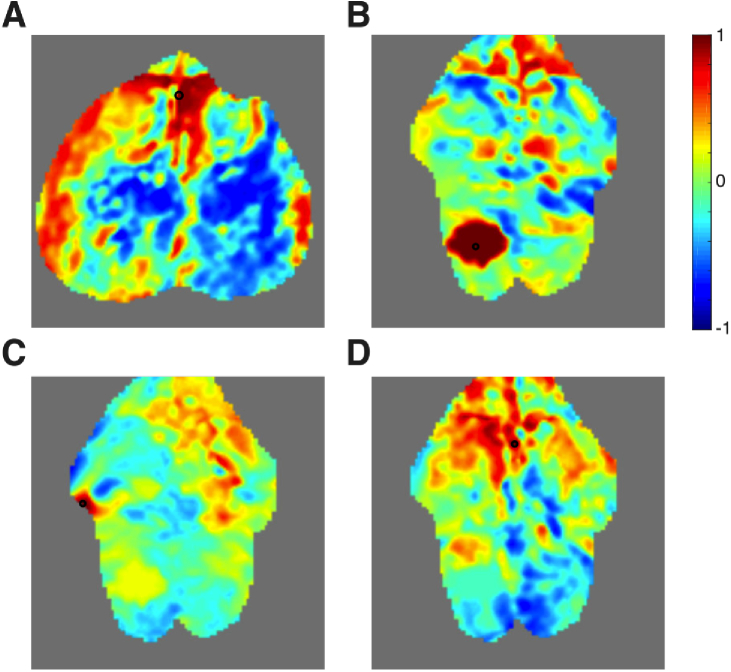
Alternatively, one could choose a pixel as a seed that failed quality metrics and was surrounded by other noisy pixels and was not interpolated using spatial smoothing (these pixels are thus available for analysis only in the manual segmentation data). Such seeds resulted in noisy functional connectivity maps without a clear neurologic basis for the correlations (Fig. 9 ). This result held regardless of the particular mask that caused a pixel to fail. Thus, when larger blocks of low quality pixels are present, their effect was noticeable and could not be removed by spatial smoothing. Masking of these pixels prevents these noisy functional connectivity maps from being present in the overall connectivity matrix, .
Fig. 9.
Functional connectivity maps performed using seeds that failed pixel-wise quality metrics. All data is after affine transformation. All seeds (black circles) shown in this figure were surrounded by other pixels that failed the quality metrics and were unable to be interpolated using spatial smoothing; thus all maps are shown using manually segmented data only. (A) A map of correlation coefficients using a seed in the frontal cortex along the sagittal sinus (mouse 1, session 5). This pixel failed the local correlation metric. (B) A seed pixel chosen from the region where the camera was saturated in the left retrosplenial cortex (mouse 3, session 3). (C) A seed pixel chosen from a region of low SNR in the left somatosensory cortex (mouse 3, session 3). (D) A seed pixel chosen from a region of low local correlation in the cingulate cortex and sagittal sinus (mouse 3, session 3). The resulting images all consist of patterns without a sensible neurologic network.
3.3. Averaging across sessions and mice
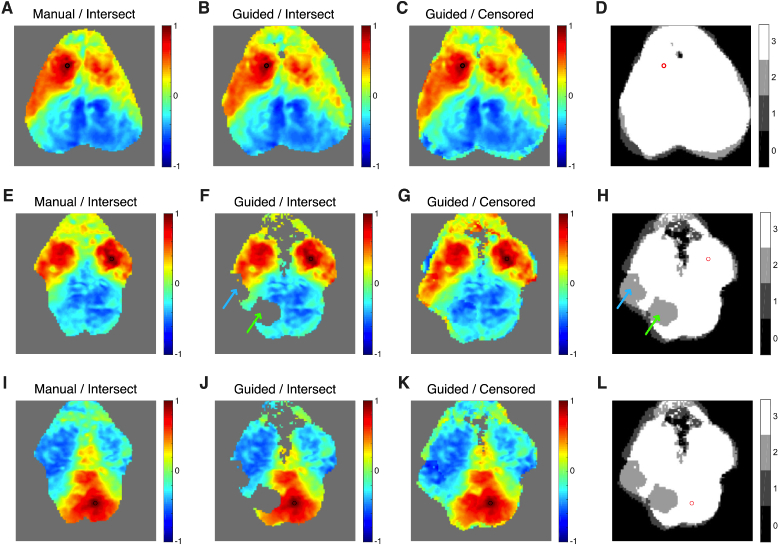
Use of the intersection method resulted in substantial drop-out of pixels when averaging across sessions. When using manual segmentation, we found that a median of 1378 pixels (8%, range: 819-2108, 5-12.9%) are lost when using intersect averaging across sessions. When using pixel-wise masking with guided segmentation in combination with the intersect averaging method, then more pixels are lost (median: 1563 pixels, 9.5%; range: 1285-2799, 7.8-17.1%). This increased loss is because the pixels excluded in each session do not always match between sessions. With censored averaging no pixels are lost. The resulting improved field-of-view is apparent in the seed-based functional connectivity maps (Fig. 10 ). In mice with a high degree of overlap between sessions, then all methods were able to do a reasonable job at preserving a high field-of-view (Fig. 10(A-D)). However, in mice wherein field-of-view varied more substantially between sessions, then the censored method resulted in a larger preserved field-of-view (compare Fig. 10(E) to Fig. 10(G) and Fig. 10(I) to Fig. 10(K)). When utilizing pixel-wise quality metrics in combination with the intersection method, the problem is even worse, as every pixel excluded in each single session necessarily reduces the overall field-of-view (Fig. 10(F, J)).
Fig. 10.
Demonstration of methods for combining data across sessions within a mouse. Data is shown after affine transformation. Data in the first row (A-D) is from mouse 2 with a seed in the left motor cortex (black or red circle). (A) Correlation coefficients from data segmented manually and then merged using the intersect method. (B) Data segmented using the guided segmentation and then merged with the intersect method. (C) Data segmented using the guided segmentation and then merged using the censored method. (D) Image showing the number of sessions contributing data for each pixel’s correlation coefficient when censored averaging is used (here, most pixels use all three sessions). (E-H) Similar data to A-D using data from mouse 3 and a seed in the right motor cortex. Note two large regions that were excluded by the pixel-wise quality metrics from one session cause drop-out in the guided segmentation / intersect method data. In the left parietal cortex, there is a region with signal loss due to camera saturation (green arrows, compare to Fig. 2(D)). In the left somatosensory cortex, there is signal loss due to instability in camera illumination (blue arrows, compare to Fig. 3(H)). The censored averaging method preserves the full field-of-view. (I-L) Similar data to A-D using data from mouse 3 and a seed in the right retrosplenial cortex.
When combining data from all mice, the improvements with censored averaging are even more apparent (Fig. 11 ). With manual segmentation and intersect averaging, correlation coefficients remain (only 11.1% of the possible correlations). With guided segmentation and intersect averaging, only correlation coefficients remain (5.9% of all possible correlations). With guided segmentation and censored averaging, correlation coefficients remain; this represents a 5.2-fold improvement over the prior standard method and 58% of all possible correlations in the field-of-view. This improvement is slightly exaggerated by the inclusion of suboptimal scans: the three runs with inadequate dental cement restrict the lateral field-of-view of the intersect method field-of-view, and the one run with a large region of camera saturation results in a large hole in left parietal cortex of the intersect method field-of-view. An alternative method to preserve field-of-view would be to simply not use data from mice with poor field-of-view or poor signal-to-noise, but this approach can exclude valuable data. Widely applicable analysis techniques should not rely on having only perfect data to work. Furthermore, the data from individual mice (e.g., Fig. 10) demonstrate that even mice with limited field-of-view still show the expected network structure and their inclusion in the overall average should improve confidence and statistical rigor for data within the imaged regions. Using all the data, even the suboptimal scans, is a more efficient use of mice and scanning time.
Fig. 11.
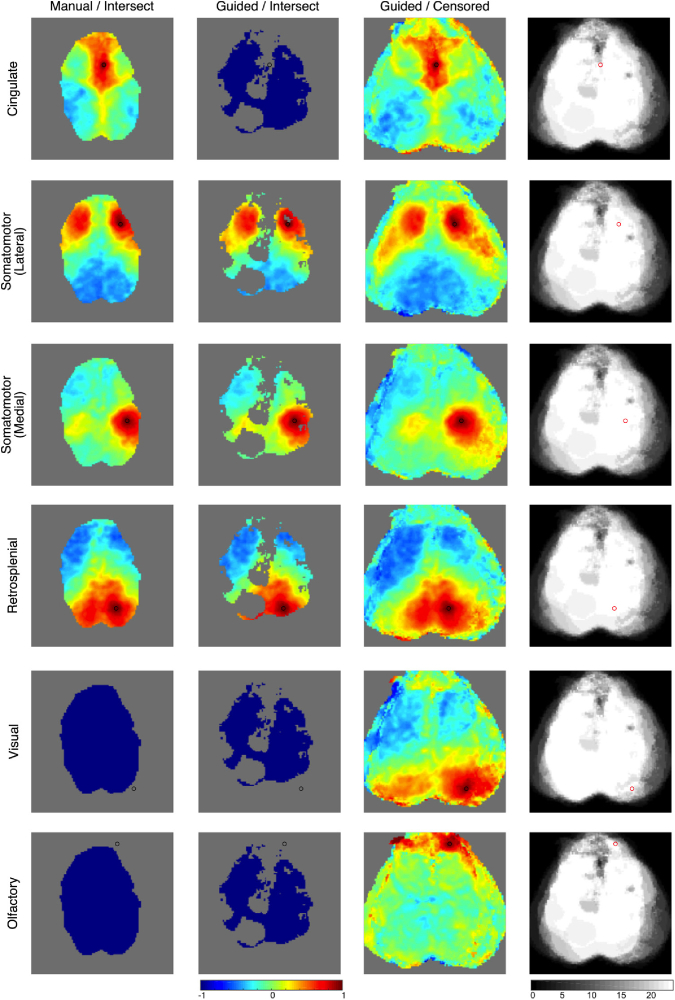
Demonstration of methods for combining data across mice. Data is shown after affine transformation. Each row is a different canonical resting-state network as shown by seed-based functional connectivity with the seed denoted by the circle (black or red). The first column uses manually segmented data merged using the intersect method. The second column is data segmented using the guided segmentation and then merged with the intersect method. The third column is data segmented using the guided segmentation and then merged using the censored method. The fourth column shows the number of sessions contributing data for each pixel’s correlation coefficient when calculated using the censored method. When seeds are selected that are outside of the field-of-view of the intersect method data, then the segmented brain is shown entirely in blue.
The wider field-of-view provided by censored averaging permits mapping of brain regions that are more lateral, anterior, and posterior. Although these areas were not present in every brain exposure, they are readily mapped by the censored method. With the intersect methods some areas such as olfactory and visual cortex are lost. Similarly, the full extent of some networks, such as the lateral somatomotor network are seen only with the censored method. Throughout most of the field-of-view, the correlation map using the censored data is smooth, and it is not readily apparent that a different set of sessions are included in each point. However, along the edges of the censored field-of-view only a small number of sessions are contributing to the overall image. In these areas, the edges between different component fields-of-view are more obvious.
4. Discussion
We have developed, demonstrated, and quantified novel visual processing methods to improve the analysis of mouse optical neuroimaging data. Pixel-wise quality metrics improved the data quality of the hemodynamic time courses and increased image quality through improved image segmentation. These findings were quantified via decreasing unintended intra- and inter-rater variation in brain segmentation. The new methods lead to improved confidence in the segmented boundaries. Additionally, since the guided segmentation is less user-dependent, the segmentation process is less dependent on expertise. Further, we developed methods to combine functional connectivity correlation coefficients even when the pixels involved differ between sessions. These methods compensate for both varying field-of-view in each cranial exposure and also the varying brain masks introduced by the pixel-wise quality metrics.
The techniques presented enable a more robust statistical treatment of imaging data, enabling finer control over data quality. One goal of this contribution is to suggest analysis methods that preserve as much usable data as possible. Ultimately, this gain could decrease the number of mice or sessions required and could increase statistical power. Rather than discarding mice with limited fields-of-view, or discarding sessions with areas of poor data quality, these data can be incorporated into the statistical model. This process is similar in concept to the fMRI technique of removing individual frames due to motion [24,25], which enables usable data to be extracted from sessions otherwise corrupted by subject motion. While on an individual session basis, the exclusion of pixels with low signal-to-noise did not visually appear to change many canonical correlation maps, more advanced metrics such as community construction and network analysis can be highly sensitive to data quality and noise. Thus, we expect that further advantages to pixel masking will be apparent in the future.
The quality metrics rely on multiple thresholds to determine which pixels to include. The coefficients chosen here were selected based on visual inspection of the data and the masks generated. Future work is necessary to determine if the values chosen here are optimal and generalizable. For example, different wavelengths of light have different path lengths in tissue, which may affect the masking parameter thresholds (e.g., , ). Additionally, other optical intrinsic signal imaging systems may have different signal-to-noise characteristics. We would, however, expect that the approaches described here should be generalizable.
Additional insight may be gained by examining the Fourier properties of the data. For example, techniques developed for fMRI such as amplitude of low frequency fluctuations (ALFF) [26] and relative ALFF (rALFF) [27] may be able to differentiate brain from other tissue types. However, the magnitudes of these metrics are not homogenous across the brain [28,29], and their utility for segmentation is unexplored. Furthermore, because optical imaging’s high sampling rate avoids the aliasing of high-frequency systemic physiology into the low frequency functional connectivity band, the values of these metrics may be different with optical imaging. This difference from fMRI may be particularly relevant for rALFF, which depends on the reference frequency band chosen for normalization. Understanding the properties of these metrics with OIS imaging will be part of our future work.
Other sources of noise in optical imaging data may require different types of filtering procedures. For example, as awake optical neuroimaging in mice becomes more prevalent [19,30], imaging quality will likely be improved by methods to remove artifacts due to motion [25]. Although mice are restrained in these studies, motion can cause systematic errors in fMRI measurements of functional connectivity even in restrained, anesthetized subjects [31]. Additionally, the effects of motion can differ between populations leading to statistical bias when performing group-level analyses [32]. Censoring individual pixels will likely be inadequate to remove such artifacts and more sophisticated methods, as have been used in fMRI [33], will be required.
Although the methods demonstrated in this manuscript concerned optical intrinsic signal imaging and resting-state functional connectivity, they should be broadly applicable to other imaging modalities. Human optical neuroimaging techniques, such as diffuse optical tomography (DOT), face similar spatial data issues as arise in mice. Variation in DOT image-pad positioning can introduce problems such as the field-of-view not being constant subject-to-subject and session-to-session. When functional data from DOT is mapped onto anatomic imaging from MRI [34,35], variation can be quantified, but this process does not ameliorate the underlying problem that variability imposes. As in prior mouse studies, the intersect method for multi-session and multi-subject averaging is commonly used [35,36], but it suffers from the same problems that were quantified in this paper. Such methods will be severely limiting for future studies, especially those in children or hospitalized patients, for example, where one might expect probe positioning to be extremely variable. Accounting for variations in a rigorous way is important to improving data reliability. The same general approach described here could be applicable to atlases for functional DOT data.
Future work will address the statistical analysis of merged data, which is nontrivial. Correlation coefficients in the final data will have been computed from a different subset of sessions, and we will need to treat the variance in an individualized manner. Then, the Fisher coefficients can be properly converted to -scores and -values. An alternative method for the analysis of resting-state functional connectivity data is independent component analysis (ICA). Similar censoring methods for ICA would be ideal, although the adaptation of ICA algorithms to comprehend partial data may be difficult. Similarly, the general concept of creating a mask to guide data censoring should be applicable to task-evoked activity (from OIS imaging, fluorescent dye imaging, or DOT). General linear model coefficients could be calculated at each pixel using a censored hemodynamic trace and expected canonical response. However, again the analysis of error and degrees of freedom necessary to calculate -values will need to take into consideration the censored nature of the data.
5. Conclusion
In conclusion, these rigorous in vivo studies demonstrate that pixel-wise quality metrics, guided segmentation, and censored averaging techniques can increase the amount of usable data and field-of-view obtainable from optical intrinsic signal imaging studies. More sessions can be included, thereby increasing subject numbers and likely increasing statistical power. Moreover, these methods increase the statistical rigor of optical neuroimaging and should enable detection of subtle effects. Ultimately, the resulting better understanding of data quality and its statistical properties will facilitate future work with more advanced methods of interpreting brain network connectivity data.
Acknowledgments
We thank Adam Bauer for help with instrumentation; Adam Bauer, Annie Bice, and Hannah Metheny for help with mouse protocols; and Theodore Satterthwaite and Zaixu Cui for help with analyzing correlation coefficients.
Funding
National Heart, Lung, and Blood Institute10.13039/100000050 (T32-HL007915); National Institute of Neurological Disorders and Stroke10.13039/100000065 (R01-NS060653); National Institute of Biomedical Imaging and Bioengineering10.13039/100000070 (P41-EB015893); Eunice Kennedy Shriver National Institute of Child Health and Human Development10.13039/100009633 (R37-HD059288); Children’s Hospital of Philadelphia10.13039/100006458.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Fox M. D., Raichle M. E., “Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging,” Nat. Rev. Neurosci. 8(9), 700–711 (2007). 10.1038/nrn2201 [DOI] [PubMed] [Google Scholar]
- 2.Fox M. D., Greicius M., “Clinical applications of resting state functional connectivity,” Front. Syst. Neurosci. 4, 19 (2010). 10.3389/fnsys.2010.00019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gorges M., Roselli F., Muller H.-P., Ludolph A. C., Rasche V., Kassubek J., “Functional connectivity mapping in the animal model: principles and applications of resting-state fMRI,” Front. Neurol. 8, 200 (2017). 10.3389/fneur.2017.00200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.White B. R., Bauer A. Q., Snyder A. Z., Schlaggar B. L., Lee J.-M., Culver J. P., “Imaging of functional connectivity in the mouse brain,” PLoS One 6(1), e16322 (2011). 10.1371/journal.pone.0016322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kura S., Xie H., Fu B., Ayata C., Boas D. A., Sakadzic S., “Intrinsic optical signal imaging of the blood volume changes is sufficient for mapping the resting state functional connectivity in the rodent cortex,” J. Neural. Eng. 15(3), 035003 (2018). 10.1088/1741-2552/aaafe4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mohajerani M. H., Chan A. W., Mohsenvand M., LeDue J., Liu R., McVea D. A., Boyd J. D., Wang Y. T., Reimers M., Murphy T. H., “Spontaneous cortical activity alternates between motifs defined by regional axonal projections,” Nat. Neurosci. 16(10), 1426–1435 (2013). 10.1038/nn.3499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Vanni M. P., Murphy T. H., “Mesoscale transcranial spontaneous activity mapping in GCaMP3 transgenic mice reveals extensive reciprocal connections between areas of somatomotor cortex,” J. Neurosci. 34(48), 15931–15946 (2014). 10.1523/JNEUROSCI.1818-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wright P. W., Brier L. M., Bauer A. Q., Baxter G. A., Kraft A. W., Reisman M. D., Bice A. R., Snyder A. Z., Lee J.-M., Culver J. P., “Functional connectivity structure of cortical calcium dynamics in anesthetized and awake mice,” PLoS One 12(10), e0185759 (2017). 10.1371/journal.pone.0185759 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vanni M. P., Chen A. W., Balbi M., Silasi G., Murphy T. H., “Mesoscale mapping of mouse cortex reveals frequency-dependent cycling between distinct macroscale functional modules,” J. Neurosci. 37(31), 7513–7533 (2017). 10.1523/JNEUROSCI.3560-16.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bero A. W., Bauer A. Q., Stewart F. R., White B. R., Cirrito J. R., Raichle M. E., Culver J. P., Holtzman D. M., “Bidirectional relationship between functional connectivity and amyloid- deposition in mouse brain,” J. Neurosci. 32(13), 4334–4340 (2012). 10.1523/JNEUROSCI.5845-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bauer A. Q., Kraft A. W., Wright P. W., Snyder A. Z., Lee J.-M., Culver J. P., “Optical imaging of disrupted functional connectivity following ischemic stroke in mice,” NeuroImage 99, 388–401 (2014). 10.1016/j.neuroimage.2014.05.051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wright P. W., Archambault A. S., Peek S., Bauer A. Q., Culican S. M., Ances B. M., Culver J. P., Wu G. F., “Functional connectivity alterations in a murine model of optic neuritis,” Exp. Neurol. 295, 18–22 (2017). 10.1016/j.expneurol.2017.05.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Quattromani M. J., Hakon J., Rauch U., Bauer A. Q., Wieloch T., “Changes in resting-state functional connectivity after stroke in a mouse brain lacking extracellular matrix components,” Neurobiol. Dis. 112, 91–105 (2018). 10.1016/j.nbd.2018.01.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fischl B., Salat D. H., Busa E., Albert M., Dieterich M., Haselgrove C., van der Kouwe A., Killiany R., Kennedy D., Klaveness S., Montillo A., Makris N., Rosen B., Dale A. M., “Whole brain segmentation: automated labelling of neuroanatomical structures in the human brain,” Neuron 33(3), 341–355 (2002). 10.1016/S0896-6273(02)00569-X [DOI] [PubMed] [Google Scholar]
- 15.Rex D. E., Shattuck D. W., Woods R. P., Narr K. L., Luders E., Rehm K., Stolzner S. E., Rottenberg D. A., Toga A. W., “A meta-algorithm for brain extraction in MRI,” NeuroImage 23(2), 625–637 (2004). 10.1016/j.neuroimage.2004.06.019 [DOI] [PubMed] [Google Scholar]
- 16.Shattuck D. W., Prasad G., Mirza M., Narr K. L., Toga A. W., “Online resource for validation of brain segmentation methods,” NeuroImage 45(2), 431–439 (2009). 10.1016/j.neuroimage.2008.10.066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bai J., Trinh T. L. H., Chuang K.-H., Qiu A., “Atlas-based automatic mouse brain image segmentation revisited: model complexity vs imaging registration,” Magn. Reson. Imaging 30(6), 789–798 (2012). 10.1016/j.mri.2012.02.010 [DOI] [PubMed] [Google Scholar]
- 18.Bauer A. Q., Kraft A. W., Baxter G. A., Wright P. W., Reisman M. D., Bice A. R., Park J. J., Bruchas M. R., Snyder A. Z., Lee J.-M., Culver J. P., “Effective connectivity measured using optogenetically evoked hemodynamics signals exhibits topography distinct from resting state functional connectivity in the mouse,” Cereb. Cortex 28(1), 370–386 (2018). 10.1093/cercor/bhx298 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Murphy T. H., Boyd J. D., Bolanos F., Vanni M. P., Silasi G., Haupt D., LeDue J. M., “High-throughput automated home-cage mesoscopic functional imaging of mouse cortex,” Nat. Commun. 7(1), 11611 (2016). 10.1038/ncomms11611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Silasi G., Xiao D., Vanni M. P., Chen A. C. N., Murphy T. H., “Intact skull chronic windows for mesoscopic wide-field imaging in awake mice,” J. Neurosci. Methods 267, 141–149 (2016). 10.1016/j.jneumeth.2016.04.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zang Y., Jiang T., Lu Y., He Y., Tian L., “Regional homogeneity approach to fMRI data analysis,” NeuroImage 22(1), 394–400 (2004). 10.1016/j.neuroimage.2003.12.030 [DOI] [PubMed] [Google Scholar]
- 22.Alexander R. A., “A note on averaging correlations,” Bull. Psychon. Soc. 28(4), 335–336 (1990). 10.3758/BF03334037 [DOI] [Google Scholar]
- 23.Silver N. C., Dunlap W. P., “Averaging correlation coefficients: should Fisher’s transformation be used?” J. App. Psychol. 72(1), 146–148 (1987). 10.1037/0021-9010.72.1.146 [DOI] [Google Scholar]
- 24.Power J. D., Mitra A., Laumann T. O., Snyder A. Z., Schlaggar B. L., Petersen S. E., “Methods to detect, characterize, and remove motion artifact in resting state fMRI,” NeuroImage 84, 320–341 (2014). 10.1016/j.neuroimage.2013.08.048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Siegel J. S., Power J. D., Dubis J. W., Vogel A. C., Church J. A., Schlaggar B. L., Petersen S. E., “Statistical improvements in functional magnetic resonance imaging analyses produced by censoring high-motion data points,” Hum. Brain Mapp. 35(5), 1981–1996 (2014). 10.1002/hbm.22307 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zang Y.-F., He Y., Zhu C.-Z., Cao Q.-J., Sui M.-Q., Liang M., Tian L.-X., Jiang T.-Z., Wang Y.-F., “Altered baseline brain activity in children with ADHD revealed by resting-state functional MRI,” Brain Dev. 29(2), 83–91 (2007). 10.1016/j.braindev.2006.07.002 [DOI] [PubMed] [Google Scholar]
- 27.Zou Q.-H., Zhu C.-Z., Yang Y., Zuo X.-N., Long X.-Y., Cao Q.-J., Wang Y.-F., Zang Y.-F., “An improved approach to detection of amplitude of low-frequency fluctuation (ALFF) for resting-state fMRI: Fractional ALFF,” J. Neurosci. Methods 172(1), 137–141 (2008). 10.1016/j.jneumeth.2008.04.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li Z., Zhu Y., Childress A., Detre J., Wang Z., “Relations between BOLD fMRI-derived resting brain activity and cerebral blood flow,” PLoS One 7(9), e44556 (2012). 10.1371/journal.pone.0044556 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yuan R., Di X., Kim E., Barik S., Rypma B., Biswal B., “Regional homogeneity of resting-state fMRI contributes to both neurovascular and task activation variations,” Magn. Reson. Imaging 31(9), 1492–1500 (2013). 10.1016/j.mri.2013.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Brier L., Landsness E., Snyder A., Wright P., Baxter G., Bauer A., Lee J.-M., Culver J., “Separability of calcium slow waves and functional connectivity during wake, sleep, and anesthesia,” Neurophotonics 6(03), 1 (2019). 10.1117/1.NPh.6.3.035002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chuang K.-H., Lee H., Li Z., Chang W.-T., Nasrallah F., Yeow L., Singh K., “Evaluation of nuisance removal for functional MRI of rodent brain,” NeuroImage 188, 694–709 (2019). 10.1016/j.neuroimage.2018.12.048 [DOI] [PubMed] [Google Scholar]
- 32.Satterthwaite T., Wolf D., Loughead J., Ruparel K., Elliott M., Hakonarson H., Gur R., Gur R., “Impact of in-scanner head motion on multiple measures of functional connectivity: Relevance for studies of neurodevelopment in youth,” NeuroImage 60(1), 623–632 (2012). 10.1016/j.neuroimage.2011.12.063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Power J., Schlaggar B., Petersen S., “Recent progress and outstanding issues in motion correction in resting state fMRI,” NeuroImage 105, 536–551 (2015). 10.1016/j.neuroimage.2014.10.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wu X., Eggebrecht A. T., Ferradal S. L., Culver J. P., Dehghani H., “Quantitative evaluation of atlas-based high-density diffuse optical tomography for imaging of the human visual cortex,” Biomed. Opt. Express 5(11), 3882–3900 (2014). 10.1364/BOE.5.003882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ferradal S. L., Eggebrecht A. T., Hassanpour M., Snyder A. Z., Culver J. P., “Atlas-based head modeling and spatial normalization for high-density diffuse optical tomography: in vivo validation against fMRI,” NeuroImage 85, 117–126 (2014). 10.1016/j.neuroimage.2013.03.069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Eggebrecht A. T., Ferradal S. L., Robichaux-Viehoever A., Hassanpour M. S., Dehghani H., Snyder A. Z., Hershey T., Culver J. P., “Mapping distributed brain function and networks with diffuse optical tomography,” Nat. Photonics 8(6), 448–454 (2014). 10.1038/nphoton.2014.107 [DOI] [PMC free article] [PubMed] [Google Scholar]