Development of Risk Prediction Equations for Incident Chronic Kidney Disease

Robert G Nelson; Morgan E Grams; Shoshana H Ballew; Yingying Sang; Fereidoun Azizi; Steven J Chadban; Layal Chaker; Stephan C Dunning; Caroline Fox; Yoshihisa Hirakawa; Kunitoshi Iseki; Joachim Ix; Tazeen H Jafar; Anna Köttgen; David M J Naimark; Takayoshi Ohkubo; Gordon J Prescott; Casey M Rebholz; Charumathi Sabanayagam; Toshimi Sairenchi; Ben Schöttker; Yugo Shibagaki; Marcello Tonelli; Luxia Zhang; Ron T Gansevoort; Kunihiro Matsushita; Mark Woodward; Josef Coresh; Varda Shalev

doi:10.1001/jama.2019.17379

. 2019 Nov 8;322(21):2104–2114. doi: 10.1001/jama.2019.17379

Development of Risk Prediction Equations for Incident Chronic Kidney Disease

Robert G Nelson ¹, Morgan E Grams ², Shoshana H Ballew ², Yingying Sang ^2,³, Fereidoun Azizi ⁴, Steven J Chadban ⁵, Layal Chaker ^6,^7,⁸, Stephan C Dunning ³, Caroline Fox ^9,¹⁰, Yoshihisa Hirakawa ¹¹, Kunitoshi Iseki ¹², Joachim Ix ^13,¹⁴, Tazeen H Jafar ^15,^16,¹⁷, Anna Köttgen ^2,¹⁸, David M J Naimark ¹⁹, Takayoshi Ohkubo ²⁰, Gordon J Prescott ²¹, Casey M Rebholz ², Charumathi Sabanayagam ^22,^23,²⁴, Toshimi Sairenchi ²⁵, Ben Schöttker ^26,²⁷, Yugo Shibagaki ²⁸, Marcello Tonelli ²⁹, Luxia Zhang ³⁰, Ron T Gansevoort ³¹, Kunihiro Matsushita ², Mark Woodward ^2,^32,³³, Josef Coresh ^2,^✉, Varda Shalev ³⁴, for the CKD Prognosis Consortium

¹Chronic Kidney Disease Section, National Institute of Diabetes and Digestive and Kidney Diseases, National Institutes of Health, Phoenix, Arizona

²Department of Epidemiology, Johns Hopkins Bloomberg School of Public Health, Baltimore, Maryland

³OptumLabs, Cambridge, Massachusetts

⁴Endocrine Research Center, Research Institute for Endocrine Sciences, Shahid Beheshti University of Medical Sciences, Tehran, Iran

⁵Charles Perkins Centre, University of Sydney, Sydney, Australia

⁶Academic Center for Thyroid Diseases, Erasmus Medical Center, Rotterdam, the Netherlands

⁷Department of Internal Medicine, Erasmus Medical Center, Rotterdam, the Netherlands

⁸Department of Epidemiology, Erasmus Medical Center, Rotterdam, the Netherlands

⁹Population Sciences Branch, National Heart, Lung, and Blood Institute, National Institutes of Health, Bethesda, Maryland

¹⁰The Framingham Heart Study, Framingham, Massachusetts

¹¹Department of Public Health and Health Systems, Nagoya University Graduate School of Medicine, Nagoya, Japan

¹²Nakamura Clinic & Okinawa Asia Clinical Investigation Synergy, Okinawa, Japan

¹³University of California, San Diego, La Jolla

¹⁴Veterans Affairs San Diego Healthcare System, San Diego

¹⁵Program in Health Services and Systems Research, Duke-National University of Singapore Medical School, Singapore

¹⁶Department of Medicine, Aga Khan University, Karachi, Pakistan

¹⁷Duke Global Health Institute, Durham, Duke University, North Carolina

¹⁸Institute of Genetic Epidemiology, Faculty of Medicine and Medical Center-University of Freiburg, Freiburg, Germany

¹⁹Sunnybrook Hospital, University of Toronto, Toronto, Ontario, Canada

²⁰Department of Hygiene and Public Health, Teikyo University School of Medicine, Tokyo, Japan

²¹Medical Statistics Team, School of Medicine, Medical Sciences & Nutrition, University of Aberdeen, Aberdeen, United Kingdom

²²Singapore National Eye Centre, Singapore Eye Research Institute, Singapore, Singapore

²³Yong Loo Lin School of Medicine, National University of Singapore, Singapore

²⁴Duke-National University of Singapore Medical School, Singapore, Singapore

²⁵Department of Public Health, Dokkyo Medical University, Tochigi, Japan

²⁶Division of Clinical Epidemiology and Aging Research, German Cancer Research Center, Heidelberg, Germany

²⁷Network Aging Research, University of Heidelberg, Heidelberg, Germany

²⁸Division of Nephrology and Hypertension, Department of Internal Medicine, St Marianna University School of Medicine, Kawasaki, Japan

²⁹Department of Medicine, University of Calgary, Calgary, Alberta, Canada

³⁰Peking University Institute of Nephrology, Division of Nephrology, Peking University First Hospital, Beijing, China

³¹Department of Nephrology, University Medical Center Groningen, University of Groningen, Groningen, the Netherlands

³²The George Institute for Global Health, University of Oxford, United Kingdom

³³The George Institute for Global Health, University of New South Wales, Australia

³⁴Medical Division, Maccabi Healthcare Services, and Sackler Faculty of Medicine, Tel Aviv University, Tel Aviv, Israel

Group Information: CKD Prognosis Consortium members appear at the end of the article.

^✉

Corresponding Author: Josef Coresh, MD, PhD, Chronic Kidney Disease Prognosis Consortium Data Coordinating Center, 2024 E Monument St, Baltimore, MD 21205 (ckdpc@jhmi.edu).

Accepted for Publication: October 15, 2019.

Published Online: November 8, 2019. doi:10.1001/jama.2019.17379

Author Contributions: Drs Grams and Coresh had full access to all the data in the study and take responsibility for the integrity of the data and the accuracy of the data analysis. The co–principal investigators are Drs Grams and Coresh.

Concept and design: Grams, Chadban, Naimark, Matsushita, Coresh, Shalev.

Acquisition, analysis, or interpretation of data: All authors.

Drafting of the manuscript: Nelson, Ballew, Sang, Naimark, Shibagaki.

Critical revision of the manuscript for important intellectual content: Grams, Ballew, Azizi, Chadban, Chaker, Dunning, Fox, Hirakawa, Iseki, Ix, Jafar, Köttgen, Ohkubo, Prescott, Rebholz, Sabanayagam, Sairenchi, Schöttker, Tonelli, Zhang, Gansevoort, Matsushita, Woodward, Coresh, Shalev.

Statistical analysis: Grams, Sang, Iseki, Prescott, Sairenchi, Woodward, Coresh, Shalev.

Obtained funding: Grams, Chadban, Tonelli, Gansevoort, Coresh.

Administrative, technical, or material support: Grams, Ballew, Chaker, Dunning, Hirakawa, Jafar, Köttgen, Ohkubo, Sabanayagam, Gansevoort.

Supervision: Grams, Azizi, Fox, Coresh, Shalev.

Other - Data collection: Köttgen.

Conflict of Interest Disclosures: Dr Grams reported receiving travel support from the Dialysis Clinic Inc Director Conference for speaking. Dr Ix reported receiving grants from University of California, San Diego. Dr Ohkubo reported receiving grants from Omron Healthcare and personal fees from Takeda Pharmaceutical. Dr Prescott reported receiving grants from the Chief Scientists Office for Scotland, the NHS Grampian Endowment Research Fund, and the NHS Grampian Endowment. Dr Tonelli reported receiving grants from the Canadian Institutes of Health Research. Dr Zhang reported receiving grants AstraZeneca. Dr Matsushita reported receiving grants from the NIH and Kyowa Hakko Kirin and personal fees from Kyowa Hakko Kirin and Healthy.io. Dr Woodward reported serving as a consultant to Amgen and Kirin. Dr Coresh reported receiving grants from the National Institutes of Health and serving as a scientific advisor to Healthy.io. No other disclosures were reported.

Group Information: CKD-PC investigators and collaborators are listed according study. ADVANCE: John Chalmers MD, PhD, Hisatomi Arima, MD, PhD, Vlado Perkovic, MBBS, PhD, and Mark Woodward, PhD, George Institute for Global Health, Australia, who is also affiliated with George Institute for Global Health, Oxford University, United Kingdom, and Department of Epidemiology, Johns Hopkins Bloomberg School of Public Health, The Johns Hopkins University, Baltimore, Maryland; ARIC: Josef Coresh, MD, PhD, Kunihiro Matsushita, MD, PhD, Morgan Grams, MD, PhD, and Yingying Sang, MSc, Department of Epidemiology, Johns Hopkins Bloomberg School of Public Health, Baltimore, Maryland; AusDiab: Kevan Polkinghorne, FRACP, MClinEpi, PhD, and Robert Atkins, FRACP, DSc, Monash University, Clayton, Australia; Steven Chadban, FRACP, PhD, University of Sydney, Sydney, Australia; Beijing: Luxia Zhang, MD, MPH, Peking University First Hospital and Peking University, Beijing, China; Lisheng Liu, MD, Beijing Hypertension League Institute, Beijing, China; Ming-Hui Zhao, MD, Peking University First Hospital and Peking-Tsinghua Center for Life Sciences, Beijing, China; Fang Wang, MD, Peking University First Hospital and Peking University Health Science Center, Beijing, China; Jinwei Wang, PhD, Peking University First Hospital, Beijing, China; CARE: Marcello Tonelli, MD, SM, Department of Medicine, University of Calgary, Calgary, Alberta, Canada; Frank M. Sacks, MD, Department of Nutrition, Harvard T. H. Chan School of Public Health, Boston, Massachusetts; Gary C. Curhan, MD, ScD, Channing Division of Network Medicine and Renal Division, Department of Medicine, Brigham and Women’s Hospital, Harvard Medical School, Boston, Massachusetts; CHS: Michael Shlipak, MD, MPH, Department of Epidemiology and Biostatistics, University of California, San Francisco, and San Francisco VA Medical Center; Mark J Sarnak, MD, MS, Division of Nephrology, Tufts Medical Center, Boston, Massachusetts; Ronit Katz, DPhil, Department of Medicine, and Kidney Research Institute, University of Washington, Seattle; Jade Hiramoto, MD, Division of Vascular and Endovasculary Surgery, Department of Surgery, University of California, San Francisco; CIRCS: Hiroyasu Iso, MD, PhD, MPH, Public Health, Department of Social Medicine, Osaka University Graduate School of Medicine, Suita, Japan; Isao Muraki, MD, PhD, Osaka Center for Cancer and Cardiovascular Disease Prevention, Osaka, Japan; Kazumasa Yamagishi, MD, PhD, Department of Public Health Medicine, Faculty of Medicine, University of Tsukuba, Tsukuba, Japan, and Health Services Research and Development Center, University of Tsukuba, Tsukuba, Japan; Mitsumasa Umesawa, MD, PhD, Department of Public Health, Dokkyo Medical University School of Medicine, Mibu, Japan; Ibaraki Health Plaza, Mito, Japan; ESTHER: Hermann Brenner, MD, MPH, German Cancer Consortium and German Cancer Research Center, Heidelberg, Germany; Ben Schöttker, PhD, and Kai-Uwe Saum, MPH, PhD, German Cancer Research Center, Heidelberg, Germany; Dietrich Rothenbacher, MD, MPH, German Cancer Research Center, Heidelberg, and University of Ulm, Ulm, Germany; Framingham: Caroline S. Fox, MD, MPH, National Heart, Lung, and Blood Institute, Framingham, Massachusetts, and Merck Research Laboratories, Boston, Massachusetts; Shih-Jen Hwang, PhD, National Heart, Lung, and Blood Institute, Framingham, Massachusetts; Geisinger: Alex R Chang, MD, MS, Jamie Green, MD, MS, and Gurmukteshwar Singh, MD, Department of Nephrology and Kidney Health Research Institute, Geisinger Medical Center, Danville, Pennsylvania; H. Lester Kirchner, PhD, Department of Biomedical and Translational Informatics, Geisinger Medical Center, Danville, Pennsylvania; GLOMMS 2: Corri Black, MBChB, MRCP, MSc, MFPH, and Angharad Marks, MBBCh, MRCP, MSc, PhD, Aberdeen Centre for Health Data Science, School of Medicine, Medical Sciences & Nutrition, University of Aberdeen, Aberdeen, Scotland; Gordon J Prescott, BSc, MSc, PhD, Medical Statistics Team, School of Medicine, Medical Sciences & Nutrition, University of Aberdeen, Aberdeen, United Kingdom and Lancashire Clinical Trials Unit, University of Central Lancashire, Preston, United Kingdom; and Laura Clark, MBChB, MD, FRCP, and Nick Fluck, BSc, MBBC, DPhil, FRCP, NHS Grampian, Aberdeen, United Kingdom; Gubbio: Massimo Cirillo, MD, University of Naples “Federico II”, Italy; HUNT: Stein Hallan, MD, PhD, Marius Øvrehus, PhD, Knut Asbjørn Langlo, MD, PhD, Norwegian University of Science and Technology and St Olav University, Trondheim, Norway; Solfrid Romundstad, MD, PhD, Norwegian University of Science and Technology and Levanger Hospital, Levanger, Norway; IPHS: Fujiko Irie, MD, PhD, Department of Health and Welfare, Ibaraki Prefectural Office, Mito, Japan; Toshimi Sairenchi, PhD, Department of Public Health, Dokkyo Medical University School of Medicine, Tochigi-ken, Japan; JHS: Adolfo Correa, MD, PhD, University of Mississippi Medical Center, Jackson; Casey M. Rebholz, PhD, Department of Epidemiology, Johns Hopkins Bloomberg School of Public Health, Baltimore, Maryland; Bessie A. Young, MD, MPH, Division of Nephrology, University of Washington and VA Puget Sound Health Care System, Seattle; L. Ebony Boulware, MD, Department of Medicine, Duke School of Medicine, Durham, North Carolina; Stanford Mwasongwe, MPH, Jackson State University, Jackson; JSHC: Tsuyoshi Watanabe, MD, PhD, Division of Nephrology, Hypertension, Endocrinology, and Diabetology/Metabolism, Fukushima Medical University School of Medicine, Fukushima, Japan, and Kunihiro Yamagata, MD, PhD, University of Tsukuba, Tsukuba, and Osaka Center for Cancer and Cardiovascular Disease Prevention, Osaka, Japan, and Kunitoshi Iseki, MD, Okinawa Heart and Renal Association, Japan; Dialysis Unit, University Hospital of the Ryukyus, Nishihara, Okinawa, Japan, and Koichi Asahi, MD, PhD, Division of Nephrology and Hypertension, Iwate Medical University, Morioka, Iwate, Japan; Maccabi: Gabriel Chodick, PhD, Epidemiology and Database Research, MaccabiTech Healthcare Services, Tel Aviv, Israel; Varda Shalev, MD, Institute for Health and Research and Innovation, Maccabi Healthcare Services and Tel Aviv University, Tel Aviv, Israel; MESA: Michael Shlipak, MD, MPH, Department of Epidemiology and Biostatistics, University of California, San Francisco, and San Francisco VA Medical Center; Mark Sarnak, MD, MS, Division of Nephrology, Tufts Medical Center, Boston, Massachusetts; Ronit Katz, DPhil, Department of Medicine, and Kidney Research Institute, University of Washington, Seattle; Carmen Peralta, MD, MAS, School of Medicine, University of California, San Francisco VA Medical Center, and Cricket Health, San Francisco, California; Mt Sinai BioMe: Erwin Bottinger, MD, and Girish N Nadkarni, MD, MPH, Department of Medicine, Division of Nephrology, Icahn School of Medicine at Mount Sinai, New York, New York; Stephen B Ellis, MS, and Rajiv Nadukuru, MS, Informatics and Information Technology, Icahn School of Medicine at Mount Sinai, New York, New York; NZDCS: Timothy Kenealy, MBCHB, PhD, Department of Medicine, University of Auckland, New Zealand; C Raina Elley, MBCHB, PhD, General Practice and Primary Health Care, University of Auckland, Auckland, New Zealand; John F Collins, MBCHB, FRACP, and Paul L Drury, MA, MB, BCHIR, Auckland District Health Board, Auckland, New Zealand; Ohasama: Takayoshi Ohkubo, MD, PhD, Kei Asayama, MD, PhD, and Masahiro Kikuya, MD, PhD, Department of Hygiene and Public Health Teikyo University, Tokyo, Japan; Hirohito Metoki, MD, PhD, Division of Public Health, Hygiene and Epidemiology, Tohoku Medical and Pharmaceutical University, Sendai, Japan; Masaaki Nakayama, MD, PhD, Kidney Center, St. Luke’s International Hospital, Tokyo, Japan; Okinawa83/93: Kunitoshi Iseki, MD, and Chiho Iseki, PhD, Clinical Research Support Center, Nakamura Clinic, Okinawa Heart and Renal Association, Okinawa, Japan; Pima: Robert G Nelson, MD, PhD and Helen C Looker, MBBS, Chronic Kidney Disease Section, National Institute of Diabetes and Digestive and Kidney Diseases, Phoenix, Arizona; William C Knowler, MD, DrPH, Diabetes Epidemiology and Clinical Research Section, National Institute of Diabetes and Digestive and Kidney Diseases, Phoenix, Arizona; PREVEND: Ron T Gansevoort, MD, PhD, and Stephan JL Bakker, MD, PhD, Department of Internal Medicine, University Medical Center Groningen, University Hospital Groningen, Groningen, the Netherlands; Hiddo JL Heerspink, PharmD, PhD, Department of Clinical Pharmacy and Pharmacology, University of Groningen, Groningen, the Netherlands; Rancho Bernardo: Simerjot K Jassal, MD, MAS, Division of General Internal Medicine, University of California San Diego and VA San Diego Healthcare, San Diego, California; Jaclyn Bergstrom, MS, Department of Family Medicine and Public Health, University of California San Diego, San Diego, California; Joachim H Ix, MD, MAS, Division of Nephrology-Hypertension, University of California San Diego and VA San Diego Healthcare, San Diego, California; Elizabeth Barrett-Connor MD, Division of Epidemiology, University of California San Diego, San Diego, California; RCAV: Csaba P Kovesdy, MD and Keiichi Sumida, MD, PhD, Medicine-Nephrology, Memphis Veterans Affairs Medical Center and University of Tennessee Health Science Center, Memphis, Tennessee; Kamyar Kalantar-Zadeh, MD, MPH, PhD, Division of Nephrology and Hypertension, Department of Medicine, University of California Irvine Medical Center, Orange, California; RSIII: Sanaz Sedaghat, PhD, Layal Chaker, MD, PhD, and M Arfan Ikram, MD, PhD, Department of Epidemiology, Erasmus University Medical Center, Rotterdam, The Netherlands; Ewout J Hoorn, MD, PhD, Department of Internal Medicine, Erasmus University Medical Center, Rotterdam, The Netherlands; Abbas Dehghan, MD, PhD, Department of Epidemiology and Biostatistics, Imperial College London, London, United Kingdom; SCREAM: Juan J Carrero, PharmD, PhD, Department of Medical Epidemiology and Biostatistics, Karolinksa Institutet, Stockholm, Sweden; Marie Evans, MD, PhD and Carl-Gustaf Elinder, MD, PhD, Department of Clinical Science, Intervention and Technology, Karolinska Institutet, Stockholm, Sweden; Björn Wettermark, PharmD, PhD, Department of Medicine, Karolinksa Institutet, Stockholm, Sweden; SEED: Tien Y Wong, MD, PhD, Charumathi Sabanayagam, MD, PhD and Ching-Yu Cheng, MD, PhD, Singapore Eye Research Institute, Singapore National Eye Centre and Ophthalmology & Visual Science Academic Clinical Program, Duke-NUS Medical School, Singapore; Riswana Banu Binte Mohamed Abdul Sokor, Singapore Eye Research Institute, Singapore; Taiwan MJ: Chi-Pang Wen, MD, DrPH, China Medical University Hospital, Taichung, Taiwan; Chwen-Keng Tsao, BS, MJ Health Management Institution, Taipei, Taiwan; Min-Kuang Tsai, MS, Institute of Population Health Sciences, National Health Research Institutes, Miaoli, Taiwan; Chien-Hua Chen, MD, MPH, Digestive Disease Center, Show-Chwan Memorial Hospital, Changhua, Taiwan; TLGS: Farhad Hosseinpanah, MD, Farzad Hadaegh, MD, and Fereidoun Azizi, MD, Research Institute for Endocrine Sciences, Shahid Beheshti University of Medical Sciences, Tehran, Iran; Mohammadhassan Mirbolouk, MD, Ciccarone Center for Prevention of Heart Disease, Johns Hopkins Medicine, Baltimore, Maryland; Tromso: Marit Dahl Solbu, MD, PhD and Bjørn Odvar Eriksen, MD, PhD, Metabolic and Renal Research Group, UiT the Arctic University of Norway and Section of Nephrology, University Hospital of North Norway, Tromso, Norway; Trond Geir Jenssen, MD, PhD, Metabolic and Renal Research Group, UiT the Arctic University of Norway, Tromso, Norway and Department of Nephrology, Oslo University Hospital, Oslo, Norway; Anne Elise Eggen, PhD, Department of Community Medicine, UiT the Arctic University of Norway, Tromso, Norway; ULSAM: Lars Lannfelt, MD, PhD, Department of Public Health and Caring Sciences, Uppsala University, Uppsala, Sweden; Anders Larsson, MD, PhD, Department of Medical Sciences, Uppsala University, Uppsala, Sweden; Johan Ärnlöv MD, PhD, Department of Neurobiology, Care Sciences and Society, Karolinksa Institutet, Stockholm, Sweden; ZODIAC: Henk JG Bilo, MD, PhD, Department of Internal Medicine, University of Groningen and University Medical Center Groningen, Groningen, The Netherlands; Gijs WD Landman, MD, Gelre Ziekenhuizen, Apeldoorn, The Netherlands; Kornelis JJ van Hateren, MD, Langerhans Medical Research Group, Zwolle, The Netherlands; Nanne Kleefstra, MD, PhD, Langerhans Medical Research Group, Zwolle, the Netherlands and Department of Internal Medicine, University Medical Center Groningen, Groningen, the Netherlands.

External Validation Cohort: OLDW: Stephan C. Dunning, MBA, OptumLabs, Minneapolis, Minnesota; Nikita Stempniewicz, MSc, John Cuddeback, MD, PhD, and Elizabeth Ciemins, PhD, MPH, MA, AMGA Alexandria, Alexandria, Virginia.

CKD-PC Steering Committee: Josef Coresh (chair), MD, PhD, Morgan E. Grams, MD, PhD, Shoshana H Ballew, PhD, Kunihiro Matsushita, MD, PhD, and Mark Woodward, PhD, Department of Epidemiology, Johns Hopkins Bloomberg School of Public Health, Baltimore, Maryland, who is also affiliated with George Institute for Global Health, Australia, and George Institute for Global Health, Oxford University, United Kingdom; Ron T Gansevoort, MD, PhD, Department of Internal Medicine, University Medical Center Groningen, University Hospital Groningen, Groningen, The Netherlands; Alex R. Chang, MD, MS, Department of Nephrology and Kidney Health Research Institute, Geisinger Medical Center, Danville, Pennsylvania; Stein Hallan, MD, PhD, Norwegian University of Science and Technology and St Olav University, Trondheim, Norway; Anna Köttgen, MD, MPH, Institute of Genetic Epidemiology, Faculty of Medicine and Medical Center - University of Freiburg, Freiburg, Germany; Csaba P Kovesdy, MD, Medicine-Nephrology, Memphis Veterans Affairs Medical Center and University of Tennessee Health Science Center, Memphis, Tennessee; Andrew S Levey, MD, Division of Nephrology, Tufts Medical Center, Boston, Massachusetts; Varda Shalev, MD, Institute for Health and Research and Innovation, Maccabi Healthcare Services and Tel Aviv University, Tel Aviv, Israel; Luxia Zhang, MD, MPH, Peking University First Hospital and Peking University, Beijing, China.

CKD-PC Data Coordinating Center: Shoshana H Ballew, PhD (assistant project director), Jingsha Chen, MSc (programmer), Josef Coresh, MD, PhD (principal investigator), Morgan E Grams MD, PhD (director of nephrology initiatives), Lucia Kwak, MSc (programmer), Kunihiro Matsushita, MD, PhD (director), Yingying Sang, MSc (lead programmer), Aditya Surapeneni, PhD (programmer), and Mark Woodward, PhD (senior statistician), Department of Epidemiology, Johns Hopkins Bloomberg School of Public Health, Baltimore, Maryland, who is also affiliated with George Institute for Global Health, Australia, and George Institute for Global Health, Oxford University, United Kingdom.

Funding/Support: Dr Köttgen was supported by grant KO 3598/5-1 from the German Research Foundation. The CKD Prognosis Consortium (CKD-PC) Data Coordinating Center is funded in part by a program grant from the US National Kidney Foundation (NKF funding sources include Boehringer Ingelheim) and by grant R01DK100446 from the National Institute of Diabetes and Digestive and Kidney Diseases. A variety of sources have supported enrollment and data collection including laboratory measurements, and follow-up in the collaborating cohorts of the CKD-PC (eAppendix 3 in the Supplement). These funding sources include government agencies such as national institutes of health and medical research councils as well as foundations and industry sponsors. (Study acronyms and abbreviations are listed in eAppendix 2 in the Supplement; most cohorts received a small [<$2000] amount of funds to offset the costs of data preparation, no compensation was provided to any individuals listed for manuscript review.)

Role of the Funder/Sponsor: The funders of the study had no role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; and decision to submit the manuscript for publication. In addition, the funders had no right to veto publication or to control the decision regarding to which journal the paper would be submitted.

Data Sharing Statement: CKD-PC has agreed with collaborating cohorts not to share data outside the consortium. Each participating cohort has its own policy for data sharing.

^✉

Corresponding author.

PMCID: PMC6865298 PMID: 31703124

Key Points

Question

Can development of chronic kidney disease be predicted using readily available demographic, clinical, and laboratory variables?

Findings

In this analysis of 5 222 711 individuals in 34 multinational cohorts from 28 countries, 5-year risk prediction equations for CKD were developed and demonstrated high discrimination (median C statistic for the equation for individuals without diabetes, 0.85; median C statistic for the equation for individuals with diabetes, 0.80) and variable calibration (69% of the study populations had a slope of observed to predicted risk between 0.80 and 1.25). Discrimination and calibration were similar in 9 external cohorts consisting of 2 253 540 individuals.

Meaning

Abstract

Importance

Early identification of individuals at elevated risk of developing chronic kidney disease (CKD) could improve clinical care through enhanced surveillance and better management of underlying health conditions.

Objective

To develop assessment tools to identify individuals at increased risk of CKD, defined by reduced estimated glomerular filtration rate (eGFR).

Design, Setting, and Participants

Individual-level data analysis of 34 multinational cohorts from the CKD Prognosis Consortium including 5 222 711 individuals from 28 countries. Data were collected from April 1970 through January 2017. A 2-stage analysis was performed, with each study first analyzed individually and summarized overall using a weighted average. Because clinical variables were often differentially available by diabetes status, models were developed separately for participants with diabetes and without diabetes. Discrimination and calibration were also tested in 9 external cohorts (n = 2 253 540).

Exposures

Demographic and clinical factors.

Main Outcomes and Measures

Incident eGFR of less than 60 mL/min/1.73 m².

Results

Among 4 441 084 participants without diabetes (mean age, 54 years, 38% women), 660 856 incident cases (14.9%) of reduced eGFR occurred during a mean follow-up of 4.2 years. Of 781 627 participants with diabetes (mean age, 62 years, 13% women), 313 646 incident cases (40%) occurred during a mean follow-up of 3.9 years. Equations for the 5-year risk of reduced eGFR included age, sex, race/ethnicity, eGFR, history of cardiovascular disease, ever smoker, hypertension, body mass index, and albuminuria concentration. For participants with diabetes, the models also included diabetes medications, hemoglobin A_1c, and the interaction between the 2. The risk equations had a median C statistic for the 5-year predicted probability of 0.845 (interquartile range [IQR], 0.789-0.890) in the cohorts without diabetes and 0.801 (IQR, 0.750-0.819) in the cohorts with diabetes. Calibration analysis showed that 9 of 13 study populations (69%) had a slope of observed to predicted risk between 0.80 and 1.25. Discrimination was similar in 18 study populations in 9 external validation cohorts; calibration showed that 16 of 18 (89%) had a slope of observed to predicted risk between 0.80 and 1.25.

Conclusions and Relevance

Equations for predicting risk of incident chronic kidney disease developed from more than 5 million individuals from 34 multinational cohorts demonstrated high discrimination and variable calibration in diverse populations. Further study is needed to determine whether use of these equations to identify individuals at risk of developing chronic kidney disease will improve clinical care and patient outcomes.

This study pools data from 34 cohorts participating in the CKD Prognosis Consortium developed a risk equation to predict risk of incident chronic kidney disease (CKD) defined as an estimated glomerular filtration rate of less than 60 mL/min/1.73 m².

Introduction

Chronic kidney disease (CKD) is a global public health problem that is associated with major adverse health events, including kidney failure, cardiovascular disease, and death. The Global Burden of Disease study estimates that nearly 697 million persons worldwide had reduced estimated glomerular filtration rate (eGFR) or increased albuminuria in 2016, an increase of 70% since 1990.¹ Globally, years of life lost due to CKD increased by 53% in the same period.¹ Chronic kidney disease is the 16th most common cause of years of life lost.² Factors associated with the increased prevalence of CKD include the aging of the population and the increasing prevalence of diabetes, hypertension, and obesity. The ability to identify individuals at risk of CKD may prevent adverse health outcomes associated with CKD. Moreover, even among those who are diagnosed with CKD, proper management may be hindered by lack of awareness of CKD and its management among clinicians and uncertainties about the underlying risk of CKD progression.

A kidney failure risk equation may help improve care for patients with established CKD,^3,4 but relatively little work has been performed to develop predictive tools to identify those at increased risk of developing CKD—defined by reduced eGFR, despite the high lifetime risk of CKD—which is estimated to be 59.1% in the United States.³ A simple risk assessment tool that helps clinicians quickly identify patients at increased risk of reduced eGFR and provides an estimate of the magnitude of risk could lead to better and more targeted surveillance strategies and potentially to better management of the factors associated with reduced eGFR. In the present study, data from multinational cohorts were used to develop and evaluate risk prediction equations for CKD defined by reduced eGFR.

Methods

This study was approved for use of deidentified data by the institutional review board at the Johns Hopkins Bloomberg School of Public Health, Baltimore, Maryland. The need for informed consent was waived by the institutional review board.

Participating Cohorts

The Chronic Kidney Disease Prognosis Consortium (CKD-PC) includes study cohorts worldwide that were identified from the general population and from patients at high risk of cardiovascular disease (eAppendix 1 in the Supplement).^4,5,6,7,8,9 (Study acronyms and abbreviations as well as funding acknowledgments are listed in eAppendixes 2 and 3 in the Supplement.) Inclusion criteria required that cohorts included at least 1000 participants, data on serum creatinine and albuminuria values, and 50 or more events of the outcome of interest. Included cohorts consisted of prospective studies, clinical trials, and administrative health care data sets. Separate risk models were developed for those with and without diabetes mellitus. The analyses among participants without diabetes included 31 cohorts, and the analyses among participants with diabetes included 15 cohorts. Within cohorts, eligible participants were 18 years or older with an eGFR of more than 60 mL/min/1.73 m² at baseline. Eligible participants had no previous end-stage kidney disease and had at least 1 serum creatinine value recorded during follow-up. Because the prevalence and incidence of CKD differ by race/ethnicity, data on race/ethnicity were analyzed from the participating cohorts. Methods used to determine race varied from cohort to cohort, but most cohorts used self-report to define race/ethnicity. Data were collected from April 1970 through January 2017.

Procedures

The CKD-EPI creatinine equation was used to calculate eGFR.¹⁰ In cohorts from which the creatinine measurement was not standardized to isotope dilution mass spectrometry, values were multiplied by 0.95 before the eGFR calculation.¹¹ We defined diabetes as fasting glucose of 126 mg/dL 7.0 mmol/L or more (≥7.0 mmol/L), nonfasting glucose of 200 mg/dL or more (≥11.1 mmol/L) hemoglobin A_1c of 6.5% or more, use of glucose-lowering drugs, or self-reported diabetes. Hypertension was defined as blood pressure of more than 140/90 mm Hg or the use of antihypertensive medications. Smoking was classified as ever smoking vs never smoking. Participants with a history of myocardial infarction, coronary revascularization, heart failure, or stroke were considered to have a history of cardiovascular disease. Measures of albuminuria were restricted to the urine albumin:creatinine ratio. Among participants with diabetes, hemoglobin A_1cvalue, or taking oral diabetes medications or insulin at baseline were also recorded.

Outcomes

The outcome of interest was incident eGFR of less than 60 mL/min/1.73 m². Additional outcomes were eGFR of less than 45 mL/min/1.73 m²and less than 30 mL/min/1.73 m², and decline in eGFR of 40%. Participants who developed end-stage kidney disease, mostly identified by procedure codes or by linkage to national registries before reaching a qualifying outpatient level of eGFR were also considered to have developed the outcome of interest. In secondary analyses, we evaluated the risk of confirmed outcomes. Outcomes were defined as confirmed if there were at least 3 measures of eGFR (1 baseline, 2 during follow-up) and the first eGFR that was lower than the threshold was confirmed by a second qualifying eGFR between 90 days and 2 years later, or if the linear slope of eGFR decline crossed the threshold during follow-up (eAppendix 1 in the Supplement). In both cases, the event date was considered the date of the first qualifying eGFR measurement.

Prediction Model Development

The prediction model was built from weighted-average hazard ratios estimated in all participating cohorts and an adjusted baseline risk estimated in cohorts with frequent outcome assessment. To estimate the hazard ratios, each study was first analyzed individually, then combined, weighting the study by the square root of the number of events in each cohort and capped at 5-times the median study weight. This method was used to ensure that the largest studies did not dominate the analysis due to small within-study variance compared with total variance. We performed a complete case analysis, excluding variables that were missing more than 50% of the time in the cohort-specific analyses. Because variables were often differentially available by diabetes status (eg, albuminuria, hemoglobin A_1c; missing data are shown in eTable 1A and B in the Supplement), models were developed separately for participants with diabetes and without diabetes. The primary model included demographic variables (age, sex, race/ethnicity), eGFR (linear splines with a knot at 90 mL/min/1.73 m²), history of cardiovascular disease, ever smoker, hypertension, body mass index (BMI), and albuminuria. The primary model for participants with diabetes also included diabetes medications (insulin vs only oral medications vs none), hemoglobin A_1cvalues, and the interaction between the 2.

The albuminuria variable was handled differently for those with vs without diabetes. For the model among participants with diabetes, missing albuminuria was treated as a dummy variable with reference at a urine albumin:creatinine ratio of 10 mg/g. For the model among participants without diabetes, for which albuminuria values were available only in a minority of individuals, a patch approach was used.¹² Models were fit in all the cohorts using all variables except albuminuria, and data were combined as described above. The weighted-average coefficients were then held constant in cohort-specific models among participants with measures of albuminuria to obtain a conditional coefficient for albuminuria, which was then combined for analyses using the weighting described above. This conditional, weighted-average coefficient for albuminuria was applied to the observed level of albuminuria minus the expected level of albuminuria (eTable 2 in the Supplement) and combined with the weighted-average coefficients for the other variables in the final model.

To obtain the adjusted baseline risk for use with the primary model, we held the weighted-average coefficients constant and fit a multivariable competing risk model in the studies with follow-up for mortality and mean time between creatinine measures of less than 1 year. The adjusted subhazard was smoothed using a Weibull distribution, and the mean was estimated using weights determined by the method described above. The prediction model then combined the mean adjusted baseline risk with the weighted-average coefficients.

Evaluation of Model Performance

To evaluate model discrimination, the Harrell C statistic was estimated within each cohort and summarized as the median and interquartile range (IQR) across studies. Model calibration was plotted using observed vs predicted risk per decile of predicted risk at 5 years in each cohort with frequent measures of creatinine (median time between 2 measurements was approximately ≤1 year and mean follow-up time was ≥2 years) and quantified using a regression of the deciles of mean observed risk on the mean predicted risk in a 0-intercept linear regression model. Calibration was assessed by visual inspection of the plots (dots showing deciles are close to the identity line) and by the slope of observed to predicted risk being near to 1.¹³ To summarize calibration, we determined the number of study populations with an observed risk within 1.25-fold that of the predicted risk (ie, with a slope between 0.80 and 1.25 [1/0.8]). These metrics of discrimination and calibration were also calculated within 9 external validation cohorts selected from OptumLabs Data Warehouse (OLDW). eAppendix 1 in the Supplement describes the methods for selecting centers for the 9 external validation cohorts. The OLDW contains deidentified longitudinal health information on enrollees and patients, including administrative claims and electronic health record data. The OLDW includes people aged 18 to 88 years, from diverse ethnicities and geographical regions across the United States (eTable 3 in the Supplement). The electronic health record–derived data include a subset that have been normalized and standardized across health systems into a single database, including information on demographics, laboratory values, encounter and discharge codes.¹⁴

To compare the newly developed models with existing equations, predicted risks using the newly developed models were compared with risks calculated using 2 published equations identified in a recent review¹⁵ (herein referred to as the Chien equation¹⁶ and the O’Seaghdha equation,¹⁷ respectively, eAppendix 4 in the Supplement). The Chien equation was developed from 5168 Chinese individuals who underwent baseline health examinations at the National Taiwan University Hospital¹⁶ and annual follow-up examinations that included measurements of serum creatinine concentration for assessing the outcome of reduced eGFR. During a median follow-up of 2.2 years, 190 individuals developed CKD. We used the Chien clinical equation, which included age, BMI, diastolic blood pressure, and history of type 2 diabetes and stroke. The O’Seaghdha prediction model was developed in the predominantly white population of Framingham, Massachusetts, using baseline serum creatinine and a subsequent measure 10 years later. Among the 2490 individuals aged 45 through 64 years included in this study, 229 developed eGFR of less than 60 mL/min/1.73 m² at 10 years. The O’Seaghdha model included age, hypertension, diabetes, eGFR category, and albuminuria values.¹⁷

The performance of the newly developed model, the Chien equation, and the O’Seaghdha equation were compared among the CKD-PC cohorts that provided individual-level participant data and that had the required variables for all equations. Differences in C statistics were estimated within all cohorts and then summarized using random-effects meta-analysis. Brier scores, the mean squared difference between the predicted risk vs observed binary outcomes, were used to evaluate which risk equation showed the best calibration within each cohort (eAppendix 4 in the Supplement).¹⁸ Brier scores were assessed only within the subset of cohorts with frequent assessments of creatinine. Comparisons of the discrimination and calibration were also performed within the 9 external validation cohorts from OLDW.

All analyses were performed using Stata version 15 (StataCorp). Statistical significance was determined using a 2-sided test with a threshold P value of <.05.

Results

Overall, 5 222 711 participants were included (eTable 4 in the Supplement), 781 627 of whom (15.0%) had diabetes. Baseline characteristics of participants in the 34 individual cohorts are shown in Table 1 according to the presence or absence of diabetes. The population without diabetes were a mean age of 54 years (SD, 16 years) and 38% were women. The population with diabetes were a mean age of 62 years (SD, 11 years) and 13% were women, owing primarily to the Veterans Administration cohort, which was 97% male.

Table 1. Baseline Characteristics of the Participants in the 31 Cohorts Without Diabetes and 15 Cohorts With Diabetes^a.

Cohort	Country	No. of Patients	Age, Mean (SD), y	Women, No. (%)	eGFR, Mean (SD), mL/min/1.73 m²	No. (%) of Patients			BMI, Mean (SD)
Cohort	Country	No. of Patients	Age, Mean (SD), y	Women, No. (%)	eGFR, Mean (SD), mL/min/1.73 m²	History of CVD	Hypertension	Smoking	BMI, Mean (SD)
Cohorts Without Diabetes
ARIC	United States	12 757	54 (6)	7082 (56)	103 (14)	980 (8)	4437 (35)	7367 (58)	27 (5)
AusDiab	Australia	6281	50 (12)	3471 (55)	88 (14)	306 (5)	1580 (25)	2528 (41)	27 (5)
Beijing	China	948	59 (9)	496 (52)	85 (12)	127 (13)	363 (38)	321 (34)	25 (3)
CARE	Canada	2923	57 (9)	343 (12)	80 (13)	2923 (100)	2432 (83)	2332 (80)	28 (7)
CHS	United States	2170	73 (4)	1341 (62)	77 (11)	409 (19)	1280 (59)	1122 (53)	27 (5)
CIRCS	Japan	10 022	54 (9)	6275 (63)	90 (14)	97 (1)	3353 (33)	3507 (35)	23 (3)
ESTHER	Germany	3394	61 (6)	1885 (56)	92 (15)	458 (13)	2213 (65)	1548 (47)	27 (4)
Framingham	United States	2353	58 (9)	1290 (55)	91 (16)	180 (8)	828 (35)	368 (16)	28 (5)
Geisinger	United States	229 448	50 (16)	132 677 (58)	95 (18)	23 403 (10)	113 953 (50)	110 640 (49)	30 (7)
GLOMMS 2	United Kingdom	24 321	61 (14)	13 598 (56)	81 (15)	1962 (8)	910 (4)	NA	NA
Gubbio	Italy	1249	54 (6)	714 (57)	85 (11)	44 (4)	443 (35)	688 (55)	28 (4)
HUNT	Norway	34 430	46 (13)	19 114 (56)	102 (15)	1170 (3)	12 377 (36)	17 992 (53)	26 (4)
IPHS	Japan	70 557	60 (10)	47 934 (68)	86 (12)	3603 (5)	33 626 (48)	19 565 (28)	23 (3)
JHS	United States	2164	48 (11)	1312 (61)	102 (17)	94 (4)	885 (41)	596 (28)	31 (7)
JSHC	China	461 797	63 (8)	279 934 (61)	94 (11)	34 567 (9)	193 996 (42)	62 947 (14)	23 (3)
Maccabi	Israel	939 309	43 (15)	546 440 (58)	104 (17)	55 138 (6)	213 398 (23)	231 695 (25)	27 (5)
MESA	United States	4954	61 (10)	2623 (53)	86 (13)	1 (0)	2051 (41)	2600 (53)	28 (5)
Mt Sinai BioMe	United States	14 590	48 (14)	8998 (62)	93 (19)	722 (5)	6385 (44)	3910 (28)	29 (7)
Ohasama	Japan	2346	60 (10)	1483 (63)	98 (11)	91 (4)	832 (35)	349 (19)	24 (3)
Okinawa8393	Japan	1624	50 (10)	957 (59)	100 (13)	0	NA	NA	24 (3)
Pima	United States	2733	28 (11)	1626 (59)	125 (13)	NA	272 (10)	793 (47)	33 (8)
PREVEND	Netherlands	5977	49 (12)	3057 (51)	97 (14)	247 (4)	1773 (30)	4160 (70)	26 (4)
Rancho Bernardo	United States	639	64 (10)	369 (58)	75 (11)	49 (8)	232 (36)	354 (56)	26 (4)
RCAV	United States	1 765 629	59 (13)	133 822 (8)	85 (15)	256 353 (15)	1 196 576 (68)	NA	29 (6)
RSIII	Netherlands	2292	56 (6)	1333 (58)	87 (12)	126 (5)	1375 (60)	1572 (69)	27 (4)
SCREAM	Sweden	716 952	52 (17)	392 827 (55)	95 (17)	40 554 (6)	177 249 (25)	NA	NA
SEED	Singapore	2358	54 (9)	1246 (53)	88 (14)	156 (7)	1164 (50)	700 (30)	26 (4)
Taiwan MJ	Taiwan	101 216	41 (12)	52 658 (52)	91 (15)	2474 (2)	16 560 (16)	26 037 (28)	23 (3)
TLGS	Iran	8502	37 (13)	4753 (56)	81 (13)	171 (2)	1404 (17)	1839 (22)	26 (5)
Tromso	Norway	6007	58 (10)	3522 (59)	95 (12)	283 (5)	3183 (53)	3877 (65)	26 (4)
ULSAM	Sweden	1142	50 (1)	0	98 (10)	5 (0)	416 (36)	NA	25 (3)
		4 441 084	54 (16)	1 673 180 (38)	93 (17)	426 693 (10)	1 996 070 (45)	509 588 (26)	27 (6)
Cohorts With Diabetes
ADVANCE	Multiple^b	9339	66 (6)	3774 (40)	83 (13)	2235 (24)	8003 (86)	4024 (43)	28 (5)
AusDiab	Australia	427	59 (11)	189 (44)	84 (13)	70 (16)	287 (67)	205 (48)	30 (6)
Beijing	China	343	62 (9)	168 (49)	85 (12)	80 (23)	184 (54)	127 (37)	25 (4)
Geisinger	United States	34 463	58 (15)	16 842 (49)	93 (18)	8606 (25)	27 251 (79)	17 563 (52)	34 (8)
HUNT	Norway	1564	54 (12)	709 (45)	95 (14)	130 (8)	932 (60)	892 (57)	28 (5)
JHS	United States	390	54 (10)	241 (62)	101 (18)	46 (12)	310 (79)	131 (34)	35 (8)
Maccabi	Israel	72 480	60 (13)	32 972 (45)	92 (15)	18 147 (25)	54 586 (75)	21 733 (30)	31 (6)
MESA	United States	659	63 (9)	304 (46)	90 (15)	0	455 (69)	343 (52)	31 (6)
Mt Sinai BioMe	United States	2652	54 (13)	1598 (60)	91 (19)	511 (19)	2013 (76)	923 (37)	32 (8)
NZDCS	New Zealand	14 819	58 (13)	7152 (48)	86 (16)	2260 (15)	10 197 (82)	6469 (44)	32 (7)
Pima	United States	933	43 (14)	577 (62)	114 (17)	NA	335 (36)	291 (40)	34 (8)
RCAV	United States	607 132	63 (10)	20 241 (3)	83 (15)	157 611 (26)	551 356 (91)	NA	32 (6)
SCREAM	Sweden	34 307	60 (16)	14 224 (41)	91 (17)	8041 (23)	20 408 (59)	NA	NA
SEED	Singapore	1029	58 (9)	508 (49)	88 (15)	151 (15)	742 (72)	311 (30)	28 (5)
ZODIAC	the Netherlands	1090	63 (11)	522 (48)	77 (12)	310 (28)	794 (73)	249 (23)	29 (5)
		781 627	62 (11)	100 021 (13)	85 (15)	198 198 (25)	677 853 (87)	53 261 (38)	32 (6)

Open in a new tab

Abbreviations: BMI, body mass index, calculated as weight in kilograms divided by height in meters squared; CVD, cardiovascular disease; eGFR, estimated glomerular filtration rate; NA, not available.

^{^a}

Racial distributions of the cohorts are available in eTable 4 in the Supplement and the citations for each study are available in eAppendix in the Supplement.

^{^b}

Participants are from Australia, Canada, China, Czech Republic, Estonia, France, Germany, Hungary, India, Ireland, Italy, Lithuania, Malaysia, Netherlands, New Zealand, Philippines, Poland, Russia, Slovakia, and United Kingdom.

Among the 4 441 084 participants without diabetes, 660 856 incident cases (14.9%) with an eGFR of less than 60 mL/min/1.73 m² occurred during a mean follow-up of 4.2 years, and 374 513 (56.7%) of them were confirmed by subsequent eGFR measurements. Among the 781 627 participants with diabetes, 313 646 incident cases (40.1%) occurred during a mean follow-up of 3.9 years, and 212 246 (67.7%) of them were confirmed by subsequent eGFR measurements. The number of participants and the total and confirmed number of events of incident reduced eGFR in cohorts with and without diabetes are shown in eTable 5 in the Supplement.

Risk Factors for Reduced eGFR

Weighted-average subhazard ratios of major risk factors for incident eGFR of less than 60 mL/min/1.73 m² are shown in Table 2 and for other eGFR thresholds in eTable 6 in the Supplement, according to the presence or absence of diabetes. Older age, female sex, black race, hypertension, history of cardiovascular disease, lower eGFR values, and higher urine albumin:creatinine ratio were each significantly associated with incident eGFR of less than 60 mL/min/1.73 m² in both cohorts with and without diabetes. Smoking was significantly associated with an incident eGFR of less than 60 mL/min/1.73 m² only in the cohorts without diabetes, and elevated HbA_1c and presence and type of diabetes medicines were significantly associated with an incident eGFR of less than 60 mL/min/1.73 m² in the cohorts with diabetes.

Table 2. Weighted-Average Subhazard Ratios of Major Risk Factors for Incident eGFR Less Than 60 mL/min/1.73 m² in Cohorts With and Without Diabetes .

Risk Factors	Subhazard Ratios (95% CI) for Incident eGFR <60 mL/min/1.73 m²
Risk Factors	No Diabetes	With Diabetes
Age, per 5 y	1.29 (1.27-1.32)	1.14 (1.13-1.15)
Women	1.20 (1.18-1.22)	1.15 (1.11-1.18)
Black race	1.20 (1.13-1.27)	1.10 (1.02-1.18)
eGFR 60-90, per –5 mL	1.58 (1.57-1.59)	1.43 (1.41-1.44)
eGFR ≥90, per –5 mL	1.37 (1.34-1.41)	1.16 (1.14-1.19)
History of CVD	1.22 (1.18-1.26)	1.21 (1.17-1.24)
Ever smoker	1.13 (1.10-1.16)	1.00 (0.96-1.04)
Hypertension^a	1.43 (1.40-1.46)	1.44 (1.39-1.50)
BMI, per 5 points	1.07 (1.05-1.08)	1.05 (1.04-1.07)
ACR, per 10-fold increase	1.42 (1.37-1.48)^b	1.45 (1.42-1.49)
HbA_1c (for oral diabetes medications), per 1%		1.06 (1.05-1.07)
Insulin vs oral diabetes medication (at 7% HbA_1c)		1.11 (1.05-1.19)
None vs oral diabetes medication (at 7% HbA_1c)		0.86 (0.83-0.89)
Interaction: HbA_1c × insulin vs oral diabetes medication, per 1%		1.02 (1.00-1.05)
Interaction: HbA_1c × no medications vs oral diabetes medication, per 1%		1.04 (1.02-1.06)
ACR missing indicator (set ACR = 10)		0.96 (0.93-1.00)

Open in a new tab

Abbreviations: ACR, urine albumin:creatinine ratio; BMI, body mass index, calculated as weight in kilograms divided by height in meters squared; CVD, cardiovascular disease; eGFR, estimated glomerular filtration rate; HbA_1c, hemoglobin A_1c.

^{^a}

Defined as blood pressure of 140/90 mm Hg or the use of antihypertensive medications.

^{^b}

ACR was modeled using a patch in the nondiabetes model in which the coefficient for ACR was estimated in the population with available ACR with the other coefficients fixed. The model allows for prediction when ACR is missing. eTables 9 and 10 in the Supplement provide absolute risk and risk difference scenarios.

Discrimination

Measures of discrimination for the 5-year predicted probability of incident eGFR of less than 60 mL/min/1.73 m², based on the predictive models, are shown separately for the cohorts with and without diabetes in eTable 7A in the Supplement. The median C statistic for the 5-year predicted probability of all eGFR events of less than 60 mL/min/1.73 m² was 0.845 (IQR, 0.789-0.890) in the cohorts without diabetes and 0.801 (IQR, 0.750-0.819) in the cohorts with diabetes, reflecting good discrimination. For confirmed eGFR events of less than 60 mL/min/1.73 m², the median C statistic was 0.869 (IQR, 0.823-0.897) in the cohorts without diabetes and 0.808 (IQR, 0.794-0.836) in the cohorts with diabetes. Measures of discrimination for the lower incident eGFR thresholds are shown in eTable 7B in the Supplement.

Predicted Absolute Risk

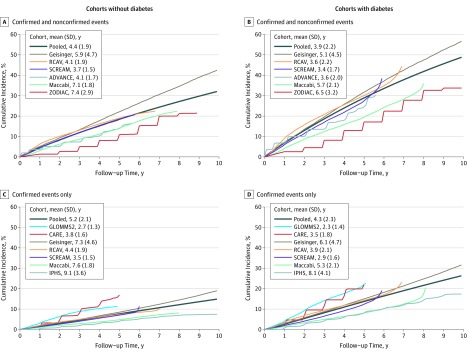
Adjusted baseline subhazards for an eGFR of less than 60 mL/min/1.73 m² were computed over time in both cohorts with frequent measures of creatinine using baseline covariates from the cohorts and weighted-average coefficients from the models (Figure 1). The figure illustrates the variability in the adjusted absolute risk across the cohorts that was unexplained by the covariates included in the models. Similar findings are shown for the lower incident eGFR thresholds for cohorts without diabetes in eFigure 1 and for cohorts with diabetes in eFigure 2 in the Supplement.

Figure 1. — Each line represents the adjusted baseline risk in an individual cohort. The risk was determined by holding the weighted-average coefficients constant and fitting a multivariable competing risk model in each study. The adjusted subhazard was smoothed using a Weibull distribution. The pooled line represents the weighted mean used in the prediction equation.

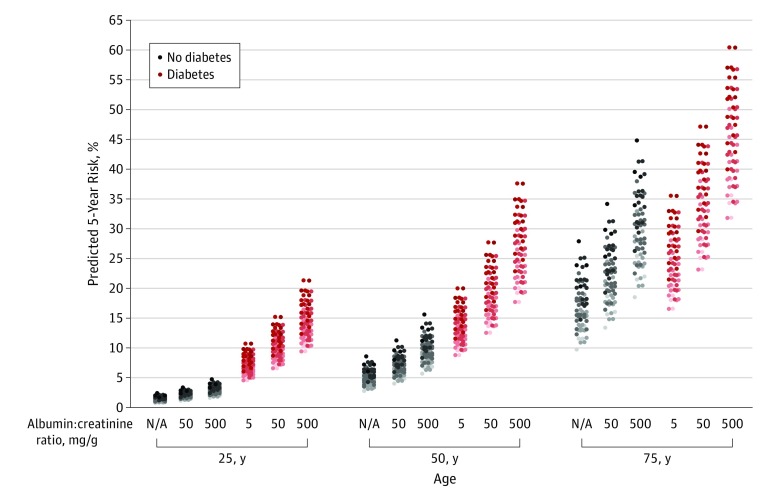
Equations for the 5-year predicted risk of incident eGFR of less than 60 mL/min/1.73 m², based on the predictive models and the mean baseline subhazards, are shown separately for individuals with or without diabetes in eTable 8 in the Supplement and are available online at http://ckdpcrisk.org/ckdrisk. The predicted 5-year absolute risk of an incident eGFR of less than 60 mL/min/1.73 m² among individuals with and without diabetes at 3 ages and for various combinations of risk factors are shown in Figure 2 and in greater detail for all 3 incident eGFR thresholds in eTables 9 and 10 in the Supplement. A wide range of risk was seen, and the level of risk was strongly associated with the demographic features and comorbid conditions. The absolute risk was generally higher among persons with diabetes than among those without diabetes and those of older age regardless of the presence or absence of diabetes. Elevated albuminuria was also significantly associated with the absolute risk regardless of the presence or absence of diabetes. The 5-year absolute risk of confirmed eGFR reduction followed the same pattern as it did for the unconfirmed end point, with lower absolute risk for the confirmed end points (eTables 9 and 10). Equations for the 5-year predicted risk of other outcomes are shown in eTables 11 and 12 in the Supplement.

Figure 2. — Predicted 5-year absolute risk of incident estimated glomerular filtration rate (eGFR) of less than 60 mL/min/1.73 m² is shown for various scenarios for 3 ages and albuminuria categories among those with or without diabetes. All 5-year risks were computed for hypothetical individuals with a baseline eGFR of 90 mL/min/1.73 m². For the 5-year predicted risk in a hypothetical individual with diabetes, the hemoglobin A_1c was also set to 7.7% and the individual was assumed to be receiving an oral diabetes medicine. Scenarios: sex, male or female; ethnicity, nonblack or black; history of cardiovascular disease, yes or no; smoker, yes or no; hypertension, yes or no; and body mass index (BMI), calculated as weight in kilograms divided by height in meters squared, 25 or 35.

Each column contains 64 dots representing 64 (all combinations of 6 binary variables) hypothetical scenarios. The dots are shaded from light to dark based on the number of risk factors present, scaled from 0 to 4 based on the presence or absence of cardiovascular disease, smoking, hypertension, and BMI of 35 or higher.

Calibration

Model calibration was assessed visually by plotting observed vs predicted risk per decile of predicted risk at 5 years in the cohorts with frequent measures of creatinine. Plots for the eGFR of less than 60 mL/min/1.73 m² end point are shown in eFigure 3 in the Supplement and for the lower eGFR end points in eFigures 4 and 5 in the Supplement. The plots reflected the performance of the equations for the primary end point in the cohorts, with 9 of the 13 study populations (69%) showing a slope of observed to predicted risk between 0.80 and 1.25 (eTable 13 in the Supplement). Calibration was generally better for the eGFR of less than 60 mL/min/1.73 m² end point than for the lower eGFR end points, where calibration was poor in some cohorts (eTables 14-15 in the Supplement). For example, for an eGFR of less 45 mL/min/1.73 m², just 5 of 13 study populations (38%) showed a slope between 0.80 and 1.25. For and eGFR of less than 30 mL/min/1.73 m², just 4 out of 11 study populations (36%) showed a slope between 0.80 and 1.25. Calibration, by design, was best in the development cohorts with the highest number of events.

External Validation

Model discrimination was tested in 18 study populations in 9 external validation cohorts (n = 2 253 540, eTable 16 in the Supplement). There were 288 462 events over 4.1 years of follow-up in the population without diabetes and 78 697 events over 3.5 years of follow-up in the population with diabetes. Discrimination was similar to that observed in the development cohorts. The median C statistic for the 5-year predicted probability of all eGFR events of less than 60 mL/min/1.73 m² was 0.84 (IQR, 0.83-0.87) in the population without diabetes and 0.81 (IQR, 0.80-0.82) in the population with diabetes (eTable 17 in the Supplement). Calibration analysis showed that 16 out of 18 study populations (89%) had a slope between 0.80 and 1.25 (eFigure 6, eTable 18 in the Supplement). Discrimination and calibration for the lower eGFR end points are shown in eFigures 7 and 8 and eTables 17 and 18 in the Supplement. For example, for an eGFR of less than 45 mL/min/1.73 m², 15 out of 18 study populations (83%) showed a slope between 0.80 and 1.25. For an eGFR of less than 30 mL/min/1.73 m², 11 out of 18 study populations (61%) showed a slope between 0.80 and 1.25. Differences in calibration could not be explained by differences in mean baseline characteristics in the underlying study populations.

Comparison to Existing Equations

The newly developed model for an eGFR of less than 60 mL/min/1.73 m² in the absence of diabetes had better discrimination than the Chien equation (random-effects analyses difference in C statistic, 0.094, 95% CI, 0.071-0.117) and the O’Seaghdha equation (random-effects analyses difference in C statistics, 0.020, 95% CI, 0.015-0.025) when compared with the CKD-PC cohorts. Similarly, the Brier score was lower using the newly developed equation in the cohorts with frequent measures of creatinine, indicating superior calibration for the newly developed equation (eTable 19 in the Supplement). In the presence of diabetes, the newly developed model had better discrimination than the Chien equation (random-effects analyses difference in C statistic, 0.107, 95% CI, 0.087-0.128) and the O’Seaghdha equation (random-effects analyses difference in C statistics, 0.037, 95% CI, 0.030-0.044) and lower Brier scores in 2 out of 3 cohorts with frequent measures of creatinine. When evaluated in the 9 external validation cohorts, model discrimination and calibration were also better using the newly developed equations compared with the Chien and O’Seaghdha equations (eTable 20 in the Supplement).

Discussion

Risk prediction models were developed that facilitated prediction of the 5-year probability of reduced eGFR in diverse populations of men and women with variable ages and ethnicity. Models were developed separately for people with vs without diabetes. Readily available demographic, clinical, and laboratory variables were used in these risk models so that risk calculators from these models could conceivably be added to electronic health records to identify patients at increased risk of developing reduced eGFR. Further study is needed to determine whether these risk equations can improve care. For example, future study could assess whether focusing resources on patients at highest risk of developing CKD improves blood pressure control and/or weight loss. Future study might also determine whether prescribing medications to improve albuminuria or control diabetes might prevent occurrence of reduced eGFR among those at risk.

Several prediction models of CKD exist for use for the general population.^16,17,19,20 Equations previously developed to identify people at risk of incident eGFR of less than 60 mL/min/1.73 m² included the Chien equation and the O’Seaghdha equation, both of which have been externally validated.^15,16,17 External validation of the Chien clinical model was previously conducted for 3205 Chinese adults from the Chin-Shan Community Cardiovascular Cohort. Moderate discrimination was observed for the clinical prediction model in the development cohort (C statistic = 0.77), but the discriminatory power of the model was greatly reduced in the external validation cohort (C statistic = 0.67).¹⁶ The O’Seaghdha risk score was validated in 1777 individuals from the ARIC study (C statistic = 0.79 in Framingham and 0.74 in ARIC).¹⁷ These prior studies did not develop separate equations for those with vs those without diabetes. The present study, which developed scores separately for people with vs without diabetes, demonstrated higher C statistics and better calibration than both the clinical Chien and the O’Seaghdha equations. This was true for the CKD-PC cohorts used in development of the equations as well as for the 9 external validation cohorts.

Risk prediction models that estimate the absolute risk of specific adverse health outcomes have become increasingly popular clinical decision-making tools in recent years, and novel approaches to analyzing existing data are emerging that may enhance prediction.²¹ Several models have been developed for estimating the risk of prevalent and incident CKD and end-stage kidney disease,^{4,16,17,19,20,22,23,24} but even those with good discriminative performance have not always performed well for cohorts of people outside the original derivation cohort.¹⁵ In data reported herein, the incidence of low eGFR varied across settings, even after adjustment for variable distribution of risk factors. Differences in the incidence of eGFR in distinct populations may explain differences in calibration in prior studies.

Calibration is an essential aspect of risk prediction, particularly when absolute risk thresholds are used to determine clinical care. A tool that overestimates risk may result in unnecessary treatment, whereas one that underestimates risk may delay optimal management. By design, calibration in the development cohorts in this study was linked to the overall weighted risk of reduced eGFR. Other strengths of this study include the large sample sizes of the nondiabetic and diabetic cohorts, and the clinical, geographic, and ethnic diversity of the individuals in those cohorts. However, calibration of the developed risk equations may be poorer for the derivation populations with lower adjusted incidence rates of reduced eGFR or for which ascertainment of reduced eGFR is more or less sensitive.

Limitations

This study has several limitations. First, the absence of albuminuria data in most cohorts of patients who did not have diabetes required that a statistical patch derived from cohorts without diabetes, but with albuminuria data, be applied to the remaining cohorts in order to estimate how including albuminuria altered the models. This approach allows valid estimation of risk even in the absence of albuminuria, although clinical assessment of albuminuria improved risk estimation and detection of early stage CKD defined by elevated albuminuria (A stages) in the absence of reduced kidney function (G stages 1-2).²⁵ Second, the risk equations developed in this study incorporated routinely collected demographic, clinical, and laboratory data, and their predictive accuracy might be enhanced by incorporating other variables, including genotype data or newly identified biomarkers of early CKD.²⁶ Third, the risk prediction equations developed in this study were intended to identify persons at increased risk of an intermediate health outcome. The risks of progression from CKD to kidney failure, cardiovascular disease, or death were not assessed by these equations. Fourth, no minimum change in eGFR was required in the primary predictive model to become a case of CKD, so someone with a baseline eGFR of 61 mL/min/1.73 m² and a follow-up eGFR of 59 mL/min/1.73 m² would be considered to have the outcome of interest. Fifth, calibration varied across setting, with particularly poor performance in some of the research cohorts. The models for eGFR of less than 45 and less than 30 mL/min/1.73 m² were poorly calibrated in many of the development cohorts, which may be due in part to the low number of events and relatively short follow-up time.

Conclusions

Equations for predicting risk of incident chronic kidney disease were developed from more than 5 million individuals from 34 multinational cohorts and demonstrated high discrimination and variable calibration in diverse populations. Further study is needed to determine whether use of these equations to identify individuals at risk of developing chronic kidney disease will improve clinical care and patient outcomes.

Supplement.

eAppendix 1. Data analysis overview and analytic notes for some of individual studies

eAppendix 2. Acronyms or abbreviations for studies included in the current report and their key references linked to the Web references

eAppendix 3. Acknowledgements and funding for collaborating cohorts

eAppendix 4. Two existing published equations and the comparison methods

eTable 1A. Missing data, by cohort, for the non-diabetes model

eTable 1B. Missing data, by cohort, for the diabetes model

eTable 2. Risk equation to estimate the expected urine albumin-to-creatinine ratio in the nondiabetic cohorts

eTable 3. Baseline characteristics for 9 health care centers from OptumLabs Data Warehouse used in external validation

eTable 4. Race/ethnicity of the participants in all 34 cohorts included in CKD-PC

eTable 5. Number of participants and the total and confirmed events of incident reduced eGFR by three eGFR thresholds in the nondiabetic and diabetic cohorts included in CKD-PC

eTable 6. Weighted average sub-hazard ratios of major risk factors for incident eGFR <45 ml/min/1.73m2 and <30 ml/min/1.73m2 in the nondiabetic and diabetic cohorts for use in the prediction equations

eTable 7A. C-statistics for the prediction equations for total and confirmed incident eGFR <60 ml/min/1.73m2 in the nondiabetic and diabetic cohorts

eTable 7B. C-statistics for the prediction equations for total and confirmed incident eGFR <45 ml/min/1.73m2 and <30 ml/min/1.73m2 in the nondiabetic and diabetic cohorts

eTable 8. Prediction equations to apply to individual patients for the 5-year absolute risk of incident eGFR <60 ml/min/1.73m2 for all events (includes confirmed and unconfirmed)

eTable 9. Predicted 5-year absolute risk for total and confirmed incident reduced eGFR for three eGFR thresholds in nondiabetic individuals according to different combinations of risk factors

eTable 10. Predicted 5-year absolute risk for total and confirmed incident reduced eGFR for three eGFR thresholds in diabetic individuals according to different combinations of risk factors

eTable 11. Prediction equations to apply to individual patients for the 5-year absolute risk of incident eGFR <45 ml/min/1.73m2, incident eGFR <30 ml/min/1.73m2, eGFR decline ≥40% for all events (includes confirmed and unconfirmed)

eTable 12. Prediction equations to apply to individual patients for the 5-year absolute risk for confirmed events

eTable 13. Calibration for eGFR <60 ml/min/1.73m2 in CKD-PC cohorts: mean observed and predicted risk of deciles, and slope of zero-intercept regression of mean observed on mean predicted risk of deciles

eTable 14. Calibration for eGFR <45 ml/min/1.73m2 in CKD-PC cohorts: mean observed and predicted risk of deciles, and slope of zero-intercept regression of mean observed on mean predicted risk of deciles

eTable 15. Calibration for eGFR <30 ml/min/1.73m2 in CKD-PC cohorts: mean observed and predicted risk of deciles, and slope of zero-intercept regression of mean observed on mean predicted risk of deciles

eTable 16. Number of participants and the total and confirmed events of incident reduced eGFR by three eGFR thresholds in the nondiabetic and diabetic cohorts included in nine OptumLabs Data Warehouse external validation cohorts

eTable 17. Discrimination of developed prediction equations in nine OptumLabs Data Warehouse external validation cohorts

eTable 18. Calibration of developed prediction equations in nine OptumLabs Data Warehouse external validation cohorts

eTable 19. Discrimination and Calibration of CKD-PC developed prediction equation vs. Chien and O’Seaghdha in CKD-PC Cohorts

eTable 20. Discrimination and Calibration of CKD-PC developed prediction equation vs. Chien and O’Seaghdha equations in nine OptumLabs Data Warehouse external validation cohorts, stratified by presence of diabetes

eFigure 1. Variation in baseline competing risk of incident eGFR <45 ml/min/1.73m2 and <30 ml/min/1.73m2 in nondiabetic cohorts with frequent measures of serum creatinine concentration

eFigure 2. Variation in baseline competing risk of incident eGFR <45 ml/min/1.73m2 and <30 ml/min/1.73m2 in diabetic cohorts with frequent measures of serum creatinine concentration

eFigure 3. Visual plots of calibration for the 5-year prediction of incident eGFR <60 ml/min/1.73m2 are shown in nondiabetic and diabetic cohorts with frequent measures of serum creatinine concentration

eFigure 4. Visual plots of calibration for the 5-year prediction of incident eGFR <45 ml/min/1.73m2 are shown in nondiabetic and diabetic cohorts with frequent measures of serum creatinine concentration

eFigure 5. Visual plots of calibration for the 5-year prediction of incident eGFR <30 ml/min/1.73m2 are shown in nondiabetic and diabetic cohorts with frequent measures of serum creatinine concentration

eFigure 6. Visual plots of calibration for the 5-year prediction of incident eGFR <60 ml/min/1.73m2 are shown in the population without and with diabetes in the 9 centers from the OptumLabs Data Warehouse

eFigure 7. Visual plots of calibration for the 5-year prediction of incident eGFR <45 ml/min/1.73m2 are shown in the population without and with diabetes in the 9 centers within the OptumLabs Data Warehouse

eFigure 8. Visual plots of calibration for the 5-year prediction of incident eGFR <30 ml/min/1.73m2 are shown in nondiabetic and diabetic cohorts within the OptumLabs Data Warehouse

References

Click here for additional data file.^{(2.3MB, pdf)}

References

1.GBD 2017 Disease and Injury Incidence and Prevalence Collaborators Global, regional, and national incidence, prevalence, and years lived with disability for 354 diseases and injuries for 195 countries and territories, 1990-2017: a systematic analysis for the Global Burden of Disease Study 2017. Lancet. 2018;392(10159):1789-1858. doi: 10.1016/S0140-6736(18)32279-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
2.GBD 2017 Causes of Death Collaborators Global, regional, and national age-sex-specific mortality for 282 causes of death in 195 countries and territories, 1980-2017: a systematic analysis for the Global Burden of Disease Study 2017. Lancet. 2018;392(10159):1736-1788. doi: 10.1016/S0140-6736(18)32203-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Grams ME, Chow EK, Segev DL, Coresh J. Lifetime incidence of CKD stages 3-5 in the United States. Am J Kidney Dis. 2013;62(2):245-252. doi: 10.1053/j.ajkd.2013.03.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Tangri N, Grams ME, Levey AS, et al. ; CKD Prognosis Consortium . Multinational assessment of accuracy of equations for predicting risk of kidney failure: a meta-analysis. JAMA. 2016;315(2):164-174. doi: 10.1001/jama.2015.18202 [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Grams ME, Sang Y, Ballew SH, et al. ; CKD Prognosis Consortium . A meta-analysis of the association of estimated GFR, albuminuria, age, race, and sex with acute kidney injury. Am J Kidney Dis. 2015;66(4):591-601. doi: 10.1053/j.ajkd.2015.02.337 [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Grams ME, Sang Y, Levey AS, et al. ; Chronic Kidney Disease Prognosis Consortium . Kidney-failure risk projection for the living kidney-donor candidate. N Engl J Med. 2016;374(5):411-421. doi: 10.1056/NEJMoa1510491 [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Coresh J, Turin TC, Matsushita K, et al. . Decline in estimated glomerular filtration rate and subsequent risk of end-stage renal disease and mortality. JAMA. 2014;311(24):2518-2531. doi: 10.1001/jama.2014.6634 [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Kovesdy CP, Coresh J, Ballew SH, et al. ; CKD Prognosis Consortium . Past decline versus current eGFR and subsequent ESRD risk. J Am Soc Nephrol. 2016;27(8):2447-2455. doi: 10.1681/ASN.2015060687 [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Matsushita K, Ballew SH, Astor BC, et al. ; Chronic Kidney Disease Prognosis Consortium . Cohort profile: the chronic kidney disease prognosis consortium. Int J Epidemiol. 2013;42(6):1660-1668. doi: 10.1093/ije/dys173 [DOI] [PubMed] [Google Scholar]
10.Levey AS, Stevens LA, Schmid CH, et al. ; CKD-EPI (Chronic Kidney Disease Epidemiology Collaboration) . A new equation to estimate glomerular filtration rate. Ann Intern Med. 2009;150(9):604-612. doi: 10.7326/0003-4819-150-9-200905050-00006 [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Levey AS, Coresh J, Greene T, et al. ; Chronic Kidney Disease Epidemiology Collaboration . Expressing the Modification of Diet in Renal Disease Study equation for estimating glomerular filtration rate with standardized serum creatinine values. Clin Chem. 2007;53(4):766-772. doi: 10.1373/clinchem.2006.077180 [DOI] [PubMed] [Google Scholar]
12.Matsushita K, Sang Y, Chen J, et al. . Novel “predictor patch” method for adding predictors using estimates from outside datasets—a proof-of-concept study adding kidney measures to cardiovascular mortality prediction. Circ J. 2019;83(9):1876-1882. doi: 10.1253/circj.CJ-19-0320 [DOI] [PubMed] [Google Scholar]
13.Alba AC, Agoritsas T, Walsh M, et al. . Discrimination and calibration of clinical prediction models: Users’ Guides to the Medical Literature. JAMA. 2017;318(14):1377-1384. doi: 10.1001/jama.2017.12126 [DOI] [PubMed] [Google Scholar]
14.OptumLabs [website]. OptumLabs and OptumLabs Data Warehouse (OLDW) descriptions and citation. https://www.manta.com/c/mb4ykhk/optum-labs-inc. May 2019. Accessed October 23, 2019.
15.Fraccaro P, van der Veer S, Brown B, et al. . An external validation of models to predict the onset of chronic kidney disease using population-based electronic health records from Salford, UK. BMC Med. 2016;14:104. doi: 10.1186/s12916-016-0650-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Chien KL, Lin HJ, Lee BC, Hsu HC, Lee YT, Chen MF. A prediction model for the risk of incident chronic kidney disease. Am J Med. 2010;123(9):836.e2-846.e2. [DOI] [PubMed] [Google Scholar]
17.O’Seaghdha CM, Lyass A, Massaro JM, et al. . A risk score for chronic kidney disease in the general population. Am J Med. 2012;125(3):270-277. doi: 10.1016/j.amjmed.2011.09.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Brier G. Verification of forecasts expressed in terms of probability. Mon Weather Rev. 1950;78(1):1-3. doi: [DOI] [Google Scholar]
19.Bang H, Vupputuri S, Shoham DA, et al. . Screening for Occult Renal Disease (SCORED): a simple prediction model for chronic kidney disease. Arch Intern Med. 2007;167(4):374-381. doi: 10.1001/archinte.167.4.374 [DOI] [PubMed] [Google Scholar]
20.Kshirsagar AV, Bang H, Bomback AS, et al. . A simple algorithm to predict incident kidney disease. Arch Intern Med. 2008;168(22):2466-2473. doi: 10.1001/archinte.168.22.2466 [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Ravizza S, Huschto T, Adamov A, et al. . Predicting the early risk of chronic kidney disease in patients with diabetes using real-world data. Nat Med. 2019;25(1):57-59. doi: 10.1038/s41591-018-0239-8 [DOI] [PubMed] [Google Scholar]
22.Tangri N, Stevens LA, Griffith J, et al. . A predictive model for progression of chronic kidney disease to kidney failure. JAMA. 2011;305(15):1553-1559. doi: 10.1001/jama.2011.451 [DOI] [PubMed] [Google Scholar]
23.Echouffo-Tcheugui JB, Kengne AP. Risk models to predict chronic kidney disease and its progression: a systematic review. PLoS Med. 2012;9(11):e1001344. doi: 10.1371/journal.pmed.1001344 [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Collins GS, Omar O, Shanyinde M, Yu LM. A systematic review finds prediction models for chronic kidney disease were poorly reported and often developed using inappropriate methods. J Clin Epidemiol. 2013;66(3):268-277. doi: 10.1016/j.jclinepi.2012.06.020 [DOI] [PubMed] [Google Scholar]
25.Kidney Disease: Improving Global Outcomes (KDIGO) CKD Work Group KDIGO 2012 Clinical Practice Guideline for the Evaluation and Management of Chronic Kidney Disease. https://kdigo.org/wp-content/uploads/2017/02/KDIGO_2012_CKD_GL.pdf. Published January 2013. Accessed October 29, 2019.
26.Fox CS, Gona P, Larson MG, et al. . A multi-marker approach to predict incident CKD and microalbuminuria. J Am Soc Nephrol. 2010;21(12):2143-2149. doi: 10.1681/ASN.2010010085 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials