Abstract
In this article, the authors aim to maximally utilize multimodality neuroimaging and genetic data for identifying Alzheimer's disease (AD) and its prodromal status, Mild Cognitive Impairment (MCI), from normal aging subjects. Multimodality neuroimaging data such as MRI and PET provide valuable insights into brain abnormalities, while genetic data such as single nucleotide polymorphism (SNP) provide information about a patient's AD risk factors. When these data are used together, the accuracy of AD diagnosis may be improved. However, these data are heterogeneous (e.g., with different data distributions), and have different number of samples (e.g., with far less number of PET samples than the number of MRI or SNPs). Thus, learning an effective model using these data is challenging. To this end, we present a novel three‐stage deep feature learning and fusion framework, where deep neural network is trained stage‐wise. Each stage of the network learns feature representations for different combinations of modalities, via effective training using the maximum number of available samples. Specifically, in the first stage, we learn latent representations (i.e., high‐level features) for each modality independently, so that the heterogeneity among modalities can be partially addressed, and high‐level features from different modalities can be combined in the next stage. In the second stage, we learn joint latent features for each pair of modality combination by using the high‐level features learned from the first stage. In the third stage, we learn the diagnostic labels by fusing the learned joint latent features from the second stage. To further increase the number of samples during training, we also use data at multiple scanning time points for each training subject in the dataset. We evaluate the proposed framework using Alzheimer's disease neuroimaging initiative (ADNI) dataset for AD diagnosis, and the experimental results show that the proposed framework outperforms other state‐of‐the‐art methods.
Keywords: Alzheimer's disease (AD), deep learning, mild cognitive impairment (MCI), multimodality data fusion
1. INTRODUCTION
Alzheimer's disease (AD) is the most common form of dementia for people over 65 years old (Chen et al., 2017; Mullins, Mustapic, Goetzl, & Kapogiannis, 2017; Rombouts et al., 2005; Zhou, Thung, Zhu, & Shen, 2017; Zhou et al., 2018). According to a recent research report from Alzheimer's association (Association, 2016), the total estimated prevalence of AD is expected to be 60 million worldwide over the next 50 years. AD is a neurodegenerative disease that is associated with the production of amyloid peptide (Suk et al., 2015), and its symptoms typically start with mild memory loss and gradual losses of other brain functions. As there is no cure for AD, the early detection of AD and especially its prodromal stage, that is, mild cognitive impairment (MCI), is vital, so that treatment can be administered to possibly slow down the disease progression (Thung, Wee, Yap, & Shen, 2016; Wee et al., 2012). On the other hand, it is also highly desirable to further classify MCI subjects into two subgroups, that is, progressive MCI (pMCI) that will progress to AD, and stable MCI (sMCI) that will remain stable. Thus, more resources can be applied directly to pMCI subjects for their treatment (Thung, Yap et al., 2018).
In search of biomarkers that can accurately identify AD and its earlier statuses, data from different modalities have been collected and examined. One of the most commonly collected data is Magnetic Resonance (MR) images, which can provide us anatomical brain information for AD study (Chen, Zhang et al., 2016; Cuingnet, Gerardin et al., 2011; Fox et al., 1996; Koikkalainen et al., 2016; Raamana et al., 2014; Raamana, Weiner et al., 2015; Sørensen, Igel et al., 2017; Thung, Wee et al., 2014; Yu Zhang, 2018; Zhanga et al., 2018). For example, Koikkalainen et al. (Koikkalainen et al., 2016) extracted volumetric and morphometric features from T1 MR images and also vascular features from FLAIR images to build a multi‐class classifier based on the disease state index methodology. Raamana et al. (2014) proposed a novel three‐class classifier to discriminate among AD, frontotemporal dementia (FTD), and normal control (NC) using volumes, shape invariants, and local displacements of hippocampi and lateral ventricles obtained from brain MR images. Raamana, Weiner et al. (2015) proposed a novel thick‐net features that can be extracted from a single time‐point MRI scan and demonstrated their potential for individual patient diagnosis. Another neuroimaging techniques, that is, Positron Emission topography (Rasmussen, Hansen, Madsen, Churchill, & Strother, 2012), which provides us functional brain information, has also been widely used to investigate the neurophysiological characteristics of AD (Chetelat et al., 2003; Escudero, Ifeachor et al., 2013; Liu et al., 2015; Mosconi et al., 2008; Nordberg, Rinne, Kadir, & Långström, 2010). Recent studies have shown that fusing the complementary information from multiple modalities can enhance the diagnostic performance of AD (Kohannim, Hua et al., 2010; Perrin, Fagan, & Holtzman, 2009; Yuan, Wang et al., 2012). For instance, Kohannim, Hua et al. (2010) concatenated attributes (or better known as features in machine learning community) derived from different modalities into a long vector and then trained a support vector machine (SVM) as classifier. The researchers in (Yuan, Wang et al., 2012; Zhang, Shen et al., 2012) used sparse learning to select features from multiple modalities to jointly predict the disease labels and clinical scores. Another work in (Suk et al., 2015) used a multi‐kernel SVM strategy to fuse multimodality data for disease label prediction. In addition, discriminative multivariate analysis techniques have been applied to the analysis of functional neuroimaging data (Dai et al., 2012; Haufe et al., 2014; Rasmussen et al., 2012). For instance, Dai et al. (Dai et al., 2012) proposed a multi‐modality, multi‐level, and multi‐classifier (M3) framework that used regional functional connectivity strength (RFCS) to discriminate AD patients from healthy controls.
Recently, imaging‐genetic analysis (Lin, Cao, Calhoun, & Wang, 2014) has been utilized to identify the genetic basis (e.g., Single Nucleotide Polymorphisms [SNPs]) of phenotypic neuroimaging markers (e.g., features in MRI) and study the associations between them. In particular, various Genome‐Wide Association Studies (GWAS) (Chu et al., 2017; Price et al., 2006; Saykin, Shen et al., 2010; Wang, Nie et al., 2012) have been done investigation on the relationship between the human genomic variants and the disease biomarkers. For example, GWAS has identified the associations between some SNPs and AD related brain regions (Biffi, Anderson et al., 2010; Shen et al., 2014; Shen, Kim et al., 2010), where the SNPs found could be used to predict the risk of incident AD at earlier stage of life even before pathological changes begin. If success, such early diagnosis may help clinicians to identify prospectus subject to monitor for AD progression and find potential treatments to possibly prevent the AD. In our study, we aim to use the complementary information from both the neuroimaging and genetic data for the diagnosis of AD and its related early statuses. Based on this study, it shows that the complementary information from multimodality data can improve the diagnosis performance.
There are three main challenges in fusing information from multimodality neuroimaging data (i.e., MRI and PET) and genetic data (i.e., SNP) for AD diagnosis. The first challenge is data heterogeneity, as the neuroimaging and genetic data have different data distributions, different numbers of features, and different levels of discriminative ability to AD diagnosis (e.g., SNP data in their raw form are less effective in AD diagnosis). Due to the heterogeneity issue, simple concatenation of the features from multimodality data will result in an inaccurate prediction model (Di Paola et al., 2010; Liu et al., 2015; Ngiam et al., 2011; Zhu, Suk, Lee, & Shen, 2016).
The second challenge is the high dimensionality issue. One neuroimage scan (i.e., MR or PET image) normally contains millions of voxels, while the genetic data of a subject has thousands of AD‐related SNPs. In this study, we address the high dimensionality issue of the neuroimaging data by first preprocessing them to obtain the region‐of‐interest (ROI) based features using a predefined template. However, we do not have similar strategy to reduce the dimensionality of genetic data. Thus, we still have a high‐dimension‐low‐sample‐size problem, as we have thousands of features (dominated by SNPs) as compared to just hundreds of training samples.
The third challenge is the incomplete multimodality data issue, that is, not all samples in the training set have the complete three modalities. This issue will worsen the small‐sample‐size issue mentioned above, if we only use samples with complete multimodality data for training. In addition, using few samples during training may also degrade the performance of the classifier algorithm that relies on a large number of training samples to learn an effective model, such as deep learning (Schmidhuber, 2015; Zhou et al., 2017).
To address the above challenges, we propose a novel three‐stage deep feature learning and fusion framework for AD diagnosis in this article. Specifically, inspired by the stage‐wise learning in (Barshan & Fieguth, 2015), we build a deep neural network and train it stage‐wise, where, at each stage, we learn the latent data representations (high‐level features) for different combinations of modalities by using the maximum number of available samples. Specifically, in the first stage, we learn high‐level features for each modality independently via progressive mapping of multiple hidden layers. After the first stage of deep learning, the data from different modality in the latent representation space (i.e., the output of the last hidden layer) are theoretically more discriminative to the target labels, and thus more comparable to each other. In other words, the heterogeneity issue of multimodality data is partially alleviated. In the second stage, we learn a joint feature representation for each modality combination by using the high‐level latent features learned from the first stage. In the third stage, we learn the diagnostic labels by fusing the learned joint features from the second stage. It is worth emphasizing that we use the maximum number of all available samples to train each stage of the network more effectively. For example, in the first stage, to learn the high‐level latent features from MRI data, we use all the available MRI data; in the second stage, to learn the joint high‐level features from MRI and PET data, we use all the samples with complete MRI and PET data; in the third stage, we use all the samples with complete MRI, PET and SNP data. In this way, the small‐sample‐size and incomplete multimodality data issues can be partially addressed. Moreover, to learn a more effective deep classification model, we further significantly increase the number of training samples by using multiple time‐point data for each training subject, if available.
The main contributions of our work are summarized as follows: (a) To our best knowledge, this is the first deep learning framework that fuses multimodality neuroimaging and genetic data for AD diagnosis. (b) We propose a novel three‐stage deep learning framework to partially address the data heterogeneity, as well as small‐sample‐size and incomplete multimodality data issues. (c) We propose to significantly increase the number of training samples by using multiple time‐point data scanned for each training subject in ADNI study, which is completely different from most of the existing methods that often consider only the data scanned at one time‐point.
The rest of this article is organized as follows. We briefly describe the background and related works in Section 2, introduce the proposed framework in Section 3, describe the materials and the data preprocessing method used in this study in Section 4, present the experimental results in Section 5, and conclude our study in Section 6.
2. BACKGROUND
2.1. Feature extraction of neuroimaging data
There are basically three approaches for extracting features from neuroimaging data for analysis (Jack, Bernstein et al., 2008): (a) voxel‐based approach, which directly extracts features by using voxel intensity values from neuroimaging data, (b) patch‐based approach, which extracts features from local image patches, and (c) region of interest (ROI) based approach, which extracts features from the predefined brain regions. Among these three approaches, the voxel‐based approach is perhaps the most straightforward method, as it uses the raw low‐level image intensity values as features. Because of that, it has the drawbacks of having high feature dimensionality and high computation load, as well as ignoring the regional information of the neuroimages as it treats each voxel in the neuroimaging data independently. In contrast, patch‐based approach can capture brain regional information by extracting features from image patch. As diseased‐related information and brain structures are more easily found in image patches, this approach generally can obtain much better classification performance than the voxel‐based approach. A higher level of information can be extracted by using brain anatomical prior, as in the ROI‐based approach. The dimensionality of ROI‐based features depends on the number of ROIs defined in the template, which is comparatively smaller than the aforementioned approaches, and thus this is a good feature reduction method that can reflect the entire brain information (Barshan & Fieguth, 2015; Cuingnet, Gerardin et al., 2011; Suk et al., 2015; Wan et al., 2012; Zhou et al., 2017). Accordingly, we also use the ROI‐based approach in this study to reduce the feature dimensionality of neuroimaging data.
2.2. Deep learning in AD study
Deep learning has been widely used in learning high‐level features and conducting classification, and achieves promising results (Barshan & Fieguth, 2015; Farabet, Couprie, Najman, & LeCun, 2013). Deep learning can effectively capture hidden or latent patterns in the data. Recently, deep learning algorithms have been successfully applied to medical image processing and analysis (Litjens et al., 2017). For instance, Zheng et al. (2016) proposed a multimodal neuroimaging feature learning algorithm with the stacked deep polynomial networks for AD study. Fakoor et al. (2013) presented a novel method to enhance cancer diagnosis from gene expression data by using unsupervised deep leaning methods (e.g., stacked auto‐encoder [SAE]). Suk et al. (2015) adopted SAE to discover the latent feature representation from the ROI‐based features, and then used a multi‐kernel learning (MKL) framework to combine latent features from multimodality data for AD diagnosis. Liu et al. (2015) also adopted an SAE‐based multimodal neuroimaging feature learning algorithm for AD diagnosis. Suk, Lee et al. (2014) adopted Restricted Boltzmann Machine (RBM) to learn multi‐modal features from 3D patches for AD/MCI diagnosis. Plis et al. (2014) adopted RBM and Deep Belief networks (DBN) to learn high‐level features from MRI and fMRI for schizophrenia diagnosis. The common limitation of these deep learning methods is that they assume the data are complete, and thus only the data with complete multimodality can be used in the training and testing. This limitation may also reduce the effectiveness of training the deep learning model, as few number of samples can be used in the training. In the next section, we show how we address this limitation by proposing a stage‐wise deep learning model.
3. PROPOSED FRAMEWORK
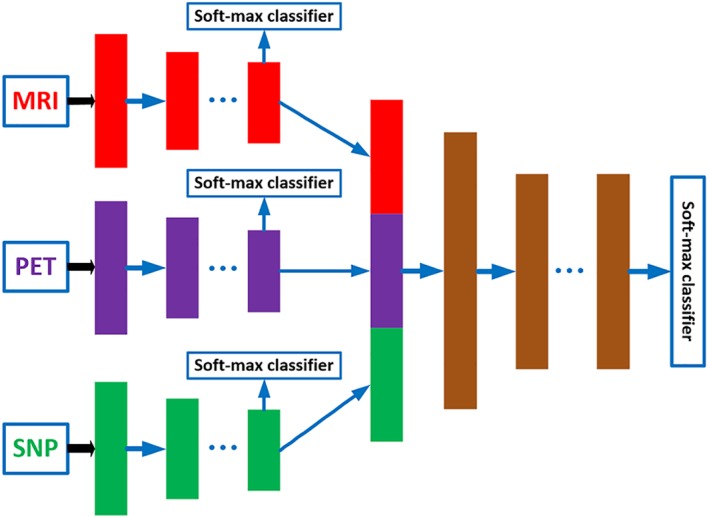
Figure 1 shows the overview of our proposed three‐stage deep feature learning and fusion framework for AD classification by using multimodality neuroimaging data (i.e., MRI and PET) and genetic data (i.e., SNP). Our framework aims to maximally utilize all the available data from the three modalities to train an effective deep learning model. There are three stages in our proposed deep learning framework, where each stage is composed of a set of different deep neural networks (DNNs), with each DNN used to learn feature representations for different combinations of modalities by using the maximum number of available samples. In particular, the first stage learns the latent representations for each individual modality, the second stage learns the joint latent representations for each pair of modalities, and finally the third stage learns the classification model using the joint latent representations from all the modality pairs. The details of each stage of the framework are described in the following.
Figure 1.
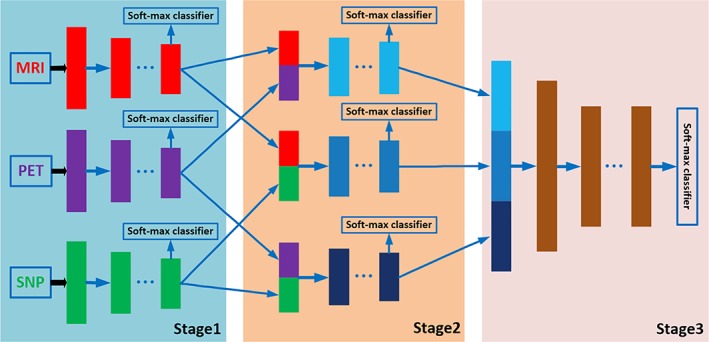
The proposed overall framework of three‐stage deep neural network for AD diagnosis using MRI, PET, and SNP data. We first learn latent representations (i.e., high‐level features) for each modality independently in stage 1. Then, in stage 2, we learn joint latent feature representations for each pair of modality combination (e.g., MRI and PET, MRI and SNP, PET and SNP) by using the high‐level features learned from stage 1. Finally, in stage 3, we learn the diagnostic labels by fusing the learned joint latent feature representations from the stage 2 [Color figure can be viewed at http://wileyonlinelibrary.com]
3.1. Stage 1 ‐ individual modality feature learning
The ROI‐based features for MRI and PET data are continuous and low‐dimensional (i.e., 93), while SNP data are discrete (i.e., 0, 1, or 2) and high dimensional (i.e., 3,123). Direct concatenation of these data will result in an inaccurate detection model, as SNP data, which are only indirectly related to the target labels, will dominate the feature learning process. In addition, there is also incomplete multimodality data issue, that is, not all samples have all the modalities and also the PET data has a far less number of samples than the numbers of MRI and SNP data. This implies that, if we train a single DNN model for all three modalities, only samples with complete multimodality data can be used, thus limiting the effectiveness of the model.
Therefore, in Stage 1 of our proposed framework, we employ a separate DNN for each individual modality, as depicted in Figure 1. Each DNN contains several fully‐connected hidden layers and one output layer (i.e., Softmax classifier). The output layer consists of three neurons for the case of three‐class classification (i.e., AD/MCI/NC classification task), or four neurons for the case of four‐class classification (i.e., AD/sMCI/pMCI/AD classification task). During the training, we use the label information from the training samples at the output layer to guide the learning of the network weights. After training, the outputs of the last hidden layer of each DNN are regarded as the latent representations (i.e., high‐level features) for the corresponding modality.
There are several advantages of this individual modality feature learning strategy. First, it allows us to use the maximum number of available training samples for each modality. For example, assume that we have N subjects, where only N1 subjects contain MRI data, N2 subjects contain PET data, and N3 subjects contain SNP data. The conventional multimodality model uses only the subjects with all three modality data, which is much less than min(N1, N2, N3). On the other hand, by using our proposed framework, we can use all the N1, N2 and N3 samples to train three separate deep learning models for three modalities, respectively. It is expected that, by using more samples in training, our model can learn better latent representations for each model. Furthermore, this setting also partially addresses the incomplete multimodality data issue, as the framework is applicable for the training set with incomplete multimodality data. Second, it allows us to use both different number of hidden layers and different number of hidden neurons (for each layer) to learn the latent representations of each modality and modality combination. We argue that, as our multimodality data are heterogeneous with different feature size and discriminability for AD diagnosis, the number of hidden layers and the number of neurons in the neural network should be modality‐dependent. For instance, for the modality with more number of features (i.e., SNPs in our case), we use more hidden layers and then gradually reduce the number of neurons for each layer to reduce the dimensionality of the modality; while for the modalities with less number of features or more direct relationship to the targets (i.e., ROI‐based MRI and PET features in our case), we can use a few number of hidden layers to obtain the latent features. This strategy is also consistent with the strategy used in previous studies that also fuse multimodality data at the later stage of the hidden layers (Ngiam et al., 2011; Srivastava & Salakhutdinov, 2012; Suk, Lee et al., 2014). As a result, the high‐level features (i.e., the output of the last hidden layer) of each modality should be more comparable to each other as they are semantically closer to the target labels, thus partially addressing the modality heterogeneity issue.
3.2. Stage 2 ‐ joint latent representation learning of two modalities
In Stage 2, we learn the feature representations for different combinations of modality pairs (i.e., MRI‐PET, MRI‐SNP, PET‐SNP). The aim of this stage is to fuse the complementary information from different modalities to further improve the performance of the classification framework. The complete DNN architecture used in Stage 2 is depicted in Figure 1 . There are a total of three DNN architectures, one for each pair of modalities. Note that, the outputs from hidden layers in Stage 1 are regarded as intermediate inputs in Stage 2, and the weights from Stage 1 can be regarded as the initial weights to initialize the DNN architecture in Stage 2. In addition, we use three outputs to train each DNN architecture. Two of the outputs are used to guide the learning of high‐level features from two different modalities, while third output is used to guide the learning of joint high‐level features for the two modalities.
Note that we also use the maximum number of available samples for this stage. For instance, to learn feature representation for the combination of MRI and PET data, we use the samples with complete MRI and PET data to train the DNN model. Using the same example of the previous section, where N1 subjects contain MRI data, N2 subjects contain PET data, N3 subjects contain SNP data, and Nmp = min(N1, N2) subjects contain both MRI and PET data. Then, we use Nmp samples to train network for modality pair of MRI & PET in Stage 2, while use N1 samples and N2 samples to train the independent MRI and PET network models, respectively. The weights learned from Stage 1 are used as initial weights for Stage 2. We use a similar strategy to train neural network for other modality pairs; thus, in Stage 2, we train totally three DNN models for three combinations of modality pairs.
3.3. Stage 3 ‐ final feature fusion of three modalities
After Stage 2, we obtain the joint feature representations of all the modality pairs. We then fuse all the joint representations in a final DNN prediction model. The architecture used in this stage is depicted as Stage 3 in Figure 1. In Stage 3, we use the learned joint high‐level features from Stage 2 as input and the target labels as output. As features from all the three modalities are involved in the DNN architecture in Stage 3, we can only use the samples with complete MRI, PET, and SNP data to train this part of network, and then fine‐tune the whole network (i.e., DNN architecture in Stage 1, Stage 2, and Stage 3). Note that the networks in Stage 1 and Stage 2 are learned by using more available training samples. This is the major advantage of stage‐wise network training which can make full use of all available samples for training. After training the whole network, we may obtain the diagnostic label for each testing sample (with complete data from three modalities) at the output layer. Due to the limited number of subjects with complete multimodality data in this study, the classification results at the last output layer may suffer from over‐fitting issue. Thus, we use majority voting strategy for all the seven soft‐max output layers in Stage 3 (shown in Figure 1), as our final classification result.
4. MATERIALS AND IMAGE DATA PREPROCESSING
We use the public Alzheimer's disease neuroimaging initiative (ADNI) database to evaluate the performance of our framework. The ADNI dataset was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and nonprofit organizations with a 5‐year public private partnership. The main goal of ADNI is to investigate the potential of fusing multimodality data, including neuroimaging, clinical, biological, and genetic biomarkers, to diagnose AD and its early statuses.
4.1. Subjects
In this study, we used 805 ADNI‐1 subjects, including 190 AD, 389 MCI, and 226 normal controls (NC) subjects, which have their MR images scanned at the first screening time (i.e., the baseline). Out of these subjects, 360 have PET data, and 737 have SNP data. The detailed demographic information of the baseline subjects is summarized in Table 1. In addition, Table 2 shows the numbers of subjects with different combinations of modalities. From Table 2, it is clear to see that some subjects have certain modalities missing, as only 360 subjects have complete multimodality data.
Table 1.
Demographic information of the baseline subjects in this study (MMSE: Mini‐mental state examination)
| Female/male | Education | Age | MMSE | |
|---|---|---|---|---|
| NC | 108/118 | 16.0 ± 2.9 | 75.8 ± 5.0 | 29.1 ± 1.0 |
| MCI | 138/251 | 15.6 ± 3.0 | 74.9 ± 7.3 | 27.0 ± 1.8 |
| AD | 101/89 | 14.7 ± 3.1 | 75.2 ± 7.5 | 23.3 ± 2.0 |
| Total | 347/458 | 15.5 ± 3.0 | 75.2 ± 6.8 | 26.7 ± 2.7 |
Table 2.
Numbers of subjects with different combinations of modalities
| Modality | MRI | PET | SNP | MRI & PET | MRI & SNP | PET & SNP | MRI & PET & SNP |
|---|---|---|---|---|---|---|---|
| Number | 805 | 360 | 737 | 360 | 737 | 360 | 360 |
After the baseline scan, follow‐up scans were acquired every 6 or 12 months for up to 36 months. However, not all the subjects came back for follow‐up scans, and also not all kinds of neuroimaging scans were acquired for each subject. Thus, the number of longitudinal data for each subject is different, and also the number of modality data at each time point is different for each subject. Nevertheless, our framework is still applicable in this case, as it is robust to incomplete multimodality data.
For the MCI subjects, we retrospectively labeled those who progressed to AD after a certain period of time as pMCI subjects, while those who remained stable as sMCI subjects. Following this convention, the labeling of sMCI/pMCI could be affected by both the reference time‐point and the time period in which the patients are monitored for conversion to AD. We considered the 18‐th month as the reference and 30 months as the time period to monitor for conversion, so that there is a sufficient number of earlier scan samples (i.e., samples at baseline, 6th and 12th month) in each cohort (i.e., pMCI and sMCI) for our study. Thus, MCI patients who were converted to AD within the 18th to 48th month (the duration of 30 months) are labeled as pMCI patients, while MCI patients whose conditions remained stable are labeled as sMCI patients. MCI patients who were progressed to AD prior to the 18th month were excluded from the study, because they were no longer MCI patients at the reference time point. Similarly, MCI patients who were converted to AD after the 48th month were also excluded to avoid ambiguity in labeling. In addition, as some MCI subjects dropped out of the study after the baseline scans, their sub‐labels (pMCI or sMCI) cannot be determined. Hence, the total number of pMCI (i.e., 157) and sMCI (i.e., 205) subjects does not match with the total number of baseline MCI subjects.
4.2. Processing of neuroimages and SNPs
For this study, we downloaded the preprocessed 1.5 T MR images and PET images from the ADNI website.1 The MR images were collected by using a variety of scanners with protocols individualized for each scanner. In order to ensure the quality of all images, ADNI had reviewed these MR images and had corrected them for spatial distortion caused by B1 field inhomogeneity and gradient nonlinearity. For PET images, which were collected by 30–60 min post Fluoro‐Deoxy Glucose (FDG) injection, multi‐operations including averaging, spatially alignment, interpolation to standard voxel size, intensity normalization, and common resolution smoothing had been performed.
After that, following some previous studies (Barshan & Fieguth, 2015; Suk et al., 2015), we further processed these neuroimages to extract ROI‐based features. Specifically, the MR images were processed using the following steps: anterior commissure‐posterior commissure (AC‐PC) correction by using MIPAV software,2 intensity inhomogeneity correction using N3 algorithm (Sled, Zijdenbos, & Evans, 1998), brain extraction using robust skull‐stripping algorithm (Wang, Nie et al., 2014), cerebellum removal, tissues segmentation using FAST algorithm in FSL package (Zhang, Brady, & Smith, 2001) to obtain three main tissues (i.e., white matter (WM), gray matter (GM), and cerebrospinal fluid), registration to a template (Kabani, 1998) using HAMMER algorithm (Shen & Davatzikos, 2002), and projection of ROI labels from the template image to the subject image. Finally, for each ROI in the labeled image, we computed the GM tissue volume, normalized it with the intracranial volume, and used it as ROI feature. Moreover, for each subject, we aligned the PET images to their respective T1 MR images by using affine registration, computed the average PET intensity value of each ROI, and regarded it as a feature. Thus, for a template with 93 ROIs, we obtained 93 ROI‐based neuroimaging features for each neuroimage (i.e., MRI or PET). In addition, for SNP data, according to the AlzGene database,3 only the SNPs belonging to the top AD gene candidates were selected. The selected SNPs were used to estimate the missing genotypes, and the illumina annotation information was also adopted to select a subset of SNPs (An et al., 2017; Saykin, Shen et al., 2010). In this study, we adopted 3,123 dimensional SNP data.
5. EXPERIMENTAL RESULTS AND ANALYSIS
5.1. Experimental setup
In this section, we evaluate the effectiveness of the proposed deep feature learning and fusion framework by considering four classification tasks: (a) NC versus MCI versus AD, (b) NC versus sMCI versus pMCI versus AD, (c) NC versus MCI, and (d) NC versus AD. For each classification task, we used 20‐fold cross‐validation for our experiments due to limited number of subjects. Specifically, we first split our dataset to 20 parts according to the subjects' unique Roster IDs (RIDs), where one part is used as testing set. Then, for the remaining RIDs, 10% is used as validation set, while 90% is used as training set. Furthermore, as the success of deep learning model relies greatly on adequate number of training samples, which enables the neural network to learn a generative nonlinear mapping of the input features to the target labels, we have taken two strategies to increase the number of samples in our study. First, we trained our model stage‐wise, where each stage of neural network learns feature representation for different modality combinations. In this way, we can use all the available samples in each stage of deep learning model training. In contrast, if we train our deep learning model directly, we can only use a limited number of samples with complete modalities. Second, as ADNI has been longitudinally collecting data for all the participating subjects and monitoring their disease status progressions, we propose to exploit these longitudinal data in our model. More specifically, we used the samples from multiple time points for all the training RIDs in our study. These two strategies can significantly increase the number of training samples to train our model. Figure 2 shows how we split the data for training, validation, and testing. For training set, we can either use the baseline data (single time‐point) or the longitudinal data (multiple time‐points) to train our deep learning model.
Figure 2.
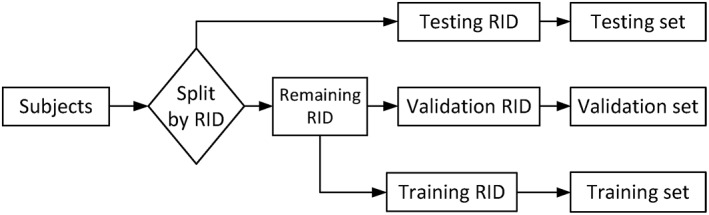
Dataset separation procedure used in our study. For the training set, we can either use the most available baseline data (single time‐point) or longitudinal data (multiple time‐points) to train our deep learning model
Next we discuss how to set the network structure of our proposed deep learning framework. For clarity, we define “hyperparameters” as the parameters that are related to the network structure (e.g., the number of layers, the number of nodes in each layer, etc.) and network learning (e.g., regularization parameters, dropout, etc.). As in many deep learning related studies, it is challenging to determine network hyperparameters. The tuning of these hyperparameters involves a lot of experience, guesswork, assumptions, prior knowledge of the data, and experiments. As the cost (in terms of time and money) to train a deep neural network for each hyperparameter combination is high due to the large number of network parameters, it is not feasible to use inner cross‐validation to determine all the hyperparameters for each fold of data. For example, for the case of using inner cross‐validation to select the number of layers and the number of neurons in each layer (while fixing other hyperparameters), we will have 5 × 5 = 25 combinations for each stage of network, even considering just 5 possible values for the number of layers and the number of neurons at each layers, respectively. As we have three modalities and three stages (but just needing one combination in the third stage) in our proposed deep neural network, there is a total of 25 × 3 × 2 + 25 = 175 hyperparameter value combinations. In each fold, if we use 5 subfolds and 5 repetitions for inner cross‐validation, we will end up with a total of 175 × 5 × 5 = 4,375 simulations in each fold of experiment. The mean computation time for each simulation is about 1 min (note that, as I used the lab server, which was shared by other lab members, to run our experiments, the computation time could be more when the server is busy). Thus, we may need about 4375/60/24 ≈ 3 days for one fold of experiment. If we use 20 fold cross‐validation and repeat for 50 times, the computation cost could become 3,000 days/GPU, which is not practical.
Due to the enormous computation cost of adopting the inner cross‐validation strategy, we have limited our search range to a small predefined range. First, we consider how to set the number of layers. We have investigated the effects of different number of layers and found that the performance could degrade when more layers are used. As we have a limited number of training samples, too many layers (thus more network parameters) will cause over‐fitting issue. Thus, we consider the number of hidden layers to be fewer than five. Second, we need to set the number of neurons in each layer. In our study, we use ROI‐based neuroimaging features for PET and MRI data. From the literature (Zhu et al., 2016), we know that not all the ROIs are related to the disease. Thus, with the feature selection, we set the number of neurons to be smaller than the number of ROI‐based input features for each neuroimaging data. Similarly, for SNP data, previous studies have indicated that only a handful of SNPs is helpful for AD diagnosis (An et al., 2017). Thus, in our study, we also use a small number of hidden neurons for SNP data.
The hyperparameter combination to be selected for each stage of network is given as follows. In Stage 1, we search the best hyperparameter setting from the following four combinations, that is, 64, 64–32, 64–32–32, 64–32–32–16. In Stage 2 and Stage 3, we select the best number of hidden layers from the following two options, that is, 32, 32–16. We use few number of layers in Stage 2 and 3, as we assume features have become more semantic (high‐level) after Stage 1 training. The details of our experiment are described as follows. In our proposed stage‐wise method, we first selected hyperparameters using the inner‐cross‐validation loop (using only the training set) in Stage 1 for each modality data (i.e., MRI, PET, SNP). Next, we fixed network architectures in Stage 1, and then implemented an inner‐cross‐validation loop to tune network architectures in Stage 2 for each modality combination (i.e., MRI + PET, MRI + SNP, MRI + PET + SNP). Finally, we fixed network architectures in Stage 1 and Stage 2, to tune network architectures in Stage 3 for three‐modality combination. Compared with the previous version of our paper (i.e., we fixed hyper‐parameters in all stages and folds), our model now selects parameter setting based on the best result of inner‐cross‐validation experiment by using only the training dataset. We used only two fold for the inner‐cross‐validation experiment to reduce the computation cost, but employed 20‐fold outer‐cross‐validation, with 50 repetitions, to get a more accurate estimate of model performance. Furthermore, L1 and L2 regularizations were also imposed on the weight matrices of the networks. The regularization parameters for L1 and L2 regularizers are empirically set to 0.001 and 0.1, respectively.
5.2. Implementation details
As described in Sec. 4.1, we totally have 737 subjects (the corresponding RID set is denoted as “Rall”), in which 360 subjects (with their corresponding RIDs denoted as “Rcom”) have complete multi‐modality data (i.e., MRI, PET, and SNP). Besides, we denote the RID set corresponding to the subjects with MRI, PET, and SNP data as “RMRI”, “RPET”, and “RSNP”, respectively. In the following, we introduce the implementation details of how to apply this dataset for our three‐stage training. First, we split the 360 subjects with complete data (“Rcom”) into 20 subsets according to their RIDs, where one of the subsets are used as testing set, and the remaining subsets are further divided into two parts: validation set (10%) and training set (90%). We denote the RIDs corresponding to the testing set as “Rte” and the RIDs corresponding to the validation set as “Rva”. In the Stage 1 of our deep learning model, we learn feature representations for each modality independently. For example, for MRI modality, we use all training subjects with available MRI data to train the MRI submodel, where the corresponding RID set used is RMRI − Rva − Rte. In other words, all MRI data corresponding to RID set RMRI − Rva − Rte (including data from other time points if using longitudinal data), are used to train our MRI model. Similarly, the corresponding RID sets used to train PET and SNP submodels are given as RPET − Rva − Rte and RSNP − Rva − Rte, respectively. It can be clearly seen that the subject sets used in training, validation, and testing are mutually exclusive. In Stage 2, we train three neural network submodels for three different combinations of modality pair using the output from Stage 1. Similar to Stage 1, we also use all available subjects to train the submodels in Stage 2. For example, for MRI + PET submodel, the corresponding RID set used is RMRI ∩ RPET − Rva − Rte (∩ denotes intersection). Similarly, the corresponding RID sets for MRI + SNP and PET+SNP submodels are given as RMRI ∩ RSNP − Rva − Rte and RPET ∩ RSNP − Rva − Rte, respectively. In Stage 3, we use the subjects with complete three modalities to train the whole network. Thus, the corresponding RID set used is RMRI ∩ RPET ∩ RSNP − Rva − Rte. It is clearly shown that we have most number of training subjects in Stage 1, smaller number of training subjects in Stage 2, and the least number of training subjects in Stage 3. In brief, in each stage, we first find the RID set corresponding to the training subjects, and then use all data corresponding to the RID set (including data from time point other than the baseline, if using longitudinal data) as training samples.
5.3. Comparison with other feature representation methods
We compared the proposed framework with four popular feature representation methods, that is, principal component analysis (PCA) (Wold, Esbensen, & Geladi, 1987), canonical correlation analysis (Bron, Smits et al., 2015; Hardoon, Szedmak, & Shawe‐Taylor, 2004), locality preserving projection (LPP) (He et al., 2006), and L21 based feature selection method (Nie et al., 2010). For PCA and LPP, we determined the optimal dimensionality of the data based on their respective eigenvalues computed by the generalized eigen‐decomposition method according to (He et al., 2006). For CCA, we optimized its regularization parameter value by cross‐validation in the range of {10−4, 10−3, ⋯, 10−2}. For L21 method, we optimized its sparsity regularization parameter by cross‐validating its value in the range of {10−4, 10−3, ⋯, 10−2}. To fuse the three modalities, we concatenated the feature vectors of the multimodality data into a single long vector for the above four comparison methods. We also compared our proposed framework with a deep feature learning method, that is, SAE (Suk et al., 2015). For this method, we obtained SAE‐learned features from each modality independently, and then concatenated all the learned features into a single long vector. We also set the hyper‐parameters of SAE to the values suggested in (Suk et al., 2015), that is, we used a three‐layer neural network for multi‐modality data by using a grid search from [100; 300; 500; 1,000]‐[50; 100]‐[10; 20; 30] (bottom‐top). As a baseline method, we further included the results for the experiment using just the original features without any feature selection (denoted as “Original”). In addition, we also compared to our method with Multiple Kernel Learning (MKL) (Althloothi, Mahoor, Zhang, & Voyles, 2014; De Bie et al., 2007), as MKL is a common multi‐modality fusion method. For this method, we first used PCA to reduce feature dimension for each modality, adopted MKL to fuse features from different modalities via a linear combination of kernels, and then used a support vector machine (SVM) classifier for classification. For MKL, we optimized the weights of different kernels by cross‐validating its value in the range of (0, 1) with the sum of weights set to 1. We used SVM classifier from LIBSVM toolbox (Chang & Lin, 2011) to perform classification for all the above comparison methods. For each classification task, we use grid search to determine the best parameters for both the feature selection and classification algorithms, based on their performances on the validation set. For instance, the best soft margin parameter C of SVM classifier was determined by grid searching from {10−4, ⋯, 104}. Also note that, for fair comparison with other comparison methods, we used only the data at baseline time‐point (i.e., corresponding to “Ours‐baseTP”) to train our network in this subsection.
In order to verify the effectiveness of our method, we have conducted the comparison experiments for two multi‐class classification tasks (i.e., NC/MCI/AD and NC/sMCI/pMCI/AD) and two binary classification tasks (i.e., NC/AD and NC/MCI). Figures 3 and 4 show the results in violin plot achieved by different methods. We choose violin plot to present our results as it can visualize the distribution of the results. In addition, in Figure 5, we show the confusion matrix results achieved by the proposed method for two multi‐class classification tasks. Note that we report the final confusion matrices by averaging the 50 repetitions of 20‐fold cross validation results. Further, we use a nonparametric Friedman test (Demšar 2006) to evaluate the performance difference between our method and other competing methods. Friedman test is generally used to test the difference between two groups of variables that are corresponding to the same set of objects. Table 3 shows the Friedman test results (in term of p‐values) by comparing the predictions between our method and each competing method. Note that smaller p‐value indicates bigger prediction difference between our method and another comparison method.
Figure 3.
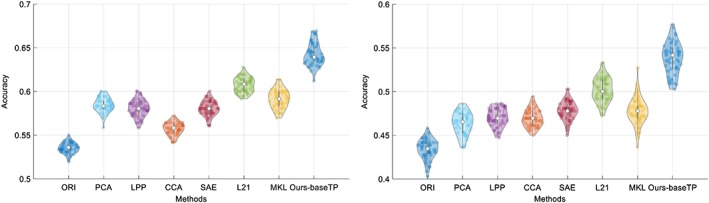
Violin plots for the distributions of classification accuracy of the two multi‐class classification tasks, that is, NC/MCI/AD (left) and NC/sMCI/pMCI/AD (right), where the hollow white dot and the box denote the median, and the interquartile range of the classification results of 50 repetitions, respectively. From the violin plot, it can be clearly seen that our proposed method outperforms other comparison methods [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 4.
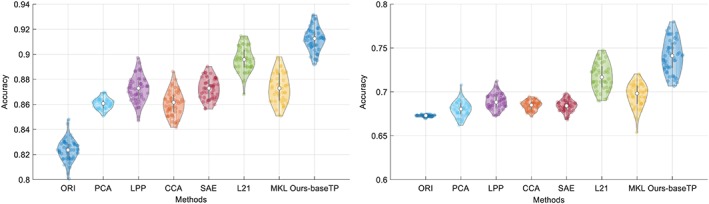
Violin plots for the distributions of classification accuracy of the two multi‐class classification tasks, that is, NC/AD (left) and NC/MCI (right), where the hollow white dot and the box denote the median, and the interquartile range of the classification results of 50 repetitions, respectively. From the violin plot, it can be clearly seen that our proposed method outperforms other comparison methods [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 5.
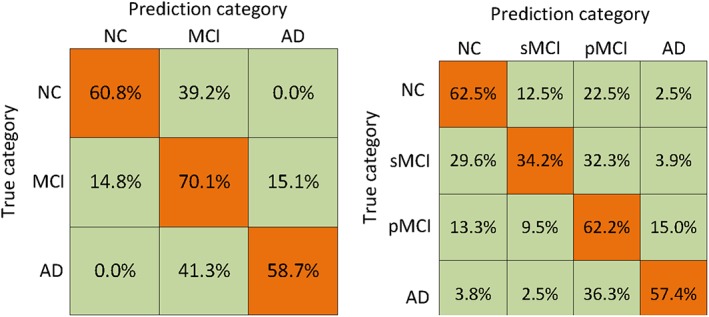
Confusion matrices achieved by the proposed method on the two multi‐class classification tasks: (left) NC/MCI/AD and (right) NC/sMCI/pMCI/AD [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 3.
p‐values of the Friedman test results between our method and other competing methods
| ORI | PCA | LPP | CCA | SAE | L21 | MKL | |
|---|---|---|---|---|---|---|---|
| NC/MCI/AD | <.00001 | <.00001 | <.00001 | <.00001 | <.00001 | <.00001 | <.00001 |
| NC/sMCI/pMCI/AD | <.00001 | <.00001 | <.00001 | <.00001 | <.00001 | <.00001 | <.0001 |
| NC/AD | <.00001 | <.00001 | <.00001 | <.00001 | <.00001 | <.00001 | <.00001 |
| NC/MCI | <.00001 | <.00001 | <.00001 | <.00001 | <.00001 | <.0001 | <.00001 |
From Figures 3, 4, 5 and Table 3, we have the following observations.
From Figures 3 and 4, it can be seen that our proposed AD diagnosis framework outperforms all the comparison methods in term of classification accuracy.
From Table 3, it can be seen that most p‐values are less than .00001, which indicates statistically significant improvement of our proposed method compared to other method under comparison. This is consistent with the accuracy comparison results using violin plots in Figures 3 and 4.
From Figure 5, we can see the percentages of both the correct and wrong classifications in each cohort of data. As the MCI is considered as the intermediate stage between AD and NC, it is much more difficult to differentiate MCI subjects from AD and NC subjects, which is supported by a relatively higher percentage of miss‐classification rate in MCI cohort.
5.4. Effects of different components of the proposed framework
We have two settings for our proposed framework, that is, “Ours‐baseTP”, which uses only the baseline time‐point data, and “Ours‐multiTP”, which exploits the longitudinal data scanned at multiple time‐points. As “Ours‐multiTP” uses more data than “Ours‐baseTP” when training the network, we expect “Ours‐multiTP” would have better generalized network and would perform better than “Ours‐baseTP”. In addition, the good performance of our proposed framework could be due to the stage‐wise feature learning strategy, which uses the maximum number of all available samples for training. In order to verify this, we also compare our proposed methods with our degraded deep learning method that do not use stage‐wise training strategy, that is, “Ours‐complete”, which uses only the baseline samples with complete three‐modality data for training, with the deep learning architecture shown in Figure 6. Figure 7 shows that comparison results for the four classification tasks. The bars labeled with “Ours‐complete” and “Ours‐baseTP” use only the baseline time‐point data, while “Ours‐multiTP” exploits the longitudinal. It can be seem from Figure 7 that the proposed methods (i.e., “Ours‐baseTP” and “Ours‐multiTP”) outperform “Ours‐complete”, implying the effectiveness of our stage‐wise feature learning and fusion strategy that can best use of all the samples in the training set, regardless of their modality completeness. Besides, we first use a nonparametric Friedman test to evaluate the performance difference between “Ours‐multiTP” and other competing methods (i.e., “Ours‐complete” and “Ours‐baseTP”), as shown in Figure 7. From Figure 7, the Friedman test results have indicated that “Ours‐multiTP” is significantly better than “Ours‐complete” and “Ours‐baseTP as demonstrated by very small p‐values. Moreover, we also use a nonparametric Friedman test to evaluate the performance difference between “Ours‐baseTP” and “Ours‐complete”, the results have verified that “Ours‐baseTP” performs better than “Ours‐complete”. In summary, our experimental results indicate that the performance of deep neural network can be improved when using more data samples.
Figure 6.
The flow of directly fusing three complete modalities by using high‐level features. Specifically, we learn latent representations (i.e., high‐level features) for each modality independently in stage 1, and then learn diagnostic labels by fusing the learned latent feature representations from stage 2 [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 7.
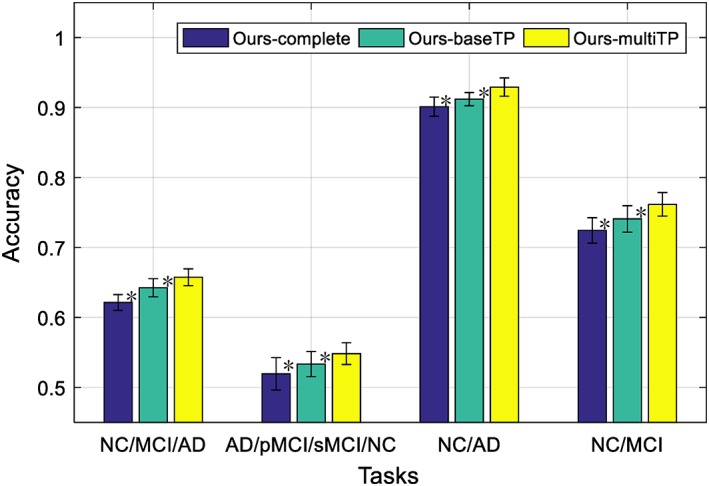
Comparison of classification accuracy for the four classification tasks by using different methods, where “ours‐complete” use baseline time‐point data with complete modalities, “ours‐baseTP” use the baseline time‐point data, while “ours‐multiTP” exploits the longitudinal data by using the data scanned at multiple time‐points (* denotes the Friedman test with p < .001) [Color figure can be viewed at http://wileyonlinelibrary.com]
5.5. Effects of different modality combinations
To further analyze the benefit of neuroimaging and genetic data fusion, Figure 8 illustrates the performance of our proposed framework for different combinations of modalities on the baseline time‐point data. Note that, in Figure 8, we show the comparison results using the base time‐point data. From Figure 8, we can see that the performance of using only MRI modality is better than using PET or SNP, and the SNP shows the lowest performance. This is understandable as SNP data are the genotype features which are least related to the diagnostic label, compared to the MRI and PET data, which are the phenotypes features that are closely related to diagnostic labels. Nevertheless, when we combined all the three modalities, the classification results are better than the results from any single modality or two‐modality combinations (bimodal). The interesting part of the results in Figure 8 is that, for bimodal that involves SNP, the classification results are not always better than the results using individual modality. For example, for PET+SNP combination, its classification result is better than the results using individual modality for four‐class (AD/pMCI/sMCI/NC) classification, but not for the three‐class (AD/MCI/NC) and two‐class (NC/AD and NC/MCI) classifications. For MRI + SNP combination, it can be seen that its performances for four‐class classification and NC/MCI tasks are better than the results using only its individual modality. These findings show that the SNP data have positive effect for four‐class classification task when it combines with MRI, PET or both modality data. The effect of SNP data in bimodal network for other classification tasks is not consistent, and, in some cases, the inclusion of SNP data will degrade the classification performance. This could be caused by the network structure that we used, which is probably not optimal for bimodal network that involves SNP. Probably we should reduce the number of neurons for the output layer of the SNP submodel, so that the less discriminant SNP features can take less contribution in bimodal network, to circumvent the negative effect of SNP data. Nevertheless, it is worth noting that when all the three modalities are used, the performance of our model is better than any single modality or bi‐modality models. Besides, we also use a nonparametric Friedman test to evaluate the performance difference between our method with three modalities and the other methods with single modality or any two‐modality combination, as shown in Figure 8, the results have indicated statistically significant improvement of our proposed method combing three modalities (i.e., MRI + PET+SNP) compared to the methods using single modality or any two‐modality combination.
Figure 8.
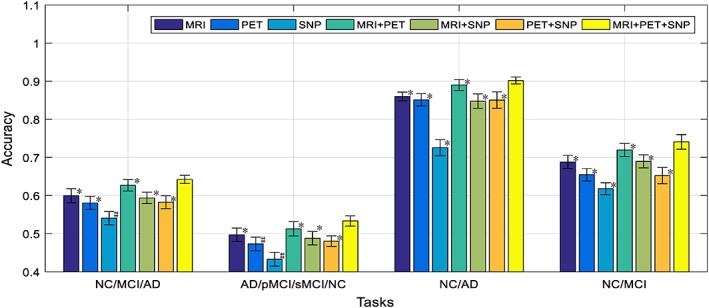
Comparison of classification accuracy of the proposed framework by using different modalities (i.e., MR, PET, and SNP) and modality combinations (i.e., MRI + PET, MRI + SNP, PET+SNP, MRI + PET+SNP) for four different classification tasks (where * denotes the Friedman test with p < .0001 and # denotes the Friedman test with p < .00001) [Color figure can be viewed at http://wileyonlinelibrary.com]
5.6. Normal aging effects
Some studies (Dukart et al., 2011; Franke, Ziegler et al., 2010; Moradi, Pepe et al., 2015) have discovered the confounding effects of normal aging and AD, that is, there are overlaps between the brain atrophies caused by normal aging and AD. In order to evaluate the impact of removing age‐related effects from the features derived from MRI and PET data, we followed a strategy described in previous studies (Dukart et al., 2011; Moradi, Pepe et al., 2015). More specifically, we first estimated the relationship between volumetric features and ages for the subjects in NC cohort by learning multiple linear regression models, where ages are used to predict brain volumetric features, with one regression model learned for each feature. Then, we removed age‐related effects by subtracting the predictions of the linear regression model from the original features of MRI and PET data, with the details described in Appendix B of Moradi, Pepe et al. (2015). For convenience, we denote “Ours‐AgeEffectRemoved” as our method with the aging effects removed. Figure 9 shows the comparison results between our methods using neuroimaging data with and without removal of normal aging effects. From Figure 9, it can be observed that that the removal of age‐related effects from MRI and PET data can indeed improve the classification performance. This is because, by removing age‐related effects, we can focus more on the AD‐related atrophies for classification. Besides, we also use a nonparametric Friedman test to evaluate the performance difference between “Ours‐AgeEffectRemoved” and “Ours‐baseTP”. From Figure 9, the Friedman test result has indicated that “Ours‐AgeEffectRemoved” is significantly better than “Ours‐baseTP”.
Figure 9.
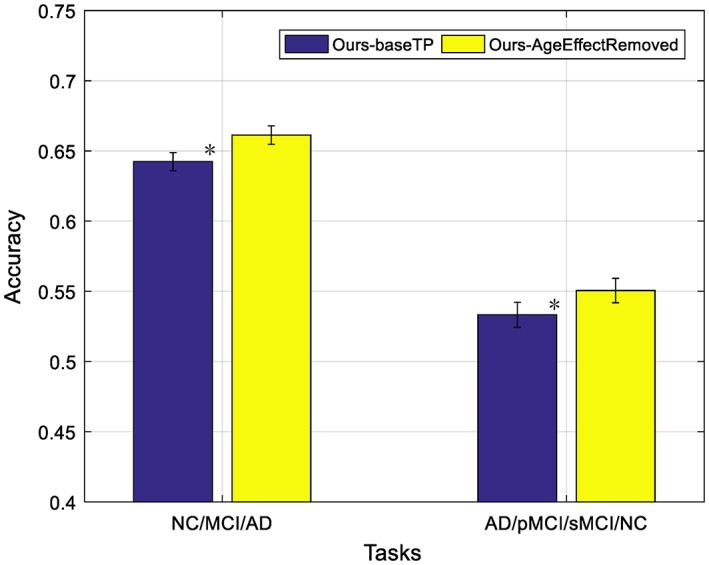
Impact of removing aging‐related effects in the two multi‐class classification tasks, where “ours‐AgeEffectRemoved” denotes our method using MRI and PET features after removing age‐related effects (* denotes the Friedman test with p < .0001) [Color figure can be viewed at http://wileyonlinelibrary.com]
5.7. The Most discriminative brain regions and SNPs
It is important to find out the most discriminative brain regions (i.e., ROIs) and SNPs for AD diagnosis. In this study, the most frequently selected ROI‐based features or SNPs in cross‐validations are regarded as the most discriminative brain regions or SNPs. These discriminative features are important as they can become the potential biomarkers for clinical diagnosis. For our proposed deep learning framework, although we did not use weight matrix W to select discriminative features directly, we can rank the features based on the l2‐norm of the weight matrix W. Specifically, for the j‐th fold, we have the weight matrix Wj in the first layer of the neural network. Each row in Wj is corresponding to one ROI (for MRI and PET data) or SNP. Then, we define the top 10 ROIs (or SNPs) as the ROIs (or SNPs) that correspond to the 10 largest summation of absolute values along the rows of Wj. Thus, for each fold, we select top 10 ROIs (or SNPs) based on their magnitudes of weights. For 20‐folds, we have 20 different sets of top 10 ROIs (or SNPs). We then define the final top ROIs (or SNPs) as the ROIs (or SNPs) with the highest selection frequency. The top 10 ROIs identified from MRI and PET data for the four classification tasks are shown in Figures 10 and 11, respectively. In MRI, hippocampal, amygdala, uncus, and gyrus regions are identified. In PET, angular gyri, precuneus, globus palladus are the top regions identified. These regions are consistent with some previous studies (Convit et al., 2000; Zhang, Shen et al., 2012; Zhu et al., 2016) and can be used as potential biomarkers for AD diagnosis.
Figure 10.
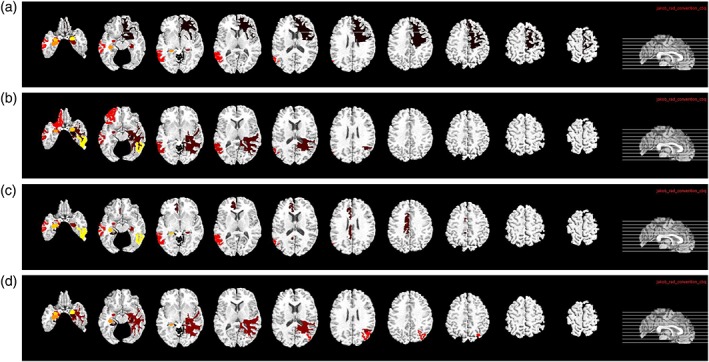
Top 10 selected ROIs from MRI data for the four different classification tasks: (a) NC/MCI/AD, (b) NC/sMCI/pMCI/AD, (c) NC/AD, and (d) NC/MCI [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 11.
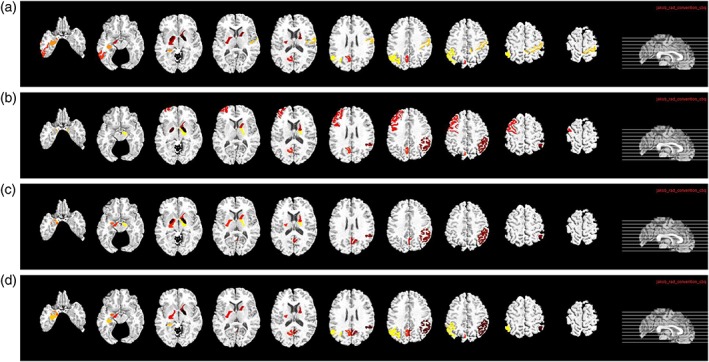
Top 10 selected ROIs from PET data for the four different classification tasks: (a) NC/MCI/AD, (b) NC/sMCI/pMCI/AD, (c) NC/AD, and (d) NC/MCI [Color figure can be viewed at http://wileyonlinelibrary.com]
The most frequently selected SNP features and their corresponding gene names are summarized in Table 4. The SNPs in APOE have shown that they are related to neuroimaging measures in brain disorders (An et al., 2017; Chiappelli et al., 2006). Besides, some SNPs are found to be from DAPK1 and SORCS1 genes, which are the well‐known top candidate genes that are associated with hippocampal volume changes and AD progression. In addition, most selected SNPs are from PICLAM, ORL1, KCNMA1, and CTNNA3 genes (An et al., 2017; Peng et al., 2016), which have been shown to be AD‐related in the previous studies. These findings indicate that our method is able to identify the most relevant SNPs for AD status prediction.
Table 4.
Most related SNPs for AD diagnosis
| Gene name | SNP name |
|---|---|
| APOE | Rs429358 |
| DAPK1 | rs822097 |
| SORCS1 | rs11814145 |
| PICLAM | rs11234495, rs7938033 |
| ORL1 | rs7945931 |
| KCNMA1 | rs1248571 |
| CTNNA3 | rs10997232 |
6. DISCUSSION
6.1. Comparison with previous studies
Different from the conventional multi‐modality fusion methods, we proposed a novel stage‐wise deep feature learning and fusion framework. In this stage‐wise strategy, each stage of the network learns feature representations for independent modality or different combinations of modalities, by using the maximum number of available samples. The main advantage is that we can use more available samples to train our model for improving prediction performance. Further, our proposed method can automatically learn representations from multi‐modality data and obtain diagnostic results using an end‐to‐end manner, while the traditional methods in the literature mostly employ feature selection, feature fusion, and classification in multiple separate steps (Peng et al., 2016; Zhang, Shen et al., 2012; Zhu et al., 2016).
In addition, Bron, Smits et al. (2015) reported results of a challenge, where different algorithms are evaluated using same set of features derived from MRI data for AD diagnosis. The features used include regional volume, cortical thickness, shape, and signal intensity values. The best performing algorithm yielded classification accuracy of 63% for three‐class (i.e., NC vs. MCI vs. AD) classification. However, the results reported in Bron et al.'s paper are not directly comparable with the results reported in our paper. First, both studies used different set of data. Bron et al.'s study used 384 subjects from three medical centers (i.e., VU University Medical Center, the Netherlands; Erasmus MC, the Netherlands; and University of Porto, Portugal), whereas our study used 805 subjects from ADNI dataset (collected from over 50 imaging centers). Furthermore, in term of the number of MCI subjects, our study has higher percentage of subjects coming from MCI cohort than the Bron et al.'s study, that is, 48.3% versus 34.1%. As MCI can be considered as the intermediate state of NC and AD, this cohort is much more challenging to be discriminated from the other two cohorts. As our ADNI dataset is unbalance (in term of disease cohorts), contains higher percentage of hard‐to‐discriminate intermediate cohort, incomplete (in term of the completeness of modalities), and heterogenous (e.g., due to over 50 image collection centers), our problem is much more challenging than the problem presented in Bron, Smits et al. (2015). Nevertheless, our method is still able to achieve 64.4% accuracy for three‐class classification task, comparable to the best result reported in Bron et al.'s study (Bron, Smits et al., 2015).
Second, the types and number of features used by both works are different. In Bron et al.'s paper (Bron, Smits et al., 2015), when using only regional volume features, the reported accuracies are 49.7% for Dolph method and 47.7% for Ledig‐VOL method, which are lower than 61% accuracy achieved by our method that only uses ROI features from MRI data. Third, the focus of both studies are different. While Bron et al.'s study is focusing on getting the best classification algorithm using a combination of multiple‐view features from the MRI data, we are focusing on improving the classification performance by using a combination of neuroimaging and genetic data. We aim at overcoming the heterogeneity and incomplete data issues of these multi‐modality data by proposing a novel deep learning based multi‐modality fusion framework. The bottom line is that the experimental results have validated the efficacy of our proposed framework as it outperforms the baseline method as well as other state‐of‐art methods. For instance, we also achieve an accuracy of 64.4% for three‐class classification using the proposed method, which is about 18% improvement over our baseline method that uses original features.
6.2. Clinical interest
AD is a progressive irreversible neurodegenerative disease. Before its disease onset, there is a prodromal stage called MCI. Some of the MCI subjects (i.e., pMCI) will progress to AD within few years, while the others (i.e., sMCI) are relatively stable and do not progress to AD within the same period. As AD is currently irreversible and incurable, the detection of its earlier stages, or multi‐class classification for different AD stages is actually of much more clinical interest. Thus, unlike many previous studies in the literature that focused on binary classification tasks (Zhang, Zhang, Chen, Lee, & Shen, 2017; Zhu, Suk et al., 2017), we focus our classification results on four different tasks: (a) NC versus MCI versus AD, (b) NC versus sMCI versus pMCI versus AD, (c) NC versus MCI, and (d) NC versus AD. The first two are multi‐class classification tasks, which is much more challenging but of more clinical interest, while the latter two are the conventional binary classification tasks, added for easier comparison with the results from previous studies. For four‐class classification task (i.e., NC vs. sMCI vs. pMCI vs. AD), our method achieves about 54% accuracy, outperforming other state‐of‐the‐art methods. This performance seems lower than the other tasks, but it is due to the increased complexity of the problem, instead of the failure of the algorithm. The bottom line is that we have shown how to make use of all available data for training a robust deep learning model for multi‐status AD diagnosis. Nevertheless, more works need to be done to improve the performance of this classification task for practical clinical usage, where the performance of this work could be used as a benchmark, and the strategy used for this work could be used as the foundation.
6.3. Future work
Although our proposed prediction method achieves promising results in four classification tasks, there are several improvements that can be considered for future work. First, our method is focusing on using ROI features as input to the deep learning model; however, such hand‐crafted features may limit the richness of structural and functional brain information from MRI and PET images, respectively. To fully unleash the power of deep learning model in learning imaging features that are useful for our classification tasks, we may have to use the original imaging data, and utilize convolution or other more advanced deep neural networks in our framework. Second, as discussed in Section 5.6 about the effects of age, we can incorporate other confounding factors (e.g., gender, education level, etc.) into the proposed framework to possibly improve the performance.
7. CONCLUSION
In this article, we focus on how to best use multimodality neuroimaging and genetic data for AD diagnosis. Specifically, we present a novel three‐stage deep feature learning and fusion framework for AD diagnosis, which integrates multimodality imaging and genetic data gradually in each stage. Our framework alleviates the heterogeneity issue of multimodality data by learning the latent representations of different modality using separate DNN models guided by the same target. As the latent representations of all the modalities (i.e., outputs of the last hidden layer) are semantically closer to the target labels, the data heterogeneity issue is partially addressed. In addition, our framework also partially addresses the incomplete multimodality data issue by devising a stage‐wise deep learning strategy. This stage‐wise learning strategy allows samples with incomplete multimodality data to be used during the training, thus also allowing to use the maximum number of available samples to train each stage of the proposed network. Moreover, we exploit longitudinal data for each training subject to significantly increase the number of training samples. As our proposed deep learning framework can use more data in the training, we achieved better classification performance, compared with other methods. All these experimental results (using ADNI database) have clearly demonstrated the effectiveness of the proposed framework, and the superiority of using multimodality data (over the case of using single modality data) in AD diagnosis.
ACKNOWLEDGMENTS
This research is partly supported by National Institutes of Health EB022880, AG053867, EB006733, EB008374, AG041721, and G049371.
Zhou T, Thung K‐H, Zhu X, Shen D. Effective feature learning and fusion of multimodality data using stage‐wise deep neural network for dementia diagnosis. Hum Brain Mapp. 2019;40:1001–1016. 10.1002/hbm.24428
Funding information Foundation for the National Institutes of Health, Grant/Award Number: EB022880, AG053867, EB006733, EB008374, AG041721
Footnotes
REFERENCES
- Althloothi, S. , Mahoor, M. H. , Zhang, X. , & Voyles, R. M. (2014). Human activity recognition using multi‐features and multiple kernel learning. Pattern Recognition, 47(5), 1800–1812. [Google Scholar]
- An, L. , Adeli, E. , Liu, M. , Zhang, J. , Lee, S. W. , & Shen, D. (2017). A hierarchical feature and sample selection framework and its application for Alzheimer's disease diagnosis. Scientific Reports, 7, 45269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Association, A. S . (2016). 2016 Alzheimer's disease facts and figures. Alzheimer's & Dementia, 12(4), 459–509. [DOI] [PubMed] [Google Scholar]
- Barshan, E. , & Fieguth, P. (2015). Stage‐wise training: An improved feature learning strategy for deep models. Feature extraction: Modern questions and challenges. Proceedings of Machine Learning Research, 44, 49–59. [Google Scholar]
- Biffi, A. , Anderson, C. D. , Desikan, R. S. , Sabuncu, M. , Cortellini, L. , Schmansky, N. , … Alzheimer's Disease Neuroimaging Initiative (ADNI) (2010). Genetic variation and neuroimaging measures in Alzheimer disease. Archives of Neurology, 67(6), 677–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bron, E. E. , Smits, M. , van der Flier, W. , Vrenken, H. , Barkhof, F. , Scheltens, P. , … Alzheimer's Disease Neuroimaging Initiative . (2015). Standardized evaluation of algorithms for computer‐aided diagnosis of dementia based on structural MRI: The CADDementia challenge. NeuroImage, 111, 562–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, C.‐C. , & Lin, C.‐J. (2011). LIBSVM: A library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST), 2(3), 27. [Google Scholar]
- Chen, X. , Zhang, H. , Gao, Y. , Wee, C. Y. , Li, G. , Shen, D. , & the Alzheimer's Disease Neuroimaging Initiative . (2016). High‐order resting‐state functional connectivity network for MCI classification. Human Brain Mapping, 37(9), 3282–3296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, X. , Zhang, H. , Zhang, L. , Shen, C. , Lee, S. W. , & Shen, D. (2017). Extraction of dynamic functional connectivity from brain grey matter and white matter for MCI classification. Human Brain Mapping, 38(10), 5019–5034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chetelat, G. , Desgranges, B. , de la Sayette, V. , Viader, F. , Eustache, F. , & Baron, J. C. (2003). Mild cognitive impairment can FDG‐PET predict who is to rapidly convert to Alzheimer's disease? Neurology, 60(8), 1374–1377. [DOI] [PubMed] [Google Scholar]
- Chiappelli, M. , Borroni, B. , Archetti, S. , Calabrese, E. , Corsi, M. M. , Franceschi, M. , … Licastro, F. (2006). VEGF gene and phenotype relation with Alzheimer's disease and mild cognitive impairment. Rejuvenation Research, 9(4), 485–493. [DOI] [PubMed] [Google Scholar]
- Chu, A. Y. , Deng, X. , Fisher, V. A. , Drong, A. , Zhang, Y. , Feitosa, M. F. , … Fox, C. S. (2017). Multiethnic genome‐wide meta‐analysis of ectopic fat depots identifies loci associated with adipocyte development and differentiation. Nature Genetics, 49(1), 125–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Convit, A. , de Asis, J. , de Leon, M. J. , Tarshish, C. Y. , de Santi, S. , & Rusinek, H. (2000). Atrophy of the medial occipitotemporal, inferior, and middle temporal gyri in non‐demented elderly predict decline to Alzheimer's disease. Neurobiology of Aging, 21(1), 19–26. [DOI] [PubMed] [Google Scholar]
- Cuingnet, R. , Gerardin, E. , Tessieras, J. , Auzias, G. , Lehéricy, S. , Habert, M. O. , … Alzheimer's Disease Neuroimaging Initiative . (2011). Automatic classification of patients with Alzheimer's disease from structural MRI: A comparison of ten methods using the ADNI database. NeuroImage, 56(2), 766–781. [DOI] [PubMed] [Google Scholar]
- Dai, Z. , Yan, C. , Wang, Z. , Wang, J. , Xia, M. , Li, K. , & He, Y. (2012). Discriminative analysis of early Alzheimer's disease using multi‐modal imaging and multi‐level characterization with multi‐classifier (M3). NeuroImage, 59(3), 2187–2195. [DOI] [PubMed] [Google Scholar]
- De Bie, T., Tranchevent, L. C., Van Oeffelen, L. M., & Moreau, Y. (2007). Kernel‐based data fusion for gene prioritization. Bioinformatics, 23(13), i125–i132. [DOI] [PubMed] [Google Scholar]
- Demšar, J. (2006). Statistical comparisons of classifiers over multiple data sets. Journal of Machine learning research, 7(Jan), 1–30. [Google Scholar]
- Di Paola, M., Di Iulio, F., Cherubini, A., Blundo, C., Casini, A. R., Sancesario, G., … Spalletta, G. (2010). When, where, and how the corpus callosum changes in MCI and AD a multimodal MRI study. Neurology, 74(14), 1136–1142. [DOI] [PubMed] [Google Scholar]
- Dukart, J., Schroeter, M. L., Mueller, K., & Alzheimer's Disease Neuroimaging Initiative. (2011). Age Correction in Dementia–Matching to a Healthy brain. PLoS One, 6, e22193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escudero, J. , Ifeachor, E. , Zajicek, J. P. , Green, C. , Shearer, J. , Pearson, S. , & Alzheimer's Disease Neuroimaging Initiative . (2013). Machine learning‐based method for personalized and cost‐effective detection of Alzheimer's disease. IEEE Transactions on Biomedical Engineering, 60(1), 164–168. [DOI] [PubMed] [Google Scholar]
- Fakoor, R., Ladhak, F., Nazi, A., & Huber, M. (2013). Using deep learning to enhance cancer diagnosis and classification. Proceedings of the International Conference on Machine Learning, 28. [Google Scholar]
- Farabet, C. , Couprie, C. , Najman, L. , & LeCun, Y. (2013). Learning hierarchical features for scene labeling. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(8), 1915–1929. [DOI] [PubMed] [Google Scholar]
- Fox, N. C., Warrington, E. K., Freeborough, P. A., Hartikainen, P., Kennedy, A. M., Stevens, J. M., & Rossor, M. N. (1996). Presymptomatic hippocampal atrophy in Alzheimer's disease: A longitudinal MRI study. Brain, 119(6), 2001–2007. [DOI] [PubMed] [Google Scholar]
- Franke, K. , Ziegler, G. , Klöppel, S. , Gaser, C. , & Alzheimer's Disease Neuroimaging Initiative . (2010). Estimating the age of healthy subjects from T 1‐weighted MRI scans using kernel methods: Exploring the influence of various parameters. NeuroImage, 50(3), 883–892. [DOI] [PubMed] [Google Scholar]
- Hardoon, D. R. , Szedmak, S. , & Shawe‐Taylor, J. (2004). Canonical correlation analysis: An overview with application to learning methods. Neural Computation, 16(12), 2639–2664. [DOI] [PubMed] [Google Scholar]
- Haufe, S. , Meinecke, F. , Görgen, K. , Dähne, S. , Haynes, J. D. , Blankertz, B. , & Bießmann, F. (2014). On the interpretation of weight vectors of linear models in multivariate neuroimaging. NeuroImage, 87, 96–110. [DOI] [PubMed] [Google Scholar]
- He, X., Cai, D., & Niyogi, P. (2006). Laplacian score for feature selection. Advances in Neural Information Processing Systems, 507–514. [Google Scholar]
- Jack, C. R. , Bernstein, M. A. , Fox, N. C. , Thompson, P. , Alexander, G. , Harvey, D. , … ADNI Study . (2008). The Alzheimer's disease neuroimaging initiative (ADNI): MRI methods. Journal of Magnetic Resonance Imaging, 27(4), 685–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabani, N. J. (1998). 3D anatomical atlas of the human brain. NeuroImage, 7, P‐0717. [Google Scholar]
- Kohannim, O. , Hua, X. , Hibar, D. P. , Lee, S. , Chou, Y. Y. , Toga, A. W. , … Alzheimer's Disease Neuroimaging Initiative . (2010). Boosting power for clinical trials using classifiers based on multiple biomarkers. Neurobiology of Aging, 31(8), 1429–1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koikkalainen, J. , Rhodius‐Meester, H. , Tolonen, A. , Barkhof, F. , Tijms, B. , Lemstra, A. W. , … Lötjönen, J. (2016). Differential diagnosis of neurodegenerative diseases using structural MRI data. NeuroImage: Clinical, 11, 435–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, D. , Cao, H. , Calhoun, V. D. , & Wang, Y. P. (2014). Sparse models for correlative and integrative analysis of imaging and genetic data. Journal of Neuroscience Methods, 237, 69–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litjens, G., Kooi, T., Bejnordi, B. E., Setio, A. A. A., Ciompi, F., Ghafoorian, M., … Sánchez, C. I. (2017). A survey on deep learning in medical image analysis. Medical Image Analysis, 42, 60–88. [DOI] [PubMed] [Google Scholar]
- Liu, S. , Liu, S. , Cai, W. , Che, H. , Pujol, S. , Kikinis, R. , … ADNI. (2015). Multimodal neuroimaging feature learning for multiclass diagnosis of Alzheimer's disease. IEEE Transactions on Biomedical Engineering, 62(4), 1132–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moradi, E. , Pepe, A. , Gaser, C. , Huttunen, H. , Tohka, J. , & Alzheimer's Disease Neuroimaging Initiative . (2015). Machine learning framework for early MRI‐based Alzheimer's conversion prediction in MCI subjects. NeuroImage, 104, 398–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosconi, L. , Tsui, W. H. , Herholz, K. , Pupi, A. , Drzezga, A. , Lucignani, G. , … de Leon, M. J. (2008). Multicenter standardized 18F‐FDG PET diagnosis of mild cognitive impairment, Alzheimer's disease, and other dementias. Journal of Nuclear Medicine, 49(3), 390–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mullins, R. J. , Mustapic, M. , Goetzl, E. J. , & Kapogiannis, D. (2017). Exosomal biomarkers of brain insulin resistance associated with regional atrophy in Alzheimer's disease. Human Brain Mapping, 38(4), 1933–1940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngiam, J., Khosla, A., Kim, M., Nam, J., Lee, H., & Ng, A. Y. (2011). Multimodal deep learning. Proceedings of the 28th international conference on machine learning (ICML‐11).
- Nie, F., Huang, H., Cai, X., & Ding, C. H. (2010). Efficient and robust feature selection via joint ℓ2, 1‐norms minimization. Advances in Neural Information Processing Systems, 1813–1821. [Google Scholar]
- Nordberg, A. , Rinne, J. O. , Kadir, A. , & Långström, B. (2010). The use of PET in Alzheimer disease. Nature Reviews Neurology, 6(2), 78–87. [DOI] [PubMed] [Google Scholar]
- Peng, J., An, L., Zhu, X., Jin, Y., & Shen, D. (2016). Structured sparse kernel learning for imaging genetics based Alzheimer's disease diagnosis. In International Conference on Medical Image Computing and Computer‐Assisted Intervention. Springer. [DOI] [PMC free article] [PubMed]
- Perrin, R. J. , Fagan, A. M. , & Holtzman, D. M. (2009). Multimodal techniques for diagnosis and prognosis of Alzheimer's disease. Nature, 461(7266), 916–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plis, S. M. , Hjelm, D. R. , Salakhutdinov, R. , Allen, E. A. , Bockholt, H. J. , Long, J. D. , … Calhoun, V. D. (2014). Deep learning for neuroimaging: A validation study. Frontiers in Neuroscience, 8, 229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price, A. L. , Patterson, N. J. , Plenge, R. M. , Weinblatt, M. E. , Shadick, N. A. , & Reich, D. (2006). Principal components analysis corrects for stratification in genome‐wide association studies. Nature Genetics, 38(8), 904–909. [DOI] [PubMed] [Google Scholar]
- Raamana, P. R. , Rosen, H. , Miller, B. , Weiner, M. W. , Wang, L. , & Beg, M. F. (2014). Three‐class differential diagnosis among Alzheimer disease, frontotemporal dementia, and controls. Frontiers in Neurology, 5, 71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raamana, P. R. , Weiner, M. W. , Wang, L. , Beg, M. F. , & Alzheimer's Disease Neuroimaging Initiative . (2015). Thickness network features for prognostic applications in dementia. Neurobiology of Aging, 36, S91–S102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen, P. M. , Hansen, L. K. , Madsen, K. H. , Churchill, N. W. , & Strother, S. C. (2012). Model sparsity and brain pattern interpretation of classification models in neuroimaging. Pattern Recognition, 45(6), 2085–2100. [Google Scholar]
- Rombouts, S. A., Barkhof, F., Goekoop, R., Stam, C. J., & Scheltens, P. (2005). Altered resting state networks in mild cognitive impairment and mild Alzheimer's disease: An fMRI study. Human Brain Mapping, 26(4), 231–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saykin, A. J. , Shen, L. , Foroud, T. M. , Potkin, S. G. , Swaminathan, S. , Kim, S. , … Alzheimer's Disease Neuroimaging Initiative . (2010). Alzheimer's disease neuroimaging initiative biomarkers as quantitative phenotypes: Genetics core aims, progress, and plans. Alzheimer's & Dementia, 6(3), 265–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidhuber, J. (2015). Deep learning in neural networks: An overview. Neural Networks, 61, 85–117. [DOI] [PubMed] [Google Scholar]
- Shen, D. , & Davatzikos, C. (2002). HAMMER: Hierarchical attribute matching mechanism for elastic registration. IEEE Transactions on Medical Imaging, 21(11), 1421–1439. [DOI] [PubMed] [Google Scholar]
- Shen, L. , Kim, S. , Risacher, S. L. , Nho, K. , Swaminathan, S. , West, J. D. , … Alzheimer's Disease Neuroimaging Initiative . (2010). Whole genome association study of brain‐wide imaging phenotypes for identifying quantitative trait loci in MCI and AD: A study of the ADNI cohort. NeuroImage, 53(3), 1051–1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen, L., Thompson, P. M., Potkin, S. G., Bertram, L., Farrer, L. A., Foroud, T. M., … Kauwe, J. S. (2014). Genetic analysis of quantitative phenotypes in AD and MCI: Imaging, cognition and biomarkers. Brain Imaging and Behavior, 8(2), 183–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sled, J. G. , Zijdenbos, A. P. , & Evans, A. C. (1998). A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Transactions on Medical Imaging, 17(1), 87–97. [DOI] [PubMed] [Google Scholar]
- Sørensen, L. , Igel, C. , Pai, A. , Balas, I. , Anker, C. , Lillholm, M. , … Alzheimer's Disease Neuroimaging Initiative and the Australian Imaging Biomarkers and Lifestyle flagship study of ageing (2017). Differential diagnosis of mild cognitive impairment and Alzheimer's disease using structural MRI cortical thickness, hippocampal shape, hippocampal texture, and volumetry. NeuroImage: Clinical, 13, 470–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava, N. and Salakhutdinov R. R. (2012). Multimodal learning with deep boltzmann machines. Advances in neural information processing systems.
- Suk, H. I., Lee, S. W., Shen, D., & Alzheimer's Disease Neuroimaging Initiative. (2014). Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. NeuroImage, 101, 569–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk, H.‐I. , et al. (2015). Latent feature representation with stacked auto‐encoder for AD/MCI diagnosis. Brain Structure and Function, 220(2), 841–859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thung, K.‐H. , Wee, C. Y. , Yap, P. T. , Shen, D. , & Alzheimer's Disease Neuroimaging Initiative . (2014). Neurodegenerative disease diagnosis using incomplete multi‐modality data via matrix shrinkage and completion. NeuroImage, 91, 386–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thung, K. H., Wee, C. Y., Yap, P. T., & Shen, D. (2016). Identification of progressive mild cognitive impairment patients using incomplete longitudinal MRI scans. Brain Structure and Function, 221(8), 3979–3995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thung, K.‐H. , Yap, P. T. , Adeli, E. , Lee, S. W. , Shen, D. , & Alzheimer's Disease Neuroimaging Initiative . (2018). Conversion and time‐to‐conversion predictions of mild cognitive impairment using low‐rank affinity pursuit denoising and matrix completion. Medical Image Analysis, 45, 68–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thung, K. H., Yap, P. T., & Shen, D. (2017). Multi‐stage diagnosis of Alzheimer's disease with incomplete multimodal data via multi‐task deep learning In Deep learning in medical image analysis and multimodal learning for clinical decision support (pp. 160–168). Quebec City, Canada: Springer. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan, J., Zhang, Z., Yan, J., Li, T., Rao, B. D., Fang, S., … Shen, L. (2012). Sparse Bayesian multi‐task learning for predicting cognitive outcomes from neuroimaging measures in Alzheimer's disease. Computer Vision and Pattern Recognition (CVPR), 2012 I.E. Conference on,16‐21 June 2012, Providence, RI, USA: IEEE.
- Wang, H. , Nie, F. , Huang, H. , Risacher, S. L. , Saykin, A. J. , Shen, L. , & For the Alzheimer's Disease Neuroimaging Initiative . (2012). Identifying disease sensitive and quantitative trait‐relevant biomarkers from multidimensional heterogeneous imaging genetics data via sparse multimodal multitask learning. Bioinformatics, 28(12), i127–i136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, Y. , Nie, J. , Yap, P. T. , Li, G. , Shi, F. , Geng, X. , … for the Alzheimer's Disease Neuroimaging Initiative . (2014). Knowledge‐guided robust MRI brain extraction for diverse large‐scale neuroimaging studies on humans and non‐human primates. PLoS One, 9(1), e77810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee, C. Y., Yap, P. T., Denny, K., Browndyke, J. N., Potter, G. G., Welsh‐Bohmer, K. A., … Shen, D. (2012). Resting‐state multi‐spectrum functional connectivity networks for identification of MCI patients. PloS one, 7(5), e37828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wold, S. , Esbensen, K. , & Geladi, P. (1987). Principal component analysis. Chemometrics and Intelligent Laboratory Systems, 2(1–3), 37–52. [Google Scholar]
- Yu Zhang, e. a. (2018). Strength and similarity guided group‐level brain functional network construction for MCI diagnosis. Pattern Recognition . [DOI] [PMC free article] [PubMed]
- Yuan, L. , Wang, Y. , Thompson, P. M. , Narayan, V. A. , Ye, J. , & Alzheimer's Disease Neuroimaging Initiative . (2012). Multi‐source feature learning for joint analysis of incomplete multiple heterogeneous neuroimaging data. NeuroImage, 61(3), 622–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, D. , Shen, D. , & Alzheimer's Disease Neuroimaging Initiative . (2012). Multi‐modal multi‐task learning for joint prediction of multiple regression and classification variables in Alzheimer's disease. NeuroImage, 59(2), 895–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Y. , Brady, M. , & Smith, S. (2001). Segmentation of brain MR images through a hidden Markov random field model and the expectation‐maximization algorithm. IEEE Transactions on Medical Imaging, 20(1), 45–57. [DOI] [PubMed] [Google Scholar]
- Zhang, Y. , Zhang, H. , Chen, X. , Lee, S. W. , & Shen, D. (2017). Hybrid high‐order functional connectivity networks using resting‐state functional MRI for mild cognitive impairment diagnosis. Scientific Reports, 7(1), 6530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, C., Adeli, E., Zhou, T., Chen, X., & Shen, D. (2018). Multi‐Layer Multi‐View Classification for Alzheimer's Disease Diagnosis. [PMC free article] [PubMed]
- Zheng, X., Shi, J., Li, Y., Liu, X., & Zhang, Q. (2016). Multi‐modality stacked deep polynomial network based feature learning for Alzheimer's disease diagnosis. Biomedical Imaging (ISBI), 2016 I.E. 13th International Symposium on, IEEE.
- Zhou, S. K., Greenspan, H., & Shen, D. (2017). Deep learning for medical image analysis. Cambridge, Massachusetts: Academic Press. [Google Scholar]
- Zhou, T., Thung, K. H., Zhu, X., & Shen, D. (2017). Feature learning and fusion of multimodality neuroimaging and genetic data for multi‐status dementia diagnosis In International Workshop on Machine Learning in Medical Imaging (pp. 132–140). Springer, Cham. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, T., Thung, K. H., Liu, M., & Shen, D. (2018). Brain‐wide genome‐wide association study for Alzheimer's disease via joint projection learning and sparse regression model. IEEE Transactions on Biomedical Engineering, in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, X. , Suk, H. I. , Lee, S. W. , & Shen, D. (2016). Subspace regularized sparse multitask learning for multiclass neurodegenerative disease identification. IEEE Transactions on Biomedical Engineering, 63(3), 607–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, X. , Suk, H. I. , Wang, L. , Lee, S. W. , Shen, D. , & Alzheimer's Disease Neuroimaging Initiative . (2017). A novel relational regularization feature selection method for joint regression and classification in AD diagnosis. Medical Image Analysis, 38, 205–214. [DOI] [PMC free article] [PubMed] [Google Scholar]


