Evaluating the organizational structure and specificity of network topology within the face processing system

Abstract

There is increasing appreciation that network‐level interactions among regions produce components of face processing previously ascribed to individual regions. Our goals were to use an exhaustive data‐driven approach to derive and quantify the topology of directed functional connections within a priori defined nodes of the face processing network and evaluate whether the topology is category‐specific. Young adults were scanned with fMRI as they viewed movies of faces, objects, and scenes. We employed GIMME to model effective connectivity among core and extended face processing regions, which allowed us to evaluate all possible directional connections, under each viewing condition (face, object, place). During face processing, we observed directional connections from the right posterior superior temporal sulcus to both the right occipital face area and right fusiform face area (FFA), which does not reflect the topology reported in prior studies. We observed connectivity between core and extended regions during face processing, but this limited to a feed‐forward connection from the FFA to the amygdala. Finally, the topology of connections was unique to face processing. These findings suggest that the pattern of directed functional connections within the face processing network, particularly in the right core regions, may not be as hierarchical and feed‐forward as described previously. Our findings support the notion that topologies of network connections are specialized, emergent, and dynamically responsive to task demands.

1. INTRODUCTION

There are thousands of empirical papers investigating the neural basis of face processing, the vast majority of which disproportionately focus on understanding the distinct functional properties of individual regions in the occipito‐temporal cortex, like the occipital face area (OFA; Gauthier et al., 2000) and fusiform face area (FFA; Kanwisher, McDermott, & Chun, 1997). There is an increasing appreciation for the network‐level interactions among these regions that produce the seemingly independent components of face perception previously ascribed to individual regions (e.g., Avidan et al., 2014; Dima, Stephan, Roiser, Friston, & Frangou, 2011; Ewbank et al., 2013; Goulden et al., 2012; Herrington, Taylor, Grupe, Curby, & Schultz, 2011; Joseph et al., 2012; Nagy, Greenlee, & Kovács, 2012; Summerfield et al., 2006). The goal of this article was to investigate the nature of these interactions and understand whether they are specific to the condition of viewing faces or vary in response to viewing other visual categories. To do so, we localized neural regions that are optimized for face processing and used a data‐driven approach to derive and quantify the topology of directed functional connections among these regions. We also evaluated whether the derived topology is category‐specific and consistent with long‐standing models of the neural basis of face processing.

The notion that the neural basis of face processing is instantiated via a distributed system of networked neural regions was articulated in a functional model nearly 20 years ago (Haxby et al., 2000). Inspired by the Bruce and Young (1986) cognitive model of face perception, Haxby and colleagues proposed that cognitively distinct aspects of face perception are supported by distinct neural systems that are organized hierarchically (see Figure 1a). Specifically, they proposed that the structural visual analysis of faces is processed by core regions (black regions in Figure 1a), including portions of the inferior occipital gyri (IOG), lateral fusiform gyri (FG), and the superior temporal sulcus (STS). They suggested that based on its anatomical location, the IOG likely provides input to the entire system. Furthermore, Haxby and colleagues proposed that extended regions (Figure 1a, blue) work in concert with the core regions to process the significance of information gleaned from the face (e.g., emotional tone of an expression, eye gaze direction; Haxby et al., 2000). These regions include the intraparietal sulcus (IPS), auditory cortex, amygdala, insula, limbic system, and anterior temporal cortex. The model was later modified to accommodate findings regarding familiar face recognition, which resulted in the inclusion of new regions and further functional organization within the model (Gobbini & Haxby, 2007). The extended system became subdivided into a person knowledge subsystem, which includes the anterior paracingulate cortex, posterior STS, anterior temporal cortex and precuneus/posterior cingulate gyrus, and an emotion subsystem, which includes the amygdala, insula, and the striatum. The authors proposed bidirectional interactions between these subsystems. Together, these two papers have been cited nearly 2,500 times, which reflects the influential nature of this functional model of face perception.

Figure 1.

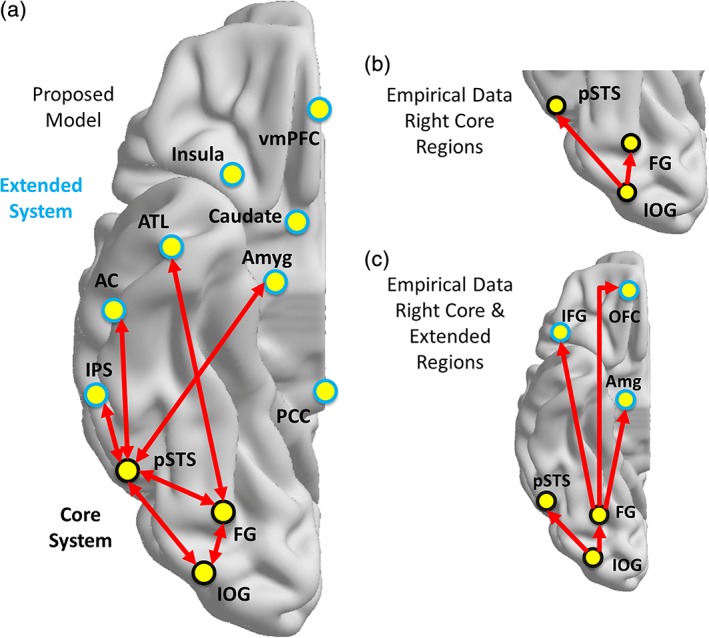
Models of functional organization within face processing network. Proposed organization of connectivity within face processing regions as defined by Haxby et al. (2000) and Gobbini and Haxby (2007) (a). Empirical findings of directed functional connections elicited during face viewing by Fairhall and Ishai (2007) among core regions (b) and core and extended regions (c) of the face processing network in the right hemisphere. Abbreviations: IOG = inferior occipital gyrus; FG = fusiform gyrus; pSTS = posterior superior temporal sulcus; IPS = intraparietal sulcus; AC = auditory cortex; ATL = anterior temporal lobe; Amyg = amygdala, IFG = inferior frontal gyrus; OFC = orbitofrontal cortex [Color figure can be viewed at http://wileyonlinelibrary.com]

Fairhall and Ishai (2007) provided some of the earliest empirical testing of the proposed organization of this functional model using effective connectivity (EC) analyses of fMRI time series data. EC reflects the influence that one neural system has over another and is measured using model parameters that explain these observed dependencies (Friston, 2011). This is in contrast to the more common approach of measuring functional connectivity, or the statistical dependence (i.e., temporal synchrony) in fMRI time series data, which is commonly quantified using correlation. Importantly, EC is dynamic, activity‐dependent, and depends on a model of interactions (Friston, 2011). Relevant to the current work, Fairhall and Ishai addressed two main questions about the functional organization of the face perception system, namely: what is the functional organization within the core system; and, how does the core system interact with the extended system? Fairhall and Ishai tested 24 models (feedforward, recurrent) separately in each hemisphere to evaluate the functional organization of the core system with the IOG as the only source of input to the other regions (FG, STS). They reported that the model in which the IOG influences both the FG and STS best characterized the data (see Figure 1b). To evaluate the patterns of connections between the core and extended regions, they modeled connections between the FG and amygdala, inferior frontal gyrus (IFG) and orbitofrontal cortex (OFC) and separately between the STS and these same extended regions under different task conditions. They reported that the model with feedforward connections between the FG and the extended regions best fit the data (see Figure 1c).

For more than a decade, these findings have had a lasting influence on the subsequent work investigating the topological organization of directed functional connections within the face processing network. Table 1 represents a summary of the existing studies using EC analyses to investigate the functional organization within some portion of the face processing network. There are two important things to note across studies. First, 32% of the studies focused exclusively on functional organization within the core regions alone. As a result, there is limited empirical testing of the predictions about the interactions between the core and extended regions and within the extended regions of functional face perception system. Second, and perhaps more importantly, only 64% of the studies empirically measured the functional organization of directed functional connections within this network. Note too that there is variability in the selected regions of interest and little convergence regarding the pattern of directional connections among these regions. The remaining 36% of existing studies assumed, rather than empirically determined, the functional network organization of directed connections within their sample. Specifically, these studies all presume similar versions of the hierarchical, feedforward topology reported by Fairhall and Ishai (2007).

Table 1.

Studies investigating effective connectivity in the face processing system organized chronologically

Study	N	Groups	Core regions	Extended regions	Other regions	Discover topology
Summerfield et al. (2006)	NR	NR	r IOG r FFA	r Amyg	r MFC	No
Fairhall and Ishai (2007)	10	TD	r/l IOG r/l FG r/l STS	r/l Amyg	r/l IFG mid OFC	Yes
Almeida et al. (2011)	38	MDD TD		r/l Amyg r/l vmPFC	r/l ACC	No
Cohen Kadosh, Kadosh, Dick, and Johnson (2011)	14	TD	r IOG r FG r STS			No
Dima et al. (2011)	40	TD	r IOG r FG	r Amyg	r IFG	No
Herrington et al. (2011)	39	TD	r/l IOG r/l FG	r/l Amyg		Yes
Goulden et al. (2012)	43	MDD TD	r V1 r FG	r Amyg	r LFC	Yes
Nagy et al. (2012)	25	TD	r OFA r FFA		r LO	Yes
Ewbank et al. (2013)	26	TD	r OFA r FFA			Yes
Furl, Henson, Friston, and Calder (2013)	18	TD	r OFA r FFA r STS	r Amyg	r V5f	Yes
Yu, Zhou, and Zhou (2013)	18	TD		r Amyg vmPFC	r NAcc	Yes
Nguyen, Breakspear, and Cunnington (2014)	24	TD	r OFA r FFA r STS		r mFG	Yes
Furl, Henson, Friston, and Calder (2015)	18	TD	r OFA r FFA r STS		BA18 V5	Yes
He, Garrido, Sowman, Brock, and Johnson (2015)	14	TD	r/l OFA r/l FFA r/l STS			Yes
Lamichhane and Dhamala (2015)	33	TD	r FFA		l PPA r dlPFC	Yes
Xiu et al. (2015)	18	TD	l IOG l FG	l Amyg	l Hipp l SPL l OFC	No
Frässle, Paulus, Krach, and Jansen (2016)	25	TD	r/l OFA r/l FFA		r/l V1	No
Frässle, Paulus, Krach, Schweinberger, et al. (2016)	20	TD	r/l OFA r/l FFA		r/l V1	Yes
Lohse et al. (2016)	30	TD CP	r OFA r/l FFA r STS	l ATL	EVA	No
Minkova et al. (2017)	30	TD SAD		r/l Amyg	OFC	No
He and Johnson (2018)	11	TD	r/l OFA r/l FFA r/l STS			Yes

NR = not reported; CP = congenital prosopagnosia; MDD = major depressive disorder; SAD = seasonal affective disorder; TD = typically developing; FFA = fusiform face area; OFA = occipital face area; STS = superior temporal sulcus; Amyg = amygdala; MFC = medial frontal cortex; IFG = inferior frontal gyrus; OFC = orbitofrontal cortex; vmPFC = ventromedial frontal cortex; ACC = anterior cingulate cortex; LFC = lateral frontal cortex; LO = lateral occipital complex; NAcc = nucleus accumbens; mFG = medial frontal gyrus; PPA = parahippocampal place area; dlPFC = dorsolateral prefrontal cortex; IOG = inferior occipital gyrus; FG = fusiform gyrus; Hipp = hippocampus; SPL = superior parietal lobule; ATL = anterior temporal lobe; EVA = early visual area.

Note. Studies are organized by year and then alphabetically. Studies that discover network topologies are those that empirically test for the topology, usually against a set of a priori determined models using Dynamic Causal Modeling. Studies that do not discover the network topology presume a model structure and then test modulation of the hypothesized network connections under different task conditions.

The reason this is noteworthy is that while the Fairhall and Ishai (2007) study was foundational, there are important limitations about the study that contextualize the findings. First, the initial analyses and model testing of the functional architecture among the core regions was evaluated on data from 10 adults and the model testing of the functional architecture between the core and extended regions was evaluated on data from five adults. As a result, it is critical that these findings be empirically investigated in other, larger samples to determine convergence in findings. Second, to compare different models of functional architecture within the face perception network, the authors used Dynamic Causal Modeling (DCM; Friston, Harrison, & Penny, 2003). DCM is a tool specifically designed for estimating EC among fMRI time series data. To empirically compare potential functional architectures of a neural system, this approach requires one to specify the models (each node and directional connection) to be tested a priori; it does not do a comprehensive comparison of all possible model structures unless they are all specified a priori (Smith et al., 2011). A consequence of this approach is that the true best model of directed functional connections may be one that was not included in the original 24 that were tested by Fairhall and Ishai (2007). Importantly, no existing study evaluating EC in the face processing network has used an approach with an exhaustive model search. Therefore, there remains a potential gap in understand about the topologic architecture of functional connections within the face processing system.

Our goal in the current work was to assess the functional architecture within the face perception system using a data‐driven approach with an exhaustive model search procedure in a larger sample and, in so doing, determine whether we generate findings that reflect predictions from the models articulated by Haxby and colleagues (Gobbini & Haxby, 2007; Haxby et al., 2000). We approached this work with three central questions. First, do we discover the same hierarchical, feedforward topology that was originally reported by Fairhall and Ishai (2007) using a computational approach that enables us to investigate all possible feedforward and feedback connections among the nodes of the core system? Second, what is the organizational structure of the functional network architecture between the core and extended regions? Specifically, what are the interactions between the core and person versus emotion subsystems within the extended system? Third, how specific is the functional network architecture among these regions during face processing compared to during processing of other kinds of visual objects? To address these questions, we included both unfamiliar and familiar face stimuli to identify the core and extended regions in the face processing network, including the bilateral FFA, right OFA, bilateral STS, posterior cingulate cortex (PCC), ventromedial prefrontal cortex (vmPFC), bilateral amygdala, and bilateral caudate nuclei. We investigated whether the brain responds with similar or different topology of directed functional connections among the core and extended face processing regions in response to perceiving faces, places, and objects.

2. MATERIALS AND METHODS

2.1. Participants

Typically developing young adults (N = 40, range = 18–26 years, 20 females) participated in the experiment. Participants were healthy and had no history of neurological or psychiatric disorders in themselves or their first‐degree relatives. They were also screened for behavioral symptoms indicative of undiagnosed psychopathology. They had normal or corrected vision, no history of head injuries or concussions, and were right handed. Written informed consent was obtained using procedures approved by the Internal Review Board of the Pennsylvania State University. Participants were recruited through the Psychology Department undergraduate subject pool and via fliers on campus. Univariate analyses of these neuroimaging data and associations between region of interest measures and behavioral performance have been reported previously (Elbich & Scherf, 2017). However, no connectivity analyses of these data have been reported prior to this work.

2.2. Experimental procedure

Prior to scanning, all participants were placed in a mock MR scanner for approximately 20 min and practiced lying still. This procedure is highly effective at acclimating participants to the scanner environment and minimizing motion artifact and anxiety (see Scherf, Elbich, Minshew, & Behrmann, 2015). The visual stimulation task has been described in previous publications (Elbich & Scherf, 2017); briefly, the task included blocks of silent, fluid concatenations of short movie clips from four conditions: novel faces, famous faces, common objects, and navigational scenes. The task was organized into twenty four 16‐s stimulus blocks (six per condition). The order of the stimulus blocks was randomized for each participant. Fixation blocks (6 s) were interleaved between task blocks, resulting in a total task time of 9 min and 24 s.

2.3. Image acquisition

Functional EPI images were acquired with prospective acquisition correction (PACE) framework for functional MRI (Thesen, Heid, Mueller, & Schad, 2000). In PACE, each 3D volume is registered to the reference image directly at the scanner. This information is provided to the console to update the scanning parameters online. PACE is the only technique for fMRI applications that allows for adequate correction of spin‐history effects (Yancey et al., 2011) and intra‐volume distortions (Speck, Henning, & Zaitsev, 2006). The use of prospective motion correction via PACE together with retrospective motion correction is superior in fMRI analyses to either alone (see Zaitsev, Akin, LeVan, & Knowles, 2017). The functional data were collected in thirty four 3 mm‐thick slices that were aligned approximately 30° perpendicular to the hippocampus, which is effective for maximizing signal‐to‐noise ratios in the medial temporal lobes (Whalen et al., 2008). This scan protocol allowed for complete coverage of the medial and lateral temporal lobes, frontal, and occipital lobes. The scan parameters were as follows; TR = 2,000 ms; TE = 25; flip angle = 80°, FOV = 210 × 210, 3 mm isotropic voxels. Anatomical images were also collected using a 3D‐MPRAGE with one hundred seventy six 1 mm³, T1‐weighted, straight sagittal slices (TR = 1,700; TE = 1.78; flip angle = 9°; FOV = 256).

2.4. Image data processing

Imaging data were analyzed using Brain Voyager QX version 2.3 (Brain Innovation, Maastricht, The Netherlands). Preprocessing of functional data included 3D‐motion correction, slice scan time correction, and filtering out low frequencies (three cycles). Given empirical findings that global signal and tissue‐based regressors can induce distant‐dependent biases in functional connectivity analyses (Ciric et al., 2017; Jo et al., 2013), we did not include these regressors in our preprocessing pipeline.

Only participants who exhibited maximum motion of less than 2/3 voxel in all six directions (i.e., no motion greater than 2.0 mm in any direction on any image) were included in the fMRI analyses. No participants were excluded due to excessive motion. In addition, we evaluated whether there were any differences in motion as a function of viewing condition, which might influence the patterns of connectivity. To do so, we computed the mean relative framewise displacement (FD) for each viewing condition separately and submitted these scores to a repeated‐measures ANOVA. There was no significant difference in motion across the conditions, F(2, 78) = 0.60, p > 0.10. Nonetheless, we centered the mean relative FD and entered it as a covariate in the subsequent analyses investigating differences in the topology of the network organization across viewing condition.

For each participant, the time series images for each brain volume were analyzed for condition differences (faces, objects, navigation) in a fixed‐factor GLM. Each condition was defined as a separate predictor with a box‐car function adjusted for the delay in the hemodynamic response using a double gamma function. The time series images were then spatially normalized into Talairach space. The functional images were not spatially smoothed in line with suggestions for processing ROIs in close proximity to one another (see Weiner & Grill‐Spector, 2011) and for extracting time series data from small anatomical regions like the amygdala and caudate nuclei.

2.5. Defining network nodes and extracting time series

2.5.1. Defining regions of interest for the network analyses

The fMRI time series data were extracted from each ROI in each participant in a two‐step process. The search space for the ROIs was initially defined by identifying face‐selective activation at the group level using a whole brain voxelwise random effects GLM that included all participants, in which visual category (famous faces, novel faces, navigation, objects) was a fixed factor and participant was a random factor. Face‐selective activation was defined by the contrast [Famous+Novel Faces] > [Objects+Navigation]. The group map was corrected for false positive activation at the whole brain level using the False Discovery Rate of q < 0.001 (Genovese, Lazar, & Nichols, 2002). Based on this group map, the following face‐related functional ROIs were defined bilaterally, FFA, OFA, PSTS, amygdala, caudate nucleus, and face‐related activation in the vmPFC and PCC were defined on the midline. The cluster of contiguous voxels nearest the classically defined FFA (i.e., Talairach coordinates right: 40, −41, −21, left: −38, −44, −19) in the middle portion of the gyrus was identified as the pFus‐faces/FFA1 (Weiner et al., 2014). We defined the OFA as the set of contiguous voxels on the lateral surface of the occipital lobe closest to our previously defined adult group level coordinates (right: 50, −66, −4, left: −47, −70, 6) (Scherf, Behrmann, Humphreys, & Luna, 2007). The posterior superior temporal sulcus (pSTS) was defined as the set of contiguous voxels within the horizontal posterior segment of the superior temporal sulcus (right: 53, −50, 11; left: −53, −52, 14) that did not extend into the ascending posterior segment of the STS. The most anterior boundary of the pSTS was where the ascending segment of the IPS intersected the lateral fissure. The PCC was defined as the cluster of voxels in the posterior cingulate gyrus above the splenium of the corpus callosum near the coordinates reported previous in studies of face processing (0, −51, 23) (Schiller, Freeman, Mitchell, Uleman, & Phelps, 2009). The vmPFC was defined as the cluster of voxels in the medial portion of the superior frontal gyrus ventral to the cingulate gyrus near coordinates reported in previous studies of social components of face processing (0, 48, −8) (Schiller et al., 2009). The amygdala was defined as the cluster of face‐selective voxels within the gray matter structure. Any active voxels that extended beyond the structure out to the surrounding white matter, horn of the lateral ventricle, or hippocampus were excluded. For the caudate nuclei, we only defined face‐selective voxels in the head of the nucleus bilaterally. This included voxels in the gray‐matter structure that did not extend into the adjacent lateral ventricle or white matter in the anterior limb of the internal capsule.

Second, to individualize and optimize the signal for each participant, we then identified the most face‐selective set of voxels within each of these group‐defined ROIs for each participant individually. For each subject, we computed a voxelwise fixed‐factor GLM and defined face‐related activation using the same contrast ([Famous+Novel Faces] > [Objects+Navigation]). Within each group‐defined ROI, we identified the peak face‐selective voxel for each participant and extract the average time series from this voxel and the surrounding 6 mm volumetric sphere. Finally, the mean time series from all the voxels in the 6 mm sphere was extracted for the EC analyses. Because the amygdalae and caudate nuclei are small structures, we also constrained the search space for the peak voxels so that the sphere would be contained within the neuroanatomy (and not extend outside the nuclei). Importantly, none of the resulting ROIs shared overlapping voxels; therefore, the time series data come from independent sets of voxels in each person. In this way, all participants have optimized data that contributed to the EC analyses. Table 2 reports the mean and standard deviation of the centroid of each individualized ROI across participants.

Table 2.

Average coordinates of individual subject regions of interest used for connectivity analyses

	Mean region coordinates (SD)
Category	ROI	X	Y	Z
Core regions	R FFA	37 (2)	−45 (5)	−17 (3)
	L FFA	−40 (1)	−43 (6)	−19 (3)
	R OFA	50 (4)	−61 (6)	6 (4)
	R pSTS	48 (6)	−39 (5)	5 (5)
	L pSTS	−58 (4)	−40 (6)	4 (4)
Extended regions	vmPFC	0 (5)	46 (6)	−9 (4)
	PCC	2 (3)	−53 (4)	22 (5)
	R Amyg	17 (2)	−7 (2)	−11 (1)
	L Amyg	−20 (2)	−8 (2)	−11 (2)
	R caudate	11 (2)	2 (5)	15 (6)
	L caudate	−12 (3)	4 (4)	12 (6)

2.5.2. Extracting time series data

Visual category‐specific time series data were extracted from each of the ROIs described above. To generate category‐specific time series data, rather than splice sections of the time series and concatenate them together, which disrupts the HRF, we modeled the interaction between the time series and each visual category separately, much like modeling a psychophysiological interaction (Friston et al., 1997; Gitelman, Penny, Ashburner, & Friston, 2003). For each participant, this process involved mean correcting the raw time series from each ROI, which normalized these data for mean differences in overall activation across individuals and ROIs. Critically, this prevents any differences in mean activation from contributing to differences in connectivity patterns. Next, the time series were deconvolved with a gamma function to model the HRF using AFNI 3dTfitter. We multiplied the deconvolved time series by the category specific time series and reconvolved the resulting interaction time series with a gamma HRF function to transform it back into the HRF domain. We did this separately for each of the three visual categories to make separate face, object, and place time series for each ROI.

Prior to submitting the time series data to GIMME, we evaluated the distributions of the time series data from each ROI in each viewing condition for violations of normality. Both the skew (−3 < × < 3) and kurtosis (−10 < × < 10) were within the tolerable ranges as recommended by Klein (2005), with the exception of the right STS during place viewing, which had high kurtosis. Importantly, GIMME can reliably recover effects when data are either normally distributed or have a skewed distribution (Henry & Gates, 2017) and empirical analyses indicate that the fit indices that we employed to evaluate GIMME (i.e., unified SEM) are robust to high kurtosis (see Lei & Lomax, 2005).

2.6. Modeling effective connectivity

We used Group Iterative Multiple Model Estimation (GIMME) to model EC within the face processing system (Gates & Molenaar, 2012). Briefly, GIMME employs unified structural equation modeling (Kim, Zhu, Chang, Bentler, & Ernst, 2007) to model both lagged (across TR) and contemporaneous (within TR) effects, both of which exist in fMRI data and need to be accounted for to decrease biases in estimates (Gates et al., 2010). In this data‐driven procedure, a null network (i.e., no connections) is initially created for all subjects. Any single directional connection is only opened into the model if it significantly improves the model fit for a majority of subjects (Gates & Molenaar, 2012). In this data set, we used an 80% criterion so that each connection that survives at the group level must be present in a minimum of 32 of 40 participants. Once the group model is determined, it is used as a prior for each individual subject model, which undergoes its own model fit procedure. This process greatly improves the recovery of true connections and determination of the direction of connections compared to traditional approaches for individual‐level analyses (Gates & Molenaar, 2012; Smith et al., 2011). Critically, no model structures have to be designated a priori for comparison. The model tests all possible model structures in a comprehensive way and overfitting is heavily protected via minimally parameterized models (see Gates & Molenaar, 2012). GIMME is freely available as an R package (gimme; Lane et al., 2015). For each participant, in each viewing condition, each model output included a directed adjacency matrix that represented the presence or absence of each directional connection and its corresponding strength (i.e., beta weight) (see Figure 2). Nonexistent connections were assigned a beta weight of 0.

Figure 2.

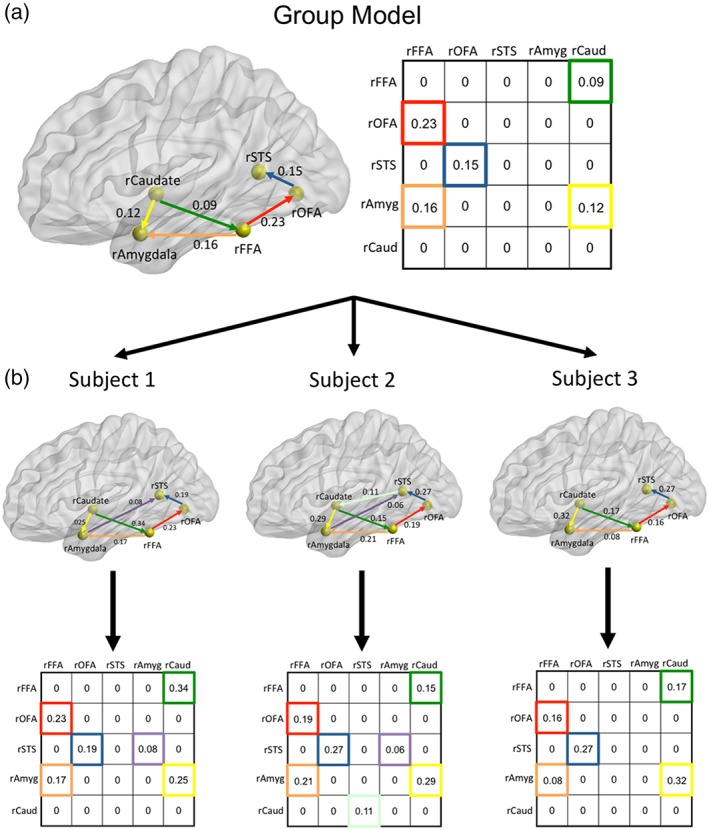
Method for deriving group and individual participant network structures using GIMME. Network map in (a) depicts an example model network with five regions for illustrative purposes. Group (a) and individual participant (b) directional connections are both derived from the GIMME analyses. The directed adjacency matrices reflect beta weights for each directional connection with the horizontal axis as the point of origin of the connection and the vertical axis as the point of destination of each connection. Note that the two sides of each matrix are not symmetrical because these are not correlational matrices; they are directed adjacency matrices. The beta weights from the individual subject adjacency matrices were submitted to the pattern analyses. Glass brain rendered using BrainNet Viewer (Xia, Wang, & He, 2013) [Color figure can be viewed at http://wileyonlinelibrary.com]

To evaluate the validity of GIMME for discovering directed functional connections in these time series data, we compared the models generated with the original time series data to null models. The null models were created by disrupting the temporal structure of the original time series fMRI data and submitting these data to the same GIMME analyses. To temporally disrupt the time series data, we phase‐shifted and randomized them (Liu & Molenaar, 2016). Specifically, for each participant the time series data from each ROI was Fourier transformed into the frequency domain. Next, we added a random number taken from a distribution of [−π, π] to all values in the newly transformed time series. The transformed data were Fourier transformed back into the time domain. These time series data were submitted to GIMME and evaluated for model fit. We predicted that the null models would have worse model fit indices compared to models derived from the temporally structured original data.

2.7. Data analyses

The analyses are organized to address the three central questions of the paper. For each analysis, we submitted phase‐shifted, randomized time series data to the same analyses to compare fit indices across participants.

Question 1: What is the Topology of Directed, Functional Connections within the Right Core Face Processing Regions?

To evaluate the topological architecture of directed functional connections within the right core regions, we submitted the time series data during face viewing from the right OFA, FFA1, and pSTS to the GIMME model.

Question 2a: What is the Topology of Directed, Functional Connections between the Right Core and Extended (Emotion vs Person) Sub‐Systems?

We conducted this analysis in a multistep process because we were interested in evaluating the potential patterns of connections between the core regions and each proposed subsystem (emotion, person) of the extended system. First, we evaluated the patterns of connections between the core and emotion subsystem by submitting the time series data during face viewing from the right OFA, FFA1, pSTS, right amygdala, and right caudate nucleus to the GIMME model. Second, we evaluated the patterns of connections between the core and person knowledge subsystem by submitting the time series data during face viewing from the right OFA, FFA1, pSTS, vmPFC, and PCC to the GIMME model.

Question 2b: What is the Topology of Directed, Functional Connections between the Bilateral Core & Extended System

Finally, to evaluate the pattern of connections in the fullest model of core and extended regions, we evaluated the topology of directed functional connections between right OFA, bilateral FFA1, pSTS, caudate nuclei, amygdala, vmPFC, PCC, during face viewing in the GIMME model.

Question 3: Is there Specificity in the Topology of Directed, Functional Connections within the Face Processing System?

To address this question, we derived models of EC for each of three viewing conditions (faces, places, objects) across the full set of 11 ROIs (bilateral core and extended regions). To empirically evaluate potential differences in the functional network architecture across viewing conditions, we employed pattern analytic methods. This analysis incorporates information about both the direction and weight of connections when comparing the overall patterns of the neural network topology. The strategy of the analysis was to quantify how different each participant's network topology is from the group mean map in each viewing condition. The underlying assumption is that if there is homogeneity in network organization during face viewing, participants will have similar network topology and similar maps to the group mean generated during face viewing. In contrast, if the network organization generated during object viewing is fundamentally different than during face viewing, there will be more heterogeneity in network organization when comparing individual subject face network topology to the group mean map generated during object viewing. These differences in network organization can be quantified in terms of Euclidean distances (ED) from the group mean map. Larger EDs indicate more heterogeneity and difference in overall network topology from the reference mean map.

To conduct these analyses, we vectorized each individual participant's adjacency matrix from each category‐specific neural network (face, place, object) separately. This generated three separate vectors of 121 (11 × 11 ROIs) units. Importantly, each vector preserved the pattern of weighted, directional connections representing the topology of network organization during each viewing condition. Next, we generated and vectorized 40 group mean vectors for each viewing condition that included n‐1 participants. This allowed us to compute the ED between each individual subject's category‐specific vector (i.e., pattern of weighted directed connections) and an independent group mean vector using the following equation:

$$\sum _{j=1}^{121}{\left(y_{\mathit{ji}}-u_j\right)}^2$$

where “y” is the subject beta vector, “u” is an independently defined group mean beta vector for each subject, “i” denotes the subject, and “j” is the connection (Deza & Deza, 2014). Specifically, for each subject, an ED was computed for each connection between the individual subject connection and the independent group mean connection across the entire pattern and then summed across all 121 connections. The EDs were then averaged across participants. EDs were computed within each visual category (e.g., individual subject face networks compared to group mean face network) and between visual categories (e.g., individual subject face networks compared to group mean object and place networks).

Given that we optimized this network to evaluate face processing in terms of the selected ROIs, we predicted that the network topology for face viewing would be unique and homogenous across subjects compared the network architecture elicited during object or place viewing. To test this hypothesis, we evaluated whether the EDs comparing individual subject topologies to the group mean topology for face viewing were smaller than the EDs comparing individual face networks to the group mean topology for the two other viewing conditions (i.e., places, objects). We submitted the ED scores from the three comparisons to a repeated‐measures ANCOVA, including the centered mean relative framewise displacement as the covariate, and conducted Bonferroni corrected post hoc tests to determine which of the EDs were different from each other. We did this for both the core model and the bilateral core and extended models separately. In addition, to evaluate whether the network organization elicited during object and/or place viewing was unique and homogenous, we conducted the same analyses for the vectors generated during object and place viewing as well.

3. RESULTS

3.1. What is the topology of directed functional connections within right core face processing regions?

Using the data‐driven approach to deriving the topology of network connections, we uncovered a different pattern of directed functional connections than has been previously reported. During face viewing, the most reliable connections across individuals originated from the pSTS to both the FFA and OFA (see Figure 3). Importantly, these group‐level connections did not arise as a result of fitting noise in the data. Recall that we used an 80% criterion in the group model which reflects that a minimum of 32 of 40 participants had to have each of these connections to survive in the group model.

Figure 3.

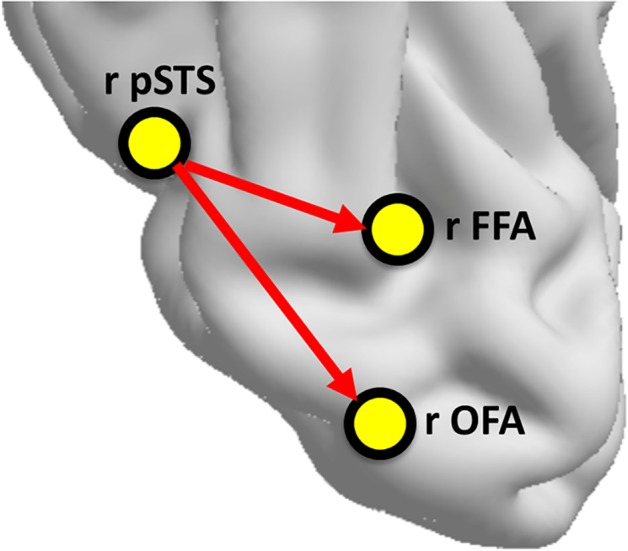
Pattern of directed functional connections among core regions during face viewing. Network organization representing group level directed functional connections among right core regions. We are only representing the most reliable group connections, which are those that are present in all 40 individual subject maps [Color figure can be viewed at http://wileyonlinelibrary.com]

3.2. What is the topology of directed functional connections between the core and extended system?

When the emotion extended subsystem ROIs are included, the functional organization among the right core regions is maintained (see Figure 4a) with directional connections from the pSTS to both the OFA and FFA. In addition, a directed connection from the right FFA to the right amygdala emerged (Figure 4a).

Figure 4.

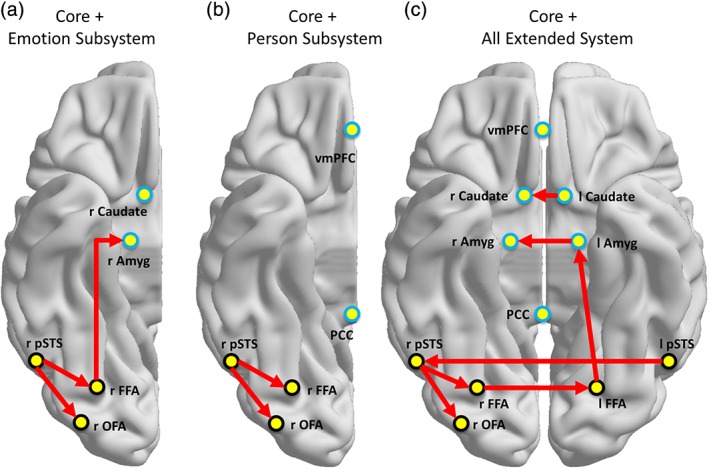
Network organization among core and extended face regions during face viewing. Network organization representing group level directed functional connections among right core and right extended regions related to emotion processing (a), right core and midline extended regions related to person processing (b), and the bilateral core and full extended system together (c) during face viewing. We are only representing the most reliable group connections, which are those that are present in all 40 individual subject maps [Color figure can be viewed at http://wileyonlinelibrary.com]

When only the person knowledge extended subsystem ROIs are included, only the functional organization within the core regions remains (Figure 4b) (see Supporting Information Table S2 for model fit statistics).

Finally, we determined the functional organization among the full set of bilateral core and extended face processing regions during face viewing. Again, the functional organization among the right core regions is consistent (see Figure 4c), indicating a robust topological organization among these three regions in the context of the overall network. Additionally, there are important interhemispheric connections between contralateral regions, including the FFA, pSTS, amygdala, and caudate nuclei. Interestingly, all of the interhemispheric connections involve the directional flow of information from the left to the right hemisphere, except in the case of the FFA, which goes in the opposite direction from the right to left hemisphere. There is also a connection between FFA and amygdala in the left, but not right, hemisphere. This is in contrast to the right hemisphere only model where the right FFA connected to the right amygdala. Finally, there are no connections with regions that are part of the person knowledge extended regions (i.e., PCC, vmPFC).

3.3. Is there specificity in the topology of directed functional connections within the face processing system?

Figure 5 depicts the group connections elicited during face, object, and place viewing across the full set of core and extended ROIs. The topological organization of connections elicited during face viewing is visually very different from those elicited during either object or place viewing. To quantify these potential differences, we vectorized and compared the configuration of weighted directed connections across each category. Figure 6 shows the distinctiveness of the neural network organization in response to each visual category plotted as a function of mean Euclidian distance (ED) between each individual participant's adjacency matrix and that of the group mean.

Figure 5.

Group maps for each visual category. Network organization representing group level directed functional connections among the bilateral core and full extended regions during face (a), object (b), and place (c) viewing. We are only representing the most reliable group connections, which are those that are present in all 40 individual subject maps [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 6.

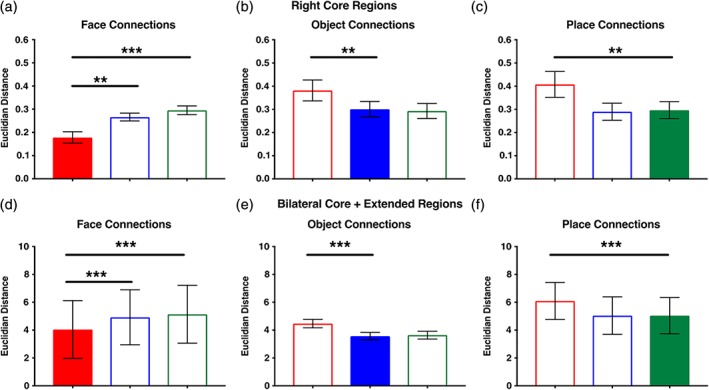
Evaluating the distinctiveness of neural network organization elicited during viewing of each visual category. We computed the Euclidian distance (ED) between each individual participant's vectorized directed adjacency matrix representing their full set of directed functional connections and the vectorized group mean directed adjacency matrix of connections comparing each visual category for the (a) core and (b) combined core and extended models. Bars represent mean ED ± 1 SEM. Colored bars represent the relative network/vector from which the ED was measured within each graph. For both types of models (core, core + extended), the global pattern of weighted, directed connections elicited during face viewing was distinct from that observed during object and place viewing. In contrast, the global patterns of weighted, directed connections elicited during object and place viewing were not distinct from one another. Note: *p < 0.05; **p < 0.01; ***p < 0.001 [Color figure can be viewed at http://wileyonlinelibrary.com]

3.3.1. Right core model (OFA, FFA, pSTS)

In Figure 6a, the individual subject patterns of face connections are compared to the group mean patterns of face, object, and place connections. The repeated‐measures ANOVA evaluating the specificity of the functional connections elicited during face viewing across participants revealed a main effect of condition, F(2, 76) = 14.7, p < 0.001, η² = 0.28, and no category × motion interaction, F(2, 76) = 0.75, p > 0.10. The post hoc comparisons indicated that the EDs were smallest from the face group mean (M = 0.18, SD = 0.16) than from both the object (M = 0.27, SD = 0.11) and place (M = 0.30, SD = 0.12) group means (p < 0.005). As predicted, across individuals the topological organization of directed functional connections generated during face viewing was homogenous and distinct from that generated during object and place viewing.

In Figure 6b, the individual subject patterns of object connections are compared to the group mean patterns of object, face, and place connections. The repeated‐measures ANOVA evaluating the specificity of the functional connections elicited during object viewing revealed a main effect of condition, F(2, 76) = 11.5, p < 0.001, η² = 0.23, but no category x motion interaction, F(2, 76) = 2.4, p > 0.10. The post hoc comparisons indicated that the EDs were smaller from the object group mean (M = 0.30, SD = 0.21) compared to the face group mean (M = 0.38, SD = 0.29), (p < 0.005). However, the EDs between the object and place viewing group means (M = 0.29, SD = 0.21) were not different (p > 0.1). In other words, the functional connections generated during object and place viewing were not significantly different from each other. This indicates that across individuals, the topological organization of functional connections generated during object viewing was relatively homogenous and distinct from that generated during face, but not place, viewing.

In Figure 6c, the individual subject patterns of place connections are compared to the group mean patterns of place, object, and face connections. The repeated‐measures ANOVA evaluating the specificity of the functional connections elicited during place viewing revealed a main effect of condition, F(2, 76) = 13.9, p < 0.001, η² = 0.27, but no category × motion interaction, F(2, 76) = 1.0, p > 0.10. The post hoc comparisons indicated that the EDs were smaller from the place group mean (M = 0.30, SD = 0.23) compared to the face group mean (M = 0.41, SD = 0.35) (p < 0.005). However, the EDs between the place and object viewing group means (M = 0.29, SD = 0.23) were not different (p > 0.1). This indicates that across individuals, the topological organization of functional connections generated during place viewing among these ROIs was relatively homogenous and distinct from that generated during face, but not object, viewing. Therefore, the functional connections generated during place and object viewing were not significantly different from each other.

In sum, the organization of the functional connections among the core face processing regions during face viewing are distinct from those elicited during place and object viewing.

3.3.2. Core + extended model

In Figure 6d, the individual subject patterns of face connections are compared to the group mean patterns of face, object, and place connections. The repeated‐measures ANOVA evaluating the specificity of the functional connections elicited during face viewing revealed a main effect of condition, F(2, 76) = 60.7, p < 0.001, η² = 0.61, but no category × motion interaction, F(2, 76) = 0.20, p > 0.10. The post hoc comparisons indicated that the EDs were smallest from the face group mean (M = 4.04, SD = 13.01) compared to both the object (M = 4.92, SD = 12.48) and place (M = 5.14, SD = 13.13) group means (p < 0.001). As predicted, across individuals the topological organization of functional connections among the core and extended regions generated during face viewing was homogenous and distinct from that generated during object and place viewing.

In Figure 6e, the individual subject patterns of object connections are compared to the group mean patterns of object, face, and place connections. Similarly, the repeated‐measures ANOVA evaluating the specificity of the functional connections elicited during object viewing revealed a main effect of condition, F(2, 76) = 48.4, p < 0.001, η² = 0.56, but no category × motion interaction, F(2, 76) = 0.04, p > 0.10. The post hoc comparisons indicated that the EDs were smaller from the object group mean (M = 3.57, SD = 1.73) compared to the face group mean (M = 4.47, SD = 1.95), (p < 0.001). However, the EDs between the object and place viewing group means (M = 3.64, SD = 1.79) were not different (p > 0.1). This indicates that across individuals, the topological organization of functional connections among the core and extended regions generated during object viewing was homogenous and distinct from that generated during face, but not place, viewing.

In Figure 6f, the individual subject patterns of place connections are compared to the group mean patterns of place, object, and face connections. Finally, the repeated‐measures ANOVA evaluating the specificity of the functional connections elicited during place viewing revealed a main effect of condition, F(2, 76) = 55.0, p < 0.001, η² = 0.59, but no category × motion interaction, F(2, 76) = 0.12, p > 0.10. The post hoc comparisons indicated that the EDs were smaller from the place group mean (M = 5.04, SD = 8.24) compared to the face group mean (M = 6.09, SD = 8.40) (p < 0.001). However, the EDs between the place and object viewing group means (M = 5.05, SD = 8.52) were not different (p > 0.1). This indicates that across individuals, the topological organization of functional connections among the core and extended regions generated during place viewing was homogenous and distinct from that generated during face, but not object, viewing.

In sum, the organization of the functional connections among the core and extended face processing regions during face viewing appears to be distinct from that during place and object viewing.

3.4. Is noise diving the distinction between face and nonface objects?

Finally, to evaluate whether the models were overfitting noise, we submitted phase‐shifted versions of the condition‐specific time series data to GIMME for analysis (Supporting Information Table S1). These results reflect that the models generated using the original time series data are not the result of overfitting random noise (see Supporting Information Tables S1 and S2). For the core region models, 85% of individual participants exhibited better model fit indices for the face viewing data compared to the models generated with the phase‐shifted, randomized time series data analysis (see Supporting Information Table S1). The phase‐shifted models generated from the object and place time series data were not able to converge on a solution and, therefore, could not be compared to data models. For the core + extended models, no model for any condition was able to converge at either the group or individual level.

4. DISCUSSION

The overarching goal of this study was to investigate the architecture of the directed functional connections within the face processing system in typically developing adults using an exhaustive data‐driven modeling approach. In so doing, we addressed three central questions. First, we determined whether, using this approach, we would uncover a similar topological structure that has been reported previously and/or presumed in much of the previous literature, which has relied on confirmatory modeling with the right IOG as the input node sending information directionally to the right FFA and right pSTS (see Table 1). Second, given the limited work in the existing literature, we investigated the functional topology of directed functional connections between the core regions and those in the extended subsystems proposed by Haxby and colleagues (Gobbini & Haxby, 2007; Haxby et al., 2000). Finally, we investigated the category‐specificity of these topologies by deriving network architectures of directed functional connections while participants were also viewing objects and places and compared the topologies directly. To address these questions, we used GIMME, which allowed us to model EC among all the a priori defined regions using an exhaustive search algorithm that reliably discovers functional connections and identifies the direction of those connections (Gates & Molenaar, 2012; Smith et al., 2011).

4.1. Evaluating topology within the core face network

We investigated all possible directional functional connections among regions identified by Haxby and colleagues (Gobbini & Haxby, 2007; Haxby et al., 2000) as part of the “core” face processing network, including the FFA1, OFA, and pSTS. We focused on the right hemisphere in these initial analyses because this is the approach taken by most studies in the existing literature (see Table 1). There are two important differences in our approach to measuring EC compared to those that predominate the existing literature. First, rather than using an a priori defined confirmatory model search approach, we employed a data‐driven exhaustive search strategy. A primary strength of this approach is that it allows for the potential to uncover topologies that were not tested or conceived previously but may best fit the data. Relatedly, we did not require input into the right OFA. This is because of reports that visual information may reach the ventral visual pathway in multiple ways including via feedback pathways from more anterior regions, like the amygdala (Hung et al., 2010; Garvert et al., 2014; Vuilleumier & Pourtois, 2007).

We found that during viewing of both familiar and unfamiliar faces, the neural network architecture does not reflect what was previously reported/presumed in prior studies (IOG ‐> FFA, IOF ‐> FFA). In contrast, we found that the right pSTS sends information to both the right OFA and right FFA (pSTS ‐> FFA, pSTS ‐> OFA). Importantly, we repeatedly discovered this topology of directed functional connections among the three right hemisphere core face regions across all the analyses of face viewing, no matter which regions were included. Critically, we ruled out the possibility that this topology reflected noise because the analyses of the phase‐shifted, randomized data do not reflect this topology.

While this functional topology of directed connections may seem surprising, it is not unprecedented. The models proposed by Haxby and colleagues hypothesize reciprocal connections among all the core regions, with no clear predictions about the directionality of a single connection (Gobbini & Haxby, 2007; Haxby et al., 2000). More recent models of the neural basis of face‐processing also predict reciprocal connections between both the pSTS and FFA/OFA (Duchaine & Yovel, 2015). Importantly, studies investigating functional connectivity within the face processing system, which cannot report anything about the directionality of connections, often report the presence of connections between the pSTS and FFA (Furl et al., 2013, 2015; Lohse et al., 2016; Nguyen et al., 2014). There are also structural pathways that would enable these functional connections to exist. Although there are questions regarding a direct structural connection between the pSTS and FFA (Gschwind et al., 2012; Pyles, Verstynen, Schneider, & Tarr, 2013), functional information could travel between the pSTS and the OFA and FFA via the ventral occipital fasciculus (VOF; Yeatman et al., 2014) as well as the dorsolateral occipital segment of the inferior longitudinal fasciculus (ILF) (Latini et al., 2017).

Beyond the differences in our analytic approach, we also used dynamic stimuli, while many of the existing studies used static line drawings or photographs. pSTS responds strongly to biologically relevant moving stimuli (Duchaine & Yovel, 2015; Girges, O'Brien, & Spencer, 2016), which may explain, in part, why the directional functional connections we identified originate from pSTS and feed into rFFA and rOFA. This hypothesis could be tested by employing static stimuli and a similar analysis approach to evaluate potential differences in the topology of the derived network connections.

These results suggest that the pattern of directed functional connections within the right core face processing regions may not be as hierarchical and feed‐forward as has been described in the literature. They also reflect that the models of the neural basis of face processing may need to be more dynamic to reflect the task‐specific nature of the elicited patterns of connections.

4.2. Evaluating topology among regions comprising the core and extended face network

A second important contribution of this work is that we investigated the topology of directional connections within the broader extended face processing network. Recall that Haxby and colleagues suggest that there are emotion and person subsystems within the extended face processing network (Gobbini & Haxby, 2007). Separately, we evaluated the topology of directed functional connections between the right core regions and the emotion subsystem extended regions (i.e., amygdala, caudate nucleus) and then between the right core regions and the person subsystem extended regions (i.e., PCC, vmPFC). Based on the patterns of EC elicited as participants passively view dynamic movie stimuli; our findings do not support much of the hypothesized functional organization proposed in the Gobbini and Haxby (2007) model. For example, the researchers predicted that the emotion subsystem has feedback connections to the core system. In contrast, we observed a feed‐forward functional connection from the right FFA to the right amygdala, when just the right hemisphere regions were evaluated. When all regions were included (i.e., bilateral core regions and both emotion and person subsystem regions), the functional connection was still feed‐forward, but from the left FFA to the left amygdala.

In contrast to the Gobbini and Haxby (2007) model predictions, we did not observe any connections between the right core and person subsystem regions. In other words, during this task, the core and person‐knowledge subsystems regions appear to be functionally independent from each other. This was also true when we include all regions (bilateral core and emotion and person subsystem extended regions) in the model. In sum, we found that the functional architecture among the right core regions did not vary even when the emotion and/or person extended regions were included in the model and the only functional interaction between the core and extended regions was via a feed‐forward functional connection from the FFA to the amygdala.

Although our results are not consistent with the predictions from the Gobbini and Haxby (2007) model, they are a bit overlapping with those from Fairhall and Ishai (2007), who reported feed‐forward connections between the right FFA and amygdala, inferior frontal gyrus, and orbitofrontal cortex. An interesting possibility to explain why our findings regarding the organization of network topology do not fit with the predictions of the predominant theoretical model is related to the task demands. Participants in this study were instructed to passively view the stimuli (although they likely implicitly recognized the famous faces). Tasks that elicit more active processing of faces (e.g., identity recognition or emotional expression detection) may engage more functional connections between the core and extended regions. This idea is consistent with the findings from studies using the DCM approach that evaluate how intrinsic connections are modulated by task demands (e.g., Fairhall & Ishai, 2007). Testing this idea will be an important next step to determine how face processing task demands alter the entire topology of functional connections within the face processing system.

4.3. Specificity of network topology within the face processing regions

The third set of findings was related to our goal of investigating the specificity of the functional network architecture among these regions for processing faces compared to other kinds of visual objects. Previous work has primarily focused on assessing differences in the modulation of network architecture within the face processing system during different face processing tasks (Cohen Kadosh et al., 2011; Fairhall & Ishai, 2007; Frässle, Paulus, Krach, & Jansen, 2016; Frässle, Paulus, Krach, Schweinberger, et al., 2016). However, there is virtually no work, as far as we can find, that specifically evaluates whether the topological structure of connections changes within the regions implicated in face processing when participants view objects from other visual categories. Evaluating this possibility is important for understanding whether the pattern of directed functional connections elicited during face viewing is potentially optimized for faces or is more generally activated across a broader set of visual object categories.

To investigate whether the global pattern of directed functional connections elicited during face viewing is different than that elicited during object or place viewing, we vectorized the adjacency matrix of weighted directed connections from each participant generated during each of the viewing conditions. We did so for the core and full core and extended regions separately, which generated a total of six distinct matrices/vectors for each participant. Importantly, this approach preserves the presence/absence, direction, and strength of each connection in each network topology. We evaluated the relative distinctiveness of each pattern of connections in each viewing conditions (face, objects, places) by comparing how similar individual participants' patterns of connections (e.g., face connections) were to each other for one condition average (e.g., average pattern of face connections) compared to another condition average (e.g., average pattern of object connections). The rationale was that if the patterns were fairly similar across the two conditions, then the patterns of connections were generally activated across this broad set of visual categories. However, if the patterns were different, then that would be evidence in favor of a more optimized pattern of connections, particularly for faces given that these regions were all defined as part of the face processing network.

We observed several findings using this approach. First, indeed the set of global connections elicited during face viewing within the core regions as well as in the entire network (core and extended regions) are reliably different from the set of connections elicited during object or place viewing. Interestingly, the set of connections elicited during object and place viewing were also reliably different from the set of connections activated during face viewing within the core regions and in the entire network (core and extended regions). However, the pattern of connections activated during object and place viewing were not reliably different from each other. In other words, the patterns of directed functional connections among the face processing regions do appear to be particularly optimized for face processing. They are different then when processing objects and places, but not in ways that uniquely identify that either of these kinds of visual objects is being processed. Importantly, this shows that indeed the face network has a distinct topology of functional connections that is optimized for viewing faces. It is critical to note that the regions comprising this topology are all centrally involved in the processing of faces, not other visual categories. Given these findings, we would presume that a set of regions “optimized” more for the processing of objects or places would produce unique patterns of connections during their respective category viewing.

4.4. Limitations and future directions

There are limitations to note from this study that we can build on in future work. First, we were not able to include the anterior temporal lobe as a region in this network analysis. This is unfortunate given its reported role in processing face identity (Kriegeskorte, Formisano, Sorger, & Goebel, 2007) and person knowledge (Gobbini & Haxby, 2007). This was primarily due to signal dropout around the preauricular sinus, which interfered with the acquisition of group level activation that could be used to constrain the ROI search space for extracting individualized time series data in the anterior temporal lobe. Second, there are other important regions for face processing that are not captured in our analyses. For example, in emotion recognition research much of the focus is on connectivity between the amygdala and multiple regions within frontal cortex, which have limited representation in models of face‐processing (Duchaine & Yovel, 2015; Gobbini & Haxby, 2007; Haxby et al., 2000). It is possible that including such regions would change the overall patterns of connections between the core and extended regions, or even among the core regions. Finally, it will be important to evaluate the validity of these findings with other EC analysis approaches and using more direct measures of neural connectivity, like intracranial electrocorticography.

5. CONCLUSIONS

Our findings regarding the organizational topology of functional connections within the face processing system suggest that we revise our understanding of this system. We provide evidence that challenges the predominant view that this system is primarily hierarchical and feedforward, particularly among the core regions. In addition, we also provide evidence that the pattern of functional connections among these regions is truly optimized for face processing. Our findings also suggest that the entire topological configuration of directional functional connections in a neural network are dynamic and responsive to task demands, even in passive viewing of different kinds of visual objects. This is a novel way of thinking about neural network organization, particularly in the face processing literature. This conceptual and methodological approach to thinking about dynamic changes and emergent properties of neural network organization could be especially useful for addressing questions about atypical neural organization in populations that struggle with multiple aspects of face processing behavior, as is the case with individuals with autism spectrum disorder and prosopagnosia.

CONFLICT OF INTEREST

None declared.

Supporting information

Supplementary Table S1

Supplementary Table S2

Elbich DB, Molenaar PCM, Scherf KS. Evaluating the organizational structure and specificity of network topology within the face processing system. Hum Brain Mapp. 2019;40:2581–2595. 10.1002/hbm.24546