Parcellation of the human hippocampus based on gray matter volume covariance: Replicable results on healthy young adults

Abstract

The hippocampus is a key brain region that participates in a range of cognitive and affective functions, and is involved in the etiopathogenesis of numerous neuropsychiatric disorders. The structural complexity and functional diversity of the hippocampus suggest the existence of structural and functional subdivisions within this structure. For the first time, we parcellated the human hippocampus with two independent data sets, each of which consisted of 198 T1‐weighted structural magnetic resonance imaging (sMRI) images of healthy young subjects. The method was based on gray matter volume (GMV) covariance, which was quantified by a bivariate voxel‐to‐voxel linear correlation approach, as well as a multivariate masked independent component analysis approach. We subsequently interrogated the relationship between the GMV covariance patterns and the functional connectivity patterns of the hippocampal subregions using sMRI and resting‐state functional MRI (fMRI) data from the same participants. Seven distinct GMV covariance‐based subregions were identified for bilateral hippocampi, with robust reproducibility across the two data sets. We further demonstrated that the structural covariance patterns of the hippocampal subregions had a correspondence with the intrinsic functional connectivity patterns of these subregions. Together, our results provide a topographical configuration of the hippocampus with converging structural and functional support. The resulting subregions may improve our understanding of the hippocampal connectivity and functions at a subregional level, which provides useful parcellations and masks for future neuroscience and clinical research on the structural and/or functional connectivity of the hippocampus.

1. INTRODUCTION

The hippocampus, located deep in the medial temporal lobe, is a key region in the limbic system. Structural and functional deficits of the hippocampus characterize numerous neurological and neuropsychiatric disorders, including Alzheimer's disease, anxiety disorder, schizophrenia, and major depression (Chen & Etkin, 2013; Geuze, Vermetten, & Bremner, 2005; Harrison, 2004; Videbech & Ravnkilde, 2004). Prior research has shown that the hippocampus participates in a range of cognitive and affective functions (Barkus et al., 2010; Strange, Witter, Lein, & Moser, 2014), which has a correlate on a complex and heterogeneous structure (Amunts et al., 2005; Carr, Rissman, & Wagner, 2010; Moser & Moser, 1998; Poppenk, Evensmoen, Moscovitch, & Nadel, 2013; Strange et al., 2014). The functional diversity (Poppenk et al., 2013; Strange et al., 2014) and structural complexity (Duvernoy, 2005) of the hippocampus suggest the existence of subdivisions within this region. The parcellation of the hippocampus into subdivisions may provide critical insights regarding the roles of the hippocampus in physiological and pathological states, including Alzheimer's disease (Iglesias et al., 2015), major depressive disorder (Roddy et al., 2019), and schizophrenia (Arnold et al., 2014), because these techniques offer a valuable tool to explore such critical questions (Eickhoff, Thirion, Varoquaux, & Bzdok, 2015; Fan et al., 2016; Glasser et al., 2016).

Human hippocampal parcellation strategies have used anatomical features; however, these studies were either mainly based on postmortem brain tissue (Amunts et al., 2005; Augustinack et al., 2014), or based on topographic landmarks, intensity changes, and geometric information (Kim et al., 2000; Mueller et al., 2007; Van Leemput et al., 2009; Yushkevich, Pluta, et al., 2015). Postmortem brain parcellation approaches may be biased by subtle, but noticeable, anatomical differences between in vivo and postmortem fixated tissue. Purely topographic landmark, intensity change, and geometric information‐based approaches take into account the internal microstructure of a brain area, but not the interregional connectivity properties of the brain areas. Therefore, a connectivity‐based parcellation may provide additional information to improve our understanding of the structural and functional specialization of the human brain. Several studies have been conducted to characterize hippocampal subregions based on the characteristics of the functional connectivity. Using a combination of meta‐analytic connectivity modeling and clustering algorithms, Chase et al. (2015) parcellated the subiculum into a bilateral anterior region, and separate posterior and intermediate regions on each hemisphere. Using the same approaches, the left hippocampus was segmented into three distinct subregions: an anterior emotional processing region, an intermediate cognitive operations region, and a posterior perceptual region (Robinson et al., 2015), while the right hippocampus was segmented into two and five subregions. Wang, Ritchey, Libby, and Ranganath (2016) did not find significantly different subregions in the hippocampus by using resting‐state functional magnetic resonance imaging (fMRI) functional connectivity. A data‐driven functional connectivity approach (masked independent component analysis, [MICA]) (Moher Alsady, Blessing, & Beissner, 2016), was also used to reproducibly define hippocampal subregions with resting‐state fMRI, and map their intrinsic functional connectivity patterns, demonstrating configurations that support longitudinal segmentation of hippocampal functions (Blessing, Beissner, Schumann, Brünner, & Bär, 2016). More recently, Beissner, Preibisch, Schweizer‐Arau, Popovici, and Meissner (2018) and Zhao et al. (2019) divided the bilateral hippocampus into 10 and 17 subregions with MICA, respectively. Despite these attempts to delineate functionally hippocampal subdivisions, subregions based on the characterization of the structural connectivity/covariance are less well defined. To date, one study has identified hippocampal subregions based on structural connections estimated using probabilistic tractography (Adnan et al., 2016). Specifically, the authors applied diffusion‐weighted imaging to divide the hippocampus into an anterior versus posterior dichotomy, and demonstrated that these structurally defined subregions differentially functionally connected to the rest of the brain.

Research over the past decade has started to identify the organizational principles that govern the topology of structural covariance networks, based on the assumption that brain structural communities covary in their morphological properties at a population level (Alexander‐Bloch, Giedd, & Bullmore, 2013). A novel valuable tool used to investigate structural covariance networks is the study of gray matter volume (GMV) covariance. GMV covariance may reflect the synchronized maturational changes mediated by axonal connections forming and reforming over the course of development (Alexander‐Bloch, Raznahan, Bullmore, & Giedd, 2013; Mechelli, Friston, Frackowiak, & Price, 2005; Montembeault et al., 2012; Zielinski, Gennatas, Zhou, & Seeley, 2010). It has been suggested that GMV covariance recapitulates functional brain networks (Seeley, Crawford, Zhou, Miller, & Greicius, 2009) and the pattern of interregional structural covariance is akin to the pattern of functional connectivity (Alexander‐Bloch, Giedd, & Bullmore, 2013), thereby driving the brain functioning in an efficient way. GMV covariance has been used to reliably parcellate brain regions such as the insula (Kelly et al., 2012) or the orbitofrontal cortex (Liu, Qin, Qi, Jiang, & Yu, 2015). These two studies (Kelly et al., 2012; Liu et al., 2015) employed GMV correlation (GMVCorr), which is a bivariate voxel‐to‐voxel correlation method that utilizes second‐order statistics to depict the association of the GMV between two voxels within the region of interest (ROI). In contrast, independent component analysis (ICA) (McKeown & Sejnowski, 1998), is a multivariate blind source separation method, which utilizes higher order statistics to model common associations across multiple voxels. MICA has been used to parcellate an ROI with fMRI data (Blessing et al., 2016; Kim, Park, & Park, 2013; Moher Alsady et al., 2016). In the present study, we introduce MICA to quantify GMV covariance for structural brain parcellation.

We utilized GMVCorr (Kelly et al., 2012; Liu et al., 2015) as well as MICA (Blessing et al., 2016; Kim et al., 2013; Moher Alsady et al., 2016), which are two different approaches to quantify GMV covariance (Mechelli et al., 2005; Xu, Groth, Pearlson, Schretlen, & Calhoun, 2009), to parcellate the human hippocampus based on T1‐weighted MRI scans from two independent data sets. We hypothesized that the combination of bivariate GMVCorr and multivariate MICA would provide converging and complementary information and improve the structural covariance parcellation. Our secondary aim was to contrast GMV covariance patterns to functional connectivity patterns on the parcellated hippocampal subregions to determine: (a) the structural and functional connection properties of these subregions and (b) whether the patterns of interregional structural covariance resemble the patterns of functional connectivity, and to quantify such resemblance.

2. MATERIALS AND METHODS

2.1. Data sets and imaging protocols

Study participants were from two independent cohorts (Beijing and Cambridge datasets) of the 1000 Functional Connectomes Project (https://www.nitrc.org/projects/fcon_1000). The corresponding institutional review boards approved for the submission of anonymized data obtained with written informed consent from each participant.

There were 198 healthy volunteers (122 females and 76 males, mean ± SD age = 21.16 ± 1.82, range 18–26 years old) in the Beijing dataset and 198 healthy volunteers (123 females and 75 males, mean ± SD age = 21.03 ± 2.31, range 18–30 years old) in the Cambridge dataset. A high‐resolution 3D magnetization‐prepared rapid gradient echo sequence was acquired for each participant, and resting‐state fMRI data were acquired using an echo‐planar imaging sequence. Scanning parameters are provided in Table 1.

Table 1.

Scanning parameter details for the data sets included in the present study

Data set	TR (ms)	FOV (mm)	Voxel size (mm × mm × mm)	Slice number	Time points
Beijing‐MRI	2,530	256	1.33 × 1.0 × 1.0	128	N/A
Cambridge‐MRI	2,200	230	1.2 × 1.2 × 1.2	144	N/A
Beijing‐fMRI	2,000	200	3.13 × 3.13 × 3.6	33	225
Cambridge‐fMRI	3,000	256	3.0 × 3.0 × 3.0	47	119

Abbreviations: FCP = Functional Connectomes Project; fMRI = functional magnetic resonance imaging; FOV = field of view; MPRAGE = magnetization‐prepared rapid gradient echo.

Note. The Cambridge data used multi‐echo MPRAGE for MRI data collection, allows increased contrast through weighted averaging of the four derived images. Other details on scanning parameters like TE, flip angle, and scanner model are not available through the 1000 FCP website.

2.2. Preprocessing

Structural MR images were preprocessed (Figure 1a) using the voxel‐based morphometry (VBM, http://dbm.neuro.uni-jena.de/vbm8/) and Statistical Parametric Mapping software toolbox (SPM12, http://www.fil.ion.ucl.ac.uk/spm). The preprocessing procedures involved four main steps: segmentation, normalization, modulation, and spatial smoothing. The first three steps were done within the VBM8 toolbox, and the spatial smoothing was implemented in the SPM toolbox. The segmentation procedure applied adaptive maximum a posterior and partial volume estimation to segment the raw images into gray matter, white matter and cerebrospinal fluid images in the native space for all subjects. Prior to high‐dimensional warping, the gray matter images were registered to the tissue probability map using affine transformation. Diffeomorphic Anatomical Registration using Exponentiated Lie Algebra was done to implement a high‐dimensional nonlinear normalization. Through the iteration of image registration and template creation, gray matter maps were normalized to their own average templates and further to the Montreal Neurological Institute (MNI) space, and resampled to a voxel size of 1.5 × 1.5 × 1.5 mm³. Thereafter, the normalized gray matter partitions were multiplied by the Jacobian determinants from the deformations to preserve the total amount of tissue in native spaces. Therefore, the regional GMV represents normalized GMV after removing the effect of variance in individual brain sizes. Finally, the gray matter images were smoothed with a 3‐mm full width at half maximum (FWHM) Gaussian kernel. After preprocessing, we obtained normalized, modulated, and smoothed GMV maps for subsequent analyses. To reduce the search space in GMVCorr calculation to meet reasonable computational and memory requirement (see below) (Chang, Yarkoni, Khaw, & Sanfey, 2012; Jung et al., 2014; Kahnt, Chang, Park, Heinzle, & Haynes, 2012), the images were additionally downsampled to 3 × 3 × 3 mm³. Thus, the final resolution was 1.5 × 1.5 × 1.5 mm³ for the hippocampal voxels and 3 × 3 × 3 mm³ for the nonhippocampal voxels.

Figure 1.

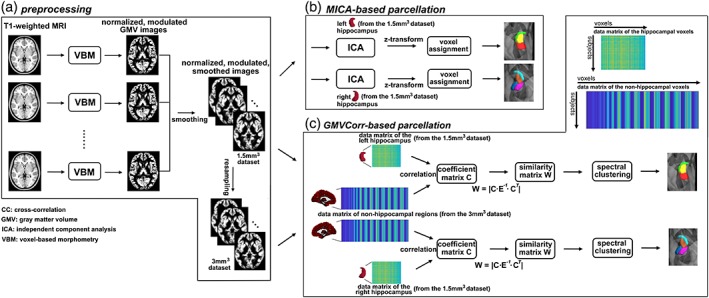
Flow diagram of the parcellation procedures in the present study. (a) Preprocessing of the T1‐weighted magnetic resonance imaging images, the output of this procedure is the normalized, modulated, and smoothed gray matter volume (GMV) images. Furthermore, we resampled the 1.5 mm³ data set into 3 mm³ resolution. (b) Masked independent component analysis (MICA)‐based parcellation procedure, including ICA, z‐transformation of the components, and voxel assignment with a winner‐take‐all strategy. (c) GMV correlation (GMVCorr)‐based parcellation procedure. The coefficient matrix C is first generated by correlating the GMV of hippocampal voxels to all of the nonhippocampal voxels. Then, a similarity matrix W is constructed from C, and is used as the input of a spectral clustering algorithm. Note that the hippocampus mask was obtained from the Harvard‐Oxford probabilistic atlas (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/Atlases) thresholded at 50% [Color figure can be viewed at http://wileyonlinelibrary.com]

One of the 198 Beijing participants was excluded for fMRI data analysis since the data was acquired in a different orientation from others. Thus, 197 and 198 participants were included in fMRI data analyses for Beijing and Cambridge dataset, respectively. The fMRI preprocessing was conducted in SPM toolbox, and steps included discarding the first five volumes, slice‐timing correction, realignment, normalization to the standard MNI template, reslicing into 3‐mm isotropic voxels, spatial smoothing using a 3‐mm FWHM Gaussian kernel, linear detrending, nuisance signal removing (24‐parameter head motion profiles, cerebrospinal fluid, and white matter signals), and temporal band‐pass filtering (0.01–0.08 Hz).

2.3. GMV covariance‐based parcellation

The left and right hippocampal ROIs were defined on the basis of the Harvard‐Oxford atlas, using a probability threshold of 50% (Beissner et al., 2018; Blessing et al., 2016; Marder et al., 2014; Zhao et al., 2019) at the MNI152 space, yielding a conservative anatomical representation with 1,267 and 1,271 voxels for the left and right hippocampus respectively (MNI152 1.5 mm space). GMV covariance quantifies the extent to which GMV covary between different regions across participants, and in the present study, GMV covariance was conducted via two approaches: voxel‐based GMVCorr (Kelly et al., 2012; Liu et al., 2015) and MICA (Moher Alsady et al., 2016). The following procedures of GMVCorr and MICA were designed to cluster hippocampal voxels that share similar GMV covariance properties together, and were implemented for unilateral hippocampus of each data set, respectively.

For GMVCorr (Figure 1c), we calculated the Pearson correlation between the GMV of each hippocampal ROI voxel (from the 1.5 × 1.5 × 1.5 mm³ set) and those from each nonhippocampal voxel in the rest of the brain (from the 3 × 3 × 3 mm³ set; downsampling was used to obtain sufficient spatial resolution for each ROI region and to meet reasonable computational and memory requirements) across all 198 subjects. The coefficient matrix C ∈ R ^v × w of all ROI voxels was calculated (v and w were the number of voxels over the ROI region and nonhippocampal regions), and a symmetric nonnegative similarity matrix W (Elhamifar & Vidal, 2013; Ge et al., 2017) was constructed from the coefficient matrix: W = |C · E ⁻¹ · C ^T|∈ R ^v × v (Zhang et al., 2015), where E was the diagonal matrix saving the column summations of the coefficient matrix C and T denoted transposition. The similarity matrix W was then fed into a spectral clustering algorithm (Ge et al., 2017; Ng, Jordan, & Weiss, 2002) to generate the final parcellations. Spectral clustering has been proven to outperform other clustering algorithms (Von Luxburg, 2007), it can be solved efficiently by standard linear algebra methods, and the implementation of spectral clustering in fMRI studies was less sensitive to initial conditions than other methods (Craddock, James, Holtzheimer, Hu, & Mayberg, 2012). With spectral clustering, a similarity graph was first built, with vertexes representing voxels and similarity matrix representing the weight of the edges connecting vertexes within a graph. The problem of spectral clustering can be formulated using this similarity graph such that edges between different parcels have low weights (which means that voxels in different subregions are dissimilar from each other) and edges within a parcel have high weights (voxels within the same subregion are similar to each other). Technically, a graph Laplacian matrix was constructed as L = D − SM, L ∈  R^v × v, D ∈  R^v × v, where D was a diagonal matrix saving the degree of each vertex (the row sum). Then, K (number of subregions) first eigenvectors u₁, u₂, … , u_K of the normalized Laplacian L^′  = D^−0.5LD^−0.5, L^′∈ R ^v × K were computed, and saved in a spectral embedding matrix U = [u₁, u₂,  … , u_K] ∈ R ^v × K as a low‐dimensional representation of the data (Von Luxburg, 2007). We subsequently generated a matrix NU ∈ R ^v × K by normalizing the rows of U to norm 1. Finally, k‐means clustering was applied to the normalized spectral embedding matrix NU. In the present study, the k‐means clustering method was executed 100 times with random initializations to ensure stability of the results.

MICA analysis (Figure 1b) was applied to parcellate the hippocampus using the GIFT toolbox (http://icatb.sourceforge.net). Spatial ICA using the InfoMax algorithm (Bell & Sejnowski, 1995) decomposed the data matrix (participants by voxels, the number of voxels was the dimension of the hippocampus from the 1.5 × 1.5 × 1.5 mm³ set) into a mixing matrix (participants by sources) and a source matrix (sources by voxels). Note that the stability of the parcellation results in this part relied on the stability of the ICA algorithm, and we selected InfoMax algorithm, which is quite stable relative to other algorithms (Correa, Adalı, & Calhoun, 2007; Ma et al., 2011). Furthermore, the component estimation was performed 100 times with varying initial conditions of the algorithm using ICASSO (Himberg, Hyvärinen, & Esposito, 2004). The number of sources was the number of clusters, which was determined by cross validation (see below). Each row of the source matrix indicates a gray matter network sharing the same regional covariance patterns. To generate the maps of subregions, the sources were transformed into z‐scores, and each voxel within the source was assigned the maximally contributed source label, that is, winner‐take‐all strategy, according to the z‐scores (Moher Alsady et al., 2016).

2.4. Determination of optimal cluster number K

To avoid an arbitrary cluster number from being chosen, we used a twofold cross‐validation strategy to determine a number that would yield optimal consistency across participants. The entire sample of each data set was randomly split into two non‐overlapping subdatasets of equal sample size. We computed the Dice's coefficient of the parcellation results from the two subdatasets. As one of the most used metrics to quantify reproducibility and similarity of parcellation in neuroimaging (Craddock et al., 2012; Hale et al., 2015; Mejia et al., 2015; Shen, Tokoglu, Papademetris, & Constable, 2013; Wang et al., 2015), the Dice's coefficient has values in the interval [0,1], with higher values indicating higher consistency. This cross‐validation procedure was conducted with varying K values (from 2 to 15) and repeated 50 times for Beijing and Cambridge dataset. We defined the optimal K to be the nontrivial (K > 2) clustering solution that demonstrated highest Dice's coefficient between subdatasets.

2.5. GMV covariance‐based hippocampal subregions overlapping with hippocampal cytoarchitectonic maps

To investigate the extent to which the GMV covariance‐based subregions were comprised of which hippocampal subfields, we calculated the overlapping ratios between each subregion and subfields of a hippocampal cytoarchitectonic map from the Anatomy toolbox (Amunts et al., 2005; Eickhoff et al., 2005). Six subfields were selected: cornu ammonis 1–3 (CA1–3), dentate gyrus, entorhinal cortex, and subiculum. Note that the inclusion of the entorhinal cortex was because the hippocampal ROIs used in the present study were slightly overlapped with the entorhinal cortex from the Anatomy toolbox. Masks of these subfields were constructed by assigning each voxel to the subfield within which it has the maximal probability. Since the CA2 and CA3 regions are small relative to other subfields and there is variability in how these subfields are defined in humans MRI data (Wisse et al., 2017; Yushkevich, Amaral, et al., 2015), we combined these two regions with CA1 and formed a single CA subfield. Subsequently, an overlap ratio between each subregion and each subfield was computed by dividing the number of overlapping voxels (between each subregion and each subfield mask) by the number of voxels in that subregion.

2.6. GMV covariance maps and resting‐state functional connectivity patterns of hippocampal subregions

To probe GMV covariance patterns of hippocampal subregions, we extracted the average GMV of each ROI (derived from intersection of each GMVCorr and ICA‐derived subregion) across participants and calculated the partial correlation coefficient between the GMV of each subregion and those of nonhippocampal voxels of the whole brain, with age and sex as nuisance covariates. To characterize the functional connectivity patterns associated with the hippocampal subregions, whole‐brain correlation analysis was conducted for each participant. Specifically, a seed‐to‐voxel correlation strategy was employed, with intersections of the GMVCorr and ICA‐derived subregions as seed regions. Whole‐brain functional connectivity patterns were produced. Specifically, the mean fMRI time series from each seed region was extracted, followed by computing the Pearson correlation coefficient between that time series and time series from all other brain voxels. Statistical tests on the Fisher's z‐transformed functional connectivity patterns were performed using one sample t test for each data set, with age, sex, and mean frame displacement of head movement as nuisance covariates. Multiple comparisons were corrected using a false discovery rate method (p < .05/14 = 0.004, Bonferroni correction was applied to correct for multiple comparisons of the seven a priori subregions tested for the two data sets). Subsequently, GMV covariance patterns were spatially correlated with functional connectivity patterns to investigate the relationships between structural and functional patterns of subregions.

2.7. Hierarchical clustering of hippocampal subregions according to GMV covariance and functional connectivity patterns

To examine how GMV covariance patterns (and functional connectivity patterns) of the hippocampal subregions resemble one another, we performed hierarchical clustering analysis on the GMV covariance patterns (and functional connectivity patterns). The clustering algorithm successively merged pairs of GMV covariance patterns (functional connectivity patterns) until all were merged into a single cluster, based on the similarity of these patterns. We used a hierarchical clustering approach with Ward's linkage rule (Ward, 1963) in the present study. For the hierarchical clustering results, the height in the dendrogram represents the dissimilarity value: the lower the values, the higher the similarity between GMV covariance patterns or functional connectivity patterns. To assess the validity and robustness of the hierarchical clustering, a cophenetic correlation coefficient was calculated for the final dendrogram to evaluate the degree to which the clustering represented the underlying similarities among the GMV covariance patterns or functional connectivity patterns. Cophenetic correlation coefficient is a measure of how faithfully the hierarchical cluster results represent the dissimilarity among observations. Specifically, it is defined as the linear Pearson correlation coefficient between the original pairwise dissimilarities and the cophenetic dissimilarities obtained from the dendrogram. The value of this coefficient varies between 0 and 1. A higher cophenetic correlation coefficient indicates a better cluster solution, and the hierarchical clustering was considered successful if the cophenetic correlation coefficient was larger than 0.75 (Cauda et al., 2012; Hao et al., 2016).

3. RESULTS

3.1. Parcellation of the hippocampus based on GMV covariance

Using the twofold cross‐validation strategy, we identified the local maxima of Dice's coefficients as K = 3 and 4 for left and right hippocampus of each data set (Beijing and Cambridge dataset) and each method (GMVCorr and MICA, Figure 2), respectively. The optimal clustering numbers for left and right hippocampus were 3 and 4 in the present study.

Figure 2.

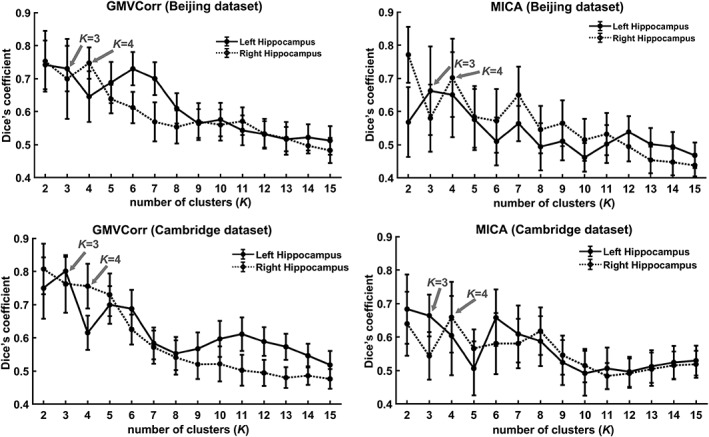
Using Dice's coefficient as an indication of the clustering consistency (interval 0–1) of the GMV covariance‐based parcellation, where larger values indicate high consistency and 1 stands for perfect match. With twofold cross‐validation technique for each data set (50 times), we found that the three and four cluster solution showed higher values than other solutions for left and right hippocampus

The parcellation results are shown in Figure 3. Using the three‐cluster scheme, the left hippocampus was parcellated into the anterior (L1), posterior‐medial (L2), and posterior‐lateral (L3) subregions. For the right hemisphere, the hippocampus was parcellated into the anterior‐medial (R1), anterior‐lateral (R2), posterior‐medial (R3), and posterior‐lateral (R4) subregions. The parcellation results were very similar in both data sets by GMVCorr and MICA methods, as evidenced by the fairly high Dice's coefficients between parcellation results from different methods and different data sets (central panel in Figure 3 with an average value of 0.76). We employed nonparametric permutation tests to determine whether the Dice's coefficients between parcellation results were significantly different from random parcellation of the ROIs. In other words, we intended to assess the significance of each of the Dice's coefficient in Figure 3. Specifically, we obtained an empirical distribution for the Dice's coefficient by randomly reallocating all voxels into different subregions and recomputing the Dice's coefficient based on the randomized results (5,000 permutations). The 95th percentile points of the empirical distributions were used as critical values to estimate p‐values, which indicate the deviation of the observed discriminative performance from those expected by chance. The histograms in Figure S1 depict the results of the permutation tests on Dice's coefficient values, and the red dots show the real observations of the Dice's coefficient in each condition. The permutation results demonstrated that the parcellation results obtained with different methods and different data sets were highly similar (all p < < .001, Bonferroni corrected, Figure S1).

Figure 3.

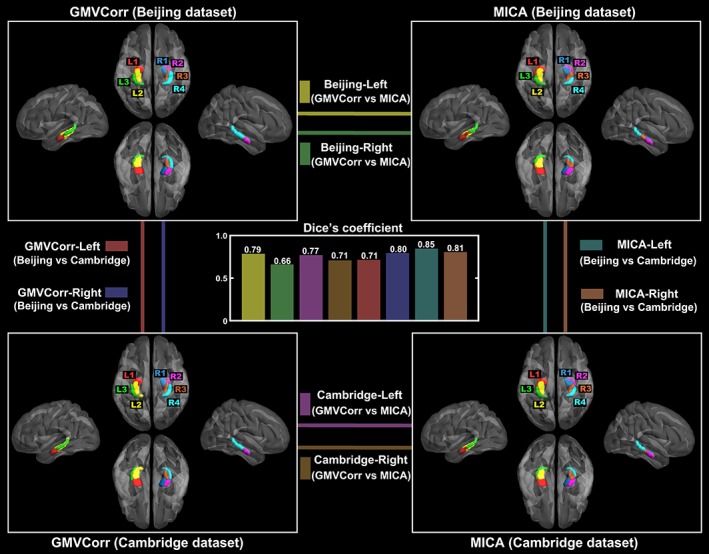
Gray matter volume correlation (GMVCorr) and masked independent component analysis (MICA)‐based parcellation schemes for the two data sets. Dice's coefficients between different parcellation methods (GMVCorr vs. MICA, within each data set) and different data sets (Beijing vs. Cambridge, within each method) are shown in the central panel, with an average value of 0.76. The parcellation results (NIFTI format) are provided in the have been released on the neuroimaging informatics tools and resources clearinghouse (NITRC) website (https://www.nitrc.org/projects/hippo_gmvc/) [Color figure can be viewed at http://wileyonlinelibrary.com]

3.2. Hippocampal subregions overlapping with hippocampal cytoarchitectonic maps

Overlapping ratios between GMV covariance‐based subregions and hippocampal subfields are shown in Figure 4. Specifically, L1, L2, R1, and R2 were mainly located in the subiculum and CA; a large portion of R3 was located in the subiculum, the remaining portion of this region overlapped with CA and dentate gyrus; L3 and R4 were mainly located in CA and dentate gyrus with similar overlapping ratios of the two subfields. All of the subregions did not largely overlap with entorhinal cortex because this subfield occupies a small portion of the hippocampal mask used in the present study (Harvard‐Oxford atlas). In addition, the subregions obtained with different methods on different data sets had similar overlapping patterns with cytoarchitectonic maps. Figure S2 presents the results with divided CA subfields (i.e., CA1, CA2, and CA3).

Figure 4.

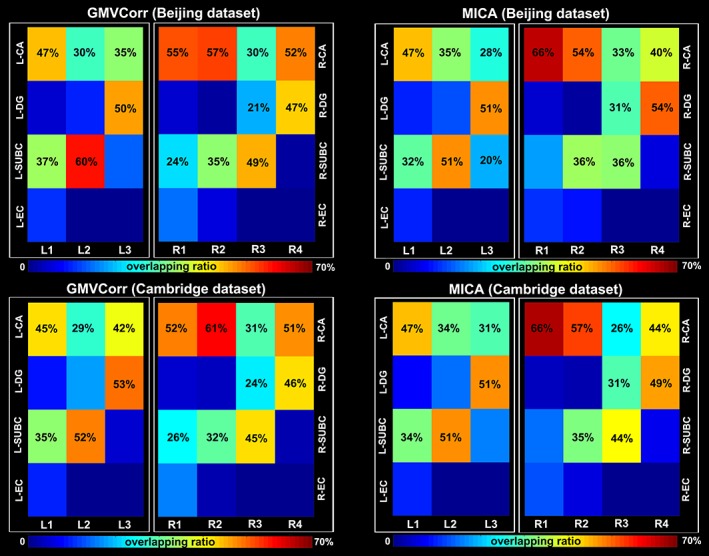
Overlapping ratios between hippocampal subregions and the cytoarchitectonic subfields. Subfields that additively occupy at least 20% of each subregion were numbered. CA = cornu ammonis; DG = dentate gyrus; SUBS = subiculum; EC = entorhinal cortex [Color figure can be viewed at http://wileyonlinelibrary.com]

3.3. GMV covariance maps, resting‐state functional connectivity patterns of hippocampal subregions and their relationships

Different GMV covariance and functional connectivity patterns were found for each subregion (Figure 5). The GMV covariance pattern of L1 included bilateral hippocampal formation (including hippocampus and parahippocampus), amygdala, putamen, caudate, insula, ventral thalamus, posterior cingulate, and bilateral temporal pole. The left posterior‐medial portion, L2, was positively correlated with the bilateral hippocampal formation, fusiform gyrus, middle cingulate, precuneus, dorsal thalamus, and left lateral parietal cortex. GMV of L3 was primarily positively correlated with bilateral hippocampal formation, ventral thalamus, cuneus, calcarine gyrus, and paracentral lobule. For the right anterior‐medial portion, R1, its GMV covariance map mainly included bilateral hippocampal formation, insula, and right middle temporal gyrus. GMV of R2 was positively correlated with bilateral hippocampal formation, amygdala, ventral thalamus, putamen, and bilateral temporal pole. GMV of R3 was positively correlated with bilateral hippocampal formation, amygdala, caudate, dorsal thalamus, precuneus, and bilateral lateral parietal cortex. GMV of R4 was mainly correlated with bilateral hippocampal formation and thalamus. The resting‐state fMRI signal of L1 positively correlated with that of bilateral hippocampal formation, amygdala, bilateral temporal pole, bilateral middle temporal gyrus, bilateral superior temporal gyrus, bilateral precentral and postcentral gyrus, supplement motor area, Please expand VMPFC, dorsomedial prefrontal cortex (DMPFC), bilateral putamen, and left angular gyrus. L2 was primarily correlated with left dorsolateral prefrontal cortex, left superior parietal cortex, left hippocampal formation, bilateral VMPFC, DMPFC, bilateral thalamus, bilateral putamen, bilateral caudate, bilateral posterior cingulate, bilateral calcarine gyrus, bilateral precuneus, and cuneus. L3 was primarily correlated with left hippocampal formation, left middle frontal gyrus, bilateral insula, bilateral lateral parietal cortex, bilateral middle temporal cortex, bilateral precuneus, and middle cingulate cortex. As for R1, its fMRI signal positivity correlated with bilateral hippocampal formation, bilateral thalamus, bilateral putamen and caudate, and supplement motor area. The functional connectivity pattern of R2 was similar to L1 by showing significant correlation with bilateral hippocampal formation, amygdala, bilateral temporal pole, middle temporal gyrus, superior temporal gyrus, precentral and postcentral gyrus, supplement motor area, VMPFC, DMPFC, bilateral putamen, and thalamus. The functional connectivity pattern of R3 included bilateral DMPFC, right middle frontal gyrus, right thalamus, putamen, caudate, bilateral posterior cingulate, bilateral calcarine gyrus and cuneus, and right lateral parietal cortex. The functional connectivity pattern of R4 included right hippocampus, right thalamus, bilateral middle cingulate, bilateral precuneus, bilateral cuneus and precuneus, and bilateral middle frontal gyrus. All structural and functional patterns were well replicated in both data sets.

Figure 5.

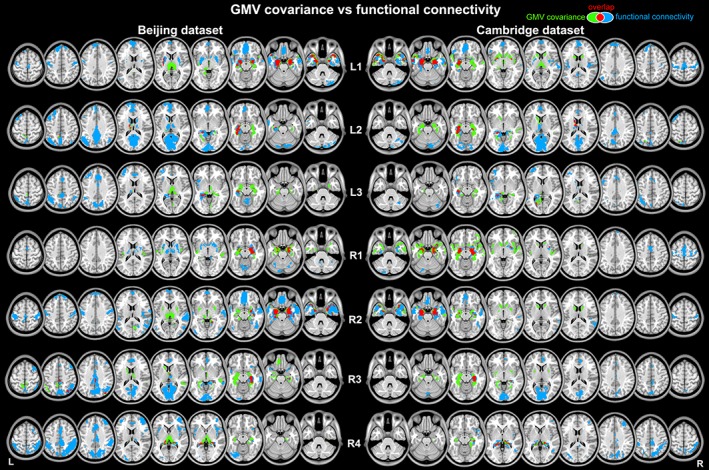
Spatial distribution of the whole brain gray matter volume (GMV) covariance and functional connectivity (FC) patterns for hippocampal subregions. For visualization purpose, the FC patterns are corrected for multiple comparisons at p < .05 (false discovery rate) with a cluster extent threshold of 50 voxels, and the GMV covariance patterns are displayed using a voxel‐level threshold of p < .005 (uncorrected) with a cluster extent threshold of 50 voxels [Color figure can be viewed at http://wileyonlinelibrary.com]

For L1, the structural and functional patterns mainly overlapped at bilateral hippocampal formation, amygdala, left putamen, bilateral middle temporal gyrus, and bilateral temporal pole. For L2, the overlapped regions included left thalamus, parahippocampus, and precuneus. For L3, the overlapped regions included middle cingulate and left parahippocampus. The structural and functional patterns of R1 overlapped at bilateral hippocampal formation and left caudate. For R2, the overlapped regions included bilateral hippocampal formation, bilateral amygdala, bilateral middle temporal gyrus, and bilateral temporal pole. For R3, the overlapped regions located at bilateral parahippocampus, fusiform, and right lateral parietal cortex. For R4, the overlapped regions were at bilateral hippocampal formation.

The correlational results between GMV covariance and functional connectivity patterns are shown in Figure 6. For each subregion, its GMV covariance pattern was most closely related to its own functional connectivity pattern (by showing maximal values, which were marked with black asterisks, in the row of the correlation matrix between GMV covariance maps and functional connectivity patterns). These results suggest that the structural covariance pattern of a particular subregion specifically corresponded with its functional connectivity pattern.

Figure 6.

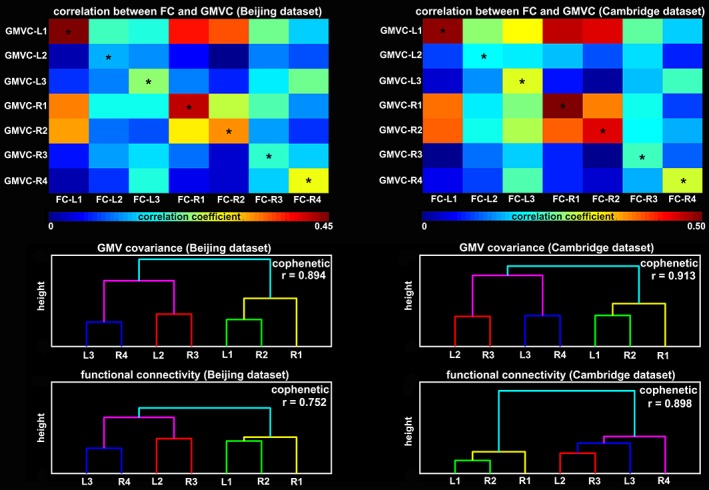
Upper panels: Spatial correlation between functional connectivity (FC) patterns and gray matter volume (GMV) covariance maps of the hippocampal subregions. Lower panels: Hierarchical dendrograms of the seven subregions according to their GMV covariance and FC patterns. The cophenetic correlation coefficients were shown in each of the dendrograms [Color figure can be viewed at http://wileyonlinelibrary.com]

The hierarchical clustering of the GMV covariance patterns grouped L1 and R2, L3 and R4, and L2 and R3 together at a very low height, suggesting high similarity in their structural covariance patterns (Figure 6, lower panel). Furthermore, the group of L1 and R2 was similar with R1, and the group of L3 and R4 merged with the group of L2 and R3. These results were replicated in both data sets. As for the hierarchical clustering of the functional connectivity patterns, Beijing and Cambridge datasets exhibited consistent results by grouping L1 and R2 (further with R1), L2 and R3 together. Nevertheless, for Beijing dataset, the group of L3 and R4 merged with the group of L2 and R3, whereas for Cambridge dataset, the group of L2 and R3 merged with L3 and R4 sequentially (Figure 6, lower panel). The cophenetic correlations of the obtained dendrograms were high (all cophenetic correlation coefficients r > .75) which suggested that the clustering solution accurately represented the underlying similarities and differences among the GMV covariance patterns or functional connectivity patterns.

4. DISCUSSION

To the best of our knowledge, this is the first study to parcellate the human hippocampus based on structural covariance and to elucidate the structural covariance and functional connectivity patterns of the hippocampus at the subregional level. Seven distinct subregions with their structural covariance and functional connectivity patterns were reproducibly identified for bilateral hippocampi across two independent data sets. We demonstrated the close correspondence between structural and functional characteristics of the hippocampal subdivisions. The bilaterally symmetric subregions exhibited similar structural and functional characteristics. Taken together, our results provide a preliminary topographical configuration of the hippocampus with converging structural and functional support, which may improve our understanding of hippocampal connectivity and functions at the level of subregions.

The hippocampus has been parcellated according to its functional connections with the rest of the brain (Blessing et al., 2016; Wang et al., 2016), whereas Adnan et al. (2016) used white matter structural connectivity to parcellate it. However, those commonly used fMRI and probabilistic tractography connectivity‐based parcellation approaches, may not be optimal for small‐sized structures like the hippocampus, due to their low spatial resolution. Inspired by the parcellation of insula (Kelly et al., 2012) and orbitofrontal cortex (Liu et al., 2015) with GMV covariance, we parcellated the human hippocampus based on this technique which emerged from high‐resolution structural images (Mechelli et al., 2005). GMV covariance examines covariation of gray matter morphology between brain regions across populations. The biological meaning of this structural covariance is not yet fully understood, but it may reflect coordinated development and/or maturational synchronization between brain regions (Alexander‐Bloch, Giedd, & Bullmore, 2013), and has been demonstrated as an efficient approach to test network hypotheses about brain aging/developmental mechanisms (Bergfield et al., 2010; DuPre & Spreng, 2017; Li et al., 2013; Montembeault et al., 2012; Nordin et al., 2018; Persson et al., 2014; Spreng & Turner, 2013; Zielinski et al., 2010) and clinical utility for patients (Heinze et al., 2015; Kim et al., 2015; Modinos et al., 2009; Montembeault, Rouleau, Provost, & Brambati, 2015; Seeley et al., 2009).

GMV covariance was recently proposed as a surrogate method for assessing structural networks between different brain regions. The concept of structural covariance networks describes the interindividual differences in regional brain structure covariation with other brain structures across the population (Alexander‐Bloch, Giedd, & Bullmore, 2013). Though the underlying biological meaning of GMV covariance is still unclear, it may reflect shared variation in gray matter morphology (Alexander‐Bloch, Raznahan, et al., 2013; Mechelli et al., 2005) and has been suggested to reflect the synchronized maturational changes medicated by axonal connections forming and reforming over the course of development (Alexander‐Bloch, Giedd, & Bullmore, 2013). To quantify the GMV covariance for parcellation, we used voxel‐by‐voxel linear correlation (GMVCorr) and MICA. These two approaches were complementary to each other in that GMVCorr is a bivariate measure of association of the GMV (across participants) between two voxels, while MICA is a multivariate analytical technique for simultaneously modeling common associations across multiple voxels. Different from GMVCorr that was designed for structural gray matter images (Mechelli et al., 2005), MICA, which is a derivative of ICA (McKeown & Sejnowski, 1998), was initially introduced to detect local functional connectivity networks in particular brain regions (Beissner, Schumann, Brunn, Eisenträger, & Bär, 2014; Dobromyslin et al., 2012; Leech, Braga, & Sharp, 2012). Recently, several studies have begun to employ MICA and fMRI to parcellate brain regions into their functional subdivisions (Blessing et al., 2016; Igelström, Webb, & Graziano, 2015; Kim et al., 2013; Moher Alsady et al., 2016). In the present study, we introduced MICA to quantify GMV covariance for structural brain parcellation for the first time.

The reproducibility of research results is a topic of concern across all scientific disciplines (Poldrack & Poline, 2015), and in particular within the neuroimaging community due to the inconsistent replication of findings. One way to address this issue is through the inspection of independent data sets, and analyzing those data sets with different and/or complementary analytic approaches (Poldrack et al., 2017). A significant strength of the present study is that we discovered highly reproducible (as evidenced by the fairly high Dice's coefficient value between parcellation results obtained with different methods on different data sets) hippocampal subregions by two complementary covariance‐based network measures (GMVCorr and MICA) from two independent data sets with different ethnic populations. The present study demonstrated that GMV covariance serves as a feasible and efficient approach to reliably parcellate the brain regions.

There are some similarities as well as differences between the parcellations of the present study and of others using fMRI data (Beissner et al., 2018; Robinson et al., 2015; Robinson, Salibi, & Deshpande, 2016; Zhao et al., 2019). The longitudinally discrete configuration of the hippocampal subregions in the present study was remarkable, given the widely known model of the long‐axis functional specialization of hippocampus (Poppenk et al., 2013; Strange et al., 2014). More importantly, our results revealed that these GMV covariance‐based subregions additionally distributed along the transverse axis, which corresponded with the spatial configuration of the cytoarchitecturally defined subfields (Amunts et al., 2005). This result is similar to those reported in the fMRI literature (Beissner et al., 2018; Moher Alsady et al., 2016; Zhao et al., 2019), where a transverse distribution of the subregions in the head of the hippocampus is found when the number of clusters was set to a relatively high number. Furthermore, most of these subregions were located in the CA1, dentate gyrus, and subiculum, because these three subfields extend along the anterior–posterior axis mostly (Yushkevich, Pluta, et al., 2015). Future studies should compare the differences between GMV covariance‐based and fMRI‐based parcellation results by fusing these multimodal data with a unified approach, for instance, joint ICA or parallel ICA (Correa, Li, Adali, & Calhoun, 2009).

Gray matter is composed of cell somata and their prolongations forming a dense mesh of connections, the neuropil, and therefore is considered as the neuroanatomical underpinning of neuronal activity. It is plausible to hypothesize that structural covariance and functional connectivity patterns ought to converge and our findings support this hypothesis by showing that the structural covariance pattern of a particular subregion specifically corresponded with its functional connectivity pattern (Figure 6). Further support was shown in a study on healthy volunteers that demonstrated a tight linkage between intrinsic functional connectivity and correlated GMV (Seeley et al., 2009). The study built on notions of small worldness in human cortical gray matter structure by demonstrating a direct, network‐based structure–function relationship. At a large‐scale network level, a more recent study demonstrated the existence of consistent structural covariance networks that corresponded well with several canonical functional networks (Guo et al., 2015). Our results were generally consistent with theirs and extended their ideas by showing that a subcortical region (i.e., hippocampus) also exhibited highly correlated structure–function relationships.

With the hippocampal subregions as seeds, we revealed the structural covariance and functional connectivity patterns with the GMV and fMRI data, respectively. The structural covariance of each subregion showed a slightly symmetrical covariance pattern, whereas the functional connectivity patterns showed a hemispheric asymmetry in many regions. For instance, the GMV of the R4 correlated with the GMV of the bilateral amygdala, bilateral hippocampal formation, and bilateral thalamus; however, the fMRI of R4 correlated primarily with the regions in the right hemisphere, especially in lateral prefrontal and lateral parietal cortex. This result suggests that human brain is functionally and anatomically asymmetric (Kimura, 1973; MacNeilage, Rogers, & Vallortigara, 2009); however, the functional asymmetry is much more striking. Moreover, the functional connectivity patterns of the anterior subregions (L1, R1, and R2) were primarily located at the anterior part of the default mode network (DMN), whereas the functional connectivity patterns of the posterior subregions (L2, L3, R3, and R4) were primarily located at the posterior part of the DMN. This result is not surprising as the hippocampus itself is often considered as a node in this network. By using hierarchical clustering algorithms on the structural covariance and functional connectivity patterns, we additionally demonstrated bilaterally symmetric subregions had similar patterns, both structurally and functionally. For instance, L2 and R3 were approximately symmetrical in their spatial configurations, and they showed similar GMV covariance patterns and functional connectivity patterns. This result was consistent with previous resting‐state network studies (Melie‐García, Sanabria‐Diaz, & Sánchez‐Catasús, 2013; Salvador et al., 2005; Stark et al., 2008) and structural covariance studies (Gong, He, Chen, & Evans, 2012; Mechelli et al., 2005; Nosarti et al., 2011) showing robust correlated spontaneous activity and structural covariance between homotopic regions. Taken together, these results suggest symmetrical subregions are homotopic in nature. This suggestion does not exclude the notion of hemisphere specialization (Robinson et al., 2016), as we found subregions showed more functional connectivity with ipsilateral regions relative to contralateral regions.

This report should be considered in light of some limitations. First, a methodological limitation of our study inherits the limitation of the GMV covariance. The GMV covariance networks are constructed from interregional correlations estimated on the basis of a group of individual images. Methods for the construction of networks from an individual MRI image are needed (Tijms, Seriès, Willshaw, & Lawrie, 2012). However, we revealed converging group‐level results with GMV covariance. Another limitation is that we lack the ethnic group information. The difference between ethnic groups on hippocampus parcellation is a topic for our future study.

In summary, on the basis of GMV covariance, we have parcellated the human hippocampus into several subregions, which were highly replicable in two independent data sets. The resulting subregions may guide future cognitive neuroscience and clinical studies focusing on the structural as well as functional connectivity of the hippocampus. We demonstrated converging and similar structural covariance and functional connectivity patterns for each hippocampal subregion and bilaterally symmetric subregions, respectively. These results further illuminate our knowledge of the topographical configurations of the hippocampus.

CONFLICT OF INTEREST

The authors declare no potential conflict of interest.

Supporting information

Figure S1 Results of the permutation tests on Dice's coefficient values, and the red dots show the real observations of the Dice's coefficient in each condition. Dice's coefficients between different parcellation methods (GMVCorr vs MICA, within each data set) and different data sets (Beijing vs Cambridge, within each method) are shown in the central panel. The color scheme of the bar graphs is the same as that of Figure 3.

Figure S2 Overlapping ratios between hippocampal subregions and the cytoarchitectonic subfields. Subfields that additively occupy at least 20% of each subregion were numbered. L1 and R1 were mainly located in the subiculum and CA1; a large portion of L2 and R3 were located in subiculum; L3 and R4 were mainly located in CA1 and dentate gyrus, and R2 was located in CA1 mainly. In addition, the subregions obtained with different methods on different data sets had similar overlapping patterns with cytoarchitectonic maps. CA1–3: cornu ammonis 1–3; DG: dentate gyrus; SUBS: subiculum; EC: entorhinal cortex.

Ge R, Kot P, Liu X, et al. Parcellation of the human hippocampus based on gray matter volume covariance: Replicable results on healthy young adults. Hum Brain Mapp. 2019;40:3738–3752. 10.1002/hbm.24628

DATA AVAILABILITY

The data that support the findings of this study are openly available in the 1000 Functional Connectomes Project at https://www.nitrc.org/frs/?group_id=296.