Network spread determines severity of degeneration and disconnection in Huntington's disease

Abstract

Trans‐neuronal propagation of mutant huntingtin protein contributes to the organised spread of cortico‐striatal degeneration and disconnection in Huntington's disease (HD). We investigated whether the network diffusion model, which models transneuronal spread as diffusion of pathological proteins via the brain connectome, can determine the severity of neural degeneration and disconnection in HD. We used structural magnetic resonance imaging (MRI) and high‐angular resolution diffusion weighted imaging (DWI) data from symptomatic Huntington's disease (HD) (N = 26) and age‐matched healthy controls (N = 26) to measure neural degeneration and disconnection in HD. The network diffusion model was used to test whether disease spread, via the human brain connectome, is a viable mechanism to explain the distribution of pathology across the brain. We found that an eigenmode identified in the healthy human brain connectome Laplacian matrix, accurately predicts the cortico‐striatal spatial pattern of degeneration in HD. Furthermore, the spread of neural degeneration from sub‐cortical brain regions, including the accumbens and thalamus, generates a spatial pattern which represents the typical neurodegenerative characteristics in HD. The white matter connections connecting the nodes with the highest amount of disease factors, when diffusion based disease spread is initiated from the striatum, were found to be most vulnerable to disconnection in HD. These findings suggest that trans‐neuronal diffusion of mutant huntingtin protein across the human brain connectome may explain the pattern of gray matter degeneration and white matter disconnection that are hallmarks of HD.

1. INTRODUCTION

Huntington's disease (HD) is an autosomal dominant neurodegenerative disease caused by pathological transcription and misfolding of the mutant huntingtin protein (Macdonald et al., 1993). Selective degeneration of medium spiny neurons in the striatum and associated neuropil is an early feature of neuropathology in HD (Mitchell, Cooper, & Griffiths, 1999). Over time, degeneration spreads locally into other regions in the basal ganglia, and distally into the frontal, cingulate, motor, and visual cortices (Mangiarini et al., 1996). In vivo MRI studies of HD have mapped the morphological consequences of cortico‐striatal progression of degeneration and disconnection (Douaud et al., 2006; Georgiou‐Karistianis et al., 2013; Hobbs et al., 2010; Kassubek et al., 2004; Poudel et al., 2014; Tabrizi et al., 2010). In particular, recent longitudinal studies have demonstrated significant degeneration of the striatum and associated cortico‐striatal white matter pathways many years prior to disease onset (Aylward et al., 2011; Poudel, Stout, et al., 2014; Ruocco, Bonilha, Li, Lopes‐Cendes, & Cendes, 2008; Tabrizi et al., 2011; Tabrizi et al., 2013). While these studies provide important insights into the overall consequence of the disease, the factors that determine, and potentially predict, the distribution of neural degeneration and disconnection remains unclear.

Emerging evidence suggests that local and distant neuron‐to‐neuron transfer of pathogenic mHTT may explain the spatial distribution of neurodegeneration in HD (see Jansen, Batenburg, Pecho‐Vrieseling, & Reits, 2017 for a review). Although the precise biomolecular mechanisms of trans‐neuronal mHTT spread remains unclear, synaptic connections play important role. For example, trans‐synaptic transfer of mHTT, involving synaptic vesicle exocytosis (Pecho‐Vrieseling et al., 2014), have been demonstrated in a mouse model of mHTT. Similarly, trans‐neuronal mHTT can spread through vesicle fusion mechanisms, leading to aggregation of mHTT in the distant but axonally connected neurons (Babcock & Ganetzky, 2015). These studies clearly highlight the role of axonal connections in mHTT spread, motivating the hypothesis that the canonical organisation of the axonal connections (human brain connectome) may determine the pattern of neuropathological changes in the HD brain. Previous studies have mapped the brain connectome using diffusion weighted imaging (DWI) based tractography and used it to predict network vulnerability in Alzheimer's and Parkinson's diseases (Raj et al., 2015; Raj, Kuceyeski, & Weiner, 2012; Yau et al., 2018). Others have also used functional connectome mapping —a macroscopic map of the functional interactions across the brain—to identify patterns of neurodegenerative distribution that begin from known pathological epicentres (Seeley, Crawford, Zhou, Miller, & Greicius, 2009; Zhou, Gennatas, Kramer, Miller, & Seeley, 2012). In HD, abnormal changes in both functional and structural brain networks precede the development of symptoms by several years (Harrington et al., 2015; Poudel et al., 2014; Werner et al., 2014). Notably, mutant huntingtin protein appears to target the regions that have high network traffic and low clustering with neighboring regions (Faria et al., 2016; McColgan et al., 2015). More recent work has also demonstrated that white matter pathways, enriched with synaptic and metabolic genes, are more vulnerable in HD (McColgan et al., 2018). However, whether propagation of pathology in HD can be modeled as a diffusion process acting within the human brain connectome remains unknown.

Here, we implemented the network diffusion model (NDM), which has been used extensively to model the distribution of pathology in other neurodegenerative diseases (Pandya, Mezias, & Raj, 2017; Raj et al., 2012; Raj et al., 2015), to investigate whether network spread can determine neural degeneration and disconnection in HD. We hypothesized that (a) the severity of degeneration in HD can be determined by network diffusion and that (b) the white matter connections linking the nodes most susceptible to diffusion are also most vulnerable to disconnection. These predictions are supported by the network‐spread hypothesis that has been tested and validated in other neurodegenerative diseases (Guo et al., 2013; Raj et al., 2012; Seeley et al., 2009; Zhou et al., 2012).

2. MATERIALS AND METHODS

2.1. Data

Data used in the current investigation are from the Australian‐based IMAGE‐HD study (Dominguez et al., 2013; Georgiou‐Karistianis et al., 2013; Poudel et al., 2015; Poudel, Egan, et al., 2014; Poudel, Stout, et al., 2014). For the current investigation, we used retrospectively age‐matched T1‐weighted and diffusion‐weighted (DWI) MRI data from 26 symptomatic HD and 26 healthy control participants from the baseline time‐point. Recruitment procedures, inclusion criteria, and MRI protocol have been published previously (Dominguez et al., 2013; Georgiou‐Karistianis et al., 2013; Poudel, Egan, et al., 2014; Poudel, Stout, et al., 2014; Poudel et al., 2015). Demographic data for the cohort used in the current investigation are provided in Table 1.

Table 1.

Demographic data of the participants in the symptomatic HD and controls used in the analysis

	Controls (n = 26)	HD (n = 26)
Age	47 ± 14	49 ± 7
UHDRS		16 ± 11
CAG		44 ± 2
DBS		377 ± 66
YSD		2 ± 2

Note: UHDRS, motor subscale score Unified Huntingtons Disease Rating Scale (pre‐HD, UHDRS < 5; symp‐HD, UHDRS ≥ 5); CAG: cytosine‐adenine‐guanine (number of repeats >40 is full penetrance); Disease Burden Score: (CAG − 35.5) × age; DBS: disease burden score; YSD: years since diagnosis.

2.2. Structural MRI data processing

The data processing pipeline used in the study have been outlined in Figure 1. MRI data for each subject were processed and analysed using widely accepted neuroimaging analysis tools, including FreeSurfer version 5.3.0 (Fischl et al., 2004), FMRIB Software Library(Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012), and MRtrix(Tournier, Calamante, & Connelly, 2012). Free‐surfer was used to parcellate the T1‐weighted MRI data into 82 distinct cortical and sub‐cortical brain regions in the brain according to the Desikan‐Killiany atlas. Free‐surfer analyses were performed on MASSIVE HPC (http://www.massive.org.au) using the “recon‐all” function. The neuroanatomical labels were inspected for accuracy in all HD and controls. To measure the severity of volume loss in each of the parcellated brain regions, the mean and SD of the volume was estimated. For each region, t‐statistics of the difference between the HD and healthy control participants were calculated using the following equation:

$$t=\frac{{\mu }_{\mathit{\text{controls}}-}{\mu }_{\mathit{HD}}}{\sqrt{\frac{{\sigma }_{\mathit{\text{controls}}}^2}{n_{\mathit{\text{controls}}}}+\frac{{\sigma }_{\mathit{HD}}^2}{n_{\mathit{HD}}}}}$$ (1)

Figure 1.

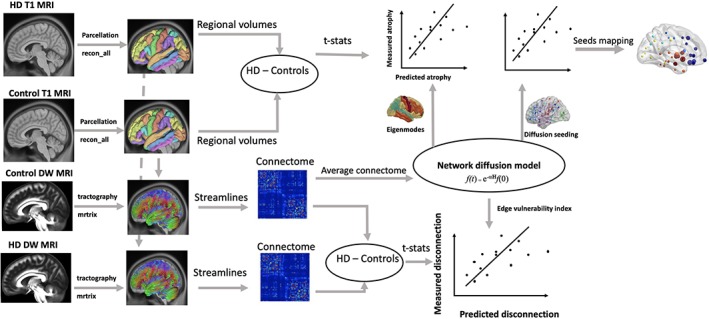
A flow diagram for the data analysis process used in the study. T1‐weighted structural MRI data from healthy controls (N = 26) and HD (N = 26) were parcellated into 82 brain regions using FreeSurfer reconall protocol. Atrophy in these regions were estimated by calculating the t‐statistics of the difference between HD and controls. Diffusion weighted MRI data from healthy controls and HD were used to generate streamlines using constrained spherical deconvolution (CSD) based tractography available in the MRtrix software. The number of streamlines and brain parcels (from FreeSurfer analysis) were combined to obtain connectome matrix, which represented total number of streamlines (edges) connecting each of the brain regions (nodes). The connectomes from healthy controls were averaged to obtain a healthy connectome matrix, which was used to model network diffusion. In the first analysis, eigenvectors of healthy connectome graph Laplacian were identified as eigenmodes of diffusion. The first five eigenmodes were statistically compared against measured atrophy (t‐statistics) using correlation analysis. In the second analysis, network diffusion was run on the healthy connectome by repeatedly initiating diffusion from each regions of the brain. Predicted degeneration for each seed region were statistically compared against measured degeneration. In the third analysis, a measure of predicted disconnection, which was calculated as total diffusion in the corresponding nodes, was estimated for network diffusion from each seed region in the brain. The predicted disconnection was statistically compared against measured disconnection (t‐statistics of the difference in number of streamlines between HD and controls) [Color figure can be viewed at http://wileyonlinelibrary.com]

2.3. Generation of structural connectome

For each individual, the cortical and sub‐cortical parcels in the T1‐weighted space were aligned to DWI space via the application of an inverse transformation matrix derived from the linear alignment of the mean fractional anisotropy (FA) to T1‐weighted images using FSL FLIRT. Constrained spherical deconvolution was used to estimate the distribution of fiber orientations at each voxel of the DWI volume. Whole‐brain probabilistic tractography was then performed, generating one million streamlines to form a representation of the axonal connections in the brain (Tournier et al., 2012). The cortical/sub‐cortical parcellation and whole‐brain tractography were combined to produce 82 × 82 connectome maps for each participant, in which the weight of the connection (edge) between each pair of parcels (nodes) represented the total number of streamlines that start/terminate within a 2 mm radius of each parcel divided by the total volume of the connected nodes. To reduce spurious connections: (a) connections with streamline count less than 10 were set to zero, and (b) a group consensus threshold of 60% was employed so that only connections that were present in at least 60% of the participants in the control group were retained for subsequent analyses.

2.4. Network diffusion model

Network diffusion model was applied on the average brain connectome generated from the healthy controls (N = 26). Connectome was generated as per the description in the previous section. Diffusion is defined as the net passive flow of particles (e.g., mHTT protein molecules) from a higher concentration region to lower concentration region until a state of equilibrium is reached. Network diffusion is used to mathematically model this diffusion process across a structure defined by a set of elements and their interconnections, such as social networks (Ma, Yang, Lyu, & King, 2008) and human brain connectome (Raj et al., 2012). An undirected brain network graph can be represented as G = (v, ε), where v is the set of brain parcels (nodes) given by v = (v₁, v₂, …, v_n) and ε is the set of connections between v _i and v _j (edge) given by ε = (v_i, v_j). The network diffusion model treats the edge (v_i, v_j) as a conduit that connects nodes v_i and v_j through which diffusion can occur. According to the diffusion model, spread of pathology at time t can be modeled as:

$$f{\left(t\right)}_{=}{\mathrm{e}}^{-\mathrm{\alpha }\mathbf{H}}f\left(0\right)$$ (2)

where f(t) denotes the vector consisting of the amount of diffusion of pathology at node v_i at time t, beginning from an initial distribution of pathology given by f(0) at time zero. H is the graph Laplacian defined as the difference between degree matrix and adjacency matrix. Αlpha (α) is the diffusivity constant (assumed to be 1 in our analyses).

The diffusion process f(t) can be estimated as:

$$f\left(t\right)={\sum }_{i=1}^N\left(e^{-\alpha ⋋t}{u}_i^{t}f\left(0\right)\right)u_i$$ (3)

where U = [u₁, u₂, u₃, …u_n] represent eigenvectors of the Laplacian matrix. As shown in a previous study (Raj et al., 2012), and replicated here (Figure S1), eigen vectors of the Laplacian matrix (eigenmodes) associated with smaller eigen values represent persistent modes of diffusion in the human brain connectome (Figure S1).

To assess which eigenmode was most representative of the pattern of atrophy in HD, absolute values of the first five eigenvectors of the Laplacian matrix and measured atrophy (t‐values of the difference between HD and controls) were correlated using Spearman's correlation. Separate correlations were also performed for cortical and sub‐cortical regions. Any correlation with p < .01 (family‐wise corrected p‐value threshold for the first five eigenmodes used in the correlation) was considered to be significant.

2.5. Repetitive network diffusion to identify the epicenters of disease

To assess whether initiating the process of diffusion from any specific region in the brain is most predictive of pattern of atrophy in HD, we simulated the process of diffusion on the healthy connectome by repeatedly initiating the diffusion from all brain regions within the Desikan‐Killiany atlas. For each region i, the network diffusion model is used to estimate the diffusion at all other regions at time t = 1 to 50, with initial condition f( ₀) set as a unit vector with 1 at the ith location and 0 elsewhere. Network diffusion was initiated from bilateral seeds, such that 41 different initial conditions were used. This process generated vectors with 82 elements at each time point. The predicted atrophy vector at all time points, f( _t), were correlated against measured atrophy (t‐value) using Spearman's correlation, resulting in 41 × 50 correlation‐time matrices. To ensure that correlation was not driven by atrophy in the seed regions, we only correlated measured atrophy and predicted atrophy after excluding the seed regions. For each seed region i, we identified the maximum correlation value, which was used as a measure of the likelihood of the region being the putative source responsible for spreading the pathology.

2.6. Identifying the most vulnerable connections

We extend the network diffusion model (Raj et al., 2012 ) to identify the edges most vulnerable to disconnection by taking disease spread process into consideration. We posit that for an edge ε _i,j, it's susceptibility to disconnection is determined by diffusion vulnerability of the corresponding nodes (v_i and v_j). To this end, we define vulnerability of an edge as the total diffusion in the corresponding nodes, given by:

$$p_{i,j}\left(t\right)=f_{i,n}\left(t\right)+f_{j,n}\left(t\right)$$ (4)

Where f _i,n(t) and f _i,n(t) represent accumulation of diffusion at node i and j at time t when node n is used as a seed. There are two variables that need to be accounted for in this definition of edge vulnerability (a) the seed node and (b) the time. To identify the best seed node and model time, we repeatedly initiate the spread from 41 bilateral regions and estimate edge vulnerability associated with each seed node at time t.

To assess whether the measure of edge vulnerability is predictive of disconnection in HD, we used the network based statistic (NBS) (Zalesky, Fornito, & Bullmore, 2010) to identify the connections showing reduced connectivity (i.e., decreased streamline density) in HD, compared to controls. For each connection, we used an unpaired t‐test to compare the change in the magnitude of the edge weight between HD and healthy controls. To test the significance of the group differences, a nonparametric permutation test was performed using 5,000 permutations, an edge‐threshold of t > 2.8, and a component‐level significance threshold of p < .05, as per a standard NBS approach.

To assess the relationship between measured disconnection and edge vulnerability, we simulated the network spread by initiating the diffusion from each bilateral pair of nodes over model times 1 to 50. Hence, for each seed region, a vector representing the vulnerability of the edges was estimated. This process generated a matrix of K times t, where K is the number of edges, and t is the model time. T‐statistics representing the difference between HD and controls were correlated (Spearman) with edge vulnerability estimated from the network diffusion model. This process generated a 41 × 50 matrix of correlation values. The seed region showing the greatest correlation between predicted and measured disconnection was identified as that most responsible for spreading disconnection in HD.

2.7. Network spread on random networks

To investigate whether network spread on the healthy human brain connectome is a significant finding, we compared the findings against network spread on random networks. To this end, we simulated network diffusion model on 2000 random network models and identified the maximum association between predicted and measured degeneration. The random networks used in the simulation maintained the weight, degree, and strength distribution of the healthy connectome. The distribution of maximum correlation between measured atrophy (t‐stats) and predicted atrophy obtained from random networks were plotted, which allowed us to compare the null model against true associations. We also tested the significance of network spread by randomly assigning the 82 brain regions with 2,000 different permutations of true atrophy vector. The distribution of maximum correlation between NDM predicted atrophy and scrambled atrophy vector provided another null model to test the significance of the true association. To investigate whether edge vulnerability identified from network diffusion model is a significant finding, we further simulated the relationship between predicted and measured disconnection using 2000 random network and 2000 randomly scrambled disconnection vectors.

3. RESULTS

3.1. Pattern of degeneration in HD compared to controls

The brain regions showing volume loss in HD compared to the healthy control group (p < .05) are listed in Table 2. The regions most affected are in the basal ganglia, with the caudate, putamen, pallidum, and accumbens showing greatest loss of volumes. In the frontal lobe, inferior frontal gyri (parstriangularis and parsopercularis), precentral gyrus, and postcentral gyrus show volume loss in HD. Other brain regions in Occipital, Parietal, and Temporal lobes were spared in our HD cohort (Table S1).

Table 2.

Comparison of regional volumes in HD and healthy controls. Only the regions showing loss of volumes in HD at p < .05 are shown in the table

Brain regions	Controls (mm3)	HD (mm3)	Control vs HD (t‐values)	Control vs HD (p‐values)
Caudate	3,712.74	2,390.85	10.96	<.00001*
Putamen	5,385.55	3,560.33	9.93	<.00001*
Pallidum	1,432.41	1,092.35	4.82	<.00001*
Accumbens area	495.87	354.8	4.57	<.00001*
Amygdala	1,695.71	1,526.41	2.64	.011
Parstriangularis	2089.42	1881.9	2.4	.02
Postcentral	6,675.98	6,254.48	2.16	.036
Parsopercularis	2,371.88	2,187.63	2.03	.047
Precentral	7,967.71	7,531.21	2.02	.049

* denotes FWE corrected.

3.2. Eigen‐modes of the healthy human brain connectome determines spatial distribution of atrophy in HD

Of the first five eigen modes, selected based on their decay characteristics, the spatial pattern associated with the fifth eigenmode captured the cortico‐striatal pattern of degeneration associated with HD (Figure 2a). There was a significant association between the measured atrophy and the atrophy predicted by the fifth eigenmode in the cortical and sub‐cortical nodes when considered together (r = .33, p = .003), as well as when subcategorized (cortical: r = .52, p < .001; sub‐cortical: r = .69, p < .001; Figure 2b). The first four eigenmodes of healthy connectome also demonstrated distinct spatial patterns, but they were not significantly associated with HD atrophy pattern (Figure S2). There was a significant correlation between the first eigenmode and average regional volume in the healthy brain generated from the healthy controls (i.e., the global effect; Figure S2).

Figure 2.

Visualization of the measured and predicted atrophy. (a) Visual comparison of measured and predicted atrophy displayed on the brain surface. The predicted atrophy is based on the absolute value of the fifth eigenmode of the healthy brain connectome Laplacian matrix. The measured atrophy pattern is based on the t‐value of the difference in grey‐matter volume in the 82 parcels from Desikan‐Killiany atlas. Colour range is chosen such that darker red represents greater atrophy. T‐values values were transformed to z‐scores for comparison. (b) Scatter plot showing linear association between predicted and measured atrophy in cortical and sub‐cortical nodes. Spearmans correlation values (r) and associated p‐values are provided within the scatter plot. The correlation analysis was performed for cortical and sub‐cortical nodes separately [Color figure can be viewed at http://wileyonlinelibrary.com]

3.3. The brain regions critical for generating the spatial distribution of atrophy

Figure 3 shows the result of repeated diffusion analysis with all 82 cortical–subcortical regions within the Desikan‐Killiany atlas as the potential origin of the disease spread across the healthy brain connectome (Figure 3a). The thalamus, accumbens, lateral orbitofrontal cortex, and insula show moderate to strong association between predicted and measured atrophy (Figures 3b,c). Maximum association between the predicted and measured atrophy was identified when diffusion was initiated from the thalamus (r = .52, p < .001) and accumbens (r = .52, p < .001). Application of network diffusion on random network showed that the findings using the healthy brain connectome are significantly different from null models. The distribution of maximum association (Pearson's correlation values) between the measured atrophy and the predicted atrophy identified from the 2,000 random networks is shown in Figure S3A. This distribution, (Gaussian with mean: 0.31 and SD: 0.042) shows that the association obtained from healthy connectome (r = .52) is much higher and statistically outside the 95% confidence interval (p < .05) of the null network. The distribution of maximum associations when the spatial location of atrophy was randomized is shown in Figure S3B, which demonstrates that reported associations predicted by network diffusion on healthy connectome cannot be explained by chance.

Figure 3.

The spatial distribution of diffusion over time in the brain networks when each of the 82 brain regions are used as starting point of diffusion. (a) Curves showing evolution of correlation between the measured and predicted atrophy when the spread was initiated from each region in the Desikan‐Killiany atlas (bilaterally). Y‐axis shows the correlation values (Pearsons correlation) and x‐axis shows time in number of years. The regions showing the highest correlation (Pearsons correlation) between the measured (t‐statistics of the difference between HD and controls) and predicted atrophy (amount of diffusion) are the thalamus, accumbens, lateral orbitofrontal cortex, and insula. (b) Scatter plot of the correlation between predicted and measured atrophy at t = 3 for the initiation of diffusion‐based spread from the thalamus. (c) Visual representation of maximum correlation values obtained for each node using spherical balls plotted on a surface brain. The size of the ball corresponds to the maximum correlation between predicted and measured atrophy. Balls are colour coded by lobe—Dark blue (frontal), light blue (motor), sky‐blue (parietal), yellow (visual), orange (temporal), and dark red (sub‐cortical) [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4. Network diffusion determines disconnection in HD

Figure 4 shows the results of network based statistical comparison of the number of white matter streamlines in HD and controls. HD compared to controls showed significant disconnection in interhemispheric connections in the motor, frontal, and parietal cortices and cortico‐striatal connections (Figure 4a). The network edges with the highest edge vulnerability index encompassed interhemispheric connections and cortico‐striatal connections. The highest association between the measured and predicted disconnection was observed when diffusion was initiated from the pallidum (r = .36, p < .001) at model time 3. The pallidum, putamen, accumbens, insula, and caudate were the regions showing the greatest association (r > .3). The association remained significant after correcting for edge weights (r = .35, p < .001). Simulations using random networks and random shuffling of the disconnection vectors show that the findings cannot be explained by chance (Figure S4).

Figure 4.

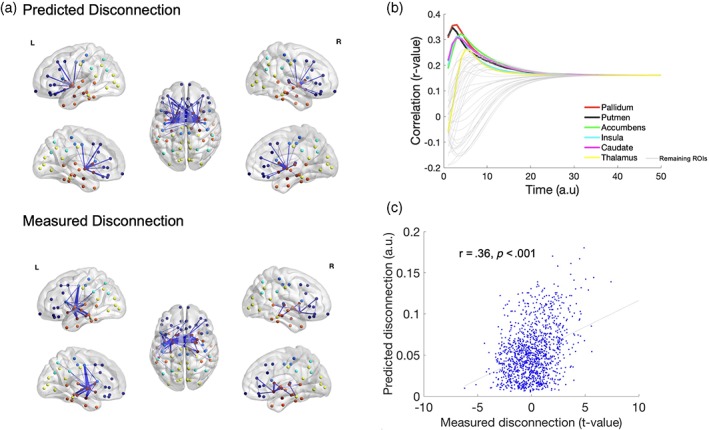
Network diffusion determines white matter disconnection in HD compared to controls. White matter disconnection in HD compared to controls was determined using network‐based statistics comparison of the number of streamlines (generated by tractography) in HD compared to controls. (a) Visualisation of the measured white matter disconnection (identified using network‐based statistics) and predicted disconnection (top 2% of the most vulnerable edges) using ball and stick plots overlaid on the surface of the brain. Balls are colour coded by lobe—Dark blue (frontal), light blue (motor), sky‐blue (parietal), yellow (visual), orange (temporal), and dark red (sub‐cortical). Connections are shown as blue lines between the nodes. (b) Curves showing evolution of correlation between measured (t‐value of the difference between HD and healthy controls) and predicted disconnection when diffusion is initiated from each region in the Desikan‐Killiany atlas (bilaterally). The regions showing the highest correlation are the pallidum, putamen, accumbens, insula, and cortex. The unit of models diffusion time t is arbitrary. (c) Scatter plot of association between predicted and measured disconnection at t = 3 when the initiation of the diffusion based spread was from the pallidum [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

We show that the trans‐neuronal spread of pathology across the brain in HD can be modeled as diffusion across the human brain structural connectome, with this model successfully recapitulating the pattern of neural degeneration and disconnection observed in HD. Seeding the diffusion process from the striatum and thalamus in particular procreates the pattern of cortical degeneration in HD. Notably, the axonal connections most culpable in the disease spread were also selectively vulnerable to disconnection, particularly when the striatum was assumed to be the disease epicenter. These findings demonstrate the potential utility for network diffusion in predicting the evolution of neural degeneration and disconnection in HD. They also provide a framework to test trans‐neuronal spread hypothesis in HD.

Degeneration in the motor cortex, prefrontal cortex, temporal cortex, and the striatum is a hallmark of symptomatic HD (Aylward et al., 2011; Dominguez et al., 2013; Ruocco et al., 2008; Tabrizi et al., 2011; Tabrizi et al., 2013). The fifth eigenmode of the healthy connectome, identified in the current study, is concordant with this selective vulnerability of the cortico‐striatal network in HD. Notably, the first four eigenmodes observed in our study were similar to the eigenmodes previously identified and found to be associated with other neurodegenerative conditions including Alzheimer's disease subtypes (Raj et al., 2012; Raj et al., 2015). Within the fifth eigenmode, the association between the predicted and measured atrophy varied according to the location of the nodes, such that the relationship was stronger in sub‐cortical nodes than in cortical nodes. This is consistent with the hypothesis that sub‐cortical regions show the earliest degeneration in HD. Diverse relationships within and between the cortical and sub‐cortical nodes may also be interpreted as macroscopic consequences of distinct neuropathological processes, such that cell‐autonomous processes may cause early striatal atrophy, whereas trans‐neuronal propagation could drive cortical atrophy. While the neurobiological underpinning of such structured distribution of the disease remains unclear, recent work from transgenic mouse models of HD suggest that both paracrine spread, via extracellular space, and neuron‐to‐neuron transmission of misfolded huntingtin protein, may play important roles (Pecho‐Vrieseling et al., 2014). Trans‐neuronal spread can also occur across synapses, which provides a putative neuro‐biological basis of disease spread through diffusion within the intrinsic networks of the brain.

When network diffusion was emulated for each brain regions, maximum correlation between predicted and measured atrophy was observed for the accumbens and thalamus. The accumbens, in particular, generated the most stable spatial pattern of diffusion, consistently recapitulating the atrophy pattern in HD over time. Previous studies have shown that the striatum, including the caudate, putamen, and accumens, show early loss of neurons and morphological changes in HD (van den Bogaard et al., 2011). Notably, the loss of neurons in these sub‐cortical structures have the greatest influence on predicting the motor and cognitive disturbances in symptomatic HD (Backman, Robins‐Wahlin, Lundin, Ginovart, & Farde, 1997). The finding of selective and targeted spread of disease from the striatum to the cortex is also consistent with the evidence of regional selectivity in cortical atrophy, as maximum degeneration is observed in the sensorimotor regions with the strongest connections to the striatum (Bohanna, Georgiou‐Karistianis, & Egan, 2011; Rosas et al., 2008). Other sub‐cortical structures such as the thalamus, amygdala, and hippocampus are relatively spared in the early stage of the disease (van den Bogaard et al., 2011). The finding that the initiation of spread from the thalamus can also predict the pattern of atrophy in HD was unexpected. The correlation between predicted and measured atrophy was also high when diffusion process was initiated from the thalamus. This finding was unexpected as the thalamus is not one of the most vulnerable regions in HD. However, the thalamus is a hub region which forms strong and dense interconnections with most of the cortical and sub‐cortical structures (van den Heuvel & Sporns, 2011). Therefore, the hubness and its proximity to the striatum may make the thalamus an important node for spatial distribution of pathology in HD.

Consistent with several previous studies, we also demonstrate significant loss of interhemispheric and cortico‐striatal white matter connections in HD (Bohanna et al., 2011; McColgan et al., 2018; Poudel et al., 2015; van den Bogaard et al., 2011; Zhang et al., 2018). Axonal degeneration has been shown to be an early pathological event in HD and has been observed even in the absence of neural degeneration (Li, Li, Yu, Shebourne, & Li, 2001; Wang et al., 2008). Axonal degeneration in HD is thought to result from the aggregation of mHTT in axons, as well as abnormal oligodendrocyte function. More importantly, axonal disconnection explains cognitive and motor impairment even in the early stages of the disease(Szabo et al., 2011). Here, we provide a framework to explain the disconnection in HD and show that connections most involved in the disease spread are also the most vulnerable. A number of previous studies have attempted to develop mechanistic framework underlying selective disconnection in HD. One study provided evidence for a direct relationship between topological length and rate of white matter degeneration in premanifest stages of HD (McColgan et al., 2017). Another recent study has demonstrated an association between gene expression profiles and loss of connections over time in HD (McColgan et al., 2018). Our finding shows that the process of diffusion itself ‐ whereby abnormal protein aggregates spread along the connections (edges) between brain regions (nodes)—may render the edges vulnerable to disconnection.

A number of important factors should be taken into consideration when interpreting our findings. The network diffusion, used in the current study, models the distribution of pathology in HD as a linear passive diffusion process. However, a number of previous studies have demonstrated that the neurobiological mechanisms underlying trans‐neuronal spread is an active process, which may involve synaptic vesicles (see Jansen et al., 2017 for a review). Hence, nonlinear active models will be necessary to better capture the neurobiological mechanisms of the disease spread in HD. The study relied on diffusion weighted imaging based tractography to infer the axonal connectivity between brain regions. Although the use of canonical human brain connectome, based on diffusion MRI and tractography, to predict atrophy spread is in line with previous studies (Pandya et al., 2017; Raj et al., 2012), a model that is informed by cellular level degeneration and detailed microconnectome is necessary to corroborate our findings. The current findings were validated only in one HD dataset (IMAGE‐HD). The data from other studies (e.g., Track‐HD, Predict‐HD) could be used to further validate network spread in HD. The findings are also limited to cross‐sectional group‐level differences in symptomatic HD compared to controls. More recent models of network diffusion, applied on Alzheimer's disease, allow individual‐level prediction of potential seeds of neurodegeneration from longitudinal MRI data (Torok et al., 2018). The implementation of longitudinal network diffusion model is necessary to causally explain the evolution of neural degeneration and disconnection in HD.

In summary, we showed that trans‐neuronal diffusion of mHTT, constrained by intrinsic structural organization of the human brain, may explain the pattern of cortical atrophy and white matter disconnection in HD. The network diffusion model helped elucidate the cortico‐striatal pathways of disease distribution and to determine why some brain regions and circuits are selectively vulnerable in HD.

DECLARATION OF INTEREST

G.F.E. reports grants from Siemens Healthcare Australia, outside the submitted work.

DATA SHARING AND ACCESSIBILITY

The code and connectivity data that support the findings of this study are openly available in github at https://github.com/govin2000/NetworkSpread. The raw neuroimaging data files are available upon request from the CHDI foundation (https://chdifoundation.org/).

Supporting information

Figure S1 Properties of eigen‐values and eigen‐vectors of healthy connectome Laplacian matrix. (A) Sorted eigen values of healthy connectome Laplacian matrix showing that most eigen‐vectors are associated with large eigen‐values. Only a small number of first few eigen vectors are associated with small eigen values. (B) Decay of the eigen modes over time, demonstrating that only the first few eigenmodes are persistent modes.

Figure S2: Spatial patterns associated with first 4 eigen‐modes of healthy connectome Laplacian matrix. 1st, 2nd, 3rd, and 4th eigenmodes are mapped onto cortical surface using free‐surfer Desikan‐Killiany Atlas (82 parcels). The 1st eigen‐mode corresponds to the healthy brain volume, as shown in the scatter plot on the left. 2nd eigen‐mode corresponds to temporal pattern. 3rd eigen‐mode corresponds to fronto‐parietal pattern. 4th eigen‐mode corresponds to Parieto‐occipital pattern. 2nd, 3rd, and 4th eigen‐modes do not show significant association with HD atrophy pattern. Red dots represent sub‐cortical nodes and blue dot represents cortical nodes.

Figure S3: Distribution of r‐statistics of the relationship between measured and predicted atrophy obtained from null networks. (A) Histogram of maximum correlation between predicted and measured atrophy in 2000 random connectomes with preserved weight, degree and strength distributions of healthy connectome (B) Histogram of maximum correlation between atrophy measured using 2000 randomly shuffled atrophy vectors and atrophy predicted by applying NDM on the healthy connectome.

Figure S4: Distribution of r‐statistics of the relationship between measured and predicted disconnection from null networks. (A) Histogram of maximum correlation between predicted and measured disconnection in 2000 random connectomes with preserved weight, degree and strength distributions of healthy connectome (B) Histogram of maximum correlation between disconnection randomly shuffled for 2000 times and disconnection predicted by applying network diffusion on healthy connectome.

Table S1: Comparison of regional volumes in HD and healthy controls, where the difference was not significant at p < .05.

Poudel GR, Harding IH, Egan GF, Georgiou‐Karistianis N. Network spread determines severity of degeneration and disconnection in Huntington's disease. Hum Brain Mapp. 2019;40:4192–4201. 10.1002/hbm.24695