Abstract
Functional connectivity network provides novel insights on how distributed brain regions are functionally integrated, and its deviations from healthy brain have recently been employed to identify biomarkers for neuropsychiatric disorders. However, most of brain network analysis methods utilized features extracted only from one functional connectivity network for brain disease detection and cannot provide a comprehensive representation on the subtle disruptions of brain functional organization induced by neuropsychiatric disorders. Inspired by the principles of multi‐view learning which utilizes information from multiple views to enhance object representation, we propose a novel multiple network based framework to enhance the representation of functional connectivity networks by fusing the common and complementary information conveyed in multiple networks. Specifically, four functional connectivity networks corresponding to the four adjacent values of regularization parameter are generated via a sparse regression model with group constraint (l2,1‐norm), to enhance the common intrinsic topological structure and limit the error rate caused by different views. To obtain a set of more meaningful and discriminative features, we propose using a modified version of weighted clustering coefficients to quantify the subtle differences of each group‐sparse network at local level. We then linearly fuse the selected features from each individual network via a multi‐kernel support vector machine for autism spectrum disorder (ASD) diagnosis. The proposed framework achieves an accuracy of 79.35%, outperforming all the compared single network methods for at least 7% improvement. Moreover, compared with other multiple network methods, our method also achieves the best performance, that is, with at least 11% improvement in accuracy.
Keywords: computer‐aided diagnosis, functional connectivity network, multi‐kernel fusion, multi‐view group‐sparse network, multi‐view learning, resting‐state functional magnetic resonance imaging (R‐fMRI)
1. INTRODUCTION
Human brain is a complex yet efficient network, in which anatomically distant brain regions are functionally integrated to perform specialized information processing. In the past two decades, resting‐state functional magnetic resonance imaging (R‐fMRI) has been widely applied as a powerful tool to explore intrinsic functional connectivity of the brain, avoiding the challenge of designing tasks and the task‐induced influences (Biswal, Yetkin, Haughton, & Hyde, 1995; Greicius, 2008; van den Heuvel & Hulshoff Pol, 2010). Functional connectivity is the temporal correlation between neural activity patterns (fMRI signals) from different brain regions, and can usually be represented by a connectivity network comprised of nodes, and edges between nodes (van den Heuvel & Hulshoff Pol, 2010). Here, the nodes are brain regions and the edges are the time correlations between two brain regions. Therefore, functional connectivity is often referred as functional connectivity networks (FCNs). FCN has been of great importance for discovering the functional organization of human brain and searching for the biomarkers of the neuropsychiatric disorders (Fornito, Zalesky, & Breakspear, 2015).
Researchers have discovered disruptions of FCN in neuropsychiatric diseases, such as Alzheimer's disease (Greicius, Srivastava, Reiss, & Menon, 2004; Wang et al., 2013), mild cognitive impair (MCI) (Bai et al., 2011; Das et al., 2013), depression (Greicius et al., 2007; Yang et al., 2016), autism spectrum disorder (ASD) (Anderson et al., 2011; Assaf et al., 2010; Cheng, Rolls, Gu, Zhang, & Feng, 2015; Ebisch et al., 2011), and schizophrenia (Wang, Xia, et al., 2014). On the other hand, machine learning techniques have been proven to be very effective in identifying biomarkers for brain disease diagnosis based on FCN (Chen, Zhang, et al., 2016; Jiang, Zhang, & Zhu, 2014; Khazaee, Ebrahimzadeh & Babajani‐Feremi, 2015; Sato et al., 2015; Wee, Yap, Zhang, Wang, & Shen, 2014; Zhang, Hu, Ma, & Xu, 2015). Here, we focus on exploring biomarkers from FCN for ASD diagnosis using state‐of‐the‐art machine learning techniques. ASD is a group of neurodevelopmental disorders that cause abnormal social behavior, impaired communication and language skills, and repetitive/stereotyped behavior (Amaral, Schumann, & Nordahl, 2008, American Psychiatric Association, 2013). It has been reported to occur in about 1% of children, resulting in immense suffering to patients and also burden to their families (Kim et al., 2011; Lai, Lombardo, & Baron‐Cohen, 2014). Recent machine learning based studies advanced the discovery of new neuroimaging‐based biomarkers for computer‐aided ASD diagnosis (Chen et al., 2015; Chen, Duan, et al., 2016; Cheng et al., 2015; Guo et al., 2017; Iidaka, 2015; Nielsen, Zielinski, Fletcher, Alexander, Lange, Bigler, Lainhart, & Anderson, 2013; Plitt, Barnes, & Martin, 2015; Price, Wee, Gao, & Shen, 2014; Wee, Yap, & Shen, 2016).
In spite of some promising results, due to the complexity and substantial heterogeneity of neuropsychiatric disorders, identifying effective biomarkers is still a challenging task, which requires more advanced feature representation method to better capture subtle disease‐related FCN disruptions. Most of the existing R‐fMRI based disease identification frameworks utilize only one FCN, from which features are extracted for classification. However, the brain is the most complex system in the human body, causing immense difficulty in understanding the functional mechanism of the brain via simple representation, such as using a single network with predefined sparsity level (Wee et al., 2014). Moreover, using only one single FCN could not comprehensively capture subtle disruptions of brain functional organization induced by neuropsychiatric disorders (Plitt et al., 2015). Each network can only capture a part of between‐group differences and identify some patients correctly, which often causes serious results, that is, certain patients cannot be identified timely to receive effective treatment. Inspired by the concept of multi‐view learning which utilizes information from multiple perspectives of an object to enhance its representation (Gong, Ke, Isard, & Lazebnik, 2014; Jin et al., 2014; Wu et al., 2016; Xu, Tao, & Xu, 2013), multiple FCNs can be used in a similar way to provide a more descriptive and informative representation on the functional organization of the brain. In the multi‐view learning, a feature set is extracted from each view to provide some different yet complementary information. For instance, we can use face images, taken from different angles, to help to identify a person. Since parts of the face or body of a person may be occluded in some images, combining information from different view images can provide a more comprehensive representation of the same person, leading to better recognition performance than using just a single view image. Similarly, multiple networks can also be considered as the multiple “views” of the functional organization of the same brain. An fMRI scan can be used to generate multiple networks, and thus multiple sets of features can be extracted from these networks. Each network is assumed to convey distinct information from other networks, and the fusion of multiple networks provides more comprehensive description of the brain, leading to better classification performance than the single network based methods.
It is worth exploring how to construct multiple networks of the brain to enhance the representation of FCNs. To our knowledge, only a few previous studies explored the construction of multiple networks for R‐fMRI based disease classification (Wee, Yap, Denny, Browndyke, Potter, Welsh‐Bohmer, Wang, & Shen, 2012a; Jie, Zhang, Wee, & Shen, 2014; Price et al., 2014). However, these methods do not construct multiple networks based on the principles of multi‐view learning and have some limitations. For example, Wee et al. (2012a) ignores the fact that the brain networks are intrinsically sparse and concatenating features for classification easily leads to overfitting in a small size of samples. Substantially, this method is single‐view learning as it does not jointly optimize information from multiple FCNs. The method proposed by Jie et al. (2014) achieves good performance for MCI detection, but has three limitations. First, similar to Wee et al. (2012a), Pearson's correlation based networks are not sparse and contain many spurious or insignificant connections, which may degrade the classification performance. Second, this method abandons some valuable topological structures when deriving consistent subnetworks across subjects, which may lead to information loss. Third, the use of predefined thresholds makes it difficult to be extended to detection of other brain diseases. The method proposed by Price et al. (2014) suffers from the need of manually selecting a subset of biologically meaningful spatial maps from all maps derived using group independent component analysis (ICA), which cannot automatically be performed for classification. The discriminative networks are required to be selected from several hundred spatial networks on multi‐scale windows for fusion classification. This method is quite complex and suitable for brain disease classification based on dynamic functional connectivity. Here, we investigate multiple network construction based on static functional connectivity using the consensus and complementary principles of successful multi‐view learning. We will overcome the limitations of the above methods, by providing an appropriate framework to enhance the representation of FCNs through fusion of multi‐view information.
For multi‐view learning, it is very crucial to extract discriminative features from multiple FCNs for classification purpose. Many R‐fMRI based disease diagnosis studies directly utilized functional connectivity as the input features to the classifier (Chen et al., 2015; Chen, Duan, et al., 2016; Cheng et al., 2015; Iidaka, 2015; Nielsen, Zielinski, Fletcher, Alexander, Lange, Bigler, Lainhart, & Anderson, 2013; Plitt, Barnes, & Martin, 2015). However, both high dimensionality and distributed variability of functional connectivity make feature selection difficult in selecting the discriminative functional connections (Varoquaux & Craddock, 2013). Compared to the connectivity‐based approaches, graph theory metrics, which provide a quantified summary on the topological organization of a network, draw considerable attention due to their meaningful interpretation, low dimensionality and easy computation (Bassett & Bullmore, 2006; He, Chen, & Evans, 2007; Li et al., 2013; Rubinov & Sporns, 2010; Sporns & Zwi, 2004). More importantly, they have been proven to be able to reveal functional connectivity abnormalities in neuropsychiatric disorders in high level representation (Baggio et al., 2014; Harrington et al., 2015; Stam et al. 2009; Wang et al., 2009, 2013; Zhang, Wang, Wu, et al., 2011). Local clustering coefficient of a node in a FCN (graph) which quantifies how close its neighboring nodes are to be a clique can be used to reflect functional segregation among the brain regions (Rubinov & Sporns, 2010). Compared to the binary clustering coefficient that considers only the number of links between the neighboring nodes, the weighted clustering coefficient uses the actual amount of interactions between the neighboring nodes to quantify the clustering of the nodes, and can thus capture connection details of network topology to provide a more comprehensive feature representation. The weighted clustering coefficients proposed by Onnela et al. (2005) have been used in Wee et al. (2012a) and Jie et al. (2014) to extract features from multiple networks for identifying MCI subjects. However, the performance of different weighted clustering coefficients should be further investigated.
In this paper, we propose a novel multiple network construction method to generate a set of FCNs with different sparsity levels of topological structures, and then fuse network level features from all FCNs to enhance feature representations. Specifically, we construct multiple FCNs with different sparsity levels by varying the regularization parameter of an l2,1‐norm based group‐constrained sparse regression model (Wee et al., 2014). This model can ensure that brain networks are sparse without spurious or insignificant connections, and topological structure of FCN for each sparsity level is identical across subjects to facilitate between‐subject comparison. We fuse multiple group‐sparse FCNs with adjacent values that are determined based on the training set, to enhance the common intrinsic topological structure and limit the error rate caused by different views. Meanwhile these group‐sparse networks with different sparsity levels provide complementary information different from each other in a granular fashion to capture subtle disease‐associated alterations in functional connectivity. To quantify the subtle differences of each group‐sparse network at local level, we compute a modified version of weighted local clustering coefficients. Specifically, we define the weighted clustering coefficients by replacing the connection status between two neighbors connected to a node in the binary clustering coefficient (Watts & Strogatz, 1998) with their connection weight. We compare the performance of the proposed method with both single network methods and other multiple network methods for identifying ASD children from typically developing (TD) children. We also compare the performance of our weighted clustering coefficient with that proposed by Onnela et al. (2005). Finally, the improvement effect of our proposed multiple network method is discussed in detail, and several most discriminative brain regions are identified and analyzed as biomarkers for ASD diagnosis.
It is noteworthy that the proposed method is different from our previous method which uses a group‐constrained sparse regression model to construct a FCN for MCI diagnosis (Wee et al., 2014). First, to the best of our knowledge, using different amount of sparsity constraint to obtain a set of networks from the same brain has not been investigated in the previous resting‐state fMRI studies. Second, these networks are used in a multi‐view way for guiding the classification, which is also new for the resting‐state functional networks. Finally, multiple brain networks often exist for each person, that is, such as including the default mode network, motor network, attention network, and salience network (Buckner, Andrews‐Hanna, & Schacter, 2008; Biswal et al., 1995; Ptak, 2012; Seeley et al., 2007; Yu et al., 2015). The integration of these multiple networks makes the brain perform effectively various tasks. This is the main reason why we would like to get more possible brain networks for better characterizing the insights of the brain at each time point.
2. MATERIALS AND METHODS
2.1. Subjects
The R‐fMRI data utilized in this study were obtained from the open‐access Autism Brain Imaging Data Exchange (ABIDE) database (http://fcon_1000.projects.nitrc.org/indi/abide/) that consists of 17 international imaging sites and was released in 2012 (Di Martino et al., 2014). The aim of ABIDE is to promote our knowledge of ASD neurobiology, biomarker discovery, and innovation of image analysis methodologies. All datasets were anonymous in accordance with HIPAA (Health Insurance Portability and Accountability Act) guidelines and 1,000 Functional Connectomes Project/INDI protocols. For more detailed information about data, one can see http://fcon_1000.projects.nitrc.org/indi/abide/.
To prevent the effects of multi‐site data during comparison, we select to evaluate the performance of the proposed method using just the R‐fMRI data acquired at New York University (NYU) Langone Medical Center, that is, the dataset with the largest sample size. Written informed consent was available from each participant. We select 45 ASD and 47 socio‐demographic‐matched TD children aged between 7 and 15 years old for the analysis. These subjects had no excessive head motion with a displacement of less than 1.5 mm or an angular rotation of less than 1.5° in any direction. There are no significant gender (ASD children: 38 males and 7 females; TD children: 36 males and 11 females; p = .3428), age (ASD children: 11.1 ± 2.3 years old; TD children: 11.0 ± 2.3 years old; p = .7773), and full intelligent quotient (ASD children: 106.8 ± 17.4; TD children: 113.3 ± 14.1; p = .0510) differences between two groups. The detailed demographic information about the used R‐fMRI data is provided in Table 1.
Table 1.
Demographic information of the subjects
| ASD | TD | p‐value | |
|---|---|---|---|
| Male/female | 38/7 | 36/11 | .3428a |
| Age (mean ± SD) | 11.1 ± 2.3 | 11.0 ± 2.3 | .7773b |
| FIQ (mean ± SD) | 106.8 ± 17.4 | 113.3 ± 14.1 | .0510 |
| ADI‐R (mean ± SD) | 38.2 ± 14.3 c | – | |
| ADOS (mean ± SD) | 13.7 ± 5.0 | – |
ASD, autism spectrum disorder; TD, typically developing; FIQ, full intelligence quotient; ADI‐R, autism diagnostic interview‐revised; ADOS, autism diagnostic observation schedule.
aThe p‐value was obtained by chi‐squared test.
bThe p‐value was obtained by two‐sample two‐tailed t‐test.
cTwo patients do not have the ADI‐R score.
2.2. Imaging acquisition and preprocessing
The R‐fMRI data were collected on a 3.0 T Siemens Allegra scanner at the NYU Langone Medical Center. During the resting‐state scan, most subjects were instructed to relax with their eyes open and stare at a white fixation cross in the center of the black screen. The acquisition time lasted for 6 min and a total of 180 volumes of EPI images were acquired (repetition time (TR)/echo time (TE) = 2,000/15 ms, flip angle = 90°, 33 slices, slice thickness = 4 mm, imaging matrix = 64 × 64).
The data were then preprocessed using the Analysis of Functional NeuroImages (AFNI) software (Cox, 1996), including removing the first 10 R‐fMRI volumes, spatial smoothing using Gaussian kernel with the full width at half maximum (FWHM) of 6 mm, signal detrending, band‐pass filtering (0.005–0.1 Hz), regression of nuisance signals (ventricle, white matter, and global signals), and normalization to the Montreal Neurological Institute (MNI) space with a resolution of 3 × 3 × 3 mm3. To decrease the effects of head motion as soon as possible, we also regressed out six head motion signals before computing the functional connectivity. The brain was parcellated into 116 regions of interest (ROIs) according to the Automated Anatomical Labeling (AAL) atlas (Tzourio‐Mazoyer et al., 2002). The average fMRI time series was computed for each ROI. After preprocessing, we obtained the average fMRI time series of 116 ROIs.
2.3. Classification framework
Figure 1 illustrates the overview of the proposed multiple network based ASD identification framework. This framework consists of four stages, including (1) multiple network construction, (2) feature extraction, (3) feature selection, and (4) feature fusion and classification. Unlike previous multiple network construction methods (Wee, Yap, Zhang, Denny, Browndyke, Potter, Welsh‐Bohmer, Wang, & Shen, 2012a; Jie et al., 2014; Price et al., 2014), we propose to construct multiple group‐sparse FCNs for each subject through different values of regularization parameter of the group‐constrained sparse regression modeling (Wee et al., 2014). Next, a modified version of weighted local clustering coefficient is extracted for every ROI in each FCN. A two‐stage feature selection method is adopted to identify the most discriminative features for each sparsity level based on the training set. Finally, a multi‐kernel support vector machine (SVM) is adopted to linearly fuse the selected features from FCNs with different levels of sparsity for ASD diagnosis. It is worth noting that we use a leave‐one‐out cross‐validation (LOOCV) to evaluate the performance of the proposed method. Specifically, feature selection and parameter optimization are solely implemented on the training set via the inner cross‐validations to guarantee automatic operation of the whole process and also to avoid the positively biased performance evaluation. In what follows, we will detail the four main stages in our study.
Figure 1.
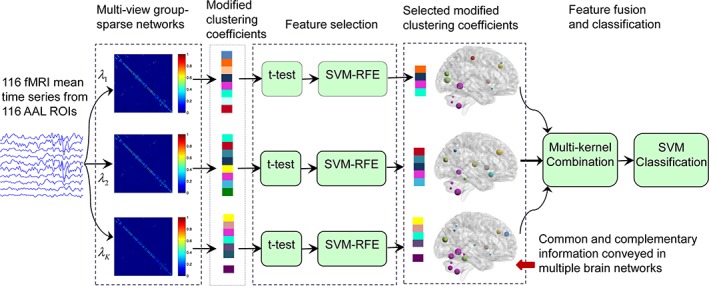
Overview of the proposed classification framework based on multi‐kernel fusion of multiple group‐sparse networks [Color figure can be viewed at http://wileyonlinelibrary.com]
2.4. Construction of multiple group‐sparse FCNs
In this study, we adopt a group‐constrained sparse regression model to infer the functional connectivity among brain regions. Furthermore, we vary the values of regularization parameter to construct multiple group‐sparse FCNs for each subject for characterizing topological structures at different levels of sparsity.
2.4.1. Construction of single group‐sparse FCN
The group‐constrained sparse regression model proposed in (Wee et al., 2014) is adopted at each individual sparsity level to ensure identical topological structures across subjects by imposing an l2‐norm based group‐constraint regularizer into the l1‐norm based sparse model in Equation (1). In the sparse model, the average time series of any ROI can be regarded as a linear combination of the time series of only a few other ROIs, which can be determined via an l1‐norm penalization based linear regression model. Assume that there are a total of N subjects, and each subject has M average time series from M ROIs, with each time series having k time points. Let represent the average time series of the i‐th ROI for the nth subject, and be a data matrix formed by concatenating time series of M ROIs (where the time series of the i‐th ROI is represented as a zero column vector) from the same subject. Sparse network modeling obtains the functional connectivity of the i‐th ROI by solving the following l1‐norm regularized optimization problem (Figueiredo, Nowak, & Wright, 2007):
| (1) |
where, is the M dimensional weighted coefficient vector, reflecting how related other ROIs are to the i‐th ROI, and λ > 0 is the regularization parameter controlling the sparsity of the weighted vector . A higher value of the regularization parameter indicates lesser number of non‐zero elements in the weighted vector. The sparse model is applied to each ROI of the same subject, respectively, to obtain a sparse FCN .
However, FCNs generated based on Equation (1) exhibit significant topological structure variability across subjects, which may potentially decline the classification performance. To overcome this problem, Wee et al. (2014) imposed an l2‐norm based group‐constraint on the generated FCNs for achieving an identical topological structure across subjects. The group‐constrained sparse regression model solves the following objective function to obtain the functional connectivity of the i‐th ROI via multi‐task learning:
| (2) |
where, is a matrix composed of the weighted coefficient vectors of the i‐th ROI from all N subjects, and ∥Wi∥2,1 denotes the summation of l2‐norms across the rows of matrix Wi. The l2,1‐norm of Wi ensures the positions of non‐zero elements of the weighted coefficient vectors to be the same for all subjects. Similarly, Equation (2) is applied to each ROI, respectively, to obtain a group‐sparse FCN . Note that these identical topological structures across subjects allow for easier and more consistent between‐subject comparison, while still allowing the variation of connectivity values (connection strength).
2.4.2. Construction of multiple group‐sparse FCNs
The regularization parameter λ controls the sparsity of the FCN and thus the topological structure. FCN generated with a larger λ is too sparse to retain important information, while FCN generated with a smaller λ is so dense that FCN contains many insignificant or spurious connections. In both cases, these less informative representations will, inevitably, deteriorate the classification performance. Generally, we can choose an appropriate value of λ to enhance the classification performance via cross‐validation on the training set. However, a single network representation is less informative for such a complex system like the human brain, and thus limits its classification performance.
Recent studies show that fusing information from multiple networks can further improve classification performance due to potential complementary information conveyed by different networks (Jie et al., 2014; Price et al., 2014). To obtain successful multi‐view learning fusion, two principles should be satisfied: consensus and complementary principles (Xu et al., 2013). The aim of consensus principle is to ensure the agreement of information on multiple different views as more as possible, which could limit the error rate caused by different views. The complementary principle requires that each view of the subject should carry different information from other views, so that multi‐view learning could utilize abundant information to characterize the subject. In the group‐constrained sparse network model, FCN becomes sparser and sparser with the increase of the regularization parameter to reflect the topological structure of FCN at different levels of sparsity. These FCNs with different sparsity levels contain not only the consistent information across networks but also the topological information different from each other. Therefore, we hypothesize that fusing information from the group‐sparse FCNs with different sparsity levels can enhance the classification performance.
To extract consistent yet complementary information for classification, we set regularization parameter to three groups of values: (a) [0.1–0.5] with a step size of 0.1, (b) [0.01–0.09] with a step size of 0.01, and (c) [0.001–0.009] with a step size of 0.001. There are a total of 23 group‐sparse FCNs generated for each subject. Four networks are chosen from these 23 FCNs, and fused to improve the classification performance, since 4 networks could provide more abundant complementary information than 2 and 3 networks. Furthermore, due to significant increment in computational complexity and the overfitting problem caused by overtraining, we do not adopt the fusion of more FCNs. The optimal values of the regularization parameters are determined empirically via cross‐validation on the training set. To satisfy the consensus principles of successful multi‐view learning, we fuse the multiple group‐sparse FCNs corresponding to any four adjacent values to enhance the common intrinsic topological structure for improving the performance. Although non‐adjacent values would provide slightly more variability among views compared to the adjacent values, it would also reduce the agreement of information on multiple different views, causing the increase of classification error rate. The optimal weights to combine multiple FCNs are determined empirically based on the classification accuracy of multi‐kernel SVM achieved using training samples. The four adjacent regularization parameter values that achieve the best accuracy are used to construct multiple FCNs for testing samples.
We further apply the Fisher's r‐to‐z transformation on each constructed FCN to improve its normality.
2.5. Feature extraction with modified weighted clustering coefficients
The graph theory metrics can provide a quantified summary of the topological organization of a functional connectivity network, and reveal functional connectivity abnormalities in neuropsychiatric disorders at a high level representation. Compared to global network measures, local network measures can characterize the properties of an individual node or brain region at a more granular level, thus providing a more sensitive and informative interpretation on the functional interactions among the brain regions (Meskaldji et al., 2013).
The local clustering coefficient quantifies the presence of clusters that reflects functional segregation among nodes. A larger clustering coefficient implies more functional segregation that allows the corresponding node and its neighbors for specialized information processing (Rubinov & Sporns, 2010), which has been successfully applied to brain disorder diagnosis (Jie et al., 2014; Wee et al., 2014, 2016). The local binary clustering coefficient refers to the fraction of a node's neighbors that are neighbors of each other in all possible neighbors (Watts & Strogatz, 1998). However, since the weighted graph conveys more information and is more sensitive to disorder‐related alterations in contrast to the binary graph (Meskaldji et al., 2013), we prefer to use the local weighted clustering coefficient as features from the constructed FCN, which happens to also be a weighted graph.
In this study, we do not use the commonly used weighted clustering coefficient proposed by Onnela et al. (2005). Instead, we propose using a modified version of weighted clustering coefficients to extract features from each FCN. To differentiate it from the former, we refer to our proposed clustering coefficients as the modified clustering coefficients.
The commonly used weighted clustering coefficient proposed by Onnela et al. (2005) is based on the geometric mean of triangles around a node (Figure 2a). The weighted clustering coefficient Ci of node i is defined as
| (3) |
Figure 2.

Illustration of Onnela's weighted clustering coefficient (a) and our modified weighted clustering coefficient (b). (a) is the sum of the geometric mean of triangles around a central node, and (b) is the sum of the strengths of red edges between the neighbors around a central node [Color figure can be viewed at http://wileyonlinelibrary.com]
where, wij, wih, and wjh are the connection strengths between nodes i and j, between nodes i and h, and between nodes j and h, respectively. The number of edges connected to node i is represented by ki, and N is the set of all nodes in the network. This clustering coefficient practically computes the sum of the geometric mean of triangles attached to a node, and has been used to extract local features for brain disease diagnosis (Wee, Yap, Denny, Browndyke, Potter, Welsh‐Bohmer, Wang, & Shen, 2012a; Jie et al., 2014; Chen, Zhang, et al., 2016). However, the above weighted clustering coefficients may not effectively capture subtle differences between two groups on the connection strengths between the neighboring nodes that are linked to a node, since it uses the weights between a node and its neighbors in the computation of clustering coefficients, which may weaken the difference of weights between the neighboring nodes (Figure 2a).
To highlight the differences on the connection strengths between the neighboring nodes, we suggest computing the weighted clustering coefficients using a method similar to the one used for computing the binary clustering coefficients (Watts & Strogatz, 1998). The only difference is that the connection status between two neighbors that are connected to a node in the binary clustering coefficient computation is replaced by their connection strength. Therefore, the modified weighted clustering coefficient is equivalent to the summation of connection strengths for the edges between a node's neighbors that are also neighbors to each other (Figure 2b), and is defined as
| (4) |
where, aij is the connection status between nodes i and j , that is, aij = 1 if there exists a link between two nodes and aij = 0 if otherwise. wjh is the connection strength for the edge that links nodes j and h. If nodes j and h are the neighbors of the node i, aijaihwjh indicates the connection strength wjh between the neighbors j and h for the node i. We substantially compute the sum of the link strengths of the subgraphs formed by the neighboring nodes that are linked to a node. The weights between a node and its neighboring nodes play the only role of indicating the existence of neighboring nodes and will not be used in the computation to emphasize the strength of the subgraph comprised by the neighboring nodes that are commonly connected to the same node (Figure 2b). We expect this modified weighted clustering coefficient to better capture between‐group differences than the conventional definition such as proposed by Onnela et al. (2005).
2.6. Feature selection using t‐test and SVM‐RFE
We design a two‐stage feature selection strategy to automatically select the most discriminative features. Figure 3 illustrates the procedure of the proposed two‐stage feature selection. We first adopt a threshold controlled statistical t‐test to select a preliminary set of features that is highly correlated to clinical status and then use the SVM recursive feature elimination (SVM‐RFE) algorithm (Guyon, Weston, Barnhill, & Vapnik, 2004) to further select the most discriminative features from this preliminary set of features based on the classification accuracy on the training set.
Figure 3.
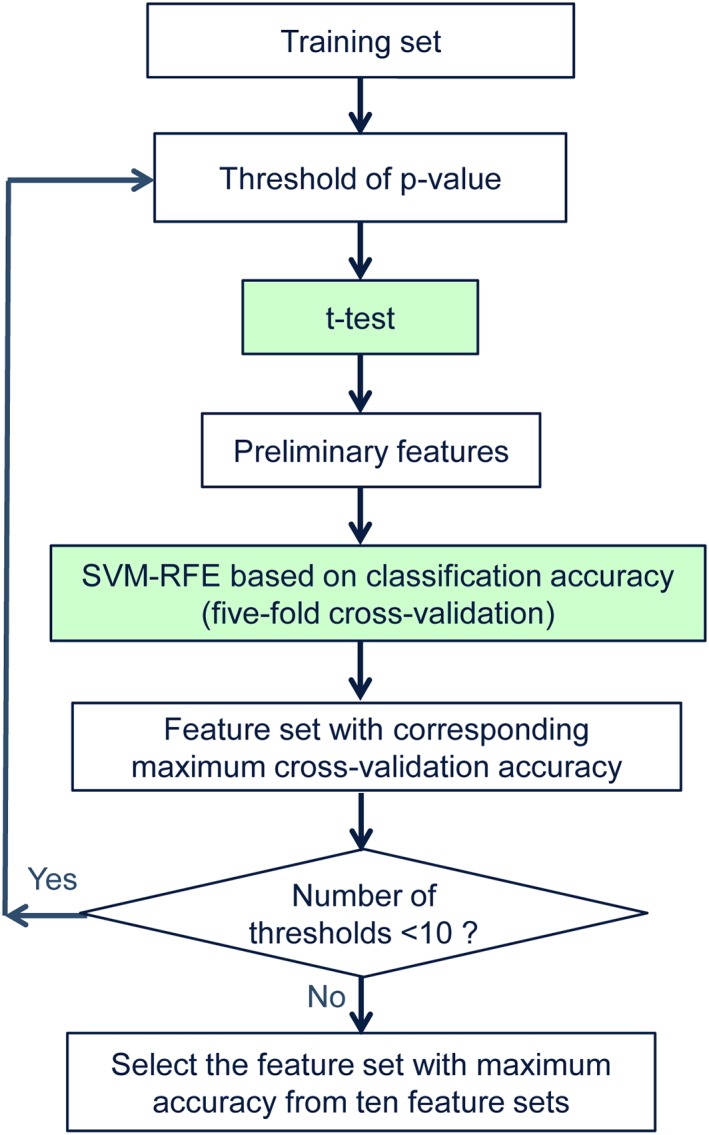
Procedure of the two‐stage feature selection [Color figure can be viewed at http://wileyonlinelibrary.com]
The two‐sample t‐test is utilized to determine the importance of each feature through comparing its correlation with clinical status. The smaller the p‐value, the stronger the discriminative power of a feature is. The features are ranked according to the ascending p‐values and a threshold is set to control for the number of features that are retained for the second stage of feature selection. This threshold has a significant influence on the final classification performance. A small threshold can retain those features with high discriminability but may fail to retain some features that are useful for classification. A large threshold can retain more features but suffer from the issue of large amount of redundant features. Therefore, we empirically determine this threshold value for each level of network sparsity through a grid search approach among a set of 10 candidate thresholds. For each threshold, SVM‐RFE, one of the most commonly used wrapper‐based feature selection methods, is carried out to select the most discriminative features based on the classification accuracy of a linear SVM using a five‐fold cross‐validation on the training set. The importance of a feature is evaluated by the classification accuracy of the remaining features when the feature is removed. The higher the accuracy, the less important the feature is. The least important feature is discarded from the surviving feature set iteratively until the surviving feature set becomes empty. We finally yield a list in which all the features are ranked according to their importance to classification in descending order. Let n be the number of features used for training a SVM classifier, determined via cross‐validation. The set of n features that achieves the highest cross‐validation accuracy is considered as the most discriminative feature set and will be used for final classification.
2.7. Multiple network fusion and classification using multi‐kernel SVM
The last step in our proposed framework is the feature fusion and classification. Here, we adopt a multiple‐kernel linear SVM (Zhang, Wang, Zhou, et al., 2011; Zhang, Shen, & Alzheimer's Disease Neuroimaging Initiative, 2012; Wee, Yap, Zhang, et al., 2012b; Wee, Yap, & Shen, 2013) to fuse multiple networks of features for ASD diagnosis. Assume that there are N training subjects and Q FCNs (or Q levels of sparsity), and and are the selected features corresponding to subject i and j for network q, respectively (i, j = 1, 2, …, N; q = 1, 2, . . , Q). μq is a nonnegative weighted coefficient. The kernel function of the multi‐kernel linear SVM is defined as a linear combination of multiple linear basis kernels:
| (5) |
where, is a linear basis kernel function for network q.
We employ a LOOCV to perform experiments to evaluate the proposed method. One subject is left out as a testing set for each cross‐validation and the remaining subjects are used as a training set. In multi‐kernel fusion, we need to select four adjacent FCNs through a five‐fold cross‐validation on the training set, and fuse the selected clustering coefficients from these FCNs via multi‐kernel SVM to identify ASD for the testing set for each fold. We first compute the linear kernel matrix of the selected clustering coefficients from each FCN for the training set. Then we linearly combine four kernel matrices from any four adjacent FCNs into one mixed‐kernel matrix using weighted coefficients. Subsequently the performance of the standard SVM using the mixed kernel is evaluated via a five‐fold cross‐validation on the training set. We equally partition the training set into five folds. Each time the subjects from one fold are repeatedly selected as the validation set and all remaining subjects in the other four folds are used for training the SVM with a mixed‐kernel. The weighted coefficients are optimized not only jointly together with other SVM parameters, but also using a coarse‐grid search approach (Zhang, Wang, Zhou, et al., 2011) through the above five‐fold cross‐validation on the training set. The range of coarse‐grid search for the weighted coefficient μq is from 0 to 1 with a step size of 0.1. We successfully compute five‐fold cross‐validation accuracy for the fusion of any four adjacent FCNs based on the training set, and select the four adjacent FCNs. Based on the identified four adjacent FCNs and their optimal weighted coefficients, we also compute the mixed‐kernel matrix for the testing set. The standard linear SVM model is trained using the mixed‐kernel matrix of the training set, and then used to identify ASD on the mixed‐kernel matrix of the left out testing sample. As we are adopting LOOCV, every subject is used as a testing sample once to predict its class label. Finally, the performance metrics are calculated according to the predicted class labels of all subjects.
We had attempted to adopt the standard multi‐kernel SVM method with joint optimization of kernel weights to carry out multi‐kernel fusion, but no good result was achieved. We thus used a coarse‐grid search approach with a five‐fold cross‐validation on the training set to optimize the weight coefficients. Based on this approach, we achieved better classification results than the standard multi‐kernel SVM method. The optimization of the weighted coefficients jointly together with other SVM parameters may cause over‐fitting, that is, good performance can be achieved on the training set, however, the performance on the testing set decreases.
2.8. Experimental settings
To evaluate the performance of the proposed method, we employ LOOCV to perform experiments. Each subject has an opportunity to be the testing set, which can produce a fair estimate for classification error.
The group‐sparse FCNs are computed using SLEP package (Liu, Ji, & Ye, 2009). In the first step of feature selection, the optimal threshold for selecting features that are highly relevant to clinical status is determined from a set of 10 candidate p‐values of [0.005, 0.05, 0.08, 0.1, 0.12, 0.15, 0.2, 0.3, 0.4, 0.5]. SVM‐RFE is then performed via a five‐fold cross‐validation, and linear SVM is implemented using LIBSVM software package (Chang & Lin, 2011). Based on the five‐fold cross‐validation results, we identify the optimal p‐value and discriminative features for each of 23 networks in each fold.
Note that the two‐stage feature selection (t‐test, and SVM‐RFE), and the determination of the weighted coefficients are performed only on the training samples. Using this nested cross‐validation method to determine both the optimal parameters and the most discriminative features ensures the generalizability of the proposed classification framework.
3. EXPERIMENTAL RESULTS
To assess the performance of the compared methods, performance metrics including the accuracy (ACC), sensitivity (SEN), specificity (SPE), positive predictive value (PPV), and negative predictive value (NPV) are calculated from the classification confusion matrix. Here, the accuracy is defined as the relative number of subjects correctly predicted in all subjects. The sensitivity measures the relative number of correct detections of ASD patients, and the specificity represents the relative number of correct detections of TD individuals. The positive predictive value refers to the relative number of true positive patients in all predicted patients with ASD, and the negative predictive value refers to the relative number of true TD individuals in all detected TD individuals.
It is noteworthy that the following results are achieved based on the clustering coefficients from FCNs. The multiple network based method uses the fused clustering coefficients as the input features of the classifier.
3.1. Effect of regularization parameter
To explore the effect of the regularization parameter λ on classification performance and sparsity, we use three groups of λ values as mentioned in the “Materials & Method” section to compute the accuracies and density for each individual FCN (Table 2). Density is defined as the ratio of the number of non‐zero elements to the total number of all elements in a graph. The classification accuracies of the single networks are above 63% for λ values between 0.05 and 0.08, including a maximum accuracy of 72.83%, with the density ranged from 12 to 14%. For λ values from the first group with the density ranged from 29 to 50%, the accuracies are less than 60%. For the third group with the density ranged from 5 to 11%, the single network provides accuracies less than 60% except a maximum accuracy of 65.22% at 8% of density.
Table 2.
Density and classification accuracy of FCNs corresponding to different regularization parameters
| Regularization parameter | Density (%) | Accuracy (%) | |
|---|---|---|---|
| Group 1 | 0.001 | 50.35 | 51.09 |
| 0.002 | 46.56 | 59.78 | |
| 0.003 | 42.73 | 52.17 | |
| 0.004 | 39.11 | 51.09 | |
| 0.005 | 36.65 | 56.52 | |
| 0.006 | 34.07 | 54.35 | |
| 0.007 | 32.11 | 50.00 | |
| 0.008 | 30.35 | 48.91 | |
| 0.009 | 28.79 | 51.09 | |
| Group 2 | 0.01 | 27.43 | 43.48 |
| 0.02 | 19.28 | 48.91 | |
| 0.03 | 16.58 | 61.96 | |
| 0.04 | 14.75 | 50.00 | |
| 0.05 | 13.78 | 63.04 | |
| 0.06 | 13.01 | 63.04 | |
| 0.07 | 12.25 | 67.39 | |
| 0.08 | 11.67 | 72.83 | |
| 0.09 | 11.36 | 59.78 | |
| Group 3 | 0.1 | 10.84 | 59.78 |
| 0.2 | 8.37 | 65.22 | |
| 0.3 | 6.70 | 44.57 | |
| 0.4 | 5.56 | 58.70 | |
| 0.5 | 4.92 | 58.70 |
We can see that the regularization parameter has significant influence on the classification performance of single group‐sparse network. The number of non‐zero elements gets less, and the FCN becomes sparser and sparser with the increase of regularization parameter. Multiple FCNs include different levels of sparsity.
3.2. Multiple FCN fusion based classification performance
The optimal regularization parameter values for the proposed multiple network based method are selected as 0.06–0.09 with a step size of 0.01 via nested cross‐validation on the training set. The classification performances of the proposed multiple network based method and four single network based methods with adjacent regularization parameter values (0.06, 0.07, 0.08, and 0.09) are shown in Table 3. The single network with a regularization parameter value of 0.08 shows the highest performance among the four single networks with an accuracy of 72.83%, a sensitivity of 77.78%, and a specificity of 68.09%. The proposed method, which fuses the clustering coefficients of FCNs with four different levels of sparsity (0.06, 0.07, 0.08, and 0.09), achieves an accuracy of 79.35%, a sensitivity of 82.22%, and a specificity of 76.60%, showing an increment of 6.52% in accuracy compared to the best performed single network. It is important to note that the proposed method outperforms the single network based methods in all other performance measures.
Table 3.
Comparison of the classification performance between the single network based methods and the proposed multiple network based method
| Method | ACC (%) | SEN (%) | SPE (%) | PPV (%) | NPV (%) |
|---|---|---|---|---|---|
| Network 1 (0.06) | 63.04 | 71.11 | 55.32 | 60.38 | 66.67 |
| Network 2 (0.07) | 67.39 | 73.33 | 61.70 | 64.71 | 70.73 |
| Network 3 (0.08) | 72.83 | 77.78 | 68.09 | 70.00 | 76.19 |
| Network 4 (0.09) | 59.78 | 77.78 | 42.55 | 56.45 | 66.67 |
| Multiple network method | 79.35 | 82.22 | 76.60 | 77.08 | 81.82 |
We have performed an additional experiment to validate the effectiveness of the adjacent value method over the non‐adjacent value methods when determining the regularization parameter values of multiple networks. To validate better performance of fusing the clustering coefficients of 4 networks than 3 and 5 networks, we carry out the above experiment based on 3, 4, and 5 networks, respectively. The non‐adjacent values are determined using two methods. First, we seek the single FCN that gives the best cross‐validation accuracy on the training set, and then incrementally add another FCN in the multiple network fusion to see whether this inclusion of new network can improve the accuracy. The single FCN that can increase the accuracy will be kept until the required number of networks has been tested. Second, we select the parameter values corresponding to the single FCNs with the best accuracy on the training set to construct multiple networks. The above two ways of parameter optimization are denoted as non‐adjacent value 1 and non‐adjacent value 2, respectively. The parameter optimization method used in this study is denoted as adjacent value. Figure 4 shows the classification results of multiple network fusion with 3, 4, and 5 networks in three ways, respectively. As shown in Figure 4a–c, the parameter optimization method using adjacent value achieves the best classification performance. Figure 4d shows that the fusion of 4 networks achieves better classification performance than the cases of using 3 and 5 networks, respectively, when adopting adjacent value method to determine the values of regularization parameter.
Figure 4.
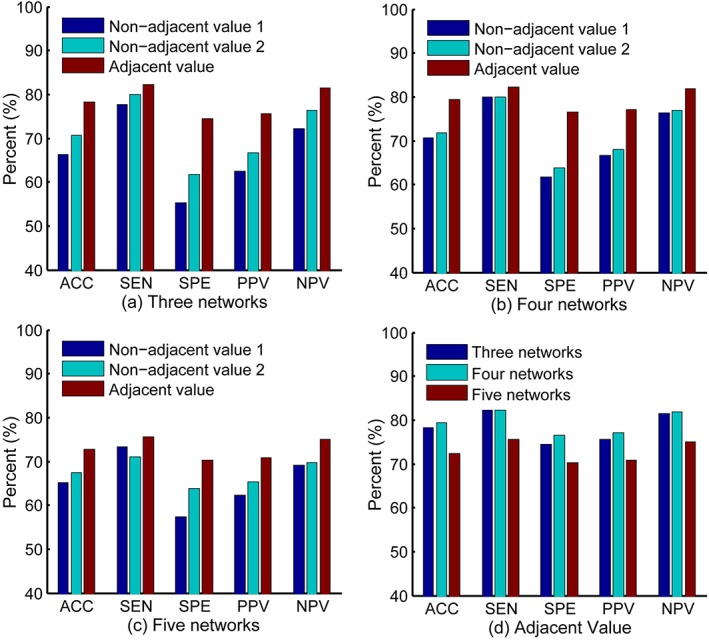
Classification performance of multiple network fusion with 3 (a), 4 (b), and 5 (c) networks in three parameter optimization ways (i.e., non‐adjacent value 1, non‐adjacent value 2, and adjacent value). (d) Performance comparison of 3, 4, and 5 networks when adopting adjacent value method. ACC, accuracy; SEN, sensitivity; SPE, specificity; PPV, positive predictive value; NPV, negative predictive value [Color figure can be viewed at http://wileyonlinelibrary.com]
The classification performance comparison between the proposed method and other multiple network based methods is summarized in Table 4. The compared multiple network based methods are: (1) Pearson correlation coefficient based method, (2) graph‐kernel based method (Jie et al., 2014), (3) sparse network estimation method without group constraint, and (4) sparse inverse covariance estimation (SICE) (Huang et al., 2010; Sun et al., 2009), respectively. Multiple Pearson correlation matrices were generated by thresholding the original Pearson correlation matrix with different thresholds ranged from 0 to 0.5 with a step size of 0.02. The graph kernel based method was also based on thresholded Pearson correlation matrices, and but used an RFE graph kernel (RFE‐GK) (Jie et al., 2014) to seek the identical topological structure that maximizes classification accuracy. We selected four optimal thresholds to achieve the best performance for both methods. The sparse network method without group constraint applied an l1‐norm sparse regression model (Equation (1)) to each subject individually without enforcing identical topological structures across subjects. The SICE introduced the sparsity constraint to the maximum‐likelihood estimation via l1‐norm regularization to obtain the inverse covariance matrix (Huang et al., 2010). We compute the sparse network and the SICE using SLEP package (Liu et al., 2009). The four multiple network based methods utilized the same classification procedures (i.e., feature extraction, feature selection, feature fusion and classification) as the proposed method, except the network construction step. The results in Table 4 demonstrate that the four compared multiple‐networks‐based methods achieve classification accuracy less than 70%. Although the sensitivity of the SICE is higher than the proposed method, its specificity 40.43% is far from satisfactory, that is, an imbalanced performance which should be avoided.
Table 4.
Comparison of the classification performance of 5 different multiple network based methods
| Method | ACC (%) | SEN (%) | SPE (%) | PPV (%) | NPV (%) |
|---|---|---|---|---|---|
| Pearson correlation | 68.48 | 75.56 | 61.70 | 65.38 | 72.50 |
| Graph kernel | 65.22 | 73.33 | 57.45 | 62.26 | 69.23 |
| Sparse | 58.70 | 66.67 | 51.06 | 56.60 | 61.54 |
| SICE | 63.04 | 86.67 | 40.43 | 58.21 | 76.00 |
| Group sparse | 79.35 | 82.22 | 76.60 | 77.08 | 81.82 |
3.3. Improvement of modified weighted clustering coefficients
Different network measures quantify different characteristics of a network and may have significant effects on classification performance. We compare the performance of the proposed weighted clustering coefficient (Table 3) with that proposed by Onnela et al. (2005) (Table 5). These clustering coefficients are computed from the FCNs generated by the group‐constrained sparse regression model. In the case of multiple network fusion, our modified weighted clustering coefficient outperforms Onnela's method in all performance measures. At the same time, the highest single network accuracy of the proposed weighted clustering coefficient is also larger than Onnela's method. From Table 5, we can see that the multiple network fusion does not achieve improved results, and has the same accuracy as the network 4 (with the best performance among single networks).
Table 5.
Classification performance of single network and multiple network methods using the weighted clustering coefficient proposed by Onnela et al.
| Method | ACC (%) | SEN (%) | SPE (%) | PPV (%) | NPV (%) |
|---|---|---|---|---|---|
| Network 1 | 56.52 | 64.44 | 48.94 | 54.72 | 58.97 |
| Network 2 | 63.04 | 80.00 | 46.81 | 59.02 | 70.97 |
| Network 3 | 64.13 | 75.56 | 53.19 | 60.71 | 69.44 |
| Network 4 | 69.57 | 80.00 | 59.57 | 65.45 | 75.68 |
| Multiple network method | 69.57 | 75.56 | 63.83 | 66.67 | 73.17 |
| The proposed method | 79.35 | 82.22 | 76.60 | 77.08 | 81.82 |
In addition, we also compare the classification performance of several network measures including connectivity strength, local efficiency, and betweenness centrality. The connectivity strength is defined as the sum of the weights of all neighboring edges connected to that node, illustrating the significance of a node in the network. The local efficiency is the average inverse shortest path length computed on node neighborhoods, and reflects how well information exchange is between its neighbors when removing a node (Achard & Bullmore, 2007). The betweenness centrality of a node is defined as the ratio of all shortest paths between two nodes that pass through a node in the network and therefore can be used to assess whether nodes are important controls of information flow (Freeman, 1977, 1978).
The comparison results are summarized in Figure 5. The proposed weighted clustering coefficient achieves the best classification performance, followed by the betweenness centrality with an accuracy of 66.3%. The connectivity strength performs the worst with an accuracy of 61.96%, while the local efficiency achieves an accuracy of 65.22%.
Figure 5.
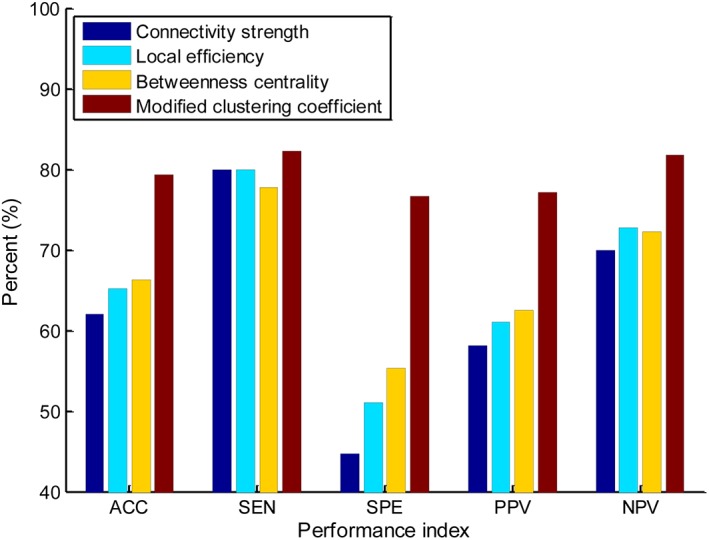
Classification performance comparison between the proposed clustering coefficient and other local network measures (such as connectivity strength, local efficiency, and betweenness centrality). ACC, accuracy; SEN, sensitivity; SPE, specificity; PPV, positive predictive value; NPV, negative predictive value [Color figure can be viewed at http://wileyonlinelibrary.com]
3.4. Top discriminative brain ROIs
We determine the discriminative brain ROIs according to their contribution to classification performance. The discriminative brain ROIs (corresponding to features) might be different for each fold due to the use of different training and testing set in each fold of the LOOCV procedure. The contribution of a ROI is thus evaluated by the ratio of occurrence of the ROI feature in LOOCV procedure. For example, for a ROI feature that is selected in 90 out of 92 LOOCV folds, its contribution is quantified as . We sort the ROI features according to their contribution measures. In Figure 6 and Table 6, we show the results of ROIs with their contributions greater than or equal to 0.5. These ROIs are selected in at least half of folds during LOOCV procedure. The mean clustering coefficients of the discriminative brain ROIs are computed from TD and ASD children, respectively, for each network and are shown in Figure 6b. In order to clearly show the difference in mean clustering coefficients between ASD and TD, the mean clustering coefficients are normalized to [−1 1]. The sizes of ROIs represent the amounts of contribution, that is, larger ROI has stronger contribution (Figure 6a). The related detailed information is shown in Table 6. As the final classification performance is achieved by fusing the features from four FCNs, we thus examine the contribution of each network in multi‐kernel SVM classification. It is noteworthy that networks contribute unequally to ASD identification, with network 3 showing the largest contribution, followed by network 2, network 1 and network 4 (Table 6), roughly in line to their individual performances (Table 3). To evaluate the significant differences between ASD and TD, the p‐value of each discriminative ROI computed based on two sample t‐test is also listed. The ROIs are grouped into different resting‐state networks represented by different colors according to previous studies (Broyd et al., 2009; Dosenbach et al., 2010; Wang et al., 2012; Andrews‐Hanna, Smallwood, & Spreng, 2014; Suk et al., 2016), including default mode network (DMN), executive attention network (EAN), visual network, sensorimotor network (SMN), cingulo‐opercular network (CON), subcortical regions and cerebellum.
Figure 6.
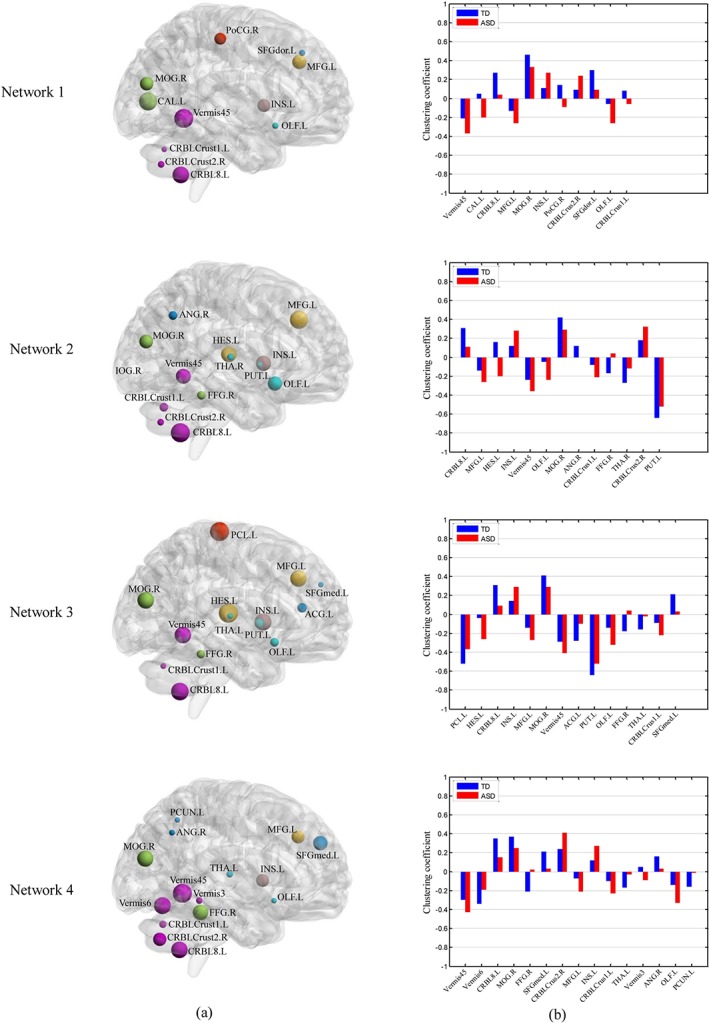
Contribution (a) and mean clustering coefficient (b) of discriminative ROIs between ASD and TD children in four FCNs. The abbreviations of the ROIs can be found in Table A1. The contributions of ROIs are visualized on a brain surface rendering and are proportional to the sizes of spheres in (a). The ROIs are related with different functional networks represented by different colors (blue: default mode network; yellow: executive attention network; green: visual network; red: sensorimotor network; brown: cingulo‐opercular network; cyan: subcortical regions; violet: regions in the cerebellum). (b) shows the comparison of the normalized mean clustering coefficient between the TD and ASD children [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 6.
The discriminative brain ROIs for each functional connectivity network
| Weight | Name of ROI | Network | Contribution | TD | ASD | p‐value | |
|---|---|---|---|---|---|---|---|
| Network 1 | 0.14 | Vermis45 | Cerebel | 0.91 | −0.21 | −0.37 | .018 |
| Cal.L | Visual | 0.89 | 0.05 | −0.20 | .001 | ||
| CRBL8.L | Cerebel | 0.85 | 0.27 | 0.04 | .011 | ||
| MFG.L | EAN | 0.79 | −0.13 | −0.26 | .095 | ||
| MOG.R | Visual | 0.77 | 0.46 | 0.33 | .068 | ||
| INS.L | CON | 0.76 | 0.11 | 0.27 | .048 | ||
| PoCG.R | SMN | 0.73 | 0.14 | −0.09 | .002 | ||
| CRBLCrust2.R | Cerebel | 0.60 | 0.09 | 0.24 | .038 | ||
| SFGdor.L | DMN | 0.59 | 0.30 | 0.09 | .001 | ||
| OLF.L | SBC | 0.59 | −0.06 | −0.26 | .002 | ||
| CRBLCrust1.L | Cerebel | 0.57 | 0.08 | −0.06 | .014 | ||
| Network 2 | 0.32 | CRBL8.L | Cerebel | 0.96 | 0.31 | 0.11 | .007 |
| MFG.L | EAN | 0.93 | −0.14 | −0.26 | .073 | ||
| HES.L | EAN | 0.84 | 0.16 | −0.20 | .000 | ||
| INS.L | CON | 0.83 | 0.12 | 0.28 | .051 | ||
| Vermis45 | Cerebel | 0.82 | −0.24 | −0.36 | .058 | ||
| OLF.L | SBC | 0.80 | −0.05 | −0.24 | .002 | ||
| MOG.R | Visual | 0.78 | 0.42 | 0.29 | .056 | ||
| ANG.R | DMN | 0.61 | 0.12 | 0.00 | .109 | ||
| CRBLCrust1.L | Cerebel | 0.61 | −0.08 | −0.21 | .029 | ||
| FFG.R | Visual | 0.60 | −0.17 | 0.04 | .001 | ||
| THA.R | SBC | 0.55 | −0.27 | −0.12 | .026 | ||
| CRBLCrust2.R | Cerebel | 0.54 | 0.18 | 0.32 | .043 | ||
| PUT.L | SBC | 0.50 | −0.64 | −0.52 | .037 | ||
| Network 3 | 0.40 | PCL.L | SMN | 0.90 | −0.52 | −0.37 | .008 |
| HES.L | EAN | 0.90 | −0.04 | −0.26 | .006 | ||
| CRBL8.L | Cerebel | 0.86 | 0.31 | 0.09 | .012 | ||
| INS.L | CON | 0.84 | 0.14 | 0.29 | .061 | ||
| MFG.L | EAN | 0.83 | −0.14 | −0.27 | .076 | ||
| MOG.R | Visual | 0.83 | 0.41 | 0.29 | .086 | ||
| Vermis45 | Cerebel | 0.83 | −0.29 | −0.41 | .043 | ||
| ACG.L | DMN | 0.63 | −0.28 | −0.10 | .025 | ||
| PUT.L | SBC | 0.63 | −0.64 | −0.52 | .037 | ||
| OLF.L | SBC | 0.61 | −0.14 | −0.32 | .003 | ||
| FFG.R | Visual | 0.60 | −0.18 | 0.04 | .001 | ||
| THA.L | SBC | 0.53 | −0.16 | −0.02 | .102 | ||
| CRBLCrust1.L | Cerebel | 0.53 | −0.09 | −0.22 | .027 | ||
| SFGmed.L | DMN | 0.52 | 0.21 | 0.03 | .015 | ||
| Network 4 | 0.14 | Vermis45 | Cerebel | 0.90 | −0.30 | −0.43 | .042 |
| Vermis6 | Cerebel | 0.84 | −0.34 | −0.19 | .066 | ||
| CRBL8.L | Cerebel | 0.83 | 0.35 | 0.15 | .007 | ||
| MOG.R | Visual | 0.82 | 0.37 | 0.25 | .082 | ||
| FFG.R | Visual | 0.80 | −0.21 | 0.02 | .001 | ||
| SFGmed.L | DMN | 0.77 | 0.21 | 0.03 | .015 | ||
| CRBLCrust2.R | Cerebel | 0.74 | 0.24 | 0.41 | .022 | ||
| MFG.L | EAN | 0.73 | −0.07 | −0.21 | .039 | ||
| INS.L | CON | 0.73 | 0.12 | 0.27 | .065 | ||
| CRBLCrust1,L | Cerebel | 0.57 | −0.10 | −0.23 | .026 | ||
| THA.L | SBC | 0.55 | −0.17 | −0.03 | .092 | ||
| Vermis3 | Cerebel | 0.55 | 0.05 | −0.09 | .063 | ||
| ANG.R | DMN | 0.53 | 0.16 | 0.03 | .086 | ||
| OLF.L | SBC | 0.52 | −0.14 | −0.33 | .003 | ||
| PCUN.L | DMN | 0.52 | −0.16 | −0.01 | .050 |
The abbreviations of the ROIs can be found in Table A1. TD, typically developing; ASD, autism spectrum disorder; DMN, default mode network; EAN, executive attention network; Visual, visual network; SMN, sensorimotor network; CON, cingulo‐opercular network; SBC, subcortical regions; Cerebel, cerebellum.
There are a total of 23 discriminative ROIs selected from all four group‐sparse networks. The common as well as the network‐specific discriminative ROIs are provided in Figure 7. The discriminative ROIs that are common across all four networks are the middle frontal gyrus, middle occipital gyrus, olfactory cortex, insula, and three regions from the left cerebellum. The abbreviations of the ROIs used in Figures 6 and 7, and Table 6 are provided in Table A1.
Figure 7.
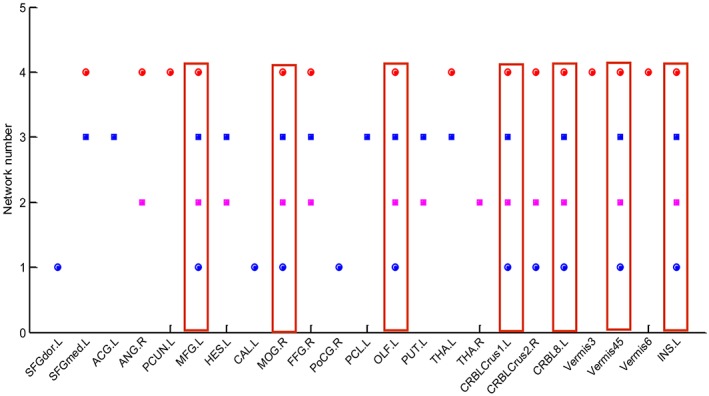
Common and network‐specific discriminative ROIs. The abbreviations of the ROIs can be found in Table A1. Common ROIs are in the red rectangle [Color figure can be viewed at http://wileyonlinelibrary.com]
4. DISCUSSION
We have investigated the fusion of the clustering coefficients of multiple group‐sparse FCNs for ASD identification. Our results have demonstrated that the proposed multiple FCN fusing method outperforms the single network methods. The fusion of the clustering coefficients of multiple FCNs enhances the representation of brain FCN and thus provides an effective and novel way to search for potential biomarkers.
4.1. Improvement of the proposed method
The regularization parameter should be selected carefully to retain appropriate connections and improve the classification performance of a single network based on the group‐constrained sparse model. It is not appropriate to set the sparsity of the FCNs to be high or low values. The FCNs cannot retain too much information if too sparse, while many insignificant or spurious connections are introduced in the network, if too dense. To obtain the optimal value of the regularization parameter, a series of values with finer intervals need to be explored on the training set. On the other hand, classification performance of a single network is limited by its less informative features.
Our brain is a complex network, thus it is difficult to fully understand the brain functional organization using only one single FCN. Motivated by the consensus and complementary principles of multi‐view learning, we fused the clustering coefficients of the FCNs with different sparsity levels to enhance the classification performance. These FCNs were generated by the same group‐constrained sparse model but with different regularization parameter values, which ensures the multiple views of data to satisfy the consensus principle. Although the difference of sparsity among the FCNs was small, their classification performance differed obviously (Table 2). This may attribute to the capability of weighted clustering coefficients in capturing subtle alterations in FCNs. Naturally, this provides a good avenue to construct multiple FCNs. Compared with single network based methods, the fusion of multiple networks can enhance the classification performance through the use of complementary information from different networks. The performance improvement of the proposed method is significant with an increase of 6.52%, compared to the highest performance of the single network based method (Table 3).
The performance of multiple network fusion depends largely on the performance of the single networks. If the individual networks have good performance, they will contribute to improve the fusion performance. However, the individual networks should share some similarities with each other to enhance common intrinsic properties that are useful for classification, which conforms to the consensus principle of successful multi‐view learning. We performed experiments by combining individual networks with non‐adjacent values (determined by two parameter optimization methods: non‐adjacent value 1 and non‐adjacent value 2) and obtained relatively poorer results (Figure 4). It is likely that non‐adjacent values would generate more variability among views compared to adjacent values, which could reduce the agreement of information on multiple views and increase the classification error rate. In contrast, the adjacent networks could not only provide complementary information among views, but also limit the error rate caused by different views, thus achieving good results (Figure 4). The number of FCNs could also have an obvious effect on the performance of multiple network fusion. The fusion of more networks could combine more abundant complementary information to enhance the performance. However, the fusion of 5 networks achieves poorer performance than the case of 4 networks (Figure 4d), since better performance on the training set cannot be generalized on the testing set. In this case, the overtraining causes the overfitting which should be avoided.
Besides the common ROIs that were selected consistently across all four networks, there were some network‐specific ROIs that contributed to achieve good classification performance, suggesting complementary information conveyed in networks with different topological structures (see Figures 6 and 7). Topological differences between three FCNs (with regularization parameter λ as 0.08, 0.07, and 0.06, respectively) and the FCN (λ = 0.09) are shown in Figure 8. With the decrease of the regularization parameter, the number of extra connections between ROIs in the sparse networks increases and shows differences in clustering coefficients. For each FCN, a feature vector consisting of clustering coefficients can capture differences of specific spatial patterns between ASD and TD children. Multiple FCNs can provide complementary information different from each other in a granular fashion. We do not simply combine all networks together, but properly select the most discriminative networks since only some features show differences between ASD and TD children. For instance, left paracentral lobule (PCL.L) in the region of insula (INS) shows different connection patterns in Figure 8a–c, and it is displayed in network 3 but not appearing in other networks in Figure 6. Network 3 shows the highest classification accuracy in all four networks. This suggests that the topological connectivity pattern in network 3 can precisely capture the difference between ASD and TD children located in PCL.L that cannot be captured by other networks.
Figure 8.
Topological differences between three FCNs [with regularization parameter λ as 0.08 (a), 0.07 (b), and 0.06 (c), respectively] and the FCN (λ = 0.09). Compared with the FCN (λ = 0.09) as benchmark, the number of extra links from three FCNs increases with the decrease of λ. The thickness of links represents the weights of connections from other ROIs to a specific ROI. The abbreviations of the ROIs can be found in Table A1 [Color figure can be viewed at http://wileyonlinelibrary.com]
We adopted the group‐constrained sparse regression model to construct multiple networks, achieving the best performance compared to other multiple network based methods (Table 4). The proposed framework benefitted from the group constraint that can enhance the performance significantly. It encoded the variability of network properties across subjects into connection strength variability and enabled direct comparison of the corresponding features from two groups. The graph kernel method also intrinsically seeks the common topological structures across subjects, but it abandons some topological structures which inevitably causes information loss. Meanwhile, it contains many spurious or insignificant connections due to using the Pearson's correlation based networks. Sparse model (without group constraint), SICE, and Pearson's correlation based methods, which do not have an identical topological structure, suffered from a large inter‐subject variability that may inhibit the actual differences between clinical groups.
The modified weighted clustering coefficients were adopted to extract the features from multiple FCNs and improved the performance of the proposed multiple network method. Our proposed weighted clustering coefficient can embody more important subtle differences of the local topological structure than that proposed by Onnela et al. (2005) (Tables 3 and 5), thus leading to the performance improvement of single networks. Further, the modified weighted clustering coefficients from networks with adjacent sparsity levels can provide more consensus and complementary information to enhance the performance of multiple network fusion. However, multiple network fusion based on the weighted clustering coefficient proposed by Onnela et al. (2005) did not show any improvement in classification performance, possibly due to lack of significant complementary information provided by multiple networks. This demonstrates that the fusion effect of multiple networks is related with the features. Compared to connectivity strength, local efficiency, and betweenness centrality, the proposed clustering coefficient showed much better discriminative ability (Figure 5), in line with our previous observation (Wee et al., 2016), suggesting that ASD children may experience abnormality in specialized information processing compared to TD children (Assaf et al., 2010; Pelphrey, Shultz, Hudac, & Vander Wyk, 2011; Murdaugh et al., 2012).
4.2. Analysis of discriminative ROIs
The discriminative brain regions identified by our method are distributed over the whole brain, and are parts of several common resting‐state networks. The identified discriminative ROIs are largely consistent with the results reported in previous ASD studies. About two thirds of the discriminative ROIs are located in the left hemisphere, in line with the previously reported left‐hemisphere hypothesis of ASD (Chandana et al. 2005; Jin, Wee, Shi, Thung, Ni, Yap, & Shen, 2015a; Jin, Wee, Shi, Thung, Yap, & Shen, 2015b).
It is worth noting that the discriminative ROIs were selected as a whole during ASD identification (Table 6). Machine learning techniques consider multiple variables simultaneously to capture spatial pattern as features, and thus can detect subtle differences that may be invisible to the univariate analysis methods such as the statistical t‐test using each variable separately (De Martino et al., 2008). Therefore, although the p‐values of most of the discriminative ROIs were smaller than 0.05, when used individually, they showed inferior classification performance than our proposed method. On the other hand, the p‐values of some discriminative ROIs were larger than or equal to 0.05, showing no significant between‐group difference individually. However, such discriminative ROIs, also indispensable, practically played a certain role in identifying ASD when combined with other ROIs. Expectedly, the contribution of each ROI is not closely related with the significant difference. Therefore, the contributions of ROIs are more important, compared to the p‐values, when using machine learning methods.
The failure of modulating the deactivation of the DMN and the abnormal connectivity of DMN with other regions have been found in ASD (Assaf et al., 2010; Murdaugh et al., 2012; Washington et al., 2014). The DMN is known to activate at rest and deactivate during task performance. The ASD children may be unable to modulate the deactivation of the DMN and suppress the mental activity during rest (Kennedy, Redcay, & Courchesne, 2006). In the present study, the left superior frontal gyrus (medial) and right angular gyrus, two functional hubs of the DMN (Andrews‐Hanna et al., 2014), were found contributed significantly to ASD prediction. The former showed lower clustering coefficient in ASD children compared to TD children (Figure 6), presumably implying the decreased ability of information processing about the self and thinking about others (Andrews‐Hanna et al., 2014; Goldberg, Harel, & Malach, 2006). The two regions are highly related with social recognition ability (Andrews‐Hanna et al., 2014) and have previously been reported to show abnormal activity or connectivity in ASD (Sato, Toichi, Uono, & Kochiyama, 2012; You et al., 2013). Other selected DMN regions including the left anterior cingulate gyrus and left precuneus have been found related to ASD pathology (Perkins, Bittar, McGillivray, Cox, & Stokes, 2015; Urbain et al., 2015). Impairment in the development of the anterior cingulate gyrus may cause social cognitive deficits in autism (Mundy, 2003). The left precuneus of ASD children showed more activity than TD children in a 2‐back working memory task, which is related with working memory impairment (Urbain et al., 2015).
The visual network is responsible for the visual processing of human brain. Regions of this network including the right middle occipital gyrus (Simard, Luck, Mottron, Zeffiro, & Soulieres, 2015), left calcarine (Libero et al., 2014; Perkins et al., 2015), and right fusiform gyrus (Scherf, Elbich, Minshew, & Behrmann, 2015; Urbain et al., 2016) have been found abnormal in ASD. In our present study, these three regions were found contributed more to ASD identification than other ROIs. Both the left middle frontal gyrus and left Heschl's gyrus, as part of the EAN, contributed much to ASD classification. The left middle frontal gyrus showed increased activity in set‐shifting task in ASD children compared to controls (Yerys et al., 2015). Left insula, region in CON, was reported highly associated with the communicative and emotional deficits of ASD (Di Martino et al., 2009; Leung, Pang, Cassel, Brian, Smith, & Taylor, 2015; Urbain et al., 2016). Left paracentral lobule of the SMN contributed the most to ASD identification in network 3 (see Figure 6), and was reported to show significant difference between ASD and TD subjects in a recent study (Cheng et al., 2015).
Our findings demonstrated that six regions in the human cerebellum (left cerebellum crust 1, right cerebellum crust 2, left cerebellum 8, vermis 3, vermis 45, and vermis 6) showed obvious contribution to ASD identification. The cerebellum besides involving in the fine motor function, plays an important role in higher cognitive functions including language (Hampson & Blatt, 2015). Some recent studies have implicated cerebellar connectivity deficits in ASD patients (Igelström, Webb, & Graziano, 2016; Khan et al., 2015; Wang, Kloth, & Badura, 2014). In addition, the left olfactory cortex, a subcortical structure which was consistently selected in all four networks, showed significant deviation in mean clustering coefficient in ASD children when compared to TD children, in line with recent finding that ASD patients experienced abnormal olfactory function (Rozenkrantz et al., 2015). Other discriminative subcortical regions including the left putamen and bilateral thalamus have also been reported to be abnormal in the previous ASD studies (Cerliani et al., 2015; Chen, Duan, Liu, et al., 2016; Estes et al., 2011; Nair et al., 2015).
4.3. Effect of different parcellation schemes
It has been shown that different parcellation schemes may have significant impact on the topological structure of the constructed networks (De Reus & van den Heuvel, 2013). “Parcellation” refers to dividing the whole brain into brain regions at the macroscale to facilitate structural or functional characterization of distinct regions (De Reus & van den Heuvel, 2013). The method proposed in this study is based on the widely used anatomically defined AAL atlas (Tzourio‐Mazoyer et al., 2002). Unlike the anatomical atlases that derived from anatomical or cyto‐architectonic segmentation, the functional parcellation scheme (i.e., CC200) proposed by Craddock et al. (2012, 2013) explored homogeneous functional connectivity in the brain, resulting in a set of spatially coherent brain regions. We examine the effects of brain parcellation scheme on our proposed method by replacing the AAL atlas with the CC200 functional atlas. We propagate the labels of CC200 atlas onto the registered fMRI images, and achieve a brain parcellation of 200 ROIs. We then compute the average time serials of each ROI and construct FCNs using the proposed method. The classification performances of AAL and CC200 atlases are shown in Table 7. Although CC200 atlas performed inferior compared to AAL atlas, it demonstrated the same performance trend, that is, the proposed method improved the ASD classification performance by fusing multiple FCNs that can characterize the same brain from different views. This observation provides strong evidence on the superiority of the proposed multi‐view method over the conventional single‐view methods, regardless of the brain parcellation schemes used.
Table 7.
Comparison of the classification performance between AAL atlas and CC200 atlas
| Method | AAL atlas (116 ROIs) | Craddock atlas (200 ROIs) | ||||
|---|---|---|---|---|---|---|
| ACC (%) | SEN (%) | SPE (%) | ACC (%) | SEN (%) | SPE (%) | |
| Network 1 | 63.04 | 71.11 | 55.32 | 70.65 | 73.33 | 68.09 |
| Network 2 | 67.39 | 73.33 | 61.70 | 68.48 | 80.00 | 57.45 |
| Network 3 | 72.83 | 77.78 | 68.09 | 70.65 | 75.56 | 65.96 |
| Network 4 | 59.78 | 77.78 | 42.55 | 65.22 | 77.78 | 53.19 |
| Multiple network method | 79.35 | 82.22 | 76.60 | 73.91 | 77.78 | 70.21 |
From Table 7, the different performance between the two atlases is because the networks using the CC200 atlas are more similar, so they could not capture abundant complementary information to enhance the classification performance. CC200 is used to construct parcellations based on homogeneous functional connectivity, while the parcellation in AAL atlas was determined based on the brain anatomical information. AAL atlas has been successfully and widely used in functional neuroimaging studies to locate the regions of the brain. In our case, the AAL atlas may be more suitable for constructing FCNs as functional connectivity relies on anatomical structure as the substrate. AAL atlas is a manual macroanatomical parcellation, and can thus provide more realistic functional connectivity patterns.
4.4. Results on validation datasets
To validate our proposed method, we have performed validation on a new independent dataset from the University of California, Los Angeles (UCLA). The data were preprocessed using the AFNI software (Cox, 1996). We use 34 ASD and 29 TD children aged between 8 and 15 years old from the UCLA_1 dataset. There are no significant gender (ASD children: 29 males and 5 females; TD children: 25 males and 4 females; p = .9178), age (ASD children: 12.5 ± 2.1 years old; TD children: 12.8 ± 1.7 years old; p = .4785), and full intelligent quotient (ASD children: 102.0 ± 13.5; TD children: 105.7 ± 10.4; p = .2371) differences between two groups. The R‐fMRI data were collected on a 3.0 T Siemens Trio scanner at UCLA. During the resting‐state scan, most subjects were instructed to relax with their eyes open and stare at a white fixation cross in the center of the black screen. The acquisition time lasted for 6 min and a total of 120 volumes of EPI images were acquired (repetition time (TR)/echo time (TE) = 3,000/28 ms, flip angle = 90°, 34 slices, slice thickness = 4 mm, imaging matrix = 64 × 64).
The classification performances of the proposed multiple network based method and four single network based methods on the UCLA_1 dataset are shown in Table 8. The proposed method fusing four FCNs achieves an accuracy of 71.43%, a sensitivity of 76.47%, and a specificity of 65.52%, showing an increment of 4.76% in accuracy compared to the best performed single network.
Table 8.
Comparison of the classification performance between the single network based methods and the proposed multiple network based method on the UCLA_1 dataset
| Method | ACC (%) | SEN (%) | SPE (%) | PPV (%) | NPV (%) |
|---|---|---|---|---|---|
| Network 1 | 42.86 | 38.24 | 48.28 | 46.43 | 40.00 |
| Network 2 | 53.97 | 47.06 | 62.07 | 59.26 | 50.00 |
| Network 3 | 66.67 | 73.53 | 58.62 | 67.57 | 65.38 |
| Network 4 | 46.03 | 55.88 | 34.48 | 50.00 | 40.00 |
| Multiple network method | 71.43 | 76.47 | 65.52 | 72.22 | 70.37 |
We have also carried out validation on the combined dataset aggregating NYU and UCLA_1 datasets (79 ASD and 76 TD children) via a 10‐fold cross‐validation. The average performance of classification results are reported across all 10 cross‐validation folds. The classification performances of the proposed multiple network based method and four single network based methods on the combined dataset are shown in Table 9. The proposed method fusing four FCNs achieves an accuracy of 73.08%, a sensitivity of 74.29%, and a specificity of 71.67%, showing an increment of 6.93% in accuracy compared to the best performed single network.
Table 9.
Comparison of the classification performance between the single network based methods and the proposed multiple network based method on combined dataset (NYU + UCLA_1)
| Method | ACC (%) | SEN (%) | SPE (%) | PPV (%) | NPV (%) |
|---|---|---|---|---|---|
| Network 1 | 63.85 | 65.71 | 61.67 | 66.67 | 60.66 |
| Network 2 | 64.62 | 71.43 | 56.67 | 65.79 | 62.96 |
| Network 3 | 66.15 | 70.00 | 61.67 | 68.06 | 63.79 |
| Network 4 | 58.46 | 65.71 | 50.00 | 60.53 | 55.56 |
| Multiple network method | 73.08 | 74.29 | 71.67 | 75.36 | 70.49 |
Our proposed method again outperforms the compared single network methods in all the measures with this independent dataset, and combined dataset. Other replicable results are included in the Supporting Information (Supporting Information Tables S1–S4). Supporting Information Tables S1 and S2 are obtained based on the UCLA_1 dataset, and Supporting Information Tables S3 and S4 based on combined dataset (NYU + UCLA_1). In Supporting Information Tables S1 and S3, the proposed method achieves the best performance compared to other multiple network based methods. In Supporting Information Tables S2 and S4, multiple network fusion based on the weighted clustering coefficient proposed by Onnela et al. did not show obvious improvement in classification accuracy compared with the best performed single networks whose accuracies were 63.49% and 60%, respectively. Therefore it shows inferior performance to our proposed method.
4.5. Age effect
Age is an important factor in the development and progression of ASD. In order to investigate the effects of age on the network structure and the accuracy of the proposed approach, we have performed experiments on the combined NYU and UCLA_1 dataset via 10‐fold cross‐validation. We divided all subjects (79 ASD and 76 TD children) into two groups according to age: the group of 7–10 years old (34 ASD and 28 TD children), and the group of 11–15 years old (45 ASD and 48 TD children). Then the proposed method was carried out on each group. The network structure and the accuracy of the proposed method for both groups are shown in Figures 9 and 10, respectively. Figure 9 shows the mean network structure with the maximum number of connections for both groups. To clearly display the network structure, only the connections with connection strength above 0.1 are shown. More connections appears in the group of 11–15 years old than in the group of 7–10 years old, implying that the connections are stronger in the group of 11–15 years old than in the group of 7–10 years old. It is expected due to the rapid growth of brain during this period of time. From Figure 10, we can see that both groups present the accuracy of 70%, inferior to the accuracy of the entire group (73.08%). Normally, dividing subjects into age groups may improve classification accuracy due to reducing the sample variation caused by age. However, in our case, due to the small sample size, further reduction based on age actually hurts the classification accuracy. On the other hand, the fact that both groups have almost same accuracy indicates that age does not affect the final classification result significantly.
Figure 9.
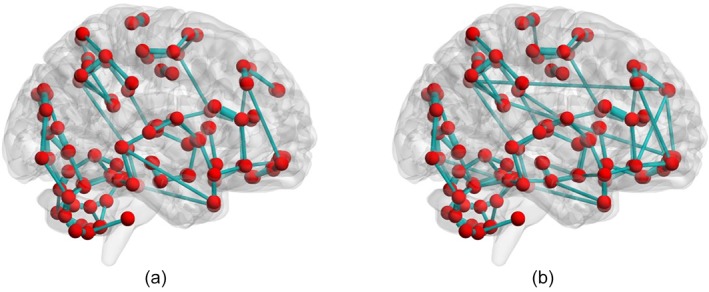
The network structures with the maximum number of connections for the group of 7–10 years old (a) and the group of 11–15 years old (b). Only the connections with connection strength above 0.1 are shown [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 10.
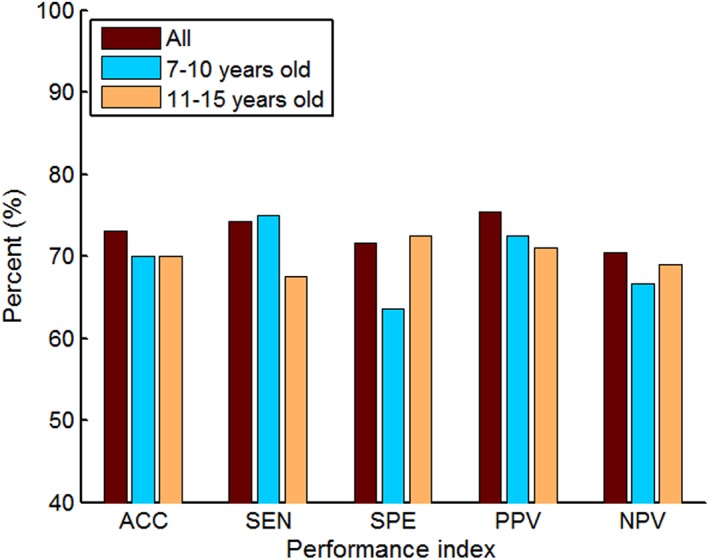
Classification performance of the entire group and the two subgroups (7–10 years old and 11–15 years old). ACC, accuracy; SEN, sensitivity; SPE, specificity; PPV, positive predictive value; NPV, negative predictive value [Color figure can be viewed at http://wileyonlinelibrary.com]
Furthermore, we have also included the age as an additional feature into the feature vector to explore how it may affect the classification accuracy. Our results demonstrated that the age was finally not selected as effective feature during cross‐validation for achieving the best classification performance, implying no significant influence by age to our classifier.
4.6. Limitation
Compared to the classification on single‐site data, classification on multi‐site data encounters a challenging problem of dealing with the heterogeneity of the data (e.g., the data variation caused by different MRI scanner types, imaging sequences, and disease evaluations; see Abraham et al. (2017) and Nieuwenhuis et al. (2017)). Multi‐site data classification is a recent study topic that can use larger aggregated data to boost the application of neuroimaging‐based classification algorithms into clinical practice. However, the heterogeneity of multi‐site data can significantly decrease the prediction accuracy of neuropsychiatric disorders. Abraham et al. (2017) have adopted some techniques to overcome the issue of data heterogeneity and achieved better classification performance using multi‐site data.
It is important to note that the aim of our work is to design a new classification framework (i.e., combination of multi‐view based FCNs and modified weighted clustering coefficient) that can more accurately identify ASD patients from healthy subjects. In order to explicitly demonstrate the advantages of our proposed framework, we evaluated the classification of performance on relatively homogeneous single‐site datasets NYU and UCLA_1, and combined dataset (NYU + UCLA_1) since classification on heterogeneous multi‐site data without appropriate handling techniques such as those suggested by Abraham et al. (2017) may hinder the comparison with other FCN construction and feature extraction methods. To overcome the heterogeneity of data, we may use an appropriate brain parcellation, align the feature distributions of different sites to the common feature space, and utilize multi‐task learning to achieve shared features, as well as adopt semi‐supervised co‐training to improve the classifier iteratively. We will consider extending the proposed framework to the heterogeneous multi‐site data in our future work.
As another future work, we would like to extend the current work to predict treatment response and disease outcome once a dataset with such information is available.
5. CONCLUSIONS
Most methods used only one FCN for exploring the biomarkers of the neuropsychiatric disorders based on R‐fMRI, which ignores the capability of multiple networks for a more comprehensive and informative representation of disease‐associated functional disruptions. In this paper, we have proposed a novel multiple network based classification framework that can generate multiple group‐sparse FCNs with different levels of network sparsity and then linearly fuse the network measures extracted from these FCNs to enhance the representation of functional connectivity networks via a multi‐view learning approach. Group‐sparse FCNs capture subtle disease‐related alterations at different levels of sparsity by varying the regularization parameter, while minimizing the inter‐subject variability through an identical network structure across subjects. We evaluated the performance of the proposed method on a dataset from the ABIDE database, and achieved the best classification performance among all compared single network based methods and multiple network based methods, suggesting that the fusion of group‐sparse FCNs with multiple levels of sparsity may provide more informative biomarkers for aiding brain disease diagnosis. The results on validation datasets also demonstrate the validity of our proposed method. In the future, for the specific studies at hand, multiple network methods could be explored to boost the representation of FCNs by fusing multi‐view information for better brain disease diagnosis.
Supporting information
Appendix S1: Supplementary Material
Appendix S2: Supplementary Material
ACKNOWLEDGMENTS
This work was partly supported by the National Natural Science Foundation of China [grant numbers 61300073, 61272356, 61463035]; and the National Institutes of Health (NIH) grants (grant numbers EB006733, EB008374, MH100217, MH108914, AG041721, AG049371, AG042599, DE022676, CA206100, AG053867, EB022880). Dr. S.‐W. Lee was partially supported by Institute for Information & Communications Technology Promotion (IITP) grant funded by the Korea government (No. 2017‐0‐00451). Primary support for the Autism Brain Imaging Data Exchange (ABIDE) by Adriana Di Martino was provided by the National Institute of Mental Health (NIMH) (K23MH087770) and the Leon Levy Foundation. Primary support for the ABIDE by Michael P. Milham and the International Neuroimaging Data‐sharing Initiative (INDI) team was provided by gifts from Joseph P. Healy and the Stavros Niarchos Foundation to the Child Mind Institute, as well as by an NIMH award to MPM (R03MH096321). The funders had no role in study design, data analysis, decision to publish, or preparation of the manuscript.
NAMES AND ABBREVIATIONS OF THE BRAIN ROIS IN THE AAL ATLAS
Table A1.
Names and abbreviations of the brain ROIs in the AAL atlas
| Index | ROI name (abbreviation) | Index | ROI name (abbreviation) |
|---|---|---|---|
| 1,2 | Precentral gyrus (PreCG) | 3,4 | Superior frontal gyrus (dorsal) (SFGdor) |
| 5,6 | Orbitofrontal cortex (superior) (ORBsup) | 7,8 | Middle frontal gyrus (MFG) |
| 9,10 | Orbitofrontal cortex (middle) (ORBmid) | 11,12 | Inferior frontal gyrus (opercular) (IFGoperc) |
| 13,14 | Inferior frontal gyrus (triangular) (IFGtriang) | 15,16 | Orbitofrontal cortex (inferior) (ORBinf) |
| 17,18 | Rolandic operculum (ROL) | 19,20 | Supplementary motor area (SMA) |
| 21,22 | Olfactory (OLF) | 23,24 | Superior frontal gyrus (middle) (SFGmed) |
| 25,26 | Orbitofrontal cortex (medial) (ORBmed) | 27,28 | Rectus gyrus (REC) |
| 29,30 | Insula (INS) | 31,32 | Anterior cingulate gyrus (ACG) |
| 33,34 | Middle cingulate gyrus (MCG) | 35,36 | Posterior cingulate gyrus (PCG) |
| 37,38 | Hippocampus (HIP) | 39,40 | Parahippocampal gyrus (PHG) |
| 41,42 | Amygdala (AMYG) | 43,45 | Calcarine cortex (CAL) |
| 45,46 | Cuneus (CUN) | 47,48 | Lingual gyrus (LING) |
| 49,50 | Superior occipital gyrus (SOG) | 51,52 | Middle occipital gyrus (MOG) |
| 53,54 | Inferior occipital gyrus (IOG) | 55,56 | Fusiform gyrus (FFG) |
| 57,58 | Postcentral gyrus (PoCG) | 59,60 | Superior parietal gyrus (SPG) |
| 61,62 | Inferior parietal lobule (IPL) | 63,64 | Supramarginal gyrus (SMG) |
| 65,66 | Angular gyrus (ANG) | 67,68 | Precuneus (PCUN) |
| 69,70 | Paracentral lobule (PCL) | 71,72 | Caudate (CAU) |
| 73,74 | Putamen (PUT) | 75,76 | Pallidum (PAL) |
| 77,78 | Thalamus (THA) | 79,80 | Heschl gyrus (HES) |
| 81,82 | Superior temporal gyrus (STG) | 83,84 | Temporal pole (superior) (TPOsup) |
| 85,86 | Middle temporal gyrus (MTG) | 87,88 | Temporal pole (middle) (TPOmid) |
| 89,90 | Inferior temporal gyrus (ITG) | 91–94 | Crust 1–2 of cerebellar hemisphere (crust) |
| 95–108 | Lobule 3–10 of cerebellar hemisphere (CRBL) | 109–116 | Lobule 1–10 of vermis (vermis) |
The odd and even indices refer to the left‐hemisphere and right‐hemisphere regions, respectively.
Huang H, Liu X, Jin Y, Lee S‐W, Wee C‐Y, Shen D. Enhancing the representation of functional connectivity networks by fusing multi‐view information for autism spectrum disorder diagnosis. Hum Brain Mapp. 2019;40:833–854. 10.1002/hbm.24415
Funding information National Natural Science Foundation of China, Grant/Award Numbers: 61300073, 61773048, 61272356, 61463035; National Institutes of Health, Grant/Award Numbers: EB006733, EB008374, MH100217, MH108914, AG041721, AG049371, AG042599, DE022676, CA206100, AG053867, EB022880; Institute for Information & Communications Technology Promotion (IITP) grant, Grant/Award Number: 2017‐0‐00451
REFERENCES
- Abraham, A. , Milham, M. P. , Di Martino, A. , Craddock, R. C. , Samaras, D. , Thirion, B. , & Varoquaux, G. (2017). Deriving reproducible biomarkers from multi‐site resting‐state data: An autism‐based example. NeuroImage, 147, 736–745. [DOI] [PubMed] [Google Scholar]
- Achard, S. , & Bullmore, E. (2007). Efficiency and cost of economical brain functional networks. PLoS Computational Biology, 3, e17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amaral, D. G. , Schumann, C. M. , & Nordahl, C. W. (2008). Neuroanatomy of autism. Trends in Neurosciences, 31, 137–145. [DOI] [PubMed] [Google Scholar]
- American Psychiatric Association . (2013). Diagnostic and statistical manual of mental disorders (5th ed.). Arlington: American Psychiatric Association Publishing. [Google Scholar]
- Anderson, J. S. , Nielsen, J. A. , Froehlich, A. L. , DuBray, M. B. , Druzgal, T. J. , Cariello, A. N. , … Lainhart, J. E. (2011). Functional connectivity magnetic resonance imaging classification of autism. Brain, 134, 3742–3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews‐Hanna, J. R. , Smallwood, J. , & Spreng, R. N. (2014). The default network and self‐generated thought: Component processes, dynamic control, and clinical relevance. Annals of the New York Academy of Sciences, 1316, 29–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf, M. , Jagannathan, K. , Calhoun, V. D. , Miller, L. , Stevens, M. C. , Sahl, R. , … Pearlson, G. D. (2010). Abnormal functional connectivity of default mode sub‐networks in autism spectrum disorder patients. NeuroImage, 53, 247–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baggio, H. C. , Sala‐Llonch, R. , Segura, B. , Marti, M. J. , Valldeoriola, F. , Compta, Y. , … Junque, C. (2014). Functional brain networks and cognitive deficits in Parkinson's disease. Human Brain Mapping, 35, 4620–4634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai, F. , Liao, W. , Watson, D. R. , Shi, Y. , Wang, Y. , Yue, C. , … Zhang, Z. (2011). Abnormal whole‐brain functional connection in amnestic mild cognitive impairment patients. Behavioural Brain Research, 216, 666–672. [DOI] [PubMed] [Google Scholar]
- Bassett, D. S. , & Bullmore, E. (2006). Small‐world brain networks. The Neuroscientist, 12, 512–523. [DOI] [PubMed] [Google Scholar]
- Biswal, B. , Yetkin, F. Z. , Haughton, V. M. , & Hyde, J. S. (1995). Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magnetic Resonance in Medicine, 34, 537–541. [DOI] [PubMed] [Google Scholar]
- Broyd, S. J. , Demanuele, C. , Debener, S. , Helps, S. K. , James, C. J. , & Sonuga‐Barke, E. J. (2009). Default‐mode brain dysfunction in mental disorders: A systematic review. Neuroscience and Biobehavioral Reviews, 33, 279–296. [DOI] [PubMed] [Google Scholar]
- Buckner, R. L. , Andrews‐Hanna, J. R. , & Schacter, D. L. (2008). The brain's default network: Anatomy, function, and relevance to disease. Annals of the New York Academy of Sciences, 1124, 1–38. [DOI] [PubMed] [Google Scholar]
- Cerliani, L. , Mennes, M. , Thomas, R. M. , Di Martino, A. , Thioux, M. , & Keysers, C. (2015). Increased functional connectivity between subcortical and cortical resting‐state networks in autism spectrum disorder. JAMA Psychiatry, 72, 767–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandana, S. R. , Behen, M. E. , Juhasz, C. , Muzik, O. , Rothermel, R. D. , Mangner, T. J. , … Chugani, D. C. (2005). Significance of abnormalities in developmental trajectory and asymmetry of cortical serotonin synthesis in autism. International Journal of Developmental Neuroscience, 23, 171–182. [DOI] [PubMed] [Google Scholar]
- Chang, C. C., & lin, C. J. (2011) LIBSVM: A library for support vector machines, ACM TIST 2011, pp. 21–27. Retrieved from http://www.csie.ntu.edu.tw/~cjlin/libsvm
- Chen, C. P. , Keown, C. L. , Jahedi, A. , Nair, A. , Pflieger, M. E. , Bailey, B. A. , & Muller, R. A. (2015). Diagnostic classification of intrinsic functional connectivity highlights somatosensory, default mode and visual regions in autism. NeuroImage Clinical, 8, 238–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, H. , Duan, X. , Liu, F. , Lu, F. , Ma, X. , Zhang, Y. , … Chen, H. (2016). Multivariate classification of autism spectrum disorder using frequency‐specific resting‐state functional connectivity‐‐a multi‐center study. Progress in Neuro‐Psychopharmacology & Biological Psychiatry, 64, 1–9. [DOI] [PubMed] [Google Scholar]
- Chen, X. , Zhang, H. , Gao, Y. , Wee, C. Y. , Li, G. , Shen, D. , & Alzheimer's Disease Neuroimaging, I. (2016). High‐order resting‐state functional connectivity network for MCI classification. Human Brain Mapping, 37, 3282–3296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng, W. , Rolls, E. T. , Gu, H. , Zhang, J. , & Feng, J. (2015). Autism: Reduced connectivity between cortical areas involved in face expression, theory of mind, and the sense of self. Brain, 138, 1382–1393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox, R. W. (1996). AFNI: Software for analysis and visualization of functional magnetic resonance neuroimages. Computers and Biomedical Research, 29, 162–173. [DOI] [PubMed] [Google Scholar]
- Craddock, R. C. , James, G. A. , Holtzheimer, P. E. , Hu, X. P. , & Mayberg, H. S. (2012). A whole brain fMRI atlas generated via spatially constrained spectral clustering. Human Brain Mapping, 33, 1914–1928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craddock, R. C. , Jbabdi, S. , Yan, C. G. , Vogelstein, J. T. , Castellanos, F. X. , Di Martino, A. , … Milham, M. P. (2013). Imaging human connectomes at the macroscale. Nature Methods, 10, 524–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das, S. R. , Pluta, J. , Mancuso, L. , Kliot, D. , Orozco, S. , Dickerson, B. C. , … Wolk, D. A. (2013). Increased functional connectivity within medial temporal lobe in mild cognitive impairment. Hippocampus, 23, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Martino, F. , Valente, G. , Staeren, N. , Ashburner, J. , Goebel, R. , & Formisano, E. (2008). Combining multivariate voxel selection and support vector machines for mapping and classification of fMRI spatial patterns. NeuroImage, 43, 44–58. [DOI] [PubMed] [Google Scholar]
- De Reus, M. A. , & van den Heuvel, M. P. (2013). The parcellation‐based connectome: Limitations and extensions. NeuroImage, 80, 397–404. [DOI] [PubMed] [Google Scholar]
- Di Martino, A. , Shehzad, Z. , Kelly, C. , Roy, A. K. , Gee, D. G. , Uddin, L. Q. , … Milham, M. P. (2009). Relationship between cingulo‐insular functional connectivity and autistic traits in neurotypical adults. The American Journal of Psychiatry, 166, 891–899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Martino, A. , Yan, C. G. , Li, Q. , Denio, E. , Castellanos, F. X. , Alaerts, K. , … Milham, M. P. (2014). The autism brain imaging data exchange: Towards a large‐scale evaluation of the intrinsic brain architecture in autism. Molecular Psychiatry, 19, 659–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach, N. U. , Nardos, B. , Cohen, A. L. , Fair, D. A. , Power, J. D. , Church, J. A. , … Schlaggar, B. L. (2010). Prediction of individual brain maturity using fMRI. Science, 329, 1358–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebisch, S. J. , Gallese, V. , Willems, R. M. , Mantini, D. , Groen, W. B. , Romani, G. L. , … Bekkering, H. (2011). Altered intrinsic functional connectivity of anterior and posterior insula regions in high‐functioning participants with autism spectrum disorder. Human Brain Mapping, 32, 1013–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estes, A. , Shaw, D. W. , Sparks, B. F. , Friedman, S. , Giedd, J. N. , Dawson, G. , … Dager, S. R. (2011). Basal ganglia morphometry and repetitive behavior in young children with autism spectrum disorder. Autism Research, 4, 212–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Figueiredo, M. A. T. , Nowak, R. D. , & Wright, S. J. (2007). Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problem. IEEE Journal of Selected Topics in Signal Processing, 1, 586–597. [Google Scholar]
- Fornito, A. , Zalesky, A. , & Breakspear, M. (2015). The connectomics of brain disorders. Nature Reviews. Neuroscience, 16, 159–172. [DOI] [PubMed] [Google Scholar]
- Freeman, L. C. (1977). A set of measures of centrality based on betweenness. Sociometry, 40, 35–41. [Google Scholar]
- Freeman, L. C. (1978). Centrality in social networks: Conceptual clarification. Social Network, 1, 215–239. [Google Scholar]
- Goldberg, I. I. , Harel, M. , & Malach, R. (2006). When the brain loses its self: Prefrontal inactivation during sensorimotor processing. Neuron, 50, 329–339. [DOI] [PubMed] [Google Scholar]
- Gong, Y. , Ke, Q. , Isard, M. , & Lazebnik, S. (2014). A multi‐view embedding space for modeling internet images, tags, and their semantics. International Journal of Computer Vision, 106, 210–233. [Google Scholar]
- Greicius, M. (2008). Resting‐state functional connectivity in neuropsychiatric disorders. Current Opinion in Neurology, 21, 424–430. [DOI] [PubMed] [Google Scholar]
- Greicius, M. D. , Flores, B. H. , Menon, V. , Glover, G. H. , Solvason, H. B. , Kenna, H. , … Schatzberg, A. F. (2007). Resting‐state functional connectivity in major depression: Abnormally increased contributions from subgenual cingulate cortex and thalamus. Biological Psychiatry, 62, 429–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius, M. D. , Srivastava, G. , Reiss, A. L. , & Menon, V. (2004). Default‐mode network activity distinguishes Alzheimer's disease from healthy aging: Evidence from functional MRI. Proceedings of the National Academy of Sciences of the United States of America, 101, 4637–4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo, X. , Dominick, K. C. , Minai, A. A. , Li, H. , Erickson, C. A. , & Lu, L. J. (2017). Diagnosing autism spectrum disorder from brain resting‐state functional connectivity patterns using a deep neural network with a novel feature selection method. Frontiers in Neuroscience, 11, 460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guyon, I. , Weston, J. , Barnhill, S. , & Vapnik, V. (2004). Gene selection for cancer classification using support vector machines. Machine Learning, 46, 389–422. [Google Scholar]
- Hampson, D. R. , & Blatt, G. J. (2015). Autism spectrum disorders and neuropathology of the cerebellum. Frontiers in Neuroscience, 9, 420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrington, D. L. , Rubinov, M. , Durgerian, S. , Mourany, L. , Reece, C. , Koenig, K. , … Rao, S. M. (2015). Network topology and functional connectivity disturbances precede the onset of Huntington's disease. Brain, 138, 2332–2346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He, Y. , Chen, Z. J. , & Evans, A. C. (2007). Small‐world anatomical networks in the human brain revealed by cortical thickness from MRI. Cerebral Cortex, 17, 2407–2419. [DOI] [PubMed] [Google Scholar]
- Huang, S. , Li, J. , Sun, L. , Ye, J. , Fleisher, A. , Wu, T. , … Alzheimer's Disease NeuroImaging, I. (2010). Learning brain connectivity of Alzheimer's disease by sparse inverse covariance estimation. NeuroImage, 50, 935–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Igelström, K. M. , Webb, T. W. , & Graziano, M. S. (2016). Functional connectivity between the temporoparietal cortex and cerebellum in autism spectrum disorder. Cerebral Cortex, pii, bhw079. [DOI] [PubMed] [Google Scholar]
- Iidaka, T. (2015). Resting state functional magnetic resonance imaging and neural network classified autism and control. Cortex, 63, 55–67. [DOI] [PubMed] [Google Scholar]
- Jiang, X. , Zhang, X. , & Zhu, D. (2014). Intrinsic functional component analysis via sparse representation on Alzheimer's disease neuroimaging initiative database. Brain Connectivity, 4, 575–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jie, B. , Zhang, D. , Wee, C. Y. , & Shen, D. (2014). Topological graph kernel on multiple thresholded functional connectivity networks for mild cognitive impairment classification. Human Brain Mapping, 35, 2876–2897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin, Y. , Shi, Y. , Zhan, L. , Gutman, B. A. , de Zubicaray, G. I. , McMahon, K. L. , … Thompson, P. M. (2014). Automatic clustering of white matter fibers in brain diffusion MRI with an application to genetics. NeuroImage, 100, 75–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin, Y. , Wee, C. Y. , Shi, F. , Thung, K. H. , Ni, D. , Yap, P. T. , & Shen, D. (2015a). Identification of infants at high‐risk for autism spectrum disorder using multiparameter multi‐scale whitematter connectivity networks. Human Brain Mapping, 36, 4880–4896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin, Y. , Wee, C. Y. , Shi, F. , Thung, K. H. , Yap, P. T. , & Shen, D. (2015b). For the infant brain imaging study (IBIS) network: Identification of infants at risk for autism using multi‐parameter hierarchical white matter connectors. Machine Learning and Medical Imaging, 9532, 170–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy, D. P. , Redcay, E. , & Courchesne, E. (2006). Failing to deactivate: Resting functional abnormalities in autism. Proceedings of the National Academy of Sciences of the United States of America, 103, 8275–8280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan, A. J. , Nair, A. , Keown, C. L. , Datko, M. C. , Lincoln, A. J. , & Muller, R. A. (2015). Cerebro‐cerebellar resting‐state functional connectivity in children and adolescents with autism spectrum disorder. Biological Psychiatry, 78, 625–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khazaee, A. , Ebrahimzadeh, A. , & Babajani‐Feremi, A. (2015). Identifying patients with Alzheimer's disease using resting‐state fMRI and graph theory. Clinical Neurophysiology, 126, 2132–2141. [DOI] [PubMed] [Google Scholar]
- Kim, Y. S. , Leventhal, B. L. , Koh, Y. J. , Fombonne, E. , Laska, E. , Lim, E. C. , … Grinker, R. R. (2011). Prevalence of autism spectrum disorders in a total population sample. The American Journal of Psychiatry, 168, 904–912. [DOI] [PubMed] [Google Scholar]
- Lai, M. C. , Lombardo, M. V. , & Baron‐Cohen, S. (2014). Autism. Lancet, 383, 896–910. [DOI] [PubMed] [Google Scholar]
- Leung, R. C. , Pang, E. W. , Cassel, D. , Brian, J. A. , Smith, M. L. , & Taylor, M. J. (2015). Early neural activation during facial affect processing in adolescents with autism Spectrum disorder. NeuroImage Clinical, 7, 203–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, J. , Jin, Y. , Shi, Y. , Dinov, I. D. , Wang, D. J. , Toga, A. W. , & Thompson, P. M. (2013). Voxelwise spectral diffusional connectivity and its applications to Alzheimer's disease and intelligence prediction. Medical Image Computing and Computer‐Assisted Intervention, 8149, 655–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libero, L. E. , Maximo, J. O. , Deshpande, H. D. , Klinger, L. G. , Klinger, M. R. , & Kana, R. K. (2014). The role of mirroring and mentalizing networks in mediating action intentions in autism. Mol Autism, 5, 50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, J., Ji, S., & Ye, J. (2009). SLEP: Sparse learning with efficient projections. Technical report. Tempe, AZ: Arizona State University.
- Meskaldji, D. E. , Fischi‐Gomez, E. , Griffa, A. , Hagmann, P. , Morgenthaler, S. , & Thiran, J. P. (2013). Comparing connectomes across subjects and populations at different scales. NeuroImage, 80, 416–425. [DOI] [PubMed] [Google Scholar]
- Mundy, P. (2003). Annotation: The neural basis of social impairments in autism: The role of the dorsal medial‐frontal cortex and anterior cingulate system. Journal of Child Psychology and Psychiatry, 44, 793–809. [DOI] [PubMed] [Google Scholar]
- Murdaugh, D. L. , Shinkareva, S. V. , Deshpande, H. R. , Wang, J. , Pennick, M. R. , & Kana, R. K. (2012). Differential deactivation during mentalizing and classification of autism based on default mode network connectivity. PLoS One, 7, e50064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair, A. , Carper, R. A. , Abbott, A. E. , Chen, C. P. , Solders, S. , Nakutin, S. , … Muller, R. A. (2015). Regional specificity of aberrant thalamocortical connectivity in autism. Human Brain Mapping, 36, 4497–4511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen, J. A. , Zielinski, B. A. , Fletcher, P. T. , Alexander, A. L. , Lange, N. , Bigler, E. D. , … Anderson, J. S. (2013). Multi‐site functional connectivity MRI classification of autism: ABIDE results. Frontiers in Human Neuroscience, 7, 599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwenhuis, M. , Schnack, H. G. , van Haren, N. E. , Lappin, J. , Morgan, C. , Reinders, A. A. , … Dazzan, P. (2017). Multi‐center MRI prediction models: Predicting sex and illness course in first episode psychosis patients. NeuroImage, 145, 246–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onnela, J. P. , Saramäki, J. , Kertész, J. , & Kaski, K. (2005). Intensity and coherence of motifs in weighted complex networks. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 71, 065103. [DOI] [PubMed] [Google Scholar]
- Pelphrey, K. A. , Shultz, S. , Hudac, C. M. , & Vander Wyk, B. C. (2011). Research review: Constraining heterogeneity: The social brain and its development in autism spectrum disorder. Journal of Child Psychology and Psychiatry, 52, 631–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perkins, T. J. , Bittar, R. G. , McGillivray, J. A. , Cox, I. I. , & Stokes, M. A. (2015). Increased premotor cortex activation in high functioning autism during action observation. Journal of Clinical Neuroscience, 22, 664–669. [DOI] [PubMed] [Google Scholar]
- Plitt, M. , Barnes, K. A. , & Martin, A. (2015). Functional connectivity classification of autism identifies highly predictive brain features but falls short of biomarker standards. NeuroImage Clinical, 7, 359–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price, T. , Wee, C. Y. , Gao, T. , & Shen, D. (2014). Multiple‐network classification of childhood autism using functional connectivity dynamics. Medical Image Computing and Computer‐Assisted Intervention, 17, 177–184. [DOI] [PubMed] [Google Scholar]
- Ptak, R. (2012). The frontoparietal attention network of the human brain: Action, saliency, and a priority map of the environment. The Neuroscientist, 18, 502–515. [DOI] [PubMed] [Google Scholar]
- Rozenkrantz, L. , Zachor, D. , Heller, I. , Plotkin, A. , Weissbrod, A. , Snitz, K. , … Sobel, N. (2015). A mechanistic link between olfaction and autism spectrum disorder. Current Biology, 25, 1904–1910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov, M. , & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52, 1059–1069. [DOI] [PubMed] [Google Scholar]
- Sato, J. R. , Moll, J. , Green, S. , Deakin, J. F. , Thomaz, C. E. , & Zahn, R. (2015). Machine learning algorithm accurately detects fMRI signature of vulnerability to major depression. Psychiatry Research, 233, 289–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato, W. , Toichi, M. , Uono, S. , & Kochiyama, T. (2012). Impaired social brain network for processing dynamic facial expressions in autism spectrum disorders. BMC Neuroscience, 13, 99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scherf, K. S. , Elbich, D. , Minshew, N. , & Behrmann, M. (2015). Individual differences in symptom severity and behavior predict neural activation during face processing in adolescents with autism. NeuroImage Clinical, 7, 53–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeley, W. W. , Menon, V. , Schatzberg, A. F. , Keller, J. , Glover, G. H. , Kenna, H. , … Greicius, M. D. (2007). Dissociable intrinsic connectivity networks for salience processing and executive control. The Journal of Neuroscience, 27, 2349–2356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simard, I. , Luck, D. , Mottron, L. , Zeffiro, T. A. , & Soulieres, I. (2015). Autistic fluid intelligence: Increased reliance on visual functional connectivity with diminished modulation of coupling by task difficulty. NeuroImage Clinical, 9, 467–478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns, O. , & Zwi, J. D. (2004). The small world of the cerebral cortex. Neuroinformatics, 2, 145–162. [DOI] [PubMed] [Google Scholar]
- Stam, C. J. , de Haan, W. , Daffertshofer, A. , Jones, B. F. , Manshanden, I. , van Cappellen van Walsum, A. M. , … Scheltens, P. (2009). Graph theoretical analysis of magnetoencephalographic functional connectivity in Alzheimer's disease. Brain, 132, 213–224. [DOI] [PubMed] [Google Scholar]
- Suk, H. I. , Wee, C. Y. , Lee, S. W. , & Shen, D. (2016). State‐space model with deep learning for functional dynamics estimation in resting‐state fmri. Neuroimage, 129, 292–307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, L., Patel, R., Liu, J., Chen, K., Wu, T., Li, J., Reiman, E., & Ye, J. (2009). Mining brain region connectivity for alzheimer's disease study via sparse inverse covariance estimation. In ACM SIGKDD09 (pp. 1335–1344).
- Tzourio‐Mazoyer, N. , Landeau, B. , Papathanassiou, D. , Crivello, F. , Etard, O. , Delcroix, N. , … Joliot, M. (2002). Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single‐subject brain. NeuroImage, 15, 273–289. [DOI] [PubMed] [Google Scholar]
- Urbain, C. , Vogan, V. M. , Ye, A. X. , Pang, E. W. , Doesburg, S. M. , & Taylor, M. J. (2016). Desynchronization of fronto‐temporal networks during working memory processing in autism. Human Brain Mapping, 37, 153–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urbain, C. M. , Pang, E. W. , & Taylor, M. J. (2015). Atypical spatiotemporal signatures of working memory brain processes in autism. Translational Psychiatry, 5, e617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel, M. P. , & Hulshoff Pol, H. E. (2010). Exploring the brain network: A review on resting‐state fMRI functional connectivity. European Neuropsychopharmacology, 20, 519–534. [DOI] [PubMed] [Google Scholar]
- Varoquaux, G. , & Craddock, R. C. (2013). Learning and comparing functional connectomes across subjects. NeuroImage, 80, 405–415. [DOI] [PubMed] [Google Scholar]
- Wang, J. , Zuo, X. , Dai, Z. , Xia, M. , Zhao, Z. , Zhao, X. , … He, Y. (2013). Disrupted functional brain connectome in individuals at risk for Alzheimer's disease. Biological Psychiatry, 73, 472–481. [DOI] [PubMed] [Google Scholar]
- Wang, L. , Zhu, C. , He, Y. , Zang, Y. , Cao, Q. , Zhang, H. , … Wang, Y. (2009). Altered small‐world brain functional networks in children with attention‐deficit/hyperactivity disorder. Human Brain Mapping, 30, 638–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, S. S. , Kloth, A. D. , & Badura, A. (2014). The cerebellum, sensitive periods, and autism. Neuron, 83, 518–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, X. , Xia, M. , Lai, Y. , Dai, Z. , Cao, Q. , Cheng, Z. , … He, Y. (2014). Disrupted resting‐state functional connectivity in minimally treated chronic schizophrenia. Schizophrenia Research, 156, 150–156. [DOI] [PubMed] [Google Scholar]
- Wang, Z. , Liu, J. , Zhong, N. , Qin, Y. , Zhou, H. , & Li, K. (2012). Changes in the brain intrinsic organization in both on‐task state and post‐task resting state. NeuroImage, 62, 394–407. [DOI] [PubMed] [Google Scholar]
- Washington, S. D. , Gordon, E. M. , Brar, J. , Warburton, S. , Sawyer, A. T. , Wolfe, A. , … VanMeter, J. W. (2014). Dysmaturation of the default mode network in autism. Human Brain Mapping, 35, 1284–1296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts, D. J. , & Strogatz, S. H. (1998). Collective dynamics of 'small‐world' networks. Nature, 393, 440–442. [DOI] [PubMed] [Google Scholar]
- Wee, C. Y. , Yap, P. T. , Denny, K. , Browndyke, J. N. , Potter, G. G. , Welsh‐Bohmer, K. A. , … Shen, D. (2012a). Resting‐state multi‐spectrum functional connectivity networks for identification of MCI patients. PLoS One, 7, e37828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee, C. Y. , Yap, P. T. , & Shen, D. (2013). Prediction of Alzheimer's disease and mild cognitive impairment using cortical morphological patterns. Human Brain Mapping, 34, 3411–3425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee, C. Y. , Yap, P. T. , & Shen, D. (2016). Diagnosis of autism spectrum disorders using temporally‐distinct resting‐state functional connectivity networks. CNS Neuroscience & Therapeutics, 22, 212–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee, C. Y. , Yap, P. T. , Zhang, D. , Denny, K. , Browndyke, J. N. , Potter, G. G. , … Shen, D. (2012b). Identification of MCI individuals using structural and functional connectivity networks. NeuroImage, 59, 2045–2056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee, C. Y. , Yap, P. T. , Zhang, D. , Wang, L. , & Shen, D. (2014). Group‐constrained sparse fMRI connectivity modeling for mild cognitive impairment identification. Brain Structure & Function, 219, 641–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, F. , Jing, X. Y. , You, X. G. , Yue, D. , Hu, R. M. , & Yang, J. Y. (2016). Multi‐view low‐rank dictionary learning for image classification. Pattern Recognition, 50, 143–154. [Google Scholar]
- Xu, C., Tao, D., & Xu, C. (2013). A survey on multi‐view learning. Computer Science. arXiv:1304.5634.
- Yang, R. , Gao, C. , Wu, X. , Yang, J. , Li, S. , & Cheng, H. (2016). Decreased functional connectivity to posterior cingulate cortex in major depressive disorder. Psychiatry Research, 255, 15–23. [DOI] [PubMed] [Google Scholar]
- Yerys, B. E. , Antezana, L. , Weinblatt, R. , Jankowski, K. F. , Strang, J. , Vaidya, C. J. , … Kenworthy, L. (2015). Neural correlates of set‐shifting in children with autism. Autism Research, 8, 386–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You, X. , Norr, M. , Murphy, E. , Kuschner, E. S. , Bal, E. , Gaillard, W. D. , … Vaidya, C. J. (2013). Atypical modulation of distant functional connectivity by cognitive state in children with autism Spectrum disorders. Frontiers in Human Neuroscience, 7, 482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu, Q. , Erhardt, E. B. , Sui, J. , Du, Y. , He, H. , Hjelm, D. , … Calhoun, V. D. (2015). Assessing dynamic brain graphs of time‐varying connectivity in fMRI data: Application tohealthy controls and patients with schizophrenia. NeuroImage, 107, 345–355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, D. , Shen, D. , & Alzheimer's Disease Neuroimaging Initiative . (2012). Multi‐modal multi‐task learning for joint prediction of multiple regression and classification variables in Alzheimer's disease. NeuroImage, 59, 895–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, D. , Wang, Y. , Zhou, L. , Yuan, H. , Shen, D. , & Alzheimer's Disease Neuroimaging Initiative . (2011). Multimodal classification of Alzheimer's disease and mild cognitive impairment. NeuroImage, 55, 856–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, J. , Wang, J. , Wu, Q. , Kuang, W. , Huang, X. , He, Y. , & Gong, Q. (2011). Disrupted brain connectivity networks in drug‐naive, first‐episode major depressive disorder. Biological Psychiatry, 70, 334–342. [DOI] [PubMed] [Google Scholar]
- Zhang, X. , H B, M. X. , & Xu, L. (2015). Resting‐state whole‐brain functional connectivity networks for MCI classification using L2‐regularized logistic regression. IEEE Transactions on Nanobioscience, 14, 237–247. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Supplementary Material
Appendix S2: Supplementary Material


