Neuronal dynamics enable the functional differentiation of resting state networks in the human brain

Abstract

Intrinsic brain activity is organized in spatial–temporal patterns, called resting‐state networks (RSNs), exhibiting specific structural–functional architecture. These networks presumably reflect complex neurophysiological processes and have a central role in distinct perceptual and cognitive functions. In this work, we propose an innovative approach for characterizing RSNs according to their underlying neural oscillations. We investigated specific electrophysiological properties, including spectral features, fractal dimension, and entropy, associated with eight core RSNs derived from high‐density electroencephalography (EEG) source‐reconstructed signals. Specifically, we found higher synchronization of the gamma‐band activity and higher fractal dimension values in perceptual (PNs) compared with higher cognitive (HCNs) networks. The inspection of this underlying rapid activity becomes of utmost importance for assessing possible alterations related to specific brain disorders. The disruption of the coordinated activity of RSNs may result in altered behavioral and perceptual states. Thus, this approach could potentially be used for the early detection and treatment of neurological disorders.

1. INTRODUCTION

Brain oscillations were first discovered by Hans Berger in the 1920s using electroencephalography (EEG) (Berger, 1929). Since then, it has been clear that brain rhythms are a ubiquitous and intrinsic feature of brain activity (Buzsaki & Draguhn, 2004; Rosanova et al., 2009; Thut, Miniussi, & Gross, 2012), which specifically emerge from the interaction between neuronal assembly activity (Buzsaki & Draguhn, 2004; Cottone et al., 2017; He et al., 2008; Mayhew, Ostwald, Porcaro, & Bagshaw, 2013), and behavioral state (Schnitzler & Gross, 2005; Thut & Miniussi, 2009). Brain waves are believed to organize neural activity at multiple temporal and spatial scales rhythmically, and thereby orchestrate local information processing as well as neuronal communication between distant brain areas (Ganzetti & Mantini, 2013; Siegel, Donner, & Engel, 2012). Since the synchronization of brain oscillations in specific frequencies, within or across brain areas, leads to changes in perception (Schulz, Zherdin, Tiemann, Plant, & Ploner, 2012), attention (Glennon, Keane, Elliott, & Sauseng, 2016), and working memory (Seidenbecher, Laxmi, Stork, & Pape, 2003), the disruption of this coordinated activity might result in, or be caused by, altered behavioral and perceptual states (2012, Babiloni et al., 2016, Ibrahim et al., 2013, Imperatori et al., 2014, Koelewijn et al., 2017, Uhlhaas & Singer, 2006, Wang et al., 2017). Accordingly, the investigation of spectral properties associated with brain regions may provide a deeper understanding of the neural mechanisms underlying human cognitive and behavioral processes.

Functional and structural changes, associated with cognitive or pathological states, have been investigated extensively using neuroimaging techniques, above all functional magnetic resonance imaging (fMRI) (Fox & Raichle, 2007; Smits et al., 2016; Alcala‐Lopez et al., 2017). In the last two decades, it has been proposed that the human brain is organized into consistent large‐scale networks (Biswal, Yetkin, Haughton, & Hyde, 1995; Damoiseaux et al., 2006; De Luca, Beckmann, De Stefano, Matthews, & Smith, 2006; Gusnard & Raichle, 2001; Raichle, 2015; Raichle et al., 2001), each of them characterized by specific structural and functional architectures (Doucet et al., 2011; Gillebert & Mantini, 2013). Using fMRI techniques, these networks have also been observed during idling condition (i.e., at rest), and, therefore, they are typically named as resting state networks (RSNs) (Greicius, Krasnow, Reiss, & Menon, 2003; Lee, Smyser, & Shimony, 2013; Raichle, 2015; Raichle et al., 2001). Subsequently, fMRI has been applied to detect functional abnormalities associated with neuropsychiatric and neurological disorders in RSNs (Bassett, Nelson, Mueller, Camchong, & Lim, 2012; Bonavita et al., 2011; Greicius, Srivastava, Reiss, & Menon, 2004; Rosazza & Minati, 2011), which is highly desirable for all cases in which patients are unable to perform tasks or actively respond to stimuli. Accordingly, the identification and development of effective biomarkers for early pathological diagnosis would result in clinical uses (Fox & Greicius, 2010). However, the limited temporal resolution of fMRI has prevented accurate detection of the underlying rapid fluctuations associated with behavioral changes (Engel, Gerloff, Hilgetag, & Nolte, 2013; He, Zempel, Snyder, & Raichle, 2010; Mayhew et al., 2016; Mayhew, Porcaro, Tecchio, & Bagshaw, 2017). Therefore, the use of alternative techniques is warranted.

Electrophysiological techniques, such as magnetoencephalography (MEG) (Brookes et al., 2011; De Pasquale et al., 2010; Hipp, Hawellek, Corbetta, Siegel, & Engel, 2012) and EEG (Liu, Farahibozorg, Porcaro, Wenderoth, & Mantini, 2017; Liu, Ganzetti, Wenderoth, & Mantini, 2018; Mantini, Perrucci, Del Gratta, Romani, & Corbetta, 2007; Yuan et al., 2016), having finer temporal resolution than fMRI, have recently enabled the investigation of intrinsic fast brain oscillations associated with RSNs (Liu et al., 2018; Van Diessen et al., 2015). In particular, it has been demonstrated that each network is characterized by a particular functional architecture related to the complexity of the information processing underlying its specific behavioral function (Engel et al., 2013). Additionally, findings suggest that RSNs present specific electrophysiological signatures (Brookes et al., 2011; Mantini et al., 2007).

In this study, beginning with the hypothesis that different RSNs might display different electrophysiological properties, we aimed to investigate how neuronal oscillations associated with RSNs are implicitly linked to behavioral and perceptual states, by looking at the unperturbed balance of these oscillations in healthy brains. To this end, we investigated the specific electrophysiological properties for each RSN, derived from high‐density EEG (hdEEG) source reconstructed signals, by using a multi‐angle approach, which integrates time and frequency information, as well as complexity measures like Higuchi's Fractal Dimension (FD) and Shannon Entropy (SE). In particular, these measurements were chosen for extracting unique features derived from the finer temporal resolution of EEG with respect to other neuroimaging techniques, such as fMRI. Then, the spectral properties and complexity metrics derived from EEG‐RSNs were given as input to a data driven approach, such as the hierarchical clustering, resulting in the differentiation of resting state brain networks based on their functional roles, as previously reported also with fMRI studies (Ding et al., 2011). More specifically, we showed that also features derived from electrophysiology lead to the separation of RSNs into two main categories: perceptual networks (PNs) and higher cognitive networks (HCNs), which are representative of lower perceptual role and higher cognitive function, respectively.

The identification of the normal dynamics of this intrinsic oscillatory activity in healthy human brains may provide a clear baseline for all transient changes due to alterations in perception or cognition. When these disruptions are associated with neurological disorders, delivering an appropriate intervention, for example, by means of neuromodulation, might contribute to restoring the physiological baseline.

2. MATERIALS AND METHODS

2.1. Subjects

The data used in this study were used in our previous study (Liu et al., 2017), which comprised of the resting‐state hdEEG signals, the electrode positions, and the individual whole‐head anatomy MRI from 19 healthy right‐handed subjects (age 28 ± 5.9 years, 5 males and 14 females). All participants reported normal or corrected‐to‐normal vision, had no psychiatric or neurological history and were free of psychotropic or vasoactive medication. Before participation in the experiment, subjects provided written informed consent to the experimental procedures, which were approved by the local Institutional Ethics Committee of ETH Zurich.

2.2. EEG and MR data acquisition

The EEG experiment was performed in accordance with the approved guidelines, in a quiet, air‐conditioned laboratory with soft natural light. Continuous 5‐min resting EEG data with eyes open were collected. To reduce eye movements and blinks, subjects were instructed to keep fixation on the center of the screen during the experiment. High‐density EEG signals were recorded at 1,000 Hz by the 256‐channel HydroCel Geodesic Sensor Net (GSN) using silver chloride‐plated carbon‐fiber electrode pellets provided by Electrical Geodesics (EGI, Eugene, Oregon). In addition, to better characterize the scalp distribution of EEG signals, all 256 sensors and three landmarks positions (nasion, left and right preauricolar) were localized prior to the EEG acquisition by using a Geodesic Photogrammetry System (GPS) (Marino, Liu, Brem, Wenderoth, & Mantini, 2016). In addition to EEG data and electrode position information, a T1‐weighted whole‐head MR image of each subject was acquired in a separate experimental session using a Philips 3 T Ingenia scanner with a turbo field echo sequence. The scanning parameters were: TR = 8.25 ms, TE = 3.8 ms, flip angle = 8°, field of view = 240 × 240 × 160, isotropic spatial resolution of 1 mm.

2.3. EEG‐derived RSNs detection

The detection of EEG‐derived RSNs was performed using the automated processing pipeline proposed by Liu et al. (2017) and validated in Liu et al. (2018), which consists of: (1) hdEEG preprocessing, involving bad‐channel detection, filtering, independent component analysis (ICA)‐based denoising, and re‐referencing (Liu et al., 2015; Porcaro, Medaglia, & Krott, 2015); (2) Volume conduction model creation, involving electrodes co‐registration, MRI segmentation and forward modeling solution; (3) Brain activity reconstruction, estimating the distribution of active brain sources that most likely generate the potentials measured over the hdEEG sensors; (4) Connectivity analysis, performing ICA on power time series of source dipoles and selecting the independent components (ICs) associated with large‐scale brain network activity.

The abovementioned pipeline was applied subject‐by‐subject. Specifically, following the hdEEG preprocessing, head model creation, and source reconstruction, spatial ICA (sICA) was performed on source‐reconstructed hdEEG signals, in order to detect the RSNs. The number of ICs was estimated by using the minimum description length (MDL) criterion (Li, Wang, Zhu, & He, 2007). As a result, we extracted 34–58 ICs, depending on the subject. Each IC comprised a spatial map. In order to select only the ICs associated with large‐scale brain networks, we performed a template‐matching procedure based on spatial similarity with RSNs derived from fMRI data. The fMRI RSNs used as templates to select and label the EEG ICs were generated from 24 healthy subjects by using sICA (Mantini et al., 2013). Eight core RSNs were identified and used for further investigations: four HCNs, including default mode network (DMN), dorsal attention network (DAN), ventral attention network (VAN), and language network (LN); four PNs, including somatomotor network (SN), auditory network (AN), visual foveal network (VFN), and visual peripheral network (VPN). Finally, we warped the individual RSN maps to the standard Montreal Neurological Institute (MNI) space, and performed statistical analysis to obtain the group‐level RSN maps. The voxel‐wise nonparametric permutation test with 5,000 permutations by FSL (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki)) was applied. The significance threshold was set to p < .01 following correction for multiple comparisons performed with the threshold‐free cluster enhancement (TFCE) method (Smith & Nichols, 2009).

2.4. EEG time series reconstruction

The workflow to obtain the neural dynamics underlying each RSN is shown in Supporting Information Figure S1. Spatial ICA finds systematically nonoverlapping, temporally coherent, brain regions without constraining the dynamics of the temporal response. It has been employed largely for the detection of fMRI‐RSNs (Beckmann, DeLuca, Devlin, & Smith, 2005)

$$D_{\mathrm{ds}}=A_{\mathrm{ds}}·S+\mathrm{\epsilon }$$

where, D_ds is the matrix of downsampled power time course in each dipole source, S is the decomposed ICs which reflect the spatial distributions, A_ds is the mixing matrix, referring to the non‐Gaussian temporal oscillations of ICs, and ε denotes the Gaussian noise. The estimation of S, $\widehat{S}$, can be obtained as following:

$$\widehat{S}=W_{\mathrm{ds}}·D_{\mathrm{ds}}$$

where, W_ds is the unmixing matrix. We selected the RSNs‐related ICs according to the spatial similarity with fMRI RSN maps. We masked the individual RSN maps and extracted the estimated neural oscillations in the masked voxels. Notably, these neural oscillations were of high temporal resolution and corresponded to each RSN. We then performed the principal component analysis (PCA) on the signals in x, y, and z orientations to obtain the principal component in each voxel. Finally, we averaged the PCs, one for each voxel, as inputs of following spectral and complexity analysis.

2.5. Characterizations of neural activity in EEG‐derived RSNs

We investigated the neurophysiological properties of the EEG‐derived RSNs from three different angles: (1) Frequency domain—power spectral density (PSD), that is, the squared modulus of the continuous Fourier transform, is a particularly useful tool for studying brain oscillations on a time scale of minutes, which is typical of an individual's “stable state” (Niedermeyer & da Silva, 2005), (2) Time domain—neuronal assembly signal power, as a function of frequency displays, satisfies the “power law” (Ramon & Holmes, 2015), and the exponent of this function corresponds to its fractality, thus we used temporal fractal dimension (FD) (Higuchi, 1988) as a signature of neural oscillations underlying brain networks, (3) Signal distribution domain—Shannon Entropy (SE) (Shannon, 1948) a measure of uncertainty or unpredictability of a signal. It is defined as the expectance of the logarithm of the corresponding distribution probabilities. Entropy quantifies how different the distribution is from a uniform one. Therefore, we can use entropy to quantify to what degree a frequency component is fluctuating from a stationary process (Rosso, 2007). Both FD and SE can be seen as complexity measures of the signal, even if they use a different property from the signal itself.

2.6. Power spectral density

PSD was estimated for the neural activity from each EEG‐derived RSN (including DMN, VAN, DAN, SN, AN, VFN, LN, and VPN), using the Welch procedure (1,024 ms duration, Hanning window, and 60% overlap). We investigated the spectral properties in the classical frequency bands, such as delta band (1–3 Hz), theta band (4–7 Hz), alpha band (8–13 Hz), beta band (14–32 Hz), gamma band (33–80 Hz with notched 50 Hz), and broadband (1–80 Hz) (IFSECN, 1974). Since we were interested in the dynamics of the RSNs in their synchronization levels, independently of the number of neurons in the network, we normalized the PSD of each RSNs to be equal to one within the 1–80 Hz frequency range.

2.7. Higuchi's fractal dimension

The FD is a measure of signal complexity, generally evaluated in the phase domain by means of the correlation dimension (Grassberger & Procaccia, 1983). Tomoyuki Higuchi proposed an algorithm to calculate FD directly in the time domain, without transforming the time series to the frequency domain or embedding data in a phase space (Higuchi, 1988). Higuchi's algorithm is based on the measure of the mean length of the curve L(k) by using a segment of k samples as a unit of measure. If L(k)∼k^−FD the curve is fractal‐like with dimension FD.

From a given time series: X(1), X(2), …, X(N) the algorithm constructs a new self‐similar time series $X_m^k$ as:

$$X_m^k:X\left(m\right),X\left(m+k\right),\dots X\left(m+\text{int}\left(\frac{N-m}{k}\right)·k\right)$$

where, m = 1, 2, …, k is the initial time, and k = 1, 2, …, k _max is the interval time. k _max is a free parameter.

The length, L _m(k), of each curve X ^k _m is calculated as:

$$L_m\left(k\right)=\frac{1}{k}\left[\sum _{i=1,\text{int}\left(\frac{N-m}{k}\right)}\left|X\left(m+\mathit{ik}\right)-X\left(m+\left(i-1\right)k\right)\right|·\frac{N-1}{\text{int}\left(\frac{N-m}{k}\right)}\right]$$

where, N is the total number of samples. In other terms, the length of curve for the time interval k, L(k), is calculated as the mean of the k values L _m(k) for m = 1, 2, …, k.

The value of FD is calculated by a least‐squares linear best‐fitting procedure as the angular coefficient of the linear regression of the graph:

$$\ln \left(L\left(k\right)\right)\approx \mathrm{FD}\ln \left(\frac{1}{k}\right)\text{for}k=1,2,\dots ,k_{\max }$$

importantly, FD does not rely on the amplitude of signal. In fact, FD remains the same even if the signal is multiplied by a constant. For each RSN, we calculated FD in time windows of 1 s, resulting, for our datasets, in 200 samples that were then averaged. The only important parameter of Higuchi's algorithm is k _max. We estimated FD for k _max = 2, …, 100. The maximum of 100 is equal to half of samples within 1‐s window (200 samples, since the frequency sampling rate is 200 Hz). For the next analysis we set k _max equal to 50, which corresponds to the median FD values for PNs and HCNs from the entire samples obtained for k _max = 2, …, 100 (Smits et al., 2016).

2.8. Shannon entropy

SE has been proposed (Shannon, 1948) as a measure of variability or uncertainty of a given random variable. SE is defined as:

$$\mathrm{SE}=-\sum _{i=1}^n{P}_i\log P_i$$

Theoretically, SE reaches its global maximum when {P_i}, the probability distribution function (pdf) of the variable under investigation, is uniformly distributed, for example, P_i = P_j, i ≠ j. In case of the measured signals, the pdf is unknown and should be estimated. An established method for estimating the pdf is the histogram method, in which the amplitude range of the signal is linearly divided into k bins so that the ratio k/N is constant (N is the number of signal samples). The ratio k/N characterizes the average filling of the histogram. The Freedman‐Diaconis rule was applied to estimate the optimal number of bins (Cohen, 2015; Ostwald, Porcaro, & Bagshaw, 2010, 2011; Porcaro, Cottone, Cancelli, Salustri, & Tecchio, 2018).

2.9. Hierarchical clustering

Hierarchical clustering was used to subdivide the eight RSNs based on the similarity of their features as derived from the neuronal dynamics, including PSD, FD, and SE. The relationships among RSNs are represented by a hierarchical tree, in which branch length reflects the degree of similarity, as assessed by a pairwise similarity function, between the RSNs. Notably, the separation of RSN groups also depends on the metric used to measure the distance between networks and on the linkage criterion which specifies the dissimilarity of networks. In this study, the Euclidean distance of PSD, FD, and SE of RSNs was used as similarity function for clustering the networks. Given an m‐by‐n data matrix X, which is treated as m (1‐by‐n) row vectors x ₁, x ₂, …, x _m, the various distances between the vector x _s and x _t are defined as follows:

$$d^2=\left(x_s-x_t\right)*{\left(x_s-x_t\right)}^T$$

and the inner squared distance calculated by minimum variance algorithm was used to measure the distance between clusters. The cluster analysis in this study was applied as shown in Statistics and Machine Learning Toolbox (https://it.mathworks.com/help/stats/hierarchical-clustering-12.html)). Following our working hypothesis, and by using the information extracted from the neural oscillations of RSNs, we expected to achieve a distinct separation of RSNs in groups, HCNs and PNs.

2.10. Statistical analysis

Since the PSD, FD, and SE values were not normally distributed, even after natural logarithm transformation, we used the nonparametric statistical analysis, which does not assume Gaussian distribution of signals. Specifically, two‐sample permutation t‐tests (10,000 permutations; p < .05) among RSNs were performed on the Spearman's correlation between FD values and band‐limited power of eight RSNs. In case of the point‐by‐point two‐sample permutation t‐tests, false discovery rate (FDR) was used to correct for multiple comparisons (Nichols & Holmes, 2002).

3. RESULTS

3.1. Spatial and temporal identification of the EEG‐derived RSNs

The spatial map and the corresponding temporal oscillations of the RSNs are illustrated in Figure 1. Specifically, we extracted eight core networks, characterized by particular spatial architectures: DMN (with posterior cingulate cortex, bilateral angular gyrus, and medial prefrontal cortex), DAN (primarily involving middle and superior occipital gyrus, parietal gyrus, inferior, and superior parietal gyrus, but lacking the middle and superior frontal gyrus, probably due to the limited spatial resolution of EEG technique), AN (primarily encompassing the bilateral middle and superior temporal gyrus), LN (including superior temporal gyrus and inferior frontal gyrus), VAN (including the inferior frontal gyrus and the middle temporal gyrus in the right hemisphere), SN (including the bilateral parietal operculum cortex and the anterior division of bilateral supramarginal gyrus), VFN (including lateral occipital cortex, parts of lingual gyrus, and occipital fusiform gyrus), and VPN (including the lingual gyrus, intracalcarine cortex, and parts of temporal occipital fusiform cortex). As described in the methods section, we reconstructed the broadband EEG data from 1 to 80 Hz for each of those networks. Once we obtained the temporal dynamics of each network, we were also able to examine the spectral and complexity properties of RSNs, in the frequency, time, and signal distribution domains, as measured by PSD, FD, and SE, respectively.

Figure 1.

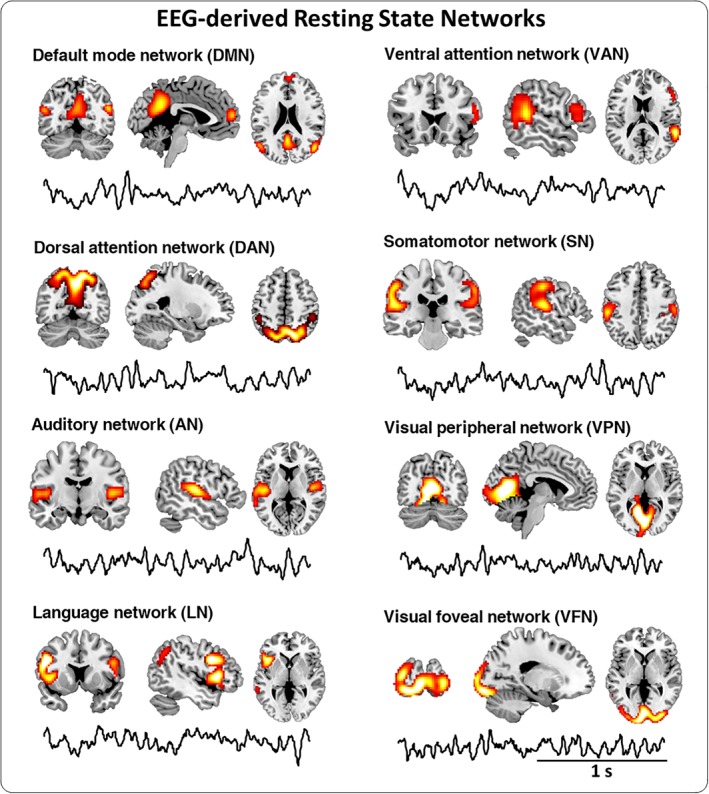
Broadband EEG‐derived resting state networks (RSNs): The spatial map and the neural oscillations of each RSN. Group‐level broadband EEG‐derived RSN maps are shown thresholded at p < .01 TFCE‐corrected. Eight RSNs were identified and labeled based on the spatial overlap with fMRI networks: language network (LN), ventral attention network (VAN), default mode network (DMN), dorsal attention network (DAN), auditory network (AN), somatomotor network (SN), visual foveal network (VFN), and visual peripheral network (VPN). An example of time course within two‐second window for each RSN is shown under the spatial map [Color figure can be viewed at http://wileyonlinelibrary.com]

3.2. EEG‐derived RSNs: Power spectrum density

The PSD curve of the neural oscillations in each RSN revealed that the brain networks can be qualitatively characterized by the power in specific frequency bands (Supporting Information Figure S2). In particular, the HCNs have higher PSD in delta and theta frequency bands compared with PNs, while the opposite trend is observed in gamma band. PSD in alpha and beta bands, however, does not show any precise trend. Following these qualitative observations, we extended our investigation in a quantitative way.

For each RSN, the band‐limited power was obtained for each band, including gamma, beta, alpha, theta, delta bands and broad bands (Figure 2). We found that the permutation t‐test on the two groups (HCNs vs. PNs) showed statistically significant differences in gamma and theta bands where HCNs had significantly lower gamma power and higher theta power (see Figure 2 first column and Table 1).

Figure 2.

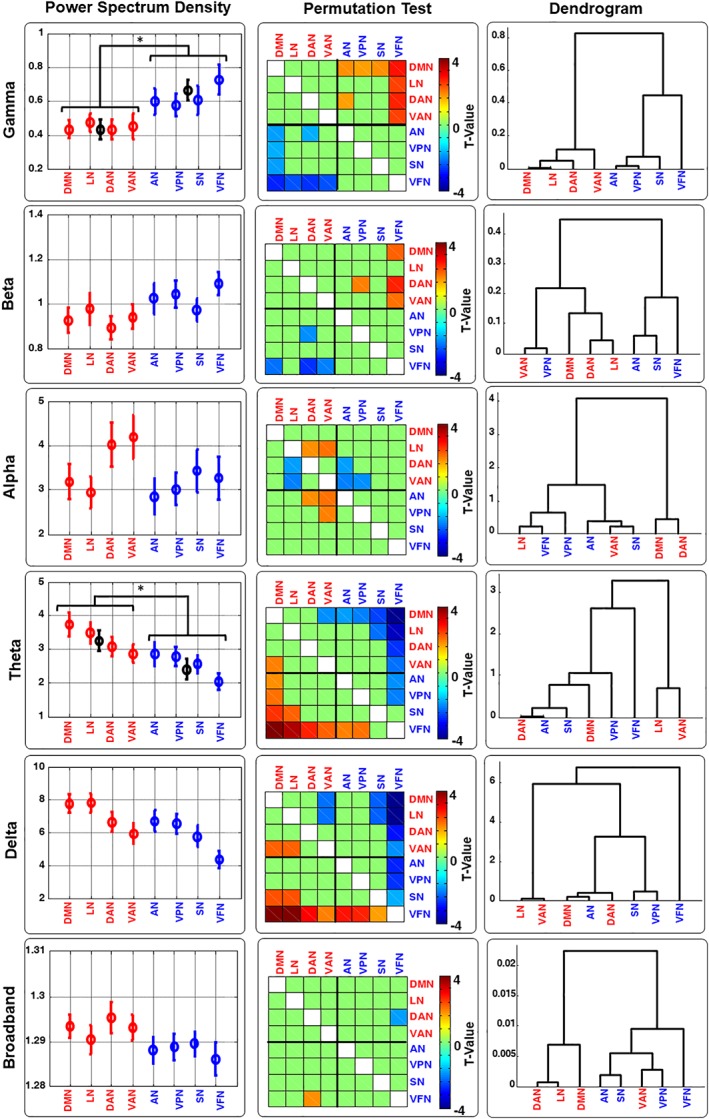
The band‐limited power of EEG‐derived RSNs. The band‐limited power Power Spectrum Density (PSD, the empty circle indicates the grand average across subjects and the vertical lines indicates the standard error [SE]). Dendrogram and permutation t‐test across all RSNs and across all bands (Delta, Theta, Alpha, Beta, Gamma, and Broadband) are shown. PSD and Permutation Test values are shown based on the sorted values obtained for the dendrogram in gamma band. For the PSD is also shown the average values and SE for the two groups HCNs (DMN, LN, DAN, and VAN) and PNs (AN, VPN, SN, and VFN) in all the case those two groups show significant difference (* indicate p < .05) [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 1.

Permutation test between HCNs and PNs

	Delta	Theta	Alpha	Beta	Gamma	BB	FD	SE	T&G
p	0.0663	0.0344*	0.2254	0.0904	0.0244*	0.1048	0.0212*	0.4279	0.0176*
T	1.5502	1.8950	0.7912	−1.3791	−2.0501	1.2773	−2.1048	−0.1808	−2.2229

^* Indicate p < .05

The order of RSNs was re‐arranged for visualization purposes, based on the distances obtained from hierarchical clustering using the gamma band PSD (see in the last column at the first row of Figure 2). The results of two‐sample permutation t‐tests (10,000 permutations; p < .05) on the band‐limited power of RSNs were shown in the middle column of Figure 2. Overall, the permutation t‐test showed certain differences among the networks, although these differences were insufficient for the discrimination of each single network. In this respect, we applied the hierarchical clustering analysis based on the Euclidean distance of the band‐limited power. We found that the hierarchical tree derived from gamma band PSD was able to successfully cluster the eight RSNs into HCNs and PNs, whereas the PSD of all the other frequency bands failed to separate the eight RSNs according to their functional roles (shown in the last column of Figure 3).

Figure 3.

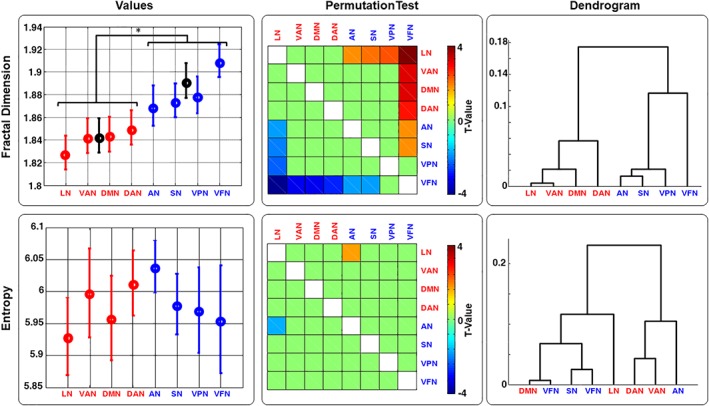
Fractal dimension and entropy for the EEG‐derived RSNs dynamics. Grand average (circle) and standard error (vertical line) for the Fractal Dimension (FD) and Entropy (E) values are shown (first column). Dendrogram (second column) and permutation Test (third column) across all RSNs and across all bands (Delta, Theta, Alpha, Beta, Gamma, and Broadband) are also shown. FD and Permutation t‐test values are shown based on the sorted values obtained for the FD dendrogram. Average values and SE for the two groups HCFNN (DMN, LN, DAN, and VAN) and P (AN, VPN, SN, and VFN) for the FD are also shown (* indicate p < .05) [Color figure can be viewed at http://wileyonlinelibrary.com]

3.3. EEG‐derived RSNs: Complexity measures

FD and SE were calculated by using the broadband neural oscillations (1–80 Hz) underlying each RSN (Figure 3). For better visualization, the eight RSNs in Figure 3 were re‐arranged based on the dendrogram tree obtained by FD (Figure 3, last column first row). Similarly to the PSD, the two‐sample permutation t‐tests (10,000 permutations; p < .05) among RSNs were performed for FD and SE. As for the PSD, permutation t‐test (PNs vs. HCNs) showed significantly higher FD values for the PNs respect to the HCNs (see Figure 3 first column and Table 1). No significant differences were found in SE values from PNs and HCNs. Also for these two complex measures, the permutation t‐test shows that there were some differences among the networks, but it was not enough to discriminate each single network.

We then applied hierarchical clustering analysis using either FD or SE features as metrics. The corresponding dendrograms were shown in the third column of Figure 3. Only FD was able to cluster the eight RSNs into two groups as HCNs and PNs.

Since the choice of the free parameter k _max has a crucial role in FD estimation, we performed the pointwise (for k = 2, …, 100) two‐sample permutation t‐tests (10,000 permutations, p < .05, FDR corrected) between HCNs and PNs FD values from HCNs and PNs exhaustively. We found that the values from PNs were higher than those from HCNs for k > 15 (see Supporting Information Figure S3).

3.4. HCNs and PNs comparison at the single‐subject level

We examined the PSN, FD and SE features from brain networks at the single subject level (Figure 4). To this end, we defined an index for highlighting the comparison between HCNs and PNs, that is, whether the features obtained for HCNs and the PNs are higher or lower with respect to each other. The index was calculated using the following formulation (HCNs − PNs)/(HCNs + PNs). This index is normalized to be between one and minus one and to be zero only when HCN and PN value are identical.

Figure 4.

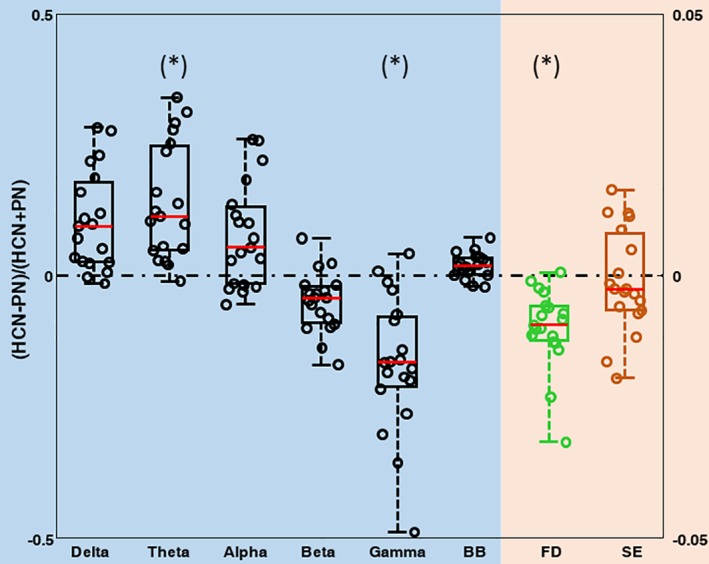
Behavioral characterization between HCNs and PNs. Boxplot and single subject distribution between HCNs and PNs. Left y axis refers to the value of the PSD in each band and broadband. Right y axis refers to FD and E values [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 4 shows that the features of HCNs are significantly higher than PNs for theta (permutation t‐test: p = .0344, t = 1.8950; Table 1) and the features of HCNs are significantly lower than PNs for gamma band (permutation t‐test: p = .0244, t = −2.0501; Table 1). Notably, we reported that, for theta band, only one subject violated this relationship, while, for gamma band, which displays an opposite trend compared with theta, only two subjects violated this relationship. FD values derived from HCNs were significantly lower than those from PNs (permutation t‐test: p = .0212, t = −2.1048; Table 1). All the other bands and SE did not reach the level of statistical significance.

3.5. Correlation between complexity measures and PSD

Since we found that gamma band and FD both enabled the separation of PNs and HCNs, through the hierarchical clustering (Figures 2 and 3), we tried to shed light on the possible relationship between these measures. To this end, Spearman's correlation between FD and the band‐limited power was calculated for each RSN and each subject (8 networks * 19 subjects, in total 152 values). FD was correlated with beta (R = 0.5847) and high correlated with gamma power (R = 0.9039), and anti‐correlated with delta (R = −0.6972), theta (R = −0.8124), alpha power (R = −0.4606), and broadband (R = −0.7462). Interestingly, the gamma power showed a significant quadratic correlation with FD with a linear goodness of fit of 5.12 and a quadratic one equal to 3.69 (see Figure 5). We also repeated the correlation analysis between SE and PSD. However, in this case no correlation was observed except for a significant inverse correlation between delta power and SE (R = −0.2548, p = .0016; see for all the other results Supporting Information Figure S4). On the other hand, since all the bands seemed to have a strong relationship with the FD, a stepwise regression was performed to investigate which bands better described the FD. For the stepwise regression, FD was used as a function of the predictor variables represented by the five power bands. Gamma and theta bands enter in the model for describing the FD (see Table 2).

Figure 5.

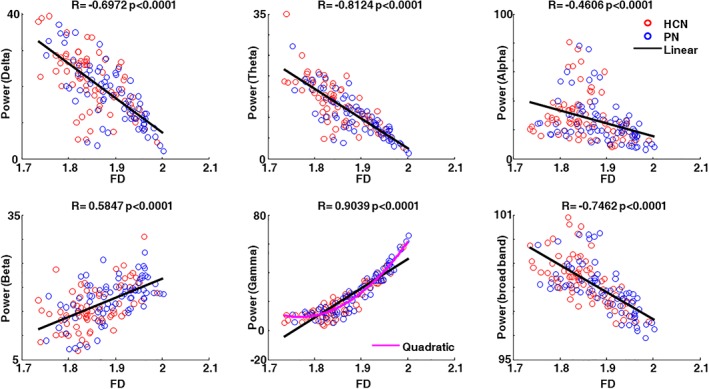
Correlation between FD and band‐limited power. Single subject Spearman correlation between FD and band‐limited power in delta, theta, alpha, beta, gamma, and broad bands. The red circle indicates HCNs and the blue circle indicates PNs. The black line indicates the linear fitting and the magenta line indicates the quadratic fitting using band‐limited power as a function of FD. The R and p values are reported on top of each subplot [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 2.

Stepwise regression analysis between FD and band limited power

	Beta Coeff.	Std.err.	Status	p
Delta	−0.0035	0.0016	Out	.0485
Theta	−0.0199	0.0029	In	3.2403e‐006
Alpha	0.0029	0.0031	Out	.3621
Beta	0.0117	0.0148	Out	.4414
Gamma	0.1347	0.0124	In	9.0521e‐009

3.6. FD and multiple bands characterization

Based on the model obtained from the stepwise analysis we performed a clustering analysis, using as a distance measure the combination of the synchronized theta and desynchronized gamma power. The results indicated that theta and gamma features were able to separate the two network groups using cluster analysis (i.e., HCNs and PNs, Figure 6). In particular, we found that PNs had higher values than HCNs in all the subjects except for one, showing an improvement compared with the results obtained for the gamma bands only (Figure 6). Moreover, permutation t‐test showed higher significance when theta and gamma were joined together relative to the other indexes (Table 1). Moreover, the Spearman correlation also increased when theta and gamma were applied together (R = 0.9852, Figure 6, last column) relative to gamma band only (R = 0.9039; Figure 5). Also in this case, a quadratic correlation was observed with a linear goodness of fit of 3.2157 (respect to 5.1239 for the only gamma) and a quadratic one equal to 2.0302 (respect to 3.6874 for the only gamma).

Figure 6.

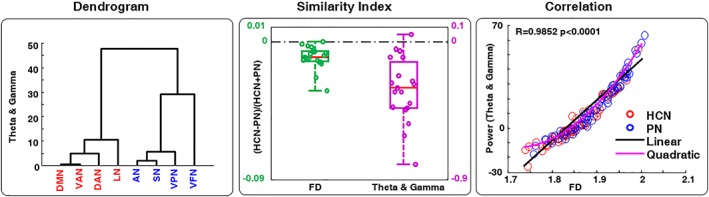
FD and multiple bands characterization. Dendrogram, Dissimilarity index, and Correlation results are reported as for the single band for the theta and gamma bands combination [Color figure can be viewed at http://wileyonlinelibrary.com]

3.7. Classification of RSNs based on neuronal activity

We found that FD, gamma band power, and the combination of theta power and gamma power were able to classify HCNs and PNs successfully for each subject, except for one, which led to 94.74% (18/19) accuracy rate. This finding suggests that it is possible to distinguish the HCNs from PNs based on their neuronal activity. Accordingly, HCNs and PNs display different oscillatory features, as expressed by spectral content, and complexity measures. More specifically, a network characterized by a small FD value is likely to belong to the category of HCNs. Similarly, if the same network displays either a low value gamma power or a low value for theta and gamma power combination, the network is associated with the HCNs. In the opposite case, the network is likely to belong to the PNs category.

4. DISCUSSION

In this study, we investigated which neural oscillations underlie RSNs in the healthy human brain, disclosing the homeostatic orchestration of brain rhythms. In particular, we were able to distinguish two groups of brain networks relative to their different functional roles (HCNs and PNs), based on their electrophysiological features.

Recent studies have shown that the electrophysiological signature of RSNs might reflect neural mechanisms supporting local specialization and global integration among brain regions (Hipp et al., 2012). We calculated the band‐limited power in six frequency bands (e.g., delta, theta, alpha, beta, gamma, and broadband) and the complexity measures in broadband (FD and SE), from RSNs source‐reconstructed hdEEG time‐courses and found that, depending on its functional role, each network presents a characteristic combination of brain rhythms.

RSNs were found to be separable based on the complexity of their functional interactions, with HCNs showing greater functional connectivity compared with the PNs, as revealed by fMRI data (Ding et al., 2011). However, the ways in which neuronal dynamics intervene in the description of the functional processes of RSNs has not yet been clarified. In this work, we have shown for the first time that neuronal dynamics also enable distinct differentiation of RSNs, which were again easily grouped in two representative categories, PNs and HCNs, each characterized by particular spectral and temporal features and explaining different functions at the behavioral level (Damoiseaux et al., 2006; Fox, Corbetta, Snyder, Vincent, & Raichle, 2006). Networks fractionation, resulting from the degree of complexity of the functional interactions in each network, was performed using measures derived from RSNs spectral features, including PSD (Figure 2), FD, and SE (Figure 3).

We showed that PNs are characterized by a higher level of synchronization in gamma band and desynchronized theta band, according to PSDs, compared with the ones associated with HCNs (Figures 2 and 4). Networks involved in higher cognitive functions, such as DMN, and DAN and VAN, involved in mediating information transfer across brain areas and attentional processes, respectively, typically exhibit oscillations in lower frequencies bands, for example, alpha and theta. On the contrary, PNs usually display high‐frequency oscillations, for example, gamma, in line with previous studies which reported a consistent contribution of gamma band in auditory and visual areas (Fries, Reynolds, Rorie, & Desimone, 2001; Kaiser, Lutzenberger, Ackermann, & Birbaumer, 2002; Womelsdorf et al., 2007). As to the structural topology, contrary to HCNs, which present a sparse spatial distribution (e.g., DMN), PNs are characterized by a very focal distribution (e.g., VFN), or bilateral distribution (e.g., AN). These findings support the previous concept that the frequency of the oscillations underlying cortical processes might relate to the distance between the brain regions exchanging information (Nunez & Srinivasan, 2006). More specifically, that slower fluctuations support information transfer on a larger spatial scale, while faster ones are involved in local processes (Canolty et al. 2006). Accordingly, neuronal interactions most likely reflect more complex dynamics that involves the co‐existence of more than one frequency band (Mantini et al., 2007), both slow and fast, also in a single network, as shown, for example, in the visual cortex (Michalareas et al., 2016). This co‐existence of different frequency bands might possibly reflect directionality of information (Hillebrand et al., 2016) or hierarchical processes (Buzsaki & Wang, 2012).

By measuring the complexity of brain oscillations, FD has proven to be a valid metric for discriminating brain areas that are functionally different from each other (Cottone et al., 2017), and for identifying different state of attention, such as in closed and open eyes conditions (Cottone et al., 2017). In addition, FD has been successfully used in neuroscience to distinguish distinct cognitive states, for example, during resting condition, sleep stages (Weiss, Clemens, Bodizs, & Halasz, 2011), external stimulation perception (Cottone et al., 2017), and to fractionate the areas of the sensorimotor cortex, regions which are closely connected and strongly interacting, but involved in different functions (Cottone et al., 2017). Furthermore, it has been shown to be a reliable indicator for the discrimination of healthy and pathological brains, as well as different stages of aging, resulting in a suitable metric for monitoring maturation and degeneration of brain function (Smits et al., 2016; Zappasodi et al., 2014; Zappasodi, Marzetti, Olejarczyk, Tecchio, & Pizzella, 2015). The variations of FD can track changes in the complexity of the neuronal dynamics, which might be related to the cognitive or perceptual impairment, as it has been previously reported for patients presenting with dementia (Smits et al., 2016; Zappasodi et al., 2015) and Alzheimer symptoms (Ahmadlou, Adeli, & Adeli, 2011).

However, two limitations have been mainly preventing the widespread use of FD (Kesic & Spasic, 2016): the unknown neurophysiological meaning and the uncertainty with regard to the most appropriate value of k _max, the only tuneable parameter associated with FD. In the present study, we revealed significant correlations between FD and band‐limited power. Also, FD could express a specific combination of brain rhythms (Figure 6), disclosing the corresponding electrophysiological basis of FD (Cottone et al., 2017; Zappasodi et al., 2015). More specifically, in our case, we found that the electrophysiological signature underlying higher FD is given by the concurrent presence of lower theta and higher gamma rhythm, as revealed by the stepwise analysis (Table 2). By looking at the correlation between FD and all the other frequency bands (Figure 5), we reported that the gamma band shows the highest linear correlation with FD, though quadratic correlation more closely fits their relationship, as displayed in Figure 5. Previous studies (Fernandez et al., 2012; Gomez, Perez‐Macias, Poza, Fernandez, & Hornero, 2013) have suggested that both gamma band and neuronal oscillations complexity separately demonstrate positive quadratic correlations with a common variable, for example, aging. Both measurements might be expressions of hidden nonlinearity. Here, we showed a similar trend in these two measurements. The effect is even more pronounced when considering the combination of gamma and theta band relative to FD (Figure 6). On the other hand, the other complexity index SE did not show any convincing correlation with the band‐limited power in any frequency band (Supporting Information Figure S4), underlying its incapacity to highlight any valid electrophysiological representation (Blanco, Garay, & Coulombie, 2013). Moreover, from the methodological point of view, we proved that the overall trend of the FD is relatively independent from the selected value of k _max, (see Supporting Information Figure S3). The band‐limited power negatively correlates with FD for the lower frequency bands, for example, delta, theta, and alpha, which are consistent with the previous literature (Cottone et al., 2017; Spasic et al., 2008; Zappasodi et al., 2015). Our finding further strengthens this phenomenon as, in our study, FD calculated for each source‐reconstructed time‐course allows providing reliable information on the actual neuronal dynamics.

RSNs in healthy individuals displayed robust spatial organizations and distinct frequency spectra (Mantini et al., 2007). Furthermore, our group level findings are consistent across almost all the individuals at the single subject level, strengthening the validity of the proposed approach, and making it potentially suitable for future clinical applications. Nonetheless, further validation in cohorts of pathological populations should be sought in future studies. These spectral features are probably associated with specific homeostatic regulations of neurotransmitters, which may change abnormally in the case of pathological states, including psychiatric disorders (Imperatori et al., 2014; Whitton et al., 2017). Accordingly, frequency disruption may occur.

fMRI has been used extensively for the identification of abnormal changes in RSNs in the presence of pathological conditions, such as depression (Greicius et al., 2007) and schizophrenia (Bluhm et al., 2007). However, the time‐scale of these abnormalities cannot adequately follow behavioral changes. Thus, alternative techniques with finer temporal resolution are warranted to detect the rapid fluctuations underlying a cognitive or perceptual state (Engel et al., 2013). Following consistent methodological improvement, mainly oriented to the increase of spatial resolution (Murias, Webb, Greenson, & Dawson, 2007), EEG has shown the potential value in a clinical environment.

We proposed a new approach for monitoring brain function and possibly detecting abnormal occurrences based on the neuronal oscillations of RSNs. More specifically, our work suggests that this innovative methodology may be a feasible way to assess brain function at rest, providing valid information about the mechanisms underlying normal brain activation and monitoring electrophysiological disruptions of RSNs. This might enable the early detection of behavioral and perceptual disorders, and provide an effective strategy for predicting or treating pathological conditions not only by pharmacological or invasive intervention, but also by noninvasive neuromodulation interventions (Feurra, Bianco, et al., 2011; Feurra, Paulus, Walsh, & Kanai, 2011) or connectivity‐guided neurofeedback (Keynan et al., 2016) with the aim of rebalancing the healthy and natural RSNs conditions. Furthermore, in this study, we have deepened our understanding of the relationships between FD and oscillatory activities previously observed (Cottone et al., 2017; Zappasodi et al., 2015) on a new network‐based level. We observed here that the brain function classification of wide or local networks can be assessed in a manner that is easy and straightforward via the single FD index.

CONFLICT OF INTEREST

The authors declare that they have no conflicts of interest.

Supporting information

Figure S1 The workflow to obtain the neural oscillations underlying RSNs.

The workflow includes following steps: (1) the power envelope of the source activity is calculated by moving averaging approach (de Pasquale et al. 2010); (2) the spatial ICA is applied on the power envelop to obtain the spatial ICs, with one IC referring to one spatial map; (3) the ICs corresponding to RSNs are then selected, according to the spatial similarity with the fMRI‐RSN templates; (4) the selected IC maps are binarized and used as mask to extract the neural dynamics underlying the each RSN; (5) PCA is applied on the neural activity with x, y and z orientations to reduce the dimension with the principle component, and finally the neural oscillations underlying one RSN are the averaged PCs across the masked individual RSN maps. Notably, all the analysis is performed on single subject level.

Figure S2. Power Spectrum Density of the neural oscillations underlying eight EEG‐derived RSNs.

The Grand average broadband PSD for each RSN is shown in the middle panel. The PSDs in Delta band (1–4 Hz), Theta band (4–8 Hz) and Alpha band (8‐15 Hz), Beta band (15–32 Hz) and Gamma band (32–48 Hz and 52‐79 Hz) corresponding to each RSN are shown in up panel and bottom panel.

Figure S3. Pint wise Fractal Dimension – PN vs. HCN

Pointwise two‐sample permutation t‐test (10,000 permutations) analysis was performed on the averaged FD values for the PN (blue curve) and HCN (red curve) networks. The blue line and red line are the averaged FD values across PNs and HCNs respectively, and the shadow areas indicate the standard error (SE). The horizontal gray line indicates the median value of the averaged PNs and HCNs, whereas the dashed horizontal gray lines indicate median value ±2*standard deviation. Dotted lines at k _max = 35 and k _max = 65 represent when the median value intercept the PN and HFN FD values. The dotted line at k _max = 50 represents the k _max value used in our study. We used false discovery rate (FDR) to correct for multiple comparisons (magenta line).

Figure S4. Spearman Correlation – E vs. PSD

Single subject Spearman correlation between FD and SE in each band and broadband is shown. Red circles indicate HFC networks and blue circles indicate P networks. Continuous black line indicates the linear fitting. R and P values are also reported.

Marino M, Liu Q, Samogin J, et al. Neuronal dynamics enable the functional differentiation of resting state networks in the human brain. Hum Brain Mapp. 2019;40:1445–1457. 10.1002/hbm.24458