Abstract
Understanding the correlation structure associated with brain regions is a central goal in neuroscience, as it informs about interregional relationships and network organization. Correlation structure can be conveniently captured in a matrix that indicates the relationships among brain regions, which could involve electroencephalogram sensors, electrophysiology recordings, calcium imaging data, or functional magnetic resonance imaging (FMRI) data—We call this type of analysis matrix‐based analysis, or MBA. Although different methods have been developed to summarize such matrices across subjects, including univariate general linear models (GLMs), the available modeling strategies tend to disregard the interrelationships among the regions, leading to “inefficient” statistical inference. Here, we develop a Bayesian multilevel (BML) modeling framework that simultaneously integrates the analyses of all regions, region pairs (RPs), and subjects. In this approach, the intricate relationships across regions as well as across RPs are quantitatively characterized. The adoption of the Bayesian framework allows us to achieve three goals: (a) dissolve the multiple testing issue typically associated with seeking evidence for the effect of each RP under the conventional univariate GLM; (b) make inferences on effects that would be treated as “random” under the conventional linear mixed‐effects framework; and (c) estimate the effect of each brain region in a manner that indexes their relative “importance”. We demonstrate the BML methodology with an FMRI dataset involving a cognitive‐emotional task and compare it to the conventional GLM approach in terms of model efficiency, performance, and inferences. The associated program MBA is available as part of the AFNI suite for general use.
Keywords: Bayesian multilevel modeling, GLM, inter‐region correlation, linear mixed‐effects modeling, matrix‐based analysis, multiplicity, null hypothesis significance testing, region pair
1. INTRODUCTION
Understanding the correlation structure associated with multiple brain regions is a central goal in neuroscience, as it informs us of potential “functional groupings” and network structure (Pessoa, 2014; Baggio et al., 2018). The correlation structure can be conveniently captured in a matrix format that reveals the relationships among a set of brain regions, which could involve electroencephalogram sensors, electrophysiology recordings, calcium imaging data, or functional magnetic resonance imaging (FMRI) data, among others. We therefore call this type of analysis matrix‐based analysis, or MBA. In the context of FMRI research, with m regions of interest (ROIs) defined across subjects, the investigator summarizes the original data into an m × m matrix for each subject. Two broad categories of MBA exist in the MRI context, depending on whether the study is functional or structural. For the former, a researcher could define a functional attribute matrix using inter‐region Pearson correlations (IRCs; other measures of association are also possible, including partial correlation and those computed in the frequency domain) of the BOLD signal among the ROIs. For the latter, one can generate a structural attribute matrix that typically summarizes properties of white matter between pairs of gray matter ROIs. Without loss of generality, we focus our discussion here on IRC matrices, which can be readily extended to other cases.
The central issue facing an investigator interested in the correlation structure of her data is to estimate the population‐level average effect of the correlation (often referred to as “functional connection”) between each region pair (RP). However, such estimation poses considerable challenges. First, correlation values are, by definition, computed over pairs of random variables (e.g., BOLD time series for FMRI data). However, the existence of “shared regions” among RPs implies that some pairwise correlations are not independent, namely, they are correlated themselves (Figure 1a). Accordingly, proper modeling requires such covariance between RPs to be accounted for. A second challenge concerns the problem of multiple comparisons. With m > 2 regions, the total number of unique effect estimates per subject is (Figure 1b). As one solution of correcting for multiple testing, permutation testing has been suggested, where a null distribution of a maximum statistic (either the maximum testing statistic or the maximum number of surviving RPs based on a cluster approach) is used to declare which RPs pass the dichotomization threshold (Zalesky, Fornito, & Bullmore, 2010).
Figure 1.
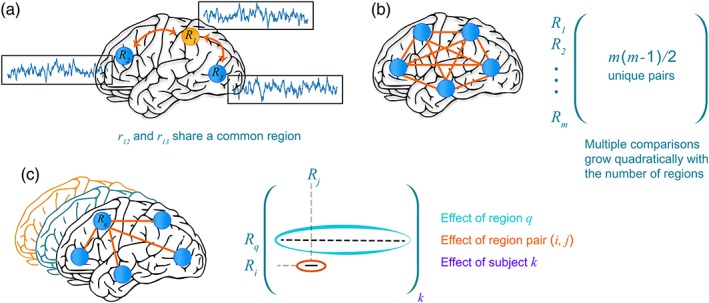
Characterizing the inter‐region correlation structure of group brain data. (a) Correlations between two pairs of brain regions, r ij, are not independent when they share a common region. Thus, when simultaneously estimating multiple correlations, such relatedness needs to be modeled and accounted for. (b) Estimating correlations leads to a multiplicity problem, in particular how to account for the simultaneous inferences of all effects in conventional hypothesis testing. In a Bayesian framework, multiplicity relates to the problem of estimating all correlations simultaneously by invoking the notion of multilevel “information sharing,” also known as partial pooling or shrinkage. (c) Within a Bayesian multilevel framework, it is possible to frame the problem in terms of estimating the population‐level effect of (1) brain region, R q, (2) RP, r ij, and (3) subject k. The estimation of the contribution of the effect of brain regions is a unique contribution of our framework, which allows investigators to characterize a region's “importance” within a principled statistical framework [Color figure can be viewed at http://wileyonlinelibrary.com]
In this article, we develop a novel multilevel Bayesian approach to capturing the intricate relationships embedded in the correlation matrix of FMRI data in a manner that addresses the challenges outlined. Our overall goal is to decompose each correlation effect into multiple components that are associated with brain regions, RPs, and subjects (Figure 1c). Our central aims are threefold. First, we address the multiplicity problem faced under the conventional univariate approach by sharing variability information across brain regions. Second, we make inferences that cannot be performed within conventional statistical approaches, including linear mixed‐effects (LME) models. In particular, we estimate parameters corresponding to the effect of RPs and each brain region. Third, and relatedly, our approach provides a statistically sound way to estimate the contribution of a brain region to the structure captured in the correlation matrix, allowing an investigator to gauge a region's “importance” (across all RPs in which it is involved). Consistent with the Bayesian approach adopted here, we encourage full reporting of estimated effects and their uncertainties, not only “significant” ones. The application to an existing dataset demonstrates the feasibility of the approach, and the associated program MBA is available as part of the AFNI suite for general use.
1.1. Preambles
Throughout this article, italic letters in lower case (e.g., α) stand for scalars or random variables; lowercase, boldfaced italic letters (a) and upper (X) cases stand for column vectors and matrices, respectively. With one group of n subjects and m > 2 regions, R 1,R 2,….,R m, the total number of unique effect estimates per subject is . For the kth subject (k = 1,2,…,n), the estimated values (e.g., correlation coefficients {r ijk}) correspond to M RPs, and they form a symmetric (r ijk = r jik, i,j = 1,2,…,m) m × m positive semi‐definite matrix with diagonals r iik = 1 (Figure 2, left). In the case of correlation coefficients, their Fisher‐transformed version (Figure 2, right) through z = arctanh(r) is usually adopted so that methods assuming a Gaussian distribution may be utilized, as Fisher z‐values are more likely to be Gaussian‐distributed than raw Pearson correlation coefficients. As stated, the question of interest focuses on the estimation of the population average effect of RP (i,j). Because and are both symmetric, inferences at the population level can be made through the M elements in the lower triangular part (i > j, shaded gray in Figure 2).
Figure 2.

Inter‐region correlation (IRC) matrix among m regions for the kth subject and its Fisher‐transformed counterpart . Due to the symmetry, only half of the off‐diagonal elements (shaded in gray) are usually considered during IRC analysis
Suppose that and are z‐values associated with correlations and of two RPs of the kth subject. When a pair of elements of the correlation matrix involves four separate regions (i.e., i 1 ≠ i 2 and j 1 ≠ j 2), we assume that they are unrelated (i.e., their correlation is 0). We denote the correlation between any two elements, and , that pivot around a common region (e.g., i 1 = i 2 or j 1 = j 2) as ρ, with an ad hoc assumption that they are the same across all regions.1 Thus, ρ characterizes the interrelatedness of and when the RPs share a common region. We further define z k = vec({z ijk,i > j}) to be the vector of length M whose elements correspond to the “column‐stacking” of the lower triangular part of the matrix Z (m) (Figure 2). That is, z is the half‐vectorization of excluding the main (or principal)/diagonal: . The variance–covariance matrix of z k can be expressed as the M × M matrix
| (1) |
where is the variance of z ijk, i > j, and P (m) is the correlation matrix that is composed of 1 (diagonals), ρ and 0 (an example is shown in Figure 3). It has been analytically shown (Chen et al., 2016) that −1/[2(m − 2)] ≤ ρ ≤ 0.5 (when m > 3) at the individual subject level, and because of the mixture of relatedness and interdependence among the elements of , it becomes crucial to capture this correlation structure P (m) in a given modeling framework.
Figure 3.

Inter‐region correlation (IRC) with m = 5 regions. Left: Pictorial representation of 5 × 5 region pairing. Unlike typical representations with solid lines in the literature, we use dashed lines here to indicate correlations, not physical connections, between regions. Right: The complex relatedness among the off‐diagonal elements in is illustrated with the correlation matrix P (5) for m = 5 regions, in which ρ represents the correlation when two elements (e.g., z 32 and z 43, colored in red) are associated with a common region (e.g., R 3) while independence (with a correlation of 0) is assumed when two elements (e.g., z 51, colored in blue, and z 32 or z 43) do not share a common region. The third index k in z ijk for subjects is dropped in this figure for clarity [Color figure can be viewed at http://wileyonlinelibrary.com]
1.2. MBA: The general linear model approach
An intuitive and straightforward approach to making estimation at the population level is to separately handle each RP under the framework of general linear model (GLM), parallel to the conventional whole‐brain voxel‐wise GLM widely adopted in neuroimaging. Thus, for the lth RP (l = 1,2,…,M),
| (2) |
where = z ijk; l indices the flattened list of RPs (i,j), i,j = 1,2,…,m (i > j); represents the population effect of the lth RP, and ɛ lk is the deviation of the kth subject on the lth RP, which is assumed to follow a Gaussian distribution. Each of the M models in Equation (2) is essentially a Student's t test for the null hypothesis of H 0: = 0. This modeling strategy has been incorporated into neuroimaging tools such as network‐based statistics (NBS; Zalesky et al., 2010), FSLNets in FSL (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012) and independent component toolbox GIFT (Calhoun, Adali, Pearlson, & Pekar, 2001).
For the convenience of model comparison, the M separate models in GLM1 (Equation (2)) can be merged into one GLM by pooling all the residuals across the M RPs (i.e., by treating the RPs as M levels of a factor in the model),
| (3) |
The GLM formulations, GLM1 in Equation (2) and GLM2 in Equation (3), can be readily extended to cases with categorical variables (e.g., between‐subjects factors such as two or more groups, or within‐subject factors such as conditions or tasks), or with quantitative explanatory variables (e.g., subject‐specific values such as age or behavioral measures).
The immediate challenges that the GLM framework in Equations 2, 3 faces are twofold. First, the irregular pattern of the correlation matrix P (m) is not explicitly accounted for by the GLMs (although, to some extent, they are implicitly treated in the process of correction for multiple testing, such as in the permutation‐based methods in NBS and FSL Randomize). The second challenge is the issues of multiplicity and arbitrary dichotomization involved: As there are a total of M models (Equation (2)) that correspond to the M RPs, it remains a daunting job to effectively and efficiently maintain an overall false‐positive rate (PFR) under the null hypothesis significance testing (NHST) framework (Baggio et al., 2018; Zalesky et al., 2010).
2. MATRIX‐BASED ANALYSIS VIA BAYESIAN MULTILEVEL MODELING
Throughout the text, Roman and Greek letters are used, respectively, to differentiate between fixed and random‐effects in the conventional statistics context. Although the terms of “fixed” and “random” effects do not strictly apply in a Bayesian framework, we use them here as we expect most readers to be familiar with the terminology. For instance, a conventional fixed‐effects parameter under ANOVA or an LME model is treated as a constant that is shared by all entities (e.g., subjects, ROIs), and a random‐effect parameter is treated as variable because its value changes from one entity (e.g., subject, ROI) to another. Major acronyms and terms are listed in Table 1.
Table 1.
Acronyms and terminology
| BML | Bayesian multilevel | LOO‐CV | Leave‐one‐out cross‐validation |
|---|---|---|---|
| ESS | Effective sample size | LOOIC | Leave‐one‐out information criterion |
| FPR | False‐positive rate | MBA | Matrix‐based analysis |
| GLM | General linear model | MCMC | Markov chain Monte Carlo |
| HMC | Hamiltonian Monte Carlo | NHST | Null hypothesis significance testing |
| ICC | Interclass correlation | PPC | Posterior predictive check |
| IRC | Inter‐region correlation | ROI | Region of interest |
| LME | Linear mixed‐effects | RP | Region pair |
2.1. Bayesian modeling based on three‐way random‐effects ANOVA
We start with a framework of MBA for m ROIs through an effect decomposition (Figure 1c) of three‐way random‐effects ANOVA or LME with three crossed random‐effects components,
| (4) |
where b 0 is the intercept or overall effect that is shared by all regions, RPs, and subjects; ξ i and ξ j are the random‐effects or deviations from the population effect b 0 for the two ROIs i and j, respectively; π k is the random‐effect attributable to subject k; and ɛ ijk is the residual term. Due to the symmetric nature of the data structure in , only half of the matrix elements excluding the diagonals (i.e., either the lower or upper triangular part of the matrix) are utilized in the model (Equation (4)), and thus the index inequality of i > j applies. The three random‐effects components, ξ i, ξ j, and π k, form a crossed (or cross‐classified) structure with a factorial (or combinatorial) layout among the levels (or indices i, j, and k) of the three factors: The first two factors are the same set of m regions while the third one codes the n subjects.
With the assumption of independent Gaussian distributions, , and , the LME0 model in Equation (4) can be solved under a three‐way random‐effects ANOVA or LME. Unlike the M separate GLMs in Equation (2) or the pooled version (Equation (3)) that treats the M RPs as separate and independent entities, each effect z ijk is decomposable as the additive effects of multiple components under the LME model in Equation (4). Such decomposition allows for more accurate effect characterization and more powerful inferences than the typical GLM approach of analyzing each RP separately, as in Equations 2, 3. For instance, related to the concept of intraclass correlation (ICC), the correlation between two RPs, (i,j 1) and (i,j 2) (j 1 ≠ j 2), that share a common region R i can be derived with the independence and i.i.d. assumptions as
| (5) |
The correlation between two RPs that do not share a common region can be trivially derived as 0. Unlike GLM approaches such as Equations 2, 3 where the RPs are assumed to be isolated and unrelated, the interrelatedness among the IRC matrix elements is maintained under the LME0 model (Equation (4)) as characterized in Equation (5) and the relatedness matrix P (m) in Equation (1).
Similarly, the correlation of an RP (i,j) between two subjects k 1 and k 2 can be derived with the independence and iid assumptions as
| (6) |
The fundamental demarcation between the GLM and LME modeling frameworks lies in the distinct assumption about the relationships between brain regions. Under the GLM framework, each region or RP is assumed to be isolated from its counterparts in two senses. First, spatial correlations among regions or RPs are ignored during the modeling stage (although their spatial relatedness is considered during the step of correction for multiple testing). In contrast, the LME model directly characterizes the interrelationships among regions and RPs, as shown in Equation (5), and the relatedness matrix P (m) in Equation (1). Second, the GLM framework assumes that no effect magnitude information is shared across regions or RPs, which is equivalent to implicitly assuming a uniform distribution of effect magnitudes for the regions. In other words, complete ignorance is represented by assuming an effect at each region being anywhere within (−∞,+∞) with equal likelihood. In contrast, under LME, region effects are assumed to follow a Gaussian distribution reflecting some similarity across regions. This loose constraint on effect magnitudes follows the same rationale as the standard Gaussian assumption applied to subjects under GLM, for instance. In summary, it is this difference in distributional assumptions (uniform vs. Gaussian) that fundamentally distinguishes the two modeling frameworks.
There are two hurdles associated with the LME0 model (Equation (4)) that have to be overcome. Although the random‐effects components, ξ i and ξ j, associated with the two regions i and j are assumed to follow the same underlying Gaussian distribution (that is why we denote them by the same symbol ξ), they would have to be treated as two separate random‐effect components when one solves the system in practice. Furthermore, because only half of the off‐diagonal elements in the matrix are utilized as inputs, the two random‐effects components, ξ i and ξ j, are generally not evenly arranged among all the RPs,2 leading to unequal estimation of the two random‐effects components. The problem can be resolved by using both upper and lower triangular off‐diagonal elements of the matrix as input, as previously adopted in LME modeling for inter‐subject correlation analysis (Chen et al., 2016). Therefore, the theoretical index constraint of i > j under the LME0 is relaxed to i ≠ j for numerical implementations. The second hurdle is that, under conventional modeling frameworks such as ANOVA and LME, we can only obtain the point estimate and the associated uncertainty (e.g., standard error) for each fixed effect (e.g., the overall effect b 0 in LME0), as well as the variances for those random‐effects components (e.g., λ 2, τ 2, and σ 2). However, the central goal is to make inferences about each RP, that is, about p ij = b 0 + ξ i + ξ j, which cannot be achieved under conventional modeling frameworks such as ANOVA and LME. In other words, the second hurdle basically renders the standard LME modeling framework unfeasible.
To be able to derive the effect at both each brain region and RP directly, we reformulate the effect decomposition of z ijk under a Bayesian framework, following our previous work (Chen et al., 2019). For example, we translate LME0 in Equation (4) to its BML counterpart,3 forming a multilevel structure with data clustered by brain region, RP, and subject:
| (7) |
Both of the above hurdles are overcome under the BML system (Equation (7)). First, only half of the off‐diagonal elements (e.g., the lower triangular part) in Z (m) are needed as input by using a multi‐membership modeling scheme4 (Bürkner, 2018). Second, with hyperpriors (e.g., weakly informed prior) for the model parameters b0, λ2, τ2, and σ 2, the model (Equation (7)) can be numerically solved and the posterior distribution for each RP (i,j) can be assessed through
| (8) |
In addition, the effects that are attributable to each region, r i, and each subject, s k, as well as their interaction (a subject's effect at a particular region), t ik, can be derived, too, via their posterior distributions with
| (9) |
| (10) |
| (11) |
respectively. The intercept b 0 is the overall effect shared by all brain regions, RPs, and subjects, which may or may not be of interest to the investigator. The factor of in the region‐specific effect formula of r i (Equation (9)) and in the region‐subject interaction effect t ik (Equation (11)) reflects the fact that the effect of each RP is evenly shared between the two associated regions. The region‐specific effect r i indicates the contribution or “importance” of an ROI relative to all other regions. Similarly, the effect of a subject s k shows, for example, whether the subject is atypical relative to the whole group.
The BML framework (Equation (7)) adopted here offers a good opportunity to discuss the conventional terminology of “fixed‐ vs. random‐effects.” Being of research interest for statistical inference, the effect at each region or RP, on the one hand, would be considered as “fixed” under the conventional framework; on the other hand, such an effect is modeled as random in the LME0 model (Equation (4)). Such a conceptual inconsistency dissolves once we abandon the distinction of fixed‐ versus random‐effects and instead differentiate two different types of effects: The effect ξ i associated with each region (or p ij in [Equation (8)] associated with each RP) is modeled under the model BML0 (Equation (7)) for the sake of statistical inference through partial pooling with a Gaussian prior, whereas the subject‐specific effect π k in the BML framework (Equation (7)) represents a varying component across subjects. In other words, the distinction between fixed‐ and random‐effects under the conventional framework is mapped to the differentiation, in the current context, between information pooling across regions and across‐subject variability.
2.2. Extensions of the multilevel Bayesian framework
The LME0 model in Equation (4) can be expanded or generalized by including two types of random‐effects interaction components: One component is the RP‐specific term, and the other component is the interaction between a region and a subject. The expansions lead to three new LME models, corresponding to three different combinations of the two extra effects:
| (12) |
| (13) |
| (14) |
where η ij is the RP‐specific effect that is associated with regions i and j (i.e., the interaction effect between regions i and j) relative to the overall effect b 0 and the two region effects, ξ i and ξ j, while ζ ik and ζ jk are the interaction effects between region i and subject k and that between region j and subject k, respectively. We note that the RP‐specific effect η ij captures the unique effect (i.e., offset or fluctuation) of each RP in addition to the overall effect b 0 and the common effects from the two involved regions, ξ i and ξ j; in the conventional ANOVA terminology, η ij acts as the interaction effect between the two regions i and j while the main effects associated with the two regions are modeled by ξ i and ξ j. The same subtlety applies to the region‐subject interactions ζ ik and ζ jk.
The two ICC measures in Equations 5, 6 can be correspondingly updated:
| (15) |
| (16) |
| (17) |
Among the four LME models, LME0 is the simplest and LME3 is the most complex and inclusive, while LME1 and LME2 are intermediate. The models can be compared based on the tradeoff between model performance and complexity (e.g., number of parameters), for example, by a likelihood ratio test or through criteria such as the Akaike information criterion or the Bayesian information criterion (Bates, Maechler, Bolker, & Walker, 2015). As the number of components in a model increases, so does the number of parameters to be estimated. For example, with m(m − 1)n data points z ijk as input, the total number of parameters involved at the right‐hand side of the model LME3 in Equation (14) is m(m − 1) + 2mn + 2 m + 1. For the model LME3 to be identifiable, the following relationship must hold:
| (18) |
To prevent LME3 from being over‐parameterized, a condition for the number of subjects, derived from a quadratic form of m based on Equation (18), is . Such a lower bound for m is a decreasing function of n; in particular.
We now consider Bayesian extensions to the primary model BML0 (Equation (7)), paralleling the three LME expansions of LME0. Specifically, by incorporating the interaction effect between the two regions of each RP, as well as the interaction effect between each region and each subject, we have three additional models (corresponding to their LME counterparts):
| (19) |
| (20) |
| (21) |
where η ij is the idiosyncratic effect for the (i,j) RP or the interaction between regions i and j, while ζ ik is the unique interaction effect between region i and subject k, and ζ jk is the unique interaction effect between region j and subject k. The two interaction effects, ζ ik and ζ jk, are considered as two members, i and j, of a multi‐membership cluster. Because of the sheer number of parameters, their LME counterparts are not always identified (e.g., because prerequisite (Equation (18)) is violated), but the Bayesian models can be analyzed given the regularization applied through priors. Indeed, even if the number of parameters surpasses the number of data points, BML can still converge with appropriate prior information. In practice, identifiability will not be a problem with typical matrix datasets in neuroimaging with, for example, at least 10 regions and subjects. Similar to the LME case, complexity increases from BML0 to BML3.
Under the extended BML models, the region and RP effects can be similarly derived from their posterior distributions as for BML0 in Equation (7). The region‐ and subject‐specific effect formulas, as well as their interactions, remain the same for these extended models as in Equations 9, 10, 11, respectively. Along the same vein, the RP‐specific effect formulation remains the same as Equation (8) for BML2 (Equation (20)), while for BML1 (Equation (19)) and BML3 (Equation (21)) it becomes
| (22) |
Which of the above models BML0–3 is the most appropriate? In other words, which and how many interaction terms should one consider among the various choices? An important aspect of the Bayesian framework is to perform the model quality check by utilizing various prediction accuracy metrics to evaluate different models. In an ideal setting, the predictive accuracy of a model would be assessed in terms of costs and benefits when applied to new datasets. However, for typical data analysis including the current context, in the absence of explicit cost–benefit functions, model evaluation can be performed in terms of information criterion scoring functions such as the widely applicable information criterion (Vehtari, Gelman, & Gabry, 2017) as well as cross‐validation. The aim of quality check is not to accept or reject the model, but rather to assess its ability to fit the data. For example, Pareto smoothed importance‐sampling leave‐one‐out cross‐validation (LOO‐CV; Vehtari et al., 2017) compares the potential model candidates by estimating the point‐wise, out‐of‐sample prediction accuracy from each fitted Bayesian model using the log‐likelihood evaluated at the posterior simulations of the parameter values, and selects the one with the lowest information criterion (if selection of a single model is desired). This accuracy tool uses probability integral transformation (PIT) checks, for example, through a quantile–quantile plot to compare the LOO‐PITs to the standard uniform or Gaussian distribution (Vehtari et al., 2017). Another qualitative approach to comparing models is to visually inspect model predictions against the original data, such as when employing posterior predictive checks (PPC) to graphically compare competing models to actual data. The underlying rationale is that, when drawing from the posterior predictive distribution, a reasonable model should generate new data that look similar to the acquired data at hand. Furthermore, as a model validation tool, PPC allows one to examine systematic differences or potential misfits of the model, similar to plotting a fitted regression model against the original data. We illustrate the use of quality checks when we apply the models to FMRI data below.
Not only can we perform model comparisons among Bayesian model candidates, but also we can compare BML and GLM models by fitting a GLM under a Bayesian framework. For example, the conventional GLM approach can be directly compared to BML models through cross‐validation (e.g., assessing posterior predictive accuracy via PPCs) by assigning a noninformative prior to the model parameters as shown with the GLM formulation (Equation (3)) Bayesianized to
| (23) |
where the parameters b p and σ 2 are assigned with corresponding hyperpriors. The Bayesianized version GLM3 is essentially the same as GLM2 in (3) with no additional information assumed. Indeed, each RP under the three GLM models is treated as an isolated entity, without information being shared among all regions and RPs as in the LME and BML models.
A second class of model extension involves incorporating one or more subject‐specific (e.g., sex, age, and behavioral measures) explanatory variables. For example, with one explanatory variable, BML1 in (19) can be directly augmented by adding a subject‐level covariate x k to,
| (24) |
where λ and μ are 2 × 2 variance–covariance matrices. Model comparisons can also be performed among various candidate models in the presence of explanatory variables, with options similar to those suggested above.
The region‐ and subject‐specific effects such as r i defined in Equation (9) and s k in Equation (10) as well as their interaction t ik can be directly applied to the BML model in Equation (24). In addition, the region‐ and RP‐specific effects associated with the covariate x under the BML (Equation (24)) can be similarly obtained:
| (25) |
| (26) |
Cases with more than one explanatory variable can be similarly formulated as in the BML models (Equation (24)). In the same vein, the research interest can be region‐specific (e.g., r i) or RP‐specific (e.g., p ij) effects for the intercepts; alternatively, the effect of interest can be region‐specific (e.g., ) or RP‐specific (e.g., ) effects of an explanatory variable.
It is worth emphasizing that a unique feature of BML modeling is that region and subject effects can be obtained through the posterior distribution of, for example, ξ i and π k, so that the investigator can (a) evaluate the relative “importance” of each ROI and (b) investigate which subjects are more atypical than others, or explore the possibility of including potential covariates based on the outlying information. Importantly, the BML framework allows one to quantify the uncertainty of each effect of interest. We believe that these properties provide a major benefit over ANOVA and LME, because such inferences on the effects of each region and each RP cannot be achieved readily under conventional frameworks.
To be able to construct a reasonable BML model, exchangeability (in the sense of de Finetti's theorem) is assumed for each entity‐level effect term (e.g., region and subject). Conditional on region‐level effects ξ i and ξ j (i.e., when the two ROIs are fixed at indices i and j), the subject effects π k can be reasonably assumed to be exchangeable since participants are usually recruited randomly from a hypothetical representative population. As for the ROI effects ξ i and ξ j, here we simply assume their exchangeability conditional on the subject effect π k (i.e., when subject is fixed at index k), and address the validity of the exchangeability assumption later in the Section 4.
2.3. Numerical implementations of the Bayesian framework
As analytical solutions are not available for BML models in general, we use numerical approaches whereby we draw samples from the posterior distributions via Markov chain Monte Carlo (MCMC) simulations. Specifically, we adopt the algorithms implemented in Stan, a probabilistic programming language and library in C++ on which the language depends (Stan Development Team, 2017). In Stan, the main engine for Bayesian inferences is adaptive Hamiltonian Monte Carlo (HMC) under the category of gradient‐based MCMC algorithms (Betancourt, 2018). The present implementations are executed with the R package brms in which multi‐membership modeling is available (Bürkner, 2017; Bürkner, 2018).
Examples of the priors for cross‐region and cross‐subject effects, as well as their interactions, were provided with each model in the previous section. For population parameters (e.g., b 0 and b 1 in Equation (24)), we adopt an improper flat (noninformative uniform) distribution over the real domain or a weakly informative distribution such as Cauchy or Gaussian depending on the amount of available data (e.g., use a noninformative prior if a large amount of information is available). As for assigning hyperpriors, we follow the general recommendations by the Stan Development Team. For example, a weakly informative prior such as a Student's half‐t(3,0,1)5 or a half‐Gaussian (with restriction to the positive side of the respective distribution) is usually applied for the scaling parameters at the region and subject level, the standard deviations for the cross‐region and cross‐subject effects, ξ i, ξ j, and π i as well as their interactions. For the covariance structure (e.g., λ in Equation (24)), the LKJ correlation prior6 is used with the shape parameter taking the value of 1 (i.e., jointly uniform over all correlation matrices of the respective dimension) (Gelman, Simpson, & Betancourt, 2017). Lastly, the standard deviation σ for the residuals utilizes a half Cauchy prior with a scale parameter depending on the standard deviation of z ijk.
Bayesian inference is usually expressed in terms of the whole posterior distribution of each effect of interest. Point estimates from these distributions, such as mean or median, can be used to illustrate centrality, while standard error or quantile‐based intervals provide an uncertainty measure or a condensed summary of the posterior distribution. To estimate the posterior distribution for an effect of interest, multiple Markov chains are usually run in parallel for a number of iterations (after the so‐called “burn‐in” iterations). To gauge the consistency of an ensemble of Markov chains, the split statistic (Gelman et al., 2014) can be used; fully converged chains correspond to , but in practice is acceptable. Another useful statistic, effective sample size (ESS), measures the number of independent draws from the posterior distribution that would be expected to produce the same amount of information of the posterior distribution as calculated from the dependent draws obtained by the MCMC algorithm. As the sampling draws are not always independent of each other, especially when MCMC chains mix slowly, one should ensure that the ESS is large enough (e.g., 200) so that quantile (or compatibility) intervals of the posterior distribution can be estimated with reasonable accuracy.
3. APPLYING BAYESIAN MULTILEVEL MODELING TO FMRI CORRELATION DATA
To illustrate our framework, we applied it to data from a previous cognitive‐emotional task (Choi, Padmala, & Pessoa, 2012). Briefly, a cohort of 41 subjects (mean age = 21, SD = 2.4, 22 females) was investigated. In each of six functional runs, 169 EPI volumes were acquired with a TR of 2,500 ms and TE of 25 ms. Each volume consisted of 44 oblique slices with a thickness of 3 mm and an in‐plane resolution of 3 × 3 mm2 (192 mm field of view). The 41 subjects performed a response‐conflict task (similar to the Stroop task) under safe and threat conditions. During all trials, after an initial 0.5‐s cue signifying the beginning of each trial, there was an anticipation period during which participants viewed a fixation cross lasting 1.75–5.75 s (with duration randomly selected), after which they performed the response‐conflict task. Trials were separated from each other by a blank screen lasting 1.75–5.75 s (again, the duration was randomly selected). During threat trials, participants received a mild shock during the anticipation period in a subset of the trials; during safe trials, shocks were never administered. Shock trials were discarded from the analysis here. To keep the trial types balanced after exclusion of physical‐shock trials, the subsequent trial type after the physical‐shock trial was always of the safe condition, which was also discarded from the analysis. A total of 54 trials were available for each condition. Finally, here we investigated the same 16 ROIs (listed in the first column of Table 2), as used in the original paper (Choi et al., 2012; see also Kinnison, Padmala, Choi, & Pessoa, 2012).
Table 2.
Region effect estimates and their uncertainties under BML
| ROI | Mean | Std err | 2.5% | 5% | 50% | 95% | 97.5% | P + |
|---|---|---|---|---|---|---|---|---|
| BF_L | 0.026 | 0.017 | −0.008 | −0.001 | 0.026 | 0.055 | 0.060 | .942 |
| BF_R | 0.024 | 0.016 | −0.007 | −0.003 | 0.024 | 0.051 | 0.057 | .924 |
| BNST_L | 0.032 | 0.017 | 0.001 | 0.005 | 0.032 | 0.061 | 0.067 | .977 |
| BNST_R | 0.029 | 0.017 | −0.002 | 0.002 | 0.028 | 0.057 | 0.062 | .960 |
| Thal_L | 0.030 | 0.017 | −0.004 | 0.001 | 0.029 | 0.059 | 0.064 | .952 |
| Thal_R | 0.036 | 0.019 | 0.000 | 0.006 | 0.035 | 0.067 | 0.073 | .976 |
| aIns_L | 0.025 | 0.017 | −0.006 | −0.001 | 0.025 | 0.053 | 0.060 | .944 |
| aIns_R | 0.025 | 0.017 | −0.008 | −0.003 | 0.025 | 0.054 | 0.059 | .937 |
| IPG_L | 0.011 | 0.017 | −0.024 | −0.018 | 0.012 | 0.039 | 0.045 | .758 |
| IPG_R | 0.014 | 0.017 | −0.021 | −0.015 | 0.014 | 0.041 | 0.047 | .794 |
| MPFC_L | 0.008 | 0.017 | −0.030 | −0.021 | 0.009 | 0.036 | 0.040 | .694 |
| MPFC_R | 0.010 | 0.017 | −0.026 | −0.019 | 0.011 | 0.038 | 0.042 | .730 |
| mIns_R | 0.012 | 0.017 | −0.023 | −0.017 | 0.012 | 0.039 | 0.045 | .764 |
| pIFG_L | 0.005 | 0.019 | −0.032 | −0.026 | 0.006 | 0.035 | 0.039 | .622 |
| pIFG_R | 0.016 | 0.017 | −0.018 | −0.011 | 0.017 | 0.043 | 0.049 | .838 |
| SMA_R | 0.021 | 0.016 | −0.010 | −0.006 | 0.021 | 0.047 | 0.052 | .908 |
Comparison of “threat” minus “safe” conditions in the FMRI dataset. Region effects (in Fisher's z‐value) for each ROI, their standard errors, 90 and 95% two‐sided quantile intervals as well as the posterior probabilities of the effects being positive (the area under the posterior density with the effect being positive), p +, were estimated through BML3 (Equation (21)). Although displaying the full posterior distributions (Figure 5) is preferable in general, tabulated results may be more feasible when the number of plots is large. The lower and upper limits of the 95% (or 90%) quantile interval are listed under the columns 2.5% (or 5%) and 97.5% (or 95%), respectively. The 50% column is the median of the posterior samples, whose difference with the “mean” column can be an indicator of distribution skewness. Rows in italics indicate that the corresponding effect lies beyond the 95% quantile interval, revealing “strong” statistical evidence for the region effect; rows in bold indicate that the corresponding effect lies beyond the 90% quantile interval (or the 95% quantile interval if the effect sign is a priori known, which is reasonable in the current example), revealing “moderate” statistical evidence for the region effect. Alternatively, the posterior probability of an effect being positive, p + (last column), can be used as statistical evidence. For example, there is some extent of the statistical evidence for the five regions of BF_L, BF_R, aIns_L, aIns_R, and SMA_R per their posterior probabilities p +. Unlike the popular practice of sharp thresholding under NHST, we emphasize the continuity of evidence as indicated by p +.
Abbreviations: BF, basal forebrain; BNST, bed nucleus of the stria terminalis; IFG, inferior frontal gyrus; IPG, inferior parietal gyrus; Ins, insula; MPFC, medial prefrontal cortex; SMA, supplementary motor area; Thal, thalamus. a, anterior; p, posterior; m, medial; L, left; R, right.
Correlation data of a 16 × 16 matrix from the n = 41 subjects were assembled from m = 16 ROIs that were analyzed and discussed in Kinnison et al. (2012). With the Fisher‐transformed z‐values of the IRC data as input, six models were evaluated: One GLM as formulated in Equation (23), four BML models (BML0 to BML3, Equations 7, 19, 20, 21), plus LME3 (Equation (14)) that shares the same effect decomposition as BML3 (Equation (21)). For comparison, the MATLAB package NBS (Zalesky et al., 2010) was used to address multiple testing involved in the GLM approach (5,000 permutations).
Among the five models (GLM and four BML models), GLM yielded the poorest results in terms of predictive accuracy assessed through LOO‐CV (Table 3), most likely due to the lack of accounting for the covariance structure in the correlation matrix due to shared regions. In contrast, the differences in terms of PPCs between the GLM approach and the BML models were subtle (Figure 4): The GLM tended to generate fewer near‐zero values (see the peak regions). Among the Bayesian models, the most complex model BML3 in Equation (21) and BML2 in Equation (20) showed substantially better predictive accuracy in terms of LOO‐CV (Table 3); they were virtually indiscernible in terms of PPC (Figure 4). For illustrative purposes, we chose BML3 here given its slight advantage over BML2.
Table 3.
Model comparisons among five candidate models via approximate LOO‐CV
| Model | GLM | BML0 | BML1 | BML2 | BML3 |
|---|---|---|---|---|---|
| GLM | −2,808.31 (101.65) | 1,735.46 (78.20) | 3,458.45 (106.53) | 1,733.56 (78.03) | 3,465.96 (105.94) |
| BML0 | −1,735.46 (78.20) | −4,543.77 (102.97) | 1,722.99 (84.14) | −1.90 (0.97) | 1,730.49 (84.13) |
| BML1 | −1,733.56 (78.03) | 1.90 (0.97) | −4,541.87 (103.04) | 1,724.89 (84.21) | 1,732.39 (84.15) |
| BML2 | −3,458.45 (106.53) | −1,722.99 (84.14) | −1,724.89 (84.21) | −6,266.76 (108.23) | 7.50 (7.39) |
| BML3 | −3,465.96 (105.94) | −1,730.49 (84.13) | −7.50 (7.39) | −1,732.39 (84.15) | −6,274.26 (108.22) |
Smaller values indicate better fit. To directly compare with the four BML models, the Bayesianized version of GLM (Equation 23) was fitted with the data at each RP separately. Each diagonal element displays the out‐of‐sample deviance measured by the leave‐one‐out information criterion (LOOIC) and the corresponding standard error (in parentheses). Each off‐diagonal element is the LOOIC difference between the two models (row vs. column) and its standard error (in parentheses). The higher predictive accuracy of the four BML models is shown by their substantially lower LOOIC. Among the four BML models, two of them, BML2 and BML3, are substantially superior to the other two. Between the two most inclusive models, BML3 (with both subject‐region and between‐region interactions) is slightly better than BML2 (with subject‐region interaction only).
Figure 4.
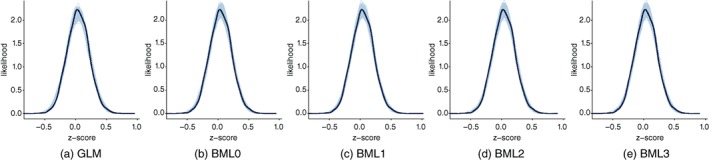
Model performance comparisons through posterior predictive checks (PPCs) and cross validations between conventional univariate GLM (a) and the four BML models (b–e). Each of the five panels shows the posterior predictive density overlaid with the raw data from the half off‐diagonal element in a 16 × 16 Fisher‐transformed IRC matrix from each of the 41 subjects for the given model: Solid black curves show the raw data (with linear interpolation) whereas the light blue cloud is composed of 500 sub‐curves each of which corresponds to one draw from the posterior distribution. Differences between the solid black curves and the light blue cloud indicate how well the respective model fits the raw data. For this particular data set, PPCs did not differentiate the five models as clearly as LOO‐CV (Table 3); the four BML models fitted the data slightly better than the GLM (Equation 23) around the peak area while the differences were negligible among the four BML models. However, for demonstrative purpose, we show the PPCs here to illustrate their use for model comparison in general [Color figure can be viewed at http://wileyonlinelibrary.com]
The summary results that are comparable between LME3 and BML3 are shown in Table 4. Among the sources of data variability, the highest was the residuals, indicating that a large amount of variability was unaccounted for. The second and third largest sources were cross‐subject effects and region‐subject interaction effects, respectively; in other words, the overall variability at the subject level as well as the variability at each ROI of individual subjects was relatively large. Finally, the variabilities across regions and across all RPs were relatively small. Per the formulas in Equation (17), the two ICC values for LME3 and BML3 indicate that the correlation between any two RPs of a subject that share a region was substantial with ρ r = 0.483 at the population level, while the correlation of any RP between two subjects was negligible with ρ s = 0.017. Table 4 includes results for the LME3 model, showing that the estimated parameters are nearly identical in both cases, despite LME being estimated via restricted maximum likelihood, and MCMC being used to estimate the BML parameters. Under LME, however, the SD can only be estimated for b 0 (which is a fixed effect); the variability of the remaining random‐effects is not estimable, which precludes direct statistical inferences involving them. Importantly, the similarity of parameter estimates between the two modeling frameworks illustrates the negligible impact of weakly informative priors (when sufficient data are available) adopted in BML.
Table 4.
| Term | BML3 | LME3 | |||||
|---|---|---|---|---|---|---|---|
| Estimate | SD | 95% QI | ESS |
|
Estimate | SD | |
| ν: Region‐subject | 0.070 | 0.002 | [0.066, 0.075] | 734 | 1.001 | 0.070 | – |
| λ: Region | 0.014 | 0.005 | [0.004, 0.026] | 321 | 1.007 | 0.013 | – |
| τ: Subject | 0.093 | 0.012 | [0.072, 0.121] | 680 | 1.002 | 0.093 | – |
| μ: Region pair | 0.011 | 0.003 | [0.004, 0.017] | 366 | 1.004 | 0.012 | – |
| b 0: Overall average | 0.040 | 0.017 | [0.005, 0.074] | 608 | 1.004 | 0.041 | 0.016 |
| σ: Residual | 0.120 | 0.001 | [0.118, 0.123] | 2000 | 0.998 | 0.120 | – |
The column headers estimate, SD, QI, and ESS are short for effect estimate in Fisher's z‐value, standard deviation, quantile interval, and effective sample size, respectively. LME3 shares the same effect components as BML3 and shows virtually the same effect estimate for the population mean b 0 and the standard deviations for those effect components despite: (a) the two modeling frameworks are solved through two different numerical schemes (REML for LME3 and MCMC for BML3); and (b) in practice the input data for LME3 had to be duplicated to maintain the balance between the two crossed random‐effects components associated with each RP. In addition, the nearly identical parameter estimates indicate that the use of priors under BML3 had a negligible effect. However, LME3 does not allow statistical inferences about region‐ or RP‐specific effects. All values under BML3 were <1.1, indicating that all the four MCMC chains converged well. The effective sample sizes (ESSs) for the population‐ and entity‐level effects were large enough to warrant quantile accuracy in summarizing the posterior distributions for the effects of interest, such as region and RP effects.
We now summarize statistical inferences with regard to the region effects from BML3. As the number of regions was relatively small (m = 16), we display all the posterior distributions as well as their 50, 90, and 95% quantiles (Figure 5). The posterior densities were roughly symmetric, but there were some irregularities in terms of distribution shape, especially around the peak for regions such as the BNST_L, BNST_R, Thal_R, aIns_R, and SMA_R. In addition, estimates of region effects can be condensed and summarized by their mean (or median), SD, quantile intervals, and posterior probability of the effect being positive, P +, as illustrated in Table 2. Because the effect of the “threat” condition was known to be higher than that of the “safe” condition from previous studies, the directionality of the RP effect was a priori known to be positive,7 and thus we could make inferences based on one‐sided (e.g., positive) intervals; for example, a 90% quantile interval corresponds to a positively sided 95% interval (cf. the posterior probability of the effect is positive, P +, in the last column of Table 2). Among the 16 regions, two of them, BNST_L and Thal_R (highlighted with green dot‐dashed boxes in Figure 5 and italicized in Table 2), exhibited “strong” statistical evidence for a region‐level effect as judged by the two‐sided 95% quantile interval; two regions, BNST_R and Thal_L (highlighted with orange dot‐dashed boxes in Figure 5 and bolded in Table 2), had “moderate” statistical evidence under the two‐sided 90% quantile interval; and five regions, BF_L, BF_R, aIns_L, aIns_R, and SMA_R, exhibited slightly weaker but still sizable statistical evidence (close to the two‐sided 90% quantile interval). Furthermore, four of those regions with sizable statistical evidence were bilateral: The basal forebrain, bed nucleus of the stria terminalis (BNST), thalamus, and anterior insula are strongly involved in threat processing (Grupe & Nitschke, 2013; Pessoa, 2013).
Figure 5.
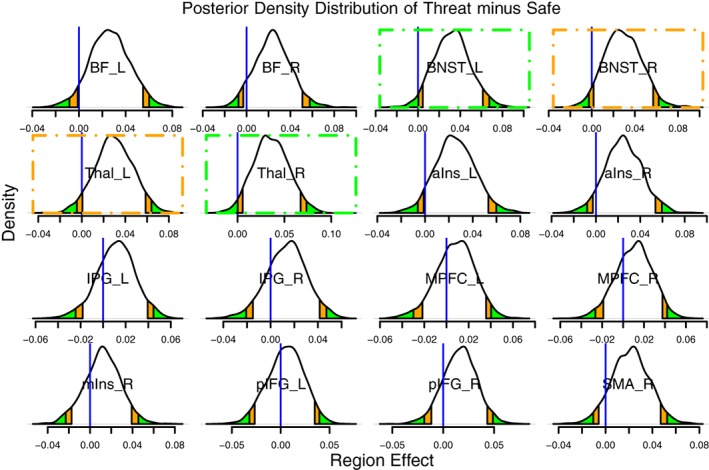
Comparison of “threat” minus “safe” conditions in the FMRI dataset. Posterior density plots of region effects (in Fisher's z‐value) for threat minus safe based on 2000 draws from BML3 (Equation 21). Each posterior probability distribution indicates the probability of observing region effects (“threat” minus “safe”). The orange and green tails mark areas outside the two‐sided 90 and 95% quantile intervals, respectively; the blue vertical line indicates the zero region effect. Consider a region such as the BNST_L: The zero region effect lies in the left green tail, indicating that the probability that the effect is positive, P +, is greater or equal to 0.975 (conversely, the probability that the effect is negative is ≤0.025). The same is true for the Thal_R; both regions are indicated with green dot‐dashed boxes. In these two cases, we can say that there is “strong” statistical evidence of a region effect. Two other ROIs (BNST_R and Thal_L; orange dot‐dashed boxes) exhibited “moderate” statistical evidence of a region effect (the blue vertical line was within the orange band). Four more ROIs forming contralateral pairs of regions (BF_L and BF_R, aIns_L and aIns_R) plus SMA_R also exhibited some statistical evidence as they were close to the typical “convenience” thresholds. Note that the posterior density provides rich information about each effect distribution, including shape, spread, and skewness. Unlike the conventional confidence interval that is flat and inconvenient to interpret, it is valid to state that, conditional on the data and model, with probability, say, 95%, the region effect lies in its 95% posterior interval. Note that the two‐sided 90% quantile interval can be interpreted as a one‐sided 95% interval if the effect of directionality is known a priori; likewise, the two‐sided 95% interval can be interpreted as a one‐sided 97.5% interval. BF, basal forebrain; BNST, bed nucleus of the stria terminalis; IFG, inferior frontal gyrus; IPG, inferior parietal gyrus; Ins, insula; MPFC, medial prefrontal cortex; SMA, supplementary motor area; Thal, thalamus; a, anterior; p, posterior; m, medial; L, left; R, right [Color figure can be viewed at http://wileyonlinelibrary.com]
The fact that almost all regions with some extent of statistical evidence were bilateral reinforces our inferences based on BML. For example, BML3 identified the BNST and the thalamus as exhibiting region‐level effects on both of their respective contralateral sides. The identification of the BNST is particularly noteworthy because of its involvement in processing threat during uncertain and more temporally extended conditions; this region has received increased attention in the past decade (Fox, Oler, Tromp, Fudge, & Kalin, 2015). For example, in a previous threat study, the “betweenness” of the BNST was shown to be modulated by anxiety scores, such that greater increases in betweenness during threat relative to safety were observed for participants with high‐ relative to low‐anxiety (McMenamin et al., 2014). The thalamus is also a key region in the processing of threat, and is at the core of cortical–subcortical signal integration that is required for determining the biological significance of stimuli and behavioral contexts (Pessoa, 2017).
In general, illustrating RP results is visually more challenging, as the number of RPs is potentially quite large, and it might not be practical to show the full results in the format of density histograms, or in the format of summarized results with mean, standard error, and quantile intervals, as illustrated for the region effects in Figure 5 and Table 2. Nevertheless, as in the current dataset, there were 120 RPs, we illustrate the posterior densities in a relatively compact fashion in Figure 6. More generally, one may present the results with a matrix format as typically seen in the literature. Figure 7 shows the results of the GLM and BML3 models side‐by‐side for comparison purposes. Note that the effect of partial pooling or shrinkage under BLM3 is evident relative to GLM: The effects at both large and small, as well as positive and negative, ends estimated under the GLM tended to be “pulled” toward to the center under BML; see larger (darker) or smaller (lighter) circles in GLM (Figure 7, left) and the corresponding slightly smaller (lighter or above zero) or larger (darker) circles under BML (Figure 7, right). In other words, since all the regions were incorporated in one platform under BML, all region‐level estimates were constrained by the prior Gaussian distribution and thus became slightly more similar to one another than their GLM counterparts. In addition, the GLM initially identified 62 RPs (Figure 7, left) as statistically significant under the one‐sided NHST level of 0.05. However, none of them survived the correction for multiple testing through the NBS permutation approach (Zalesky et al., 2010). As a direct comparison, 33 RPs from BML3 (Figure 7 right) exhibited comparable statistical evidence (i.e., based on a comparable 95% one‐sided quantile intervals); they constituted a subset of the 62 RPs identified under the GLM without multiple testing correction.
Figure 6.
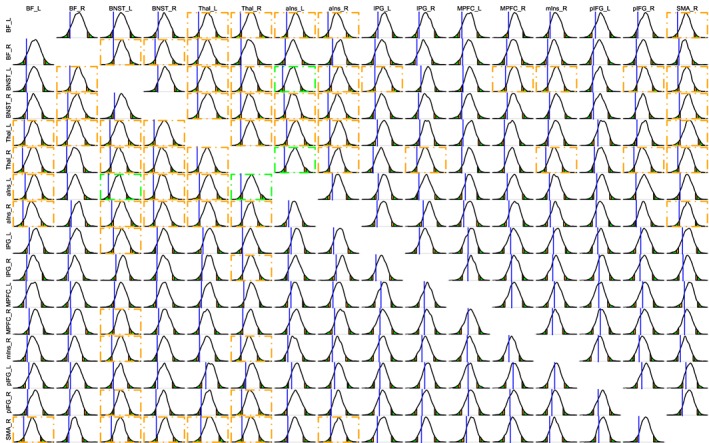
Comparison of “threat” minus “safe” conditions in the FMRI dataset. Posterior density plots for the effect magnitude (Fisher's z‐value) of “threat” minus “safe” are shown for all RPs based on BML3 (Equation 21). As in Figure 5, the blue vertical line marks the location of zero effect, orange and green areas under the density curve show the ranges outside the 90 and 95% quantile intervals, respectively. The orange and green dot‐dashed boxes highlight the RPs that display some extent of statistical evidence as in Figure 5. The empty entries along the diagonal correspond to the correlation value of 1 along the diagonal of the matrix [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 7.

Comparisons of RP effects between GLM3 (Equation 23) on the left and BML3 (Equation 21) on the right for the FMRI dataset. The empty entries correspond to the correlation value of 1 along the diagonal. The effect magnitude (Fisher's z‐value) of threat minus safe is symbolized with both circle size and color scheme (color bar, far right). The impact of partial pooling (or shrinkage) under BML3 is evident as the effects for most RPs are “pulled” toward the middle relative to their GLM counterparts. Following the coloring convention of other figures, RPs are colored with a green or orange background based on the strength of statistical evidence (95 or 90% two‐sided quantiles). As the directionality of the effect was known a priori (i.e., positive for the contrast of “threat” relative to “safe”), one‐sided effects were considered here. Therefore, the 90 or 95% two‐sided quantile intervals shown with a color background can be viewed as equivalent to one‐sided 95 or 97.5% interval. With GLM3, 62 RPs were identified as statistically significant (one‐sided, 0.05; green and orange boxes) without correction for multiple testing. With BLM3, 33 RPs exhibited “moderate” to “strong” statistical evidence and they formed a subset of those 62 RPs declared under GLM3. When cluster‐level correction was applied to GLM3 (FPR of 0.05 with NBS, one‐sided testing), no RPs survived. As discussed in the text, multiplicity is dissolved in the BML model through partial pooling. We encourage researchers to report the full results, thus avoiding dichotomous interpretations [Color figure can be viewed at http://wileyonlinelibrary.com]
4. DISCUSSION
In a recent article, we addressed issues associated with correcting for multiple testing in FMRI activation data (Chen et al., 2019). We converted the traditional voxel‐wise GLM into a region‐based BML via a step‐wise model building process (univariate GLM → two‐way random‐effects ANOVA or crossed random‐effects LME → BML). As BOLD responses in the brain share approximately the same scale and range, the region‐based BML approach allows information to be pooled across regions to jointly help estimate effect magnitudes at each individual ROI.
4.1. Summary of Bayesian multilevel modeling for matrix‐based analysis
In this article, we applied the same modeling approach of information sharing and regularization to matrix‐based data analysis. Specifically, we described a multilevel Bayesian approach to modeling the correlation structure across brain regions, as in FMRI correlation matrices. To help the conceptual and inferential migration from univariate GLM to multilevel BML, as an intermediate step, we formulated a series of LME models. Among them, LME0 contained three crossed random‐effects terms and is essentially a traditional three‐way random‐effects ANOVA. The other three LME models were extensions of LME0 incorporating various interactions among random‐effects variables. The inclusion of these interaction terms led the way to the development of the corresponding BML counterparts. A central novelty of our overall approach is the idea of decomposing the correlation structure into multiple additive effects, including region, RP, and subject effects; thereafter their interactions can be modeled seamlessly. In particular, our approach takes into account the covariance structure of the data, namely the fact that RPs share common regions, hence variance. As the data are modeled by a single, unified model, issues related to multiplicity automatically disappear. Finally, within the Bayesian framework, effects of interest can be directly summarized via posterior distributions without having to resort to thresholding decisions, which we believe is an attractive feature of the approach.
Let us recapitulate the differences between the LME and BML frameworks that explain the rationale behind our adoption of the latter. The two frameworks are essentially the same in terms of effect decompositions; the different expressions under the BML formulation are meant to explicitly indicate the conditionality involved. However, there is one fundamental difference between the two approaches and one crucial consequence for our intended goals. Consider the LME3 and BML3 models. Two distinct parameter sets coexist under LME. The first set of parameters is considered epistemic in the sense that the relevant effects are treated to be intrinsic, unknown but constant (e.g., the overall effect b 0 shared across all regions and subjects), and are thus referred to as “fixed‐effects” under LME3. In contrast, the second set of parameters is aleatoric in the sense that the associated effects are considered unknown and random (e.g., region‐, RP‐ and subject‐specific effects, ξ i, ξ j, η ij, and π k), and are accordingly called “random‐effects” under LME3. At least two considerations, one conceptual and the other practical, are involved in the differentiation of fixed‐ versus random‐effects under LME. The conceptual aspect emphasizes the different treatment of the two parameter types while the practical aspect focuses on the question of research interest and the feasibility of the parameterization. Fixed‐effects are usually the focus of investigation while random‐effects are embedded in the model to account for variability across measuring entities (e.g., regions, subjects); that is, one or a few effects are targeted as fixed‐effects (e.g., population effects for experimental conditions) while other entities are sampled as representatives of random‐effects (e.g., subjects). In stark contrast, the distinction between fixed‐ and random‐effects dissolves under BML. For example, even the overall effect b 0 across all regions and subjects is considered fundamentally aleatoric (with an uninformative or weakly informative prior). Despite the introduction of priors and hyperpriors, the two modeling frameworks produce virtually identical estimates for fixed‐effects parameters and random‐effects variances (Table 4). However, the differential treatment of model parameters under LME and BML results in a crucial bifurcation. Under LME, we can estimate parameters and uncertainty of fixed‐effects (e.g., b 0), but we can only obtain the variances (e.g., λ 2, μ 2, and τ 2) for the random‐effects variables, not the individual random‐effect parameters (e.g., region‐, RP‐, and subject‐specific effects, ξ i, ξ j, η ij, and π k). Consequently, under LME, we cannot achieve our goal of making inferences at the region and region‐pair levels, whereas, under BML, we can directly assess these effects with MCMC. Although LME cannot be directly adopted for MBA, it serves as a useful intermediate step between GLM and BLM. See Figure 8 for an overall summary.
Figure 8.

Relationships among the modeling frameworks. The flowchart illustrates the differences in model formulation, assumptions, and inferential capabilities (using GLM1, LME3, and BML3 as examples). Although the LME framework does not allow the analyst to achieve the goal of making inferences about the effects of interest at the region‐pair level ( or p ij = b 0 + ξ i + ξ j + η ij, where l codes the combined indices i and j for the two involved regions), it serves as an intermediate step in the conceptual transition from the univariate GLM paradigm to BML. Effects at the region level, can be further inferred through BML, but not under GLM or LME [Color figure can be viewed at http://wileyonlinelibrary.com]
The MBL approach was illustrated here with correlation data from FMRI. However, the approach can be applied to datasets in matrix form generally, with one matrix per subject. Besides correlation coefficients, such matrix format includes, but is not limited to, coherence, entropy, mutual information, and white matter properties (e.g., fractional anisotropy, mean diffusivity, radial diffusivity, and axial diffusivity). In addition, the diagonals in the matrices (which equaled 1 and were not informative in the present case) can be incorporated into the model when appropriate (e.g., entropy), and missing data in the matrix are allowed when the effects of RPs are deemed uncertain or nonexistent (e.g., in the context of DTI data when brain lesions are present.)
We derived our approach by starting with a population analysis strategy with ANOVA or linear mixed‐effects (LME) that incorporated region, RP, and subject effects. These models were then converted into their respective counterparts within a Bayesian framework. A central feature of the approach was to not assume the RPs as isolated and unrelated (as under the conventional GLM approach), but instead treat the individual regions as inherently associated with each other through a Gaussian distribution assumption. As a result, instead of each region (or RP) being assumed to follow a uniform distribution with equal likelihood on the real domain (−∞,+∞) under GLM, the effects across regions are loosely constrained and regularized through a Gaussian distribution under BML. In our view, the Bayesian approach helps to mitigate, or possibly dissolve, the multiple testing issue under the conventional GLM based on three perspectives:
The higher efficiency of BML lies in the overall modeling strategy. The fundamental issue with the conventional univariate modeling approach in neuroimaging in general, and correlation analysis through GLM in particular, is an inefficient two‐step process: Initially assume that voxels or RPs are independent of each other, and build as many models as the number of elements; then, handle the multiple testing issue using spatial relatedness as leverage to partially recover the efficiency loss. In contrast, we construct a single, integrative BML model through which the effect decomposition more accurately accounts for the intricate interrelationships of the data structure.
The benefit of partial pooling through regularization under BML is to avoid information waste. The conventional GLM allows each region and RP to independently take values with equal likelihood within (−∞,+∞), which is equivalent to assuming a noninformative uniform prior or a Gaussian prior with an infinite variance in the Bayesian terminology. On the surface, a noninformative prior does not inject much “subjective” information into the model and should be preferred. In other words, it might be considered a desirable property from the NHST viewpoint, since noninformative priors are independent of the data. Because of this “objectivity” property, one may insist that noninformative priors should be used all the time. Counterintuitively, a “noninformative” prior may become, in fact, too informative (see below).
The high efficiency of information sharing among regions through BML can be conceptualized as a tug of war between two extremes: Complete pooling and no pooling. Complete pooling assumes no variability across brain regions or RPs; they are assumed to be homogeneous. Complete pooling is unrealistic in the brain (the brain is differentiated across regions of course), but serves as an anchor for comparison. The other extreme of no pooling is adopted in neuroimaging as a standard approach of massively univariate modeling and provides another interesting anchor. Through modeling each RP individually, the conventional GLM offers the best fit separately, but each RP is considered autonomous and independent of each other. At the same time, a few disadvantages are associated with no pooling: (a) it wastes the prior knowledge that the regions and RPs share some similarity in terms of effect size; (b) it carries the risk of overfitting, poor inference, or predictive ability regarding future data; (c) to control for multiplicity, one has to compromise in efficiency through paying the price of potential over‐penalization by considering spatial extent; and (d) it may over and/or underestimate some effects, leading to type S (sign) and type M (magnitude) errors.
In contrast, with BML, we loosely constrain the regions through a weakly informative prior (i.e., Gaussian distribution). With a regularizing prior, partial pooling usually leads to more conservative inferences and achieves a counterbalance between homogenization and independence. Specifically, BML treats each region via a random process that adaptively regularizes the regions, and conservatively pools the effect of each region and RP toward the “center.” In this manner, the BML methodology sacrifices model performance in the form of a potentially poorer fit in samples (observed data) for the sake of better inference and better fit (prediction) in out‐of‐sample data (future data) through partial pooling (McElreath, 2016). Whereas BML may fit each individual region or RP more poorly than univariate GLM, BML improves collective fitting and overall model performance, as illustrated through model comparisons in Table 3.
-
3.
Instead of focusing on the conventional concepts of false positives and false negatives, BML effectively controls two different types of error: Errors of incorrect sign (type S) and incorrect magnitude (type M; Chen et al., 2019; Gelman & Carlin, 2014). From the NHST perspective, one may wonder about scenarios when BML still commits substantial type I errors: Is the false‐positive rate under BML higher than its GLM counterpart? We would argue that the situation is not as severe for two reasons: (a) the concept of false‐positive rate and the associated NHST strategy is qualitatively different from the Bayesian perspective which is often interested in modeling the data, not in making dichotomous decisions (Chen et al., 2019; Gelman & Carlin, 2014); and (b) inferences under BML most likely have the same directionality as the true effect because type S errors are well controlled under BML (Gelman & Tuerlinckx, 2000). Consider the following two scenarios: (a) when power is low, the likelihood under the NHST to mistakenly infer that the healthy group is “higher” than, say, the autistic group could be sizable (e.g., with a type S error of 30%); and (b) with the type S error rate controlled under, for example, 3.0%, the BML approach might exaggerate the magnitude difference between the two groups by, say, two times. Whereas the second scenario is problematic, we expect that most researchers would view the first scenario as more problematic. Taken together, in place of dealing with multiplicity and false positives under the massively univariate GLM, the regularization across ROIs and RPs under BML aims to prevent sizable errors of incorrect directionality and magnitude.
A special note about model selection concerns the presence of explanatory variables. In general, when no between‐subjects variables are involved, we recommend the use of BML3 because it is the most inclusive model; when one or more between‐subjects variables are incorporated, we recommend a model in the form of Equation (24). As seen with the experimental data, the most inclusive model BML3 clearly outperformed its less inclusive counterparts when no between‐subject variables were involved (Table 3). However, when at least one between‐subject explanatory variable is present, a model (i.e., Equation (24)) without the interaction effects explicitly modeled between regions and subjects should be considered due to the conflict between the explanatory variables and the interaction terms. Specifically, if the interaction effects, such as ζ ik and ζ jk in BML2 (Equation (20)) and BML3 (Equation (21)), were included in the model, cross‐subject variability at each region would be largely explained by the interaction effects ζ ik and ζ jk, leaving little for the effect of interest, ξ 1i and ξ 0j. Therefore, when the region‐specific effect associated with a between‐subject explanatory variable (e.g., group difference or age effect at each ROI) is the research focus, it is a prerequisite that such effect is not substantially absorbed by the interaction effects between regions and subjects.
4.2. Potential advantages of Bayesian multilevel modeling of correlation matrices
The adoption of a Bayesian multilevel framework offers the following advantages over traditional GLM approaches:
Generality. As BML and LME usually share a corresponding modeling structure, BML can handle data structures subsumed under LME, such as Student's t tests, ANOVA, regression, ANCOVA, and GLM. In particular, missing data can be modeled as long as the missingness can be considered random. Therefore, BML can be reasonably applied, for example, to analysis with DTI even if white matter “connections” are not detected in some participants. More generally, BML is superior to LME in dealing with complicated data structures. In particular, the number of parameters under LME with a sophisticated variance–variance structure could be high, leading to overfitting and convergence failure with the maximum likelihood algorithm; in contrast, the priors under BML help overcome overfitting and convergence issues.
Hierarchization. When applied to correlation matrices, the crucial feature of BML is the disentangling of each RP effect into the additive effects of the two involved regions, plus other interaction effects. Thanks to this untangling process, both region‐ and RP‐specific effects can be retrieved through their posterior distributions, which would not be achievable under LME. The reason is that as each effect under LME is categorized as either fixed‐ or random‐effects, only the fixed‐effects components (e.g., b 0 in LME0‐3) can be inferred with effect estimates and uncertainties while random‐effects components (e.g., region effect ξ i, RP effect η ij, interaction between region and subject ζ ik in LME0‐3) would be assessed with their variances. In contrast, as all effect components are considered random under the Bayesian framework they can be estimated with their respective posterior distributions (either directly or through reassembling), as illustrated in Table 2, Figures 5, 6, 7. Thus, the multilevel approach allows one to address different aspects of the input correlation data, from individual regions to RPs.
Extraction of region effects. A unique feature of the present approach is that it can estimate region‐level effects. In this manner, the approach more accurately characterizes the contribution of a region through an integrative model that leverages hierarchical effects at multiple levels. We propose that this property allows the assessment of region “importance” in a manner that is statistically more nuanced than those commonly used in graph‐theoretic analysis (such as “hubs” and “degrees”). In addition, note that region‐level effects at present cannot be obtained through alternative GLM‐based methodologies such as NBS, FSLnets, and GIFT.
Integration and efficiency. BML builds an integrative platform and achieves high efficiency through sharing and pooling information across all entities involved in the system. Specifically, instead of modeling each RP separately as with the conventional GLM approaches, BML incorporates multiple testing as part of the model by assigning a prior distribution (e.g., Gaussian) among the regions (i.e., treating ROIs as random‐effects). Thus, the multilevel approach conservatively “shrinks” the original effects toward the center. In essence, instead of leveraging cluster size or the strength of statistical evidence as in traditional approaches, BML leverages the “common information” among regions.
Full reporting. The estimation of posterior distributions under a Bayesian framework (Figure 4) provides rich and detailed information about each effect of interest, and avoids the need for thresholding under NHST and the resulting dichotomization of results—the latter effectively creates a two‐class system of results, some deemed “significant” and worthy of being reported, and some that are not “significant” and thus should be ignored. However, the popular practice of only reporting “statistically significant” results in neuroimaging not only wastes data information, but also distorts the full results as well as perpetuates the reproducibility crisis because of the fact that the difference between a “significant” result and a “nonsignificant” one is not necessarily significant (Cox et al., 1977). In other words, the omnipresent adoption of artificial dichotomization tends to nurture an illusion that “statistically significant” results are “proven to be true,” while anything below the threshold is effectively “nonexistent.” Although it might be natural for humans to categorize continuous variables, the typical data in neuroimaging and the underlying mechanisms do not necessarily follow such discretization. Thus, fully presenting a continuous spectrum avoids reliance on artificial thresholding. We encourage the practice of fully reporting the results while highlighting some of the results with strong evidence. For one, full reporting allows appropriate meta‐analyses and helps promote reproducibility. For example, even if the evidence for an effect is at the level of 89% level,8 reporting it allows the evidence to inform for future studies, as well as allowing it to be included in potential meta‐analyses.
Validation. The capability of model checking (e.g., PPCs, Figure 5) and validation (e.g., leave‐one‐out cross‐validation, Table 3) under BML is possibly unmatched in the conventional GLM framework (including permutation testing). The determination coefficient R 2 in a classic statistical model measures the proportion of the variance in the data that can be accounted for by the explanatory variable(s). However, it does not provide a well‐balanced metric for model performance. For instance, a regression model fitted with high‐order polynomials may behave well with the current data, but its predictability with a new dataset could fail severely. Therefore, a more effective approach is to evaluate the model through visual verifications of PPCs and LOO‐CV with the data at hand (Vehtari et al., 2017).
4.3. Potential limitations of the Bayesian multilevel approach
Despite the potential strengths of our approach described above, there are also several challenges and potential limitations. First, currently, computational demands are relatively high. With today's computers, as the number of regions m and the number of subjects n increase, the runtime can be hours, days, or even months. At present, parallelization can only be achieved across MCMC chains, but not within each chain; ongoing developments aim to take advantage of multi‐threading, which may allow within‐chain parallelization in the future. Second, it is possibly problematic to assume the effect decomposition adopted here, namely to consider each RP effect z ijk as given by additive contributions. Such additivity is bound to be vulnerable to assumption violations (although it is adopted in most statistical models). Despite the vulnerability and the potential risk of poor fitting, we emphasize that model quality can be directly assessed through various validation methods such as LOO‐CV and PPCs (see Figure 4). Third, one concern is that the exchangeability requirement of BML assumes that no differential information is available across the ROIs in the model. However, it should be noted that exchangeability captures symmetry among the ROIs in a sense that does not require independence. In other words, an independent and identically distributed set of entities (e.g., ROIs) is exchangeable, but not vice versa (every exchangeable set of entities (e.g., ROIs) is identically distributed; Gelman et al., 2014). Under some circumstances, ROIs can be expected to share some information and to not be fully independent, especially when they are anatomically contiguous or more functionally related than other ROIs (e.g., corresponding regions in opposite hemisphere). However, the exchangeability is an epistemological assumption that renders a convenient approximation of a prior distribution by a mixture of i.i.d. distributions (de Finetti's theorem; Gelman et al., 2014). Bayesian estimation builds on posterior distributions without invoking the notion of degrees of freedom, and the violation of exchangeability usually leads to negligible effects on the final shape of posterior distributions, except for the precise sequence in which the posterior draws occur (McElreath, 2016). In contrast, conventional statistics heavily relies on the concept of degrees of freedom, and the presence of temporal autocorrelation in time series data may cause the underestimation of associated variances. Fourth, one aspect of Bayesian modeling that is potentially more controversial relates to the notion of the “subjectivity” of priors. We note, however, that the major prior for the cross‐region components, ξ i and ξ j, is a Gaussian distribution. In this respect, the approach does not appreciably differ from similar assumptions about subject variability and residuals under conventional statistical models, such as regression, AN(C)OVA, GLM, and LME. Furthermore, in general, the impact of priors for other model parameters (e.g., intercept or population effect and the variances for the prior distributions) is usually negligible if the amount of data is nontrivial and if the priors/hyperpriors are weakly informative. On the other hand, with hyperpriors, Bayesian models can solve systems that would be over‐parameterized and over‐fitted under GLM or LME. Critically, by regularizing the estimation, the Bayesian framework allows statistical estimations that are not feasible under conventional frameworks.
It should be emphasized that a principled Bayesian workflow includes a full series of prior predictive checks, model sensitivity analysis, and PPC, as well as computational/numerical considerations (Gelman et al., 2014). Although we only demonstrated the use of PPC for model comparison and cross‐validation, the other steps are important in accurately capturing the data structure and in achieving robust inferences. For example, simulated data can be generated from prior distributions and then fitted with the model at hand, and numerical divergence of Markov chains (e.g., ) during computation of posterior distributions can be checked. Furthermore, simulation‐based calibration can be utilized to assess whether estimated posterior parameters follow the same distribution as the true model parameters adopted to generate simulated data. It is beyond the scope of the present investigation to systematically explore the full Bayesian workflow, but we plan to investigate these additional aspects in the future. Nevertheless, we believe that the adoption of uninformative and/or weakly informative hyperpriors combined with sufficient data (e.g., at least 10 regions and 10 subjects) poses minimal concerns regarding modeling validity.
5. CONCLUSIONS
The Bayesian multilevel modeling framework developed in the present paper can be applied to any matrix‐based analysis. Through decomposing the effect at each element of the correlation matrix into multiple components such as row, column, subject as well as their interactions, we have described a Bayesian multilevel model that more accurately captures the data structure and associated interrelatedness. Importantly, as a principled compromise between local and global effects through partial pooling, the multilevel Bayesian framework allows the investigator to efficiently make statistical inferences at both region and RP levels under a single unified model. Finally, we encourage researchers to adopt a philosophy of reporting the full results (instead of dichotomizing into “significant” and “nonsignificant” results), thus minimizing information loss while enhancing reproducibility.
ACKNOWLEDGMENTS
The research and writing of the paper were supported (GC, PAT, and RWC) by the NIMH and NINDS Intramural Research Programs (ZICMH002888) of the NIH/HHS, USA. LP's research was supported in part by the National Institute of Mental Health (R01 MH071589 and R01 MH112517). We thank Vitria Adisetiyo for her help and are indebted to the Stan Development Team for their technical support. The computations were performed and the figures were generated with the R language for statistical computing (R Core Team, 2018). Constructive comments and suggestions from two anonymous reviewers helped us improve the manuscript in terms of readability, clarity, and rigorousness. This work utilized the computational resources of the NIH HPC Biowulf cluster. (http://hpc.nih.gov).
Chen G, Bürkner P‐C, Taylor PA, et al. An integrative Bayesian approach to matrix‐based analysis in neuroimaging. Hum Brain Mapp. 2019;40:4072–4090. 10.1002/hbm.24686
Funding information National Institute of Mental Health, Grant/Award Numbers: MH071589, MH112517, ZICMH002888
Endnotes
The assumption of identical correlation ρ for all regions may be relaxed. However, per Occam's razor, such a parsimonious hypothesis with fewer adjustable parameters will have a posterior probability with “sharper” predictions (Jeffreys & Berger, 1992). More generally, it may be profitable to assume varying correlation among RPs based on anatomical and/or functional information concerning the clustering of brain regions. Such extensions deserve further exploration in future work.
With region pairs, there are totally 2 M = m(m ‐ 1) indices. Therefore, when m is odd, each index repeats even (i.e., m − 1) times, a balanced distribution between the two random‐effects factors can be achieved through the following rearrangement: if the difference between the two indices i and j is odd, switch their order (i.e., z ij effectively changes to z ji); otherwise, no change is made. However, when m is even (i.e., m − 1 is odd), balance cannot be reached but can be approximated in the sense that the first index is alternately one more (or less) than the second one.
The effect decomposition of the BML model remains the same as its LME counterpart. The different model expression here is adopted to emphasize the framework shift and the fact that the outcome under BML is conditional on the parameters and priors.
In theory, the multi‐membership scheme can also be implemented under the conventional LME.
See https://en.wikipedia.org/wiki/Folded-t_and_half-t_distributions for the density p(ν,μ,σ 2) of folded nonstandardized t‐distribution, where the parameters ν, μ, and σ 2 are the degrees of freedom, mean, and variance.
The LKJ prior (Lewandowski, Kurowicka, & Joe, 2009) is a distribution over symmetric positive‐definite matrices with the diagonals consisting of 1s.
The posterior probability of the effect being negative at a region is p − = 1 − p +. As p + takes into account the directionality of the effect, it is directly related to making one‐sided (in this case positive) or two‐sided statistical (positive or negative) inferences. The quantile of a two‐sided inference always has a corresponding quantile of a one‐sided inference, and vice versa. For example, a two‐sided 90% quantile interval can be used to derive a positively‐sided 95% interval, and a two‐sided 95% quantile interval to a positively‐sided 97.5% interval.
The use of the 89 and 97% levels was proposed by McElreath (2016), only partly in jest, as arbitrary values (simply because they are prime numbers), and as a potential antidote to the unchallenged use of the “magic” 95% level widely adopted across the experimental sciences.
REFERENCES
- Baggio, H. C. , Abos, A. , Segura, B. , Campabadal, A. , Garcia‐Diaz, A. , Uribe, C. , … Junque, C. (2018). Statistical inference in brain graphs using threshold‐free network‐based statistics. Human Brain Mapping, 39(6), 2289–2302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates, D. , Maechler, M. , Bolker, B. , & Walker, S. (2015). Fitting linear mixed‐effects models using lme4. Journal of Statistical Software, 67(1), 1–48. 10.18637/jss.v067.i01 [DOI] [Google Scholar]
- Betancourt, M. , 2018. A conceptual introduction to Hamiltonian Monte Carlo. arXiv:1701.02434
- Bürkner, P. (2017). Brms: An R package for Bayesian multilevel models using Stan. Journal of Statistical Software, 80(1), 1–28. 10.18637/jss.v080.i01 [DOI] [Google Scholar]
- Bürkner, P. (2018). Advanced Bayesian multilevel modeling with the R package brms. The R Journal, 10(1), 395–411. [Google Scholar]
- Calhoun, V. , Adali, T. , Pearlson, G. , & Pekar, J. (2001). A method for making group inferences from functional MRI data using independent component analysis. Human Brain Mapping, 14, 140–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, G. , Shin, Y. ‐W. , Taylor, P. A. , Glen, D. , Reynolds, R. C. , Israel, R. B., & Cox, R. W. (2016). Untangling the Relatedness among Correlations, Part I: Nonparametric Approaches to Inter‐Subject Correlation Analysis at the Group Level. NeuroImage, 142, 248–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, G. , Xiao, Y. , Taylor, P. A. , Riggins, T. , Geng, F. , & Redcay, E. (2019). Handling multiplicity in neuroimaging through Bayesian lenses with multilevel Modeling. Neuroinformatics. 10.1007/s12021-018-9409-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi, J. M. , Padmala, S. , & Pessoa, L. (2012). Impact of state anxiety on the interaction between threat monitoring and cognition. NeuroImage, 59(2), 1912–1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox, D. R. , Spjøtvoll, E. , Johansen, S. , van Zwet, W. R. , Bithell, J. F. , Barndorff‐Nielsen, O. , & Keuls, M. (1977). The role of significance tests. Scandinavian Journal of Statistics, 4(2), 49–70. [Google Scholar]
- Fox, A. S. , Oler, J. A. , Tromp, D. P. , Fudge, J. L. , & Kalin, N. H. (2015). Extending the amygdala in theories of threat processing. Trends in Neurosciences, 38(5), 319–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman, A. , & Carlin, J. B. (2014). Beyond power calculations: Assessing type S (sign) and type M (magnitude) errors. Perspectives on Psychological Science, 9(6):641–651. [DOI] [PubMed] [Google Scholar]
- Gelman, A. , Carlin, J. B. , Stern, H. S. , Dunson, D. B. , Vehtari, A. , & Rubin, D. B. (2014). Bayesian data analysis (3rd ed.). London: Chapman & Hall/CRC Press. [Google Scholar]
- Gelman, A. , Simpson, D. , & Betancourt, M. (2017). The prior can often only be understood in the context of the likelihood. Entropy, 19(10), 555. [Google Scholar]
- Gelman, A. , & Tuerlinckx, F. (2000). Type S error rates for classical and Bayesian single and multiple comparison procedures. Computational Statistics, 15, 373–390. [Google Scholar]
- Grupe, D. W. , & Nitschke, J. B. (2013). Uncertainty and anticipation in anxiety: An integrated neurobiological and psychological perspective. Nature Reviews Neuroscience, 14(7), 488–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffreys, W. H. , & Berger, J. O. (1992). Sharpening Ockham's razor on a Bayesian strop. American Scientist, 23(3):1259. [Google Scholar]
- Jenkinson, M. , Beckmann, C. F. , Behrens, T. E. , Woolrich, M. W. , & Smith, S. M. (2012). FSL. NeuroImage, 62, 782–790. [DOI] [PubMed] [Google Scholar]
- Kinnison, J. , Padmala, S. , Choi, J. M. , & Pessoa, L. (2012). Network analysis reveals increased integration during emotional and motivational processing. The Journal of Neuroscience, 32(24), 8361–8372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewandowski, D. , Kurowicka, D. , & Joe, H., 2009. Generating random correlation matrices based on vines and extended onion method. Journal of Multivariate Analysis, 100, 1989–2001. [Google Scholar]
- McElreath, R. (2016). Statistical rethinking: A Bayesian course with examples in R and Stan. London: Chapman & Hall/CRC Press. [Google Scholar]
- McMenamin, B. W. , Langeslag, S. J. E. , Sirbu, M., Padmala, S., & Pessoa, L. (2014). Network organization unfolds over time during periods of anxious anticipation. J Neurosci, 34, 11261–11273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pessoa, L. (2013). The cognitive‐emotional brain: From interactions to integration. Cambridge, MA: MIT Press. [Google Scholar]
- Pessoa, L. (2014). Understanding brain networks and brain organization. Physics of Life Reviews, 11(3), 400–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pessoa, L. (2017). A network model of the emotional brain. Trends in Cognitive Sciences, 21(5), 357–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team . (2018). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; https://www.r-project.org/ [Google Scholar]
- Stan Development Team , 2017. Stan modeling language users guide and reference manual, Version 2.17.0. Retrieved from: http://mc-stan.org
- Vehtari, A. , Gelman, A. , & Gabry, J. (2017). Practical Bayesian model evaluation using leave‐one‐out cross‐validation and WAIC. Statistics and Computing, 27(5), 1413–1432. [Google Scholar]
- Zalesky, A. , Fornito, A. , & Bullmore, E. T. (2010). Network‐based statistic: Identifying differences in brain networks. NeuroImage, 53, 1197–1207. [DOI] [PubMed] [Google Scholar]


