Abstract
It has been known for decades that head motion/other artifacts affect the blood oxygen level‐dependent signal. Recent recommendations predominantly focus on denoising resting state data, which may not apply to task data due to the different statistical relationships that exist between signal and noise sources. Several blind‐source denoising strategies (FIX and AROMA) and more standard motion parameter (MP) regression (0, 12, or 24 parameters) analyses were therefore compared across four sets of event‐related functional magnetic resonance imaging (erfMRI) and block‐design (bdfMRI) datasets collected with multiband 32‐ (repetition time [TR] = 460 ms) or older 12‐channel (TR = 2,000 ms) head coils. The amount of motion varied across coil designs and task types. Quality control plots indicated small to moderate relationships between head motion estimates and percent signal change in both signal and noise regions. Blind‐source denoising strategies eliminated signal as well as noise relative to MP24 regression; however, the undesired effects on signal depended both on algorithm (FIX > AROMA) and design (bdfMRI > erfMRI). Moreover, in contrast to previous results, there were minimal differences between MP12/24 and MP0 pipelines in both erfMRI and bdfMRI designs. MP12/24 pipelines were detrimental for a task with both longer block length (30 ± 5 s) and higher correlations between head MPs and design matrix. In summary, current results suggest that there does not appear to be a single denoising approach that is appropriate for all fMRI designs. However, even nonaggressive blind‐source denoising approaches appear to remove signal as well as noise from task‐related data at individual subject and group levels.
Keywords: artifacts, denoising, fMRI, head motion, signal‐to‐noise
1. INTRODUCTION
Although the exact mechanisms of the blood oxygen level‐dependent (BOLD) signal remain actively debated (Petzold & Murthy, 2011; Attwell et al., 2010), most functional magnetic resonance imaging (fMRI) studies attribute BOLD changes to glutamate‐mediated signaling in neurons/astrocytes and associated hemodynamic response. However, it has been known for decades (Friston, Williams, Howard, Frackowiak, & Turner, 1996) that fluctuations in the BOLD signal are also related to head motion, physiological noise, and other scanner artifacts (Power, Schlaggar, & Petersen, 2015; reviewed in Caballero‐Gaudes & Reynolds, 2017). Head motion is perhaps the largest single problem, reducing intersubject and intrasubject reliability (Lund, Norgaard, Rostrup, Rowe, & Paulson, 2005; Van Dijk, Sabuncu, & Buckner, 2012) and increasing signal variance (Bullmore et al., 1996; Friston et al., 1996; Power et al., 2014). Excessive head motion is especially prevalent in young, very old and neuropsychiatric samples (Fair et al., 2007; Greicius, 2008; Power et al., 2015), and exhibits a complex interaction with individual variability in functional organization that may partially be biologically based (i.e., trait) rather than artifactual (Siegel et al., 2016; Zeng et al., 2014).
Although prospective motion correction techniques, externally monitored techniques with and without real‐time feedback, and multiecho acquisition schemes have all been developed (Gonzalez‐Castillo et al., 2016; Maclaren, Herbst, Speck, & Zaitsev, 2013), retrospective correction algorithms remain the most prevalent techniques for mitigating the impact of motion artifacts on signal. Retrospective motion correction techniques typically occur in two distinct steps: motion detection and the subsequent correction of this motion using a rigid body transformation based on various cost functions (reviewed in detail in Johnstone et al., 2006; Oakes et al., 2005; Mayer, Franco, Ling, & Canive, 2007). The motion parameters (MPs) themselves are typically referred to as capturing “absolute” displacement from a reference image, whereas the N − (N − 1) derivative of each MP has been operationally defined as framewise displacement (FD; Power et al., 2014) or relative motion (Mayer et al., 2007). The six original MPs, their respective derivatives and squares (24 total) are frequently used as nuisance‐based regressors (i.e., denoising) to account for additional motion‐related variance from the time series (Power et al., 2014; Satterthwaite et al., 2013). However, motion affects fMRI measurements in a complex fashion for several seconds after the actual physical displacement occurs (Friston et al., 1996; Power et al., 2014). Therefore, other techniques for removing motion‐related variance, including “scrubbing” (i.e., the direct censoring or removing of individual images with high motion), scrubbing plus interpolation, and scrubbing plus band‐pass filtering and/or spike regression, have also been suggested (Power et al., 2015; Caballero‐Gaudes & Reynolds, 2017).
More sophisticated blind‐source separation techniques have also been applied to solely remove head motion artifacts (Pruim et al., 2015) or motion plus other physiological, hardware, or thermal noise sources from fMRI data, including multiband artifact (Burgess et al., 2016; Dong, Huang, Yang, Weng, & Wang, 2009; Griffanti et al., 2014; Salimi‐Khorshidi et al., 2014; Tohka et al., 2008). Most blind‐source approaches have utilized independent component analysis (ICA), which has been applied to both resting state and task‐related fMRI data (Calhoun, Adali, Pearlson, & Pekar, 2001; Smith et al., 2009). During ICA, a predetermined number of components are generated and subsequently labeled (manual or through classification) as belonging to an “artifact” or “signal” class. Artifact components are then regressed against the original time series to partial out associated variance. ICA procedures have been observed to denoise data at a level that is superior to nuisance‐based regression approaches (Kochiyama et al., 2005; Pruim et al., 2015), with inclusion of global signal estimates producing the best result in connectome‐style acquisitions (Burgess et al., 2016). These improved denoising results could be secondary to the fact that ICA approaches can regress out additional artifacts in the data other than those that are specific to head motion (Iacovella & Hasson, 2011). ICA‐based denoising techniques also reduce false positive classification relative to motion scrubbing (Middlebrooks et al., 2017) and improve group level statistical power potentially through denoising (Pruim et al., 2015) or by increasing correlation with the design matrix (Dong et al., 2009).
Importantly, the majority of recent studies have focused on the effects of denoising on resting state (rsfMRI) scans (Power et al., 2015) with a single recent publication on task data (Glasser et al., 2018). Importantly, the optimal strategy for reducing motion‐related variance and other artifacts may be dependent on task design (Johnstone et al., 2006), with different strategies potentially more appropriate for rsfMRI, block‐design (bdfMRI) and event‐related (erfMRI) tasks (Caballero‐Gaudes & Reynolds, 2017). Critically, the relationships between intrinsic neural activation (i.e., measured during rsfMRI) and head motion/physiological artifacts are much more difficult to quantify given the lack of an explicit model (i.e., design matrix) differentiating “signal” from noise (Power et al., 2014; Saad et al., 2012), and the potential relationship that exists between the two (i.e., respiratory‐related bulk head movement; Iacovella & Hasson, 2011). Head motion can either be correlated (i.e., time‐locked with stimuli), anticorrelated (i.e., time‐locked with “baseline” states) or independent of the primary regressors of interest in task‐based fMRI (Mayer et al., 2007), a relationship that may vary with stimulus duration. Moreover, the average (i.e., global) gray matter (GM) signal is also frequently correlated with the design matrix in task‐based fMRI (especially bdfMRI), which further complicates recent discussions regarding the removal of global signal in rsfMRI (Burgess et al., 2016; Power, Plitt, Laumann, & Martin, 2017). Thus, in contrast to previously discussed positive results (Glasser et al., 2018; Griffanti et al., 2014; Pruim et al., 2015), it is not surprising that several other studies have reported marginal or significant signal loss from various denoising approaches across a variety of different fMRI designs (Bright & Murphy, 2015; Pujol et al., 2014; Tohka et al., 2008).
The current experiment therefore examined the effects of MP nuisance‐based regression analyses (0, 12, or 24 parameters), motion only ICA denoising (Pruim et al., 2015) and more global ICA denoising approaches (Griffanti et al., 2014) on multiband, high temporal resolution (TR = 460 ms) erfMRI and bdfMRI data. Similar to previous studies (Dong et al., 2009; Johnstone et al., 2006), our primary variable of interest was a direct statistical comparison of percent signal change (PSC) values in brain regions with known signal (i.e., task‐related activations) and regions that typically exhibit artifacts (i.e., ventricles, white matter [WM], and edges) at the group level. This metric was primarily selected due to the simplicity in terms of interpreting significance of results compared to the complexity associated with interpreting other motion‐based metrics (Power et al., 2015). Based on previous studies (Kochiyama et al., 2005; Pruim et al., 2015), we predicted that ICA denoising techniques would outperform MP only nuisance‐based regression, resulting in higher statistical values in signal areas and variation in noise regions in task‐based fMRI data. We also predicted that erfMRI data would benefit more from denoising than bdfMRI (Johnstone et al., 2006). Secondary analyses examined the effect of denoising on single‐subject contrasts. Finally, given the time‐consuming nature of manual classification, we also determined the generalizability of classifiers derived from one design type to other fMRI tasks (e.g., bdfMRI, erfMRI, and rsfMRI).
2. METHODS
2.1. Participants
The primary dataset consisted of 46 healthy participants (28 males; mean age = 31.8 ± 7.4 years; mean education = 15.2 ± 1.9 years) collected during an erfMRI (AX Continuous Performance Test [AX‐CPT]) and rsfMRI paradigm on a 32‐channel coil with multiband capabilities (Ryman et al., 2019). Forty‐four of these subjects also completed a relatively short duration bdfMRI (multimodal attention task [MMAT]). Secondary replication and extension analyses were conducted on data from (a) an additional unique sample of 64 healthy participants (35 males; mean age = 29.33 ± 8.23 years) who completed the MMAT task using a 12‐channel coil (Mayer, Ryman, Hanlon, Dodd, & Ling, 2016) and (b) 30 adolescents (21 males; mean age = 14.23 ± 1.76 years) on the same 32‐channel coil using a bdfMRI task with longer block duration (CO2 challenge). All participants provided informed consent according to institutional guidelines at the University of New Mexico School of Medicine.
2.2. Task descriptions
An intermodal version of the AX‐CPT was used as our erfMRI design (Ryman et al., 2019). Briefly, participants were exposed to a continuous stream of letters that were presented in either the visual (i.e., the cues) or auditory (i.e., the probes) modality. Participants responded with their right index finger if the target sequence was completed (i.e., “yes” response) and with their right middle finger for all other cases (i.e., “no” response). Letter sequences were presented in a pseudorandom order, such that within each run target trials (AX) occurred with 70% frequency and each of the nontarget trials (AY, BX, and BY) occurred with 10% frequencies. A variable delay was used between the cue offset and probe onset (interstimulus interval: 2,760–3,680 ms), as well as between the probe offset and subsequent cue onset (intertrial interval: 3,790–4,980 ms) to decrease temporal expectations and allow better modeling of the hemodynamic response function (HRF). The design matrix was well‐conditioned with minimal evidence of collinearity.
Primary bdfMRI analyses were based on a previously published task with shorter block lengths (Mayer et al., 2016). All multisensory stimuli (cues and targets) were presented foveally and binaurally via a rear projection screen and headphones (head‐centered). Each block began with a multisensory (audiovisual) cue indicating the sensory modality for focused attention (“HEAR” = attend‐auditory; “LOOK” = attend‐visual; 300 ms duration). After 1,000 ms, cues were followed by a string of congruent or incongruent multisensory numeric stimuli (target words = “ONE,” “TWO,” or “THREE”; 300 ms duration) at either low (0.33 Hz; three trials per block) or high (0.83 Hz; six trials per block) rates of stimulus frequency over a 6,300 ms duration (entire block length = 7,600 ms). Participants were asked to maintain constant head and eye positioning (visual fixation on a centrally presented cross) and to respond with a right‐handed button press. The interblock interval varied between 3,900 and 5,740 ms. The design matrix was well‐conditioned with minimal evidence of collinearity.
These specific erfMRI and bdfMRI tasks, and associated contrasts, were selected primarily because of their wide use and evidence of replicability in the cognitive neuroscience literature, the robustness of activation with chosen contrasts, and the availability of selected task data across multiple coil and TR configurations.
2.3. Imaging acquisition and analyses
High‐resolution 5‐echo multiecho magnetization prepared rapid acquisition gradient echo (MPRAGE) T1‐weighted data (TR = 2,530 ms; echo times [TE] = 1.64, 3.5, 5.36, 7.22, and 9.08 ms; inversion time = 1,200 ms; flip angle = 7°; number of excitations [NEX] = 1; slice thickness = 1 mm; field of view [FOV] = 256 mm; matrix size = 256 × 256; isotropic voxels = 1 mm3) were collected for structural images on a 3T Siemens Trio Tim scanner for all tasks. Echo‐planar imaging (EPI) for the AX‐CPT, MMAT, rsfMRI, and CO2 challenge data were collected using a single‐shot, gradient‐echo echo‐planar pulse sequence (TR = 460 ms; TE = 29 ms; flip angle = 44°; multiband acceleration factor = 8; NEX = 1; slice thickness = 3 mm; FOV = 248 mm; matrix size = 82 × 82; resolution = 3.02 × 3.02 × 3.00 mm3 voxels). Fifty‐six interleaved transversal slices were selected to provide whole‐brain coverage. The first three images of each run were eliminated to account for T1 equilibrium effects. A single‐band reference image (SBREF) was also acquired to facilitate registration with the T1 image. Two EPI spin‐echo distortion mapping prescan sequences (TR = 7,220 ms; TE = 73 ms; flip angle = 90°; refocus flip angle = 180°; slice thickness = 3 mm; FOV = 248 mm; matrix size = 82 × 82; 56 interleaved slices; 3.02 × 3.02 × 3.00 mm3 voxels) with reversed phase encoding directions (anterior → posterior; posterior → anterior) were also collected to correct for susceptibility‐related artifacts.
For the 12‐channel data, a high‐resolution 5‐echo multiecho MPRAGE T1 sequence (TR = 2.53 s, 7° flip angle, NEX = 1, slice thickness = 1 mm, FOV = 256 mm, resolution = 256 × 256) was collected. EPIs were collected using a single‐shot, gradient‐echo echo‐planar pulse sequence (TR = 2,000 ms; TE = 29 ms; flip angle = 75°; FOV = 240 mm; matrix size = 64 × 64). Foam padding and paper tape were used with all participants across 12‐ and 32‐channel coils to prophylactically reduce the likelihood of head motion.
Preprocessing steps for functional data were conducted individually for each run (Figure 1). Anomalous time series data were first identified and replaced based on values from the previous and subsequent image using Analysis of Functional NeuroImages's (AFNI) despiking protocol (Cox, 1996). All timeseries data were then temporally interpolated to the first slice to account for differences in slice acquisition. Data were then spatially registered in two‐ (2dImReg) and three‐dimensional (3dvolreg) space using AFNI software programs to the SBREF image to reduce the effects of head motion. The initial six motion regressors (three rotational and three translational) were directly estimated from the rigid registration of each image to SBREF followed by computation of derivatives and squares. Susceptibility‐induced field distortion was subsequently estimated and corrected using FMRIB Software Library (FSL) Topup (Andersson, Skare, & Ashburner, 2003; Smith et al., 2004). The next set of preprocessing steps varied based on the different denoising protocols described in detail below (Figure 1).
Figure 1.
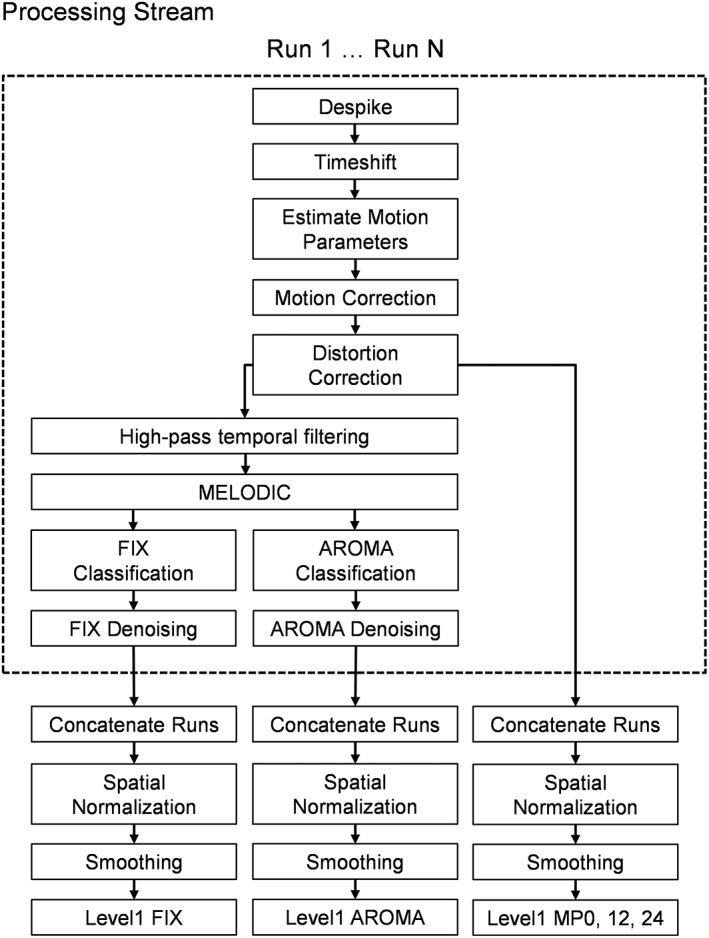
The individual steps within the preprocessing, denoising, and subject‐level (Level 1) analyses for the FIX, AROMA, and motion parameter (MP; 0, 12, or 24 parameters) pipelines utilized in the current study. Based on current published recommendations, each run for the FIX and AROMA pipelines was individually denoised (denoted by dashed box in figure)
After each individual denoising pipeline, each run of task data was then concatenated, converted to standard stereotaxic coordinate space (Talairach & Tournoux, 1988) using a nonlinear algorithm (AFNI 3dQwarp; template = TT_N27) and spatially blurred using a 6‐mm Gaussian full‐width at half‐maximum filter.
2.4. FIX denoising
Individual runs of preprocessed AX‐CPT and MMAT data were prepared for FSL FIX according to the FSL documentation (Griffanti et al., 2014; Salimi‐Khorshidi et al., 2014) to prevent signal intensity shifts between runs affecting the time series. Data were high‐pass filtered (cutoff period: 100.0 s) prior to running MELODIC. Following MELODIC, the resulting components (ICAall) from 20 individuals (i.e., a single run from the AX‐CPT task) were manually classified as noise (ICAnoi) or signal (ICAsig) by two independent raters based on previously described criteria (Salimi‐Khorshidi et al., 2014). Any discrepancies between the two raters were resolved by a third party, with the final results subsequently used to train the classifier.
A secondary aim of the study was to determine whether classification accuracy depended on experimental design (erfMRI vs. bdfMRI vs. rsfMRI) or whether classifiers generalized across designs. A completely independent set of 20 AX‐CPT, 21 MMAT, and 20 resting state runs were therefore manually classified using the same methodology as a “gold standard” from which to determine classification accuracy for each task. The classification probability output of FIX requires a threshold to provide a binary classification into noise or signal. To determine an appropriate threshold, our training set was evaluated with the FIX leave‐one‐out accuracy testing which charts the true positive rate (TPR) and true negative rate (TNR) at several thresholds. A threshold of 20% for classifying noise components was selected as the best balance of TPR and TNR using previously described methodology (Griffanti et al., 2014).
Following classification, motion regressors in the FIX pipeline were high‐pass filtered to match the imaging data. MPs were then mean‐centered and variance normalized. Next, each run of the task data was denoised with the FIX “soft‐clean” method, a three‐step method to remove the variance unique to the noise components while attempting to avoid the removal of variance that may be shared with signal components (Griffanti et al., 2014). The first step of the soft‐clean method regresses out 24 different MPs corresponding to the six rigid body adjustments, their derivatives, and their squares (C mot) from the task data (Y all). Importantly, the constant term (β0) is eliminated from the model to maintain scale (Y res = Y all − C mot). Similarly, MPs were also regressed against each individual component, again excluding β0 from the model (ICAres = ICAall − C mot). To estimate the contribution of all components, the residualized task data was modeled against the residualized component time series to acquire beta weights (Yres = β0 + βICAres). Finally, the sums of the weighted noise components were subtracted from the residualized task data to remove the unique contribution of the artifact components and derive the final denoised data (Yclean = Yres − ∑ βICAnoi).
2.5. AROMA denoising
To make ICA denoising pipelines comparable, preprocessed AX‐CPT and MMAT individual run data were denoised with the procedure recommended in the AROMA manual (nonaggressive option) using the MELODIC data from the first step of the FIX processing. This therefore included high‐pass filtering of the data. The AROMA denoising procedure automates the selection of motion‐related artifacts by assessing four features of each component: high‐frequency content, correlation to the MPs, edge fraction, and cerebrospinal fluid (CSF) fraction (Pruim et al., 2015). A component exceeding either a CSF fraction >10%, a high‐frequency content >35%, or a combined maximum MP correlation/edge fraction threshold was subsequently classified as a noise artifact by the AROMA algorithm. Noise component time series were subsequently filtered from the data using FSL fsl_regfilt based on the following algorithm (Ydenoised = Y − Xnβn).
2.6. Regression‐based denoising approaches
Our MP pipelines directly regressed motion from task data using a general linear model (ordinary least squares). Specifically, either 0 MPs (baseline model: MP0), 6 MPs and their derivatives (MP12), or 6 MPs, their derivatives and their squares (MP24) were included as nuisance regressors in a general linear model at the subject level for each of the various tasks.
2.7. Task comparisons and primary outcome variables
Following each denoising pipeline, a voxel‐wise deconvolution analysis (AFNI's 3dDeconvolve) generated a single HRF for each trial type relative to the baseline state. Error trials were modeled separately to eliminate error variance (Mayer et al., 2012). For our erfMRI AX‐CPT task, the HRF was modeled for the first 13.8 s following onset of cues or probes. MMAT HRFs were based on the first 22.08 s following block onset. Based on our previous publications (Mayer et al., 2016; Ryman et al., 2019), PSC was calculated by summing all beta coefficients between 3.68 and 5.06 s (AX‐CPT) or 4.14 and 8.28 s (MMAT) post‐onset, corresponding to the peak period of the HRF, then dividing by the average of the constant term across the individual runs.
The primary outcome variable was a t‐statistic resulting from pairwise PSC comparisons at the group level. This metric informs as to whether differences in the denoising pipelines were statistically meaningful and robust enough to be detected using standard thresholding criteria. Secondary analyses examined whether denoising pipelines differences were driven by changes in the mean or variance of PSC. The latter were further quantified with Pitman–Morgan tests, which specifically test for differences in paired samples based on the bivariate normal distribution. Importantly, denoising algorithms may have different effects in noise regions such as the ventricles or edge of the brain (reducing amplitude and/or variance) versus task‐related activations (ideally reducing only variance). All voxel‐wise results were corrected for multiple comparisons at p < .05 based on 10,000 Monte Carlo Simulations (parametric value <0.001 and cluster threshold = 1,664 μL) using the spherical autocorrelation correction in AFNI (Cox, Chen, Glen, Reynolds, & Taylor, 2017). More liberal thresholding (i.e., voxels below family‐wise error (FWE)‐corrected threshold values) are presented in figures solely to provide a more nuanced depiction of potential pipeline differences.
Quality control PSC plots (QC PSC) plotted mean FD and absolute displacement relative to PSC values in both signal and noise regions of interest (ROIs; Power et al., 2015). GM, WM, and CSF tissue masks were generated using SPM (v12) and the TT_N27 template (i.e., our registration target) from AFNI (see Supplemental Methods). The primary sensorimotor cortex (SMC) and supplementary motor area (SMA) were empirically defined as signal regions based all tasks/trials commonly involving a button press. The ventrolateral prefrontal cortex (VLPFC) was defined using a 12‐mm sphere (Talairach coordinates: 49, 28, and 10) and has been shown to be active across all selected contrasts (Dolcos, Wang, & Mather, 2014; Mayer et al., 2016; Mayer, Franco, Canive, & Harrington, 2009; Ryman et al., 2019). Thus, any potential effects on signal should be greatest within motor regions with differential motor requirements (MMAT task; frequency contrast) whereas the VLPFC should be more sensitive for cognitive contrasts (AX‐CPT: AY vs. AX trials; MMAT: incongruent vs. congruent trials) and frequency effects.
Secondary analyses examined the impact of various denoising pipelines on t‐statistics at the individual subject‐level and how this relationship was moderated by head motion. For subject‐level t‐statistics, the numerator represents a comparison of the magnitude of beta coefficients associated with different conditions of interest (i.e., incongruent vs. congruent trials; high vs. low frequency trials) whereas the denominator of the t‐statistic represents trial‐by‐trial variability. Subject‐level t‐statistics were averaged across the same three signal (SMC, SMA, and VLPFC) and noise (edge, CSF, and WM) ROI used in group‐level comparisons, and plotted against each other based on the different denoising pipelines.
3. RESULTS
3.1. Classification accuracy as a function of design
Our first objective was to determine whether results from a classifier trained on one design type (here erfMRI) generalized to other experimental designs (bdfMRI and rsfMRI) using identical acquisition parameters. Results (Table 1) from the classifier on the erfMRI AX‐CPT data indicated a mean TPR of 99.2% and a mean TNR of 97.5% at the selected threshold of 20% across our manually classified testing runs. Results from the classification of the bdfMRI MMAT task were similar with a mean TPR of 99.5% and a mean TNR of 96.9%. Classification accuracy was also high for rsfMRI data (TPR = 99.3%; TNR = 95.3%). An average of 77.43% of all components (range 62.32–94.87%) from the FIX pipeline were classified as noise across both runs and subjects for the erfMRI, 78.23% (range 63.51–95.28%) for the bdfMRI task and 79.34% (range 65.22–92.47%) for the rsfMRI task (see Supplemental Materials for actual component numbers). In summary, current results suggest that artifacts and signal components are relatively consistent across rsfMRI, erfMRI, and bdfMRI designs when the same scanning parameters are applied. Thus, it may only be necessary to train a classifier once for a single acquisition sequence and generalize this classifier to other design types.
Table 1.
Single run FIX classification accuracies across a range of thresholds. Values are presented as mean across tested datasets. Accuracies are given as mean of signal (TPR) and noise (TNR) components correctly classified when compared to manual classification
| Threshold | 1 | 2 | 5 | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|---|
| AX‐CPT (remainder of runs) | ||||||||
| TPR | 100.0 | 100.0 | 100.0 | 100.0 | 99.2 | 98.7 | 97.5 | 95.3 |
| TNR | 93.9 | 94.7 | 95.7 | 96.6 | 97.5 | 98.0 | 98.5 | 98.8 |
| MMAT | ||||||||
| TPR | 100.0 | 100.0 | 100.0 | 100.0 | 99.5 | 98.7 | 97.4 | 97.4 |
| TNR | 93.3 | 93.7 | 94.7 | 95.8 | 96.9 | 97.9 | 98.6 | 98.8 |
| Resting state | ||||||||
| TPR | 100.0 | 100.0 | 100.0 | 100.0 | 99.3 | 99.0 | 99.0 | 98.3 |
| TNR | 90.0 | 91.2 | 92.8 | 94.1 | 95.3 | 96.5 | 97.0 | 97.3 |
Note. The AX‐CPT task results were validated on a different set of participants than those used to train classifier.
Abbreviations: AX‐CPT, AX Continuous Performance Test; MMAT, multimodal attention task; TNR, true negative rate; TPR, true positive rate.
3.2. Denoising effects in erfMRI design
No clusters survived FWE correction during paired comparisons of MP24 versus MP0 (Figure 2a) or MP24 versus MP12 (Supplemental Figure S2A) during the AX‐CPT task. Uncorrected data (i.e., all voxels p < .05) are displayed in figures to provide a more nuanced view of pipeline differences. Quantitative comparisons indicated a reduced variance mostly in edge areas for MP24 versus MP0 suggestive of improvement in denoising in noise regions with additional MPs. Not surprisingly, the PSC density functions (Figure 2a) from the MP24 and MP0 pipelines were predominantly overlapping in both signal and noise ROI.
Figure 2.
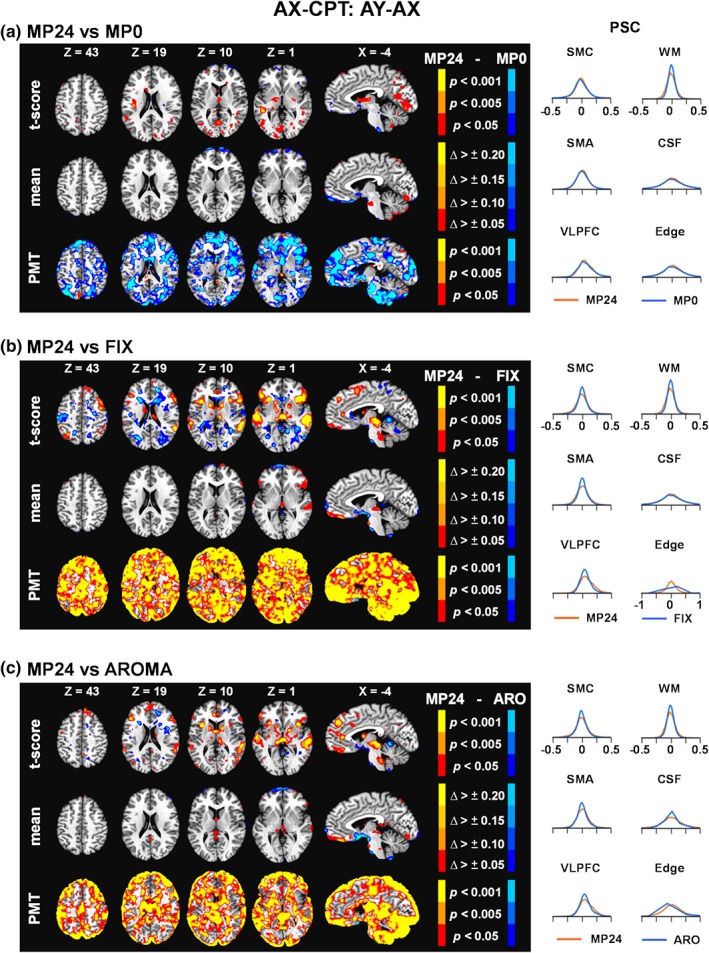
Results comparing the 24 motion parameter (MP24) pipeline relative to the 0 motion parameter pipeline (MP0; Panel a), the FIX pipeline (Panel b), and the AROMA pipeline (ARO; Panel c) for the AY–AX trial contrast of the AX continuous performance test (AX‐CPT). For each panel, the first row corresponds to the paired t‐score results comparing percent signal change (PSC) values across pipelines at the group level, the second row average change (Δ) scores in the mean, and the third row the Pitman–Morgan test (PMT) results. Axial (Z) and sagittal (X) slices correspond to the Talairach atlas. All pipeline comparisons are fully corrected for family wise error for formal reporting of results in the paper. In contrast, AX‐CPT results are presented at multiple uncorrected p values (.05 = red or dark blue coloring; .005 = dark orange or light blue coloring; .001 = yellow or cyan coloring) in the figure to provide a more nuanced view of potential pipeline differences. The magnitude of mean change values across pipelines are also represented with various color coding (Δ > ±0.05 = red or dark blue coloring; Δ > ±0.10 = dark orange or navy blue; Δ > ±0.15 = dark yellow or light blue; Δ > ±0.20 = yellow or cyan). For all panels, greater MP24 values are always depicted with warm colors. The right side of each panel presents density plots for PSC values within a priori selected regions of interest (see Supplemental Figure S1), predominantly corresponding to either task‐related signal (SMC, sensorimotor cortex; SMA, supplementary motor area; VLPFC, ventrolateral prefrontal cortex) or artifacts (WM, white matter; CSF, cerebrospinal fluid; Edge, perimeter of brain mask). Density plots are color‐coded based on the direction of subtraction of pipelines (i.e., MP24 values always plotted in red) in the left side of the panels [Color figure can be viewed at http://wileyonlinelibrary.com]
To maximize consistency across comparisons, data from the MP24 pipeline results were next compared to FIX and AROMA pipeline results for the AX‐CPT task. Results indicated that PSC values were significantly higher following FWE corrections within the bilateral dorsolateral prefrontal cortex (BA 9), anterior insula/VLPFC (BAs 13/47), auditory cortex (BAs 21/22), and the thalamus for MP24 relative to FIX pipeline (Figure 2b). Importantly, several of these regions are commonly activated during reactive cognitive control tasks (Braver, 2012) or corresponded to the sensory modality of the auditory target (i.e., signal regions). A cluster of significantly lower PSC for MP24 relative to FIX was present in the right parahippocampal gyrus (BA 19). Similarly, the MP24 pipeline resulted in significantly higher PSC in the right auditory cortex (BAs 21/22) and thalamus when compared to AROMA (Figure 2c), with evidence of increased signal (i.e., subthreshold) also present in the bilateral anterior insula/VLPFC and left auditory cortex. Quantitative assessment indicated that PSC variance was increased for MP24 relative to AROMA pipeline primarily around volume edges, with FIX showing similar but more global reductions in variance relative to the MP24 pipeline across the entire brain. Both FIX and AROMA denoising resulted in a more peaked PSC density distribution within signal areas whereas variable effects were observed in noise ROI (Figure 2b,c). Signal loss is most evident within the VLPFC, where a clear leftward shift is observed in the distribution function comparing AY relative to AX trials.
In summary, in contrast to previous results (Johnstone et al., 2006), current results indicated statistically similar performance regardless of whether 0, 12, or 24 MPs were utilized to remove artifact during an erfMRI task. Moreover, utilization of various ICA approaches (FIX and AROMA) resulted in small (mean) but statistically significant decreases in PSC (t‐statistics) in task activated regions as well as significant reductions in the variance for both task‐activated and noise (greater reduction) regions.
3.3. Denoising effects in bdfMRI design
Similar to erfMRI, no clusters survived FWE correction during voxel‐wise paired comparisons of MP24 versus MP0 or MP24 versus MP12 for either the cognitive (congruent vs. incongruent; Figure 3a and Supplemental Figure S2B) or frequency (high frequency vs. low frequency; Figure 4a and Supplemental Figure S2C) contrasts. PSC density functions were also mostly overlapping across the three different MP pipelines. Quantitatively, the variance was again consistently lower in the volume edge area for the MP24 relative to MP0 pipeline for the frequency contrast. However, the cognitive task, results were more mixed with both increased and decreased variance for the MP24 relative to MP0 pipeline. As a result, FIX and AROMA pipelines were again compared only to MP24 pipeline.
Figure 3.
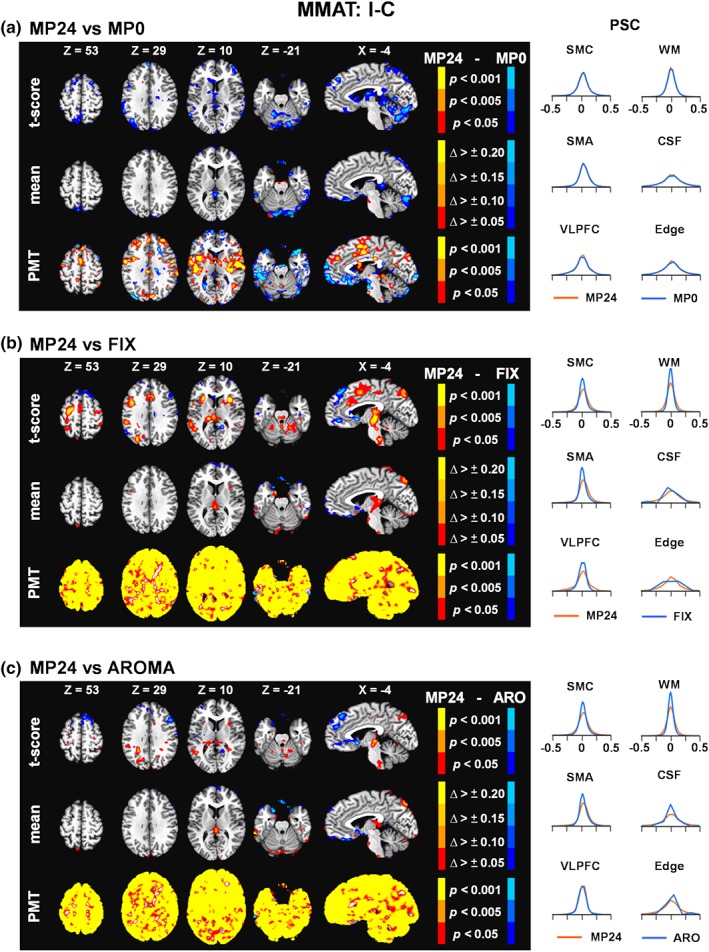
Results comparing the 24 motion parameter (MP24) pipeline relative to the MP0 (Panel a), the FIX pipeline (Panel b), and the AROMA pipeline (ARO; Panel c) for the incongruent minus congruent (I − C) trial contrast of the multimodal attention task at the group level (MMAT). The selected axial (Z) and sagittal (X) slices from the Talairach atlas were changed to best represent data for this contrast. However, all other aspects of the figure are identical to Figure 2. Δ, change; CSF, cerebrospinal fluid; Edge, perimeter of brain mask; PMT, Pitman‐Morgan test; PSC, percent signal change; SMA, supplementary motor area; SMC, sensorimotor cortex; VLPFC, ventrolateral prefrontal cortex; WM, white matter [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 4.
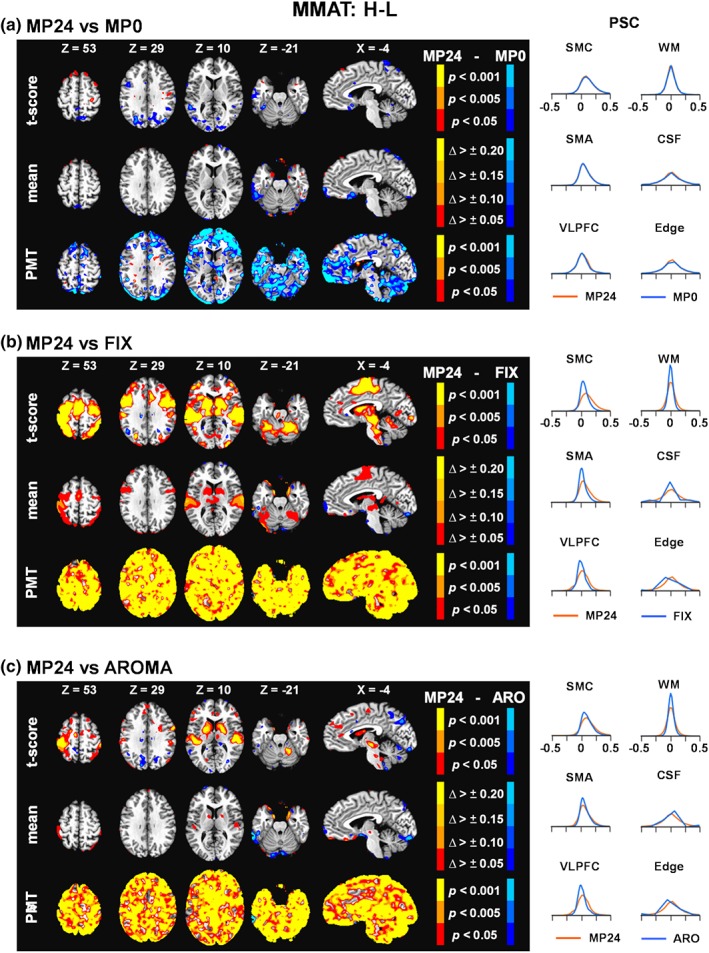
Results comparing the 24 motion parameter (MP24) pipeline relative to the MP0 (Panel a), the FIX pipeline (Panel b), and the AROMA pipeline (ARO; Panel c) for the high minus low (H − L) frequency trial contrast of the multimodal attention task at the group level (MMAT). The selected axial (Z) and sagittal (X) slices from the Talairach atlas were changed to best represent data for this contrast. However, all other aspects of the figure are identical to Figure 2. Δ, change; CSF, cerebrospinal fluid; Edge, perimeter of brain mask; PMT, Pitman‐Morgan test; PSC, percent signal change; SMA, supplementary motor area; SMC, sensorimotor cortex; VLPFC, ventrolateral prefrontal cortex; WM, white matter [Color figure can be viewed at http://wileyonlinelibrary.com]
MP24 PSC values were consistently higher relative to FIX following FWE corrections within the cognitive control network during congruent versus incongruent contrasts (Figure 3b) and within sensory and motor areas when examining effects associated with stimulus frequency (Figure 4b). Specifically, a single cluster of significantly higher PSC was present in the red nucleus for the cognitive control contrast for MP24 relative to FIX (Figure 3b, present in X = −4). Statistically significant increased PSC was observed in the medial frontal gyri (BA 6), anterior cingulate gyrus (BAs 24/32), bilateral primary motor cortex (BAs 3/6), auditory cortex (BAs 22/41), visual cortex (BAs 17–19), bilateral putamen and thalamus, and Lobule VI of the cerebellum for the MP24 relative to FIX pipelines.
There were no statistically significant differences between the AROMA and MP24 pipelines during the cognitive control contrast (Figure 3c). However, the MP24 pipeline was associated with significantly higher PSC relative to the AROMA pipeline (Figure 4c) within the bilateral auditory cortex (BAs 22/41), left primary motor cortex (BAs 3/40), and putamen and lentiform nucleus for high relative to low frequency stimuli. A quantitative assessment of images and their underlying distributions showed widespread, increased variance of the MP24 PSC relative to both FIX and AROMA. Reduction in the mean amplitude of PSC was also more evident for the stimulus frequency relative to cognitive control contrasts for both FIX and AROMA pipelines, and corresponded to regions where significant statistical differences relative to the MP24 pipeline were detected. Finally, the VLPFC PSC density functions were shifted left for cognitive contrasts whereas the SMC and SMA were shifted left for stimulus frequency contrasts for the FIX (larger shift present in most ROI) and AROMA (smaller shift only present in certain ROI) pipelines (Figures 3b,c and 4b,c).
3.4. QC PSC results
The QC PSC plots comparing mean FD with PSC data indicated a minimal relationship between motion and noise ROI (r = .02) in the minimally denoised (MP0) pipeline for the AX‐CPT data (Figure 5a). A positive but relatively weak relationship (small effect size) was also observed between mean FD and PSC in signal ROI (r = .12) for MP0, which was subsequently reduced or completely eliminated following the various denoising pipelines (MP12, MP24, FIX, and AROMA). In general, the QC PSC plots indicated that stronger relationships may exist between FD and noise ROI in the minimally denoised (MP0) pipeline for both the cognitive (I − C; r = −.17) and stimulus frequency (H − L; r = .18) contrasts for the bdfMRI data. Somewhat surprisingly, this relationship was variably affected by the denoising pipelines, with a reduction in the correlation for the H − L contrast whereas AROMA and FIX increased the correlation for the I − C contrast. The strength of the relationship between motion and signal ROI varied as a function of contrast in the MP0 pipeline (I − C: r = −.22; H − L: r = .09) and followed the same pattern in terms of an increased (FIX and AROMA for I − C) or reduced (all pipelines for H − L) correlation following denoising. These results were largely the same when absolute displacement was compared with PSC data (Supplementary Figure 3).
Figure 5.
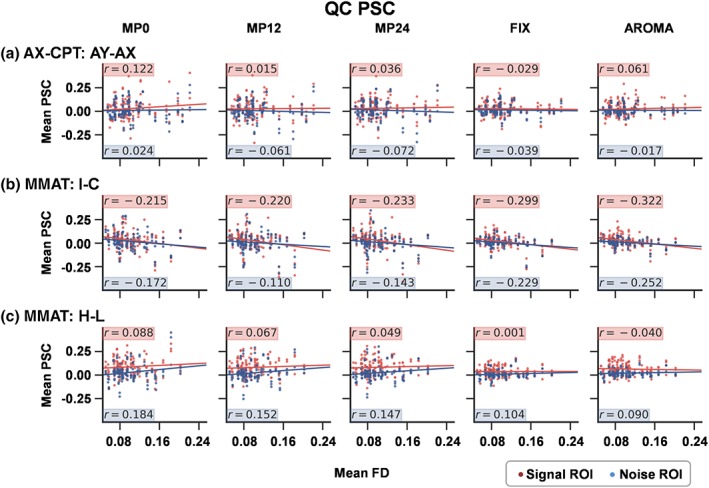
Quality control (QC) percent signal change (PSC) plots for the event‐related functional magnetic resonance imaging (fMRI) AY–AX contrast (Panel a) and block‐design fMRI incongruent − congruent (I − C; Panel b) and high − low (H − L; Panel c) contrasts for the 0 (MP0), 12 (MP12), and 24 (MP24) motion parameter, FIX, and AROMA pipelines. Each plot expresses the relationship between mean framewise displacement (FD) and PSC separately for both signal (red dots/highlighting) and noise (blue dots/highlighting) regions of interest (ROI; see Supplemental Figure S1) across all participants. The magnitude of the relationship is expressed by the correlation coefficient (r) and graphically depicted with a linear regression line [Color figure can be viewed at http://wileyonlinelibrary.com]
In summary, current results showed minimal differences at the group level for the inclusion of either 12 or 24 MPs in a regression model relative to no regressors. Similar to erfMRI findings, the use of two denoising algorithms (FIX and AROMA) eliminated signal as well as noise during our bdfMRI task, with the amount of signal loss being largest during the FIX pipeline. QC PSC plots indicated complex relationships between head motion and PSC values in both noise and signal regions, which were variably affected by the different denoising algorithms.
3.4.1. Potential confounding effects from estimation of constant coefficient
Our principle analyses compared various denoising algorithms using PSC as the dependent variable as is typically performed in the majority of task‐related analyses reported in the literature. However, the calculation of PSC depends not only on the magnitude of the beta coefficients corresponding to task regressors (PSC numerator), but also on the magnitude of the constant coefficient (PSC denominator). To ensure that the various denoising algorithms were not differentially affecting baseline calculations, analyses were repeated across erfMRI and bdfMRI designs utilizing the baseline coefficient as the dependent variable rather than PSC. Results (Supplemental Figure S4) indicated significant differences (i.e., surviving FWE correction) in the baseline coefficient during MP24 versus FIX and MP24 versus AROMA comparisons around the edge of the brain for both erfMRI and bdfMRI designs. In contrast, there were no significant clusters that survived following false positive correction in the MP24 versus MP0 comparisons. The edge regions are prone to partial voluming effects, and are known to be particularly affected by head motion (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012). Importantly, these same regions also exhibited higher PSC standard deviation (SD) for the MP24 pipeline (see Figures 2, 3, 4), further highlighting the potential benefits that ICA‐based denoising algorithms have in these regions. However, there were no significant differences in baseline coefficients within signal regions, minimizing the likelihood that a differential estimate of baseline coefficients explains our findings of signal loss at the group level.
3.4.2. Effects of denoising pipelines on single‐subject statistical values
Previous results focused on the effects of denoising pipelines on group level statistics. However, the methods and the metrics for measuring the efficacy of denoising strategies are actively debated and may vary across individuals due to their relative degree of motion (Ciric et al., 2017; Power et al., 2015). We therefore examined how denoising pipelines differentially affected single‐subject statistics by directly plotting t values from the congruent versus incongruent and high versus low stimulus frequency contrasts across the tested pipelines. Equivalent performance across the various denoising pipelines should theoretically result in an X = Y reference line on subject‐level t‐statistics (see Figure 6). Participants were further divided into three groups based on their mean FD. Results were collapsed across the three signal and noise ROI utilized for presenting group level results.
Figure 6.
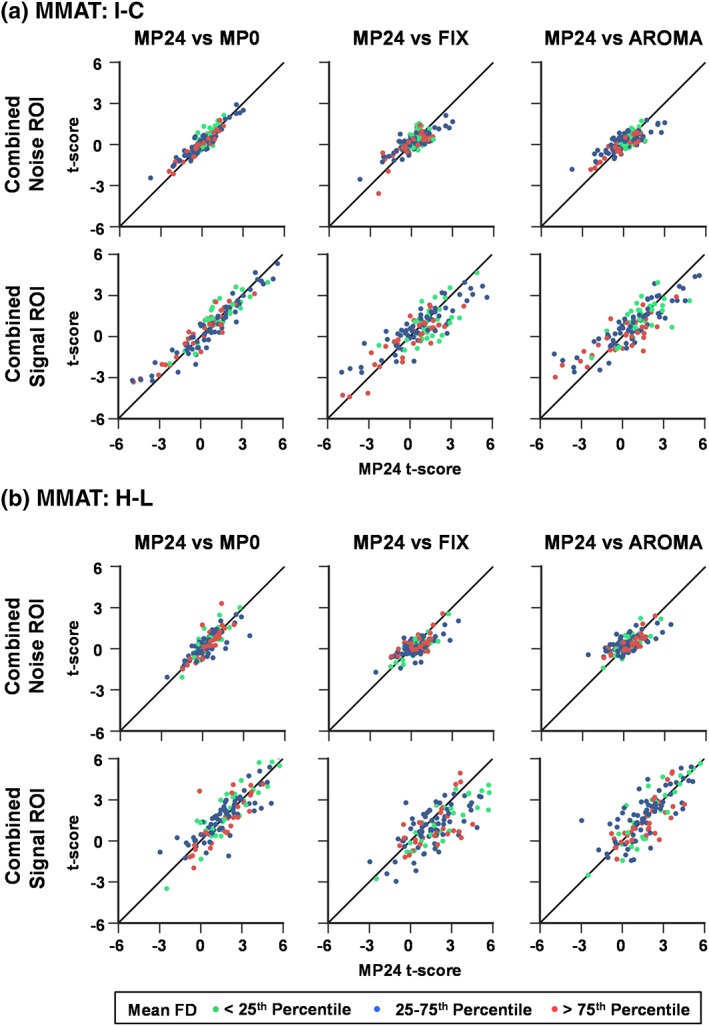
Results comparing subject‐level t‐scores of the 24 motion parameter (MP24; x axis) pipeline relative to the MP0, FIX, and AROMA pipelines (y axis) for the cognitive (incongruent [I] − congruent [C]; Panel a) and frequency (high [H] − low [L]; Panel b) contrasts of block‐design functional magnetic resonance imaging. The solid black line represents the X = Y reference line, which should be the expected pattern if the denoising pipelines resulted in equivalent t statistics. Participant data are plotted across the three signal (sensorimotor cortex, supplementary motor area, and ventrolateral prefrontal cortex) and noise (white matter, CSF, and edge) ROI within each individual panel (each participant is represented by three points). Participants are divided into three groups based on mean framewise displacement (FD) from the multimodal attention task (MMAT) task. Participants with mean FD below the 25th percentile are plotted in green, those between the 25th and 75th percentile are plotted in blue, and those above the 75th percentile are plotted in red. Results indicated that the FIX pipeline resulted in signal loss relative to the MP24 pipeline (i.e., rightward shift of points from the reference line), which was most evident in signal regions and for the frequency contrast [Color figure can be viewed at http://wileyonlinelibrary.com]
The noise ROI followed the expected X = Y pattern, with minimal effects from the different denoising pipelines and generally decreased scatter around the reference line. These results could potentially be due to reduced variance in the t‐statistics for noise regions (i.e., the t‐statistic is expected to approximate the null distribution in noise regions during task contrasts). In contrast, the FIX pipeline resulted in reduced t‐statistic values relative to the MP24 pipeline (i.e., rightward shift of points from the reference line) in signal ROI, which was greater for the frequency (large shift) relative to the congruency (smaller shift) contrast. Increased variability in data scatter around the reference line was also evident for signal ROI, although this did not appear to be related to the individual's degree of head motion as measured by mean FD. In contrast to group level results, there were minimal discernable differences in terms of deviation from the reference line between the MP24 and AROMA pipelines.
3.5. Replication and extension of motion parameter denoising in bdfMRI
In contrast to previous work (Johnstone et al., 2006), current data provide no clear evidence of detriments or advantages for motion‐based regressors as part of standard denoising protocols in erfMRI relative to bdfMRI designs. To ensure that current results were not limited to the associated factors of increased temporal resolution, multiband factor, and/or head‐coil diameter used in newer sequences, the MP0 and MP24 nuisance regressor pipelines were repeated on a dataset of 64 healthy controls who performed an identical bdfMRI task using a standard 12‐channel coil without multiband acceleration and TR = 2,000 ms (Mayer et al., 2016).
The inner diameter of the Siemens 32‐channel head coil is known to be much smaller than the 12‐channel coil. Therefore, it was not surprising that FD was significantly greater for the 12‐ relative to 32‐channel cohort (t 116.5 = 5.6; p < .001), even when FD was corrected for differences in TR acquisition time (see Supplemental Results). Similar to our principal analyses, the cognitive contrast resulted in a single significant cluster of higher PSC in right cingulate gyrus for MP0 relative to MP24 (Supplemental Figure S5A) whereas the comparison of MP24 to MP0 for the sensory contrast was nonsignificant for the 12‐channel/slower TR data (Supplemental Figure S5B). A quantitative assessment of images again showed the expected decrease in the variance of PSC for the MP24 relative to MP0 pipeline primarily around brain edges. These findings therefore represent either a full (MP0 vs. MP12) or partial replication (MP0 vs. MP24) of the motion regression analyses across two independent datasets with different TRs and head coil configurations.
Next, we considered whether the differences between previous and current findings could result from the correlation structure between the design matrix and MPs. The overall design matrix (i.e., all trial types) from each erfMRI and bdfMRI task across both 12‐ and 32‐channel coils was therefore correlated with each of the primary six motion regressors (Table 2). The mean correlation across the six motion regressors in our bdfMRI was 0.07 (SD = 0.02; maximum = 0.11), with a similar value observed for our erfMRI task (mean = 0.04; SD = 0.02; maximum = 0.07). Thus, the magnitude of correlation between task and motion regressors in both our erfMRI and bdfMRI designs was similar to previously reported erfMRI (mean = 0.09; SD = 0.02; maximum = 0.13) designs (Johnstone et al., 2006), whereas the correlation was much larger in previously reported bdfMRI (mean = 0.22; SD = 0.06; maximum = 0.36) designs (Johnstone et al., 2006). Correlations between the design matrix and FD were of decreased magnitude relative to absolute displacement, and also similar in magnitude across erfMRI and bdfMRI designs.
Table 2.
Correlation of design matrix with the mean of translational and rotation MP for both absolute and framewise displacement
| Absolute displacement | Framewise displacement | ||||||
|---|---|---|---|---|---|---|---|
| Source | Design | Mean | SD | Max | Mean | SD | Max |
| Johnstone et al. (2006) | erfMRI | 0.09 | 0.02 | 0.13 | – | – | – |
| AX‐CPT 32‐ch | erfMRI | 0.04 | 0.02 | 0.07 | 0.01 | 0.01 | 0.03 |
| Johnstone et al. (2006) | bdfMRI | 0.22 | 0.06 | 0.36 | – | – | – |
| MMAT 32‐channel | bdfMRI | 0.07 | 0.02 | 0.11 | 0.02 | 0.01 | 0.04 |
| MMAT 12‐channel | bdfMRI | 0.10 | 0.02 | 0.14 | 0.04 | 0.01 | 0.07 |
| CO2 32‐channel | bdfMRI | 0.25 | 0.14 | 0.71 | 0.02 | 0.01 | 0.04 |
Abbreviations: AX‐CPT, AX Continuous Performance Test; bdfMRI/erfMRI, block‐design/event‐related functional magnetic resonance imaging; CO2, CO2 challenge; Max: Maximum; MMAT, multimodal attention task; SD, standard deviation.
Another potential difference between current and previous findings was the shorter block length used in our bdfMRI design. We therefore examined the effects of motion regressor denoising on an additional dataset of 30 healthy adolescents during an extended (block length = 35 s) inhalation of a 5% CO2 gas mixture relative to room air (block length = 30 ± 5 s). These data were collected using the same multiband sequence and were preprocessed identically to the primary datasets for nuisance‐based MP regression pipelines only. Results following FWE correction indicated reduced PSC for MP24 relative to MP0 within the bilateral precentral gyri (BAs 4/43), postcentral gyri (BAs 2/3), medial frontal gyri (BA 6), the inferior parietal lobule (BA 40), middle frontal gyri (BA 9), insula (BA 13), and basal ganglia (Figure 7a). The MP12 pipeline also indicated statistically significant increased signal in several regions relative to MP24 (Figure 7b). QC PSC plots indicated a similar magnitude in relationship between mean FD and PSC in signal/noise ROI (Figure 7c) relative to the shorter block task (MMAT; Figure 5b, c), with minimal effect of MP12 and MP24 on the magnitude of the relationship. However, in contrast to the shorter MMAT task, the mean correlation between the CO2 challenge task and motion regressors was much higher (r = .25; SD = 0.14; maximum = 0.71).
Figure 7.
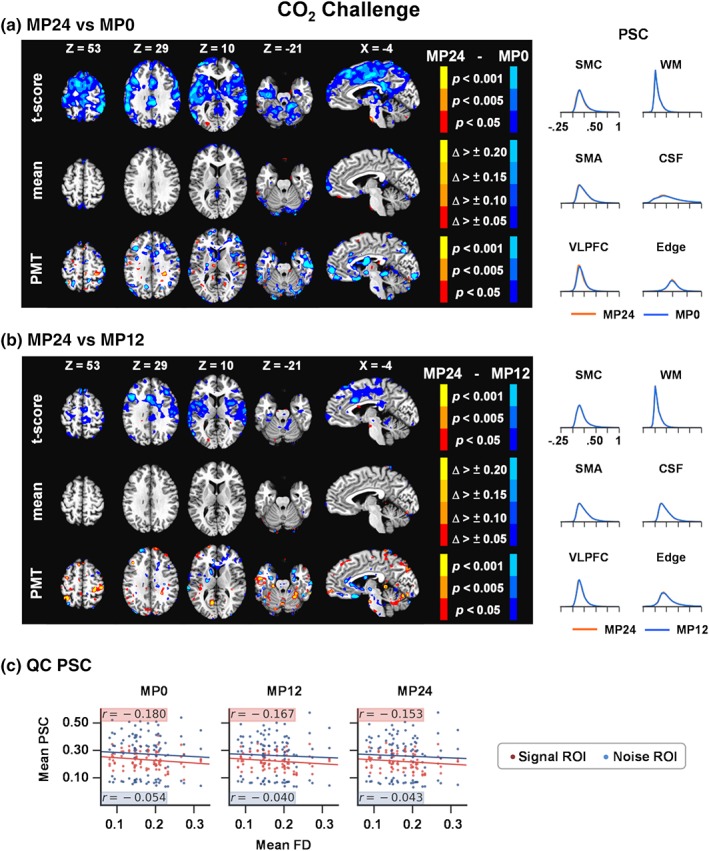
Results comparing the 24 motion parameter (MP24) pipeline relative to the MP0 (Panel a) and MP12 parameters (Panel b) pipeline during the CO2 challenge task at the group level. The selected axial (Z) and sagittal (X) slices from the Talairach atlas were changed to best represent data for this contrast. However, all other aspects of Panels a and b of the figure are identical to Figure 2. Panel c shows quality control (QC) PSC plots for the CO2 challenge task, depicting the relationship between mean framewise displacement (FD) and PSC separately for both signal (red dots/highlighting) and noise (blue dots/highlighting) regions of interest (ROIs; see Figure 5) for the MP0, MP12, and MP24 pipelines. Δ, change; CSF, cerebrospinal fluid; Edge, perimeter of brain mask; PMT, Pitman‐Morgan test; PSC, percent signal change; SMA, supplementary motor area; SMC, sensorimotor cortex; VLPFC, ventrolateral prefrontal cortex; WM, white matter [Color figure can be viewed at http://wileyonlinelibrary.com]
4. DISCUSSION
The field of fMRI continues to rapidly progress both in terms of data acquisition techniques (e.g., simultaneous multislice selection; Barth, Breuer, Koopmans, Norris, & Poser, 2016) and novel analyses to improve on signal‐to‐noise and contrast‐to‐noise properties (Griffanti et al., 2014; Power et al., 2014; Pruim et al., 2015; Satterthwaite et al., 2013). Current results suggest that alterations in both pulse sequences (i.e., shorter TR) as well as hardware (i.e., smaller 32‐ vs. 12‐channel coil) directly impact the physical measurement of head motion in the scanning environment, indicating that appropriate “cutoffs” for acceptable head motion requires constant reevaluation (Power et al., 2015) and may be better determined in a sample‐specific fashion (Ling et al., 2012; Mayer et al., 2007). Previous studies have reported benefits (Glasser et al., 2018; Griffanti et al., 2014; Pruim et al., 2015) as well as costs (Bright & Murphy, 2015; Pujol et al., 2014; Tohka et al., 2008) for various denoising algorithms, with the majority of more recent studies focused on rsfMRI data (Power et al., 2015).
In contrast to a priori predictions, current results utilizing a relatively straightforward metric (PSC magnitude) and QC PSC plots indicated that both FIX (Griffanti et al., 2014) and AROMA (Pruim et al., 2015) denoising algorithms removed task‐related activity (“signal”) as well as noise (reduced variance in edge regions) from high‐temporal resolution erfMRI and bdfMRI paradigms relative to a 24 MP approach at the group level. The loss of signal was not a result of differential effects of denoising on the baseline coefficient in these task‐activated regions. In general, the degree of signal loss was greater for FIX relative to the AROMA algorithm for both individual and group level statistics relative to MP regression.
The degree of signal loss was relatively consistent across the cognitive contrasts in both erfMRI and bdfMRI designs at the group level, with a noticeable increase in signal loss for a comparison with highest contrast‐to‐noise properties (i.e., the robust manipulation of stimulus frequency rate). Both FIX and AROMA algorithms quantitatively decreased noise (as measured by signal variance) in task‐related regions as well as ROI susceptible to artifacts, particularly in the edge of the brain (Pruim et al., 2015). Importantly, given the lack of a ground truth in fMRI analyses, and the higher susceptibility of certain regions to artifact, we cannot rule out that the decrement in task‐related activity following ICA‐based denoising strategies within a priori signal regions was not the removal of other physiological noise sources. However, the loss of activity may be particularly detrimental in patient studies, where large between‐subject variance renders the testing of smaller group‐wise effect sizes particularly challenging, especially in light of more stringent false positive corrections (Eklund, Nichols, & Knutsson, 2016).
Importantly, our denoising approach was conservative both in terms of the inclusion of artifact components in our FIX training set and the utilization of the “nonaggressive” or “soft‐clean” settings for both methods. Aggressive cleaning has been shown to reduce mean amplitude in lower frequency ranges of rsfMRI data relative to soft cleaning (Griffanti et al., 2014). Although not directly tested in the current experiment, signal loss may be greater in task‐based data if more aggressive denoising methods/options are utilized depending on the correlation structure of the data. It is recommended that the FIX classifier be first trained with local data whereas AROMA automates artifact component selection (Pruim et al., 2015). As both FIX and AROMA resulted in signal loss relative to more standard motion regression, it is therefore unlikely that errors in component identification (i.e., incorrect manual classification of signal as noise components) during the training of the FIX classifier accounted for current results. In addition, FIX attempts to remove multiple noise sources from the data (Griffanti et al., 2014), whereas AROMA is designed to be more specific to motion artifact (Pruim et al., 2015). Collectively, these results suggest that ICA‐based denoising procedures, as currently recommended, may not sufficiently isolate the noise from task‐related signal in both erfMRI and bdfMRI designs.
In contrast to the previous seminal study on nuisance‐based MP regression in task‐based fMRI (Johnstone et al., 2006), we did not observe any statistically significant detriments or benefits for using 12 or 24 MPs relative to no parameters in erfMRI and more typical (i.e., block length of less than 10 s) bdfMRI designs across two independent samples. Current results also indicated a benefit for reducing edge noise that monotonically increased with the addition of MP estimates to the denoising procedure (edge noise MP0 > MP24 ≈ MP12) across most task designs and contrasts. Signal loss was observed with the inclusion of additional MPs (MP12 and MP24 pipelines) in a bdfMRI design that involved much longer block lengths (30 ± 5 s). Importantly, the correlation between the task regressor and MPs was approximately double in the long bdfMRI design relative to both erfMRI and short bdfMRI designs. Considered collectively, current and previous (Johnstone et al., 2006) results suggest that the degree of correlation between absolute displacement and task regressors is a critical factor for determining whether or not MPs should be included in task‐based fMRI designs, and how the removal of MPs will affect group‐level results. The relationship with FD may be less critical. Thus, MP regression may confer limited benefits for shorter duration block designs in adults (Churchill et al., 2012) but may improve signal detection in higher motion cohorts (Evans, Todd, Taylor, & Strother, 2010).
There are several limitations to our study. First, in order to more directly compare pipelines, MELODIC was performed on unsmoothed data followed by smoothing of denoised data as recommended for FIX (Griffanti et al., 2014) but not AROMA (Pruim et al., 2015). Thus, the order and inclusion (time‐slice correction, high‐pass filtering, run concatenation, etc.) of data preprocessing steps (Caballero‐Gaudes & Reynolds, 2017; Ciric et al., 2017; Glasser et al., 2018), as well as the choice of group‐based relative to single‐subject ICA (Du et al., 2016), are important considerations for any denoising pipeline. However, it is beyond the scope of the current study to examine all potential permutations of preprocessing steps or task type/length that could be employed in task‐based data analyses. Similarly, as succinctly stated in several recent review articles (Ciric et al., 2017; Power et al., 2015), the methods and the metrics for measuring the “success” of various denoising strategies are being actively developed and evaluated at both the single‐subject and group level. Previous results indicate that “different metrics” favor “different methods” (i.e., multiple tradeoffs), a finding that was also observed in the current study in primary analyses, single‐subject results and the QC PSC plots. Finally, the utilization of a medical gas administration task for the longer bdfMRI analyses may have confounded effects on respiration rate and associated BOLD fluctuations (Birn, Diamond, Smith, & Bandettini, 2006) with increased head motion. Future studies should consider utilizing extended cognitive, motor, or sensory tasks where this confound does not exist.
In summary, the field of fMRI denoising is rapidly evolving with no clear indication on which techniques are truly superior (Caballero‐Gaudes & Reynolds, 2017; Power et al., 2015). It is likely that there will not be a one‐size fits all approach, especially when contrasting the various properties of task‐related versus rsfMRI and the multiple tradeoffs (e.g., distance‐dependent artifacts, loss of degrees of freedom) that occur with different denoising methods. Current results suggest that even the nonaggressive options of several ICA approaches appear to remove signal as well as noise from task‐related data relative to nuisance‐based motion regression approaches at both the single‐subject and group level. Finally, in contrast to long‐standing recommendations (Johnstone et al., 2006), nuisance‐based MP regression approaches may be appropriate for bdfMRI designs if minimal correlation exists between MPs and the design matrix.
CONFLICT OF INTEREST
The authors declare no potential conflict of interest.
Supporting information
APPENDIX S1 Supplemental Material
ACKNOWLEDGMENTS
The authors would like to thank Diana South and Catherine Smith for their assistance with data collection. This work was supported by the National Institutes of Health (grant numbers 1R01MH101512‐01A1 and 1R01NS098494‐01A1) to A.R.M. The funding agencies had no involvement in the study design, data collection, analyses, writing of the manuscript, or decisions related to submission for publication.
Mayer AR, Ling JM, Dodd AB, Shaff NA, Wertz CJ, Hanlon FM. A comparison of denoising pipelines in high temporal resolution task‐based functional magnetic resonance imaging data. Hum Brain Mapp. 2019;40:3843–3859. 10.1002/hbm.24635
Funding information National Institutes of Health, Grant/Award Numbers: 1R01NS098494‐01A1, 1R01MH101512‐01A1
Data Availability: The data that support the findings of this study come from multiple funded grants. These data will be openly available in FITBIR at https://fitbir.nih.gov, reference number FITBIR‐STUDY0000339, and the RDOC database at https://nda.nih.gov, reference ID number 2102, upon completion of the studies.
DATA AVAILABILITY
The data that support the findings of this study come from multiple funded grants. These data will be openly available in FITBIR at https://fitbir.nih.gov, reference number FITBIR‐STUDY0000339, and the RDOC database at https://nda.nih.gov, reference ID number 2102, upon completion of the studies.
References
REFERENCES
- Andersson, J. L. , Skare, S. , & Ashburner, J. (2003). How to correct susceptibility distortions in spin‐echo echo‐planar images: Application to diffusion tensor imaging. NeuroImage, 20, 870–888. [DOI] [PubMed] [Google Scholar]
- Attwell, D. , Buchan, A. M. , Charpak, S. , Lauritzen, M. , Macvicar, B. A. , & Newman, E. A. (2010). Glial and neuronal control of brain blood flow. Nature, 468, 232–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth, M. , Breuer, F. , Koopmans, P. J. , Norris, D. G. , & Poser, B. A. (2016). Simultaneous multislice (SMS) imaging techniques. Magnetic Resonance in Medicine, 75, 63–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn, R. M. , Diamond, J. B. , Smith, M. A. , & Bandettini, P. A. (2006). Separating respiratory‐variation‐related fluctuations from neuronal‐activity‐related fluctuations in fMRI. NeuroImage, 31, 1536–1548. [DOI] [PubMed] [Google Scholar]
- Braver, T. S. (2012). The variable nature of cognitive control: A dual mechanisms framework. Trends in Cognitive Sciences, 16, 106–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bright, M. G. , & Murphy, K. (2015). Is fMRI 'noise' really noise? Resting state nuisance regressors remove variance with network structure. NeuroImage, 114, 158–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore, E. , Brammer, M. , Williams, S. C. , Rabe‐Hesketh, S. , Janot, N. , David, A. , … Sham, P. (1996). Statistical methods of estimation and inference for functional MR image analysis. Magnetic Resonance in Medicine, 35, 261–277. [DOI] [PubMed] [Google Scholar]
- Burgess, G. C. , Kandala, S. , Nolan, D. , Laumann, T. O. , Power, J. D. , Adeyemo, B. , … Barch, D. M. (2016). Evaluation of denoising strategies to address motion‐correlated artifacts in resting‐state functional magnetic resonance imaging data from the Human Connectome Project. Brain Connectivity, 6, 669–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caballero‐Gaudes, C. , & Reynolds, R. C. (2017). Methods for cleaning the BOLD fMRI signal. NeuroImage, 154, 128–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun, V. D. , Adali, T. , Pearlson, G. D. , & Pekar, J. J. (2001). A method for making group inferences from functional MRI data using independent component analysis. Human Brain Mapping, 14, 140–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchill, N. W. , Oder, A. , Abdi, H. , Tam, F. , Lee, W. , Thomas, C. , … Strother, S. C. (2012). Optimizing preprocessing and analysis pipelines for single‐subject fMRI. I. Standard temporal motion and physiological noise correction methods. Human Brain Mapping, 33, 609–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciric, R. , Wolf, D. H. , Power, J. D. , Roalf, D. R. , Baum, G. L. , Ruparel, K. , … Satterthwaite, T. D. (2017). Benchmarking of participant‐level confound regression strategies for the control of motion artifact in studies of functional connectivity. NeuroImage, 154, 174–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox, R. , Chen, G. , Glen, D. R. , Reynolds, R. C. , & Taylor, P. A. (2017). FMRI clustering in AFNI: False positive rates redux. Brain Connectivity, 7, 152–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox, R. W. (1996). AFNI: Software for analysis and visualization of functional magnetic resonance neuroimages. Computers and Biomedical Research, 29, 162–173. [DOI] [PubMed] [Google Scholar]
- Dolcos, F. , Wang, L. , & Mather, M. (2014). Current research and emerging directions in emotion‐cognition interactions. Frontiers in Integrative Neuroscience, 8, 83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong, G. , Huang, Z. , Yang, Z. , Weng, X. , & Wang, P. (2009). Enhance fMRI Data Analysis by RAICAR. In 2009 3rd International Conference on Bioinformatics Engineering (pp. 1–4), IEEE.
- Du, Y. , Allen, E. A. , He, H. , Sui, J. , Wu, L. , & Calhoun, V. D. (2016). Artifact removal in the context of group ICA: A comparison of single‐subject and group approaches. Human Brain Mapping, 37, 1005–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eklund, A. , Nichols, T. E. , & Knutsson, H. (2016). Cluster failure: Why fMRI inferences for spatial extent have inflated false‐positive rates. Proceedings of the National Academy of Sciences of the United States of America, 113, 7900–7905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans, J. W. , Todd, R. M. , Taylor, M. J. , & Strother, S. C. (2010). Group specific optimisation of fMRI processing steps for child and adult data. NeuroImage, 50, 479–490. [DOI] [PubMed] [Google Scholar]
- Fair, D. A. , Schlaggar, B. L. , Cohen, A. L. , Miezin, F. M. , Dosenbach, N. U. , Wenger, K. K. , … Petersen, S. E. (2007). A method for using blocked and event‐related fMRI data to study "resting state" functional connectivity. NeuroImage, 35, 396–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston, K. J. , Williams, S. , Howard, R. , Frackowiak, R. S. , & Turner, R. (1996). Movement‐related effects in fMRI time‐series. Magnetic Resonance in Medicine, 35, 346–355. [DOI] [PubMed] [Google Scholar]
- Glasser, M. F. , Coalson, T. S. , Bijsterbosch, J. D. , Harrison, S. J. , Harms, M. P. , Anticevic, A. , … Smith, S. M. (2018). Using temporal ICA to selectively remove global noise while preserving global signal in functional MRI data. NeuroImage, 181, 692–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez‐Castillo, J. , Panwar, P. , Buchanan, L. C. , Caballero‐Gaudes, C. , Handwerker, D. A. , Jangraw, D. C. , … Bandettini, P. A. (2016). Evaluation of multi‐echo ICA denoising for task based fMRI studies: Block designs, rapid event‐related designs, and cardiac‐gated fMRI. NeuroImage, 141, 452–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius, M. (2008). Resting‐state functional connectivity in neuropsychiatric disorders. Current Opinion in Neurology, 21, 424–430. [DOI] [PubMed] [Google Scholar]
- Griffanti, L. , Salimi‐Khorshidi, G. , Beckmann, C. F. , Auerbach, E. J. , Douaud, G. , Sexton, C. E. , … Smith, S. M. (2014). ICA‐based artefact removal and accelerated fMRI acquisition for improved resting state network imaging. NeuroImage, 95, 232–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iacovella, V. , & Hasson, U. (2011). The relationship between BOLD signal and autonomic nervous system functions: Implications for processing of "physiological noise". Magnetic Resonance in Medicine, 29, 1338–1345. [DOI] [PubMed] [Google Scholar]
- Johnstone, T. , Ores Walsh, K. S. , Greischar, L. L. , Alexander, A. L. , Fox, A. S. , Davidson, R. J. , & Oakes, T. R. (2006). Motion correction and the use of motion covariates in multiple‐subject fMRI analysis. Human Brain Mapping, 27, 779–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochiyama, T. , Morita, T. , Okada, T. , Yonekura, Y. , Matsumura, M. , & Sadato, N. (2005). Removing the effects of task‐related motion using independent‐component analysis. NeuroImage, 25, 802–814. [DOI] [PubMed] [Google Scholar]
- Ling, J. , Merideth, F. , Caprihan, A. , Pena, A. , Teshiba, T. , & Mayer, A. R. (2012). Head injury or head motion? Assessment and quantification of motion artifacts in diffusion tensor imaging studies. Human Brain Mapping, 33, 50–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lund, T. E. , Norgaard, M. D. , Rostrup, E. , Rowe, J. B. , & Paulson, O. B. (2005). Motion or activity: Their role in intra‐ and inter‐subject variation in fMRI. NeuroImage, 26, 960–964. [DOI] [PubMed] [Google Scholar]
- Maclaren, J. , Herbst, M. , Speck, O. , & Zaitsev, M. (2013). Prospective motion correction in brain imaging: A review. Magnetic Resonance in Medicine, 69, 621–636. [DOI] [PubMed] [Google Scholar]
- Mayer, A. R. , Franco, A. R. , Canive, J. , & Harrington, D. L. (2009). The effects of stimulus modality and frequency of stimulus presentation on cross‐modal distraction. Cerebral Cortex, 19, 993–1007. [DOI] [PubMed] [Google Scholar]
- Mayer, A. R. , Franco, A. R. , Ling, J. , & Canive, J. M. (2007). Assessment and quantification of head motion in neuropsychiatric functional imaging research as applied to schizophrenia. Journal of the International Neuropsychological Society, 13, 839–845. [DOI] [PubMed] [Google Scholar]
- Mayer, A. R. , Ryman, S. G. , Hanlon, F. M. , Dodd, A. B. , & Ling, J. M. (2016). Look hear! The prefrontal cortex is stratified by modality of sensory input during multisensory cognitive control. Cerebral Cortex, 27, 2831–2840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer, A. R. , Teshiba, T. M. , Franco, A. R. , Ling, J. , Shane, M. S. , Stephen, J. M. , & Jung, R. E. (2012). Modeling conflict and error in the medial frontal cortex. Human Brain Mapping, 33, 2843–2855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks, E. H. , Frost, C. J. , Tuna, I. S. , Schmalfuss, I. M. , Rahman, M. , & Old, C. A. (2017). Reduction of motion artifacts and noise using independent component analysis in task‐based functional MRI for preoperative planning in patients with brain tumor. American Journal of Neuroradiology, 38, 336–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oakes, T. R. , Johnstone, T. , Ores Walsh, K. S. , Greischar, L. L. , Alexander, A. L. , Fox, A. S. , & Davidson, R. J. (2005). Comparison of fMRI motion correction software tools. NeuroImage, 28, 529–543. [DOI] [PubMed] [Google Scholar]
- Petzold, G. C. , & Murthy, V. N. (2011). Role of astrocytes in neurovascular coupling. Neuron, 71, 782–797. [DOI] [PubMed] [Google Scholar]
- Power, J. D. , Barnes, K. A. , Snyder, A. Z. , Schlaggar, B. L. , & Petersen, S. E. (2012). Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. NeuroImage, 59, 2142–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power, J. D. , Mitra, A. , Laumann, T. O. , Snyder, A. Z. , Schlaggar, B. L. , & Petersen, S. E. (2014). Methods to detect, characterize, and remove motion artifact in resting state fMRI. NeuroImage, 84, 320–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power, J. D. , Plitt, M. , Laumann, T. O. , & Martin, A. (2017). Sources and implications of whole‐brain fMRI signals in humans. NeuroImage, 146, 609–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power, J. D. , Schlaggar, B. L. , & Petersen, S. E. (2015). Recent progress and outstanding issues in motion correction in resting state fMRI. NeuroImage, 105, 536–551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruim, R. H. , Mennes, M. , van, R. D. , Llera, A. , Buitelaar, J. K. , & Beckmann, C. F. (2015). ICA‐AROMA: A robust ICA‐based strategy for removing motion artifacts from fMRI data. NeuroImage, 112, 267–277. [DOI] [PubMed] [Google Scholar]
- Pujol, J. , Maciá, D. , Blanco‐Hinojo, L. , Martinez‐Vilavella, G. , Sunyer, J. , de la Torre, R. , … Harrison, B. J. (2014). Does motion‐related brain functional connectivity reflect both artifacts and genuine neural activity? NeuroImage, 101, 87–95. [DOI] [PubMed] [Google Scholar]
- Ryman, S. G. , El Shaikh, A. A. , Shaff, N. A. , Hanlon, F. M. , Dodd, A. B. , Wertz, C. J. , & Mayer, A. R. (2019). Proactive and reactive cognitive control rely on flexible use of the ventrolateral prefrontal cortex. Human Brain Mapping, 40, 955–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad, Z. S. , Gotts, S. J. , Murphy, K. , Chen, G. , Jo, H. J. , Martin, A. , & Cox, R. W. (2012). Trouble at rest: How correlation patterns and group differences become distorted after global signal regression. Brain Connectivity, 2, 25–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salimi‐Khorshidi, G. , Douaud, G. , Beckmann, C. F. , Glasser, M. F. , Griffanti, L. , & Smith, S. M. (2014). Automatic denoising of functional MRI data: Combining independent component analysis and hierarchical fusion of classifiers. NeuroImage, 90, 449–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite, T. D. , Elliott, M. A. , Gerraty, R. T. , Ruparel, K. , Loughead, J. , Calkins, M. E. , … Wolf, D. H. (2013). An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting‐state functional connectivity data. NeuroImage, 64(10), 240–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel, J. S. , Mitra, A. , Laumann, T. O. , Seitzman, B. A. , Raichle, M. , Corbetta, M. , & Synder, A. Z. (2016). Data quality influences observed links between functional connectivity and behavior. Cerebral Cortex, 27, 4492–4502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, S. M. , Fox, P. T. , Miller, K. L. , Glahn, D. C. , Fox, P. M. , Mackay, C. E. , … Beckmann, C. F. (2009). Correspondence of the brain's functional architecture during activation and rest. Proceedings of the National Academy of Sciences of the United States of America, 106, 13040–13045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, S. M. , Jenkinson, M. , Woolrich, M. W. , Beckmann, C. F. , Behrens, T. E. , Johansen‐Berg, H. , … Matthews, P. M. (2004). Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage, 23(Suppl. 1), S208–S219. [DOI] [PubMed] [Google Scholar]
- Talairach, J. , & Tournoux, P. (1988). Co‐planar stereotaxic atlas of the human brain. New York, NY: Thieme. [Google Scholar]
- Tohka, J. , Foerde, K. , Aron, A. R. , Tom, S. M. , Toga, A. W. , & Poldrack, R. A. (2008). Automatic independent component labeling for artifact removal in fMRI. NeuroImage, 39, 1227–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk, K. R. , Sabuncu, M. R. , & Buckner, R. L. (2012). The influence of head motion on intrinsic functional connectivity MRI. NeuroImage, 59, 431–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng, L. L. , Wang, D. , Fox, M. D. , Sabuncu, M. , Hu, D. , Ge, M. , … Liu, H. (2014). Neurobiological basis of head motion in brain imaging. Proceedings of the National Academy of Sciences, 111, 6058–6062. [DOI] [PMC free article] [PubMed] [Google Scholar]
Data citation
- Mayer, A.R. (2018). A Multidimensional Investigation of Cognitive Control Deficits in Psychopathology. RDOCdb (https://nda.nih.gov): ID#2102.
- Mayer, A.R. (Ongoing). The Impact of Diffuse Mild Brain Injury on Clinical Outcomes in Children. FITBIR (https://fitbir.nih.gov): FITBIR‐STUDY0000339.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
APPENDIX S1 Supplemental Material
Data Availability Statement
The data that support the findings of this study come from multiple funded grants. These data will be openly available in FITBIR at https://fitbir.nih.gov, reference number FITBIR‐STUDY0000339, and the RDOC database at https://nda.nih.gov, reference ID number 2102, upon completion of the studies.


