Evolution of white matter tract microstructure across the life span

Abstract

The human brain undergoes dramatic structural change over the life span. In a large imaging cohort of 801 individuals aged 7–84 years, we applied quantitative relaxometry and diffusion microstructure imaging in combination with diffusion tractography to investigate tissue property dynamics across the human life span. Significant nonlinear aging effects were consistently observed across tracts and tissue measures. The age at which white matter (WM) fascicles attain peak maturation varies substantially across tissue measurements and tracts. These observations of heterochronicity and spatial heterogeneity of tract maturation highlight the importance of using multiple tissue measurements to investigate each region of the WM. Our data further provide additional quantitative evidence in support of the last‐in‐first‐out retrogenesis hypothesis of aging, demonstrating a strong correlational relationship between peak maturational timing and the extent of quadratic measurement differences across the life span for the most myelin sensitive measures. These findings present an important baseline from which to assess divergence from normative aging trends in developmental and degenerative disorders, and to further investigate the mechanisms connecting WM microstructure to cognition.

1. INTRODUCTION

In‐depth understanding of normal human brain changes across the life span is required to link maturational processes during childhood to degenerative processes of old age and to provide an informed basis from which to study patterns of divergence in brain disorders. Life span studies of the postmortem human brain have demonstrated structural changes to total brain volume (Dekaban & Sadowsky, 1978), myelination (Benes, Turtle, Khan, & Farol, 1994; Yakovlev & Lecours, 1967), and synaptic density (Huttenlocher, 1979; Huttenlocher & de Courten, 1987). These studies typically describe rapid changes to brain organization during childhood and adolescence, followed by a slowing of developmental processes in young adulthood, before achieving a maturational peak, reversing in trend, and declining in later adulthood and old age. Theories within the aging literature have suggested that life span tissue processes may obey a retrogenic sequence ordering, which can be broadly broken down into “gain‐predicts‐loss” and “last‐in‐first‐out” hypotheses of aging (Raz, 2000; Reisberg et al., 2002; Yeatman, Wandell, & Mezer, 2014). The gain‐predicts‐loss hypothesis predicts that the rate of tissue change during development equals the rate of decline during old age. Equivalently, knowledge of a tissue state in late‐childhood should predict the tissue state at a symmetric age postpeak. The last‐in‐first‐out hypothesis predicts that structures that develop slower ontogenetically will also be the most vulnerable to age‐related decline. Previous assessments of this theory have formulated the problem in different fashions (Davis et al., 2009; Douaud et al., 2014; Yeatman et al., 2014), often using qualitative assessments (Brickman et al., 2012; Gao et al., 2011; Madden et al., 2012; Stricker et al., 2009; Ziegler et al., 2012).

Findings in recent years have made it apparent that the white matter (WM) plays a critical role in cognitive development, normal cognition, and cognitive decline in old age (Ameis & Catani, 2015; Bells et al., 2017; Filley & Fields, 2016). Most of the studies investigating age‐related changes in human WM have focused on diffusion tensor imaging (DTI; Basser, Mattiello, & LeBihan, 1994). These investigations report robust increases in fractional anisotropy (FA) and decreases in mean diffusivity (MD) during childhood and adolescence (Barnea‐Goraly et al., 2005; Eluvathingal, Hasan, Kramer, Fletcher, & Ewing‐Cobbs, 2007; Schmithorst, Wilke, Dardzinski, & Holland, 2002), and reverse trends in old age (Abe et al., 2002; Cox et al., 2016; Ota et al., 2006; Pfefferbaum et al., 2000). A number of recent studies have extended investigations to cover most of the life span, revealing the full extent of nonlinear “U‐shaped” and “inverted U‐shaped” life span trajectories within the major WM tracts, typically reaching peak maturation between the early twenties and mid‐forties (Kochunov et al., 2012; Lebel et al., 2012; Westlye et al., 2010; Yeatman et al., 2014).

One potential confound of the DTI analyses relates to the inherent nonspecificity of the measurement, where observed changes in FA may be due to changes to any combination of axonal dispersion, fiber crossing, myelination, or axonal densities (Beaulieu, 2002; Jones, Knösche, & Turner, 2013). In an attempt to provide more easily interpreted and specific microstructural measures, the neurite orientation dispersion and density imaging (NODDI) biophysical model of diffusion has been proposed (Zhang, Schneider, Wheeler‐Kingshott, & Alexander, 2012). The few studies that have investigated aging effects using NODDI point toward increased sensitivity to aging differences as compared to DTI, increased fiber dispersion with age and increased axonal packing during adolescence/young adulthood (Billiet et al., 2015; Chang et al., 2015; Kodiweera, Alexander, Harezlak, McAllister, & Wu, 2016). The investigation of nonlinear life span trajectories was precluded in these studies due to the relatively small sample sizes and the inclusion of few subjects over the age of 55 years. One recent study investigated aging effects in later life (45–77 years) using the NODDI model in a large cohort of over 3,000 individuals (Cox et al., 2016). The findings from this work suggest that axonal packing decreases in old age and that, for most tracts, a nonlinear model better approximates data.

Beyond the microstructural measures provided by diffusion‐weighted imaging (DWI), the development of noninvasive MR biomarkers for myelin has facilitated early investigations into myelin development and decline across the life span. One such quantitative magnetic resonance imaging (qMRI) methodology—multiparameter mapping (MPM; Weiskopf et al., 2013), provides estimates for the magnetization transfer (MT) and relaxation rates R1 and R2*, each providing a level of sensitivity to local myelination and/or iron deposition (Draganski et al., 2011; Fukunaga et al., 2010; Lutti, Dick, Sereno, & Weiskopf, 2014; Stüber et al., 2014). Recent findings suggest significant demyelination in human WM with age (Callaghan et al., 2014; Draganski et al., 2011), particularly in later life after myelination has matured to a peak density before reversing in trend and declining with age (Li et al., 2014; Yeatman et al., 2014). As an extension to myelin imaging, recent work has proposed a method for noninvasively estimating the g‐ratio (Stikov et al., 2011; Stikov et al., 2015). Preliminary investigations of g‐ratio change across the life span in small imaging cohorts (n = 38–92) have reported linear increases with age in the deep WM (Cercignani et al., 2016), with little age‐related change observed across the mid‐sagittal portion of the corpus callosum (Berman, West, Does, Yeatman, & Mezer, 2017).

In this study, we combine DTI tractography with DWI and MPM tissue microstructure characterization to provide a detailed assessment of multiparametric tissue differences across the life span (7–84 years) in a large cohort of healthy individuals (n = 801). Cross‐validation was used to select appropriate aging models for each of the quantitative microstructure measurements and robust curve fitting approaches applied to estimate ages of peak maturation within a tract. Finally, age, sex, and hemisphere associations were investigated using multiple linear regression.

2. MATERIALS AND METHODS

2.1. Subjects

A total of 801 healthy volunteers (410 females) were recruited from the Lausanne regional area of Switzerland based on fliers, university newsletters and, for the majority of subjects (N = 624), their ongoing participation in the CoLaus | PsyCoLaus cohort (Preisig et al., 2009). Study approval was granted by the local Ethics Committee and informed consent was collected for all subjects and/or a parent/guardian. Subjects were aged between 7 and 84 years (mean age 50 ± 17 years) and distributed as follows: 106 subjects aged 7–24 years; 108 subjects aged 25–39 years; 245 subjects aged 40–54 years; 242 subjects aged 55–69 years; and 100 subjects aged 70–84 years. Subjects had no self‐reported history of neurological of psychiatric disease and were screened carefully for brain abnormalities and movement artifacts. Given the absence of substantive differences in tract characteristics between right‐ and left‐handed subjects (Cox et al., 2016), we chose not to assess handedness as part of our investigation.

2.2. MR data acquisition

All imaging was performed on a 3T whole‐body MRI system (Magnetom Prisma; Siemens Medical Systems, Erlangen, Germany) using a 64‐channel RF receive head coil and body coil for transmission.

2.2.1. Multiparametric mapping

The qMRI protocol consisted of three whole‐brain multiecho 3D fast low angle shot acquisitions with predominantly MT‐weighted (MTw: TR/α = 24.5 ms/6°), proton density‐weighted (PDw: TR/α = 24.5 ms/6°), and T1‐weighted (T1w: 24.5 ms/21°) contrast (Helms, Dathe, & Dechent, 2008; Helms, Draganski, Frackowiak, Ashburner, & Weiskopf, 2009; Weiskopf et al., 2013). Multiple gradient echoes with minimum at 2.34 and 2.34 ms echo spacing were acquired for each contrast with 1 mm isotropic (ISO) voxel size, field of view (FOV), matrix size = 256 × 240 × 176), and alternating readout polarity. The number of echoes was 6/8/8 for the MTw/PDw/T1w acquisitions to keep the TR value identical for all contrasts. Parallel imaging was used along the phase‐encoding direction (acceleration Factor 2 with GRAPPA reconstruction) (Griswold et al., 2002), partial Fourier (Factor 6/8) was used along the partition direction. Data were acquired to calculate maps of the RF transmit field B1+ using the 3D echo‐planar imaging (EPI) spin echo and stimulated echo method described in Lutti et al. (2012) and Lutti, Hutton, Finsterbusch, Helms, and Weiskopf (2010). The total acquisition time was 27 min.

A subset of participants (N = 84, 7–75 years) underwent an equivalent 1.5 mm³ MPM protocol. The acquisition parameters for this protocol differed for the following parameters: FOV = 240 × 225 × 180 mm³ and matrix size = 160 × 150 × 120. The total acquisition time was 13 min. Image resolution was included as a regressor in all curve fitting and statistical models.

2.2.2. Diffusion‐weighted imaging

The diffusion‐weighted MRI data were acquired using a 2D EPI sequence with the following parameters: TR/TE = 7420/69 ms, parallel GRAPPA acceleration factor = 2, FOV = 192 × 212 mm², matrix size = 96 × 106, 70 axial slices, 2 mm ISO voxel dimension, 118 isotropically distributed diffusion sensitization directions (15 at b = 650 s/mm², 30 at b = 1,000 s/mm², and 60 at b = 2,000 s/mm²) and 13 at b = 0 images interleaved throughout the acquisition. The lower resolution acquisition used for a subset of participants (N = 84, 7–75 years) was acquired using the same 118 direction sampling scheme and the following imaging parameters: TR/TE = 3906/88 ms, parallel GRAPPA acceleration factor = 0, FOV = 192 × 209 mm², matrix size = 96 × 106, 60 axial slices, 2.2 mm ISO voxel dimension, and multiband factor = 2.

2.3. MR data preprocessing

2.3.1. Structural data

The R2*, MT, and R1 quantitative maps were calculated as previously described (Draganski et al., 2011) using in‐house software running under SPM12 (Wellcome Trust Centre for Neuroimaging, UCL, London, UK; http://www.fil.ion.ucl.ac.uk/spm) and MATLAB (MathWorks, Sherborn, MA). The R2* maps were estimated from the regression of the log‐signal of the eight PD‐weighted echoes. The MT and R1 maps were computed as described in Helms et al. (2008), using the MTw, PDw, and T1w images averaged across all echoes. The maps were corrected for local RF transmit field inhomogeneities using the B1+ maps computed from the 3D EPI data (Helms et al., 2008) and for imperfect RF spoiling using the approach described by Preibisch and Deichmann (2009).

2.3.2. Diffusion preprocessing

DWIs were preprocessed to correct for eddy currents and subject motion using the FSL EDDY tool (Andersson & Sotiropoulos, 2016) and the gradient directions were appropriately rotated to correct for subject movement (Leemans & Jones, 2009). The B0 maps acquired as part of the structural imaging session were used to correct for EPI susceptibility distortions with the SPM field mapping toolbox (Hutton et al., 2002). The DWI images were then rigid body aligned to the MT image with the aid of the mean b = 0 image using SPM12.

DTI maps were estimated on the b = 0 s/mm², b = 650 s/mm², and b = 1,000 s/mm² data using a constrained nonlinear least‐squares algorithm (Koay, Chang, Carew, Pierpaoli, & Basser, 2006). The NODDI (Zhang et al., 2012) maps were processed with the AMICO toolbox (Daducci, Canales‐Rodriguez, & Zhang, 2015) using multishell diffusion data across all of the acquired b‐values. For each subject, we thus generated DTI tissue microstructure maps for FA and MD, in addition to NODDI maps for intracellular volume fraction (ICVF) and orientation dispersion index (ODI).

2.3.3. g‐Ratio estimation

The g‐ratio is defined as the ratio between the axonal diameter and the myelinated fiber diameter and represents a fundamental property of axonal morphology and conduction (Waxman, 1975). Here, we apply a recently developed technique (Campbell et al., 2014; Mohammadi et al., 2015; Stikov et al., 2015) which estimates the g‐ratio using a combination of noninvasive diffusion microstructure and myelin imaging measures. The g‐ratio—g, was estimated voxelwise via the following equation:

$$g=\sqrt{\frac{1}{1+\frac{\mathrm{MVF}}{\mathrm{AVF}}}}=\sqrt{\frac{1}{1+\frac{\mathrm{\alpha MT}}{\left(1‐\mathrm{\alpha MT}\right)\left(1-{\nu }_{\mathrm{iso}}\right){\nu }_{\mathrm{ic}}}}}$$

where MVF is the myelin volume fraction, AVF is the axonal volume fraction, MT is the quantitative MT measurement, and ν_iso/ν_ic are, respectively, the ISO and ICVF estimates from the NODDI diffusion model. We estimated the normalization factor, α, by following the previous literature (Cercignani et al., 2016; Mancini et al., 2017; Mohammadi et al., 2015). A region of interest (ROI) was selected in the splenium of 11 subjects (mean age 26.5 ± 1.41 years) and a value of α = 0.23 chosen as the median normalization factor required to constrain the splenium g‐ratio to a value of 0.7 across subjects, mirroring reported g‐ratio values made in the splenium using electron microscopy (Graf von Keyserlingk & Schramm, 1984).

2.4. Tractography and microstructure sampling

The AFQ software package (Yeatman, Dougherty, Myall, Wandell, & Feldman, 2012) was used to estimate average tissue microstructural properties across 20 bilateral and callosal tracts (Figure 1). The subset of DWI data used to calculate the DTI maps was provided to the software and used to generate a whole brain tractogram using default settings (step size = 1 mm; FA threshold = 0.2; angle threshold = 30°). More advanced High Angular Resolution Diffusion Imaging (HARDI) tractography procedures were tested but determined to provide little benefit to tract identification while introducing additional instabilities in certain subjects. After fully automated individual tract segmentation and cleaning procedures, the accepted streamlines were used to sample each of the previously computed tissue microstructure maps (MT, R1, R2*, g‐ratio, FA, MD, ICVF, and ODI) and averaged along the tract length to provide mean tissue microstructure estimates for each of the tracts and metrics. Correlation matrices for all the microstructure measurements across three example tracts are provided in Figure S1, Supporting Information. The spatial extent of each tract was restricted by WM plane ROIs as part of the default AFQ processing procedure. This step aims to ensure that the most consistent core segment of a tract is selected for comparison across individuals. The final segments used for the tract definitions are shown in Figure 1. Whole brain tractography segmentations for a representative subject are shown in Figure S2, Supporting Information. As part of a secondary analysis, each tract was sampled at 100 segments along the length between the 2 WM plane ROIs. The aging models described below were then fit to each tract segment to determine the variability of the aging parameters along a tract's length for each MRI parameter (Figure S3, Supporting Information).

Figure 1.

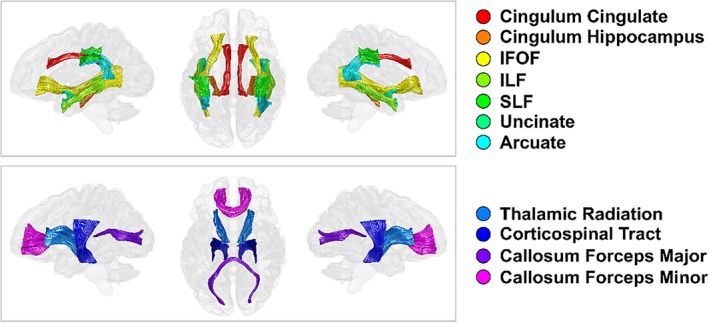
Major white matter (WM) tracts of interest. Tracts dissected using an automated fiber identification procedure on whole brain tractograms and restricted for analysis by WM plane regions of interest. Tracts are rendered in left‐lateral, superior, and right‐lateral views [Color figure can be viewed at http://wileyonlinelibrary.com]

2.5. Curve fitting

We considered three possible aging trajectory models (linear, quadratic, and Poisson curve), each of which has been identified as a suitable description of tract evolution across the life span for a particular microstructure measurement (Bartzokis et al., 2012; Cox et al., 2016; Kochunov et al., 2012; Lebel et al., 2012; Yeatman et al., 2014). The linear model describes the relationship between age and tract microstructure according to the following equation:

$$Y={\mathrm{\beta }}_1+{{\mathrm{\beta }}_2}^{*}\mathrm{Age}$$

where Y is a tract microstructure measurement (e.g., for MT) while β₁ and β₂ parameterize the intercept and slope, respectively. The quadratic curve extends the linear model via the following equation:

$$Y={\mathrm{\beta }}_1+{\mathrm{\beta }}_2*\mathrm{Age}+{\mathrm{\beta }}_3*{\mathrm{Age}}^2$$

where β₃ parameterizes a nonlinear quadratic aging term. The Poison curve model is capable of modeling asymmetric nonlinear aging trajectories as described by the following equation:

$$Y={\mathrm{\beta }}_1+{\mathrm{\beta }}_2*\mathrm{Age}*{\exp }^{‐{\mathrm{\beta }}_3*\mathrm{Age}}$$

Linear and quadratic models were evaluated using a GLM, which included additional regressors for sex, resolution, hemisphere, and sex–age interactions. The Poisson curve was estimated using a nonlinear optimization in MATLAB after the regression of covariates. Model selection was performed for each microstructure metric using repeated fivefold cross‐validation. For each tract, a total of 10⁴ repetitions were performed, each time using a randomized division of subjects into folds. The winning model was selected as the model which minimized mean cross‐validated error across fold, repetitions and tracts. Bootstrapping with replacement was repeated 1,000 times using the winning model to estimate the age at which tract microstructure measurements peaked. Peak age was estimated for the quadratic and Poisson curve models as the age at which the measurement first derivative with respect to age equaled zero (the global minima/maxima). The mean of the bootstrapped sampling distribution was taken as the peak age estimate and SE were calculated as the SD of the bootstrapped sampling distribution.

2.6. Age, sex, and hemisphere associations

GLMs were run to test for the association of age, sex, hemisphere, image resolution, and their interactions for each tract and metric. Two GLMs were considered, one which included only first‐order aging terms:

$$\mathrm{Age}+\mathrm{Sex}+\text{Resolution}+\text{Hemisphere}+\mathrm{Age}\times \mathrm{Sex}+\mathrm{Age}\times \text{Resolution}+\mathrm{Age}\times \text{Hemisphere}$$

and a second GLM which included a second‐order aging term:

$$\mathrm{Age}+{\mathrm{Age}}^2+\mathrm{Sex}+\text{Resolution}+\text{Hemisphere}+\mathrm{Age}\times \mathrm{Sex}+\mathrm{Age}\times \text{Resolution}+\mathrm{Age}\times \text{Hemisphere}$$

The Akaike information criterion was used to assess which of the two GLMs was best supported by a tract's life span microstructure trajectory. Independent and dependent variables were normalized prior to model estimation in order to obtain standardized beta coefficients ($\widehat{\mathrm{\beta }}$). We report standardized beta coefficients as effect sizes alongside the model probability values in our results.

2.7. Retrogenesis of WM tracts

We investigated the retrogenesis hypothesis by assessing whether a simple quadratic aging model (symmetric) was a more appropriate description of microstructure evolution over the human life span than either linear or Poisson curve models (asymmetric). Here, we formulate the problem in terms of age of maturity predicting the extent of quadratic tissue difference over the life span. First, each tissue measurement of a tract was normalized by the mean across subjects to determine the percentage deviations from the sample mean. Second, a GLM containing regressors for age, sex, hemisphere, resolution, and their interactions (see the second‐order aging model in Section 2.6) was evaluated for each tract and metric to estimate quadratic aging terms. Finally, Pearson's correlations were made between the bootstrapped peak age estimates and quadratic aging effects to quantitatively test the prediction that age of maturity predicts percentage tissue variation across the major WM fiber bundles. This approach to formulating the last‐in‐first‐out hypothesis assesses the relationship between two fundamental life span curve parameters and, by the nature of the quadratic term, tests the prediction that late maturation is associated with an accelerated rate of decline postpeak and a greater absolute level of microstructural difference from adolescence to old age.

3. RESULTS

3.1. Quality control

For quality control of MRI data, we use both qualitative and quantitative assessments based on R2* signal homogeneity in brain's WM. SDR2* is a measure of intrascan motion artifact, validated against motion history (Castella et al., 2018). SDR2* values below 4 s⁻¹ have been reported in the absence of head motion (1.5 mm³ data). The peak/mean values of the histogram are 3.47/3.81 s⁻¹ for our 1 mm³ data. In Figure S4 (Supporting Information), we show a histogram of the SDR2* values calculated from the high‐resolution (1 mm³) and low‐resolution (1.5 mm³) data sets. SDR2* stays for the SD of R2* estimates in WM derived from the multiecho PD‐ and T1‐weighted data.

3.2. Life span differences within WM tracts

Each of the WM tracts followed similar general life span trajectories. MT, R1, g‐ratio, FA, ICVF, and ODI measurements most accurately followed a quadratic aging model, while R2* and MD trajectories were better fit using a Poisson curve. MT, R1, and ICVF showed a positive slope from adolescence into adulthood before reaching a peak and declining into old age at a rate symmetric to that observed before the peak; we observed a positive slope of R2* toward adulthood before reaching a peak value and then showing a flatter negative slope; MD trends were opposite to R2*, characteristically with initial negative slope, achieving a minimum, and then demonstrating a positive slope at a slower rate; FA and ODI are characterized by opposite patterns of age‐associated differences, though certain tracts showed very little quadratic change or inverted trajectories across the life span; the g‐ratio showed a period of relative stability from adolescence into the third decade before increasing with further age.

The estimates for age of peak MT, R1, R2*, g‐ratio, MD, and ICVF were robust and had SE of 0–6 years (mean error ± 3.2 years; Figure 2). For FA and ODI, the estimates for peak age were less reliable with average SE of 13.2 and 10.6 years, respectively. The reliability of peak age estimates relates to the extent of nonlinear (quadratic) aging effects within a tract and this, as well as the precise timing of peak maturation, can vary substantially from tract to tract and, in the cases of FA and ODI, even along a tract's length (Figure S3, Supporting Information). The percentage difference of a tissue measurement at age 15 years to the peak age and the percentage difference from peak age to age 75 years are provided in Table 1. These values provide an overview of the absolute tissue measurement differences observed during maturation and decline.

Figure 2.

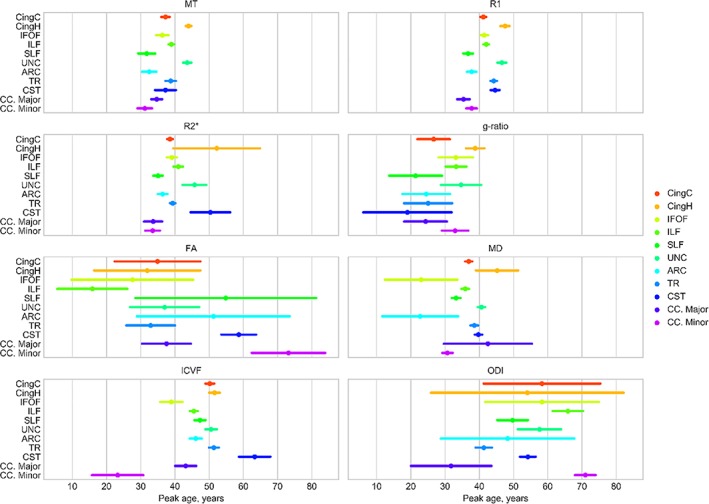
The relative timings of tract microstructure peaks for MT, R1, R2*, g‐ratio, FA, MD, ICVF, and ODI. The mean bootstrapped age of peak microstructural development is shown for each tract (circle) along with the bootstrapped SE (bars). The age scale is consistent across all measurement types. ARC = arcuate fasciculus; CC. Major = corpus callosum forceps major; CC. Minor = corpus callosum forceps minor; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; TR = thalamic radiations; UNC = uncinate fasciculus [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 1.

Percentage measurement change during maturation and senescence. Maturation defined as percentage change from age 15 to peak; senescence defined as percentage change from peak to age 75

	CingC	CingH	IFOF	ILF	SLF	UNC	ARC	TR	CST	CC. Major	CC. Minor	Mean ± Std
FA
Maturation	0.71	0.72	0.11	0.09	‐3.17	1.41	‐2.99	‐1.05	‐3.23	1.02	‐11.49	‐1.62 ±3.71
Senescence	‐2.36	‐4.45	‐3.67	‐6.45	‐0.31	‐2.95	0.40	4.64	0.55	‐2.42	0.00	‐1.55 ±3.01
ICVF
Maturation	6.06	8.78	2.23	5.15	3.69	10.04	3.22	6.10	5.09	2.98	0.21	4.87 ±2.85
Senescence	‐2.87	‐3.40	‐4.65	‐4.56	‐2.60	‐4.36	‐2.69	‐2.47	‐0.35	‐3.61	‐5.58	‐3.38 ±1.42
g‐ratio
Maturation	‐0.19	‐0.97	‐0.34	‐0.45	‐0.04	‐0.48	‐0.10	‐0.13	‐0.01	‐0.11	‐0.45	‐0.30 ±0.28
Senescence	2.76	2.14	1.54	2.26	2.21	1.61	2.07	2.18	1.53	2.40	2.36	2.10 ±0.39
MD
Maturation	‐3.24	‐2.60	‐1.27	‐3.56	‐2.49	‐4.51	‐1.12	‐3.54	‐2.75	‐1.92	‐2.45	‐2.68 ±1.01
Senescence	3.49	0.54	5.72	4.35	4.13	3.22	4.07	3.17	2.11	0.88	5.68	3.40 ±1.69
MT
Maturation	3.10	7.24	2.51	4.27	1.19	7.21	1.29	3.28	1.73	2.04	1.45	3.21 ±2.20
Senescence	‐8.53	‐7.75	‐7.89	‐9.22	‐7.47	‐8.06	‐7.32	‐7.37	‐4.50	‐8.18	‐10.06	‐7.85 ±1.39
ODI
Maturation	6.03	8.67	6.50	11.12	6.35	9.94	4.41	7.64	13.95	‐1.25	21.59	8.63 ±5.81
Senescence	‐0.33	5.13	‐0.92	‐0.39	‐3.17	‐1.68	‐2.50	‐11.33	‐3.63	7.47	‐0.09	‐1.04 ±4.82
R1
Maturation	3.53	6.54	3.32	4.05	1.71	6.54	1.89	4.74	2.88	1.80	2.30	3.57 ±1.76
Senescence	‐5.70	‐4.41	‐5.20	‐5.79	‐5.18	‐5.00	‐4.87	‐5.02	‐2.95	‐6.54	‐5.94	‐5.15 ±0.94
R2*
Maturation	7.17	12.18	6.84	6.74	4.34	10.41	4.34	8.92	7.20	3.75	3.69	6.87 ±2.79
Senescence	‐5.77	‐1.89	‐5.19	‐4.14	‐5.38	‐3.49	‐4.60	‐6.45	‐1.64	‐5.41	‐5.63	‐4.51 ±1.58

ARC = arcuate fasciculus; CC. Major = corpus callosum forceps‐major; CC. Minor = corpus callosum forceps‐minor; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; TR = thalamic radiations; UNC = uncinate fasciculus.

3.3. Limbic tracts

Life span trajectory scatterplots for the cingulum‐cingulate and cingulum‐hippocampus tracts are shown in the first two rows of Figures 3 and 4. The peak ages of the cingulum‐cingulate were intermediate relative to the other tracts (Figure 2). In contract, the cingulum‐hippocampus displayed exceptionally late maturation for MT, R1, R2*, g‐ratio, and MD. We observed a positive slope of MT, R1, and R2* during maturation that were moderate for the cingulum‐cingulate (MT/R1/R2*, 3.1%/3.5%/7.2%) but large for the cingulum‐hippocampus (7.2%/6.5%/12.2%). Negative slopes during senescence were generally moderate for both tracts although the cingulum‐hippocampus showed a particularly small decline in R2* (1.9%). The ODI developmental estimates in the cingulum‐hippocampus approximated a linearly increasing slope. The peak age and maturation estimates for ODI in the cingulum‐hippocampus should therefore be interpreted with caution and this uncertainty is reflected in the bootstrapped confidence interval of Figure 2. Across the other tissue measurements, the two tracts possessed relatively intermediate values of maturation and decline.

Figure 3.

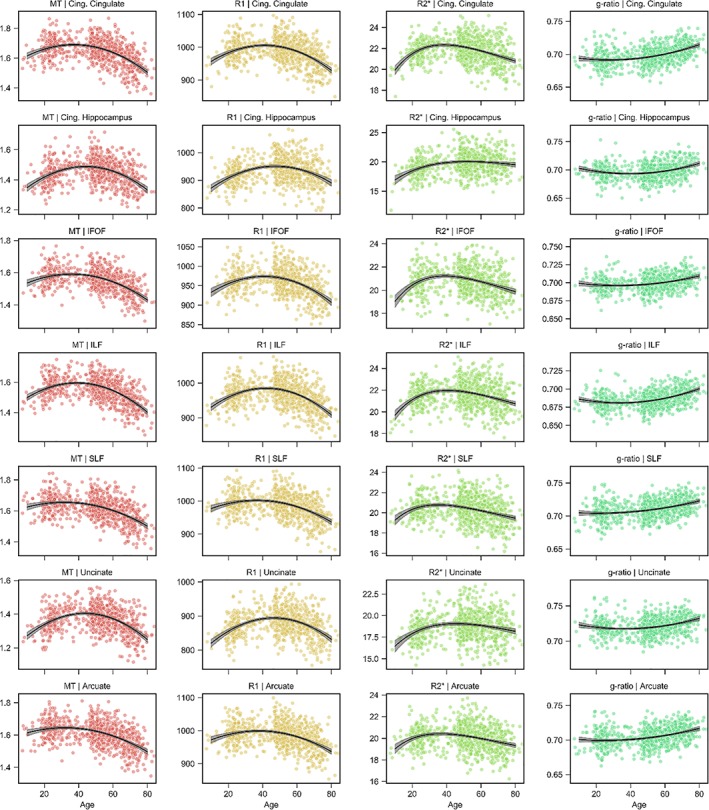
Association fiber trajectories for MT, R1, R2*, and g‐ratio. Scatterplots indicate the tract microstructure measurement distribution across the sample with age; black lines denote the aging regression line for quadratic (MT, R1, g‐ratio) or Poisson curve (R2*) models (gray shading 95% CI). Red: MT; orange: R1; green: R2*; turquoise: g‐ratio. ARC = arcuate fasciculus; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; TR = thalamic radiations; UNC = uncinate fasciculus [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 4.

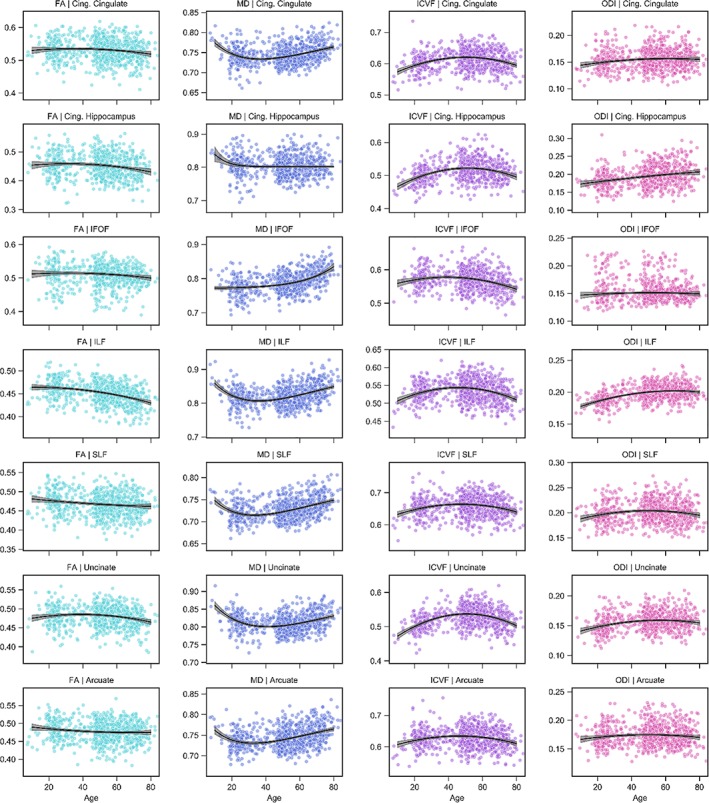
Association fiber trajectories for FA, MD, ICVF, and ODI. Scatterplots indicate the tract microstructure measurement distribution across the sample with age; black lines denote the aging regression line for quadratic (FA, ICVF, ODI) or Poisson curve (MD) models (gray shading 95% CI). Light blue: FA; dark blue: MD; purple: ICVF; pink: ODI. ARC = arcuate fasciculus; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4. Association tracts

The life span trajectories for the association fibers are shown in Rows 3–7 of Figures 3 and 4. The inferior fronto‐occipital fasciculus (IFOF) attains its peak value early for FA, MD, and ICVF while peaking at intermediate ages for all other tissue measures (Figure 2); the inferior longitudinal fasciculus (ILF) peaks early for FA, late for ODI and at intermediate ages for all other measurements; the superior longitudinal fasciculus (SLF) peaks relatively early for MT, R1, R2*, and g‐ratio with intermediate peak ages for the other measures; the uncinate fasciculus observes a late peak for MT and R1 with all other measurements taking intermediary ages; the arcuate fasciculus is the earliest to peak for MD and also peaks relatively early for MT, R1, and R2*. Of note, we see that the IFOF has a relatively small amount of difference during senescence for the g‐ratio (1.5%), a small amount of MD difference during maturation (1.3%) and a large amount of MD difference during decline (5.7%); the uncinate displays steep positive slope during development for ICVF (10.0%), MD (4.5%), MT (7.2%), R1 (6.5%), and R2* (10.4%); and the arcuate exhibits only a small difference during maturation for MD (1.1%).

3.5. Projection tracts

The aging trajectories of the thalamic radiation and corticospinal tract projection fibers are shown in the first two rows of Figures 5 and 6. The thalamic radiations typically peak at intermediate‐to‐late ages for all tissue measures excluding ODI, which peaks earlier than all pathways excluding the forceps minor of the corpus callosum. The corticospinal tract peaks late for the R1, R2*, and FA and, most notably, the ICVF measurements while peaking earliest for the g‐ratio. Across the remaining measures, the corticospinal tract peaks at intermediate values. Table 1 contains the percentage difference in tissue measurements during maturation and decline for the projection tracts. We highlight the large differences in FA (4.6%), ODI (11.3%), and R2* (6.5%) during senescence for the thalamic radiations; the corticospinal tract was particularly stable after peak maturation, exhibiting little difference during senescence for the ICVF (0.4%), MT (4.5%), R1 (3.0%), and R2* (1.6%) measures.

Figure 5.

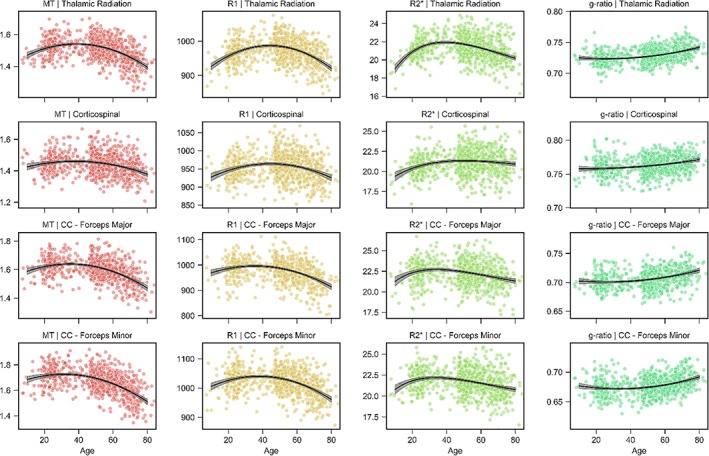
Projection and callosal fiber trajectories for MT, R1, R2*, and g‐ratio. Scatterplots indicate the tract microstructure measurement distribution across the sample with age; black lines denote the aging regression line for quadratic (MT, R1, g‐ratio) or Poisson curve (R2*) models (gray shading 95% CI). Red: MT; orange: R1; green: R2*; turquoise: g‐ratio. CC: Corpus callosum [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 6.

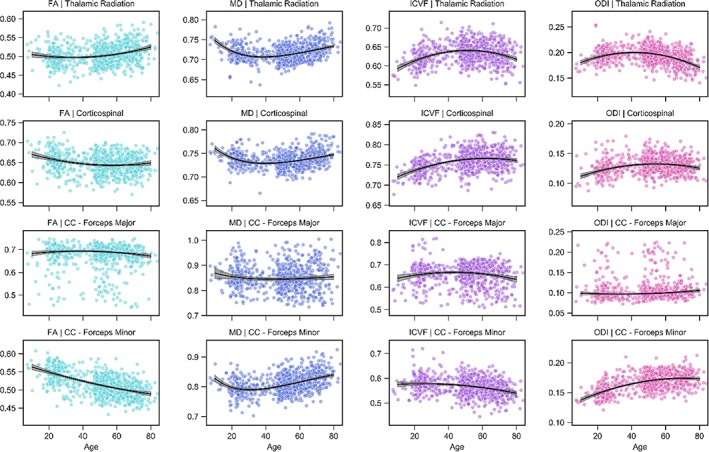
Projection and callosal fiber trajectories for FA, MD, ICVF, and ODI. Scatterplots indicate the tract microstructure measurement distribution across the sample with age; black lines denote the aging regression line for quadratic (FA, ICVF, ODI) or Poisson curve (MD) models (gray shading 95% CI). Light blue: FA; dark blue: MD; purple: ICVF; pink: ODI. CC: corpus callosum [Color figure can be viewed at http://wileyonlinelibrary.com]

3.6. Commissural tracts

The life span trajectory curves for the commissural tracts of the corpus callosum—the forceps major (occipital) and the forceps minor (frontal)—are presented in the bottom two rows of Figures 5 and 6. We observe that the commissural fibers are often some of the earliest to mature across the multiple tissue measurements (Figure 2). The forceps major peaks early across R1, R2*, g‐ratio, ICVF, and ODI measurements while peaking at relatively intermediate ages across the remaining tissue measures. Similarly, the forceps minor peaks particularly early across MT, R1, R2*, MD, and ICVF measurements while also peaking exceptionally late in FA and ODI measures, both of which are sensitive to alterations of fiber crossing and dispersion. The amount of tissue measurement difference during maturation and decline for the commissural fibers can differ quite substantially as compared to the other major tracts of the brain (Table 1). The forceps major displays little difference during maturation for R1 (1.8%) and R2* (3.8%), and senescence for MD (0.88%), while also following an inverted ODI trend, decreasing during maturation (1.3%) and increasing during senescence (7.5%); the forceps minor shows particularly large difference during maturation for FA (11.5%) and ODI (21.6%), small differences during maturation for ICVF (0.2%) and R2* (3.7%), with large differences during senescence for ICVF (5.6%), MD (5.7%), and MT (10.1%).

3.7. Tract associations with age, sex, image resolution, and hemisphere

Associations with age were predominantly nonlinear excluding FA, ODI, and g‐ratio measurements across a few isolated tracts (Figure 7 and Tables S1–S4, Supporting Information), indicating reducing tissue difference slopes with age up to a peak value before a reversal and steeping of slopes with further increases in age. These general aging curve trends lead to the inverted U‐shaped (e.g., MT, R1, R2*, ICVF) and U‐shaped (e.g., MD, g‐ratio) life span trajectories detailed in Figures 3, 4, 5, 6. Significant quadratic aging terms (p < 0.001) were consistently observed for MT (−2.15 ≤ $\widehat{\mathrm{\beta }}$≤ −1.08), R1 (−2.12 ≤ $\widehat{\mathrm{\beta }}$ ≤ −1.25), R2* (−1.49 ≤ $\widehat{\mathrm{\beta }}$ ≤− 0.8), g‐ratio (0.31 ≤ $\widehat{\mathrm{\beta }}$ ≤0.85), MD (0.73 ≤ $\widehat{\mathrm{\beta }}$ ≤2.04), and ICVF (−1.67 ≤ $\widehat{\mathrm{\beta }}$ ≤0.60) with a degree of spatial heterogeneity observed across tracts (Figure 8 and Tables S1–S4, Supporting Information). Quadratic associations with age were particularly robust in association (IFOF, ILF, SLF, arcuate, and uncinate fasciculi), thalamic radiation and cingulum bundles (Figure 7). In contrast, the corticospinal tract and callosal pathways generally exhibited more modest nonlinear associations with age. Significant though less consistent quadratic aging terms were observed for the water diffusion coherence measures of FA (−0.55 ≤ $\widehat{\mathrm{\beta }}$ ≤0.81) and ODI (−1.58 ≤ $\widehat{\mathrm{\beta }}$ ≤0.54; Tables S1–S4, Supporting Information). The quadratic aging model was found to provide a significantly better fit than a linear model for all metrics and tracts except for FA in the ILF for which older age was significantly associated with lower coherence of water diffusion ($\widehat{\mathrm{\beta }}$ = −0.43).

Figure 7.

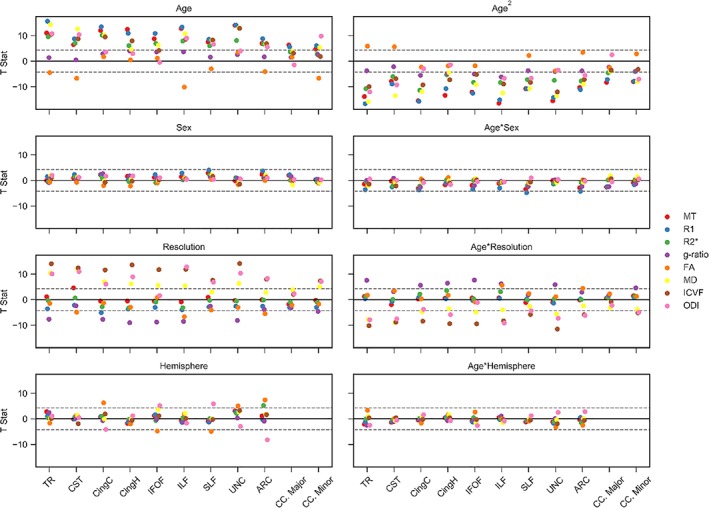
Tissue measurement associations with age, sex, resolution and hemisphere. GLMs were used to estimate T‐statistics for MT, R1, R2*, g‐ratio, FA, MD, ICVF, and ODI with age, sex, resolution, hemisphere, and their interactions with age. Male, high resolution and left hemisphere coded as 0. The valence of the g‐ratio and MD associations has been reflected for visualization purposes across each of the panels. Horizontal dashed gray lines display the FWE‐corrected significance level at p ≤ 0.001. Full details of the regression coefficients are provided in Tables S1–S4, Supporting Information [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 8.

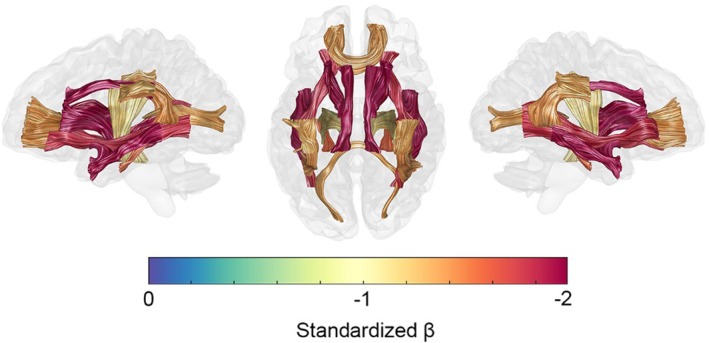
Spatial heterogeneity of R1 quadratic aging effects. A glass brain visualization with 20 major fascicles displayed on left‐lateral, superior, and right‐lateral views. Age2 coefficient values (standardized βs) are from the GLM model results detailed in Figure S1, Supporting Information [Color figure can be viewed at http://wileyonlinelibrary.com]

Sex differences and their interactions with age were modeled for all tracts and tissue measurements (Figure 7 and Tables S1–S4, Supporting Information). Sex differences were generally weak and inconsistent, with the only significant results showing trends for higher R1 in males in the SLF ($\widehat{\mathrm{\beta }}$ = 0.28) and arcuate fasciculus ($\widehat{\mathrm{\beta }}$ = 0.26). Interactions between age and sex were significant for R1 across the thalamic radiation, cingulum cingulate, IFOF, SLF, and arcuate fasciculus ($\widehat{\mathrm{\beta }}$ ≤ −0.27), and for MT in the SLF ($\widehat{\mathrm{\beta }}$ = −0.25), suggestive of a marginally higher association with age in females as compared to males.

Associations with MR imaging resolution were generally small and insignificant for MT, R1, and R2* with larger effects apparent for the diffusion derived MD, ODI, ICVF, and g‐ratio measurements. The lower resolution scans were typically associated with higher MD ($\widehat{\mathrm{\beta }}$ ≥ −0.71) and lower ODI, ICVF, and g‐ratio values ($\widehat{\mathrm{\beta }}$ ≤ 0.94). A secondary analysis in the subset of subjects with high‐resolution scans (n = 718) produced highly consistent age, sex, and hemisphere associations with those observed in the full data set (Figure S5, Supporting Information).

Asymmetries in tract microstructure were examined for all bilateral tracts (Figure 7 and Tables S1–S4, Supporting Information). Associations by hemisphere revealed left–right asymmetries in FA and ODI for several bilateral tracts. FA was higher and ODI lower in the left hemisphere for the cingulum‐cingulate (FA | ODI; $\widehat{\mathrm{\beta }}$ = 0.45 | $\widehat{\mathrm{\beta }}$ = −0.31) and the arcuate fasciculus ($\widehat{\mathrm{\beta }}$ = 0.52 | $\widehat{\mathrm{\beta }}$ = −0.57) and in the right hemisphere for the IFOF ($\widehat{\mathrm{\beta }}$ = −0.45 | $\widehat{\mathrm{\beta }}$ = 0.48) and SLF ($\widehat{\mathrm{\beta }}$ = −0.34 | $\widehat{\mathrm{\beta }}$ = 0.39). Further left‐sided asymmetries were observed with higher FA in the left uncinate fasciculus ($\widehat{\beta }$ = 0.41), higher R2* in the left arcuate ($\widehat{\beta }$ = 0.38) and lower MD in the left IFOF ($\widehat{\mathrm{\beta }}$ = −0.31). There were no significant associations between hemispheres for any of the MT, R1, g‐ratio, or ICVF measurements. Interactions between age and hemisphere were weak to nonexistent across all tracts and measurements excluding FA in the thalamic radiations, for which we observed a trend toward larger associations with age in the left versus right hemisphere ($\widehat{\mathrm{\beta }}$ = 0.26).

3.8. Spatial heterogeneity of g‐ratio

Peak g‐ratio values for the major WM fasciculi are presented in Figure 9. Tract specific g‐ratio values were found in the range 0.67–0.76, centered around the value used for calibration (g = 0.7, see Section 2.3.3). The forceps minor of the corpus callosum achieves the lowest value of all the fasciculi (g = 0.67). The association fibers of the brain and the forceps major reach intermediate g‐ratios centered around g = 0.7 (cingulum‐cingulate, g = 0.69; cingulum‐hippocampus, g = 0.69; IFOF, g = 0.7; ILF, g = 0.68; SLF, g = 0.70; uncinate, g = 0.71; arcuate, g = 0.70; forceps major, 0.70). The thalamic radiations (g = 0.72) and the corticospinal tract (g = 0.76) attain relatively higher peak g‐ratio values. Across all tracts, the g‐ratio remains reasonably stable around these peak values into the third decade (Figures 3 and 5). After this period of stability, g‐ratios are observed to begin increasing at ever accelerating rates with age (Table S2, Supporting Information). The cingulum‐cingulate, forceps major, and forceps minor show the greatest percentage difference from their peak up until age 75 (2.36–2.76%) while the corticospinal tract and IFOF exhibit the smallest percentage g‐ratio difference with increasing age (1.53 and 1.54%, respectively).

Figure 9.

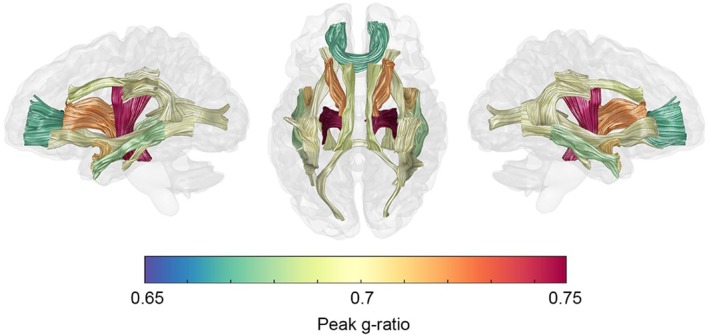
Spatial heterogeneity of peak g‐ratio values. A glass brain visualization with 20 major fascicles displayed on left‐lateral, superior, and right‐lateral views. Peak values were estimated from the peak age estimates of Figure 2 and the aging curves of Figures 3 and 5 [Color figure can be viewed at http://wileyonlinelibrary.com]

3.9. Retrogenesis of WM tracts

In support of the “last‐in‐first‐out” hypothesis, robust correlations (r ≥ 0.65) between age of peak maturation and quadratic aging effects were observed for MT (r = 0.81), R1 (r = 0.66), R2* (r = 0.65), and g‐ratio (r = 0.82) measurements (Figure 10). Conversely, peak age was negatively correlated with quadratic aging effect for ODI (r = −0.66). Weak and inconsistent correlations were seen for the FA (r = −0.23), MD (r = 0.12), and ICVF (r = 0.32) measurements. Across the MT, R1, R2*, and ICVF microstructure measurements, the corticospinal tract is a noticeable outlier, typically exhibiting weaker quadratic aging effects than the age of maturity would suggest.

Figure 10.

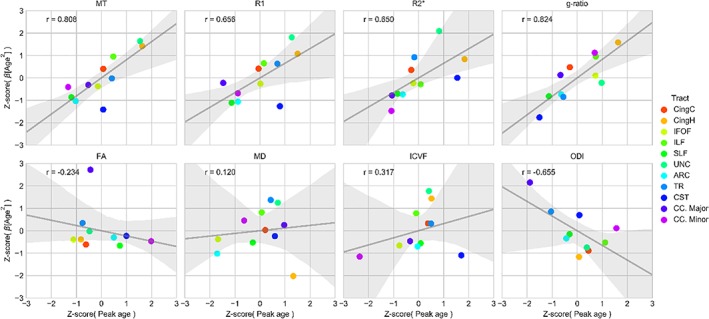
Testing the last‐in‐first‐out hypothesis of aging. The last‐in‐first‐out hypothesis predicts that a later developmental timing for a tract is associated with increased vulnerability on old age. The age of peak maturation was correlated with the quadratic aging effects of a tract across MT, R1, R2*, g‐ratio, FA, MD, ICVF, and ODI measurements. Gray line indicates linear regression line (shaded area 95% bootstrapped CI). Pearson's r correlation annotated in upper left of each box. ARC = arcuate fasciculus; CC. Major = corpus callosum forceps major; CC. Minor = corpus callosum forceps minor; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; TR = thalamic radiations; UNC = uncinate fasciculusforceps majorforceps minor [Color figure can be viewed at http://wileyonlinelibrary.com]

The “gain‐predicts‐loss” hypothesis necessitates symmetric developmental and aging trajectories relative to a peak. We find robust evidence for this hypothesis across MT, R1, and ICVF measures, which are best described by a symmetric quadratic aging model (Figures 3, 4, 5, 6). A quadratic aging model also best describes g‐ratio, FA, and ODI measurements though the quadratic aging effects, and therefore the evidence for symmetric maturation and decline, is less robust (Figure 8 and Tables S1–S4). R2* and MD measurements have highly asymmetric periods of maturation and decline which do not align well with the predictions of the “gain‐predicts‐loss” hypothesis.

4. DISCUSSION

This study contributes to our understanding of changes in WM microstructure across the human life span. We observe robust nonlinear aging effects across tissue measurements and tracts. Using a combination of qMRI measures, we demonstrate that R1, MT, and MD were the most sensitive parameters to aging effects across the major WM fascicles of the brain. After reaching a peak level of microstructural organization, the major WM tracts degrade with increasing age, losing myelin, decreasing in microstructural organization, and deviating from the optimal g‐ratio needed for efficient signal conduction.

A more detailed look at tract microstructure trajectories suggests that the brain maturation period between adolescence and mid‐adulthood could be associated with steeper positive slope of the estimates of myelination (MT, R1, R2*) and microstructural organization (FA, MD, ICVF, ODI) in association fasciculi and thalamic radiations. The corticospinal tract and corpus callosum segments follow similar trajectories during this period but with a smaller amount of microstructural difference, indicative of their early development and stability (Bartzokis et al., 2012; Kinney, Brody, Kloman, & Gilles, 1988; Yakovlev & Lecours, 1967; Yeatman et al., 2014). During senescence, we observe a reversal with aging associations that are in line with predicted life span trends, adding considerable support to the findings of past investigations (Callaghan et al., 2014; Chang et al., 2015; Cox et al., 2016; Kochunov et al., 2012; Lebel et al., 2012; Li et al., 2014; Saito, Sakai, Ozonoff, & Jara, 2009; Sexton et al., 2014; Westlye et al., 2010; Yeatman et al., 2014).

The estimates at which each tract reaches peak maturity are in good agreement with previous studies investigating life span differences in R1 (Yeatman et al., 2014) and MD (Hasan et al., 2010; Lebel et al., 2012; Westlye et al., 2010). The ages of peak maturation for the corticospinal tract and callosal connections vary more widely across microstructure measures and this may be reflective of their relative stability over the life span (weaker quadratic aging effects) and advanced levels of maturation before the end of adolescence (Lebel, Walker, Leemans, Phillips, & Beaulieu, 2008; O'Muircheartaigh et al., 2014; Tamnes et al., 2010). Sex differences were observed across five tracts for R1 but were generally weak and inconsistent, which corroborates previous findings with differences observed varyingly across corticospinal, cingulum, ILF, and forceps major tracts (Abe et al., 2002; Cox et al., 2016; Lebel et al., 2012; Ota et al., 2006). Hemispheric associations were most robustly observed for FA in the cingulum‐cingulate, IFOF, SLF, uncinate, and arcuate fasciculi. Across these tracts, leftward asymmetries were found for the cingulum‐cingulate, arcuate and uncinate fasciculi, and rightward asymmetries observed in the IFOF and SLF. These findings support published DTI studies reporting hemispheric differences in tract microstructure across various age ranges (Cox et al., 2016; Hasan et al., 2010).

One unique aspect of our investigation is the inclusion of g‐ratio measurements (Stikov et al., 2011; Stikov et al., 2015) in a large life span cohort of 801 subjects. Here, we demonstrate that peak g‐ratio levels have tract specific values in the range 0.67–0.76, consistent with previous findings in younger adults (20–40 years; Cercignani et al., 2016). This might be in part due to the similar method used for calibration. A comparison between the g‐ratio aging trajectories shown here and those calculated from myelin volume fraction obtained from PD estimates would be of high interest. PD‐based estimates of the g‐ratio do not require calibration (Berman et al., 2017; Duval et al., 2017) and differences arising from such a comparison might highlight changes in macromolecular content with age.

Our findings suggest that the largest investments in myelination for a given axonal caliber occur in the anterior callosal fibers (forceps minor) while conversely the lowest myelination investments occur in corticospinal fibers. Of the two previous life span g‐ratio studies, both had fewer than 100 participants which precluded the investigation of nonlinear associations with age (Berman et al., 2017; Cercignani et al., 2016). Here, with a much larger sample size, we observed quadratic aging effects for the g‐ratio across all tracts excluding the corticospinal tract and forceps major, both of which are well developed by young adulthood and showing a steady positive slope in their g‐ratio values thereafter. A contrasting report by Berman et al. (2017) found little evidence of g‐ratio associations with age in callosal subregions. This discrepancy may result from the linear models applied in their investigation and their lower density of subjects at higher ages, as our results suggest that the increasing steepness of the g‐ratio slope becomes most apparent from the third decade onward. The observed positive slope of g‐ratio across all tracts during senescence provides evidence of widespread demyelination processes in the aging human brain which cannot be explained as the sole consequence of axonal degeneration. Investigations in the experimental animal have shown extended periods of myelin degradation in aging primates in the absence of overt axonal loss (Peters, 2009; Peters & Sethares, 2003). However, it has been challenging to determine how translatable these findings are to human aging due to the shorter life span of rhesus monkeys (Tigges, Gordon, McClure, Hall, & Peters, 1988) and the extensive phylogenetic changes observed in human WM (Rilling et al., 2008; Schoenemann, Sheehan, & Glotzer, 2005). Our results provide empirical evidence of myelin sensitive degradation processes occurring in the human brain during normal aging.

Our findings of stronger age‐related FA decline in anterior relative to posterior brain regions replicate previous findings (for review, see Madden et al., 2012). Given the abundance of DTI studies investigating the impact of age on WM microstructure, there remains much controversy about the specificity of the DTI‐derived index of FA toward particular tissue property change. Consistent with a recent report looking at the effects of age on brain's WM using not only DTI‐derived metrics, but also T2 relaxation‐based estimates of myelin water fraction, we observed relatively weak relationships between FA and age in the majority of investigated WM tracts (Arshad, Stanley, & Raz, 2016). Along the same lines, FA and ODI showed the greatest variability and uncertainty in terms of peak age across all investigated WM tracts. These results might imply that for a subset of tracts FA and ODI measures increase/decrease monotonically over the life span and/or contain a relatively large amount of variance unaccounted for by our aging models. This lack of nonlinear association with age could reflect the fact that FA and ODI are sensitive to a mixture of fiber organizational properties that could vary even over the length of a tract (see Figure S3, Supporting Information), hampering the straightforward neurobiological interpretation of age‐related FA and ODI changes in the brain. Furthermore, both DTI and NODDI models are known to underestimate the complexity of the diffusion microstructure problem. We therefore advise cautious interpretation of the obtained FA and ODI results (Beaulieu, 2002; Jones et al., 2013; Novikov, Fieremans, Jespersen, & Kiselev, 2016; Veraart, Fieremans, & Novikov, 2019; Vos, Jones, Jeurissen, Viergever, & Leemans, 2012).

The estimation of the fiber g‐ratio involved the calibration of the MT values into estimates of myelin volume fraction. In‐line with (Cercignani et al., 2016; Mohammadi et al., 2015), this calibration was conducted using a healthy g‐ratio value of 0.7 in the splenium of a subset of young adults. Note that this calibration is made under the assumption that the ratio between myelin and other macromolecules, which both contribute to MT values, is uniform across WM and age (Campbell et al., 2017). Deviation from this assumption might result in inaccurate g‐ratio estimates. In the context of aging, cellular processes such as inflammation might lead to the detection of spurious change in g‐ratio values.

The noticeable differences in microstructural aging trends across the brain, in terms of both heterochronicity and spatial heterogeneity, provide support for the last‐in‐first‐out retrogenesis hypothesis of aging (Raz, 2000). We demonstrate a strong correlational relationship between peak maturational timing and the extent of quadratic measurement difference across the life span for the most myelin sensitive measures, suggesting a relationship between extended ontological development during adulthood and senescent vulnerability to myelin loss. This effect is also apparent when comparing tract aging curves side‐by‐side (Figure S6, Supporting Information). This supports the findings in post mortem and DWI studies which have reported distinct ontological differences between early myelinating projection and posterior callosal fibers, and the later developing frontal and association pathways (Huttenlocher & Dabholkar, 1997; Kinney et al., 1988; Lebel et al., 2012; Stricker et al., 2009; Westlye et al., 2010). Support for the last‐in‐first‐out hypothesis was less consistent for the DWI‐related measures. One recent study by Yeatman et al. (2014) formulating quantitative definitions for the retrogenesis hypotheses found in contrast to our results no direct evidence for the last‐in‐first‐out hypothesis using R1 and MD measurements. One potential explanation for this discrepancy comes from the differences in hypothesis formation. While we focused on peak timing predicting the rate of quadratic (accelerating) microstructure change either side of the peak, Yeatman et al. (2014) used a piecewise linear model to test the relationship between peak age and the duration of maturational stability (plateau). Our combined findings suggest that the late myelination of a region is predictive of relative levels of myelin reorganization (during decline and postadolescent maturation) but not the duration of peak maturational stability (Yeatman et al., 2014).

The gain‐predicts‐loss hypothesis (Reisberg et al., 2002) necessitates that symmetric aging trends should occur either side of a maturational peak. A cross‐validated model selection procedure designated a symmetric (quadratic) aging model for MT, R1, g‐ratio, FA, ICVF, and ODI measurements. R2* and MD displayed highly asymmetric aging trends which were better described using an asymmetric Poisson curve model. These findings are in good agreement with the Yeatman et al. (2014) assessment of the gain‐predicts‐loss hypothesis that found supportive evidence for R1 but not MD tissue measurements.

Our study population includes a representative subsample from the CoLaus (Firmann et al., 2008) | PsyCoLaus (Preisig et al., 2009) longitudinal cohort with available deep phenotyping for relevant cardiovascular risk factors, psychiatric comorbidities, level of education, socioeconomic status, to name but a few. Given the number and complexity of the presented brain imaging characteristics, we deliberately decided not to include any of the above‐mentioned variables in our statistical design and acknowledge this as potential limitation of our study. We excluded any individuals with known neurodegenerative or psychiatric disease and screened all imaging data for overt pathology or signs of neurovascular abnormalities. One potential concern for cross‐sectional study designs is that modeled trajectories may inaccurately describe within‐subject aging trends (Lindenberger, von Oertzen, Ghisletta, & Hertzog, 2011). Though the present study provides a well‐powered investigation into cross‐sectional aging trajectories, a full examination of intraindividual trends will require future prospective imaging studies which, in a fully longitudinal design, would require many decades of work to cover a comparable age range.

Given the lack of significant main effects of sex and its interaction with age on the tract specific measures of tissue properties, we abstained from controlling for head/brain size in our analyses. However, we acknowledge the potential impact of head/brain size on connectivity strength, which according to the Ringo hypothesis shows sex independent effects that could affect the obtained results (Hänggi, Fövenyi, Liem, Meyer, & Jäncke, 2014; Ringo, 1991). A further consideration for this study relates to the quality of the diffusion measurements and sampling schemes. The diffusion acquisition was made using a highly optimized sequence of 118 imaging volumes and preprocessed images underwent a detailed quality checking process. The tractography was performed using an automated procedure (Yeatman et al., 2012) which eliminated any investigator bias in tract definitions. Furthermore, the tract sampling scheme used here applies a Gaussian weighting function to weight points at the tract core more highly than peripheral streamlines, reducing the influence of partial volume effects at the tract periphery. Despite these controls, we cannot rule out the possibility of partial volume effects biasing certain tract microstructure measurements (Vos, Jones, Viergever, & Leemans, 2011) and as with previous investigations, we advise caution when interpreting the data. The cingulum‐hippocampus is a particularly difficult tract to delineate and although we observed only a weak streamline count correlation with age (r = −0.12), we advise caution when interpreting the results involving this tract.

In conclusion, this monocentric study provides an important contribution to our understanding of microstructural organization of the WM across the human life span. The well‐powered study sample of 801 individuals affords the description of detailed nonlinear aging trends across 20 major WM pathways of the brain. Heterochronicity and spatial heterogeneity across tracts and microstructure measurements highlights the importance of using multiple tissue measurements to investigate each region of the WM. Our data on g‐ratio evolution over the human life span provides novel aging associations and an important baseline from which to assess dysfunctional g‐ratio development and maintenance in a variety of psychiatric disorders (Du & Ongür, 2013). Furthermore, a quantitative assessment of the retrogenesis hypotheses of aging provides additional support for prolonged myelin maturation being associated with greater myelin reorganization and vulnerability with age. These findings present an important baseline from which to assess divergence from normative aging trends in developmental and degenerative disorders, and to further investigate the mechanisms connecting WM microstructure to cognition.

CONFLICT OF INTEREST

The authors do not have any conflicts of interest to declare.

Supporting information

Figure S1 Correlational relationships across tissue measurements in three example tracts. Pearson correlations (left) and partial correlations (right) were estimated across subjects in the cingulum cingulate, cortico‐spinal tract and uncinate fasciculus for all tract‐parameter combinations

Figure S2. Tract segmentations in a representative individual. Tracts dissected using an automated fiber identification procedure on whole brain tractograms. Tracts are rendered in left‐lateral, superior, and right‐lateral views

Figure S3. Consistency of aging parameters along tract profiles. MRI tissue measurements were sampled along the length of three representative tracts (the cortico‐spinal, corpus callosum forceps minor, and the uncinate fasciculus) before fitting the same aging models used to fit the tract averaged measures. Peak value and Age2 (quadratic aging) effects at each segment along a tract were normalized by the average estimate along the tract length, providing a measure of deviation from the tract average at any point along the length

Figure S4. SDR2* values in white matter computed from the PDw and T1w data in the 1 and 1.5 mm data sets. This parameter is a measure of intra‐scan motion artifact, validated against the history of the motion during the scans. SDR2* values below 4 s⁻¹ are typically observed in the absence of head motion at 1.5 mm³ resolutions and below 4.35 s⁻¹ at 1 mm³ resolution

Figure S5. Tissue measurement associations with age, sex, and hemisphere in all subjects imaged at the higher resolution (n = 718). GLMs were used to estimate T‐statistics for MT, R1, R2*, g‐ratio, FA, MD, ICVF, and ODI with age, sex, hemisphere, and their interactions with age. Associations were highly consistent to models results when including the additional low‐resolution subjects (see Figure 7). Male and left hemisphere coded as 0. The valence of the g‐ratio and MD associations has been reflected for visualization purposes across each of the panels. Horizontal dashed gray lines display the FWE‐corrected significance level at p ≤ 0.001

Figure S6. Side‐by‐side comparisons of tract aging trajectories for three example tissue measures. The data used to visualize these curves are the same as that used in Figures 3–6. We provide these additional representations to help highlight the differences in maturational timing and extent for the aging curves of different white matter tracts. ARC = arcuate fasciculus; CingH = cingulum‐hippocampus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; UNC = uncinate fasciculus

Table S1 Regression models of age, sex, hemisphere, and resolution on tract‐averaged white matter MT and R1. Standardized βs (p values) and adjusted R ² reported. Associations significant at p < 0.001 (uncorrected) highlighted in bold. Male, high resolution and left hemisphere coded as 0. ARC = arcuate fasciculus; CC. Major = corpus callosum forceps major; CC. Minor = corpus callosum forceps minor; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; TR = thalamic radiations; UNC = uncinate fasciculus

Table S2. Regression models of age, sex, hemisphere, and resolution on tract‐averaged white matter R2* and g‐ratio. Standardized βs (p values) and adjusted R ² reported. Associations significant at p < 0.001 (uncorrected) highlighted in bold. Male, high resolution and left hemisphere coded as 0. ARC = arcuate fasciculus; CC. Major = corpus callosum forceps major; CC. Minor = corpus callosum forceps minor; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; TR = thalamic radiations; UNC = uncinate fasciculus

Table S3. Regression models of age, sex, hemisphere, and resolution on tract‐averaged white matter FA and MD. Standardized βs (p values) and adjusted R ² reported. Associations significant at p < 0.001 (uncorrected) highlighted in bold. Male, high resolution and left hemisphere coded as 0. ARC = arcuate fasciculus; CC. Major = corpus callosum forceps major; CC. Minor = corpus callosum forceps minor; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; TR = thalamic radiations; UNC = uncinate fasciculus

Table S4. Regression models of age, sex, hemisphere, and resolution on tract‐averaged white matter ODI and ICVF. Standardized βs (p values) and adjusted R ² reported. Associations significant at p < 0.001 (uncorrected) highlighted in bold. Male, high resolution and left hemisphere coded as 0. ARC = arcuate fasciculus; CC. Major = corpus callosum forceps major; CC. Minor = corpus callosum forceps minor; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; TR = thalamic radiations; UNC = uncinate fasciculus

Table S5. Regression models of age, sex, hemisphere, and resolution on AFQ derived mm³ tract volume estimates. Standardized βs (p values) and adjusted R ² reported. Associations significant at p < 0.001 (uncorrected) highlighted in bold. Male, high resolution and left hemisphere coded as 0. ARC = arcuate fasciculus; CC. Major = corpus callosum forceps major; CC. Minor = corpus callosum forceps minor; CingC = cingulum‐cingulate; CingH = cingulum‐hippocampus; CST = corticospinal tract; IFOF = inferior fronto‐occipital fasciculus; ILF = inferior longitudinal fasciculus; SLF = superior longitudinal fasciculus; TR = thalamic radiations; UNC = uncinate fasciculus

Slater DA, Melie‐Garcia L, Preisig M, Kherif F, Lutti A, Draganski B. Evolution of white matter tract microstructure across the life span. Hum Brain Mapp. 2019;40:2252–2268. 10.1002/hbm.24522