Evaluation of different cerebrospinal fluid and white matter fMRI filtering strategies—Quantifying noise removal and neural signal preservation

Abstract

This study examines the impact of using different cerebrospinal fluid (CSF) and white matter (WM) nuisance signals for data‐driven filtering of functional magnetic resonance imaging (fMRI) data as a cleanup method before analyzing intrinsic brain fluctuations. The routinely used temporal signal‐to‐noise ratio metric is inappropriate for assessing fMRI filtering suitability, as it evaluates only the reduction of data variability and does not assess the preservation of signals of interest. We defined a new metric that evaluates the preservation of selected neural signal correlates, and we compared its performance with a recently published signal–noise separation metric. These two methods provided converging evidence of the unfavorable impact of commonly used filtering approaches that exploit higher numbers of principal components from CSF and WM compartments (typically 5 + 5 for CSF and WM, respectively). When using only the principal components as nuisance signals, using a lower number of signals results in a better performance (i.e., 1 + 1 performed best). However, there was evidence that this routinely used approach consisting of 1 + 1 principal components may not be optimal for filtering resting‐state (RS) fMRI data, especially when RETROICOR filtering is applied during the data preprocessing. The evaluation of task data indicated the appropriateness of 1 + 1 principal components, but when RETROICOR was applied, there was a change in the optimal filtering strategy. The suggested change for extracting WM (and also CSF in RETROICOR‐corrected RS data) is using local signals instead of extracting signals from a large mask using principal component analysis.

1. INTRODUCTION

Data from functional magnetic resonance imaging (fMRI) based on the blood oxygenation level‐dependent (BOLD) signal (Ogawa et al., 1990) are burdened by a relatively large amount of noise. The fMRI noise is a manifestation of many different confounding sources, such as thermal motion, instabilities of the MR scanner, and the vital functions and motion of the scanned subject (Liu, 2016). Many approaches for filtering noise from fMRI data have been introduced (for a comprehensive review, see Caballero‐Gaudes and Reynolds, 2017). The two main types of filtering options differ substantially: nuisance signals (which are regressed out of the data) can be computed using a mathematical model or they can be data‐driven. The mathematical modeling methods involve using the simultaneously measured data of another modality (e.g., ECG/pulse oximetry, pneumatic belt for breathing measurement), and this data is used as a basis for noise modeling (Birn et al., 2008; Chang et al., 2009; Chang and Glover, 2009; Glover et al., 2000). The data‐driven method extracts nuisance signals directly from fMRI data using various techniques, including multivariate decomposition methods such as principal component analysis (PCA) and/or independent component analysis (ICA) (Behzadi et al., 2007; Thomas et al., 2002). The use of such decomposition methods is based on the assumption that they can separate useful signals and noise.

Noise management is important especially in connectivity analyses, that is, when computing seed functional connectivity (FC) (Weissenbacher et al., 2009), in graph theory analysis based on FC (Gargouri et al., 2018) and in analyses studying task‐modulated intrinsic fluctuations where noise management also plays a role, for example, in psychophysiological interactions (Barton et al., 2015). This is because the complicated spatiotemporal structure of noise (Jo et al., 2010) introduces (even long‐distance) correlations to the data, and hence, the connectivity estimate can be biased.

In this work, we focus on data‐driven filtering of fMRI data using extracted cerebrospinal fluid (CSF) and white matter (WM) signals. These nuisance signals are commonly used for filtering fMRI data, because it is thought that signals of neural origin are not present in CSF/WM compartments, that is, the CSF/WM signals reflect only the physiological/hardware noise that contaminates even gray matter (GM), which is the compartment of interest. From this point of view, it seems plausible to use such nuisance signals as estimates of noise and to regress them out of the data to increase the signal‐to‐noise ratio (SNR) in GM. However, evidence has emerged that CSF and WM compartments also contain fluctuations related to neural activity (Gawryluk et al., 2014; Renvall et al., 2014), especially when using scanners with stronger magnetic induction (Mazerolle et al., 2013).

A commonly used approach for computing CSF‐ and WM‐related nuisance signals is based on extracting the fMRI time series from the CSF and the WM masks, respectively, and on the subsequent computation of representative signals using the PCA (Liu, 2016). These PCA component time series are then regressed out of the data. The original PCA‐based correction method (CompCor; Behzadi et al., 2007) was followed by advanced version of the method (Soltysik et al., 2015). These methods were primarily validated on task‐based fMRI data for improving the detection power of activations linked directly to performing a given task. A substantial step in such a scenario is the orthogonalization step, that is, nuisance signals are orthogonalized to signals of interest, that is, the time course of the task BOLD signal—the “ground truth” signal. This step ensures the correctness of the filtering—noise is removed and the signal(s) of interest, that is, modeled task activation(s), are preserved in the data. Such PCA‐based filtering approaches are also commonly used for connectivity analyses as a clean‐up step before analysis (Caballero‐Gaudes and Reynolds, 2017). The original paper introducing this basic PCA‐based denoising method, however, cautioned that “Finally, this exclusion approach is not easily extended to resting‐state (RS) experiments aimed at studying functional connectivity. Future work addressing the applicability of CompCor to these types of studies would be useful.” (Behzadi et al., 2007). This is because the knowledge of what “signals of interest” is often unknown in the RS fMRI and in experiments studying task‐modulated intrinsic fluctuations/connectivity (Cole et al., 2014), and therefore, the orthogonalization step cannot be performed. For example, when extracting the fMRI time series from a specific GM region of interest serving as a seed for FC, these time series contain signals of interest but also include variability originating in noise processes.

The next issue related to using such a method practically is deciding how many top PCA components from the CSF and WM compartments should be chosen and then regressed out from the data. The original CompCor paper (Behzadi et al., 2007) and a more recent methodological paper using CompCor (Muschelli et al., 2014) suggest estimating these numbers using different criteria. The original paper evaluates the number of top components that are “meaningful,” that is, not the result of random noise in data; the more recent paper uses arbitrary criterion—the set of CSF/WM signals (i.e., top CSF/WM components) must explain at least 50% of the time‐series variance in CSF/WM compartments. Both such estimations are subject‐specific. In fact, the numbers of PCA components are often taken as “fixed” (Caballero‐Gaudes and Reynolds, 2017) in fMRI‐based neuroimaging. For example, five CSF and five WM PCA signals are used as the default settings in the CONN toolbox (https://www.nitrc.org/projects/conn) and in many other studies using different software (e.g., Baniqued et al., 2018); there are also studies involving other fixed numbers of these nuisance PCA‐based signals, for example, a recent fMRI FC study by Tillman (Tillman et al., 2018) used three CSF and three WM signals.

Because the nuisance signals are regressed out in a voxel‐by‐voxel manner, the evaluation of such filtering is often based on assessing the resulting fMRI signal modification in individual voxels. This is commonly done by evaluating the decrease in temporal standard deviation (SD), or alternatively the increase in the temporal SNR (tSNR), defined as the ratio between the mean value of the fMRI signal over time to its SD (Behzadi et al., 2007; Curtis and Menon, 2014). The tSNR approach was originally used in studies assessing the quality of fMRI data acquisition (Gonzalez‐Castillo et al., 2011; Kruger et al., 2001) and then became routinely used for data filtering performance. For data filtering, nevertheless, we should not define the best filtering as the one that “improves” the tSNR most, that is, reduces the data variability most (assuming that the filtering does not influence the filtered signal's mean), because the data variability bears not only the noise but also the BOLD signals of interest, and the tSNR metric does not distinguish between these two sources of variability. If all the variability were to be regressed out from the data, it would cause zero SD of the fMRI signals (i.e., there would be no time evolution of the BOLD signal, just a series of identical brain scan volumes). Such an “ideal” filtering would result in tSNR ~∞. Of course, this is an extreme example, but practically, with a very high number of regressors involved in the filtering design matrix, the tSNR would increase rapidly and the BOLD signals would be severely suppressed. This limitation of the tSNR metric for evaluating SNR of BOLD‐related fluctuations was confirmed by a recent study (DeDora et al., 2016) using an fMRI phantom as the ground‐truth model.

The aim of this study is to examine the suitability of this type of filtering using different numbers of CSF/WM PCA components derived from differently defined CSF/WM masks. Also, more locally specific nuisance signals, reflecting potentially distinct noise processes in different parts of the CSF/WM compartments, are used as additional noise estimates to evaluate their filtering properties. As a tool for this evaluation, we use a combination of two metrics evaluating nuisance regression strategies, taking into account the preservation of neural‐related BOLD signals that manifest in fMRI data as a correlation structure of interest. We define the first metric to reflect the reduction of data variability with respect to the preservation of large‐scale brain network‐related variability. This metric is mathematically defined as a ratio between two measures: (a) the percentage of complete data variance explained by nuisance regressors and (b) the signal of interest variance explained by the nuisance regressors. The signals of interest are derived as time courses of ICA components representing intrinsic fluctuations of well‐known neural networks (and additionally, the task BOLD signal in task data). The evaluation of the first metric enables the assessment of the performance of particular CSF/WM filtering variants in terms of preserving the signal of interest and suppressing the noise, that is, improving the potential for BOLD SNR; later in the text, this metric is denoted as impBSNR (for a detailed explanation, see Section 2.4.1). The second metric used, published by Shirer (Shirer et al., 2015), is signal–noise separation or SNS. The SNS metric tells how different filtering strategies preserve valid FC, that is, correlations between pairs of neural network in‐brain regions, and how they suppress FC between the in‐brain regions and voxels outside the brain. The rationale of the second metric is that the true FC exists between the in‐brain regions of particular neural networks, and that the potential existence of FC between the brain and the regions outside the brain is, apparently, artificial. For a demonstration of this phenomenon, see Figure 3 in (Jo et al., 2010), which clearly shows that nuisance signals derived from the inside of the brain can correlate with the noise in the out‐brain voxel time series, suggesting that there is noise correlation structure that is present also across the GM in‐brain voxels but is not specific to the brain.

It can be assumed that after the impBSNR and SNS are computed, these metrics will provide very similar results because they both reflect a similar quality of the (filtered) data. If true, the final step is to generalize the results by combining these two metrics. This evaluation is done specifically for task data and RS data separately, because the character of neural signal patterns presumably differs between task and RS data in terms of spatial extent and BOLD amplitude (Arbabshirani et al., 2013) and in overall network configurations, for example, local/global efficiencies and modular integrations (Di et al., 2013). The whole evaluation of different data‐driven filtering approaches is tested on data with and without a model‐based correction for physiological noise, RETROICOR (Glover et al., 2000), to test whether the suggested form of data‐driven filtering differs for preprocessing involving model‐based filtering. This is motivated by an observation reported in the seminal CompCor paper (Behzadi et al., 2007) suggesting that RETROICOR filtering and data‐driven CSF/WM filtering have similar effects. However, in a study of model‐based filtering (Reynaud et al., 2017), both the model‐driven and data‐driven filtering were used together; this combined approach is often used in functional neuroimaging studies in general. As a last step, recommendations derived from the two metrics are formulated and conclusions about preferred filtering forms are tested for validation on the simple examples of task‐based and RS‐based connectivity. We focused on the task‐based connectivity of regions implicated in selected tasks and task‐based and RS‐based connectivity of the intrinsic BOLD signal fluctuations of the default mode network (DMN) (Raichle and Snyder, 2007) with a focus on its main hub, the precuneus (Utevsky et al., 2016). We have chosen the precuneus because it has widespread connections with other brain regions, suggesting its importance in a wide spectrum of information processing and cognitive functions (Cavanna and Trimble, 2006).

2. MATERIALS AND METHODS

The current study uses four data sets, each consisting of task data and RS data. The impBSNR metric uses a set of neural‐linked BOLD signals to assess CSF/WM data‐driven filtering of cortical and subcortical GM by nuisance signals obtained by different extraction options. The next step is to generalize these results, that is, to find a universal indication of how to optimally preprocess the fMRI data using data‐driven filtering. The SNS metric is computed for all data sets and generalized across the data sets in the same way as the impBSNR metric.

We used various approaches to compare different options for extracting CSF and WM signals. Different areas for signal extraction and different numbers of signals are tested, including different numbers of nuisance PCA components from CSF/WM compartments and/or “local” nuisance signals (i.e., signals from particular single voxels/spheres located in distinct areas of CSF/WM compartments). The CSF/WM masks defined with various strictness and/or spatial extents are used to demarcate particular compartments. Testing the different areas for signal extraction makes it possible to examine whether different compartment areas can provide different information about the underlying noise structure. For example, Sweetman and Linninger showed that the pattern of liquor flow during the cardiac cycle varies in different parts of the CSF compartment (Sweetman and Linninger, 2011); different areas of WM may also contain different noise components.

The four used data sets were acquired on a 3T scanner but differ in acquisition parameters, especially in the number of volumes and TRs (time to repeat, i.e. scan time)—two data sets' TRs are long, that is, ≥2 s; the other two data sets' TRs are short, that is, <720 ms. The kinds of tasks were the second factor of variability between data sets—two tasks have no explicit motor output; the other two involve motor output that can cause different noise patterns because of imposing more task‐correlated noise to the data (Seto et al., 2001). In all data sets, the physiological recordings, that is, heartbeat and breathing, were available. We excluded all subjects with inadequate quality of physiological recordings, poor fMRI data coverage, or insufficient task performance. See Table 1 for a brief overview of data set fMRI acquisition settings, final numbers of subjects, and tasks used. Detailed information about all data sets including removed subjects is in the Supporting Information Supplementary Methods Section S.1.1.

Table 1.

Overview of used data sets—every data set consists of a task session and RS session with the same or very similar acquisition settings (Data set 2). N values represent the number of subjects, F represents number of females

Data set	Task	Volumes	Task TR (ms)	RS TR (ms)	N (F)	Age mean (±SD) (years)
1	Visual—checkerboards versus rest	156	2,000	2,000	19 (10)	24.8 (±3.4)
2	Aperception test—keypresses	200	2,490	2,480	26 (13)	25.6 (±4.2)
3	Semantic decision task—silent reading of sentences versus string viewing	660	650	650	19 (11)	24.7 (±3.8)
4	Reading task—overt reading of nonwords versus simple checkerboard viewing	665	704	704	25 (12)	23.3 (±2.9)

2.1. Preprocessing of fMRI and structural data

All fMRI data sets were preprocessed in SPM12 (Functional Imaging Laboratory, Wellcome Department of Imaging Neuroscience, Institute of Neurology at University College London, UK). Every data set was preprocessed in two different ways—without RETROICOR (NC, not corrected) and with RETROICOR (RC, RETROICOR corrected). The preprocessing pipeline contained realign and unwarp; filtering with RETROICOR (RC variant only) in a slice‐wise fashion respecting the original timing of particular slices (Jones et al., 2008); co‐registration of high‐resolution anatomical image to mean functional scan; normalization of high‐resolution anatomical image to standard MNI space and segmentation into (MNI‐normalized) segments of GM, WM, and CSF; normalization of functional data to standard stereotactic space (Montreal Neurological Institute, MNI) using normalization parameters estimated from the co‐registered anatomical image; and smoothing of functional data using isotropic Gaussian kernel with full with half maximum of 5 mm FWHM.

Individual high‐resolution structural T1‐weighted images were segmented using a standard Statistical Parametric Mapping (SPM) 12 segmentation procedure to obtain subject‐specific probability maps of GM, WM, and CSF. All these probability maps were resampled to the resolution of fMRI data.

2.2. Versions of CSF signal extraction

We tested 19 versions of CSF signal extraction. All variants of CSF extraction are listed in Table 2. We used two general CSF templates with different spatial extents—a mask of the lateral ventricles (LV) and a mask of the ventricular system (VS) including the LV, third ventricle, fourth ventricle, and superior cistern. We then used restricted variants of these two templates—we restricted it with a group‐specific CSF mask—to obtain lateral ventricles (group‐specific) (LVGS) and ventricular system (group‐specific) (VSGS) variants. The group‐specific CSF mask was taken as the next mask variant of the CSF compartment, spanning voxels from the whole‐brain CSF compartment including cortical subarachnoid space. From these five masks, we extracted the time series of all in‐mask voxels, computed PCA, and used:

Table 2.

Overview of CSF extraction variants with corresponding abbreviations used in subsequent figures in the Result section

Variant and abbreviation	Type of extraction	Number of signals	CSF mask
(1) 1LV	PCA	1	Lateral ventricles (general template)
(2) 1LVGS	PCA	1	Lateral ventricles (group‐specific)
(3) 1VS	PCA	1	Ventricular system (general template)
(4) 1VSGS	PCA	1	Ventricular system (group‐specific)
(5) 1CSFallGS	PCA	1	Group‐specific CSF mask
(6) 2LV	PCA	2	Lateral ventricles (general template)
(7) 2LVGS	PCA	2	Lateral ventricles (group‐specific)
(8) 2VS	PCA	2	Ventricular system (general template)
(9) 2VSGS	PCA	2	Ventricular system (group‐specific)
(10) 2CSFallGS	PCA	2	Group‐specific CSF mask
(11) 5LV	PCA	5	Lateral ventricles (general template)
(12) 5LVGS	PCA	5	Lateral ventricles (group‐specific)
(13) 5VS	PCA	5	Ventricular system (general template)
(14) 5VSGS	PCA	5	Ventricular system (group‐specific)
(15) 5CSFallGS	PCA	5	Group‐specific CSF mask
(16) 4V	Single voxels	4	Left, right/anterior, posterior horns of lateral ventricles from group‐specific mask
(17) 4Sp	Mean from spherical ROIs	4	Left, right / anterior, posterior horns of lateral ventricles from group‐specific mask
(18) 6V	Single voxels	6	Left, right/anterior, posterior horns of lateral ventricles; third ventricle; superior cistern from group‐specific mask
(19) 6Sp	Mean from spherical ROIs	6	Left, right/anterior, posterior horns of lateral ventricles; third ventricle; superior cistern from the group‐specific mask

One top PCA time series—Variants 1 to 5 in Table 2,

Two top PCA time series—Variants 6 to 10 in Table 2, and

Five top PCA time series—Variants 11 to 15 in Table 2.

General masks of the LV and VS were created from the SPM template of CSF—this probability map was thresholded at 0.5, and particular compartments were delineated manually. The group‐specific CSF mask was computed as an intersection of individual (subject‐specific) thresholded CSF masks obtained from a segmentation procedure of anatomical images; these individual masks were thresholded at 0.5. The group masks were computed for every data set separately.

We also extracted sets of signals from distinct regions of the whole compartment: these consisted of four and six single voxels from the group‐specific CSF mask, Variants 16 and 18, respectively, in Table 2, and four and six mean signals from clusters constructed as intersections of spheres (radius 1 cm) with the group‐specific CSF mask, Variants 17 and 19, respectively, in Table 2; for the location of the extraction areas for Variants 16 to 19, see Table 2, and for their exact coordinates, see Supporting Information Supplementary Table 1.

As an example, all CSF masks for Data set 1 are depicted in Figure 1. It is clear that templates restricted with group‐specific CSF mask contain fewer voxels, warranting better specificity (i.e., a lower probability of partial volume artifacts contaminating the extracted signals with signals from the subcortical GM, for example, caudate nucleus). The group‐specific CSF mask alone, without intersection with CSF templates, contains voxels adjacent to the cortical surface; this increases the risk of accidentally extracting signals from the cortical GM.

Figure 1.

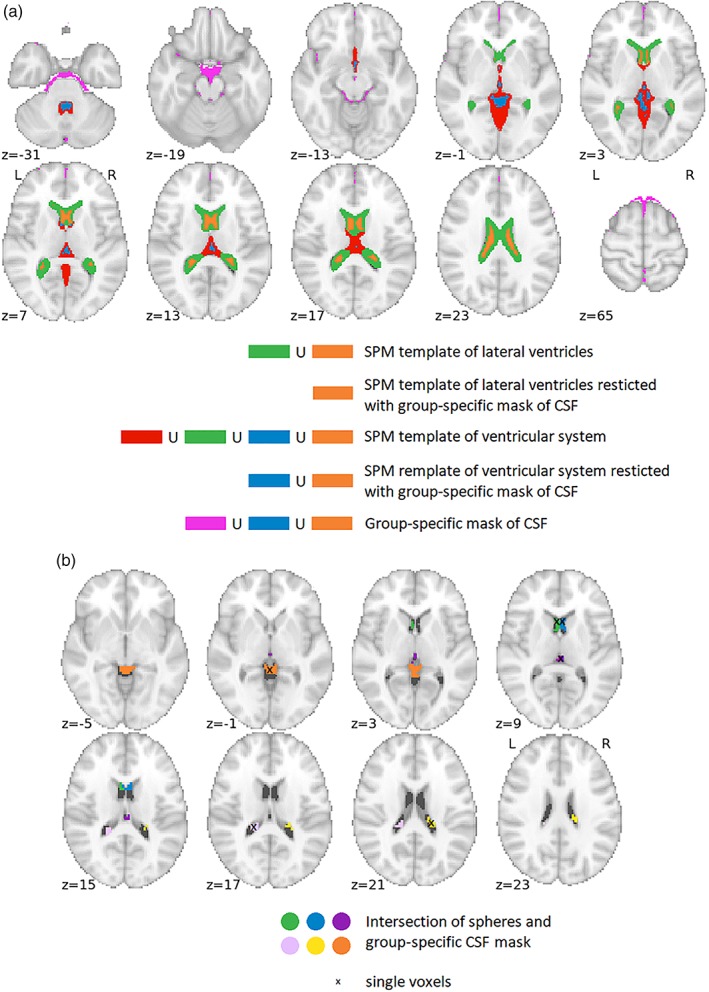
Masks for CSF signal extraction for Data set 1; (a) masks corresponding to Variants 1 to 15 from Table 2; (b) masks corresponding to Variants 16 to 19. The ∪ stands for union operation. Coordinates for single voxels/sphere centers (x, y, z) in millimeters in the standard MNI space: anterior horn of right lateral ventricle (3, 14, 8); anterior horn of left lateral ventricle (−3, 14, 8); posterior horn of right lateral ventricle (18, −31, 20); posterior horn of left lateral ventricle (−18, −37, 17); third ventricle (0, −25, 8); and superior cistern (0, −40, −1) [Color figure can be viewed at http://wileyonlinelibrary.com]

2.3. Versions of WM signal extraction

We tested eight versions of WM signal extractions (see Table 3). Again, we used a general template and a data‐derived mask of the WM compartment. The general template was created as an SPM WM probability map thresholded at a value of 0.9; for the WM template, a different threshold value than the one used with the CSF template (0.5) was used because of the incomparable probabilistic values of CSF and WM and to properly separate WM from GM in the proximity of the cortical sulci and at the subcortical GM (despite this, the volume of “central” WM mass remained large). The group‐specific WM mask was computed as the intersection of individual thresholded WM masks obtained from a segmentation procedure of anatomical images; these individual masks were thresholded at 0.9. The group masks were computed for every data set separately. We also extracted sets of signals from distinct regions of the whole compartment: these consisted of four single voxels from the group‐specific WM mask, Variant 7 in Tables 3 and 4 mean signals from clusters constructed as intersections of spheres (radius 1 cm) with the group‐specific WM mask, Variant 8 in Table 3; for the location of the extraction areas for Variants 7 and 8, see Table 3, and for their exact coordinates, see Supporting Information Supplementary Table 1.

Table 3.

Overview of WM extraction variants with corresponding abbreviations used in subsequent figures in the Result section

Variant of WM mask & abbreviation	Type of extraction	Number of signals	WM mask
(1) 1SPM	PCA	1	Thresholded SPM template
(2) 1GS	PCA	1	Group‐specific WM map
(3) 2SPM	PCA	2	Thresholded SPM template
(4) 2GS	PCA	2	Group‐specific WM map
(5) 5SPM	PCA	5	Thresholded SPM template
(6) 6GS	PCA	5	Group‐specific WM map
(7) 4V	Single voxels	4	Left, right/anterior, posterior WM mass
(8) 4Sp	Mean from spherical ROIs	4	Left, right/anterior, posterior WM mass

Table 4.

Overview of significant differences between group medians of unnormalized impBSNR values and value of 1 across different CSF/WM filtering variants. Every cell contains two percentage ratios, impBSNR >1/ impBSNR <1; the higher and lower counts of impBSNR >1 compared to impBSNR <1 are marked in italic and bold, respectively

Data set 1	Winning	Equivalent	One PCAs strict	Five PCAs strict	Five PCAs large
Task NC	87.5/0	75/0	87.5/0	75/0	50/0
Task RC	75/0	75/0	75/0	50/0	12.5/0
RS NC	66.7/0	0/0	0/0	0/33.3	0/50
RS RC	16.7/0	0/0	0/0	0/0	0/50

Data set 2	Winning	Equivalent	1 PCAs strict	5 PCAs strict	5 PCAs large
Task NC	75/0	87.5/0	75/0	75/0	87.5/0
Task RC	75/0	25/0	75/0	50/16.7	50/0
RS NC	83.3/0	33.3/0	66.7/0	33.3/0	33.3/0
RS RC	50/0	33.3/0	50/0	33.3/0	0/0

Data set 3	Winning	Equivalent	1 PCAs strict	5 PCAs strict	5 PCAs large
Task NC	25/25	25/16.7	25/25	25/50	12.5/62.5
Task RC	25/25	25/37.5	25/50	16.7/75	0/75
RS NC	0/0	0/0	0/0	0/66.7	0/100
RS RC	0/33.3	0/16.7	0/33.3	0/100	0/100

Data set 4	Winning	Equivalent	1 PCAs strict	5 PCAs strict	5 PCAs large
Task NC	37.5/0	37.5/0	25/0	37.5/50	25/50
Task RC	25/0	37.5/0	25/0	25/62.5	12.5/62.5
RS NC	50/16.7	0/0	16.7/0	16.7/50	0/66.7
RS RC	16.7/0	0/0	0/33.3	0/66.7	0/100

As an example, all WM masks for Data set 1 are depicted in Figure 2. It is clear that the group‐specific WM mask contains more voxels in the callosal WM, whereas the mask derived from the SPM template contains voxels adjacent to cortical GM and voxels probably overlapping with subcortical GM. This suggests better sensitivity and specificity of the group‐specific WM mask.

Figure 2.

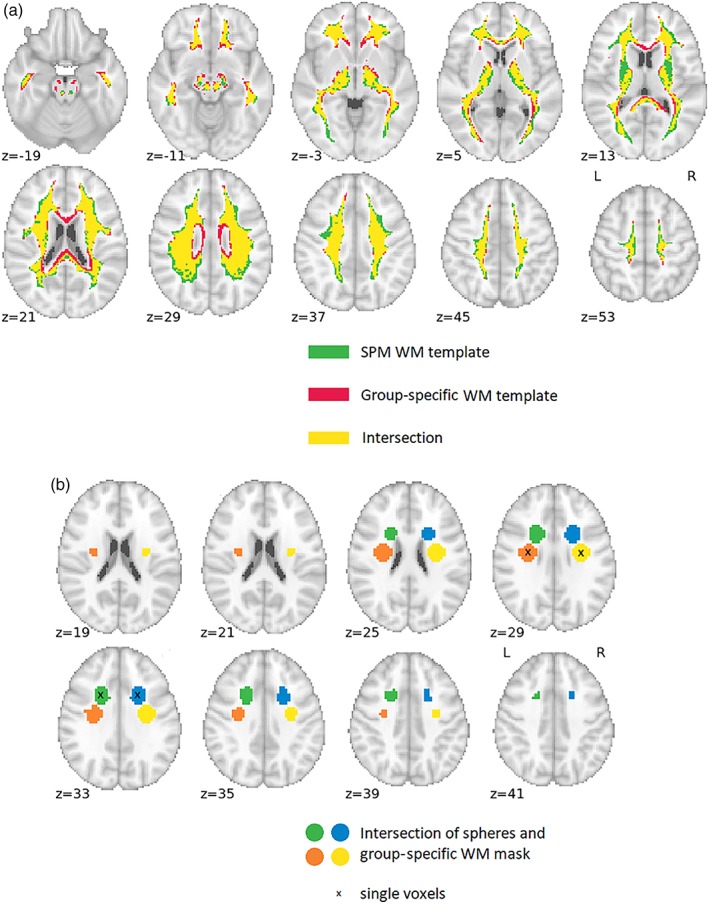
Masks for WM signal extraction for Data set 1; (a) masks corresponding to Variants 1 to 6 from Table 3; (b) masks corresponding to Variants 7 and 8. Coordinates for single voxels/sphere centers (x, y, z) in millimeters in the standard MNI space: anterior right (21, 11, 32); anterior left (−21, 11, 32); posterior right (30, −10, 29); and posterior left (−30, −10, 29) [Color figure can be viewed at http://wileyonlinelibrary.com]

2.4. Evaluation of data‐driven filtering suitability

We used two metrics to evaluate the effect of fMRI data filtering with particular nuisance signal sets: (a) potential for BOLD signal‐to‐noise improvement (impBSNR); (b) SNS. CSF/WM signals are commonly used with motion parameters (MPs) estimated from the realign preprocessing step (Friston et al., 1996) in one filtering design matrix (Jo et al., 2010; Weissenbacher et al., 2009). To assess the variability between particular CSF/WM variants with higher sensitivity, we first regressed out the MPs from all of the time series (i.e., GM data, estimates of neural signal correlates for impBSNR metric and CSF/WM regressors); we then performed the CSF/WM filtering and evaluation of impBSNR metric values. The filtering effect of CSF/WM regressors in addition to the regressor set containing only the MPs is exactly the same as CSF/WM filtering alone when working with all the time series filtered for the effects of MPs. However, the relative variability of impBSNR between particular CSF/WM variants are higher using the MP‐regressed out time series; therefore, the sensitivity for observing differences of filtering effects across different CSF/WM variants is higher. Time courses were also high‐pass filtered using the HP filter implemented in SPM12 with a default cut‐off frequency of 1/128 s. We took this step because the lowest frequencies of fMRI data contain a variability of no interest, hardware drifts (Smith et al., 1999), and they are routinely filtered out in fMRI studies.

2.4.1. The impBSNR metric

We define this metric, improvement potential of BOLD SNR, as a ratio between the GM data coefficient of determination and the neural signal coefficient of determination, that is, a ratio between the explained portion of variance in specific GM data and the explained portion of variance of a specific neural BOLD signal:

$${\text{impBSNR}}_{\text{Signal}}^{\text{Data}}=\frac{R_{\mathrm{GM}\text{Data}}^2}{R_{\text{Neural Signal}}^2}=\frac{\frac{{\sigma }_{\text{Expl}\mathrm{GM}\text{Data}}^2}{{\sigma }_{\mathrm{GM}\text{Data}}^2}}{\frac{{\sigma }_{\text{Expl Neural Signal}}^2}{{\sigma }_{\text{Neural Signal}}^2}}.$$

Using all CSF/WM signal sets, impBSNR for every subject has two dimensions with size 19 × 8; the versions of “data” and “signal” are explained subsequently in this section.

To compute the impBSNR in our study, the GM data (impBSNR numerator) were taken as signals extracted from cortical and subcortical GM using the masks from the Automated Anatomical Labeling (AAL) atlas of GM (Tzourio‐Mazoyer et al., 2002). For cortical GM, all cortical areas were put together by conjunction. The mask of subcortical GM was created in the same way; however, we included only the following structures (bilaterally): amygdala, caudate, putamen, pallidum, and thalamus; we did not include the cerebellum in the subcortical GM mask because we did not have full cerebellar acquisition coverage in every data set. The intersection of the AAL cortical or subcortical GM areas with the joint mask of data coverage for all four data sets (i.e., in‐brain mask estimated by SPM) formed our masks of GM data in which we assess the variability reduction by CSF/WM filtering. See Supporting Information Supplementary Figure 1 for the spatial extent of our cortical and subcortical GM coverage. The motivation for using the AAL atlas as a mask of GM is that this atlas is often used for parcellation of fMRI data in connectivity analyses.

As the neural signals (impBSNR denominator), we used the BOLD time courses of three ICA components of well‐known brain networks: DMN, motor network, and visual network. In the task data, we additionally added the modeled BOLD signal task time course. Modeled task‐related signals have strong correlates in data with large spatial extents localized in GM and relevant to contexts of particular tasks, suggesting their relevance to neural processes; see Supporting Information Supplementary Figure 2 for activation maps of all four tasks. The task‐related signals consisted of one representative time course in every data set—when there was more than one type of trial/motor action, we chose the one linked with the strongest/largest activation pattern—that is, simple keypresses in Data set 2 (see Supporting Information Supplementary Section S.1.2.3 for details) and blocks of reading of nonwords in Data set 4 (see Supporting Information Supplementary Section S.1.4.3 for details).

The ICA components were computed in the GIFT toolbox using group ICA with the number of components estimated using the minimum descriptive length criterion (Li et al., 2007). The estimated ICA components were then back‐reconstructed for individual subjects using the GICA3 algorithm (Erhardt et al., 2011), and the three ICA components of the default mode, motor, and visual networks were selected manually on the basis of visual inspection of their spatial patterns. Proceeding based on the group ICA ensures that particular ICA components were estimated in a stable way across subjects and fMRI runs (analyses for corresponding data set‐specific task and RS runs were computed together—we ran eight group ICA models—separately for every data set and for the NC/RC preprocessing variant).

After extracting the GM data and computing the ICA components, the next step was to compute the percentage of explained variability. We used all combinations of CSF (19 variants) and WM (8 variants) filtering approaches, that is, 152 filtering options. We evaluated the explained variance of data for every single GM voxel, resulting in 26,684 and 2,429 values for cortical and subcortical GM, respectively. This was done for every filtering option, subject, and NC/RC preprocessing variant. Analogically, we computed explained variances of neural signals, resulting in four values for task data and three values for RS data. This was done for every subject and NC/RC variant. Mean values (across voxels) of explained cortical and subcortical GM variance were computed. Consequently, the impBSNR values were computed as a ratio between the particular mean of the explained data variances and the explained variances of neural signals. For a schematic overview of the impBSNR computation pipeline, see Figure 3. These impBSNR values were logarithmized (using a logarithm with a base of 10) because of log‐normal distribution of basic impBSNR (all the impBSNR values mentioned further in the text are meant to be logarithmized).

Figure 3.

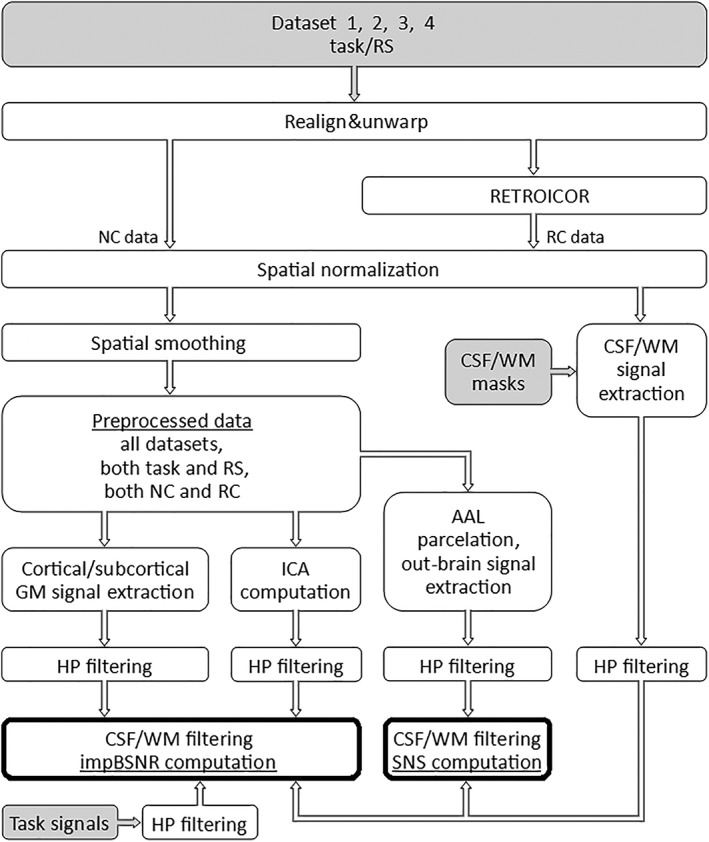
Schematic pipeline depiction of fMRI data preprocessing and computation of the impBSNR and SNS for various CSF/WM nuisance signal filtering. The gray fields are the inputs and the fields with bold boundaries are the outputs

This computation procedure resulted in eight and six (number of neural signal estimates × number of GM data masks for task and RS data, respectively) impBSNR subject‐specific matrices—separately for task NC, task RC, RS NC, and RS RC fMRI runs.

2.4.2. The SNS metric

The SNS metric is defined as the ratio of the strengths of meaningful within‐brain functional connections to the strengths of meaningless functional connections represented by FC between in‐brain areas and non‐brain time series, respectively.

For brain parcellation, we involved AAL areas with data coverage greater than 100 voxels. From these areas, the first PCA components were extracted as representative BOLD signals. We then classified particular AAL areas as members of various large‐scale brain networks based on their physiological relatedness to specific functions (Laird et al., 2011); see Supporting Information Supplementary Table 2 for an overview of the involved AAL areas and their membership in specific networks. The SNS computation follows: in total, 58 ROIs were taken as part of 15 networks with 236 mutual within‐network connections examined by evaluating simple parametric correlation coefficients. For the modeling of false FC, we took the time series from 200 out‐brain voxels and computed 200 × 58 parametric correlation coefficients between out‐brain time series and AAL signals. The SNS metric is mathematically evaluated as a two‐sample t‐test between the “real” correlations and “false” correlations; therefore, these t‐values express SNS values. For a schematic overview of the SNS computation pipeline, see Figure 3.

This SNS computation procedure was repeatedly applied to all signals filtered by 152 particular combinations of CSF/WM regressors (i.e., 19 CSF × 8 WM).

As a result, we obtained SNS subject‐specific matrices with two dimensions and size of 19 (CSF) × 8 (WM)—separately for task NC, task RC, RS NC, and RS RC fMRI runs.

2.4.3. Generalization/averaging of impBSNR and SNS results

To generalize the results from various “subtypes” of impBSNR (i.e., using different estimates of neural signals and data from cortical/subcortical GM) and to generalize impBSNR values and across tasks, we average particular metric matrices gradually across these three “mergeable” factors—neural signal type, GM data mask, and data set (in the SNS, there is just one such factor—data set). The reason for collapsing impBSNR across these factors is the generalizability of the results. As we want to evaluate the usefulness of particular filtering strategies separately for task and RS data and NC and RC data, the factors of task/rest and NC/RC preprocess are retained.

Every time before performing the averaging across different levels of particular mergeable factors, we compute the correlations of the median (across subjects for a particular data set) metric matrices that should be averaged. This computation serves as a tool for assessing the similarity of metric values between levels of a particular factor. We report all the correlations obtained between all levels of the tested factor for all possible values of the remaining mergeable factors in the Supporting Information Supplementary Material.

Assuming that the absolute values of impBSNR and SNS could differ across the data sets, and that impBSNR values could differ across factors, we normalize particular metric matrices before performing the averaging. This ensures comparable contributions of variability across filtering variants from all averaged metric values to the resulting “mean” matrix. This normalization step should retain the intersubject variability and make the resulting metric values comparable in terms of the median metric value and variability across particular filtering options. To achieve this, we compute the across‐subject median of the matrix to be averaged and compute the across‐filtering variants median and across‐filtering variability (inter quartile range) from this across‐subject median matrix. The median metric value of “group‐median” filtering variants is subtracted from corresponding subject‐specific metric matrices, and the subject‐specific matrices are also divided by the estimated variance (interquartile range) of group‐median filtering variants (see Supporting Information Supplementary Figure 3 for a schematic depiction of the metric values normalization procedure). This makes the group “average” of the metric value equal to zero and sets the unitary variance of the group “average” of filtering options, resulting in relative metric values.

As a last step, after merging the corresponding metric submatrices (and possibly impBSNR and SNS metric matrices together, resulting in a combined SNR—combSNR—metric), we find the best—winning—filtering option in terms of the highest metric relative value and compute the “equivalent” filtering options, that is, options that do not differ significantly from the best one. This is assessed by a one‐tailed pair Wilcoxon signed rank test, taking into consideration the group median and the intersubject variability. The threshold is p < .05 with false discovery rate (FDR) correction for multiple comparisons.

2.4.4. Comparison of the unnormalized impBSNR and SNS values and their variance across factors

Because we evaluate just the relative metric values, which allows us to generalize results (and to make relative comparisons between filtering variants), we also evaluate the filtering of “real” effects reflected by unnormalized metric values. The unnormalized impBSNR values are compared to the value of one (i.e., equal filtering of neural signal correlate and data filtering) and SNS values to SNS values from MP‐only filtered data, to observe whether there is potential for “real” improvement caused by a particular CSF/WM filtering variant and whether the particular effects are significant. We show these comparisons for selected variants of CSF/WM filtering with different metric values and across task/RS conditions, NC/RC preprocessing, and particular data sets. The CSF/WM filtering variants shown are:

1. winning variant

2. equivalent variant

3. variant using 1 + 1 PCA components from strict masks of CSF/WM (i.e., a mask of the LV restricted by the group‐specific CSF mask and the group‐specific WM mask)—a variant similar to variants widely used in connectivity studies,

4. variant using 5 + 5 PCA components extracted from strict masks—a variant similar to variants used in connectivity studies using, for example, the CONN toolbox or justified by the need for “robust” filtering (compared to 1 + 1 PCA option),

5. variant using 5 + 5 PCA components from the whole group‐specific CSF compartment and WM template—the variant exploiting CSF signals proximate to cortical surface and group‐nonspecific WM, therefore being potentially the most prone to contain neural signal correlates.

These variations of unnormalized impBSNR and SNS values between levels of particular nonmergeable factors are reported using simple descriptive statistics. We also test the difference of impBSNR values between levels of mergeable factors, that is, cortical versus subcortical GM data and between different neural signal correlates used for impBSNR. All testing in this section uses a two‐tailed pair Wilcoxon signed rank test, thresholded at p < .05 with FDR correction for multiple comparisons.

2.5. Evaluation of variance filtered by RETROICOR

It is necessary to point out the portion of variance captured by RETROICOR, because it is apparent that RC data sets have lower variance, because of the model‐based filtering during the preprocessing step, than the corresponding NC ones. Data‐driven filtering should then have theoretically less (quantitatively) impact. We computed the average‐explained variance for every subject (across in‐mask GM cortical and subcortical voxels) and then computed the mean and SD of these values to obtain data set‐specific values.

2.6. Validation of impBSNR‐based and SNS‐based conclusions on connectivity analyses

We use the knowledge derived in Section 2.4 to observe the impact of different filtering strategies on task‐driven and RS connectivity. The generalized psychophysiological interaction (gPPI) method (McLaren et al., 2012) assesses task‐driven connectivity, that is, changes of connectivity caused by changes in the contextual task condition or stimulus type. The FC seed‐based connectivity (Biswal et al., 1995) is used in RS data. We chose Data set 1 and Data set 3, including (both block design) a visual checkerboard task and a semantic decision task, respectively, and both including RS.

For both task‐connectivity analyses, we chose seeds in cluster peak activation maxima, right posterior cuneus, and left posterior superior temporal gyrus (lSTS), for Task 1 and Task 3, respectively. We chose the precuneus for both task and RS‐connectivity as local deactivation maxima. Masks of all seeds were defined as a sphere (radius 1 cm) centered at the coordinates:

Right cuneus—(18, −91, 1), Task 1 activation,

lSTS—(−60, −40, 11), Task 3 activation,

Precuneus—(3, −58, 44), Task 1 deactivation,

Precuneus—(3, −52, 38), Task 3 deactivation.

All coordinates listed as x, y, z in millimeters in the standard MNI space. The seed signal was computed as the first PCA component of the signals from the sphere. We compute gPPI/FC whole‐brain connectivity in a voxel‐wise manner; for Data set 3, we added also event‐related responses to individual models to avoid detecting trial‐based coactivation within the gPPI effect (O'Reilly et al., 2012). The maps of gPPI/FC effects (with gender as the only covariate of no interest) are tested with one sample t‐test to obtain group statistics. All connectivity analyses are done only in GM voxels, because this is our primary compartment of interest—we expect meaningful connectivity results only in GM and therefore also all the evaluation of impBSNR and SNS metrics was done only for GM voxels.

Because our aim is to assess the influence of the different filtering strategies and not to make statistics‐based neurobiological inference from gPPI and FC results, we threshold gPPI connectivity maps at p < .005 uncorrected for multiple comparisons and RS FC maps at p < .05 FWE corrected for multiple comparisons. These different threshold levels are because of naturally weak PPI effects (O'Reilly et al., 2012) and relatively robust results of seed FC.

3. RESULTS

3.1. Evaluation of data‐driven filtering suitability

3.1.1. The impBSNR metric

First, we compared across‐subject median impBSNR values among different levels of particular factors. The values of these median impBSNR matrices do not have normal distribution; therefore, the similarity of these impBSNR variations across different CSF/WM variants was assessed by nonparametric Spearman's correlation, using a threshold of p < .05 FDR corrected. The corresponding correlation values and their significance (also for the whole process of merging) are described in the Supporting Information Supplementary Methods Section S.2.1.

The across‐subject mean impBSNR values, after consecutive merging across all mergeable factors, are depicted in Figures 4 and 5, for task and RS data sets, respectively. It is clear that variants consisting of 5 + 5 PCA components perform worse than the other regressor sets, in terms of impBSNR, in both task and RS data for both NC and RC variants. The use of RETROICOR in task data shifts the best variants from 1 + 1 PCA CSF and WM variants to a variant exploiting one CSF PCA and local WM signals. The use of RETROICOR in RS data extends the best variants from one CSF PCA and local WM signals to variant‐exploiting local signals from both CSF and WM compartments.

Figure 4.

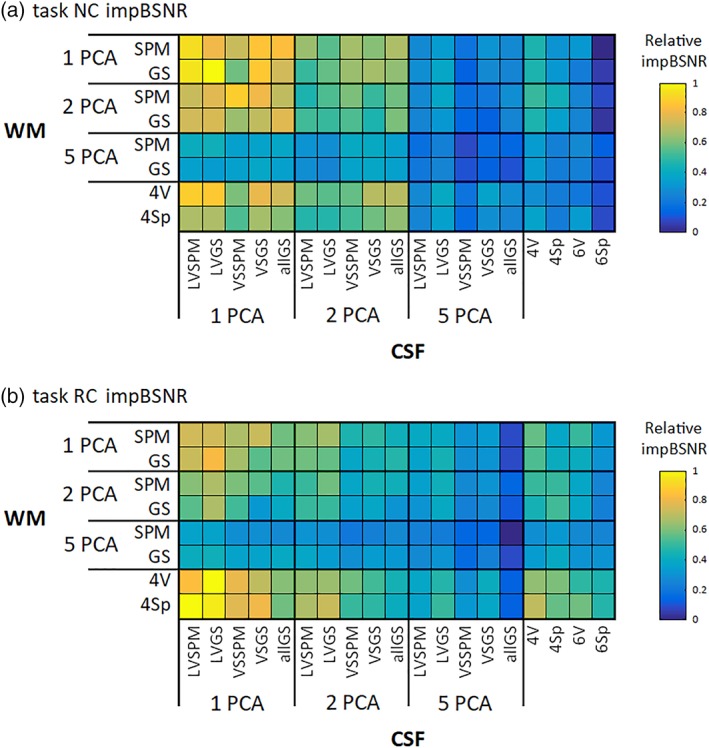
Relative values of the impBSNR metric for (a) NC and (b) RC task data across all combinations of CSF/WM regressor sets. The values are collapsed across all mergeable factors and medians across subjects are shown [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 5.

Relative values of the impBSNR metric for (a) NC and (b) RC RS data across all combinations of CSF/WM regressor sets. The values are collapsed across all mergeable factors, and medians across subjects are shown [Color figure can be viewed at http://wileyonlinelibrary.com]

3.1.2. The SNS metric

The across‐subject median SNS values do not have normal distribution; therefore, the similarity of these mean SNS variations across different CSF/WM variant was assessed by Spearman's correlation using a threshold of p < .05 FDR corrected. We evaluated correlations between the group‐median SNS values from all four tasks. The values of the Spearman's correlation coefficients can be found in the Supporting Information Supplementary Methods Section S.2.2.

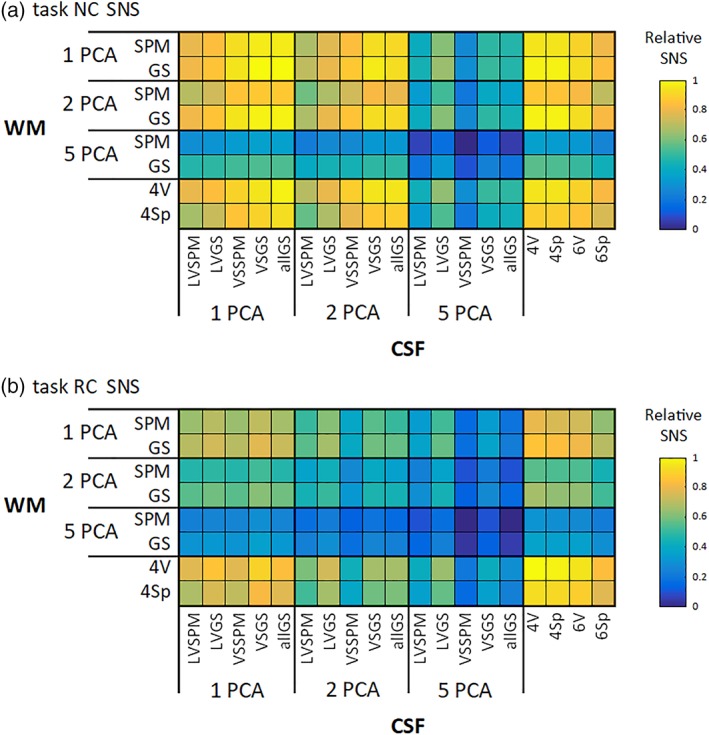
The across‐subject median SNS values after merging across the only factor “task” are depicted in Figures 6 and 7, for task and RS data sets, respectively. It is clear that variants consisting of 5 + 5 PCA components perform worse than the other regressor sets, in terms of SNS. There is a similar shift between task and RS data and between NC and RC variants as in impBSNR (described in the previous section). The only difference from impBSNR is that there is less difference of two PCA variant performances than of one PCA and local signals.

Figure 6.

Relative values of the SNS metric for (a) NC and (b) RC task data across all combinations of CSF/WM regressor sets. The values are medians across subjects [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 7.

Relative values of the SNS metric for (a) NC and (b) RC RS data across all combinations of CSF/WM regressor sets. The values are medians across subjects [Color figure can be viewed at http://wileyonlinelibrary.com]

3.1.3. Generalization/averaging of impBSNR and SNS results and estimation of best filtering options

To assess the similarity of impBSNR and SNS results, we computed correlations between across‐subject mean values of impBSNR and SNS. The mutual correlations were positive and significant in 100% of cases in all preprocessing variants and both RS and task data. Having such converging results, we combined these two metrics. All matrices of metric values were normalized, and the corresponding matrices were averaged, resulting in the combSNR metric.

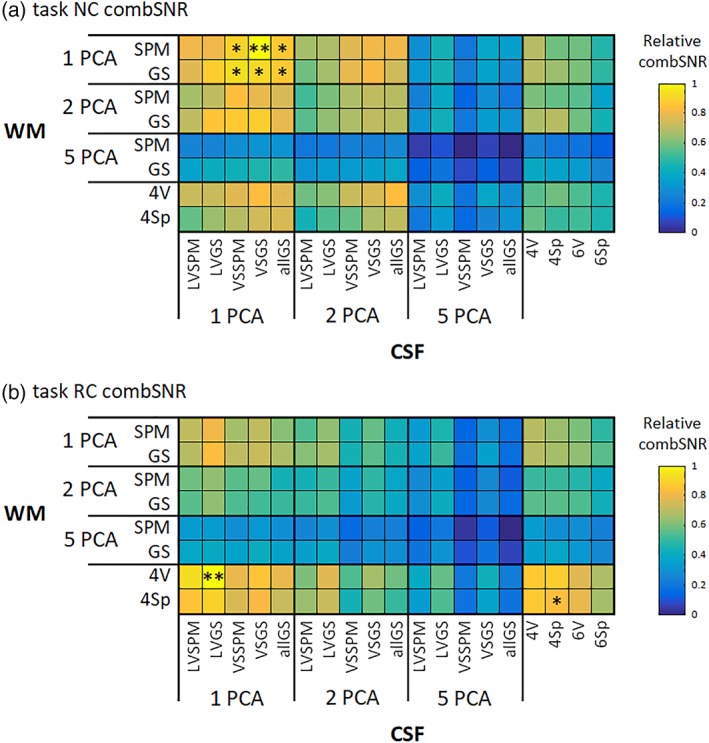
We evaluated the best variant of CSF/WM regressor set combinations for every task/RS and for NC/RC data. After this, we evaluated equivalent variants (i.e., variants not significantly differing). The results are in Figures 8 and 9, for task and RS data, respectively.

Figure 8.

Relative values of the combination of impBSNR and SNS metrics (i.e., combSNR) for (a) NC and (b) RC task data across all combinations of CSF/WM regressor sets. The values are medians across subjects. The best filtering option is marked by two asterisks; the equivalent options are marked by a single asterisk [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 9.

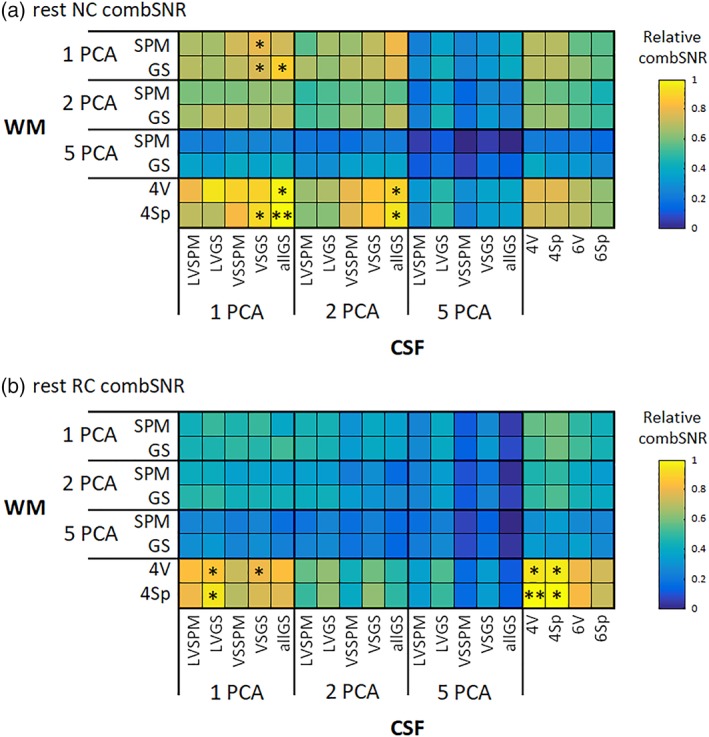
Relative values of the combination of impBSNR and SNS metrics (i.e., combSNR) for (a) NC and (b) RC RS data across all combinations of CSF/WM regressor sets. The values are medians across subjects. The best filtering option is marked by two asterisks; the equivalent options are marked by a single asterisk [Color figure can be viewed at http://wileyonlinelibrary.com]

The best combinations of regressor sets for filtering in terms of combSNR metric were:

For task NC: CSF 1VSGS ± WM 1SPM, (i.e., one PCA component from the group‐specific mask of the whole VS and one PCA from a general WM template),

For task RC: CSF 1LVGS ± WM 4V, (i.e., one PCA component from the group‐specific mask of the LV and four signals from spheres located intersected with group‐specific WM),

For RS NC: CSF 1allGS ± WM 4Sp, (i.e., one PCA component from the group‐specific mask of the whole CSF compartment and four signals from single WM voxels),

For RS RC: CSF 4V ± WM 4Sp, (i.e., four signals from single CSF voxels and four signals from spheres located intersected with group‐specific WM).

The equivalent variants are listed in the Supporting Information Supplementary Results Section S.2.4. It is clear (as in impBSNR and SNS alone) that in task data, the one PCA variants are preferable to RS data, where especially WM “local” regressors sets, that is, single voxels/spheres, are preferred. The same holds true when comparing NC and RC preprocessing. The “extreme” case is RS RC data, where single voxels/spheres for both CSF and WM perform best.

It is clear that variants consisting of 5 + 5 PCA components perform worse than the other regressor sets, in terms of combSNR. However, the best of the five PCA CSF and five PCA WM variants is the CSF 5LVGS ± WM 5GS—for all four combinations of task/RS and NC/RC—this variant's filtering performance is still low when compared to winning or equivalent to winning variants but bears mentioning because its performance is also shown in the further sections (together with 5 + 5 PCA variant from the least strict masks).

3.1.4. Comparison of unnormalized impBSNR and SNS values and their variance across factors

Unnormalized impBSNR values

We compared the unnormalized impBSNR values belonging to particular selected filtering options to the value of one (i.e., equal filtering of neural signal correlate and data filtering) to observe whether the CSF/WM increasing/decreasing metric values is significant.

There are eight and six impBSNR (values having two GM data mask, and four and three neural signal correlates, in task and RS data, respectively) for every combination of NC/RC preprocessing and every task/RS data set. We computed the significance of the difference between the value of one and particular group impBSNR values. The percentage ratios of significantly different impBSNR group medians are listed in Table 4—in every cell of the table, there are two values representing the percentage ratios of impBSNR >1/impBSNR <1, that is, a ratio of 50/25 means that half (50%) of the eight or six impBSNR values was significantly higher than 1, that a quarter (25%) were significantly lower than 1, and that in (unreported resting) a quarter (25%) it did not differ from the value of 1.

It is clear that:

1. there is substantial variance across data sets,

2. task data exhibits higher numbers of impBSNR >1 and lower numbers of impBSNR <1 than RS data sets,

3. NC data exhibits higher numbers of impBSNR >1 and lower numbers of impBSNR <1 than RC data.

Considering also values not shown in Table 4, we did not observe significantly different behavior between cortical and subcortical GM data unless 5 + 5 PCA components were used (then, generally lower impBSNR values were observed in subcortical GM). We observed significantly higher impBSNR values of task‐related BOLD signal impBSNR than impBSNR values exploiting other neural signal correlates (i.e., ICA components) in task data. We also observed differences between other impBSNR using different neural signal correlates when using “worse” filtering (across both task and RS data sets).

Unnormalized SNS values

We compared the unnormalized SNS values belonging to particular selected filtering options to SNS values from MP‐only filtered data to observe whether the CSF/WM increasing/decreasing of metric values is significant.

The group medians of SNS values and their comparisons to CSF/WM unfiltered data (i.e., filtered with six MPs only) are reported in Table 5.

Table 5.

Overview of group medians of unnormalized SNS values across different CSF/WM filtering variants and their significant differences from CSF/WM unfiltered data (i.e., filtered only with 6MPs); these differences are marked with plus and minus signs, and their significance is marked with asterisks. Significant positive and negative differences are marked in italic and bold, respectively

Data set 1	6MPs only	Winning	Equivalent	One PCAs strict	Five PCAs strict	Five PCAs large
Task NC	111.3	112.6+	115+	110.1*−	88.1*−	85.6*−
Task RC	117.7	107.3*−	108.7*−	108.8*−	85.3*−	79.4*−
RS NC	125	123.6−	123.5−	120.5*−	90.4*−	78.9*−
RS RC	126.8	127+	117.6*−	107.1*−	85.6*−	78.2*−

Data set 2	6MPs only	Winning	Equivalent	One PCAs strict	Five PCAs strict	Five PCAs large
Task NC	128.8	129.9*+	132.2*+	121.6*−	100.4*−	95.2*−
Task RC	134.9	120.4*−	125.5*−	115.3*−	93.5*−	87.3*−
RS NC	132.9	138.6+	133.9+	118.6*−	105.7*−	90.9*−
RS RC	148.7	138.1−	127.5*−	120.7*−	99.9*−	85.8*−

Data set 3	6MPs only	Winning	Equivalent	One PCAs strict	Five PCAs strict	Five PCAs large
Task NC	166.5	170.6+	159.2−	169.9+	131.4*−	120*−
Task RC	170.1	162−	162.7*−	145.01*−	124.5*−	108.1*−
RS NC	176.9	169.8−	182.4+	178.7+	128.2*−	117.8*−
RS RC	181.8	174.2−	167.9‐	141.2*−	126.2*−	107.7*−

Data set 4	6MPs only	Winning	Equivalent	One PCAs strict	Five PCAs strict	Five PCAs large
Task NC	187.2	193.3+	188+	186.1−	167.2*−	140.6*−
Task RC	191.5	193.6+	191.8+	188.2−	143.8*−	122.4*−
RS NC	182.1	181.1−	182−	179.3−	156.6*−	135.7*−
RS RC	188.7	184.4−	184.8−	167.7*−	140.4*−	119.8*−

It is clear that:

1. There is substantial variation of SNS values across data sets,

2. For the winning variant, there is no systematic change of SNS compared to CSF/WM unfiltered data,

3. The “worse” the CSF/WM variant is the greater the decrease in SNS (less evident in NC data),

4. RC variants have generally higher SNS values in CSF/WM unfiltered data.

3.2. Evaluation of variance filtered by RETROICOR

We did not observe consistent across‐data set differences between cortical and subcortical GM nor between task and RS data. The values of explained variances are listed in Table 6.

Table 6.

Evaluation of variance filtered by RETROICOR in (a) cortical GM; (b) subcortical GM

(a)	Task 1	Task 2	Task 3	Task 4
Cortical GM	20.7 ± 4.5%	14.9 ± 5%	10.5 ± 3%	8.6 ± 2.9%
Subcortical GM	24.4 ± 4.6%	20.6 ± 6.2%	7.5 ± 1.7%	7.1 ± 2%

(b)	RS 1	RS 2	RS 3	RS 4
Cortical GM	19.3 ± 5%	18.6 ± 3.5%	9.2 ± 2.7%	11.6 ± 3.7%
Subcortical GM	22.8 ± 4.4%	23.9 ± 4.9%	6.7 ± 1.8%	8.8 ± 2.2%

3.3. Validation of impBSNR‐based and SNS‐based conclusions on connectivity analyses

We computed task‐related (gPPI) and RS (FC) analysis of connectivity as described in Section 2.6. To show the impact of different CSF/WM filtering strategies, different variants of CSF/WM filtering were involved (see Section 2.4.4 for details):

1. CSF/WM unfiltered data,

2. winning variant (listed in Section 3.1.3),

3. equivalent variant:

   For task NC—one PCA component from the group‐specific CSF mask of the whole CSF compartment and one PCA from the group‐specific WM mask;

   For task RC – four CSF mean signals from spheres located in the group‐specific CSF map and four WM mean signals from spheres located in the group‐specific WM map;

   For RS NC – one PCA component from the group‐specific CSF mask of the whole CSF compartment and one PCA component from the group‐specific WM mask;

   For RS RC – one PCA from a CSF mask of group‐specific LV and four WM signals from single voxels located in WM;

4. variant using 1 + 1 PCA component from strict masks of CSF/WM,

5. variant using 5 + 5 PCA components extracted from the strict masks,

6. variant using 5 + 5 PCA components from the potentially “worst”/large masks.

The results of group gPPI effect from the activated seed (right cuneus) for Data set 1 are presented in Figures 10 and 11 for NC and RC variants, respectively. A negative gPPI effect is located bilaterally in the calcarine sulcus and posterior parts of the bilateral lingual gyri. The localization of this negative gPPI effect is stable across all filtering strategies; only its strength and number of suprathreshold voxels vary (in both NC and RC variants, it diminished for 5 + 5 PCA from large masks; in RC, it also diminished for 1 + 1 PCA from strict masks and increased rapidly in 5 + 5 PCA variant from strict masks). Positive gPPI effects are in the posterior cingulate cortex/precuneus and left angular gyrus—these are generally stronger in the RC variant. In addition, there is a positive gPPI effect in the ventromedial prefrontal cortex in the RC variant for CSF/WM unfiltered and winning CSF/WM filtering variants. For the winning CSF/WM variant in NC data, the positive precuneus gPPI effect diminishes; in 1 + 1 PCA from strict masks in NC data, there is also a positive gPPI effect in the medial part of the superior frontal gyrus.

Figure 10.

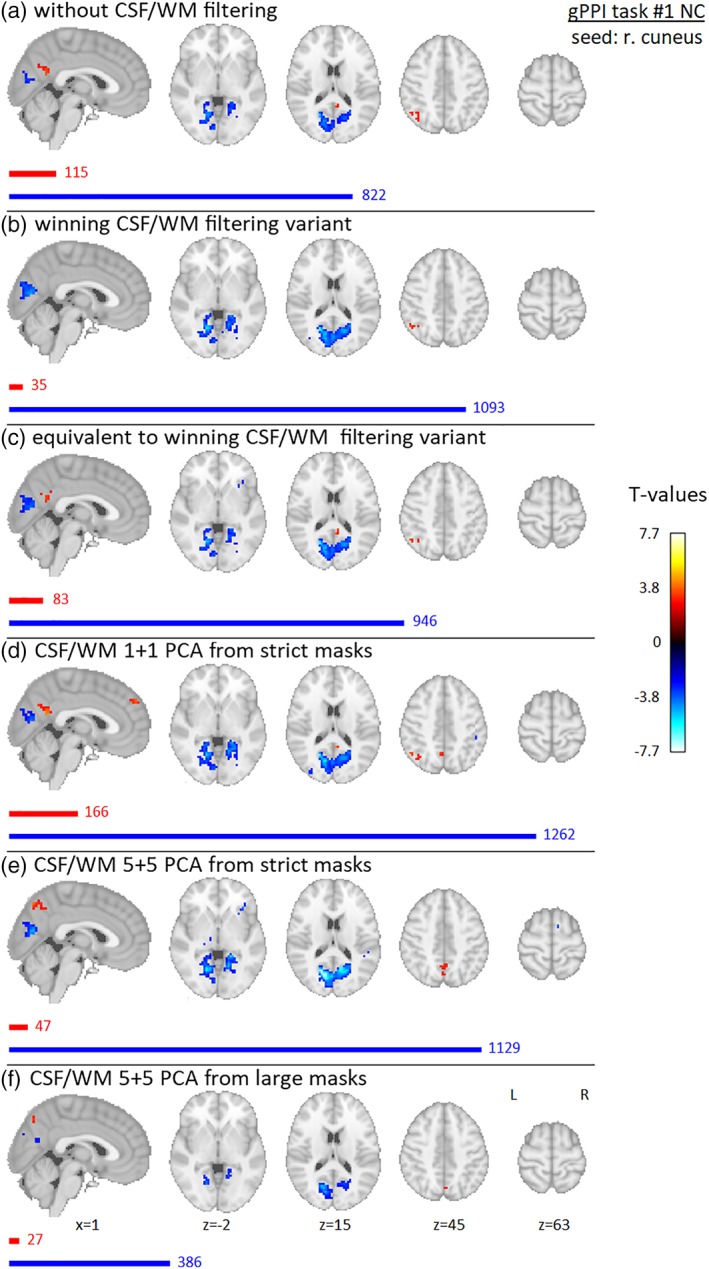
Results of group gPPI effect seeded in right cuneus (flickering checkerboards vs resting baseline) for Data set 1, NC preprocessing variant, for different filtering strategies—(a) without filtering of CSF/WM signals, (b) winning variant (1 + 1 PCA components from CSF mask of group‐specific ventricular system and WM general template), (c) equivalent variant (1 + 1 PCA components from group‐specific CSF mask of whole CSF compartment and group‐specific WM mask), (d) 1 + 1 PCA components from strict masks (group‐specific mask of lateral ventricles and group‐specific WM mask), (e) 5 + 5 PCA components from strict masks (same as in (d)), (f) 5 + 5 PCA components from “large” masks (group‐specific CSF mask of whole CSF compartment and general WM template). Nineteen subjects were involved in the analysis, and gender was added into the group model as a covariate of no interest. Maps are thresholded at p < .005 uncorrected for multiple comparisons. Red and blue bars with corresponding numbers indicate the numbers of significant voxels with positive and negative effects respectively [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 11.

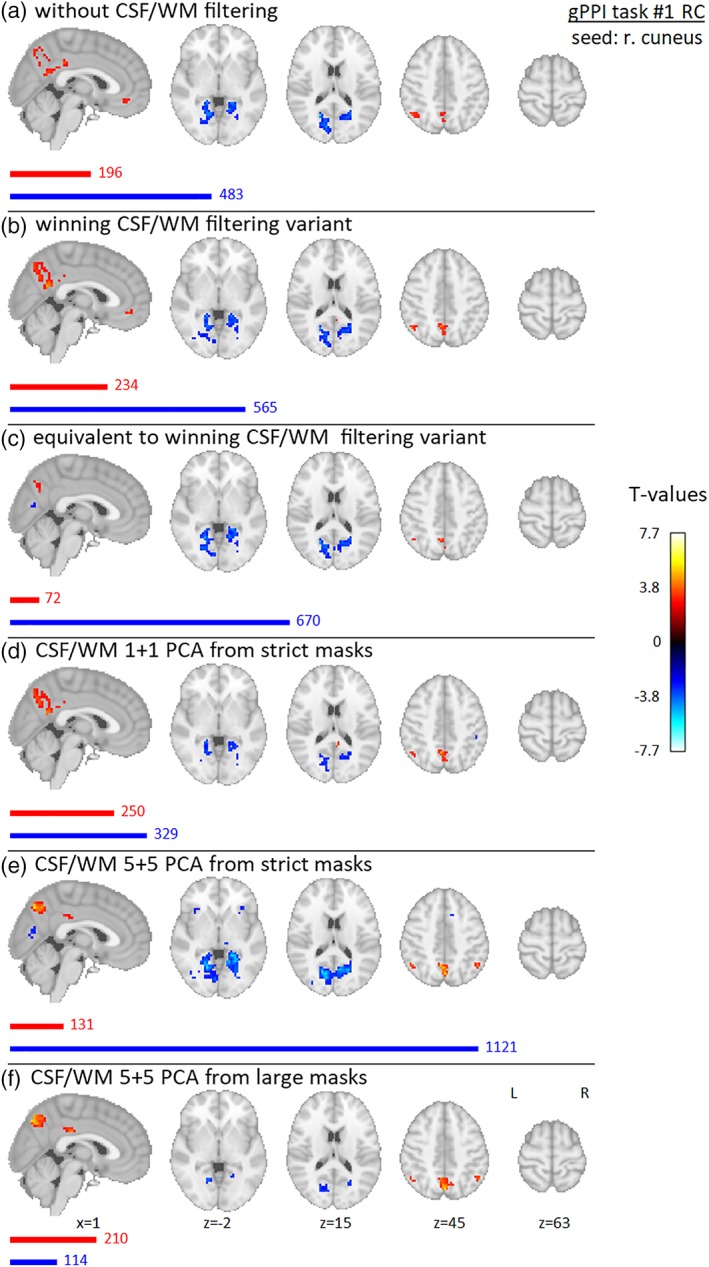
Results of group gPPI effect seeded in right cuneus (flickering checkerboards vs resting baseline) for Data set 1, RC preprocessing variant, for different filtering strategies—(a) without filtering of CSF/WM signals, (b) winning variant (one PCA component from CSF mask of group‐specific lateral ventricles and four WM signals from single voxels located in WM), (c) equivalent variant (four CSF mean signals from spheres located in group‐specific CSF map and four WM mean signals from spheres located in group‐specific WM map), (d) 1 + 1 PCA components from strict masks (group‐specific mask of lateral ventricles and group‐specific WM mask), (e) 5 + 5 PCA components from strict masks (same as in (d)), (f) 5 + 5 PCA components from “large” masks (group‐specific CSF mask of whole CSF compartment and general WM template). Nineteen subjects were involved in the analysis, and gender was added into the group model as a covariate of no interest. Maps are thresholded at p < .005, uncorrected for multiple comparisons. Red and blue bars with corresponding numbers indicate the numbers of significant voxels with positive and negative effects respectively [Color figure can be viewed at http://wileyonlinelibrary.com]

The results of group FC for Data set 1 are presented in Figures 12 and 13 for NC and RC variants, respectively. In CSF/WM unfiltered data, there are positive FC located bilaterally in the precuneus, posterior and middle cingulate cortex, superior and inferior parietal lobules, angular gyri, precentral and postcentral gyri, superior and middle frontal gyri, medial prefrontal area, thalamus, hippocampus, right putamen, and right caudate (FC effect was significant in the bilateral putamen and the caudate in RC data). With winning, equivalent filtering, and 1 + 1 PCA CSF/WM filtering, there is a reduction of FC suprathreshold voxels and this reduction is located in the precentral and postcentral gyri, hippocampus, putamen, and thalamus (thalamus partially remaining significant only with right‐lateralization in RC data and in some of these filtering strategies). For the 5 + 5 PCA filtering variants, the FC effect is further reduced in all clusters.

Figure 12.

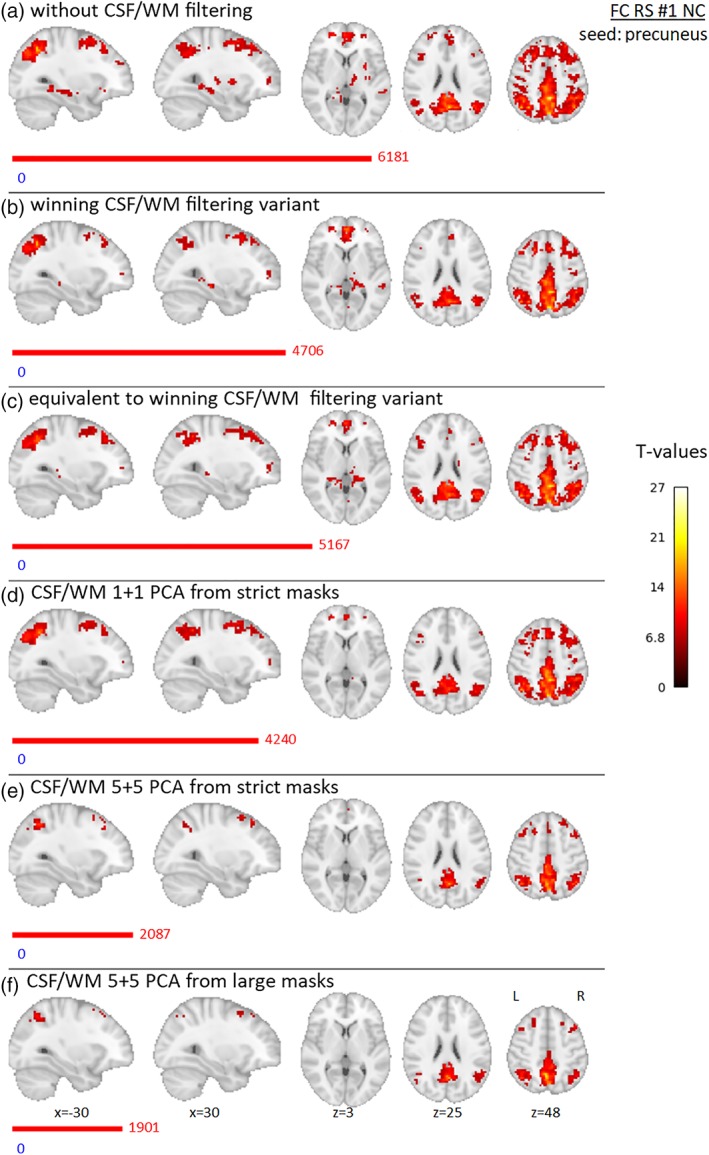
Results of group precuneus RS FC effect for Data set 1, NC preprocessing variant, for different filtering strategies—(a) without filtering of CSF/WM signals, (b) winning variant (one PCA component from group‐specific CSF mask of whole CSF compartment and four WM mean signals from spheres located in group‐specific WM map), (c) equivalent variant (1 + 1 PCA components from group‐specific CSF mask of whole CSF compartment and from group‐specific WM mask), (d) 1 + 1 PCA components from strict masks (group‐specific mask of lateral ventricles and group‐specific WM mask), (e) 5 + 5 PCA components from strict masks (same as in (d)), (f) 5 + 5 PCA components from “large” masks (group‐specific CSF mask of whole CSF compartment and general WM template). Nineteen subjects were involved in the analysis, and gender was added into the group model as a covariate of no interest. Maps are thresholded at p < .05, FWE corrected for multiple comparisons. Red and blue bars with corresponding numbers indicate the numbers of significant voxels with positive and negative effects respectively [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 13.

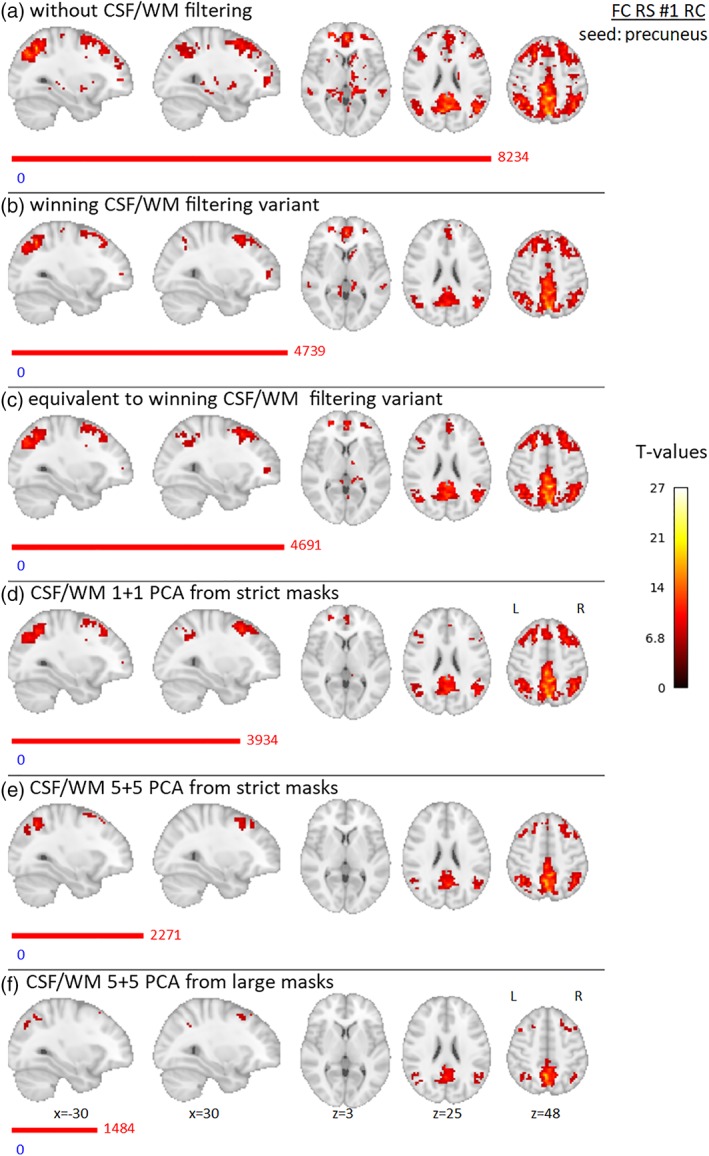
Results of group precuneus RS FC effect for Data set 1, RC preprocessing variant, for different filtering strategies—(a) without filtering of CSF/WM signals, (b) winning variant (four single voxels in CSF and four WM mean signals from spheres located in group‐specific WM map), (c) equivalent variant (one PCA component from CSF mask of group‐specific lateral ventricles and four WM signals from single voxels located in WM), (d) 1 + 1 PCA components from strict masks (group‐specific mask of lateral ventricles and group‐specific WM mask), (e) 5 + 5 PCA components from strict masks (same as in (d)), (f) 5 + 5 PCA components from “large” masks (group‐specific CSF mask of whole CSF compartment and general WM template). Nineteen subjects were involved in the analysis, and gender was added into the group model as a covariate of no interest. Maps are thresholded at p < .05, FWE corrected for multiple comparisons. Red and blue bars with corresponding numbers indicate the numbers of significant voxels with positive and negative effects respectively [Color figure can be viewed at http://wileyonlinelibrary.com]

The results of group gPPI effect from the deactivated seed (precuneus) for Data set 1 are presented in Supporting Information Supplementary Figures 4 and 5 for NC and RC variants, respectively. The results of the group gPPI effect from the activated seed (precuneus) for Data set 3 are presented in Supporting Information Supplementary Figures 6 and 7 for NC and RC variants, respectively. The results of group gPPI effect from the deactivated seed for Data set 3 are presented in Supporting Information Supplementary Figures 8 and 9 for NC and RC variants, respectively. The results of group FC for Data set 3 are presented in Supporting Information Supplementary Figures 10 and 11 for NC and RC variants, respectively.

4. DISCUSSION

In this study, we examined the suitability of different possible options for data‐driven filtering of fMRI data using CSF and WM nuisance signals. This filtering is used as a step before/during connectivity analyses (i.e., for studying intrinsic brain fluctuations and their spatial relations) in task and RS data. However, as noted in the Introduction, these nuisance signals may be contaminated by time courses of signals of interest. In simple task activation analyses, the data filtering may become easier—the time course of interest can be simply regressed out of the nuisance signals before the nuisance signals are removed from data (Behzadi et al., 2007; Soltysik et al., 2015), but this cannot be done in the connectivity analysis because the signals of interest are unknown. A combination of the data‐driven model with a common variant of model‐based filtering, RETROICOR, was also assessed.

Several options for nuisance signal extraction were tested, including single voxels/spheres distributed in CSF/WM compartments and different numbers of PCA components computed from signals of whole compartments delineated with different degrees of precision.

To test the impact of different filtering strategies, we defined a new metric, impBSNR, as a modification of the classical tSNR metric, which is defined as defined as the ratio between the mean value of the fMRI signal over time to its temporal SD. The new metric is motivated by the fact that the tSNR metric does not consider the variability source and simply assumes that increases of tSNR (reduction of data variability, when assuming that nuisance signal regression does not influence the signal mean) lead to better data quality. This would be true only if all the data variability was noise, with no signal fluctuations of interest (but if this were true, there would be no need to measure the time evolution of brain images). To address this problem, impBSNR takes into account not only data variability reduction but also the preservation of signals of interest estimated with ICA (and the task signal in task data). If a lower‐performing set of regressors would explain a high portion of useful signals relative to data variability (low impBSNR), such a regressor could not only reduce useful signals in the data but also potentially falsely introduce useful signal variability to the time series. For instance, in voxels where few or no useful signal(s) were originally present, the estimation of regressor beta weight would be influenced mainly by the variance of the noise in the data; subtracting the regressor with such weight also subtracts inappropriately multiplied useful signal(s) that are present in the regressor. This would impose useful signal variability on the data. Such a nuisance regression, with regressors “contaminated” by useful signal(s), may therefore result in increases in the false negative rate in FC analyses (by disrupting useful signals in the data) but also in increases in false positives (by introducing them to the data). Similarly, if the regressor contains, in addition to noise, a high‐signal variability, the signal may be subtracted and noise may be added to the voxel time series where high signal and low noise variability is present.

It is important to note that the data contain yet more neural signal correlates, and these three main components (and the task signal in task data) are not the only “meaningful” signals in the data. Despite this, impBSNR, using these three or four signals, provides better clues about filtering suitability than simple tSNR. The unsuitability of tSNR for estimating data filtering performance was recently reported in the literature (DeDora et al., 2016).

The second metric used was SNS. This metric had been published and its performance tested (Shirer et al., 2015). SNS evaluates the ratio between FC within brain networks (i.e., meaningful functional connections) and FC of areas inside the brain with areas outside the brain (i.e., meaningless functional connections). We observed that these metrics yield very similar results and provide converging evidence about the suitability of different nuisance signal regression approaches.

By averaging the results from both metrics (to improve the result robustness), we obtained combSNR metric. The particular combSNR values across different filtering strategies for task data (Figure 8) and RS data (Figure 9) and for their NC and RC variants of preprocessing were compared. We observed that regression sets containing 5 + 5 CSF/WM PCA components perform poorly when compared to other variants. The commonly used approach consisting of 1 + 1 PCA components performed better only in the task NC data. There was a trend in task RC data and in RS NC data sets that the “local” nuisance signals (i.e., from single voxels or small spheres) provide better data filtering. This is more apparent for WM signals, but for the RS RC data, it applies for both CSF and WM. It is logical that after RETROICOR preprocessing, there is less noise in the nuisance time series and therefore a higher risk of extracting also some information of interest. In the RS data, the amplitude of brain network BOLD signals is lower, and the network activity overlaps more than in the task condition (Arbabshirani et al., 2013). From our results, it seems that the noise and useful signals are also harder to separate in RS. When considering the effect of CSF/WM mask strictness, we did not observe clear evidence that less strict masks perform consistently worse. A common practice in functional neuroimaging studies is to construct a mask with strict thresholding of CSF/WM probability maps and subsequently erode them to reduce their spatial extent. The rationale behind this is the motivation to exclude voxels that potentially contain part of GM (because of partial volume artifacts). We constructed our CSF/WM templates with relatively liberal thresholds (0.5 and 0.9 for CSF and WM, respectively) and compared the performance of corresponding nuisance signals with group‐restricted CSF WM masks. These group masks were also constructed using liberal thresholds, but the group intersection resulted in spatial restriction. We did not use subject‐specific masks to have comparable numbers of mask voxels across subjects.

When considering absolute impBSNR values (see Table 4), it is important to note that intrinsic fluctuations in task data are less prone to useful signal disruption by nuisance signal regression. For the RS data, the risk is higher, especially in the RC variant. It is apparent that there is subtle variance in particular filtering strategies performance across data sets in terms of unnormalized impBSNR. This may be caused by substantially different acquisition settings (Data sets 1 and 2 were scanned conventionally with long TR, and Data sets 3 and 4 were scanned with short TR using simultaneous multislice acquisition). However, the number of data sets in our work does not make it possible to draw statistical conclusions about this. There is also variability across impBSNR values using different neural signal correlates. Despite relatively high numbers of impBSNR significantly higher than 1 (i.e., first value of cells ≥ 75 in Table 4) for some data sets when using winning/equivalent or 1 + 1 PCAs from strict masks, there is still some portion of impBSNR (using different neural signal correlates and GM data mask) that exhibits different behavior. Conversely, the distribution of the particular significance of impBSNR lower than 1 (i.e., more explained neural signal correlate than explained data, suggesting that filtering worsens the BOLD SNR) was not systematic for any specific impBSNR version—we did not observe consistent patterns (e.g., impBSNR using DMN ICA signal and cortical GM data) of such low values across data sets. The last issue to address concerning the impBSNR metric is the values of the absolute portions of data and signal explained variability. See Supporting Information Supplementary Figures 12 and 13 for an example using DMN ICA signal and cortical GM data. It is clear that when using winning variants consisting of 1 + 1 PCA nuisance set (tasks NC, Supporting Information Supplementary Figure 7a–d) or one PCA for CSF and four local WM signals (tasks RC, Supporting Information Supplementary Figure 7e–h and RS NC, Supporting Information Supplementary Figure 8a–d) or both CSF and WM local signals (RS RC, Supporting Information Supplementary Figure 8e–h), the percentage ratio of explained data and signal variance are in the orders of units. This is in contrast to the 5 + 5 PCA variant (even when using strict masks) where explained variances are around 20%.

The variation of SNS values across different filtering strategies and their comparison to the MP‐only filtered data (see Table 5) exhibits rather nonsignificant changes for winning and equivalent variants for NC data. This is probably because proper filtering removes the correlation structure that is not specific only to brain tissue, see Figure 3 in (Jo et al., 2010). Concerning RC data, significant SNS reduction can be seen after winning or equivalent WM/CSF filtering (in comparison with the “6MPs only” version) in some data sets. This can be explained: the noise effects spanning the whole scanned volume are suppressed by RETROICOR, and subsequent WM/CSF filtering can suppress more neural BOLD signal variability in the data.

As a final step, we applied different nuisance regression variants before gPPI and FC analyses.

The gPPI analyses were seeded in task‐positive regions and in the task‐deactivated region (the precuneus) in two data sets. The FC analyses were seeded in the precuneus.

The spatial distribution of gPPI effects from task‐positive regions (see Figures 10 and 11 for Task 1, and Supporting Information Supplementary Figures 6 and 7 for Task 3) was consistent for a given seed across CSF/WM filtering strategies. Despite this, there was rather unsystematic variability in terms of suprathreshold voxels, including strengthening of gPPI effect when using 5 + 5 PCAs compared to 1 + 1 PCAs (Figure 11, Supporting Information Supplementary Figures 6 and 7).

There were very similar results in gPPI from precuneus for task Data set 1 (both NC and RC preprocessing, Supporting Information Supplementary Figures 4 and 5, respectively) in CSF/WM unfiltered data and in all other CSF/WM filtering variants excluding 5 + 5 PCA variants. This was similar for the gPPI analysis in the NC version of task Data set 3 (see Supporting Information Supplementary Figure 8); in the RC version (see Supporting Information Supplementary Figure 9), there was a decrease in the number of suprathreshold voxels. The 5 + 5 PCA variants caused substantial reduction in numbers of suprathresholded voxels of gPPI effect from the precuneus in both tasks (Supporting Information Supplementary Figures 4, 5, 8, and 9).

This suggests complex interactions between (generally weak) gPPI effects and data filtering, which is consistent with our previous work (Barton et al., 2015). The difference in sensitivity may be caused not only by noise reduction but also by useful signal variability manipulation—if we disrupt the seed neural signal, we can expect sensitivity reduction; if we regress out part of the (possibly task‐modulated) signals related to different neural networks, we can impose false gPPI effects to the regions where these effects were not originally present, or it can lead to a reduction of data variability that is relevant (i.e., of neural origin), and its removal will cause a higher sensitivity of current gPPI effect detection. Moreover, it is important to note that there is variability of absolute impBSNR values for different neural signals and GM data masks (see Table 4)—it is likely that for different seed regions and different tasks, such data‐driven filtering may have a different impact on PPI/gPPI analyses. Nevertheless, the best improvement of data quality and result correctness will be reached with the recommended filtering strategy.

When evaluating the FC results, we observed a common DMN pattern. For both NC and RC data in RS Data set 1 (see Figures 12 and 13), there was a decrease of apparently artificial FC when proper CSF/WM filtering was done compared to unfiltered data—i.e., FC of the precuneus with pericentral regions that are not part of the DMN as commonly reported in the literature and with subcortical structures not typically being part of the RS pattern of the DMN (Bluhm et al., 2011). This was more evident in NC data. We observed diminishing FC with the hippocampi in CSF/WM filtered compared to MP‐only filtering, and this connectivity was generally weaker in RC data. This observation of hippocampus FC is contradictory to its FC in Data set 3 (see Supporting Information Supplementary Figures 5 and 6)—hippocampal FC was increasing in NC data for proper CSF/WM filtering compared to unfiltered data, and it was present in CSF/WM unfiltered RC data. This hippocampal correlation may be artificial in RS Data set 1 because of the significant amount of pulse and breathing artifacts filtered with RETROICOR (data not shown). However, the hippocampus has been also reported as a part of the DMN (Vincent et al., 2008); therefore, in the RS Data set 3, the true connectivity might be masked by artifacts and revealed after proper filtering. These two data sets differed in the acquisition (long and short TRs, respectively); therefore, the artifacts and real connectivity may also differ for this reason. A general DMN RS pattern was also observed in RS Data set 3, without apparently artificial FC. When using 5 + 5 PCA variants in RS FC, we observed substantial decreases of detected effects, suggesting the disruption of signals of interest and hence the weakening of connectivity patterns. All these observations are in line with corresponding rows in Tables 4 and 5.

Concerning fMRI data types that were not involved in our study, caution should be taken especially when analyzing data with special acquisition settings, such as multiecho data with subsequent use of ICA‐based denoising methods (Dipasquale et al., 2017), data acquired with a low flip angle (Gonzalez‐Castillo et al., 2011), and in functional imaging of the spinal cord (Fratini et al., 2014), where noise management is very important but there may be different distributions and properties of noise. Although these cases of fMRI are rather special, there is rapid development and routine use of new fMRI acquisition methods (such as multiecho data and MR‐encephalography (Zahneisen et al., 2011) that make it possible to reach repetition times less than 100 ms), and the proper form of CSF/WM filtering may differ from the ones reported in the current study. Data from 7T magnetic resonance imaging machines may also exhibit different nuisance regression behavior (Jorge et al., 2013). Some specific kind of CSF/WM filtering can also be beneficial for the phase fMRI data denoising (Hagberg et al., 2012; Petridou et al., 2009). Future research may focus on combining ICA‐based denoising methods for both classical single echo data (Perlbarg et al., 2007; Salimi‐Khorshidi et al., 2014) and multiecho data and interactions of these denoising methods with CSF/WM regression.

Because fMRI (both task and RS) connectivity is often used to study the pathology of various diseases and to find pathological connectivity patterns that can serve in the classification and hence in the detection of disease, it is important to point out that noise processes may differ under such pathological conditions. It has been reported that CSF pulsation in neurodegenerative disease may be altered (Kiviniemi et al., 2016). Properties of WM‐linked noise were also observed to be different in schizophrenia than in healthy controls (Cheng et al., 2015). It is important to keep in mind that if nuisance regression has a different effect on the patients than on the control group, false positive group differences may occur. This should be avoided by evaluating noise filtering effects for both groups in terms of not only noise suppression (e.g., tSNR) but also neural signal preservation (i.e., impBSNR).

Our recommendation is to suggest concrete trends in nuisance regression (local WM signals for RS NC and task RC data instead of the popular 1 + 1 PCA approach, and both CSF and WM local signals in RC RS data) and to point out the potential benefit of impBSNR estimation belonging to recommended CSF/WM variants prior to CSF/WM filtering. Even when the SNS provided very similar values in terms of metric value variations between particular CSF/WM filtering strategies, we do not suggest using it for evaluating the absolute filtering effect. When comparing SNS values of CSF/WM filtered data (even with winning variant) to MPs‐only filtered data, we observed mainly nonsignificant changes or SNS reduction (not SNS increase). However, the impBSNR >1 clearly suggests data quality improvement, or impBSNR <1 suggests more disruptions of signals of interest. This may lead to the conclusion that the suggested CSF/WM filtering may not have a positive effect (i.e., impBSNR values not significantly higher than 1), particularly in some RC RS data sets (as in the RC RS data in Data set 3, see Table 4), and therefore, such filtering should be omitted (this is consistent with the near absence of an effect in RS Data set 3 FC, see Supporting Information Supplementary Figures 10 and 11). However, in all observations except this single one, the recommended filtering evaluation provided significantly improved data quality.

The physiological noise because of heart action and breathing includes also low‐frequency artificial fluctuations caused by cardiac rate variability (Shmueli et al., 2007) and breathing depth and breathing rate variations—that is, variation of breathing volume per time (Birn et al., 2008). Many methods were introduced to account for these artifacts; for review, see (Murphy et al., 2013). However, recent research findings (Golestani et al., 2017) demonstrate that the link between these low‐frequency fluctuations and the BOLD signal is more complex. In addition to the noise processes, there is also a clear correspondence between the activity of large‐scale brain networks implicated in autonomic processing and changes in heart rate and breathing variations (Fan et al., 2012). It has been demonstrated that correction for these fluctuations may disrupt the detection of the pharmacologically induced effects affecting RS FC involved in autonomic processing (Khalili‐Mahani et al., 2013). Because of the complexity of this issue and to keep our article concise and focused on commonly used noise correction strategies, we did not involve such correction procedures in the current analyses.

The last potential area of interest is CSF/WM regression in studies examining the FC of WM. Recent studies suggest the potential of this method to study brain function in healthy subjects (Ding et al., 2018; Peer et al., 2017) and also under pathological conditions (Jiang et al. 2018). The specific form of nuisance regression may differ from our reported results since we focused on GM denoising only.

5. CONCLUSION

We assessed the suitability of a broad range of different forms of data‐driven CSF/WM nuisance regression strategies in four task and RS data sets, and interaction of CSF/WM nuisance regression with model‐based RETROICOR filtering. To assess this, we defined one new metric—impBSNR, and we also used one recently introduced metric—SNS. We observed converging results across two metrics and across all data sets. The results showed the use of higher numbers of PCA components from CSF and WM disrupts signals of interest with very high probability. We observed that use of the first PCA signal from WM may disrupt useful signals in RS data and in RETROICOR‐corrected task data. Our results suggest that in the RS data after RETROICOR correction, not only the first PCA time series from WM but also the first PCA from CSF may cause a part of the useful signals to be regressed out of the data. Instead of using the first PCA, we recommend using local signals extracted from single voxels/small spheres.

Supporting information

Supplementary Table 1 The exact coordinates of single voxels/sphere centers for CSF/WM extraction. All coordinates are listed as (x, y, z) in mm in the standard MNI space

Supplementary Table 2 overview of AAL areas involved in SNS analysis and their relatedness to specific networks, the “ICN” and number marks denote individual networks in the original paper; more details are shown in (Laird et al., 2011). Networks are not complete; we involved areas with data coverage>100 voxels

Supplementary Table 3 Spearman's correlation coefficients for impBSNR matrices based on different neural signal models, for both GM data types, both NC/RC preprocessing variants, and all tasks. Asterisks mark significant positive correlation (p < .05 FDR corrected)

Supplementary Table 4 Spearman's correlation coefficients for impBSNR matrices based on different neural signal models, for both GM data types, both NC/RC preprocessing variants, and all RS datasets. Asterisks mark significant positive correlation (p < .05 FDR corrected)

Supplementary Table 5 Coefficients of Spearman's correlation between impBSNR matrices based on cortical and subcortical GM data types, both NC/RC preprocessing variants, and all task datasets. Asterisks mark significant positive correlation (p < .05 FDR corrected)

Supplementary Table 6 Coefficients of Spearman's correlation between impBSNR matrices based on cortical and subcortical GM data types, both NC/RC preprocessing variants, and all RS datasets. Asterisks mark significant positive correlation (p < .05 FDR corrected)

Supplementary Table 7 Coefficients of Spearman's correlation between impBSNR matrices from different task datasets. Asterisks mark significant positive correlation (p < .05 FDR corrected)

Supplementary Table 8 Coefficients of Spearman's correlation between impBSNR matrices from different RS datasets. Asterisks mark significant positive correlation (p < .05 FDR corrected)

Supplementary Table 9 Coefficients of Spearman's correlation between SNS matrices from different task datasets. Asterisks mark significant positive correlation (p < .05 FDR corrected)

Supplementary Table 10 Coefficients of Spearman's correlation between SNS matrices from different RS datasets. Asterisks mark significant positive correlation (p < .05 FDR corrected)

Supplementary Figure 1

Supplementary Figure 2

Supplementary Figure 3

Supplementary Figure 4

Supplementary Figure 5

Supplementary Figure 6

Supplementary Figure 7

Supplementary Figure 8

Supplementary Figure 9

Supplementary Figure 10

Supplementary Figure 11

Supplementary Figure 12

Supplementary Figure 13

Supplementary Appendix S1

Bartoň M, Mareček R, Krajčovičová L, et al. Evaluation of different cerebrospinal fluid and white matter fMRI filtering strategies—Quantifying noise removal and neural signal preservation. Hum Brain Mapp. 2019;40:1114–1138. 10.1002/hbm.24433