Charting shared developmental trajectories of cortical thickness and structural connectivity in childhood and adolescence

Abstract

The cortex is organised into broadly hierarchical functional systems with distinct neuroanatomical characteristics reflected by macroscopic measures of cortical morphology. Diffusion‐weighted magnetic resonance imaging allows the delineation of areal connectivity, changes to which reflect the ongoing maturation of white matter tracts. These developmental processes are intrinsically linked with timing coincident with the development of cognitive function. In this study, we use a data‐driven multivariate approach, nonnegative matrix factorisation, to define cortical regions that co‐vary together across a large paediatric cohort (n = 456) and are associated with specific subnetworks of cortical connectivity. We find that age between 3 and 21 years is associated with accelerated cortical thinning in frontoparietal regions, whereas relative thinning of primary motor and sensory regions is slower. Together, the subject‐specific weights of the derived set of cortical components can be combined to predict chronological age. Structural connectivity networks reveal a relative increase in strength in connection within, as opposed to between hemispheres that vary in line with cortical changes. We confirm our findings in an independent sample.

1. INTRODUCTION

Brain development during childhood and adolescence has been well‐characterised in recent years using magnetic resonance imaging (MRI) (Mills et al., 2016). MRI provides a noninvasive method to examine neuroanatomy at a multiple scales. Analyses of structural MRI have found that the volume of grey and white matter follows different developmental trajectories during childhood.

Longitudinal analyses describe widespread and regionally variable decreases in cortical volume and thickness over childhood, with the largest decreases in thickness observed in the parietal lobe and the smallest changes in primary sensory‐motor cortex (Tamnes et al., 2017; Vijayakumar et al., 2016; Wierenga, Langen, Oranje, & Durston, 2014). During childhood, observable patterns of cortical thinning, in part, reflect changes to the tissue microstructure (Huttenlocher, 1979; Pakkenberg & Gundersen, 1997; Vértes & Bullmore, 2015). Over the same period, significant maturation of the brain's white matter occurs, with increases in overall volume and continuing axonal myelination (Lebel & Beaulieu, 2011; Lebel & Deoni, 2018; Tamnes et al., 2010).

The cortex is organised into broadly hierarchical functional systems with distinct neuroanatomical characteristics, including neuronal density and cortico‐cortical connectivity (Collins, Airey, Young, Leitch, & Kaas, 2010; Felleman & Van Essen, 1991; Markov et al., 2013). Areal differences in cortical cytoarchitecture mirror this hierarchy (Collins et al., 2010), a pattern that is reflected by macroscopic measures of cortical morphology (Wagstyl, Ronan, Goodyer, & Fletcher, 2015). At a microscopic level, neuronal density is inversely related to cortical thickness (Cahalane, Charvet, & Finlay, 2012; Schüz & Palm, 1989; Wagstyl et al., 2015), whereas synaptic density tends to increase with increasing thickness (Schüz & Palm, 1989).

Diffusion‐weighted MRI allows the delineation of macroscale areal connectivity, changes to which reflect the ongoing maturation of white matter tracts. These developmental changes vary in timing and extent in a regional pattern that likely reflects the functional organisation of the brain. Studies using diffusion MRI have shown markers of tissue organisation, including fractional anisotropy (FA), increase with age during childhood (Lebel, Walker, Leemans, Phillips, & Beaulieu, 2008), with maturation of commissural and projection fibres regions preceding intrahemispheric association fibres (Lebel & Beaulieu, 2011). The effects of white matter maturation on structural connectivity measures reveal large‐scale topological organisation of the structural connectome with measures of network efficiency and modularity increasing over childhood and adolescence (Baum et al., 2017; Zhao et al., 2015).

It is likely these developmental processes are intrinsically linked (Van Essen, 1997; Herculano‐Houzel, Mota, Wong, & Kaas, 2010; Mota & Herculano‐Houzel, 2012) with timing coincident with the development of cognitive function (Blakemore & Choudhury, 2006). In children, evidence of increased cortical thinning and white matter maturation from MRI is associated with improved cognitive performance (Kharitonova, Martin, Gabrieli, & Sheridan, 2013; Krogsrud et al., 2018; Squeglia, Jacobus, Sorg, Jernigan, & Tapert, 2013).

Regional variation in both grey and white matter development reflects the functional organisation of the brain, with lower order motor and sensory regions developing before areas that support complex, executive function. In a recent study, Sotiras et al. used a data‐driven, multivariate method for dimension reduction, nonnegative matrix factorisation (NMF), to identify a set of regional patterns of coordinated decreases in cortical thickness during adolescence (Sotiras et al., 2017). They found that changes in cortical thickness were spatially heterogeneous, with regional variation mirroring functional organisation and genetic patterning (Sotiras et al., 2017). This modular organisation is supported by evidence that cortical regions can be defined based on the extent of their shared anatomical connections (Bullmore & Sporns, 2012; Hilgetag, Burns, O'Neill, Scannell, & Young, 2000). Both neuronal density and dendritic spine density are correlated to areal connectivity (Beul & Hilgetag, 2019; Scholtens, Schmidt, de Reus, & van den MP, 2014), and white matter networks derived from MRI can similarly be split in subnetworks of connections, or modules, that appear to support known cortical systems, vary together with age and can be disrupted in neurodevelopmental disorder (Ball, Beare, & Seal, 2017; Baum et al., 2017; Faskowitz, Yan, Zuo, & Sporns, 2018). Therefore, macroscopic markers of brain development, including cortical thickness and measures of white matter connectivity reflect regionally‐varying patterns of complex, interlinked microscopic processes across the white and grey matter.

Multivariate methods, including NMF, are well‐suited to neuroimaging analysis, enabling pattern discovery in large, complex data sets (Ball, Beare, & Seal, 2017; Beckmann & Smith, 2005; Calhoun, Liu, & Adalı, 2009; Sotiras, Resnick, & Davatzikos, 2015). Recently, a number of multivariate methods have been described that aim to integrate measures from different imaging modalities (Groves, Beckmann, Smith, & Woolrich, 2011; Sui, Adali, Yu, & Calhoun, 2012). This allows correlated patterns to be identified across imaging types, providing multiple views of developmental processes across tissue compartments. NMF is particularly apt for MRI analysis given that most MR‐derived anatomical measures are nonnegative (cortical thickness, tissue volume, FA, etc.) (Sotiras et al., 2015). When applied to anatomical data, NMF returns sparse components that represent local patterns, or components, of covariation that permit interpretation as regions of coordinated growth or maturation (Sotiras et al., 2015, 2017). We have previously applied this method to structural network data, revealing subnetworks or network components, with connections that vary together across subjects (Ball, Beare, & Seal, 2017).

In this article, we aim to combine these approaches to describe how patterns of regional change in cortical thickness are associated with specific patterns of change to structural connectivity networks during childhood and adolescence. In a large development cohort, we demonstrate that NMF provides hierarchical decomposition of the cortex based on regional differences in cortical thickness change over time. Additionally, using a supervised NMF approach, we define specific patterns of structural connectivity that vary over the population in line with each cortical pattern.

2. METHODS

2.1. Data

Data were acquired from the PING Study (Jernigan et al., 2016). The PING cohort comprises a large, typically‐developing paediatric population with participants from several U.S. sites included across a wide age and socioeconomic range. The human research protections programs and institutional review boards at all institutions participating in the PING study approved all experimental and consenting procedures, and all methods were performed in accordance with the relevant guidelines, regulations and PING data use agreement (Brown et al., 2012). Written informed consent was obtained for all PING participants. Exclusion criteria included: (a) neurological disorders; (b) history of head trauma; (c) preterm birth (less than 36 weeks); (d) diagnosis of an autism spectrum disorder, bipolar disorder, schizophrenia, or mental retardation; (e) pregnancy; and (f) daily illicit drug use by the mother for more than one trimester (Jernigan et al., 2016). Similar proportions of males and females participated across the entire age range.

The PING cohort included 1,493 participants aged 3 to 21 years, of whom 1,249 also had neuroimaging data. Of these, n = 763 imaging data sets were available to download.

2.2. Neuroimaging

At each site, pulse sequences were optimised for equivalence in contrast properties across scanner manufacturers and models (Brown et al., 2012; Jernigan et al., 2016). T1‐weighted images were acquired using standardised 3‐Tesla high‐resolution 3D RF‐spoiled gradient echo sequences with prospective motion correction (PROMO). Image resolution was 1 × 1 × 1.2 mm (Siemens) or 0.9375 × 0.9375 × 1.2 mm (GE). Diffusion data were acquired using axial 2D EPI scans with 30‐directions, b‐value = 1,000, resolution 2.5 × 2.5 mm (Siemens) or 1.875 × 1.875 (GE) and slice thickness = 2.5 mm with a corresponding reverse‐encoded b = 0 map for EPI B₀‐distortion correction. Detailed acquisition parameters for each scanner manufacturer can be viewed at: http://pingstudy.ucsd.edu/resources/neuroimaging-cores.html.

Quality control for the PING data is detailed in Jernigan et al. (2016). In brief, images were inspected for excessive distortion, operator compliance or scanner malfunction. We performed additional, on‐site, visual quality control assessment of T1 and diffusion data. This involved a visual inspection of T1 volumes for motion or image acquisition or reconstruction artefacts. In addition, we included only diffusion data with at least one complete 30‐direction acquisition, after inspection for slice‐dropouts or motion artefacts. Five participants were removed due to excessive motion in T1‐weighted images; a further 312 were removed due to a lack of matched 30‐direction sequences (n = 232), or due to motion or image artefacts (n = 80).

This resulted in a final cohort of n = 456 participants with both T1‐weighted and 30‐direction diffusion data from five scan sites (mean age + S.D [range] = 12.6 + 4.91 [3.2–21.0] y, 233 male [51.1%]). Site/scanner‐specific demographic data are shown in Table S1.

2.3. Discovery and validation cohorts

The full cohort was split into discovery and validation cohorts prior to analysis. A random subset of 152 subjects (33%) were removed and retained as a held‐out validation cohort.

2.4. Image processing

T1 MRI data were processed as in Ball Adamson, Beare, & Seal, (2017). Briefly, vertex‐wise maps of cortical thickness were constructed with FreeSurfer 5.3 (http://surfer.nmr.mgh.harvard.edu). This process includes removal of non‐brain tissue, transformation to Talairach space, intensity normalisation, tissue segmentation, and tessellation of the grey matter/white matter boundary followed by automated topology correction. Cortical geometry was matched across individual surfaces using spherical registration (Dale, Fischl, & Sereno, 1999; Fischl et al., 2002; Fischl & Dale, 2000; Fischl, Sereno, & Dale, 1999). Any images that failed initial surface reconstruction, or returned surfaces with topological errors, were manually fixed and resubmitted to FreeSurfer until all data sets completed reconstruction. To reduce computational load, data were downsampled to the fsaverage5 surface comprising 10,242 vertices per hemisphere and smoothed to 10 mm FWHM.

Diffusion data were preprocessed using MRtrix 3.0 (http://www.mrtrix.org/). Data were first denoised and corrected for EPI distortions using topup/eddy (Andersson & Sotiropoulos, 2016; Veraart, Fieremans, & Novikov, 2016). The diffusion signal at each voxel was then modelled using a tensor model, from which we calculated FA (Basser & Pierpaoli, 1996).

2.5. Whole‐brain tractography

Prior to tractography, each T1 image was segmented into three tissue classes (grey matter, white matter, and cerebrospinal fluid) using FSL's FAST (Zhang, Brady, & Smith, 2001) and the cortical grey matter parcellated into n = 220 cortical regions‐of‐interest derived from subdivisisions of the Desikan‐Killiany anatomical atlas using easy_lausanne (https://github.com/mattcieslak/easy_lausanne) (Daducci et al., 2012; Hagmann et al., 2008). Tissue segmentations and parcellations were transformed into diffusion space using Boundary‐Based Registration (Greve & Fischl, 2009) followed by nonlinear registration using ANTS (Avants, Epstein, Grossman, & Gee, 2008).

Probabilistic whole‐brain fibre‐tracking was performed using wild bootstrap diffusion tensor tractography (Jones, 2008) implemented in MRtrix3. Ten million streamlines were generated per participant with a step size of 1 mm. Streamlines were seeded from the grey/white matter interface and anatomically constrained using a 5‐tissue‐type (5TT) mask (Smith, Tournier, Calamante, & Connelly, 2012).

Structural connectivity matrices (of size 220 × 220) were constructed by identifying streamlines that connected cortical regions‐of‐interest using a 2‐mm radial search from streamline endpoints. For each pair of connected regions, connection strength was estimated by calculating mean FA along all connecting streamlines.

After discounting connections that were zero across all subjects, connectivity matrices were subject to a consistency‐based thresholding, retaining the top 10% most consistent edges across subjects and resulting in n = 1,538 edges in the final set of networks (Roberts, Perry, Roberts, Mitchell, & Breakspear, 2017).

2.6. Site correction

To correct for possible effects of acquisition site on the initial NMF decomposition, we used ComBat harmonisation (https://github.com/ncullen93/neuroCombat) to estimate and remove linear site effects from vertexwise measures of cortical thickness (see also Figure S3). This method has been shown to remove unwanted sources of scan variability in multisite analyses of cortical morphometry measures (Fortin et al., 2018). We did not apply this method to the connectivity data. Instead, due to the removal of site variation from the H matrix (see below), we only consider edges that vary with each cortical component, and therefore do not vary with site.

2.7. Projective NMF

We decomposed cortical thickness data into a set of nonnegative, orthogonal components using projective NMF (Ball, Beare, & Seal, 2017; Sotiras et al., 2015, 2017; Yang & Oja, 2010).

Briefly, NMF is a multivariate method that models an n feature × m sample data matrix, V, as the product of two nonnegative matrices: W with dimensions n × r and H with dimensions r × m, such that V ≈ WH. Generally, the number of basis components r < min(m, n), thus WH represents a low‐rank approximation of the original data in V (Lee & Seung, 1999).

In projective NMF, the matrix, H is replaced with W^TV such that V ≈ WW^TV. PNMF confers a number of benefits over standard NMF including fewer learned parameters and increased sparsity of the resulting matrix W (Yang & Oja, 2010).

In this context, the columns of W represent a set of components, each comprising cortical regions that covary together across the study population and W^TV provides a corresponding set of subject‐specific weights, one per component (Sotiras et al., 2015). Together, these elements can be combined to approximately reconstruct any subject's original data set.

We implemented PNMF in Python (3.6.3), performing 20,000 iterations each time. Before NMF, each subject's cortical data were normalised to unit norm as an equivalent operation to correcting each vertex for mean cortical thickness, while ensuring nonnegativity.

2.8. Supervised NMF

To identify structural connections that covary with each of the cortical components, we performed a supervised NMF decomposition of the structural connectivity data. We derive the subject loadings from the PNMF decomposition of the cortical data: $H=W_{\text{cortical}}^{T}V$ and decompose the connectivity data, V_conn by iteratively updating W_conn to minimise the (Euclidean) distance between the original and reconstructed matrices, subject to nonnegativity constraints, while ensuring H remains fixed:

$$\underset{W\ge 0,H\ge 0}{\min }F=\frac{1}{2}\sum _{\mathit{ij}}{\left[V_{\mathit{ij}}-{\left(\mathit{WH}\right)}_{\mathit{ij}}\right]}^2$$

This results in a set of orthogonal network components, each comprising a sparse set of (topologically) localised connections (i.e., : the edge structure of different components does not overlap) and each varying across the population in line with a given cortical component. As with the cortical data, each subject's connectivity was normalised prior to NMF.

2.9. Reconstruction error, cross‐validation, and age prediction

For each set of components, we calculated the root mean square error (RMSE) between the original data matrices and matrices reconstructed from the NMF components for both cortical thickness and structural connectivity. To reduce bias in our error estimation, we employed Wold holdouts (Wold, 1978), masking a random subset of 20% of elements from each data matrix during NMF estimation and calculating error within the held‐out subset. Holdouts were repeated five times and reconstruction error averaged across repeats.

In addition, to demonstrate the low‐rank data representations retains relevant neurobiological signal, we used each set of component timecourses to predict chronological age. We used Gaussian process regression implemented in scikit‐learn (v0.20.0) to estimate age for each subject based on their individual component weights within a 10‐fold cross‐validation framework (Cole et al., 2017). For each set of components, age prediction error was calculated as the mean absolute difference between predicted and chronological age.

2.10. Modelling component timecourses

For each component, we used generalised additive models (GAMs) to model the relationship between age and component weight using the mgcv package in Rv3.5.1 (Wood, 2017). GAMs are flexible models that allow a data‐driven estimation of (possibly nonlinear) relationships between variables. Component weight was modelled as a smooth function of age, estimated using penalised thin plate regression splines with automatic smoothness estimation maximising marginal likelihood (ML) (Wood, 2003, 2011). For each component, we additionally tested the inclusion of main effects of sex and site alongside age and compared model fit using the Akaike information criterion (AIC).

2.11. Network component analysis

To test whether network components comprised edge sets that were significantly enriched for connection involving regions within the corresponding cortical components, we modelled each component's edge count using a hypergeometric distribution. We calculated the probability that the observed proportion of edges connecting within (or between) cortical components was drawn as a random sample from the full (thresholded) network:

$$p=1-\sum _{i=0}^x\frac{\left(\genfrac{}{}{0pt}{}{K}{i}\right)\left(\genfrac{}{}{0pt}{}{M-K}{N-i}\right)}{\left(\genfrac{}{}{0pt}{}{M}{N}\right)}$$

where p is the upper cumulative probability of finding x or more edges connecting at least one region within a given cortical module drawn randomly without replacement from a set of edges of size N, given the overall number of edges connecting at least one region within a given cortical module, K, and the size of the complete set of edges in the thresholded network, M.

For all components, we calculated both the enrichment ratio (i.e., : the proportion of network component edges connected to a given cortical component divided by the proportion in the whole network) and the hypergeometric probability, p, for edges connecting at least one region within a given module. We corrected p‐values using false discovery rate (FDR) to account for multiple comparisons.

2.12. Hierarchical decomposition

Hierarchical clustering was performed using Ward's linkage based on Euclidean distance between the component timecourses. The cophenetic correlation was calculated between pairwise similarity and dendrogram distance of component timecourses as a measure of hierarchical organisation. Statistical significance was determined using random permutations (p < .05, n = 10,000).

2.13. Neurocognitive data

In addition to imaging data, participants in the PING study undertook comprehensive behavioural and cognitive assessments (NIH Toolbox Cognition Battery, NTCB). The NTCB comprises a set of tests that measure abilities across several cognitive domains, including cognitive flexibility, inhibitory control, and working memory, resulting in eight measures of cognitive performance (for full details of these measures in the PING cohort refer to Akshoomoff et al., 2014). In total, n = 253 (83%) in the discovery cohort and n = 124 (82%) had both imaging and neurocognitive data.

To test associations between individual component weights and cognitive performance, we first modelled each cognitive score as a smooth function of age with an additional main effect of sex using a GAM (Akshoomoff et al., 2014). For each scale, the residuals of this model represent individual performance at a level greater or lesser than expected for a given age and sex. Similarly, the residuals of the nonlinear component model described above represent relative regional thickness that is greater or lesser than expected for a given age.

As performance across scales is closely correlated within individuals, and in order to avoid a large number of related statistical tests, we combined the standardised residuals of each of the cognitive models using PCA. This resulted in a set of components, each a linear combination of the original, residualised NTCB variables. Finally, we modelled associations between the weight of each NMF component (also residualised to age and sex) and the first 2 NTCB principal components (PCs) using a linear model, correcting for multiple tests using FDR. Statistical analysis was performed in Rv3.5.1.

2.14. Data availability

PING data are available via the NIMH Data Archive (ID 2607). Dataset identifier(s): [DOI: https://doi.org/10.15154/1503353].

3. RESULTS

3.1. Reconstruction error and age prediction

In the discovery cohort, we performing projective NMF to decompose cortical thickness data into 2, 5 10, 15, and 20 components and used the resulting component timecourses to derive a corresponding set of structural connectivity components.

To determine how well the full thickness and connectivity data sets were represented by each set of NMF components, we calculated reconstruction error at each level using five repeated Wold holdouts (Figure 1). As expected, training error decreased with increasing number of NMF components for both cortical thickness and structural connectivity. In contrast, reconstruction error of held‐out data points increased moderately for cortical thickness (mean RMSE for 2, 5, 10, 15, and 20 components: 0.001634, 0.001636, 0.001638, 0.001640, and 0.001641, respectively). For structural connectively, test error remained relatively stable across component sets, decreasing slightly from 0.00766 for 2 components to 0.007652 for 20 components.

Figure 1.

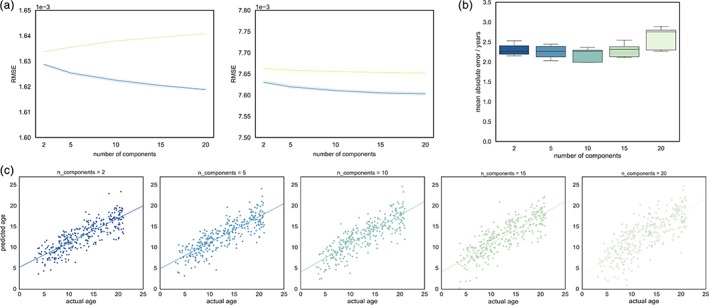
Reconstruction error and age prediction for increasing number of NMF components. (a) Reconstruction errors (RMSE; root mean squared error in terms of Euclidean‐normed cortical thickness or connectivity values), averaged over 5 Wold holdouts, for cortical thickness (left) and structural connectivity data (right). Error for training datapoints (blue) and held‐out test datapoints (green) are shown with 95% C.I. (b) Mean absolute error in age prediction is shown, averaged over 10 cross‐validation folds for each set of NMF components. (c) Individual age predictions are shown for each set of components [Color figure can be viewed at http://wileyonlinelibrary.com]

To demonstrate that relevant biological information was retained by the low‐dimensional data representation formed by each set of components, we used Gaussian process regression to predict age from the set of component timecourses at each level. Prediction error was estimated using 10‐fold cross‐validation within the discovery cohort (Figure 1b). Figure 1c shows individual, cross‐validated predictions of age based on each of the NMF component sets. Mean absolute error in age estimation was similar across all component sets with the lowest error observed in the 10 component set (mean MAE ± S.D = 2.18 ± 0.18) and highest in the 20 component set (2.60 ± 0.30).

As reconstruction errors and age prediction were relatively similar between component sets, we initially progress by focusing on the five component set only. For comparison, decompositions of cortical thickness and structural connectivity into 2, 5, and 10 components are shown in Figure S1.

3.2. Cortical thickness components

Figure 2 shows the result of projective NMF decomposition of cortical thickness data into five components, along with corresponding component timecourses. Each image represents the spatial distribution of component weights across the cortex, highlighting regions that vary across the population together. Each map is associated with a timecourse that describes the relative contribution of that component to the full data set and reflects how cortical thickness within the regions described by each map varies over time.

Figure 2.

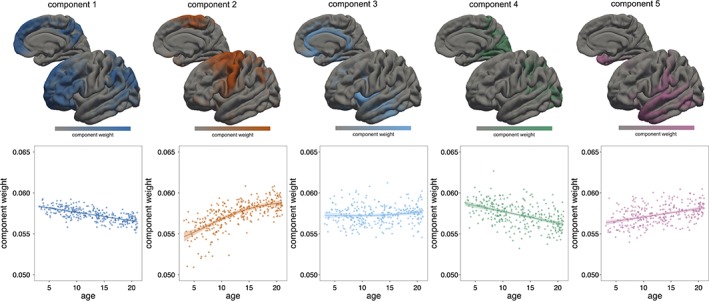
Cortical NMF components. Spatial maps for the five‐component solution are shown with associated timecourses. Components weights are normalised to account for the mean trend in cortical thickness over time [Color figure can be viewed at http://wileyonlinelibrary.com]

As each subject's data were normalised to a unit norm prior to NMF decomposition, the component timecourses in Figure 2 are effectively corrected for mean trends over time. We find that overall, mean cortical thickness decreased between 3 and 21 years (Figure 3). Thus, the timecourses presented in Figure 2 show changes relative to this overall trend and a decrease over time represents a regional decrease that is faster than the mean trend and vice versa. The effect of this normalisation is shown in Figure 3.

Figure 3.

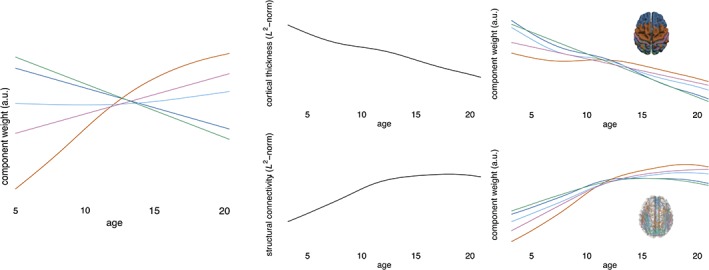
Normalising component weights. Components weights for the 5‐component solution are shown overlaid on each other (left). Prior to NMF decomposition each subject's data were normalised to unit norm. The GAM‐derived trajectory for the norm of the raw data is shown in the centre column, revealing the mean trend for cortical thickness (top) and connectivity (bottom). Combining the normalised trajectories with the group mean shows the raw trajectories of each component (right). Colours are coded according to cortical component [Color figure can be viewed at http://wileyonlinelibrary.com]

To determine if this cortical decomposition captured relevant information regarding the possible functional organisation of the cortex, we compared the spatial configuration of each cortical component to a canonical set of functional networks previously described in an independent data set (Yeo et al., 2011). We found a largely discrete mapping between cortical components and functional networks (Figure S2). Components mapped to frontoparietal and default mode networks (component 1), primary somato‐motor (component 2), ventral attention and limbic networks (components 3 and 5), and primary visual networks (component 4).

Component 1 (dark blue, Figure 2) groups together dorsolateral and medial frontal cortex with lateral parietal cortex and the precuneus. Together, cortical thickness in these regions decreases between 3 and 21 years of age. In contrast, component 2 groups together primary and supplementary motor cortex, which relative to the mean trend, increases over the same age span. Component 3 primarily includes insular and cingulate cortex and remains relatively stable over time. The final two components comprise primary visual cortex (component 4) and primary sensory along with superior temporal cortex and the anterior temporal horn (component 5), regions that increase (component 4) and decrease (component 5) relative to the mean trend over time. There were no significant differences between male and female timecourses for any component (Table S2). Similarly, after applying ComBat harmonisation to the cortical thickness data prior to NMF, there were no significant site effects on component weight (Table S2; Figure S3).

3.3. Structural connectivity components

The timecourses derived from the initial projective NMF were used to drive a supervised decomposition of structural connectivity data to identify groups of connections that share the same relative trajectory over the population as each of the cortical components. As with the cortical data, connectivity data were normalised prior to decomposition. The mean trend in edge strength, indexed by FA, followed an upward course, increasing rapidly to around 12 years before plateauing. The mean trend and raw (unnormalised) component timecourses are shown in Figure 3. Figure 4 shows the corresponding structural connectivity subnetworks for each cortical component in Figure 2. The top 25% of edges based on component weight are shown for each subnetwork.

Figure 4.

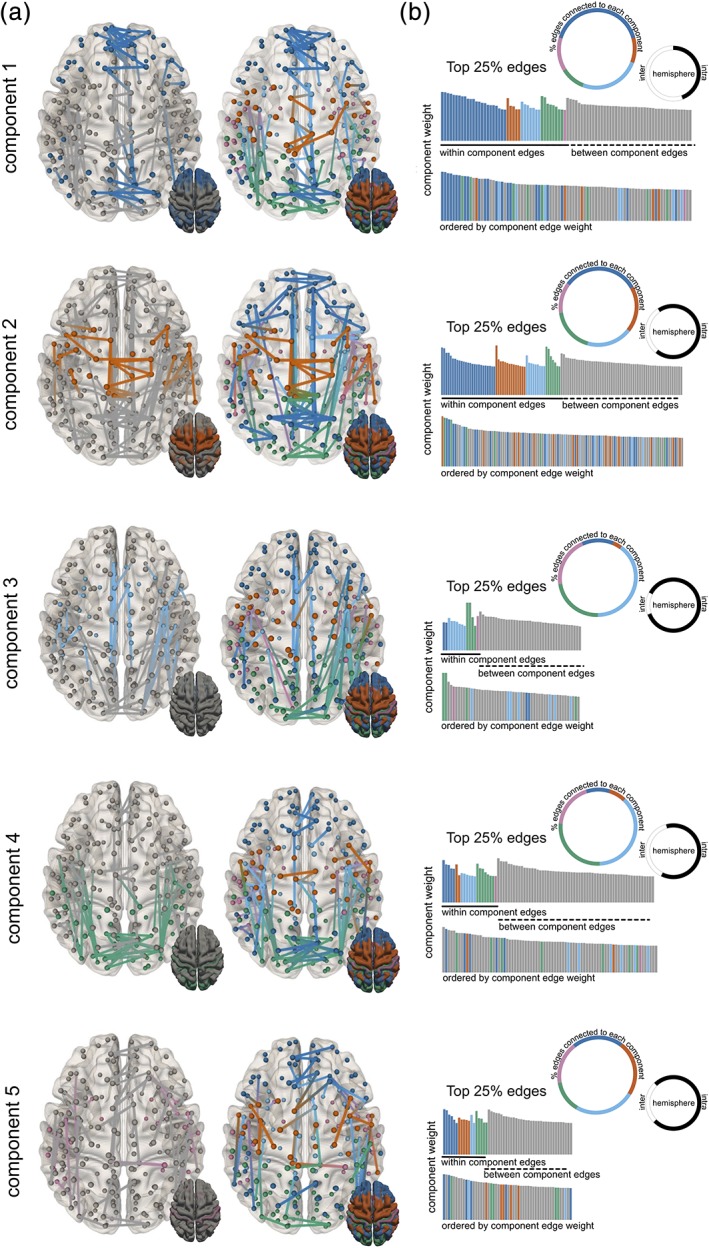
Connectivity NMF components. (a) Connectivity subnetworks are shown in the same order as corresponding cortical components. The top 25% edges based on component weight are coloured based on connections to the corresponding component (left) or all components (right) with the colour along each edge representing the membership of nodes at each end (b) networks are summarised based on the proportion of edges connected different modules (coloured circle), the proportion of interhemispheric and intrahemispheric edges (black/white circle) and as a histogram of edge weights ordered by within‐ or between‐modules connectivity (top) and edge strength (bottom) [Color figure can be viewed at http://wileyonlinelibrary.com]

The NMF decomposition resolved five distinct connectivity subnetworks, each of which contained connections both within and between the corresponding cortical components. Connectivity components 1 and 2 comprised approximately 50% within‐ and 50% between‐component edges (Figure 4b). In contrast, between‐component edges formed the majority of connections in connectivity components 3 (74%), 4 (75%), and 5 (64%). We found that connectivity components 1–4 were all enriched for connections to regions within their corresponding cortical components (Table 1), with significant enrichment in components 3 and 4 (FDR‐corrected p < .05). No components had a significantly larger proportion of edges that did not involve corresponding cortical regions than was expected by chance (Table 1).

Table 1.

Enrichment of connectivity component edges for connections to corresponding cortical components

	Connected to cortical component		Not connected to cortical component
Component	Enrichment	p	Enrichment	p
1	1.19	.091	0.86	.94
2	1.32	.074	0.92	.95
3	1.57	.0021a	0.68	.99
4	1.58	.0005a	0.73	.99
5	0.92	.674	1.03	.45

^aFDR corrected p < .05.

Connectivity components 1, 2, and 4 all displayed a significantly larger proportion of connections between hemispheres than was expected given the overall proportion of interhemispheric and intrahemispheric connections in the full network (enrichment ratio = 4.9, 2.4, and 3.1, respectively, all FDR corrected p < .05). Component 1 contained a large proportion (~55%) of interhemispheric connections between homologous regions in medial frontal cortex (Figure 4a,b) and edges within the corresponding cortical component formed the top ~10% when ordered by component weight (dark blue, Figure 4b). Within component 1, interhemispheric edges are also present between homologous regions in primary visual and motor cortex (cortical components 2 and 4) and intrahemisphere connections between insular and ventral parietal cortex (components 3 and 4). As shown by the timecourses in Figure 2, the relative contribution of this subnetwork to the full connectivity data set changes at a slower rate that the mean trend, with component weight (along with component 4) higher relative to other components at 3 years of age, and lowest at 21 years (Figure 3).

Edges forming the second connectivity component followed a similar distribution of intracomponent and intercomponent connections (Figure 4a), but with a smaller proportion of interhemispheric connections compared to component 1. The component weight increased rapidly over the age range resulting in the largest relative contribution to the full network at the end of the age range (Figure 3). Unlike connectivity component 1, the majority of the strongest edges do not connect primarily within regions of the corresponding cortical component. Connections are present between frontal and parietal regions (cortical component 1) and between hemispheres in supplemental motor (component 3), frontal, parietal (component 1), and visual cortex (component 4).

Unlike the other components, connectivity component 3 was not enriched for interhemisphere connections (enrichment = 0.95, p = .62) and is represented largely by intrahemispheric connections (87%) between different cortical components, with a large proportion of edges connecting one or more nodes in cortical component 3 or 4 (Figure 4b). We tested whether connectivity between specific cortical regions was over‐represented within any connectivity component (Table S3). We found significant enrichment for connections between cortical components 3 and 4 within connectivity component 3 (enrichment = 3.38, p = .0008). As with cortical component 3, the relative strength of this subnetwork increases over time with the mean trend (Figure 3).

This reciprocal connectivity is also evident in connectivity component 4, with 64% of edges connecting to a node in either cortical component 3 or 4. The fourth subnetwork was also enriched interhemispheric edges with extensive connections between occipital regions within the corresponding cortical component (Figure 4a; Table 1).

Connectivity component 5 contains no edges that connect solely within the corresponding cortical component. Instead connections are evenly distributed between cortical components (Figure 4b). As with connectivity component 2, component weight increases relative to the mean trend over the age range.

3.4. Component hierarchy

To determine whether NMF provides a hierarchical decomposition, that is, : by splitting larger components into smaller constituent parts. We performed projective NMF on the cortical thickness data, specifying 20 components and clustered the cortical maps and corresponding structural connectivity networks according to a hierarchical clustering of the component timecourses (Figure 5). There was a significant correlation between timecourse similarity over the 20 components and distance along the clustering dendrogram (cophenetic correlation = 0.66, p < .001 10,000 random permutations). By combining maps and networks from the higher level decomposition according to the hierarchical clustering algorithm, we were able to recapture patterns derived from NMF decompositions at coarser levels (2, 5, and 10 components (Figure 5b,c) demonstrating a stable, hierarchical decomposition of both data sets.

Figure 5.

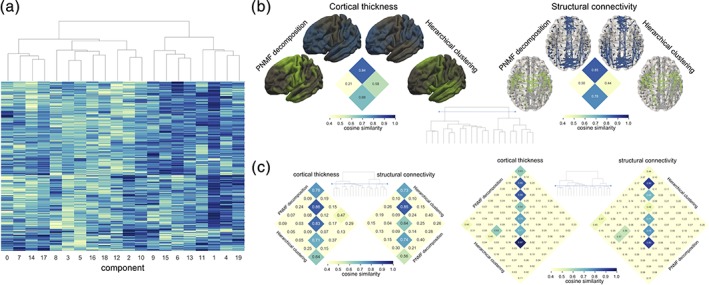
Hierarchical decomposition of NMF components. (a) 20 NMF components are clustered based on similarity of component weights across subjects. (b) The spatial similarity between NMF decompositions at a level of 2 components are shown with maps constructed through the addition of hierarchically clustered components at lower levels. (c) Similarity matrices are shown at the 5 and 10 component level [Color figure can be viewed at http://wileyonlinelibrary.com]

3.5. Association with cognitive performance

Using neurocognitive scores from the NTCB, we tested for associations between component weight and cognitive performance. Initial models showed age accounted for a significant proportion of variance (R ²: 0.41–0.60) in each cognitive score (Table S4). After accounting for variation due to age and sex, standardised, residualised cognitive scores were combined using PCA, with the first 2 principal components (PCs) together explaining >55% of the remaining variance. After FDR correction to account for multiple tests, we found two significant linear associations between the second PC and NMF components 1 and 4. These results showed a small positive correlation (R ² = 0.03, p = .008) between relatively slower thinning in frontal and parietal regions and improved performance in attention‐related tasks and relatively poorer performance in vocabulary and reading tasks with the opposite relationship (R ² = 0.03, p = .005) in component 4 (visual and lateral parietal cortex) (Figure S4).

3.6. Validation cohort

For validation, we repeated the NMF decomposition of cortical thickness and structural connectivity data into five components in the remaining, held‐out subsample (n = 152). The similarity of the resultant cortical maps and connectivity subnetworks are shown in Figure 6, ordered by average similarity to matched components in the discovery cohort. Average cosine similarity was significantly higher between matched components compared to unmatched (t = 4.83, p < .001) and ranged from 0.4 (component 5) to 0.57 (component 2). Matching was performed separately for cortical and connectivity components; similarity was higher for cortical thickness maps (range: 0.53–0.64; matched vs. unmatched: t = 5.75, p < .001) compared to connectivity subnetworks (0.27–0.50; t = 3.24, p = .004). Component timecourses were similar between discovery and validation samples (Figure S5). We also found similar patterns of edge enrichment in the network components with enrichment for edges connected to corresponding cortical component in network components 1 and 2 (enrichment = 1.24, 2.48; p = .09, p = .00002*, respectively, *FDR corrected p < .05) and all components enriched for interhemispheric connections (all p < .05), although we did not find any enrichment for connections between specific cortical components. Repeating the cognitive associations in the validation sample, we found a small, nonsignificant, positive correlation (r = 0.07) between PC2 and component 1 but no association between PC2 and component 4.

Figure 6.

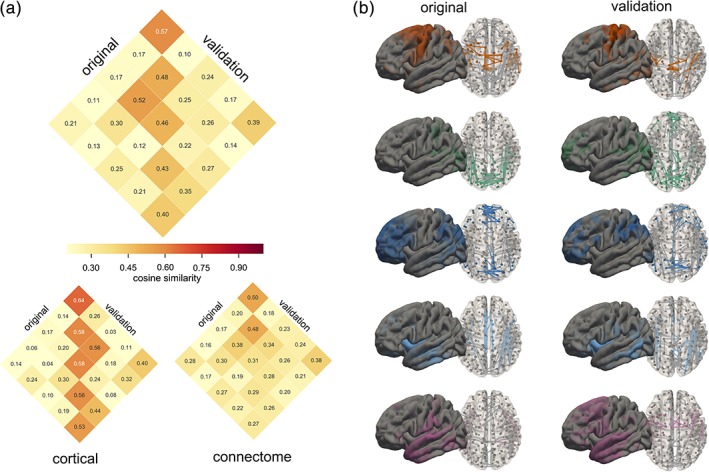
Comparison of discovery and validation cohorts. (a) the average similarity between matched components in the original and validation cohorts are shown (top), within corresponding matrices for similarity of cortical maps and connectivity networks. (b) Comparison of cortical and connectivity components from the original and validation cohorts, ordered by average similarity [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

In this study, we employ data‐driven, matrix factorisation methods to decompose the developing cortex into a set of modules containing areas that covary together with age and are correlated with specific structural connectivity subnetworks.

We find that increasing age between 3 and 21 years is associated with accelerated thinning of frontoparietal regions, whereas relative thinning of primary motor and sensory regions is decreased. Together, the weights of each set of components can be combined to predict chronological age and can be decomposed further into sets of smaller submodules while retaining overall data structure. Through the use of a second, supervised decomposition, we define a set of connections, with an overall weight that varies across the population according to the same trajectory as each of the cortical components. From this, we determine that connections between cortical areas within the same hemisphere increase in strength with age faster than connections between hemispheres, as well as observing patterns of differential maturation in connections within and between cortical modules.

Previously, Sotiras et al. used NMF to demonstrate that the cortex can be split into a set of components, or modules, that covary together, capture developmental change over time, and reflect the organisation of large‐scale functional networks (Sotiras et al., 2017). Here, we replicate these findings in a separate cohort, extending their observations to test the hierarchical properties of NMF decomposition as well as combining this approach with diffusion MRI to map out covarying patterns of structural connectivity. The PING cohort has a wider age range than the Philadelphia Neurodevelopmental Cohort studied by Sotiras et al. and overall, it is promising that our findings support those previously described in an independent developmental cohort; we define a set of cortical components with spatial patterns that reflect known functional systems including: frontoparietal, primary motor, sensory, and cortical limbic systems (Sotiras et al., 2017; Yeo et al., 2011). These patterns replicate well in an independent subset of the cohort. We find an overall decrease in cortical thickness with age (Figure 3), this support recent findings in multiple longitudinal cohorts demonstrating a broadly monotonic decrease in thickness over time in the same age range (Tamnes et al., 2017). After correcting for this mean trend, we observe regional differences in rate of change in thickness across cortical components. In contrast to Sotiras et al., where raw (not normalised) cortical data were used for NMF, no differences were observed between sexes in component trajectory, suggesting any sex differences were captured by the differences in mean thickness. Focusing on the five component model, we find that cortical thinning was fastest in components 1 and 4 comprising regions in dorsolateral frontal and parietal cortex, precuneus and primary visual cortex, and slowest in primary and supplementary motor, primary sensory and superior temporal cortex. Regional modelling of cortical thickness has found similar patterns, broadly respecting the organisational hierarchy of the cortex (Fjell et al., 2015; Tamnes et al., 2010, 2017; Vijayakumar et al., 2016). The differential rate of thinning is greatest in association cortex (component 1) compared to primary motor and sensory regions (components 2 and 5), with the exception of the visual cortex (component 4). We anticipate these differences in regional rate of change reflects the differential progress of microstructural processes including synaptic pruning (Huttenlocher, 1979), although recent evidence has suggested that apparent cortical thinning in the visual cortex may be dependent on tissue contrast changes due to intracortial myelination, rather than synaptic remodelling (Natu et al., 2018).

Our use of supervised NMF to derive a corresponding set of connectivity subnetworks that covary over the population in line with each cortical component allow the direct comparison of cortical and white matter development. Other studies have employed different methods to study concomitant changes across both tissue compartments. These approaches include inspection and comparison of white matter properties directly subjacent to different cortical regions (Croteau‐Chonka et al., 2016), or examination of white matter tracts from specific cortical gyri (Jeon, Mishra, Ouyang, Chen, & Huang, 2015) or connections between cortical areas that displaying significant age‐related changes in surface area in childhood (Cafiero, Brauer, Anwander, & Friederici, 2019). A strength of our approach is that we used a data‐driven method to select important connections based on their covariation with each cortical component. This allows the derivation of spatially (topologically) independent subnetworks, where connections are not shared between components, that vary together across the population (Ball, Beare, & Seal, 2017). Importantly, this form of supervised decomposition can be applied to any data set, imaging or otherwise, that is (or has been transformed to be) nonnegative and is shared by the same participants.

In contrast to previous approaches, this method does not restrict white matter connections to those that exclusively connect to the corresponding cortical component, instead selecting groups of edges where change over time relative to the mean trend mirrors that seen in the cortex. The mean trend in connectivity strength revealed a relatively quick increase that slows at around 12 years reaching a plateau by late adolescence. Similar trends in white matter maturation, as indexed by FA, have been described previously using tractographic approaches (Chen, Zhang, Yushkevich, Liu, & Beaulieu, 2016). Overall, connectivity component 2 showed the most rapid increases, with components 1 and 4 the slowest.

Connectivity component 1 exhibited the largest proportion of within‐module connections and was significantly enriched for connections to/from regions within its corresponding cortical component, with a large proportion of edges between homologous regions in frontal and parietal cortex. There were significantly more edges within this component connecting between hemispheres and, as with the cortical component, the relative contribution of these edges to the full network decreases with age, rising slowest between 3 and 21 years. In contrast, connectivity component 2 contained a lower proportion of interhemispheric connections (though still more than expected by chance) with edges that show the largest increase with age and connecting predominately within hemisphere. Similarly, edge strength within component 5 increases rapidly with age, plateauing later than components 1 or 4. Edges were not significantly enriched for between‐hemisphere connections and were predominantly within hemisphere These findings support observations from diffusion tractography studies that found that interhemispheric commissural tracts display earlier maturation compared to within‐hemisphere association fibres such as the superior longitudinal and fronto‐occipital fasciculi (Lebel & Beaulieu, 2011). A large proportion of reciprocal connectivity was observed between subnetworks associated with the spatially adjacent cortical components 3 and 4, supported by connection within connectivity component 3, with a number of edges connecting one areas in each component, although the cortical components showed differential change over time. Component 4, comprising a larger portion of interhemispheric edges decreasing in strength relative to the mean compared to component 3. Connectivity component 5 was the only network that was not significantly enriched for edges connecting to its corresponding cortical component. This relatively distributed subnetwork contained edges connecting to all cortical components, predominately within hemisphere. Therefore, this component may represent an integrative network process that facilitates communication across the network and have been shown to increase during adolescence (Dennis et al., 2013).

Using our NMF approach, we found that changes in focal cortical components were associated with contemporaneous changes in relatively distributed connectivity subnetworks. As the cortical and connectivity components were linked by a shared timecourse, this likely reflects a combination of developmental processes occurring simultaneously within the brain. Cafiero et al. recently demonstrated that streamlines passing through regions of myelinating white matter in early childhood terminate within large swathes of the developing cortex (Cafiero et al., 2019). We chose FA to define white matter connectivity strength, a partial proxy for white matter myelination in the developing brain (Lebel & Beaulieu, 2011). As such, developmental changes in the core white matter, through which all major white matter tracts pass will likely impact a wide range of structural network connections. Despite this, we identified specialised networks with preferential connections to corresponding cortical regions in 4 out of 5 components. We suggest that this likely reflects the differential developmental trajectories of major tract systems that carry connections to/from focal cortical regions (Lebel & Beaulieu, 2011).

To test whether individual variance in regional cortical development was associated with neurocognitive parameters, we performed an additional analysis examining association between component weight and performance on a suite of cognitive tests. We found only weak associations between differential thinning in frontparietal regions (component 1) and visual and lateral parietal regions (component 4) and performance, that did not explain susbstantial variance in the cognitive score. Indeed, as with previous studies in this cohort, we found that age accounted for the majority of individual variance (Akshoomoff et al., 2014), whereas only a small degree of variation could additionally be accounted for by neuroanatomical measures, after correcting for age (Ball, Adamson, et al., 2017). This analysis does not provide strong support for a relationship between regional patterns of relative cortical thickness and cognitive performance but, as noted by Akshoomoff et al., the large age range of the PING cohort means that the majority of variance in the data will be accounted for by age differences. This conclusion would benefit from additional studies designed to compare performance within larger cohorts across a smaller age range, such as the ongoing ABCD study (Casey et al., 2018).

As is often the case with unsupervised methods, the appropriate choice of component number poses a difficult challenge. We performed NMF using five different levels: 2, 5, 10, 15, and 20 and compared how well the resulting components could reconstruct the original data, and how well the resulting timecourses could be used to predict chronological age. Overall, we did not find significant differences between the different levels of resolution. Reconstruction error was relatively stable across all component sets, as was age prediction error for all levels except for n = 20. Overall, age prediction error was in range with previous “brain age” estimates (Ball, Adamson, et al., 2017; Cole et al., 2017; Franke, Luders, May, Wilke, & Gaser, 2012) confirming that utility of NMF for providing useful low‐rank representations of large imaging data sets (Varikuti et al., 2018).

As the prediction errors were relatively stable, we chose to focus on the five component set for ease of interpretation. We provide additional images of cortical and network components in Figure S1 for comparison. We also note that, using split‐half repeats as a measure of reliability, Sotiras et al. found the most reliable decompositions at similarly coarse levels (2, 7, and 18). The fact that reconstruction error did not significantly change when increasing the number of components suggested that the bulk of the original data matrix was captured by the lowest level of decomposition (i.e., two components), and that increasing the decomposition resolution further resulted in a subdivision of these two, larger components. To test this hypothesis, we performed a hierarchical clustering of the highest resolution decomposition, combining cortical and connectivity components based on the similarity of their timecourses. We found that there was significant hierarchical structure in the NMF decompositions and could largely recapture the original 2‐component solution by combining a number of smaller components (Figure 4). This may allow future studies to compare findings even if different numbers of components are specified.

We suspect that the broadly hierarchical decomposition may also explain why cortical error reconstruction did not improve with increasing numbers of components as may be expected (Figure 1a). We note that the RMSE for two or five components is not significantly different and we think this behaviour, in part, reflects that the same information is captured with 2 as with 5 components, as the lower resolution components can be viewed as a weighted combination of the components resulting from the higher resolution decomposition. Further understanding of this behaviour may be gained through the use of multilayer NMF methods that respect the hierarchical structure of the data (Cichocki & Zdunek, 2007).

Finally, we performed a within‐cohort validation, running the NMF decompositions separately in a held‐out subset of the full cohort. We found that, in general, similar spatial maps were defined in the validation set. Similarity was higher in the cortical components compared to the connectivity components, suggesting that the decomposition of the connectivity data may be more variable, or more dependent on sample size.

We note some limitations to this work. Firstly, there are a number of considerations when performing structural connectivity analysis: how to parcellate the brain, which algorithm to use for tractography, how to threshold the connectivity matrix. However, it remains unclear which methods are the best choice for structural connectivity analyses (Zalesky et al., 2010, 2016) We were limited in our choices in some respect due to the lack of high angular resolution diffusion data. Our method took advantage of state‐of‐the‐art approaches to limit false positives, including the use of anatomical constraints (Smith et al., 2012), we also thresholded our matrices based on a measure of edge weight consistency shown to improve estimate of consistent networks across subjects (Roberts et al., 2017). While this process may reduce the subject‐level variability in the group, we view it as an essential step to remove possible noise sources from the data. Changing the threshold would result in a slightly different set of edges and therefore altered network components, though we anticipate that the core patterns shown in Figure 5 would be retained. Indeed, we have previously found this when investigating the effects of changing the initial edge thresholds before NMF decomposition of network data (Ball, Beare, & Seal, 2017). Secondly, we used a large multisite cohort for this study. Site and scanner variance can impact neuroanatomical measures derived from MRI (Fortin et al., 2018; Schnack et al., 2010). Here, we employed a method for control of batch effects, ComBat, and found that unwanted site variance was significantly less apparent within component timecourses (Figure S3). We did not apply this form of site correction to the connectivity data as, although this method had been applied to parametric diffusion maps, for example, : FA (Fortin et al., 2017), inter‐site variation may affect the initial whole‐brain tractography prior to FA weighting. Instead, due to the removal of site variation from the H matrix, we only consider edges that vary with each cortical component, and therefore do not vary with site. Due to this, we were not able to perform our method in the reverse direction, performing PNMF first in the connectivity data, followed by supervised NMF of the cortical data. Additionally, this study is cross‐sectional and our conclusions would be strengthened by observing within subject longitudinal changes that mirror the cross‐sectional age‐related trends reported here.

In summary, we use a data‐driven, multivariate method to identify patterns of regional cortical development that have a hierarchical structure and reliable identified across independent cohorts. We find that these components share developmental trajectories with distinct subnetworks of structural connectivity.

Supporting information

Table S1 PING demographics by scan site/scanner

Table S2: Model fit and terms for each NMF component

Table S3: Enrichment of edges between specific cortical components for each connectivity network

Table S4: Variance explained in cognitive scores by models of age and sex

Figure S1: NMF decompositions into 2, 5 and 10 components.

Figure S2: Mapping of NMF components onto functional networks.

Figure S3. Removing site variance.

Figure S4: Associations between NTCB scores and component weights.

Figure S5: Normalised component trajectories for the discovery (top) and validation (bottom) cohorts.

Ball G, Beare R, Seal ML. Charting shared developmental trajectories of cortical thickness and structural connectivity in childhood and adolescence. Hum Brain Mapp. 2019;40:4630–4644. 10.1002/hbm.24726