Neural mechanisms of vibrotactile categorization

Abstract

The grouping of sensory stimuli into categories is fundamental to cognition. Previous research in the visual and auditory systems supports a two‐stage processing hierarchy that underlies perceptual categorization: (a) a “bottom‐up” perceptual stage in sensory cortices where neurons show selectivity for stimulus features and (b) a “top‐down” second stage in higher level cortical areas that categorizes the stimulus‐selective input from the first stage. In order to test the hypothesis that the two‐stage model applies to the somatosensory system, 14 human participants were trained to categorize vibrotactile stimuli presented to their right forearm. Then, during an fMRI scan, participants actively categorized the stimuli. Representational similarity analysis revealed stimulus selectivity in areas including the left precentral and postcentral gyri, the supramarginal gyrus, and the posterior middle temporal gyrus. Crucially, we identified a single category‐selective region in the left ventral precentral gyrus. Furthermore, an estimation of directed functional connectivity delivered evidence for robust top‐down connectivity from the second to first stage. These results support the validity of the two‐stage model of perceptual categorization for the somatosensory system, suggesting common computational principles and a unified theory of perceptual categorization across the visual, auditory, and somatosensory systems.

1. INTRODUCTION

The processing of stimuli from the environment into internal representations that guide behavior is fundamental to cognition. Perceptual categorization, the mapping of sensory stimuli to category labels, is a crucial aspect of this process. Across sensory modalities (vision, audition, touch), a universal principle of perceptual processing in the brain is a “simple‐to‐complex” multistage hierarchy, in which receptive field size and tuning complexity increases from primary sensory areas to higher level regions (Pleger & Villringer, 2013; Rauschecker & Scott, 2009; Romo & Salinas, 2001; Ungerleider & Haxby, 1994).

How does this hierarchy support perceptual categorization? Several monkey and human studies provide evidence for a processing hierarchy comprising two fundamental stages (Riesenhuber & Poggio, 2000; Ashby & Spiering, 2004; Jiang et al., 2007, 2018): (a) a “bottom‐up” perceptual learning stage in sensory cortices, in which neurons acquire increased selectivity for stimulus features and (b) a “top‐down” second, task‐dependent stage in higher cortical areas, which receives input from the first stage in sensory cortex and learns to categorize the stimulus. This hierarchical framework is computationally simple (it requires supervised learning only at the top, without the need to propagate task errors down the processing hierarchy) yet powerful, because sensory representations in the first stage can be flexibly reused by different modules in the second stage, depending on task demands (Riesenhuber & Poggio, 2000). Two key predictions of the two‐stage model is that following learning of a categorization task, the first stage shows selectivity for the physical features of the stimulus, and this representation should not be biased for any one task (e.g., show no explicit category representation). Such an ability is a key element for human cognition that often involves categorizing the same physical stimulus along different dimensions (e.g., categorizing a human face as male or female, happy or sad, etc.).

Jiang et al. (2007) first provided evidence for this two‐stage model in the visual system. They trained participants to categorize a stimulus space of morphed cars. Increased shape selectivity was identified in the lateral occipital cortex after training. Category selectivity, in contrast, was localized to the lateral prefrontal cortex. These findings were subsequently generalized to the auditory system (Jiang et al., 2018) by training human participants to categorize a morphed set of monkey calls. Sharpened tuning to monkey call features (without explicit category representation) was observed in the left posterior superior temporal cortex, and category selectivity for different types of monkey calls was found in prefrontal cortex.

The foregoing findings hint at a universal model of perceptual categorization, reflecting a similar computational goal of categorization across sensory modalities: the grouping of physically similar stimuli into the same category, and dissimilar stimuli into different categories. To what degree the two‐stage model applies to the somatosensory system, the third major sensory modality, is unknown, however. Previous investigations of haptic and vibrotactile (VT) perception suggest that the somatosensory system is also hierarchically organized in a “simple‐to‐complex” hierarchy (Bodegård, Geyer, Grefkes, Zilles, & Roland, 2001; Hernández et al., 2010; Kim et al., 2014). It has even been found that neurons at intermediate levels of the visual and somatosensory systems have similar tuning properties for object shape (Yau, Pasupathy, Fitzgerald, Hsiao, & Connor, 2009). Yet, no neuroimaging study so far has investigated VT categorization by training human participants to identify VT categories. We here trained human participants to categorize VT stimuli and used representational similarity analyses (RSA; Kriegeskorte & Kievit, 2013) of functional magnetic resonance imaging (fMRI) data to characterize the neural representations of the trained stimuli. Evidence was found for the two‐stage model in the somatosensory system. In order to also characterize information flow across the hierarchy, we built upon a recently developed dynamical model that allows extracting quantitative estimates of connectivity (Gilson, Moreno‐Bote, Ponce‐Alvarez, Ritter, & Deco, 2016). We found robust top‐down connectivity from the second to first stage of the hierarchy during task performance. Our findings are consistent with a common computational mechanism of perceptual categorization that generalizes across sensory systems, supporting a unified theory of perceptual categorization and learning.

2. METHODS

2.1. Participants

Fourteen right‐handed healthy adults (ages 18–28 years, mean age = 23.6 years, 10 females) were enrolled in the study. Georgetown University's Institutional Review Board approved all experimental procedures, and written informed consent was obtained from all participants before the experiment. Participants were paid for their participation.

2.2. VT device

A (17.4 × 11.0 cm²) 14‐channel magnetic resonance imaging (MRI)‐compatible VT stimulator array was organized as two rows of seven stimulators (Figure 1a), with on‐center stimulator spacing of 2.54 cm. To ensure that the stimulators would maintain contact with the volar forearm, the array comprised four rigid modules connected with stiff plastic springs. Velcro straps were used to firmly mount the device to the arm while bending the array to conform to the arm's shape. The modules closest to the wrist (9.7 × 5.0 cm²) each contained four stimulators, and the other two modules (7.1 × 5.0 cm²) each had three stimulators. The piezoelectric bimorph stimulator wafers (http://www.piezo.com, model Q220‐A4‐303YB) were sandwiched between two manufactured printed circuit boards (two‐layer 1.5 mm FR‐4 epoxy glass laminate) with 2.15 mm spacing between boards. Custom 3D‐printed plastic contactors (with 4.6 mm diameters) were epoxied to the bimorph's moving ends and protruded through 6.4 mm diameter surround holes in each circuit board. With no applied voltage to the piezoelectric bimorphs, the contactors were flush with the circuit board surface facing the skin. During operation, a constant +57 V voltage applied to all stimulators retracted the contactors into the surround, and each applied −85 V pulse drove the contactor into the skin. All pulses were identical—the drive signal was a square wave, with a pulse time (−85 V) of 2 ms, and with unpowered intervals of 1 ms between power reversals to protect the switching circuitry.

Figure 1.

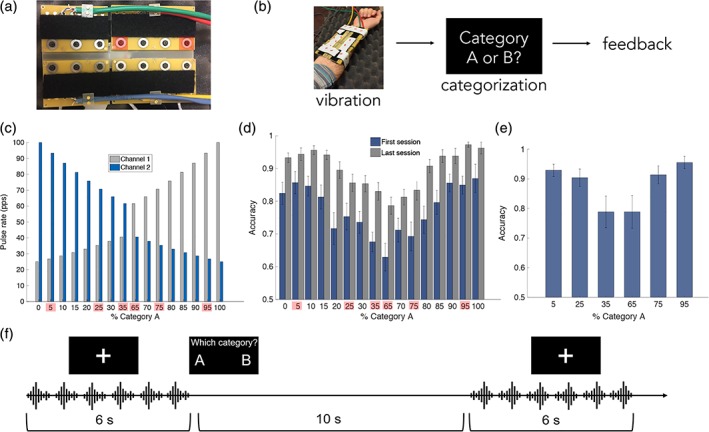
Vibrotactile (VT) device and stimuli, training paradigm and performance, and fMRI paradigm. (a) Fourteen‐channel MRI‐compatible VT stimulator array used for VT categorization training. Each VT stimulus was comprised of two concurrently active channels (highlighted in red). (b) In each trial during training, a VT stimulus was presented to the right forearm. Participants indicated their categorization decision with a button press with their left hand. Following incorrect trials, the correct category label was displayed on the screen, and participants were given the opportunity to replay the stimulus. (c) The Category A prototype consisted of a high‐pulse‐rate vibration toward the elbow (Channel 1; light blue) and a low‐pulse‐rate vibration toward the wrist (Channel 2; dark blue). The Category B prototype was the opposite. The set of training stimuli was generated by morphing parametrically between the category prototypes. In both A and B, the six stimuli used in the fMRI scans are highlighted in red. (d) Training performance (d) and (e) in‐scanner performance. Error bars indicate SEM across subjects (N = 14). (f) Participants completed an fMRI scan after category training in which they actively categorized the VT stimuli. VT stimulus repetitions were presented in 6‐s blocks. At the end of each block, the category labels appeared on the screen and the participant indicated their choice with a button press [Color figure can be viewed at http://wileyonlinelibrary.com]

The control system comprised the power supplies (−85 V, +57 V), high voltage switching circuits to apply these voltages to the piezoelectric bimorphs, and a digital control system that accepted from a controlling computer's serial COM port the digital records specifying a stimulus (comprising the times and channels to output pulses on), and a command to initiate stimulus output.

2.3. Stimuli

VT pulse trains were presented to the right volar forearm using the multichannel VT array. We used a morphing algorithm to create a quasi‐continuous stimulus space, divided into two categories (Figure 1c) (Chevillet, Jiang, Rauschecker, & Riesenhuber, 2013; Jiang et al., 2007; Jiang et al., 2018). Morphed stimuli permitted precise control of the physical features and category membership of VT stimuli. Each stimulus morph consisted of two concurrently active channels spaced 7.62 cm apart. The Category A prototype comprised a pulse train at a high rate (100 pulses per second [pps]) closer to the elbow and a pulse train at a lower rate (25 pps) closer to the wrist. The Category B prototype was the opposite with regard to the positions of the higher and lower pulse‐rate stimuli: 25 pps closer to the elbow, and 100 pps vibration closer to the wrist. A set of 18 training stimuli was generated by morphing between category prototypes in 1/10 octave steps (Figure 1c), such that the pulse rate of one active channel increased and the pulse rate of the other active channel decreased with each step along the morph line. Category membership was defined by the spatial location of the higher pulse rate channel relative to the lower pulse rate channel while overall stimulus energy was matched across Categories A and B.

2.4. Categorization training

To examine how the brain learns to assign categories to VT patterns, we trained participants to categorize the VT stimulus morphs (Figure 1b). On each trial, a VT stimulus was presented followed by the category labels (“gark” and “skay,” shown as “A” and “B” in the figures for simplicity) on the screen. Participants indicated their categorization decision with a button press with their left hand corresponding to the spatial position of the correct label (left vs. right). The position of the labels swapped on each block to mimic the design of the fMRI experiment (see below). Following incorrect trials, the correct category label was displayed on the screen, and participants were given the opportunity to replay the stimulus. No feedback was given for correct trials. Each training session comprised six blocks of 144 trials each. During the first training session, the distance from the tip of the middle finger to the VT device was recorded for each subject so that the device was consistently positioned in the same location on the right forearm for each session.

To facilitate training progression, we used a weighting system in which the stimuli that participants' miscategorized most often were presented more frequently than stimuli that were correctly categorized. In each block, the stimuli were evenly distributed over 66% of the trials. The four stimuli that were most often miscategorized from the previous block were used in the remaining 33% of trials. Participants were trained to 92.5% accuracy, based on pilot studies in which participants took between five and eight sessions to reach this performance level, comparable to training times in our previous studies of categorization in the visual and auditory domains (Jiang et al., 2007, 2018).

2.5. Categorization fMRI scan

Echo planar images (EPI) images from six short‐block runs were collected. Each run lasted 7.6 min and began and ended with a 10‐s fixation period. Within each run, VT stimulus repetitions were presented in 6‐s blocks, with a 10‐s interblock interval (Figure 1f). To boost the stimulus‐driven blood oxygen level‐dependent (BOLD) signal, six repetitions of the same morph were presented in each block. Six morphs were included in the scans: Three morphs from Category A (95, 75, and 65% Category A morphs), and three morphs from Category B (35, 25, and 5% Category A morphs; Figure 1c). At the end of each block, the category labels appeared on the screen and the participant indicated their categorization decision with a button press with their left hand. The position of the category labels on the screen was alternated every run so that there were no systematic differences in activation between categories due a specific button press being associated with a single category.

2.6. MRI acquisition

MRI data were acquired at Georgetown University's Center for Functional and Molecular Imaging using an EPI sequence on a 3‐Tesla Siemens TIM Trio scanner. A 12‐channel head coil was used (flip angle = 90°, repitition time (TR) = 2040 ms, echo time (TE) = 29 ms, field‐of‐view (FOV) = 205 mm, 64 × 64 matrix). Thirty‐five interleaved axial slices (thickness = 4.0 mm, no gap; in‐plane resolution = 3.2 × 3.2 mm²) were acquired. Two hundred and twenty‐nine EPI images were acquired in each run, and six total runs were acquired for each subject. A T1‐weighted magnetization‐prepared rapid acquisition with gradient echo (MPRAGE) anatomical image (resolution 1 × 1 × 1 mm³) was also acquired for each subject.

2.7. fMRI data preprocessing

Image preprocessing was performed in SPM12 (http://www.fil.ion.ucl.ac.uk/spm/software/spm12/). The first four acquisitions of each run were discarded to allow for T1 stabilization, and the remaining EPI images were slice‐time corrected to the middle slice and spatially realigned. EPI images for each subject were coregistered to their anatomical image. The anatomical image was then segmented and the resulting deformation fields for spatial normalization were saved for later use when normalizing the RSA maps.

2.8. Diffusion‐tensor imaging preprocessing and tractography

For each participant, diffusion‐tensor imaging (DTI) was used to evaluate the white‐matter intracortical connectivity. Diffusion parameters were as follows: TR = 7,500 ms, TE = 87 ms, flip angle = 90°, voxel size = 2.5 × 2.5 × 2.5 mm³, one average, 80 directions, and b value 900 s/mm². Each DTI volume underwent motion and eddy current correction using the FSL package. For each voxel, a diffusion tensor was built using dtifit and a probabilistic diffusion model was constructed using bedpostx (Behrens et al., 2003, 2007).

2.9. Univariate analysis

Realigned and slice‐time corrected functional images were normalized to Montreal Neurological Institute (MNI) space and smoothed with an isotropic 6‐mm Gaussian kernel for univariate analysis. The onset of each block was modeled using a canonical hemodynamic response function. Six motion parameters generated from realignment were included as regressors of no interest. Contrast images were generated for the contrast of all stimulus conditions relative to an implicit baseline and entered into a one‐sample t test against 0 using SPM's second‐level routines.

2.10. Representational similarity analysis

In RSA (Kriegeskorte & Kievit, 2013), the dissimilarity of neural activation patterns elicited in response to different stimuli is compared to a hypothesized model of the representational structure of those stimuli. RSA permits the testing of specific hypotheses about the structure of neural representations and facilitates the localization of these representations in the brain. A hypothesized model of representation is tested by constructing a representational dissimilarity matrix (RDM) in which each entry (Row i, Column j) corresponds to the expected dissimilarity between Stimuli i and j. To test for category selectivity, we constructed an RDM in which all stimuli within a category had a dissimilarity coefficient of 0, whereas all stimuli in different categories had a dissimilarity coefficient of 1 (Figure 3a). Importantly, the button presses required to categorize a stimulus as Category A or B was swapped after each run. Therefore, by counterbalancing the motor responses required to indicate categorization decisions, we ensured that category‐related responses could be dissociated from motor responses.

Figure 3.

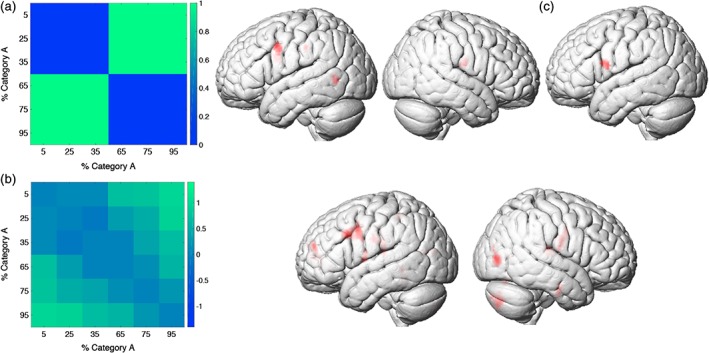
Representational similarity analysis. (a) Category‐selective representational dissimilarity matrix (RDM; left) and category‐RSA (right). (b) Stimulus‐selective RDM (left) and stimulus‐RSA (right). (c) Category‐RSA, controlling for stimulus‐selectivity using a partial correlation. All maps are thresholded at a voxel‐wise p < 0.001 and cluster‐level p < 0.05, FWE corrected [Color figure can be viewed at http://wileyonlinelibrary.com]

To construct a stimulus‐selective RDM, we analyzed the results of a stimulus discrimination behavioral experiment performed by a subset of participants (n = 10) that participated in the training and fMRI experiments. Participants performed a same/different discrimination task using the six morphs from the fMRI experiment. On each trial, pairs of stimuli were presented with a 400‐ms interstimulus interval. Participants were required to respond within 1.5 s. Participants first performed 20 practice trials with feedback, and then completed seven blocks of 72 trials each with no feedback. The same number of “same” and “different” trials was used. To construct an RDM from these data, d‐prime measures were computed for each pair of stimuli (Green & Swets, 1966). d‐Prime combines information about successfully detected “different” trials with false alarms, and thus accounts for response biases (e.g., responding “different” on all of the trials). An RDM was calculated for each individual subject. A mean RDM was calculated across subjects, which was then used in the RSA (Figure 3b). RDMs were consistent across subjects; the RDMs for all individual participants correlated with the mean RDM with a mean Pearson r = 0.82 ± 0.06. Finally, to test for category selectivity while controlling for stimulus selectivity, we performed an additional whole‐brain RSA using partial Spearman correlations (Xu et al., 2018) between the neural dissimilarity matrix and the category‐selective RDM, controlling for the stimulus‐selective RDM.

RSA was performed using the CoSMoMVPA toolbox (Oosterhof, Connolly, & Haxby, 2016) (http://www.cosmomvpa.org) and custom MATLAB code. Each of the six VT stimulus morphs was modeled as a regressor in a first‐level model. The onset of each block was modeled using a canonical hemodynamic response function. Six motion parameters generated from realignment were included as regressors of no interest. T‐statistic images were generated for the contrast of each stimulus condition relative to an implicit baseline. T‐statistic maps were used, because t values divide the beta estimate for each voxel by the estimate of its SE, thereby reducing the influence of highly variable response estimates (Misaki, Kim, Bandettini, & Kriegeskorte, 2010). RSA was first performed on unsmoothed data and in participants' native space, and then the RSA results for each individual subject were normalized to MNI space for statistical analysis. We performed a searchlight procedure (Kriegeskorte, Goebel, & Bandettini, 2006), in which the multivoxel response pattern associated with each VT morph was extracted from within a sphere of 30 voxels (similar results were obtained for a range of searchlight sizes from 20 to 100 voxels), and the dissimilarity between patterns for each stimulus pair was calculated (1—Pearson correlation distance). The mean of each feature (i.e., voxel) across conditions was subtracted prior to computing the dissimilarity for each stimulus pair (Diedrichsen & Kriegeskorte, 2017). The neural dissimilarity matrix for each searchlight was then Spearman‐rank correlated to the category‐selective RDM, and the resulting correlation coefficient was assigned to the voxel at the center of the searchlight. This procedure was repeated for all searchlights across the entire brain, generating a whole‐brain map of Spearman correlation coefficients between the neural dissimilarity matrix and the category‐selective RDM. The resulting correlation coefficient maps were Fisher‐z‐transformed (atanh function in MATLAB) to conform to statistical assumptions for second‐level parametric statistics. The Fisher‐transformed maps for each subject were normalized to MNI space, smoothed with an isotropic 6‐mm Gaussian kernel, and submitted to one‐sample t tests against 0 using SPM's second‐level routines. All analyses were thresholded at a voxel‐wise p < 0.001 and cluster‐level p < 0.05, FWE corrected.

2.11. Whole‐cortex EC analysis: Overview

The term “effective connectivity (EC)” refers to the causal impact a brain region's activity exerts over another (Friston, 2011), according to a dynamical model. We built on a recently developed method (Gilson et al., 2016) to estimate, for each subject, directed interactions between functional brain regions. In contrast to the widely used dynamic causal modeling (Friston, 2011; Friston, Harrison, & Penny, 2003), our method for the estimation of EC relies on a simpler model for local activity and on linear activity propagation without modeling the hemodynamic response explicitly. In particular, we used a noise‐diffusion network that incorporates long‐range anatomical connectivity. These simplifications allow us to efficiently estimate whole‐cortex EC between 200 regions (chosen from a brain atlas (Finn et al., 2015; Shen, Tokoglu, Papademetris, & Constable, 2013)), thus obviating the need to confine the computation of functional connectivity and interactions to limited a priori sets of region of interest (ROI) that might not include all relevant network nodes. The model was tuned such that it approximated the empirical spatiotemporal fMRI functional connectivity. The resulting model parameters can be interpreted as EC between regions.

2.12. Brain parcellation for EC analysis

The brain atlas from (Finn et al., 2015; Shen et al., 2013) was used to parcellate the brain into functional regions. Analyses were restricted to the 200 cortical regions out of the total number of 268 brain regions, omitting subcortical regions and the cerebellum. The parcellation image is publicly available on the BioImage Suite NITRC page (https://www.nitrc.org/frs/?group_id=51). The atlas ROIs were brought into each subject's native space using the inverse normalization parameters estimated during segmentation of anatomical image.

In order to identify which nodes in this parcellation correspond to the ROIs identified in the RSA, the overlap of atlas parcels with stimulus‐selective and category‐selective clusters was evaluated using a selectivity index for each Region i (Figure 4), defined as: ${\mathit{SI}}_i=\left(o_i^{\mathrm{cat}}-o_i^{\text{stim}}\right)/\left(o_i^{\mathrm{cat}}+o_i^{\text{stim}}\right)$, where $o_i^{\mathrm{cat}}$ and $o_i^{\text{stim}}$ are the overlap in percent with the RSA maps for category selectivity and stimulus selectivity, respectively. The selectivity index ranged between −1 (purely stimulus selective) and +1 (purely category selective).

Figure 4.

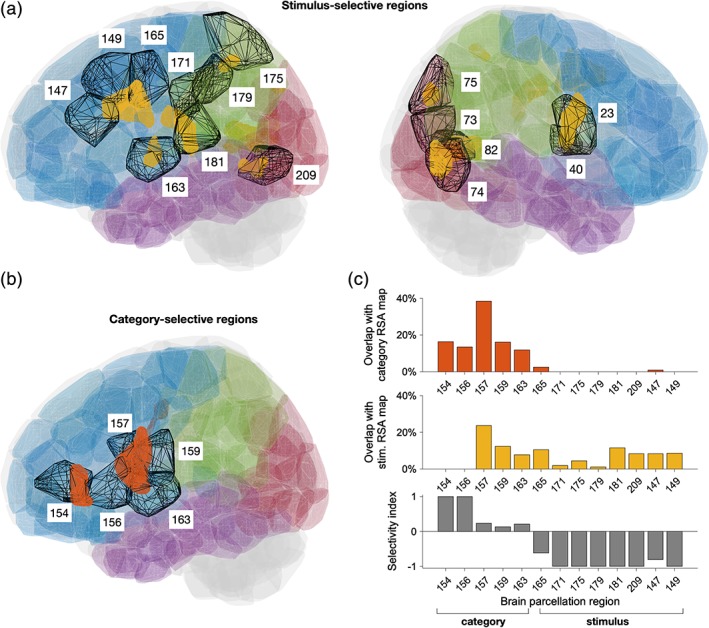
Brain atlas for whole‐brain effective connectivity analysis and selected regions of interest. (a) Atlas regions overlapping with stimulus‐selective clusters identified using RSA (clusters with significant RSA selectivity are shown in yellow), see also Table 2. (b) Atlas regions overlapping with category‐selective clusters (shown in orange), see also Table 3. (c) Percentage of category‐selective (top) and stimulus‐selective (middle) voxels inside each of the selected left cortical regions. Bottom: The selectivity index (see Section 2) indicates the atlas regions that are predominantly category‐selective (values close to 1) or stimulus‐selective (values close to −1) [Color figure can be viewed at http://wileyonlinelibrary.com]

2.13. Structural connectivity

In order to constrain our whole‐cortex computational model, we limited EC estimation to anatomically plausible connections between distant brain regions (Gilson et al., 2016). We inferred these connections by first estimating white‐matter connectivity between the cortical regions defined by our functional parcellation (see above). We used the probabilistic tractography algorithm implemented in FSL's FDT tool on the DTI volumes obtained from 21 subjects (eight subjects that participated in the current study and 13 additional subjects). For each voxel, a diffusion tensor was built using DTIFIT. A probabilistic diffusion model was constructed using bedpostX (Behrens et al., 2003, 2007). Volume masks for the fiber tracking algorithm were created from the atlas regions by transforming them into DTI space with a transformation matrix created in FSL FLIRT. Probabilistic tractography (ProbtrackX, Behrens et al., 2003, 2007) was performed using the voxels in these masks as seeds and targets. Second, we constructed individual structural connectomes from the resulting connectivity values. The connection probability P_ij between Regions j and i was computed as the fraction of seeded tracks in Region j that terminated in the target Region i. Directionality of connections cannot be determined from diffusion MRI. We therefore averaged the obtained estimates for P_ij and P_ji for each pair of regions. Third, we averaged the resulting probability matrix across subjects in order to obtain a group‐averaged connectome. We binarized the group structural connectivity matrix by applying a threshold which retained 40% overall connectivity. All our EC results remain valid for connectivity values between 20 and 50%.

2.14. ROI time series

Prior to EC estimation, the fMRI data were further preprocessed in the CONN‐fMRI toolbox (Whitfield‐Gabrieli & Nieto‐Castanon, 2012). Noise due to white matter and CSF signals were regressed out using CompCor (Behzadi, Restom, Liau, & Liu, 2007). For each recording session, we extracted the average BOLD signal time course across all voxels within each of the 200 functional regions. For each run, we subtracted the mean signal for each region and divided the time series by the average variance of the 200 regions in order to get the normalized BOLD time series $s_i^t$ for each Region i.

2.15. Model of cortical dynamics

We modeled the whole‐cortex dynamics as a noise diffusion process, where the activity in each node was determined by: (a) fluctuations in the individual input to each region, described by a diagonal covariance matrix Σ and (b) recurrent network connectivity, described by a weight matrix C. Each individual weight C_ij corresponded to the EC from source Region j to target Region i. The model is described in detail in Gilson et al. (2016). In brief, the local dynamics in each node follows an Ornstein–Uhlenbeck process, where the activity in node x_i decays exponentially with constant τ_x and is affected by the rest of the network via $d{x}_i=\left(\frac{-x_i}{{\tau }_x}+{\sum }_{j\ne i}{C}_{\mathit{ij}}{x}_j\right)\mathit{dt}+d{B}_i$. The local fluctuations in each node follow a Wiener process dB_i with variance Σ_ii. Essentially, the model decomposes functional connectivity into two sets of parameters: EC C and local variability Σ.

2.16. Parameter optimization procedure

We tuned the model by iteratively updating the network parameters C and Σ in order to minimize the difference between the model covariance matrices $Q_{\mathit{ij}}^0$, $Q_{\mathit{ij}}^1$ and the empirical functional connectivities ${\widehat{Q}}_{\mathit{ij}}^0$, ${\widehat{Q}}_{\mathit{ij}}^1$, where $Q_{\mathit{ij}}^0=\frac{1}{T-1}{\sum }_{t=1}^{T-1}{s}_i^t{s}_j^t$ and $Q_{\mathit{ij}}^1=\frac{1}{T-1}{\sum }_{t=1}^{T-1}{s}_i^t{s}_j^{t+1}$ (likewise for ${\widehat{Q}}_{\mathit{ij}}^0$ and ${\widehat{Q}}_{\mathit{ij}}^1$ that were computed across T = 1,350 time points separated by TR = 2.04 s). Crucially, including the time‐shifted covariance matrices $Q_{\mathit{ij}}^1$ and ${\widehat{Q}}_{\mathit{ij}}^1$ in the optimization allows for the estimation of asymmetric EC (Gilson et al., 2016).

Model parameters were tuned with an efficient iterative algorithm based on Lyapunov optimization (for details, see Gilson et al. (2016) and (2018)). The model was initialized with zero connectivity (all C_ij = 0) and unit variances (all Σ_ii = 1). The structure of the weight matrix C was determined by the binarized structural connectivity matrix SC (see above): only connection weights between regions that were anatomically connected were iteratively updated (so that C_ij ≥ 0) and other connections remain zero. The optimization rates were set to ɛ_C = 5 × 10⁻⁴ and ɛ_Σ = 0.01 in all analyses. For each subject, the intrinsic time constant τ_x of the corresponding model was estimated from the autocovariance decay of BOLD activity averaged over all regions: ${\tau }_x=\mathrm{TR}\bullet \frac{n}{{\sum }_{i=1}^n\log \left({\widehat{Q}}_{\mathit{ii}}^0\right)-\log \left({\widehat{Q}}_{\mathit{ii}}^1\right)}$. We obtained τ_x = 0.8591, ∙ TR ± 0.0338, ∙ TR (mean ± standard error of the mean). The goodness of fit of the functional connectivity obtained for the optimal model parameters was measured using Pearson correlation and yielded results comparable to previous studies despite our finer parcellation (mean correlation of model functional connectivity (FC) and empirical FC ± SEM across subjects was r = 0.646 ± 0.017 for $Q_{\mathit{ij}}^0$ and r = 0.442 ± 0.020 for $Q_{\mathit{ij}}^1$; Gilson et al., 2018: r = 0.7, Messé, Rudrauf, Benali, & Marrelec, 2014: r = 0.6).

2.17. Effective drive

We defined the effective drive (ED) to measure how the activity at Region j propagated to Region i: ${\mathrm{ED}}_{\mathit{ij}}=C_{\mathit{ij}}\sqrt{Q_{\mathit{jj}}^0}$, where $\sqrt{Q_{\mathit{jj}}^0}$ is the SD of fluctuations in Region j (Gilson et al., 2018). To quantify the direction of signal flow between two connected Regions j and i, we compute the difference between the ED ED_ij − ED_ji, so that positive values indicate stronger drive from j → i and negative values a stronger drive from i → j (Figure 5b). Finally, to compare the ED across subjects, we define the effective drive index (EDI) for a Region j as ${\mathrm{EDI}}_j=\frac{\sum _i{\mathrm{ED}}_{\mathit{ij}}-{\mathrm{ED}}_{\mathit{ji}}}{\sum _i{\mathrm{ED}}_{\mathit{ij}}+{\mathrm{ED}}_{\mathit{ji}}}$, that is, the sum of ED differences with all target Regions j, normalized by the overall ED between the regions (Figure 5d,e).

Figure 5.

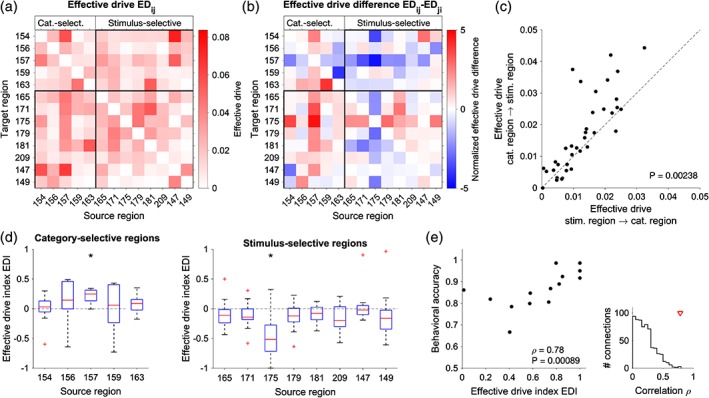
Effective connectivity between category‐selective and stimulus‐selective regions. (a,b) Average effective drive (ED) (a) and corresponding ED difference (b) for selected regions (left cortex). Note that the ED difference between Regions i and j is the same as between Regions j and i, but with opposite sign, that is, if Region j drives Region i, then Region i is driven by Region j to the same degree. ED was estimated for each of the 14 subjects and then averaged across subjects. (c) Relationship of average ED between category‐selective and stimulus‐selective regions. The drive from category‐selective regions to stimulus‐selective regions is significantly larger than in the opposite direction (Wilcoxon test, p = 0.00238, N = 40, z = −3.03). (d) Effective drive index (EDI) defined as the sum of ED differences of a source region with all target regions normalized by the total ED between the regions (see Section 2). EDI tends to be positive for connections from category‐selective regions to stimulus‐selective regions (left) and negative for connections from stimulus‐selective regions to category‐selective regions (right). (*) indicates individually significant connections (Wilcoxon test, p < 0.05; Bonferroni corrected). (e) Relationship between the EDI of regions 157 (left precentral gyrus, category selective) and 175 (left inferior parietal, stimulus selective) and behavioral accuracy (Spearman correlation ρ = 0.785, p = 0.000892, N = 14 95% confidence interval for ρ = 0.445 to 0.959 obtained using bootstrap). The inset (right) shows the EDI–accuracy correlation between all cortical regions. The red triangle indicates the value observed for the EDI of Regions 157 and 175 [Color figure can be viewed at http://wileyonlinelibrary.com]

2.18. Relationship between EDI and behavioral accuracy

We quantified this relationship using Spearman correlation (Figure 5e). The 95% confidence interval for the correlation coefficient was estimated as the 2.5th and 97.5th percentile of the correlation coefficients evaluated in 1,000 bootstrap samples obtained by randomly resampling with replacement from the 14 subjects.

3. RESULTS

3.1. Behavior

3.1.1. Category training

Participants required 5.64 ± 3.07 sessions on average to reach 92.5% categorization accuracy. To test for training effects, a paired t test was performed for each morph comparing the accuracies for the first and last training session. All morphs showed a significant improvement in accuracy from the first to last session (all p < 0.05; Figure 1d). Additionally, median reaction time significantly decreased from the first to last training session for all stimuli (all p < 0.05). Outlier reaction times defined as two SD above or below the mean reaction time were removed prior to statistical testing. These results indicate that participants' categorization performance improved significantly as a result of training.

3.1.2. In‐scanner behavior

The average categorization accuracy across all morphs and participants in the fMRI experiment was 88.0 ± 1.9% (SEM), see Figure 1e.

3.2. Univariate fMRI analysis

Several regions were significantly activated in response to VT stimulation of the right forearm, including bilateral supplementary motor area, precentral gyri, left postcentral gyrus, left supramarginal gyrus and inferior parietal lobule, and right inferior and middle frontal gyrus (Table 1 and Figure 2). To gain a better picture of the neuronal selectivity underlying these responses, we performed a series of RSA.

Table 1.

Location and cluster extent for all regions with significant activation. Clusters are thresholded at a voxel‐wise p < 0.001 and cluster‐level p < 0.05, FWE corrected

Brain regions	Extent (voxels)	Peak MNI coordinates (x, y, z)	t‐Statistic
L PreCG (BA 6)	112	−58, 6, 42	5.20
L supramarginal gyrus (BA 40), inferior parietal lobule, postcentral gyrus (BA 2, 3, 4)	3,574	−50, −28, 30	10.60
		−54, −34, 50
		−62, −26, 46
R anterior insula, inferior frontal gyrus, middle frontal gyrus	1,989	34, 28, 4	7.41
		30, 22, 12
		44, 14, 12
R cerebellum (anterior and posterior lobe)	675	24, −64, −22	6.25
		40, −54, −28
		34, −48, −32
L cerebellum (anterior and posterior lobe)	1,298	−32, −48, −30	5.77
		−22, −62, −46
		−10, −80, −30
L occipital lobe (lingual gyrus, cuneus, posterior fusiform)	385	−18, −94, 10	5.46
		−22, −76, −6
		−12, −88, −4

PreCG = precentral gyrus.

Figure 2.

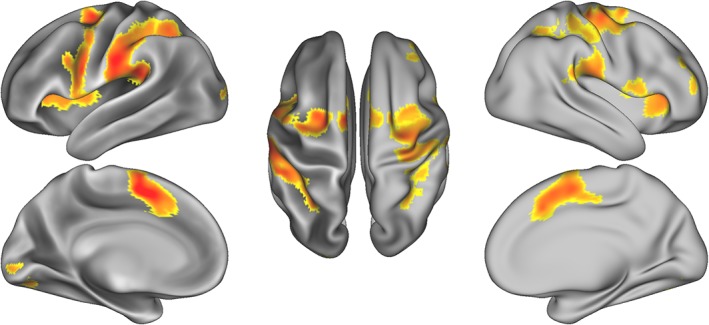
fMRI activation in response to vibrotactile stimulation of the right forearm. Results are thresholded at a voxel‐wise p < 0.001 and cluster‐level p < 0.05, FWE corrected [Color figure can be viewed at http://wileyonlinelibrary.com]

3.3. Representational similarity analysis

RSA performed with the category selective RDM (Figure 3a) identified the left precentral gyrus (PreCG), left supramarginal gyrus, left posterior middle temporal gyrus, and right postcentral gyrus (voxel‐wise p < 0.001 and cluster‐level p < 0.05, FWE corrected; Table 2 and Figure 3a).

Table 2.

Location and cluster extent for all significant category‐selective ROIs identified in the RSA. Clusters are thresholded at a voxel‐wise p < 0.001 and cluster‐level p < 0.05, FWE corrected

Brain regions	Extent (voxels)	Peak MNI coordinates (x, y, z)	t‐Statistic
L PreCG	112	−58, 6, 42	5.20
L supramarginal gyrus	58	−44, −28, 38	5.56
L inferior frontal gyrus	56	−42, 2, 24	4.73
R postcentral gyrus	71	54, −12, 22	4.72
L posterior middle temporal gyrus	81	−54, −60, 2	4.85

PreCG = precentral gyrus; ROI = region of interest.

RSA performed with the stimulus selective RDM (Figure 3b) identified selectivity in a number of regions including bilateral postcentral gyri and parietal opercula, right middle occipital gyrus and calcarine sulcus, left posterior middle temporal gyrus, and left PreCG (voxel‐wise p < 0.001, FWE cluster‐level corrected; Table 3 and Figure 3b).

Table 3.

Location and cluster extent for all significant stimulus‐selective ROIs identified in the RSA. Clusters are thresholded at a voxel‐wise p < 0.001 and cluster‐level p < 0.05, FWE corrected. Corresponding brain parcellation regions from Finn et al. (2015) that overlap with each cluster are used for estimating EC

Brain regions	Extent (voxels)	Peak MNI coordinates (x, y, z)	t‐Statistic	Corresponding brain parcellation regions
L postcentral gyrus, parietal operculum	135	−52, −24, 20	4.91	171, 181, 159
R postcentral gyrus, parietal operculum	234	52, −8, 26	5.27	23, 40, 62
R middle occipital gyrus	195	44, −78, 4	6.79	73, 74
R cuneus, precuneus	52	12, −80, 36	5.04	75
L posterior middle temporal gyrus	56	−46, −64, 0	4.51	181, 192, 209
L superior parietal lobule	42	−22, −48, 48	5.43	175, 179
R calcarine sulcus	216	12, −68, 6	6.59	82
L PreCG, superior temporal gyrus	61	−58, −2, 6	4.88	163
L PreCG	373	−46, 14, 36	5.94	165

EC = effective connectivity; PreCG = precentral gyrus; ROI = region of interest.

The category‐RSA and stimulus‐RSA results identified many of the same regions (e.g., left PreCG, left supramarginal gyrus). This is not surprising because the category‐RDM and stimulus‐RDM used in the RSA are correlated (Pearson r = 0.74), as similar stimuli in general also belong to the same category, except for similar stimuli on opposite sides of the category boundary. Conversely, dissimilar stimuli often belong to different categories, but some pairs of dissimilar stimuli belong to the same category. To disentangle stimulus‐ and category selectivity in our analyses, we therefore performed an additional whole‐brain RSA using partial correlations. At each searchlight, we performed a partial Spearman correlation between the neural dissimilarity matrix and the category‐selective RDM, controlling for the stimulus‐selective RDM. Conceptually, a partial correlation that controls for stimulus selectivity is equivalent to a test of the dissimilarity for stimulus pairs that maximally differ between the category‐selective and stimulus‐selective RDMs (Figure 3a,b). This focuses on stimuli near the category boundary. A category selective region will have a sharp transition in the neuronal responses to stimuli on either side of the category boundary driven by differences in category membership (a hallmark of perceptual categorization, for example, (Freedman, Riesenhuber, Poggio, & Miller, 2001)), whereas a stimulus selective region will show a more gradual change in response driven by differences in stimulus features. Interestingly, and compatible with the prediction of the two‐stage model, this analysis revealed a single category‐selective brain region, a region in the left ventral PreCG (Table 4 and Figure 3d). Further supporting the two‐stage model of perceptual categorization, no category selectivity was found in the somatosensory cortices (p > 0.01, uncorrected).

Table 4.

Location and cluster extent for all significant category‐selective ROIs, identified using a category‐RSA controlling for stimulus‐selectivity using a partial correlation. Clusters are thresholded at a voxel‐wise p < 0.001 and cluster‐level p < 0.05, FWE corrected. Corresponding brain parcellation regions from Finn et al. (2015) that overlap with each cluster are used for estimating EC

Brain regions	Extent (voxels)	Peak MNI coordinates (x, y, z)	t‐Statistic	Corresponding brain parcellation regions
L PreCG	56	−62, 4, 16	4.32	157, 159, 165

EC = effective connectivity; PreCG = precentral gyrus; ROI = region of interest.

3.4. Whole cortex EC

In order to gain insight into how stimulus‐selective and category‐selective brain regions interact with each other during VT categorization, we conducted a model‐based whole‐cortex EC analysis. This method allowed us to simultaneously estimate the directed EC, that is, the causal influence that a brain region exerts onto another one, between all 200 cortical regions in our parcellation (Figure 4). This means that the model‐based EC takes into account the impact of the global network configuration on the information flow between stimulus‐selective and category‐selective ROIs. Our whole‐cortex model (see Section 2) combines the structural connectivity between brain regions obtained using diffusion MRI with a dynamical model of local neural activity. The model parameters were then optimized to explain the empirically observed spatiotemporal functional connectivity, which results in an estimate of EC between anatomically connected regions.

We focused on the interaction between cortical regions that overlapped with the stimulus‐ and category‐selective clusters identified with RSA (Figure 4; see also Tables 2 and 3). First, we verified that the functional brain atlas that we used provided a sufficiently fine parcellation of the cortex so that functional regions mainly overlap with either stimulus‐selective or category‐selective clusters (Figure 4c). We found that only 1 of the 13 regions that we considered (Region 159, part of the left postcentral gyrus) overlapped to a similar degree with both stimulus‐selective and category‐selective clusters. We thus grouped the brain atlas regions in category‐selective and stimulus‐selective regions (Figure 4c).

We ran the EC analysis for each individual subject and then averaged the ED (the product of EC with the variability of local BOLD fluctuations, see Section 2) across subjects. The average ED revealed a pattern of connectivity: the majority of category‐selective regions exerted a stronger influence on stimulus‐selective regions than vice versa (Figure 5a,b; the rectangles mark stimulus → category and category → stimulus connections). This dominance of category → stimulus drive was statistically significant when considering all connections between category‐ and stimulus‐selective regions (Figure 5c; Wilcoxon test, p = 0.00238). Notably, the category‐selective region with the largest ED difference was region 157 (PreCG; Figure 5d), the region with the highest overlap with the category‐selective RSA clusters (36%; Figure 4c). In all subjects, Region 157 was driving stimulus‐selective regions rather than being driven by them, and the corresponding ED difference was significant (Wilcoxon test, p = 0.00024, N = 14). The regions that were strongly driven by this region included the stimulus‐selective regions 171 (postcentral and supramarginal gyri) and Region 175 (superior parietal lobule). In addition, we found that Region 175 received more overall input from category‐selective regions than it provided to them in 12 out of 14 subjects (Figure 5d; Wilcoxon test, p = 0.0017, N = 14). These results suggest a hierarchy between stimulus‐selective and category‐selective regions, with a dominance of top‐down signaling from category‐selective regions in the PreCG to stimulus‐selective areas.

Finally, we examined whether the top‐down drive was predictive of the subjects' performance in the categorization task. We selected the stimulus‐selective and category‐selective region with the strongest ED difference (175 and 157, respectively) and found a strong positive correlation between the behavioral accuracy and the dominance of the top‐down signals over bottom‐up signals between them (Figure 5e; Spearman's ρ = 0.785, p = 0.000892). This suggests a functional role of top‐down information flow in VT categorization decisions.

4. DISCUSSION

The grouping of sensory stimuli into categories is a fundamental function of the nervous system. Despite our remarkable ability for perceiving and identifying objects through touch (Klatzky, Lederman, & Metzger, 1985), perceptual categorization in the somatosensory system is the least understood of the three major sensory modalities. This study, for the first time, characterized the neural mechanisms of perceptual categorization of trained VT stimuli in humans. We tested the hypothesis that categorization in the somatosensory system, analogous to the visual and auditory systems, utilizes a multistage processing hierarchy in which early stages in sensory cortex are selective for the physical features of the stimuli, while later stages are selective for category membership. Indeed, we found that representations in somatosensory cortex showed selectivity for the physical features of the stimuli with no explicit category representation, while category selectivity was localized to ventral PreCG. Finally, EC analysis revealed coupling between category‐selective and stimulus‐selective regions.

Our data are consistent with a two‐stage model of perceptual categorization in the somatosensory system. To identify brain areas that were selective for the physical similarity and category membership of the VT stimuli—information that cannot be extracted using conventional univariate techniques—we utilized RSA, a technique that goes beyond traditional univariate analyses in that it characterizes the neural representations of stimuli and permits the testing of hypotheses regarding the organization of these representations. Using RSA and a category‐selective RDM, we identified category selectivity in several regions including the left ventral preCG, the left SMG, and the left posterior middle temporal gyrus. Because the category‐selective RDM was highly correlated with the stimulus‐selective RDM, we performed a second category‐selective RSA using partial correlations to control for stimulus selectivity. The RSA using partial correlations to control for stimulus selectivity identified the left ventral preCG as the only category‐selective region, consistent with the prediction of the two‐stage model that the higher level cortical areas are responsible for explicit category representation.

The primary advantage of the two‐stage model is computational flexibility: By segregating neural representations of the physical features in sensory cortex from the category membership of a stimulus in higher level cortex, representations in sensory cortex can be re‐used in support of new tasks by downstream brain regions (Riesenhuber & Poggio, 2000). Computationally, the location of the category‐selective stage is irrelevant, and our theoretical paper (Riesenhuber & Poggio, 2000) had already suggested the possibility of finding category circuits in brain areas other than prefrontal cortex, for example, in anterior IT. In this context, our finding of category‐selectivity in the ventral preCG in VT categorization therefore stands in interesting contrast to two previous studies investigating category learning in the visual (Jiang et al., 2007) and auditory (Jiang et al., 2018) systems, in which category‐selectivity was identified in prefrontal cortex (however, see Helie, Roeder, & Ashby, 2010, which found that activity in ventral PreCG correlated with categorization performance on a visual categorization task). The finding of category selectivity in the left ventral PreCG, the location of ventral premotor cortex, in the present study might suggest differences in category circuits between the different modalities. Another explanation is the intriguing possibility that the categorization of VT stimuli in our trained participants might have been more automatic than in those studies: There is increased engagement of motor systems and disengagement of other systems as experience with learned categories increases (Seger & Miller, 2010). For example, there is increased engagement in the prefrontal cortex of humans early in the learning of a stimulus–response classification task; however, engagement shifts to premotor cortex as the task becomes more automatic (Boettiger & D'Esposito, 2005). Taken together, these results could suggest that the somatosensory system may possess a greater propensity for automaticity during perceptual categorization than do the auditory and visual systems, perhaps due to the close correspondence between the somatosensory and motor systems. Our finding of category selectivity in the ventral PreCG, the location of ventral premotor cortex, is consistent with prior monkey studies that have identified premotor cortex as an important region in the decision‐process network underlying the categorization of VT stimuli (Romo & de Lafuente, 2013). It will be interesting in future studies to image participants as they are learning the categorization task.

Some recent studies can contribute to interpreting our results. A recent fMRI study used multivariate pattern analysis (MVPA) to identify selectivity for the frequency of VT stimuli in the left postcentral and supramarginal gyri (Kim, Chung, Chung, Bulthoff, & Kim, 2016). In another MVPA‐fMRI study, Kim et al. (2014) successfully decoded VT stimulus location from the posterior parietal cortex and the supramarginal gyrus. Consistent with these studies, we identified stimulus selectivity in the postcentral and supramarginal gyri, among other regions. The finding of frequency selectivity for VT stimuli in the postcentral gyrus in Kim et al. (2016), but not spatial selectivity (Kim et al., 2014), suggests that the postcentral gyrus in our study was representing categories based on the frequency content of VT stimuli.

Previous monkey electrophysiological (Romo & de Lafuente, 2013) and human neuroimaging studies (Pleger & Villringer, 2013) of VT decision making have identified a network of regions including prefrontal, premotor, motor, and sensory cortices that are involved in encoding perceptual choice. Importantly, due to the sluggish nature of the BOLD response in human fMRI studies, it has been unclear which regions contribute to sensory, decision, and motor related processes. In a recent human fMRI study, Wu, Velenosi, Schröder, Ludwig, and Blankenburg (2018) designed a VT frequency discrimination task with saccade responses that permitted the isolation of activity underlying perceptual choices from sensory and motor processes. This design allowed the authors to determine if the previously identified premotor structures still encode perceptual choice independent of action selection. Using MVPA, they identified information about perceptual choice independent of action selection in a premotor region (frontal eye fields), as well as the intraparietal sulcus and lateral prefrontal cortex. This result is consistent with our suggestion that the left premotor cortex encodes the category of trained VT stimuli, and not simply motor‐related processes.

A novelty of our study was the application of a new EC (EC) methods to gain a more detailed understanding of the cortical network underlying VT categorization. The model of EC applied here has been shown to reveal interesting properties of fMRI resting state dynamics that are not captured by temporal correlations of activity alone (Gilson et al., 2016; Glomb, Ponce‐Alvarez, Gilson, Ritter, & Deco, 2017; Rolls, Cheng, Gilson, Qiu, & Psychiatry, 2018). Recently, it has also been applied to task‐based fMRI (Gilson et al., 2018; Gravel et al., 2017; Senden et al., 2017). EC takes into account how the cortical network dynamics reflect task‐related processing because EC depends both on changes in response to stimulus processing and the (task‐dependent) network configuration (Gilson et al., 2018). For example, Gilson et al. (2018) analyzed the differences between rest and a passive movie viewing condition and found that changes in both ROI activity and in EC between the ROIs contributed to differences in FC between the two conditions. Applying this method to our data revealed strong top‐down connectivity of category‐selective to stimulus‐selective regions, demonstrating that whole‐cortex EC provides a valuable tool to gain insights into the information flow between cortical regions in task‐based fMRI.

We identified both bottom‐up (from stimulus selective to category selective regions) as well as top‐down (category selective to stimulus selective regions) EC. We quantified asymmetry in this bottom‐up and top‐down connectivity and found stronger top‐down influences. In the visual system, top‐down feedback connections greatly outnumber feedforward connections (Salin & Bullier, 1995). While the proportion of feedforward and feedback connections in the somatosensory hierarchy is not known, our results suggest that like in the visual system there may be a greater preponderance of feedback connections in the somatosensory system. What might the function of this top‐down influence be? A previous study from our lab (Scholl, Jiang, Martin, & Riesenhuber, 2014) used EEG rapid adaptation techniques to identify three phases of neuronal activity in visual perceptual categorization: posterior activity up to 200 ms following stimulus onset, anterior activation after 200 ms, and finally posterior activity again after 300 ms. We hypothesized that the late signal after 300 ms might be feedback activity from a reentrant signal, in line with a number of studies reporting reentrant activation associated with conscious awareness (Del Cul, Baillet, & Dehaene, 2007; Fahrenfort, Scholte, & Lamme, 2007). According to one theory of conscious perception known as the “global neuronal workspace” hypothesis, subliminal perception of stimuli results in activity primarily limited to sensory regions, while conscious perception results in long‐range, reverberating patterns of recurrent activity between sensory and higher level cortical regions (Del Cul et al., 2007). Under this interpretation, the strong top‐down influence of anterior category selective regions over posterior stimulus selective regions may be a marker of reentrant activity responsible for conscious awareness of the VT stimulus.

In summary, our data provide evidence for the two‐stage model of perceptual categorization in the somatosensory system with stimulus selectivity in sensory cortex and category selectivity in extra‐sensory areas. These results, together with our earlier findings from the visual (Jiang et al., 2007; Scholl et al., 2014) and auditory (Jiang et al., 2018) domains, suggest that the primary sensory modalities (vision, audition, and touch) all utilize a common neurocomputational mechanism for perceptual categorization.

CONFLICT OF INTEREST

The authors declare no competing conflict of interest.

Malone PS, Eberhardt SP, Wimmer K, et al. Neural mechanisms of vibrotactile categorization. Hum Brain Mapp. 2019;40:3078–3090. 10.1002/hbm.24581