Characterizing the role of the pre‐SMA in the control of speed/accuracy trade‐off with directed functional connectivity mapping and multiple solution reduction

Abstract

Several plausible theories of the neural implementation of speed/accuracy trade‐off (SAT), the phenomenon in which individuals may alternately emphasize speed or accuracy during the performance of cognitive tasks, have been proposed, and multiple lines of evidence point to the involvement of the pre‐supplemental motor area (pre‐SMA). However, as the nature and directionality of the pre‐SMA's functional connections to other regions involved in cognitive control and task processing are not known, its precise role in the top‐down control of SAT remains unclear. Although recent advances in cross‐sectional path modeling provide a promising way of characterizing these connections, such models are limited by their tendency to produce multiple equivalent solutions. In a sample of healthy adults (N = 18), the current study uses the novel approach of Group Iterative Multiple Model Estimation for Multiple Solutions (GIMME‐MS) to assess directed functional connections between the pre‐SMA, other regions previously linked to control of SAT, and regions putatively involved in evidence accumulation for the decision task. Results reveal a primary role of the pre‐SMA for modulating activity in regions involved in the decision process but suggest that this region receives top‐down input from the DLPFC. Findings also demonstrate the utility of GIMME‐MS and solution‐reduction methods for obtaining valid directional inferences from connectivity path models.

1. INTRODUCTION

The strategies people use to complete cognitive tasks not only have implications for task performance but also reflect individual and contextual differences in the brain and behavior. In a common example, people can adjust their performance to meet task demands by either emphasizing accurate responding at the cost of speed or increasing the speed of responding at the cost of accuracy. The ability to implement this type of strategy adjustment, known as speed/accuracy trade‐off (SAT), has been found to be of high relevance for applied research in areas as diverse as normative aging (Forstmann et al., 2011; Ratcliff, Thapar, & McKoon, 2004), attention problems in childhood (Mulder et al., 2010; Weigard & Huang‐Pollock, 2014) and obsessive‐compulsive disorder (Erhan et al., 2017).

Numerous explanations for the neural implementation of SAT have been posited and supported by a burgeoning literature involving computational modeling, cellular recording in nonhuman primates, and human neuroimaging (for a thorough review, see: Standage, Blohm, & Dorris, 2014). Of these theories, we focus herein on explanations of this phenomenon that are rooted in formal “bounded accumulator” models (Bogacz, Wagenmakers, Forstmann, & Nieuwenhuis, 2010; Rae, Heathcote, Donkin, Averell, & Brown, 2014), as these models are commonly used in neuroimaging studies on the roles of human brain regions in SAT. Such models frame choice response time (RT) tasks as a race between accumulators that gather noisy evidence for each response over time and assume that a response is initiated when one of the accumulators reaches a predetermined threshold of evidence (Bogacz et al., 2010). Lowering the distance the accumulator must travel to surpass the threshold leads to faster, but more error‐prone responding, and raising this distance has the opposite effect. Within this framework, a “cortical” theory (Van Veen, Krug, & Carter, 2008) of SAT holds that, under speed‐emphasis, brain regions involved in top‐down control (e.g., the dorsolateral prefrontal cortex; DLPFC) send a nonselective excitatory signal to regions involved in the accumulation or integration of sensory evidence, increasing their baseline activity and reducing the accumulators' distance‐to‐threshold (van Veen et al., 2008). A distinct, “striatal” theory holds that, under speed‐emphasis, excitatory input to motor regions, mediated by top‐down connections from the pre‐supplemental motor area (pre‐SMA) to the striatum, effectively lowers the threshold for response initiation, which would also lead to distance‐to‐threshold reductions (Forstmann et al., 2008, 2010, 2011).

Several additional lines of work have posited distinct explanations for the behavioral changes observed in SAT. First, recent empirical research involving both cognitive modeling (Rae et al., 2014) and single‐cell recordings (Heitz & Schall, 2012) has provided evidence that speed emphasis causes changes to the rate of evidence accumulation in addition to distance‐to‐threshold reductions. Furthermore, other theoretical accounts challenge the assumption that distance‐to‐threshold changes are the primary driver of SAT. Specifically, work using attractor network models, which replicate features of neural circuits putatively responsible for decision making, has suggested that a common excitatory input to decision circuit controls SAT by altering the strength of network dynamics, rather than through the modulation of thresholding (Furman & Wang, 2008; Roxin & Ledberg, 2008; Standage, Wang, & Blohm, 2014). However, Standage, Blohm, and Dorris (2014) proposed that a “unifying” account, in which top‐down excitatory signals project to both decision‐making attractor networks and to thresholding circuitry, is plausible given the current state of evidence in the SAT literature.

Hence, although current theories disagree about how specific decision processes change in SAT, most share the assumption that regions widely believed to be involved in sensory evidence accumulation or motor thresholding receive an excitatory input under speed emphasis, and that this input is provided by regions involved in the top‐down control of strategy adjustment (Standage, Blohm, & Dorris, 2014; Standage, Wang, & Blohm, 2014). Prior human neuroimaging work aimed at testing the “cortical” and “striatal” accounts of SAT has suggested that several regions previously found to be involved in cognitive control processes, including the dorsolateral prefrontal cortex (DLPFC: van Veen et al., 2008), the pre‐SMA (Forstmann et al., 2010, 2011), and the anterior cingulate cortex (ACC; van Maanen et al., 2011), may be the source of such control signals. Of these regions, the pre‐SMA has arguably received the most support for playing a central role in the coordination of SAT. Neural activity in the pre‐SMA as measured by functional magnetic resonance imaging (fMRI) and the integrity of white matter connections between this region and striatum have both been found to display a correlational relationship with individual differences in SAT‐related distance‐to‐threshold changes, as measured by parameters from bounded accumulator models (Forstmann et al., 2008, 2010, 2011; Mansfield, Karayanidis, Jamadar, Heathcote, & Forstmann, 2011). Furthermore, transcranial magnetic stimulation of the right pre‐SMA has been repeatedly demonstrated to experimentally alter the same parameters (Berkay, Eser, Sack, Çakmak, & Balcı, 2018; Georgiev et al., 2016; Tosun, Berkay, Sack, Çakmak, & Balcı, 2017). However, a comprehensive understanding of the pre‐SMA's role in SAT is currently lacking, in part because the strength and directionality of functional connections between this region and other regions believed to be involved in the control of SAT, as well as with those linked to evidence accumulation and motor thresholding, is currently unclear.

Previous work on neural connectivity between regions putatively involved in SAT has either employed measures of structural connections (e.g., white matter tract strength; Forstmann et al., 2010, 2011) or psychophysiological interactions (PPI: van Veen et al., 2008; Green, Biele, & Heekeren, 2012). Although these methods both have distinct advantages, they do not provide straightforward evidence of the directionality of connectivity between regions. Furthermore, previous studies have typically offered a limited window into connections between this set of regions, such as only exploring connectivity between the pre‐SMA and striatum (Forstmann et al., 2010, 2011) or clarifying the DLPFC's connections with other structures, but not connectivity between those structures (van Veen et al., 2008). Without a comprehensive description of directional connections between regions putatively involved in the control of SAT, and others putatively involved in more basic decision processes, crucial questions remain about the source of the hypothesized top‐down control signal and how the functional role of the pre‐SMA differs from that of other regions. For example, it remains unclear whether the pre‐SMA and DLPFC play distinct roles in implementing SAT strategy changes (e.g., by influencing separate regions involved in decision processing), or whether the pre‐SMA coordinates strategy changes in response to a control signal from the DLPFC.

Thus, a region‐of‐interest based directed connectivity analysis is needed to characterize directional relationships between these regions at the network level during SAT. However, fMRI network modeling methods have displayed mixed success in establishing the directionality of connections. In a landmark simulation/recovery study, Smith et al. (2011) found that methods designed to do so, such as Granger causality and the Bayes net algorithms available at the time, generally performed poorly; directional connections were identified with only 65–78% accuracy under ideal conditions. There have, however, been subsequent advances in preprocessing steps (the use high pass filters) and in the development of novel network algorithms which have produced several methods with great promise for identifying the directionality of connections using fMRI data (Mumford & Ramsey, 2014).

Group iterative multiple model estimation (GIMME; Gates & Molenaar, 2012), which implements unified structural equation models (uSEM; Gates, Molenaar, Hillary, Ram, & Rovine, 2010) to characterize both sample‐ and individual‐level directed connectivity patterns, is one such method. By accounting for contemporaneous and time‐lagged relationships between regions of interest (ROIs) in a data‐driven manner, uSEMs allow researchers to make person‐specific inferences about the presence and directionality of functional connections between multiple ROIs that are unbiased by sequential dependencies found in fMRI time series data (Gates et al., 2010). They do this by integrating SEMs to estimate contemporaneous connections between ROIs and vector autoregressions (VARs) to estimate lagged connections. GIMME, in turn, provides a method for fitting these models to sample‐level data with the goal of establishing which connections are common to a group, while also allowing for substantial heterogeneity between the connectivity maps of individuals (Gates & Molenaar, 2012). The combination of uSEM and GIMME methods was able to correctly identify the presence and directionality of roughly 90% of connections in Smith et al. (2011) simulation data set, demonstrating a marked improvement over other methods (Gates & Molenaar, 2012). Due to the accuracy and efficacy of these methods, they have previously been used to investigate directional connectivity in the domains of brain injury (Hillary et al., 2011), tobacco cessation (Zelle, Gates, Fiez, Sayette, & Wilson, 2017) and changes in brain functioning associated with alcohol use in college students (Beltz et al., 2013). Thus, they are ideal for clarifying directional connections between the numerous regions that are putatively involved in SAT.

Despite this impressive performance, however, uSEMs, and thus, GIMME are subject to the multiple solutions problem common to all cross‐sectional path analyses; there is often more than one possible network that fits the data well (Beltz & Molenaar, 2016; MacCallum, Wegener, Uchino, & Fabrigar, 1993). This is most likely to occur when contemporaneous relationships are stronger than lagged relationships, causing the data‐driven search process to decide between bi‐directional contemporaneous paths that, without the modeling of lagged relationships, would produce equivalent improvements to model fit. To address this issue, Beltz and Molenaar (2016) created GIMME for multiple solutions (GIMME‐MS) that estimates all possible solution sets; they also validated selection procedures for selecting the optimal model in a simulation study. Although GIMME‐MS has been previously applied to behavioral time series data (Beltz, Wright, Sprague, & Molenaar, 2016), it has not been previously applied to functional connectivity analyses.

In the current study, we apply these state‐of‐the‐art methods to fMRI time series data collected while participants were asked to implement SAT during a perceptual decision task. We aim to accomplish two interrelated goals. First, the methodological goal of the study is to determine whether the application of GIMME‐MS to this fMRI data set provides evidence of equivalent solutions, and, if this is the case, to use the multiple solution‐reduction procedures validated by Beltz and Molenaar (2016) to find an optimal set of models. Second, the substantive goal of the study is to use these models to investigate the presence and directionality of connections between regions that are putatively involved in the control of SAT and those putatively involved in more basic decision‐making processes, such as evidence accumulation (e.g., parietal areas) or motor thresholding (e.g., the striatum). Although we had no strong or preregistered predictions of our own, we sought to assess whether the results of this analysis were consistent with what would be expected given previous theories of SAT. We were most interested in whether the analysis would reveal strong positive connections from one or more of the former regions (the DLPFC, ACC, or pre‐SMA) to one or more of the latter, which may reflect the top‐down excitatory signal that is posited by several theories. Although the pre‐SMA is arguably the region most heavily implicated in playing a role in the control of SAT (at least from studies using a bounded accumulator model framework), we also sought to determine whether this region receives top‐down input from a distinct region (e.g., the DLPFC), potentially reflecting a higher‐order control signal. In this way, we address gaps in the previous literature on the connectivity of brain regions associated with SAT and demonstrate the utility of uSEM and GIMME‐MS for doing so.

2. METHOD

2.1. Participants

Eighteen healthy adults (6 males, Mean age = 24.22, SD = 6.04),1 who were recruited from an undergraduate student and community sample, participated in the study. All participants were required to (a) be right‐handed, (b) report no history of traumatic brain injury, neurological disease, or major medical conditions, (c) be native English speakers, and (d) display no contraindications to MRI procedures. No participants needed to be excluded for exceeding the cutoff for excessive motion (>3 mm movement in any direction within a run).

2.2. Behavioral task and paradigm timing

Participants completed a numerosity discrimination task, a paradigm well‐described by evidence accumulation models (Ratcliff & McKoon, 2008), in which they were presented with an array of asterisks in a box and were asked to decide whether the stimulus contained “many” or “few” asterisks. “Many” stimuli were boxes (289 × 289 pixels) presented as black on a white background containing 56–60 asterisks, distributed at random on an invisible 10 × 10 grid, while “few” stimuli contained 41–45 asterisks. Participants' responses were made by pressing buttons on a button box that was placed under their right hand in the scanner; they pressed the button under their index finger for “many” and the button under their middle finger for “few”.

The timing of the experimental paradigm (Figure 1) was similar to that used by Forstmann et al. (2008), which allowed the neural responses associated with speed/accuracy strategy changes to be modeled as distinct from neural responses associated with the actual decision‐making process. Prior to each trial, participants saw a 4,000 ms verbal cue that indicated whether they should emphasize speed (“FAST”) or accuracy (“ACC”) in the coming decision. This cue was followed by a jittered period, in which a fixation cross was presented for either 0, 2,000, or 4000 ms (selected at random) before the presentation of the numerosity discrimination stimulus. The stimulus was presented for 1,500 ms, followed by a 500 ms “feedback” period and another jittered period, in which a fixation cross was presented for either 0, 2,000, or 4,000 ms (selected at random) before the presentation of the next instructional cue. The “feedback” period was the same length of time for all trials and conditions, and typically involved only the presentation of a fixation cross, but other stimuli were occasionally presented during this time to encourage strategy use. Specifically, in the Accuracy‐emphasis condition, participants were informed that their response was incorrect if they made an error (“INCORRECT”, presented in red lettering). In the Speed‐emphasis condition, participants were informed that their performance was not fast enough if their response was longer than 700 ms (“TOO SLOW”, presented in red lettering). The 700 ms deadline was selected based on earlier pilot testing of the task, which indicated that this deadline was effective at encouraging SAT without reducing participants' accuracy rates in Speed‐emphasis condition to near‐chance levels. Trials with RTs greater than this deadline (20.3% of the trials in the Speed‐emphasis condition) were included in all behavioral and model‐based analyses, as removing them would make RT distributions in the Speed‐emphasis condition difficult to compare to those in the Accuracy‐emphasis condition, and would force the formal model of behavioral data (see below) to be fit to truncated distributions.

Figure 1.

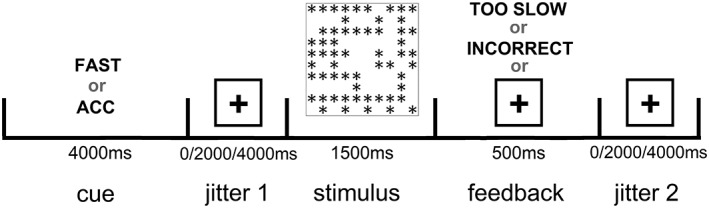
Schematic of the behavioral task and fMRI paradigm timing

Participants completed five functional imaging runs of the task, each of which contained 17 trials in each of the two conditions, leading to a total sample of 170 trials per person. The presentation order of the Speed‐ and Accuracy‐emphasis cues was varied pseudorandomly from trial to trial (i.e., a given trial may have the same type of cue as the trial that preceded it, or a cue for the alternate condition, with equal probability). Given the fast pace of the task, two “null” trial periods were also pseudorandomly interspersed in each run to compensate for the overlap of neural responses between adjacent trials. These “null” trials were simply periods of fixation cross‐presentation that lasted anywhere between 6 and 14 s, varying in increments of 2 s and with an average duration of 10 s. In addition, a fixation cross was presented for 10 s at the beginning and end of each run to improve estimates of baseline neural activity.

2.3. MRI data acquisition

Participants were scanned with a Siemens Trio 3‐T MRI scanner, using a 12‐channel head coil. Prior to functional imaging, a whole‐brain, high‐resolution T1‐weighted structural image was collected (TR = 1,650 ms, TE = 2.03 ms, flip angle = 9°, 160 sagittal slices, 1 mm slice thickness, 256 field of view, 1 mm isotropic voxels) for inter‐subject spatial normalization. Each functional imaging run included 190 T2*‐weighted MR images, collected using an echoplanar imaging (EPI) sequence (TR = 2000 ms, TE = 25, flip angle = 80°, 34 axial slices, 3 mm slice thickness, 192 field of view, 3 mm isotropic voxels).

2.4. Model‐based analysis of behavioral data

Correct and error response time data were fit to the linear ballistic accumulator model (LBA; Brown & Heathcote, 2008) in dynamic models of choice (DMC; Heathcote, Lin, Strickland, Gretton, & Matzke, 2018; Heathcote, Lin, & Gretton, 2017, https://osf.io/pbwx8/), a free set of functions for fitting evidence accumulation models in a hierarchical Bayesian framework with the R language (R Core Team, 2013). The LBA model frames decisions as a race between two or more accumulators that gather evidence at a linear, deterministic rate over time for each response. The average rate of evidence accumulation for each accumulator is defined by the “drift rate” parameter (v). In a typical implementation, the average rate of accumulation for the correct response on a given trial (vc) is estimated separately from the average rate of accumulation for erroneous responses (ve). When one of the two accumulators reaches the threshold for a response, determined by a “threshold” parameter (b), the corresponding response is initiated. The model also contains parameters for between‐trial variability in the rate of evidence accumulation (distributed normally: sv), between‐trial variability in the start point of the accumulation process (distributed uniformly: A), and the time in an RT that is taken up by peripheral processes unrelated to the decision (t0). For the current model fit, vc and ve were allowed to vary by stimulus type (many/few) and b was allowed to vary by response type (many/few) to address any potential stimulus or response biases. To identify the model, sv for the error accumulator, only, was fixed at 1 as a scaling parameter (Donkin, Brown, & Heathcote, 2009).

Although a large body of work, reviewed in the introduction, has found that thresholds (b) are lower under Speed‐ than under Accuracy‐emphasis, more recent work has provided evidence that drift rates (vc, ve: Rae et al., 2014) also differ by SAT condition. Furthermore, it is also possible that Speed‐emphasis reduces nondecision time (t ₀), as suggested by earlier neuroimaging evidence (Rinkenauer, Osman, Ulrich, Müller‐Gethmann, & Mattes, 2004). Therefore, in order to select an optimal set of LBA parameters to vary by SAT condition, we conducted a small model‐selection analysis in which five models (named Models A through E) were estimated, and each allowed different sets of parameters to vary by SAT: (a) threshold only, (b) threshold and drift rates, (c) threshold and nondecision time, (d) threshold, drift rates, and nondecision time, and (e) a “null” model in which none of the parameters were allowed to vary by SAT. For all models, a hierarchical Bayesian version of the LBA was implemented to estimate posterior distributions over individual‐level model parameter values and group‐level parameter values, which assumed that the individual‐level parameter values fell in normal distributions described by a mean (μ) and a standard deviation (σ) parameter (Turner, Sederberg, Brown, & Steyvers, 2013). Specific details of the estimation procedure and priors are reported in Supporting Information. Two standardized indices of relative fit for Bayesian models, the Watanabe–Akaike information criterion (WAIC; Watanabe, 2010) and deviance information criterion (DIC; Spiegelhalter, Best, Carlin, & Linde, 2014), both indicated that Model B, which only allowed threshold (b) and drift rate (vc, ve) parameters to vary by SAT, provided the best fit (Supporting Information Table S1), consistent with the findings of Rae et al. (2014). Model B was therefore used for all subsequent analyses. Although this model selection procedure addressed the relative fit of models with different parameter constraints, we also ensured that the model displayed good absolute fit by assessing how well it described primary effects in the behavioral data using posterior predictive plots (Gelman, Meng, & Stern, 1996), as described in section 3.

Inference about parameter value differences between conditions was conducted by calculating posterior difference distributions of μ parameter values, counting the proportion of samples for which one value was greater than the other, and using these proportions to calculate odds ratios (ORs) to quantify evidence for effects. An OR of 5:1, for example, indicates that there is a 5 to 1 chance that the difference distribution supports the hypothesis that a difference exists. As ORs provide a continuous measure of the degree of evidence for effects (in contrast to significance tests), we followed prior work (Winkel et al., 2016) by adopting interpretation guidelines similar to those used by Jeffreys' (1961) in the context of Bayes factors for categories of evidence: positive evidence (OR > 3:1), substantial evidence (OR > 10:1), strong evidence (OR > 30:1), and decisive evidence (OR > 100:1). Effects with very weak evidence (OR < 3:1) were not interpreted.

2.5. fMRI preprocessing, GLM analysis, and ROI selection

fMRI analyses were primarily conducted using Statistical Parametric Mapping (SPM8: http://www.fil.ion.ucl.ac.uk/spm/software/spm8/) but also involved the use of several individual programs from the Analysis of Functional Neuroimages (AFNI; Cox, 1996) software package, as noted below. Pre‐processing involved the following procedures performed using SPM8 programs: (a) slice timing correction (interpolation to the first slice in the series), (b) realignment with the first image in the time series to adjust for subject motion (least‐squares rigid‐body transformation; quality = .99, separation = 4, smoothing = 5.65), (c) co‐registration of the functional and high‐resolution anatomical images (maximization of normalized mutual information), (d) spatial normalization of the functional data to the T1 MNI template using the high‐resolution anatomical image to estimate transformation parameters (12‐parameter affine registration followed by a nonlinear discrete cosine transform; nonlinear iterations = 16, nonlinear regularization = 1, nonlinear frequency cutoff = 25, 3 mm isotropic voxels), and (e) spatial smoothing with a 5.65 mm FWHM Gaussian kernel.

Initial single‐subject general linear model (GLM) analyses were conducted to facilitate functional ROI selection. Four regressors of interest, convolved with the canonical hemodynamic response function (HRF), were included: (a) speed‐emphasis preparatory cues, (b) accuracy‐emphasis preparatory cues, (c) speed‐emphasis trials, and (d) accuracy‐emphasis trials. In addition, motion realignment parameters were included as nuisance regressors, a standard high‐pass filter (128 s) was applied to address low‐frequency drift, and the AR(1) estimate was used to address global autoregressive noise. Following model estimation, statistical maps of parameter estimates for three contrasts of interest were calculated at the individual level: (a) a contrast to identify regions that displayed greater activity during preparation for speed‐emphasis trials (Speed Cue > Accuracy Cue), (b) a contrast to identify regions that displayed greater activity during preparation for Accuracy‐emphasis trials (Accuracy Cue > Speed Cue), and (c) a contrast to identify regions that were primarily involved in the decision process itself, rather than in the neural response to the preparatory cue (Trials > Cues).

As GIMME‐MS estimates several features of the data, the number of multiple solutions and difficulty with model convergence increases exponentially with the number of ROIs; the method is best suited to models involving 6–10 regions (Beltz & Gates, 2017). Although some alternative connectivity analysis methods permit the inclusion of many more ROIs (e.g., simple correlation, principal components analysis), these methods are limited in their ability to test temporal or directional effects, which are of key interest in the current study. Hence, we used previous research to select a number of ROIs within the optimal range for GIMME models. Two broad categories of ROIs (Supporting Information Table S2) were included: (a) regions which had been previously linked to the top‐down control of SAT and to motor thresholding by prior research, and (b) regions putatively involved in evidence accumulation for the numerosity decision task used in the current study. For the former type of ROI, we conservatively selected a handful of regions, taking coordinates from prior research to directly extend a previous line of work on the pre‐SMA‐linked control of SAT and to facilitate generalization (e.g., avoid making inferences unique to the current sample's characteristics). Regions previously found to be involved in strategy adjustment for Speed‐emphasis, specifically the right pre‐SMA and right striatum (Forstmann et al., 2008) and the left and right DLPFC (Van Veen et al., 2008), were defined as 10 mm radius spheres centered about Talairach coordinates from the original studies, transformed to MNI coordinates using the procedure proposed by Lancaster et al. (2007). Of note, although these regions were selected a priori, analyses of task‐related activity drawn from them (reported in Supporting Information Materials) replicated previous findings; consistent with Forstmann et al. (2008), the pre‐SMA and striatum, but not the DLPFC, were more active during Speed‐ than Accuracy‐emphasis cues. A functional ROI (Accuracy Cue > Speed Cue) corresponding to the anterior cingulate cortex (ACC) was also selected because van Maanen et al. (2011) provided evidence that this region is involved in trial‐to‐trial response threshold adjustments during Accuracy‐emphasis.

For the latter type of ROI, we combined a priori knowledge with a data‐driven approach to identify regions involved in evidence accumulation during the specific decision task used in our experimental paradigm. We first inspected the array of regions that were active during decisions (the Trials > Cues contrast, which had greater power due to the increased number of events in each condition) and selected those for which there was a strong reason to believe they were involved in evidence accumulation, based on evidence from prior research. The right insula was selected because a prior study implicated this region in the domain‐general accumulation of sensory evidence for perceptual decisions (Ho, Brown, & Serences, 2009). The right intraparietal sulcus (IPS) was selected due to an abundance of evidence that this region encodes information about numerosity (Chochon, Cohen, Van De Moortele, & Dehaene, 1999; Dormal, Dormal, Joassin, & Pesenti, 2012; Piazza, Pinel, Le Bihan, & Dehaene, 2007) and is also involved in evidence accumulation (Kühn et al., 2011; Shadlen & Newsome, 2001). Additional details on ROI definition and validation are reported in Supporting Information Materials.

2.6. Connectivity analysis with GIMME‐MS

2.6.1. Extraction of ROI time series

As a goal of the study was to determine whether differences between Speed‐ and Accuracy‐emphasis could be detected in connectivity relationships between the preidentified regions, we sought to fit two uSEM models that would primarily reflect connectivity in each condition. Although an approach in which connectivity during the cues and decision trials within each condition could also be dissociated may have provided insight into changes in connectivity during different processing stages, we were more interested in relationships which we expected to persist throughout the cue and decision period (i.e., top‐down connections that increased baseline activity in putative evidence accumulation regions). Therefore, we collapsed cues and trials from the same SAT conditions in our analysis in order to maximize statistical power to detect these relationships and to allow us to identify lagged relationships which may begin during the cue phase and end during the trial phase. First, a GLM was fit with methods that were identical to those described above, except that the task regressors for cues and trials in the Speed‐emphasis condition were left out of the model. As the residual images from this model contained variance from the un‐modeled Speed‐emphasis condition but did not contain variance explained by the Accuracy‐emphasis condition or nuisance regressors, this time series was used to probe connectivity specific to the Speed‐emphasis condition. Similarly, a second GLM was fit in which only the task regressors for the cues and trials in the Accuracy‐emphasis condition were left out of the model, and the residual time series that resulted was used to probe connectivity specific to the Accuracy‐emphasis condition. Residual data, averaged within each ROI mask, was extracted from both residual time series using AFNI's 3dmaskave program and entered into GIMME‐MS separately to create a Speed‐emphasis model and an Accuracy‐emphasis model.

2.6.2. Search algorithm and solution reduction

GIMME‐MS, a free software that is programmed in MATLAB (MathWorks, 2010) and calls LISREL (Jöreskog & Sörbom, 1993), uses a data‐driven search approach to fit uSEM models with contemporaneous (at a given time point t) and time‐lagged (e.g., t + 1) relationships between ROIs in several steps. GIMME‐MS estimates lagged relationships at the t + 1 order, which was reasonable for these data (i.e., relationships at the t + 2 order were unlikely to be systematically meaningful) because first‐order models are thought to be sufficient to explain relationships in task‐based fMRI data (Beltz & Molenaar, 2015).

By estimating a model that includes paths relevant to the entire group, and subsequently using this model as the starting point for individual‐level searches, GIMME's search method has been demonstrated to produce results that are both representative of homogeneous effects that are common to the group and of heterogeneity between subjects (Beltz & Gates, 2017; Gates & Molenaar, 2012). As the estimation of directional contemporaneous relationships can produce multiple equivalent solutions (e.g., those in which ROI A predicts ROI B at the same time point vs. the reverse effect), GIMME‐MS offers an improvement on the previous version of GIMME by generating all possible equivalent solutions for comparison (Beltz & Molenaar, 2016).

First, as in the original GIMME program (Gates & Molenaar, 2012), GIMME‐MS fits a “null” model to the single‐subject covariance matrices, and uses Lagrange multiplier tests (Sörbom, 1989) to determine which one of the possible contemporaneous or lagged relationships, if estimated, would improve model fit the most for the sample overall (in this case, for 100% of participants). A new model that contains the selected path is estimated, and Lagrange multiplier tests are again used to select the remaining path that would best improve model fit for the group. This search procedure is repeated until Lagrange multiplier tests indicate that the model fit for the group would no longer be significantly improved by the addition of any remaining paths. In the event that two paths would produce equivalent improvements in fit at a given step, which most frequently occurs when a contemporaneous path has a large Lagrange multiplier test early in the search process (Beltz & Molenaar, 2016), GIMME‐MS estimates two separate models in which each direction of the path is estimated in a separate model before the search process continues for each model. This procedure is repeated for each instance of equivalent solutions during the search process, leading to the generation of multiple group‐level models. Third, a “trimming” procedure is employed to remove paths that may have become nonsignificant during the search process.

Finally, an individual‐level search process is enacted that follows a procedure parallel to the group procedure. The search begins with a model that only includes the group‐level paths, and Lagrange multiplier tests are again used to free paths that would best improve model fit for the individual until fit would no longer be significantly improved by the estimation of any remaining paths. Instances in which two paths produce equivalent improvements in fit at the individual level are dealt with in the same way as those at the group level: both solutions are estimated and parallel search processes are conducted until the fit for all possible individual‐level solutions can no longer be improved. Finally, after all, individual‐level models were estimated for all group‐level model solutions that were previously identified, models were checked to ensure that the trimming process was successful and that the estimation of model parameters was accurate, in accordance with common practices for time series analysis (Lütkepohl, 2005). The best individual‐level solutions for each group‐level solution were selected using AIC (Beltz et al., 2016). Following this, the AIC was averaged across participants for each group‐level solution for comparison (displayed in Supporting Information Table S3) and used to select the best‐fitting model.

2.6.3. Summary analyses of connectivity maps

After the best‐fitting models were selected for each Speed‐/Accuracy‐emphasis condition, several analyses were conducted to meet the study's goals. First, to identify major directed connections of regions putatively involved in the control of SAT and those putatively involved in evidence accumulation for the decision, group frequency maps (Hillary et al., 2011), which represent paths that are present for various proportions of the sample, were generated for each condition. Second, to investigate whether the between‐condition differences in individual‐level paths shown on these maps were statistically meaningful, McNemar's mid‐p test for binary matched‐pairs data (Fagerland, Lydersen, & Laake, 2013) was applied to determine whether a path was present for a larger proportion of the sample in one of the two conditions. Finally, to determine the importance of the pre‐SMA relative to other regions in the network, we calculated the total edges, a network metric which was simply defined as the total number of contemporaneous and lagged connections (excluding autoregressive paths) in any direction, for each region. This metric was entered into repeated measures ANOVAs to quantify differences between ROIs and Speed/Accuracy conditions. Regions with a greater number of connections in the network were assumed to play an outsized role in the modulation of SAT. Therefore, we expected that the pre‐SMA would show the highest number of total edges and that individual differences in total edges for this region would correlate with SAT‐related changes in relevant LBA model parameters (e.g., b and v).

2.7. Brain‐behavior correlations

We conducted a between‐subjects correlation analysis to identify relationships between changes in LBA model parameters (i.e., response threshold and drift rate) and connectivity metrics. To compare our results to those reported by Forstmann et al. (2008), we also examined correlations between LBA parameter changes and univariate effects within the striatum and pre‐SMA ROIs. However, as the small sample of participants in the current study may lead to Type II errors or unstable estimates of correlation coefficients, we note that these results should be interpreted with some caution.

Individual‐level parameter estimates from hierarchical models are not independent, making them inappropriate for entry into traditional correlational tests (Boehm, Marsman, Matzke, & Wagenmakers, 2018), and our sample was relatively small for correlational analyses. Therefore, a “plausible values” analysis (Ly et al., 2017; Marsman, Maris, Bechger, & Glas, 2016), implemented with functions in DMC, was conducted to estimate posterior distributions of the population's correlation coefficient (Pearson's r) for the relationship between changes in LBA model parameters and neural covariates. This analysis first calculates the posterior distribution for the sample's correlation coefficient by assessing the correlation between the neural covariate and each individual‐level posterior sample and then follows methods outlined by Ly, Marsman, and Wagenmakers (2018) and Ly et al. (2017) to estimate posterior distributions for the population. Calculation of the population posterior used a uniform prior, spanning r values from −1 to 1. Similar to our tests of parameter value differences between conditions, we used ORs to make inferences about the level of evidence for correlational relationships. These ORs were calculated by comparing the proportions of the posterior density that were above, vs. below, 0, and were interpreted using the same criteria outlined above for strength of evidence (e.g., >3:1 = “positive”).

3. RESULTS

3.1. Behavioral and LBA model results

Behavioral summary statistics demonstrated that participants successfully implemented a speed/accuracy trade‐off in response to the experimental manipulation. In accuracy rate, there were main effects of Stimulus, F(1,17) = 15.88, η² = 0.48, p < 0.001, in which individuals were more accurate on “many” trials, and of Speed/Accuracy condition, F(1,17) = 23.82, η² = 0.58, p < 0.001, in which individuals were more accurate in the Accuracy‐emphasis condition. In mean RT, main effects of Stimulus, F(1,17) = 24.02, η² = 0.59, p < 0.001, and Speed/Accuracy condition, F(1,17) = 15.40, η² = 0.48, p = 0.001, were also detected; individuals had faster responses to “many” stimuli and had faster responses in the Speed‐emphasis condition.

Joint cumulative distribution function plots (Figure 2a) suggested that the LBA model provided a good description of differences in the accuracy and latency of responses between SAT conditions, on aggregate. The most apparent misfit occurred for the longest quantiles of error trials. Assessments of how well the model accounted for the data at the individual level (Supporting Information Materials) confirmed that the model provided a good description of SAT‐related increases in RT and accuracy for every participant in the sample. Hence, data from all participants were retained for model‐based analyses.

Figure 2.

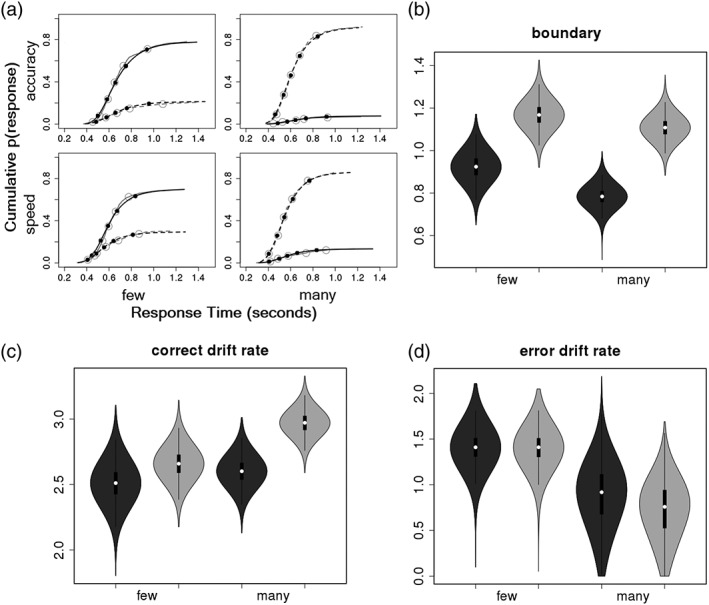
Plots illustrating model fit and posterior distributions of LBA parameter values. (a) Cumulative probability of a response plotted against RT for five main RT quantiles (dots: .10, .30, .50, .70, .90) and for smaller, 1% quantiles (lines), for each speed/accuracy condition and type of stimulus: Gray = empirical data, black = posterior predictive data from the LBA model, solid lines = “few” responses, dotted lines = “many” responses. (b) Violin plots, which display box plots of posterior samples within kernel density plots of the same samples, of group μ estimates of the b parameter for “few” and “many” responses. For all violin plots: Dark gray = speed‐emphasis, light gray = accuracy‐emphasis. (c) Violin plots of group μ estimates of the vc parameter for “few” and “many” stimuli. (d) Violin plots of group μ estimates of the ve parameter for “few” and “many” stimuli

Posterior distributions for group μ LBA parameters of interest are displayed in Figure 2 as violin plots, which contain a box plot of the samples displayed within a kernel density plot, to demonstrate the uncertainty in parameter estimates and degree of overlap. As expected, there was decisive evidence for reductions in response boundary (b) in the Speed‐, relative to Accuracy‐emphasis, condition (OR > 1,000:1). There was also strong evidence for a response bias in b (OR = 43.4:1), where b for “many” was lower than b for “few”, and positive evidence for an interaction effect (OR = 3.8:1), in which this bias appeared to be more pronounced in the Speed‐emphasis condition. There was decisive evidence for slower accumulation of correct information (vc) in the Speed‐, relative to Accuracy‐emphasis, condition (OR = 136.4:1). There was also strong evidence for a stimulus bias (OR = 38.7:1), with faster vc for “many”, relative to “few” stimuli, and positive evidence for an interaction (OR = 5.9:1), suggesting this bias was also more pronounced under Speed‐Emphasis. There was weak evidence for a Speed/Accuracy condition effect (OR = 1.7:1) or interaction effect (OR = 1.7:1) in ve, but decisive evidence for a stimulus bias (OR = 151.5:1), with faster ve for “few”, relative to “many” stimuli. In sum, the model‐based analyses indicate that the SAT effects in behavioral summary statistics can be explained by both lower b and slower vc, consistent with the findings of Rae et al. (2014).

3.2. Directed functional connectivity analysis

3.2.1. Model comparison and selection

The search algorithm produced four group‐level solutions (hereafter denoted as S1–S4) for each Speed‐/Accuracy‐emphasis condition and multiple solutions for almost all individual‐level models derived from these group‐level solutions (ranging up to 35 per person). All group‐level solutions had relatively few paths (Figure 3a), and all of these paths involved only the right DLPFC, left DLPFC, pre‐SMA, and IPS ROIs. Inspection of the group paths revealed that the group‐level solutions were mostly identical between Speed/Accuracy conditions, with the exception of S3 in the Speed‐emphasis condition, which contains a lagged path from the IPS to pre‐SMA that is not present in S3 for the Accuracy‐emphasis condition. However, AIC suggested that there were substantial differences in how well each of these group‐level solutions fit the data from each condition (Supporting Information Table S3); S4 was preferred by AIC for the Speed‐emphasis condition, while S1 was preferred for the Accuracy‐emphasis condition. These models were therefore selected for further analysis.

Figure 3.

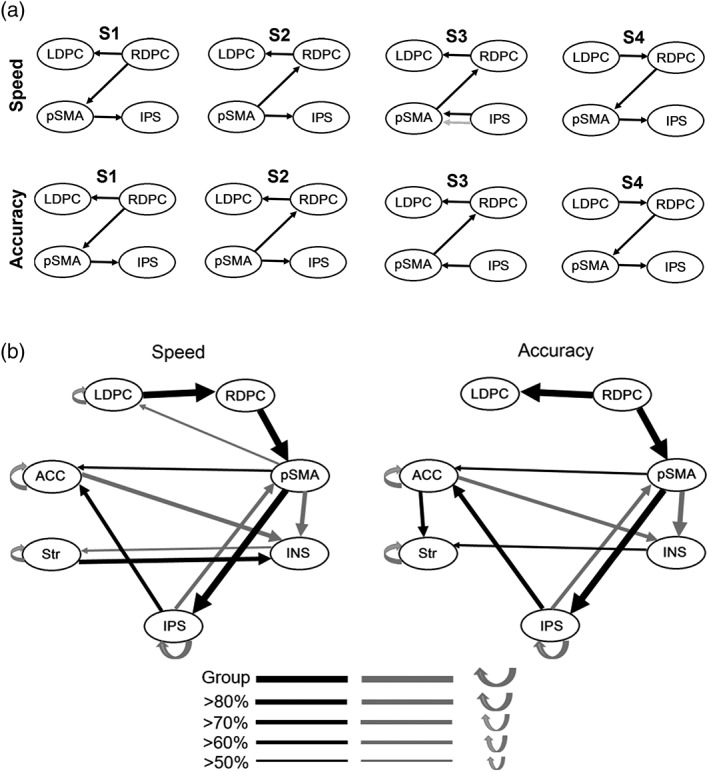
Group‐level path modeling results from GIMME‐MS. (a) Multiple group‐level solutions for the Speed‐ and Accuracy‐emphasis connectivity models. Black lines denote contemporaneous paths while gray lines denote lagged paths. Only the four ROIs, out of seven total, that were involved in the relatively sparse group models are shown. (b) Group frequency maps of all contemporaneous (black) and lagged (gray) group‐level paths and majority individual‐level paths (present in >50% of the sample) for the best‐fitting models of the Speed‐ and Accuracy‐emphasis conditions. Returning arrows indicate autoregressive paths. LDPC = left DLPFC; RDPC = right DLPFC, pSMA = pre‐SMA; ACC = anterior cingulate; INS = insula; Str = striatum; IPS = intraparietal sulcus

3.2.2. Frequency and between‐condition differences in major directed connections

Figure 3b displays group frequency maps for the selected model in each condition, which denote paths that were statistically significant (p < 0.05) for the proportion of individuals noted in the map. As uSEM models are, fundamentally, individual‐level models, statistical significance testing occurs at the level of individual participants. Group frequency maps, therefore, provide an estimate of the proportion of individuals in the population that display these significant relationships. We interpreted all group‐level paths, which were statistically significant for every individual in our sample, and all “majority paths”, which were significant for at least 50% of the group, as these paths would be most likely to generalize to other groups of subjects from the same population as our sample.

The group frequency maps indicated several notable findings. First, the right and left DLPFC do not display major direct inputs to either the IPS or insula, and appear to be relatively isolated from most other regions in the network. However, the DLPFC does communicate with the rest of the network through the right DLPFC's direct input to the pre‐SMA. The pre‐SMA, in turn, provides major input to both the IPS (contemporaneous) and insula (lagged). Inspection of the standardized beta weights of these input paths in both the Speed‐ and Accuracy‐emphasis conditions (Supporting Information Table S4) revealed that they were positive for the vast majority of participants, suggesting that these connections were excitatory. Second, the ACC receives input from another putative top‐down control region, the pre‐SMA, but also receives input from the IPS and displays a lagged output to the insula. Third, despite previous evidence that greater structural connectivity between the pre‐SMA and the striatum predicts more effective control of SAT (Forstmann et al., 2010), there were no directed functional connections between these two structures that were consistently present among most members of the group. Closer inspection of individual models revealed that connections between these structures were, in fact, common; the majority of individuals displayed at least one contemporaneous or lagged connection between the pre‐SMA and striatum in both conditions (94% in Accuracy‐emphasis, 83% in Speed‐emphasis). Therefore, the present results suggest that these structures display functional connectivity with each other during the control of SAT, but the lack of a majority path between them indicates that the directionality and temporal characteristics (contemporaneous vs. lagged) of these connections are heterogeneous.

For group‐level paths, the only clear difference between Speed‐emphasis and Accuracy‐emphasis conditions was the change in directionality of the connection between the left and right DLPFC. For individual‐level paths, no p values from McNemar's tests of SAT condition‐related differences survived correction for multiple comparisons using the Benjamini–Hochberg method (Benjamini & Hochberg, 1995).

3.2.3. Total edges and network hubs

When the total edges of each participant were entered into an ROI by Speed/Accuracy condition anova, there was a significant main effect of ROI, F(6,102) = 8.42, η² = 0.33, p < 0.001, but there was no main effect of Speed/Accuracy condition or interaction between the two factors. Inspection of Figure 4 indicates that the effect of ROI was primarily driven by the pre‐SMA, which displayed several more connections, on average, than the other ROIs, suggesting that this region is a major hub of the network. To further probe this effect, and ensure that the pre‐SMA was a hub for the majority of the sample (i.e., that the effect is not driven by a few participants), individuals' hubs were defined as the region, or regions, that displayed the most total edges for that individual. Consistent with the group result, the pre‐SMA was the most common hub (Supporting Information Table S5); this region, either by itself or in combination with the ACC, served as a network hub for the majority of participants in both the Speed‐emphasis (56% of participants) and Accuracy‐emphasis (67% of participants) conditions. Of note, the ACC appeared to be the next most common hub in both conditions (29% in Speed, 23% in Accuracy), consistent with the relatively large number of edges it displays compared to most other regions (Figure 4). Thus, results suggest that the pre‐SMA, and, to a much lesser extent, the ACC, appear to act as major hubs of the network of regions investigated in the current study.

Figure 4.

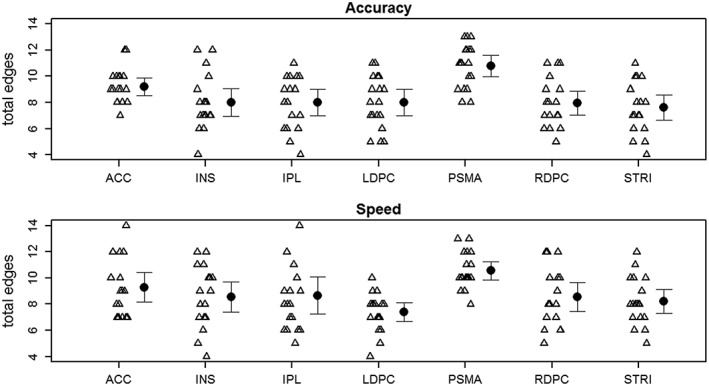
The total number of edges of each region for Speed‐emphasis and Accuracy‐emphasis conditions. Triangles represent the values of each individual. Circles represent the group mean, with error bars indicating 95% confidence intervals. LDPC = left DLPFC; RDPC = right DLPFC, PSMA = pre‐SMA; ACC = anterior cingulate; INS = insula; STRI = striatum; IPS = intraparietal sulcus

3.3. Brain‐behavior correlations

Changes in the response threshold (b) and correct drift rate (vc) parameters, which were both reduced under Speed‐emphasis, were used to investigate brain‐behavior correlations. Posterior distributions from the Speed‐emphasis condition for each parameter were averaged and subtracted from the average of those from the Accuracy‐emphasis condition, and the resulting change distributions were entered into the plausible values analysis. Thus, a positive correlation would indicate that larger values of the neural covariate predict a larger change in b or vc between Speed‐ and Accuracy‐emphasis conditions. On the basis of the substantive results described above, several covariates were used. First, we examined whether the current study's fMRI data set replicates results reported by Forstmann et al. (2008), in which univariate activation within the striatum and pre‐SMA correlates with changes in the b parameter. Second, given the apparent importance of the pre‐SMA as a hub region, individuals' total edges for this region (averaged between conditions) were used as a covariate.

Use of these covariates revealed several relationships for which there was at least positive (OR > 3:1) evidence (Figure 5). Similar to findings of Forstmann et al. (2008), the magnitude of decreases in the b parameter appeared to be positively related to Speed Cue > Accuracy Cue univariate contrast values for both the pre‐SMA (OR = 5.1:1) and striatum (OR = 12.8:1). However, there was little evidence that univariate fMRI effects in either region were related to changes in the vc parameter (all ORs < 3:1). There was moderate evidence that individuals' total number of edges for the pre‐SMA was positively related to the magnitude of change in the vc parameter (OR = 4.8:1), but little evidence for the same relationship with change in b (OR = 1.4:1). Hence, greater complexity of the pre‐SMA's connectivity, between subjects, predicts greater reductions in the quality of evidence under Speed‐emphasis.

Figure 5.

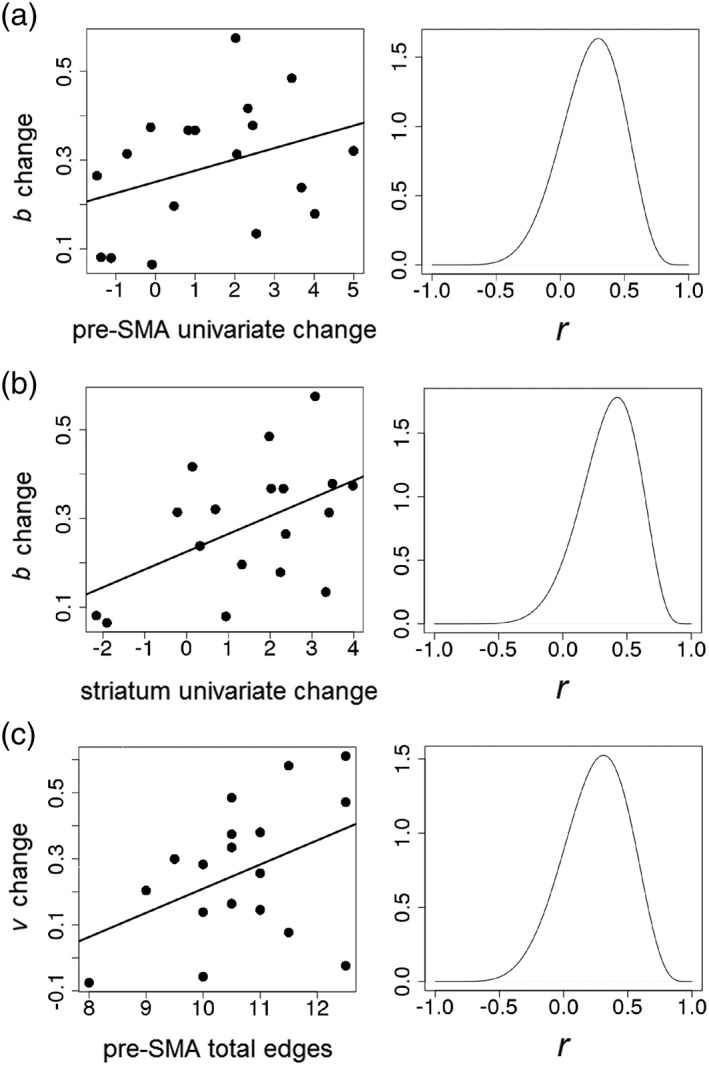
Scatterplots with the mean of individuals' posterior distributions of changes in LBA parameter values (Accuracy–Speed) on the y‐axis and neural covariates on the x‐axis for all relationships with at least positive (OR > 3:1) evidence. Density plots to the right of each scatterplot represent the posterior distribution of the Pearson's r value for each relationship

4. DISCUSSION

The current study revealed directional connections between brain regions involved in SAT by applying GIMME‐MS (Beltz & Molenaar, 2016) to fMRI time series data collected while participants were instructed to alternately emphasize speed or accuracy during a numerosity decision task. A behavioral analysis using the LBA model (Brown & Heathcote, 2008) demonstrated that the experimental paradigm was effective at reducing response thresholds and the quality of decision evidence in the speed‐emphasis condition, consistent with previous research on SAT (Rae et al., 2014). ROIs consisted of regions found to be involved in the control of SAT and motor thresholding in prior studies (DLPFC, pre‐SMA, striatum, and ACC; Forstmann et al., 2008; Van Veen et al., 2008; van Maanen et al., 2011), as well as regions previously found to be involved in evidence accumulation for decisions (IPS, right insula; Ho et al., 2009, Kühn et al., 2011; Shadlen & Newsome, 2001).

GIMME‐MS produced a large number of equivalent solutions at the group and individual levels, likely reflecting the substantial time‐locked (i.e., contemporaneous) connections between ROIs that occur during the completion of a directed task. Using validated procedures (Beltz & Molenaar, 2016), these solutions were subsequently pared down to an optimal set, and used for inference. Although it is not possible to establish a precise level of confidence for the choice of these solutions, we note that the simulation study conducted by Beltz and Molenaar (2016) demonstrated that AIC was able to recover the correct model in all cases in which it was used and that the true model parameters from the simulations were within the 95% confidence intervals of model parameters recovered in the AIC‐selected model. Thus, GIMME‐MS was vital to making accurate and informed inferences about directed functional connectivity. This is a unique strength of this method in applications where estimates of directionality are needed, as most connectivity approaches do not consider directionality, let alone produce sets of models to verify it (Smith et al., 2011).

The most noteworthy findings from this analysis concerned the respective roles of the DLPFC and pre‐SMA. Although previous work had found increased connectivity between the DLPFC and a broad set of regions involved in decision processing during speed emphasis (van Veen et al., 2008), the uSEM analyses implemented in GIMME‐MS suggested that the DLPFC shows few direct connections with other putatively related ROIs. Rather, it appears to influence other ROIs through its top‐down influence on the pre‐SMA, which, in turn, shows directional connections to regions thought to be involved in evidence accumulation (the IPS and insula) and others involved in top‐down control (the ACC). These connections appeared to be top‐down in nature, with the exception of a time‐lagged path from the IPS to the pre‐SMA, which may serve as a “feedback” process for the contemporaneous path in the opposite direction. Furthermore, analyses of a graph theoretical metric (total edges) indicated that the pre‐SMA, but not the DLPFC, is a major hub in the network of SAT‐associated regions, as demonstrated by its disproportionate number of connections and hub status for the majority of individuals.

Taken together, this pattern of findings suggests that the pre‐SMA serves as the primary region involved in the coordination of SAT, consistent with previous research using univariate fMRI (Forstmann et al., 2008, 2010, 2011; Mansfield et al., 2011) and transcranial magnetic stimulation (Berkay et al., 2018; Georgiev et al., 2016; Tosun et al., 2017). It makes a crucial extension of this work by being the first directed functional connectivity analysis to provide evidence that the pre‐SMA implements adjustments to SAT by sending top‐down control signals to an array of other regions, and coordinates SAT in response to a higher‐order control signal from the DLPFC. The finding that beta weights of the pre‐SMA's top‐down connections to regions putatively involved in gathering evidence for the decision (IPS, insula) were positive for most individuals is consistent with numerous theories positing that a nonselective excitatory signal modulates baseline neural activity in evidence accumulation regions (Furman & Wang, 2008; Roxin & Ledberg, 2008; Standage, Blohm, & Dorris, 2014; van Veen et al., 2008). Although the assumed status of the pre‐SMA as a “motor region” may cast doubt on the idea that it controls areas thought to be involved in sensory processing, the pre‐SMA has been previously implicated in a variety of nonmotor functions, including mental rotation and sequence processing (Cona, Marino, & Semenza, 2017; Cona & Semenza, 2017; Leek, Yuen, & Johnston, 2016). We did not directly assess structural connections between the regions used in our connectivity analysis to demonstrate their biological plausibility, but doing so is a crucial next step for future work.

Notably, the current data are not necessarily inconsistent with the original “cortical” hypothesis (Bogacz et al., 2010; van Veen et al., 2008) that the DLPFC, due to its role in context processing (Miller & Cohen, 2001), is the source of signals controlling SAT. Rather, they suggest that the pre‐SMA may mediate top‐down signals from the DLPFC to the rest of the cortex. The previous connectivity study by van Veen et al. (2008) revealed that the DLPFC's connections with the pre‐SMA and other regions involved in decision making were stronger under speed‐emphasis. However, as the analysis was limited to connections between the DLPFC and other regions, and did not address their directionality, it would not have been able to uncover evidence for a mediating role of the pre‐SMA. Thus, the ROI‐based directed connectivity analysis approach used in the current study provides complementary information to this previous analysis and reveals distinct mechanistic roles for the DLPFC and pre‐SMA in the control of SAT that would not have been uncovered otherwise.

Furthermore, the between‐subjects correlation analyses revealed an intriguing distinction between univariate and connectivity measurements of pre‐SMA activity, as it relates to LBA model parameter changes in SAT. Univariate activation estimates in the pre‐SMA appeared to be related to the magnitude of individuals' reductions in response threshold (b), consistent with previous research (Forstmann et al., 2008), but individuals' number of connections with the pre‐SMA was only related to reductions of evidence quality (vc) in the speed‐emphasis condition. In the context of theories that implicate reduced distance‐to‐threshold as the primary mechanism of SAT, this dissociation may be interpreted as indicating that the pre‐SMA's broad excitatory influence on other regions plays a crucial role in speed‐emphasis, but that it may have a negative effect on decision‐making processes if the influence is too broad. If the pre‐SMA interacts with a wider array of structures in some individuals than in others, it may generate more neural noise under speed emphasis in these individuals, leading to less efficient processing of decisions. Given that other models and empirical studies suggest that speed emphasis both reduces distance‐to‐threshold and impacts the rate of evidence accumulation (Heitz & Schall, 2012; Rae et al., 2014), the dissociation may provide clues as to the neural correlates of changes in these distinct features of accumulator models.

The current findings also have implications for the “striatal” theory of SAT, which holds that the striatum receives a top‐down signal from a control region, such as the pre‐SMA, under speed emphasis that causes the basal ganglia to release broad inhibitory influence over the cortex, lowering the threshold for motor responding (Forstmann et al., 2008). In apparent contradiction with work that found a relationship between individuals' changes in response thresholds and the structural integrity of connections between the pre‐SMA and striatum (Forstmann et al., 2010), we found no major directional connections between these two structures. The vast majority of subjects displayed at least one contemporaneous or lagged connection between the pre‐SMA and striatum, but the temporal characteristics and directionality of the connection differed between subjects. Thus, functional connectivity between these structures may be heterogeneous between participants, potentially reflecting strategy differences in the implementation of SAT (e.g., a sub‐group of individuals may increase activity in thresholding circuitry via the striatum, but other individuals may use strategies that do not involve the striatum). Another possibility is that the functional relationship between these structures changes dynamically over the course of the task (e.g., shifting between excitatory and inhibitory influences at different processing stages). Modifications to uSEM's application would be required to test those hypotheses because the method assumes stationarity (i.e., that the character of relationships between ROIs does not change over time) for each time series. Finally, as the current analysis was limited to a subset of a priori ROIs, we cannot rule out the possibility that effects that are consistent with the striatal account of SAT may have become apparent had more motor regions been included in the analysis (e.g., primary motor cortex).

In addition to providing insights about the neural mechanisms of SAT, the current results have two major implications for studies employing connectivity analyses, both in the SAT literature and elsewhere. First, the results demonstrate the utility of the uSEM and GIMME methods for both providing insights into the directionality of connections and revealing connectivity characteristics that are common to the group vs. unique to individuals. The former strength of these methods allowed for a compelling account of the cascade of top‐down regulation in the network of regions involved in SAT. The latter allowed for analyses that assessed how parameters from a formal cognitive model relate to individual differences in connectivity, in line with recent calls for a “model‐based” cognitive neuroscience (Forstmann & Wagenmakers, 2015). It also allowed heterogeneous relationships between ROIs (e.g., between the striatum and pre‐SMA) to be characterized as such. Second, the findings of multiple equivalent solutions at both the group and individual levels strongly suggest that GIMME‐MS and solution‐reduction strategies should be implemented when using uSEM to infer directional connectivity from fMRI data. The use of these strategies is particularly important when the direction of connections is highly relevant to the research question, as in the current case. Furthermore, as the majority of paths in the study were contemporaneous, and as previous simulations demonstrated that this feature is likely to lead to multiple solutions (Beltz & Molenaar, 2016), our findings underscore the need to explicitly address multiple solutions in situations where contemporaneous connections are dominant.

Although the current study focused on SAT‐related connectivity during both cues and trials, a pressing question for future work is whether connectivity properties differ between these distinct processes. A related question is whether trial‐to‐trial adjustments in response thresholds that occur for reasons beyond experimental manipulations of SAT (e.g., posterror increases in thresholds; Dutilh et al., 2012) can be linked to distinct connectivity patterns. Future studies may be able to investigate these questions by integrating methods which explicitly model stimulus input, such as extended‐unified SEM (euSEM; Gates, Molenaar, Hillary, & Slobounov, 2011) with GIMME‐MS. Models that include stimulus input may also be able to address whether features of the input HRF beyond magnitude (e.g., onset time or duration) influence connectivity. However, given that these extensions increase the complexity of already‐complex uSEM models, implementing them would require careful consideration of model identifiability and, likely, the inclusion of a relatively small number of ROIs.

The current findings are compelling, but some special considerations and limitations are relevant to their interpretation. First, the sample of participants was relatively small. However, as the time series data used in our analysis had many more observations than time series data previously used to validate the GIMME/uSEM method (60–200 time points, vs. the 950 time points used in the current study; Gates & Molenaar, 2012; Lane, Gates, Pike, Beltz, & Wright, 2018), this analysis likely had relatively high power to detect functional connections between ROIs at the individual subject level. As accurate recovery of connections present in a group can be obtained with as few as 10 subjects (Gates & Molenaar, 2012), we can be reasonably confident that the path counts reported in the group frequency maps closely approximate the true number of connections in the sample. Second, as the sample was two‐thirds female, it is possible that results may not generalize well to other samples with more male participants. Third, the between‐subjects correlation analyses were unable to identify strong links between connectivity metrics and LBA model parameters, potentially due to the relatively small participant sample size. Fourth, although the time series data entered into the analysis were not deconvolved with the HRF, there is some indication that consideration of the HRF may impact inferences drawn from similar connectivity analysis methods (e.g., Granger causality; Wu et al., 2013). Although the implications of this work for GIMME/uSEM‐based methods are unclear, it underscores the need for future systematic exploration of how deconvolution may alter results from these methods. Fifth, the procedure used to investigate changes in connectivity between speed and accuracy conditions did not reveal many differences. This was surprising, because cues that encourage speed‐emphasis, relative to accuracy‐emphasis, have been found to increase univariate activation of the pre‐SMA in both previous work (Forstmann et al., 2008) and the current study (see Supporting Information Materials), suggesting that the top‐down relationship between the DLPFC and pre‐SMA should become stronger in this condition. However, two methodological details may explain this apparent discrepancy. It is possible that the level of pre‐SMA activation detected by univariate methods does not reflect the pre‐SMA's covariation with other ROIs. Moreover, given that uSEM uses information from the entire time series, rather than just that associated with specific events, the directed connections it reveals may be those that are most stable across the time series, rather than context‐specific connections associated with these events. Thus, as outlined above, data from this study should be interpreted together with complementary work that used methods of assessing context‐specific connectivity in SAT (Van Veen et al., 2008). Sixth, we relied on previous fMRI research on SAT to select a small number of ROIs for our connectivity analysis rather than taking a full‐brain data‐driven approach agnostic to prior findings. As a result, the regions we included almost certainly represent only a small portion of the regions that are essential to complete the decision task, and our results may have been different had we used a connectivity analysis approach which allowed inclusion of more ROIs. Our current approach allowed us to directly assess whether patterns of connectivity were consistent with previous theories of the neural basis of SAT, but it also risked the possibility of entrenching these theories by restricting the ROIs included in the analysis. As this trade‐off between specificity in providing tests of existing theories and sensitivity to detecting patterns that may inform alternative theories is inherent in the scientific process, this issue must be addressed by future work which complements ours by taking a large‐scale network‐based or exploratory approach. Seventh, the numerosity task used in this study is different from decision tasks used in prior work on SAT; several previous studies have used the “moving dots” task, in which participants decide whether a cloud of dots, some of which are moving at random while a subset moves in a single direction, appears to move to the left or right (Forstmann et al., 2008, 2010, 2011; Ivanoff, Branning, & Marois, 2008; van Maanen et al., 2011), and Van Veen et al. (2008) used a modified version of the Simon task, in which participants had to respond as to the color of a square presented to the right or left of a fixation point. Although we assumed herein that brain regions involved in cognitive control during our numerosity task overlapped with those identified in prior studies, it is possible that different systems may be involved, requiring replication of our findings in other decision paradigms.

Finally, as our analysis focused heavily on explanations for SAT that adopt an accumulate‐to‐threshold framework, it may be difficult to extend our inferences to theories of SAT rooted in attractor models (Furman & Wang, 2008; Roxin & Ledberg, 2008; Standage, Blohm, & Dorris, 2014; Standage, Wang, & Blohm, 2014). Relatedly, our results do not address another leading theory of SAT, which posits that the subthalamic nucleus (STN), in response to a control signal from the ACC or pre‐SMA, raises response thresholds under accuracy‐emphasis by inhibiting motor circuitry (Bogacz et al., 2010; Frank et al., 2015; Frank, Scheres, & Sherman, 2007). We did not include the STN in this analysis because of evidence that the spatial resolution provided by a 3‐Tesla MRI scanner is not high enough to effectively distinguish STN activity from that of surrounding subcortical structures (de Hollander, Keuken, & Forstmann, 2015). However, a recent study using ultra‐high‐resolution (7‐Tesla) MRI found evidence of functional connectivity between the ACC and STN (Keuken et al., 2015). Although the current analysis did not reveal a clear role for the ACC, this prior work suggests that the ACC may be involved in shifting response thresholds under accuracy emphasis through its influence on the STN. Thus, future work integrating ultra‐high‐resolution functional imaging with connectivity analyses may be able to assess the role of the STN in the larger network.

In sum, we used a state‐of‐the‐art combination of the uSEM and GIMME connectivity analysis methods (Gates & Molenaar, 2012), and novel approaches for selecting optimal solutions among models (Beltz & Molenaar, 2016), to provide an informative account of directional relationships between brain regions involved in the control of SAT, and the pre‐SMA in particular. This analysis both demonstrated the need for multiple solution‐reduction procedures when assessing cross‐sectional path models of fMRI connectivity, as these procedures provide a potent tool for establishing evidence for the directionality of functional connections, and allowed us to make several substantive discoveries. We found evidence that the pre‐SMA is the primary region involved in the top‐down coordination of SAT through its influence on a broad set of other brain areas, but that this region may receive higher‐order top‐down control signal from the DLPFC to trigger strategy changes. Combined with findings suggesting that increases in striatal output under speed emphasis may also drive SAT, the results are consistent with the unifying account of Standage, Blohm, and Dorris (2014), who posit that SAT may be governed by the modulation of activity in both evidence accumulation and thresholding circuitry. Finally, as GIMME‐MS allowed us to obtain a formal group‐level model that putatively explains directional relationships between the DLPFC, pre‐SMA and IPS during SAT, this model can now be fit to other data sets in confirmatory analyses that can both test whether our results are robust and extend them to answer new questions. In this way, GIMME‐MS provides a model‐based approach to directional connectivity analysis that can explicitly contribute to the growth of cumulative knowledge about SAT and other cognitive phenomena.

Supporting information

Supporting information

Weigard A, Beltz A, Reddy SN, Wilson SJ. Characterizing the role of the pre‐SMA in the control of speed/accuracy trade‐off with directed functional connectivity mapping and multiple solution reduction. Hum Brain Mapp. 2019;40:1829–1843. 10.1002/hbm.24493