Shared and distinct neural circuitry for nonsymbolic and symbolic double‐digit addition

Abstract

Symbolic arithmetic is a complex, uniquely human ability that is acquired through direct instruction. In contrast, the capacity to mentally add and subtract nonsymbolic quantities such as dot arrays emerges without instruction and can be seen in human infants and nonhuman animals. One possibility is that the mental manipulation of nonsymbolic arrays provides a critical scaffold for developing symbolic arithmetic abilities. To explore this hypothesis, we examined whether there is a shared neural basis for nonsymbolic and symbolic double‐digit addition. In parallel, we asked whether there are brain regions that are associated with nonsymbolic and symbolic addition independently. First, relative to visually matched control tasks, we found that both nonsymbolic and symbolic addition elicited greater neural signal in the bilateral intraparietal sulcus (IPS), bilateral inferior temporal gyrus, and the right superior parietal lobule. Subsequent representational similarity analyses revealed that the neural similarity between nonsymbolic and symbolic addition was stronger relative to the similarity between each addition condition and its visually matched control task, but only in the bilateral IPS. These findings suggest that the IPS is involved in arithmetic calculation independent of stimulus format.

1. INTRODUCTION

Humans possess the unique capacity to encode and manipulate mathematical operations using culturally acquired symbols (e.g., “three” or “3” representing three items). The phylogenetic origins for symbolic mathematical abilities are heavily debated. According to one influential proposal, symbolic arithmetic abilities are rooted in the neural circuitry that evolved to represent approximate nonsymbolic quantities (e.g., array of objects; Dehaene, 1997; Dehaene, Molko, Cohen, & Wilson, 2004). In support of this hypothesis, the ability to discriminate and manipulate nonsymbolic representations, termed the approximate number sense (ANS), is ubiquitous throughout the animal kingdom and emerges early in human development (Barth et al., 2006; Cantlon, Merritt, & Brannon, 2016; Halberda, Ly, Wilmer, Naiman, & Germine, 2012; McCrink, Shafto, & Barth, 2017; McCrink & Wynn, 2004). Recent studies have reported that ANS acuity predicts some of the variance in symbolic mathematical performance (Fazio, Bailey, Thompson, & Siegler, 2014; Schneider et al., 2016). Moreover, measures of ANS acuity in infants and young children predict symbolic mathematics later in development (Libertus, Feigenson, & Halberda, 2011). These correlations suggest that the ANS may provide cognitive scaffolding for symbolic mathematics. If so, we might expect the same brain regions to be active when people make symbolic and nonsymbolic numerical judgments. Indeed some studies have found overlapping brain regions recruited during symbolic and nonsymbolic numerical comparisons (Holloway, Price, & Ansari, 2010).

An alternate view however is that there is no biologically evolved capacity for number and that the ANS is only tangentially or indirectly related to symbolic mathematical ability (Núñez, 2017). Consistent with this perspective, fMRI studies have found format dependent neural activation for symbolic and nonsymbolic representations (e.g., Cohen Kadosh, Muggleton, Silvanto, & Walsh, 2010). Furthermore, studies that have examined the spatial patterns of neural activity for symbolic and nonsymbolic representations of number have reported disparate neural representational structures (Bulthé, De Smedt, & Op de Beeck, 2014; Damarla & Just, 2013; Lyons, Ansari, & Beilock, 2015; Lyons & Beilock, 2018). Diverging patterns of brain activity suggest that symbolic and nonsymbolic representations may rely on distinct neural resources.

However, an essential aspect of the human mathematical mind is the ability to perform operations across symbolic and nonsymbolic representational formats, for example, quickly summing the total number of people in a large crowd. Recent cognitive‐training studies have found that practice with nonsymbolic addition and subtraction problems (e.g., adding and subtracting sets of dots) leads to enhanced symbolic arithmetic abilities, suggesting a causal link between nonsymbolic and symbolic calculations (Hyde, Khanum, & Spelke, 2014; Park, Bermudez, Roberts, & Brannon, 2016; Park & Brannon, 2013, 2014; Szkudlarek & Brannon, 2018). Such findings suggest the possibility that there may be a common set of neural mechanisms supporting both nonsymbolic and symbolic arithmetic (Bugden, DeWind, & Brannon, 2016). Thus, an intriguing possibility is that the relationship between nonsymbolic and symbolic representations is stronger when performing mental arithmetic than when comparing quantities.

Many prior studies support the role of the IPS in the estimation, comparison, and manipulation of numerical magnitudes across different stimulus formats (Dehaene, Piazza, Pinel, & Cohen, 2003). In contrast, when participants engage in verbal encoding of numbers and retrieve arithmetic facts, the left perisylvian areas that are commonly associated with language processing, including the angular gyrus (AG) are recruited (Dehaene et al., 2003; Grabner et al., 2007; Grabner et al., 2009; Grabner et al., 2009). Other studies suggest that there may be a neural dissociation between quantity manipulation and verbal encoding of symbolic numerals when people engage in single‐digit approximate versus exact arithmetic (Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Stanescu‐Cosson et al., 2000). In these tasks, participants were presented with a single‐digit symbolic operation followed by two numerical choices. On some trials, participants were presented with two numerals where neither was the precise sum and asked to choose the value that was approximately correct. However, on other trials, one of the numerical choices was the correct sum and participants were required to choose the exact answer. Approximate judgments elicited greater activity in the bilateral IPS relative to exact calculations, whereas exact calculations evoked activity in a network of language‐related regions, including the left AG (Dehaene et al., 1999; Stanescu‐Cosson et al., 2000). These findings suggest that performing gross estimations using numerical symbols relies heavily on quantity manipulations, whereas exact arithmetic elicits direct retrieval strategies. However, Klein, Nuerk, Wood, Knops, and Willmes (2009) did not find a distinction between approximate and exact symbolic addition when the target and distractor choices were matched across both conditions (Klein et al., 2009).

Two other prior studies explored the neural basis of approximate and exact arithmetic but used nonsymbolic stimuli in the approximate conditions. Peters, Polspoel, Op de Beeck, and De Smedt (2016) had 9‐ to 12‐year‐old children perform nonsymbolic approximate and symbolic exact‐subtraction tasks. They found, like Dehaene et al., 1999 and Stanescu‐Cosson, Pinel, van De Moortele, et al. (2000), that approximate nonsymbolic subtraction elicited greater activity in the bilateral IPS relative to exact symbolic subtraction (Peters et al., 2016). In contrast, exact symbolic subtraction showed greater activation in the bilateral AG relative to nonsymbolic subtraction. In another study, Venkatraman, Ansari, and Chee (2005) explored both exact and approximate addition across both nonsymbolic and symbolic formats of a number using quantities less than five in adults. For both nonsymbolic and symbolic addition, participants were asked to either approximate or calculate the exact answer and to make a response from two presented numerals. A single control task was included for both nonsymbolic and symbolic addition to examine common brain regions associated with the addition tasks. Common neural activation was found in the bilateral anterior IPS across approximate and exact nonsymbolic and symbolic addition (across all four addition conditions); however, the study failed to find a dissociation between symbolic and nonsymbolic addition in the left perisylvian language areas. One limitation of these prior studies is that they have relied exclusively on very small values, and therefore, participants may have relied on exact representations of number and therefore not have recruited neural systems associated with approximate nonsymbolic processes. A second limitation is that even in the study that orthogonalized the factor of exact and approximate with that of symbolic and nonsymbolic addition, participants were required to make their final judgments in all conditions with Arabic numerals (Venkatraman et al., 2005). This trial structure thus may have encouraged participants to convert nonsymbolic magnitudes into symbolic representations and so cannot provide a compelling case that the common neural resources observed are used in both nonsymbolic and symbolic arithmetic.

Although the majority of brain imaging data reviewed above suggests a dissociation between exact and approximate arithmetic, an open question is whether nonsymbolic approximate arithmetic and exact symbolic arithmetic rely on some shared neural resources when operating over large quantities. Is there a neural locus for a format‐invariant computational process such as addition? Here, we used high‐resolution fMRI to examine the relationship between nonsymbolic and symbolic arithmetic. We tested whether solving double‐digit symbolic arithmetic problems and approximate arithmetic problems on dot arrays (which we will refer to here as nonsymbolic arithmetic) activate shared neural circuitry. Importantly, we designed control tasks for both of these addition conditions that were matched for visual, motor, and attentional processes to isolate domain‐specific neural processes associated with performing each of these types of arithmetic. Venkatraman et al., 2005 found the IPS to support both approximate and exact single‐digit arithmetic. We predict that we would also find common neural signals in the bilateral IPS when performing double‐digit addition irrespective of format. The bilateral IPS is consistently implicated in mathematical operations across different formats of number (Dehaene et al., 2003). We additionally explored neural activation that was unique to performing symbolic addition relative to nonsymbolic addition and vice versa.

2. METHODS

2.1. Participants

Thirty‐five healthy adult participants from the University of Pennsylvania community were run in the study. Eleven participants were excluded from the sample, either due to chance performance on one of the conditions (n = 1), technical difficulties (n = 7), scanning artifacts (n = 1), an inability to complete the scanning session (n = 1), or having three runs in which the degree of motion exceeded our motion criteria (>3 mm total drift and/or >1.5 mm jump between volumes; n = 1), yielding a final sample of 24 healthy adult participants (17 female, age range: 18–34 years, M age = 21.92 years, SD = 3.07). All participants were native English speakers, had normal or corrected‐to‐normal vision, and were right‐handed (assessed using the Edinburgh Assessment of Handedness). None of the participants reported any neurological or psychiatric illness. The sample was ethnically diverse (e.g., four Caucasian, eight Asian, eight African American, one Caribbean American, two multi‐racial, and one Hispanic). The methods were approved by the institutional review board at the University of Pennsylvania.

2.2. Experimental design

2.2.1. Arithmetic tasks

On each trial, participants were tasked to mentally sum two sequentially presented visual dot arrays (nonsymbolic addition) or two double‐digit numerals (symbolic addition) and to indicate whether a third presented value was the correct sum or not (see Figure 1a,b). Forty‐eight different addition problems were administered, each twice, for a total of 96 trials each for the symbolic and nonsymbolic formats. Similar to the stimuli used in the paradigm of Klein et al. (2010), no problems containing 0 as an operand (e.g., 14 + 0) or equal values of the operands (e.g., 14 + 14 and 14 + 24) were included. The magnitude of the first operand ranged between 12 and 68, whereas the second ranged between 12 and 38. The position of the larger operand (first vs. second) was counterbalanced. The operands were the same for both the nonsymbolic and symbolic addition tasks. Half of the trials had the correct sum while the other half contained the incorrect sum. In the symbolic condition, the incorrect probes differed from the correct result by a numerical distance of either ±2 or ±10 to minimize solution strategies based on parity of the operands or by focusing solely on the units position to form a response (Klein et al., 2010). The incorrect sums in the nonsymbolic addition task differed from the correct solution by +/− a ratio of either 0.3, 0.35, or 0.4 (ratio here is defined as the smaller number divided by the larger) with the numeric absolute values between 23 and 107 (see Table A1 for a complete list of problems).

Figure 1.

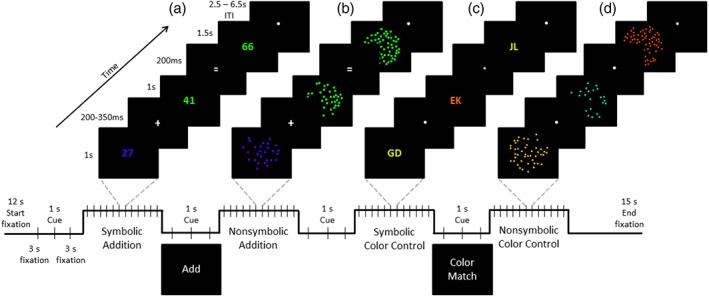
An illustration of the timing parameters for a trial from each of the experimental tasks. (a) An example of an incorrect symbolic‐addition trial. (b) An example of a correct nonsymbolic‐addition trial. (c) An example of a matched color‐control trial for the symbolic task. (d) An example of a nonmatched color‐control trial for the nonsymbolic arithmetic task [Color figure can be viewed at http://wileyonlinelibrary.com]

2.3. Color‐matching control tasks

For both of the above arithmetic tasks, there was a color‐matching control task. In these, participants judged whether a third stimulus matched either the first or second stimulus in color (Figure 1c,d). For the nonsymbolic addition color‐matching control task, the stimuli were identical to that used in the corresponding nonsymbolic addition task. For the symbolic addition color‐control task, the stimuli were letters rather than numbers. The trial structure of the control tasks was directly matched to the addition trials such that participants were required to remember the color information from the first two stimuli until the presentation of the third stimulus, at which time they were required to indicate whether the third stimulus matched either of the previous stimuli in color. There were 48 different target colors, each administered twice, for a total of 96 trials for each control task. On half of the trials, the third stimulus was identical in color to the first or second stimulus (counterbalanced), whereas on the other half of the trials, the colors differed by varying the hue along the RGB scale (Table A2). The colors for the nonmatched trials were selected through pilot testing to best match accuracy on the comparable addition tasks. Paralleling the arithmetic tasks, the color hues of the nonmatching probes ranged from close to far away in distance along the RGB scale from the target color (Table A2). The color‐matching tasks therefore controlled for sensory, motor, and attentional neural resources to isolate the domain‐specific computation processes associated with adding symbolic and nonsymbolic quantities.

2.4. Dot stimuli

Dot arrays for the nonsymbolic addition and color‐matching tasks were constructed such that individual dot size and field area (i.e., the smallest bounding box that can be drawn around the dot array) were held constant within a given trial (i.e., across all three sets dot‐arrays within a given trial). Field area is the invisible circle that defines the maximum convex hull of the dot stimuli. The diameter of individual dots within an array for a given trial was randomly selected from four different sizes (i.e., 7, 9, 11, and 13 pixels). Similarly, the field area for each trial was randomly selected from four different sizes (i.e., 350, 375, 400, and 425 pixels). Accordingly, the dot size and density were uninformative of numerosity within a given trial. Although visual perceptual cues have been shown to impact performance during nonsymbolic comparison tasks (Leibovich & Henik, 2014), these cues have minimal influence on performance during sequential presentation of dot stimuli (Smets, Moors, & Reynvoet, 2016).1

2.5. Procedure

Each participant completed a battery of behavioral tasks and received practice on the experimental scanner tasks (in counterbalanced order) before the date of the MR session. The behavioral tasks were not analyzed for the present study and are thus not described here. The MR session consisted of the two experimental arithmetic tasks and the two color‐matching control tasks described above. All four scanner tasks were presented with E‐prime 2.0 software (Psychological Software Tools, Pittsburgh, PA) and displayed on a monitor mounted behind the scanner. The participants viewed the stimuli through a mirror mounted on top of the head coil. The four tasks were presented across eight experimental runs for each participant. Functional runs began with a 12‐s fixation screen followed by four mini‐blocks of the nonsymbolic‐addition, symbolic‐addition, nonsymbolic color‐control, and symbolic color‐controls tasks, and ended with a 15‐s fixation screen. Before each block, participants were presented with a 1‐s cue screen that indicated whether they were to perform an addition task or a color‐matching task in that block. There were 12 trials for each condition presented in a run. Figure 1 illustrates the common trial structure for all four tasks. In each trial, the first stimulus was presented for 1 s, followed by a screen with either an addition‐symbol for the addition task or a fixation‐dot for the color‐match task for an average duration of 250 ms (jittered between 200 and 350 ms). The second operand stimulus was then presented for 1 s, followed by an equal‐sign screen (addition task) or fixation‐dot screen (color‐match task) for 200 ms. Then, the third stimulus (either the correct or incorrect sum for the addition task, or a color match or a color mismatch in the color‐matching task) was presented for 1.5 s regardless of when the participant made a response. After the presentation of each trial, a jittered inter‐trial fixation screen ranging randomly between 2,500 ms and 6,500 ms in duration was presented (steps of 500 ms, with a mean of 4,500 ms).

Each run was 7.67 min in duration. The order of conditions within each run was presented in a counterbalanced order using a Latin square design to minimize order and carry‐over effects across runs. There were four different orders, each presented twice. Participants received the same instructions for both the nonsymbolic and symbolic addition tasks such that they were asked to sum the first two presented quantities (whether they were arrays of dots or Arabic numerals) and indicate whether the third presented quantity was the correct or incorrect sum. They were not explicitly asked to perform exact or nonsymbolic operations to derive the sum. For the color‐matching task, participants were instructed to focus on the color of each stimulus, and make a response to indicate whether the third presented stimulus color matched that of either the first or second stimulus. Participants were asked to make their selection as quickly and accurately as possible via a button box. The entire scanning protocol was approximately 1 hr and 10 min.

2.6. fMRI data acquisition and preprocessing

Structural and functional scans were acquired on a 3 T Siemens Prisma whole‐body MRI scanner using a 32‐channel head coil. A high resolution T1‐weighted structural scans were collected using MPRAGE sequence (FOV = 240 mm; TR = 2.2 s; TE = 4.67 ms; Voxel size = 1.0 mm³; Flip angle = 8 deg; Matrix = 256 × 256; Slices = 160). The T2* functional images were collected using a multi‐echo planar imaging sequence (EPI) with the following parameters: slices = 76; FOV = 220 mm; TR = 2.0 s; slice thickness = 2 mm, no gap; TE = 32 ms; multiband acceleration factor = 4; flip angle = 50°. The first six volumes were discarded prior to the start of each run to establish magnetic equilibrium.

The fMRI data were preprocessed and analyzed using the Brain Voyager QX 3.4 software package (Brain Innovation, Maastricht, Netherlands). Functional runs with greater than 3 mm drift across the entire run and/or greater than 1.5 mm motion between adjacent volumes were excluded (across all the subjects, three runs were excluded). Three participants completed 5, 6, or 7 runs rather than 8, because of scanner failures. Functional images were corrected for differences in slice‐time acquisition, head motion, linear trends, and low‐frequency noise. Following an automatic initial alignment, a fine‐tuning alignment using a gradient‐driven affine transformation was performed to align functional images to the T1 high‐resolution anatomical images. Functional images were spatially smoothed with a 6 mm full‐width at half maximum Gaussian smoothing kernel. The realigned functional data were subsequently normalized by transforming them into Talairach space (Talairach & Tournoux, 1988) for statistical analysis.

2.7. Statistical analyses

For each participant, the functional runs were modeled using a general linear model (GLM). The design matrix included event‐related predictors of the correct trials for the symbolic and nonsymbolic addition trials and for the symbolic and nonsymbolic color‐matching control tasks. Additionally, the instruction cues, errors, and six motion parameters were included as regressors of no interest. A two‐gamma hemodynamic response function was used to model the expected BOLD signal (Friston, Josephs, Rees, & Turner, 1998). The neural signal was modeled as epochs with the duration of each trial defined as the onset of the first stimulus until the participant made a response following the third stimulus. This procedure accounts for the confounding effects related to task differences in response time (Grinband et al., 2011a, 2011b; Li et al., 2017).

A whole‐brain random‐effects GLM analysis was used to analyze the group data. Initially, we performed two voxel‐wise t‐test statistical maps to contrast the neural signals associated with nonsymbolic and symbolic addition separately relative to their respective control tasks (i.e., nonsymbolic addition > nonsymbolic control; symbolic addition > symbolic control). Next, to reveal regions that responded to both nonsymbolic and symbolic addition more than in their control conditions, a conjunction of random effects analysis was performed across these two contrasts. For the conjunction of both contrasts, we examined brain regions where both nonsymbolic and symbolic addition were jointly activated using a minimum statistic approach (Nichols, Brett, Andersson, Wager, & Poline, 2005). In other words, this approach establishes brain regions that are activated for both contrasts (not just one or the other).

To scrutinize the sensitivity of coactivation found in the conjunction analysis, we conducted a follow‐up representational similarity analysis (RSA; Kriegeskorte et al., 2008) to test the strength of the relationship between the neural signals associated with symbolic and nonsymbolic addition and their respective control tasks. The parietal and inferior temporal brain regions (found in the conjunction analysis) are part of the neural circuitry that has been implicated for numerical and mathematical processing (e.g., Amalric & Dehaene, 2016). However, common neural signals for nonsymbolic and symbolic addition do not necessarily imply a shared neural mechanism among both tasks, and instead could reflect functionally different neural patterns within the same brain regions (Peelen & Downing, 2007; Peelen, Wiggett, & Downing, 2006). Accordingly, we carried out this a representational similarity analysis using nonspatially smoothed brain data to provide finer grain tools at the voxel level to examine the neural activation patterns associated with representing symbolic and nonsymbolic addition (Kriegeskorte, Mur, & Bandettini, 2008; Mur, Bandettini, & Kriegeskorte, 2009). In particular, the voxels in the parietal and inferior temporal brain regions that we used for these analyses were defined for each subject based on the main effect of addition > control tasks (collapsed across symbolic vs. nonsymbolic) at p < .001 (cluster corrected to p < .05), and the representational similarity analyses between the various conditions were then applied to these voxels.

Next, pair‐wise zero‐order correlations were computed using neural estimates extracted from all voxels for symbolic and nonsymbolic addition, as well as for each control task within each region. Because correlation coefficients are bounded between −1 to +1 and not normally distributed, we next transformed the r‐values using Fisher's z transformation: z = arctanh(r). The z‐values for each zero‐order pairwise correlation (e.g., symbolic and nonsymbolic addition; symbolic addition and symbolic color control; nonsymbolic addition and nonsymbolic color control) were averaged across subjects. We then tested whether the strength of the relationship between symbolic and nonsymbolic addition was significantly stronger than the relationships between symbolic and nonsymbolic addition and their respective visually matched control tasks. We hypothesized that if co‐activation in the regions of interest for symbolic and nonsymbolic addition is indicative of a shared underlying neural mechanism for addition, then the correlation between the parameter estimates for symbolic and nonsymbolic addition would be significantly stronger relative to the relationship they each have with the neural signals evoked for the visually similar control tasks.

Finally, we assessed whether there were brain regions that showed greater neural signals specifically (i.e., not shared) for nonsymbolic or symbolic addition after subtracting out activity associated with their control tasks. At the single‐subject level, we subtracted each control task from its respective addition task. To examine activity that was greater for nonsymbolic addition relative to symbolic addition, we then subtracted the difference between nonsymbolic addition and its control from the difference in symbolic addition and its respective control task (symbolic addition > symbolic color‐control) > (nonsymbolic addition > nonsymbolic color‐control). The opposing contrast was conducted to isolate neural signals for nonsymbolic addition relative to symbolic addition, after subtracting out the respective control‐task activity (nonsymbolic addition > nonsymbolic color‐control) > (symbolic addition > symbolic color‐control task). At the group level, we then tested whether the differences in the single‐subject contrast maps were significantly different from zero.

The resulting statistical maps were initially calculated using an uncorrected primary statistical threshold of p < .001 (Woo, Krishnan, & Wager, 2014). In the conjunction of random effects analysis, the independent contrasts of interest must both statistically modulate the BOLD signal in a region. To achieve an initial uncorrected statistical threshold of 0.001, we used a Dunn Sidak correction based on the number of contrasts included in the conjunction (α_sid = 1 − [1 – 0.001]^1/m, m = number of contrasts; Šidák, 1967). For the conjunction of two contrasts, the initial statistical map was set to p value = .002. The resulting statistical maps were further corrected for multiple comparisons using a cluster‐correction thresholding method (Forman et al., 1995; Goebel, Esposito, & Formisano, 2006). A Monte Carlo simulation procedure was used to estimate the cluster‐level false‐positive rates for each map. After 1,000 iterations, the minimum cluster size that yielded a false positive rate of p = .05 for each contrast was used to threshold each map.

3. RESULTS

3.1. Behavioral results

Mean reaction time (RT) and accuracy for each task are presented in Table 1. Trials in which participants failed to respond were excluded from the behavioral and neural analyses.2 A repeated‐measures anova on accuracy revealed a main effect of task, [F(2.25, 51.83) = 3.62, p = .03, η _p ² = 0.14]. Greenhouse–Geisser correction was applied, because the Mauchly's test of sphericity indicated that the assumption of sphericity was violated, W = 0.41, p = .002) A Bonferroni correction was applied to correct for multiple comparisons, such that a result was identified as significant when the p value was less than .008 (0.05/6 comparisons). Paired‐samples t tests revealed that participants were more accurate on the symbolic color task compared to the nonsymbolic color task [t(23) = 4.32, p < .001]. Relative to the p = .008 threshold, no other significant task differences were found (nonsymbolic addition vs. nonsymbolic color [t(23), 2.42, p = .02]; nonsymbolic color vs. symbolic addition [t(23) = 0.12, p = .91]; nonsymbolic addition vs. symbolic addition [t(23) = 2.82, p = .03]; symbolic color vs. symbolic addition [t(23) = 1.81, p = .08]; nonsymbolic addition vs. symbolic color [t(23) = 0.61, p = .55].

Table 1.

Task performance values

	Mean accuracy (SD)	Mean reaction time (SD)
Nonsymbolic addition	0.89 (0.09)	787.80 (143.20)
Nonsymbolic color‐control	0.84 (0.07)	796.60 (150.00)
Symbolic addition	0.84 (0.08)	972.80 (271.6)
Symbolic color‐control	0.88 (0.05)	795.80 (148.70)

A repeated‐measures anova on the RTs revealed a main effect of task [F(1.52, 34.94) =18.78, p < .001, η _p ² = 0.45]. Greenhouse–Geisser correction was applied, because the Mauchly's test of sphericity indicated that the assumption of sphericity was violated (W = 0.13, p < .001). Paired samples t test revealed that participants were significantly slower during the symbolic addition, compared to the other tasks (nonsymbolic addition task [t(23) = 4.99, p < .001], the symbolic color task [t(23) = 4.64, p < .001], and the nonsymbolic color task [t(23) = 4.56, p < .001]. No other task differences were found (nonsymbolic addition vs. nonsymbolic color [t(23) = 0.46, p = .65]; nonsymbolic color vs. symbolic color [t(23) = 0.08, p = .94]; nonsymbolic addition vs. symbolic color [t(23) = 0.42, p = .68].

3.2. fMRI results

3.2.1. Nonsymbolic‐addition (NA) versus its color‐control condition

A whole‐brain voxel‐wise t test analysis was conducted to examine differences in the BOLD signal between nonsymbolic addition and its color‐matching control condition. A fronto‐parietal network including the bilateral intraparietal sulcus (IPS), the right superior parietal lobule (SPL), the bilateral inferior temporal gyri (ITG), the right inferior frontal (IFG), and middle frontal gyri (MFG) showed greater activity for the nonsymbolic addition task relative to its color‐matching control (Figures 2a and 4, Table 2).

Figure 2.

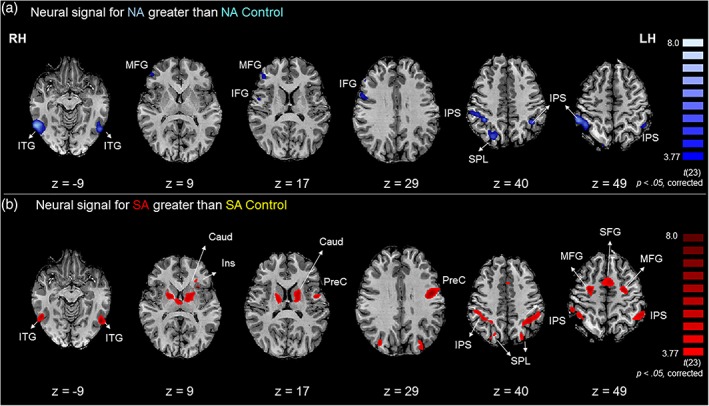
Neural signal for nonsymbolic and symbolic addition relative to their respective control tasks. (a) Brain regions that demonstrated significantly greater neural signal for nonsymbolic addition (NA) relative to nonsymbolic color‐control task (NA control), overlaid on individual slices in the horizontal plane. Regions in dark blue show greater activity for nonsymbolic addition relative to nonsymbolic color‐control. (b) Brain regions that demonstrated significantly greater neural signal for symbolic addition (SA) relative to symbolic color‐control (SA control) tasks. Red clusters show greater signal for symbolic addition relative to symbolic color‐control. RH = right hemisphere; LH = left hemisphere; IPS = intraparietal sulcus; ITG = inferior temporal gyrus; IFG = inferior frontal gyrus; Ins = insula; MFG = middle frontal gyrus; SPL = superior parietal lobule; Caud = caudate; PreC = precentral gyrus; the initial threshold was set to p < .001; cluster corrected for multiple comparisons to p < .05. The minimum cluster size observed following Monte Carlo simulations that were observed for these brain activations was 54 and 57 functional voxels for the nonsymbolic addition greater than color‐control and for symbolic addition greater than color‐control contrasts, respectively

Figure 4.

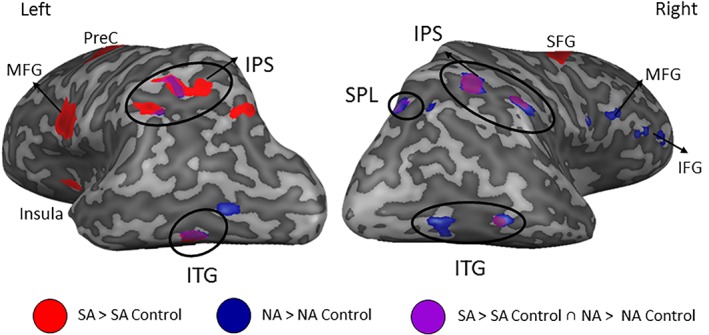
Surface illustration of the overlapping neural signal for nonsymbolic and symbolic addition greater than the color control tasks. The red clusters are brain regions that showed greater neural signal for symbolic addition relative to symbolic color‐control. The blue clusters are brain regions that showed greater neural signal for nonsymbolic addition relative to nonsymbolic color‐control. The purple clusters circled in black represent the conjunction of both symbolic and nonsymbolic addition greater than both color‐control tasks. PreC = precentral gyrus, IPS = intraparietal sulcus; ITG = inferior temporal gyrus; SPL = superior parietal lobule; SFG = superior frontal gyrus; MFG = middle frontal gyrus; SA = symbolic addition; NA = nonsymbolic addition [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 2.

A list of the anatomical regions and the location of the peak voxel for each whole brain contrast

Anatomical region	Hem	t	Tal coordinates			Number of voxels
NA > NA control
Intraparietal sulcus	R	6.70	52	−35	49	4,124
Intraparietal sulcus	L	5.37	−38	−43	40	1,172
Inferior temporal gyrus	R	7.43	55	−52	−7	4,607
Inferior temporal gyrus	L	6.23	−49	−59	−5	2,154
Superior parietal lobule	R	5.32	23	−66	41	1,560
Inferior frontal Gyrus	R	4.85	48	4	21	1,139
Middle frontal Gyrus	R	4.94	45	33	25	1,388
SA > SA control
Intraparietal sulcus	R	6.05	40	−40	44	2,265
Intraparietal sulcus	L	5.95	−37	−43	39	3,781
Superior parietal lobule	L	5.15	−25	−70	35	1,370
Superior parietal lobule	R	4.95	30	−70	31	825
Inferior temporal gyrus	R	5.94	50	−49	−9	981
Inferior temporal gyrus	L	7.18	−50	−57	−10	1,619
Middle frontal gyrus	R	6.65	25	−2	51	2,325
Middle frontal gyrus	L	5.98	−26	−3	51	2,297
Caudate	R	5.22	18	5	11	2,472
Caudate	L	6.30	−17	3	21	3,471
Insula	L	4.35	−25	18	5	653
Superior frontal gyrus	R/L	5.30	−4	9	49	1919
Precentral gyrus	L	6.79	−42	0	21	3,480

Note. The number of voxels is presented in anatomical space (1 mm³). NA = nonsymbolic addition, SA = symbolic addition, Control = color‐matching task, R = right, L = left.

3.3. Symbolic addition (SA) versus its color‐control condition

A voxel‐wise t test comparing brain regions activated during symbolic addition relative to its color‐matching control task revealed a large network of regions across the parietal, temporal, and frontal lobes that showed greater BOLD signal for symbolic addition relative to the color‐control task. These regions included clusters in the bilateral IPS and SPL, the left precentral gyrus, the bilateral ITG, as well as clusters in the frontal cortex (Figure 2b and 4, Table 2).

3.3.1. Conjunction of (NA > NA color‐control) ∩ (SA > SA color‐control)

To directly test which regions were active for both the nonsymbolic addition and the symbolic addition relative to their respective control tasks, a conjunction analysis was performed. The results from this analysis revealed that common neural activation was found for nonsymbolic and symbolic addition relative to their control tasks in the bilateral IPS and ITG, as well as in the right superior parietal lobule (SPL), suggesting that these regions play an important role in addition irrespective of format (Table 3, Figures 3 and 4).

Table 3.

A list of the anatomical regions and the location of the peak voxel for the conjunction whole‐brain contrast and contrasts examining unique activity for symbolic and nonsymbolic addition

Anatomical region	Hem	t	Tal coordinates			Number of voxels
(SA > SA control) ∩ (NA > NA control)
Intraparietal sulcus	R	5.36	40	−40	47	2,660
Intraparietal sulcus	L	5.37	−38	−43	40	1,680
Inferior temporal gyrus	R	5.92	50	−50	−9	1,280
Inferior temporal gyrus	L	5.80	−50	−58	−7	1,367
Superior parietal lobule	R	4.11	19	−67	42	723
(SA > SA control) – (NA > NA control)
Caudate	R	5.22	13	−5	17	3,202
Caudate	L	5.75	−12	−1	10	3,368
Superior frontal gyrus	R/L	4.70	0	2	49	404
Medial frontal gyrus	R	5.36	16	2	57	1,340
Medial frontal gyrus	L	4.41	−24	−6	63	559
Precentral gryus	L	5.10	−47	0	20	2,055
Cuneus	L	4.82	−6	−57	5	1,640
Cuneus	L	4.67	−9	−83	21	531
Cerebellum	R/L	5.50	1	−55	−31	584
(NA > NA control) – (SA > SA control)
Lingual gyrus	L	4.99	−15	−96	3	1,178
Middle occipital gyrus	L	5.74	−37	−73	−4	693
Parahippocampal gyrus (extending into fusifrom gyrus)	R	5.02	28	−39	−12	1,077
Fusiform gyrus	L	4.65	−26	−73	−16	447
Angular gyrus	L	7.38	−51	−58	36	1,210

Note. The number of voxels are presented in anatomical space (1 mm³). NA = nonsymbolic addition, SA = symbolic addition, Control = color‐matching control task, R = right, L = left.

Figure 3.

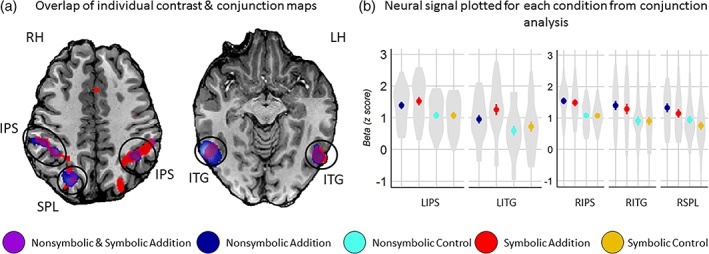
Overlapping neural signal for both nonsymbolic and symbolic addition relative to their respective control tasks. (a) Neural signal across nonsymbolic and symbolic addition tasks displayed on a single subject's brain image. The purple clusters circled in black represent the significant regions showing greater activity in the conjunction analysis for both nonsymbolic and symbolic addition relative to their respective controls. The minimum cluster size for the conjunction analysis following Monte Carlo simulation was 60 voxels. (b) The mean beta parameters are plotted for each condition for clusters showing greater activity for both nonsymbolic and symbolic addition relative to their controls. Error lines are one standard error from the mean. The violin plots illustrate the density of individual participant mean beta values. RH = right hemisphere, LH = left hemisphere, IPS = intraparietal sulcus; SPL = superior parietal lobule; ITG = inferior temporal gyrus [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4. Representational similarity analysis

To further probe whether, and the degree to which, activation in the bilateral IPS, the right SPL, and bilateral ITG for both nonsymbolic and symbolic addition evoked similar patterns of activation at the voxel level in these areas, we conducted a follow‐up representational similarity analysis (RSA; Kriegeskorte, Mur, Ruff, et al., 2008). Five regions were defined using a whole‐brain analysis where voxels were included if they showed a main effect of addition task relative to their respective control tasks (Figure 5a). This allowed us to perform the RSA in larger regions of interest bounding the bilateral IPS, the right SPL, and the bilateral ITG. More specifically, we tested whether the strength of the correlation coefficient in these areas between nonsymbolic and symbolic addition was significantly stronger than the correlation coefficients between nonsymbolic addition and its visually matched control task and between symbolic addition and its visually matched control task. We hypothesized that if co‐activation in the regions of interest for symbolic and nonsymbolic addition is indicative of a shared underlying neural mechanism, then the correlation between parameter estimates in each voxel for symbolic and nonsymbolic addition would be significantly stronger relative to the relationships they have with the neural signals evoked for visually similar control tasks.

Figure 5.

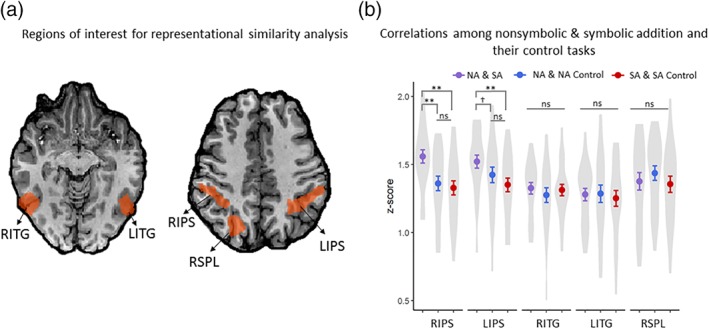
The results of the representational similarity analysis. (a) Regions characterized by the main effect of the experimental task (relative to their respective control conditions) that were submitted to the RSA analysis. The total number of anatomical voxels included in each region of interest was the following: RIPS = 5,609; LIPS = 5,117; RSPL = 4,389; RITG = 3,890; LITG = 3,320. (b) The Fishers z‐values relating the neural correlations between nonsymbolic and symbolic addition, nonsymbolic addition and its color‐control, as well as between symbolic addition and its color‐control for each region of interest. The points represent mean z‐values; the bars represent one standard error from the mean across the z‐values for individual subjects and the violin plot is the density distribution of the individual subject z‐values. R = right; L = left; IPS = intraparietal sulcus; SPL = superior parietal lobule; ITG = inferior temporal gyrus; NA = nonsymbolic addition; SA = symbolic addition; **p < .001; †p < .05; ns = not significant [Color figure can be viewed at http://wileyonlinelibrary.com]

One‐way ANOVAs were conducted to test the differences in correlation coefficients (Fishers z‐scores) within each of the brain regions. We found that for the bilateral IPS, the pattern of neural signal during symbolic addition was more strongly correlated with that of nonsymbolic addition than the pattern of neural signals of each addition task with that of each of their respective control task, [RIPS, F(2,46) = 17.17, p < .001, η ² = 0.43; LIPS, F(2, 46) = 8.48, p < .001, η ² = 0.27]. This relationship did not hold in the other areas, however, with the pattern of neural signal between the addition tasks not being significantly different relative to the correlations between each addition task and its respective control condition in either the right superior parietal lobule[ F(2, 46) = 1.88, p = .16, η ² = .08], or the bilateral ITG [RITG, F(2,46) = 0.52, p = .60, η ² = 0.02; LITG, F(2, 46) = 0.38, p = .69, η ² = 0.02 (Table 4 and Figure 5b). Thus, although both addition tasks also elicited greater neural signal in the bilateral ITG and the right SPL relative to their respective control tasks, the r coactivity‐pattern similarity in these other two regions did not significantly different relative to the pattern similarity between the addition tasks and their respective control tasks. Collectively these findings suggest that the bilateral IPS contribute similarly when performing addition independent of format, whereas the right SPL and bilateral ITG would appear to make distinct neural contributions for nonsymbolic and symbolic addition.

Table 4.

Differences in the neural similarity between nonsymbolic and symbolic addition relative to the neural similarity associated with their respective control tasks in each region of interest

Brain region	Correlation difference		t	df	p	Cohen's d
LIPS	NA & SA	NA & NA control	2.34	23	.03	.48
	NA & SA	SA & SA control	4.26	23	<.001	.87
	NA & NA control	SA & SA control	1.70	23	.10	.35
RIPS	NA & SA	NA & NA control	5.22	23	< .001	1.07
	NA & SA	SA & SA control	5.45	23	< .001	1.11
	NA & NA control	SA & SA control	.69	23	.50	.14
LITG	NA & SA	NA & NA control	−.14	23	.89	−.03
	NA & SA	SA & SA control	.70	23	.49	.14
	NA & NA control	SA & SA control	.85	23	.40	.17
RITG	NA & SA	NA & NA control	1.04	23	.31	.21
	NA & SA	SA & SA control	.31	23	.76	.06
	NA & NA control	SA & SA control	−.63	23	.54	−.13
RSPL	NA & SA	NA & NA control	−1.56	23	.13	−.32
	NA & SA	SA & SA control	.43	23	.67	.09
	NA & NA control	SA & SA control	1.99	23	.06	.41

Note. Paired samples t‐tests. L = left, R = right, IPS = intraparietal sulcus, ITG = inferior temporal gyrus, SPL = superior parietal lobule, NA = nonsymbolic addition, SA = symbolic addition. Bonferroni correction significance threshold p = .017.

3.5. Nonsymbolic addition > symbolic addition

To examine regions that showed activity that was specific for nonsymbolic addition, we conducted the following contrast: (nonsymbolic addition > nonsymbolic color‐control) – (symbolic addition > symbolic color‐control). The left angular gyrus, as well as clusters within the occipital lobe including the visual primary cortex and clusters in the extrastriate cortex, showed greater neural signal for nonsymbolic addition relative to symbolic addition after subtracting out the neural signal associated with the respective control tasks (Table 3, Figure 6).

Figure 6.

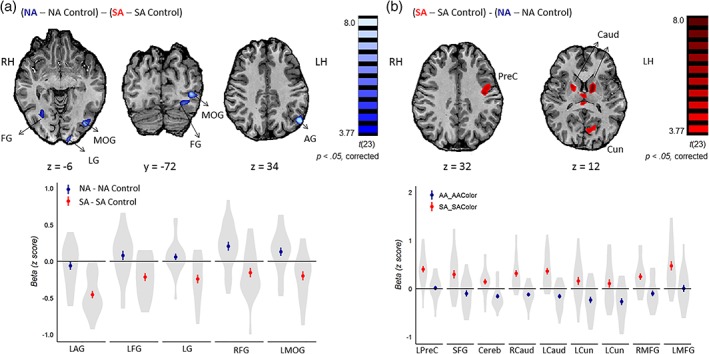
Brain regions that showed distinct neural activity for symbolic and nonsymbolic addition. (a)Brain regions that showed significantly greater activity for nonsymbolic addition after subtracting out activity for symbolic addition, after subtracting out the activity for their respective color‐matching control tasks. The minimum cluster size was 42 voxels. (b)Brain regions that showed significantly greater activity for symbolic addition relative to nonsymbolic addition, after subtracting out the activity for their color‐matching control tasks. The minimum cluster size was 48 voxels. The difference in mean parameter estimates for symbolic addition and its color‐control task are plotted in red, and the differences in the nonsymbolic addition and its color‐control task are plotted in dark blue in regions that show greater activity for symbolic addition and nonsymbolic addition respectively. The lines are standard errors from the mean. The violin plots reflect the density of the differences in mean parameter estimates for individual participants. RH = right hemisphere; LH = left hemisphere; AG = angular gyrus; FG = fusiform gyrus; MOG = middle occipital gyrus; PreC = precentral gyrus; SFG = superior frontal gyrus; Cereb = cerebellum; Caud = caudate; LG = lingual gyrus; Cun = cuneus; MFG = medial frontal gyrus [Color figure can be viewed at http://wileyonlinelibrary.com]

3.6. Symbolic addition > nonsymbolic addition

Conversely, to identify regions that showed greater activation for symbolic addition, we conducted the following contrast: (symbolic addition > symbolic color‐control) – (nonsymbolic addition > nonsymbolic color‐control). The results of this analysis revealed nine regions that showed significantly greater activity for symbolic addition, including the bilateral caudate, bilateral medial frontal gyrus, left precentral gyrus, and superior frontal gyrus (Table 3, Figure 6).

4. DISCUSSION

The main goals of our study were to identify any shared neural resources that support format‐invariant addition, while also delineating neural resources that were uniquely supporting nonsymbolic versus symbolic addition. Prior studies have characterized a neural dissociation between single‐digit approximate arithmetic (both symbolic and nonsymbolic) and exact symbolic arithmetic, such that exact arithmetic has been shown to elicit language‐mediated processes in the left angular gyrus (AG), while approximate arithmetic has been associated with greater recruitment of the bilateral intraparietal sulcus (IPS; Dehaene et al., 1999; Peters et al., 2016; Stanescu‐Cosson, Pinel, van De Moortele, et al., 2000). Yet, these studies generally used small numerical values and task designs that encouraged mentally converting nonsymbolic representations into symbolic format (Venkatraman et al., 2005). Here we contrasted symbolic and nonsymbolic addition with large numerical values and compared them to visual control conditions to test for format‐invariant neural circuitry for the addition computation.

A conjunction analysis of nonsymbolic and symbolic addition revealed common neural activations for nonsymbolic and symbolic addition in the bilateral IPS, in addition to a cluster in the right superior parietal lobule (SPL), and in the bilateral inferior temporal gyri (ITG). However, a representational similarity analysis revealed that only the IPS showed stronger neural similarity between the two addition tasks than between each addition task and its visually similar control task. This is notable in that the physical similarity between each addition condition and its control task was far greater than the physical similarity between the two addition conditions. In other words, stronger neural similarity in the IPS for the two addition conditions (as compared to each addition condition relative to its control condition) indicate that these activations patterns were driven by the task demands more than by the visual input. Our study thus provides novel evidence of a shared neural mechanism in the bilateral intraparietal sulcus (IPS) that specifically supports double‐digit addition regardless of stimulus format. Our finding is consistent with prior studies that found bilateral IPS involvement when performing nonsymbolic arithmetic (Dehaene et al., 1999; Peters et al., 2016) and when solving exact symbolic calculations (Venkatraman et al., 2005), while providing further evidence based on similarity of the voxel activity patterns within this area for these two types of arithmetic calculation.

An alternate interpretation of our findings however is that the bilateral IPS were recruited by both tasks because the arithmetic tasks required representing magnitudes not because they required addition. Indeed, prior studies have found bilateral IPS activation during both passive and active symbolic and nonsymbolic numerical comparison paradigms (Eger et al., 2009; Fias, Lammertyn, Reynvoet, Dupont, & Orban, 2003; Holloway et al., 2010; Piazza, Pinel, Le Bihan, & Dehaene, 2007). However, multiple lines of evidence support a format‐dependent representation of numerical magnitude in the IPS. For example, using transcranial magnetic stimulation (Cohen Kadosh et al., 2010), as well as fMR adaptation (Cohen Kadosh et al., 2011). Cohen Kadosh and colleagues found differential modulation of the neural signal in the IPS that was dependent on the format of representation of numerical magnitudes. Furthermore, multivariate studies have found that symbolic and nonsymbolic numerical stimuli show distinct underlying neural circuitry in the bilateral IPS (Bulthé et al., 2014; Damarla & Just, 2013; Lyons et al., 2015). Using representational similarity analysis, Lyons et al. (2015) found that the underlying neural structure at the voxel level for representing nonsymbolic quantities was distinct or unrelated to their respective symbolic representations. These studies together using different univariate and multivariate approaches thus failed to provide evidence that would support a shared representational structure for symbolic and nonsymbolic magnitudes in the IPS (Bulthé et al., 2014; Damarla & Just, 2013; Lyons et al., 2015). These sources of evidence support distinct neural representations for nonsymbolic and symbolic single‐digit quantities. It remains an open question whether symbolic and nonsymbolic double‐digit magnitudes share greater neural similarity relative to single‐digit magnitudes discussed in the above studies. The nonsymbolic color‐matching control task included the same nonsymbolic magnitudes as the nonsymbolic addition task, and therefore, neural activity associated with passively activating numerical representations when performing color judgments would have been removed through the subtraction of control task activity. Although we subtract activation associated with passively viewing nonsymbolic magnitudes, our design does not allow us to assess whether the IPS is engaged in computation above and beyond representing quantity. While our findings clearly suggest that common regions of the IPS are recruited when people perform addition over dissimilar stimuli, future studies are necessary to ascertain whether the IPS is the actual central locus of the computational process itself.

Another alternative explanation for our findings is that both types of addition recruit domain‐general working‐memory resources. Working memory plays a critical role in arithmetic performance (Dumontheil & Klingberg, 2012) and has been shown to also engage the bilateral IPS during non‐numerical working memory tasks (Dumontheil & Klingberg, 2012; Zago & Tzourio‐mazoyer, 2002). Accordingly, greater neural similarity for nonsymbolic and symbolic addition could be solely driven by the recruitment of domain‐general working‐memory resources when performing arithmetic. We attempted to rule out this hypothesis by designing control tasks that were similar to the experimental tasks in their reliance on working memory, while also controlling for sensory and attentional differences. In the control tasks, participants continuously held and updated the colors for the first and second stimuli until a judgment was made upon the presentation of the third stimulus. Neural activity in the bilateral IPS found for nonsymbolic and symbolic addition was more similar than the neural activity between the addition tasks and their respective control tasks. Therefore, we propose that neural similarity between nonsymbolic and symbolic addition is not solely driven by shared working memory processes, but rather that the similarity is driven by the manipulation of numerical magnitudes when performing arithmetic. Future work is necessary to explore other possible domain‐general executive processes that may also be at work here.

We further found greater neural activation in the bilateral ITG for both symbolic and nonsymbolic addition relative to the control tasks. While earlier theory and findings posited that the ITG was involved in visually processing Arabic numerals, more recent data have suggested a more inclusive role of the ITG in processing both numerals and complex mathematics (Abboud, Maidenbaum, Dehaene, & Amedi, 2015; Amalric & Dehaene, 2016; Daitch, Foster, Schrouff, & Rangarajan, 2016; Dehaene et al., 2003; Dehaene & Cohen, 1995; Yeo, Wilkey, & Price, 2017). We extend these findings by demonstrating that the ITG is involved in the operation of both nonsymbolic and symbolic addition. The representational similarity analyses, however, suggests that distinct voxels within the ITG were activated for nonsymbolic versus symbolic addition, rather than showing the voxel‐pattern similarity that was observed in the IPS. Future studies are necessary to further explore the differential neural mechanisms of the ITG when performing complex mathematics across different formats of numerical representations.

In addition to common neural activity for nonsymbolic and symbolic addition, we found a network of regions that were more strongly engaged during symbolic addition relative to nonsymbolic addition, after subtracting out activity for their respective control tasks. These regions include the bilateral caudate, as well as left‐lateralized clusters in the inferior frontal (IFG) and precentral gyri. The precise role(s) these regions play when performing symbolic arithmetic is less clear. Activation of the precentral gyrus during symbolic arithmetic (Arsalidou & Taylor, 2011; Pesenti, Thioux, Seron, & De Volder, 2000; Venkatraman et al., 2005), has been proposed to possibly be associated with using finger‐counting‐based representations when performing single‐digit arithmetic (Pesenti et al., 2000; Zago et al., 2001). Additionally, the caudate and the IFG have been implicated not only in a variety of symbolic numerical and calculation tasks but also in learning, attention, and working memory tasks (Ischebeck, Zamarian, Schocke, & Delazer, 2009; Nomura & Reber, 2008; Song & Jiang, 2006). One possibility, consistent with meta‐analysis conducted by Arsalidou and Taylor (2011), is that the caudate may play a role in determining the sequence of information, whereas the inferior frontal gyrus could be involved in the processing of rules that accompany performing double‐digit complex addition (Arsalidou & Taylor, 2011).

We further found that the left AG was engaged more for nonsymbolic relative to symbolic addition. At first blush, this may seem surprising because the left AG is commonly found to be involved in the verbal coding and retrieval of arithmetic facts and so it might have been expected to be more involved in the symbolic arithmetic task (Dehaene et al., 2003; Grabner, Ansari, et al., 2009; Grabner, Ansari, Koschutnig, & Reishofer, 2013; Ischebeck, Zamarian, Egger, Schocke, & Delazer, 2007). An alternate proposal suggests that the left AG supports the automatic mapping of overlearned arithmetic problems to their respective solutions in memory (Ansari, 2008; Grabner et al., 2013). However, neither our nonsymbolic nor our symbolic arithmetic conditions were likely to have invoked exclusively fact retrieval because in the symbolic condition, we employed double‐digit values and the incorrect answer differed from the correct solution by a large amount on half the trials. Thus, while participants may have employed iterative retrieval on a subset of the trials when the decade and unit sums were small it is unlikely that this was the only strategy employed (Klein, Willmes, et al., 2010).

Consistent with our results, studies have found greater neural deactivation in the left AG for multi‐digit relative to single‐digit multiplication (Delazer et al., 2003; Grabner, Ischebeck, et al., 2009; Klein, Moeller, et al., 2010; Stanescu‐Cosson, Pinel, De Moortele, et al., 2000; Zago et al., 2001). The left AG is also a node in the default mode network (Raichle et al., 2001), and is involved in a host of cognitive processes (Seghier, 2013). Thus it might be more apt to interpret our results as showing greater deactivation for symbolic addition relative to nonsymbolic addition due to the greater difficulty of the symbolic condition and therefore the greater deactivation of the default network in the symbolic condition (e.g., Buckner, Andrews‐Hanna, & Schacter, 2008). Future research is needed to further disentangle the role of the AG in complex symbolic arithmetic.

Finally, we found areas that showed greater activation for nonsymbolic addition relative to symbolic addition, after subtracting out the activity in their respective color‐control tasks. Greater activity in the middle occipital gyrus for nonsymbolic addition compared to symbolic addition is consistent with prior studies that found that areas in the lateral occipital cortex were sensitive to the number of visual elements presented (Peters, De Smedt, & Op de Beeck, 2015; Sokolowski, Fias, Mousa, & Ansari, 2017; Xu & Chun, 2006). Recent electroencephalogram (EEG) studies have found modulation of the ERP signal specific to changes in numerosity early in the time course along sites in the visual cortex for nonsymbolic number processing (even when accounting for visual properties of the stimuli; Fornaciai & Park, 2017; Park, Dewind, Woldorff, & Brannon, 2016). Thus, the clusters found in the visual cortex align with recent evidence suggesting that the visual cortex is uniquely sensitive to nonsymbolic numerical representations.

In light of the present findings, it would be of value in future research to explore the role of the IPS in different types of computations. A closer examination of the different types of computations that are supported by similar neural circuitry would elucidate the neural mechanisms associated with the manipulation of magnitudes. If the IPS activity truly reflects mental computation, then the mental addition of continuous quantities such as line length may recruit the same regions in IPS. A second intriguing question is whether training on nonsymbolic arithmetic problems would induce neural plastic changes within the bilateral IPS that might facilitate complex symbolic arithmetic. If indeed there is a causal relationship between nonsymbolic arithmetic performance and symbolic arithmetic performance, we hypothesize that improvements on symbolic arithmetic would be accompanied by changes in neural activation within the bilateral IPS. Alternately, are behavioral changes in training accompanied by changes in a distributed network of regions that may or may not include the IPS? Third, to further interrogate whether the manipulation of nonsymbolic quantities provides a critical scaffold for symbolic arithmetic development, future fMRI studies will be necessary to explore whether the IPS is involved in performing nonsymbolic arithmetic in young children who have yet to develop symbolic arithmetic skills. Such findings would further shed light on how manipulating nonsymbolic quantities can provide the scaffolding for learning symbolic arithmetic.

In summary, consistent with prior reports, we found that nonsymbolic and symbolic addition elicited distinct networks of brain regions that were specific to the format of representations. Symbolic addition elicited a left‐lateralized network including left precentral gyrus. In contrast, nonsymbolic addition activated small clusters in the occipital lobe supporting the role of the visual cortex in processing nonsymbolic quantities. Our analyses also revealed, however, that nonsymbolic and symbolic addition both engaged the bilateral IPS relative to control tasks that were matched to the addition tasks for sensory, motor, and attentional processes. Furthermore, the underlying activation patterns within the IPS had greater similarity between the two addition tasks than each task had to its visually matched control task. Our findings thus provide strong evidence that the bilateral IPS are recruited when people engage in addition regardless of numerical format.

CONFLICT OF INTEREST

The authors of this article have declared no conflicts of interest

Table A1.

The addition problems and their distractors for symbolic and nonsymbolic addition

	Problem	Correct	Symbolic probe	Nonsymbolic probe
1	14 + 12	26	28	87
2	12 + 16	28	26	93
3	18 + 12	30	40	86
4	14 + 13	27	37	90
5	13 + 15	28	38	93
6	16 + 13	29	19	97
7	14 + 15	29	27	97
8	14 + 17	31	33	103
9	18 + 14	32	34	107
10	14 + 19	33	31	94
11	18 + 15	33	35	94
12	16 + 19	35	33	100
13	18 + 17	35	45	100
14	18 + 19	37	35	106
15	14 + 21	35	37	100
16	21 + 15	36	26	103
17	16 + 21	37	39	93
18	21 + 18	39	37	98
19	17 + 23	40	50	100
20	24 + 16	40	30	100
21	13 + 25	38	48	95
22	26 + 12	38	28	95
23	14 + 26	40	30	100
24	27 + 13	40	30	100
25	24 + 38	62	64	25
26	39 + 27	66	64	26
27	27 + 41	68	66	27
28	42 + 31	73	75	26
29	26 + 45	71	61	25
30	31 + 45	76	86	27
31	46 + 37	83	73	25
32	29 + 47	76	78	27
33	48 + 36	84	82	25
34	28 + 49	77	87	27
35	51 + 26	77	87	27
36	51 + 29	80	90	24
37	16 + 52	68	66	27
38	52 + 36	88	78	26
39	18 + 53	71	73	28
40	25 + 53	78	68	23
41	54 + 16	70	60	28
42	54 + 23	77	79	27
43	12 + 56	68	66	27
44	15 + 56	71	81	28
45	61 + 14	75	77	26
46	38 + 61	99	89	30
47	64 + 23	87	97	26
48	68 + 19	87	85	26

Table A2.

The target and distractor colors of the stimuli

	Color target	Distractor color
1	0,24,255	0,139,255
2	0,62,255	90,0,255
3	0,101,255	90,0,255
4	0,139,255	0,255,255
5	0,178,255	0,255,219
6	0,204,255	0,255,193
7	0,216,255	0,126,255
8	0,242,255	0,255,154
9	0,255,255	0,101,255
10	0,255,219	0,216,255
11	0,255,193	0,126,255
12	0,255,180	0,139,255
13	0,255,141	11,255,0
14	0,255,103	126,255,0
15	0,255,26	0,255,180
16	0,255,64	0,255,193
17	11,255,0	191,255,0
18	49,255,0	229,255,0
19	88,255,0	0,255,141
20	126,255,0	0,255,141
21	165,255,0	255,244,0
22	204,255,0	255,193,0
23	229,255,0	75,255,0
24	242,255,0	255,154,0
25	255,231,0	165,255,0
26	255,193,0	255,77,0
27	255,154,0	255,116,0
28	255,116,0	255,219,0
29	255,77,0	255,206,0
30	255,39,0	255,154,0
31	255,13,0	255,0,152
32	255,0,0	255,0,152
33	255,0,36	255,0,191
34	255,0,75	255,0,229
35	255,0,229	167,0,255
36	255,0,216	255,0,75
37	255,0,191	219,0,255
38	255,0,152	255,0,0
39	255,0,114	255,0,0
40	244,0,255	255,0,152
41	206,0,255	255,0,152
42	167,0,255	103,0,255
43	129,0,255	0,24,255
44	103,0,255	26,0,255
45	90,0,255	180,0,255
46	51,0,255	129,0,255
47	26,0,255	141,0,255
48	13,0,255	0,126,255

Bugden S, Woldorff MG, Brannon EM. Shared and distinct neural circuitry for nonsymbolic and symbolic double‐digit addition. Hum Brain Mapp. 2019;40:1328–1343. 10.1002/hbm.24452