Developmental changes in functional brain networks from birth through adolescence

Abstract

Investigation of the brain connectome using functional magnetic resonance imaging (fMRI) and measures derived from graph theory analysis has emerged as a new approach to study brain development, cognitive function, and neurophysiological disorders. Here we use graph theory analysis to examine the influence of age, sex, and neurocognitive measures on developmental changes to the global and regional topology of functional brain networks derived from fMRI data recorded in 189 healthy subjects from the age of 0–18 years during rest. We observed that Global Efficiency and Rich‐Club coefficient increased with age and Local Efficiency and Small‐Worldness decreased with age, while Modularity at the global level showed an inverted U‐shaped trajectory during development. Marginally significant differences were observed in Local Efficiency, Small‐Worldness, and Modularity at a global level between boys and girls throughout development. We also examine the effects of neurocognitive measures in boys and girls globally and locally. Our results provide new insight to understand brain maturation of functional brain connectome and its relation to cognitive development from birth through adolescence.

1. INTRODUCTION

The architecture of human brain functional networks, now known as the human connectome, has recently been studied explosively using resting state functional MRI (r‐fMRI). Spontaneous fluctuations in the brain can be measured by blood oxygen level dependent (BOLD) signals using functional magnetic resonance imaging (fMRI) (Mateo, Knutsen, Tsai, Shih, & Kleinfeld, 2017). Functional connectivity in this data has been defined as inter‐regional temporal correlations among spontaneous BOLD fluctuations in different regions of the brain at rest. Graph theory has emerged as a new approach to investigate the complex functional network topology of the human brain connectome (Robinov & Sporns, 2010). Application of graph theory to functional brain networks has revealed important topological properties that influence human behavior including: efficient network architecture, Small‐Worldness, which reflects an optimal balance between segregation and integration in information processing between regions (Achard, Salvador, Whitcher, Suckling, & Bullmore, 2006; Salvador et al., 2005), modular structure, central communication hubs, and Rich‐Club organization which is formed by the densely interconnected hubs in healthy adults (Cao et al., 2014; Van den Heuvel, Kahn, Goñi, & Sporns, 2012; Van den Heuvel & Sporns, 2011).

Previous studies using graph theory approaches to analyze fMRI data have demonstrated age‐related changes in the brain functional connectome. Some of the earliest studies examining the efficiency of functional networks in younger and older adults reported that older adults showed decreased global and Local Efficiency (Achard & Bullmore, 2007) while network Modularity is not significantly changed from younger adults to older adults (Meunier, Achard, Morcom, & Bullmore, 2009). More recently topological properties of the functional connectome have been found to change significantly during child development (Bullmore & Sporns, 2009, 2012; Di Martino et al., 2014), raising the question of how they emerge and change from birth to adolescence.

Some recent studies have shown that sex and cognitive functions correlate with specific features of functional brain networks during development. Examining sex effects on intelligence and functional connectivity in language networks, boys with higher IQ exhibited more modular functional architecture with age, while girls with higher IQ exhibited a more connected functional architecture with age (Schmithorst & Holland, 2006). Similarly, girls developed a greater interhemispheric connectivity for intelligence with age, while boys developed a greater connectivity in the left inferior frontal gyrus (Schmithorst & Holland, 2007). There is also evidence that significant sex differences exist in the network properties of structural and functional brain networks in adults (Schmithorst & Holland, 2007; Smith et al., 2014). Based on these earlier studies on the interaction of sex and developmental on trajectories of brain networks, we sought to explore the influence of age, sex, and cognitive ability on more specific topological measures of developing brain networks from birth through adolescence, using graph theory to analyze r‐fMRI data from 189 healthy children aged from 0 to 18 years.

Following age appropriate normalization and parcellation of the brain imaging data into 200 regions of interest, we estimated functional connectivity from the temporal correlations between the fMRI time series from pairs of the 200 regions. The resulting correlation matrix from each individual was used to construct a binary network reflecting the topological organization of a functional brain network. Specifically, we hypothesized that sex and neurocognitive measures would influence topological properties of the functional brain connectome at both the global and regional levels. Using graph theory, we tested whole brain functional network topology for differences in global network properties between boys and girls and cognitive ability. Hypothesizing a significant relationship between specific brain networks and developing cognitive and language skills, we further explored the influence of IQ and language measures on specific brain networks where significant relationships were detected in network topology.

2. MATERIALS AND METHODS

2.1. Participants

One hundred and eighty‐nine (n = 189) participants were selected from Cincinnati MR Imaging of Neurodevelopment (C‐MIND) (http://research.cchmc.org/c-mind) database of functional neuroimaging and behavioral data from typically developing children. The C‐MIND database only contains data from normally developing children with strict exclusion of chronic illness, gestation less than 37 or greater than 42 weeks, birth weight less than the 10th percentile, history of head trauma with a loss of consciousness, special education, orthodontic braces or other metallic implants and standard MRI compatibility contraindications. The study was approved by the Institutional Review Board at Cincinnati Children's Hospital Medical Center; informed consent and assent (where appropriate) were obtained from a parent/guardian and the participant. In participants of age 5 years and under, additional preparation time was allowed at each session to acclimate the child to the scanner environment. During this time, study personnel used a step‐by‐step approach to introduce the equipment, including the headphones and microphone for in‐scanner communication. Details of methodology for scanning young children are available (Vannest et al., 2014). Participants between the ages 0 and 2 years of age were scanned while asleep. Participants between the ages 3 and 18 years of age were scanned while awake. All participants were native English speakers with demographics reflecting the regional racial and ethnic distribution (64% Caucasian, 23% African‐American, 9% Multi‐ethnic, 1% Asian, Pacific Islander, 2% unknown) and a median household income of $62,500 (see Figure 1 for detailed demographic information).

Figure 1.

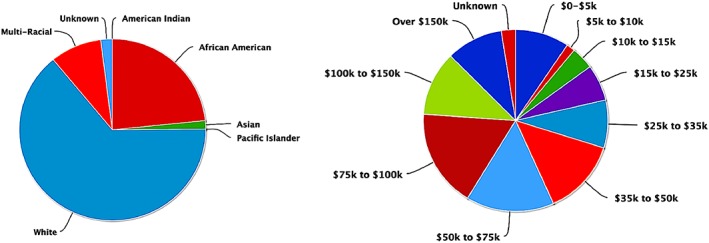
Graphs showing racial, ethnic, and income distribution of participants [Color figure can be viewed at http://wileyonlinelibrary.com]

2.2. MRI acquisition

One hundred and fifty‐six (n = 156) subjects were imaged on a Philips 3 T Achieva system and a 32‐channel head coil. About 33 subjects were imaged on a Siemens Magnetom Trio‐Tim scanner. EPI–fMRI scan parameters between the scanners were homogenized to minimize systematic variation in the data from the two machines. TR/TE = 2,000/35 ms, FOV = 24 cm × 24 cm, matrix = 80 × 80, and slice thickness = 4 mm, yielding spatial resolution of 3 × 3 × 4 mm. Thirty‐six slices were acquired, covering the entire brain. One hundred and fifty whole‐brain volumes were acquired. Prior to acquisition of the functional image data, the scanner was programmed to execute a “dummy scan” interval consisting of 2 TR periods, for which the scans were not recorded. In addition, the first acquired image was also discarded during post‐processing to insure image contrast at relaxation equilibrium. Total scan time for resting state acquisition plus dummy scans was 5 min 8 s.

Techniques detailed elsewhere (Byars et al., 2002, Vannest et al., 2014) were used to acclimatize the participants to the MRI procedure and render them comfortable inside the scanner. Soft head restraints were used to minimize head motion. In addition to the fMRI scans, whole‐brain T1 weighted inversion recovery fast gradient echo scans were acquired for anatomical co‐registration. All imaging was performed on 3 T MRI scanners. Comparison of resting state fMRI data between scanners was performed to insure compatibility of the data sets. Statistical comparison of results from connectivity network analysis with and without the Siemens data included did not change our results significantly.

2.3. Data analysis

2.3.1. Preprocessing

For the resting state functional connectivity analysis, all images were preprocessed in SPM8. The resting state functional image series was corrected for head motion by realigning all images to the mean of all functional volumes. The data of nine subjects were discarded from further analysis due to head motion because they had a higher mean frame‐wise displacement (mFD) than group average (Yan et al., 2013). Among the remaining 189 subjects, the head motion parameters showed no significant correlation with age.

The head‐motion‐corrected functional data were processed as follows. The mean functional image was co‐registered to a corresponding T1‐weighted high‐resolution image. To optimize segmentation and normalization across the age span of all subjects, we created age specific templates for five age groups: 0–2, 3–5, 6–8, 9–12, and 13–18 years. After motion correction, structural images were brain‐extracted and tissue‐type segmentation was implemented. The resulting images were then aligned to MNI space using nonlinear registration and then averaged to create an age‐specific template in SPM8. T1‐weighted images were re‐segmented into gray matter, white matter, and cerebrospinal fluid (CSF) using the age specific probability maps and then all functional images were normalized to these templates and resampled to voxel size 2 × 2 × 2 mm. Subsequently, normalized functional images were smoothed with 8 mm FWHM kernel.

Spatial smoothing of fMRI data can increase the signal to noise ratio (Friston et al.,1995; Maas & Renshaw, 1999; Worsley & Friston, 1995) and reduce resampling related artifacts after registration (Maisog & Chmielowska, 1998). Previous studies suggest that the effective FWHM should be 2–3 times the voxel size (Pajula & Tohka, 2014; Worsley & Friston, 1995). In our study, the data from all subjects were smoothed with 8 mm FWHM kernel. To test the effect of spatial smoothing on smaller, neonatal brains, we reprocessed data from all neonates up to the age of 1 year using a smaller smoothing kernel of 6 mm. We found that the magnitude of spatial smoothing did not affect the functional brain networks measures computed in this study. Consequently, because the all data is acquired with the same resolution we elected to use a consistent smoothing kernel of 8 mm for all subjects.

2.3.2. Functional brain networks construction

A major consideration in graph theory approaches to functional brain imaging data is how to define the nodes of the network. Many previous studies have used anatomical atlases as nodes (Merhar et al., 2016; Wu et al., 2013). However, anatomical atlases often have poor functional homogeneity and do not present functional connectivity patterns accurately (Craddock, James, Holtzheimer, Hu, & Mayberg, 2012). A whole brain parcellation method was recently introduced based on a data‐driven approach to generate functionally homogeneous regions of interest (ROIs) by spatially parcellating whole‐brain resting state fMRI data into regions of maximal coherence in the time course of voxels within each ROI (Craddock et al., 2012). This method can be used to create a parcellation atlas of any desired number of ROIs, though it has been shown that 150–200 ROIs provides a good compromise between functional homogeneity of the regions, interpretability of connectivity results and computational data reduction. We implemented this method for parcellation of normalized whole brain data. The pyClusterROI software (http://ccraddock.github.io/cluster_roi/) was used to parcellate whole brain functional data of each group into 200 regions.

2.3.3. ROI‐to‐ROI functional connectivity

With 200 ROIs defined in the normalized and pre‐processed resting state brain imaging data from all subjects, we computed functional connectivity using the Conn functional connectivity toolbox (Whitfield‐Gabrieli & Nieto‐Castanon, 2012). The residual BOLD time‐series was extracted from gray matter voxels within the 200 defined ROIs in the preprocessed resting state fMRI data. The resting state fMRI time series was corrected on a voxel‐by‐voxel basis using the anatomical component correction (aCompCor) method, which removes the principal components attributed to white matter and cerebrospinal fluid signals (Behzadi, Restom, Liau, & Liu, 2007) and eliminates the need for a global signal regression (Chai, Castañón, Öngür, & Whitfield‐Gabrieli, 2012; Murphy, Birn, Handwerker, Jones, & Bandettini, 2009). Additional post‐processing of time series data was performed using the Artifact Detection Tool (ART) (Mazaika, Hoeft, Glover, & Reiss, 2009) to identify image frames at the subject level with extreme motion (>1 mm relative to time series average) as outliers. These frames as well as six subject‐specific motion parameters and their first derivatives, were also calculated as potential confounds in subsequent analysis stages. The residual BOLD time‐series in each voxel was band‐pass filtered at 0.008–0.08 Hz to focus on low frequency fluctuations (Fox et al., 2005).

Following the temporal preprocessing of fMRI data, an ROI‐to‐ROI functional connectivity analysis was performed by grouping voxels into the 200 ROIs defined from the age specific atlases, and estimating the 200 × 200 correlation matrix for each subject by computing Pearson's correlation coefficients between each ROI time‐series and the time‐series of all other ROIs. These correlation coefficients for each subject were converted to z‐values using Fisher's transform to improve the normality. False discovery rate (FDR; p < .05) was used to correct for multiple comparisons in calculating the significance of each ROI–ROI connection (Benjamini & Hochberg, 1995).

2.3.4. Functional network analysis

Using a threshold of p < .05 (FDR corrected), significant correlation values in the covariance matrix between all 200 ROIs were assigned a binary value of 1 when the connection between region i and region j was present and 0 otherwise, to construct an unweighted connectivity matrix from each of the 200 ROIs for each participant. Graph theory analysis was computed using the Brain Connectivity Toolbox (http://www.brain-connectivity-toolbox.net/) which operates on the unweighted covariance matrix. To explore global topological properties of the whole brain functional networks, we computed Global Efficiency, Local Efficiency, Small‐Worldness, Modularity, and Rich‐Club coefficient. Here, the global network parameters are briefly defined as follows.

Global efficiency is defined as the average inverse shortest characteristic path length between all pairs of nodes (Latora & Marchiori, 2001). Global efficiency for a network G with N nodes is given as:

$$E_{\text{glob}}\left(G\right)=\frac{1}{N\left(N-1\right)}\sum _{1\le i,j\le N,i\ne j}\frac{1}{L_{\mathit{ij}}}$$

where, L_ij is the characteristic path length between nodes i and j in the network.

Local efficiency is computed as the average of the global efficiency of each node's neighborhood sub‐graph:

$$E_{\mathrm{loc}}\left(G\right)=\frac{1}{N}\sum _{1\le i\le N}{E}_{\text{glob}}\left(G_i\right)$$

where, G_i is the sub‐graph of the nearest neighbors of node i. In contrast to global efficiency, local efficiency represents the capacity to transfer information within the neighbors of a given node, and a high Local Efficiency reflects efficient information transfer in the immediate neighborhood of each node (Latora & Marchiori, 2001).

Betweenness centrality of a node is the fraction of shortest paths between all other pairs of nodes in the network that actually pass through the node of interest (Freeman, 1978). This measure has been used to identify the most central nodes in a network, which reflects the importance of the specific node in transferring information to other nodes. A node with high betweenness centrality is crucial to efficient communication.

Node degree (k) is computed as the number of links to other nodes in the network.

Modularity (Q) quantifies the degree to which the network may be partitioned into a subdivision that has higher connections with each other than with the rest of the network (Newman, 2006).

Small‐worldness is an important model that quantifies the balance between network segregation and integration. To examine small‐world properties of a network the normalized clustering coefficient γ = C/C_rand and normalized characteristic path length λ = L/L_rand are computed (Watts & Strogatz, 1998). C and L are the clustering coefficient and the characteristic path length of a network and C_rand and L_rand are the mean clustering coefficient and the characteristic path length of the matched random networks. Clustering coefficient (C) is described as the fraction of the node's neighbors that are also neighbors of each other. Characteristic path length (L) is defined as the average of the shortest path length between all pairs of nodes. Typically, a network is considered a small‐world when it meets the following conditions: γ > 1, σ>1, and λ ≈ 1; where, σ = (C/C_rand)/(L/L_rand).

The Rich‐Club coefficient of a network is calculated over a range of degree k after removing all nodes with degree ≤k. The Rich‐Club coefficient ∅(k) for any k is computed as the ratio of connections between the remaining nodes E_k> with a degree of at least k and the total number of possible connections between them. The Rich‐Club coefficient ∅(k) is given formally by the following:

$$\varnothing \left(k\right)=\raisebox{1ex}{$2E_{k>}$}\!\left/ \!\raisebox{-1ex}{$N_{k>}\left(N_{k>}-1\right)$}\right.$$

We computed the normalized Rich‐Club coefficient ∅_norm(k) for the unweighted connectivity matrices as follows:

$${\varnothing }_{\mathrm{norm}}\left(k\right)=\raisebox{1ex}{$\varnothing \left(k\right)$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\mathrm{rand}}\left(k\right)$}\right.$$

where, ∅_rand(k) is the average Rich‐Club coefficient over 1,000 random networks.

A normalized Rich‐Club clustering coefficient ∅_norm(k) > 1 over a range of k indicates Rich‐Club organization in the network (Van den Heuvel & Sporns, 2011).

2.4. Correlation of network topology with age, sex, and behavioral measures

To assess whether the observed changes in network properties relate to age, sex, or neurocognitive abilities in the children, we evaluated the effects of association of these measures with global and regional network properties. For each child, the age in months at the time of the resting state fMRI scan and the sex were extracted from the C‐MIND database. All children in the C‐MIND study participated in an extensive neurocognitive assessment battery within a few weeks of the functional MR imaging session. Neurocognitive testing included tests of general intellectual function [Wechsler Intelligence Scales: Wechsler Pre‐school and Primary Scale of Intelligence, Third Edition (WPPSI‐III, ages 2:6–5); Wechsler Intelligence Scale for Children, Fourth Edition (WISC‐IV, ages 6–16) Wechsler Adult Intelligence Scale, Fourth Edition (WAIS‐IV, ages 17 and 18, Wechsler, 1981) and vocabulary (the Expressive Vocabulary Test‐2 (EVT‐2) (Williams, 2007).

We found no significant correlation between age and neurocognitive measures (p > .5) and no significant difference between boys and girls (p > .6). Scores from these tests are included in statistical analysis models with brain network measures to pin point brain regions and connections that facilitate greater cognitive ability during development. Younger participants were excluded from the analysis because neurocognitive data were not available.

2.5. Statistical analysis

To determine the changes in the functional networks across development, a general linear model (GLM) was applied to analyze the effects of age, sex and neurocognitive measures and their interactions on the network parameters. We performed multiple linear regressions which included age and age² as predictors with sex and mean frame‐wise displacement (mFD) derived from the head motion parameters (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012) as other covariates to detect the linear and quadratic developmental trajectories. The GLM models were determined as follows:

$$Y_1={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\text{xage}+{\mathrm{\beta }}_2\text{xsex}+{\mathrm{\beta }}_3\text{xmFD}$$

$$Y_2={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\text{xage}+{\mathrm{\beta }}_2\mathrm{x}{\mathrm{age}}^2+{\mathrm{\beta }}_3\text{xsex}+{\mathrm{\beta }}_4\text{xmFD}$$

To examine the sex‐related differences and their development we used another GLM model including age, sex, and sex‐by‐age interactions to examine both positive (boys > girls) and negative (girls > boys) contrasts as well as positive and negative age‐by‐sex interactions.

$$Y_3={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\text{xage}+{\mathrm{\beta }}_2\text{xsex}+{\mathrm{\beta }}_3\text{xsexxage}+{\mathrm{\beta }}_4\text{xmFD}$$

For the analysis of the IQ‐related differences, we first applied a multiple linear regression Y₃ on both IQ and each network parameter to model the effects of age, sex, and their interactions.

All statistical analysis was performed in RStudio (https://www.rstudio.com).

3. RESULTS

3.1. Age and sex effects on global network properties

Brain functional network topology correlated significantly (p < .05, FDR‐corrected) with age during development. Figure 2 demonstrates the developmental trajectories of key global network parameters from 0 to 18 years of age. Children who slept during the r‐fMRI scan are indicated by open circles as the data point in Figure 2 to emphasize sleep as a potential confound for parameter estimates in this part of the curves. Positive age‐related changes (p < .0001) were found in Global Efficiency (Figure 2a), but negative age‐related changes were found in Local Efficiency and Small‐Worldness (Figure 2b,c). Modularity exhibited negative quadratic age effect (inverted U‐shaped) (p = .001) (Figure 2d).

Figure 2.

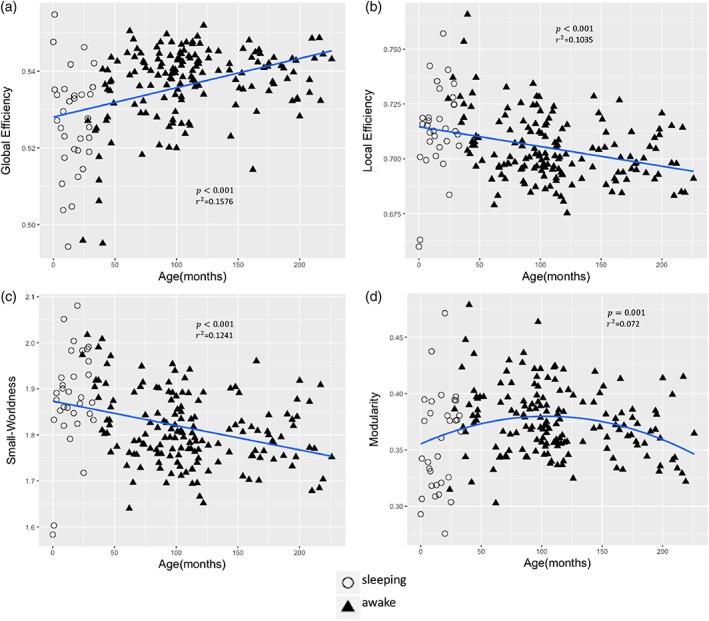
Global network measures as a function of age. (a) Global efficiency. (b) Local efficiency. (c) Small‐Worldness. (d) Modularity. p < .05, FDR correction was applied to correct for multiple comparisons [Color figure can be viewed at http://wileyonlinelibrary.com]

We found significant sex differences (p < .05, uncorrected) in Local Efficiency, Small‐Worldness, and Modularity in which the boys showed significantly higher values when compared with the girls (Figure 3b–d). Age‐by‐sex interaction in global network measures as reflected in Global Efficiency and Small‐Worldness did not reach significance (Figure 3a,c). When we adjust the sex comparison analysis for multiple testing using FDR correction, the comparison between boys and girls shows a trend for boys to have higher values of the Local Efficiency (p = .0531, FDR‐corrected), Small‐Worldness (p = .0531, FDR‐corrected) and Modularity (p = .0531, FDR‐corrected). These trends are important and indicate that with more subjects, the sex differences in connectivity may become significant. Using Degree, as a measure of which nodes are most highly connected within a functional brain network we identified the hub regions across all subjects (Van den Heuvel & Sporns, 2013). We found that the hubs differed slightly in the youngest group, but the brain hubs were predominantly located in the default mode network, attention related regions and visual cortex (Figure 4a, dark dots). The hubs in default mode, attention, and visual networks are listed in Table 1. The Rich‐Club architecture was also observed in the topology as the hub regions were more densely connected among themselves than with other brain regions. We observed that the Rich‐Club architecture increased during childhood (p = .04149, FDR‐corrected) with high variability from 5 to 12 years (Figure 4b). No significant sex differences were found in Rich‐Club coefficient of the functional brain networks across the age span.

Figure 3.

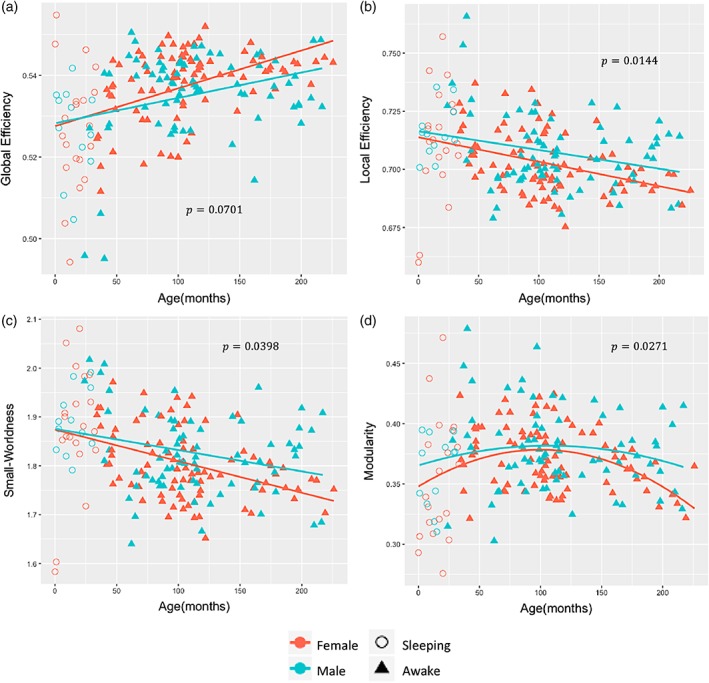
Sex difference in brain network topology with age. (a) Global efficiency. (b) Local efficiency. (c) Small‐Worldness. (d) Modularity [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 4.

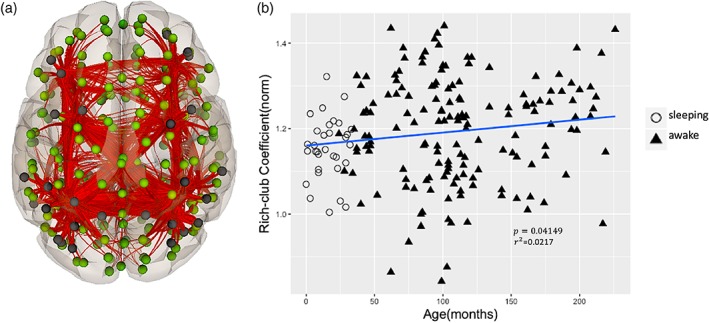
Rich‐Club trends in the developing connectome. (a) Hub regions and connections. The black dots represent the hub regions. (b) Age‐related change in normalized Rich‐Club coefficient. p < .05, FDR correction was applied for multiple comparisons [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 1.

Hub regions in default mode, attention, and visual networks and MNI coordinates of the center of each region

Network	Region	MNI(x, y, x)
Default mode	Left lateral parietal	(−39, −77, 33)
	Right lateral parietal	(47, −67, 29)
	Posterior cingulate cortex	(1, −61, 38)
Attention	Left intraparietal sulcus	(−39, −43, 52)
	Right intraparietal sulcus	(39, −42, 54)
	Left posterior parietal cortex	(−46, −58, 49)
	Right posterior parietal cortex	(52, −52, 45)
	Left lateral prefrontal cortex	(−43,33,28)
	Right lateral prefrontal cortex	(41,38,30)
Visual	Primary visual	(2, −79, 12)
	Visual ventral	(0, −93, −4)
	Visual dorsal	(−37, −79, 10)

3.2. Neurocognitive measures and sex effects

Examining all participants together we found no significant IQ effect on global network measures. However, when boys and girls were analyzed separately, significant IQ‐related differences were observed in relationship with Global Efficiency, Local Efficiency, Small‐Worldness, and Modularity. For the developmental trajectories, the boys had higher Local Efficiency, Small‐Worldness, and Modularity but lower Global Efficiency.

When boys and girls are examined together we find regional positive correlations between IQ and the local graph measures in specific regions in interest. Regions with significant correlations in this analysis are defined by functional parcellation as described above but labeled using anatomical brain atlases for reference purposes. Linear decreases between Global Efficiency and IQ, and Degree and IQ, but linear increase between average path length and IQ were found in the left middle temporal gyrus (MTG[L]). Linear increases were also found between Local Efficiency and IQ, and Clustering Coefficient and IQ in the right superior frontal gyrus (SFG[R]) (Figure 5a,e). Significant positive quadratic changes were found in the right posterior parietal cortex (PPC[R]), lateral prefrontal cortex (LPFC[R]), and inferior frontal gyrus (IFG[R]) between Local Efficiency and IQ, and Clustering Coefficient and IQ (Figure 5f,k).

Figure 5.

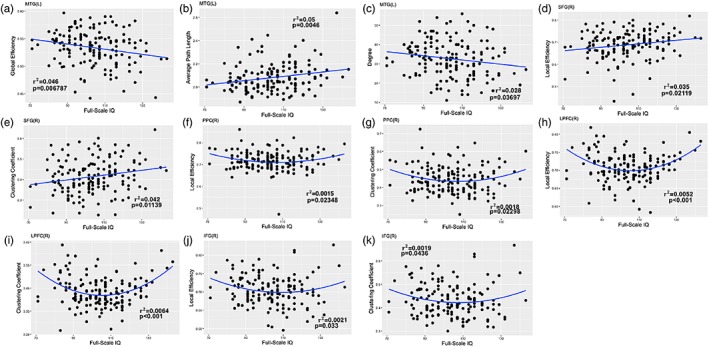
Local network measures as a function of IQ [Color figure can be viewed at http://wileyonlinelibrary.com]

Treating boys and girls as a single group, we also identified that there were correlations between specific brain regions and language ability as reflected in the EVT‐2 vocabulary measure. There was a negative linear correlation between nodal Global Efficiency and EVT‐2 in the left inferior frontal gyrus (IFG[L]). In contrast, positive linear correlations were found between the Average Path Length in IFG(L) and IFG(R)) and EVT‐2, and Small‐Worldness, Clustering Coefficient and IQ in IFG(L). Similarly, correlations between Average Path Length and IQ, and Clustering Coefficient and IQ exhibited positive linear changes, but negative quadratic change between Small‐Worldness and EVT‐2 in the left posterior superior temporal gyrus (pSTG(L)) (Figure 6). There was no significant sex effect between nodal network parameters in language regions and EVT‐2. In this analysis 113 subjects aged between 3 and 11 years were included.

Figure 6.

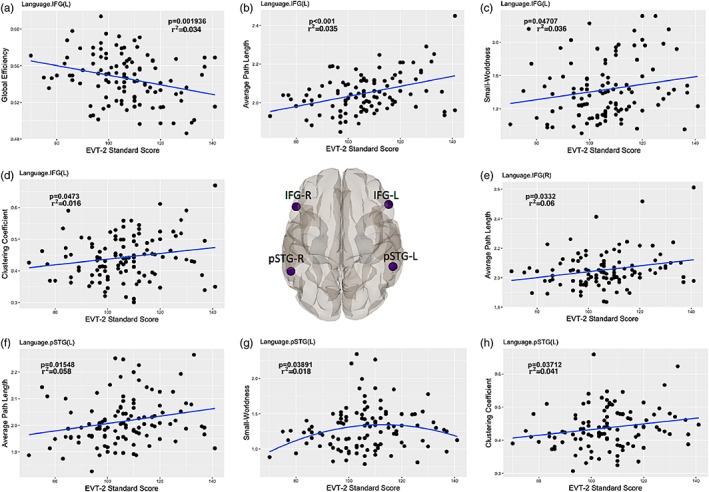
Local network measures as a function of expressive vocabulary test scores in inferior frontal gyrus (IFG) and posterior superior temporal gyrus (pSTG) [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

In this study, we investigated the topological organization of functional brain networks derived from r‐fMRI in healthy children in an age range from 0 to 18 years and analyzed the effects of age, sex and neurocognitive measures on the network properties both globally and locally. The main findings included the following: (i) functional brain networks from birth through adolescence showed linear increases in Global Efficiency and Rich‐Club coefficient, but linear decreases in Local Efficiency and Small‐Worldness, while Modularity showed negative quadratic change (Figure 2); (ii) boys exhibit a higher Local Efficiency, Small‐Worldness, and Modularity when compared with girls (Figure 3); (iii) functional brain hubs were located in default mode, fronto‐parietal, and visual networks across development (Figure 4); (iv) regional network parameters positively correlated with IQ and language measures (Figures 5 and 6).

Collectively, we detected significant topological modifications of the human brain connectome from birth through adolescence which appear to be influenced by sex and cognitive abilities.

Earlier studies have reported age‐associated changes in the global network properties showing that Local Efficiency and Small‐Worldness were reduced while Global Efficiency was not affected by age (Cao et al., 2014; Geerligs, Renken, Saliasi, Maurits, & Lorist, 2014). In this study, we find that Global Efficiency of brain functional networks increased but Local Efficiency decreased with age. A high Global Efficiency indicates the capacity of rapid information exchange among the distributed elements (Bullmore & Sporns, 2012). In contrast to Global Efficiency, a high Local Efficiency reflects efficient information transfer in the immediate neighborhood of each node (Latora & Marchiori, 2001). Previous functional brain network studies have reported no significant change in Global Efficiency during development and adulthood and increases in Local Efficiency during development and its reduction with aging which are partly in accordance with our findings (Cao et al., 2014). Differences between those results and our findings may be related to the regional parcellation of the brain that was used in the previous study for graph construction (90 vs. 200 nodes in the present study), which has a limited ability to represent functional networks due to coarse nodes which encompasses disparate functional areas (Power et al., 2011). In addition, we detected a negative age effect on Small‐Worldness during childhood which is consistent with previous results that have shown a reduction in Small‐Worldness with age. Recent studies showed that Small‐Worldness is established in functional brain networks early during development (Fransson, Åden, Blennow, & Lagercrantz, 2010; Scheinost et al., 2016), remaining stable in children and young adults (Wu et al., 2013). Therefore, our study provides further support for the previous results that functional brain networks display consistent small‐world properties from birth through adolescence.

Along with these changes, functional brain networks were found to be highly modular, reflecting higher intra‐network connectivity than inter‐network connections in younger adults. In this study, we have found that Modularity changed throughout brain development (Figure 2d) which aligns with previous findings (Cao et al., 2014; Fair et al., 2009). Similarly, we detected Modularity with an inverted U‐shaped developmental trajectory, indicating that the brain's functional Modularity increased until approximately 8 years of age and decreased at older age. This indicates that functional brain networks may become less differentiated with age which is also in accordance with previous studies (Geerligs et al., 2014).

Highly connected hub regions in the “Rich‐Club” play a crucial role in global information integration among parallel and distributed brain networks. Previous studies observed that hubs of functional brain networks were mainly located in the default mode, fronto‐parietal, and visual networks (Cole, Pathak, & Schneider, 2010; Liang, Zou, He, & Yang, 2013; Zuo et al., 2011). A recent study also suggested that functional brain hubs are stable over development (Hwang, Hallquist, & Luna, 2012). Our results in Figure 4 are consistent with these findings. Recent work elucidated the Rich‐Club configuration of human brain structural and functional networks in healthy adults (Cao et al., 2014; Collin, Sporns, Mandl, & van den Heuvel, 2013; Van den Heuvel et al., 2012). We also observed the existence of Rich‐Club organization in the functional connectome during childhood with a significant, positive age effect, in accordance with previous studies (Cao et al., 2014). Rich‐Club organization provides an important contribution to information transfer between different brain regions.

Previous fMRI studies indicated that functional interactions between multiple brain regions during a task or at rest are strongly related to neurocognitive measures (Gray, Chabris, & Braver, 2003; Song et al., 2008). Previous research has shown a positive correlation between IQ and fMRI brain activation in the middle temporal gyrus during a verb generation task (Schmithorst & Holland, 2006). Therefore, in addition to age and sex effects we investigated the correlation between cognitive measures and functional brain network topology. No significant correlation was observed between full‐scale IQ and global network measures. However, when we examined girls and boys separately, we found significant IQ related differences with age between boys and girls. This is not consistent with the recent study in adults (Van den Heuvel, Stam, Kahn, & Pol, 2009), which found that intelligence is highly correlated with both local and global efficiencies of functional brain networks. IQ‐related changes in the regional, nodal parameters were found in frontal, parietal and temporal brain regions (LPPC, PPC, MTG, STG, and IFG). Consistent with our results, Wu et al. also reported IQ‐related changes in local nodal parameters in frontal and temporal regions during development (Wu et al., 2013). At least one previous study on functional connectivity has also shown that brain network connectivity is related to intelligence (Song et al., 2008). Furthermore, several brain regions mainly involved in attention showed a positive correlation with IQ. Though we did not find local network correlations with IQ, we did discover significant correlations between language ability (EVT‐2 standard scores) and network topology in several language‐related brain regions (IFG‐L, STG‐L). Overall, our findings suggest that topology of brain networks related to attention, memory and language, underlie differences in intelligence and language ability in children throughout development.

In prior studies of developmental changes in structural and functional brain networks, the effect of age has been demonstrated in different age groups (Cao et al., 2014; Fransson et al., 2010; Meunier, Lambiotte, Fornito, Ersche, & Bullmore, 2009; Wu et al., 2013). However, the interaction of brain network topology with sex and cognitive abilities during development have not been studied thoroughly. Our study adds to the understanding of functional brain network development from birth through adolescence in healthy children by examining the growth trajectories of global network topology as a function of age and sex during childhood. An important observation is that key graph measures characterizing global and regional brain network topology do not appear to follow linear or monotonic trajectories as networks organize for improved efficiency during childhood.

4.1. Limitations

The developmental trajectories in brain network topology outlined in this report are subject to several limitations in the study design. First, while the sample size is substantial and larger than any study of normal brain connectivity development to‐date, the variance in network topology estimates is large as illustrated in the scatter plots in the figures. Consequently, the parameters describing the quadratic regression fits to the trajectories have substantial uncertainty. While the figures clearly illustrate the dynamic trends of brain network topology through development, they are not sufficiently precise to allow individual predictions about brain age, IQ, or other cognitive outcomes.

WPPSI‐III and EVT‐2 IQ and language measures were only administered to children age 30 months and older. This further limits the sample size for testing IQ and language effects on global and regional brain network topology. While we found differences in developmental trajectories for global network measures when we treated boys and girls separately, the smaller sample size for the IQ and language measures may be responsible for not detecting these differences as a function of cognitive ability in the sample tested. Several large‐scale developmental neuroimaging studies are currently underway such as the ABCD Study (https://abcdstudy.org) and the ECHO Study (https://www.nih.gov/echo) that will include thousands of children and should provide more exact estimates of average trajectories as well as a potential for training algorithms to make individual predictions of outcomes. Longitudinal studies within individuals through development rather than a cross‐sectional study as described here should reduce variance in growth trajectories (Szaflarski et al., 2006, 2012) of human brain connectomes during development and both of the studies mentioned above include longitudinal components.

Many of the children under the age of 3 years included in our study population were asleep during the fMRI scan. Sleep has been shown to influence the BOLD signal and brain connectivity (DiFrancesco, Robertson, Karunanayaka, & Holland, 2013; Manning, Courchesne, & Fox, 2013; Redcay, Kennedy, & Courchesne, 2007; Wilke, Holland, & Ball, 2003). The circle data points in Figures 1, 2, 3 indicates the age range of birth to 2 years when children were encouraged to sleep during the fMRI scan. The high variance in this age range may partly be due to the variation in consciousness levels in this group of participants and sleep may also introduce a bias in the estimates of the network parameters we have examined.

Finally, we attempted to explore the age‐related changes of functional brain networks over a continuous age range starting from birth through adolescence. Neonatal and toddler brains differ in size and cortical thickness compared with adolescent brains. To minimize age bias in our parcellation, we created age specific probability maps during preprocessing to use as templates for segmentation and normalization of structural images. Functional images were then normalized and resampled to voxel size 2 × 2 × 2 mm using the structural normalization transformations for each age group. Subsequently, normalized functional images were smoothed with 8 mm FWHM kernel. This process produces the most accurate normalization and segmentation we can achieve prior to parcellation. To the best our knowledge, this is the first study that has applied graph theoretical analysis to investigate the development of functional brain networks using functional parcellation from birth through adolescence. Further research will be necessary to determine how to most accurately scale neonatal brain parcellation to the adolescent and adult equivalents.

5. CONCLUSIONS

We detected significant age‐ and sex‐related changes in the developmental trajectories of the functional brain connectome which show different rates of maturation of functional brain networks in boys and girls. We also explored the correlation of neurocognitive measures and the regional network properties by combining neuroimaging data and behavioral measures. This approach may provide novel insight into the neural underpinnings of behavioral and cognitive variability in individuals during development. Overall, the current study reveals the dynamics of the functional brain connectome globally and locally and provides a background for evaluation of network anomalies associated with neurological disorders in children.

Gozdas E, Holland SK, Altaye M, CMIND Authorship Consortium . Developmental changes in functional brain networks from birth through adolescence. Hum Brain Mapp. 2019;40:1434–1444. 10.1002/hbm.24457