Reduced cortical thickness in Heschl's gyrus as an in vivo marker for human primary auditory cortex

Abstract

The primary auditory cortex (PAC) is located in the region of Heschl's gyrus (HG), as confirmed by histological, cytoarchitectonical, and neurofunctional studies. Applying cortical thickness (CTH) analysis based on high‐resolution magnetic resonance imaging (MRI) and magnetoencephalography (MEG) in 60 primary school children and 60 adults, we investigated the CTH distribution of left and right auditory cortex (AC) and primary auditory source activity at the group and individual level. Both groups showed contoured regions of reduced auditory cortex (redAC) along the mediolateral extension of HG, illustrating large inter‐individual variability with respect to shape, localization, and lateralization. In the right hemisphere, redAC localized more within the medial portion of HG, extending typically across HG duplications. In the left hemisphere, redAC was distributed significantly more laterally, reaching toward the anterolateral portion of HG. In both hemispheres, redAC was found to be significantly thinner (mean CTH of 2.34 mm) as compared to surrounding areas (2.99 mm). This effect was more dominant in the right hemisphere rather than in the left one. Moreover, localization of the primary component of auditory evoked activity (P1), as measured by MEG in response to complex harmonic sounds, strictly co‐localized with redAC. This structure–function link was found consistently at the group and individual level, suggesting PAC to be represented by areas of reduced cortex in HG. Thus, we propose reduced CTH as an in vivo marker for identifying shape and localization of PAC in the individual brain.

1. INTRODUCTION

Heschl's gyrus (HG), also known as the anterior transverse temporal gyrus (Penhune, Zatorre, MacDonald, & Evans, 1996; Destrieux, Fischl, Dale, & Halgren, 2010), originates medially at the retroinsular region and joins the lateral rim of the supratemporal plane (Rademacher et al., 2001; Schneider et al., 2005; Wang, 2013). Apart from common findings describing single transverse gyri, a multitude of more complex morphological variants of HG have already been observed, namely: sulcus intermedius (SI), indenting partially the transverse gyrus along its mediolateral extension (Penhune et al., 1996), common stem duplications (CSD), complete posterior duplications (CPD) (Abdul‐Kareem & Sluming, 2008; Marie et al., 2015; Marie, Maingault, Crivello, Mazoyer, & Tzourio‐Mazoyer, 2016; Moerel, De Martino, & Formisano, 2014), and furthermore multiple duplications (MD) of HG (Benner et al., 2017; Turker et al., 2017). Interestingly, the macroscopic gyrification and size of HG have been found to be highly stable already at primary school age (Seither‐Preisler, Parncutt, & Schneider, 2014). This implies that age‐related changes would not modify the characteristic structural shape of HG.

HG contains the main portion of the primary auditory cortex (PAC), as demonstrated by cytoarchitectonic (Fullerton & Pandya, 2007; Morosan et al., 2001; Rademacher et al., 2001), functional (Da Costa et al., 2011; De Martino et al., 2015; Formisano et al., 2003; Moerel et al., 2014; Saenz & Langers, 2014), and myelin‐based studies (Sigalovsky, Fischl, & Melcher, 2006; Wasserthal, Brechmann, Stadler, Fischl, & Engel, 2014). Thereby, PAC has been found to localize more in the anterolateral two‐thirds of HG as illustrated by cyto‐ and chemoarchitectonic studies (Hackett, Preuss & Kaas, 2001; Rademacher, Caviness, Steinmetz, & Galaburda, 1993; Sweet, Dorph‐Petersen, & Lewis, 2005), functional MRI (Patterson et al., 2002; Da Costa et al., 2011; Moerel et al., 2014; Schönwiesner, Dechent, Voit, Petkov, & Krumbholz, 2015), and furthermore visualized by probabilistic atlases (Penhune et al., 1996; Rademacher et al., 2001) and modern multimodal approaches (Glasser et al., 2016). Moreover, characteristic left–right asymmetries for PAC localization which were independent of shape and gyrification of HG have been reported (Galaburda and Sanides, 1980; Rademacher et al., 2001; Morosan et al., 2001; Sigalovsky et al., 2006). In an early cytoarchitectonic study by Von Economo & Horn (1930), it has already been observed that PAC in the left hemisphere is consistently more elongated along the axis of HG and reaches toward the lateral end compared to the right side. On the cellular level, characteristic granular koniocortex is found to constitute PAC, consisting of a very prominent lamina IV, a rarefied lamina V, and a high density of neurons of extremely small size particularly in the right hemisphere (Von Economo & Horn, 1930). In general, thinner koniocortex is found in the receptive areas of neocortex, that is, primary sensory cortex, where sensory fibers arrive from the thalamus (Triarhou, 2007). In addition, postmortem studies have reported very heterogeneous and regionally specific cortical thickness (CTH) values across the human cerebral cortex ranging between 1–4.5 mm and an overall average of approximately 2.5 mm (Zilles, 1990). While koniocortex of primary sensory areas shows the lowest CTH values, magnopyramidal cortex of the primary motor area displays the highest CTH values (Brodmann, 1909; Von Economo & Koskinas, 1925). As a consequence, it is plausible to assume that auditory koniocortex, that is, PAC, corresponds to a region of reduced (lower) CTH in modern MRI‐based measurements.

In histological studies, the auditory area has been said to cluster into subareas according to the underlying cytoarchitecture of the laminar pattern that is organized in a stepwise manner (Fullerton & Pandya, 2007). The width of single layers in specific cortical areas and their ratio to one another can vary significantly (Brodmann, 1909) which suggests that corresponding CTH values need to be interpreted on the basis of the areas' cortical cytoarchitecture. While the cortical surface area of a region is determined by the proliferation of the early neuronal progenitors and the number of its proliferative units, the CTH is directly proportional to the neuronal output of the individual proliferative units, that is to say, the number of cells produced by each column (Pontious, Kowalczyk, Englund, & Hevner, 2008; Rakic, 1988). An important role has been ascribed to the so‐called intermediate progenitor cells, that is, transient progenitor cells that are located in the periventricular zone. They are thought to directly impact the neuronal output of their respective proliferative units, influencing the cellular composition of individual sublayers and thus the laminar and total CTH (Pontious et al., 2008). However, as the cytoarchitecture of the cortex can only partially be explained by its cellular components alone, it seems conclusive that CTH requires additional investigation of the axonal composition and myeloarchitecture to fully comprehend its determining factors (Anderson, Southern & Powers, 1999). In fact, almost as much as 60% of gray matter (GM) volume is composed of axons and dendrites, while neuronal cell bodies and synapses account for merely 1/7 of GM (Bennett, 2011). There is a growing body of evidence that greater intracortical neuropil growth, that is, higher synaptic density, is linked to greater laminar width (De Felipe, Alonso‐Nanclares, & Arellano, 2002), and furthermore that intra‐ and subcortical myelin proliferation stretches the cortex along its tangential surface. Those inner‐cortical processes are assumed to result in the higher cortical surface area and reduced CTH (Marie et al., 2016; Seldon, 2005; van Essen, 1997). These findings have corroborated the theory that cortical morphogenesis can at least partially be explained by the tension forces exerted by axons on the radial and tangential planes of the cortex (van Essen, 1997).

Over the past decade, the metric of CTH has received increasingly more attention by neuroscientists as a consequence of new accessible methods for the automated computation of CTH using T1‐weighted MRI data (Haidar & Soul, 2006; Jones, Buchbinder, & Aharon, 2000; Kabani, Le Goualher, MacDonald, & Evans, 2001; Lerch & Evans, 2005; MacDonald, Kabani, Avis, & Evans, 2000). This has created new opportunities to investigate normal age‐related cortical changes as well as neurodegenerative diseases associated with cortical atrophy, for example, in Alzheimer's and Huntington's disease (Fischl & Dale, 2000; Rosas et al., 2002), or cortical thickening in migraine (DaSilva, Granziera, Snyder, & Hadjikhani, 2007). Moreover, it appears that CTH analysis has especially become attractive for the investigation of functional‐anatomical relationships because the biological and histological significance complements the information yielded by morphometric analyses (Bermudez, Lerch, Evans, & Zatorre, 2009; Dickerson et al., 2008). The increasing demands of more accurate CTH measurements in the neuroimaging field have necessitated the development of automated algorithms for the computation of CTH, as implemented by different methodological approaches (Fischl & Dale, 2000; Jones et al., 2000; MacDonald et al., 2000). All of them faced similar challenges aiming at overcoming artifacts which are inherent to MRI data acquisition such as intensity bias, under‐sampling, and lack of contrast to clearly separate gray matter from white matter (WM; MacDonald et al., 2000). Further difficulties are caused by the three‐dimensional anatomy of the human neocortex with its convoluted pattern of gyri and sulci facilitating partial volume effects, that is to say, the blurring of the borders of closely adjacent cortical substructures (Jones et al., 2000; MacDonald et al., 2000; Shafee, Buckner, & Fischl, 2015). These challenges have partially been fixed by higher resolutions of newer MRI scanners as well as by modern automated methods providing confident measures of CTH (Haidar & Soul, 2006; Kabani et al., 2001; Lerch & Evans, 2005). In recent in vivo studies assessing CTH, areas containing HG and surrounding regions have been classified as a single region termed AC (Foster & Zatorre, 2010; Hyde et al., 2007) or as a part of the supratemporal plane (Bermudez et al., 2009), which does not allow drawing conclusions about subregions of HG. Despite these limitations, Meyer et al. found HG to constitute the thinnest of five investigated auditory regions (namely, HG, Heschl's sulcus [HS], planum temporale [PT], planum polare and STG) in both hemispheres, showing mean CTH values of 2.43 ± 0.28 mm for the left and 2.53 ± 0.29 mm for the right hemisphere (Meyer, Liem, Hirsiger, Jäncke, & Hänggi, 2014). These findings are in line with Sigalovsky et al. (2006) who found CTH in several subareas of HG to rank around 2.6 mm. Further neuroimaging studies have confirmed heterogeneous CTH values across the cortex (Fischl & Dale, 2000; Jones et al., 2000) as well as the unequal distribution of CTH values between gyri and sulci, with the CTH at the crowns of gyri averaging 2.7 mm as opposed to 2.2 mm measured at the grounds of sulci (Fischl & Dale, 2000; van Essen, 1997). However, modern MRI‐based CTH analyses in the search for an adequate in vivo marker of PAC are still a challenge because of the high inter‐individual structural variability of AC.

Using electrophysiological methods such as electroencephalography (EEG) or magnetoencephalography (MEG), the primary auditory evoked P1 response as evoked by sinusoidal or complex harmonic sound stimulation can be considered as a reliable functional marker of PAC which has been illustrated by intracranial (Godey, Schwartz, De Graaf, Chauvel, & Liegeois‐Chauvel, 2001; Liegeois‐Chauvel, Musolino, Badier, Marquis, & Chauvel, 1994) and electrophysiological studies (Schneider et al., 2002, 2005; Wengenroth et al., 2014). Particularly, MEG provides not only a high temporal resolution but also, compared to EEG, a suitable spatial resolution for source localization of primary responses (Scherg, 1990). Since the P1 response complex may include not only primary activation but also, to a minor proportion, early secondary pitch‐sensitive responses of lateral HG (Yvert et al., 2001; Schneider et al., 2005), it is important to separate the earlier primary component by appropriate constraints (Schneider et al., 2002; Wengenroth et al., 2014). In a combined MRI and EEG study, Liem, Zaehle, Burkhard, Jancke, and Meyer (2012) have reported thinner CTH to be associated with larger N1 amplitude in lateral HG. Furthermore, it is well‐known that auditory response patterns differ between children and adults under influence of maturational learning processes. Age‐related plasticity seems to affect secondary response patterns more likely, while the primary response characteristics are already present in early childhood (Sharma, Kraus, McGee, & Nicol, 1997) and elementary school age (Seither‐Preisler et al., 2014). Therefore, the P1 component can be seen as a stable marker of elementary sound detection in both children and adults.

In this study, we propose that the combined measurement of structural MRI‐based CTH analysis and MEG‐based functional activity is a new approach to clarify if regions of reduced CTH in HG are of primary auditory origin and if this method is suitable to study their inter‐individual variability in shape and localization. In a large cohort of 60 children and 60 adults, we investigated the individual CTH distribution in the region of HG, as measured by structural MRI, in relation to individual HG morphology and to primary auditory source activity, as measured by MEG. We hypothesize that the spatial and temporal characteristics of the primary auditory evoked responses may provide functional support for applying CTH analysis as a structural in vivo marker for PAC, even in the individual brain. Furthermore, group‐averaged CTH mapping was used to compare the average distribution and lateralization of regions of reduced CTH in AC in relation to age.

2. MATERIALS AND METHODS

2.1. Subjects

In this study, two independent samples of 60 children aged 8–11 years (mean age 9.7 ± 0.72 years; 27 male, 33 female) and 60 adults aged 18–55 years (mean age 34.0 ± 9.6 years; 28 male, 32 female) without any neurological, developmental, or learning disorders were selected. Children were recruited as a part of the research project “AMseL: Audio‐ and neuroplasticity of musical learning” funded by the German Federal Ministry of Education and Research (BMBF) (Seither‐Preisler et al., 2014; Serrallach et al., 2016). Adults were chosen as an arbitrary sample from the normal population as part of the Heisenberg program “Sound perception between outstanding musical abilities and auditory dysfunction: The neural basis of individual predisposition, maturation, and learning‐induced plasticity in a lifespan perspective” funded by the German Research Foundation (DFG). Considering musical expertise, both groups constituted a representative sample of the normal population, including 46 children/42 adults with no or little and 14 children/18 adults with more intensive musical practice (average intensity of musical practice; children: > 7 h/week × years, adults: > 15 h/week averaged across the last 3 years). Standardized screening of musical aptitude also reflected the typical age‐related distribution of the normal population (average total score of music audiation; children: 65 ± 0.8, adults: 60 ± 1.5 out of 80), which was assessed using the Intermediate Measures of Music Audiation (IMMA‐test) for children and the Advanced Measures of Music Audiation (AMMA‐test) for adults (Gordon, 1986, 1989). The local research ethics committee of the Medical Faculty of the University of Heidelberg approved all experimental procedures in accordance with the Helsinki declaration. For young subjects, parents provided informed consent in written form and subjects informed assent.

2.2. MRI acquisition, image processing, and CTH analysis

High‐resolution T1‐weighted 3D MR images of the brain (magnetization‐prepared rapid acquisition of gradient echo sequence: echo time 4.38 ms, repetition time 1930 ms, 1 mm³ isotropic resolution, flip angle 15°, 176 contiguous sagittal slices, and matrix size 256 mm) were acquired for all children and adults at 3 Tesla (Magnetom Trio, Siemens, Erlangen, Germany) using a 12‐channel head coil. In addition, T2‐weighted sequences were obtained and assessed by a neuroradiologist to rule out pathology. Image preprocessing, CTH analysis, cortex‐based alignment (CBA), and region of interest (ROI) analysis were performed with Brain Voyager QX 2.8 Software (Brain Innovation, Maastricht, Netherlands) from pseudonymized data.

The individual preprocessing of T1 weighted images included (a) Intensity inhomogeneity correction, (b) brain extraction, (c) AC‐PC transformation, and (d) Talairach space transformation (Talairach & Tournoux, 1988) (Figure 1a). Subsequently, Brain Voyager's “Automatic Segmentation Pipeline” was computed for each subject separately to improve the quality of individual whole‐brain segmentations and to prepare the preprocessed morphological data for following individual CTH and CBA computing (http://brainvoyager.com/bv/doc/UsersGuide/Segmentation/TheAutomaticCortexSegmentationPipeline.html). First, the image resolution was converted from 1.0 to 0.5 mm³ iso‐voxel size for optimizing the following CTH computing. Based on the 0.5 mm³ data the cerebellum and subcortical structures such as the brain stem were removed using an automatically generated mask, and a sigma filter was applied to enhance homogeneity and tissue contrast by smoothing intensity values around each voxel. The borders for the separation of GM, WM and cerebrospinal fluid (CSF) were identified (Figure 1b). Whole‐brain CTH values were then calculated for each hemisphere and subject separately resulting in individual CTH maps (Figure 1c).

Figure 1.

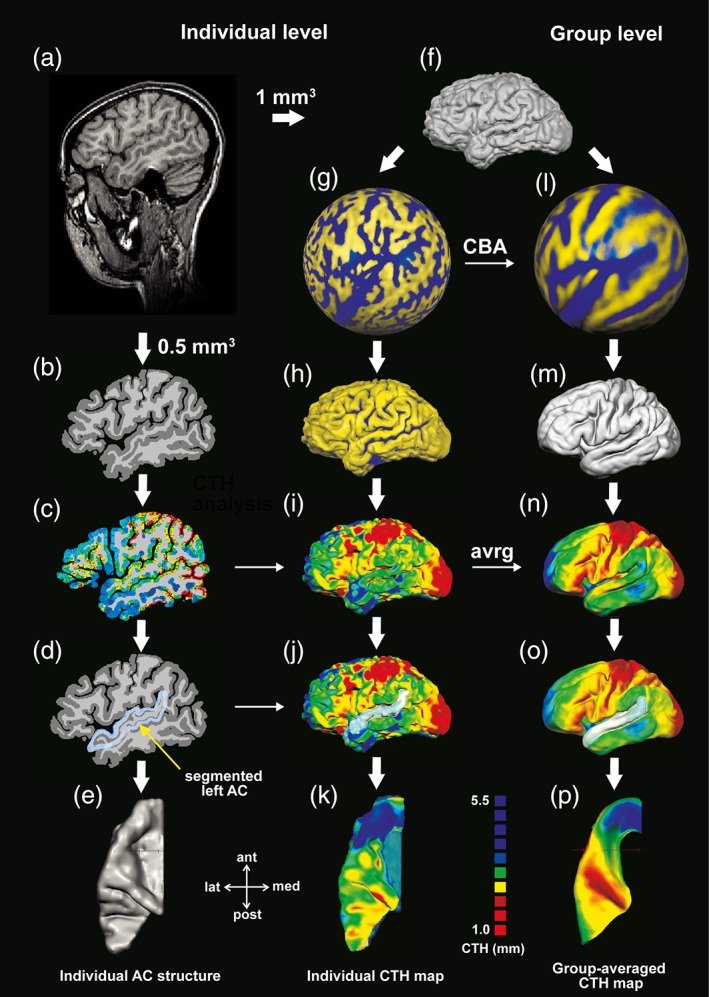
Successive procedure for measuring individual and group‐averaged CTH. (a–e) Whole‐brain preprocessing, extraction of AC, and calculation of individual CTH maps for each hemisphere separately. (f–k) 3D reconstruction of individual whole‐brain surfaces including CTH mapping and extraction of AC for each individual and hemisphere. (l–p) co‐registration of individual hemispheres (during CBA process) followed by group‐averaged 3D reconstruction of the whole‐brain surface, CTH mapping, and extraction of AC

2.3. Individual segmentation of AC

In parallel to the CTH analyses, segmentation and 3D reconstruction of individual AC was performed based on a stepwise semi‐automatic procedure using BrainVoyager QX software (Figure 1d). In particular, the superior temporal plane including HG, anterior superior temporal gyrus (aSTG) and planum temporale (PT) was segmented slice‐by‐slice along the Sylvian fissure based on sagittal images, employing standard definitions of the anatomical landmarks of AC (Penhune, Cismaru, Dorsaint‐Pierre, Petitto, & Zatorre, 2003; Rademacher et al., 2001; Wong et al., 2008) and according to established criteria (Benner et al., 2017; Schneider et al., 2005; Wengenroth et al., 2014). Thereby, the HG was defined as the most anterior transverse gyrus within the supratemporal plane located between the first transverse sulcus and Heschl's sulcus (HS). In the case of multiple gyration, transverse gyri posterior to the first HG were considered to be posterior HG duplications. The PT was defined as the plane cortical structure posterior to the HG. A complete HS (cHS) posterior to HG was considered as the anterior border of the PT. In the case of multiple complete posterior duplications of HG, the anterior border of PT was specified as the last complete transverse sulcus posterior to the duplications. The posterior border of PT was determined to be the origin of the ascending ramus (if present), the medial border to be the insular cortex, and the inferior border to be the supratemporal sulcus. For the correct identification of PT, HG, and occurring duplications, a critical step was the visualization of sulcal boundaries based on 3D reconstruction of the AC surface (Figure 1e). This established segmentation procedure has previously been applied in several previous studies (Benner et al., 2017; Schneider et al., 2005; Schneider & Wengenroth, 2009; Seither‐Preisler et al., 2014; Serrallach et al., 2016; Wengenroth et al., 2014; Wengenroth, Blatow, Bendszus, & Schneider, 2010) and allows a clear identification of HG, PT and possible duplications as needed for further ROI‐based analyses.

2.4. Cortical reconstruction and CTH mapping

On the individual level, subsequent surface reconstruction was performed for demonstrating the GM–CSF boundary (pial surface) which improved the accurate estimation of the individual morphology of the cortical surface. Hemispheres were separated and a surface mesh was reconstructed based on the 1.0 mm³ data. The resulting surface vertices were gradually interpolated (20 iterations, smoothing force: 0.07) for optimized visualization (Figure 1f). Individually reconstructed surface meshes were converted into spheres, containing corresponding vertices of the original surface mesh while preserving the original curvature information (Figure 1g). Each resulting sphere was matched to a standard sphere separately, that is, each vertex on the standard sphere was mapped to the closest vertex on the morphed sphere with a defined number of vertices per hemisphere. A folded mesh representation was created for each individual sphere, while preserving the curvature information of the original mesh (Figure 1h). Individual whole‐brain CTH maps were generated based on the previous CTH analyses (Figure 1C) and superimposed on the reconstructed surfaces. A reconstructed surface‐mask of individual ACs was transferred separately to the surface of each hemisphere (Figure 1i–j). The last step involved the extraction of individual ACs and corresponding superimposed CTH maps (Figure 1k).

On the group level, all resulting surfaces were structurally aligned using curvature information reflecting the gyral folding pattern aiming at improving intersubject spatial correspondence (Frost and Goebel, 2012; Goebel et al., 2006). To preserve the underlying distribution of CTH, CBA procedure was applied which matches the spheres by iteratively progressing from highly to slightly smoothed curvature maps using an individual target sphere (Fischl, Sereno, & Dale, 1999; Goebel et al., 2006). The results of the CBA processing were displayed in a group‐aligned sphere representing the co‐registered curvature information (Figure 1l) and afterwards converted to group‐averaged hemispheres for both, adults and children (Figure 1m). Individual CTH maps were group‐aligned and averaged by integrating the co‐registration information obtained from individual CBA processing, and superimposed on the group‐averaged hemispheres (Figure 1n). A reconstructed surface‐mask of average ACs was transferred to the group‐averaged surface of each hemisphere separately (Figure 1o). The last step involved the extraction of the masked ACs and corresponding CTH maps for each group (children and adults) and hemisphere separately (Figure 1p).

2.5. ROI definitions

Based on the individual segmentation of ACs, the individual structure of HG was systematically parcellated in (a) medial HG (mHG), covering the posteromedial two‐thirds of HG (Figure 2, blue area), and (b) lateral HG (lHG), covering the remaining lateral part of HG (Figure 2, green area), including potential CSDs or CPDs according to Schneider et al. (2005) and Benner et al. (2017). Thereby, the region of HG was defined to originate medially at the retroinsular region and to extend to the lateral rim of the supratemporal plane (Rademacher et al., 2001; Schneider et al., 2005; Wang, 2013). The lateral part of HG, known to host pitch perception centers, has usually been ascribed to be part of the medial STG (Pandya, 1995; Liem et al., 2012; Meyer et al., 2014; Poliva, 2015).

Figure 2.

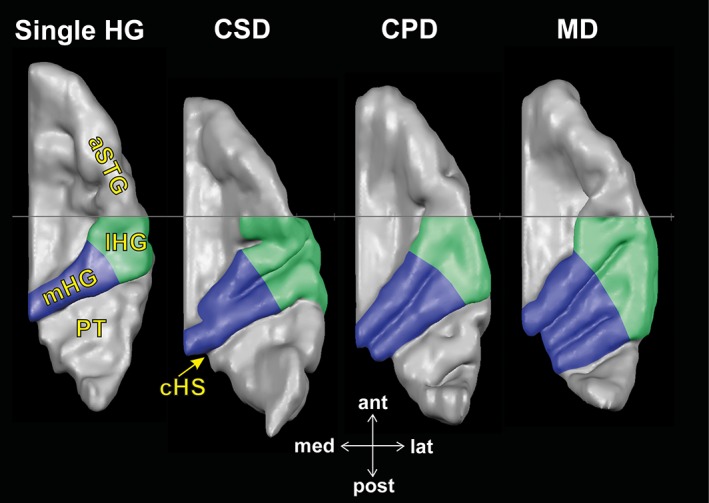
Top view on the supratemporal plane demonstrating the topography of the auditory cortex based on individual segmentation. Three examples of right hemispheric ACs illustrate typical variations of HG: Single transversal Heschl's gyrus (single HG), common stem duplication (CSD), complete posterior duplication (CPD), and multiple duplication (MD). The posteromedial two‐thirds of HG are colored in blue (mHG), the remaining anterolateral part of HG in green (lHG). In posterior direction, HG is separated from the planum temporale (PT) by the first complete Heschl's sulcus (cHS). In the anterior direction, HG is separated from the anterior supratemporal gyrus (aSTG) by the y = 0 axis, delineating the lHG's anterior border (visible as a gray line)

In addition, CTH‐based ROIs were used to systematically describe the hypothesized effect of lateralization, which cannot adequately quantified by the two anatomically predefined ROIs (mHG, lHG). Preliminary CTH analyses of our research revealed that the anatomically predefined region of mHG is only in the right hemisphere an adequate predictor for PAC, however not in the left hemisphere, related to the observed structural and functional leftward asymmetry. Therefore, we defined two further CTH‐based ROIs that were derived from the individual CTH maps: (Figure 1h): (a) the largest continuous region of reduced CTH in AC (redAC, see red areas in Figure 3) and (b) the surrounding belt region of thicker AC (subAC). Since the transition between the individual CTH values of redAC and subAC occurred abruptly around 2.5 mm (magnitude ~0.5 mm) we used a corresponding distinction in the color‐scale of generated CTH maps to emphasize this threshold (red to yellow, see Figures 3 and 4). Furthermore, the locations of the centers of reduced AC (centAC) were determined by decreasing the individual threshold of the computed CTH maps and by identifying the smallest coherent area within redAC.

Figure 3.

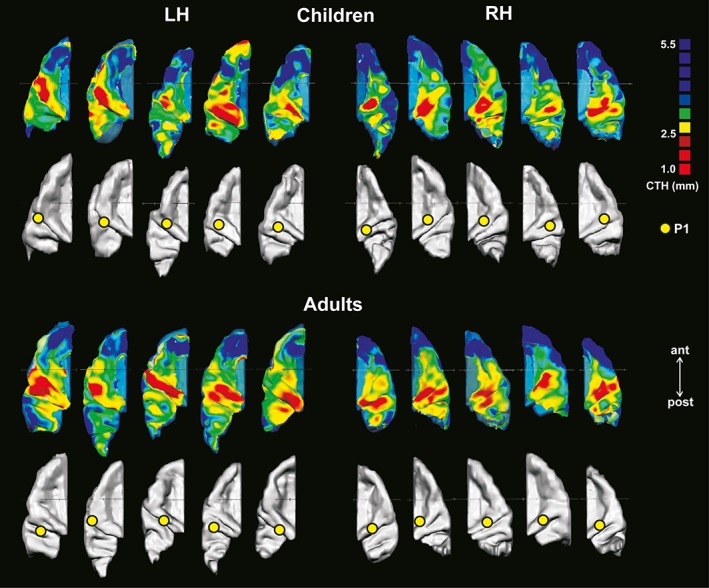
Examples of individual CTH distribution and auditory evoked P1 responses which are shown for five children (top) and five adults (bottom) mapped on the 3D reconstructed left and right ACs separately. Inter‐individual and interhemispheric differences are visible in shape and size of cortical regions with higher (green) and lower (red) CTH (upper panels), as well as in localization of the primary auditory evoked P1 response (yellow open circles; lower panels). Overall, the localization of areas with reduced CTH varies largely across the lateral and medial portions of HG and expands toward posterior duplications of HG in several cases

Figure 4.

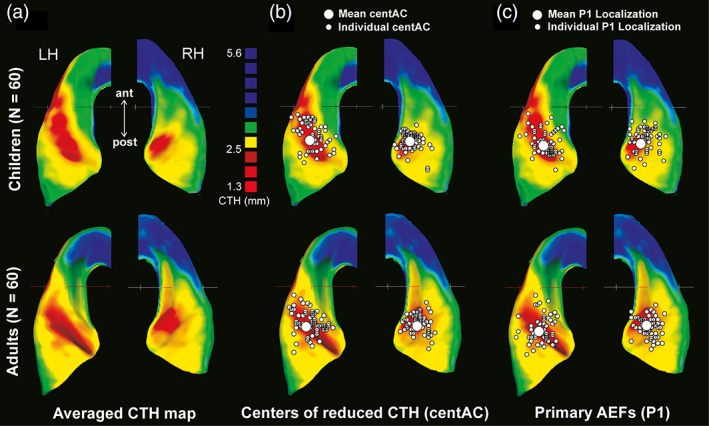
(a) Average maps of the CTH distribution were mapped separately for both groups (60 children, 60 adults) and projected onto the corresponding structural averaged ACs respectively. The grouped CTH maps were thresholded to distinguish the areas of reduced CTH (centAC, CTH < 2.6 mm, indicated in red) from thicker surrounding areas (indicated successively in yellow, green and blue). The left hemisphere exhibits a more even distribution of CTH along the entire extent of HG, whereas the right hemisphere reveals a markedly thinner medial portion of HG as compared to its lateral portion. (b) Localizations of the individual centers of reduced AC (small white circles) in relation to the CTH maps and group‐averaged localization (large white circles). (c) Localizations of the individual primary auditory evoked P1 responses (small white circles) in relation to the corresponding CTH maps and group‐averaged localization (large white circle)

2.6. Magnetoencephalography

Auditory evoked fields (AEFs) were recorded using a Neuromag‐122 whole‐head MEG system in response to a pseudorandomized sequence of seven different simple instrumental tones (piano, guitar, flute, bass clarinet, trumpet, violin, and drums) and five artificial simple harmonic complex tones that have successfully been employed in earlier studies (Schneider et al., 2005; Seither‐Preisler et al., 2014; Serrallach et al., 2016; Wengenroth et al., 2014). These stimuli evoke both the earlier primary auditory P1 response occurring about 30–80 ms after tone onset and the later secondary auditory N1 and P2 auditory responses occurring about 90–250 ms after tone onset. To enhance the primary response, subjects were measured in the MEG without any task. To control their vigilance, they were instructed to listen to the sounds in a relaxed state and to watch a silent movie. Each of the stimuli was presented 100 times in pseudorandomized order (tone length 500 ms, interstimulus interval range 300–400 ms, total length of the stimulation 15 min). The AEFs were recorded with a bandpass filter of 0.00 (DC)–330 Hz and a sampling rate of 1,000 Hz. Data analysis was conducted with the BESA Research 6.0 software (MEGIS Software GmbH, Graefelfing, Germany). Prior to averaging, data were inspected to exclude automatically external artifacts using the event‐related fields ERF module. By applying the automatic Artifact Scan tool, on average 3–7 noisy (bad) channels were excluded, and around 10% of all epochs exceeding a gradient of 600 fT/cm s and amplitudes either exceeding 3,000 fT/cm, or falling below 100 fT/cm, were rejected from further analysis. Thereby, the major part of endogenous artifacts, like eye blinks, eye movements, cardiac activity, face movements, and muscle tensions could be accounted for. A baseline‐amplitude calculated over the 100 ms interval before the onset of the tones was subtracted from the signals. The responses of each subject were first collapsed into a grand average (about 1000 artifact‐free epochs after the rejection of 10% of artifact‐afflicted or noisy epochs) in a 100 ms prestimulus to 400 ms poststimulus time window.

Spatio‐temporal source modeling was performed to separate the primary response complex from the later secondary responses using one equivalent dipole in each hemisphere (Scherg, 1990; Schneider et al., 2002, 2005; Seither‐Preisler et al., 2014; Wengenroth et al., 2014). The P1 wave is a composite response complex comprising separate peaks of the earlier primary and later secondary auditory activity and shows large inter‐individual differences with respect to shape, number of subpeaks, and timing of peak latencies. Therefore, the fitting intervals were adjusted from peak onset time either toward the saddle point in case of a two‐peak complex or toward the main peak latency in case of a merged single P1 peak. Due to developmental maturation, the P1 response complex occurs around 30–70 ms after tone onset in adults (Schneider et al., 2005), but considerably later around 60–95 ms in primary school children (Ponton, Eggermont, Khosla, Kwong, & Don, 2002; Seither‐Preisler et al., 2014; Serrallach et al., 2016; Sharma et al., 1997). For both, children and adults, the response‐dependent time windows were clearly detectable from the course of the individual source waveforms and could clearly be separated from the following later secondary N1 response, which typically starts to develop at the age of 8–10 years (Seither‐Preisler et al., 2014). In a first step, the primary source activity was modeled based on one regional source in each hemisphere using the predefined fitting intervals. In a second step, the localization of the fitted regional sources was kept fixed and the dipole orientation was then fitted to the direction with the highest global field power, keeping its main orientation toward the vertex.

2.7. Statistical analyses

All statistical analyses were carried out with the software package IBM SPSS Statistics, version 24 (SPSS Inc., Chicago, IL). For the MRI data, a three‐way anova with “age‐group” (children vs. adults) as a grouping factor and “hemisphere” (right vs. left) and “region” (redAC and subAC) as repeated measurement factors were calculated to analyze possible differences in CTH. An analogous analysis was performed to test for CTH differences between anatomically predefined regions (mHG vs. lHG).

For the MEG data, two‐way anovas were performed for the x‐ and y‐coordinates of the P1 component with “age group” (children vs. adults) as a grouping factor and “hemisphere” (right vs. left) as a repeated measurements factor. In the case of significant interactions, the mean values of interest were compared with the Tukey‐HSD. Moreover, correlation analyses were performed to analyze interdependencies between the MRI and MEG data and corrected for age (partial correlation with age held constant). Since not all MEG localization parameters were normally distributed, nonparametric statistics were determined.

3. RESULTS

3.1. Cortical thickness patterns

CTH measures were computed for HG and surrounding areas for children and adults (see section 2). The resulting CTH values are listed in Table 1. The ANOVA on CTH yielded a significant main effect “region” (F[1,118] = 345.1, p = 7.8 × 10⁻³⁷, part. η ² = 0.75), with the CTH of redAC being 0.65 mm thinner compared to the surrounding areas of subAC. Mean CTH values were for redAC 2.34 ± 0.024 (SEM) mm and for subAC 2.99 ± 0.025 mm (pooled across age‐group and hemispheres). There was a nonsignificant trend for the interaction “age‐group × region” (F[1,118] = 3.76, p = .055, part. η ² = 0.031). In children, the differences between the thinner and thicker HG regions were slightly larger compared to adults [children: CTH(redAC) = 2.39 ± 0.034 mm, CTH(subAC) = 3.11 ± 0.035 mm; adults: CTH(redAC) = 2.29 ± 0.034 mm, CTH(subAC) = 2.87 ± 0.035 mm; pooled across hemispheres]. Tukey‐HSD tests revealed that the group difference was significant (p < .01) only for subAC (0.24 mm), but not for redAC (0.10 mm).

Table 1.

Cortical thickness values of AC and specific subareas of HG

	LH		RH
	Range (mm)	Mean ± SEM (mm)	Range (mm)	Mean ± SEM (mm)
	Children
Complete AC	2.50–3.30	3.00 ± 0.021	2.71–3.40	3.07 ± 0.018
redAC	1.38–3.29	2.40 ± 0.050	1.60–3.26	2.38 ± 0.043
subAC	2.06–4.79	3.03 ± 0.061	2.21–3.76	3.19 ± 0.043
mHG	1.98–3.64	2.77 ± 0.037	1.87–3.96	2.63 ± 0.044
lHG	1.63–3.56	2.72 ± 0.044	2.18–3.68	3.02 ± 0.039
	Adults
Complete AC	2.44–3.27	2.82 ± 0.021	2.57–3.14	2.88 ± 0.018
redAC	1.82–3.23	2.38 ± 0.036	1.46–3.41	2.20 ± 0.049
subAC	2.21–3.64	2.84 ± 0.26	1.91–3.95	2.90 ± 0.049
mHG	2.07–3.01	2.62 ± 0.027	1.76–2.97	2.37 ± 0.035
lHG	1.85–3.13	2.58 ± 0.032	1.77–3.66	2.67 ± 0.050

Range = range of the individual CTH values; RH = right hemisphere; LH = left hemisphere; mHG = medial Heschl's gyrus; lHG = lateral Heschl's gyrus; redAC = region of reduced thickness in AC; subAC = surrounding belt region of thicker AC; SEM = standard error of mean.

There was a significant interaction “hemisphere x region” (F[1,118] = 15.9, p = .0001, part. η ² = 0.12). Differences between redAC and subAC were larger in the right hemisphere (0.76 mm) compared to the left hemisphere (0.54 mm; RH: mean CTH(redAC) = 2.29 ± 0.033 mm; CTH(subAC) = 3.05 ± 0.033; LH: CTH(redAC) = 2.39 ± 0.031; CTH(subAC) = 2.93 ± 0.035; pooled across age‐groups). Furthermore, we observed that CTH in children's HG was on average 0.17 mm thicker compared to CTH in adult's HG (CTH[children] = 2.75 ± 0.024 mm; CTH(adults) = 2.58 ± 0.024 mm; main effect “age‐group”: F[1,118] = 24.9, p = .000002, part. η ² = 0.18; pooled across regions and hemispheres). The anova on the centers of redAC showed centAC to be located significantly more laterally in the left hemisphere compared to the right hemisphere (LH: x = −51.1 ± 0.44 mm; RH: x = 44.7 ± 0.34 mm; F[1,118] = 179.6, p = 1.8 × 10⁻²⁵, part. η ² = 0.60; pooled across age‐groups). This characteristic hemisphere effect was similar in children and adults (Table 2) and could also clearly be distinguished from the individual and averaged CTH maps (Figures 3 and 4a,b): in left AC, redAC was on average more evenly distributed over the entire HG, partly extending into anterolateral direction toward aSTG. Right AC revealed a more medial distribution of redAC, extending toward posterior HG duplications and the PT.

Table 2.

Hemispheric differences in the localization of centAC and primary auditory evoked P1 responses

	LH	RH
	Children
x‐coord. centAC	−51.0 ± 0.62	44.7 ± 0.48
y‐coord. centAC	−14.5 ± 0.84	−15.4 ± 0.57
x‐coord. P1 response	−51.7 ± 0.61	45.2 ± 0.57
y‐coord. P1 response	−18.2 ± 0.79	−15.5 ± 0.75
	Adults
x‐coord. centAC	−51.2 ± 0.61	44.7 ± 0.49
y‐coord. centAC	−18.3 ± 0.73	−17.5 ± 0.59
x‐coord. P1 response	−50.6 ± 0.54	44.3 ± 0.49
y‐coord. P1 response	−21.0 ± 0.92	−16.2 ± 0.70

x, y = stereotaxic Talairach coordinates; RH = Right hemisphere; LH = left hemisphere; Values in mm ± SEM (standard error of mean).

In consistency with previous studies, single HGs were observed to be three (children) to five (adults) times more frequently in the left compared to the right hemisphere. Posterior duplications of HG (CSDs, CPDs, and MDs) occurred more frequently in right hemispheres of both groups (Table 3) which corroborates Pfeiffer's rule that HG duplications are more frequent in the right hemisphere (Pfeiffer, Bumke, & Forster, 1936). The localization of redAC was limited to aHG for two‐thirds of all cases in the left‐ and for about half of all cases in the right hemisphere for both, children and adults. Furthermore, redAC was observed to extend toward HG duplications in about one‐third of all cases, however more frequently in the right compared with the left hemisphere.

Table 3.

Distribution of redAC localization in relation to different HG shapes

	LH					RH
N (%)	Single HG	CSD	CPD	MD	Total	Single HG	CSD	CPD	MD	Total
	Children
redAC on aHG	21 (36)	2 (3)	8 (14)	8 (14)	39 (66)	8 (14)	4 (7)	8 (14)	11 (19)	31 (53)
redAC on aHG & dupl.		3 (5)	7 (12)	7 (12)	17 (29)		7 (12)	9 (15)	9 (15)	25 (42)
redAC on dupl.		2 (3)		1 (2)	3 (5)		1 (2)		2 (3)	3 (5)
Total	21 (36)	7 (12)	15 (25)	16 (27)	59 (100)	8 (14)	12 (20)	17 (29)	22 (37)	59 (100)
	Adults
redAC on aHG	28 (47)	1 (2)	1 (2)	9 (15)	39 (65)	10 (17)	3 (5)	5 (8)	9 (15)	27 (45)
redAC on aHG & dupl.		3 (5)	3 (5)	10 (17)	16 (27)		11 (18)	4 (7)	13 (22)	28 (47)
redAC on dupl.		3 (5)	2 (3)		5 (8)		1 (2)	2 (3)	2 (3)	5 (8)
Total	28 (47)	7 (12)	6 (10)	19 (32)	60 (100)	10 (10)	15 (25)	11 (18)	24 (40)	60 (100)

RH = right hemisphere; LH = left hemisphere; aHG = anterior Heschl's gyrus; CSD = common stem duplication; CPD = complete posterior duplication; MD = multiple duplications; Number of cases: N (%).

3.2. Functional evidence by magnetoencephalography

The morphological findings were reflected in the source localization of the primary auditory evoked response (P1) to auditory stimulation, as measured by MEG (see section 2). After spatiotemporal source modeling individual spatial coordinates of P1 dipoles were superimposed onto the averaged AC surface reconstruction including the CTH distribution. Overall, P1 dipoles localized within the HG region of redAC in most cases in both hemispheres (Figure 4c). On average, we observed left‐ to right‐asymmetric P1 sources in both children and adults: left‐hemispheric sources were significantly more lateral (x‐coordinate left: −51.2 ± 0.4 mm, right: 44.8 ± 3.7 mm; F[1,118] = 146.1, p = .22*10⁻²², part. η ² = 0.55) and more posterior (y‐coordinate left: −19.6 ± 0.6 mm, right: −16.2 ± 0.5 mm; F[1,118] = 20.2, p = .000016, part. η ² = 0.15). The left–right asymmetry showed similar patterns in the children and adult population (no interaction “age‐group × hemisphere” for x‐coordinate). However, the mean y‐coordinate localized significantly more anterior for the children compared to the adults (children: y = −16.9 ± 0.6 mm; adults: y = −19.0 ± 0.6 mm; F(1,118) = 7.0, p = .009, part. η ² = 0.06).

The localization of the functional primary auditory evoked P1 component, measured by MEG in response to complex harmonic sounds, consistently co‐localized with the coordinates of centAC (partial correlations corrected for age: x‐coordinate left: r = .44, p = 3.6 × 10⁻⁷; x‐coordinate right: r = .58, p = 4.1 × 10⁻¹²; y‐coordinate left: r = .63, p = 1.3 × 10⁻¹⁴; y‐coordinate right: r = .37, p = .000023; pooled across age‐group; Figure 5).

Figure 5.

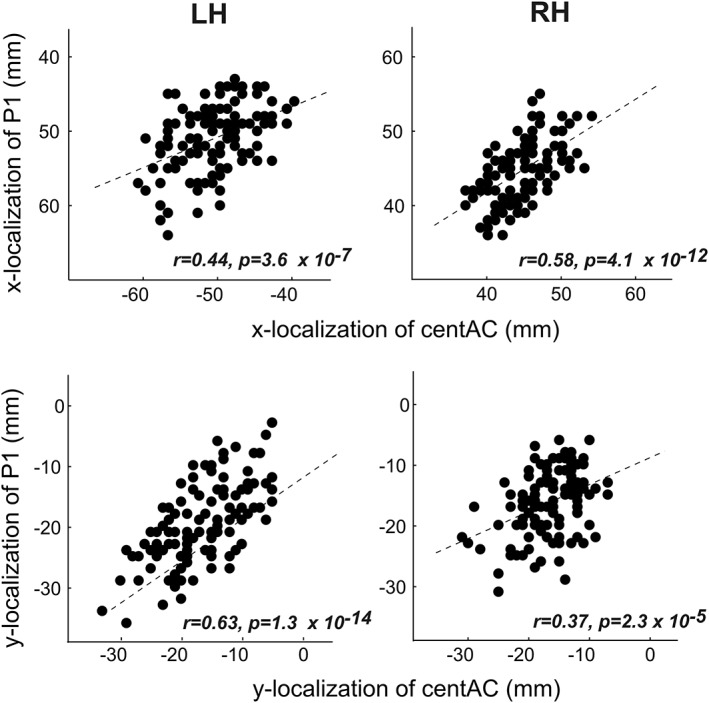
Correlations between localization of the primary auditory evoked responses (P1) and localization of the centers of reduced CTH in AC (centAC) in the x‐direction (upper panels) and y‐direction (lower panels)

3.3. The medial region of HG as a predictor of PAC in the right hemisphere

Furthermore, CTH measures of the anatomically predefined regions mHG and lHG were compared (see section 2 and Figure 2). Overall, mHG showed thinner CTH compared to lHG [CTH(mHG) = 2.60 ± 0.019 mm; CTH(lHG) = 2.70 ± 0.029 mm; F(1,118) = 15.1, p = .00017, part. η ² = 0.11]. Comparing the hemispheres, this effect turned out to be present only on the right side [CTH(mHG) = 2.50 ± 0.029 mm, CTH(lHG) = 2.80 ± 0.042 mm], however not in the left hemisphere [CTH(mHG) = 2.69 ± 0.023 mm, CTH(lHG) = 2.62 ± 0.037 mm; interaction “hemisphere x region”: F(1,118) = 55.9, p = 1.47 × 10⁻¹¹, part. η ² = 0.32). Comparing the groups, children showed 0.23 mm larger CTH values in marked contrast to adults [CTH(children) = 2.77 ± 0.020 mm; CTH(adults) = 2.54 ± 0.020 mm; main effect “age‐group”: F(1,118) = 32.8, p = 8.09 × 10⁻⁸, part. η ² = 0.22). Furthermore, children showed lower CTH values in the left hemisphere [CTH(children) LH = 2.73 ± 0.034 mm, RH: 2.81 ± 0.042 mm], whereas for adults the inverse effect was observed [mean CTH(adults) LH = 2.58 ± 0.034 mm, RH: 2.49 ± 0.042 mm; interaction “age‐group × hemisphere”: F(1,118) = 5.3, p = .023, part. η ² = 0.043).

3.4. Summary of the main results

In both, children and adults, we found contoured regions of reduced CTH, as delineated by redAC, along with the mediolateral extension of HG, illustrating large inter‐individual variability with respect to shape, localization, and lateralization. In the right hemisphere redAC localized more within the medial portion of HG, more frequently extending toward posterior duplications of HG. In the left hemisphere, redAC was distributed more laterally, reaching more toward the anterolateral portion of HG (Figure 4). In both hemispheres, regions of redAC were found to be 0.65 mm thinner on average (mean CTH of 2.34 ± 0.02 mm) compared to surrounding areas of subAC (2.99 ± 0.03 mm). This difference between redAC and subAC was found to be larger in the right hemisphere (Δ = 0.76 mm) compared to the left (Δ = 0.54 mm), and slightly larger in children (Δ = 0.72 mm) compared to the adults (Δ = 0.58 mm). Furthermore, average CTH (pooled across redAC, subAC and hemispheres) was 0.17 mm thicker in children (2.75 ± 0.02 mm) than in adults (2.58 ± 0.02 mm). The localization of centAC was observed to be shifted about ~6 mm more laterally on HG in the left hemisphere compared to the right. This characteristic leftward lateralization of centAC was similar in children and adults (see Table 2 and Figure 4). The localization of the early primary component of auditory evoked fields (P1), as measured by MEG in response to complex harmonic sounds, strictly co‐localized with centAC (see Figure 5). Resulting P1 dipoles were found to generally localize within the HG region of redAC (Figure 4c) showing a lateral shift of 6.4 mm in the left hemisphere, in accordance with left‐lateralized localization of centAC. This leftward asymmetry of P1 localization was found similarly in children and adults, whereas a shift of 2.1 mm in posterior direction was observed in the adults. Moreover, mHG turned out to be an adequate predictor for reduced CTH only in the right hemisphere, however not in the left hemisphere, related to the observed structural and functional leftward asymmetry.

4. DISCUSSION

In this study, we propose that the combined analysis of structural CTH and functional response patterns by MEG is an appropriate method to identify PAC in HG and to observe its inter‐individual differences in the variability in shape, localization, and lateralization. The primary auditory evoked P1 component, derived from MEG in response to complex harmonic sounds, co‐localized consistently with centAC at the group and individual level. Therefore, a separation of the early component of the primary auditory evoked response from later secondary components by means of spatiotemporal source modeling was crucial (see Methods). This structure–function link surpasses the attempts of earlier studies and corroborates the idea to use CTH measures to identify primary sensory areas.

4.1. Localization and lateralization of PAC

The reliable and precise localization of PAC in humans remains a challenge (Sigalovsky et al., 2006) and histological analysis is still the most accurate method to distinguish PAC from surrounding secondary AC. In recent histological studies, the localization of PAC, deriving from cytoarchitectonic probability maps, could only be approximated to the medial two‐thirds of HG (Morosan et al., 2001). This approximation seems to be insufficient, especially if considering the HG's high inter‐individual structural variability (Abdul‐Kareem & Sluming, 2008; Benner et al., 2017; Campain & Minckler, 1976) and the weak correlation between macro‐anatomical landmarks of AC with cytoarchitectonic features of PAC while auditory koniocortex shows likewise considerable intersubject variability in location and extent (Morosan et al., 2001; Rademacher et al., 1993, 2001; Sweet et al., 2005; Von Economo & Horn, 1930). In early histological investigations by Von Economo & Koskinas (1925) and Von Economo & Horn (1930), PAC has already been found to correspond roughly to the macroscopic landmarks delineated by HG which are conceded to merely posit a region of probability, while cases of PAC extending into areas posterior of HG have been reported by them as well They have suggested that the entire koniocortex (corresponding to area TC) covers the same surface area in both hemispheres, and have noted that the major part of PAC consisting of true koniocortex (corresponding to area TC1) is larger on the left than on the right. Moreover, their results have shown area TC to be more elongated in the left hemisphere, stretching along the axis of HG reaching its anterolateral end. Conversely, they have argued that in the right hemisphere PAC mainly extends toward the anteroposterior direction, readily covering posterior duplications of HG, while being more limited to HG's medial portion. More recently, cytoarchitectonic studies have observed characteristic interhemispheric differences for PAC on the cellular level. For instance, Morosan et al. (2001) have reported a higher cell density in all, but the most lateral subdivision of PAC (Te1.2, which is considered a transition zone) in the left hemisphere. Furthermore, Hutsler and Gazzaniga (1996) have found greater cell size of pyramidal cells in layer III in the left as opposed to the right PAC, suggesting greater column width, which in turn could imply greater surface area. Supporting histological evidence stems from fundamental research by Seldon (1981, 1982) who investigated the functional column width of PAC and found functional units to have a greater diameter in left as opposed to right PAC. Furthermore, he described more tangential dendritic connections in left PAC, while right PAC showed preferred vertical dendritic connections. Moreover, Rademacher et al. (1993) have explicitly noted a leftward asymmetry of BA 41 (Brodmann area corresponding to PAC) in 60% of subjects, although a later study has demonstrated 44% of subjects with a leftward asymmetry of PAC, while only 26% of subjects have shown to have a rightward asymmetry (Rademacher et al., 2001). Some studies, however, have not found such asymmetries (Galaburda, Sanides, & Geschwind, 1978), or even a rightward asymmetry (Geschwind & Levitsky, 1968), even though it has been suggested that contradictory findings can be attributed to differing definitions of HG or PAC or varying methodological approaches (Abdul‐Kareem & Sluming, 2008). In addition, several MRI and postmortem studies have reported remarkable interhemispheric differences with respect to HG morphology (Campain & Minckler, 1976; Chiarello, Kacinik, Manowitz, Otto, & Leonard, 2004; Dorsaint‐Pierre et al., 2006; Galuske et al., 2000; Musiek & Reeves, 1990; Penhune et al., 1996; Penhune et al., 2003; Sigalovsky et al., 2006). However, recent studies have demonstrated that CTH and cortical surface area measurements should be considered to be independent neuroanatomical traits because CTH is distinct from cortical surface area in the contribution to cortical volume (Eyler et al., 2011; Greve et al., 2013; Meyer et al., 2014; Meyer et al., 2016; Panizzon et al., 2009; Winkler et al., 2010).

Considering postmortem analyses, there are obvious limitations. Therefore, in recent research, structural and functional MRI has been used in addition to histological investigations to optimize PAC mapping, and progress has been made here especially in generating probabilistic (Penhune et al., 1996; Rademacher et al., 2001) and tonotopic maps (Da Costa et al., 2011; Fischl & Dale, 2000; Formisano et al., 2003; Moerel et al., 2014; Schönwiesner et al., 2015). Progress in MRI technology and methods enables to measure myelin content for example, based on the R1‐relaxation rate. Recent studies in that field have shown a stronger intracortical myelination particularly within primary sensory areas such as PAC (Glasser et al., 2016; Glasser & van Essen, 2011; Shafee et al., 2015; Van Essen, Glasser, Dierker, Harwell, & Coalson, 2012; Wasserthal et al., 2014), and furthermore left‐lateralized myelination in HG suggesting a link to language function (Sigalovsky et al., 2006). In fact, the highest proportion of heavily myelinated deeper layers of the cortex has been found in the precentral and postcentral gyrus as well as in the core region of HG (Rowley et al., 2015). Thus, area‐specific differences in intracortical myelination should be considered when using novel automated methods for CTH estimation based on T1 images, as the exact GM‐WM border of the higher myelinated primary cortex may be difficult to determine within the deeper cortical layers (Glasser & van Essen, 2011). However, existing knowledge from histological studies shows primary sensory cortex to constitute relatively thin cortical regions (Brodmann, 1909; Fischl & Dale, 2000; Lyall et al., 2015), consisting of heterotypic granular koniocortex composed of extremely small cell size, even of the pyramidal cells of layer III, and a rarefied layer V (Triarhou, 2007; Von Economo & Koskinas, 1925). Furthermore, probabilistic cytoarchitectonial maps have been found to match with specific myeloarchitectural features only in the primary cortex (Dinse et al., 2015; Eickhoff et al., 2005). Considering the co‐localization between high intracortical myelination and thinner cortex estimations within primary auditory areas, as measured also by modern quantitative R1 mapping (Lutti, Dick, Sereno, & Weiskopf, 2014), it is reasonable to conclude that areas of reduced CTH within HG correspond to PAC.

Here, we observed an overall posteromedial–anterolateral CTH gradient across HG toward aSTG, showing highest CTH values toward the temporal pole, however gradually thinning out toward the PT, which has previously been shown in CTH measures by Sigalovsky et al. (2006). In particular, our CTH analysis revealed significantly reduced cortex in the central core region of HG (redAC) compared to the surrounding belt areas of subAC (CTH range of complete AC: 2.6–3.4 mm), which is in line with comparable MRI‐ and histological studies reporting a similar CTH range across the supratemporal plane (~2.4–3.3 mm; Rosas et al., 2002; Meyer et al., 2014). Furthermore, average redAC was found to localize roughly within anterior HG bilaterally, but differed markedly regarding size and location between hemispheres: In right hemispheres, redAC was confined more to mHG partially extending posteriorly toward HG duplications and PT, whereas in left hemispheres the area of redAC was spread out more toward the lateral end of HG, covering a larger HG surface area. The identified areas of reduced CTH show high correspondence with the location of PAC, backing the notion that PAC is represented by more evenly elongated, larger, and laterally displaced areas on the left, but more medially confined and smaller areas on the right hemisphere.

4.2. Functional evidence and structure–function link

Gradients of CTH across sensory cortices have been found to significantly correlate with the structural hierarchy level of sensory areas from primary to higher‐order areas and related functional processing hierarchies in both humans and macaque (Glasser et al., 2016; Wagstyl, Ronan, Goodyer, & Fletcher, 2015). The hierarchy level of sensory areas increases with and is predicted by the CTH gradient within auditory, visual, and somatosensory cortices, demonstrating primary sensory areas to be consistently thinner than surrounding higher‐order areas. Furthermore, CTH shows to follow other related gradients to hierarchies of connectivity and cytoarchitecture, while each of these measures has its own advantages also with respect to functional implications. Although sensory processing cannot easily be simplified, the related structural hierarchy is assumed to index functional hierarchies and therefore differences in hierarchical function may be reflected by inter‐individual variability in cytoarchitecture and CTH. Thus, it can be suggested that a CTH gradient, which extends from thinner primary sensory to thicker higher‐order areas, offers an additional biomarker reflecting systematic changes in cortical cytoarchitecture, structural hierarchy and related hierarchy of cortical function (Wagstyl et al., 2015). In a study searching for CTH patterns in musicians Bermudez et al. (2009) have found thicker cortex mainly in posterior supratemporal (secondary) and dorsolateral frontal regions within musicians compared to nonmusicians. Interestingly, the same study has shown thinner cortex in a number of areas including also lateral temporal (secondary) and posterodorsal frontal (higher‐order) cortices among a subgroup of absolute pitch possessors compared with nonpossessors. Further studies that performed combined structural and functional neuroimaging have reported higher functional activation in thinner cortices, for example, found in frontoparietal areas (attention network) during a written language task (Lu et al., 2009), or in supratemporal areas on the right AC (auditory core/belt) during basic auditory perception (Liem et al., 2012). Overall, these findings suggest a highly specialized and efficient neural organization in areas of reduced CTH, such as in PAC, which may provide computational power optimized for the corresponding (sensory) functions.

Our observed structural asymmetries of redAC in terms of surface area and localization were supplemented by functional correlates in the left and right AC, namely the primary auditory evoked P1 response. Compared to fMRI, the source localization of electrophysiological data is usually rather variable and is largely dependent on the method used, although this method is reliable within individuals. In marked contrast to EEG, MEG provides a suitable spatial resolution for source localization of primary responses (Scherg, 1990). Here, we used a well‐established MEG stimulation protocol where the P1 source waveforms were modeled from grand‐averaged sensor responses including more than 1,000 single events and robustly localized in the region of PAC (Schneider et al., 2005; Seither‐Preisler et al., 2014; Serrallach et al., 2016). It should be noted that not all MEG localization parameters were normally distributed in the present study and therefore nonparametric statistics were computed (see section 2). Importantly, co‐localization of structural (centAC) and functional (P1) spatial coordinates was specifically observed when spatiotemporal source modeling was applied to separate the early primary responses from later secondary MEG components (as opposed to probing the localization of the average MEG dipoles, representing the sum of primary and secondary responses).

Our demonstrated hemispheric asymmetries in the localization of P1 are consistent with the previously reported bilateral asynchrony of the primary auditory response in children (Seither‐Preisler et al., 2014), while adult musical experts show a more balanced, symmetric localization of the primary auditory fields (Schneider et al., 2005). Moreover, the lateralization demonstrated for the location of PAC reflects the complementary organization of left and right AC, resulting in a variety of functional asymmetries such as spatial and temporal processing (Zatorre & Belin, 2001), rapid and slow speech segments (Meyer, Elmer, & Jäncke, 2012; Poeppel, 2003), spectral and fundamental pitch perception (Schneider et al., 2005), and encoding of music and speech (Tervaniemi & Hugdahl, 2003; Zatorre, Belin, & Penhune, 2002; Zatorre & Gandour, 2008). Recent fMRI studies aimed at localizing PAC by mapping its tonotopy in response to pure tones and thus have demonstrated that PAC is located within HG (Da Costa et al., 2011; Formisano et al., 2003; Humphries, Liebenthal, & Binder, 2010; Langers & van Dijk, 2012; Moerel et al., 2014; Saenz & Langers, 2014; Schönwiesner et al., 2015; Van Dijk & Langers, 2013). Furthermore, studies by Yoo et al. (2005) and Devlin et al. (2003) both have reported increased BOLD‐responses of left PAC as opposed to right PAC. Repeated MRI measurements have isolated a predominant leftward functional asymmetry in PAC during both linguistic and simple tonal stimulations (Yoo et al., 2005), while increased BOLD‐responses to monaurally presented tones in the left PAC have found to be independent of which ear the sound was presented to (Devlin et al., 2003). The functional asymmetry of PAC observed in these studies is in line with our results demonstrating a greater surface area of redAC, presumably PAC, in the left hemisphere in relation to corresponding P1 localizations.

4.3. Inter‐individual variability

The gross morphology of HG demonstrates a remarkably high inter‐individual structural variability (Campain & Minckler, 1976; Schneider et al., 2002, 2005; Golestani, Molko, Dehaene, Le Bihan, & Pallier, 2007; Golestani, Price, & Scott, 2011; Seither‐Preisler et al., 2014; Marie et al., 2015, 2016; Turker et al., 2017) which is linked to specific functional extensions of AC, particularly in cases of pronounced HG duplications (Wengenroth et al., 2010, 2014; Serrallach et al., 2016; Benner et al., 2017). Here we observed a likewise high inter‐individual variability of CTH across HG, showing that redAC was not always confined to mHG, but varied considerably with respect to size, localization, and anterolateral extension. This observation is consistent with the variability of PAC localization across HG, which has previously been reported by cytoarchitectonic studies (Hackett et al., 2001; Rademacher et al., 2001; Von Economo & Horn, 1930). Particularly, individual analysis showed markedly thinner regions in subjects with CSDs and CPDs to be limited more to the anterior portion of HG. Although PAC is roughly limited to HG, it can extend further posteriorly toward PT or anteriorly into the planum polare, which is also backed by functional evidence using MEG (Benner et al., 2017; Wengenroth et al., 2014) and fMRI (Da Costa et al., 2011).

4.4. Age‐related effects

Comparing the results of children and adults, we found broad consistency across the groups with respect to average localization, shape, extension, lateralization, and overall variability of the measured CTH values across HG. However, on average, CTH was slightly reduced in adults compared with children showing 0.17 mm thicker cortex within HG. We further observed enhanced CTH in the right AC of the children compared to the left side, suggesting that maturation processes may develop faster in the right temporal lobe. Accordingly, recent structural neuroimaging studies have observed faster maturation of the right superior temporal regions during early childhood (Leroy et al., 2015). Furthermore, elementary school children exhibit a developmental advantage in the right hemisphere, as reflected by faster auditory processing of the primary auditory response (Seither‐Preisler et al., 2014). Particularly, children with developmental and learning disorders (AD[H]D, Dyslexia, Williams–Beuren syndrome) show a systematic left‐hemispheric delay of 10–40 ms in the primary auditory response (Serrallach et al., 2016; Wengenroth et al., 2010). Interestingly, musically experienced subjects demonstrate a remarkable synchronization of the left and right auditory responses, indicating an efficient interplay between the hemispheres (Seither‐Preisler et al., 2014; Serrallach et al., 2016).

The more evenly interhemispheric CTH distribution in adults indicates a stronger balance of GM density between hemispheres. These age‐related group differences are in accordance with the general observation that GM density of the temporal cortex increases until adolescence (Shaw et al., 2008; Sowell et al., 2004), reaching a plateau at the age of ~17 years (Giedd et al., 1999) and decreases during adulthood (Vandekar et al., 2015). Effects of locally different cortical thinning and thickening during youth and adolescence have also found to be related to the local cortical topology (Thompson, 1900; Von Economo & Koskinas, 1925; Vandekar et al., 2015). Moreover, changes in WM architecture during cortical maturation seem to spatially be associated with a decline in CTH with age (Vandekar et al., 2015). Thus, maturational changes in WM structure might be related to differences in CTH across the gyral topology. Although WM development and associated myelination changes are supposed to have an impact on the thickness of neocortex, the regional cortical development might be descriptive of WM development only to a moderate degree. In a structural MRI study with 168 healthy subjects between 8 and 30 years, Tamnes and colleagues have found regional age‐related effects of cortical thinning, an increase in WM volume, and also changes in diffusion parameters in major tracts. They have shown that age‐related changes may occur generally in cortex and WM microstructure regions. However, they have reported relatively little cortical thinning in the temporal and frontal lobes during development and their results do not indicate a regionally tightly linked pattern of age‐related changes in CTH and underlying WM properties. Therefore, they have concluded that cortical thinning in adolescence cannot fully be explained by WM maturation in adjacent areas. This finding may implicate that proliferation of myelin into the periphery of cortical neuropil is not likely to be the sole factor accounting for the observed effects of cortical thinning during adolescence (Tamnes et al., 2010).

At the functional level, auditory evoked fields as measured by EEG and/or MEG show distinct maturational and learning‐induced changes in the course of AC development from early infancy to adolescence (Dehaene‐Lambertz & Spelke, 2015; Kral & Sharma, 2012; Meyer et al., 2011; Ponton et al., 2002; Serrallach et al., 2016; Sharma et al., 2005; Sharma, Nash, & Dorman, 2009). In particular, later secondary N1 and P2 responses just start to develop at elementary school age (Seither‐Preisler et al., 2014). Nevertheless, from that age on, primary auditory evoked fields can clearly be identified and separated from the later N1 and P2 responses. The electrophysiological response timing patterns and magnitudes depend on musical aptitude, specific auditory skills, and furthermore the presence of certain auditory processing disorders (Schneider et al., 2002; Serrallach et al., 2016; Wengenroth et al., 2014).

5. CONCLUSION

By performing MEG and CTH analyses in two independent samples of 60 children and 60 adults, we were able to investigate age‐related characteristics of gross‐morphological structural markers in AC. As expected, areas of redAC were found within HG, corroborating the general consensus of PAC localization. However, areas of redAC were more confined to the medial two‐thirds of HG in the right hemisphere, while covering a greater surface area and stretching further laterally along the extent of HG in the left hemisphere. The observed interhemispheric differences confirm previous evidence on the functional, cytoarchitectonic, and cellular level. Particularly, the asymmetric localization of redAC may originate from increased column width, cell size, and density generally found in PAC in the left hemisphere. The presented structure–function link between primary auditory evoked responses and centAC surpasses the attempts of earlier studies and corroborates the idea to use CTH measures to identify primary sensory areas. Finally, a large inter‐Individual variability was observed with respect to the extent, shape, and localization of redAC. As children and adults showed similar localization and lateralization of regions of reduced CTH along left and right HG, we propose redAC to be a suitable in vivo marker of PAC in humans. This structural marker is strongly supported by the functional results of the primary auditory evoked fields. Furthermore, PAC shows remarkable differences in extent and localization between hemispheres. Future research should aim at improving the methodological approach on the whole‐brain level to account for age‐related specificities, maturational influences, and possible sex differences.

AUTHOR CONTRIBUTIONS

Data acquisition and data analysis: SZ, JB, BZ, and PS. Study design, data interpretation, and writing of the manuscript: SZ, JB, MB, MW, MC, and PS. Statistical analyses with SPSS: ASP and MC. Providing tool and methodology for data acquisition and data analysis: JB, AH and RG. Medical assistance: AS. All authors discussed the results and implications and commented on the manuscript.

CONFLICT OF INTEREST

The authors declare no competing financial interests.

Zoellner S, Benner J, Zeidler B, et al. Reduced cortical thickness in Heschl's gyrus as an in vivo marker for human primary auditory cortex. Hum Brain Mapp. 2019;40:1139–1154. 10.1002/hbm.24434