Discriminating between neurofibromatosis‐1 and typically developing children by means of multimodal MRI and multivariate analyses

Abstract

Neurofibromatosis Type 1 leads to brain anomalies involving both gray and white matter. The extent and granularity of these anomalies, together with their possible impact on brain activity, is still unknown. In this multicentric cross‐sectional study we submitted a sample of 42 typically developing and 38 neurofibromatosis‐1 children to a multimodal MRI assessment including T1, diffusion weighted and resting state functional sequences. We used a pipeline involving several features selection steps coupled with multivariate statistical analysis (supporting vector machine) to discriminate between the two groups while having interpretable models. We used MRI indexes measuring macro (gray matter volume) and microstructural (fractional anisotropy, mean diffusivity) characteristics of the brain, as well as indexes of brain activity (fractional amplitude of low frequency fluctuations) and connectivity (local and global correlation) at rest. We found that structural indexes could discriminate between the two groups, with the mean diffusivity leading to performance as high as the combination of all structural indexes combined (accuracy = 0.86), while functional indexes had worse performances. The MRI signature of NF1 brain pathology is a combination of gray and white matter abnormalities, as measured with gray matter volume, fractional anisotropy, and mean diffusivity.

1. INTRODUCTION

Neurofibromatosis type 1 (NF1) is an autosomal dominant genetic disorder. It is one of the most common genetic disorder, with a prevalence of 1 in 3,500 (Kayl & Moore, 2000). NF1 is a neurocutaneous disorder due to the dysregulation in the production of the protein neurofibromin, which is implicated in synaptic plasticity and thus memory and learning (Johnston, 2004).

From a cognitive viewpoint, children with NF1 can show impairment in executive functions including attention and working memory (Schwetye & Gutmann, 2014), in phonological processing (Chaix et al., 2018), in visuo‐spatial abilities (Hyman, Shores, & North, 2005) and social cognition (Chisholm et al., 2018). Together with cognitive impairment, children with NF1 show several intracranial manifestations, as macrocephaly, corpus callosum enlargement, and nontumorous deep gray and white matter changes (Dubovsky et al., 2001; North, 2000). One of the most striking intracranial manifestation in NF1 are the so‐called “unidentified bright objects” (UBO), region of hyperintensities visible in T2‐weighted (and partially T1‐weighted) MRI images, mostly observed in the cerebellum, brain stem, thalamus and basal ganglia of children and adolescents affected by NF1 (DeBella, Poskitt, Szudek, & Friedman, 2000; National Institutes of Health Consensus Development Conference., 1988; Sevick et al., 1992).

In recent years, several studies have tried to uncover the neural signature of this pathology with the view to extend knowledge beyond the macroscopic brain differences between NF1 and healthy children as obtained from visual assessment of MRI imaging. As regards gray matter, it has been reported greater volume in several subcortical regions (i.e., thalamus, putamen, pallidum, hippocampus, caudate, amygdala, and accumbens) and lower volume in an extended fronto‐parieto‐temporal network (Huijbregts et al., 2015) and specifically in the superior temporal gyrus (Pride et al., 2014) in NF1 subjects compared to controls. However, morphometric differences between NF1 and typically developing children have not always been found using canonical univariate analyses (Duarte et al., 2014). White matter abnormalities in NF1 have also been inquired, using both T1 and DWI derived indexes. Concerning WM morphometry, the most consistent finding is an increase in the volume of the corpus callosum (Cutting et al., 2002; Duarte et al., 2014; Dubovsky et al., 2001; Kayl, Moore, Slopis, Jackson, & Leeds, 2000), whose microstructure also demonstrates abnormalities as inquired by DWI (Wignall et al., 2010; Zamboni, Loenneker, Boltshauser, Martin, & Il'yasov, 2007). See (Payne, Moharir, Webster, & North, 2010) for a complete review of structural finding in NF1 subjects. Studies using DWI to inquire NF1 subjects white matter microstructure chiefly used a region of interest approach, focusing on the corpus callosum and other specific tracts (e.g., Koini, Rombouts, Veer, Van Buchem, & Huijbregts, 2017), thus using a model‐driven approach that may have led to miss important characteristic of NF1 pathology. DWI has also been used to study the microstructural basis of the UBOs, showing that UBOs have increased axial, radial, and mean diffusivity, as well as reduced fractional anisotropy, suggesting altered microstructural compartmentalization, rather than demyelination and axonal degeneration (Billiet et al., 2014).

Beyond the structure and microstructure of GM and WM, several studies have focused on functional abnormalities in NF1 subjects using electroencephalography (EEG), positron emission tomography (PET), and task‐related and resting‐state fMRI. As for EEG, it has been shown that NF1 children differ from matched controls during low level visual processing in term of alpha oscillation amplitude in the parieto‐occipital cortex (Ribeiro et al., 2014). EEG also highlighted differences between NF1 and controls during higher level attentional task as flanker task (Bluschke et al., 2017) and covert attentional task (Silva et al., 2016). As for fMRI, NF1 children showed reduced activation in a set of area within the salience network (i.e., inferior occipital gyrus, fusiform gyrus/posterior cerebellum, pre‐SMA and inferior frontal gyrus) during a GO–NO GO task (Pride, Korgaonkar, North, Barton, & Payne, 2017). NF1 children also show reduced recruitment of key brain areas related to working memory (i.e., dorsolateral prefrontal cortex and posterior parietal cortex) as well as atypical task‐related connectivity during a working memory task (Ibrahim et al., 2017). Other studies have observed reduced deactivation of the default mode network (DMN) in NF1 subjects relative to controls during low level visual stimulation (Violante et al., 2012a) or spatial working memory task (Ibrahim et al., 2017). Interestingly, a previous clinical study showed that the drug lovastatin, that ameliorate cognitive symptoms in NF1 patients, increase long range connectivity within the regions of the DMN. Finally, Tomson et al. (2015), have shown abnormal network‐related measures in the connectome of children affected by NF1 using graph‐theory.

A handful of studies have used multimodal imaging to elucidate specific hypothesis about the physiopathology of NF1. For example, Violante et al. (2016) combined magnetic resonance spectroscopy (MRS) and [(11)C]‐flumazenil (a GABAA receptors radio tracer) and find lower GABA+ and reduced GABAA receptor binding in adult NF1 compared to controls. The same group combined high‐density EEG during a GO/NO GO task and MRS to study the relationship between the GABAergic system, neurophysiology and impulsivity in NF1. They confirmed reduced GABA+ in the medial frontal and occipital cortex and found an abnormal correlation between GABA+ level in the medial frontal cortex and response style in the GO/NO GO task relative to controls (Ribeiro et al., 2015). This same group also combined a rhythmic motor task with EEG and fMRI finding behavioral, oscillatory and brain activation (i.e., greater recruitment of extra‐pyramidal system) differences between NF1 adults and matched controls (Silva et al., 2018). Although these previous multimodal studies improved our knowledge of NF1 physiopathology they were limited in their scope by the specific hypothesis they were testing, or by methodological limitation (MRS can be performed only with an ROI approach) or by using a specific cognitive task. On the other hand, multimodal MRI protocols, including acquisitions sensitive to different and complementary tissue characteristics, can be used to help finding the “imaging signature” of a disease, that is, the set of diffuse and subtle alterations that are bound to be present in a neurological condition, without using any a priori ROIs. The statistical approach to make best use of the complementary information provided by multimodal MRI imaging are multivariate analyses. This type of analyses allows for the identification of subtle and diffuse cerebral alterations that may attain different tissues, while taking into account the interdependency between these alterations. The idea of using multivariate analyses to observe subtle differences between NF1 patients and healthy controls has already been considered by Duarte et al. (2014) who used supporting vector machine to discriminate between NF1 children and adults and their healthy counterparts. Although the authors reach a very high classification accuracy, this study only used T1‐related GM and WM volumes as features, limiting the insight to the macrostructural alteration present in NF1 patients. We used a multimodal MRI acquisition protocol including T1‐weighted, diffusion weighted, and resting state functional MRI, coupled with state‐of‐the‐art machine learning approach (Meng et al., 2017) to discriminate between NF1 and healthy children and uncover the multimodal signature of NF1. Our method relies heavily on data‐driven features reduction to find the model that best discriminate between the two groups while retaining the minimum number of features, in order to have more interpretable model. In turn, having an interpretable model can improve our knowledge and foster a better understanding of the core NF1 pathophysiology.

2. MATERIALS AND METHODS

2.1. Subjects

The study was cross‐sectional and performed as a collaboration between two French national NF1 referral centers in Toulouse and Aix‐Marseille. The study was systematically proposed to all children who had been diagnosed with NF1 in accordance with the Neurofibromatosis Conference statement (1988), and who were between 8 and 12 years old. All children included were right‐handed. The group of children with NF1 was compared with a group of typically developing children (TD). All the children were examined by a neuropediatrician, and the absence of “café au lait” spots and other symptoms of NF1 was assumed to exclude an NF1 diagnosis for children in the TD group. In both groups, children with a known neurological or psychiatric disorder (epilepsy, brain tumor as known symptomatic glioma, autism) or uncorrectable hearing or visual impairment were excluded. Included children did not have any sign of mental retardation (WISC total IQ superior to 70 or/and subtest Similarities and Picture concepts scaled scores superior to 7). Children with suspicion of attention deficit hyperactivity disorder (ADHD) were excluded from the study as assessed through parent and clinician ratings on the DSM‐V diagnostic criteria for ADHD (< six inattention and six hyperactive/impulsive symptoms). Following this inclusion and exclusion criteria we included 80 children: 42 TD (21 in Toulouse and 21 in Marseille) and 38 NF1 (21 in Toulouse and 17 in Marseille).

The study was approved by the local ethics committees (CPP) in Toulouse and Aix‐Marseille and was conducted in accordance with the Declaration of Helsinki. We obtained written informed consent from the parents and their children.

2.2. MRI acquisition

Toulouse: MRI images were acquired using a Philips Achieva dStream 3.0 T MRI scanner equipped with a 32‐channel head coil.

Rs‐fMRI: echo planar imaging (EPI) sequence. Time repetition (TR)/time echo (TE) = 3,000/40 ms, flip angle (FA) = 90°, field of view (FOV) = 240 mm, matrix = 80 × 80, voxel size = 3.0 × 3.0 × 3.0 mm, 46 axial slices. Each scan session was 600 s long and included 200 volumes.

T1‐weighted images: fast field echo (FFE). TR/TE = 8.1/3.7 ms, FOV = 240 mm, matrix = 240 × 240 × 170, voxel size = 1 × 1 × 1 mm, 170 sagittal slices.

DWI: TR/TE = 9146/92, voxel size = 2 × 2 × 2 mm, 34 noncollinear directions, b = 0/1,000, matrix = 112 × 112.

Fluid attenuated inversion recovery: TR/TE = 3,054/50, FOV 240 mm, in‐plane resolution = 1 × 0.1 mm, slice thickness = 2 mm, matrix = 240 × 240.

Marseille: MRI images were acquired using a Siemens Magnetom Skyra 3.0 T MRI scanner equipped with a 32‐channel head coil.

Rs‐fMRI: EPI sequence. TR/TE = 2,540/30 ms, FA = 90°, FOV = 192 mm, matrix = 64 × 64, voxel size = 3.0 × 3.0 × 3.0 mm, 45 axial slices. Each scan session was 635 s long and included 250 volumes.

T1‐weighted images: MPRAGE. TR/TE = 1,900/2.5 ms, FOV = 230 mm, matrix = 256 × 158 × 192, voxel size = 0.9 × 0.9 × 0.9 mm.

DWI: TR/TE = 9,400/89, voxel size = 2 × 2 × 2, 30 noncollinear directions, b = 0/1,000, matrix = 128 × 128.

Fluid attenuated inversion recovery: TR/TE = 8,370/104, FOV 240 mm, in‐plane resolution = 0.75 × 0.75, slice thickness = 4 mm, matrix = 320 × 320.

2.3. Images preprocessing

2.3.1. T1 images

T1 images were segmented in gray matter and white matter volume map using CAT12 (http://www.neuro.uni-jena.de/cat/; Gaser & Dahnke, 2016). This toolbox is an improvement over the VBM8 toolbox: briefly, the tissue probability maps are only used in a first (affine) registration step, the actual segmentation being performed using an adaptive MAP approach with local adaptation of local intensity changes to deal with varying tissue contrast (Dahnke, Ziegler, & Gaser, 2012; Gaser & Dahnke, 2016). The final normalization is performed using DARTEL (Ashburner, 2007). The gray matter tissue maps were modulated using the determinant of the Jacobian (linear and nonlinear component, thus allowing to observe absolute tissue volume). CAT12 also outputs an estimate of the TIV for each subject as a sum of the volume of the gray matter, white matter, and cerebrospinal fluid. This value was used to compare brain volume between groups and to correct structural imaging data for TIV. Note that modulated gm volume maps were corrected for total intracranial volume (TIV) by taking the residuals of a linear model with gm volume at each voxel as dependent variable and TIV as independent variable. This ensures that any gm cluster discriminating between NF1 and TD does so over and beyond the global effect of head/brain size. CAT12 also includes an automatic quality assessment (QA) for each segmented image, providing a normalized QA value on a continuous scale that consider resolution, bias and noise present in the images. This value is then transformed in a note from A to E, with images with note lower than D usually discarded from the analysis. None of our subjects had a QA note lower than D.

2.3.2. Resting state images

rs‐fMRI data were analyzed using the conn toolbox (Whitfield‐Gabrieli & Nieto‐Castanon, 2012). Briefly, all images were time‐slicing corrected, unwarped and realigned to the first volume and normalized to the standard EPI template provided with SPM12 (Friston et al., 2007). We used three smoothing levels for EPI images: no smoothing, 4 mm FWHM smoothing and 8 mm FWHM smoothing (see Section 2.3.4). We also used the art toolbox (http://nitrc.org/projects/artifact_detect/) to detect corrupted volumes, defined as volume with more than 2 mm movement in any direction or a root mean squared change in bold signal from volume to volume greater than 9. Noise correction was performed using aCompCor (Behzadi, Restom, Liau, & Liu, 2007), that regresses out from the functional time‐series the first two principal components of the time‐series extracted from white matter and CSF. Moreover, six movement regressors calculated during realignment plus their time derivatives and their quadratic values were regressed out from the BOLD time‐series. Volumes deemed corrupted were also regressed out. No subjects showed a mean framewise displacement greater than 2 mm. Note that the CONN preprocessing pipeline outputs QA measurement that can be accounted for in statistical analyses for group comparison purpose. From these variables we retained the mean movement and the mean global signal change for each subject and used them to test for possible differences in fMRI acquisition quality between the two groups.

After preprocessing and denoising we calculated the fraction of amplitude of low frequency fluctuations (fALFF). fALFF measures the proportion of the power of each frequency at the low‐frequency range (0.01–0.08 Hz) to that of the entire frequency range (0–0.25 Hz), thus providing a normalized quantity that it is thought to reflect local activity at rest (Zou et al., 2008). We also calculated two basic indexes of brain connectivity at rest: local and global correlation. The former is the average correlation of each voxels with its 18 neighbors while the latter is the average correlation of each voxel with every other voxel in the brain. They can be roughly taken as index of segregation and integration within the brain. Note that the fALFF, local correlation, and global correlation maps are calculated using smoothed images and thus are intrinsically smoothed at the same size as input images (i.e., no smooth, 4 mm, and 8 mm, see Section 2.3.4).

2.3.3. Diffusion weighted images

DWI were processed using fsl 5.0 (Mark Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012). In particular, DWI images were corrected for eddy current and realigned using eddy_correct, then a standard tensor model was fit to each images in order to calculate fractional anisotropy (FA) and mean diffusivity (MD; Behrens et al., 2003). FA images were nonlinearly normalized onto the standard FA template provided with FSL using FLIRT (M Jenkinson & Smith, 2001) for the affine registration and FNIRT for the nonlinear registration (Anderson, Jenkinson, & Smith, 2010). As QA variables we calculated the average between volumes frame displacement and the between volume mean global signal change (measured with DVARS) in order to test for DWI quality differences between the two groups.

2.3.4. Smoothing

Studies on the effect of spatial smoothing on the performance of multivariate analyses of structural and functional MRI data have led to contrasting results finding better accuracy for smoothed data (Monté‐Rubio et al., 2018), worse accuracy for data smoothed at larger kernel (Misaki, Luh, & Bandettini, 2013) or an insensitivity to preprocessing choices, including smoothing (Laconte et al., 2005). In the light of these conflicting evidences, we decided to use different levels of smoothing for our analyses: no smoothing, smoothing with a 4 mm FWHM Gaussian kernel, and smoothing with an 8 mm FWHM Gaussian kernel. The results from the three smoothing levels were qualitatively comparable (although with better performance for no smoothing). We report the results of the analysis performed with unsmoothed images in the main text of the manuscript, and the results of 4 mm and 8 mm smoothing in Supporting Information (for images smoothed with 8 mm FWHM see supplementary analyses—8 mm smoothing, pages 3–10 and Figures S3–S8; for images smoothed with 4 mm FWHM see supplementary analyses—4 mm, pages 11–15 and Figures S9–S14).

2.4. Machine learning pipeline

The machine learning pipeline consisted of several features selection and reduction steps detailed below.

2.4.1. Matrix reshaping and range normalization

Separately for each modality, images were reshaped from 3D matrix to 2D matrix with subjects × voxels dimensions after being masked for the relevant mask (i.e., a liberal gray matter mask for gm fALFF, local correlation and global correlation, and white matter for FA and MD). These matrices were then normalized so that the values were comprised between 0 and 1. Before entering the pipeline, we removed variance related to TIV and centers of acquisition from the gray matter, FA and MD features. We also removed mean framewise displacement and mean global signal variation from fALFF, local correlation, and global correlation features. This was achieved by taking the residual of a linear model having the features values at each voxel as dependent variable and the nuisance variables as independent variables. In Supporting Information we report the results of a similar procedure (i.e., removing of nuisance variables) but without centers, to inquire a possible effect of the center of acquisition on the discrimination accuracy (see Table S1 for unsmoothed images, Table S3 for images smoothed with 8 mm FWHM kernel, and Table S5 for images smoothed with 4 mm FWHM kernel). Briefly, there were no differences between the two approaches.

2.4.2. Variance thresholding

Similarly to (Meng et al., 2017) we reasoned that features with only minor variation among subjects (i.e., with a low variance) would not be useful to separate different group. For this reason, we adopted a simple variance features reduction step in which, for each modality, we eliminated the 25% of features with the lowest variance. This step can be considered conceptually similar to the one described by (Wilhelm‐Benartzi et al., 2013) and a more liberal version adapted to classification problem of the one proposed in (Meng et al., 2017).

2.4.3. Relieff based features selection

Relieff (Kira & Rendell, 1992; Kononenko, Šimec, & Robnik‐Šikonja, 1997) is a features selection algorithm that is widely used in the machine learning literature. It estimates a weight for each feature by comparing, for each case, the distance of the closest intra and interclass cases in that feature space and increasing the weight if the distance is greater for the interclass than for the intraclass case. For each modality, we submitted the features surviving the variance threshold to the Relieff algorithm (as implemented in the CORElearn package for R (Robnik‐Sikonja & Savicky, 2017)). In order to select the most relevant features we use a scree test approach (Mori, Hasegawa, Suenaga, & Toriwaki, 2000) as implemented in (Meng et al., 2017). We calculated the selection threshold as the first minimum of the second derivative of the sorted (in decreasing order) and smoothed (via a loess regression (Cleveland, Grosse, & Shyu, 1992)) Relieff weights. This is equivalent to find the point at which the speed of the function approach to zero (i.e., the Relieff weight values drop dramatically). Note that the smoothing applied in this step is not in brain space, but in features space (i.e., the 2D sorted weights) and is applied only for easiness of calculation of the second derivatives. It influences the features weights but not the features values. Only features with a weight exceeding the threshold were retained.

2.4.4. Spatial clustering of the features

Features from brain imaging are intrinsically nonindependent. This is partially due to the smoothing applied to the images, but it is above all related to the fact that voxels that lie close usually belong to the same anatomical/functional region. In the light of this, spatially cluster features (i.e., voxels) that are close to each other is an effective and meaningful way of reducing the number of features. For each modality, we submitted the features surviving the Relieff threshold to a spatial clustering algorithm: contiguous voxels were assigned the same cluster (this step was performed using the spatstat package in R (Baddeley, Rubak, & Turner, 2015)). Finally, we extracted the average signal for each cluster, thus effectively reducing the number of features for each modality from hundreds to tens.

2.4.5. Merging of modalities and subset selection

After the spatial clustering step, we merged all the modalities in one matrix (having dimensions [subjects] × [N of clusters from all modalities]. Even after Relieff selection and spatial clustering, some clusters may be not very informative, and some clusters may convey redundant information (e.g., spatially overlapping low FA and high MD may actually capture similar characteristics of the white matter). For this reason, we performed subset selection based on correlation. This selection step is aimed to find the subset of features (i.e., clusters in the case at hand) that maximizes the predictive power relative to the outcome while minimizing redundancy among clusters (measured as collinearity) (Kohavi & John, 1997; Tripoliti, Fotiadis, Argyropoulou, & Manis, 2010). The subset selection was performed using the select.cfs function (Wang et al., 2005) of the Biocomb package (Novoselova, Wang, Pessler, & Klawonn, 2017). The outcome of this step is a subset of clusters in the order of tens (or lower): the low number of clusters help the interpretability of the model while maximizing the discriminative power.

2.4.6. Fitting of the model

Finally, the model was fitted using the sequential minimal optimization (SMO) algorithm (Platt, 1998; Schölkopf & Smola, 2002) with a polynomial kernel. The model was fitted using the RWeka package (Hornik, Buchta, & Zeileis, 2009), a wrapper of the java‐based software Weka (Witten, Ian, Frank, Hall, & Mark, 2011). The free parameters of the SMO algorithm are the order of the polynomial and the lambda (i.e., allowed error). We left these parameters to the default value of, respectively, 5 and 10.

2.4.7. Cross validation scheme

We adopted a 10‐fold full cross‐validation scheme. This means that each step in the machine learning pipeline (except for the images reshaping and range normalization) were performed within the cross‐validation framework. At each iteration, we divided our sample in a 90% training sample and a 10% testing sample. The feature selection and reduction steps were carried out using the training sample. Similarly, the SMO model was fitted using only the training set. Then we used the clusters found in the training sample as features for the test sample and fitted the model using only the test sample. This procedure was repeated 10 times and the predicted values for each fold were stacked to have a prediction for each subject in the sample. We then calculated accuracy and balanced accuracy (i.e., the average of sensitivity and specificity, to account for the unbalanced sample) for the stacked predictions. We repeated the whole cross validation Scheme 10 times, using 10 different folding, in order to have an estimate of the variability of the performance. For each model, we report the average accuracy, specificity, and sensitivity over the 10 CV repetitions, as well as the range of p‐values obtained and the median p‐value across the 10 repetitions.

We used the variability between folds (i.e., different training samples) to assess the discriminant power of the features (i.e., voxels): we counted, for each voxel, the number of folds that was selected by the pipeline over the 100 total folds (i.e., 10 folds times 10 repetitions). Throughout the figures in this article, voxels are color‐coded according to the number of folds they have been chosen.

2.4.8. Modalities included

We started by fitting a model including each modality at a time. Then, in the light of the results of the single modality, we combined all the structural modalities (i.e., GM, FA, and MD, “structural model” hereafter) and the structural modalities plus local correlation (“complete model” hereafter).

2.5. Statistical analysis

We compared sex distribution between groups by means of a fisher exact test. TIV was normally distributed and we compared it between groups by means of a two‐sample t‐test. Age, rs‐fMRI mean movement, rs‐fMRI mean global signal change, DWI mean movement, DWI mean global signal change, and QA evaluation from CAT12 were non‐normally distributed and were compared using Wilcoxon rank signed tests. If QA variables for a certain modality were found to differ between the two groups, the variance related to those variables were removed from the relevant modality before fitting the discriminant model.

Following (Combrisson & Jerbi, 2015) we used binomial cumulative distribution testing in order to assess the statistical significance of the classification pipelines. Briefly, classical binomial testing relies on the assumption that the theoretical chance level in a classification task is $\frac{1}{c}$ where c is the number of classes. However, this is only true when the number of observations is (or approach to) infinite. Whenever we are dealing with a sample of finite amount, the chance level depends on the sample size. One way of taking this into account is to assume that the classification error follows a binomial cumulative distribution and calculate the number of correctly classified observations that allows to say that the classification accuracy depart from chance with an α level of certitude. This can be achieved using the binomial cumulative distribution function as follow Observation Correctly Classified(α) = binomial CDF (1 − α, n, chance level), where α is the desired statistical threshold, n is the sample size and chance level is the probability to correctly classify an observation at random. We used the qbinom function in R to calculate the binomial cumulative distribution function, testing five statistical thresholds (0.95, 0.99, 0.999, 0.9999, 0.99999). Unlike (Combrisson & Jerbi, 2015) study, we had an unbalanced sample, so instead of a chance level of 0.5 we used a chance level of $\frac{\text{most represented class}}{n}$ (i.e., 0.525). The reason to choose this chance level is that with unbalanced classes, the best expected random model is a model that simply classifies all observations as members of the most represented class. Combrisson (Combrisson & Jerbi, 2015) has shown that the binomial cumulative distribution function method yields similar results as permutations method, even if this latter is slightly more conservative for small sample. For each model we report the range of p values and their median calculated over the 10 repetitions.

To ascertain that the correct classification of subjects was independent from the center of acquisition we performed a X square test for each discriminant model comparing the distribution of correct and incorrect classified subjects within each center with the null distribution.

In order to gain insights about the nature of the differences between NF1 and TD children found using the SMO algorithm we extracted the relevant values from the modality‐specific clusters that appeared in more than 50 folds and compared them using independent sample t‐tests while accounting for multiple comparisons within each modality using Bonferroni correction.

2.6. Unidentified bright object segmentation

We wanted to have empirical evidence of how much UBOs were responsible for the discriminative power of our models. To this aim one of the author (FN) manually segmented the UBO on the FLAIR images of the NF1 patients. These segmentations were subsequently normalized onto the MNI 152 template using a combination of linear (T2 toward T1, T1 toward template) registration using FLIRT (Jenkinson & Smith, 2001). An overlap map was calculated where each voxel has a value equal to the ratio of the number of NF1 subjects having UBOs at that voxel to the total number of NF1 subjects having UBOs. We binarized the overlap map and measured the degree of overlap with the clusters resulting from the multivariate pipelines by means of the Jaccard index (i.e., $\frac{A\cap B}{A\cup B},\mathrm{it}\mathrm{can}$ take value from 0 to 1). We also registered the presence of UBOs as a categorical variable (present/absent) and performed a Fisher exact test to ascertain whether or not there was a relationship between being correctly classified and the presence of UBOs. In Supporting Information we report the results of a supporting analysis performed removing all voxels in which at least one individual had an UBO (see Table S2 for unsmoothed images, Table S4 for images smoothed with 8 mm FWHM kernel and Table S6 for images smoothed with 4 mm FWHM kernel). Briefly, the results were roughly the same.

3. RESULTS

3.1. Demographic variables

We included 42 TD and 38 NF1 children. Neither age (TD = 121 ± 13.9 months old, NF1 = 116 ± 16.5 months old, t = −1.79, p = .09) nor sex distribution (TD = 22 F/20 M; NF1 = 15 F/23 M, odds ratio = 0.60, p = .27) differed between the two groups. The TIV differed between groups: TD = 1,489.4 ± 134.26 mm³; NF1 = 1,587.32 ± 141.75 mm³, t = −3.16, p = .002.

3.2. QA MRI variables

The QA measures from the T1 structural images were comparable between groups (TD [median ± IQR] = 84.9 ± 3.60; NF1 = 85.5 ± 3.27, W = 847, p = .64). Similarly, mean framewise displacement and global signal were comparable between the two groups for DWI images (displacement: TD (median ± IQR) = 0.98 ± 0.40 mm; NF1 = 1.1 ± 0.75 mm, W = 821, p = .83; global signal change: TD (median ± IQR) = 199 ± 24; NF1 = 207 ± 18.4, W = 919, p = .24). On the other hand, there were group differences for the mean framewise motion displacement (TD (median) = 0.16 ± (IQR) .23 mm; NF1 = 0.24 ± 0.37 mm, W = 588, p = .043) and mean global signal variation (TD (median) = 0.87 ± (IQR) 0.15; NF1 = 1 ± 0.36, W = 539, p = .013) from rs‐fMRI. Thus, we decided to treat the TIV, the mean framewise motion displacement, the mean global signal variation from rs‐fMRI and the site of acquisition (Toulouse/Aix‐Marseille) as nuisance variables. Specifically, before entering the data in the pipeline, we removed from the relevant modalities the variance related to the nuisance variables by taking the residuals of a linear model with value at each voxel as dependent variable and the nuisance variables as independent variables.

3.3. UBO

We identified UBOs in 18 out of 38 NF1 children included in the study, 11 (out of 21) acquired in Toulouse and 7 (out of 18) acquired in Marseille. There was no difference in the distribution of children with and without UBOs in the two sites (odds ratio = 0.64, p = .53). Figure 1 report the frequency of occurrence of UBO for each voxel within the children with UBOs.

Figure 1.

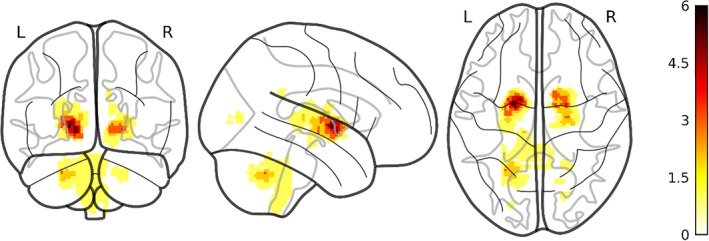
UBOs overlap. Number of subjects displaying UBOs within each voxel superimposed to a glass brain. Note that the colorbar report the absolute number of children rather than the proportion. UBO, unidentified bright objects [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4. Single modality models

3.4.1. Gray matter volume

Using only the gray matter volume we could correctly classify on average 55 (±2) subjects out of 80 (accuracy = 0.69 95%CI [0.66–0.70], specificity = 0.78 95%CI [0.72–0.80], sensitivity = 0.61%CI [0.57–0.65] (range of p values = .0001–.05, median = 0.01). There was no relationship between UBOs presence and correct classification (p values range = .33–1, median = 0.75). There was no effect of center on the probability of a subject of being correctly classified (p values range = .13–1, median = 0.71). The Jaccard index of the overlap between the UBOs and the clusters found using only gm as features was 0.033.

The gray matter volume clusters were mainly localized in the thalamus, the hippocampus, and the striatum while also including cortical regions mainly localized in the medial occipital lobe (Figure 2). Thirty clusters were present in more than 50 folds. NF1 had greater volume relative to controls in a large cluster spanning the thalamus, the striatum, the parahippocampal gyrus, the brainstem and part of the cerebellum (p < .001) and in smaller isolated clusters within the right thalamus (p < .02), the anterior division of the right parahippocampal gyrus (p = .034), the right V lobule of the cerebellum (p = .036) and in the left IX lobules of the cerebellum (p = .031). Inversely, clusters in the left intracalcarine cortex (p < .001), the left (p = .004) and right (p = .016) lingual gyrus and in the posterior part of the temporal fusiform gyrus (p = .013) showed greater volume for the TD relative to the NF1.

Figure 2.

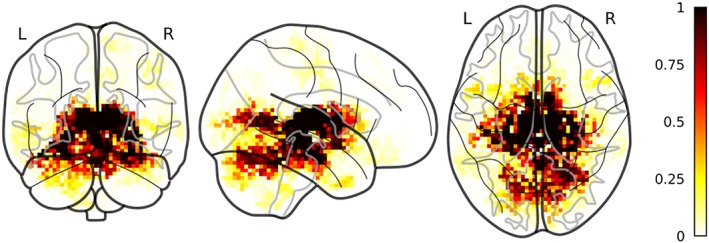
Selected GM clusters. Discriminant GM clusters between NF1 and TD color coded according to the proportion of folds where a certain cluster was selected by the pipeline. Clusters are superimposed to a glass brain in MNI space [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4.2. FA

Using only the FA we could correctly classify on average 65(±2) subjects out of 80 (accuracy = 0.82 95%CI [0.80–0.84], specificity = 0.88 95%CI [0.86–0.90], sensitivity = 0.75 95%CI [0.73–0.77] (range of p values = .00001–.00001, median = 0.00001). There was no relationship between UBOs presence and correct classification (p values range = .067–1, median = 0.57). There was no effect of center on the probability of a subject of being correctly classified (p values range = .063–1, median = 0.70). The Jaccard index of the overlap between the UBOs and the clusters found using only gm as features was 0.12. The FA clusters included the genu and the splenium of the corpus callosum, as well as clusters localized in the internal capsule and the inferior fronto‐occipital fasciculus (Figure 3). A cluster observed in all folds spanned the brainstem and the ventral part of the cerebellum. Nine clusters were present in more than 50 folds, covering the bilateral brainstem and cerebellum and the bilateral internal capsule. For all clusters NF1 children showed significantly lower FA than TD (all ps < .026).

Figure 3.

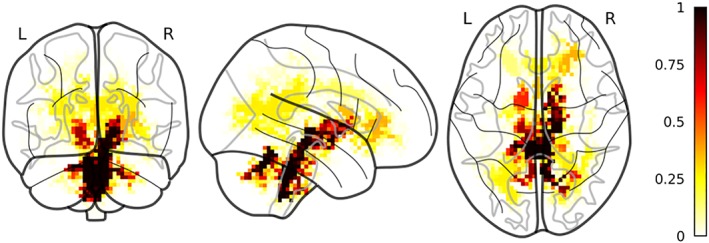
Selected FA clusters. Discriminant FA clusters between NF1 and TD color coded according to the proportion of folds where a certain cluster was selected by the pipeline. Clusters are superimposed to a glass brain in MNI space [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4.3. MD

Using only the MD we could correctly classify on average 69 (±1) subjects out of 80 (accuracy = 0.86 95%CI [0.85–0.87], specificity = 0.89 95%CI [0.87–0.90], sensitivity = 0.83 95%CI [0.80–0.86] (range of p values = .00001–.00001, median = .00001). There was no relationship between UBOs presence and correct classification (p values range = 0.41–1, median = 0.86). There was no effect of center on the probability of a subject of being correctly classified (p values range = .079–.9, median = 0.71). The Jaccard index of the overlap between the UBOs and the clusters found using only MD as features was 0.079.

MD clusters were spread out in the white matter bilaterally. We also observed MD cluster in the left and right crus as well as in the left and right pallidum and left and right thalamus (Figure 4). Finally, we also observed clusters in the gray matter, particularly in the temporo‐occipital part of the right inferior temporal gyrus, in the parahippocampal gyrus bilaterally and in the temporal pole bilaterally. Thirty clusters were observed in more than 50 folds. The NF1 children showed greater MD in all these clusters (all significant ps < .001).

Figure 4.

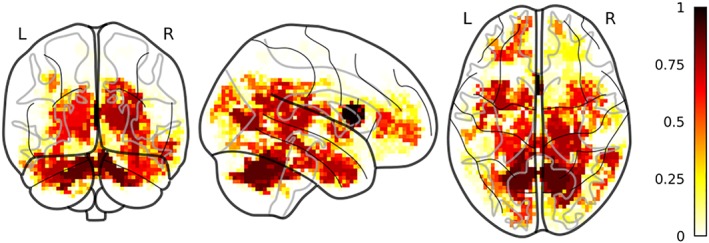
Selected MD clusters. Discriminant MD clusters between NF1 and TD color coded according to the proportion of folds where a certain cluster was selected by the pipeline. Clusters are superimposed to a glass brain in MNI space [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4.4. fALFF

fALFF alone could not discriminate between the two groups: on average only 45 (±2) were correctly classified (accuracy = 0.56 95%CI [0.54–0.58] (range of p values = .05–.7, median = 0.3).

3.4.5. Global correlation

Global correlation alone could not discriminate between the two groups: on average only 50 (±4) subjects out of 80 were correctly classified (accuracy = 0.63 95%CI [0.59–0.65] (range of p values = .01–.3, median = 0.1).

3.4.6. Local correlation

Local correlation correctly classified on average 52(±3) subjects out of 80 (accuracy = 0.64 95%CI [0.62–0.67], specificity = 0.68 95%CI [0.64–0.72], sensitivity = 0.61 95%CI [0.55–0.65] (range of p values = .001–.2, median = 0.03). There was no relationship between UBOs presence and correct classification (p values range = .33–1, median = 0.64). There was no effect of center on the probability of a subject of being correctly classified (p values range = .06–.1, median = 0.74). The Jaccard index of the overlap between the UBOs and the clusters found using only local correlation as features was 0.019.

Local correlation clusters were located in the left and right precuneus and superior parietal lobule, in the right precentral gyrus and the right supramarginal gyrus, in the left frontal operculum, in the right and left Heschl's gyrus, in the left frontal orbital cortex, the bilateral frontal pole, the right superior temporal gyrus and the right middle temporal gyrus (Figure 5). Twenty‐five clusters were observed in more than 50 folds. In three of them, NF1 had significantly higher local correlation relative to TD, specifically in a cluster spanning the bilateral supplementary motor cortex (p = .01), a cluster in the left crus I of the cerebellum (p = .032) and a cluster in the posterior division of the left inferior temporal gyrus (p = .002). On the contrary, in clusters in the anterior division of the right middle temporal gyrus (p = .013), in the right (p < .001) and left (p < .001) precuneous/lateral occipital cortex, and in the left (p < .001) and right (p < .001) posterior cingulate cortex TD showed higher local correlation than NF1 children.

Figure 5.

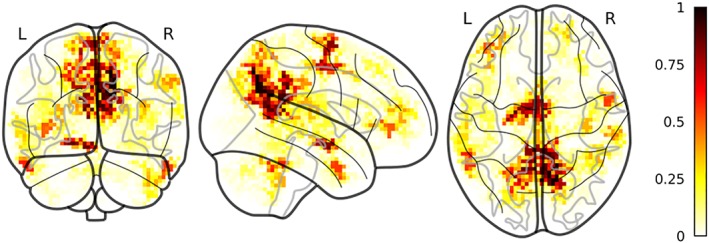
Selected local correlation clusters. Discriminant local correlation clusters between NF1 and TD color coded according to the proportion of folds where a certain cluster was selected by the pipeline. Clusters are superimposed to a glass brain in MNI space [Color figure can be viewed at http://wileyonlinelibrary.com]

3.5. Structural model

Using only index pertaining to brain structure (i.e., gm volume, FA and MD) we could correctly on average 68 (±2) subjects out of 80 (accuracy = 0.84 95%CI [0.82–0.86], specificity = 0.87 95%CI [0.85–0.89], sensitivity = 0.82 95%CI [0.77–0.86] (range of p values = .00001–.0001, median = 0.00001). There was no relationship between UBOs presence and correct classification (p values range = .32–1, median = 0.58). There was no effect of center on the probability of a subject of being correctly classified (p values range = .13–.1, median = 0.30). The Jaccard indexes of the overlap between the UBOs and the clusters of the different modalities were similar to those found for the modalities in isolation (gm = 0.09, MD = 0.09, FA = 0.12).

The clusters found for the different modalities were similar to those found using the modality in isolation, although lower frequencies of occurrence can be observed for GM and MD (Figure S1).

3.6. Complete model

We combined in one model all the indexes that, taken in isolation, could discriminate between the two groups. This model could correctly classify on average 65 (±3) subjects out of 80 (accuracy = 0.81 95%CI [0.79–0.84], specificity = 0.85 95%CI [0.81–0.88], sensitivity = 0.77 95%CI [0.75–0.80] (range of p values = .00001–.00001, median = 0.00001). There was no relationship between UBOs presence and correct classification (p values range = .04–1, median = 0.57). There was no effect of center on the probability of a subject of being correctly classified (p values range = .26–.1, median = 0.91). The Jaccard indexes of the overlap between the UBOs and the clusters of the different modalities were similar to those found for the modalities in isolation (GM = 0.057, MD = 0.084, FA = 0.11, local correlation = 0.19). The clusters found for the different modalities were similar to those found using the modality in isolation, although lower frequencies of occurrence can be observed for GM, MD and for some clusters of local correlation (Figure S2)

4. DISCUSSION

Using multimodal MRI acquisitions focusing on gray matter morphology and white matter microstructure coupled with multivariate analyses, we showed that it is possible to discriminate between NF1 and healthy children. On the other hand, we found that of the indices pertaining to brain activity and connectivity, only local correlation could discriminate the two groups, while global correlation and fALFF could not. We showed that the discrimination performance obtained including all structural indexes together (i.e., GM volume, FA, and MD) or even combination of structural and functional indexes (i.e., GM, FA, MD, and local correlation) is not higher than the performance resulting from the single‐modality models but as high as the performance obtained using MD only. This suggest that diffuse microstructural abnormalities, possibly related to variations in the barriers restricting the movement of water (e.g., cell membranes; Bosch et al., 2012), can be regarded as the central MRI marker of NF1 brain pathology. This hypothesis is in line with the results of the anatamo‐pathological study of Di Paolo et al. (1995) highlighting a modification of the water content of the myelin in NF1 individuals. Moreover, we showed that the performance of the structural model is independent from the presence of UBOs and that the discriminative clusters are only minimally overlapping with the regions where UBOs appear more frequently in our sample. Moreover, a supplementary analysis performed excluding voxels where at least one subject had UBOs led to comparable results as the original analysis. Note however that the relative high slice thickness acquired in one of the two centers (4 mm) may have biased the volume of the UBOs we found. The spatial distribution of the gray matter volume discriminative clusters is in accord with previous findings and with the known pathology of NF1. We found an involvement of the caudate nucleus and the thalamus bilaterally, two structures that have been reported to have greater volume in NF1 than in healthy children (Huijbregts et al., 2015). These regions were also found to have high discriminative power by Duarte et al. (2014) using multivariate methods. Similarly to Duarte et al. (2014), we found an involvement of the medial occipital lobe and the parahippocampal gyrus. These structures are involved in visuospatial abilities, whose impairment is one of the most frequently reported cognitive deficit in NF1 children (Hyman et al., 2005). It is noteworthy that the direction of the univariate effect we found for the GM clusters was similar to those found by Duarte et al. (2014), with subcortical structure having greater GM volume in NF1 children and medial occipital lobe cluster having lower GM values in NF1 children relative to TD. Contrary to previous studies, we did not found an involvement of the associative cortex (Duarte et al., 2014; Pride et al., 2014). This could be because using our pipeline, only the most discriminative clusters have a chance to be retained, as cluster carrying redundant information are excluded from the final model. In this sense, it can be suggested that subcortical, medial temporal, and medial occipital abnormalities are the core morphological deficit of NF1 pathology, with associative cortex involvement may be being less central to NF1 brain pathology. On the other hand, difference in preprocessing pipeline for T1 images (different software, different template, and different modulation) could account for this discrepancy in the results. Note that the results of univariate analysis, concerning not only gray matter but also the other modalities, should be taken with caution, as the nature of multivariate analysis does not allow to comment on the discriminative power of each cluster in isolation.

Finding obtained from white matter microstructure are partially in line with previous findings in the literature. We found an involvement of the corpus callosum, whose macrostructure and microstructure have been reported to be abnormal in NF1 (Aydin et al., 2016; Filippi, Watts, Duy, & Cauley, 2013; Pride et al., 2010). This involvement was only evident using MD, and it was most stable (i.e., observed in a higher number of folds) in the genu of the corpus callosum than in the splenium, while it is this latter that has been most commonly found to be abnormal in NF1 children (Aydin et al., 2016; Filippi et al., 2013). However, the direction of the univariate differences between the group was consistent with previous finding, with NF1 having higher MD than TD children, suggesting a less organized or a less myelinated white matter. Generally, for MD we found a diffuse involvement of the white matter, with the univariate analyses showing that NF1 had higher MD values relative to TD children in all the clusters. This finding confirms and extends those of a recent study that found that whole‐brain MD, as well as MD measured in the anterior thalamic radiation, the cingulate bundle and the superior longitudinal fasciculus, was higher for NF1 than for TD (Koini et al., 2017). MD discriminative clusters were also observed in the bilateral thalamus and putamen, showing that microstructural abnormalities are not confined to white matter.

These microstructural abnormalities are in line with the cognitive phenotype of NF1 patients. The predominant MD abnormalities in the right hemisphere fits well with impaired visuo‐spatial ability (Vogel, Bowers, & Vogel 2003; Wu et al., 2016) and social cognition (De Pisapia et al., 2014; Mitchell & Phillips, 2015). Impairment of the thalamus and of its projections on the visual and frontal cortex may contribute to the executive and/or the visuo‐spatial deficits in NF1. Finally, the involvement of medial structures such as the cingulate cortex and the corpus callosum goes well with the high frequency of attentional abnormalities in this population.

For the first time, we also found localized FA abnormalities in the brain stem and cerebellar white matter in absence of (or independent from) UBOs, with TD showing higher FA than NF1. Brain stem and cerebellum are two common locations of UBOs (Ertan et al., 2014; Ferraz‐Filho et al., 2012). FA values were lower in UBOs relative to spared white matter (Billiet et al., 2014; Ertan et al., 2014; Ferraz‐Filho et al., 2012). Interestingly, in our sample these regions were not the one where UBOs appeared with the higher frequency. The fact that they were nonetheless selected as discriminant using FA suggests that microstructural abnormalities in these regions can exist even when UBOs are not present (or not visible). Noteworthy, Ferraz‐Filho et al. (2012) used longitudinal data to show that FA is reduced in region where UBOs were presented at baseline even after reduction or disappearance of UBOs themselves.

Including all the structural modalities together led to a performance as high as that of the model that only included MD. The clusters selected for the different modalities taken together were extremely similar to those selected in the single‐modality pipeline. The fact that the discriminative clusters resulting from the combined pipeline were similar to those found using the modality in isolation suggest that the different indexes used bring indeed complementary information, as our pipeline was conceived to minimize redundant features. The fact that despite this complementary information the combined pipeline did not perform better than the model including only MD can be related to an additive effect of noise coming from different modalities: since MD already reached a quite high accuracy, the benefit of adding other modalities could have been masked by the addition of independent noise that this entails. Note, however, that this is a tentative interpretation and that a more systematic study about signal‐to‐noise ratio in the different modalities is needed for a definitive response. This result suggests that the MRI signature of NF1 brain pathology is a widespread structural abnormality that involve both subcortical and cortical gray matter, together with white matter. Moreover, the white matter abnormalities may be related to both fibers structural organization and myelination, as both FA and MD are discriminative, although in different brain regions.

Here it needs to be addressed the difference in performance between our classifiers and those in Duarte et al. (2014). Indeed, Duarte et al. reached higher accuracy using GM and WM volume separately (highest accuracy using GM volume = 0.89; highest accuracy using WM volume = 0.87) than any of our classifiers. It should be noticed that Duarte et al. used WM volume, rather than indexes of WM microstructure, as we did. Moreover, they tried different thresholds for the number of voxels included in their models, and there was a clear effect of this choice on their results (when including only 100 voxels the accuracy was 0.83 for GM volume and 0.78 for the WM volume, lower than ours). We did not try different thresholds for the number of voxels included, preferring a data‐driven method based on the scree plot of the relieff weights. This data‐driven method could have been suboptimal for the task at hand, leading to lower accuracies. At the same time, it ensures independence in the choice of the best hyperparameters of the model, which might have not been the case in the Duarte's study. Another important aspect that may explain classifier accuracy difference with the previous study by Duarte et al. (2014) is that of features reduction. Following Meng et al. (2017) we wanted to build a model capable not only of high accuracy and of using the interdependencies between features, but also of privileging the interpretability of the results. To this end, we performed several features selection steps, ending up with only tens of features in the final models, rather than the hundred that was the minimum features number used by Duarteet al. Moreover, for the sake of interpretability (and computing time), we down sampled all images to an isotropic 3 mm voxels, while Duarteet al. used images in the original resolution of 1.5 mm isotropic voxels. This could have reduced our ability to detect more subtle differences and thus lowered our accuracy. This is partly in line with the fact that we have obtained better results with unsmoothed rather than smoothed images: the gain in the spatial alignment related to smoothing are probably weaker than the loss in the spatial specificity of the signal. Another source of difference could have been the multicentric nature of our study. Even if we took care of removing the variance related to the centers of acquisition (and the results were comparable when we did not remove center‐related variance), intrinsic differences between the images acquired in the two centers could have lowered our performance.

Indexes related to the brain activity and connectivity at rest were less successful in discriminating between the two groups. fALFF and global correlation could not discriminate between the two groups, while local correlation reached a lower performance than any of the structural indexes. It is important to underline that in term of absolute performance, the three functional measures were not so different among them, and all fared worse than the worse structural measure. For this reason, one should consider with caution the fact that local correlation performance was significant while fALFF and global correlation performance were not. The relative poor performance of functional measures goes rather well with a previous FDG PET study that measured brain metabolism and hence activity in adults with NF1 and that showed only a small cluster of hypoactivity in the thalamus (Apostolova et al., 2015). On the other hand, brain activity during certain cognitive tasks has been shown to differ between NF1 and TD children (Pride et al., 2017; Violante et al., 2012). Task‐evoked functional indexes could be better suited to differentiate between the two groups. Our results using indexes of connectivity are also partly in accord with those of Tomson et al. (2015) who showed that both modularity (i.e., an index of clustering of neighboring nodes) and long‐distance connectivity (in particular antero‐posterior) were different between NF1 and TD. Given that local and global correlation can be conceived as rough index of local clustering and longer distance connectivity, respectively, our study confirms abnormal short‐distant functional connectivity as part of the NF1 phenotype. Of notice, adding local correlation to the structural indexes did not improve the overall performance of the model, even if the clusters found using this model were extremely similar to those found using single modality. Subtler connectivity indexes related to graph‐theory analyses may be better suited to discriminate between NF1 and TD (Tomson et al., 2015). Similarly, seed based or RSN connectivity based on network known to be affected in NF1 (e.g., DMN) could indeed discriminate between the two groups (Ibrahim et al., 2017; Violante et al., 2012b). However, the complexity of these methods in term of analyses choices (e.g., seed based vs. ICA based, choice of the seed region[s], choice of the parcellation in the case of graph‐theory measures) make them better suited for future focused studies. Another possibility is that more direct measures of brain metabolism at rest could lead to better discrimination performance. A recent study by Schütze et al. (2018) was able to predict a composite cognitive measure in a sample of children and adult with NF1 using 18F‐FDG PET brain imaging at rest and Gaussian Process Regression. It is reasonable that the same measure would be useful to discriminate between NF1 and controls. All in all, rs‐fMRI seems not to be well suited for discriminating between NF1 and controls, but task‐related fMRI, more subtle connectivity‐measure and metabolic imaging performed with 18F‐FDG PET may be better suited for the task.

Another reason for the poor performance of the fMRI related indexes could be the noise removal step we performed before fitting the model: while for the structural indexes we only removed variance from TIV and center of acquisition, for the fMRI related indexes we also removed mean movement‐ and mean global signal change‐related variance. Part of the signal relevant for discrimination could have been removed together with the noise.

To conclude, we showed that the core MRI signature of NF1 is a diffuse microstructural abnormality, possibly related to variations in the barriers restricting the movement of water (e.g., cell membranes; Bosch et al., 2012). Complementary abnormalities were observed for GM volume (abnormalities in the subcortical nuclei and the medial temporal lobe), for FA (in the cerebellum and brainstem) and MD (diffuse bilaterally and extending both in the white and the gray matter). Local correlation was also discriminative, although to a lesser extent and with low sensitivity. It would be of interest to study now the possible link between these characteristic brain abnormalities and the neuropsychological profile of patients with NF1.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

Supporting information

Appendix S1: Supplementary Information

Nemmi F, Cignetti F, Assaiante C, et al. Discriminating between neurofibromatosis‐1 and typically developing children by means of multimodal MRI and multivariate analyses. Hum Brain Mapp. 2019;40:3508–3521. 10.1002/hbm.24612