Abstract
The transition from early adulthood to the elder is marked by functional and structural brain transformations. Many previous studies examined the correlation between the functional connectivity (FC) and aging using resting‐state fMRI. Results showed that the changes in FC are linked to aging as well as the cognitive ability changes. However, some researchers proposed that the FC is not static but dynamic changes during the resting‐state fMRI scan. In this study, we examined the correlation between the resting‐state dynamic functional network connectivity and age using resting scan data of 434 subjects. The results suggested: (a) age is negatively associated with variability of dynamic functional network connectivity state; (b) the dwell time of each age range spends in each state is different; (c) the dynamic graph metrics curve of each age ranges is different and 19–30 age range has the largest average global efficiency and average local efficiency; (d) some dynamic functional network connectivity measures were correlated to the certain cognitive ability. Overall, the results suggested the changes in dynamic functional network connectivity measures may be a characteristic of the aging process and in further investigations may provide a deep understanding of the aging process.
Keywords: aging, dynamic functional network connectivity, graph theory, Wechsler adult intelligence scale
1. INTRODUCTION
With the increasing of age, our brain undergoes structural and functional changes (Betzel et al., 2014). For brain structures, previous studies revealed that there was a tendency toward cortical “disconnection”, that is, a rapid decline of within‐network covariance in aging process (Betzel et al., 2014; DuPre & Spreng, 2017). This “disconnection” was also presented in resting‐state functional connectivity during the aging process. For example, the execute control network, which is involved in attention, memory, and executive control functions, has a decreased interaction of within‐network during the aging process. (Chan, Park, Savalia, Petersen, & Wig, 2014). Therefore, it is important to investigate changes in functional brain network pattern across the lifespan, which provided a whole brain level understanding of the aging process. (Zuo et al., 2017).
Functional connectivity (FC) describes how the neural activity of two brain regions interact with each other over time, which is usually measured by the Pearson correlation coefficient between their fMRI time series (Biswal, Yetkin, Haughton, & Hyde, 1995). Many previous studies examined the difference of FC in age using resting‐state functional connectivity analysis. Results showed that the changes in FC are linked to cognitive ability and behavioral changes, which are correlated with aging (Fair et al., 2018; Power, Fair, Schlaggar, & Petersen, 2010; Thomason et al., 2008). However, these studies may not be enough to finely describe the changes in functional brain network pattern across the lifespan (Fair et al., 2018; Greicius, 2008; Power et al., 2010; Thomason et al., 2008; Van den Heuvel and Hulshoff Pol, 2010). This depiction of change neglects the dynamic characteristic of the brain's FC, with the potential assumption that FC remains constant throughout the resting period (Biswal et al., 1995; Fox et al., 2005). However, recent research showed that the brain functional network is not static but dynamic reconfiguration during the resting‐state fMRI scan.
Recently, a growing body of research examined the dynamic FC in healthy subjects and patients with neuropsychiatric diseases (Calhoun, Miller, Pearlson, & Adali, 2014). For example, Allen et al., (2014) examined resting‐state FC dynamics in healthy young adults, revealed unanticipated FC states and challenged the conventional assumption that resting‐state FC remains stationary. In a follow‐up study, the authors found resting‐state dynamic FC have a difference between schizophrenia and healthy groups, that is, patients show significant differences in dwell times in multiple states (Damaraju et al., 2014). Besides resting‐state dynamic FC, researchers also examined task dynamic FC and found that there was a direct link between cognitive performance and the dynamic reorganization of the network structure of the brain (Tsvetanov, et al., 2016). Furthermore, researchers found that there was a link between resting‐state dynamic FC and concurrently collected electroencephalography (EEG) data, which suggested that the resting‐state dynamic FC has a physiological basis (Allen et al., 2018). Another study evaluated replicability of dynamic FC states using resting‐state fMRI data of 7,500 subjects, and the results showed that dynamic FC states are similar across groups (Abrol, Chaze, Damaraju, & Calhoun, 2016). These collective findings imply that dynamic FC is a promising avenue for clinical neuroimaging and can enrich our knowledge of the functional organization of the human brain.
In this study, we investigated the relationship between dynamic FC and aging. Based on the previous studies on dynamic connectivity (Allen et al., 2014; Damaraju et al., 2014; Hutchison & Morton, 2015), we compared the dynamic functional network connectivity (FNC) measures in different age cohorts. Firstly, group independent component analysis (ICA) was used to extract resting‐state networks (RSNs), and then dynamic FNC matrices were created using sliding time windows and Pearson correlation approaches. Subsequently, the K‐means algorithm was employed to cluster these matrices into different dynamic states which are the average patterns that FC matrix tends to return to during the resting state scan. Then we calculated the dynamic FNC measures based on the clustering results, such as the dwell time of each individual subject spends in each state, and compare these measures in different age cohorts. Lastly, we described the states by calculating their network graph metrics including local efficiency, global efficiency, as well as hub areas. Besides, we examined the associated between dynamic FNC and intelligence. Overall, we suggested the study of dynamic FC can unveil flexibility in the functional coordination between different sub‐networks and in further investigations may provide a deep understanding of brain changes and aging.
2. MATERIALS AND METHODS
2.1. Subjects
The large sample was drawn from an ongoing project exploring the associations among individual development in brain structure and function, cognitive ability, and mental health (Wei, et al., 2018). A total of 494 healthy volunteers were recruited from Southwest University (SWU) by means of the campus network, advertisements on bulletin boards and through face‐to‐face communications, but 60 participants were excluded due to large head motion (FD > 0.2 mm) (Laumann et al., 2016). Thus, the final sample was composed of 434 subjects (165 males; mean age = 44.44, SD = 17.28; age range = 19–80). All participants were required to be healthy and none had a history of psychiatric disorder or substance abuse (including illicit drugs and alcohol), and MRI contraindications. The project was approved by the SWU Brain Imaging Center Institutional Review Board, and written informed consent was obtained from each subject prior to the study. Participants received payment depending on time and tasks completed.
2.2. Image acquisition
All functional images were obtained from a 3‐T Siemens Magnetom Trio scanner (Siemens Medical, Erlangen, Germany) at the Brain Imaging Research Central in Southwest University, Chongqing, China. The whole‐brain resting‐state functional images were acquired using T2‐weighted gradient echo planar imaging (EPI) sequence: slices = 32, repetition time (TR)/echo time (TE) = 2000/30 ms, flip angle = 90°, field of view (FOV) = 220 mm × 220 mm, thickness = 3 mm, slice gap = 1 mm, matrix = 64 × 64, resulting in a voxel with 3.4 × 3.4 × 4 mm3. During the functional images acquisition, participants were asked to close eyes, keep still, and not to fall asleep (confirmed by all participants immediately after the experiment). The scan lasted for 484 s and acquired 242 volumes in total for each subject. Additionally, high‐resolution T1‐weighted anatomical images were acquired for each participant (TR = 1900 ms; TE = 2.52 ms; inversion time = 900 ms; flip angle = 9°; resolution matrix = 256 × 256; slices = 176; thickness = 1.0 mm; voxel size = 1 × 1 × 1 mm3).
2.3. Data preprocessing
The sMRI (1 × 1 × 1 mm3) data was processed by using SPM8 (Welcome Department of Cognitive Neurology, London, UK; http://www.fil.ion.ucl.ac.uk/spm) implemented in MATLAB 2012a (MathWorks Inc., Natick, MA). Each sMRI was first displayed in SPM8 to check quality. Firstly, the reorientation of the images was manually set to the anterior commissure. Then, the images were segmented into gray matter, white matter, and cerebrospinal fluid by using the segmentation tool in SPM8.
The resting‐state fMRI data were preprocessed using data processing assistant for resting‐state fMRI (DPARSF, http://resting-fmri.sourceforge.net/) implemented in the MATLAB 2012a (Math Works, Natick, MA) platform. Resting‐state fMRI preprocessing steps included the following: eliminate first 10 time points of each subject, slice timing correction, realignment, registration functional images (MNI pace), normalization (3 × 3 × 4 mm3), smoothing (FWHM = 6 mm), band pass filtering (0.023–0.18 Hz) (Gonzalez‐Castillo et al., 2015; Leonardi & Van De Ville, 2015), nuisance regressors included white matter and cerebrospinal fluid signals in addition to 24 movement regressors derived by expansion, frames with frame wise displacement (FD) > 0.2 mm were censored. The residual effects of motion was regressed out in group statistical analysis by including mean FD derived with Jenkinson's relative root mean square (RMS) algorithm as a regressor of no interest. These preprocessing steps were followed by the standard protocol published (Yan, Wang, Zuo, & Zang, 2016).
2.4. Head motion correction
Recent studies have demonstrated that head motion has a substantial impact on dynamic FC (Laumann et al., 2016;Siegel et al., 2016). So we used the following steps to further minimize the effects of head motion. Artifacts were reduced using excluding subjects with high head‐motion, nuisance regression (excluding censored frames), interpolation (Power et al., 2014), and band pass‐filtering (0.023 < f < 0.18 Hz) (Gonzalez‐Castillo et al., 2015; Leonardi & Van De Ville, 2015). Nuisance regressors included the cerebrospinal fluid signals, white matter, and their derivatives, in addition to 24 movement regressors derived by expansion (Friston, Williams, Howard, Frackowiak, & Turner, 1996; Yan et al., 2013). Subjects with max head motion >2 mm and 2.0° were censored (Laumann et al., 2016),
2.5. Group independent component analysis
Group ICA was performed using the GIFT toolbox (http://mialab.mrn.org/software/gift). Following the Allen et al. (2014), we used a relatively high model order (number of components, C = 100) to achieve a “functional parcellation” of refined cortical and subcortical components corresponding to known anatomical and functional segmentations. In group ICA, principal component analysis (PCA) was used to reduce the dimension of fMRI data at two levels. First, fMRI data of each subject were decomposed into 150 principal components (PCs). Then the reduced data of all participants were concatenated and further decomposed into 100 PCs using the expectation–maximization algorithm (Roweis, 1998). The Infomax algorithm was then used to find independent components. This algorithm was repeated 20 times in ICASSO (http://www.cis.hut. fi/projects/ica/icasso) and spatial maps (SMs) were estimated as the modes of the component clusters. Based on visual recognition and calculating spatial Pearson correlation, 41 components were discarded and a total of 59 components were identified as intrinsic connectivity networks (ICNs) for future analysis. Finally, following a previous study, we performed additional post processing steps on time courses of the 59 ICNs, including (a) removing linear, quadratic, and cubic trends, (b) regressing out six realignment parameters and their temporal derivatives, (c) low‐pass filtering (0.15 Hz), and (d) removing spikes to ensure that artifactual spikes do not negatively impact the signal analysis (Allen et al., 2014).
2.6. Dynamic FNC computation
Before dynamic FNC computation, the time courses of RSNs were temporally bandpass filtered (0.023–0.18 Hz) (Gonzalez‐Castillo et al., 2015; Leonardi & Van De Ville, 2015) to reduce the effects of low‐frequency drift and high‐frequency physiological noise. The dynamic FNC was computed using a sliding‐window correlation approach. Since there was currently no formal consensus regarding the window length, we selected the length (22TR) according to a former study with a Gaussian of σ = 3 TR (Allen et al., 2014). The window was shifted with a step of 1 TR, resulting in 210 windows. In each window, the time courses of each pair of the 59 RSNs were used to calculate FNC (Pearson's correlation coefficient) and a 59 × 59 correlation matrix was obtained. A Fisher's r‐to‐z transformation was then applied to all FNC matrices to improve the normality of the correlation distribution as r is the Pearson correlation coefficient and z is approximately normally distributed.
2.7. K‐means clustering
For the dFNC patterns reoccur within subjects across time and across subjects, we applied the k‐means algorithm to divide the dFNC windows into separate clusters. The clustering algorithm was applied to a subset of all windows that showed greater variance in FNC, and was repeated 150 times to increase the likelihood of escaping local minima, with random initial cluster centroid positions (Allen et al., 2014; Liu et al., 2016). Subsampling was chosen both to reduce redundancy between windows (the chosen time step of 1 TR induces high autocorrelation in FC time series) and to reduce computational costs. The optimal number of clusters was estimated as five using the elbow criterion (Ketchen & Shook, 1996), which is calculated as the maximum ratio of within‐cluster distance and between‐cluster distance across a set of candidate cluster numbers (2 to 10 in our study). Finally, the resulting centroids of subsample were used as starting points to cluster all data into five clusters. A k of 4 and 6 was used respectively to validate the robustness of our results (see SI.B).
2.8. State analysis
In addition, we performed an exploratory experiment in which we calculated and compared temporal metrics derived from each subject's state vector (Allen et al., 2014). Specifically, we computed four measures in each subject, including: (a) frequency of each state, measured as the number of windows in each state; (b) dwell time of each state, measured as the number of consecutive windows in each state. While the current window and the next window have the same certain state, the dwell time of the certain state plus one; (c) total number of transitions, measured as the total number of situation that window state from one state switched to another state; and (d) frequency of each state transition, measured as the number of situation that the window state switched from the certain state to another state, for example, the frequency of State 1–3 means that the number of situation that the window state from State 1 switched to State 3.
A similarity to previous research (Hutchison and Morton (2015), parametric tests (Pearson correlation) were utilized to evaluate the correlation between age and these measures, and head motion is regressed out as nuisance covariates.
2.9. Dynamic graph metrics curve of different age ranges
Before the analysis, each connection matrix of cluster centroids was converted to a z‐value connection matrix that is normally distributed by using Fisher's r‐to‐z transform. Thresholding the dynamic functional network connectivity matrices is critical to obtain a sparse adjacency matrix. Using absolute thresholding method may ultimately change the properties of the original global and local FC, which may bias the comparisons of graph‐theoretic metrics between different groups of subjects (Song et al., 2014). Therefore, we applied a proportional network threshold of 15% (Whitfield‐Gabrieli & Nieto‐Castanon, 2012). We globally thresholded all dynamic functional network connectivity matrixes at a fixed threshold (K = 0.15), and then measured local and global efficiency based on weighted adjacency matrix by using Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/) (Whitfield‐Gabrieli & Nieto‐Castanon, 2012). Global efficiency is the average inverse shortest path length and usually as an index of global integration. (Latora & Marchiori, 2001). Local efficiency is the efficiency of the local subgraph of a node i that contains only the direct neighbors of node i, and it usually as a measure of local connectedness (Latora & Marchiori, 2001).
By the dFNC computation, each subject can get 210 FC matrixes and their global efficiency. Then we averaged the global efficiency of 210 connectivity matrixes of a subject as the global efficiency of this subject. Next, we divided the subjects into six groups according to their ages, each age span of 10 years (19–30; 31–40; 41–50; 51–60; 61–70; 71–80). Thus, we can calculated average global efficiency of each age group and compared the differences in average global efficiency between different age groups.
As for local efficiency, we summed the local efficiency of nodes that within a sub‐network as the local efficiency of this sub‐network. Similarly, we averaged local efficiency of a sub‐network of 210 connectivity matrixes of a subject as the local efficiency of this sub‐network of this subject. Previous literatures indicted that DMN (Damoiseaux et al., 2008; Biswal et al., 2010; Evers, Klaassen, Rombouts, Backes, & Jolles, 2012), CCN (Elizabeth DuPre & R. Nathan Spreng, 2017), and SN (Tsvetanov et al., 2016) are more susceptible to the effects of aging. Therefore, we averaged local efficiency of three sub‐networks (DMN, CCN, and SN) of each age group and compared the differences in average local efficiency of three sub‐networks between different age groups.
Besides, the sample was not equally distributed among the age groups. Each age groups have 149, 32, 63, 103, 59, and 28 samples, respectively. Considering the distribution may impact the differences in graph metrics among age groups, we randomly sampled 28 subjects from each age group and made them a new sample. To ensure the stability of results, we repeated extract new sample and compare the graph metrics among different age groups in new samples 100 times.
Lastly, we plotted the dynamic graph metrics curve of different age ranges to visually observe the difference in the time‐varying of graph metrics in different age groups. Firstly, we averaged the global efficiency of a certain time window (connectivity matrixes) of all subjects who belongs to an age group as the global efficiency of this time window of this age group. Thus, the average global efficiency of each age group changes dynamically over the time window. Similarly, we averaged the local efficiency of three sub‐networks (DMN, CCN, and SN) of a certain time window (connectivity matrixes) of all subjects who belongs to an age group as the local efficiency of three sub‐networks of this time window of this age group. Thus, the average local efficiency of three sub‐networks of each age group changes dynamically over the time window.
2.10. Topological properties of discrete functional connectivity states
To characterize the state topological properties, we globally thresholded the state matrix at a fixed threshold (K = 0.15), calculated global efficiency, sub‐network local efficiency, and the degree of every node of every matrices, and then listed the hub nodes of matrices according to their degree (The Brain Connectivity Toolbox, http://www.brain-connectivity-toolbox.net/). With global efficiency, local efficiency, and hub regions of each state, we can depict the topological characteristic of each state.
2.11. The correlation between Wechsler adult intelligence scale and state
The Wechsler Adult Intelligence Scale (WAIS) is an IQ test designed to measure intelligence and cognitive ability in adults and older adolescents (Kaufman & Lichtenberger, 2005). The WAIS‐R, a revised form of the WAIS, and consisted of six verbal and five performance subtests (Wechsler, 1981). Firstly, we investigated the relationship between age, state indexes (frequency of each state; dwell time of state; numbers of transitions), and total score of WAIS. Secondly, we chose one of verbal subsets, called similarity, which measures abstract verbal reasoning as well as semantic knowledge. In this section, participants are given two words or concepts and required to describe how they are similar. The reasons we chose the similarity subscales is as follows. Firstly, the similarity subset (measuring abstract verbal reasoning and semantic knowledge) is considered relatively stable across the aging (Ardila, 2007). If similarity subset changes with aging, then others will theoretically change. Secondly, some elder didn't complete all the WAIS items, and the completion rate of similarity subset is highest. We examined the relationship between similarity (the subtest of the Wechsler Adult Intelligence Scale‐Revised Chinese revision [WAIS‐RC; Gong, 1992]), state indexes, and age. Lastly, we tested the relationship between block design test (the subtest of the Wechsler Adult Intelligence Scale‐Revised Chinese revision (WAIS‐RC; Gong, 1992), state indexes, and age. The block design test, which is thought to evaluate fine motor skills, processing speed, and visuospatial ability, is most affected by age (Hoogendam, Hofman, van der Geest, van der Lugt, & Ikram, 2014).
3. RESULTS
3.1. Static functional network connectivity
Figure 1 displays the ICNs identified by the group ICA approach. Network components are shown in Figure 1.Based on their anatomical and presumed functional properties, ICs are grouped into sub‐cortical (SC), auditory (AUD), somatomotor (SM), visual (VIS), cognitive control (CC), default‐mode (DM), and salience (SN) networks by spatial correlation and visual recognition. The manually identified ICNs are very similar to a previous study (Allen et al., 2014). These ICNs are also similar to those observed in previous studies using a higher model order (Smith et al., 2009; Allen et al., 2011) and cover the majority of subcortical and cortical gray matter regions. Figure 2 displayed the static FC between ICNs, computed over the entire scan length and averaged across subjects.
Figure 1.
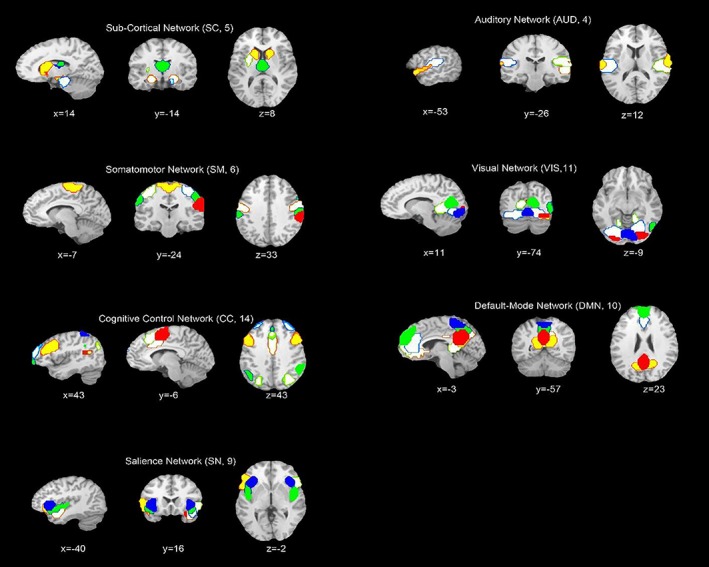
Composite maps of the 59 identified intrinsic connectivity networks (ICNs), sorted into seven sub‐networks. Each color in the composite maps corresponds to a different ICN [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 2.
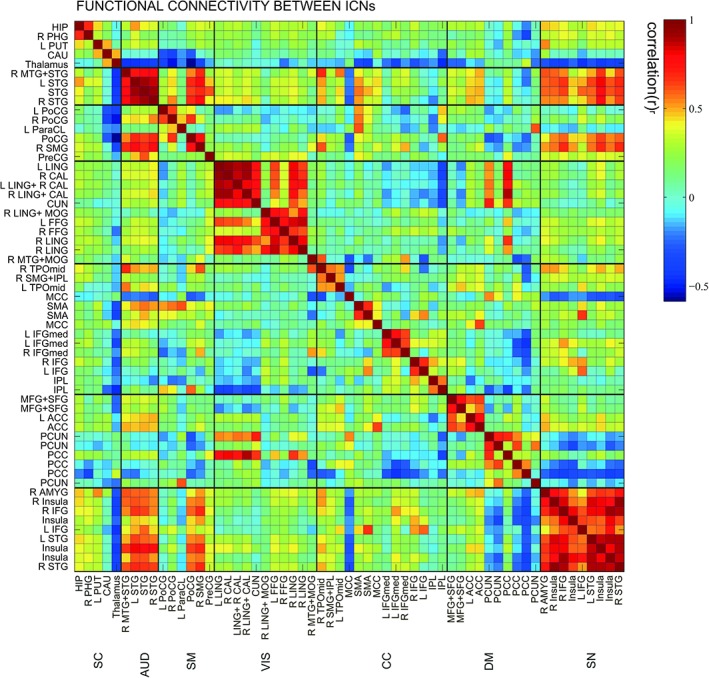
Static functional network connectivity matrix of ICNs during rest computed over the entire scan length and averaged over subjects [Color figure can be viewed at http://wileyonlinelibrary.com]
3.2. The duration and transition of connectivity states as a function of age
In addition to the static FNC, we can also examine the frequency of states as a function of time and the transitions between them. Figure 3 shows the state assignments as a function of time in four example subjects. As we would see, functional networks tend to sustain single state during a long period, while transition times are rarely less. We can characterize transition behavior by calculating the frequency changing from one state to another.
Figure 3.
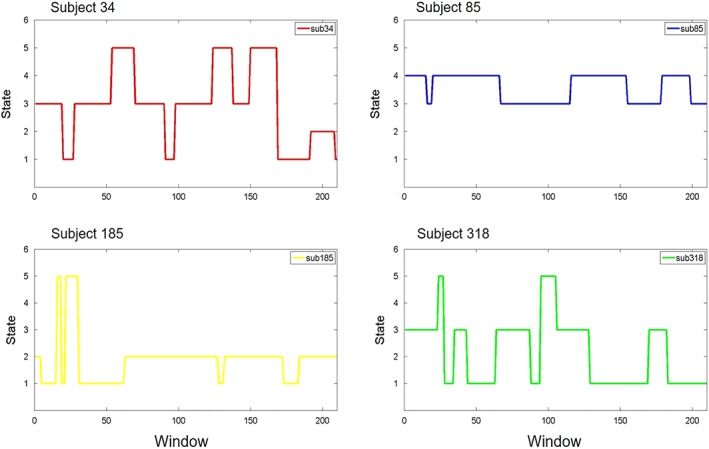
The state assignments as a function of time for the four example subjects. Examples of FC dynamics for Subject 34, Subject 85, Subject 185, Subject 318 [Color figure can be viewed at http://wileyonlinelibrary.com]
The total dwell time (the sum of dwell time of all states) of states was positively correlated with age (r = 0.20, p = .000, n = 434), while the total transition of states was negatively correlated with age (r = −0.20, p = .000, n = 434). The states indexes at rest were correlated with age (See Table 1), the distribution of each state in each age ranges is shown in Figure 4. The gender ratio in the sample is not balanced, so we used the Independent Sample t test to examine the gender impact in the measures of the dynamic states. Results suggested that the significant gender difference in State 1–2 (t = 8.29, p = .004), State 1–3 (t = 8.29, p = .004), State 2–1 (t = 6.49, p = .011), State 2–3 (t = 14.50, p = .000), and State 3–1 (t = 4.61, p = .032). The only dynamic state (State 2–3) was both correlated with age and gender.
Table 1.
The state index expressed at rest was correlated with age
| State index | r | p |
|---|---|---|
| Total dwell time | 0.20 | 0.000 |
| Total transition time | −0.20 | 0.000 |
| Frequency of state 1 | 0.32 | 0.000 |
| Frequency of state 3 | −0.238 | 0.000 |
| Frequency of state 4 | −0.19 | 0.000 |
| Frequency of state 5 | 0.11 | 0.022 |
| Transition times of 1–5 | 0.19 | 0.000 |
| Transition times of 2–3 | −0.15 | 0.002 |
| Transition times of 3–2 | −0.12 | 0.015 |
| Transition times of 3–4 | −0.20 | 0.000 |
| Transition times of 3–5 | −0.17 | 0.000 |
| Transition times of 4–3 | −0.21 | 0.000 |
| Transition times of 5–1 | 0.16 | 0.001 |
| Transition times of 5–3 | −0.14 | 0.003 |
| Head motion | 0.41 | 0.000 |
Figure 4.
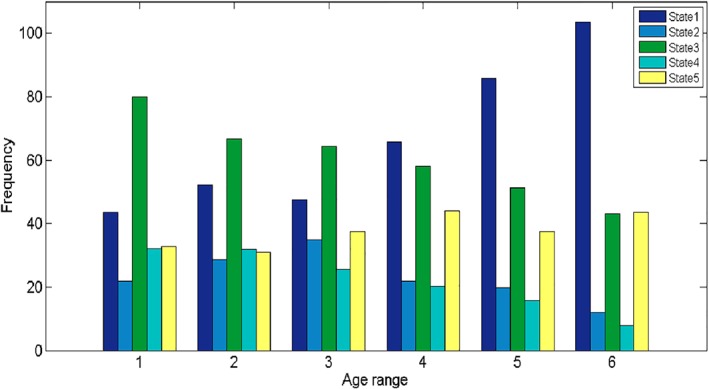
The distribution of each state in each age range [Color figure can be viewed at http://wileyonlinelibrary.com]
Besides, recent studies have demonstrated that head motion has a substantial impact on dynamic FC (Laumann et al., 2016;Siegel et al., 2016). Therefore, we examined the correlation between head motion (mean frame wise displacement) and state indexes. The results indicated head motion is negatively correlated with the frequency of State 3 (r = −0.15, p = .002) and the times of transition of State 3–5 (r = −0.10, p = .034).
3.3. Dynamic graph metrics curve of different age ranges
To characterize the age effects on the global network topological properties, two key graph metrics were employed, global efficiency, and local efficiency, which were all calculated based on weighted networks.
Firstly, we found significant differences between different age groups in the global and local efficiency (see Table 2). The difference is observed in the global efficiency (global efficiency: r = −0.24, p = .000), 19–30 years old age range has significant greater global efficiency than 51–60, 61–70, and 71–80 years old age range. The correlation between sub‐network local efficiency and age (DMN Elocal: p = .055, r = −0.092; CC_Elocal: p = .019, r = −0.11; SN_Elocal: p = .000, r = −0.19) behaved differently. Intriguingly, no matter which network, its local efficiency of 19–30 age range is the highest.
Table 2.
Global efficiency and local efficiency of each age group
| Age range | N | Global efficiency | DMN local efficiency | CC local efficiency | SN local efficiency |
|---|---|---|---|---|---|
| 19–30 | 149 | 0.351 | 0.601 | 0.603 | 0.616 |
| 31–40 | 32 | 0.347 | 0.598 | 0.580 | 0.599 |
| 41–50 | 63 | 0.341 | 0.588 | 0.577 | 0.607 |
| 51–60 | 103 | 0.334 | 0.576 | 0.575 | 0.571 |
| 61–70 | 59 | 0.328 | 0.566 | 0.552 | 0.553 |
| 71–80 | 28 | 0.325 | 0.578 | 0.562 | 0.534 |
| Numbers of significant results (in 100 times) | 94 | 11 | 16 | 79 |
Secondly, we compared the global efficiency and local efficiency among different age groups in new sample. We ran the above‐mentioned analysis 100 times and reported the ratio of significant result (p < .05) in Table 2. The results indicated that the difference between different age groups in global efficiency is reliable and stable and that in the local efficiency of different sub‐networks is unstable.
Besides, we have plotted the dynamic graph metrics curve of different age ranges (see Figure 5).
Figure 5.
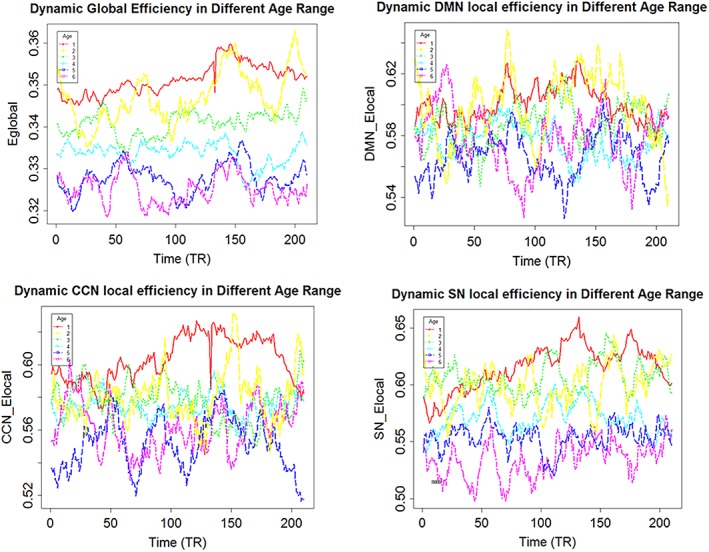
The varying curve of different age ranges in the time course. The global efficiency of young age range was always higher than it of the older age range in whole time course. The DMN local efficiency of elderly reached its peak at the beginning, while it of young reached its peak in the intermediate process. The CCN local efficiency of elderly reached its peak at the beginning, while it of young reached its peak in the second half. The SN local efficiency of elderly maintained a relative low level, while it of young had been growing up [Color figure can be viewed at http://wileyonlinelibrary.com]
3.4. Characteristic of dynamic functional connectivity states
We used sliding window approach to estimate dFNC network for each subject. For the dFNC patterns reoccur within subjects across time and across subjects, we then applied the K‐means algorithm to divide the dFNC windows into separate clusters. Figure 6 shows the centroids of the five dFNC states. In State 1, the whole network displayed slight and moderate negative connectivity. State 2 showed the high positive correlation among AUD, SMN, and VIS, while the negative correlation between SCN and other networks. In State 3, there are negative connections between DMN and other networks as well as SCN and others. In State 4, the whole network displayed slight and moderate positive connectivity, and the high positive coupling among AUD, SMN, and VIS appeared again. In State 5, AUD, SMN, and SN were negatively correlated with DMN and it displayed a whole negative pattern.
Figure 6.
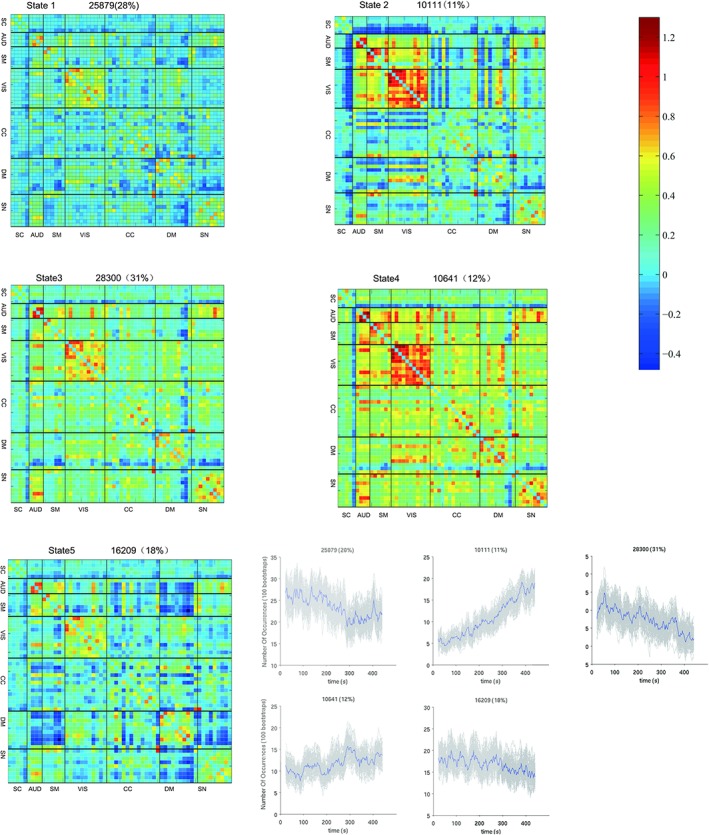
The centroids of the 5 dFNC states. In State 1, the whole network displayed slight and moderate negative connectivity. State 2 showed the high positive correlation among AUD, SMN, and VIS, while the negative correlation between SCN and other networks. In State 3, there are negative connections between DMN and other networks as well as SCN and others. In State 4, the whole network displayed slight and moderate positive connectivity, and the high positive coupling among AUD, SMN, and VIS appeared again. In State 5, AUD, SMN, and SN were negatively correlated with DMN and it displayed a whole negative pattern [Color figure can be viewed at http://wileyonlinelibrary.com]
To characterize the state topological properties, we applied a proportional network threshold of 15% and calculated global efficiency, sub‐network local efficiency and degree based on thresholded weighted networks (See Table 3). It's worth noting that State 4 has the largest global efficiency, DMN local efficiency, CC local efficiency and SN local efficiency. The hub nodes (the node of the top three degree) are located in visual and auditory cortex, DMN (posterior cingulate cortex) and CCN (supplementary motor area).
Table 3.
Graphic indexes of each state
| State indexes | State 1 | State 2 | State 3 | State 4 | State 5 |
|---|---|---|---|---|---|
| Global efficiency | 0.1938 | 0.2069 | 0.2388 | 0.3049 | 0.2005 |
| DMN local efficiency | 0.3442 | 0.3025 | 0.3830 | 0.5334 | 0.4610 |
| CCN local efficiency | 0.2932 | 0.2316 | 0.3929 | 0.4190 | 0.3625 |
| SN local efficiency | 0.3847 | 0.4412 | 0.5327 | 0.6566 | 0.4454 |
| Hub node | VIS(71,28), DMN(52) | VIS(71,55,28,54) | VIS(71,28), AUD(51,63) | VIS(28,71,55) | AUD(63), VIS(28), CCN(47) |
| N | 25,879 | 10,111 | 28,300 | 10,641 | 16,209 |
IC labels: 28, 47, 51, 52, 54, 55, 63, 71.
3.5. The correlation between WAIS and age
Firstly, the total score of WAIS and similarity were both negatively correlated with age (total score: r = −0.51, p = .000, n = 82; similarity: r = −0.49, p = .000, n = 93), and similarity was negatively correlated with transition of State 3–1 (r = −0.22, p = .031, n = 93). However, the box block design is inversely correlated to age (r = −0.53, p = .000, n = 82) and frequency of State 5 (r = −0.26, p = .019, n = 82), while the correlation between age and the frequency is not significant (r = 0.15, p = .18, n = 82). However, we think age is positively correlated with the frequency of State 5, as the total samples (n = 434) suggested the two factors are positively correlated (r = 0.11, p = .022). The size and age range of the subsample (n = 82, age range: 23–65) may be the cause of that statistical significance failed to reach borderline in subsample.
3.6. Robustness analysis
Some literature (Gonzalez‐Castillo et al., 2015; Leonardi & Van De Ville, 2015) recommend removing frequency components below 1/w (where w is the length of the window), so we used a band pass filtering of 0.023–0.18 Hz. However, others (Abrol et al., 2016; Damaraju et al., 2014) low‐pass filtered time series with a high frequency cutoff of 0.15 Hz by Gift software (http://mialab.mrn.org/software). To examine our main results, we use the second filtering parameter to reanalysis the correlation between aging and dynamic FC.
We examined the frequency of states as a function of time and the transitions between them. As our previous results, FC tends to sustain single state during a long period, while transition times are rarely less. The total dwell time (the sum of dwell time of all states) of states were positively correlated with age (r = 0.14, p = .003), while the total transition of states were negatively correlated with age (r = −0.14, p = .003). The results verified the previous finding. As aging process occurring, the pattern of functional connectivity tended to keep stable in resting period. Some states indexes were correlated with age (See SI.D), and the distribution of each state in each age range was shown in SI.E.
Then we compared the states of two analyzes (states identified in first analysis and robust analysis). Firstly, we calculated the Pearson correlation coefficient among states. Considering the correlation coefficient and visual pattern, we think State 5_second is similarity with State 4_first (See SI.F). Secondly, we applied a proportional network threshold of 15% and calculated the global efficiency, sub‐network local efficiency, and degree of each state. The State 5_second, just like State 4_first, had greatest global efficiency and sub‐network local efficiency (See SI.G). Lastly, SI.H showed the centroids of the intrinsic states.
4. DISCUSSION
4.1. Brain's dynamics functional network connectivity over aging
The present study examined the effect of age on dynamic whole‐brain FC. The analysis revealed five recurring FC states departed with substantial internetwork correlation variability. During the resting‐state period, the non‐random distribution of states in different age ranges suggested that dynamic changes of large‐scale brain network may be a fundamental feature of aging process.
Firstly, the number of transitions occurring between multi‐connectivity states and the rate of transition between states were all higher among younger than older participants. It may be suggested that the thinking is more active for young people than older people, or the speed of mind change is faster during the resting period.
Secondly, the frequency of occurrence State 1 and 5 increased over aging, while the same parameter for State 3 and 4 decreased over aging. This suggests that the patterns of State 1 and 5 occur more in the older life span, while the patterns of State 3 and 4 occur more in the young life span. The State1 and state 5 displayed a whole negative connectivity network, while State 3 and 4 had more positive connectivity among sub‐networks. This may indicated the functional brain network of young may be inclined to presented integrate pattern, while it of the elder may be inclined to presented segregate pattern during the rest period.
Thirdly, a number of studies have proposed that head motion can substantially affect functional connectivity (Power et al., 2012; Yan et al., 2013; Laumann et al., 2016;Siegel et al., 2016), however, the correlation between head motion and state dwell time is not significant in this work, which verified the dynamic FC over time is not artifacts. In this work, head motion was negatively correlated with the frequency of State 3, while positively correlated with age, and the frequency of State 3 was negatively correlated with age. Maybe the State 3 reflects the psychological characteristics associated with head movement, such as control ability, which decreases in the aging process. That is to say, head motion changes systematically with age, which may reflect true neurobiological effects of aging. (Geerligs, Tsvetanov, & Henson, 2017).
Lastly, our results suggested that dwell time is positively correlated with age, while previous literature (Hutchison & Morton, 2015) reported the dwell time is negatively correlated with age. One possible reason is that previous sample mainly focused 9–32 age range; however, the age range of our subjects included 19–80. After 32 years old, dwell time is still increasing, and 40 years old is a turning point, twists, and turns down. The different results may be caused by that we have adopted a larger age span sample. Another reason is that the two results are not necessarily comparable as we use a different number of states.
4.2. The difference among age groups in graph metrics
In this study, we examined the difference among age groups in global efficiency and local efficiency. The 19–30 age group has significant greater global efficiency and local efficiency of sub‐networks than older age group. Young have greater global efficiency than elder maybe because they have more amounts of State 4, which has largest global efficiency in all states. In State 4, the whole brain functional network displayed slight and moderate positive connectivity, and the high positive coupling among AUD, SMN, and VIS. The state distribution again verified that the functional brain network of young presented more integrate patterns than it of elder during the rest period. It is the first time to examine age impact in the graph metrics using the dynamic functional network connectivity, which provides a new perspective to observe the brain response of different people in the resting‐fMRI scan. For example, the peak and valley values of local efficiency of DMN for young and elder occurs at different points in the scanning process, which maybe means that young and elder has different cognitive processing methods.
Previous researches finding of the correlation between age and graph metrics based static functional brain network connectivity are controversial. Some found that the global efficiency of brain functional network showed no significant relationship with age (Cao et al., 2014), some indicated that increasing global efficiency is accompanied by aging (Chan et al., 2014; Sala‐Llonch et al., 2014), and others thought young have greater global efficiency than elder (Achard & Bullmore, 2007). It is necessary to make abundant of researches to find the respective meaning of static and dynamic results.
4.3. The correlation of cognitive ability and state
Firstly, the total score of WAIS and similarity were both negatively correlated with age, and similarity was negatively correlated with transition of State 3–1. The negative correlation between age and the total score of WAIS may be resulted from that the numbers of elder are few in the behavior sample and their scores are relatively low. The similarity is used to evaluate the abstract verbal reasoning as well as semantic knowledge (Wechsler, 1981). Although the ability is relatively stable in the aging process, the response speed may be influenced. In the State 3, AUD, SM, and VIS displayed the high positive correlation between networks, and the SN displayed high positive correlation within the network. This pattern maybe means that the individual is alert and receive the information from the surrounding (Kucyi, Hove, Esterman, Hutchison, & Valera, 2017). In State 1, the whole network displayed slight and moderate negative connectivity, though the AUD, SM, and VIS displayed a slight positive correlation between networks. This pattern maybe suggests that the individual experiences the resting state and decreases the attention to the outsides (Kucyi et al., 2017). Therefore, the higher this transition frequency, the more the individual's attention is to the inner world. Thus, the less attention to the outside world may be resulted the lower the similarity score.
Secondly, the box block design is inversely correlated to age and frequency of State 5, while the correlation between age and the frequency is not significant. However, we think age is positively correlated with the frequency of State 5, as the total samples (n = 434, age range: 19–80) suggested the two factors are positively correlated. The size and age range of the subsample (n = 82, age range: 23–65) may be the cause of that statistical significance failed to reach borderline in subsample. The block design test evaluates fine motor skills, processing speed, and visuospatial ability, which are decreasing accompanied by age increasing (Hoogendam et al., 2014). In State 5, AUD, SMN, and SN were negatively correlated with DMN and it displayed a whole negative pattern. The pattern of State 5 in elder may reflect a true decreasing in certain cognitive abilities.
5. CONCLUSION
The findings motivate a reconceptualization of the link between aging and FC. The previous model assumed that FC remains static throughout the resting period, neglecting the dynamic feature of the brain's functional connectivity. Our results instead suggest that these networks are, like aging process themselves, transient, and dynamic. There are also some limitations to note in our study. One potential problem is that although we provided robust analysis, the direct relationship between aging and brain state requires utilizing the independent sample (Zuo et al., 2014; Shafto et al., 2014) to verify the reliability of the results, and this work is in prepared. Secondly, using fMRI data alone, it is not possible to determine whether network changed as aging increased structure connectivity between brain regions, or whether the topological changes were merely a necessary temporary state. Besides, using functional imaging across development are age‐associated motion artifacts and physiological signals (Power et al., 2012; Lehmann, White, Henson, & Geerligs, 2017; Geerligs et al., 2017), however, the impact of these factors on dynamic FC can be minimized by larger sampling (Zuo & Xing, 2014; Zuo et al., 2014), rigorous head motion control (Laumann et al., 2016; Siegel et al., 2016) or simultaneous psychological recordings. Furthermore, Van Den Heuvel et al. (2017) found lower levels of overall FC in either the patient or control group will often lead to differences in network efficiency and clustering, therefore, examine the overall FC strength across age ranges seems essential. Finally, we plan to investigate the underlying significance of states in more detail using methods such as time‐varying analysis. Future work would focus on depicting the cognitive symbolize of connectivity state. There is a lot of useful information that we can learn from characterizing the network properties of each state individually; however, we are left with properties across multiple states.
Supporting information
Figure SI.C Cluster centroids for k = 4 to 6. The gray rectangle highlights the clustering result presented in the main text. The total number and percentage of occurrences are listed above each centroid.
Apendix S1 Supplementary Information.
ACKNOWLEDGMENTS
This research was supported by the National Natural Science Foundation of China (31470981; 31571137; 31500885), National Outstanding young people plan, the Program for the Top Young Talents by Chongqing, the Fundamental Research Funds for the Central Universities (SWU1509383,SWU1509451,SWU1609177), Natural Science Foundation of Chongqing (cstc2015jcyjA10106), Fok Ying Tung Education Foundation (151023), General Financial Grant from the China Postdoctoral Science Foundation (2015M572423, 2015M580767), Special Funds from the Chongqing Postdoctoral Science Foundation (Xm2015037, Xm2016044), Key research for Humanities and social sciences of Ministry of Education (14JJD880009).
Xia Y, Chen Q, Shi L, et al. Tracking the dynamic functional connectivity structure of the human brain across the adult lifespan. Hum Brain Mapp. 2019;40:717–728. 10.1002/hbm.24385
Funding information Fok Ying Tong Education Foundation, Grant/Award Number: 151023; National Natural Science Foundation of China, Grant/Award Numbers: 314709813150088531571137, 31470981; 31571137; 31500885; Ministry of Education, Grant/Award Number: 14JJD880009; Chongqing Postdoctoral Science Foundation, Grant/Award Number: Xm2015037, Xm2016044; China Postdoctoral Science Foundation, Grant/Award Number: 2015M572423, 2015M580767; Fok Ying Tung Education Foundation, Grant/Award Number: 151023; Natural Science Foundation of Chongqing, Grant/Award Number: cstc2015jcyjA10106; Fundamental Research Funds for the Central Universities, Grant/Award Number: SWU1509383,SWU1509451, SWU1609177
Contributor Information
Hong Chen, Email: chenhg@swu.edu.cn.
Jiang Qiu, Email: qiuj318@swu.edu.cn.
REFERENCES
- Abrol, A. , Chaze, C. , Damaraju, E. , & Calhoun, V. D. (2016). The chronnectome: Evaluating replicability of dynamic connectivity patterns in 7500 resting fMRI datasets. Paper presented at the 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, (pp. 5571–5574). [DOI] [PubMed]
- Achard, S. , & Bullmore, E. (2007). Efficiency and cost of economical brain functional networks. PLoS Computational Biology, 3(2), e17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen, E. A. , Erhardt, E. B. , Damaraju, E. , Gruner, W. , Segall, J. M. , Silva, R. F. , … Calhoun, V. D. (2011). A baseline for the multivariate comparison of resting‐state networks. Frontiers in Systems Neuroscience, 5, 2. doi: 10.3389/fnsys.2011.00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen, E. A. , Damaraju, E. , Plis, S. M. , Erhardt, E. B. , Eichele, T. , & Calhoun, V. D. (2014). Tracking whole‐brain connectivity dynamics in the resting state. Cerebral Cortex, 24, 663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen, E. A. , Damaraju, E. , Eichele, T. , Wu, L. , & Calhoun, V. D. (2018). EEG signatures of dynamic functional network connectivity states. Brain Topography, 31(1), 101–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ardila, A. (2007). Normal aging increases cognitive heterogeneity: Analysis of dispersion in WAIS‐III scores across age. Archives of Clinical Neuropsychology, 22(8), 1003–1011. [DOI] [PubMed] [Google Scholar]
- Betzel, R. F. , Byrge, L. , He, Y. , Goñi, J. , Zuo, X. N. , & Sporns, O. (2014). Changes in structural and functional connectivity among resting‐state networks across the human lifespan. NeuroImage, 102Pt 2(2), 345. [DOI] [PubMed] [Google Scholar]
- Biswal, B. , Yetkin, F. Z. , Haughton, V. M. , & Hyde, J. S. (1995). Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magnetic Resonance in Medicine, 34, 537–541. [DOI] [PubMed] [Google Scholar]
- Biswal, B. B. , Mennes, M. , Zuo, X.‐N. , Gohel, S. , Kelly, C. , Smith, S. M. , et al. (2010). Toward discovery science of human brain function. Proceedings of the National Academy of Sciences of the United States of America, 107, 4734–4739. 10.1073/pnas.0911855107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun, V. D. , Miller, R. , Pearlson, G. , & Adali, T. (2014). The chronnectome: Time‐varying connectivity networks as the next frontier in fMRI data discovery. Neuron, 84, 262–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao, M. , Wang, J. H. , Dai, Z. J. , Cao, X. Y. , Jiang, L. L. , Fan, F. M. , … Milham, M. P. (2014). Topological organization of the human brain functional connectome across the lifespan. Developmental Cognitive Neuroscience, 7, 76–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan, M. Y. , Park, D. C. , Savalia, N. K. , Petersen, S. E. , & Wig, G. S. (2014). Decreased segregation of brain systems across the healthy adult lifespan. Proceedings of the National Academy of Sciences, 111(46), E4997–E5006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damaraju, E. , Allen, E. A. , Belger, A. , Ford, J. M. , McEwen, S. , Mathalon, D. H. , … Turner, J. A. (2014). Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia. NeuroImage: Clinical, 5, 298–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux, J. S. , Beckmann, C. F. , Arigita, E. J. S. , Barkhof, F. , Scheltens, P. , Stam, C. J. , … Rombouts, S. A. R. B. (2008). Reduced resting‐state brain activity in the “default network” in normal aging. Cerebral Cortex, 18, 1856–1864. 10.1093/cercor/bhm207 [DOI] [PubMed] [Google Scholar]
- DuPre, E. , & Spreng, R. N. (2017). Structural covariance networks across the lifespan, from 6–94 years of age. Network Neuroscience, 1(3), 302–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evers, E. A. T. , Klaassen, E. B. , Rombouts, S. A. , Backes, W. H. , & Jolles, J. (2012). The effects of sustained cognitive task performance on subsequent resting state functional connectivity in healthy young and middle‐aged male school teachers. Brain Connectivity, 2, 102–112. 10.1089/brain.2011.0060 [DOI] [PubMed] [Google Scholar]
- Fair, D. A. , Dosenbach, N. U. , Church, J. A. , Cohen, A. L. , Brahmbhatt, S. , Miezin, F. M. , … Schlaggar, B. L. (2007). Development of distinct control networks through segregation and integration. Proceedings of the National Academy of Sciences, 104(33), 13507–13512. [Google Scholar]
- Friston, K. J. , Williams, S. , Howard, R. , Frackowiak, R. S. , & Turner, R. (1996). Movement‐related effects in fMRI time‐series. Magnetic Resonance in Medicine, 35(3), 346–355. [DOI] [PubMed] [Google Scholar]
- Fox, M. D. , Snyder, A. Z. , Vincent, J. L. , Corbetta, M. , Van Essen, D. C. , & Raichle, M. E. (2005). The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences of the United States of America, 102, 9673–9678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geerligs, L. , Tsvetanov, K. A. , & Henson, R. N. (2017). Challenges in measuring individual differences in functional connectivity using fMRI: The case of healthy aging. Human Brain Mapping, 38, 4125–4156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong, Y. X. (1992). Chinese version of the Wechsler adult intelligence scale (WAIS‐RC) (p. 35150). Changsha: Hunan Map Publishing House. [Google Scholar]
- Greicius, M . (2008). Resting‐state functional connectivity in neuropsychiatric disorders. Current opinion in neurology, 21(4), 424–430. [DOI] [PubMed] [Google Scholar]
- Gonzalez‐Castillo, J. , Hoy, C. W. , Handwerker, D. A. , Robinson, M. E. , Buchanan, L. C. , Saad, Z. S. , & Bandettini, P. A. (2015). Tracking ongoing cognition in individuals using brief, whole‐brain functional connectivity patterns. Proceedings of the National Academy of Sciences, 112(28), 8762–8767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison, R. M. , & Morton, J. B. (2015). Tracking the brain's functional coupling dynamics over development. Journal of Neuroscience, 35(17), 6849–6859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoogendam, Y. Y. , Hofman, A. , van der Geest, J. N. , van der Lugt, A. , & Ikram, M. A. (2014). Patterns of cognitive function in aging: The Rotterdam study. European Journal of Epidemiology, 29(2), 133–140. [DOI] [PubMed] [Google Scholar]
- Tsvetanov, K. A. , Henson, R. N. A. , Tyler, L. K. , Razi, A. , Geerligs, L. , Ham, T. E. , & Rowe, J. B. (2016). Extrinsic and intrinsic brain network connectivity maintains cognition across the lifespan despite accelerated decay of regional brain activation. The Journal of Neuroscience, 36(11), 3115–3126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman, A. S. , & Lichtenberger, E. O. (2005). Assessing adolescent and adult intelligence, Hoboken, New Jersy: John Wiley & Sons Inc. [Google Scholar]
- Ketchen, D. J., Jr. , & Shook, C. L. (1996). The application of cluster analysis in strategic management research: An analysis and critique. Strategic Management Journal, 17, 441–458. [Google Scholar]
- Kucyi, A. , Hove, M. J. , Esterman, M. , Hutchison, R. M. , & Valera, E. M. (2017). Dynamic brain network correlates of spontaneous fluctuations in attention. Cerebral Cortex, 27(3), 1831–1840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latora, V. , & Marchiori, M. (2001). Efficient behavior of small‐world networks. Physical Review Letters, 87(19), 198701. [DOI] [PubMed] [Google Scholar]
- Laumann, T. O. , Snyder, A. Z. , Mitra, A. , Gordon, E. M. , Gratton, C. , Adeyemo, B. , … McCarthy, J. E. (2016). On the stability of bold fmri correlations. Cerebral Cortex, 27(10), 4719–4732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann, B. C. , White, S. R. , Henson, R. N. , & Geerligs, L. (2017). Assessing dynamic functional connectivity in heterogeneous samples. NeuroImage, 157, 635–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leonardi, N. , & Van De Ville, D. (2015). On spurious and real fluctuations of dynamic functional connectivity during rest. NeuroImage, 104, 430–436. [DOI] [PubMed] [Google Scholar]
- Liu, F. , Wang, Y. , Li, M. , Wang, W. , Li, R. , Zhang, Z. , & Chen, H. (2016). Dynamic functional network connectivity in idiopathic generalized epilepsy with generalized tonic‐clonic seizure. Human Brain Mapping, 38(2), 957–973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power, J. D. , Barnes, K. A. , Snyder, A. Z. , Schlaggar, B. L. , & Petersen, S. E. (2012). Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage, 59(3), 2142–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power, J. D. , Fair, D. A. , Schlaggar, B. L. , & Petersen, S. E. (2010). The development of human functional brain networks. Neuron, 67, 735–748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power, J. D. , Mitra, A. , Laumann TO , Snyder, A. Z. , Schlaggar, B. L. , & Petersen, S. E. (2014). Methods to detect, characterize, and remove motion artifact in resting state fMRI. NeuroImage, 84, 320–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roweis, S. (1998). EM algorithms for PCA and SPCA. Neural Information Processing Systems, 10, 626–632. [Google Scholar]
- Sala‐Llonch, R. , Junqué, C. , Arenaza‐Urquijo, E. M. , Vidal‐Piñeiro, D. , Valls‐Pedret, C. , Palacios, E. M. , … Bartrés‐Faz, D. (2014). Changes in whole‐brain functional networks and memory performance in aging. Neurobiology of Aging, 35(10), 2193–2202. [DOI] [PubMed] [Google Scholar]
- Shafto, M. A. , Tyler, L. K. , Dixon, M. , Taylor, J. R. , Rowe, J. B. , Cusack, R. , … Henson, R. N. (2014). The Cambridge centre for ageing and neuroscience (Cam‐Can) study protocol: A cross‐sectional, lifespan, multidisciplinary examination of healthy cognitive ageing. BMC Neurology, 14(1), 204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel, J. S. , Mitra, A. , Laumann, T. O. , Seitzman, B. A. , Raichle, M. , Corbetta, M. , & Snyder, A. Z. (2016). Data quality influences observed links between functional connectivity and behavior. Cerebral Cortex, 27(9), 4492–4502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, S. M. , Fox, P. T. , Miller, K. L. , Glahn, D. C. , Fox, P. M. , Mackay, C. E. , … Laird, A. R. (2009). Correspondence of the brain's functional architecture during activation and rest. Proceedings of the National Academy of Sciences, 106, 13040–13045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song, J. , Birn, R. M. , Boly, M. , Meier, T. B. , Nair, V. A. , Meyerand, M. E. , & Prabhakaran, V. (2014). Age‐related reorganizational changes in modularity and functional connectivity of human brain networks. Brain Connectivity, 4(9), 662–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomason, M. E. , Chang, C. E. , Glover, G. H. , Gabrieli, J. D. , Greicius, M. D. , & Gotlib, I. H. (2008). Default‐mode function and task‐induced deactivation have overlapping brain substrates in children. NeuroImage, 41, 1493–1503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel, M. P. , de Lange, S. C. , Zalesky, A. , Seguin, C. , Yeo, B. T. , & Schmidt, R. (2017). Proportional thresholding in resting‐state fMRI functional connectivity networks and consequences for patient‐control connectome studies: Issues and recommendations. NeuroImage, 152, 437–449. [DOI] [PubMed] [Google Scholar]
- Wechsler, D. (1981). Scale‐revised (Vol. 1, p. 309). New York: W. A. I. The Psychological Corporation. [Google Scholar]
- Wei, D. , Zhuang, K. , Ai, L. , Chen, Q. , Yang, W. , Liu, W. , … Qiu, J. (2018). Structural and functional brain scans from the cross‐sectional Southwest University adult lifespan dataset. Scientific data, 5. [DOI] [PMC free article] [PubMed]
- Whitfield‐Gabrieli, S. , & Nieto‐Castanon, A. (2012). Conn: A functional connectivity toolbox for correlated and anticorrelated brain networks. Brain Connectivity, 2, 125–141. [DOI] [PubMed] [Google Scholar]
- Yan, C. G. , Cheung, B. , Kelly, C. , Colcombe, S. , Craddock, R. C. , Di Martino, A. , … Milham, M. P. (2013). A comprehensive assessment of regional variation in the impact of head micromovements on functional connectomics. NeuroImage, 76, 183–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan, C. G. , Wang, X. D. , Zuo, X. N. , & Zang, Y. F. (2016). DPABI: Data Processing & Analysis for (resting‐state) brain imaging. Neuroinformatics, 14, 339–351. 10.1007/s12021-016-9299-4 [DOI] [PubMed] [Google Scholar]
- Zuo, X. N. , Anderson, J. S. , Bellec, P. , Birn, R. M. , Biswal, B. B. , Blautzik, J. , … Milham, M. P. (2014). An open science resource for establishing reliability and reproducibility in functional connectomics. Scientific Data, 1, 140049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo, X. N. , He, Y. , Betzel, R. F. , Colcombe, S. , Sporns, O. , & Milham, M. P. (2017). Human Connectomics across the life span. Trends in Cognitive Sciences, 21, 32–45. [DOI] [PubMed] [Google Scholar]
- Zuo, X. N. , & Xing, X. X. (2014). Test‐retest reliabilities of resting‐state fmri measurements in human brain functional connectomics: A systems neuroscience perspective. Neuroscience & Biobehavioral Reviews, 45, 100–118. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure SI.C Cluster centroids for k = 4 to 6. The gray rectangle highlights the clustering result presented in the main text. The total number and percentage of occurrences are listed above each centroid.
Apendix S1 Supplementary Information.


