A difference degree test for comparing brain networks

Abstract

Recently, there has been a proliferation of methods investigating functional connectivity as a biomarker for mental disorders. Typical approaches include massive univariate testing at each edge or comparisons of network metrics to identify differing topological features. Limitations of these methods include low statistical power due to the large number of comparisons and difficulty attributing overall differences in networks to local variation. We propose a method to capture the difference degree, which is the number of edges incident to each region in the difference network. Our difference degree test (DDT) is a two‐step procedure for identifying brain regions incident to a significant number of differentially weighted edges (DWEs). First, we select a data‐adaptive threshold which identifies the DWEs followed by a statistical test for the number of DWEs incident to each brain region. We achieve this by generating an appropriate set of null networks which are matched on the first and second moments of the observed difference network using the Hirschberger–Qi–Steuer algorithm. This formulation permits separation of the network's true topology from the nuisance topology induced by the correlation measure that alters interregional connectivity in ways unrelated to brain function. In simulations, the proposed approach outperforms competing methods in detecting differentially connected regions of interest. Application of DDT to a major depressive disorder dataset leads to the identification of brain regions in the default mode network commonly implicated in this ruminative disorder.

1. INTRODUCTION

In recent years, graph theoretical tools have become increasingly important in the analysis of brain imaging data. In particular, evaluations of the associations between spatially distinct regions have led to valuable insights into the brain's organization in health and disease. Functional connectivity (FC), which measures the coherence between neurophysiological time series (Friston, 1994), has been extremely valuable in identifying disease‐induced modifications to cortical and subcortical (SUB) communication. In fact, altered cortical activity has been observed in major depressive disorder (MDD) (Craddock, Holtzheimer, Hu, & Mayberg, 2009; Drysdale et al., 2017), Alzheimer's disease (Stam, Jones, Nolte, Breakspear, & Scheltens, 2006), and schizophrenia (Liu et al., 2008; Rubinov & Sporns, 2010). While Pearson correlation is a widely used FC measure, alternate association metrics such as partial correlations (Wang, Kang, Kemmer, & Guo, 2016), mutual information (Salvador et al., 2005), and coherence (Bassett et al., 2011) are finding favor. Brain networks have become particularly important since the FC measures offer different perspectives on coactivation between brain regions, and many studies agree that psychiatric disorders and neurodegenerative diseases manifest as disruptions in local and global FC (Pandya, Altinay, Malone, & Anand, 2012).

Recently, Simpson and Laurienti (2016) classify the growing literature on network connectivity methods into two categories based on the intentions to compare connectivity differences locally at the edge level or network‐wide topological features. Many of the developed methods investigate differences at the edge level. In fact, the earliest approach tests for group differences at each edge in the network (Nichols & Holmes, 2002). For a network with N regions, this requires multiple testing corrections since N(N‐1)/2 unique edges must be assessed. Unfortunately, controlling the familywise error rate or false discovery rate (FDR) leads to a reduction in power to detect group differences at the edge level. The sum of powered score (SPU), adaptive SPU test (Pan, Kim, Zhang, Shen, & Wei, 2014), and PARD (Chen, Kang, Xing, & Wang, 2015) leverage edge level differences to assess overall deviation in the networks (Kim, Wozniak, Mueller, & Pan, 2015). While they can lead to highly powered tests, there are practical difficulties in selecting the optimal tuning parameter. Furthermore, the tests do not specifically identify edges, regions, or structures contributing to overall network differences, which complicate interpretation of the results. Shehzad et al. (2014) propose a distance‐based framework for detecting voxels associated with a phenotypic outcome such as disease status. Unlike the previous approaches, the authors use clustering to select statistically meaningful voxels which avoids the power reduction inherent in multiple testing correction procedures.

Other approaches assume differences in brain connectivity contribute to coordinated, connected disruptions across multiple brain subsystems. The popular network‐based statistic (NBS) (Zalesky, Fornito, & Bullmore, 2010) identifies collections of differentially weighted edges (DWEs) forming interconnected subcomponents but has limited exploratory value. A key assumption is that altered edges form connected subnetworks (Kim et al., 2015). The NBS is severely underpowered to detect differences in the networks if this assumption is violated (Zalesky et al., 2010). Furthermore, the NBS does not provide a principled approach for thresholding significant DWEs. As shown in Kim, Wozniak, Mueller, Shen, and Pan (2014), the NBS performance is reported across a grid of thresholds. In simulations, one can heuristically tune the threshold to produce the best performance. However, threshold selection becomes substantially more difficult in real data applications. In simulations and real data applications, we find that the NBS (extent) is unable to detect connected components spanning the difference network across a wide range of thresholds. We note that the NBS is fundamentally different from the DDT. Whereas the NBS detects fully connected components comprised of DWEs, the DDT is attuned to local clustering of DWEs at each node.

Other methods (Rudie et al., 2013; Wang et al., 2015) have focused on comparing graph metrics across networks, using two sample t tests to test for differences. Unfortunately, these tests are often underpowered to detect group differences (Kim et al., 2014), and there are doubts on the suitability of two‐sample t tests to compare some network metrics (Fornito, Zalesky, & Bullmore, 2010). Alternatively, nonparametric approaches utilize permutation tests (Simpson, Lyday, Hayasaka, Marsh, & Laurienti, 2013; Zalesky et al., 2010) to assess differences in the networks' topological features or generate random networks (Bassett et al., 2009) in order to construct distributions for network metrics of interest under the null hypothesis and then use these reference distributions to evaluate the significance of the observed network features. However, generating an appropriate null network is nontrivial. Existing approaches attempt to randomly rewire edges while preserving the degree distribution and the clustering coefficient (Bansal, Khandelwal, & Meyers, 2009; Maslov & Sneppen, 2002; Volz, 2004). Unfortunately, the network generation schemes are sensitive to the desired network measure (see Fornito, Zalesky, and Breakspear (2013) for an overview) and may not provide a complete picture of the network differences reflected by alternate summary measures.

In this article, we propose a difference degree test (DDT) to identify brain regions contributing to local and global disruptions in cortical communication. The DDT is composed of two steps: (a) identify edges that are differentially weighted across populations and (b) identify hub nodes incident to a statistically significant number of such edges. Despite the naming convention, the difference degree is not the difference of the nodal degree in the connectivity matrices. Rather, it assesses the incongruency of the observed number of DWEs incident to a region with the expected count in a network replicating only nuisance structures. Our approach relies on accurate estimation of the difference network, referred to in earlier literature as the differential statistical parametric network (Ginestet, Fournel, & Simmons, 2014). Edge weights in the difference network represent the statistical significance of between‐group comparisons between all region pairs. The Hirschberger–Qi–Steuer (HQS) algorithm (Hirschberger, Qi, & Steuer, 2007) allows us to perform the two steps of the DDT using the derived difference network. The algorithm produces null networks which follow the first and second moment characteristics of the observed difference network. Such networks preserve the nuisance topology present in the observed network while simultaneously annihilating all intrinsic structure. We identify important edges by leveraging distributional properties of the HQS‐generated null networks. The cutoff value defining the suprathresholded edges ensures the null and observed networks attain a common density. This is especially important given the well‐reported positive relationship between many network features and the network's density. From the adjacency matrices, we subsequently identify brain regions incident to a statistically significant number of such edges.

HQS is paramount to both steps of the DDT. Notably, the algorithm generates random networks that are appropriately matched to the observed network. In contrast, naively generated random networks, that is, random edge rewiring and random edge sampling, produce nulls which annihilate intrinsic and nuisance topologies present in the observed network. Although these approaches can quickly generate random network configurations, the graphs are inappropriate benchmarks for the observed network. Any inference based on this collection of nulls will be severely impacted. Further, conclusions about the sources of disrupted cortical communication are likely erroneous.

Through extensive simulations, we illustrate that the proposed method has greater power to detect differentially connected nodes across networks compared to standard multiple testing procedures, while also maintaining reasonable control over false positives. Furthermore, the adaptive threshold selection procedure leads to increased power to detect DWEs across the network as compared to Bonferroni and FDR correction procedures. Additionally, the adaptive threshold approach under the proposed method can automatically adapt to different network settings and hence is more generalizable compared to “hard” thresholding approaches assuming a fixed threshold. Finally, we apply the proposed approach to a MDD dataset, which leads to meaningful findings regarding disrupted brain connectivity attributed to the disorder.

The rest of this article is organized as follows. In Section 2, we discuss the construction of null difference networks, the proposed procedure, simulated data setting for the numerical studies, and functional magnetic resonance imaging (fMRI) preprocessing details. We present simulation and real data results in Sections 3.1 and 3.2, respectively. Section 4 presents a discussion of practical and clinical significance.

2. METHODS

2.1. Data application

Existing literature has identified multiple brain regions implicated in MDD. For example, patients exhibit reduced connectivity in the frontoparietal network (FPN) as well as modified activity in areas such as the insula (Deen, Pitskel, & Pelphrey, 2010), amygdala (Sheline, Gado, & Price, 1998), hippocampus (Lorenzetti, Allen, Fornito, & Yuücel, 2009; Schweitzer, Tuckwell, Ames, & O'brien, 2001), dorsomedial thalamus (Fu et al., 2004; Kumari et al., 2003), subgenual, and dorsal anterior cingulate cortex (Mayberg et al., 1999). We apply the DDT to an MDD resting‐state (rs) fMRI study (Dunlop et al., 2017) to investigate brain regions contributing to differences in overall functional network organization in the affected population.

To construct brain network, we choose the 264‐node system defined by Power et al. (2011). Each node is a 10 mm diameter sphere in standard MNI space representing a putative functional area consistently observed in task‐based and rs‐fMRI meta‐analysis. We focus upon 259 nodes located in cortical and subcortical regions, excluding a few nodes lying in the cerebellum. Each node is assigned to one of 12 functional modules defined in Power et al. (2011): sensor/somatomotor (SM), cingulo‐opercular task control (CIO), auditory (AUD), default mode network (DMN), memory retrieval (MEM), visual (VIS), FPN, salience (SAL), subcortical (SUB), ventral attention network (VAN), dorsal attention network (DAN), and uncertain (UNC).

We measure the functional association between all pairs of brain regions with Pearson correlation and partial correlation. Partial correlations are estimated using the DensParcorr R package (Wang et al., 2016). For both correlation measures, we conduct the between‐group tests on the Fisher Z‐transformed correlation coefficient at each edge and derive both the unadjusted p‐values when confounding variables are not accounted for and also the adjusted p‐values when they are accounted for. We construct the difference networks based on the model‐free and model‐based between‐group test p‐values for connectivity measured by both Pearson correlation and partial correlation. We apply the two variations of the proposed DDT to identify brain regions incident to a statistically significant number of DWEs. Subsequently, we investigate the distribution of the DWEs across the networks as well as between and within functional modules. Although the NBS is widely used, it did not detect any group differences over a wide range of thresholds, including that suggested by Zalesky et al. (2010).

2.1.1. Subjects and preprocessing

The data consists of rs‐fMRI scans from 20 MDD subjects and 19 healthy subjects. MDD patients are on average 45.8 years old (SD: 9.6 years) and 50% male. The matched healthy participants are 47% male and 43 years old (SD: 8.9 years). MDD patients exhibited severe symptoms (mean score 19 (SD: 3.4)) as measured by the 17‐item, clinician‐rated Hamilton Rating Scale for Depression (Brown et al., 2008).

During rs‐fMRI scans, participants were instructed to rest with eyes closed without an explicit task. Data were acquired on a 3T Tim Trio MRI scanner with a 12‐channel head array coil. fMRI images were captured with a z‐saga sequence to minimize artifacts in the medial prefrontal cortex and orbitofrontal cortex due to sinus cavities (Heberlein & Hu, 2004). Z‐saga images were acquired interleaved at 3.4 × 3.4 × 4 mm³ resolution in 30 4‐mm thick axial slices with the parameters field of view = 220 × 220 mm², repetition time = 2,920 ms, echo time = 30 ms for a total of 150 acquisitions and total duration 7.3 min. Several standard preprocessing steps were applied to the rs‐fMRI data, including despiking, slice timing correction, motion correction, registration to MNI 2 mm standard space, normalization to percent signal change, removal of linear trend, regressing out the cerebrospinal fluid, white matter, and six movement parameters, band‐pass filtering (0.009–0.08), and spatial smoothing with a 6 mm Full Width Half Maximum Gaussian kernel.

2.2. Numerical studies

We conduct extensive simulation studies to assess the performance of the DDT. Our primary interest is how well the DDT detects regions incident to many DWEs. Additionally, we assess the performance of the DDT's thresholding procedure for identifying DWEs. Unless otherwise noted, the generated networks contain N = 35 nodes, and we consider sample sizes of 20 and 40 for each of the two groups. For the first set of simulations, we consider the case where there is only one node in the network incident to a specified number of DWEs. Without loss of generality, we refer to it as Node 2, and assess whether the proposed DDT can accurately identify this node. We consider both DDT methods, that is, aDDT based on parametric percentiles and eDDT based on empirical percentiles in the adaptive thresholding step. Three network structures are considered in the simulation: (a) random, (b) small world, and (c) hybrid. Random networks contain edges that are equally likely to be positive or negative for all connections. We generate this structure by sampling edge weights independently from an N (0, .04) distribution, which produces a connectivity matrix with no structural zeros. The small world network retains the cliquishness of the regular lattice and the short path length of the random network. Additionally, it retains small world properties observed in functional and structural brain networks (Bassett & Bullmore, 2006; Hilgetag & Goulas, 2016; Salvador et al., 2005). The hybrid network seeks to fuse the block diagonal structure observed in real brain networks, while maintaining the small worldness inherent to human brains. The “blocks” correspond to functional modules observed in the brain such as the DMN and VIS networks.

In order to evaluate the performance of our method, we simulate data similar to that of Chen et al. (2015) and Zalesky et al. (2010). All subjects share a common base brain network, B, which is a correlation matrix generated according to the random, small world, and hybrid network structure. The hybrid network structure is a subset of the interregional correlations for one healthy individual in the major depression disorder study. The random correlation network structure is generated by cross correlating N time series, where each contains 500 timepoints sampled from a zero mean multivariate normal distribution with a diagonal covariance structure. Finally, the small world correlation structure is generated from inhouse functions that define a small world precision matrix. We covert this structure to a partial correlation matrix using the transformation proposed by Whittaker (1990).

We perturb the edge weights in B to induce subject‐level correlation network while controlling the distribution of DWEs across the populations. For subjects i ₁ = 1, …, n ₁ and i ₂ = 1, …, n ₂ in the two groups, we generate the subject‐level networks, H _i1 and H _i2, as follows: for n ₁ subjects in Group 1, H _i1 = B + W _i1, where W _i1 ∈R^N × N,w _ij,i1 ∼ N(0, .02) for 1 ≤ i < j ≤ N = 35 and w _ij,i1 = 0 ∀ i = j; for n ₂ subjects in population two, H _i2 = B + W _i2 where W _i2 ∈ R^N × N. Let I be the set of differentially connected nodes where I = {2} for the first set of simulation. For i ∈ l, we generate q off‐diagonal elements corresponding to the DWEs in the ith row and column edges connected with i from N(.1, .02) and other edges of i from N(0, .02). For i ∉ I, we have w _ij,i2 ∼ N(0, .02). We consider q = 4, 7, and 11 to assess our method's power to detect differentially connected region(s) when the number of DWEs increases. We construct the difference network with model‐free p‐values, where we conduct a two sample t test and record one minus the p‐value as the weight for each edge in the difference network.

We compare the performance of DDT to that of two other tests. The first comparison method (T _(10%)) is a standard two sample t test of local nodal degree. For this test, we threshold the subject‐specific correlation matrices to attain 10% density, evaluate the subject‐level degree measure at each node and then perform a two sample t test to compare the nodal degree across groups. We also investigated but did not include the results obtained from 15% density and 1% network density, which were less powerful in detecting differentially connected regions than 10% density. We also consider two binomial tests which are similar to DDT in that they directly assess the number of DWEs incident to a node but differ from DDT in that they apply some multiple comparison corrections to detect the DWEs. Specifically, the first binomial test, Bin_B, applies a Bonferroni correction to detect the DWEs (Tyszka, Kennedy, Paul, & Adolphs, 2013) and the second binomial test, Bin_F, implements a less stringent FDR multiple testing correction. For both binomial tests, each node's difference degree is the sum of all DWEs incident to it. Finally, we consider the performance of the NBS (extent). The method does not detect group differences across a wide range of thresholds and significance levels.

In the second set of simulations, we assess the methods' performances when there are three differentially connected regions. We consider two scenarios in this setting. First, the network size is fixed while the number of DWEs varies with q = 4, 7, and 11. Second, we fix the proportion of DWEs for the differentially connected nodes to be 30% while increasing the size of the network. We report various metrics to quantify the methods' accuracy in detecting differentially connected nodes across the simulations. The false positive rate (FPR) is calculated as ${\sum }_{s=1}^S{\sum }_{n=1}^{N}I\left({\widehat{R}}_{n,s}=1,R_n=0\right)/\left(S*N\right)$ and quantifies the chance that each method incorrectly identifies a differentially connected region. The true positive rate (TPR) is calculated as ${\sum }_{s=1}^S{\sum }_{n=1}^{N}I\left({\widehat{R}}_{n,s}=1,R_n=1\right)/\left(S*N\right)$ and measures the correct identification. Here, S is the total number of simulations. ${\widehat{R}}_{n,s}$ takes the value 1 if region n in simulation s is selected as differentially connected and 0 otherwise. R _n is a binary indicator of whether region n is differentially connected in the ground truth. We compare accuracy in selecting truly differentially connected regions by Matthews correlation coefficient (MCC) (Johnstone, Milward, Berretta, Moscato, & Initiative, 2012), which is a popular measure for accessing the correspondence between predicted and true class labels. MCC, which is computed as $\raisebox{1ex}{$\mathrm{TP}\times \mathrm{TN}-\mathrm{FP}\times \mathrm{FN}$}\!\left/ \!\raisebox{-1ex}{$\sqrt{\left(\mathrm{TP}+\mathrm{FP}\right)\left(\mathrm{TP}+\mathrm{FN}\right)\left(\mathrm{TN}+\mathrm{FP}\right)\left(\mathrm{TN}+\mathrm{FN}\right)}$}\right.$, takes values in [−1,1] where 1 indicates perfect agreement between the predicted and true class labels, 0 no agreement, and −1 inverse agreement. In this formula, TP, TN, FP, and FN denote the number of nodes that are true positives, true negatives, false positives, and false negatives, respectively. In a supplementary analysis of the simulation results, we assess the performance of the adaptive thresholding procedures presented in Section 2.3.5 in correctly detecting DWEs. We compare the MCC in selecting the true DWEs based on the proposed aDDT and eDDT thresholding procedures with that based on two hard thresholds at .95 and .99 as well as based on multiple comparison corrections thresholds using the Bonferroni and FDR methods.

In the third set of simulations, we investigate the performance of the DDT when the DWEs form a connected component (contrast) as examined in Zalesky et al. (2010). First, we sample a random network and estimate the minimal spanning tree (igraph R package) which defines the contrast. We modify the settings in the first simulation where the DWEs comprising the contrast have unit mean in one group and zero mean in the second group (unit variance in both groups). All other edges are sampled from a standard normal distribution. We simulate 1,000 datasets where each dataset contains 20 contrast‐free networks and 20 contrast‐incorporated networks. We report the number of times each node is selected as a differentially connected region across all simulation runs.

2.3. DDT methodology

2.3.1. Brain network construction

In network analysis of neuroimaging data, the brain can be represented as a graph defined by a finite set of nodes (brain regions) and edges showing the statistical association between pairs of nodes. For N regions in the node set η, the network is represented as a symmetric N × N connectivity matrix, G, which can be thresholded to obtain the adjacency matrix A, representing the edge set of the network. For selection of the node system, the naive approach is to treat each voxel as a putative region of interest. This approach results in an extremely high‐dimensional connectivity matrix that not only poses challenges for subsequent analyses, but also tends to be unreliable and noisy. A more common approach is to define nodes based on anatomically defined brain structures, for example, automated anatomical labeling atlas (Tzourio‐Mazoyer et al., 2002) and Harvard–Oxford atlases (Fischl et al., 2004; Frazier et al., 2005). When analyzing brain functional networks, it is suggested to parcellate the brain into putative functional areas based on clusters of voxels exhibiting similar signals in rs‐fMRI data (Craddock et al., 2009). Some widely used examples of functionally defined node systems are the Power 264 node system (Power et al., 2011), Yeo (Yeo et al., 2011), and Gordon (Gordon et al., 2014) atlases, among others.

For brain networks based on fMRI, the edges represent the coherence in the temporal dynamics between the blood oxygen‐level‐dependent signal between node pairs. In this article, we utilize undirected measures of connectivity such as Pearson and partial correlation, where Pearson correlation measures the marginal association between two regions and partial correlation measures their association conditioned on all other regions in the network. Given the heavy debate on the merits and disadvantages of each correlation measure in brain network analysis (Kim et al., 2015; Liang et al., 2012), we investigate both and compare the findings.

The resulting network, G, is a weighted graph representing undirected statistical associations between all pairs of nodes. Often, a thresholding procedure is applied to produce a binary adjacency matrix, A, where a value of 1 in the (i,j)th entry indicates a connection between the respective regions. This network formulation is particularly advantageous as it simplifies calculations of graph metrics and leads to intuitive metric definitions (see Bullmore and Bassett (2011); Rubinov and Sporns (2010) for more details).

Since we are interested in between‐group differences in functional networks, we consider a difference network which is defined on the same node system as the functional network but the edges represent the strength of between‐group differences in the functional connections. Details of the difference network construction are presented in the following section. We focus on the number of thresholded edges incident to each region in the difference network, which we call the difference degree. Similar to the interpretation of nodal degree in connectivity matrices, we focus upon this metric as it suggests regions contributing to local differences in the network architecture across diseases or conditions. We believe that a brain region incident to a large number of DWEs is potentially responsible for overall differences in brain network topology, without being sensitive to any particular network summary measure commonly used to capture connectome differences.

2.3.2. Difference network construction

Suppose we are comparing networks between two groups with n _r subjects in group r (r = 1, 2). Denote ${\mathrm{G}}^{{\mathrm{k}}_{\mathrm{r}}}$ = {$g_{r,\mathit{ij}}^{k_r}$} (k _r = 1, …, n _r) as the estimated brain connectivity matrices for the k _r ^th subject in the rth group (r = 1,2) and $g_{r,\mathit{ij}}^{k_r}$ denotes the connectivity measure (such as the Pearson or partial correlation) between nodes i and j (i, j ∈ η = {1, …, N}) for the k _rth subject in the rth group. The first step of DDT is to construct a N × N difference network D = {d _ij: i, j ∈ η}, where d _ij represents the statistical significance of population‐level differences in the connection strength between nodes i and j, that is,

$$d_{\mathit{ij}}=1-p\left(\left\{g_{1,\mathit{ij}}\right\},\left\{g_{2,\mathit{ij}}\right\}\right)\in \left[0,1\right)$$ (1)

where p({g _1,ij},{g _2,ij}) is the p‐value of a between‐group difference test based on the estimated connectivity measures at edge (i,j) across subjects in the two groups. For example, one can obtain the p‐value by applying two‐sample t test to {$g_{r,\mathit{ij}}^{k_1}$} and {$g_{r,\mathit{ij}}^{k_2}$}. We will provide more detailed discussion on how to derive the p‐values from various types of between‐group tests in Section 2.3.3. From Equation (1), each element in the difference network d _ij serves as our measure of the difference of the edge connectivity g _r,ij between the two groups, with larger values (i.e., smaller p‐values) corresponding to larger group differences at the (i,j)th edge, and vice versa. Note that D = {d _ij} is a symmetric matrix where ∀i,j ∈η, d _ij = d _ji, and d _ij = 0 for i = j given that we are not interested in the diagonal elements.

From the difference network D = {d _ij}, we can derive the difference adjacency matrix A = {a _ij}, where a _ij represents the presence of group differences in the connection between nodes i and j, that is,

$$a_{\mathit{ij}}=I\left(d_{\mathit{ij}}>\tau \right)$$ (2)

where τ is a threshold for selecting edges which are differentially weighted. When d _ij exceeds the threshold, τ, or equivalently the p‐value for the group test is smaller than 1 − τ, we obtain a _ij = 1 indicating the presence of group difference at the edge (i,j). Otherwise, a _ij = 0 represents no group difference at the edge (i,j). In the following section, we will present a data‐driven adaptive threshold selection method for finding τ.

Based on the difference adjacency matrix A, we define the following difference degree measure for the ith node (i = 1,…,N),

$$d_i=\sum _{j\in \mathrm{\eta },j\ne i}{a}_{\mathit{ij}}$$ (3)

The difference degree measure, d _i, represents the number of connections to node i that are significantly different between the two groups as captured by edge‐wise p‐values without multiplicity adjustments. In subsequent steps of the DDT, d _i will be used as the test statistic for investigating node i's contribution to disrupted communication in the brain. While the difference network provides edge‐level information on between‐group differences, it is widely accepted that cognitive deficits in mental diseases are demarcated by disruptions in systems (Catani & ffytche, 2005). Thus, collections of connected DWEs are more consistent with the system wide disruption paradigm than evaluation of individual DWEs. The DWEs incident to each node form a locally connected component and indicate that irregular activity at the node of interest contributes to differentiated coactivation with adjacent regions. Investigation at the nodal level not only has biological justification, but also substantially improves the multiple testing problem. The number of statistical tests scales linearly with the network's size rather than quadratically at the edge level. The notion of disruptions in subsystems has also been used in previous work to mitigate the multiplicity problem common to network comparisons (Zalesky et al., 2010).

2.3.3. Deriving p‐value from between‐group tests

The p‐value used to define the difference network in Equation (1) can be derived based on various between‐group testing procedures. The p‐values fall into two categories: model‐free and model‐based. The model‐free p‐values are derived based on parametric or nonparametric tests between the two groups of subjects without accounting for the subjects' biological or clinical characteristics. The common choices of such tests include the two‐sample t test, the nonparametric Wilcoxon rank sum test, or the permutation test. The model‐based p‐values are derived from regression models where the subject‐specific connectivity measure (or some transformation) is modeled in terms of group membership and other relevant factors such as age and gender that may affect the brain connectivity. These p‐values for between‐group difference can then be derived based on the test of the parameter in the model associated with the group covariate. This model‐based p‐value reflects the degree of group differences while controlling for potential confounding effects. In many neuroimaging studies, subjects' group memberships are not based on randomization but rather based on observed characteristics. In this case, the distribution of subjects' demographic and clinical variables tends to be unbalanced between the groups and there often exist some potential confounding factors in between group comparisons (Satterthwaite et al., 2014). For such studies, it may not be the case that the model‐based p‐values more accurately reflect group‐induced variation in FC as compared with model‐free p‐values.

We note that when computing the difference network in Equation (1), the proposed approach does not apply a multiple testing correction to the edge‐wise between‐group test p‐values. Such multiplicity adjustment often reduces the power to detect DWEs. Additionally, since our goal is to detect differentially expressed nodes in the brain network, a multiplicity adjustment on the edge‐wise tests is not crucial, provided the falsely identified DWEs are more or less uniformly distributed across the nodes without systematic differences. In such a case, the threshold τ in Equation (2), which is chosen using an appropriately constructed null distribution as in Section 2.3.4, automatically adjusts for falsely identified DWEs occurring across nodes. Indeed, extensive simulation studies where the proposed method is able to control false positives at a nominal value.

2.3.4. Null distribution generation

After constructing the difference network D = {d _ij} and deriving the difference degree measure, d _i, for each node, the next step in the DDT procedure is to conduct a statistical test to evaluate whether there is significant group difference in the connections to the node. As a standard strategy in hypothesis testing, we will evaluate the test statistic, d _i, with respect to its null distribution under the hypothesis that there are no between‐group differences. For this purpose, we first derive the null distribution by generating difference networks under the null hypothesis.

We present a procedure for generating null difference networks that maintain some of the fundamental characteristics of the observed difference networks but have a random pattern of between‐group differences which is expected under the null hypothesis. Since the elements in the difference network lie within a restricted range, that is, (0,1), we first apply a logit transformation, that is,

$$\overline{D}=\left\{{\overline{d}}_{\mathit{ij}}:{\overline{d}}_{\mathit{ij}}=\text{logit}\left(d_{\mathit{ij}}\right)\in \left(-\infty ,\infty \right);i<j;i,j\in \mathit{\eta }\right\}$$ (4)

We define the first and second moment characteristics for the observed difference network as follows:

$$\overline{e}=E\left[\overline{d}\right]\text{and}\overline{v}=\mathrm{Var}\left[\overline{d}\right]\text{for}\mathrm{i}<j,e=E\left[\overline{d}\right]\text{for}\mathrm{i}=\mathrm{j}$$

where $\overline{e}$ represents the mean of the off‐diagonal elements, e represents the mean of the diagonal element, and $\overline{v}$ is the variance of the off‐diagonal elements.

In the following, we present a procedure for generating a null difference network C ∈ IR^N × N whose first and second moment characteristics match that of the observed difference network and preserves its true topology. Motivated by the HQS algorithm, we propose to generate C based on the multiplication of a random matrix and its conjugate transpose

$$\mathbf{C}=\mathbf{L}*{\mathbf{L}}^{\mathbf{T}}$$ (5)

where L ∈ R ^N × m. Based on the formulation of Hirschberger et al. (2007), we generate l _ij ∼ N(μ, σ ²) where $\mu =\sqrt{\overline{e}/m}$ and $\sigma =-{\mu }^2+\sqrt{{\mu }^4+\frac{\overline{v}}{m}}$ and m = min{2,⌊$\frac{e-\overline{e}}{v}$ ⌋}, where ⌊·⌋ is the floor function. Based on this specification, we can show that

$$E\left[\mathit{cij}\right]=\overline{e},\mathrm{Var}\left[\mathit{cij}\right]=\overline{v},\text{and}E\left[\mathit{cii}\right]=e,$$

Please see Equations A3, A4 for details. The generated null difference network $\overline{\mathbf{C}}$ maintains the first and second moment characteristics of the observed difference network $\overline{\mathbf{D}}$. Finally, we transform $\overline{\mathbf{C}}$ through the inverse logit function to obtain a null difference network C such that c _ij ∈ (0, 1).

The proposed generation procedure has several appealing features. First, it is a very fast algorithm for generating null networks. Second, the generated null difference network, $\overline{\mathbf{C}}$, preserve the first and second moment characteristics of the observed difference network $\overline{\mathbf{D}}$. An important advantage in maintaining these fundamental properties of the observed network is that it will help make the generated null network a meaningful reference for comparison with the observed network. For example, to perform meaningful comparison of the connectivity structure between two networks, a critical condition is that the two networks must have similar number of edges (Fallani, Richiardi, Chavez, & Achard, 2014). This condition would be violated if there exists a significant difference in the average connectivity measure between the two networks in the sense that the network with higher average connectivity is associated with larger number of edges. By generating null networks with the same first and second moment as the observed network, the proposed procedure makes sure the comparison between the observed network against the null networks would not be confounded by their differences in the fundamental characteristics. More importantly, replication of the first and second moments allows the null networks to preserve the nuisance topology of the observed difference network while annihilating intrinsic group structures of the observed network. As discussed in Zalesky, Fornito, and Bullmore (2012), benchmarking against such null networks permits identification of the intrinsic topology in the observed network.

2.3.5. An adaptive threshold selection method

Recall that after obtaining the difference network $\overline{\mathbf{D}}=\left\{{\overline{d}}_{\mathit{ij}}\right\}$, we need to threshold it to derive the difference adjacency matrix $\overline{\mathbf{A}}=${${\overline{a}}_{\mathit{ij}}$}. If ${\overline{d}}_{\mathit{ij}}>\gamma ,\overline{a}=1$, indicating the presence of a group difference at the edge (i,j) where γ = logit(τ). Otherwise, ${\overline{a}}_{\mathit{ij}}$ = 0 represents no group difference at the edge (i, j).

In the existing between‐group network tests, the threshold value is typically selected by a multiple comparison method that controls the familywise error rate or the FDR. Others select a prespecified cutoff or grid over a range of cutoffs (Zalesky et al., 2010). We propose to adaptively select the threshold based on the distribution of the between‐group test statistic. Specifically, the ${\tilde{c}}_{\mathit{ij}}$ are independent and identical samples from the mixture distribution, H(.),

$$\mathrm{H}\left({\tilde{c}}_{\mathit{ij}}\right)\mathbf{=}\frac{2{\sigma }^2}{4}\mathit{T}\mathbf{-}\frac{2{\sigma }^2}{4}\mathit{Q}$$ (6)

where T and Q are noncentral χ ² and central χ ² random variables, respectively. Each variable in the mixture distribution depends only on the mean and variance of the observed data (see the Appendix section). We propose two ways to select the threshold, γ as the 95th quantile: (a) aDDT which uses the theoretical critical value based on the parametric mixture distribution in Equation (6), and (b) eDDT which uses the empirical critical value based on the empirical distribution. The numerical advantages and disadvantages of each of the two thresholding methods will be addressed in the simulation studies. Since the null difference network, $\overline{\mathbf{C}}$, is generated in a way that it matches the first and second moments of the observed difference network, $\overline{\mathbf{D}}$, the selected threshold value γ will automatically adapt to the properties of the observed difference network. Compared to hard thresholding approaches which use a fixed cutoff value, our threshold selection method can potentially provide an adaptive and general approach for choosing suitable threshold values for different studies. Once the threshold value γ is computed as above, one can apply it to the generated null difference networks $\overline{\mathbf{C}}$ to obtain difference adjacency matrices $\overline{\mathbf{A}}\mathit{=}\left\{{\overline{a}}_{\mathit{ij}}\right\}$ such that ${\overline{a}}_{\mathit{ij}}=1\text{if}\overline{c}>\gamma$ and 0 otherwise.

The proposed threshold selection procedure controls the selection of false positive edges, while circumventing the loss of power inherent in existing multiplicity corrections methods. This is achieved by adaptively selecting the threshold based on the distribution of the elements in the difference network. Similar approaches (Kundu, Mallick, & Baladandayuthapani, 2018; Newton, Noueiry, Sarkar, & Ahlquist, 2004) have effectively controlled Type I error by using the empirical distribution of edge probabilities to select a threshold in order to detect important connections. We do note that this thresholding procedure does not guarantee a universally optimal choice. The selected threshold is only utilized to control the Type I error in the weak sense at the edge level and may be suboptimal with respect to other manual or automatic thresholding procedures. However, simulations show that it leads to superior performance in detecting the nodes of interest.

2.3.6. Difference degree test

In this section, we present a statistical test for the difference degree measure, d _i, for node i based on the generated null difference networks. ${\overline{d}}_i$ essentially is a count variable representing the number of connections out of a total of N − 1 connections of node i that show between‐group difference. Therefore, we can model d _i with a binomial distribution. Under the null, d _i ∼ f ^null = Binomial(N‐1, $p_i^{\text{null}}$) where $p_i^{\text{null}}$ is the expected probability for each connection of node i to demonstrate between‐group difference under the null hypothesis. We can estimate the null probability $p_i^{\text{null}}$ based on the generated null difference networks, that is,

$${\widehat{p}}_i^{\text{null}}=\frac{1}{U\left(N-1\right)}{\sum }_{u=1}^U{\sum }_{j\in \mathit{\eta },j\ne i}{\overline{a}}_{\mathit{ij}}^{\left(u\right)}$$ (7)

where U is the total number of null networks and ${\overline{a}}_{\mathit{ij}}^{\left(u\right)}$are elements of uth thresholded null network, ${\overline{\mathbf{A}}}^{\left(\mathit{u}\right)}$. By comparing the observed d _i against the null distribution, we identify all regions incident to more DWEs than is expected by chance. Our proposed procedure is summarized in Algorithm (1).

Algorithm 1: Difference Degree Test

1: Construct difference network $\overline{\mathit{D}}={\left\{{\overline{d}}_{\mathit{ij}}\right\}}_{i,j}$


2: Obtain first and second moments of $\overline{\mathit{D}}$, that is, $\overline{e}=E\left({\overline{d}}_{\mathit{ij}}\right)$ and ${\sigma }^2=\mathrm{Var}\left({\overline{d}}_{\mathit{ij}}\right)$


3: Generate U null Difference Networks, ${\overline{\mathit{C}}}^m$(u = 1,..,U) based on $\overline{e}$ and 
σ2


4: Apply the adaptive threshold selection method to find the threshold, 
γ


5: Apply threshold to $\overline{\mathit{D}}$ to obtain the difference adjacency matrix $\mathbf{A}={\left\{{\overline{a}}_{\mathit{ij}}\right\}}_{i,j}$ and 
d
i for node i

6: Generate the null distribution for $d_i\sim \text{Binomial}\left(N-1,p_i^{\text{null}}\right)$. See Equation (7) for the form of $p_i^{\text{null}}$


7: Assess the statistical significance of the number of DWEs at node i.

3. RESULTS AND DISCUSSION

3.1. Numerical studies

Table 1 displays accuracy measures for identifying one differentially connected node across two populations in the first set of simulations. Generally, the proposed DDT methods, that is, aDDT and eDDT, exhibit larger TPR than the t tests and the binomial tests across various sample sizes and network structures. The binomial tests achieve the lowest FPR, which is attributed to the Bonferroni and FDR multiple testing corrections. However, the multiplicity corrections reduce the power to detect the correct region. The t test attains the nominal Type I error rate (α = .05). For all methods, the TPR improves when the sample size increases and the number of differentially connected edges increase. Overall, the two proposed DDT approaches exhibit superior performance as compared to the other tests. Among the two DDT methods, eDDT typically exhibits higher TPR, but the latter has a slightly higher FPR, although the FPR under both approaches is less than the nominal level of .05. In Figure 1, we see the significant edges in the true difference network structure as well as those detected by eDDT, aDDT, Bonferroni, and FDR multiplicity corrections. Clearly, aDDT and eDDT performances identify the same significant edges while the Bonferroni and FDR corrections produce many false negatives. Such performance at the edge level permits our methods to detect the correct nodes of interest and contributes to the superior TPR and FPR values observed in the simulations.

Table 1.

FPR and TPRs for the random, small world, and hybrid network structures. Competing methods are aDDT (theoretical DDT), eDDT (empirical DDT), Bin_B (binomial, Bonferroni correction), Bin_F (binomial, FDR corrected), and t test (10% density)

			n 1 = n 2 = 20					n 1 = n 2 = 40
			DDT		Binomial		t Test	DDT		Binomial		t Test
	Network structure	DWE	aDDT	eDDT	BinB	BinF	10%	aDDT	eDDT	BinB	BinF	10%
FPR	Random	4	0.021	0.046	0.002	0.001	0.052	0.019	0.046	0.002	0.002	0.052
		7	0.022	0.047	0.002	0.002	0.051	0.017	0.044	0.002	0.002	0.054
		11	0.020	0.046	0.002	0.002	0.052	0.014	0.044	0.003	0.002	0.055
		20	0.017	0.045	0.000	0.003	0.057	0.008	0.033	0.001	0.004	0.060
	Small world	4	0.022	0.046	0.001	0.001	0.050	0.019	0.045	0.002	0.002	0.054
		7	0.023	0.046	0.002	0.002	0.051	0.016	0.044	0.002	0.002	0.051
		11	0.020	0.045	0.002	0.002	0.052	0.012	0.042	0.003	0.002	0.055
		20	0.019	0.045	0.000	0.003	0.054	0.008	0.033	0.001	0.003	0.058
	Hybrid	4	0.024	0.042	0.001	0.002	0.054	0.019	0.045	0.001	0.001	0.055
		7	0.022	0.045	0.002	0.001	0.055	0.018	0.045	0.002	0.002	0.059
		11	0.020	0.046	0.002	0.002	0.054	0.015	0.046	0.002	0.002	0.064
		20	0.017	0.045	0.001	0.003	0.058	0.009	0.034	0.001	0.003	0.063
TPR	Random	4	0.370	0.458	0.036	0.049	0.111	0.710	0.891	0.123	0.112	0.203
		7	0.631	0.767	0.240	0.292	0.230	0.977	0.991	0.747	0.738	0.379
		11	0.893	0.885	0.694	0.686	0.450	1.000	0.999	0.999	0.998	0.619
		20	0.994	0.991	0.981	0.999	0.791	1.000	1.000	1.000	1.000	0.962
	Small world	4	0.287	0.505	0.040	0.034	0.131	0.699	0.913	0.113	0.123	0.227
		7	0.639	0.738	0.274	0.226	0.155	0.982	0.994	0.784	0.764	0.307
		11	0.895	0.908	0.696	0.692	0.551	1.000	0.999	0.998	0.999	0.840
		20	0.994	0.991	0.981	0.999	0.791	1.000	1.000	1.000	1.000	0.962
	Hybrid	4	0.284	0.423	0.042	0.052	0.255	0.650	0.884	0.136	0.114	0.435
		7	0.571	0.675	0.225	0.222	0.524	0.974	0.995	0.707	0.719	0.650
		11	0.874	0.888	0.693	0.693	0.681	0.999	1.000	0.997	0.994	0.739
		20	0.996	0.988	0.875	0.993	0.820	1.000	1.000	1.000	1.000	0.978

Abbreviations: DDT, difference degree test; DWE, differentially weighted edge; FPR, false positive rate; TPR, true positive rate.

Figure 1.

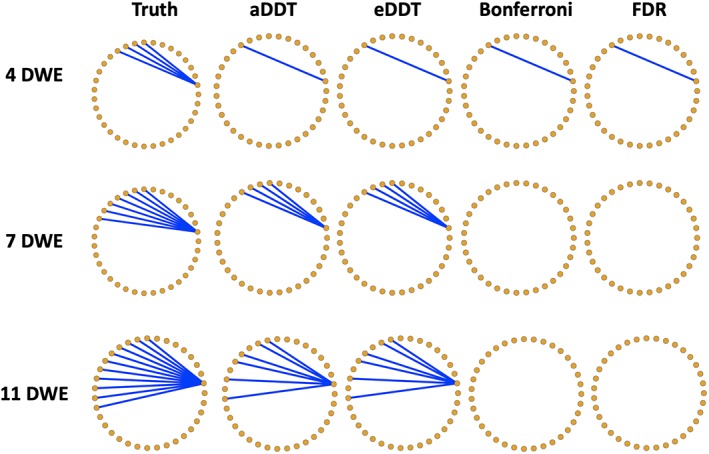
Graphical illustration of the true contrasts containing 4, 7, and 11 DWEs incident to the node of interest for a random network of 35 regions. Blue edges are true positives detected by the respective method. The Bonferroni correction and FDR are underpowered to detect significant edges while the aDDT and eDDT estimates consistently detect the same set of significant edges. DDT, difference degree test; DWE, differentially weighted edge; FPR, false positive rate [Color figure can be viewed at http://wileyonlinelibrary.com]

The advantages of the proposed aDDT and eDDT over the alternative methods persist in the second set of simulations where three regions are differentially connected. In Figure 2, across all network structures with a fixed number of nodes (N = 35) and with 4, 7, or 11 DWEs incident to each of the three nodes of interest, the DDT methods have the highest power to detect the regions of interest while attaining FPR comparable to that of T _(10%). We note that our method is superior to the multiplicity corrected Binomial tests when the differentially connected regions are incident to a small to moderate number of DWEs and is comparably powered to detect differentially connected nodes as the FDR corrected tests when the number of DWEs is large. Furthermore, as in the first simulation setting, eDDT typically exhibits higher TPR than aDDT, but the former has slightly higher FPR compared to aDDT. Notably, both methods exhibit FPR values close to the nominal level of 0.05.

Figure 2.

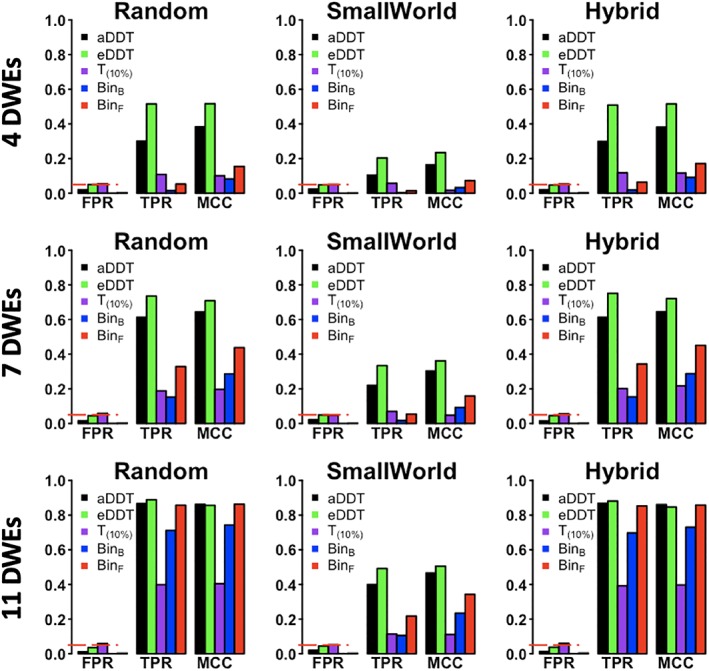
Comparison of eDDT, aDDT, t test (T _(10%)), binomial tests (Bin_F, Bin_B) in the second set of simulations with three differentially connected nodes incident to 4 (first row), 7 (second row), and 11 (third row) DWEs. The TPR, FPR, and MCC are presented for all methods across the three network structures considered and the red dashed line demarcates the nominal significance level (.05). DDT exhibits superior performance in detecting the differentially connected nodes while not exceeding the allowable Type I error rate. DDT, difference degree test; DWE, differentially weighted edge; FPR, false positive rate; MCC, Matthews correlation coefficient; TPR, true positive rate

We also examine at the performance of the approaches as the number of nodes increases, while keeping the proportion of DWEs incident to the region of interest fixed at 30%. Figure 3 clearly illustrates the advantages of DDT for detecting regions incident to DWEs, while having a comparable or lower FPR as the network's size increases. Consistent with Table 1 and Figure 2, eDDT exhibits the best TPR while the multiplicity corrected binomial tests have the smallest FPR, although the FPR levels under the DDT approaches are less than or equal to the nominal level across varying numbers of nodes. However, the TPR for eDDT and aDDT becomes increasingly similar as the number of regions is increased.

Figure 3.

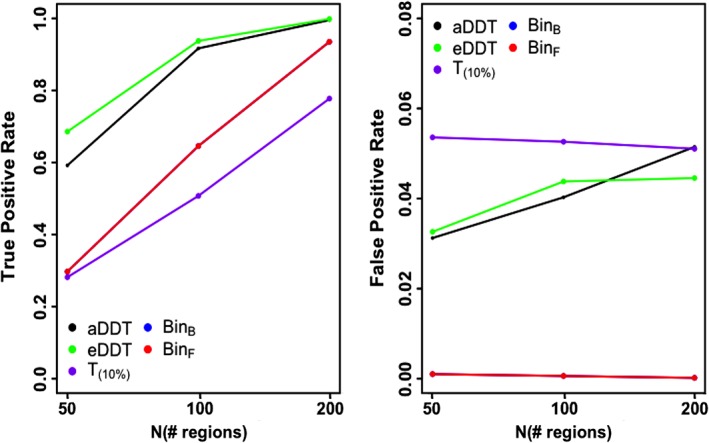
Performance of aDDT, eDDT, t test(T _10%), and binomial (Bin_B, Bin_F) tests in identifying the differentially connected node as the network size increases and the proportion of DWEs is fixed at 30%. (Note, the results of the Bin_B, Bin_F tests are very close and hence the two lines overlap) DDT, difference degree test; DWE, differentially weighted edge

Although detection of regions incident to a significant number of DWEs is our primary focus, we also investigate the performance of the thresholding procedure for detecting DWEs in a supplementary analysis in terms of the MCC values. Figure 4 indicates that aDDT's and eDDT's adaptive thresholding procedures outperform the Bonferroni and FDR multiplicity corrections over varying proportion of DWEs. Moreover, our method also exhibits superior MCC than the arbitrary hard threshold of 0.95, and at least one of the aDDT and eDDT approaches perform as well as the conservative hard threshold set at 0.99 as the proportion of DWEs across the network increases. The superior performance of the eDDT and aDDT are attributed to the liberal cutoffs selected by the methods' adaptive thresholding procedure (Figure 5.). Specifically, the Bonferroni threshold is 8.4e‐5 and FDR thresholds have a mean of 6e‐4 while the proposed eDDT and aDDT methods select much more liberal thresholds (mean threshold: 8e‐3 based on eDDT and 1.9e‐2 based on aDDT, respectively).

Figure 4.

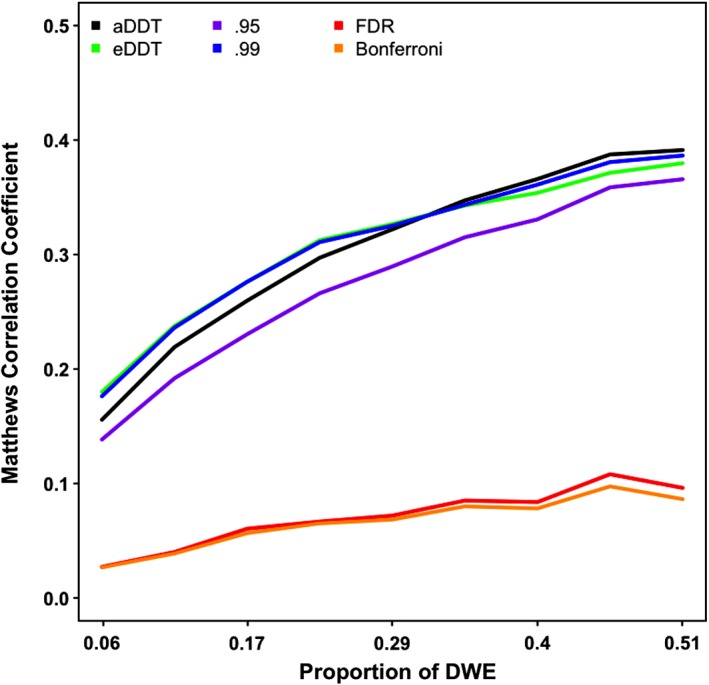
Comparison of thresholding procedures implemented in aDDT and eDDT as well as four competitors (.95 and .99 hard threshold; FDR and Bonferroni multiplicity corrections) in detecting DWEs. DDT, difference degree test; DWE, differentially weighted edge; FPR, false positive rate

Figure 5.

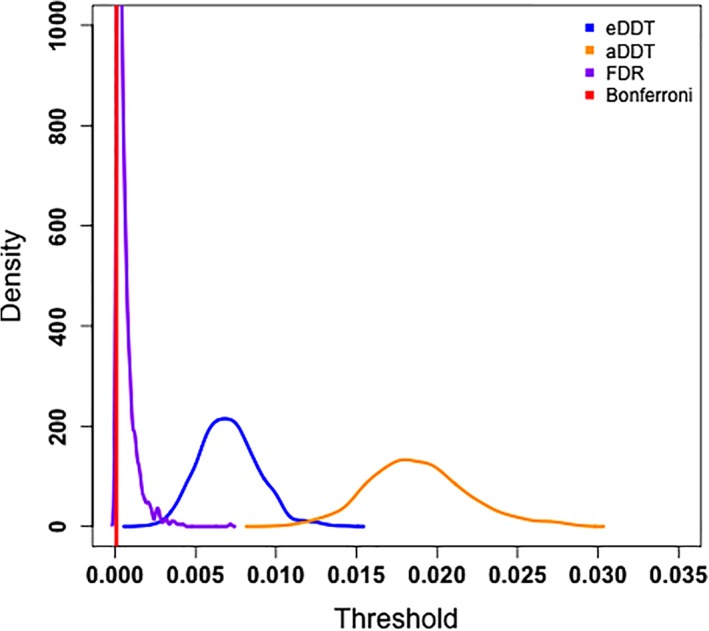
The density of the selected threshold for identifying differentially weighted edges over 1,000 simulations. eDDT and aDDT produce more liberal thresholds than the Bonferroni and FDR multiplicity corrected thresholds. DDT, difference degree test; FPR, false positive rate

Finally, we see that the proposed methods select hub nodes composing a connected component that spans the difference network (Figure 6). All of the investigated methods correctly identify Node 2 as the key hub node of between‐group differences with the largest number of DWEs between groups. Other than this common finding, the two binomial tests based on multiple comparisons have the smallest number of positive findings across the methods, only detecting Nodes 3 and 31 in a small proportion of the 1,000 simulations. Therefore, they missed some of the differentially connected hub nodes such as Nodes 8 and 17. On the other hand, T _(10%) has the largest number of positive findings, detecting between‐group differences at every node. T _(10%) has the highest FPR, mistakenly detecting nodes such as Nodes 21, 30, and 35 that do not have any DWEs with any other nodes and are completely disconnected in the contrast structure. The aDDT and eDDT results are between these two extremes and detect most of the hub nodes with multiple DWEs in the true contrast structure. Specifically, aDDT tends to detect nodes that are incident to at least three DWEs while eDDT identifies regions incident to at least two DWEs. Removal of any of the hub regions detected by the aDDT and eDDT—particularly Node 2—decomposes the structure into smaller, isolated components that are difficult to detect with the NBS. Furthermore, our proposed methods (aDDT and eDDT) do not detect any nodes that are completely disconnected from the contrast structure nor does it select peripheral nodes that have only on DWE (i.e., Node 4).

Figure 6.

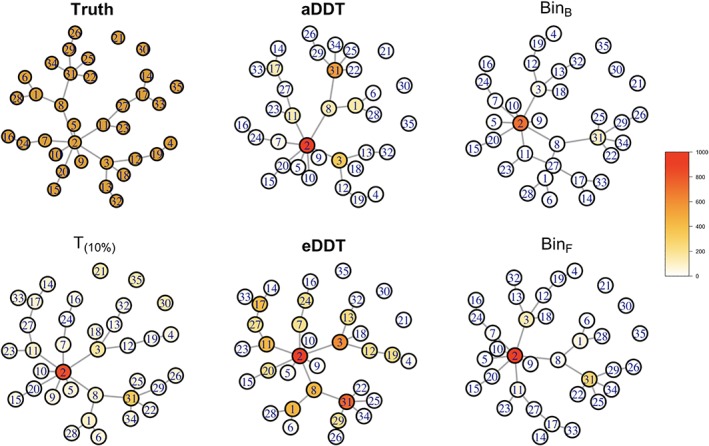
Simulation results based on the setting in the NBS paper. The figure shows the true contrast structure (truth) where the edges in the contrast structure represent differentially weighted edges between groups. The figure shows the edges and nodes that are detected as differentially connected between groups based on the proposed aDDT, eDDT methods, and the existing t test (T _(10%)) and binomial tests with multiple comparison corrections of Bonferroni and FDR (BinB, BinF). Nodes are color coded based on the number of times, it is selected as a differentially connected node across 1,000 simulations. DDT, difference degree test; FPR, false positive rate; NBS, network‐based statistic

3.2. Data application

Table 2a and b lists the top 20 differentially connected nodes for model‐based Pearson and partial correlations. Pearson correlation generally leads to more DWEs incident to nodes. Thirty percent of the regions identified in Table 2a are located in the SM module while 20% are in the DMN. Similarly, Table 2b shows DMN nodes are extremely prominent (35%) as well as the FPN and CIO which compose the task control system. These results suggest that altered connectivity in the DMN differentiates the brain networks in the MDD population from healthy controls. Similar trends are observed for Bin_B and Bin_F. We find that the FDR‐corrected binomial test detects 37 regions incident to a statistically significant number of DWEs while the Bonferroni‐adjusted test identifies 34 regions. Nineteen of these regions are also detected by our approach and can be found in Table 2a. The NBS did not detect any differences between the brain networks in the healthy and MDD populations across a wide range of parameter settings. We note that the NBS relies assumes the DWEs form connected components spanning multiple functional subnetworks (Kim et al., 2015). However, the method is substantially underpowered to detect differences in the networks if this assumption is not met (Zalesky et al., 2010). The poor performance of the NBS on our data suggests that connected component assumption is potentially overly restrictive.

Table 2.

Top 20 differentially connected nodes in the major depressive disorder study based on (a) model‐based Pearson correlations and (b) model‐based partial correlations

(a) Model‐based Pearson correlations
X	Y	Z	Name	Module	#DWE
−53	−22	23	SupraMarginal_L (aal)	AUD	29
52	7	−30	Temporal_Pole_Mid_R (aal)	DMN	27
46	16	−30	Temporal_Pole_Mid_R (aal)	DMN	26
29	1	4	Putamen_R (aal)	SUB	26
47	−30	49	Postcentral_R (aal)	Sensory/SM hand	23
10	−46	73	Precuneus_R (aal)	Sensory/SM hand	19
−24	−91	19	Occipital_Mid_L (aal)	VIS	19
−54	−23	43	Parietal_Inf_L (aal)	Sensory/SM hand	18
31	33	26	Frontal_Mid_R (aal)	SAL	18
51	−29	−4	Temporal_Mid_R (aal)	VAN	18
13	−33	75	Postcentral_R (aal)	Sensory/SM hand	16
−46	31	−13	Frontal_Inf_Orb_L (aal)	DMN	16
23	10	1	Putamen_R (aal)	SUB	16
−44	12	−34	Temporal_Pole_Mid_L (aal)	DMN	15
31	−14	2	Putamen_R (aal)	SUB	15
−38	−27	69	Postcentral_L (aal)	Sensory/SM hand	14
−60	−25	14	Temporal_Sup_L (aal)	AUD	14
27	16	−17	Insula_R (aal)	UNC	14
52	−2	−16	Temporal_Mid_R (aal)	DMN	14
50	−20	42	Postcentral_R (aal)	Sensory/SM hand	13
(b) Model‐based partial correlations
−31	19	−19	Frontal_Inf_Orb_L (aal)	UNC	15
24	32	−18	Frontal_Sup_Orb_R (aal)	UNC	13
−38	−15	69	Undefined	Sensory/SM hand	13
−26	−40	−8	ParaHippocampal_L (aal)	DMN	13
−31	−10	−36	Fusiform_L (aal)	UNC	13
17	−91	−14	Lingual_R (aal)	UNC	12
−16	−46	73	Parietal_Sup_L (aal)	Sensory/SM hand	11
23	33	48	Frontal_Sup_R (aal)	DMN	11
−28	−79	19	Occipital_Mid_L (aal)	VIS	11
37	−81	1	Occipital_Mid_R (aal)	VIS	11
−42	−55	45	Parietal_Inf_L (aal)	FPN	11
−54	−23	43	Parietal_Inf_L (aal)	Sensory/SM hand	10
7	8	51	Supp_Motor_Area_R (aal)	CIO	10
−45	0	9	Rolandic_Oper_L (aal)	CIO	10
−60	−25	14	Temporal_Sup_L (aal)	AUD	10
−13	−40	1	Precuneus_L (aal)	DMN	10
−68	−23	−16	Temporal_Mid_L (aal)	DMN	10
−10	39	52	Frontal_Sup_Medial_L (aal)	DMN	10
22	39	39	Frontal_Sup_R (aal)	DMN	10
−8	48	23	Frontal_Sup_Medial_L (aal)	DMN	10

Abbreviations: AUD, auditory; CIO, cingulo‐opercular task control; DMN, default mode; FPN, frontoparietal network; SAL, salience; SUB, Subcortical; SM, somatomotor; VAN, ventral attention; VIS, visual; UNC, uncertain.

Figure 7 displays the distribution of DWEs across the respective difference network. Here, we group the nodes based on the functional module assignment provided in Power et al. (2011). The diagonal blocks represent within‐module connections while the off‐diagonal blocks represent between‐module connections. For Pearson model‐free and model‐based analyses, we identified 793 and 776 DWEs, respectively. For partial correlations, we identified 458 DWEs based on model‐free p‐values and 772 DWEs for model‐based p‐values. The Pearson correlation derived difference networks exhibit spatial clustering of DWEs, specifically within the SM and between the SUB and VIS functional modules. Table 3 reports the consistently and inconsistently detected DWEs when comparing the four difference networks investigated, that is, model‐free/model‐based Pearson correlation networks and model‐free/model‐based partial correlation networks. Insignificant edges persist across all the difference networks considered and account for as much as 90% of the edges in the networks. Generally, the findings are more consistent between the model‐free and model‐based p‐values within the same correlation measure and less consistent across correlation measure.

Figure 7.

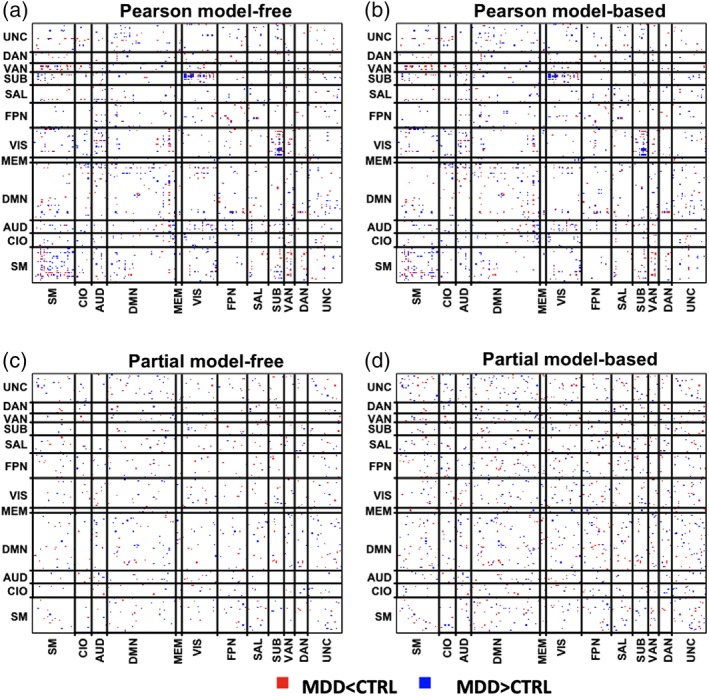
Differentially weighted edges detected by eDDT in the major depressive disorder study under the four difference network configurations: (a) model‐free Pearson and (b) model‐based Pearson, (c) model‐free partial, (d) model‐based partial. Red edges indicate the average edge weight in the MDD population is statistically smaller than in healthy adults whereas blue edges demarcate the average edge weight is statistically larger in the MDD group. The network is decomposed into 12 functional modules: sensor/somatomotor (SM), cingulo‐opercular task control (CIO), auditory(AUD), default mode (DMN), memory retrieval (MEM), visual (VIS), frontoparietal task control (FP), salience (SN), subcortical (sub), ventral attention (VAN), dorsal attention (DAN), and uncertain (UNC)

Table 3.

Consistency of DWEs detected in four types of difference networks. We show the consistency of results for each pair of the four difference networks. Based on the consistency results, edges are classified into four possible categories. Values presented in the table are the number of edges in each consistency results category

		Consistency and inconsistency in between‐group test results a
Difference network		Sig in I	Insig in I	Sig in I	Insig in I
I	II	Sig in II	Insig in II	Insig in II	Sig in II
Pearson model‐free	Pearson model‐based	662	32,504	131	114
Pearson model‐free	Partial model‐free	51	32,392	691	406
Pearson model‐based	Partial model‐based	73	31,936	703	699
Partial model‐based	Partial model‐free	454	32,936	4	318

^aThe four consistency results categories: (1) Sig in I, Sig in II: edges that demonstrate significant between‐group differences based on the difference network estimated in Models I and II; (2) Insig in I, Insig in II: edges that demonstrate insignificant between‐group differences based on the difference network estimated in Models I and II; (3) Sig in I, Insig in II: edges that demonstrate significant between‐group differences based on the difference network in Model I but insignificant results based on Model II; (4) Insig in I, Sig in II: edges that demonstrate insignificant between‐group differences based on the difference network based on Model I but significant results based on Model II.

The distribution of DWEs within and between functional modules provides insight into disrupted communication among functionally segregated subsystems in the brain. We conduct analysis to identify functional modules that are associated with higher number of DWEs as compared with other modules. Specifically, we propose the following chi‐square statistic to help identify functional module pairs for which there are unusually high number of DWEs than what is expected by chance,

$${\chi }_{g1,g2}^2=\frac{{\left(Q_{g1,g2}-E_{g1,g2}\right)}^2}{E_{g1,g2}}$$ (8)

where g ₁ ∈ {1,…,Z} and g ₂ ∈ {1,…,Z} are indices corresponding to one of the Z = 12 functional modules. When g ₁ = g ₂, (g ₁,g ₂) represents a within module block, whereas it represents a between‐module block when g ₁ = g ₂. Q _(g1,g2) represents the observed number of DWEs in the (g ₁,g ₂) block and E_(g1,g2) represents the expected number of DWEs in the (g ₁,g ₂) block when the edges distribute randomly across the module blocks in the network. Let |g| represent the total number of nodes within the gth module, and p ^* represents the proportion of DWEs among all the edges across the network. It is straightforward to see that E _g1,g2 = p**[$\frac{\left|g_1\right|*\left(\hspace{0.17em}|g_2|-1\right)}{2}$] for within module blocks, that is, g ₁ = g ₂, and E _g1,g2 = p ^**[|g ₁|*|g ₂|] for between‐module blocks.

Figure 8 displays functional modules and module pairs exhibiting a significantly high number of DWEs based on the thresholded chi‐square test statistic (see Table A1 for raw counts). The results are derived from the model‐free Pearson correlations (Figure 8a) and model‐based Pearson correlations (Figure 8b), respectively. Based on model‐free Pearson correlations (Figure 8a), there are significantly high number of DWEs within the sensorimotor module and between the module pairs of sensorimotor–VAN, sensorimotor–DAN, VIS–AUD, SUB—AUD, and SUB–VIS. After accounting for age and gender, the model‐based Pearson correlations (Figure 8b) also exhibit a large number of DWEs within the sensorimotor module and between the module pairs of sensorimotor–VAN, VIS–AUD, and SUB–VIS. However, the model‐based Pearson correlations no longer show significantly high number of DWEs between the sensorimotor–DAN and SUB–AUD module pairs. Instead, the model‐based correlations find significant number of DWEs between the SUB‐memory module pair which is not identified by the model‐free Pearson correlations.

Figure 8.

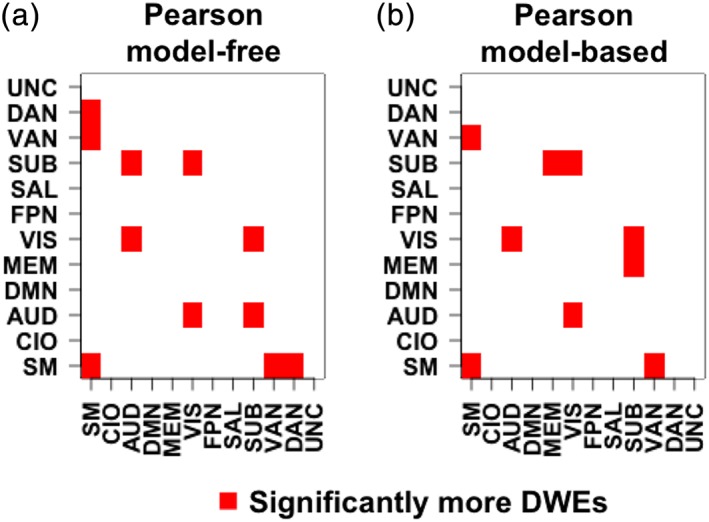
Heat map of the X ² statistic for (a) model‐free Pearson correlations and X (_g1,g2) and (b) model‐based Pearson correlations. Red squares indicate modules with more statistically significant differentially weighted edges (DWEs) than would be expected by random chance. We control the overall false discovery rate by only selecting module pairs with a multiplicity corrected p‐value <.05 [Color figure can be viewed at http://wileyonlinelibrary.com]

Many of our findings between and across functional modules have been previously reported in the MDD literature. In particular, our method identifies nodes in the frontal cortex and cingulate that are consistent with investigations of connectivity features that distinguish MDD patients from healthy controls (Menon, 2010; Menon, 2011). In addition, we reveal new brain regions connected to these well‐established regions. Further, we identify nodes in the DMN, executive control network, and SAL network that are well described in previous studies (Sheline et al., 2009; Sheline, Price, Yan, & Mintun, 2010; Yu et al., 2019). Our results also highlight new findings on hub regions in the association cortex that link to these established networks. Thus, our method detects established brain regions that are clinically relevant to MDD as well as new brain regions that could further elucidate the mechanisms by which MDD disrupts cortical communication.

4. CONCLUSION

While the estimation of brain networks is gaining increasing attention in the neuroimaging literature, the fundamental question of how brains differ in functional organization across disease populations is not yet resolved. Our proposed method exhibits two strengths. First, our automated threshold selection permits identification of DWEs without sacrificing power as is the case with many methods dependent upon multiplicity corrections. Second, we use the generated null networks to test if each brain region is incident to more DWEs than would be expected by random chance. Finally, we note that the eDDT and aDDT scale well as the number of brain regions increases. On a 2.3 GHz Intel Core i5 laptop, neither approach exceeds 15 s for up to 500 brain regions. We additionally investigated extremely high dimensional networks containing 1,000 regions. The computation times remained low for the eDDT (1.5 min) and the aDDT (1.3 min).

The aDDT and eDDT readily incorporate a broad class of connectivity measures including but not limited to correlation coefficients. Specifically, the difference network, D, could be derived from testing group differences based on various types of connectivity measures, such as correlations or mutual information. Provided we have a valid between‐group test, the null network scheme is unaffected by the choice of the connectivity measure. For example, to test group differences in correlations, we apply the Fisher Z‐transformation, which is typically applied to this measure prior statistical testing. For other connectivity measures, we recommend a similar strategy to appropriately transform it to ensure valid between‐group test results. We note that the Gaussian distribution used to generate the null network is not assumed for the connectivity measure but rather for the difference network derived from the between‐group test.

We hypothesize that network wide dysconnectivity is driven by brain regions that irregularly communicate with other regions. The results from the real data analysis suggest that the DDT appropriately identifies problematic brain regions in major depressive disorder. The existence of differential connectivity between nodes in the AUD and VIS networks (Figure 5) has previously been observed (Eyre et al., 2016). Further, multivariate pattern analyses have suggested that the most discriminative FC patterns lie within and across the VIS network, DMN, and affective network (Zeng et al., 2012). The parahippocampal gyrus, which we detect as a problematic region (Table 2), has also been suggested as a region with differentiated connectivity patterns in depressed populations. Our simulation results demonstrate superior performance of the proposed DDT tests. Although the binomial test's FPR is smaller than DDT, its ability to detect differentially connected nodes is severely attenuated. DDT maintains the an acceptable false positive rate while achieving higher TPRs than the t test across all network structures and sample sizes considered. Simulations indicate DDT's adaptive threshold selection is superior to conservative FDR and Bonferroni adjustments. An obvious limitation to this work is the i.i.d. assumption on edge weights in the null networks. However, it is non‐trivial to extend our method to account for such dependence. One way to account for the dependence is to sample rows of C, the null network in Equation (5), from a multivariate normal distribution. Unfortunately, this would require a priori specification on the covariance structure between brain regions which is often unknown. Furthermore, Equation (6), which is critical to our thresholding procedure and node‐level inference, would need rederivation since the current results are based on the i.i.d. assumption. Thus, extensive methodological developments will be required to generate null networks which incorporate edge dependencies. Although the independence assumption did not severely impact the method's performance relative to suitable competitors, it is likely that incorporation of interedge dependence structures will lead to better power to detect differentially connected nodes.

CONFLICT OF INTEREST

The authors declare that they have no conflict of interest.

Appendix 1.

PROOF FOR HQS PROCEDURE

In Section 2.3.4, we suggest that sampling l _ij ∼ N(μ, σ ²) appropriately allows for the condition that that $E\left(c_{\mathit{ij}}\right)=\overline{e}$ and $\mathrm{Var}\left(c_{\mathit{ij}}\right)=\overline{v}$. We now provide details for the distribution of $c_{\mathit{ij}}={\sum }_{k=1}^m{l}_{\mathit{ik}}\times l_{\mathit{kj}}$. Consider l _ik ,l _kj ∼ N(μ, σ ²) for k = 1,..,m. Then,

$$c_{\mathit{ij}}=\sum _{k=1}^m{l}_{\mathit{ik}}{l}_{\mathit{kj}}=\frac{1}{4}\sum _{k=1}^m{\left(l_{\mathit{ik}}+l_{\mathit{kj}}\right)}^2-\frac{1}{4}\sum _{k=1}^m{\left(l_{\mathit{ik}}-l_{\mathit{kj}}\right)}^2.$$ (A1)

Note that for l _ik, l _kj ∼ N(μ, σ ²),

$$\begin{array}{c}\frac{l_{\mathit{ik}}+l_{\mathit{kj}}}{\sqrt{2}\sigma }\sim N\left(\frac{2\mu }{\sqrt{2}\sigma },1\right)\Rightarrow \frac{{\left(l_{\mathit{ik}}+l_{\mathit{kj}}\right)}^2}{2{\sigma }^2}\sim \underset{1}{\overset{2}{\chi }}\left(\frac{4{\mu }^2}{2{\sigma }^2}\right)\\ \frac{l_{\mathit{ik}}-l_{\mathit{kj}}}{\sqrt{2}\sigma }\sim N\left(0,1\right)\Rightarrow \frac{{\left(l_{\mathit{ik}}-l_{\mathit{kj}}\right)}^2}{2{\sigma }^2}\sim \underset{1}{\overset{2}{\chi }}\end{array}$$

We can introduce constants and rewrite (A1) as

$$\begin{array}{c}\sum _{k=1}^m{l}_{\mathit{ik}}{l}_{\mathit{kj}}=\frac{1}{4}\sum _{k=1}^m{\left(l_{\mathit{ik}}+l_{\mathit{kj}}\right)}^2-\frac{1}{4}\sum _{k=1}^m{\left(l_{\mathit{ik}}-l_{\mathit{kj}}\right)}^2\\ \sum _{k=1}^m{l}_{\mathit{ik}}{l}_{\mathit{kj}}=\frac{2{\sigma }^2}{4}\sum _{k=1}^m\frac{{\left(l_{\mathit{ik}}+l_{\mathit{kj}}\right)}^2}{2{\sigma }^2}-\frac{2{\sigma }^2}{4}\sum _{k=1}^m\frac{{\left(l_{\mathit{ik}}-l_{\mathit{kj}}\right)}^2}{2{\sigma }^2}\\ \sum _{k=1}^m{l}_{\mathit{ik}}{l}_{\mathit{kj}}=\frac{2{\sigma }^2}{4}\mathbf{T}-\frac{2{\sigma }^2}{4}\mathbf{Q}\end{array}$$ (A2)

where T is a noncentral χ² with m df and noncentrality parameter $m\times \left(\frac{4{\mu }^2}{2{\sigma }^2}\right)$ and Q is a central χ² with m df. Utilizing the first moment of noncentral χ² and central χ² distributions, we see that

$$\begin{array}{c}E\left[\frac{2{\sigma }^2}{4}\mathit{T}-\frac{2{\sigma }^2}{4}\mathit{Q}\right]=\frac{2{\sigma }^2}{4}\mathrm{E}\left[\mathbf{T}\right]-\frac{2{\sigma }^2}{4}\mathrm{E}\left[\mathbf{Q}\right]\\ =\frac{2{\sigma }^2}{4}\left(m+\frac{4m{\mu }^2}{2{\sigma }^2}\right)-\frac{2{\sigma }^2}{4}m\\ =m{\mu }^2=\overline{e}\end{array}$$ (A3)

and

$$\begin{array}{c}\mathrm{Var}\left[\frac{2{\sigma }^2}{4}\mathit{T}-\frac{2{\sigma }^2}{4}\mathit{Q}\right]=\frac{2{\sigma }^2}{4}\mathrm{Var}\left[\mathbf{T}\right]-\frac{2{\sigma }^2}{4}\mathrm{Var}\left[\mathbf{Q}\right]-\left(\frac{4{\sigma }^4}{16}\right)\mathrm{Cov}\left(\mathbf{T}\mathbf{,}\mathbf{Q}\right)\\ =\frac{4{\sigma }^4}{16}\left(2\left(m+2\left(\frac{4m{\mu }^2}{2{\sigma }^2}\right)\right)\right)+\frac{4{\sigma }^4}{16}2m\\ \begin{array}{c}=m{\sigma }^4+2{\sigma }^{2}m{\mu }^2\\ \begin{array}{c}=m{\sigma }^4+2{\sigma }^{2}m{\mu }^2+m{\mu }^4-m{\mu }^4\\ =m{\left({\sigma }^2+{\mu }^2\right)}^2-m{\mu }^4=\overline{v}\end{array}\end{array}\end{array}$$ (A4)

To see the Cov(T,Q) = 0, we note that ${\left(x,y\right)}^{\prime }\sim \mathrm{MVN}\left(\tilde{\mu },\tilde{\sum }\right)$ where $\tilde{\mu }=\mu \times 1_{2m}\mathit{\text{for}}{1}_{2m}$ a vector of one's in R^2m and $\tilde{\sum }=\mathrm{diag}\left(\sum ,\sum \right)$ is a block matrix with ∑ = diag(σ², …, σ²) ∈ R^2m × 2m. Multiplying the multivariate random vector by an appropriate matrix, P, we have (x₁ + y₁, …, x_m + y_m, x₁ − y₁, …, x_m − y_m)^′ ∼ MVN((2μ, …, 2μ, 0, …, 0)^′, P∑P^′). By the partitioning of the full covariance matrix, we see that (x₁ + y₁, …, x_m + y_m)^′ ⊥ (x₁ − y₁, …, x_m − y_m)′. Consider $f\left(x\right)=\frac{1}{2{\sigma }^2}\left(\underset{1}{\overset{2}{x}}+\dots +\underset{m}{\overset{2}{x}}\right)$. Since f(.) is a continuous function, we have f(x₁ + y₁, …, x_m + y_m) ⊥ f(x₁ − y₁, …, x_m − y_m). By definition of f(.), we have T ⊥ Q which implies Cov(T,Q) = 0.

Table A1.

Within and between functional module, DWE in the major depressive disorder study. Bold values indicate statistically significant number of DWE between the respective functional modules—Sensory/somatomotor (SM), cingulo‐opercular task control (CIO), auditory (AUD), default mode network (DMN), memory retrieval (MEM), visual (VIS), frontoparietal network (FPN), salience (SAL), subcortical (SUB), ventral attention network (VAN), dorsal attention network (DAN), and uncertain (UNC)

(A) Pearson, model‐free
	SM	CIO	AUD	DMN	MEM	VIS	FPN	SAL	SUB	VAN	DAN	UNC
SM	55
CIO	11	1
AUD	14	4	1
DMN	36	22	21	42
MEM	6	0	0	7	0
VIS	29	14	28	32	1	4
FPN	10	1	9	26	1	11	7
SAL	11	2	12	15	1	4	9	2
SUB	20	3	12	6	5	63	2	1	2
VAN	25	6	2	15	0	8	2	2	2	0
DAN	20	0	4	9	0	9	3	2	2	2	0
UNC	22	10	3	43	5	13	11	9	9	4	2	5

(B) Pearson, model‐based
	SM	CIO	AUD	DMN	MEM	VIS	FPN	SAL	SUB	VAN	DAN	UNC
SM	46
CIO	9	1
AUD	12	4	1
DMN	27	25	22	45
MEM	3	0	0	5	0
VIS	29	14	27	26	4	3
FPN	9	0	7	30	1	12	7
SAL	10	2	8	16	1	6	12	4
SUB	16	3	9	10	6	54	1	1	2
VAN	23	5	2	15	0	6	2	2	2	0
DAN	17	0	2	9	0	14	3	3	1	2	0
UNC	20	9	1	48	4	14	10	12	9	4	3	5

(C) Partial, model‐free
	SM	CIO	AUD	DMN	MEM	VIS	FPN	SAL	SUB	VAN	DAN	UNC
SM	6
CIO	2	0
AUD	2	3	3
DMN	25	6	12	21
MEM	2	1	0	6	0
VIS	12	5	7	16	1	7
FPN	13	4	5	19	1	7	3
SAL	9	6	1	16	0	5	6	1
SUB	4	0	0	11	1	8	5	5	1
VAN	2	3	0	11	0	4	0	3	1	0
DAN	6	3	1	9	0	4	1	5	3	1	1
UNC	15	6	2	32	2	11	10	8	9	2	4	6

(D) Partial, model‐based
	SM	CIO	AUD	DMN	MEM	VIS	FPN	SAL	SUB	VAN	DAN	UNC
SM	9
CIO	7	0
AUD	8	4	3
DMN	47	15	17	36
MEM	3	1	1	9	0
VIS	16	8	11	30	5	11
FPN	20	8	7	40	3	19	7
SAL	14	10	2	22	1	9	11	4
SUB	7	4	2	18	2	12	8	8	1
VAN	8	3	1	19	1	8	2	6	2	0
DAN	6	4	4	17	0	6	4	7	4	3	3
UNC	30	13	7	49	5	22	16	10	13	7	7	10

Higgins IA, Kundu S, Choi KS, Mayberg HS, Guo Y. A difference degree test for comparing brain networks. Hum Brain Mapp. 2019;40:4518–4536. 10.1002/hbm.24718

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.