Neural correlates of time distortion in a preaction period

Abstract

An intention to move distorts the perception of time. For example, a visual stimulus presented during the preparation of manual movements is perceived longer than actual. Although neural mechanisms underlying this action‐induced time distortion have been unclear, here we propose a new model in which the distortion is caused by a sensory–motor interaction mediated by alpha rhythm. It is generally known that viewing a stimulus induces a reduction in amplitude of occipital 10‐Hz wave (“alpha‐blocking”). Preparing manual movements are also known to reduce alpha power in the motor cortex (“mu‐suppression”). When human participants prepared movements while viewing a stimulus, we found that those two types of classical alpha suppression interacted in the third (time‐processing) region in the brain, inducing a prominent decrease in alpha power in the supplementary motor cortex (SMA). Interestingly, this alpha suppression in the SMA occurred in an asymmetric manner (such that troughs of alpha rhythm was more strongly suppressed than peaks), which can produce a gradual increase (slow shift of baseline) in neural activity. Since the neural processing in the SMA encodes a subjective time length for a sensory event, the increased activity in this region (by the asymmetric alpha suppression) would cause an overestimation of elapsed time, resulting in the action‐induced time distortion. Those results showed a unique role of alpha wave enabling communications across distant (visual, motor, and time‐processing) regions in the brain and further suggested a new type of sensory–motor interaction based on neural desynchronization (rather than synchronization).

1. INTRODUCTION

When we make a saccade to a clock, the second hand is sometimes perceived to pause momentarily (Yarrow, Haggard, Heal, Brown, & Rothwell, 2001). Professional tennis players report a feeling of a ball “slowing‐down” before striking it (called the “zone” in sports psychology; Murphy & White, 1995). These are known as examples in which actions distort our perception of time. Although an increasing number of studies have accumulated behavioral evidence for this action‐induced time distortion (Hagura, Kanai, Orgs, & Haggard, 2012; Iwasaki et al., 2017; Merchant & Yarrow, 2016; Morrone, Ross, & Burr, 2005; Press, Berlot, Bird, Ivry, & Cook, 2014; Tomassini & Morrone, 2016; Yokosaka, Kuroki, Nishida, & Watanabe, 2015; Yon, Edey, Ivry, & Press, 2017), no study has revealed specific neural mechanisms underlying it.

A hallmark of the time distortion is that it can be induced even when actions are not executed. In one study (Hagura et al., 2012), subjects viewed a visual stimulus continuously presented on a screen (about 1,200 ms). In a half of trials, they performed a reaching movement to the screen immediately after the stimulus went off (action trials), while no movement was required in the other half (no‐action trials). The duration of the same stimulus was perceived longer in action than no‐action trials, indicating that action preparation dilated a subjective length of a stimulus in a preaction period. An intention to move (motor commands in the brain) therefore is sufficient to affect time perception.

Another point is that the action‐induced time dilation cannot be explained by general changes in attention or arousal level related to actions. Our previous study compared the dilation effect in two different conditions (Iwasaki et al., 2017). The first condition was the same as above (Hagura et al., 2012). Subjects viewed a continuous visual stimulus (950–1,450 ms) and, in action trials, performed manual movements when it went off (filled‐interval condition, Figure 1a). In the second condition, they watched two briefs (17 ms) flashes successively presented (inter‐flash interval: 950–1,450 ms), performing actions in response to the second flash (unfilled‐interval condition, Figure 1b). Note that those two conditions differed only in the presence/absence of continuous visual inputs in a preaction period. Nevertheless, they produced different results; action preparation dilated subjective duration of the continuous stimulus, while no dilation was observed in the inter‐flash interval (Figure 2a). Therefore, the time distortion was caused by a combination of two factors, action preparation (motor factor) and continuous sensory inputs (visual factor).

Figure 1.

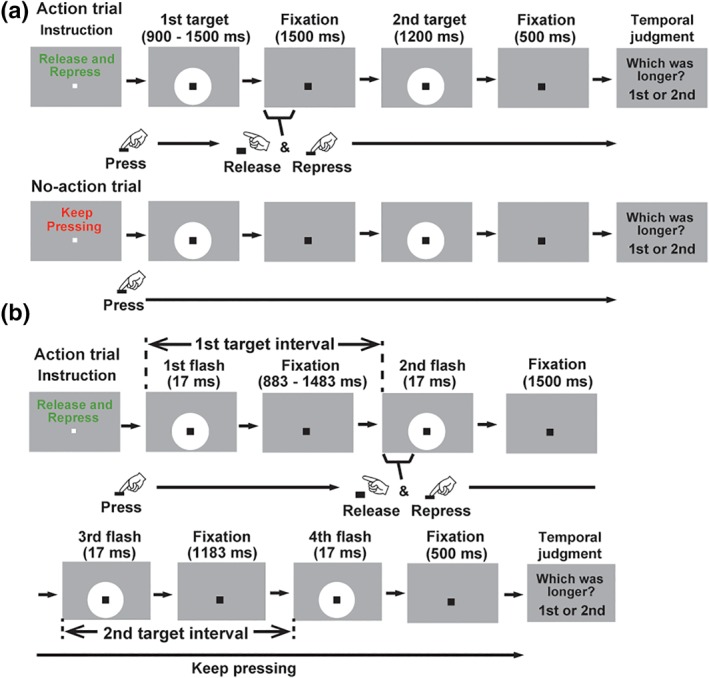
Structures of trials. (a) Filled‐interval condition. Subjects read an instruction message (“Release and Repress” or “Keep Pressing”, randomized across trials) and started each trial by pressing a button with their right hands. In action trials (upper panels), they released and repressed the button as soon as a white disk (first target, 900–1,500 ms) went off. They then viewed the second target (1,200 ms) and answered whether the first or second target was presented longer (temporal judgment task). The lower panels illustrate a control (no‐action) trial in which subjects performed no action but kept pressing the button until a screen for the temporal judgment task was shown. Time distortion induced by action preparation was measured by a difference in subjective duration of the first target between the action and no‐action trials. (b) Unfilled‐interval condition. Four flashes of a white disk were presented in each trial. Subjects compared an interval between the first and second flashes (first target) with that between the third and fourth flashes (second target). In action trials, they performed the release and repress movements to the second flash, while no action was necessary for control trials (not shown in this figure). Illustrations were adopted from our previous study (Iwasaki et al., 2017) with permission from Elsevier [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 2.

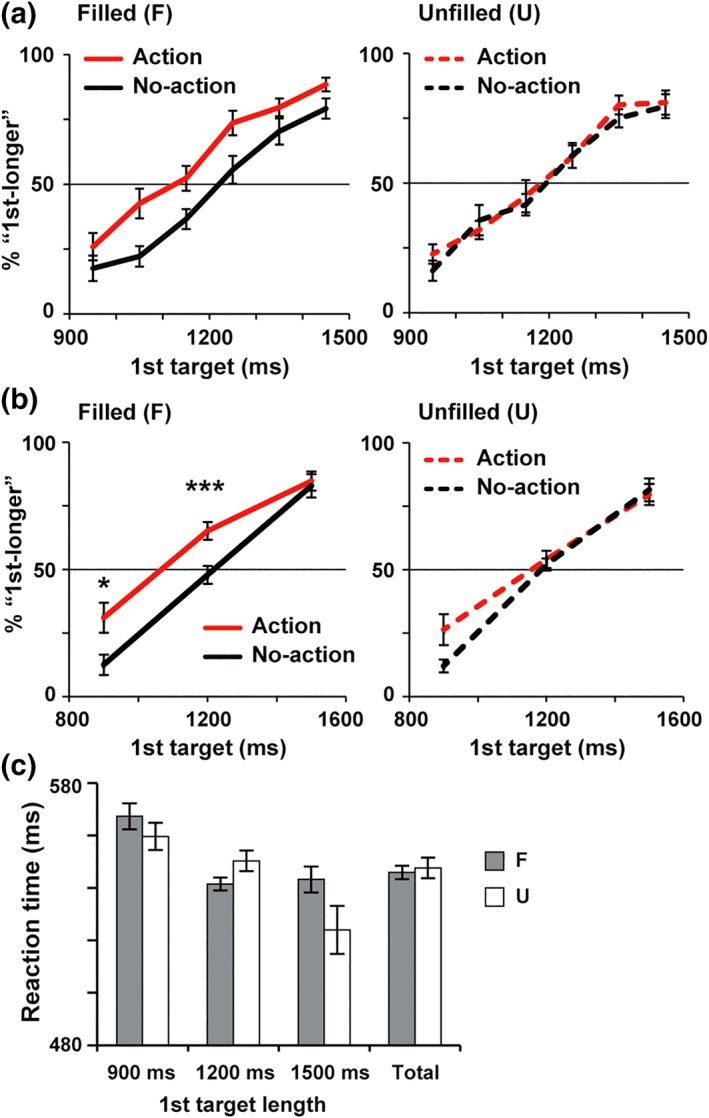
Behavioral data. (a) Percentages of trials in which subjects reported the first target as longer than the second (%“first‐longer”) as a function of actual lengths of the first target. Illustrations were adopted from our previous study (Iwasaki, Tomita, & Noguchi, 2017) with permission from Elsevier. Red and black lines denote action and no‐action trials, respectively. Action preparation generally increased %“ first‐longer” in filled‐interval condition (left panel) but not in unfilled‐interval condition (right panel). (b) The %“ first‐longer” in the present MEG study. Consistent with (a), an action‐induced time dilation was selectively observed in filled‐interval condition, showing an interaction of visual (filled/unfilled) × motor (action/no‐action) factors. (c) Reaction time (an interval from an end of the first‐target period to a completion of release and repress movements). No difference was observed in any pairs of filled (F, gray) and unfilled (U, white) conditions (see section 3 for details). In this and subsequent figures, all error bars denote SE across 18 subjects. *p < .05, ***p < .001 [Color figure can be viewed at http://wileyonlinelibrary.com]

Based on those behavioral data, here we investigate neural mechanisms of this simplest type of time distortion induced by action preparation (Hagura et al., 2012; Iwasaki et al., 2017). A whole‐brain imaging with magnetoencephalography (MEG) would allow us to record neural responses related to time perception, such as a slow build‐up (climbing) activity in the medial frontal region (Elbert, Ulrich, Rockstroh, & Lutzenberger, 1991; Macar, Vidal, & Casini, 1999; Merchant, Zarco, Perez, Prado, & Bartolo, 2011; Parker, Chen, Kingyon, Cavanagh, & Narayanan, 2014; Pfeuty, Ragot, & Pouthas, 2003; Wittmann, 2013) and neural oscillations at various frequencies (Bartolo & Merchant, 2015; Fujioka, Ross, & Trainor, 2015; Kulashekhar, Pekkola, Palva, & Palva, 2016; Wiener & Kanai, 2016). Our previous results (Iwasaki et al., 2017) predict some sort of visual–motor interaction occurring in the time‐processing regions in the brain (Harrington, Haaland, & Knight, 1998; Ivry & Spencer, 2004; Lewis & Miall, 2003; Merchant, Harrington, & Meck, 2013).

2. MATERIALS AND METHODS

2.1. Participants

Eighteen subjects (11 females, age: 18–48) were collected for the present MEG study. This sample size was based on the power analysis using G*Power 3 (Faul, Erdfelder, Lang, & Buchner, 2007). An expected effect size was taken from our previous data (Iwasaki et al., 2017) with the power (1 − beta) set at >0.80. All participants had normal vision and showed the action‐induced time dilation. Informed consent was received from each subject after the nature of the study had been explained. All experiments were carried out in accordance with guidelines and regulations approved by the ethics committee of Kobe University and the National Institute for Physiological Sciences, Japan.

2.2. Stimuli and task

Visual stimuli were generated using the MATLAB Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) and presented on a screen at a refresh rate of 60 Hz. An experiment consisted of two conditions (filled‐ and unfilled‐interval conditions) conducted in separate blocks. In the filled‐interval (F) condition (Figure 1a), each trial started with an instruction screen indicating manual movements required in that trial. A message on the instruction screen was either “Release and Repress” (action trial) or “Keep Pressing” (no‐action trial). When subjects read the message and pressed a button with their right hands, the message went off and a color of a white fixation point (0.22 × 0.22 deg) changed into black. After a random delay of 800–1,200 ms, a white disk (first target, 3.59 × 3.59 deg) appeared over the fixation for 900, 1,200, or 1,500 ms (variable across trials), which was followed by a fixation‐only screen for 1,500 ms. In action trials (“Release and Repress”), subjects had to release a button when the first target went off, and press it again. Importantly, both of those “release” and “repress” actions should be performed as quickly as possible, within 700 ms from an offset of the first target. Otherwise, they saw an error message informing an abortion of a current trial (the aborted trial was repeated later). In no‐action trials (Keep Pressing), on the other hand, subjects had to keep pressing a button even after the first target went off (an error message was shown when they released the button). Subjects then saw the second target (white disk) presented at the same position as the first target. The duration of the second target was 1,200 ms in every trial, although this information was unknown to subjects. After another fixation screen of 500 ms, a task screen (“Which was longer? first or second”) was presented that allowed subjects to release the button and prompted them to perform a temporal judgment task. In this task, subjects compared the duration of the first target (900–1,500 ms) with that of the second (1,200 ms). They pressed one button when they felt the first target was longer than the second and pressed another to indicate the reverse (those buttons for the temporal judgment task were different from the one used for the button‐press actions).

In the unfilled‐interval (U) condition, basic structures of a trial were the same as the filled condition except that an amount of time (that should be compared in the temporal judgment task) was defined as an interval between two brief flashes. As shown in Figure 1b, one trial involved four flashes of a white disk. The duration of each flash was 17 ms. Subjects compared an interval (stimulus onset asynchrony or SOA) between the first and second flashes (first target) with that between the third and fourth flashes (second target). The SOA in the first target ranged from 900 to 1,500 ms whereas SOA in the second target was fixed at 1,200 ms. An instruction screen of “Release and Repress” required subjects to perform the release and repress movements as quickly as possible in response to the second flash (action trial). No release action was necessary for the no‐action trial.

One experimental session (block) contained 50 trials in which 25 action trials were randomly intermixed with 25 no‐action trials. The duration/SOA of the first target was also randomized within the session, is set at 900 ms (8 trials), 1,200 ms (34 trials), or 1,500 ms (8 trials). As described below, we mainly analyzed MEG data when the first target was 1,200 ms (1,200 ms trials), because the time dilation effect was maximized when the first and second target shared the same length (Iwasaki et al., 2017). Subjects performed six sessions, three for the filled condition and the other three for the unfilled condition. An order of the two conditions was counterbalanced across subjects.

We analyzed behavioral data by measuring a percentage of trials in which subjects indicated the first target as longer than the second (%“first‐longer”). As shown in Figure 2, the %“ first‐longer” generally increased as a function of physical duration/SOA of the first target (900–1,500 ms). If action preparation induced a dilation of subjective time, this would be observed as an increase in %“ first‐longer” at all lengths of the first target (Hagura et al., 2012; Iwasaki et al., 2017).

2.3. MEG measurements and basic data analyses

Neural activity was measured by a whole‐head MEG system (Vector‐view, ELEKTA Neuromag, Helsinki, Finland). This system recorded neuromagnetic signals from 102 different positions over the scalp using 204 planer‐type sensors (two sensors per recording position). One sensor measured latitudinal directions of changes in neuromagnetic signals and the other sensor measured changes in longitudinal directions (sampling rate: 1 kHz, analog band‐pass filter: 0.1–330 Hz). Signals from those two sensors at the same recording position were integrated into data analyses (see below). Neuromagnetic waveforms measured by those planar‐type sensors reflected neural activity in the cerebral cortex just below the recording position (Nishitani & Hari, 2002). Other details about MEG measurements were shown in our previous publications (Noguchi & Kakigi, 2006; Noguchi, Kimijima, & Kakigi, 2015; Suzuki, Noguchi, & Kakigi, 2014).

We performed basic analyses of MEG data using Brainstorm (Tadel, Baillet, Mosher, Pantazis, & Leahy, 2011), a free software downloadable from https://neuroimage.usc.edu/brainstorm. First, neuromagnetic signals in the first‐target periods were segmented and averaged across trials to yield an event‐related field (ERF). An epoch for the averaging ranged from −800 to 2,000 ms relative to the onset of the first target, with a 100‐ms period just before the target (−100 to 0 ms) used as a baseline. Trials in which signal variations were larger than 4,500 fT/cm were excluded from analysis. To evaluate the strength of neural responses at each of 102 recording positions, we integrated ERFs of two (latitudinal and longitudinal) sensors at each position. This integration was performed by calculating a vector norm (root sum square) of the two sensors, as shown below (Noguchi, Yokoyama, Suzuki, Kita, & Kakigi, 2012).

$$\sqrt{x_i^2+y_i^2}$$

Where x and y indicate MEG signals (fT/cm) in the latitudinal (x) and longitudinal (y) sensors at the recording position i (1–102). Note that, after this conversion into vector norms, strong neuromagnetic responses are always shown as upward (not downward) shifts of the ERF waveforms (vector‐norm ERF, Figures 3 and 5). To normalize inter‐individual differences in magnitudes of neuromagnetic responses, the vector‐norm ERFs were transformed into percent changes (% change) from the baseline and then averaged across subjects.

Figure 3.

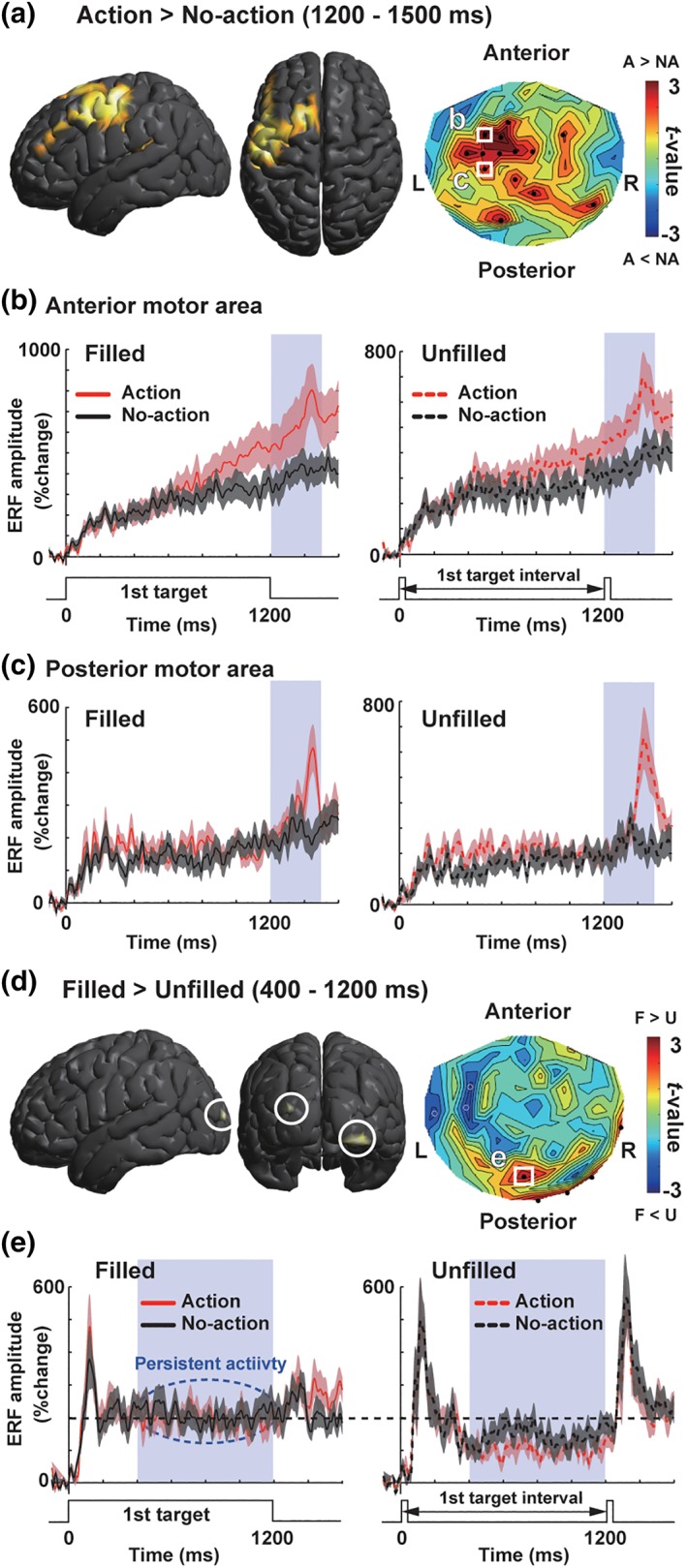
Basic results of ERF analyses. (a) Neuromagnetic activity induced by the release and repress movements (motor factor) when the first target length was 1,200 ms (1,200 ms trials). Left and middle panels show lateral and top views of a source‐space t‐map (SPM 12) comparing action (A) and no‐action (NA) trials. In this and subsequent figures, thresholds of source‐space maps were lowered into p < .005 for visual purpose only. A right panel shows a sensor‐space t‐map. The t‐values comparing mean amplitudes of vector‐norm ERFs (1,200–1,500 ms) between action and no‐action trials were color‐coded on a contour map depicted over a two‐dimensional (2D) layout of 102 sensor positions. (b) Vector‐norm ERFs at a sensor over the anterior motor region (see a white square in a). Red and black lines denote action and no‐action trials (background shading: SE across 18 subjects). Build‐up increases of ERFs in a preaction (first‐target) period indicate that this region was related to both preparation and execution of manual movements. (c) Vector‐norm ERFs in the posterior motor region. Sharp increases of ERFs around 1,400 ms suggested that this region was related to the execution of manual movements. (d,e) Comparison of filled and unfilled conditions (visual factor). An onset of a white disk (first target) elicited strong MEG responses in all types of trials (0–400 ms). This was followed by a persistent activity stronger in filled than unfilled conditions (400–1,200 ms), which reflected a continuous presentation of the white disk [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 5.

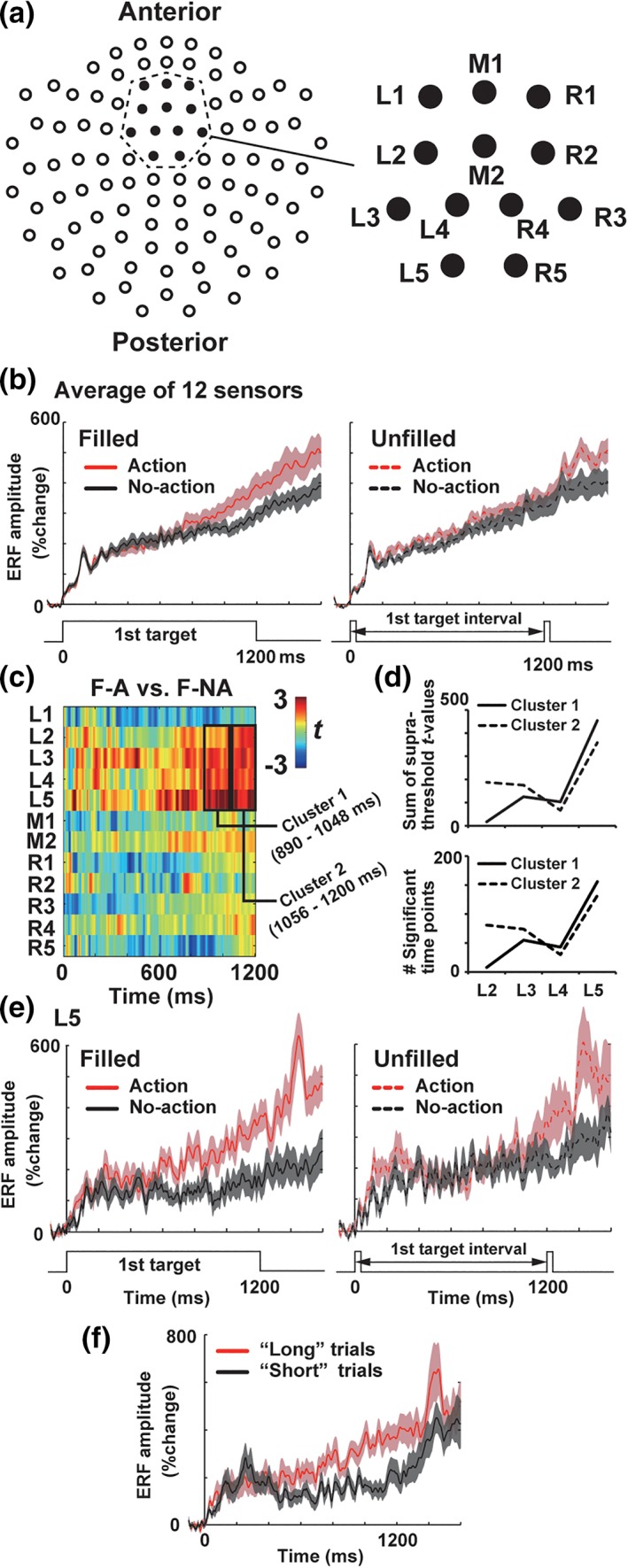
Definition of a ROI (region of interest). (a) A 2D layout of 102 sensor positions (left) and 12 sensors over the SMA (right) defined in our previous study (Noguchi & Kakigi, 2006). The spatiotemporal cluster‐based analysis (see section 2) were performed over the 12 sensors (L1–L5 over the left SMA, R1–R5 over the right SMA, and M1–M2 on a midline). (b) Vector‐norm ERFs averaged across the 12 sensors over the SMA. (c) Results of point‐by‐point paired t test. We compared amplitudes of vector‐norm ERFs between F‐A and F‐NA trials at each time point and each sensor position. Resultant t‐values were color‐coded and plotted as a function of time. Two spatiotemporal clusters were identified at L2–L5 (890–1,048 ms and 1,056–1,200 ms) showing stronger neural activity in F‐A than F‐NA trials. (d) Sums of supra‐threshold (> 2.11) t‐values (upper panel) and numbers of supra‐threshold time points (lower panel) within cluster 1 (890–1,048 ms, solid lines) and cluster 2 (1,056–1,200 ms, dotted lines). Data at individual sensors (L2–L5) are separately shown. (e) Vector‐norm ERFs at the L5. Action preparation produced a larger build‐up activity than no‐action trials in filled but not in unfilled conditions. This resembled the visual–motor interaction in behavioral data (Figure 2). (f) Results of the response‐based (trial‐by‐trial) analysis at the L5. We pooled the data in filled and unfilled conditions, comparing trials in which first target were judged as longer than the second (“long” trials, red) with those in which the first target was judged as shorter (“short” trials, black) [Color figure can be viewed at http://wileyonlinelibrary.com]

2.4. Statistical analyses of MEG data (overview)

In the following sections, we analyzed the MEG data using a variety of methods. After defining a sensor of interest by the cluster‐based permutation approach (section 2.6), we applied the time‐frequency (TF) decomposition to MEG waveforms at this sensor (section 2.7). Coefficients of the Granger causality (section 2.8) and the baseline‐shift index (BSI; section 2.10) were also estimated. In all analyses, statistical comparisons across conditions (e.g., action vs. no‐action trials) were made on a univariate measure, using a paired t test or repeated‐measures anova. A threshold of statistical significance was set at p ≤ .05 (two‐sided), except for an analysis on Statistic Parametric Mapping 12 (p ≤ .001, see section 2.5 below).

2.5. Source estimations of ERFs

We estimated anatomical source locations of MEG signals (Figure 3a) with the minimal norm (MN) approach implemented in Brainstorm. First, a spherical head model for forward solutions was constructed for each subject, using positional information of MEG sensors and a template brain from the Montreal Neurological Institute. The forward model was then inverted with the MN approach, which converted MEG waveforms at 204 sensors into a current density map of multiple dipoles placed on the cortical surface. Finally, the current density map (cortical activation map) was normalized into the sLORETA measure, to compensate for a depth‐dependent reduction of MEG signals. Noise covariance matrix for those MN estimations was computed from MEG signals in a prestimulus period (−800 to 0 ms).

For second‐level (group‐level) analyses across all subjects, the cortical activation map of each subject was exported into Statistic Parametric Mapping 12 (SPM12, available online at http://www.fil.ion.ucl.ac.uk/spm/). Differences between conditions (e.g., action trial vs. no‐action trial in Figure 3a) were evaluated by the random‐effect analysis (voxel‐wise paired t tests and repeated‐measures anova) of SPM12. The threshold for statistical significance was p = .001, uncorrected.

2.6. Definition of a region of interest

A purpose of the present study was to elucidate neural mechanisms of the time dilation effect emerging from an interaction of the visual and motor factors. To this end, we started our analyses by searching for neural correlates of this effect (Figure 4). The first candidate was medial premotor (Crowe, Zarco, Bartolo, & Merchant, 2014; Merchant, Perez, Zarco, & Gamez, 2013) or the supplementary motor cortex (SMA) (Coull, Vidal, & Burle, 2016; Schwartze, Rothermich, & Kotz, 2012), a core region of the cortico‐thalamic‐basal ganglia circuit (Akkal, Dum, & Strick, 2007) for time perception (Merchant & Yarrow, 2016). This region is known to show a “temporal accumulator” activity that slowly grows up as a function of an elapsed time from a stimulus onset (Elbert et al., 1991; Merchant et al., 2011; Parker et al., 2014). The amplitude of this activity was closely correlated with a subjective length of the stimulus (Macar et al., 1999; Pfeuty et al., 2003).

Figure 4.

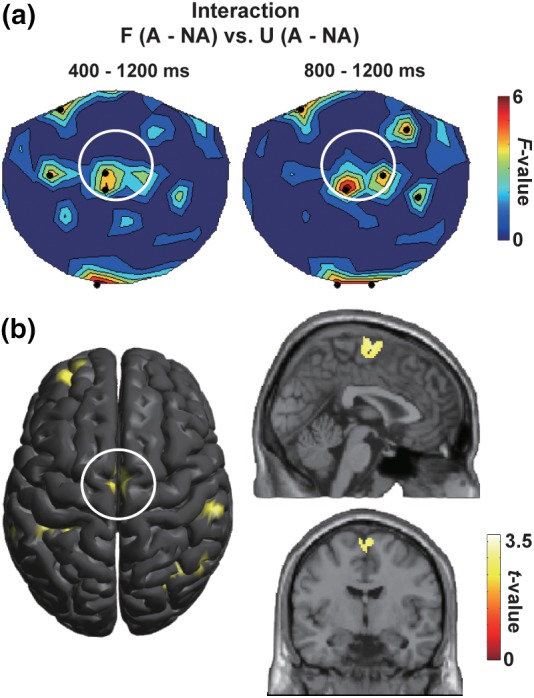
Neural correlates of the action‐induced time dilation. (a) The F‐maps showing an interaction of visual (filled/unfilled) and motor (action/no‐action) factors (repeated‐measures anova) at 400–1,200 ms (left) and 800–1,200 ms (right). A difference between filled‐action (F‐A) and no‐action (F‐NA) trials was compared with a difference between unfilled‐action (U‐A) and no‐action (U‐NA) trials. Black dots indicate sensors showing a significant (p < .05) interaction. The F‐values at local maxima over the front‐midline region (white circle) were 5.19 (p = .036) in the left panel and 6.92 (p = .018) in the right panel. (b) Source locations of the medial frontal activity showing the interaction of visual and motor factors (estimated by SPM using a contrast of [F‐A, F‐NA, U‐A, U‐NA] = [1, −1, −1, 1]). Talairach coordinates of a local maximum was x = 1, y = −7, z = 65 (Brodmann area 6). This area (supplementary motor area or SMA) has been known as a core region for the processing of time information [Color figure can be viewed at http://wileyonlinelibrary.com]

Indeed, both of our sensor‐space analysis (Figure 4a) and source‐space analysis (Figure 4b) on ERFs indicated a significant interaction of visual and motor factors in the SMA. We thus focused on this region and further searched for sensor positions (within the SMA) and time periods in which the time dilation effect was most prominently reflected in neuromagnetic signals. First, we selected 12 MEG sensors that can represent neural activity in the SMA, based on our previous study (Noguchi & Kakigi, 2006). Those consisted of five sensors over the left hemisphere (L1–L5, Figure 5a), five over the right hemisphere (R1–R5), and two on a midline (M1 and M2). Mean VEFs across the 12 sensors (Figure 5b) indicated that this region overall showed stronger neural responses in action than no‐action trials in filled but not in unfilled conditions (consistent with the interaction F‐maps in Figure 4). Second, we compared amplitudes of the vector‐norm VEFs between action and no‐action trials in filled condition (F‐A vs. F‐NA) at each time point (from 0 to 1,200 ms) and each sensor position. Results of those “point‐by‐point paired t tests” are color‐coded and shown in Figure 5c.

Finally, spatiotemporal clusters showing a significant difference between F‐A and F‐NA trials were identified by the cluster‐based permutation approach (Cichy, Pantazis, & Oliva, 2014; Maris & Oostenveld, 2007). Briefly, this approach searched for a sequence of data points (cluster) at which two ERFs significantly differed from each other (p < .05, sample‐level significance) based on their temporal and spatial adjacency. Through random permutations of original ERFs for 1,000 times, we generated a distribution of a maximum cluster‐level statistic (a sum of t‐values within each cluster) under a hypothesis of null effect. A cluster‐level threshold was then determined as an upper 2.5‐% tail of this null distribution. A difference between two ERFs was considered as significant only when spatiotemporal clusters in actual ERFs exceeded this cluster‐level threshold.

The permutation approach above identified two significant clusters in the left SMA (L2–L5), one at 890–1,048 ms (cluster 1:159 time points, p ≤ .021) and another at 1,056–1,200 ms (cluster 2:145 time points, p ≤ .015). As shown in Figure 5d, time points with the sample‐level significance were concentrated at the L5 sensor. For example, almost all time points (156 out of 159 in cluster 1 and 132 out of 145 in cluster 2) at this sensor satisfied the sample‐level significance (lower panel of Figure 5d). The chi‐square tests on numbers of significant time points across the L2–L5 showed inhomogeneous distributions of those points both in cluster 1 (χ ²[3] = 314.5, p < .001, ϕ = 0.703) and cluster 2 (χ ²[3] = 145.8, p < .001, ϕ = 0.501). We thus chose the L5 as a target sensor in the present study and performed subsequent analyses (e.g., estimations of the Granger causality and the BSI, see below) using the data at this sensor.

2.7. TF analyses

We investigated neural oscillation signals in the first‐target period. A TF transform using complex Morlet wavelets was applied to MEG data (central frequency: 1 Hz, time resolution at full width at half maximum: 3 s), which converted neuromagnetic waveforms into power spectra of time (−800 to 2,000 ms) × frequency (1–60 Hz). Those TF spectra were then averaged across trials and combined between latitudinal and longitudinal sensors at each sensor position. To show relative changes in power over time (Figure 6a), we performed a baseline correction of the TF data (Grummett et al., 2014). For each frequency, all data from −800 to 2,000 ms were converted into dB change from the baseline period (−200 to 0 ms), as shown by

$$y=20\times {\log }_{10}\left(x/u\right),$$

where x and y indicate powers before and after the baseline correction, and u indicates a mean over the baseline period. All statistical analyses on the TF data were performed at the L5, focusing on the two critical periods (890–1,048 ms and 1,056–1,200 ms) that had been identified through the spatiotemporal cluster‐based approach on ERFs (section 2.6).

Figure 6.

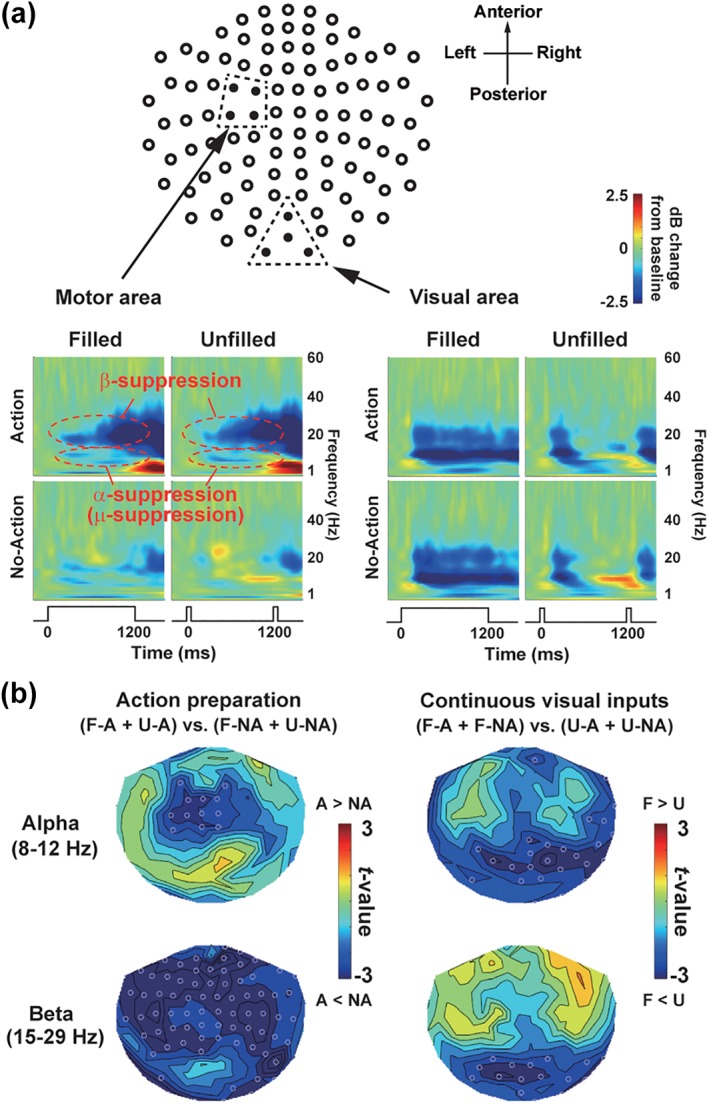
Results of TF analyses. (a) Mean TF spectra over the motor (left) and visual (right) regions. In the left motor region, action preparation induced suppression (desynchronization) of alpha (8–12 Hz) and beta (15–29 Hz) rhythms. In the visual region, continuous visual inputs in filled condition induced persistent suppression of alpha and beta rhythms. (b) Spatial distribution of the alpha and beta suppression at 400–1,200 ms. Left: t‐maps of action versus no‐action (motor factor). Right: t‐maps of filled versus unfilled (visual factor). Open white dots indicate sensors showing a significant (p < .05) difference. Note complementary patterns of motor and visual factors; action preparation induced desynchronization in anterior brain regions, while continuous visual inputs induced desynchronization at posterior sensors [Color figure can be viewed at http://wileyonlinelibrary.com]

2.8. Granger causality analyses

We then performed the bivariate Granger causality analysis between ERFs and alpha power at the L5, using the multivariate Granger causality (MVGC) toolbox on MATLAB (Barnett & Seth, 2014). First, we prepared two‐time series (ERF and alpha power) from 0 to 1,200 ms (Figure 7b). The time series of alpha power (one‐dimensional array of 1,200 data) was computed by averaging powers from 8 to 12 Hz in TF spectrum at the L5. We ensured stationarity of input data (time series) by segmenting them into short epochs of 100 ms, on the logic that shorter windows are more likely to be stationary (Barnett & Seth, 2014). A linear trend in each time series was then removed, which was also effective to improve stationarity. The number of time lags (model order) was estimated by Akaike Information Criterion with a maximum set to be 20. Based on those lags, we calculated time‐domain bivariate Granger causality between ERFs at the L5 and alpha power at the L5. Statistical significance of Granger coefficients was tested by theoretical null distribution, adjusting for multiple hypotheses. Since we repeated this analysis over 12‐time windows of 100 ms (0–100, 100–200,…, and 1,100–1,200 ms), resultant p values were corrected for multiple comparisons by a factor of 12 (the Bonferroni method).

Figure 7.

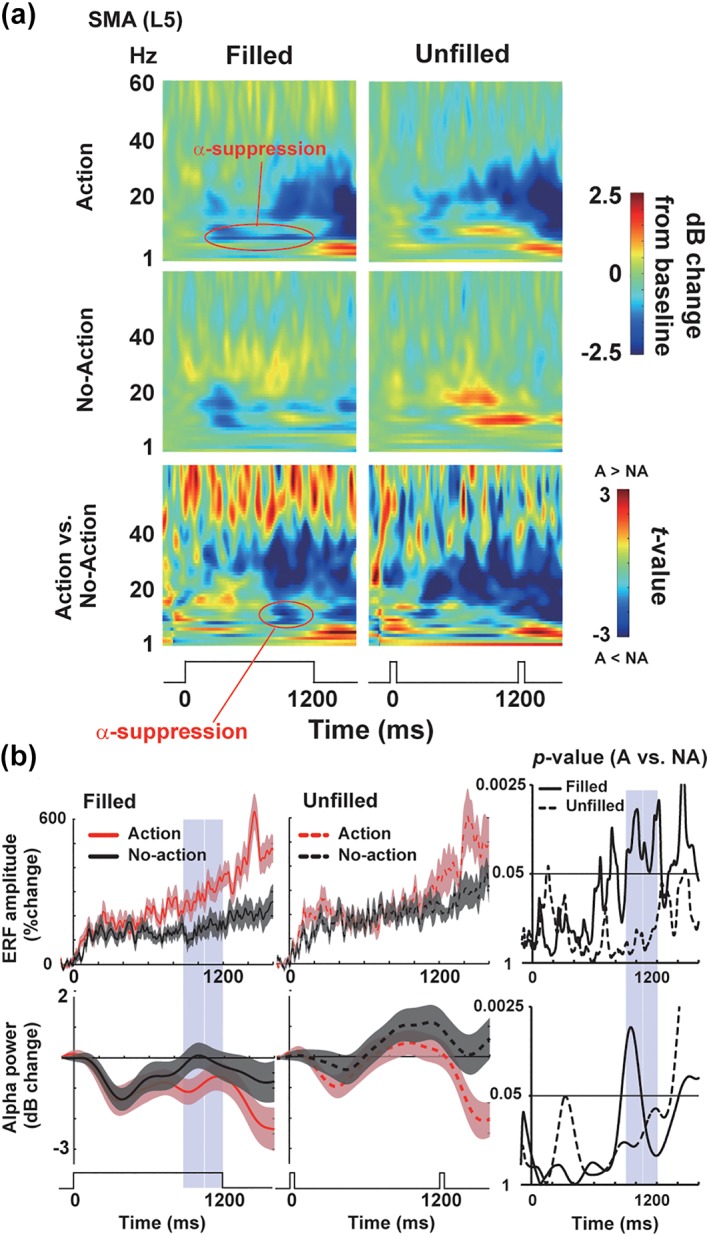
Neural oscillations in the SMA. (a) The TF spectra over the left SMA (L5). The color‐coded matrices of t‐values (comparing oscillatory powers between action vs. no‐action trials) were shown at the bottom. An interaction of motor and visual factors can be seen as the suppression of alpha rhythm in F‐A (filled‐action) trials. (b) The ERFs (upper panels) and changes in alpha power (lower panels) at the L5. The time series of alpha power was computed by averaging powers from 8 to 12 Hz in the TF spectrum. Right: Changes in p values of point‐by‐point t test (action vs. no‐action). A moving average over 41 time points is applied for visual purpose only. Blue shades denote time periods (890–1,048 ms and 1,056–1,200 ms) in which differences in ERFs between action and no‐action trials exceeded a cluster‐level threshold of significance (see section 2 and Figure 5c) [Color figure can be viewed at http://wileyonlinelibrary.com]

2.9. Response‐based analysis

To investigate a direct relationship between the behavioral and MEG data, we performed the response‐based analysis (Figure 8). Based on behavioral responses in the temporal judgment task, all trials in a given condition (e.g., F‐A) were classified into “long” trials (in which the first target was judged longer than the second) or “short” trials (in which the first target was judged shorter). Comparisons of ERFs (Figure 8a) and TF spectra (Figure 8b) between those “long” and “short” trials would reveal neural components associated with subjective lengths of the first target.

Figure 8.

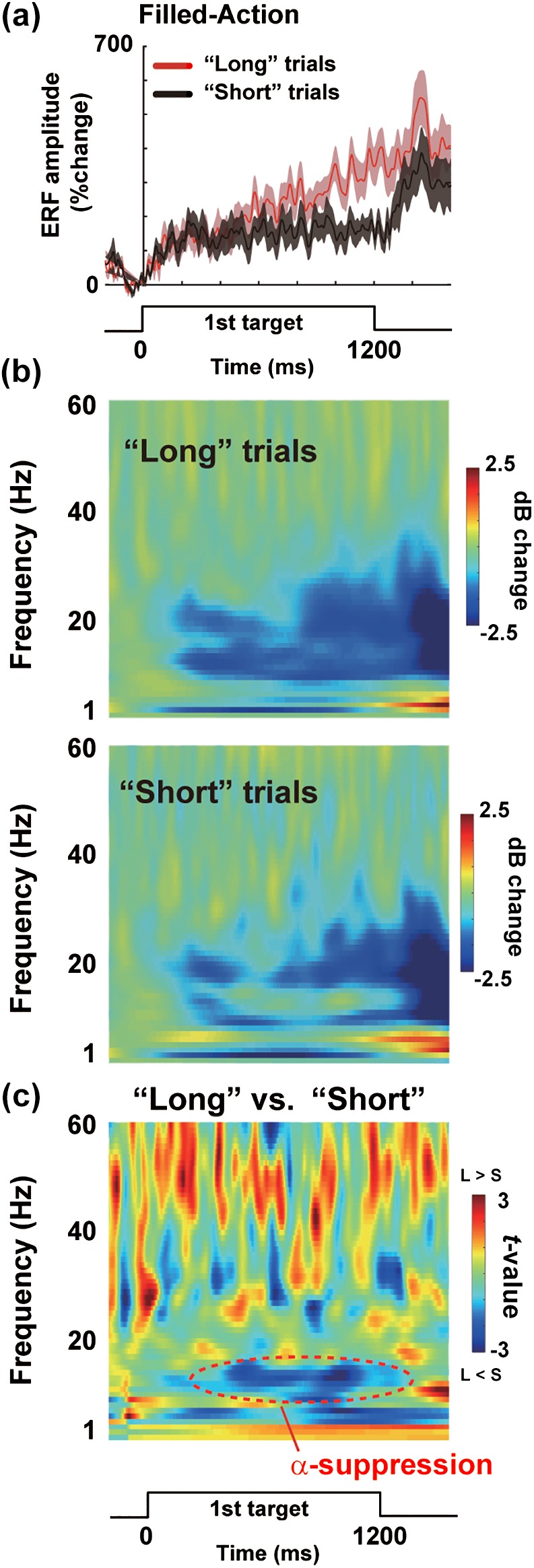
Results of the response‐based analysis in F‐A trials. (a) Vector‐norm ERFs at the L5 in “long” trials (red) and “short” trials (black). (b) TF spectra in the “long” and “short” trials. (c) The color‐coded matrices of t‐values comparing oscillatory powers between “long” and “short” trials. Behavioral effects of time dilation were closely coupled with a decrease in alpha power [Color figure can be viewed at http://wileyonlinelibrary.com]

2.10. Baseline‐shift index

Recent studies of electroencephalography (EEG) and MEG indicated that an asymmetric modulation of neural oscillations can produce slow evoked responses in event‐related potentials (ERPs) and ERFs (Mazaheri & Jensen, 2010; Nikulin, Linkenkaer‐Hansen, Nolte, & Curio, 2010). Schematic illustrations of this asymmetric modulation are shown in Figure 9. As described below, the TF analysis over the SMA showed significant suppression of alpha power induced by action preparation in Filled condition (see section 3 and Figure 7). If this suppression occurred in an asymmetric manner such that troughs of alpha rhythm were modulated stronger than peaks (black line in the right panel of Figure 9a), this would produce a slow shift of an averaged waveform (ERF) into upward direction (red line). It is possible that larger ERFs in action than no‐action trials (Figure 5e, left) resulted from this asymmetric suppression of alpha rhythm. To test this hypothesis, we computed the BSI, a measure to quantify the asymmetric (nonzero mean) modulation of neural oscillations (Nikulin et al., 2010).

Figure 9.

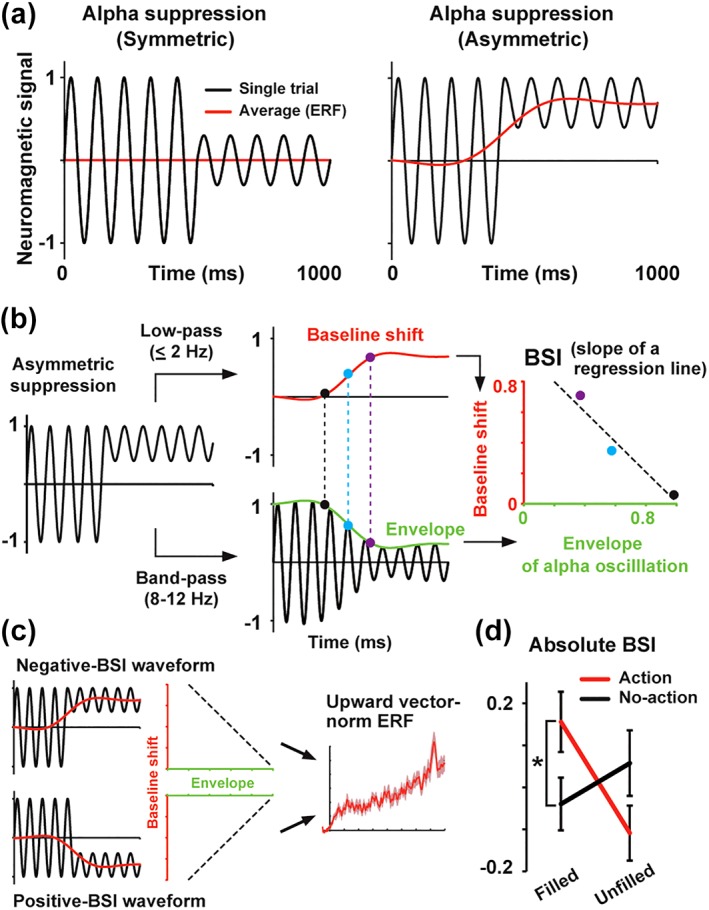
Asymmetric suppression of alpha rhythm. (a) Schematic illustrations of a build‐up ERF emerging from alpha suppression. Black and red lines indicate single‐trial and averaged waveforms, respectively. When alpha rhythm is suppressed in a symmetric manner (left panel), no baseline shift (slow change) would be observed in an averaged waveform. When alpha rhythm is suppressed in an asymmetric manner such that troughs are modulated stronger than peaks (right panel), this would produce a slow shift of an averaged waveform. (b) Computational procedures of the baseline‐shift index (BSI), a measure to quantify the asymmetric (nonzero mean) modulation of neural oscillations (Nikulin et al., 2010). See section 2 for details. The BSI was defined as a scaling factor (slope of a regression line) relating an envelope of alpha oscillation (green) to a slow component (red) in a single‐trial waveform. Note the temporal correspondence of dots with the same color (black, cyan, and purple). (c) Negative‐ and positive‐BSI waveforms. Both types of asymmetric modulation would produce a large deflection of vector‐norm ERF. (d) Absolute BSIs computed from waveforms (800–1,200 ms) at the L5. Relative differences from a baseline period (−400 to 0 ms) are shown. A significant interaction between the visual and motor factors was observed. Those results suggest that asymmetric suppression of alpha rhythm caused the larger build‐up activity (Figure 5) and the time dilation in F‐A compared with F‐NA trials (Figure 2). *p < .05 [Color figure can be viewed at http://wileyonlinelibrary.com]

As shown in Figure 9b, we filtered MEG waveform of each trial (at 800–1,200 ms) in two different ways. First, slow changes in neuromagnetic signals were isolated with a low‐pass filter of ≤2 Hz (baseline‐shift component, red line). Second, an amplitude envelope of a carrier wave (alpha rhythm) was extracted using a band‐pass filter (8–12 Hz) and the Hilbert transform (envelope, green line). We then performed a linear regression between the envelope and baseline‐shift component. The BSI was defined as a slope of this regression line (a scaling factor relating the envelope to baseline shift). As shown in Figure 9c, the BSI becomes negative when troughs of the carrier wave are modulated stronger than peaks but becomes positive when peaks are modulated stronger than troughs. Since both negative‐ and positive‐BSI waveforms would produce a large deflection of vector‐norm ERF, we computed an absolute BSI after the BSI in each trial was averaged across trials. A large absolute BSI indicates that changes in oscillation amplitude of a carrier wave (alpha rhythm) strongly modulate slow components of a MEG waveform. Based on the results of the ERF and Granger causality analyses (see below), we investigated the symmetry of alpha suppression at the SMA (L5) after 800 ms. The BSIs obtained from the waveforms at 800 to 1,200 ms were baseline‐corrected using the BSIs at −400 to 0 ms. Those corrected BSIs were statistically evaluated by a repeated measures two‐way anova of condition (filled/unfilled) × action (action/no‐action) and post hoc tests with a correction of multiple comparisons (the Bonferroni method).

3. RESULTS

3.1. Behavioral data

Figure 2b shows the %“ first‐longer” in the present MEG study. A three‐way anova of condition (filled/unfilled) × action (action/no‐action) × first‐target lengths (900/1,200/1,500 ms) yielded significant main effects of action (F[1,17] = 9.28, p = .007, η ² = 0.35) and first‐target lengths (F[1.18,20.12] = 134.7, p < .001, η ² = 0.89) as well as a significant interaction of condition × action (F[1,17] = 5.08, p = .038, η ² = 0.23). A two‐way anova focusing on the 1,200 ms trials (main data of MEG analyses, see below) indicated a significant main effect of action (F[1,17] = 13.63, p = .002, η ² = 0.45) and a condition × action interaction (F[1,17] = 12.95, p = .002, η ² = 0.43). Post hoc tests with Bonferroni correction revealed a significant difference between action and no‐action trials in filled (F) condition (p = .0004) but not in unfilled (U) condition (uncorrected p = .52). The difference between two types of action trials (F‐A vs. U‐A) was also significant (t[17] = 4.16, p = .0007, Cohen's d = 0.76). These data were consistent with those in our previous study (Figure 2a), demonstrating a dilation of subjective time selectively induced in filled condition.

Figure 2c shows the reaction time of manual movements in action trials. A two‐way anova of condition × first‐target lengths yielded a significant main effect of first‐target lengths (F[2,34] = 17.06, p < .001, η ² = 0.50) and a significant interaction (F[1.31,22.26] = 5.05, p = .027, η ² = 0.23). No main effect of condition was observed (F[1,17] = 1.04, p = .32, η ² = 0.06). Post hoc test for each length indicated no difference between filled and unfilled conditions (900 ms trials: uncorrected p = .15, 1,200 ms trials: p = .10, 1,500 ms trials: p = .11).

3.2. Neural correlates of action‐induced time dilation

Behavioral data replicated the time dilation effect emerging from a combination of continuous visual inputs of the first target (visual factor) and action preparation (motor factor). We then investigated neuromagnetic activity (event‐related fields or ERFs) when this effect was induced. Especially, we focused on MEG data when the first target was 1,200 ms (1,200 ms trials) because the time dilation effect was maximized when the first and second target shared the same length (Iwasaki et al., 2017). Basic results of ERF analyses on the motor and visual factors were shown in Figure 3. Release‐and‐repress movements by a right hand evoked strong MEG responses in a broad region over the left hemisphere (Figure 3a). An anterior part of this motor‐related region showed a build‐up (ramping‐up) activity beginning from a preaction (first‐target) period (Figure 3b), indicating that this part was related to both preparation and execution of manual movements. In contrast, neural activity in a posterior motor region (roughly corresponding to the primary motor cortex) reflected an execution of actions (Figure 3c). In the visual cortex (Figure 3d,e), an onset of first target (white disk) evoked a transient increase of vector‐norm ERFs (0–400 ms). Waveforms in filled condition also showed a persistent neural activity (400–1,200 ms) to a continuous presentation of the first target, while those in unfilled condition did not.

We then explored neural correlates of the time dilation effect. Both sensor‐space F‐map (Figure 4a) and source‐space analyses (Figure 4b) indicated the medial frontal region showing an interaction of visual and motor factors. A center of this regions was located in Brodmann area 6 (Figure 4b, right panels), corresponding to the supplementary motor area (SMA). We thus focused on this region and further searched for sensor position(s) and time period(s) in which neural activity mirroring the time dilation effect was clearly seen. The spatiotemporal cluster‐based approach (Cichy et al., 2014; Maris & Oostenveld, 2007) revealed two significant clusters over the left SMA (L2–L5, Figure 5c), one at 890–1,048 ms (cluster 1) and another at 1,056–1,200 ms (cluster 2). Further analyses using the chi‐square tests indicated that time points with the sample‐level significance were highly concentrated at the L5 sensor (see section 2 and Figure 5d). Figure 5e shows vector‐norm ERFs at the L5. Larger ERFs in action than no‐action trials were observed in filled condition (left) but not in unfilled condition (right), which resembled the behavioral data (Figure 2b). A close relationship between behavioral data and ERFs over the SMA was also seen when the first‐target was 900 and 1,500 ms (Figure S1 in Supporting Information). Furthermore, we found that MEG signals at the L5 reflected subjective lengths of stimuli (Figure 5f); the amplitude of ERFs was larger when subjects judged the first target as longer than the second (“Long” trials) compared with when they judged the first target as shorter (“Short” trials).

These results were highly consistent with a previous literature. Many studies reported a critical role of the SMA in the processing of time information (Coull et al., 2016; Schwartze et al., 2012). The build‐up activity in this region is known as a “temporal accumulator,” since it grows as a function of an elapsed time from a stimulus onset (Elbert et al., 1991; Merchant et al., 2011; Parker et al., 2014). Indeed, the amplitude of this activity was closely correlated with a subjective length of the stimulus (Macar et al., 1999; Pfeuty et al., 2003). Our results thus showed that the action‐induced time dilation (Figure 2) was represented in the neural activity in the SMA, a key node in the cortico‐thalamic‐basal ganglia timing circuit (Merchant, Harrington, & Meck, 2013).

3.3. Neural oscillations in the SMA region

The ERF analyses showed an interaction of the visual and motor factors in the SMA, revealing a neural correlate of the dilation effect. It remains unclear, however, what mechanisms in the brain enabled this visual–motor interaction in the time‐processing region. We approached this issue by investigating neural oscillatory signals since mounting evidence indicated that those signals play an important role in neural communications across distant regions (Buzsaki & Watson, 2012; Gupta & Chen, 2016). Figure 6 displays basic results of the TF analysis on the visual and motor factors. Prominent changes induced by action preparation were observed over the motor‐related region in the left hemisphere (Figure 6a, left), as a decrease in beta (15–29 Hz) power (Pfurtscheller & Lopes da Silva, 1999) in a preaction period. We also found a decrease in alpha power (8–12 Hz), which would correspond to the “mu‐suppression” (Jasper & Andrews, 1938; Matsumoto et al., 2010). In the visual cortex (Figure 6a, right), the suppressions in alpha and beta bands were continuously observed in filled condition but not in an unfilled condition (400–1,200 ms). Spatial distributions of the alpha and beta suppressions over 102 sensor positions were shown in t‐maps in Figure 6b. Note complementary patterns of motor and visual factors; action preparation induced a desynchronization of alpha and beta rhythms in anterior brain regions (left panels), while continuous visual inputs induced the alpha/beta desynchronization at posterior sensors (right panels).

Figure 7a shows TF spectra at the L5 over the left SMA. One can see that this area showed the visual–motor interaction; a combination of continuous visual inputs (filled condition) and preparation of manual movements (action trials) produced suppression of alpha rhythm in F‐A (filled‐action) trials. We compared in Figure 7b the changes in neural activity (ERFs) and alpha power over time. The alpha power averaged over 890–1,200 ms (critical periods that had been identified by the cluster‐based approach on ERFs) was significantly different between F‐A and F‐NA (t[17] = 2.25, p = .038, d = 0.43).

We further investigated a causal relationship between ERFs and changes in alpha power at the L5 using the Wiener–Granger causality analysis (Granger, 1969). Differential time series (F‐A minus F‐NA) of ERFs and alpha power were analyzed with the MVGC toolbox on MATLAB (Barnett & Seth, 2014). In a time window of 800–900 ms, we found significant causality from alpha power to the ERFs (Granger coefficient = 0.161, corrected p = .0064), while causality from the ERFs to alpha power was nonsignificant (Granger coefficient = 0.05, uncorrected p = .09). Those results suggested that a dissociation of ERFs between F‐A and F‐NA trials (beginning from 890 ms) resulted from temporal dynamics of alpha rhythm in the same time window (800–900 ms), although results of the Granger causality analysis should be interpreted cautiously (Stokes & Purdon, 2017).

A close relationship between the ERFs and alpha suppression was also seen in our response‐based analysis (Figure 8). In this analysis, we compared F‐A trials in which subjects judged the first target as longer than the second target (“long” trials) and those in which they did not (“short” trials). Larger ERFs in the “long” than “short” trials were observed at the L5 (Figure 8a). The TF spectra at the same position revealed a decrease in alpha power in the “long” compared to “short” trials (Figure 8b, c). Those results showed that the behavioral effect of time dilation (Figure 2) was tightly coupled with a larger ERF and the suppression of alpha rhythm in the SMA.

3.4. Asymmetric modulation of alpha rhythm

Results of the TF analyses suggested that the visual–motor interaction in the SMA was mediated by alpha rhythm. As a final analysis, we tested a possibility that the build‐up activity in the SMA (Figure 5) can be directly explained by the suppression of alpha power (Figure 7).

Recent EEG/MEG studies indicated that asymmetric suppression of neural oscillations can produce slow evoked responses in an averaged waveform (Mazaheri & Jensen, 2010; Nikulin et al., 2010). As described above, the SMA showed the suppression of alpha rhythm in F‐A trials. If this suppression occurred in an asymmetric manner such that troughs of alpha rhythm were modulated stronger than peaks (black line in the right panel of Figure 9a), this would produce an upward shift of ERF (red line). It is possible that larger ERFs in F‐A than F‐NA trials (Figure 5e) resulted from this asymmetric suppression of alpha rhythm. We thus computed the BSI, a measure to quantify the asymmetric (nonzero mean) modulation of neural oscillations (Nikulin et al., 2010). Briefly, the BSI is a scaling factor relating an envelope of the alpha wave (green line in Figure 9b) to a slow component (red line) of the same waveform. A large absolute BSI indicates that asymmetric changes in the amplitude of alpha rhythm strongly modulate slow components of ERFs.

Results of the BSI analysis at the L5 are shown in Figure 9d. A two‐way anova indicated no main effect of condition (F[1,17] = 1.31, p = .27, η ² = 0.07) or action (F[1,17] = 0.04, p = .84, η ² = 0.002), but yielded a significant interaction (F[1,17] = 11.49, p = .003, η ² = 0.40). Post hoc tests with the Bonferroni correction revealed a significant difference between action and no‐action trials in filled (corrected p = .02) but not unfilled (uncorrected p = .14) conditions. These data supported a possibility that a combination of visual and motor factors induced the asymmetric suppression of alpha rhythm in the SMA, causing a larger build‐up ERF (Figure 5) and the time dilation effect in F‐A compared with F‐NA trials (Figure 2).

In Figure 10, we investigated neural oscillatory signals other than alpha band, such as delta (2–4 Hz), theta (5–7 Hz), beta (15–29 Hz), and gamma (30–59 Hz). No frequency band showed the visual–motor interaction that can explain the behavioral results. Regarding the BSIs, a three‐way anova of frequency (theta/beta/gamma) × condition × action indicated no main effect or interaction (F ≤ 4.299, p > .05, η ² ≤ 0.202 for all). Two‐way anova applied for each frequency band also indicated no effect or interaction (F ≤ 4.265, p > .05, η ² ≤ 0.201 for all).

Figure 10.

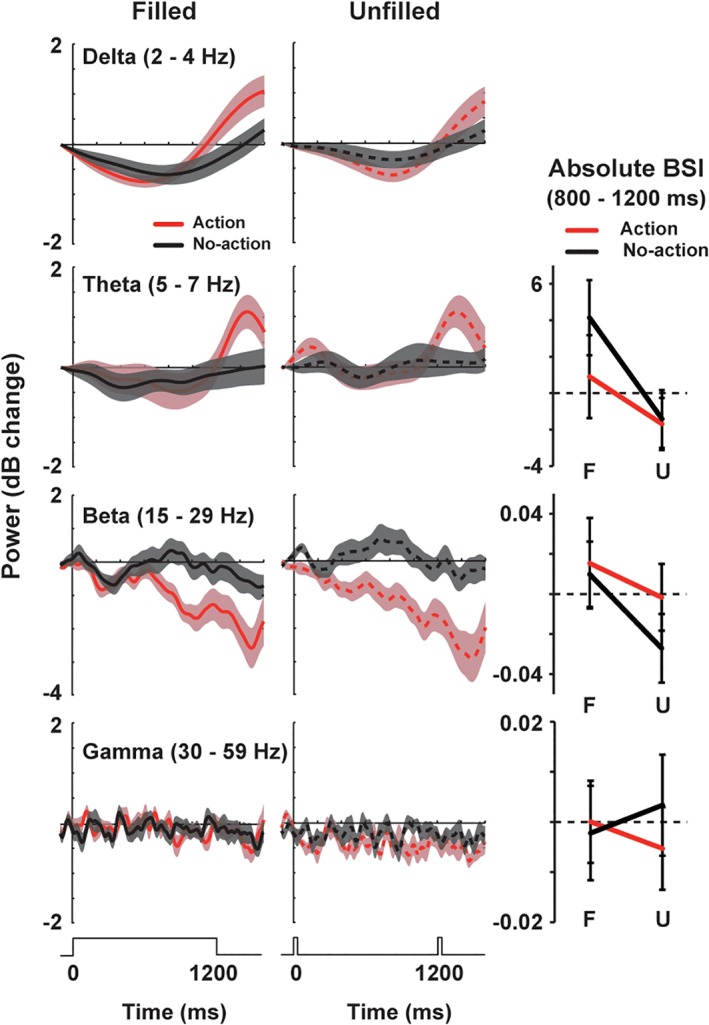
Power changes in delta (2–4 Hz), theta (5–7 Hz), beta (15–29 Hz), and gamma (30–59 Hz) rhythms at the L5. The BSIs are also displayed in the right column (mean ± SE). The BSIs in delta band are not shown because this band (2–4 Hz) partially overlaps with a slow component of a baseline shift (≤2 Hz) in calculating BSIs. No frequency band showed a significant interaction between the visual and motor factors [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

We presently investigated brain mechanisms underlying the action‐induced time dilation. First, we found the neural correlates of the dilation effect in the SMA. The build‐up activity (ERFs) in this area was modulated by action preparation in filled but not unfilled conditions, which paralleled the behavioral results. Analyses on neural oscillations further revealed that such patterns of ERFs were linked with asymmetric suppression of the alpha rhythm in the same region.

4.1. A role of alpha rhythm in time perception

Our results pointed out a close relationship between alpha wave and time perception. Alpha wave is a basic rhythm of neural oscillations widely seen in the brain. Perceiving a visual stimulus generally induces a reduction in alpha rhythm over the occipital region (Berger, 1929; Niedermeyer, 1997). Preparing manual movements also attenuates alpha power over the precentral region (“mu‐suppression”) (Jasper & Andrews, 1938; Matsumoto et al., 2010). The present study showed that, when subjects prepared movements while viewing a stimulus, those two types of changes interacted in the third (time‐processing) region in the brain, producing the alpha suppression in F‐A trials (Figure 7). Such interaction between the motor and visual factors was not observed in other frequency bands (Figure 10), highlighting a selective role of alpha rhythm in neural communications across distant (visual, motor, and time‐processing) regions.

The present data, however, do not exclude a possibility that oscillatory signals other than alpha band are involved in time perception. It has been shown that neural oscillations of various frequencies, such as delta (Arnal, Doelling, & Poeppel, 2015; Cravo, Rohenkohl, Wyart, & Nobre, 2013), beta (Bartolo & Merchant, 2015; Fujioka et al., 2015; Kononowicz & van Rijn, 2015; Kulashekhar et al., 2016), and gamma bands (Bartolo, Prado, & Merchant, 2014; Sperduti, Tallon‐Baudry, Hugueville, & Pouthas, 2011), contribute to accurate estimation and prediction of time. A recent view, therefore, is that a dominant frequency for timing behaviors is context‐dependent (Wiener & Kanai, 2016); the brain recruits different frequencies of oscillation signals based on the temporal features of the task being performed. Alpha rhythm played an important role in the present study probably because the time dilation effect emerged from an integration of motor commands with continuous visual inputs, both of which were closely associated with alpha oscillation.

4.2. Neural interaction mediated by desynchronization

A hallmark of the present results was that an interaction of visual and motor factors in the SMA was mediated by “desynchronization” of alpha rhythm. This makes a sharp contrast with previous studies because neural communications across distant regions have been traditionally associated with synchronization (increase in power or coherence in phase) of oscillatory signals (Engel, Fries, & Singer, 2001; Fries, 2005; Gupta & Chen, 2016; Hipp, Engel, & Siegel, 2011). As shown by the BSI analyses (Figure 9), alpha suppression in the present study occurred in an asymmetric manner, modulating peaks more strongly than troughs, or vice versa. Such an asymmetric (or nonzero mean) suppression can induce a slow shift of neural waveforms (Mazaheri & Jensen, 2010; Nikulin et al., 2010), causing larger ERFs and longer time percepts in action than no‐action trials. Our results thus indicated a new form of sensory–motor interaction mediated by the desynchronization (not synchronization) of neural activity. Although we focused on a mechanism of time perception in the present study, this model of interaction based on asymmetric desynchronization might be applicable to other types of integration effects, such as action‐induced enhancement of visual perception (Gutteling et al., 2015; Tomassini, Spinelli, Jacono, Sandini, & Morrone, 2015).

4.3. An implication for neural models of time perception

Previous studies have proposed a number of computational models on time perception (Addyman, French, & Thomas, 2016; Hass & Durstewitz, 2016; Mauk & Buonomano, 2004; Merchant & Averbeck, 2017). The most classical one would be the pacemaker‐accumulator model (Gibbon, 1992; Treisman, 1963). In this model, neural pulses from the “pacemaker” start to flow into the “accumulator” when the brain perceives an onset of the interval that should be timed. A total amount of pulses accumulated at an offset determines a subjective length of that interval. This process of temporal accumulation has been frequently associated with a build‐up of neural activity in the medial frontal region (Macar et al., 1999; Pfeuty et al., 2003). On the other hand, another class of models assumes that time perception was achieved by multiple neural oscillators with different frequencies in the cortex. In the striatal beat frequency model (Matell & Meck, 2004), an onset of an interval causes the phase‐resetting of the cortical oscillators. Time is indicated by striatal neurons of the basal ganglia, because these neurons work as a coincidence detector of the cortical neurons, reading out the state of the oscillators at an offset of the interval.

In the current study, we found the build‐up activity in the SMA reflecting the time illusion by action preparation. This result is consistent with the pacemaker‐accumulator model assuming the neural accumulation process for time estimation. On the other hand, we also found that the temporal dynamics of the build‐up activity was tightly coupled with changes in alpha rhythm, which underscored a critical role of oscillatory signals in time perception. Therefore, our results suggest an importance of an integrative approach that combines key concepts or elements in previous models (temporal accumulators and cortical oscillators) to elucidate neural mechanisms for the temporal phenomenon.

4.4. Adaptive function of the time dilation in a preaction period

As described in section 1, a continuous visual stimulus presented during action preparation is perceived longer. What is a functional benefit or advantage of this time dilation effect? This point was originally discussed in Hagura et al., 2012. They proposed that time dilation in a preaction period might be related to an increase in the speed of sensory processing before motor execution. When we plan quick (ballistic) movements in rapidly changing environments, it is important for the brain to obtain as much sensory information as possible so that it can be used to adjust motor commands. Dilating time in a preaction period would facilitate this acquisition and storage of information, maximizing opportunities to change or stop the planned actions before actual execution.

We presume, however, that this mechanism of time dilation sometimes might be disadvantageous, because it causes imprecise perception (overestimation) of a preaction period (Iwasaki et al., 2017). For accurate perception of time, it would be better for the brain not to dilate a period in which no stimulus is shown (e.g., unfilled interval). The time dilation effect selectively observed in filled condition (Figure 2) therefore might reflect a strategy of the brain to maximize the processing of visual inputs while avoiding unnecessary errors in time perception. Further study is necessary to examine this hypothesis from the viewpoint of neural activity.

4.5. Limitation

We finally referred to a limitation of our study. As described in section 1, our filled condition and unfilled condition were balanced in general changes in attention or arousal level, because subjects performed the same tasks in both conditions (the temporal judgment and action execution). Indeed, reaction times of manual movements in F‐A trials were not significantly different from those in U‐A trials (Figure 2c), suggesting an equal level of arousal between the two conditions. One should note, however, that some types of attention are stimulus‐driven and automatically attracted to sensory stimuli (e.g., bottom‐up attention). This would raise a possibility that the time dilation in the present study partly emerged from a continuous allocation of attention to a disk in filled condition. In F‐A trials, participants were required to attend to the disk for its entirety, as the offset of this disk was the go signal to perform the action. This continuous allocation of attention might dilate subjective time of the first target because attending to a stimulus increases its apparent duration (Mattes & Ulrich, 1998). In contrast, there was no stimulus in unfilled interval to which participants would continuously attend. No dilation effect was therefore observed in unfilled trials, even when subject performed manual actions to the second flash. In short, our present data were not sufficient to exclude a possibility that the time dilation reflected enhanced attention emerging from a combination of the visual factor (continuous visual inputs) and the motor factor (action preparation). This point should be controlled in future studies on action‐induced time distortion.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

Supporting information

Figure S1 Vector‐norm ERFs when the 1st target was 900 ms (900 ms trials, lower left) and 1,500 ms (1,500 ms trials, lower right). Data at a representative sensor for the supplementary motor area (SMA) are shown. Background shadings denote SE across subjects. Consistent with behavioral data in filled‐interval (F) condition (top panel, identical to Figure 2b), the amplitude of action trials (A) tended to be larger than no‐action (NA) trials in 900 ms trials but not in 1,500 ms trials. The difference between F‐A and F‐NA in 900 ms trials, however, did not reach cluster‐level significance, presumably because of a smaller number of trials (8 per session) compared to that in 1,200 ms trials (34 per session).

Iwasaki M, Noguchi Y, Kakigi R. Neural correlates of time distortion in a preaction period. Hum Brain Mapp. 2019;40:804–817. 10.1002/hbm.24413