Abstract
Neurovascular coupling mechanisms give rise to vasodilation and functional hyperemia upon neural activation, thereby altering blood oxygenation. This blood oxygenation level dependent (BOLD) contrast allows studies of activation patterns in the working human brain by functional MRI (fMRI). The BOLD‐weighted fMRI signal shows characteristic transients in relation to functional activation, such as the so‐called initial dip, overshoot, and post‐stimulus undershoot. These transients are modulated by other physiological stimuli and in disease, but the underlying physiological mechanisms remain incompletely understood. Capillary transit time heterogeneity (CTH) has been shown to affect oxygen extraction, and hence blood oxygenation. Here, we examine how recently reported redistributions of capillary blood flow during functional activation would be expected to affect BOLD signal transients. We developed a three‐compartment (hemoglobin, plasma, and tissue) model to predict the BOLD signal, incorporating the effects of dynamic changes in CTH. Our model predicts that the BOLD signal represents the superposition of a positive component resulting from increases in cerebral blood flow (CBF), and a negative component, resulting from elevated tissue metabolism and homogenization of capillary flows (reduced CTH). The model reproduces salient features of BOLD signal dynamics under conditions such as hypercapnia, hyperoxia, and caffeine intake, where both brain physiology and BOLD characteristics are altered. Neuroglial signaling and metabolism could affect CBF and capillary flow patterns differently. Further studies of neurovascular and neuro‐capillary coupling mechanisms may help us relate BOLD signals to the firing of certain neuronal populations based on their respective BOLD “fingerprints.”
Keywords: BOLD signal, capillary transit time heterogeneity, modeling, neuro‐capillary coupling, neurovascular coupling, oxygen transport
1. INTRODUCTION
Functional magnetic resonance imaging (fMRI) is widely used to localize neural activity in the resting and task‐activated brain. Most fMRI studies are based on blood‐oxygen‐level dependent (BOLD) contrast, due to its sensitivity to blood flow changes created by neuronal activity via neurovascular coupling mechanisms. During functional activation, cerebral blood flow (CBF) generally increases more than oxygen metabolism, which causes the oxygen extraction fraction (OEF) to decrease, and consequently, causes the blood oxygenation to increase compared to the resting state. The BOLD signal captures changes in blood oxygenation as they arise during changes in physiological state, either as a result of changes in neuronal activity, in response to altered blood gas levels, or other vasoactive stimuli, owing to the different magnetic properties of oxygenated and deoxygenated blood. Briefly, deoxyhemoglobin (dHb) and oxyhemoglobin are characterized by different magnetic susceptibilities. Accordingly, the presence of dHb in the blood causes a spatially varying magnetic susceptibility at the microscopic scale. Such local magnetic field inhomogeneities, in turn, lead to signal attenuation on the voxel scale via rapid dephasing of nearby spins. The BOLD effect is therefore sensitive primarily to the dHb content within a voxel, and hence to both blood's dHb concentration and local blood volume. As a result, the BOLD signal is not only sensitive to the local changes in CBF, but also to factors that influence the dHb content, including the OEF and the cerebral blood volume. A dynamic model of the BOLD signal that accounts for factors which affect oxygen extraction efficacy could improve our understanding of brain tissue oxygenation and its dynamical regulation when compared with experimental measurements of BOLD, CBF, and cerebral blood volume.
Buxton, Wong, and Frank (1998), along with Mandeville et al. (1999), have pioneered the development of biophysical models relating changes in CBF and dHb content to the BOLD signal. The balloon model (Buxton et al., 1998) ascribes the changes in blood volume solely to changes in with some delay, and assumes that only the venous compartment contributes to the BOLD signal. Although it may seem counterintuitive, negative BOLD transients paralleled by elevated CBF have been reported in chronic stroke patients (Blicher et al., 2012), and in patients with steno‐occlusive artery disease after vasodilator challenge (Siero et al., 2015a). The balloon model has been used to provide putative explanations for some of these puzzling experimental observations, including the negative signal observed by Siero et al. (2015a), and for the initial dip (Hu and Yacoub, 2012; Siero et al., 2015b) and post‐stimulus undershoot, both of which are negative portions of the BOLD signal. Although this model has provided insights into the origins of these poorly understood transients, it cannot fully explain why the BOLD signal sometimes remains negative after activation. Indeed, the relation between CBF and the blood volume in the venous compartment (V v) has been reported to vary across different areas in the brain, and even across different cortical depths (Tian et al., 2010; Yacoub, Ugurbil, & Harel, 2006; Zhao, Jin, Wang, & Kim, 2007). In some cases, a negative BOLD signal is observed although the venous blood volume increase does not lag behind CBF, in which case the so‐called balloon effect cannot account for the phenomenon (Yacoub et al., 2006; Zhao et al., 2007). In biophysical models such as those developed by Buxton et al., and by Mandeville et al., realistic assumptions are made regarding the time course of the venous blood compartment volume V v. In particular, V v is not determined only by CBF at time t, but also at earlier times. In contrast, for example, in Buxton et al. (1998) and Buxton, Uludağ, Dubowitz, and Liu (2004), is determined only by CBF and the metabolism at time t, but not at earlier times. Accordingly, they assume that the cerebral metabolic rate of oxygen (CMRO2), OEF, and CBF are related to each other by the relation , where C A is the arterial oxygen concentration. As discussed in greater detail below, in this equation, the term corresponds to the rate at which oxygen is extracted from plasma to the tissue. This equation is therefore true only when oxygen concentration in the tissue is at equilibrium, that is, only at steady state.
Recently, we have examined the effects of capillary transit time heterogeneity (CTH) on oxygen extraction theoretically (Angleys, Østergaard, & Jespersen, 2015; Jespersen and Østergaard, 2012; Rasmussen, Jespersen, & Østergaard, 2015). CTH is a parameter that allows the quantification of capillary blood flow heterogeneity, and is defined as the standard deviation of the capillary transit time (Jespersen and Østergaard, 2012). We proposed hypotheses on the effects of capillary dysfunction in disease that are now supported by experimental work (Eskildsen et al., 2017; Østergaard et al., 2013). This work has shown that blood flow homogenization is an effective means to facilitate oxygen extraction. In fact, homogenization of capillary flow patterns during hyperemia appears to be an intrinsic property of microvascular networks. Accordingly, analyses of vascular anatomical networks show that CTH decreases in proportion with mean transit time (MTT) as blood flow increases in passive, compliant microvascular networks (Rasmussen et al., 2015). Furthermore, several experimental studies suggest that blood flow is actively redistributed at the capillary level: on the one hand, during functional activation, it has been reported that blood flow homogenizes beyond what would be expected in passive, compliant networks (Gutiérrez‐Jiménez et al., 2016; Schulte, Wood, & Hudetz, 2003; Stefanovic et al., 2008), and on the other hand, studies show less homogenization than one would expect in such networks under conditions of hypercapnia (Gutiérrez‐Jiménez et al., 2017; Hudetz, 1997; Villringer, Them, Lindauer, Einhäupl, & Dirnagl, 1994), resulting in increased blood flow without substantial increase in oxygen availability. The way changes in CBF are triggered and flow homogenization is controlled remain poorly understood, and it is not clear whether it involves primarily feed‐forward or feedback mechanisms. Improved erythrocyte deformability upon oxygen release is thought to represent one metabolic feedback mechanism by which blood flow can be increased in capillaries with elevated oxygen utilization (Wei et al., 2016). Other studies have identified feed‐forward mechanisms by which contractile capillary pericytes dilate in response to glutamatergic neurotransmission and thus take part in the regulation of blood flow (Hall et al., 2014; Peppiatt, Howarth, Mobbs, & Attwell, 2006; Winkler, Bell, & Zlokovic, 2011). It should be noted that only pericytes located on the capillary bifurcations and branches closest to the feeding arteriole are contractile, while pericytes located in the middle and venular portion of the capillary bed are seemingly specialized to undertake blood brain barrier (BBB) function and to control the extravasation of immune cells, respectively (Attwell, Mishra, Hall, O'farrell, & Dalkara, 2016). Meanwhile, some controversy has emerged as to whether capillary pericytes or indeed arteriolar smooth muscle cells (SMCs) control blood flow at the microscopic level (see Hall et al., 2014, but also Fernandez‐Klett et al., 2010; Hill et al., 2015). This controversy partly owes to the term “precapillary arterioles” being used to describe cells originally defined as pericytes (Attwell et al., 2016). Importantly, capillaries have been observed to dilate 1 to 2 s prior to upstream arterioles (Hall et al., 2014), coinciding with a homogenization of capillary flows (Lee, Wu, & Boas, 2015). If pericyte dilation gave rise to an overall reduction in vascular resistance upstream, blood flow would increase immediately (or rather, after a delay, which equals the distance between the points where capillary and arterial diameters were measured, divided by the speed of sound in blood), so the observation by Hall et al. (2014) and Lee et al. (2015) contradicts the notion that local changes in capillary perfusion elicit functional hyperemia. Rather, information about neuronal activity may be signaled via astrocytes to local pericytes (Mishra et al., 2016), while both pericytes (Hall et al., 2014) and endothelial cells (Longden et al., 2017) seemingly transmit this signal upstream. The “decoupling” of the capillary distribution of blood from upstream vascular resistance is ascribed to the corpuscular nature of blood and the so‐called phase‐separation effect (Schmid, Reichold, Weber, & Jenny, 2015): the differential separation of erythrocytes and plasma among downstream branches as blood encounters microvascular bifurcations. Here, erythrocytes tend to enter the branch with the higher flow, increasing its hematocrit. In capillary‐sized vessels, such increases in hematocrit and linear density cause vascular resistance to increase, limiting the inflow of more erythrocytes. This so‐called self‐regulation effect thus tends to equate blood flows among branches downstream of microvascular branches over time (Schmid et al., 2015). Importantly, the phase separation and self‐regulation effects are thought to allow redistribution of plasma and erythrocytes such that the concentration of erythrocytes, and hence the abundance of oxygen, can increase in specific capillaries, without affecting net blood flow. This effect may be facilitated and augmented by the oxygenation‐dependency of erythrocyte deformability (Wei et al., 2016). Indeed, simulations in artificial microvascular networks suggest that pericyte dilations tend to redistribute erythrocytes within the microvascular network, rather than affect blood flow (Schmid et al., 2015). These findings therefore suggest that capillary flow patterns, and thereby oxygen extraction efficacy, are indeed actively regulated by neuro‐capillary coupling mechanisms—a term used to distinguish neurovascular coupling mechanisms, which converge on arterioles to alter CBF according to metabolic demands, from mechanisms that affect capillary flows. Models that disentangle the effects of CTH and CBF on the BOLD signal would hence provide an important means of demonstrating whether neuro‐capillary coupling mechanisms exist, and how they might interact with the neurovascular coupling mechanisms that converge on upstream arterioles (Jespersen and Østergaard, 2012).
In this study, we develop a dynamic three‐compartment model to predict OEF, the CMRO2, and the oxygen tension in the extravascular compartment. The model is designed to take the effects of CTH on oxygen extraction into account, while explicitly incorporating oxygen metabolism, in order to alleviate the aforementioned simplifying assumptions used in previous models (Buxton et al., 2004, 1998). Following earlier work, our model includes a venous compartment to predict the BOLD signal from the CBF and OEF time courses. Applying our model to several physiological conditions, we examine whether the incorporation of CTH effects better explains the transients observed in literature reports, especially the initial dip and post‐stimulus undershoot phenomena observed in relation to functional activation.
2. METHODS
2.1. Dynamic three‐compartment model
Figure 1 shows the schematic overview of our approach to compute CMRO2, the tissue oxygen partial pressure , and the BOLD signal, along with the variables needed for this computation. Briefly, oxygen is considered in three compartments: hemoglobin, plasma, and extravascular tissue. The oxygen concentration C in the blood includes oxygen bound to hemoglobin and dissolved in the blood plasma. The cooperativity of oxygen binding to hemoglobin is approximated by the empirical Hill equation:
| (1) |
where is the concentration of bound oxygen, B is the maximum amount of oxygen that can be bound to hemoglobin, P p is the oxygen partial pressure in plasma, P 50 is the oxygen partial pressure at half hemoglobin saturation, and n is the Hill coefficient. The total content of oxygen is , where is the concentration of oxygen in the plasma, equal to , with Henry's constant. The total oxygen content is then related to the oxygen partial pressure in plasma by
| (2) |
Figure 1.
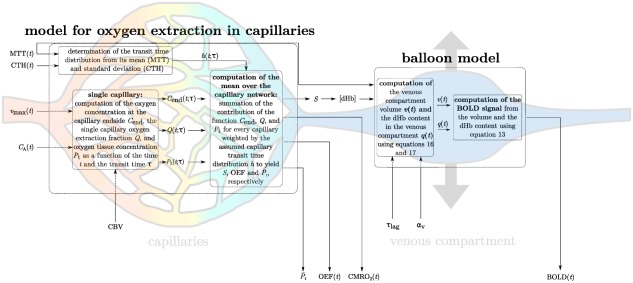
Schematic illustrating the procedure for computing the BOLD signal, given the time courses of MTT, CTH, and . In the first step, the deoxyhemoglobin concentration at the capillary end is computed. In the second step, the venous compartment volume is computed from . The BOLD signal is finally computed from the deoxyhemoglobin concentration and venous compartment volume. Abbreviations: CMRO2, cerebral metabolic rate of oxygen; CTH, capillary transit time heterogeneity; MTT, mean transit time; OEF, oxygen extraction fraction; , mean oxygen concentration in the tissue; S, oxygen saturation; , maximum metabolic rate of oxygen; please refer to Table 1 for other variables [Color figure can be viewed at http://wileyonlinelibrary.com]
The net flux of oxygen across the capillary membrane is assumed to be proportional to the difference between plasma oxygen tension (P p) and tissue oxygen partial pressure (P t), with an equal forward and reverse rate constant k. Following the approach detailed in Valabrègue, Aubert, Burger, Bittoun, and Costalat (2003), the two equations governing the oxygen concentration in the vascular and extravascular compartments can be written as:
| (3) |
| (4) |
where Hillsinv is a function that relates the oxygen partial pressure in plasma to the total oxygen content in blood, that is, the solution of Equation (2) for P p. In practice, Equation (2) is solved for 1000 different C values ranging from 0 to . The function that associates P p to the different C values is then interpolated to get P p from C for any oxygen concentration between 0 and . Equations (3) and (4) are solved numerically with stiff ordinary differential equations (ODE) solvers (ODE23tb in Matlab R2016b), as no analytical solution exists for these equations. In Equation (4), the term accounts for the metabolism, assumed to be governed by Michaelis–Menten kinetics (Michaelis and Menten, 1913). The model constants and variables are described in Table 1, and they were assigned generally accepted literature values. Note that the transit time in a given capillary is a function of time, and is subject to changes for example as a consequence of an increase in blood flow. Here, is the instantaneous transit time in the capillary defined by the relation , where L is the capillary length and is the instantaneous blood speed in the capillary at time t. The oxygen extraction fraction for a single capillary Q can be computed from the solution of Equations (3) and (4):
| (5) |
Table 1.
Different variables used in the model
| Symbol | Name, definition | Value | Unit | |||
|---|---|---|---|---|---|---|
|
|
Parameter used to describe venous compartment compliance | 0.44 (CTH model) 0.60 (Buxton model) | no unit | |||
| αH | Henry constant |
|
|
|||
| B | Maximum amount of oxygen that can be bound to hemoglobin | 19.43 |
|
|||
| C A | Arterial oxygen concentration in blood | 18.59 (up to 20.60 in Figure 7) |
|
|||
| C B | Concentration of oxygen bound to hemoglobin | Given by Equation (1) |
|
|||
|
|
Oxygen concentration at the capillary end (single capillary) |
|
|
|||
| C V | Venous oxygen concentration in blood |
|
|
|||
| C | Oxygen concentration in the blood |
|
||||
|
|
Mean oxygen concentration in the blood over the capillary length |
|
||||
| C p | Oxygen concentration in plasma |
|
|
|||
|
|
Capillary blood volume | 1.4 |
|
|||
| k | Rate constant for oxygen | 88 | 1/s | |||
|
|
Michaelis–Menten parameter for oxygen metabolism | 5 |
|
|||
| n | Hill constant | 2.8 | no unit | |||
| P p | Oxygen partial pressure in plasma |
|
|
|||
| P t | Oxygen partial pressure in the extravascular compartment (single capillary) |
|
||||
|
|
Mean oxygen concentration (pressure) in the extravascular compartment over the capillary network |
|
||||
| P V | Oxygen partial pressure in plasma in the venous compartment |
|
|
|||
| P 50 | Oxygen partial pressure at which oxygen saturation is equal to 0.5 | 26 |
|
|||
| Q | Single capillary extraction fraction | No unit | ||||
| q | deoxyhemoglobin content in a voxel normalized to its baseline value | No unit | ||||
|
|
BOLD signal amplitude | No unit | ||||
| S | Oxygen saturation | No unit | ||||
|
|
Parameter used to describe venous compartment compliance | 13 (CTH model) 14.5 (Buxton model) | s | |||
|
|
Mean transit time in the venous compartment assumed at baseline | 3 | s | |||
| v | Volume of the venous compartment, normalized to baseline value. | No unit | ||||
|
|
Maximum rate at which oxygen is metabolized | 4.18 |
|
|||
|
|
Relative volume of the venous compartment | No unit | ||||
|
|
Volume of the venous compartment during baseline | 3 |
|
In Equations (3) and (5), the factor can be written as under the assumption that , with being the concentration at the capillary end, determined from the arterial oxygen concentration C A and the extraction fraction Q:
| (6) |
Note that Q at time t depends on the transit time at earlier times in a given capillary. The net OEF is given by summing over capillaries:
| (7) |
where h is the probability density function of the assumed transit time distribution. Note that OEF is equal to the ratio , where C V is the venous concentration, assumed to be equal to the mean oxygen concentration in capillaries:
| (8) |
and that this quantity is not necessarily equal to the ratio of oxygen consumed to oxygen supplied, that is, the equation is not necessarily true in transient regime, mostly because P t shortly increases before being consumed as during steady state (see Figure 2 and corresponding main text in the results section). Another consideration related to the capillary transit time also prevents this equation from being fulfilled immediately after a change in CBF or CTH. See the section 4.2: OEF transients in the discussion for more details about this point. Next, we must specify how transit times evolve in time. For this purpose, we take MTT and CTH to be given functions of time, as determined by the specific physiological changes induced by the experimental paradigm and discussed in detail below. Note that in this model, capillary blood volume (CBV) is assumed to be constant. CBF and MTT are therefore related to each other through the central volume theorem: , such that CBF is entirely determined by MTT. The transit time distribution is then assumed to conform to a gamma distribution at all times with parameters α and β adjusted to the instantaneous mean and standard deviation . While this leaves considerable freedom for the time evolution in the individual capillaries, we here choose the N capillaries to have transit times corresponding to the quantiles for the current gamma distribution. In practice, we label capillaries with for , and assign transit time to the i th capillary according to:
| (9) |
where is the inverse cumulative gamma distribution. It can be shown that if u is a value sampled from a uniform distribution on , then follows the distribution h with parameters α and β. Furthermore, we can show that averages are conveniently computed by summing directly over the capillaries (quantiles), for example:
| (10) |
and more generally, for any function f over the capillary network that depends on the transit time τ:
| (11) |
Figure 2.
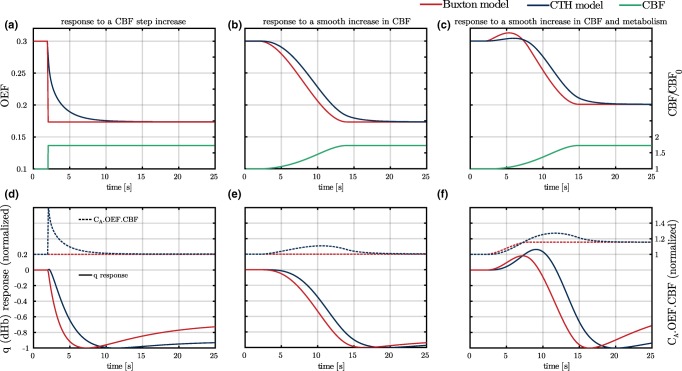
(a–c) OEF responses to different CBF (green curves) increases using the model used in Buxton et al. (2004, 1998) (Buxton model, red curves) and our model (CTH model, blue curves). In panels a and b, the metabolism is assumed to be constant, while it increases by 15% in panel c 900 ms prior to the increase in CBF. (d–f): q (deoxyhemoglobin) responses (plain lines) and time courses of the quantity (dashed lines) are shown under same conditions as panels (a–c). When using CTH model, to visualize the sole effect of CBF on oxygen extraction from the plasma, oxygen metabolism is assumed to be saturated, that is, the value of the parameter is smaller (0.001 mmHg) than elsewhere in the article. Abbreviations: CBF, cerebral blood flow; OEF, oxygen extraction fraction [Color figure can be viewed at http://wileyonlinelibrary.com]
In particular, is equal to
| (12) |
with Q denoting the function defined in Equation (5). Computation of other quantities is detailed in the Appendix. In practice, to sum the contribution of every capillary over the network, we solved Equations (3) and (4) for 1000 different τ functions (i.e., 1000 different ui values, as defined in Equation (9)). We then interpolated the value of and to get an approximation of these variables for any τ function defined in Equation (9). This model for oxygen extraction is then combined with the balloon model (Buxton et al., 1998) to predict the dynamics of the BOLD response. The latter model is calibrated for and . The BOLD signal is evaluated from the equation (Buxton et al., 1998):
| (13) |
where (Buxton et al., 2004; Valabrègue et al., 2003) is the relative volume of the venous compartment at baseline, (Angleys et al., 2015; Jespersen and Østergaard, 2012) is the oxygen extraction fraction at baseline, and q and v denote the dHb content in a voxel and the venous compartment blood volume, respectively, both relative to their baseline values. In Equation (13), the first term describes the contribution from the extravascular compartment, the second term the contribution from the intravascular compartment, and the third term the effects of a change in volume. Expressing that the derivative of the venous compartment volume is the difference between the inflow and the outflow, v fulfills the relation:
| (14) |
where is the flux which comes out of the capillary network, normalized to its baseline value, and is the transit time in the venous compartment at baseline. Unless differently stated, we take , which corresponds to . The outflow is assumed to be a function of the volume (Buxton et al., 2004):
| (15) |
Combining Equations (14) and (15), v must be the solution of the differential equation:
| (16) |
with the initial condition (normalized to its baseline value).
The dHb content of venous blood can be expressed as , where S is the hemoglobin oxygen saturation as it enters the venous compartment, and a constant converting the maximum concentration of oxygen bound to hemoglobin (B) to the corresponding hemoglobin concentration. Treating the balloon as a well‐mixed compartment, the clearance rate of dHb from the tissue is times the average venous concentration. By scaling these variables with their value at rest, the equation for q can be written as:
| (17) |
In practice, the hemoglobin saturation S is computed from the venous oxygen tension:
| (18) |
with P V being derived from the venous concentration:
| (19) |
Note the difference between the models from Buxton et al. (2004, 1998), where OEF at time t only depends on metabolism and blood flow at time t but not at earlier times, and our model, where OEF is calculated taking the effect of differential oxygen extraction from individual capillary pathways, as well as their transients, into account, while explicitly incorporating the effects of metabolism, cf. Equation (4).
2.2. Model calibration and BOLD signal predictions under different physiological conditions
To illustrate the behavior of our model under different physiological conditions, we allowed blood supply, its microscopic distribution, and tissue oxygen utilization to vary over time. Accordingly, the model's three input parameters (MTT, CTH, ) were modeled as trapezoidal functions, with rise times and durations that could be varied in order to illustrate how the temporal dynamics of intrinsic physiological variables affect the predicted onset, duration, and recovery of the BOLD signal. Table A1 in the appendix gives an overview of the timing used for the model's input parameters under each condition. To specify our model, we used literature findings of the models input parameters whenever possible, and examined whether realistic parameters choices were in fact consistent with literature observations of BOLD transients. We discuss these assumptions in detail in the discussion.
2.2.1. Hypercapnia
We assumed that metabolism ( ) remains constant during brief episodes of elevated arterial . Consistent with our findings in hypercapnic mice (Gutiérrez‐Jiménez et al., 2017), we assumed that CTH decreases relatively less than MTT in our model of hypercapnic hyperemia. Accordingly, CBF is assumed to increase by 73%.
2.2.2. Functional activation
During stimulation, oxygen utilization ( ) was assumed to increase by 15%, unless otherwise stated. Based on our experimental findings in mice (Gutiérrez‐Jiménez et al., 2016), CTH was assumed to decrease more than during hypercapnia (−61% vs −32%), but with a similar increase in CBF as in hypercapnia ( ). The CBF response was assumed to lag the increase in oxygen metabolism by 900 ms based on the experimental demonstration that energy‐requiring glutamate signaling elicits capillary dilations which is followed by elevated CBF and capillary flux homogenization a second or more later (Hall et al., 2014; Lee et al., 2015).
2.2.3. Functional activation and hyperoxic hypercapnia
For functional activation during superphysiological oxygen and levels, we calibrated model parameters in agreement with the report in (Gauthier, Madjar, Tancredi, Stefanovic, & Hoge, 2011), in the condition where the gas administered to the subject was composed of and . Accordingly, CBF was set to increase by and arterial blood oxygen content to increase by . For stimulation plus hyperoxic hypercapnia, CBF was assumed to first increase (20 s to 41 s) to the level of hyperoxic hypercapnia (above) and then to increase (53 s to 71 s) even more ( ), this time accompanied by an increase in metabolism ( ) and a decrease in CTH (–70%).
2.2.4. Functional activation and caffeine intake
We hypothesized that the effects of caffeine on red blood cell deformability (Mauro, Murphy, Thomson, Venbrux, & Morgan, 2014) caused CBF (and CTH) to change more easily and thus faster (see discussion and also Liu et al., 2004). Accordingly, we assumed that the time taken for CBF to increase to its maximum value decreased from 12 s to 6.3 s after caffeine intake, while the time between CTH begins to decrease and CBF then starts to increase decreased from 600 ms to 300 ms after caffeine intake. We also assumed that baseline CBF was reduced by 20%, and that the CBF response was 20% larger than during functional activation without caffeine intake (Chen and Parrish, 2009).
2.2.5. Glycolysis during functional activation
While lactate is involved in the regulation of cerebral arterial/arteriolar tone (Attwell et al., 2010; Gordon, Choi, Rungta, Ellis‐Davies, & MacVicar, 2008), its effects on capillary diameters has mainly been studied in the retina. Here, lactate in combination with low oxygen tension has been reported to relax pericytes, while elevated oxygen levels tend to constrict pericytes (Yamanishi, 2005). This mechanism, as well as the improved deformability of erythrocytes after their unloading of oxygen in areas of elevated oxygen metabolism (see introduction), provide putative mechanisms by which blood dynamically redistributes at the cellular level to those areas with the highest metabolic demands. To illustrate the effects of such a metabolic feedback mechanism on the BOLD signal, we therefore hypothesized that lactate production during functional activation (Mangia et al., 2007), which may indeed reflect differential extraction properties of oxygen and glucose (Angleys, Jespersen, & Østergaard, 2016), is associated with blood flow homogenization, and hence CTH reduction. Accordingly, we assumed that lactate production during stimulation gives rise to CTH reduction lasting 20 s to 30 s after the end of the stimulus, reflecting the time taken by lactate to be cleared from the tissue, causing a slow CTH recovery. In the study by Lee et al. (2015), such a persistent capillary flow homogenization was observed in one animal, while two others showed more heterogeneous capillary flows after activation. More experiments are clearly needed to verify whether lactate and oxygen combined might act as metabolic feed‐back signal by which oxygen extraction can be modulated.
2.2.6. Calibration of remaining parameters
The parameters (during baseline), , and k were calibrated as described in Angleys et al. (2016). Briefly, and are calibrated assuming that metabolism is 80% saturated at baseline. k is calibrated for the model to predict at baseline. Parameters and were calibrated to yield post‐stimulus undershoots of equal amplitude when the two models compared in this study were applied to functional activation (Figure 6). This calibration allowed us to more easily compare predictions with both models under different conditions. Accordingly, when using the model used in Buxton et al. (2004, 1998), referred to as the Buxton model, and . For our model, referred to as CTH model, and .
Figure 6.
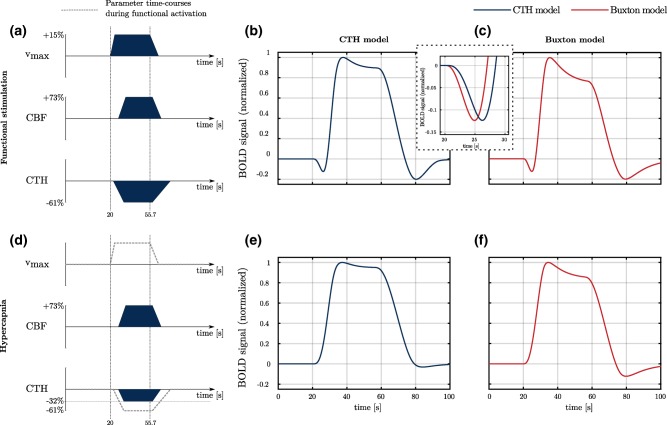
BOLD responses (normalized to the maximum) to different parameter time courses using our model (CTH model) and the model used in Buxton et al. (2004, 1998) (Buxton model). In panels a and d are represented the time course of the different parameters used in these conditions (filled dark blue). The dashed box between panels b and c shows the BOLD signal predicted with both models at a shorter time scale than in panels b and c. It therefore makes it possible to appreciate the delay between the two predicted signals. The gray dashed line (panel d) corresponds to time courses of parameters under condition of functional activation (Figure 6a), and is shown as a reference. Note that for clarity, the different parameter time courses are not to scale. Parameters and have been adjusted in both model for the post‐stimulus undershoot to be of equal amplitude in panels b and c. In panels c and f (Buxton model), parameter is equal to 0.60 and to 14.5 s, while it is equal to 0.44 s and 13 s, respectively, when using CTH model. Abbreviations: CBF, cerebral blood flow; OEF, oxygen extraction fraction [Color figure can be viewed at http://wileyonlinelibrary.com]
3. RESULTS
In this section, we first assess whether our model yields realistic predictions in terms of OEF responses to changes in CBF (Figure 2). We then evaluate the influence of each input parameter on the predicted BOLD signal (Figures 3, 4, 5). Finally, we apply our model to conditions resembling those of functional activation and hypercapnia (Figure 6), stimulation during hyperoxic hypercapnia (Figure 7), and stimulation after caffeine intake (Figure 8). In the discussion, we compare our predictions against literature reports. In Figures 2 and 6–8, CTH model predictions are compared to those of the Buxton model.
Figure 3.
Contributions of CBF, CTH, and the metabolism to the BOLD signal during functional activation. While the increase in CBF tends to increase the BOLD signal, blood flow homogenization and increase in metabolism tend to decrease it [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 4.
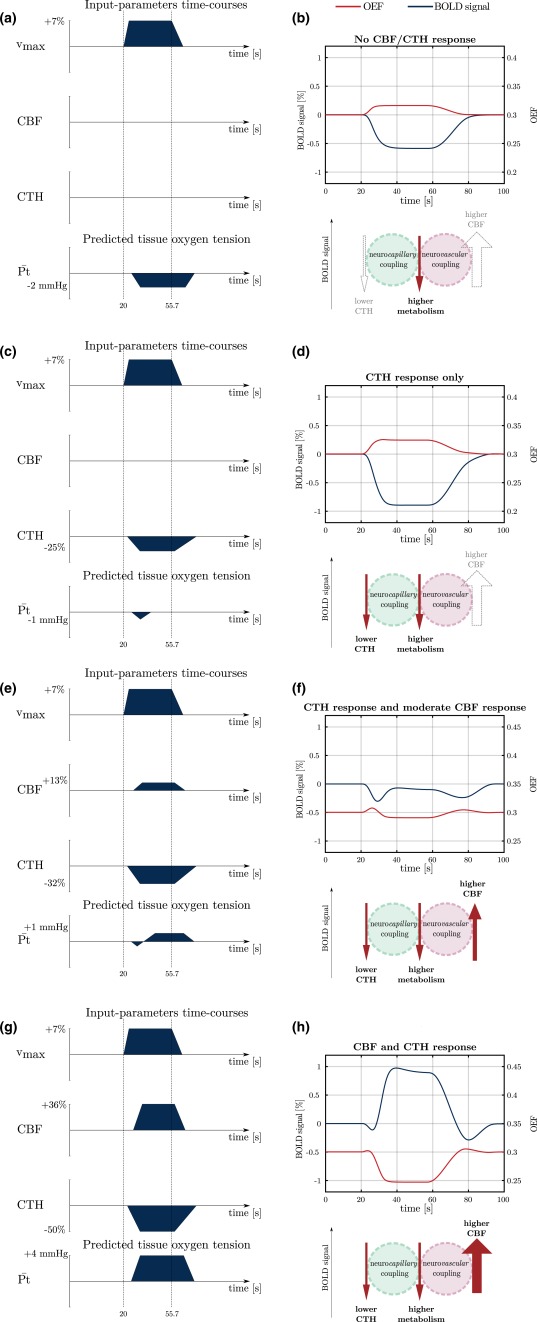
Influence of the amplitude of CBF and CTH responses on the BOLD signal amplitude (blue curves) and on OEF (red curves). In this figure, the metabolism and the blood flow responses are assumed to be reduced by half compared to the description in Section 2.2. CTH response is assumed to be reduced accordingly. On the left hand side of the figure, the dark blue fillings indicate the temporal dynamic of , CBF, and CTH and predictions for the mean tissue oxygen tension. Note that for clarity, the different parameter time courses are not to scale. Under the BOLD signal, a schematic similar to Figure 3 shows the different contributions to the BOLD signal [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 5.
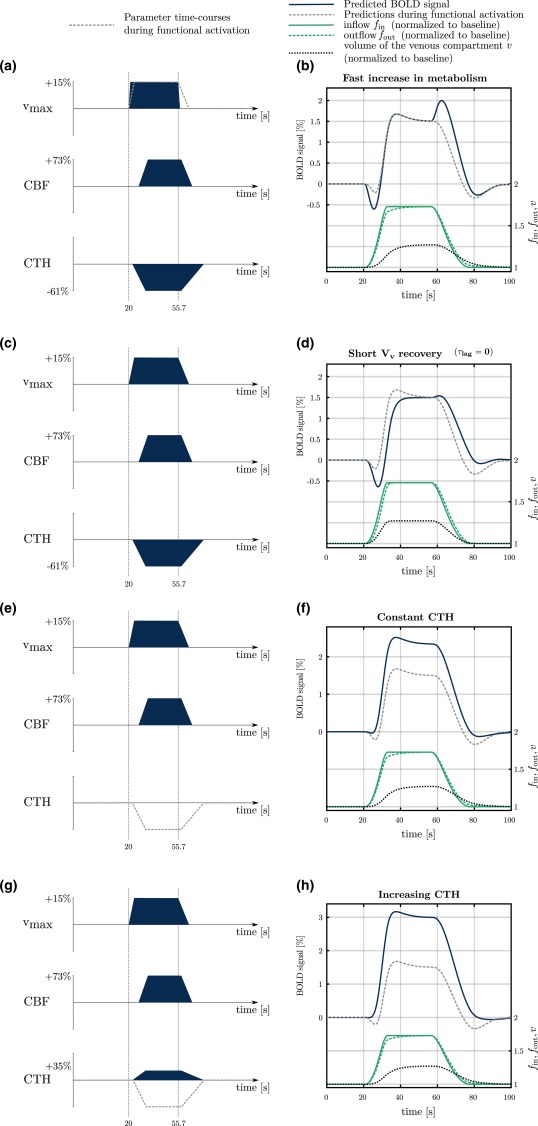
Influence of the temporal dynamics of CTH, the metabolism and V v on the BOLD signal shape and transients. The gray dashed lines in panels on the left indicate the time courses of input parameters during functional activation used in the rest of the manuscript. The corresponding BOLD signal predictions are shown in the panels on the right. The temporal dynamics of the blood flow into ( ) and out of ( ) the venous compartment, and the dynamics of V v (v) are also indicated. In the first condition, rise time and recovery time are assumed to be equal to 900 ms and 3 s, respectively, compared to 6 s and 21 s in the rest of the study. In the second condition, the parameter is assumed to be equal to 0 s, compared to 12 s in the rest of the study. As a consequence, CBF and V v are assumed to vary in synchrony. In the third condition, CTH is assumed to be constant. In the last condition, CTH is assumed to increase [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 7.
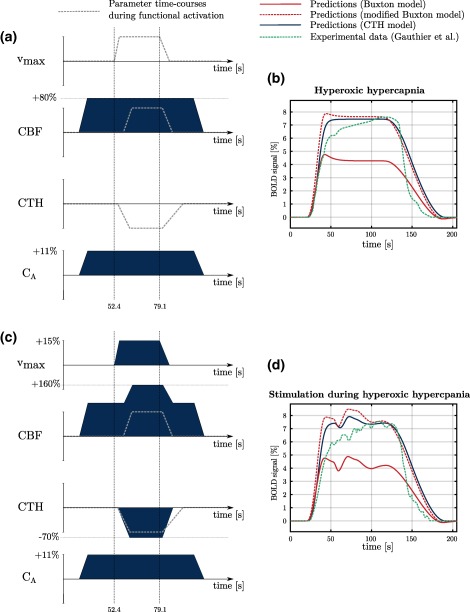
BOLD signal predictions under conditions inspired from hyperoxic hypercapnia. Under these conditions, hyperoxia is associated with increased oxygen arterial concentration (C A). On the right hand side of the figure, our predictions (CTH model, blue line), predictions made with Buxton and colleagues’ model (red lines) and experimental data (green line) are displayed. See main text for explanation regarding differences between red solid and red dashed lines. For predictions with the modified Buxton model, parameters and were set to 0.475 and 19.75 s, respectively, following the calibration described in methods section. To allow comparison of our predictions with experimental data, green curve width has been adjusted. However, no amplitude adjustment has been made. The green curve amplitude is therefore accurately reproduced from Gauthier et al. (2011) [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 8.
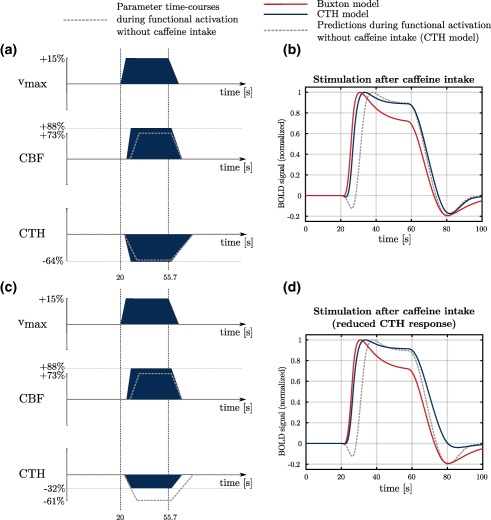
BOLD signal predictions under conditions inspired from stimulation after caffeine intake. Predictions made with our CTH model are shown with the blue curve and predictions based on Buxton et al.'s model (red curve) are shown for comparison. In the first condition (labeled stimulation after caffeine intake), the CBF response is quicker (onset time = 600 ms after metabolism increase; rise time = 6.3 s) and slightly more important ( ) than during functional activation without caffeine (+73%; onset time = 900 ms after metabolism increase; rise time = 12 s). The CTH response varies accordingly (rise time = 6.6 s; decrease by 64%; vs rise time = 12.6 s and decrease by 61%). In the second condition (labeled stimulation after caffeine intake reduced CTH response), we made the hypothesis that caffeine intake is associated with lactate production, and hence with reduced baseline CTH and reduced CTH response (−32%). CBF in both conditions follows the same time course. Baseline CBF (and CTH) is assumed to be 20% smaller than in other conditions. Accordingly, in this figure, [Color figure can be viewed at http://wileyonlinelibrary.com]
3.1. OEF response to elevated CBF
Figure 2a shows the OEF response to a step increase in CBF ( ) starting at time , while the metabolism ( ) is assumed to remain constant. Whereas the Buxton model predicts that OEF reaches its steady state value instantaneously, the CTH model predicts that this takes about 5 s. We discuss this behavior in more detail in the discussion. In Figure 2b, a slower ( ) and hence more realistic increase in CBF is assumed, while the metabolism still remains constant. The CTH model shows a response delayed by about 2 s compared to the Buxton model. This can be understood by observing panel a, where the OEF predicted by the Buxton model follows changes in CBF instantaneously, while, in reality, it takes longer time for the OEF to respond. In Figure 2c, an increase in metabolism is assumed to occur 900 ms before the increase in CBF. Figure 2c shows the same 2 s shift as observed in Figure 2b. Furthermore, as a consequence of the increase in metabolism prior to the increase in CBF, an OEF overshoot is predicted with both models, although this is noticeably more pronounced in the Buxton model.
Panels (2d–f) show the q (dHb) response (plain lines) in the three conditions discussed above. They further illustrate the differences between the Buxton BOLD model and our CTH model, and how these translate into differences in the predicted BOLD signal. To more easily comprehend timing differences between both models, the q response has been normalized to its maximum amplitude. Panel d (response to a CBF step increase) shows that the q response predicted with the Buxton model is smooth despite the stiff OEF response (panel 2a). The shift of about observed for OEF in the three different conditions (panels a–c) is also observed for the dHb response. Panels d–f also show the rate at which oxygen is extracted from the plasma, which is equal to the product . In the case of the Buxton model, the relation is assumed to be true at all times. The product is therefore constant in the two first panels (d–e), and it exactly follows the time course of our parameter in the last panel (f). In contrast, our CTH model accounts in particular for changes in extravascular oxygen content shortly following changes in CBF, and the rate at which oxygen is extracted from plasma ( ) is therefore not always at balance with the rate at which it is metabolized ( ). For instance, an increase in CBF generally gives rise to an increase in P t. This leads therefore to the inequality: , as observed in panels d and e. In panel f, on the contrary, the blue curve is under the red one from 3 s to 7 s, which means in this case that : Because in this condition the metabolism is assumed to increase before CBF, the tissue oxygen tension is expected to shortly decrease, before increasing again (from 7 s to 20 s).
In summary, Figure 2 shows that (a) OEF as predicted by our model seems to behave realistically and that (b) in comparison with our model, the Buxton model shows somewhat unrealistic OEF predictions, which would be expected to translate into timing differences when compared to actual BOLD signal.
3.2. BOLD signal dependency on the temporal dynamics of CBF, CTH, , and metabolism
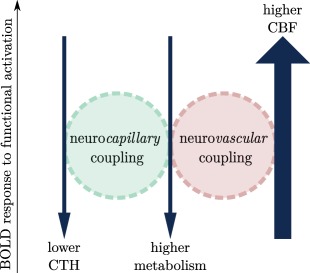
Figure 3 illustrates how CBF, CTH and the metabolism contribute to the BOLD signal response during functional activation. The increase in metabolism is associated with enhanced oxygen demand and extraction, and therefore contributes to a negative BOLD signal. The redistribution of blood flow to a more homogeneous pattern across capillaries upon neural activation increases oxygen availability. As a consequence, it also contributes to decrease the BOLD signal. Neurovascular coupling, that is, the increase in blood flow mediated by dilation of upstream arterioles, leads on the contrary to an increase in the BOLD signal during functional activation. This latter contribution is generally larger than the combined negative contributions of metabolism and CTH during functional activation, and the BOLD response is therefore generally positive. This is illustrated in Figure 3 with arrows of different thickness, indicating that the contribution of CBF is much higher than that of lower CTH and higher metabolism. Figure 3 is reproduced in different panels of Figure 4 to provide an easy overview of the conditions our model was applied to.
In Figures 5, 6, 7, 8, the gray dashed lines in panels on the left indicate the time courses of input parameters during functional activation, shown as a reference.
Figures 4 and 5 assess the influence of each input parameter on the BOLD signal. More specifically, Figure 4 illustrates how the BOLD signal (right panels) amplitude is predicted to vary according to the amplitude of CBF and CTH responses, as shown in the left panels, while Figure 5 illustrates how the BOLD signal transients are predicted to vary according to the temporal dynamics of V v, the metabolism ( ), and CTH. In Figure 4, metabolism responses are assumed to be reduced by half compared to the description in Section 2.2 to more clearly evaluate the potential effect of blood flow homogenization on tissue oxygen tension during modest metabolism increases. The first condition in Figure 4 shows the predicted BOLD signal when tissue oxygen utilization increases in the absence of any changes in CBF or CTH (panels 4a and 4b). The predicted BOLD signal is negative, as a consequence of the elevated oxygen metabolism, which results in higher oxygen extraction and hence in an increase in deoxyhemoglobin concentration. This response is similar in shape to BOLD responses reported during visual activation in chronic stroke patients (Blicher et al., 2012), during motor activation in patients with severely impaired blood supply due to intracranial artery disease (Röther et al., 2002), after acetazolamide administration in patients with steno‐occlusive artery disease (Siero et al., 2015a), and to optical intrinsic signals observed during forepaw stimulation in rats, where the vascular response is impaired by hypotension (Masamoto, Vazquez, Wang, & Kim, 2008). The model predicts that increase in metabolism is accompanied by a decrease in mean tissue oxygen tension.
The second condition (panels 4c and 4d) shows the predicted BOLD signal when tissue oxygen utilization increases in the absence of any changes in CBF, but paralleled by a reduction in CTH to meet the metabolic needs of the tissue. Note that in this case, neuronal activity is predicted to result in a negative deflection of the BOLD signal of larger amplitude than in previous condition, as a consequence of the combined action of metabolism and the redistribution of blood flow (see Figure 3 and the associated schematic in panel 4d). Unlike the previous condition, neuronal metabolism in this case is not accompanied by a reduction in tissue oxygen tension, except for the small and short reduction in tissue oxygen tension that remains which is mostly due to the mismatch between the CTH and the response. Instead, homogenization of capillary flow patterns increases oxygen extraction efficacy, even in the absence of any accompanying change in CBF (Jespersen and Østergaard, 2012). We discuss the significance of negative BOLD contributions further below.
The third condition (panels 4e,f) shows the predicted BOLD signal in a condition where the increase in metabolism is accompanied by a reduction in CTH and a modest increase in CBF (+13%). The predicted BOLD signal amplitude is almost equal to zero: the oxygen extraction fraction decreases because of the increase in blood flow, but this latter only compensates for the increased oxygen extraction fraction associated with the increase in metabolism and with the decrease in CTH.
The last condition in Figure 4 (panels 4g and h) shows the predicted BOLD signal in a condition where the increase in metabolism is accompanied by a reduction in CTH and an increase in CBF, as generally observed during functional activation. The predicted BOLD is positive, owing to the decreased oxygen extraction associated with the blood flow increase. In this condition, the contribution of the blood flow is therefore larger than the combined contribution of metabolism and CTH that tend to reduce the BOLD signal amplitude (see Figure 3 and the associated schematic in panel 4h). The predicted mean tissue oxygen tension increases.
Figure 5 shows the BOLD responses in four different conditions where all parameters but one are calibrated as described in Section 2.2 (functional activation). In the first condition, rise time is shorter than what is described in the aforementioned section. In the second condition, the parameter is equal to zero, which means that V v and CBF are assumed to be time‐locked. In the two last conditions, CTH is assumed to be constant or to decrease, respectively, which is a means to assess the influence of this parameter on the initial dip and post‐stimulus undershoot. Note that the temporal dynamics of , and v are identical in panels b, f, and h, because the CBF response, as well as values of parameters and are the same under these three conditions, while is set to zero in panel d. The first condition in Figure 5 shows that the speed by which oxygen metabolism increases to its maximum rate and then returns to its baseline value has significant impact on the shape of the BOLD response. In Figure 5a,b, the rise time and recovery time (blue line) is sevenfold shorter than what assumed in the rest of the study (gray dashed line). The rapid increase in oxygen utilization contributes to a large initial dip in the BOLD signal: Meanwhile, the rapid recovery of generates a BOLD signal overshoot at the end of stimulation, owing to the sudden decrease in OEF before CBF has time to decrease. Such a phenomenon is not generally observed in task activation studies and in the models of BOLD responses to functional activation below, the recovery time was therefore set to a larger value. Figure 5d shows the predicted BOLD signal in relation to functional activation when local venous volume V v varies in synchrony with CBF, that is, . Note that the initial dip of the BOLD signal becomes shallower, while the post‐stimulus undershoot becomes deeper, as increases. Figure 5e–h illustrates the role of CTH on the BOLD signal amplitude and transients. Figure 5f shows a condition where CTH remains constant. The initial dip and the post‐stimulus undershoot become shallower, as CTH response is reduced. Figure 5h shows a condition where CTH increases. The amplitude of the BOLD signal increases even further compared to the previous condition where CTH is constant, the initial dip completely disappears and the post‐stimulus undershoot becomes shallower.
Figure 6a–c compares the BOLD signal during functional activation predicted by our model (CTH model) to the signal predicted by the Buxton model. The BOLD response predicted by the CTH model shows three transients, namely the initial dip (between 21 and 27 s in the figure), overshoot (35 s to 40 s) and post‐stimulus undershoot (70 s to 90 s). The effect of CTH on the initial dip and post‐stimulus undershoot is discussed in more detail in the next section. The BOLD responses predicted with the CTH and Buxton models, respectively, are similar in this condition and show transients of approximately the same amplitude. The dashed box between panels b and c makes it possible to more precisely see the 1.5 s delay between initial dips predicted with both models. Note that this delay is approximatively the same as observed for the OEF and q responses in Figure 2. In both models, the overshoot is a consequence of the balloon effect, and it is more pronounced in the Buxton model than in the CTH model as a consequence of the larger value used for and in the first model. The predictions show more substantial differences in the second condition (hypercapnia: Figure 6d–f): In particular, the CTH model predicts no initial dip (panel e) and almost complete absence of undershoot, owing mainly to the smaller CTH response. On the contrary, while the Buxton model does not predict any initial dip (panel f) due to the constant metabolism, it does predict an undershoot of approximately same amplitude as in the previous condition (stimulation). Indeed, literature studies report undershoot under conditions of functional stimulation but not during hypercapnia, despite similar CBF response (Donahue et al., 2009; Hua, Stevens, Huang, Pekar, & van Zijl, 2011).
Figure 7 shows the BOLD signal predicted with our model (blue line) and with the model used in Buxton et al. (2004) (red lines) during a condition of combined severe hypercapnia ( ) and hyperoxia ( ). In this figure, we used two versions of the model developed by Buxton and colleagues: one version is similar to what is described in Buxton et al. (2004) (red solid line). The other version (modified Buxton model, red dashed line) takes into account that the rate of entry of deoxyhemoglobin in the venous compartment is more accurately described by the quantity than by the oxygen extraction fraction. In other words, the term used in Equation (5) in Buxton et al. (1998) is replaced in the modified Buxton model by , as used elsewhere in our model (see Equation (17)), thereby relaxing the assumption of a fully oxygenated hemoglobin concentration made in Buxton et al. (2004, 1998). These predictions are compared to experimental data under same conditions (green dashed line, Gauthier et al., 2011). The signal time curve amplitude predicted by our model (blue curve) is about fourfold larger than for other conditions and shows no initial dip, no overshoot and no undershoot. Figure 7d, in turn, shows the predicted BOLD signal during combined severe hyperoxic hypercapnia and functional activation. Apart from some extra ripples, the BOLD signal is remarkably similar to the one predicted in the resting condition (Figure 7b, blue curve), although the CBF response to stimulation is preserved. The BOLD signal seems to be saturated in that the effect on the BOLD signal of the parallel increase in metabolism, CBF, and blood flow homogenization is almost undistinguishable. Our model shows good agreement with experimental data (green line). In particular, the signal maximal amplitude in both conditions, as well as the absence of clear response during stimulation (Figure 7d), are accurately predicted. The slow increase in the signal observed by Gauthier et al. from 6% ( in the figure) to about 7.5% ( ) may be due to the progressive CBF increase observed experimentally. This is in contrast to our model, where a simpler time course is employed to describe the change in CBF (see panels 7a and 7c). In both conditions (panels 7b and 7d), the original (i.e., nonmodified, red solid line) Buxton model predicts a signal of smaller amplitude compared to the modified version: under hyperoxic hypercapnia, oxygen dissolved in the plasma represents more than 5% of the total oxygen content. While the quantities and are almost similar under normoxic conditions, they can differ a lot under hyperoxic conditions, and such a behavior was therefore expected. Note however that this affects mostly the amplitude of the signal and not its shape. Predictions based on the modified Buxton model (red dashed line) are close to those based on our CTH model, although the Buxton model shows a small overshoot after the first CBF increase (45 s to 50 s, panels 7b and 7d). The effect of stimulation in panel 7d is also more visible with the Buxton model than with CTH model.
Finally, in Figure 8, we apply our model to a condition inspired from stimulation after caffeine intake (panels 8a and 8b). Predictions based on the Buxton model are shown for comparison (red line). It would have been informative to compare our predictions with experimental results as we did under previous condition (Figure 7). However, while initial dip (post‐stimulus undershoot) shows a tendency to be reduced after ingestion of (a high dose of) caffeine (Behzadi and Liu, 2006; Chen and Parrish, 2009; Liu et al., 2004), BOLD signal of different amplitudes have been reported in these studies, where different stimuli and caffeine doses were employed, making comparison between studies difficult. We therefore chose to refer to the main observations made in these studies, that is, reduced initial dip and in some cases reduced post‐stimulus undershoot, rather than comparing directly our model predictions to experimental results. The predicted BOLD signal (CTH model, blue line) shows no initial dip and is otherwise similar to that predicted with the CTH model during activation without caffeine intake (gray dashed line). Quicker CBF response assumed during stimulation after caffeine intake has a similar effect on the initial dip as predicted by the Buxton model. In panels 8c and 8d, we examined whether reduced CTH prior to and during stimulation could explain the reduced post‐stimulus undershoot observed during stimulation after intake of high caffeine doses (Liu et al., 2004). To test this hypothesis, we assumed faster CTH recovery, lower baseline CTH and smaller CTH response than in previous condition. In this condition, the resulting BOLD signal shows a reduced post‐stimulus undershoot and is otherwise similar to the signal predicted in the previous condition (blue line). The Buxton model does not include the effects of CTH changes. The predicted signal is therefore similar to the previous condition.
4. DISCUSSION
In this study, we developed a dynamic model of the BOLD signal, taking the effects of CTH and tissue oxygen utilization on the dynamics of oxygen extraction in the brain during physiological stimuli into account. The main finding in our study is that the incorporation of CTH into our model leads to better qualitative agreement between BOLD signal predictions and experimental data than when CTH is not included. Importantly, the different transients predicted in the BOLD signal now reflect an interplay between realistic changes in CTH, CBF, and metabolism, taking their values at time t but also at earlier times into account when computing OEF, in contrast to other models, such as the Buxton model (Buxton et al., 2004, 1998), which takes only the history of CBF into account when determining the venous compartment volume, but not when computing OEF.
4.1. Our model applied to different physiological conditions
Our working hypothesis is that reductions in capillary resistance cause a reduction in CTH, and hence a more efficient oxygen extraction for a given tissue oxygen tension. Pericytes have been reported to dilate 1 s to 2 s prior to upstream vasodilation (Hall et al., 2014), similar to the timing of early red blood cell velocity changes caused by increased erythrocyte deformability (Wei et al., 2016). Similarly, distal‐to‐proximal signaling via capillary endothelial cells (Longden, Hill‐Eubanks, & Nelson, 2016) might contribute to the early homogenization of capillary erythrocyte flux observed about one second prior to upstream arteriole vasodilation by optical coherence tomography (Lee et al., 2015). We expect this homogenization effect to last as long as the glutamatergic signaling and elevated ATP needs are present. In Figures 5 and 6, we examined whether this early CTH reduction may cause an initial dip in the sensory‐evoked BOLD signal due to a reduction in tissue dHb concentration, as observed experimentally in several optical imaging and fMRI studies (Ernst and Hennig, 1994; Hu, Le, & Uǧurbil, 1997; Malonek and Grinvald, 1996; Menon et al., 1995; Thompson, Peterson, & Freeman, 2004). We found that, together with the effect of the delayed CBF increase (compared to the metabolism), this early decrease in CTH does contribute to the formation of the initial dip. To our knowledge, this is the first time that change in capillary flux heterogeneity is proposed to contribute to the initial dip, whose origin remains unclear (see Buxton, 2012 for in‐depth discussion). Interestingly, our model predicts that the initial dip relies on the interplay between several parameters, namely the fast increase in metabolism (compared to CBF) and early flux homogenization, while the delayed changes in V v contribute to attenuate the dip, as illustrated in Figure 5. Note that other parameters could also contribute to the formation of the initial dip, such as early changes in blood volume (Sirotin, Hillman, Bordier, & Das, 2009). Here, we propose that CTH, possibly along with other parameters, may play a major role in the initial dip. Needless to say, this hypothesis should be examined experimentally.
Our study provides a framework for understanding how passive and active changes in capillary flow patterns affect the BOLD signal. While our models identify certain features of neuro‐capillary coupling phenomena, much work remains before we fully understand the underlying physiological mechanisms, and how these affect brain oxygenation and BOLD signals in individual subjects. For example, our simulations suggest that the initial dip may reflect an instance of active neuro‐capillary coupling, rather than increased oxygen extraction from a “passive” microvasculature with a parallel drop in tissue oxygen tension. Experimental studies may be needed to examine whether neurovascular coupling mechanisms indeed adjust arteriolar tone and regional CBF while mechanisms operating closer to, or within individual capillary beds serve to prevent critical drops in cellular oxygen tension during changing physiological conditions. Indeed, recent reports suggest that glutamatergic neurotransmission relaxes pericytes/precapillary arterioles and then elicit upstream vasodilation (Hall et al., 2014; Hill et al., 2015; Peppiatt et al., 2006). Of note, the BOLD response recorded in millimeter‐sized MRI voxels reflects the combined activity of different cell types, and our model suggests the response further depends on whether the involved neuron subtypes rely differently on neuro‐capillary coupling mechanisms (affecting local capillary flows) and neurovascular coupling mechanisms (dilating upstream arterioles), respectively, to meet their metabolic demands. Inhibitory interneurons, which modulate cortical activity via gamma butyric acid (GABA), for example, comprise 15%–20% of cortical neurons (Buzsáki, Kaila, & Raichle, 2007). The energy expenditure of GABAergic neurotransmission is inherently difficult to determine, as it reduces the activity of the more numerous glutamatergic neurons, thereby “saving” energy (Buzsáki et al., 2007). Studies of GABA receptor blocker action on capillary pericytes suggest that GABA acts as capillary dilator (Peppiatt et al., 2006) while the action on GABAergic neurotransmission on upstream arterioles is less well understood (Buzsáki et al., 2007). BOLD signal amplitudes are negatively correlated with parenchymal GABA levels as measured by magnetic resonance spectroscopy (Chen, Silva, Yang, & Shen, 2005; Donahue, Near, Blicher, & Jezzard, 2010; Muthukumaraswamy, Edden, Jones, Swettenham, & Singh, 2009; Muthukumaraswamy, Evans, Edden, Wise, & Singh, 2012; Northoff et al., 2007). In fact, Goense, Merkle, and Logothetis (2012) ascribed negative BOLD signals in cortical layers with limited CBF responses to capillary dilations induced by inhibitory neural activity, although a similar phenomenon was not observed in humans (Huber et al., 2014). We speculate that the models presented here may help disentangle whether neuron subtypes, such as GABAergic and glutamatergic neurons, rely differently on neurovascular and neuro‐capillary coupling mechanisms to meet their metabolic demands. To this end, in vivo microscopy studies may prove useful as they provide means of estimating cellular activity and both arteriolar and capillary hemodynamics at high temporal resolution. See, for example, Kleinfeld et al. (2011) for discussions and Uhlirova et al. (2016) for detailed studies of microvascular hemodynamic responses to GABAergic interneuron activity.
In vitro studies show that lactate acts as a pericyte dilator in the retina if oxygen tension is low (Yamanishi, 2005), and extracellular lactate inhibits the reuptake of prostaglandin into astrocytes (Attwell et al., 2010), causing vasodilation. Therefore, lactate, which is produced during functional stimulation (Hu and Wilson, 1997; Madsen, Cruz, Sokoloff, & Dienel, 1999; Prichard et al., 1991; Sappey‐Marinier et al., 1992), might reduce CTH during the stimulus and post‐stimulus periods. Our study did not allow us to test whether lactate production and its subsequent clearance from the extravascular space produce a prolonged reduction in CTH. Instead, we examined whether a prolonged (20–30 s) decrease in CTH could affect the shape of the BOLD signal in ways that are consistent with the post‐stimulus undershoot. To test this hypothesis theoretically, we applied our model to several conditions: In Figure 5, we examined whether such a long CTH recovery could modulate the shape of the BOLD signal in a way consistent, for example, with the post‐stimulus undershoot. Our findings support this notion: the undershoot predicted by our model is the result of a long V v and long CTH recovery, as illustrated collectively by Figure 5d,f, showing that the undershoot vanishes as soon as there is no long V v ‐ or long CTH recovery. Accordingly, the duration and amplitude of the post‐stimulus undershoot is influenced by the time it takes to CTH and V v to recover. In particular, longer CTH recovery would lead to longer BOLD undershoot of higher amplitude. Interestingly, other parameters in our model can also contribute to the undershoot, such as a small CBF undershoot (not shown). These results are in agreement with several studies suggesting that the post‐stimulus undershoot relies on a complex interplay of different parameters. For example, in two studies in cat imaged with high‐field fMRI, Yacoub et al. (2006) and Zhao et al. (2007) observed an undershoot in the signal coming from both superficial and deeper tissue, whereas a long V v recovery was only observed in the surface vessels, suggesting that this transient cannot be attributed to the particular time course of only one parameter, but rather to the combined action of several parameters.
We then applied our model to different other conditions to further test the accuracy of our predictions, and the plausibility of our assumptions regarding the time courses of CTH and its role on the BOLD signal. Hypercapnia elicits a CBF increase of approximately the same magnitude as during functional activation, but the degree of flow homogenization is smaller than during functional activation (Gutiérrez‐Jiménez et al., 2017). Furthermore, hypercapnia is not believed to elicit any significant increase in metabolism (Chen and Pike, 2010; Yang and Krasney, 1995) compared to functional activation. Accordingly, we expect no lactate production and hence no long CTH recovery period as that expected during functional activation. Interestingly, hypercapnia has been reported to give rise to a BOLD signal with no undershoot (Donahue et al., 2009; Hua et al., 2011). In Figure 6, we showed that a reduced CTH response was associated with a BOLD response with much smaller undershoot compared to functional activation. We therefore propose that the absence of undershoot observed during hypercapnia could be explained by the absence of lactate production under this condition, and hence to the reduced CTH response compared to functional activation. Importantly, we showed that our model can disentangle conditions with different BOLD responses although they show similar CBF time course and constant metabolism. As illustrated in Figure 6, this is in contrast for example to the model used in Buxton et al. (2004, 1998) which, under conditions of constant metabolism, only relies on CBF time course to predict the BOLD signal, and therefore cannot distinguish two conditions with identical CBF responses: the undershoot is predicted to vanish with our model when we mimicked condition of hypercapnia, in agreement with experimental reports, but remains almost intact when using the Buxton model. The main contribution to the undershoot in the Buxton model is that of the balloon effect, that is, prolonged , which is only driven by the dynamics of CBF. As the CBF response is assumed to be the same under both conditions in Figure 6, the Buxton model predicts almost the same undershoot under both conditions. In contrast, in the CTH model, both long CTH and V v recovery contribute to the undershoot. The undershoot predicted from the CTH model is therefore largely reduced in panel 6e, where rapid CTH recovery is assumed, compared to panel 6b.
We then applied our model to a physiological condition inspired by the study of Gauthier et al. (2011), in which BOLD signals were acquired in human under conditions of severe hypercapnia ( ) and hyperoxia ( ). While hyperoxic hypercapnia is associated with a BOLD signal of high amplitude, the response to functional activation in that condition is almost unnoticeable despite the preserved perfusion response, as if the BOLD signal was saturated. Our model does predict this interesting effect. In the model, CTH is assumed to be constant in this condition. We propose that this may reflect the shunting of the blood flow through thoroughfare channels (TFC). TFC refers to a shunt from arteries to veins bypassing capillaries, which has been observed in the human brain (Hasegawa, Ravens, & Toole, 1967). Although such a shunt would not necessarily lead to an elevated CTH, because a large part of the blood would travel through the vasculature with same transit time, it would have the same effect on OEF. Of note, the OEF predicted under this condition (14%) and the oxygen saturation at capillary end (91%) is equal to that reported by Gauthier et al. (2011) under conditions of hyperoxic hypercapnia. We also tested this condition with the Buxton model, which has been slightly modified to relate the BOLD signal to the deoxyhemoglobin concentration more directly than the original version. Predictions with the Buxton model show a small overshoot after the first CBF increase and the effects of stimulation are more visible than with the CTH model. It is interesting to note that unlike under conditions of hypercapnia (Figure 6d–f), the Buxton model as implemented here shows almost no undershoot at the end of the hyperoxic/hypercapnic episode. This observation can be explained by the dynamics of the CBF response, which is assumed to be much slower under conditions of hyperoxic hypercapnia than under conditions presented in Figure 6: while it takes 21 s for CBF to return to the baseline value in Figure 6, it is assumed to take 72 s in Figure 7. Interestingly, an undershoot persists, albeit barely noticeable, in contrast to what is predicted with the CTH model.
Finally, we applied our model to conditions inspired by reports on functional activation studies after caffeine intake, assuming that caffeine is associated with a faster CBF response. Caffeine is a phosphodiesterase inhibitor, a class of agents known to increase the flexibility of erythrocytes, and thus to facilitate their passage through the lumen of the much smaller capillaries. We therefore expect caffeine consumption to be associated with faster and easier homogenization of capillary flow patterns during episodes of elevated metabolic demands, consistent with observations of improved oxygen extraction after caffeine ingestion in other tissue types, including muscle. Caffeine also exerts an excitatory effect on neurons by blocking adenosine receptors, which endogenous adenosine would otherwise occupy to inhibit neural activity. Moreover, caffeine blocks receptors on cerebral vasculature, resulting in vasoconstriction and reduced CBF. As receptors are more prone to upregulation than receptors, caffeine may elicit a higher metabolism increase in nonregular coffee users than in regular coffee users, while CBF may be reduced to the same extent for both groups (see Laurienti et al., 2002 for in‐depth discussions). This selective upregulation could explain that cerebral lactate production is observed in nonregular coffee users but not in regular coffee users (Dager et al., 1999). In Figure 8b, we observed that a fast and early CBF response could explain the disappearance of the initial dip, as observed in Behzadi and Liu (2006). Assuming that the effects of caffeine depends on the dose, CBF and the metabolism may increase in a dose‐dependent manner, leading to nonoxidative metabolism and pronounced lactate production after uptake of a high caffeine dose. In nonregular coffee users, high quantities of lactate have been observed in tissue for several dozens of minutes following caffeine intake (Dager et al., 1999). Accordingly, we hypothesize that lactate production could lead to a blood flow homogenization before, during, and after stimulation, and therefore to a lower baseline CTH and smaller CTH response than in the previous condition (without long CTH recovery as a consequence of presence of lactate also after stimulation). Interestingly, we showed in Figure 8d that such a CTH reduction could explain the smaller post‐stimulus undershoot after a high caffeine dose as observed in (Chen and Parrish, 2009; Liu et al., 2004). Applying the Buxton model to this condition leads to the same conclusion regarding the initial dip as with the CTH model: a quicker CBF response reduces the initial dip. However, it is not possible to assess the effects of reduced changes in capillary blood flow redistribution with the Buxton model, which predicts therefore same BOLD signal under both conditions in Figure 8.
In summary, we propose that the reduced initial dip associated with caffeine intake is caused by fast CBF response, and we speculate that the reduced undershoot observed after uptake of a high caffeine dose reflects production of lactate and hence reduced CTH response.
It would have been also interesting to apply our model to conditions of hypocapnia, where the blood flow would be expected to homogenize at the same time as it decreases, to sustain adequate CMRO2 levels. We hope that experimental data will be available in the future to allow us to further study neuro‐capillary coupling mechanisms under hypocapnic conditions.
4.2. OEF transients
In Figure 2, we examined the OEF response to a step increase in CBF to assess whether our model behaves realistically. Examining OEF transients is of primary importance, as it will directly influence the time course of the predicted BOLD signal. Theoretically, at least two reasons compel OEF to be continuous, even in the extreme case where CBF shows unphysiological time courses by changing instantaneously. First, the increase in CBF affects mainly the total transit time (i.e., the actual time spent in the capillary) of blood elements close to the capillary origin, while it hardly impacts that of end‐capillary blood elements. Consequently, the new OEF value is reached only when capillaries are filled with blood elements which never experienced the velocity before CBF increase, that is, after a time equal to the transit time in that capillary. Second, upon CBF increase, the oxygen concentration in the extravascular compartment tends toward a new equilibrium, affecting the concentration gradient between plasma and tissues, and hence OEF, for several seconds. Figure 2b,c illustrates the differences between the two models in term of OEF responses to more realistic, continuous, CBF time courses. Of particular importance, Figure 2c shows that OEF transients are predicted to be of different amplitudes depending on the model considered, with the model used in Buxton et al. (2004, 1998) showing a large OEF overshoot when metabolism increases, leading to substantial differences in term of predicted BOLD signals. Furthermore, it is interesting to note that the 1.5 s delay between OEF responses predicted with the Buxton and the CTH model translates approximately into the same delay in the dHb response (Figure 2e,f), and in turn in the BOLD response (Figure 6), where it is particularly obvious for the initial dips. This delay is of crucial importance, as it is of the same order of magnitude as the duration of the initial dip observed in the BOLD signal.
4.3. Limitations of the study
In this study, we model the microvascular distribution of blood by just one parameter, CTH. In this way, one can explore the role of the microcirculation in oxygen extraction (Angleys et al., 2015; Jespersen and Østergaard, 2012; Rasmussen et al., 2015) and glucose extraction (Angleys et al., 2016) in terms of a single parameter, which can be estimated in both animals (Gutiérrez‐Jiménez et al., 2016) and humans (Mouridsen, Hansen, Østergaard, & Jespersen, 2014). In maintaining this simplicity, our model is less straightforward to relate to direct observations of the microcirculation than models that incorporate the morphology and topology of the microvascular bed when calculating oxygen extraction and BOLD signals (Gagnon et al., 2015). Incorporation of the phase separation and self‐regulation effects (Section 1) also increases model complexity (Lücker, Secomb, Weber, & Jenny, 2017), but the associated change in hematocrit in capillaries that experience rapid redistribution of flow may provide means of characterizing the effects of pericyte dilations on the distribution of erythrocytes and their oxygen load. Accordingly, optical imaging studies would detect such increases in capillary hematocrit as a fast increase in total hemoglobin concentration, which might in turn be interpreted as a localized increase in local blood volume. Such changes have indeed been reported (Chen, Bouchard, McCaslin, Burgess, & Hillman, 2011; Hillman et al., 2007; Sirotin et al., 2009; Srinivasan and Radhakrishnan, 2014). The relative timing of localized changes in deoxy‐hemoglobin content and total hemoglobin may provide important clues regarding the coupling of arterial and capillary hemodynamics, respectively (Berwick et al., 2008, 2005), and thus the origin of the initial dip. It should be kept in mind, however, that a wide range of mechanisms, including central innervation of both arteries and microvessels, may affect the timing and extent of vasodilation and capillary redistribution of flow, respectively.
Although a lot of methods have been developed to quantify CMRO2 or CMRO2 change, the precise time needed for the metabolism to increase upon stimulation, and for that increase to affect mitochondrial activity, remain unknown. We therefore felt that it was important to evaluate the influence of this parameter. In this study, we assumed that the metabolism is determined by two parameters: , which accounts for the oxygen demand, and P t, which accounts for the oxygen availability in the tissue compartment around each capillary. Figure 5 shows that steep changes in , when compared to CBF, leads to an initial dip with a larger amplitude, and also to an overshoot at the end of the stimulation. In our study, we based our predictions on the assumption that the rise times for and CBF, respectively, are of comparable durations, thus matching the transients that have been observed experimentally. Note that shorter or longer time to rise would lead to similar conclusions as long as CBF's time to rise is of comparable duration.
In this study, we followed the approach detailed in Valabrègue et al. (2003) and treated individual capillaries as a compartment with homogeneous oxygen concentration, thus minimizing the amount of numerical computation. We assessed the validity of this assumption by comparing our results in steady state with those obtained with our previous model (Angleys et al., 2015) where this simplification is not made (results not shown). We observed that the predicted CMRO2 with the two models over a range of MTT and CTH values differ by less than 5%.
Our model relies on the calibration of several parameters (rate constant k, Michaelis–Menten parameters and and )—See Section 2.2.6 for more details about their calibration. While we based our assumptions on literature reports whenever possible, values or dynamics of parameters such as CTH remain unavailable or poorly documented. Although the chosen parametrization is inevitably arbitrary to some extent, our model has been applied to many different conditions. Accordingly, the good agreement between experimental data and our predictions for each of them is unlikely to be attributable to input parameters fine tuning. Moreover, when it was not possible to calibrate a parameter directly from the literature, we checked that our calibration gives rise to a realistic situation. For instance, and have been calibrated in the Buxton and CTH model to show realistic and similar initial dips and undershoots in Figure 6. With this calibration, V v is predicted to lag 3 s to 5 s behind CBF (see Figure 5), which is of same order of magnitude as reported values in the literature (Mandeville et al., 1998; Yacoub et al., 2006). When doing this calibration, we assumed that prolonged is the main contributor to the post‐stimulus undershoot in the Buxton model, while the predicted undershoot relies on both long CTH and long recovery in the CTH model. The balloon effect (long recovery) therefore needs to be relatively stronger with the Buxton model than with the CTH model to predict an undershoot of same amplitude, and the parameter , in turn, needs to take a larger value (0.60 with the Buxton model compared to 0.44 with the CTH model).
Note however that although long and CTH recoveries are the main contributors to the undershoot in the Buxton and CTH models, changes in also contribute to this negative portion of the BOLD signal in these two models: an increase in gives rise to a negative BOLD signal, as shown in Figure 4a. This negative contribution to the BOLD signal decreases its amplitude and in turn increases the amplitude of the post‐stimulus undershoot, both relatively to the signal maximum amplitude and in absolute value. When calibrating and , we disregarded mechanisms such as long metabolism recovery or CBF undershoot, which have been hypothesized to contribute to the post‐stimulus undershoot in some studies (Donahue et al., 2009; Hua et al., 2011). While taking these effects into account in our calibration, as well as getting more accurate predictions would improve our predictions, it is important to keep in mind that parameters such as , , or the dynamics of CTH, CBF, and , may also vary between brain areas and indeed among vertical layers (Gutiérrez‐Jiménez et al., 2016; Tian et al., 2010; Yacoub et al., 2006; Zhao et al., 2007).
In this study, the time courses of the different input parameters MTT, CTH, and are assumed to be smooth interpolation of trapezoidal functions. In reality, however, the blood flow does not increase at a fixed rate, but is characterized by smoother change. In particular during the off‐period, the rate at which CBF increases varies more gradually than what assumed in our model. To assess the effects of these sudden temporal changes assumed in our model on the BOLD signal transients, we applied our model to a condition where MTT and CTH vary more gradually than what assumed in the rest of the study. This left the BOLD signal transients essentially unchanged. Indeed, OEF and V v, which are used to derive the variables q and v are continuous and show smooth relaxation, even in the (unrealistic) case of noncontinuous CBF response (Figure 2). As a consequence, the influence of sudden changes in CBF on the BOLD signal in our model is limited. The rate at which CBF increases (rise time), however, has a strong influence on the transients (Figure 5a,b). In this study, the effects of changes in blood partial pressure of CO2 (pCO2) on the oxygen dissociation curve of hemoglobin (the Bohr Effect) have not been taken into account. Increase in pCO2 between conditions, or between arterioles and venules would shift the dissociation curve and lead to higher oxygen delivery, and therefore to increased BOLD signal amplitude, while the shape of the signal would be expected to be only modestly affected. Including the Bohr effect would be possible by modeling how change in pCO2 would affect oxygen dissociation curve of hemoglobin (Dash & Bassingthwaighte, 2004, 2010). While the Bohr Effect is likely to have limited influence on oxygen extraction during, for example, functional activation under conditions of normoxia, it will have more substantial effect under conditions of hypercapnia where pCO2 varies a lot, conditions under which the model has been applied in this study (Figure 6). Note that under conditions of hyperoxic hypercapnia (Figure 7), oxygen saturation levels are high (saturated in arterial blood and saturated at the capillary end). Accordingly, the shift of the oxygen dissociation curve in this condition will occur in the uppermost region of the sigmoidal curve and its effect will therefore be limited.
In this study, the BOLD signal is evaluated from the relationship 13 derived in Buxton et al. (1998) and is calibrated for and . This relationship has been updated in Buxton, Miller, Wong, and Frank (1999) according to
| (20) |
and is used in subsequent work (Buxton et al., 2004). In Equation (20), parameters ki have been calibrated for a field strength of and are equal to and (Buxton et al., 1999; Obata et al., 2004). These parameters have also been calibrated for a field strength of in another study (Mildner, Norris, Schwarzbauer, & Wiggins, 2001), where they are equal to , , and (Mildner et al., 2001). Because scanners have become more prevalent than scanners, we assessed the influence of the relationship used on the predicted BOLD signal. We found that the choice of the relationship to relate q and v to the BOLD signal has only little influence: in particular the three different relationships (Equations (13) and (20) with parameters ki calibrated for field strengths of and , respectively) give rise to initial dip and post‐stimulus undershoot of similar amplitude, suggesting that our conclusions do not depend on this particular choice. The amplitude of the BOLD signal, however, differs more substantially from one relationship to another.
To our knowledge, this is the first study where the BOLD signal is predicted, taking into account the effect of CTH, although the influence of CTH on OEF has been recently assessed dynamically using modeling (Rasmussen et al., 2015). Note however that several aspects make these two models different: First, in the model developed by Rasmussen et al., concentration in single capillaries was assumed to have reached steady state after each iteration. In contrast, in our model, we do not assume steady state condition at any moment and CTH is introduced explicitly. Second, while Rasmussen et al. modeled the extravascular compartment as a single extravascular compartment being affected by the transit time in every capillary, we modeled independent extravascular compartment around each capillary with no oxygen transfer between them. Although cells primarily receive oxygen from the nearest capillaries, the conditions under which contributions from more distant capillaries are indeed negligible, remain unclear.
We speculate that neuronal subtypes may reveal distinct BOLD “fingerprints” by virtue of their preference for utilizing neuro‐capillary coupling (redistribution of blood among capillaries) or neurovascular coupling (vasodilation) to meet their metabolic demands. It should be kept in mind, however, that aging and disease related changes in capillary function may alter individual BOLD dynamics to much larger extent. See, e.g., Østergaard et al. (2013) for a discussion of progressive capillary dysfunction and the possibility that hyperemia may no longer improve tissue oxygenation in cases where capillary “shunting” of oxygenated blood becomes extreme, cf. the inverse BOLD signals observed after vasodilation by Siero et al. (2015a).
5. CONCLUSIONS
In this study, we present for the first time a model to predict the BOLD signal dynamically, including the effects of blood flow homogenization, while employing a limited number of parameters. Although we had to employ several simplifying assumptions, we showed that the different variables used to predict the BOLD signal behave realistically and in agreement with literature reports. Applying the model to several conditions, we showed that, based on realistic parameter time courses, it can predict the BOLD signal, and in particular its transients, with reasonable accuracy. The origins of these transients have been studied for decades and although several hypotheses have been formulated, it is the first time, to our knowledge, that a model is able to bridge different plausible conjectures. In future work, it would be interesting to test the hypothesis formulated here experimentally, for example, by accurately determining the time courses of the BOLD signal, CBF, and the volume in the venous compartment, while controlling CTH. This would provide a way to assess the effects of CTH on the BOLD signal experimentally. Furthermore, we speculate that our interpretation of the BOLD signal in terms of the physiology of the microcirculation may open new avenues in terms of studying neuro‐capillary coupling mechanisms by neuroimaging methods.
DISCLOSURE/CONFLICT OF INTEREST
The authors declare no conflict of interest.
ACKNOWLEDGMENTS
This study was supported by the Danish National Research Foundation (CFIN), the Danish Ministry of Science, Innovation, and Education (MINDLab), and the VELUX Foundation (ARCADIA). The authors wish to thank Eugenio Gutiérrez‐Jiménez for fruitful discussions and artwork.
APPENDIX A.
is computed from the following equation:
| (A.1) |
where , with being the inverse of the cumulative distribution function . Its probability density function is defined as . See Angleys et al. (2016) for details about its derivation.
CMRO2 is computed as the sum of the rate at which oxygen is metabolized in every capillary:
| (A.2) |
Table A1 gives the precise time parametrization used under each conditions in this study.
Table A1.
Model parameters time courses used in different conditions the model was applied to
| Fig. (panel) | param. | tii | tif | rt | tdi | tdf | dt | |
|---|---|---|---|---|---|---|---|---|
| 2(a, d) |
|
‐ | ‐ | ‐ | ‐ | ‐ | ‐ | |
| CBF | 2 | 2+ϵ | ϵ | ‐ | ‐ | ‐ | ||
| CTH | 2 | 2+ϵ | ϵ | ‐ | ‐ | ‐ | ||
| 2(b, e) |
|
‐ | ‐ | ‐ | ‐ | ‐ | ‐ | |
| CBF | 2 | 14 | 12 | ‐ | ‐ | ‐ | ||
| CTH | 2 | 14 | 12 | ‐ | ‐ | ‐ | ||
| 2(c, f) |
|
2 | 8 | 6 | ‐ | ‐ | ‐ | |
| CBF | 2.9 | 14.9 | 12 | ‐ | ‐ | ‐ | ||
| CTH | 2.3 | 14.9 | 12.6 | ‐ | ‐ | ‐ | ||
| 4(a, b) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | ||
| CTH | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | ||
| 4(c, d) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | ||
| CTH | 20.3 | 32.9 | 12.6 | 56.6 | 92.6 | 36 | ||
| 4(e, f) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | 20.9 | 32.9 | 12 | 56.6 | 77.6 | 21 | ||
| CTH | 20.3 | 32.9 | 12.6 | 56.6 | 92.6 | 36 | ||
| 4(g, h) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | 20.9 | 32.9 | 12 | 56.6 | 77.6 | 21 | ||
| CTH | 20.3 | 32.9 | 12.6 | 56.6 | 92.6 | 36 | ||
| 5(a, b) |
|
20 | 20.9 | 0.9 | 55.7 | 58.7 | 3 | |
| CBF | 20.9 | 32.9 | 12 | 56.6 | 77.6 | 21 | ||
| CTH | 20.3 | 32.9 | 12.6 | 56.6 | 92.6 | 36 | ||
| 5(c, d) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | 20.9 | 32.9 | 12 | 56.6 | 77.6 | 21 | ||
| CTH | 20.3 | 32.9 | 12.6 | 56.6 | 92.6 | 36 | ||
| 5(e, f) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | 20.9 | 32.9 | 12 | 56.6 | 77.6 | 21 | ||
| CTH | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | ||
| 5(g, h) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | 20.9 | 32.9 | 12 | 56.6 | 77.6 | 21 | ||
| CTH | 20.3 | 32.9 | 12.6 | 56.6 | 92.6 | 36 | ||
| 6(a–c) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | 20.9 | 32.9 | 12 | 56.6 | 77.6 | 21 | ||
| CTH | 20.3 | 32.9 | 12.6 | 56.6 | 92.6 | 36 | ||
| 6(d–f) |
|
‐ | ‐ | ‐ | ‐ | ‐ | ‐ | |
| CBF | 20.9 | 32.9 | 12 | 56.6 | 77.6 | 21 | ||
| CTH | 20.9 | 32.9 | 12 | 56.6 | 77.6 | 21 | ||
| 7(a, b) |
|
‐ | ‐ | ‐ | ‐ | ‐ | ‐ | |
| CBF | 20 | 41 | 21 | 116 | 188 | 72 | ||
| CTH | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | ||
| 7(c, d) |
|
52.4 | 58.4 | 6 | 79.1 | 100.1 | 21 | |
| CBF | (20)* 53.3 | (41)* 70.7 | (21)* 17.4 | (116)* 80 | (188)* 101 | (72)* 21 | ||
| CTH | 52.7 | 70.7 | 18 | 80 | 101 | 21 | ||
| 8(a, b) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | 20.6 | 26.9 | 6.3 | 56.6 | 77.6 | 21 | ||
| CTH | 20.3 | 26.9 | 6.6 | 56.6 | 92.6 | 36 | ||
| 8(c, d) |
|
20 | 26 | 6 | 55.7 | 76.7 | 21 | |
| CBF | 20.6 | 26.9 | 6.3 | 56.6 | 77.6 | 21 | ||
| CTH | 20.3 | 26.9 | 6.6 | 56.6 | 77.6 | 21 |
All values are given in second and refer to the time axis of the figures presented in this study. tii, time at which the parameter begins to increase; tif, time at which the parameter stops to increase; rt: rise time, ; tdi, time at which the parameter begins to decrease; tdf, time at which the parameter stops to decrease; dt: decay time, .
*Values in parentheses refers to CBF increase due to hypercapnia.
Angleys H, Jespersen SN, Østergaard L. The effects of capillary transit time heterogeneity on the BOLD signal. Hum Brain Mapp. 2018;39:2329–2352. 10.1002/hbm.23991
Funding information Danish National Research Foundation (CFIN); Danish Ministry of Science, Innovation, and Education (MINDLab); VELUX Foundation (ARCADIA)
REFERENCES
- Angleys, H. , Jespersen, S. N. , & Østergaard, L. (2016). The effects of capillary transit time heterogeneity (CTH) on the cerebral uptake of glucose and glucose analogs: Application to FDG and comparison to oxygen uptake. Frontiers in Computational Neuroscience, 10, 103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angleys, H. , Østergaard, L. , & Jespersen, S. N. (2015). The effects of capillary transit time heterogeneity (CTH) on brain oxygenation. Journal of Cerebral Blood Flow & Metabolism, 35(5), 806–817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attwell, D. , Buchan, A. M. , Charpak, S. , Lauritzen, M. , MacVicar, B. A. , & Newman, E. A. (2010). Glial and neuronal control of brain blood flow. Nature, 468(7321), 232–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attwell, D. , Mishra, A. , Hall, C. N. , O'farrell, F. M. , & Dalkara, T. (2016). What is a pericyte? Journal of Cerebral Blood Flow & Metabolism, 36(2), 451–455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behzadi, Y. , & Liu, T. T. (2006). Caffeine reduces the initial dip in the visual BOLD response at 3 T. NeuroImage, 32(1), 9–15. [DOI] [PubMed] [Google Scholar]
- Berwick, J. , Johnston, D. , Jones, M. , Martindale, J. , Martin, C. , Kennerley, A. J. , … Mayhew, J. E. (2008). Fine detail of neurovascular coupling revealed by spatiotemporal analysis of the hemodynamic response to single whisker stimulation in rat barrel cortex. Journal of Neurophysiology, 99(2), 787–798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berwick, J. , Johnston, D. , Jones, M. , Martindale, J. , Redgrave, P. , McLoughlin, N. , … Mayhew, J. E. W. (2005). Neurovascular coupling investigated with two‐dimensional optical imaging spectroscopy in rat whisker barrel cortex. European Journal of Neuroscience, 22(7), 1655–1666. [DOI] [PubMed] [Google Scholar]
- Blicher, J. U. , Stagg, C. J. , O'shea, J. , Østergaard, L. , MacIntosh, B. J. , Johansen‐Berg, H. , … Donahue, M. J. (2012). Visualization of altered neurovascular coupling in chronic stroke patients using multimodal functional MRI. Journal of Cerebral Blood Flow & Metabolism, 32(11), 2044–2054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton, R. , Miller, K. , Wong, E. , & Frank, L. (1999). Application of the balloon model to the BOLD response to stimuli of different duration. In: Proceedings of the 7th Annual Meeting of ISMRM, Philadelphia. p. 1735.
- Buxton, R. B. (2012). Dynamic models of BOLD contrast. NeuroImage, 62(2), 953–961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton, R. B. , Uludağ, K. , Dubowitz, D. J. , & Liu, T. T. (2004). Modeling the hemodynamic response to brain activation. NeuroImage, 23(Supplement 1), S220–S233. [DOI] [PubMed] [Google Scholar]
- Buxton, R. B. , Wong, E. C. , & Frank, L. R. (1998). Dynamics of blood flow and oxygenation changes during brain activation: The balloon model. Magnetic Resonance in Medicine, 39(6), 855–864. [DOI] [PubMed] [Google Scholar]
- Buzsáki, G. , Kaila, K. , & Raichle, M. (2007). Inhibition and brain work. Neuron, 56(5), 771–783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, B. R. , Bouchard, M. B. , McCaslin, A. F. H. , Burgess, S. A. , & Hillman, E. M. C. (2011). High‐speed vascular dynamics of the hemodynamic response. NeuroImage, 54(2), 1021–1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, J. J. , & Pike, G. B. (2010). Global cerebral oxidative metabolism during hypercapnia and hypocapnia in humans: Implications for BOLD fMRI. Journal of Cerebral Blood Flow & Metabolism, 30(6), 1094–1099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, Y. , & Parrish, T. B. (2009). Caffeine dose effect on activation‐induced BOLD and CBF responses. NeuroImage, 46(3), 577–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, Z. , Silva, A. C. , Yang, J. , & Shen, J. (2005). Elevated endogenous GABA level correlates with decreased fMRI signals in the rat brain during acute inhibition of GABA transaminase. Journal of Neuroscience Research, 79(3), 383–391. [DOI] [PubMed] [Google Scholar]
- Dager, S. R. , Layton, M. E. , Strauss, W. , Richards, T. L. , Heide, A. , Friedman, S. D. , … Posse, S. (1999). Human brain metabolic response to caffeine and the effects of tolerance. American Journal of Psychiatry, 156(2), 229–237. [DOI] [PubMed] [Google Scholar]
- Dash, R. K. , & Bassingthwaighte, J. B. (2004). Blood HbO2 and HbCO2 dissociation curves at varied O2, CO2, pH, 2,3‐DPG and temperature levels. Annals of Biomedical Engineering, 32(12), 1676–1693. [DOI] [PubMed] [Google Scholar]
- Dash, R. K. , & Bassingthwaighte, J. B. (2010). Erratum to: Blood HbO2 and HbCO2 dissociation curves at varied O2, CO2, pH, 2,3‐DPG and temperature levels. Annals of Biomedical Engineering, 38(4), 1683–1701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donahue, M. J. , Near, J. , Blicher, J. U. , & Jezzard, P. (2010). Baseline GABA concentration and fMRI response. NeuroImage, 53(2), 392–398. [DOI] [PubMed] [Google Scholar]
- Donahue, M. J. , Stevens, R. D. , de Boorder, M. , Pekar, J. J. , Hendrikse, J. , & van Zijl, P. C. M. (2009). Hemodynamic changes after visual stimulation and breath holding provide evidence for an uncoupling of cerebral blood flow and volume from oxygen metabolism. Journal of Cerebral Blood Flow & Metabolism, 29(1), 176–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ernst, T. , & Hennig, J. (1994). Observation of a fast response in functional MR. Magnetic Resonance in Medicine, 32(1), 146–149. [DOI] [PubMed] [Google Scholar]
- Eskildsen, S. F. , Gyldensted, L. , Nagenthiraja, K. , Nielsen, R. B. , Hansen, M. B. , Dalby, R. B. , … Østergaard, L. (2017). Increased cortical capillary transit time heterogeneity in Alzheimer's disease: A DSC‐MRI perfusion study. Neurobiology of Aging, 50, 107–118. [DOI] [PubMed] [Google Scholar]
- Fernandez‐Klett, F. , Offenhauser, N. , Dirnagl, U. , Priller, J. , & Lindauer, U. (2010). Pericytes in capillaries are contractile in vivo, but arterioles mediate functional hyperemia in the mouse brain. Proceedings of the National Academy of Sciences, 107(51), 22290–22295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gagnon, L. , Sakadzic, S. , Lesage, F. , Musacchia, J. J. , Lefebvre, J. , Fang, Q. , … Boas, D. A. (2015). Quantifying the microvascular origin of BOLD‐fMRI from first principles with two‐photon microscopy and an oxygen‐sensitive nanoprobe. The Journal of Neuroscience, 35(8), 3663–3675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauthier, C. , Madjar, C. , Tancredi, F. , Stefanovic, B. , & Hoge, R. (2011). Elimination of visually evoked BOLD responses during carbogen inhalation: Implications for calibrated MRI. NeuroImage, 54(2), 1001–1011. [DOI] [PubMed] [Google Scholar]
- Goense, J. , Merkle, H. , & Logothetis, N. K. (2012). High‐resolution fMRI reveals laminar differences in neurovascular coupling between positive and negative BOLD responses. Neuron, 76(3), 629–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon, G. R. J. , Choi, H. B. , Rungta, R. L. , Ellis‐Davies, G. C. R. , & MacVicar, B. A. (2008). Brain metabolism dictates the polarity of astrocyte control over arterioles. Nature, 456(7223), 745–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutiérrez‐Jiménez, E. , Angleys, H. , Rasmussen, P. M. , Mikkelsen, I. K. , Mouridsen, K. , & Østergaard, L. (2017). The effects of hypercapnia on cortical capillary transit time heterogeneity (CTH) in anesthetized mice. Journal of Cerebral Blood Flow & Metabolism, 38(2), 290–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutiérrez‐Jiménez, E. , Cai, C. , Mikkelsen, I. K. , Rasmussen, P. M. , Angleys, H. , Merrild, M. , … Ostergaard, L. (2016). Effect of electrical forepaw stimulation on capillary transit‐time heterogeneity (CTH). Journal of Cerebral Blood Flow & Metabolism, 36(12), 2072–2086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall, C. N. , Reynell, C. , Gesslein, B. , Hamilton, N. B. , Mishra, A. , Sutherland, B. A. , … Attwell, D. (2014). Capillary pericytes regulate cerebral blood flow in health and disease. Nature, 508(7494), 55–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasegawa, T. , Ravens, J. R. , & Toole, J. F. (1967). Precapillary arteriovenous anastomoses: Thoroughfare channels in the brain. Archives of Neurology, 16(2), 217–224. [DOI] [PubMed] [Google Scholar]
- Hill, R. , Tong, L. , Yuan, P. , Murikinati, S. , Gupta, S. , & Grutzendler, J. (2015). Regional blood flow in the normal and ischemic brain is controlled by arteriolar smooth muscle cell contractility and not by capillary pericytes. Neuron, 87(1), 95–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillman, E. M. C. , Devor, A. , Bouchard, M. , Dunn, A. K. , Krauss, G. , Skoch, J. , … Boas, D. A. (2007). Depth‐resolved optical imaging and microscopy of vascular compartment dynamics during somatosensory stimulation. NeuroImage, 35(1), 89–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu, X. , Le, T. H. , & Uǧurbil, K. (1997). Evaluation of the early response in fMRI in individual subjects using short stimulus duration. Magnetic Resonance in Medicine, 37(6), 877–884. [DOI] [PubMed] [Google Scholar]
- Hu, X. , & Yacoub, E. (2012). The story of the initial dip in fMRI. NeuroImage, 62(2), 1103–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu, Y. , & Wilson, G. S. (1997). A temporary local energy pool coupled to neuronal activity: Fluctuations of extracellular lactate levels in rat brain monitored with rapid‐response enzyme‐based sensor. Journal of Neurochemistry, 69(4), 1484–1490. [DOI] [PubMed] [Google Scholar]
- Hua, J. , Stevens, R. D. , Huang, A. J. , Pekar, J. J. , & van Zijl, P. C. (2011). Physiological origin for the BOLD poststimulus undershoot in human brain: Vascular compliance versus oxygen metabolism. Journal of Cerebral Blood Flow & Metabolism, 31(7), 1599–1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber, L. , Goense, J. , Kennerley, A. J. , Ivanov, D. , Krieger, S. N. , Lepsien, J. , … Möller, H. E. (2014). Investigation of the neurovascular coupling in positive and negative BOLD responses in human brain at 7t. NeuroImage, 97, 349–362. [DOI] [PubMed] [Google Scholar]
- Hudetz, A. G. (1997). Regulation of oxygen supply in the cerebral circulation In Harrison D. K., Delpy D. T. (Eds.), Oxygen transport to tissue XIX. No. 428 in advances in experimental medicine and biology (pp. 513–520). Springer US. [DOI] [PubMed] [Google Scholar]
- Jespersen, S. N. , & Østergaard, L. (2012). The roles of cerebral blood flow, capillary transit time heterogeneity, and oxygen tension in brain oxygenation and metabolism. Journal of Cerebral Blood Flow & Metabolism, 32(2), 264–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinfeld, D. , Blinder, P. , Drew, P. J. , Driscoll, J. D. , Muller, A. , Tsai, P. S. , & Shih, A. Y. (2011). A guide to delineate the logic of neurovascular signaling in the brain. Frontiers in Neuroenergetics, 3, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurienti, P. J. , Field, A. S. , Burdette, J. H. , Maldjian, J. A. , Yen, Y.‐F. , & Moody, D. M. (2002). Dietary caffeine consumption modulates fMRI measures. NeuroImage, 17(2), 751–757. [PubMed] [Google Scholar]
- Lee, J. , Wu, W. , & Boas, D. A. (2015). Early capillary flux homogenization in response to neural activation. Journal of Cerebral Blood Flow & Metabolism, 36(2), 375–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, T. T. , Behzadi, Y. , Restom, K. , Uludag, K. , Lu, K. , Buracas, G. T. , … Buxton, R. B. (2004). Caffeine alters the temporal dynamics of the visual BOLD response. NeuroImage, 23(4), 1402–1413. [DOI] [PubMed] [Google Scholar]
- Longden, T. A. , Dabertrand, F. , Koide, M. , Gonzales, A. L. , Tykocki, N. R. , Brayden, J. E. , … Nelson, M. T. (2017). Capillary K+‐sensing initiates retrograde hyperpolarization to increase local cerebral blood flow. Nature Neuroscience, 20(5), 717–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longden, T. A. , Hill‐Eubanks, D. C. , & Nelson, M. T. (2016). Ion channel networks in the control of cerebral blood flow. Journal of Cerebral Blood Flow & Metabolism, 36(3), 492–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lücker, A. , Secomb, T. W. , Weber, B. , & Jenny, P. (2017). The relative influence of hematocrit and red blood cell velocity on oxygen transport from capillaries to tissue. Microcirculation, 24(3), e12337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madsen, P. L. , Cruz, N. F. , Sokoloff, L. , & Dienel, G. A. (1999). Cerebral oxygen/glucose ratio is low during sensory stimulation and rises above normal during recovery: Excess glucose consumption during stimulation is not accounted for by lactate efflux from or accumulation in brain tissue. Journal of Cerebral Blood Flow & Metabolism, 19(4), 393–400. [DOI] [PubMed] [Google Scholar]
- Malonek, D. , & Grinvald, A. (1996). Interactions between electrical activity and cortical microcirculation revealed by imaging spectroscopy: Implications for functional brain mapping. Science (New York, N.Y.), 272(5261), 551–554. [DOI] [PubMed] [Google Scholar]
- Mandeville, J. B. , Marota, J. J. A. , Ayata, C. , Zaharchuk, G. , Moskowitz, M. A. , Rosen, B. R. , & Weisskoff, R. M. (1999). Evidence of a cerebrovascular postarteriole windkessel with delayed compliance. Journal of Cerebral Blood Flow & Metabolism, 19(6), 679–689. [DOI] [PubMed] [Google Scholar]
- Mandeville, J. B. , Marota, J. J. A. , Kosofsky, B. E. , Keltner, J. R. , Weissleder, R. , Rosen, B. R. , & Weisskoff, R. M. (1998). Dynamic functional imaging of relative cerebral blood volume during rat forepaw stimulation. Magnetic Resonance in Medicine, 39(4), 615–624. [DOI] [PubMed] [Google Scholar]
- Mangia, S. , Tkc, I. , Gruetter, R. , Van de Moortele, P.‐F. , Maraviglia, B. , & Ugurbil, K. (2007). Sustained neuronal activation raises oxidative metabolism to a new steady‐state level: Evidence from 1H NMR spectroscopy in the human visual cortex. Journal of Cerebral Blood Flow & Metabolism, 27(5), 1055–1063. [DOI] [PubMed] [Google Scholar]
- Masamoto, K. , Vazquez, A. , Wang, P. , & Kim, S.‐G. (2008). Trial‐by‐trial relationship between neural activity, oxygen consumption, and blood flow responses. NeuroImage, 40(2), 442–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauro, M. A. , Murphy, K. P. J. , Thomson, K. R. , Venbrux, A. C. , & Morgan, R. A. (2014). Image‐guided interventions. OCLC, 851089452. [Google Scholar]
- Menon, R. S. , Ogawa, S. , Hu, X. , Strupp, J. P. , Anderson, P. , Uǧurbil, K. (1995). BOLD based functional MRI at 4 Tesla includes a capillary bed contribution: Echo‐planar imaging correlates with previous optical imaging using intrinsic signals. Magnetic Resonance in Medicine, 33(3), 453–459. [DOI] [PubMed] [Google Scholar]
- Michaelis, L. , & Menten, M. L. (1913). Die kinetik der invertinwirkung. Biochemistry, z 49(333–369), 352. [Google Scholar]
- Mildner, T. , Norris, D. G. , Schwarzbauer, C. , & Wiggins, C. J. (2001). A qualitative test of the balloon model for BOLD‐based MR signal changes at 3t. Magnetic Resonance in Medicine, 46(5), 891–899. [DOI] [PubMed] [Google Scholar]
- Mishra, A. , Reynolds, J. P. , Chen, Y. , Gourine, A. V. , Rusakov, D. A. , & Attwell, D. (2016). Astrocytes mediate neurovascular signaling to capillary pericytes but not to arterioles. Nature Neuroscience, 19(12), 1619–1627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mouridsen, K. , Hansen, M. B. , Østergaard, L. , & Jespersen, S. N. (2014). Reliable estimation of capillary transit time distributions using DSC‐MRI. Journal of Cerebral Blood Flow & Metabolism, 34(9), 1511–1521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthukumaraswamy, S. D. , Edden, R. A. , Jones, D. K. , Swettenham, J. B. , & Singh, K. D. (2009). Resting GABA concentration predicts peak gamma frequency and fMRI amplitude in response to visual stimulation in humans. Proceedings of the National Academy of Sciences, 106(20), 8356–8361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthukumaraswamy, S. D. , Evans, C. J. , Edden, R. A. , Wise, R. G. , & Singh, K. D. (2012). Individual variability in the shape and amplitude of the BOLD‐HRF correlates with endogenous GABAergic inhibition. Human Brain Mapping, 33(2), 455–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Northoff, G. , Walter, M. , Schulte, R. F. , Beck, J. , Dydak, U. , Henning, A. , … Boesiger, P. (2007). GABA concentrations in the human anterior cingulate cortex predict negative BOLD responses in fMRI. Nature Neuroscience, 10(12), 1515–1517. [DOI] [PubMed] [Google Scholar]
- Obata, T. , Liu, T. T. , Miller, K. L. , Luh, W.‐M. , Wong, E. C. , Frank, L. R. , … Buxton, L. R. (2004). Discrepancies between BOLD and flow dynamics in primary and supplementary motor areas: Application of the balloon model to the interpretation of BOLD transients. NeuroImage, 21(1), 144–153. [DOI] [PubMed] [Google Scholar]
- Østergaard, L. , Aamand, R. , Gutiérrez‐Jiménez, E. , Ho, Y.‐C. L. , Blicher, J. U. , Madsen, S. M. , … West, M. J. (2013). The capillary dysfunction hypothesis of Alzheimer's disease. Neurobiology of Aging, 34(4), 1018–1031. [DOI] [PubMed] [Google Scholar]
- Peppiatt, C. M. , Howarth, C. , Mobbs, P. , & Attwell, D. (2006). Bidirectional control of CNS capillary diameter by pericytes. Nature, 443(7112), 700–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prichard, J. , Rothman, D. , Novotny, E. , Petroff, O. , Kuwabara, T. , Avison, M. , … Shulman, R. (1991). Lactate rise detected by 1H NMR in human visual cortex during physiologic stimulation. Proceedings of the National Academy of Sciences, 88(13), 5829–5831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen, P. M. , Jespersen, S. N. , & Østergaard, L. (2015). The effects of transit time heterogeneity on brain oxygenation during rest and functional activation. Journal of Cerebral Blood Flow & Metabolism, 35(3), 432–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Röther, J. , Knab, R. , Hamzei, F. , Fiehler, J. , Reichenbach, J. R. , Büchel, C. , & Weiller, C. (2002). Negative dip in BOLD fMRI is caused by blood flow—Oxygen consumption uncoupling in humans. NeuroImage, 15(1), 98–102. [DOI] [PubMed] [Google Scholar]
- Sappey‐Marinier, D. , Calabrese, G. , Fein, G. , Hugg, J. W. , Biggins, C. , & Weiner, M. W. (1992). Effect of photic stimulation on human visual cortex lactate and phosphates using 1H and 31P magnetic resonance spectroscopy. Journal of Cerebral Blood Flow & Metabolism, 12(4), 584–592. [DOI] [PubMed] [Google Scholar]
- Schmid, F. , Reichold, J. , Weber, B. , & Jenny, P. (2015). The impact of capillary dilation on the distribution of red blood cells in artificial networks. American Journal of Physiology ‐ Heart and Circulatory Physiology, 308(7), H733–H742. [DOI] [PubMed] [Google Scholar]
- Schulte, M. L. , Wood, J. D. , & Hudetz, A. G. (2003). Cortical electrical stimulation alters erythrocyte perfusion pattern in the cerebral capillary network of the rat. Brain Research, 963(1–2), 81–92. [DOI] [PubMed] [Google Scholar]
- Siero, J. C. W. , Hartkamp, N. S. , Donahue, M. J. , Harteveld, A. A. , Compter, A. , Petersen, E. T. , & Hendrikse, J. (2015a). Neuronal activation induced BOLD and CBF responses upon acetazolamide administration in patients with steno‐occlusive artery disease. NeuroImage, 105, 276–285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siero, J. C. W. , Hendrikse, J. , Hoogduin, H. , Petridou, N. , Luijten, P. , & Donahue, M. J. (2015b). Cortical depth dependence of the BOLD initial dip and poststimulus undershoot in human visual cortex at 7 Tesla. Magnetic Resonance in Medicine, 73(6), 2283–2295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirotin, Y. B. , Hillman, E. M. C. , Bordier, C. , & Das, A. (2009). Spatiotemporal precision and hemodynamic mechanism of optical point spreads in alert primates. Proceedings of the National Academy of Sciences, 106(43), 18390–18395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivasan, V. J. , & Radhakrishnan, H. (2014). Optical coherence tomography angiography reveals laminar microvascular hemodynamics in the rat somatosensory cortex during activation. NeuroImage, 102, 393–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefanovic, B. , Hutchinson, E. , Yakovleva, V. , Schram, V. , Russell, J. T. , Belluscio, L. , … Silva, A. C. (2008). Functional reactivity of cerebral capillaries. Journal of Cerebral Blood Flow & Metabolism, 28(5), 961–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson, J. K. , Peterson, M. R. , & Freeman, R. D. (2004). High‐resolution neurometabolic coupling revealed by focal activation of visual neurons. Nature Neuroscience, 7(9), 919–920. [DOI] [PubMed] [Google Scholar]
- Tian, P. , Teng, I. C. , May, L. D. , Kurz, R. , Lu, K. , Scadeng, M. , … Devor, A. (2010). Cortical depth‐specific microvascular dilation underlies laminar differences in blood oxygenation level‐dependent functional MRI signal. Proceedings of the National Academy of Sciences, 107(34), 15246–15251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhlirova, H. , Kılıç, K. , Tian, P. , Thunemann, M. , Desjardins, M. , Saisan, P. A. , Sakadžić, S. , … Devor, A. (2016). Cell type specificity of neurovascular coupling in cerebral cortex. eLife, 5, e14315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valabrègue, R. , Aubert, A. , Burger, J. , Bittoun, J. , & Costalat, R. (2003). Relation between cerebral blood flow and metabolism explained by a model of oxygen exchange. Journal of Cerebral Blood Flow & Metabolism, 23(5), 536–545. [DOI] [PubMed] [Google Scholar]
- Villringer, A. , Them, A. , Lindauer, U. , Einhäupl, K. , & Dirnagl, U. (1994). Capillary perfusion of the rat brain cortex. An in vivo confocal microscopy study. Circulation Research, 75(1), 55–62. [DOI] [PubMed] [Google Scholar]
- Wei, H. S. , Kang, H. , Rasheed, I.‐Y. D. , Zhou, S. , Lou, N. , Gershteyn, A. , … Nedergaard, M. (2016). Erythrocytes are oxygen‐sensing regulators of the cerebral microcirculation. Neuron, 91(4), 851–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler, E. A. , Bell, R. D. , & Zlokovic, B. V. (2011). Central nervous system pericytes in health and disease. Nature Neuroscience, 14(11), 1398–1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yacoub, E. , Ugurbil, K. , & Harel, N. (2006). The spatial dependence of the poststimulus undershoot as revealed by high‐resolution BOLD‐ and CBV‐weighted fMRI. Journal of Cerebral Blood Flow & Metabolism, 26(5), 634–644. [DOI] [PubMed] [Google Scholar]
- Yamanishi, S. (2005). Extracellular lactate as a dynamic vasoactive signal in the rat retinal microvasculature. American Journal of Physiology ‐ Heart and Circulatory Physiology, 290(3), H925–H934. [DOI] [PubMed] [Google Scholar]
- Yang, S.‐P. , & Krasney, J. A. (1995). Cerebral blood flow and metabolic responses to sustained hypercapnia in awake sheep. Journal of Cerebral Blood Flow & Metabolism, 15(1), 115–123. [DOI] [PubMed] [Google Scholar]
- Zhao, F. , Jin, T. , Wang, P. , & Kim, S.‐G. (2007). Improved spatial localization of post‐stimulus BOLD undershoot relative to positive BOLD. NeuroImage, 34(3), 1084–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]


