The morphology of the human cerebrovascular system

Abstract

While several methodologies exist for quantifying gray and white matter properties in humans, relatively little is known regarding the spatial organization and the intersubject variability of cerebral vessels. To resolve this, we developed a fast, open‐source processing algorithm using advanced vessel segmentation schemes and iterative nonlinear registration to isolate, extract, and quantify cerebral vessels in susceptibility weighting imaging (SWI) and time‐of‐flight angiography (TOF‐MRA) datasets acquired in a large cohort (n = 42) of healthy individuals. From this, whole‐brain venous and arterial probabilistic maps were generated along with the computation of regional densities and diameters within regions based on popular anatomical and functional atlases. The results show that cerebral vasculature is highly heterogeneous, displaying disproportionally large vessel densities in brain areas such as the anterior and posterior cingulate, cuneus, precuneus, parahippocampus, insula, and temporal gyri. On average, venous densities were slightly higher and less variable across subjects than arterial. Moreover, regional variations in both venous and arterial density were significantly correlated to cortical thickness (R = 0.42). This publicly available new atlas of the human cerebrovascular system provides a first step toward quantifying morphological changes in the diseased brain and serving as a potential regression tool in fMRI analysis.

1. INTRODUCTION

The human brain consumes about 20% of the daily intake of oxygen and glucose, which are supplied to the cortex via arteries, arterioles, and capillaries and drained via the venous system and large sinuses (Schmid, Barrett, Jenny, & Weber, 2017). It is well documented that acute impairment of the cerebral arteries can cause collateral damage (Ossenkoppele et al., 2015) and that venous atrophy may play an important role in the early stages of a number of neurological disorders (Gorelick, Counts, & Nyenhuis, 2016; Kaufman, Milstein, Kaufman, & Milstein, 2013). Nevertheless, despite the existence of many neuroimaging tools for segmenting and quantifying the brains gray and white matter, relatively few publicly available methods exist for the noninvasive investigation of cerebral vasculature. There are several reasons why developing this is important: First, having the ability to compare the vascular tree between healthy controls and patient populations in an automated fashion (i.e., similar to a VBM analysis [Ashburner & Friston, 2000]) would allow for a better quantification of normal variations in vessel density and diameter while potentially localizing cerebrovascular defects. Second, both the timing (Jahanian, Christen, Moseley, & Zaharchuk, 2018; Provencher, Bizeau, Gilbert, Bérubé‐Lauzière, & Whittingstall, 2018) and amplitude (Vigneau‐Roy, Bernier, Descoteaux, & Whittingstall, 2013) of functional magnetic resonance imaging (fMRI) signals are influenced by the underlying venous vasculature (Provencher et al., 2018; Vigneau‐Roy et al., 2013), thus making it difficult to correctly interpret the source (i.e., neuronal or vascular) of interarea or intersubject differences (Jahanian et al., 2018; Kay et al., 2018; Roy et al., 2009). In this respect, a freely available atlas highlighting such vascular heterogeneity might be useful for studies where such measures are missing.

Noninvasive imaging techniques such as time‐of‐flight magnetic resonance angiography (ToF‐MRA) and susceptibility weighting imaging (SWI) also referred to as high‐resolution venous venography have the potential to permit visualization of the large arteries and veins, respectively, on a single‐subject basis. ToF‐MRA (with venous saturation) is based on the flow and movement of protons in the blood through the imaging plane. To measure the flow, the signal in the slice below the one that is imaged is saturated with rapid RF pulses which suppress background or stationary tissues, whereas fresh‐moving blood entering the slice after the RF pulse will retain its signal intensity and create contrast between blood and background tissue, highlighting arterial vessels with a contrast that decreases with the flow (Muhs et al., 2007). SWI, on the other hand, exploits the differences in phase changes between venous blood (i.e., deoxyhemoglobin) and surrounding cerebral tissues, highlighting the venous vessels (Reichenbach & Haacke, 2001) uniformly across the brain. Both ToF‐MRA and SWI are routinely used in clinical applications, though rarely used when interpreting fMRI results. Some of this has to do with the fact that a major difficulty in the successful extraction of the vasculature from either SWI or ToF lies in the density of the cortical arterial and venous network, which varies considerably in branching, size, surrounding tissues, and curvature across subjects (Duvernoy, Delon, & Vannson, 1981). The cortical vasculature is, therefore, a highly difficult system to model. Although single‐subject depiction and labeling of the vasculature is possible, very few vascular atlas from SWI or ToF exists in the literature (Nowinski et al., 2011), and group‐based quantifications of both veins and arteries are rare. Although some efforts have been made to assess the probability of finding major arteries from group‐based ToF‐MRA acquisitions (Dunas et al., 2017; Nils Daniel Forkert et al., 2012; Viviani, 2016), no study to our knowledge has combined both arterial and venous vessels into a single, freely available atlas. The main conclusions from these previous studies are that (1) no general process currently exists to validate those results other than comparing the major known vessels qualitatively to data from other fields (angiography, neurosurgery, neuroradiology, etc.) and (2) that registration often fails to properly align the vessel trees at smaller branches and thus necessitates many subjects (or samples) to minimize misregistration steps. This could, at least in part, explain the low number of probabilistic atlases of brain arteries (Dufour et al., 2011; Nils Daniel Forkert et al., 2012) and veins (N. D. Forkert et al., 2013; Ward et al., 2018).

As the need for dedicated tools to assess cerebral vasculature is growing, our goal was to construct the first whole‐brain probabilistic vascular density atlases for both human cerebral arteries (using ToF‐MRA) and veins (using SWI) in the same group of participants. The main objectives were threefold: (1) The development of two algorithms, the multi‐scale Frangi diffusive filter (MSFDF), based on vessel recognition, centerline, and diameter extraction and the recursive vascular registration refinement (ReVaR), an iterative nonlinear registration to extract the vessels of 42 participants and minimize their high intersubject variability. (2) The quantification of the voxel‐wise probabilistic maps of veins and arteries. (3) The regionwise quantification of vascular densities and diameters within commonly used anatomical and functional atlases. The resulting algorithms and probabilistic maps in MNI space, part of the Braincharter package, will be freely available for public use at https://github.com/braincharter/vasculature.

2. MATERIALS AND METHODS

2.1. Participants and data acquisition

Approval for this study was obtained from the Centre Hospitalier Universitaire de Sherbrooke ethics committee. All participants provided written informed consent and all experiments were conducted according to the principles expressed in the Declaration of Helsinki. Participants were an average of 22 (20–31) years old (n = 42). Anthropometric data were all within the normal range. MRI data were acquired using a 3 T Philips Scanner, where noise‐reduction headphones and head cushions were used to minimize motion artifacts. Each MRI session started with an anatomical T1‐weighted 1 mm isotropic MPRAGE (TR/TE 7.8/3.54 ms) acquisition, followed by a whole‐brain multi‐band ToF angiography acquisition (200 × 200 × 120 FOV, TR/TE 23/3.6 ms, voxel size of 0.625 × 0.625 × 1.3 mm) using a venous inflow suppression (saturation band placed on the upstream side of each slice to avoid contaminating the signal through venous inflows) and a high‐resolution multi‐echo SWI sequence (230 × 230 × 160 FOV, TR 28 ms, TE 6.9/12.6/18.3/24.0 ms, voxel size of 0.6 × 0.6 × 1.2 mm) to visualize cerebral arteries and veins, respectively.

2.2. Anatomical MRI processing

As the T1 images acquired on a 3 T scanner are prone to magnetic field biases that deform and artificially increase the gray‐level contrasts locally, a bias correction was first applied using ITK N4 bias correction (Tustison et al., 2010). Using the mindboggle‐OASIS template (Klein & Tourville, 2012), the T1 images were skull‐stripped and denoised using an edge‐preservative, nonlocal mean spatial denoising algorithm carried out using ANTs (Avants et al., 2011). The registration to the MNI space using a nonlinear SyN registration was then done using ANTs, which was also used to extract the cortical thickness for each voxel of the gray matter as well as the gray matter, white matter, and CSF classification for each voxel of the brain.

2.3. SWI and ToF preprocessing

For each subject, both ToF and SWI were preprocessed using an in‐house approach, MSFDF, with each step described here (Figure 1): (i) The original ToF and SWI were denoised using a non‐local mean denoising approach (Avants et al., 2011; Bernier, Chamberland, Houde, Descoteaux, & Whittingstall, 2014) to enhance image quality. (ii) A Bayesian Gaussian mixture with Dirichlet process was used (Pedregosa et al., 2011) to obtain a binary classification of voxels (vessels vs nonvessels). This image‐intensity thresholding approach provides a coarse preselection of candidate voxels associated to vasculature. (iii) This map was further refined by only retaining voxels exhibiting tubular geometry (i.e., vessels) by combining multiple Frangi scores (Bizeau et al., 2018; Frangi, Niessen, Vincken, & Viergever, 1998), which were obtained using different smoothing on the images (10 scales, from 0.5 to 3.0 of Gaussian FWHM), from which the maximum score was retained. This multiscale scheme allowed the extraction of vessels over different sizes. After combination, 10 iterations of a vessel enhancement diffusion (VED) filter were sequentially applied to further smooth the combined scale images (Enquobahrie, Ibanez, Bullitt, & Aylward, 2007; Manniesing, Viergever, & Niessen, 2006). (iv) This image was intensity‐normalized and thresholded (50%) to obtain both whole‐brain arterial and venous maps. (v) To compute the diameters, a thinning algorithm was employed to compute the centerline of the vessels while (vi) the ridge distance was extracted inside the vessel tree. (vii) The ridge distances were finally masked with the centerlines to obtain a measure of diameter at each voxel. To put all vessel‐related maps in a stereotaxic space, a nonlinear registration between the original non‐skull‐stripped SWI‐ToF and T1 was applied. The T1 was then nonlinearly aligned to the MNI T1 0.5 mm space (Avants et al., 2011), and both transformations were concatenated and applied to all ToF and SWI vessel maps. As multiecho SWI is prone to the appearance of arteries in later echoes, which could impact our analysis, we also computed the intersection between ToF and SWI images and removed these voxels from the SWI venous tree. Finally, we used the GM, WM and CSF classification (using ANTs) and computed the vascular density of each tissue type using a ratio between the voxels identified as a vessel and the total number of voxel per tissue type.

Figure 1.

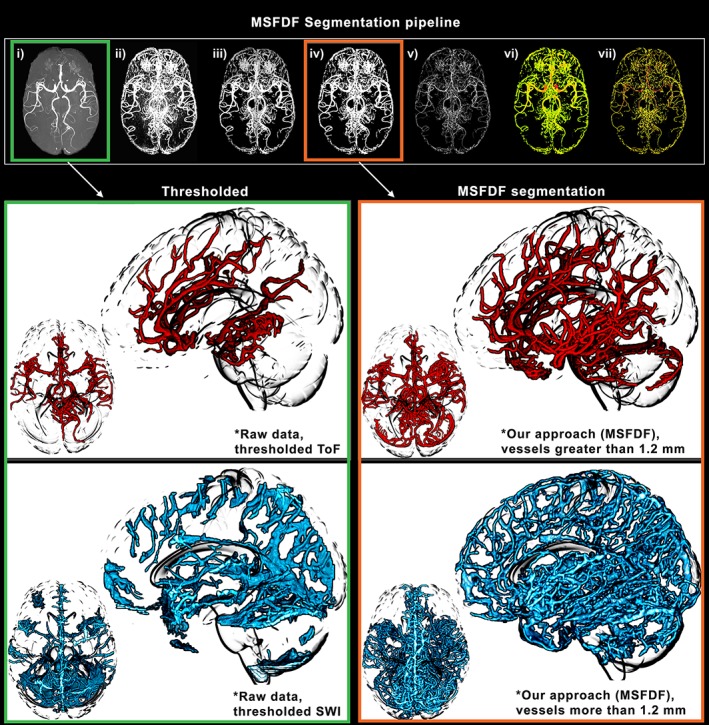
Illustration of our vessels segmentation pipeline. The extraction of small vessels (~1 mm) necessitates a complex pipeline of image processing due to inconsistencies in signal‐to‐noise ratio and intensity leveling across regions of the brain. (a–g) Each step of the segmentation and diameter extraction explained in the Methods section is shown here. Green: manual thresholding of a ToF and SWI image from a single subject. Orange: vessels extracted using our multiscale Frangi diffusion filter (MSFDF) pipeline on the same ToF

However, vessel configuration greatly varies between subjects (Ghanavati, Lerch, & Sled, 2014), thus an additional registration step involving both the vessel trees and the original image was applied on all the images to build a proper template. Here we developed the recursive vascular registration (ReVaR) refinement, an iterative back‐projection scheme involving 5 iterations of non‐linear registration. At each step, the algorithm uses a combination of the subject vasculature to the previous iteration's updated mean of all subject vasculature (weight: 90%) and their T1 image to the MNI T1 to prevent hard deformations of the cortex (weight: 10%). From these, the vessel maps are then averaged and filtered using the previously defined VED filter. To obtain the probability maps, the mean of the thresholded‐normalized vascular map was then computed (step [iv]) which resulted in voxel‐based venous and arterial density maps, a 1–100 scale of vessel probability per voxel in the MNI 0.5 mm space (see Figure 2 [top] for single‐subject and atlas 3D reconstruction of venous and arterial trees).

Figure 2.

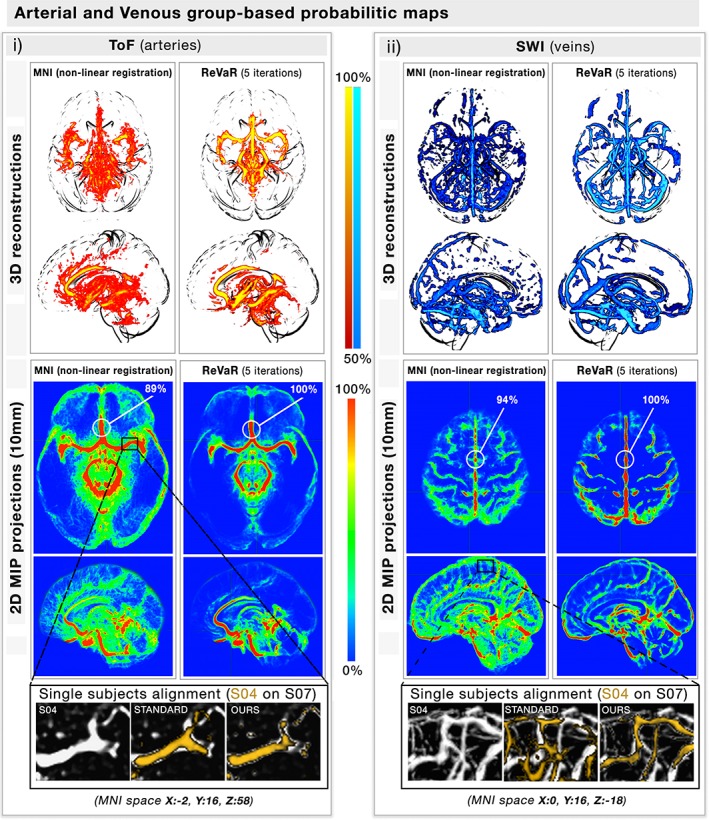
Venous and arterial probabilistic mapping. (a,b) The figure illustrates on both a 3d view (top) and a 10 mm MIP projection (bottom) how our (b) recursive vascular registration refinement (ReVaR), involving an iterative back‐projection scheme involving 5 iterations of nonlinear registration, performed compared to (a) using a standard nonlinear registration. The coloration represents for each voxel the probability of finding a vessel at that location. The zoom section illustrates the alignment of the vessels of two single subjects, with and without our approach [Color figure can be viewed at http://wileyonlinelibrary.com]

2.4. Anatomical and functional atlases

Aside from voxelwise estimates, regional vascular densities were also investigated using different atlases. Four well‐established atlases were selected from the literature, two functional and two anatomical parcellations. For the structure‐based atlases, Freesurfer (Fischl et al., 2004) aparc‐aseg parcellation based on 42 ispsilateral regions of the gray matter formed from a label‐propagation algorithm and the Harvard‐Oxford probabilistic atlas covering 48 cortical areas and currently used by FSL (Desikan et al., 2006) were investigated. For the function‐based atlases, the bootstrap analysis of stable clusters (BASC) parcellation (Bellec, 2013; Bellec, Rosa‐Neto, Lyttelton, Benali, & Evans, 2010), a compilation of multi‐scale bootstrapped k‐mean formed regions from 43 resting‐state fMRI (here the 64 regions BASC parcellation) and the multisubject dictionary learned probabilistic atlas (MSDL) covering well‐known resting‐state networks (39 distinct regions) were used. For all these atlases, Nilearn (Abraham, Dohmatob, Thirion, Samaras, & Varoquaux, 2014) was used to extract the venous and arterial densities and diameters of all subjects for each region. In each atlas, for each region, mean venous density (regional mean of venous maps obtained at step [iv]), mean arterial density (regional mean of arterial maps obtained at step (iv)), mean venous diameter (the regional nonzero mean of venous maps obtained at step [vii]), mean arterial diameter (the regional nonzero mean of venous maps obtained at step (vii)), and mean cortical thickness (regional mean) are reported.

3. RESULTS

3.1. Voxelwise intersubject variability and arterial/venous diameters

The voxel‐based probability maps for veins and arteries are shown in Figure 2 (here, 100% indicates the voxel was classified as a vessel in all 42 subjects). On average, the spatial overlap of voxels identified as being both venous and arterial was 11.27 ± 3.06%, and located near the edges of the largest arteries (i.e., basilar and posterior cerebral arteries) indicating that image SNR was sufficient to reliably separate the two vessel types. The voxels overlapping the arteries in the venous trees were removed and omitted from the analysis. As expected, the main arterial (communicating arteries) and venous (transversal, superior, and inferior sagittal sinuses) structures were identified in the vast majority of subjects while the smaller vessels were more variable across subjects (Figure 2). The figure also shows that the intersubject probability tends to decrease along with the diameter further in the vessel tree. To quantify this, the Pearson correlation between X and Y was computed using all voxels located on a single‐subject vascular tree (Figure 3 top), which were then regrouped into 1,000 regions using a k‐mean algorithm for simplification (Figure 3 bottom). Indeed, vessel diameter was significantly correlated to its probability score both at the voxel‐ and clustered level (veins: R = 0.46; arteries: R = 0.52, p < .001). This suggests that smaller vessels are more structurally variable than larger ones.

Figure 3.

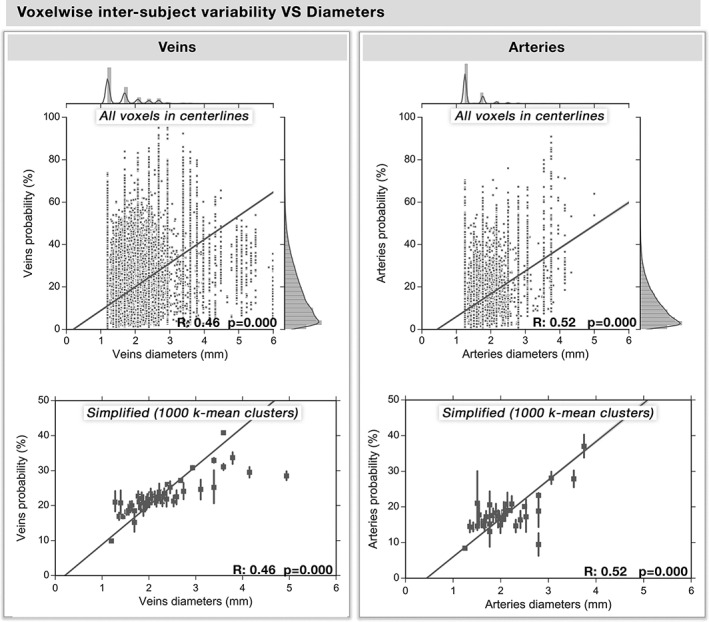
Voxelwise intersubject probabilities versus diameters. Based on the voxels along one single‐subject venous and arterial centerlines of their vessel trees, the relation between vessel diameter and the voxelwise group‐based venous and arterial intersubject probabilities are shown here. (a,b) Each dot represents a voxel along the centerline of the vascular tree, whereas the regression line and the 95% interval of confidence of the linear fit (shaded areas) are computed separately for each type of vasculature and are represented in yellow (p < .0001). The histogram of their distribution is also shown above and on the right of the graph. (c,d) For simplification and a better illustration of the relation, we regrouped the voxels in 1,000 classes of equal size using k‐mean clustering, with the standard deviation represented on each dot by a line

3.2. Regional arterial/venous densities and cortical thickness

A thresholded (top 10%) venous and arterial density map overlaid on four atlases is shown in Figures 4 and 5, respectively. The complete spatial distributions involved in the study are shown for each atlas in Supporting Information, Figures S1–S4. Arterial density varied across regions, with the densest areas located in the visual, lateral and frontal areas, which is in agreement with the locations of the large known arteries (communicating arteries). Similarly, the spatial distribution of venous density coincided with the functional and anatomical atlases (Figure 5). The highest venous densities were located near central areas of the frontal, parietal, and visual areas for both atlases, following the largest sinuses (transversal, superior, and inferior sagittal sinuses). Note how both venous and arterial densities were highest near the insula and anterior cingulate. Indeed, regional variations in venous density was highly correlated to arterial density (Figure 6, R: [0.54, 0.62, 0.69, 0.75], all p < .001). The mean densities, diameters, and cortical thicknesses for the most vascularized regions of each atlas are reported in Table 1.

Figure 4.

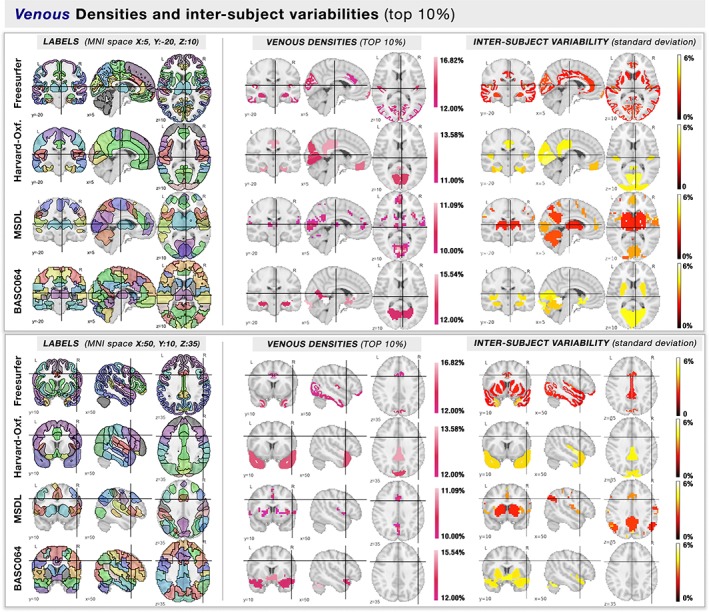
Atlas regions with highest venous densities (top 10%). On two different MNI coordinates (squares, above & below), we show the (column left) labels of the template where each brain region is color‐coded randomly, and (column right) the regions with the highest venous densities (top 10%) are color‐coded by their mean value of density. Each row represents a different atlas [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 5.

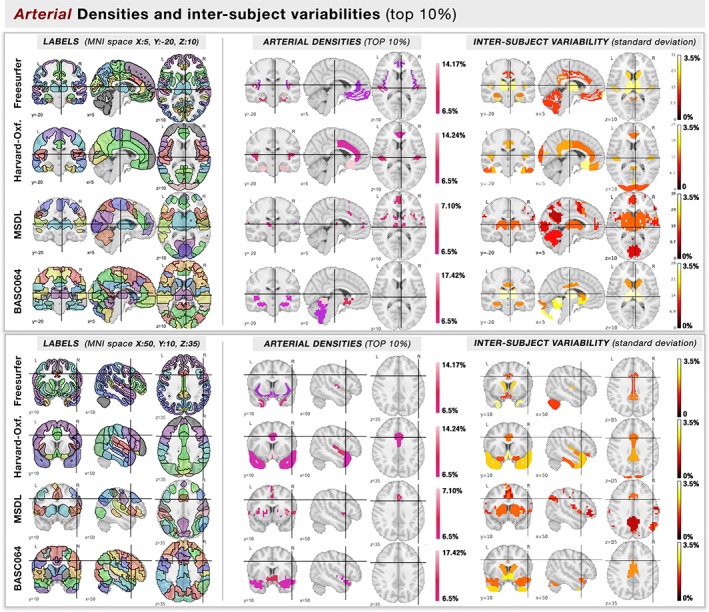
Atlas regions with highest arterial densities (top 10%). On two different MNI coordinates (squares, above & below), we show the (column left) labels of the template where each brain region is color‐coded randomly, and (column right) the regions with the highest arterial densities (top 10%) are color‐coded by their mean value of density. Each row represents a different atlas [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 6.

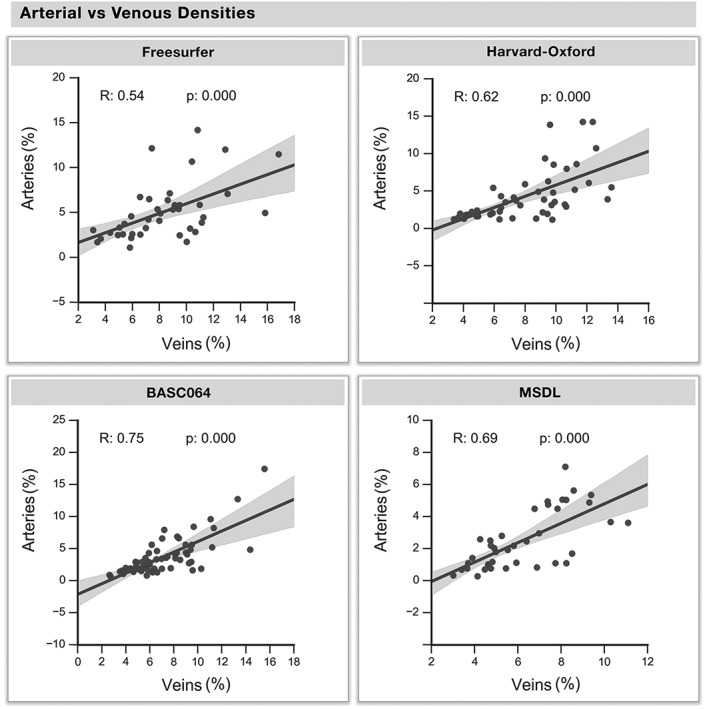
Arterial versus venous density. The venous and arterial densities of all regions are corresponded across regions. Each dot represents a region of each atlas, whereas the regression line and the 95% interval of confidence of the linear fit (shaded areas) are computed separately for each atlas

Table 1.

Summary of cortical regions with the highest vascular densities per atlas (top 10%)

Atlas	Region	Venous density (%)	Arterial density (%)	Venous diameter	Arterial diameter	Cortical thickness
BASC064	Posterior cingulate/cuneus	14.9 ± 5.11	12.71 ± 2.65	1.03 ± 0.15	1.61 ± 0.15	2.42 ± 0.12
	Anterior cingulate	12.8 ± 3.94	10.55 ± 2.03	0.87 ± 0.28	1.36 ± 0.22	3.88 ± 0.31
	Parahippocampal gyrus	10.81 ± 3.62	8.30 ± 1.60	0.86 ± 0.28	1.14 ± 0.22	2.41 ± 0.19
	Temporal gyrus	10.42 ± 3.71	9.64 ± 1.44	0.84 ± 0.26	0.99 ± 0.15	2.04 ± 0.27
	Occipital/lingual gyrus	13.73 ± 4.17	5.07 ± 1.59	0.77 ± 0.22	0.65 ± 0.13	1.85 ± 0.11
Freesurfer	Posterior cingulate/cuneus	12.01 ± 2.18	6.32 ± 1.71	0.88 ± 0.26	1.12 ± 0.22	2.99 ± 0.26
	Anterior cingulate	10.21 ± 3.51	7.05 ± 1.34	0.73 ± 0.26	1.36 ± 0.19	3.88 ± 0.38
	Parahippocampal gyrus	11.12 ± 3.74	6.27 ± 1.60	0.93 ± 0.30	1.14 ± 0.22	2.91 ± 0.24
	Temporal gyrus	12.15 ± 2.73	12.11 ± 2.77	0.90 ± 0.26	1.44 ± 0.26	3.24 ± 0.48
	Occipital/lingual gyrus	9.95 ± 3.32	6.01 ± 1.33	0.77 ± 0.22	0.76 ± 0.23	0.85 ± 0.11
Harvard‐Oxford	Posterior cingulate/cuneus	10.02 ± 4.14	4.34 ± 2.08	0.75 ± 0.28	0.65 ± 0.13	1.96 ± 0.26
	Anterior cingulate	10.75 ± 3.47	14.01 ± 2.29	0.67 ± 0.22	1.29 ± 0.22	3.01 ± 0.25
	Parahippocampal gyrus	12.02 ± 3.89	14.76 ± 2.41	0.90 ± 0.30	1.48 ± 0.22	3.14 ± 0.33
	Temporal gyrus	12.61 ± 4.59	11.33 ± 1.44	0.88 ± 0.32	0.90 ± 0.13	1.57 ± 0.30
	Culmen/lingual gyrus	12.90 ± 4.38	6.01 ± 1.31	0.86 ± 0.28	0.86 ± 0.15	2.34 ± 0.11
MSDL	Posterior cingulate/cingulate	15.80 ± 3.52	5.32 ± 1.14	1.14 ± 0.37	1.05 ± 0.24	4.52 ± 0.26
	Anterior cingulate	15.17 ± 5.11	9.61 ± 1.66	1.18 ± 0.43	1.16 ± 0.26	4.31 ± 0.66
	Cingulate	14.71 ± 5.97	10.34 ± 2.00	1.12 ± 0.43	1.18 ± 0.32	3.97 ± 0.65
	Temporal gyrus/insula	14.73 ± 4.78	10.41 ± 1.80	1.12 ± 0.49	1.33 ± 0.34	5.13 ± 0.75
	Lingual gyrus	17.66 ± 4.87	5.75 ± 1.25	1.31 ± 0.49	0.99 ± 0.26	3.44 ± 0.65

The GM, WM, and CSF classification of each voxel of the vascular trees are reported on Figure 7, where most of the vasculature (85%–90%) was classified as GM or CSF (mean of all subjects: arteries: GM = 46.4% ± 1.5%, WM = 15.1% ± 2.1%, CSF = 39.1% ± 4.1%; veins: GM = 42.8% ± 0.9%, WM = 9.9% ± 2.5%, CSF = 47.0% ± 4.3%). The vascular density of each tissue type is also shown, where the proportion of voxels per tissue type was greater in the CSF than for GM and WM (arteries: GM = 3.6% ± 1.6%; WM = 2.1% ± 0.6%; CSF = 8.3% ± 1.5%; veins: GM = 7.0% ± 2.3%; WM = 2.3% ± 1.8%; CSF = 47% ± 4%).

Figure 7.

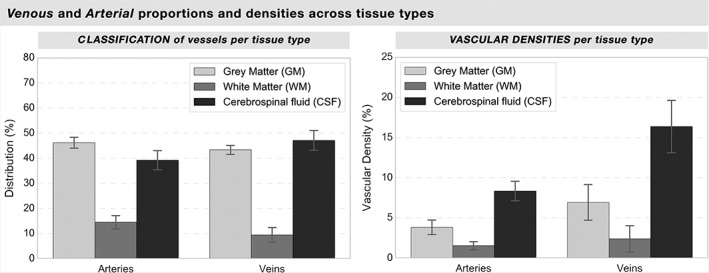
Arterial versus venous classification and density per tissue type. For each subject, each voxel classified as a vessel was classified as gray matter, white matter, or CSF according to the ANTs three‐tissues type classification. The left histogram illustrates the ratio of the vascular tree's voxels classified as their corresponding tissue location, while the right histogram shows the vascular density of each tissue type (ratio of vascular voxels vs nonvascular voxels in all the brain for each tissue type). The variations between subjects are illustrated as standard deviations

Regional variations in average cortical thickness positively correlated with venous density in all atlases (Figure 8, R = [.30, .35, .44, .59], p = [.036, .001, .003, <.001]). The arteries were also significantly correlated to cortical thickness in all atlases but the BASC064 functional atlas (see Supporting Information, Figures S5–S8, R = [.29, .36, .38], p = [.042, .012, .005]).

Figure 8.

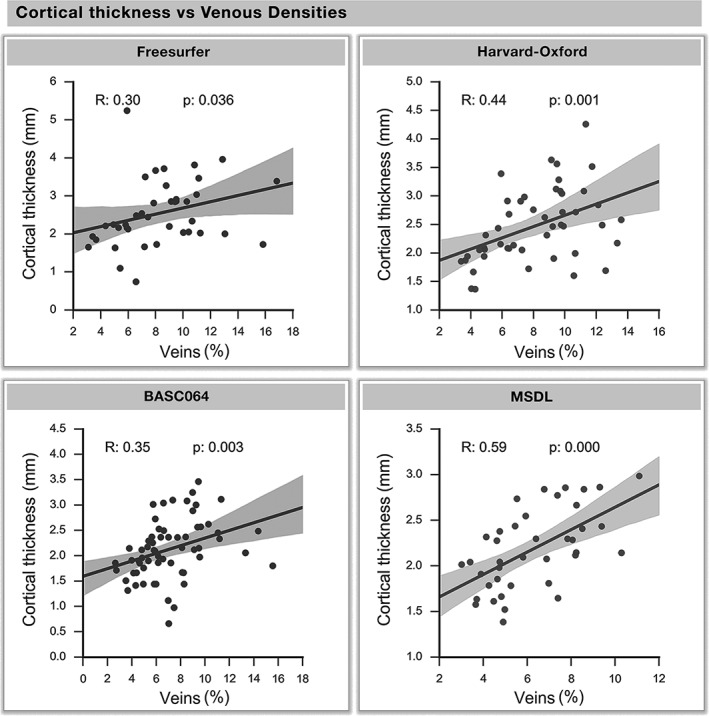
Cortical thickness versus venous density. The cortical thickness and venous density of each region are corresponded across all atlases. Each dot represents a region of an atlas, whereas the regression line and the 95% interval of confidence of the linear fit (shaded areas) are computed separately

4. DISCUSSION

Despite the numerous tools for the quantification of gray matter and white matter properties in humans, it remains challenging to study the spatial organization and variability of cerebral vessels and assess their impact on brain function. Therefore, the main goal of this study was to create a probabilistic whole‐brain atlas of human cerebral architecture of both cerebral veins and arteries based on three main novel approaches: First, the development of the MSFDF approach for segmenting vessels and the ReVaR tuning to successfully align cerebral vessels from SWI and ToF‐MRA acquisitions for group‐based comparison which resulted in a voxel‐based probabilistic atlas of veins and arteries. Second, the extraction of vessel statistics such as density and diameter and their comparison to each other as well as to measures of cortical thickness in regions defined in four widely used atlases (anatomically and functionally defined) which showed that certain brain areas are disproportionality more vascularized than others and that vascular density is significantly correlated to cortical thickness throughout the brain. Third, the analysis of how vessel diameter directly influences inter‐subject variability in vessel segmentation and registration indicated that smaller vessels are spatially more variable than larger ones. Taken together, we believe that these novel findings, including the now publicly available voxel‐wise and region‐wise maps of the vascularization in the Braincharter package on https://github.com/braincharter/vasculature, will improve research into the role of brain vasculature in neuroanatomical and functional studies.

4.1. Voxelwise venous and arterial probability maps

Our voxel‐wise probabilistic maps of the cerebral vasculature (Figure 2) highlight the spatial consistency of the major arterial and venous structures across subjects. On average, intersubject variability decreased with increasing vessel diameter (Figure 3) where vessels with diameters >∼2.5 mm tended to be most stable across subjects. This is in line with another study which examined cerebral veins in 10 subjects and reported high intersubject probabilities near the major veins, including in the superior sagittal sinus, dural sinuses, straight sinus, and internal cerebral veins (Ward et al., 2018). Notably, this relationship was also observed in arteries (Figure 3, R = [.46, .52], all p < .001).

Moreover, to the best of our knowledge, no group‐based probabilistic venous atlas with a relatively large number of healthy subjects (more than 10) exists in the literature (Nils Daniel Forkert et al., 2012), making ours the first publicly available. Our segmentation results are similar to the probabilistic map of vasculature based on 10 subjects (Ward et al., 2018) and a deterministic map of large vein atlases, showing clearly the transversal, superior, and inferior sagittal sinuses among others (Kiliç & Akakin, 2008) (Figure 2, yellow arrows). Overall, our results show that, using our 7‐steps MSFDF processing algorithm based on vessel extraction and ReVaR's iterative nonlinear registration refinement, subjects were co‐aligned better and more thoroughly and we were able to obtain more precise co‐registrations to overcome the higher intersubject variability in small vessels, as indicated by our increased probability scores.

While others have previously computed voxel‐based arterial atlases with results similar to ours, those atlases do not include venous data. In one study, Dunas et al. (2017) produced a labeled probability atlas of arteries using more than 100 older participants' 4D flow MRI angiography scans. They mainly focused on the labeling of large arteries since they used an intensity thresholding method to extract the vasculature (Dunås et al., 2016). Similarly, in another study, Viviani et al. (Viviani, 2016) constructed a ToF‐based atlas from 38 ToF‐MRA acquisitions and reported inter‐subject probabilities of ∼80% in the largest arterial structures using an affine co‐registration, which rapidly decreased in smaller arteries along the vessel tree. In our case, we do not, at this time, label our arteries as done elsewhere (Dunas et al., 2017), but our method (MSFDF) allows to extract smaller vessels (see Figure 1, left vs right). Ultimately, these could be labeled, similar to the work of Dunas et al., into well‐known arteries based by group‐based segmentation or with the help of a single‐subject deterministic atlas or segmentation (Bizeau et al., 2018). Finally, Forkert et al. (2012) created an arterial atlas based on 700 subjects with an affine co‐registration of vessels extracted from high‐resolution ToF‐MRA and reported a 60% occurrence for the bilateral carotid arteries and inter‐subject probabilities of up to 40% for the bilateral proximal middle cerebral artery and basilar artery. In contrast, we observed much higher probabilities across the brain (probabilities of up to 100%, Figure 2), even in smaller vessels, with a similar number of acquisitions (42 subjects) (probability of up to 70% in smaller vessels, Figure 3). These differences could be explained by our ReVaR approach, which improves the co‐localization of the subject's vascular tree.

4.2. Regionwise atlas‐based venous and arterial density maps

As voxel‐wise group‐based analysis relies heavily on proper registration, and thus low intersubject variability, additional vascular analysis was conducted on several different brain parcellations. The quantification of specific brain areas are highly dependent on their parcellation scheme (Arslan et al., 2017; Thirion, Varoquaux, Dohmatob, & Poline, 2014; Yao, Hu, Xie, Moore, & Zheng, 2015). In fact, the definition of regions based on tissue type (such as gray or white matter) or functional areas is the key factor in studying their properties for both structural and functional data. As the choice of parcellation can influence the outcome of the statistical analysis (Bernier, Croteau, Castellano, Cunnane, & Whittingstall, 2017), differences in the atlases' statistical analysis were expected, especially between functional and anatomical ones. However, all analysis conducted in each parcellation yielded similar results. It can be safely concluded that our results are independent of parcellation type.

Looking at the vessels penetrating the cortex, a strong and consistent correlation was found between venous and arterial densities across atlases (Figure 6), with the anterior and posterior cingulate, cuneus, precuneus, parahippocampus, insula, and temporal gyri being more vascularized (top 10%, from 10% to 18% for veins and 6.5% to 17% for arteries). Interestingly, some of these regions (i.e., parahippocampal, insular, and temporal areas) were found to exhibit the most variability in fMRI connectivity strength (Chamberland et al., 2017; Mueller et al., 2013). In addition, Eklund, Nichols, and Knutsson (2016) reported the posterior cingulate as being the brain area most susceptible to false positives, and it is exactly this area that we find as also among the most heavily vascularized. As it stands, it is unclear how vasculature is related to these fMRI findings, though including this as regressor might be an important application for our atlases. More specifically, one approach might consist of correcting regional or subject differences in fMRI signal amplitude and/or latency according to their vascular density (Provencher et al., 2018).

Unexpectedly, a strong and positive relationship was observed between venous density and cortical thickness (Figure 8). To ensure that the difference in resolution between our vascular data and the T1 images (0.6 × 1.2 mm vs 1 × 1 mm) did not impact our analysis, we also computed the cortical thickness relationship with venous density using T1 images resampled to 0.6 × 1.2 mm, but this did not significantly change the results (veins vs cortical thickness; before: R = .30, .44, .35, .59; after: R = .31, .42, .35, .59; not shown in the results). Two possible interpretations can be drawn from this relation: (1) A larger supply of blood is needed where the gray matter is thickest to properly feed the region with nutriments and, consequently, drain it back to the heart. This is in agreement with a study in mice showing that brain regions with high vascular density also have high cell counts (Tsai et al., 2009). However, this is based on the assumption that cortical thickness is a reliable marker of neuronal packing density, which is yet to be confirmed (Kanai & Rees, 2011). (2) A recent study showed that increased CBV (via vessel vasodilation) induces an overestimation of cortical thickness and gray matter volume due to changes in T1 tissue values (Tardif et al., 2017). It is therefore possible that brain areas with inherently large vessels (or with a high density of small vessels), and hence high CBV, affect the T1‐weighted intensity of nearby gray matter voxels, leading to an overestimation of thickness. This would be in line previous other studies that recommend the use of T2 (Helms, Kallenberg, & Dechent, 2006) or FLAIR images combined with T1 images to ensure a better classification of gray‐matter tissue and venous vessels at the edge of the brain (Viviani, 2016; Viviani et al., 2017). In addition, other studies have investigated the potential misclassification of vessels as gray matter (Helms et al., 2006; Viviani et al., 2017). Our results are in line with this and demonstrate the potential vascular confound in cortical thickness measurements and thus open the possibility of using SWI data in conjunction with T1 images to improve cortical thickness estimates. Importantly, it also reinforces the importance of taking vascular structure into account when interpreting cortical thickness, for example, in neurodegenerative pathologies that are related to vascular impairments.

Finally, we observed a higher density of veins compared to arteries (Figures 4, 5, 6), regardless of the atlas used. For all regions across atlases, the regional density of arteries was more than a half compared to the density of veins. Although this is in line with previous studies which report a higher proportion of veins compared to arteries in humans by factors ranging from 1.33 (Blakemore & Jennett, 2001) to 2.5 ± 0.5 (Blinder et al., 2013; Nguyen, Nishimura, Fetcho, Iadecola, & Schaffer, 2011; Shih et al., 2012), other studies concluded the opposite: the proportion of arteries was higher than veins in humans (Duvernoy et al., 1981) and primates (Guibert, Fonta, & Plouraboué, 2010; Weber, Keller, Reichold, & Logothetis, 2008). Although our results seem to coincide with the first group (more veins than arteries), it is still unclear whether these findings are due to inherent differences in the biological vasculature or technical limitations (the nature of the SWI and ToF‐MRA sequences): More specifically, SWI sensitivity is globally the same across the brain at all time points (Haacke et al., 2007), whereas the ToF‐MRA signal drops progressively in its initial intensity as the velocity progressively decreases throughout the vascular system (Ishimaru et al., 2007). The latter could affect arterial extraction in the cortex, resulting in artificially lower artery count. We are also limited to a venous and arterial diameter of 0.6 mm, which excludes the brain's venules, arterioles, and capillaries. Nevertheless, as the venous and arterial densities are strongly correlated, this is likely not a major issue for our conclusion, that is, venous and arterial brain densities co‐vary regionally.

4.3. Application to partial volume correction or voxel‐based morphometry

Some analyses would benefit from having a probabilistic atlas of the vasculature. Aside from complementing the extraction of cortical thickness as mentioned before, partial volume correction (PVC) could be applied based on the vasculature. Typically, tissue‐probability maps of gray (GM) and white matter (WM) are often used for PVC in positron emission tomography (PET) studies, where experimental data are adjusted by the proportion of GM or WM (Dukart & Bertolino, 2014; Harri, Mika, Jussi, Nevalainen, & Jarmo, 2007; Oakes et al., 2007). PVC has been used, mainly, to overcome spatial resolution limitations of PET acquisitions, based on the hypothesis that for voxel‐ or region‐based analysis, quantitative assessments may result in significant bias in their estimates due to PVC. Using an approach familiar to that already implemented for GM/WM corrections, PVC techniques could be considered for correction of vascular confounds. Surprisingly, however, vascular structure is rarely considered when interpreting region‐ or group‐based PET. The quantification of glucose metabolism using a fluorodesoxyglucose (FDG) tracer is based on kinetic models which include a blood volume correction factor (vb), often set to a global constant (or even 0 or no correction) (Alf, Martić‐Kehl, Schibli, & Krämer, 2013; Bernier et al., 2017). By fixing the vb parameters using vascular probability maps instead, the extracted glucose uptake may be more specific and less variable between subjects. In addition, vascular maps could be used to localize vascular confounds in different patient groups (i.e., as for VBM analysis).

Last, it is expected that subsequent studies using high‐field systems (i.e., 7 T‐MRI) will yield more information on smaller vessels (arterioles and venules) which were likely missed in this 3 T study due to the relatively low spatial resolution (0.6 mm). Deep‐learning algorithms also show promising results in retinal vessel segmentation (Chen, 2017), and might be of interest if translated to SWI and ToF images to further improve the segmentation process. Ultimately, another avenue for potential improvement would be to use these probabilistic atlases as priors in the vessel segmentation step, similar to using tissue‐type or spatial priors to reduce false positives and obtain smoother results (Beriault, Xiao, Collins, & Pike, 2015).

5. CONCLUSION

Based on noninvasive imaging, we are the first to show how both the density and size of veins and arteries vary proportionally, and that cortical thickness seems to partially follow this relationship. Four functionally and anatomically defined atlases were created in this study, and their region‐ and voxel‐based probabilistic maps of vascular density are freely available for fundamental and clinical studies using vascular‐based measurements (https://github.com/braincharter/vasculature). This study highlights the importance of including vesselness in functional measurements, and therefore, suggests the use of our maps for PVC as it is already done for partial gray‐matter correction.

Supporting information

Appendix S1: Supplementary figures

Bernier M, Cunnane SC, Whittingstall K. The morphology of the human cerebrovascular system. Hum Brain Mapp. 2018;39:4962–4975. 10.1002/hbm.24337