At the core of reasoning: Dissociating deductive and non‐deductive load

Abstract

In recent years, neuroimaging methods have been used to investigate how the human mind carries out deductive reasoning. According to some, the neural substrate of language is integral to deductive reasoning. According to others, deductive reasoning is supported by a language‐independent distributed network including left frontopolar and frontomedial cortices. However, it has been suggested that activity in these frontal regions might instead reflect non‐deductive factors such as working memory load and general cognitive difficulty. To address this issue, 20 healthy volunteers participated in an fMRI experiment in which they evaluated matched simple and complex deductive and non‐deductive arguments in a 2 × 2 design. The contrast of complex versus simple deductive trials resulted in a pattern of activation closely matching previous work, including frontopolar and frontomedial “core” areas of deduction as well as other “cognitive support” areas in frontoparietal cortices. Conversely, the contrast of complex and simple non‐deductive trials resulted in a pattern of activation that does not include any of the aforementioned “core” areas. Direct comparison of the load effect across deductive and non‐deductive trials further supports the view that activity in the regions previously interpreted as “core” to deductive reasoning cannot merely reflect non‐deductive load, but instead might reflect processes specific to the deductive calculus. Finally, consistent with previous reports, the classical language areas in left inferior frontal gyrus and posterior temporal cortex do not appear to participate in deductive inference beyond their role in encoding stimuli presented in linguistic format.

1. INTRODUCTION

The mental representations and processes underlying deductive reasoning in humans have long been discussed in the psychological literature (e.g., Braine & O'Brien, 1998; Johnson‐Laird, 1999; Osherson, 1975; Rips, 1994). Over the past 18 years, non‐invasive neuroimaging methods have played a growing role in investigating how the human mind achieves deductive inferences (see Monti & Osherson, 2012; Prado, Chadha, & Booth, 2011 for a review). At least in the context of propositional and categorical problems, two main hypotheses have emerged concerning the localization of the neural substrate of this ability. On the one hand, some have proposed that the centers of language, and in particular regions within what has traditionally been referred to as Broca's area, in the left inferior frontal gyrus, are critical to deductive reasoning. Reverberi and colleagues, for example, have shown that in the context of simple propositional and categorical inferences, premise integration consistently activates the left inferior frontal gyrus (particularly within Brodmann areas (BA) 44 and 45; see Reverberi et al., 2010, 2007). This region has thus been suggested to be involved in the extraction and representation of the superficial and formal structure of a problem, with other frontal regions, such as the orbital section of the inferior frontal gyrus (i.e., BA47), also contributing to representing the full logical meaning of an argument (Baggio et al., 2016; Reverberi et al., 2012).

On the other hand, a number of studies have failed to uncover any significant activation within Broca's area for propositional and categorical deductive inferences (Canessa et al., 2005; Kroger, Nystrom, Cohen, & Johnson‐Laird, 2008; Monti, Osherson, Martinez, & Parsons, 2007; Monti, Parsons, & Osherson, 2009; Noveck, Goel, & Smith, 2004; Parsons & Osherson, 2001; Rodriguez‐Moreno & Hirsch, 2009), even under much more naturalistic experimental conditions (Prado et al., 2015). An alternative hypothesis has thus been proposed under which logic is subserved by a set of language‐independent regions within frontopolar (i.e., BA10) and frontomedial (i.e., BA8) cortices, among others (Monti & Osherson, 2012; Monti et al., 2007, 2009). Consistent with this proposal, neuropsychological investigations have shown that lesions extending at through medial BA8 are sufficient to impair deductive inference‐making, as well as meta‐cognitive assessments of inference complexity, despite an anatomically intact Broca's Area and ceiling performance on neuropsychological assessments of language function (Reverberi, Shallice, D'agostini, Skrap, & Bonatti, 2009).

As discussed elsewhere, a number of experimental factors might help reconcile the divergence of results, including (i) the complexity of the deductive problems (typically much greater in studies failing to uncover activation in Broca's area), (ii) the specific task employed to elicit deductive reasoning, such as argument generation, which is correlated with detecting activation in the left inferior frontal gyrus, versus argument evaluation, which correlates with failing to uncover such activation, and (iii) the degree to which participants are trained prior to the experimental session (see Monti & Osherson, 2012 for a review). In the present work we will mainly address the first point with respect to the possibility that activity in the so‐called “core” regions of deductive inference (and particularly left frontopolar cortex) might in fact reflect, partially or entirely, increased load on non‐deductive processes (e.g., greater working memory demands) imposed by hard deductions (cf., Kroger et al., 2008; Prado, Mutreja, & Booth, 2013). For, inasmuch as complex deductions impose greater load on deductive processes, and thereby increase the need for branching, goal‐subgoal processing, and the simultaneous consideration of multiple interacting variables, as is likely in the load design used in Monti et al. (2007), the “workspace” of working memory must also undergo increased load (Halford, Wilson, & Phillips, 2010).

Of course, there is broad agreement that deductive inference is best understood as relying on a broader “cascade of cognitive processes requiring the concerted operation of several, functionally distinct, brain areas” (Reverberi et al., 2012, p. 1752; see also discussion in Prado et al., 2015) beyond those we considered above. Posterior parietal cortices, for example, are often observed across propositional, categorical, and relational deductive syllogisms, although with a preponderance of unilateral activations in propositional and categorical deductions and bilateral activations for relational problems (e.g., Knauff, Fangmeier, Ruff, & Johnson‐Laird, 2003; Knauff, Mulack, Kassubek, Salih, & Greenlee, 2002; Kroger et al., 2008; Monti et al., 2009; Noveck et al., 2004; Prado, Der Henst, & Noveck, 2010; Reverberi et al., 2010, 2007; Rodriguez‐Moreno & Hirsch, 2009). Dorsolateral frontal regions also appear to be recruited across different types of deductive problems (e.g., Fangmeier, Knauff, Ruff, & Sloutsky, 2006; Knauff et al., 2002; Monti et al., 2007, 2009; Reverberi et al., 2012; Rodriguez‐Moreno & Hirsch, 2009) and might possess interesting hemispheric asymmetries in their functional contributions to deductive inference making (see discussion in Prado et al., 2015). Nonetheless, the present study is specifically meant to address the significance of regions that have been previously proposed to encapsulate processes which lie at the heart of deductive reasoning (Monti et al., 2007, 2009) vis‐à‐vis the concern that it is “[…] not clear whether the results found by Monti et al. (2007) reflect deduction or working memory demands” (Kroger et al., 2008, p. 90).

In what follows, we report on a 3T functional magnetic resonance imaging (fMRI) study in which we tested whether the pattern of activations that has been previously characterized as “core” to deductive inference (Monti et al., 2007, 2009; see Monti & Osherson, 2012 for a review) might instead reflect activity resulting from increased general non‐deductive cognitive load (a view we will label the general cognitive load hypothesis). Specifically, using a 2 × 2 design (simple/complex, deductive/non‐deductive), we compare the effect of non‐deductive (e.g., working memory) versus deductive load on the putative “core” regions of deduction. Using a forward inference approach (Henson, 2006; see also Heit, 2015 for a discussion on the relevance of this approach to the field of the neural basis of human reasoning), under the general complexity hypothesis, activity in frontopolar and frontomedial cortices should be elicited equally by deductive and non‐deductive load. Conversely, under our previous interpretation of these regions, deductive load alone should elicit activity within these areas. As we report below, contrary to the general cognitive load hypothesis, non‐deductive load fails to elicit significant activation in the so‐called “core” regions of deduction which, in fact, appear sensitive to the interaction of load and deductive problems, further establishing the genuine tie between these areas and cognitive processes that sit at the heart of the deductive (specifically, propositional) inference.

2. MATERIALS AND METHODS

2.1. Participants

Twenty (eight female) undergraduates from the University of California, Los Angeles (UCLA), participated in the study for monetary compensation after giving written informed consent, in accordance with the Declaration of Helsinki and with the rules and standards established by the UCLA Office of the Human Research Protection Program. All participants were right‐handed native English speakers with no prior history of neurological disorders and had no prior formal training in logic. Ages ranged from 18 to 23 years old (M = 20.4 years, SD = 1.4).

Before being enrolled in the fMRI component of the study participants underwent a screening procedure similar to that used in Canessa et al. (2005) in which they had to achieve an accuracy level of 60% or better on each of the four task types to be performed in the neuroimaging session (i.e., the simple and complex deductive and non‐deductive tasks, see below). Prospective participants were recruited via the UCLA Psychology Department's SONA system, which provides a means for undergraduates to participate in psychology experiments for academic credit. The pre‐test, in which participants received no feedback on either individual problems or overall performance, utilized the same experimental stimuli as those employed in the neuroimaging session, although presented in a different random order, and occurred on average 5.3 months (SD = 4.6 month) prior to the fMRI session, to minimize the possibility of practice effects. A correlational analysis showed that there was no relationship between the amount of time that elapsed between the screening and imaging visit and the participants' accuracy at the imaging session (both overall and individually for any subtask). Importantly, participants did not undergo training on the task (e.g., of the sort used, for example, in Reverberi et al., 2007).

2.2. Task

In each trial, participants were presented with a triplet of sentences (henceforth “arguments”), asked to engage in a deductive or non‐deductive task, and then, after a brief (3 s) delay, prompted to respond (see Figure 1 for a depiction of the task timeline).

Figure 1.

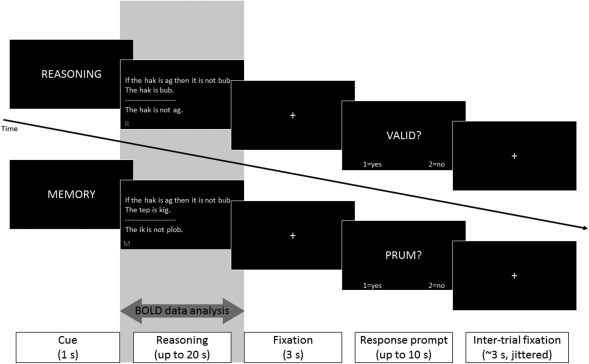
Experimental design. Sample deductive (complex; top) and non‐deductive (simple; bottom) trials. The gray area highlights the period relevant for the BOLD data analysis. (In the original displays the bottom left reminder cue appeared in red)

In the deductive condition, participants were asked to assess the logical status (i.e., (in)validity) of the argument, which they were probed on at the response prompt. Following previous work (Monti et al., 2007), half the arguments were subjectively simple to assess while the remainder were subjectively complex (henceforth simple and complex deductive conditions, respectively; see below for further details). While we adopted an empirical definition of deductive load, it is clear that the simple deductive arguments, which were structured around the logical form of modus ponens (which refers to inferences that conform to the valid propositional rule, “If P then Q; P; therefore Q”) were low in both general cognitive load and relational complexity (defined as the “the number of interacting variables represented in parallel” Halford, Wilson, & Phillips, 1998, p. 851). Conversely, the complex deductive arguments, which were structured around the logical form of modus tollens (inferences that conform to the valid propositional rule, “If P then Q; not Q; therefore not P”), were higher in both relational complexity and in general cognitive load than the simple deductive arguments. (We take it to be uncontroversial that, under the view that working memory serves “as the workspace where relational representations are constructed,” Halford et al., 2010, increased relational complexity must be accompanied by increased working memory demands.) In the non‐deductive trials, participants were asked to retain in memory the presented sentence triplet or a mentally manipulated version of the triplet (simple and complex non‐deductive conditions, respectively) for a later recognition test. The response prompt contained a fragment which participants had to respond to by determining whether it was part of the presented argument (in simple non‐deductive trials) or the mentally manipulated argument (in complex non‐deductive trials). The rule for manipulating the argument in the complex non‐deductive trials required participants to mentally replace the first term of the first statement with the last term of the third statement, and the last term of the first statement with the last term of the second statement (see Figure 2 for an example). It is this mentally manipulated version of the argument that participants were then to retain for the ensuing recognition test. This complex non‐deductive task was specifically designed in order to elicit abstract, but non‐deductive, rule‐based manipulation of the stimuli and tax participants' cognitive resources (as confirmed by the response time and accuracy analysis reported below).

Figure 2.

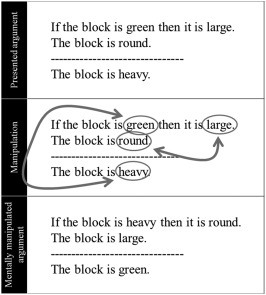
Example mental manipulation trial. Top: presented argument; middle: rules for manipulating the triplet; bottom: argument participants had to retain in memory for the later response prompt

2.3. Stimuli

The stimuli for this experiment consisted of 128 arguments. The 64 arguments employed for the deductive trials were obtained from eight logical forms validated in our previous work (Monti et al., 2007; see also Table 1). The eight logical forms give rise, when instantiated into English (see below), to four pairs of logical arguments of which two are deductively valid and two are deductively invalid. Within each pair, arguments were linguistically matched but of varying deductive difficulty, with one argument appearing consistently more difficult than the other in terms of response time, subjective complexity judgment, and binary forced choice (see Monti et al., 2007). Arguments were instantiated into natural language by replacing the logical connectives (i.e., →, ¬, ˄, ˅) with their standard English translation (i.e., “If … then …”, “not”, “and”, “or”) and by replacing logical variables (i.e., ‘p, q, r‘) with features of an imaginary block (e.g., “large”, “round”, “green”; henceforth concrete instantiation) or meaningless pseudo‐words (e.g., “kig”, “frek”, “teg”; henceforth abstract instantiation) modeled on the items of the Nonsense Word Fluency subtest of the DIBELS assessment (Good, Kaminski, Smith, Laimon, & Dill, 2003). Each logic form was instantiated four times with concrete materials and four times with abstract materials. In each instantiation, the logical variables were replaced with a different object feature or nonsense word so that each specific instantiation was unique. To illustrate, consider the following logic form:

p → ¬q

p

¬q

Table 1.

Logical forms used in stimuli, with sample arguments

Validity	Cognitive load	Formal structure	Block argument examples	Nonsense phoneme argument examples
Valid	Low	p → ¬q p ¬q	If the block is green then it is not small. The block is green. —————————— The block is not small.	If the hak is kig then it is not gop. The hak is kig. —————————— The hak is not gop.
Valid	Low	(p˅q) → ¬r p ¬r	If the block is either heavy or large then it is not blue. The block is heavy. —————————— The block is not blue.	If the hak is either kig or ik then it is not gop. The hak is kig. —————————— The hak is not gop.
Valid	High	(p˅q) → ¬r r ¬p	If the block is either red or square then it is not large. The block is large. —————————— The block is not square.	If the hak is either ag or bub then it is not frek. The hak is ag. —————————— The hak is not frek.
Valid	High	p → ¬q q ¬p	If the block is large then it is not blue. The block is blue. —————————— The block is not large.	If the hak is ag then it is not bub. The hak is bub. —————————— The hak is not ag.
Invalid	Low	(p˄q) → ¬r p ¬r	If the block is both blue and square then it is not large. The block is blue. —————————— The block is not large.	If the tep is both kig and ob then it is not plob. The tep is kig. —————————— The tep is not plob.
Invalid	Low	¬p → (q˅r) ¬p q	If the block is not red then it is either square or small. The block is not red. —————————— The block is square.	If the hak is not trum then it is either stas or plob. The hak is not trum. —————————— The hak is stas.
Invalid	High	(p˄q) → ¬r r ¬p	If the block is both square and small then it is not blue. The block is blue. —————————– The block is not square.	If the tep is both grix and ag then it is not ik. The tep is ik. —————————— The tep is not grix.
Invalid	High	¬p → (q˅r) ¬q p	If the block is not blue then it is either small or light. The block is not small. —————————— The block is blue.	If the tep is not trum then it is either frek or ob. The tep is not frek. —————————— The tep is trum.

By systematically replacing the logic variables (i.e., ‘p, q’) with propositions describing the features of an imaginary block, we can obtain a concrete instantiation of the above logic form:

If the block is green then it is not small.

The block is green.

___________________

The block is not small.

Replacing the features of an imaginary block with nonsense pseudo‐words results in an abstract instantiation of the same logic form:

If the kig is teg then it is not frek.

The kig is teg.

___________________

The kig is not freg.

The remaining 64 stimuli, employed in the non‐deductive trials, were obtained by taking the deductive arguments described above and shuffling the sentences across triplets (without mixing concrete and abstract instantiations) so that, within each argument, no common variable was shared amongst all three statements. The absence of common variables across the three statements ensured that, despite being presented with stimuli superficially analogous to those featured in deductive trials, participants could not engage in any deductive inference‐making. To illustrate:

If the block is large then it is not green.

The block is square.

___________________

The block is not heavy.

Abstract non‐deductive instantiations were obtained analogously to the abstract deductive ones (see Figure 1 for one such example).

2.4. Design and procedure

The 128 trials were distributed across four runs of 32 trials each. Within each run participants performed eight trials per each condition (simple/complex, deductive/non‐deductive). Within each run, trials were presented (pseudo‐)randomly, under the sole constraint that no two consecutive trials were of the same condition. Each run featured a different pseudo‐random ordering of the trials, and participants were randomly allocated to one of two different orderings of the runs.

As depicted in Figure 1, each trial started with a one second verbal cue, presented visually, informing the participant which task they were about to perform. Deductive conditions (i.e., simple and complex) were prompted with the verbal cue “REASONING,” while non‐deductive conditions were prompted with the verbal cue “MEMORY,” for simple trials, and “SWITCH,” for complex trials. Next, the full argument was presented, with all three premises being displayed simultaneously. Given the randomized task order, to help participants keep track of which condition they were supposed to be performing on each trial a small red reminder cue (“R,” “M,” or “S”) was displayed in the lower left corner of the screen, alongside the argument. Each triplet was available, on‐screen, for a maximum of 20 s, or until participants pressed the “continue” button (with their right little finger) to signal that they were ready to move to the response prompt. In the deductive trials participants would press the “continue” button upon reaching a decision as to the logical status of the argument, whereas in the non‐deductive trials they would press the “continue” button upon having sufficiently encoded the presented triplet (easy condition) or the mentally manipulated triplet (complex condition). At this stage, the button‐press was only employed to indicate that the participant was ready to move to the response phase, and was thus the same in all trials regardless of condition. Upon the button press, or the elapsing of the allotted 20 s, a fixation cross appeared, for three seconds, followed by a response prompt. In deductive trials, the response prompt displayed the question “VALID?” to which participants had to respond yes or no. In non‐deductive trials, the response prompt displayed a probe to which participants had to respond yes or no as to whether it was part of the presented argument (in simple non‐deductive trials) or the mentally manipulated argument (in complex non‐deductive trials). In the simple non‐deductive trials the probe was a single word (e.g., “GREEN?”) whereas in the complex non‐deductive trials the probe was a fragment (e.g., “…is not blop. The ik …”). For example, given the argument shown in Figure 2, a correct response screen might read “…is large. The block is green.” which is indeed part of the mentally manipulated argument (Figure 2, bottom), whereas an incorrect response screen might read “…is round. The block is heavy.” which is not part of the mentally manipulated argument. This design allowed us to ensure that participants could not simply recognize that terms in the response prompt were present in the argument, as they could do in the simple non‐deductive trials. (As we will show in the results section, the behavioral data confirm the difficulty of the task.) The response phase lasted up to a maximum of 10 s, and participants were instructed to answer (for all trial types equally) with the index finger to signal a ‘yes’ response and the middle finger to signal a ‘no’ response. Upon their response (or elapsing of the 10 s), a fixation cross signaled the end of the trial and remained on screen for a randomly jittered amount of time (on average 3 s), prior to the beginning on the following trial.

The average time needed to complete each of the four runs was 12.5 min. The full session, inclusive of the four functional runs, as well as structural data acquisition and brief resting periods in between runs, lasted between 75 and 105 min.

2.5. fMRI data acquisition

All imaging data were acquired on a 3 Tesla Siemens Tim Trio MRI system at the Staglin IMHRO Center for Cognitive Neuroscience (CCN) in the Semel Institute for Neuroscience and Human Behavior at the University of California, Los Angeles. First, T2* sensitive images were acquired using a gradient echo sequence (TR = 2,500 ms, TE = 30 ms, FA = 81°, FoV = 220 × 220) in 38 oblique interleaved slices with a distance factor of 20%, resulting in a resolution of 3 × 3 × 3.6 mm. Structural images were acquired using a T1‐sensitive MPRAGE (magnetization‐prepared 180° radio‐frequency pulses with rapid gradient‐echo; TR = 1900 ms, TE = 2.26 ms, FA = 9°) sequence, acquired in 176 axial slices, at a 1‐mm isovoxel resolution.

2.6. fMRI data analysis

Functional data were analyzed using FSL (FMRI Software Library, Oxford University; Smith et al., 2004). The first four volumes of each functional dataset were discarded to allow for the blood oxygenation level dependent (BOLD) signal to stabilize. Next, each individual echo planar imaging time series (EPI) was brain‐extracted, motion‐corrected to the middle time‐point, smoothed with an 8 mm FWHM kernel, and corrected for autocorrelation using pre‐whitening (as implemented in FSL). Data were analyzed using a general linear model inclusive of four main regressors focusing, as done in previous work, on the data acquired during the reasoning periods of each trial (cf., Christoff et al., 2001; Kroger et al., 2008). The four regressors marked the onset and duration of each condition separately (i.e., simple non‐deductive, complex non‐deductive, simple deductive, complex deductive). Specifically, each regressor marked the time from which an argument appeared on screen up to the button press indicating that the participant was ready to proceed to the answer prompt screen (i.e., the “Reasoning” period show in Figure 1 and shaded in gray). In other words, these four regressors captured—for each trial type—the time during which the participants were encoding and reasoning over the stimuli up to when they felt ready to go to the answer prompt screen. It is important to stress that, in order to account for response‐time differences across tasks, we explicitly factor the length of each trial in our regressors, thereby adopting what is known as a “variable epoch” GLM model (Henson, 2007). This approach has been previously shown to be physiologically plausible and to have higher power and reliability for detecting brain activation (Grinband, Wager, Lindquist, Ferrera, & Hirsch, 2008), and is conventionally used in tasks where RTs are likely to vary across trials and/or conditions (see, for example, Christoff et al., 2001; Crittenden & Duncan, 2014; Strand, Forssberg, Klingberg, and Norrelgen, 2008). A conventional double gamma response function was convolved with each of the regressors in order to account for the known lag of the hemodynamic mechanisms upon which the blood oxygenation level dependent (BOLD) signal is predicated (Buxton, Uludag, Dubowitz, & Liu, 2004). Finally, to moderate the effects of motion, the six motion parameter estimates from the rigid body motion correction, as well as their first and second derivative and their difference, were also included in the model as nuisance regressors. For each run, we performed four contrasts. First, we assessed the simple effect of load for deductive (D) and non‐deductive (ND) trials (i.e., [complex > simple]_ND and [complex > simple]_D), and, following, we assessed the interaction effect of load and task type (i.e., [complex – simple]_ND > [complex – simple]_D and [complex – simple]_D > [complex – simple]_ND). In order to avoid reverse activations (Morcom & Fletcher, 2007), each contrast was masked to only include voxels for which the sum of the z‐score statistic of the minuend and subtrahend was equal to or greater than zero (cf., DeWolf, Chiang, Bassok, Holyoak, and Monti, 2016). For the simple effect of load in deduction, for example, the mask was created by only including voxels for which $[z_{{\left(Complex-Fix\right)}_D}+\hspace{0.17em}{z}_{{\left(Simple-Fix\right)}_D}\hspace{0.17em}\ge 0]$ while, for the interaction effect the mask was created by only including voxels for which $[z_{{(Complex-Simple)}_D}+\hspace{0.17em}{z}_{{(Complex-Simple)}_{ND}}\hspace{0.17em}\ge 0$]. This procedure ensures that a voxel cannot be found active merely because the subtrahend is negative (i.e., less active than baseline/fixation) while the minuend is not greater than zero (i.e., not more active than baseline/fixation; see DeWolf et al., 2016).

Prior to group analysis, single subject contrast parameter statistical images were coregistered to the Montreal Neurological Institute (MNI) template with a two‐step process using 7° and 12° of freedom. Group mean statistics were generated with a mixed effects model accounting for both the within‐session variance (fixed‐effects) as well as the between‐session variance (random‐effects) with automatic outlier de‐weighting. Group statistical parameteric maps were thresholded using a conventional cluster correction, based on random field theory, determined by Z > 2.7 and a (corrected) cluster significance of p < .05 (Brett, Penny, & Kiebel, 2003; Worsley, 2004, 2007). Considering the recent debate on the validity of using cluster‐based correction methods in fMRI analyses, it is important to point out that, given the existing published data on the topic (e.g., Woo, Krishnan, & Wager, 2014; Eklund, Nichols, & Knuttson, 2016), our specific approach is not expected to suffer from greater than nominal (.05) familywise error rate (FWE). Specifically, (i) we are using a conservative cluster determining threshold (CDT; Z > 2.7, i.e., ∼p < .003) which falls below the envelope of liberal primary thresholds which might result in an “anti‐conservative bias” (i.e., 0.01 < CDT < 0.005; see Woo et al., 2014, p. 417) and, consistent with the previous point, (ii) the data presented in Eklund et al. (2016) suggest that the use of cluster correction with a CDT of p < .003, with FSL's FLAME1 algorithm (Beckman, Jenkinson, & Smith, 2003; Woolrich, Behrens, Beckmann, Jenkinson, & Smith, 2004) and with an event related design, should yield a valid analysis (i.e., within the nominal 5% error rate; cf., Eklund et al. 2016, Figure 1, p. 7901).

3. RESULTS

3.1. Behavioral results

Across all participants and conditions, the mean accuracy was 90.2% (SD = 4.94%), and the mean response time was 10.48 s (SD = 3.1 s). Two separate 2 × 2 repeated‐measures ANOVA were conducted to test the effects of load (simple vs. complex) and task (deductive vs. non‐deductive) on accuracy and response time (respectively).

With regard to accuracy (see Supporting Information Figure S1a), we found a significant interaction between load and task type (F(1, 19) = 9.03, p = .007, ${\widehat{\mathrm{\omega }}}_p^2$  = .05) mainly driven by a larger load effect for non‐deductive trials (M = 98%, SD = 2.7%, and M = 78.8%, SD = 8.7%, for simple and complex trials, respectively) as compared to that observed for deductive trials (M = 96.25%, SD = 7.56% and M = 87.81%, SD = 10.96%, respectively). Effect sizes reported here, based on the unbiased ${\widehat{\mathrm{\omega }}}_p^2$, as opposed to the conventional ${\widehat{\mathrm{\eta }}}_p^2$, were calculated using the formulae provided by Maxwell & Delaney, 2004). We also found a significant main effect of both load and task type (F(1, 19) = 66.95, p < .001, ${\widehat{\mathrm{\omega }}}_p^2$  = .39, and F(1, 19) = 6.547, p = .02, ${\widehat{\mathrm{\omega }}}_p^2$  = .02, respectively). Specifically, participants exhibited lower mean accuracy in complex trials (M = 83.3%), as compared to simple ones (M = 97.1%), and in non‐deductive trials (M = 88.4%), as compared to deductive ones (M = 92.0%).

With regard to response time (see Supporting Information Figure S1b), we again found a significant interaction between the load and task type (F(1, 19) = 5.97, p = .02, ${\widehat{\mathrm{\omega }}}_p^2$ = .01), which was mainly driven by a larger difference in response times across simple and complex trials for non‐deductive materials (M = 8.85 s, SD = 4.41 s, and M = 15.12 s, SD = 3.83 s, respectively) as compared to deductive ones (M = 6.79 s, SD = 2.11 s, and M = 11.18 s, SD = 3.45 s, respectively). We also found a significant main effect for both load and task type with regard to response time (F(1, 19) = 170.30, p < .001, ${\widehat{\mathrm{\omega }}}_p^2$ = .32; and F(1, 19) = 30.76, p < .001, ${\widehat{\mathrm{\omega }}}_p^2$  = .1, respectively). Specifically, participants exhibited longer response times in complex trials (M = 13.15 s), as compared to simples trials (M = 7.82 s), and in non‐deductive trials (M = 11.98 s), as compared to reasoning trials (M = 8.99 s). The response time analysis included both correct and incorrect trials (as done in previous work; e.g., Prado et al., 2013; Reverberi et al., 2010, 2007).

3.2. Neuroimaging results

Subtraction of simple non‐deductive trials from complex ones uncovered a number of significant activations across posterior parietal and frontal regions. As depicted in Figure 3a (in blue; see Table 2 for a full list of activation maxima), significant activations were uncovered in bilateral middle frontal gyri (MFG; spanning BA8 and BA6), precuneus (Prec; BA7), left lateralized superior and inferior parietal lobuli (SPL and IPL; in BA7 and BA40, respectively), and angular gyrus (AG; BA39). The subtraction of simple deductive trials from complex ones resulted in a very different pattern of activations (see Figure 3a, green areas, and Table 3 for full list of activation maxima). Consistent with previous work (Monti et al., 2007, 2009), maxima were uncovered in regions previously reported as being “core” to deductive reasoning, such as the left middle frontal gyrus (in BA10), and the bilateral medial frontal gyrus (MeFG; in BA8; also referred to as the pre‐supplementary motor area, pre‐SMA), as well as “support” regions of deductive inference, including bilateral MFG (spanning BA8 and BA6 in the right hemisphere, and BA9 and BA10/47 in the left), superior and inferior parietal lobuli (BA7 and BA40, respectively), left superior frontal gyrus (SFG; in BA8), and right lateralized cerebellum (in crus I). The overlap between the two load subtractions was minimal (see Figure 3a, in purple), and mostly confined to “bleed‐over” at the junction of the more dorsal MFG cluster uncovered in the non‐deductive comparison, and the more ventral MFG cluster observed in the deductive comparison.

Figure 3.

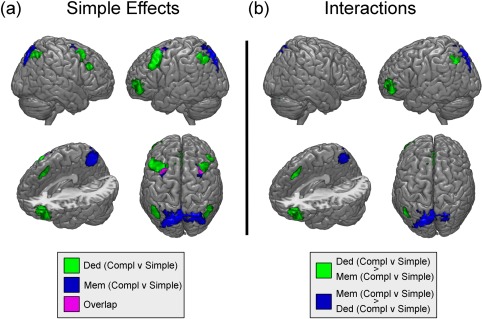
Imaging results: (a) Activations for the complexity subtraction for memory (in blue) and logic (in green) materials (overlap shown in purple); (b) Activations for the interaction of complexity by materials [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 2.

Activations for memory complexity subtraction (i.e., complex memory minus simple memory)

MNI coordinates
x	y	z	Hem	Region label (BA)	Z‐score
Frontal lobe
−24	12	46	L	Middle Frontal Gyrus (8)	5.35
−26	2	54	L	Middle Frontal Gyrus (6)	5.24
24	12	44	R	Middle Frontal Gyrus (8)	4.89
30	2	68	R	Middle Frontal Gyrus (6)	2.93
Parietal lobe
−6	−62	54	L	Precuneus (7)	7.52
−6	−64	50	L	Precuneus (7)	6.92
10	−66	52	R	Precuneus (7)	6.81
−10	−68	58	L	Superior Parietal Lobule (7)	6.69
−36	−80	30	L	Angular Gyrus (39)	6.55
−36	−50	42	L	Inferior Parietal Lobule (40)	5.79

Table 3.

Activations for reasoning complexity subtraction (i.e., complex minus simple reasoning)

MNI coordinates
x	y	z	Hem	Region label (BA)	Z‐score
Frontal Lobe
−42	22	36	L	Middle Frontal Gyrus (9)	5.39
−48	46	−2	L	Middle Frontal Gyrus (10/47)	4.75
−52	24	36	L	Middle Frontal Gyrus (9)	4.66
−34	16	54	L	Superior Frontal Gyrus (8)	4.38
−38	14	54	L	Superior Frontal Gyrus (8)	4.29
−8	24	50	L	Medial Frontal Gyrus (8)	4.19
38	14	50	R	Middle Frontal Gyrus (8)	4.13
−6	28	46	L	Medial Frontal Gyrus (8)	4.13
−36	54	−2	L	Middle Frontal Gyrus (10)	4.05
36	20	52	R	Middle Frontal Gyrus (8)	3.87
−6	38	38	L	Medial Frontal Gyrus (8)	3.63
−6	38	42	L	Medial Frontal Gyrus (6)	3.62
42	22	52	R	Middle Frontal Gyrus (8)	3.42
40	20	38	R	Precentral Gyrus (9)	3.33
34	18	62	R	Middle Frontal Gyrus (6)	3.32
12	26	42	R	Medial Frontal Gyrus (6)	3.22
Parietal lobe
−46	−54	40	L	Inferior Parietal Lobule (40)	4.03
44	−60	40	R	Inferior Parietal Lobule (40)	3.83
−44	−58	42	L	Inferior Parietal Lobule (40)	3.69
−44	−58	46	L	Inferior Parietal Lobule (40)	3.67
−44	−62	52	L	Superior Parietal Lobule (7)	3.63
−42	−64	44	L	Inferior Parietal Lobule (40)	3.60
50	−60	50	R	Inferior Parietal Lobule (40)	3.55
44	−60	58	R	Superior Parietal Lobule (7)	3.49
42	−68	46	R	Superior Parietal Lobule (7)	3.39
50	−60	46	R	Inferior Parietal Lobule (40)	3.39
Cerebellum
36	−74	−28	R	Crus I	3.95
32	−70	−32	R	Crus I	3.69
32	−76	−28	R	Crus I	3.65
38	−68	−40	R	Crus I	3.56

As shown in Figure 3b (see Tables 4 and 5 for full list of activation maxima), the interaction analysis revealed that non‐deductive load, as compared to deductive load, specifically recruited foci in bilateral SPL, as well as left lateralized Prec (BA7), AG at the junction with the superior occipital gyrus (BA19/39), and MFG (BA6). Conversely, deductive load, as compared to non‐deductive load, uncovered significant activations within bilateral MeFG (BA8 bilaterally, and BA9 in the left hemisphere), left junction of the SFG and MFG (BA10), left MFG (in BA10, BA10/47, and BA47), left SFG (BA6), left SPL and IPL (BA7, BA40, respectively), and right cerebellum (crus I).

Table 4.

Activations for the first interaction contrast, showing where the difference between complex memory and simple memory was greater than the difference between complex reasoning and simple reasoning

MNI coordinates
x	y	z	Hem	Region label (BA)	Z‐score
Frontal lobe
−24	0	52	L	Middle Frontal Gyrus (6)	4.01
−22	2	48	L	Middle Frontal Gyrus (6)	3.79
Parietal lobe
−36	−82	28	L	Angular Gurys/Superior Occipital Gyrus (19/39)	6.06
−10	−68	56	L	Superior Parietal Lobule (7)	5.82
−6	−62	54	L	Precuneus (7)	5.69
−18	−66	56	L	Superior Parietal Lobule (7)	5.29
−18	−70	52	L	Precuneus (7)	5.08
12	−66	54	R	Superior Parietal Lobule (7)	5.05

Table 5.

Activations for the second interaction contrast, showing where the difference between complex reasoning and simple reasoning was greater than the difference between complex memory and simple memory

MNI coordinates
x	y	z	Hem	Region label (BA)	Z‐score
Frontal lobe
−6	40	38	L	Medial Frontal Gyrus (9)	4.77
2	32	46	R	Medial Frontal Gyrus (8)	4.45
−4	38	48	L	Medial Frontal Gyrus (8)	4.41
−48	46	−2	L	Middle Frontal Gyrus (10/47)	4.38
−36	60	−2	L	Middle/Superior Frontal Gyrus (10)	4.31
−48	48	−8	L	Middle Frontal Gyrus (10/47)	4.22
−44	52	6	L	Middle Frontal Gyrus (10)	3.68
−40	36	−6	L	Middle Frontal Gyrus (47)	3.26
−12	22	62	L	Superior Frontal Gyrus (6)	3.09
Parietal lobe
−52	−60	40	L	Inferior Parietal Lobule (40)	4.99
−54	−54	54	L	Inferior Parietal Lobule (40)	3.57
−48	−62	52	L	Inferior Parietal Lobule (40)	3.25
−42	−68	52	L	Superior Parietal Lobule (7)	2.83
Cerebellum
32	−72	−34	R	Crus I	5.01
40	−76	−34	R	Crus I	4.67

4. DISCUSSION

The present study reports two main findings. First, we have shown that deductive reasoning is supported by a distributed set of frontoparietal regions closely matching our previous reports (Monti et al., 2007, 2009). Second, we have shown that the putative “core” regions for deductive inference cannot be interpreted as merely responding to general (i.e., non‐deductive) cognitive load and/or increased working memory demands (Kroger et al., 2008; Prado et al., 2013). We discuss each point in turn.

Consistent with previous reports, our results favor the idea that deductive reasoning is supported by a distributed network of regions encompassing frontal and parietal areas (Monti et al., 2007, 2009; Rodriguez‐Moreno & Hirsch, 2009; Prado et al., 2015). In light of recent discussions concerning the replicability of psychological and neuroimaging findings (Barch & Yarkoni, 2013; Pashler & Wagenmakers, 2012) it is particularly noteworthy that coordinates of the activation foci reported here match closely those reported in three previous experiments by our group (Monti et al., 2007, 2009; see Supporting Information Figure S12 for a visual comparison) despite different samples, stimuli, MR systems, and analysis methods. In particular, we find that complex deductive inferences, as compared to simpler ones, consistently recruit regions previously described as “core” to deductive reasoning (including left rostrolateral (in BA10) and medial (BA8) prefrontal cortices) which are proposed to be implicated in the construction of a derivational path between premises and conclusions. In addition, complex deductive inferences also recruited a number of (content‐independent) “cognitive support” regions across frontal and parietal areas which were previously described as subserving non‐deduction specific processes (cf., Monti et al., 2007, 2009). The dissociation between “core” and “support” regions is also supported by a neuropsychological study (Reverberi et al., 2009) in which patients with lesions extending to medial frontal cortex (encompassing “core” BA8) demonstrated specific deficits in deductive and meta‐deductive ability, while patients with lesions to left dorsolateral frontal cortex (encompassing “support” regions) only displayed deductive deficits in the presence of working memory impairments (while retaining meta‐deductive abilities; i.e., the ability to judge the complexity of an inference). This pattern of impairment can be seen as important independent and cross‐methodological support for the view that medial frontal cortex plays a central role in representing the overall structure of sufficiently complex deductive arguments, while left dorsolateral frontal cortex (likely in conjunction with parietal regions) only serves a supporting role, perhaps as a kind of “memory space” for the representation of deductive arguments (Monti et al., 2007; Reverberi et al., 2009).

Our second finding relates to the alternative interpretation of the previously described “core” regions of deductive reasoning (left rostrolateral frontopolar cortex in particular; i.e., BA10) as reflecting a more general, non‐deductive, increase in “cognitive difficulty” and/or working memory demands (Kroger et al., 2008; Prado et al. 2013). The results of the present study, however, do not support this view. Indeed, in contrast to the results for deductive trials, when performed over the non‐deductive trials, the load contrast failed to elicit any significant activity in the proposed “core” regions of deduction (left BA10 and medial BA8). Rather, it highlighted a different set of regions, including middle frontal gyrus (BA8, 6), precuneus (BA7), superior and inferior parietal lobule (BA7, 40), and angular gyrus (BA39), consistent with previous literature on working memory (Kirschen, Chen, Schraedley‐Desmond, & Desmond, 2005; Koechlin, Basso, Pietrini, Panzer, & Grafman, 1999; Owen, McMillan, Laird, & Bullmore, 2005; Ranganath, Johnson, & D'esposito, 2003; Ricciardi et al., 2006). This result further supports the view that the cognitive processes implemented within areas identified as core to deductive reasoning cannot be reduced to merely reflecting increased working memory demands, and might rather be integral to “identify[ing] and represent[ing] the overall structure of the proof necessary to solve a deductive problem” (Reverberi et al., 2009; p. 1113). Indeed, anterior prefrontal cortex has been previously associated with processes such as relational complexity (Halford et al., 1998, 2010; Robin & Holyoak, 1995; Waltz et al., 1999), and BA10 in particular has been found to activate in response to tasks requiring relational integration, keeping track of and integrating multiple related variables and sub‐operations, and the handling of branching subtasks (Charron & Koechlin, 2010; Christoff et al., 2001; De Pisapia & Braver, 2008; Koechlin et al. 1999b; Kroger et al., 2002; Ramnani & Owen, 2004), all of which are analogous to the kinds of processes that may be involved in evaluating deductive inferences. Similarly, previous research has associated medial BA8 with processes such as executive control, the choosing and coordinating of sub‐goals, and resolving competition between rules to transform a problem from one state into another (Fletcher & Henson, 2001; Koechlin, Corrado, Pietrini, & Grafman, 2000; Posner & Dehaene, 1994; Volz, Schubotz, & Cramon, 2005). Of course, it should be noted that the current study, as well as our previous work, focuses on the propositional inferences (as defined in Garnham & Oakhill, 1994, p.60). Yet, previous work suggests that these results might well extend to propositional inferences in natural discourse (which, however might also depend on additional contributions from the right frontopolar cortex; Prado et al., 2015) and categorical syllogisms (Prado et al., 2013; Rodriguez‐Moreno & Hirsch, 2009), further generalizing the idea that processes of relational integration might well explain the role of left rostrolateral PFC in deductive inference making (Prado et al., 2013).

Finally, our results further add to a growing body of evidence failing to detect any involvement of Broca's area in deductive inference‐making across propositional, set‐inclusion and relational problems (e.g., Canessa et al., 2005; Fangmeier et al., 2006; Knauff et al., 2002; Monti et al., 2007, 2009; Parsons & Osherson, 2001; Prado & Noveck, 2007; Rodriguez‐Moreno & Hirsch, 2009; Prado et al., 2015), and is consistent with neuropsychological work demonstrating that damage spanning at least one of the “core” regions (medial BA8) impairs deductive inference‐making, as well as appreciation for the difficulty of an inference, despite the absence of any damage in the left IFG and ceiling performance in clinical tests of language (Reverberi et al., 2009).

In interpreting these findings, a number of important issues should be considered. First, although our behavioral results replicate the classic differential performance across modus ponens and modus tollens type inferences, accuracy in the modus tollens type inferences was higher than typically reported in classic studies (i.e., 87% in our work vs. 63% in Taplin, 1971; 62% in Wildman & Fletcher, 1977). Nonetheless, our accuracy rates are in line with a number of behavioral and neuroimaging reports (e.g., 94% in Prado et al. 2010, 84% in Luo, Yang, Du, & Zhang, 2011; between 80% and 88% in Bloomfield & Rips 2003; 79% in Knauff et al., 2002; 78% in Trippas, Thompson, & Handley, 2017; 75% in Evans, 1977; and above 90% in the Wason Selection Task as implemented in Li, Zhang, Luo, Qiu, & Liu, 2014, Qiu et al., 2007, Liu et al., 2012)1 as well as developmental work showing that by age 16 accuracy rates for modus tollens range between 78% and 87% (Daniel et al., 2006). We do stress, however, that although our participants did not undergo any overt training (e.g., training to criterion; see for example Reverberi et al., 2007) and reported no formal training in logic, our procedure selected high‐performance individuals in the sense that they had to meet a 60% accuracy criterion across each of the four conditions (complex/simple, deductive/non‐deductive). Thus, our approach also favored participants with good performance in working memory (as captured by the SWITCH task), which is known to be an important variable in deductive reasoning (e.g., Toms, Morris, & Ward, 1993; Handley, Capon, Copp, & Harper, 2002; Capon, Handley, & Dennis, 2003; Markovitz et al., 2002). In addition, it is also possible that self‐selection operated, to some extent, among participants volunteering to take part in a study on “higher cognition.” Second, as shown by our behavioral results, deductive and non‐deductive tasks were not fully matched for difficulty (as captured by response time and accuracy). Indeed, we did find a significant difference between memory and logic difficulty (i.e., a significant interaction), with complex non‐deductive trials being harder to evaluate than complex deductive trials, and with the difference between simple and complex non‐deductive trials being larger than that for simple and complex deductive trials. This imbalance should make it all the more likely that, if the general cognitive load hypothesis were correct (i.e., that BA10 and BA8m are recruited by non‐deductive cognitive load), the simple effect of load for non‐deductive trials (i.e., [complex > simple]_ND) as well as the interaction effect of load and task type (i.e., [complex – simple]_ND > [complex – simple]_D) should uncover activity within the “core” areas. Yet, as we reported, this was not the case. Rather, it was the simple effect of load for deductive trials (as well as the interaction effect of load and task type (i.e., [complex – simple]_D > [complex – simple]_ND) that uncovered activity within left rostrolateral and mediofrontal cortex. In this sense, the lack of exact matching of difficulty across types of tasks works against our hypothesis and thus makes our test all the more stringent. Finally, our design contained a small asymmetry across deductive and non‐deductive taks. Simple and complex deductive trials were signaled with the same cue (i.e., REASONING) whereas simple and complex non‐deductive trials were signaled with different cues (i.e., MEMORY and SWITCH, respectively). Nonetheless, the close matching of the neuroimaging results presented above and previous work (cf., Wager & Smith, 2003; Monti et al., 2007, 2009) suggests that this might not have significantly affected our results.

In conclusion, this experiment shows that deductive inference making is based on a distributed network of regions including frontal and frontomedial “core” areas, the activation of which cannot be reduced to working memory demands or cognitive difficulty. Rather, these regions appear to be involved in processes that are at the heart of deductive inference (e.g., finding the derivational path uniting premises and conclusion; (cf., Monti & Osherson, 2012; Reverberi et al., 2009). Furthermore, our findings are also consistent with the idea that “[l]ogical reasoning goes beyond linguistic processing to the manipulation of non‐linguistic representations” (Kroger et al., 2008, p. 99).

CONFLICTS OF INTEREST

The authors have no conflicts to declare.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supporting Information

Supporting Information

Supporting Information

Coetzee JP, Monti MM. At the core of reasoning: Dissociating deductive and non‐deductive load. Hum Brain Mapp. 2018;39:1850–1861. 10.1002/hbm.23979