Noninvasive extraction of microsecond‐scale dynamics from human motor cortex

Abstract

State‐of‐the‐art noninvasive electromagnetic recording techniques allow observing neuronal dynamics down to the millisecond scale. Direct measurement of faster events has been limited to in vitro or invasive recordings. To overcome this limitation, we introduce a new paradigm for transcranial magnetic stimulation. We adjusted the stimulation waveform on the microsecond scale, by varying the duration between the positive and negative phase of the induced electric field, and studied corresponding changes in the elicited motor responses. The magnitude of the electric field needed for given motor‐evoked potential amplitude decreased exponentially as a function of this duration with a time constant of 17 µs. Our indirect noninvasive measurement paradigm allows studying neuronal kinetics on the microsecond scale in vivo.

1. INTRODUCTION

Events in the brain occur on a wide range of time scales, from those of molecular mechanisms to behavior, learning, and maturation. The events in the fast end of the spectrum are too brief to be measured with noninvasive electromagnetic recordings, such as electroencephalography or magnetoencephalography, which are limited to time scales of 1 ms at best (Fedele et al., 2015). Faster phenomena have been studied, for example, by invasive single‐cell recordings, such as the patch‐clamp method (Bean, 2007).

Ion‐channel kinetics has been mainly studied at reduced temperatures in vitro (Baranauskas and Martina, 2006). The ion‐channel kinetics depends on the temperature: At 10°C, the time constant for the activation of the voltage‐gated sodium channels is of the order of 1 ms; at room temperature, it is about 200 µs (Martina and Jonas, 1997; Baranauskas and Martina, 2006). At body temperature, the action potential waveform and its conduction velocity suggest an activation time constant lower than 60 µs for myelinated human nerves (Wesselink et al., 1999), which makes the activation too brief to be measured directly even in vitro. There are, however, indirect methods—e.g., observing which specific stimulus waveforms cause a cell to fire—that can inform us about the activation dynamics on time scales faster than those of the recorded signals. Such an indirect approach was utilized to measure, for example, the membrane time constant of the frog sciatic nerve before modern high‐speed amplifiers existed (Lapicque, 1907). A suitable indirect protocol can improve the temporal sensitivity of both noninvasive and invasive recordings.

Although fast, voltage‐gated‐sodium‐channel activation is not instantaneous. Individual channels have a random nonzero latency to open after membrane depolarization (Aldrich et al., 1983). This latency results in the so‐called vulnerable period, during which an action potential due to electrical stimulation can be suppressed by an opposing phase of the stimulation (van den Honert and Mortimer, 1979). The strength–duration relationship of the vulnerable period has been studied with invasive electrical stimulation of, for example, sciatic and auditory nerves; by adjusting the interphase gap between the two parts of a biphasic stimulus, the vulnerable period has been shown to last ∼100 µs (van den Honert and Mortimer, 1979; Shepherd and Javel, 1999). McKay and Henshall (2003) measured how the duration of the interphase gap in cochlear implant stimulation of humans affects perception, reporting that the current required to maintain the same loudness decreased exponentially with the gap duration with a time constant of about 20 µs. However, as Carlyon et al. (2005) pointed out, this estimate had high uncertainty and could also be explained by the different auditory thresholds to different stimulation frequencies. Hiwaki and Ueno (1991, 1993) observed a similar reduction with magnetic nerve stimulation. They gave trapezoidal magnetic pulses with 100‐µs rise and fall times to a single subject and observed that increases in the interphase gap (in the range of 0–100 µs) reduced the excitation threshold of the brachial plexus. In addition to their measurements, Hiwaki and Ueno (1991, 1993) performed a computer simulation of a myelinated nerve at constant stimulation intensity but with two different interphase gaps; at a suitable intensity, only the longer gap resulted in an action potential. As an earlier generalization of this, in his simulations, Reilly (1989) had observed a qualitatively similar reduction in the excitation threshold as a function of the interphase gap in an electrically stimulated myelinated nerve. Similarly to biphasic electrical stimulation, Havel et al. (1997) observed for trapezoidal magnetic stimulation that nerve excitation thresholds remained essentially unchanged with longer interphase gaps ranging from 100 to 30,000 µs (they tested rise and fall times between 120 and 2,500 µs). The main limitation of these studies lies in their qualitative comparison between measurements and simulations. In addition, these studies were limited to the peripheral nervous system. Here, we demonstrate that similar kinetics can be studied with transcranial magnetic stimulation (TMS) directly from the human cortex in vivo.

TMS is a noninvasive brain‐stimulation method with both clinical and research applications. It allows, for example, in vivo measurement of the stimulus strength–duration time constant from the primary motor cortex (M1) (Barker et al., 1991). In TMS, a brief (<1 ms) magnetic pulse induces an electric field in the brain. The induced electric field—typically of the order of 100 V/m—drives electric current, which accumulates charge at the cell membranes, causing local de‐ or hyperpolarization (Figure 1a–c). A sufficiently strong TMS pulse to M1 produces in the corresponding muscle a motor evoked potential (MEP), which can be measured with electromyography (EMG). The strength–duration time constant of the motor cortex cell assembly, of the order of 200 µs, can be found by varying the TMS pulse duration in a TMS–EMG experiment and determining the pulse strength needed to obtain a given MEP amplitude (Barker et al., 1991; Peterchev et al., 2013; D'Ostilio et al., 2016). Because this time constant is relatively long, the membrane potential remains nearly constant on the microsecond scale in the absence of external stimulation (Figure 1c). Here, we use this property to study microsecond‐scale dynamics in the human motor cortex to learn about the kinetics of voltage‐gated sodium channels.

Figure 1.

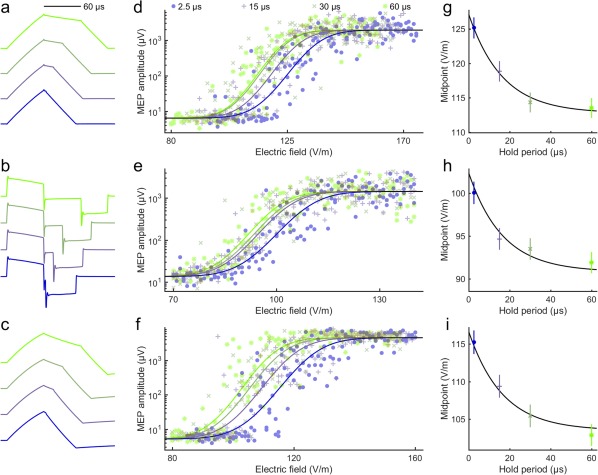
Data of the three participants. Waveforms of (a) the TMS coil current, (b) induced electric field, and (c) depolarization of a passive membrane (with a 200‐µs membrane time constant) for four hold periods. (d–f) MEP amplitudes and fitted sigmoidal functions as a function of the induced electric field for the three subjects. (g–i) Exponential fits to the midpoints of the input–output curves as a function of the hold period. The obtained activation time constant of the exponential function is 16.5 µs (95% confidence interval: 14.2–19.2 µs) and reduction in the midpoint between no hold period and a long hold period is 11.3% (95% confidence interval: 10.7%–11.9%). The error bars indicate 95% confidence intervals of the midpoints. The colors link the data of the different panels

We applied single TMS pulses to M1 of volunteer subjects to measure noninvasively the strength–duration relationship for the stimulation needed to overcome the vulnerable period. We argue that this relationship might inform us about the rate of voltage‐gated ion‐channel activation near the action potential firing threshold.

2. MATERIALS AND METHODS

Three healthy right‐handed males (28, 31, and 24 years old) with no contraindications for TMS participated in the study after giving their written informed consent. The study was approved by the Coordinating Ethics Committee of the Hospital District of Helsinki and Uusimaa and was carried out in accordance with the Declaration of Helsinki.

2.1. Data acquisition

We measured TMS‐elicited peak‐to‐peak MEP amplitudes with surface EMG from the relaxed abductor pollicis brevis (APB) muscle of the dominant hand of three healthy participants. During the experiment, the participant sat in a chair and was instructed to keep his right hand relaxed. EMG was recorded from the right APB muscle with surface electrodes in a belly–tendon montage connected to an EMG device (Nexstim eXimia, http://www.nexstim.com), which has a 500‐Hz low‐pass filter (sampling frequency 3,000 Hz).

Single‐pulse TMS was administered with our custom‐made device (Koponen et al., 2017), which allows flexible control of the pulse waveforms. The applied monophasic waveforms were designed to mimic biphasic electrical stimuli with an adjustable interphase gap. Thus, they contained three distinct parts (see Figure 1a–b): a 60‐µs period with rising coil current, a middle part with near‐constant current, and a final section that brought the current back to zero. We refer to the middle part as the hold period, as during this period the membrane potential remains nearly constant (Figure 1c). The hold period ranged from 2.5 to 60 µs. The waveforms of the coil current and the induced electric field were measured with a Rogowski current probe (PEM CWT 60B, http://www.pemuk.com) and a search coil connected to an oscilloscope, respectively.

TMS was delivered with our energy‐optimized figure‐of‐eight coil (Koponen et al., 2017). To ensure reproducible stimulation, the coil position and orientation with respect to the subject's head was tracked with the Nexstim eXimia neuronavigation system and individual magnetic resonance images. The electric‐field values reported in this article refer to those measured with our TMS characterizer in a spherically symmetric conductor model (Nieminen et al., 2015; Koponen et al., 2017). With the shortest (2.5 µs) hold period, we determined the APB hotspot, that is, the location in the left M1 that for a given TMS intensity (defined as the maximum amplitude of the induced electric field) produced the largest MEPs. All subsequent pulses were delivered to this target.

We measured the resting motor threshold (RMT) for pulses with 2.5‐ and 60‐µs hold periods. RMT was defined as the lowest intensity that produced MEPs ≥50 µV in at least 10 out of 20 consecutive trials (Rothwell et al., 1999). The interstimulus interval (ISI) during the RMT measurement was randomized between 2 and 3 s. Next, to evaluate the difference in the MEP amplitudes due to these two pulse types, we applied a sequence containing 21 pulses of both types in randomized order. The intensity of the pulses was now the mean of the measured RMTs; ISI was randomized between 4 and 6 s. The sequence started by administering one 2.5‐µs and one 60‐µs pulse in random order; data from these two pulses were not used in the analysis. Finally, we measured the input–output curves for four pulse types (hold periods of 2.5, 15, 30, and 60 µs). We generated a randomized‐order pulse set containing these pulse types. The intensity values for each pulse type covered uniformly the range from intensities producing no responses to those that resulted in maximal MEP amplitudes. We split the pulse sequence into nine pulse trains separated by short breaks of a few minutes. Each subsequence contained 65–74 pulses; ISI was randomized between 4 and 6 s. The first pulse in each subsequence was a 2.5‐µs‐hold‐period pulse at 100% RMT, and it was discarded from the analysis. The order of the pulses in all sequences was randomized, as the variability in the TMS‐evoked MEPs shows a hysteresis‐like phenomenon: a large MEP due to a stronger stimulation intensity is more likely to be followed by a large MEP even at lower intensity (Möller et al., 2009). Thus, there is a systematic interpulse correlation, which is likely due to a systematic change in the initial states of the targeted neurons. With randomization, any systematic changes are reduced to an increase in the random variability of the initial state of the targeted neurons, which will manifest itself as a slight increase in the variability of MEP amplitudes.

2.2. Data analysis

We rejected trials containing muscle preactivation or noise exceeding ±10 µV in the 100‐ms time window preceding the stimulation and determined the peak‐to‐peak MEP amplitudes in the accepted trials.

The difference in the RMT for pulses with the 2.5‐ and 60‐µs hold periods for each participant was assessed by assuming that the probability of evoking an MEP ≥50 µV increases monotonically with TMS intensity: we counted the number of MEPs exceeding this threshold for both pulse types and applied one‐tailed Fisher's exact test (Fisher, 1956) to assess the hypothesis that the pulse with the longer hold period had a lower RMT.

The measured input–output curves were used to determine the activation time constant τ that characterizes the dependence of the MEPs on the hold period. First, similar to Peterchev et al. (2013), we fitted a hierarchical Gaussian sigmoid model to the data on logarithmic scale in the least‐squares sense:

$$y\left(E\right)=n_i+a_i·\mathrm{e}\mathrm{r}\mathrm{f}\left(\left(E-m_{i,j}\right)/m_{i,j}/b_i\right),$$

where $y$ is the logarithm of the MEP amplitude, $E$ is the magnitude of the induced electric field, $n_i$, $a_i$, and $b_i$ are subject‐specific constants, and $m_{i,j}$ is a subject‐ and waveform‐specific constant ( $i=\left\{\mathrm{1,2},3\right\}$, $j=\left\{\mathrm{1,2},\mathrm{3,4}\right\}$). The model assumed a common noise floor ( $n_i$), slope ( $b_i$), and MEP saturation level ( ${n_i+a}_i$) for the pulse types; only the midpoint of the sigmoid curves ( $m_{i,j}$) was assumed specific for a given pulse type. The fit and the 95% confidence intervals for the midpoints were calculated using nlinfit and nparci functions (Matlab R2015b, http://www.mathworks.com), respectively. The activation time constant was obtained by fitting an exponential model to the hold period and the sigmoid midpoints in the least‐squares sense:

$$m_{i,j}=d_i\cdot \left(1+c·\mathrm{e}\mathrm{x}\mathrm{p}\left(-T_j/\mathrm{\tau }\right)\right),$$

where $T_j$ is the hold period and $c$ is a model‐specific and $d_i$ is the subject‐specific constant. For $N$ subjects, this model has $2+N$ degrees of freedom to explain $4\cdot N$ data points. Thus, for any number of subjects, the model has to explain more data points than there are variables. To estimate the 95% confidence interval for the activation time constant, we sampled 1,000 sigmoid midpoints for each subject and waveform using the estimated covariance matrix (given by nlinfit) of the hierarchical Gaussian sigmoid model fit and determined the activation time constant by fitting the exponential model to these (each sampled exponential model was fitted in the linear scale as a nonlinear model with nlinfit). The exponential model is sensitive only to the differences in the durations of the hold periods. Thus, it is insensitive to the onset of the time intervals; the same activation time constant would be observed even if $T_j$ would contain, for example, the combined duration of the first phase of the pulse and the hold period. A further advantage of the selected exponential model is that it contains an implicit linear model: should the data result from an approximately linear reduction in threshold with increasing hold period, the upper limit of the confidence interval for the activation time constant would tend to infinity.

2.3. Neuron model

To test whether the measured effects could be explained by the voltage‐gated channel kinetics, we built a model of a single long straight myelinated axon based on the fine‐tuned nerve fiber model by Wesselink et al. (1999) and implemented with Matlab its TMS adaption described by Salvador (2009). This model depicts a simple, peripheral neuron with Hodgkin–Huxley‐type kinetics. In this model, the sodium current is proportional to $m^{3}h$, where $m$ is the activation and $h$ is the inactivation variable of voltage‐gated sodium channels; the potassium current is proportional to $n^4$, where $n$ is the activation variable of the fast potassium current. Such kinetics and geometry have been used to model pyramidal axons (De Geeter et al., 2016; Manola et al., 2007) in which a putative activation site lies. The activation and inactivation variables follow a Hodgkin–Huxley‐like first‐order rate equation with two voltage‐dependent parameters each ( $\mathrm{\alpha }$ and $\mathrm{\beta }$ in Wesselink et al., 1999). The time constant for this equation is ${\left(\mathrm{\alpha }+\mathrm{\beta }\right)}^{-1}$. The model parameters specified the fiber geometry for axons with a diameter from 5 to 15 µm; we implemented models with 5‐, 10‐, and 15‐µm diameters. The effect of the induced electric field on the transmembrane current was modelled similarly to Nagarajan et al. (1993), the numerical integration was performed with the Crank–Nicolson method similarly to Salvador (2009) with a 1/32‐µs time step (native sampling rate of the waveform), and the threshold intensity was found with the bisection method. In the simulations, we assumed that the membrane was at rest before the stimulation. The numerical stability of the selected time step was verified by repeating the simulations with a 1‐µs time step, which introduced a maximum relative error of 0.01 in the simulated thresholds.

The model used the measured TMS pulse waveforms (sampling rate 32 MHz) after low‐pass filtering with a first‐order Butterworth filter (cut‐off frequency 2 MHz) to reduce high‐frequency noise. To avoid phase distortion, the filter was applied in both forward and reverse time using the filtfilt function (Matlab R2015b). The numerical stability of the selected cutoff frequency was verified by repeating the simulations with a lower cutoff frequency (0.5 MHz); this caused only negligible changes in the simulated thresholds (maximum relative error < 0.001). The spatial distribution of the induced electric field in the simulations was computed in cylindrical geometry with a boundary element method solver based on Stenroos et al. (2007) and with reciprocity similarly to Nummenmaa et al. (2013). The cylinder diameter was 50 mm and its conductivity 0.33 S/m; the axon was 5 mm from the surface closest to the coil and parallel to the cylinder axis.

2.4. Modified neuron model

The experimental data and the neuron model manifest a qualitatively similar response to changes in the hold period. They, however, do not match quantitatively (see Results). To identify which—if any—model parameters affect this match, we performed a simple regression with all three rate parameters of the model (sodium activation, sodium inactivation, and potassium activation) and all three ion conductivities (leakage conductivity, potassium conductivity, and sodium permeability).

2.5. Depolarization of passive membrane

The depolarization of a passive membrane due to TMS (Figure 1c) was computed as the convolution between the electric field and truncated exponential function:

$$\Delta V\left(t\right)\propto {\int }_{-\mathrm{\infty }}^{t}d{t}^{\prime }\cdot E\left(t^{\prime }\right)\cdot {\frac{1}{{\mathrm{\tau }}_{\mathrm{m}}}e}^{(t^{\prime }-t)/{\mathrm{\tau }}_{\mathrm{m}}},$$

where $\Delta V$ is the membrane depolarization, $t$ is the time, $E$ is the electric field, and ${\mathrm{\tau }}_{\mathrm{m}}$ is the membrane time constant (Corthout et al., 2001; Peterchev et al., 2013).

3. RESULTS

The RMT of a pulse with a 60‐µs hold period was lower than that of a pulse with a 2.5‐µs hold period for the three subjects by 15%, 11%, and 9%, respectively. With a stimulation intensity in‐between the two individual RMT intensities, the 60‐µs‐hold‐period pulse resulted in more frequent muscle responses than the 2.5‐µs pulse, with MEPs ≥ 50 µV in 20/20 versus 9/20, 20/20 versus 6/20, and 18/20 versus 3/20 trials for subjects 1–3, respectively. The difference in the RMT was statistically significant for each subject (p = 0.00007, 0.000002, and 0.000002, respectively, one‐tailed Fisher's exact test). As both waveforms have an identical maximum depolarization, this difference cannot be explained with the monoexponential model used by Barker et al. (1991). Thus, we can justify the model we used to fit the secondary, activation time constant to the data.

The measured MEP amplitudes for pulses with different hold periods as a function of the induced electric field are shown in Figure 1d–f. In these data, we observed an activation time constant of about 17 µs for the abolition of the vulnerable period (Figure 1g–i). This activation time constant is much shorter than the 200 µs strength–duration time constant for motor cortex neurons or large‐diameter myelinated axons activated by TMS, which has been measured by varying the duration of the first phase of the electric field (Barker et al., 1991; D'Ostilio et al., 2016; Peterchev et al., 2013); thus, it likely relates to some faster process.

The exponential dependency of the measured MEP input–output curve midpoints on the hold period is similar to that of the simulated action potential threshold in a myelinated axon (Figure 2). In the simulations, the exponential behavior is mostly due to continued sodium‐channel activation during the hold period, which manifests itself with the increasing $m$ during the hold period in Figure 3. Thus, a longer hold period results in a lower action potential threshold (Figure 2). With the model parameters by Wesselink et al. (1999), the simulations have both a slightly longer activation time constant and a larger reduction in the relative threshold than the measured data; both the activation time constant and the reduction are outside of the 95% confidence interval of the experimental result. In the model, the two values appear coupled. By conducting the regression described in Section 2.4, we could match the simulated activation time constant with the measured one by increasing the rate of sodium channel activation, but could not match the observed behavior by adjusting either of the two other rate parameters or the three membrane conductance values of the model. A match, however, could still potentially be generated with other modifications of the model. An increase of the modelled rate of sodium channel activation by a factor of 3.5 (by multiplying both $\mathrm{\alpha }$ and $\mathrm{\beta }$ by 3.5) results in identical activation time constant (16.5 µs) and almost identical reduction in the relative threshold in the simulated (11.6% for an axon with a 10‐µm diameter) and measured (11.3%) data. We found that the model‐geometry‐related parameters—that is, the axon diameter and the myelin‐sheath geometry, which were defined as a function of axon diameter for the model parameters—had negligible effect on the activation time constant and the reduction in the action potential threshold as a function of the hold period for axon diameters from 5 to 15 µm.

Figure 2.

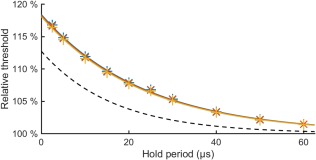
Simulated strength–duration relationship. Simulated action potential threshold relative to that of a pulse with long hold period as a function of the hold period for () 5‐µm, () 10‐µm, and () 15‐µm axon models (activation time constants 23.5–23.8 µs, reduction in the relative thresholds 15.3%–15.5%). The dashed line shows the exponential fit to the measurement data from Figure 1 (activation time constant 16.5 µs, reduction 11.3%)

Figure 3.

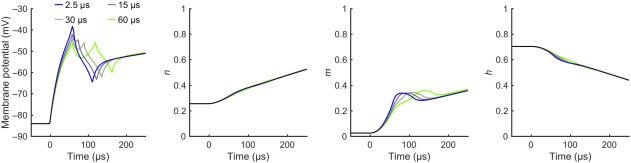
Simulated activation of an axon. Simulated activation of a long straight myelinated axon (diameter 10 µm) with the pulse waveforms with 2.5‐, 15‐, 30‐, and 60‐µs hold periods from Figure 1b. The membrane potential and the gating variables $n$, $m$, and $h$ are shown for the node with the strongest initial activation, that is, the node with the largest electric field gradient. For each waveform, the data are plotted for the lowest stimulation intensity to evoke an action potential

4. DISCUSSION

We measured how microsecond‐scale changes in the waveform of TMS applied to the motor cortex affect muscle responses. The simulation with a simplified neuron model suggests that the observed effect could be explained by the kinetics of voltage‐gated sodium channels in neuronal membranes (Bromm & Frankenhaeuser, 1968). These channels have somewhat similar dynamics to that of the Hodgkin–Huxley‐model‐like sodium channels (Horn & Vandenberg, 1984), although they possibly open more synchronously (Naundorf et al., 2006). The individual channels open at random latencies after depolarization, which, in simplified Hodgkin–Huxley‐like models, manifests as a delay in the increase of the sodium current. In both cases, the activation kinetics result in higher firing threshold for pulses with shorter hold periods. Consequently, the measured activation time constant for the reduction in motor threshold roughly describes the rate at which the net sodium influx increases at the stimulation site, which should correspond to the characteristic latency of the opening of sodium channels near the threshold potential. The observed 17‐µs activation time constant (95% confidence interval: 14.2–19.2 µs) is similar to the one estimated by McKay and Henshall (2003) from the human cochlear‐implant stimulation at three distinct interphase gaps of 8.4, 45, and 100 µs. Their estimate for a similar time constant was 23 µs; however, they had no estimate for the uncertainty of their result.

Our finding means that by noninvasive measurement we can study neuronal membrane kinetics that occur on time scales much shorter than the neuronal or membrane time constants. Our approach of estimating these kinetics from the strength–duration relationship of the vulnerable period allows circumventing the inherent bandwidth limitations of direct measurements. From the TMS point of view, the observed reduction in the RMT means that monophasic TMS with near‐rectangular pulse waveform behaves like charge‐balanced biphasic electrical stimulation, where the waveform of the later parts of the pulse is known to have an impact on the stimulation intensity (van den Honert and Mortimer, 1979). Thus, shorter monophasic TMS pulses with shorter fall times should result in even more selective stimulation of predominantly larger fibers (Gorman and Mortimer, 1983).

The observed nonlinear effects of the neuronal membrane are more sensitive to small variations in the pulse waveforms than the effects due to the linear membrane properties, which are manifested even with the sinusoidal pulse waveforms conventional to TMS. Measuring these active dynamics seems to require a TMS device with near‐rectangular electric‐field waveform, as previous experiments with conventional sinusoidal waveforms have found no difference between half‐sinusoidal and quarter‐sinusoidal current waveforms with long hold periods (Sommer et al., 2006; Delvendahl et al., 2014). The observed nonlinear effects also suggest a small refinement in the exact timing of the activation due to TMS. TMS produces inherently charge‐balanced stimulation with zero net charge accumulation. Consequently, a TMS pulse is thought to trigger many practically simultaneous action potentials in the targeted neuronal population at the moment of peak membrane depolarization (Corthout et al., 2001). Our results with nonzero hold periods suggest a more dispersed timing for the triggering of action potentials at around and after the peak depolarization. These differences, however, should be of the order of the estimated activation time constant, much less than the duration of synaptic transmission, and thus, have little or no influence on the observed MEPs or other evoked responses.

In the future, noninvasive TMS–EMG measurements of the ion‐channel dynamics may be useful in studying how individuals respond to pharmacological substances that affect ion channels, as, for example, voltage‐gated sodium channels are therapeutic targets in epilepsy treatment (Mantegazza et al., 2010). The ability to measure the kinetics of these channels may also find applications in the diagnosis of channelopathies (George, 2005; Vincent et al., 2006). To move beyond the motor areas, one may measure effects of TMS with electroencephalography (Komssi et al., 2004; Kähkönen et al., 2005).

5. CONCLUSION

To conclude, we demonstrated noninvasive measurement of microsecond‐scale dynamics from the human motor cortex. This exceeds the abilities of previous noninvasive in vivo methods by at least an order of magnitude. The developed protocol opens new possibilities in evaluating how ion channels are affected, for example, by pharmacological substances or neurological diseases. The demonstrated measurement principle could also be translated to invasive or in vitro studies to allow even more detailed experiments.

CONFLICT OF INTEREST

RJI is an advisor and a minority shareholder of Nexstim Plc., and JON has received unrelated consulting fees from the company. The other authors declare no conflict of interest.

Koponen LM, Nieminen JO, Mutanen TP, Ilmoniemi RJ. Noninvasive extraction of microsecond‐scale dynamics from human motor cortex. Hum Brain Mapp. 2018;39:2405–2411. 10.1002/hbm.24010