Core networks and their reconfiguration patterns across cognitive loads

Abstract

Different cognitively demanding tasks recruit globally distributed but functionally specific networks. However, the configuration of core networks and their reconfiguration patterns across cognitive loads remain unclear, as does whether these patterns are indicators for the performance of cognitive tasks. In this study, we analyzed functional magnetic resonance imaging data of a large cohort of 448 subjects, acquired with the brain at resting state and executing N‐back working memory (WM) tasks. We discriminated core networks by functional interaction strength and connection flexibility. Results demonstrated that the frontoparietal network (FPN) and default mode network (DMN) were core networks, but each exhibited different patterns across cognitive loads. The FPN and DMN both showed strengthened internal connections at the low demand state (0‐back) compared with the resting state (control level); whereas, from the low (0‐back) to high demand state (2‐back), some connections to the FPN weakened and were rewired to the DMN (whose connections all remained strong). Of note, more intensive reconfiguration of both the whole brain and core networks (but no other networks) across load levels indicated relatively poor cognitive performance. Collectively these findings indicate that the FPN and DMN have distinct roles and reconfiguration patterns across cognitively demanding loads. This study advances our understanding of the core networks and their reconfiguration patterns across cognitive loads and provides a new feature to evaluate and predict cognitive capability (e.g., WM performance) based on brain networks.

1. INTRODUCTION

Imaging neuroscience has helped researchers conceptualize the brain as a system of networks. A surge in brain science research has been continuously fertilized by advancements in graph theory and imaging techniques, including improvements in spatiotemporally enhanced functional magnetic resonance imaging (fMRI). In large‐scale brain network studies, the entire brain is first parcellated into functionally specific units (network nodes) from a functional (Glasser et al., 2016) or structural perspective (Fan et al., 2016), with the connectivities between node‐pairs (network edges) then characterized using a variety of functional or structural measurements (Bullmore & Sporns, 2009; Sporns, 2011). In this manner, brain network theory can provide a quantitative method for describing the way in which the brain works, predict whether a brain is on a developmental or aging track (Dosenbach et al., 2010), and evaluate whether the brain is in certain neuropsychiatric or neuropsychological states (Fornito & Harrison, 2012).

The general architecture of brain networks during transitions between different mental states (e.g., resting or performing tasks; Cole et al., 2013) has been identified previously. Researchers are increasingly interested in the underlying dynamics of brain networks, which may shed light on the roles of different brain regions or why the brain remains in a specific mental state (Bullmore & Sporns, 2012). Brain dynamics have been investigated at different temporal scales (Hutchison et al., 2013), from several seconds, to minutes, to weeks, and even to years. In particular, by comparing brain networks in different mental states, including resting and task states, it is possible to study global network reconfigurations and functional node dynamics, which provide critical clues for dissecting the ways that different functional units collaborate to implement a specific task (Cohen & D'Esposito, 2016).

As variable cognitive load paradigms, working memory (WM) tests have been widely used to evaluate memory maintenance and update performance, as well as to assess fluid intelligence and academic capacity (Eriksson, Vogel, Lansner, Bergstrom, & Nyberg, 2015; Ullman, Almeida, & Klingberg, 2014). Both the identification of WM core networks and their interactions and transitions across various cognitive load levels have attracted considerable attention in neuroscience (Eriksson et al., 2015). However, researchers are far from reaching a consensus regarding the composition of core networks in WM or from discovering how they interact and segregate at different WM load levels. Although Cole and colleagues (2013) identified the FPN as the most flexible network, that is, the one most likely to change across a variety of tasks, Vatansever, Menon, Manktelow, Sahakian, and Stamatakis (2015), using the same measure of globally variable connectivity, identified the dorsal attention network (DAN), visual cortex, and DMN as the most flexible networks when the brain confronts different cognitive loads (resting and 0–3 backs WM; see Figure 4 in Vatansever et al., 2015). Furthermore, due to its role in information maintenance, the active participation of the primary sensory cortex is well known, e.g., involvement of the visual cortex in visuospatial WM (Mueller et al., 2016). However, earlier study also identified the primary sensory cortex as a stable module, even across different load levels (Braun et al., 2015). Thus, efforts have been made to understand the reconfiguration of WM core networks. For example, Liang and colleagues (2016) specifically examined interactions of the DMN, FPN, and salience network (SN) across cognitive loads (0–3 backs WM) and, more recently, Bolt and colleagues (2017) investigated changes in global network topology and hub structure from the resting to task states. However, it is still unclear how global and core networks of WM cohesively reconfigure across cognitive loads, and whether such reconfigurations reflect behavioral performance.

Figure 4.

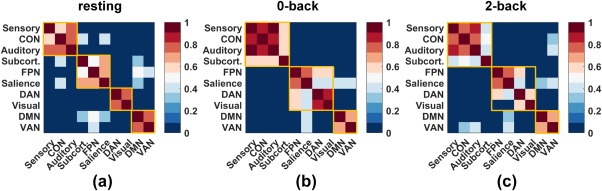
Modular partitions of the 10 networks for the three mental states: that is, resting, 0‐back, and 2‐back. For each state, modular partitioning was computed using Equation 1. The nodal assignment matrix was then obtained for each subject. The noise in the network assignment was removed by subtracting a random nodal association matrix (null model; Bassett et al., 2013), and the final partition was obtained as the consensus partition using Equation 1. Yellow squares mark the communities identified using Equation 1 for each of the three mental states [Color figure can be viewed at http://wileyonlinelibrary.com]

In this study, we analyzed resting state and WM task fMRI data from the Human Connectome Project (HCP) S500 release (Van Essen et al., 2013) to identify WM core networks, defined as the most flexible networks across cognitive loads or networks with the strongest connections in cognitive loads. Network reconfiguration was investigated at both the global network (network of the entire brain) and subnetwork levels (subnetworks of FPN and DMN, as defined in Power et al., 2011). The reconfiguration intensity of the global network was evaluated by the dissimilarity of the modular partitions in two states (see Figure 2). We further examined whether global reconfiguration intensity was correlated with WM performance. At the subnetwork level, we used nodal connectivity diversity (NCD, as in Figure 1b) to quantify the connectivity reconfiguration flexibility, where higher NCD between brain states indicated more intense reconfiguration. We also examined connection strength (see Equation (2)) to evaluate which connectivities or subnetworks dominated the reconfiguration. Reconfiguration flexibility and dominant subnetworks in reconfiguration may facilitate the identification of WM core networks and clarify how these core networks cohesively reconfigure to adapt to WM loads. We hypothesized that network reconfiguration intensity would be associated with WM performance, both at the global level and at the level of core networks associated with WM.

Figure 2.

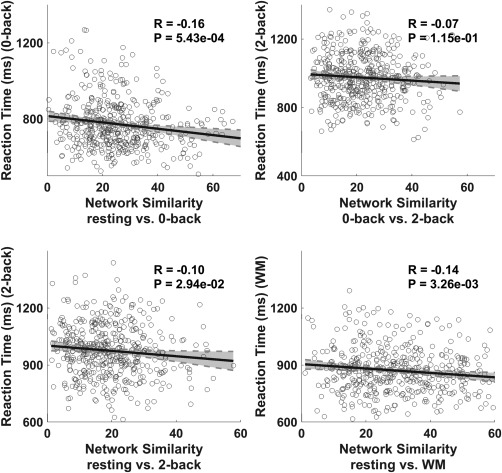
Correlations between intensity of the network reconfigurations and WM score (reaction time). First three panels are correlation plots for the three mental state pairs, that is, resting versus 0‐back, 0‐back versus 2‐back, and resting versus 2‐back, respectively. Last panel is the correlation plot between the resting state and WM (concatenating 0‐back and 2‐back)

Figure 1.

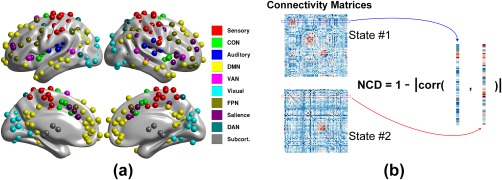
Illustrations of the ROI distributions across the brain (panel a) and definition of nodal connectivity diversity (NCD; panel b). In panel a, the ROIs, as defined in (Power et al., 2011), are color coded for the 10 networks, and were the network nodes used for the following network analyses. To compute the NCD for a node between two states, the connection profiles in the two states were extracted (labeled in blue and red boxes/curves, respectively), with Pearson correlation coefficients then computed. NCD is one minus the absolute value of the correlation coefficient [Color figure can be viewed at http://wileyonlinelibrary.com]

2. MATERIALS AND METHODS

2.1. Dataset and preprocessing

The dataset was extracted from the Human Connectome Project (HCP) dataset S500 release. We used the same data collection descriptions applied in our previous work on a partially overlapping portion of the HCP dataset (Zuo, Song, Fan, Eickhoff, & Jiang, 2016). Briefly, the dataset was collected on a 3T MRI Skyra scanner (Siemens, Germany) using a standard 32 channel head coil. The magnetic field produced by the coil was modeled to provide customized distortion correction. The primary scanning parameters were: repetition time (TR), 720 ms; echo time (TE), 33.1 ms; flip angle, 52°; field of view, 208 × 180 mm; slice thickness, 2.0 mm; and voxel size, 2.0 mm isotropic cube (Van Essen et al., 2013).

The minimally preprocessed resting and task fMRI dataset received from the HCP S500 was processed as follows (Glasser et al., 2013): (a) gradient nonlinearity distortion; (b) 6 degrees of freedom (DOF) FSL/FLIRT‐based motion correction; (c) FSL/topup‐based distortion correction and scalp stripping; (d) registration to T1 image space; and (e) FSL/FNIRT‐based registration to MNI 2 mm space. After receiving the data, we further scrubbed the frames with excessive head motions based on >0.5 mm criterion (the percentage of frames with excessive motion was 1.6% for resting data and 1.5% for WM) and corrected the frames by interpolation (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012). We then band‐pass filtered the data at 0.009–0.08 Hz to reduce low‐frequency drift and high‐frequency noise (Vatansever et al., 2015). The mean signal, five principal components of white matter and cerebrospinal fluid (CSF), and movement parameters and their derivatives (Movement_parameters.txt file in the HCP S500 release) were regressed out as confounding factors to remove physiological noise. The above principal components were derived separately by decomposing the regional signal masked by the eroded white matter and CSF (Behzadi, Restom, Liau, & Liu, 2007). As we used a series of regions of interest (ROIs) in this study to sample gray matter of the entire brain (described below), a smoothing step was not applied to reduce the signal interactions between neighboring ROIs. In addition, as there is no current consensus regarding physiological interpretation of global signal regression (Murphy, Birn, Handwerker, Jones, & Bandettini, 2009), and previous evidence has revealed that global signals potentially affect correlations and anti‐correlations between networks (Chang et al., 2016; Liu, Nalci, & Falahpour, 2017; Wong, DeYoung, & Liu, 2016), we conducted separate study in which the global signals were and were not regressed out to validate our findings.

The HCP S500 dataset contained records from 512 subjects. Certain data were excluded based on the following criteria: (a) data reported on the known issues page of the HCP website, https://wiki.humanconnectome.org/display/PublicData/HCP+Data+Release+ Updates%3A+Known+Issues+and+Planned+fixes; (b) data that did not have a sufficient number of frames (correct number of frames for each mental state is described in Barch et al., 2013); (c) data for which the task fMRIs did not have a full explanatory variable (EV) record; (d) data acquired without left‐right (LR) or right‐left (RL) phase encoding; (e) data from subjects whose performance records (reaction time [RT] and accuracy in WM tasks) were recognized as outliers (as we were not sure whether these subjects were normally actively engaged in task execution) by the Grubbs test (Grubbs, 1969) based on a confidence level of 0.05 (implemented by Francisco Garcia in https://cn.mathworks.com/matlabcentral/fileexchange/28501-tests-to-identify-outliers-in-data-series). In the end, 448 subjects (188 males and 260 females, aged 29.1 ± 3.5 years for the entire sample) were used for subsequent analyses. The original task datasets included seven conventional tasks, that is, WM, gambling, motor, language, social cognition, relational processing, and emotion processing (see Table 1 in Barch et al., 2013); however, the current study only utilized the WM dataset with 0‐back and 2‐back sessions plus separate resting sessions to sequentially compare network integration and segregation at different cognitive demand loads. The WM test in the HCP is a variant of the traditional visuospatial WM test and effectively activates well‐known WM‐related functional regions (see Table 1 in Barch et al., 2013). In this study, for computing simplicity, only session #1 (recorded as REST1 in HCP) for the resting state was used.

Table 1.

Correlations between the NCD of each network and WM scores (reaction time)

	resting vs. 0‐back		0‐back vs. 2‐back		resting vs. 2‐back
	R	p Value	R	p Value	R	p value
Sensory	.08	7.40E‐02a	–.01	.83	.05	.34
CON	.18	1.04E‐04b	.05	.25	.07	.12
Auditory	.14	2.90E‐03b	.04	.38	.09	.05
DMN	.26	3.43E‐08b	.10	.03a	.15	1.76E‐03b
VAN	.10	3.08E‐02b	.01	.91	.07	.12
Visual	.13	5.15E‐03b	.09	.07	.07	.11
FPN	.23	6.54E‐07b	.13	.01a	.19	7.10E‐05b
Salience	.21	6.01E‐06b	.11	.02a	.14	2.48E‐03b
DAN	.19	3.79E‐05b	.06	.18	.10	.04a
Subcort.	.05	.27	.06	.21	.08	.10

R indicates the correlation coefficient and p value is the significance level.

^a p Value reached significance (p < .05).

^b p Value survived multiple comparison correction by FDR (p < .05).

2.2. Functional network constructions

The functional connectivities in the three states (i.e., resting, 0‐back, and 2‐back) were determined separately. During WM execution, to reduce the effects of hemodynamic delays from the previous conditions, the first 10 frames (∼8 s) from each block were discarded and five frames (∼4 s) of the next block were concatenated (Liang, Zou, He, & Yang, 2013). To alleviate bias introduced by the phase encoding directions during fMRI scanning, the functional connectivities were constructed separately by computing the Pearson correlation coefficients in two datasets consisting of the LR and RL phase‐encoding directions and then averaging the connectivities after Fisher z‐transformation. Before calculating the functional connectivity of the task fMRI time series, mean task activity was regressed out and the residuals were used for network construction (Cole et al., 2013). Rather than a voxel‐wise connectivity analysis, which has a huge computational burden, we used the mean time series of all voxels in 5‐mm spheres around the ROI groups proposed by Power et al. (2011). This grouping scheme contains 264 ROIs distributed over the brain (including the cerebral cortex, subcortical nucleus, and cerebellum) grouped into 10 putative networks, including the sensory network, cingulo‐opercular network (CON), auditory network, subcortical network, FPN, SN, DAN, visual cortex network, DMN, and ventral attention network (VAN; Figure 1a), along with three other undetermined networks (Cole et al., 2013; Vatansever et al., 2015).

2.3. Modular partitioning and measurement of the global network reconfigurations

To measure the global network reconfigurations that occur when the brain confronts different cognitively demanding situations, for example, resting and WM (including 0‐back and 2‐back), the random coefficient (Traud, Kelsic, Mucha, & Porter, 2011) was used to evaluate the similarity between the individual modular partitions between states. Because data collection in the three mental states mentioned above took different lengths of time, using a predefined, absolute threshold to remove noisy and weak connections will result in different network densities, thereby making it impossible to compare modular partitions. Therefore, at this stage, the functional networks in the different states were thresholded by their connectivity densities and then binarized to discover existing connections. To address the bias that could result from using different thresholds, three incremental thresholds (5%, 10%, and 15%) were adopted to validate the results (Bullmore & Sporns, 2009; Rubinov & Sporns, 2010; van Wijk, Stam, & Daffertshofer, 2010).

In general, to explore the modularity of the second‐level network created by interaction (signed) between the 10 predefined networks (Power et al., 2011), we used an extended version of modularity maximization to simultaneously consider the positive and negative links (Bassett et al., 2011):

$$Q_{\pm }=\frac{1}{2w^{+}+2w^{-}}\sum _{i,j\in A}\left[A_{ij}-\left({\mathrm{\gamma }}^{+}\frac{w_i^{+}{w}_j^{+}}{2w^{+}}-{\mathrm{\gamma }}^{-}\frac{w_i^{-}{w}_j^{-}}{2w^{-}}\right)\right]\mathrm{\delta }\left(g_i,\hspace{0.17em}{g}_j\right),$$ (1)

where, A is the connectivity matrix with elements $A_{ij}$ (i, j = 1, 2…M, M is the number of nodes), $w_i^{+}={\sum }_j{A}_{ij}^{+}$ and $w_i^{-}={\sum }_j{A}_{ij}^{-}$ are the degrees of node i in $A^{+}$ (positive component of A) and ${-A}^{-}$ (negative component of A), respectively, and $A=A^{+}{-A}^{-}$ where $w^{+}$ and $w^{-}$ indicate total connection strength in ${-A}^{+}$ and ${-A}^{-}$, respectively; ${\mathrm{\gamma }}^{+}$ and ${\mathrm{\gamma }}^{-}$ are the resolution parameters for the optimal modular index; $g_i$ indicates the region assignment for node i; and $\mathrm{\delta }$ indicates that only the fraction where the two nodes are in the same region will be counted in the final modular index. To obtain the modular partitions of the global network (264 nodes), as the network was binarized as described above, only the positive items in Equation (1) were counted. In this study, the default resolution parameter $\mathrm{\gamma }\hspace{0.17em}=\hspace{0.17em}1$ was adopted when applying the generalized Louvain method (http://netwiki.amath.unc.edu/GenLouvain/GenLouvain; Mucha, Richardson, Macon, Porter, & Onnela, 2010). To validate the robustness of this finding, $\mathrm{\gamma }$ values from 0.4 to 1.6 with an incremental step of 0.2 were tested (see Supporting Information, Figure S2). Moreover, to reduce the likelihood of biasing random walk while optimizing modularity, we repeated the solution 100 times and the partition associated with the largest modularity index was selected as the final partition scheme and was thus used to choose the modularity index (Vatansever et al., 2015).

2.4. Nodal flexibility measurement: Nodal connectivity diversity (NCD)

After examining the global network reconfiguration, we further ascertained which subnetworks dominated the network reconfigurations. In the subsequent analysis, the fully‐weighted functional connectivities (Fisher z‐transformation of Pearson correlation coefficients between node‐pairs) were used rather than the binarized ones to conserve connectivity information (Bassett et al., 2011; Vatansever et al., 2015). By definition, the NCD describes the distance between connection profiles of a node in two mental states, that is, NCD = 1‐|corr(s1,s2)|, where s1 and s2 indicate the connectional profiles in state #1 and #2, respectively (see Figure 1b, where “corr” is the Pearson correlation coefficient and “|·|” is the absolute value, with NCD constrained within the range [0, 1]). This distance measure is popular in mathematics and signal processing and has been recently used in neuroscience (Schultz & Cole, 2016). In contrast to the global variable connectivity measure proposed by Cole et al. (2013), the NCD treats the nodal connectivity profile as a full vector instead of a compressed scalar value. This method allows comprehensive evaluation of the connectivity transitions. In this stage, two sequential state‐pairs were counted, that is, resting versus 0‐back and 0‐back versus 2‐back.

2.5. Connection strength measurement

The connection strength between two networks is defined in Equation (2) as follows:

$$I=\frac{1}{K·L}\sum _{\begin{array}{c}i\in network\#1,\hspace{0.17em}\\ j\in network\#2\end{array}}{|A}_{ij}|,$$ (2)

where, $A_{ij}$ is the element in the connectivity matrix that is the same as in Equation (1), K and L denote the size of the two interacting networks, respectively, with K⋅L used to normalize connection strength to reduce the effect of different network sizes. Connection strength indicates communication abilities between networks (Liao et al., 2013; Zuo et al., 2012). The internal connection strength of a given network is computed by constraining the nodes i and j of the connection inside the network.

Furthermore, modular partitioning of the 10 × 10 connection strength matrices between the 10 predefined networks was achieved using Equation (1) for each mental state for each subject. The modularity maximization method in Equation (1) identified the communities in which the intra‐interactions were strong, but the inter‐interactions were weak. A consensus partition was then derived across all 448 subjects for the three mental states (i.e., resting, 0‐back, and 2‐back) by statistical testing, which compared the network association matrix to a random network association matrix (null model; Bassett et al., 2013).

2.6. Comparing change trends in connectivity between two states

The change trends in connection strength between two mental state pairs, that is, resting versus 0‐back and 0‐back vs. 2‐back, were investigated. The overall strategy was to perform group comparisons between each pair of networks across subjects for each connection. Because the lengths of the time series for the three mental states were not identical, the z‐test statistic was used, and is defined in Equation (3) as follows (Diedenhofen & Musch, 2015):

$$Z_{\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}=\frac{z_1-z_2}{\sqrt{\frac{1}{N_1-3}+\frac{1}{N_2-3}}},$$ (3)

where, $z_1$ and $z_2$ are the two connection strengths (Fisher z‐transformation of the correlation coefficients) to be compared, and $N_1$ and $N_2$ are respectively the lengths of the time series for which the connection strengths $z_1$ and $z_2$ were computed. For a given significance level, for example, α = 0.05 in which the critical value was $\pm 1.96$, each connection was labeled as 1 (connection in the latter state increased compared to the former state) or −1 (otherwise). To define the change trends in connection strength between two mental states, the above labels along the connections between the two networks (normalized by K⋅L, as defined in Equation (2)) were summed, and a one sample t test was performed to determine whether the change trend was significantly positive (increasing) or negative (decreasing).

3. RESULTS

3.1. Intensity of global network reconfiguration correlates to WM performance

We investigated, from a global perspective, whether the intensity of network reconfiguration was related to WM performance. Based on the three density threshold levels (5%, 10%, and 15%) for binarizing the connectivity network, our results consistently demonstrated that the similarities between modular partitions in the two mental states were significantly correlated to the RT values in the WM task executions (p < .05 after FDR correction for multiple comparisons, using the mafdr function in Matlab version 2012; Figure 2 shows results for the 15% density threshold, Supporting Information, Figure S1 shows the results for the 5% and 10% density thresholds). We also varied the resolution parameters ( $\mathrm{\gamma }=[0.6,\hspace{0.17em}1.4]$ with step = 0.2) to evaluate the influence of $\mathrm{\gamma }$ and confirmed the robustness of the findings (see Supporting Information,Figure S2). These results collectively showed that, when global network reconfigurations were considered, the greater the number of functional network reconfigurations, the worse was the performance on the WM tasks. It should be noted that the regression in Figure 2 only addressed a small portion of variance. Furthermore, after regressing out the global signal, similar correlation results were achieved (see Validation section in Supporting Information). However, this finding did not clarify which networks had dominant roles during the reconfiguration; thus, this was the goal of the following analyses.

3.2. FPN is the most stable and dominant network when the brain confronts different cognitively demanding loads

To identify the most/least flexible networks between WM loads, the NCD measure (defined in Figure 1b) was used to evaluate the flexibility of each network. Of the 10 networks, the FPN showed the least flexibility (Figure 3a). However, the FPN also exhibited overwhelmingly dominant connection strength to the entire brain, as defined in Equation (2) (Figure 3b), over all other networks, except for the subcortical network. The subcortical network has heterogeneous and complex functional components globally regulating other networks (Hibar et al., 2015), resulting in strong global connection strength. The differences in NCD and global connection strength between the FPN and other networks were almost all significant when tested using paired t tests (p < .005, FDR corrected for multiple comparisons), except for the interaction strength between FPN and DAN in the 0‐bk state (p = .18), though it still showed a consistent trend (see Supporting Information, Table S3 for detailed p values).

Figure 3.

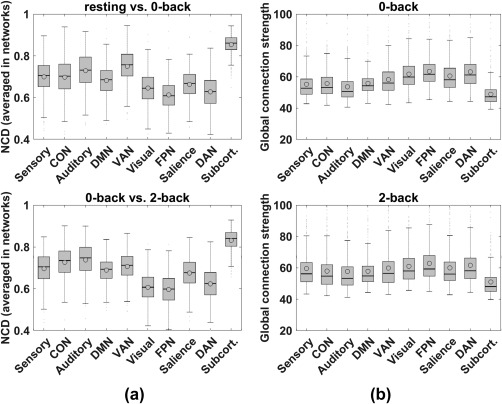
Enhanced quartile boxplots (circles and horizontal lines inside each box indicate mean and median values of subjects, respectively) for flexibility analyses using NCD (panel a) and connection strength analyses (panel b). Panel a: x‐axis indicates the 10 networks and y‐axis is average NCD for each network. Top plot is for the sequential mental state pairs, resting versus 0‐back, and the bottom plot is for 0‐back versus 2‐back. Each set of error bars indicates SE across the 448 subjects. In each box, the horizontal line indicates median NCD and the circle indicates mean NCD. Panel b: Annotations are similar to those in panel a, except the y‐axis indicates global connection strength from the examined network to the whole brain, separately for 0‐back (top) and 2‐back (bottom)

3.3. Functionally grouped networks across different mental states

Having identified the FPN as the most dominant but inflexible network when the brain confronts different cognitively demanding loads, we further explored how the 10 networks were functionally grouped when the brain was in each of the three mental states. For the resting state, four communities were identified from the 10 networks, whereas three communities were recognized for the 0‐back and 2‐back states, respectively. Figure 4 presents the modular allegiance matrices, which indicate the percentage of the subjects (448 in total) that generated the same modular assignment for each element (network‐pair). The yellow squares mark the communities identified using Equation (1) for each mental state, with four communities for the resting state (panel A) and three communities for the 0‐back and 2‐back states, respectively. These results collectively showed that, without considering the auxiliary networks, the networks in both the 0‐back and 2‐back task states were consistently composed of two communities: that is, the FPN‐group, which contained the FPN, SN, DAN, and visual network; and the DMN‐group, which contained the DMN and VAN. Furthermore, the visual network became detached from the FPN and SN in the 2‐back task in contrast to their association in the 0‐back task. To validate the robustness of these findings, we changed resolution parameter $\mathrm{\gamma }$ from 0.4 to 1.6 with a step of 0.2, repeated the modular partitioning using the different $\mathrm{\gamma }$ values, and generated the same results (see Supporting Information, Figure S3).

We further examined which of the 10 networks reorganized in the same direction as the global network, specifically whether the reconfigurations of the 10 networks correlated with task performance (RT), as shown in Figure 2. The correlation coefficients and their significance levels are listed in Table 1. The correlation analyses showed that, in contrast with the resting state, most networks reconfigured in the same direction as the global network in the 0‐back state (p < .05, after FDR correction), including the FPN‐ and DMN‐groups. Furthermore, the FPN‐ and DMN‐groups, especially the FPN, SN, and DMN, maintained their reconfigurations in the same direction as the global network in the 2‐back state (p < .05, after FDR correction). In contrast to the 0‐back state, however, the visual network was less engaged in the FPN‐group in the 2‐back state. Considering possible confounding factor effects, we also conducted similar analyses after regressing out sex, age, and head motions, and yielded consistent results (see Supporting Information, Table S1).

3.4. Change trends in connection strength between core networks

We found that the FPN‐ and DMN‐groups were the core functional networks, which intensively reconfigured in the same direction as the global network when the brain was confronted with different cognitively demanding loads (i.e., resting, 0‐back, and 2‐back) in the WM test. Thus, we next examined whether the connection strength between these core networks changed sequentially in the three mental states. The z‐test statistic (Equation (3)) showed that, for the sequential transitions from resting to 0‐back and from 0‐back to 2‐back, the interactions between the FPN‐ and DMN‐groups increased continuously (t(447) > 1.65, p < .05). Furthermore, the intra‐interaction within the FPN‐group increased in the 0‐back state. For connectivity changes between the FPN and other networks from 0‐back to 2‐back, we found no consistent output when the global signal was or was not regressed out (see Validation section in Supporting Information), thus we marked this changing direction as undetermined (dashed line in right‐bottom panel in Figure 6).

Figure 6.

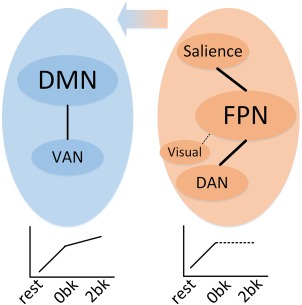
Illustration of core network reconfigurations across cognitively demanding loads, sequentially from resting state, to 0‐back, and then to 2‐back. The two colored ellipses indicate the DMN‐group (left panel in blue, including the DMN and VAN) and FPN‐group (right panel in orange, including the FPN, SN, DAN, and visual network). Left‐bottom plot indicates that the interaction between the DMN and VAN increased continually from low to high demand. Right‐bottom plot indicates that the interactions within the FPN‐group increased during the transition from resting to 0‐back. Central arrow indicates the rewiring trend from other networks to the DMN. Dashed lines indicate the undetermined interaction change direction across states as no consistent results were achieved with or without regressing out the global signal [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

In this study, we globally explored network reconfigurations across cognitive loads (resting state and visuospatial WM test) and found that the FPN was consistently the most dominant network (with the strongest connection strength over the brain) but had the least flexibility in responding to changes in the task state compared with other networks. The FPN‐group (FPN, SN, DAN, and visual network) and DMN‐group (containing DMN and VAN) actively regulated the entire network. Furthermore, they consisted of core networks across cognitive loads and exhibited the same behavior as the global reconfiguration in correlation analyses with WM performance (RT). When the brain changed from the resting state to 0‐back (lower load), both the FPN‐ and DMN‐groups increased their intra‐connections and the visual network also strengthened its interactions with other networks. As the load increased (from 0‐back to 2‐back), the FPN‐group became undetermined, and the connectivity changes between the FPN and other networks from 0‐back to 2‐back showed no consistency when the global signal was or was not regressed out (see Validation section in the Supporting Information). In addition, some of its members, including the visual network, SN, and DAN, became significantly rewired to the DMN (as illustrated in Figures 5 and 6).

Figure 5.

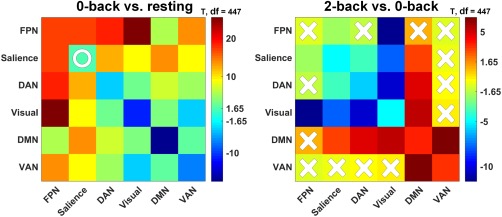
Connectivity comparisons between sequential mental state‐pairs, that is, 0‐back versus resting and 2‐back versus 0‐back. Red indicates an increase from lower to higher demand and blue indicates the opposite. In each panel, X indicates that the connectivity comparison failed to reach significance (p < .05) and O indicates that the significance did not survive FDR correction (p < .05) [Color figure can be viewed at http://wileyonlinelibrary.com]

4.1. FPN‐group and DMN‐group globally regulate network reconfiguration

Modularity maximization for the 10 networks generated the FPN‐group (FPN, SN, DAN, and visual network) and DMN‐group (DMN and VAN). The FPN had the least flexibility but the strongest connections over the global brain at the different cognitive loads (0‐back and 2‐back). As an extrapolative study, when we used the participation coefficient (Guimera & Nunes Amaral, 2005) based on the network partition of Power et al. (2011), the DMN was recognized as one of the most flexible among the 10 networks across the WM loads (see Supporting Information, Figure S6). Topological changes in the brain network between the resting and task states have been uncovered previously, both for changes in hub regions and changes in overall network structure (Bolt, Nomi, Rubinov, & Uddin, 2017; Schultz & Cole, 2016), though with the latter showing little change (Cole, Bassett, Power, Braver, & Petersen, 2014). Our results provided more detailed reconfiguration patterns for the subnetworks and unveiled the relationships between connectivity reconfigurations and behavioral performance.

A striking number of studies have shown that the FPN is the central control network during WM cognitive demands (Eriksson et al., 2015). Due to its central role in global control, the FPN is also called the central executive network (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008) or executive control network (Thompson, Waskom, & Gabrieli, 2016). The FPN consists of distributed anatomical regions across the brain, including the lateral prefrontal cortex (PFC), inferior frontal gyrus (IFG), pre‐/post‐central sulcus, superior parietal lobule (SPL), and intraparietal sulcus (IPS; Ptak, Schnider, & Fellrath, 2017; Rottschy et al., 2012), which are activated in mental simulation (Grezes & Decety, 2001; Zacks, 2008), visuospatial attention, and working memory tasks (Owen, McMillan, Laird, & Bullmore, 2005; Rottschy et al., 2012). Moreover, the dorsal FPN, including the dorsal premotor cortex and SPL/IPS, is the core system of the FPN for action emulation, and is a domain‐general system supporting various cognitive functions (Ptak et al., 2017). Adaptive participation of the FPN has been shown across cognitive loads (Owen et al., 2005), and its internal functional connectivity is strongly associated with WM loads (Bray, Almas, Arnold, Iaria, & MacQueen, 2015). Functional connectivity or activation within the FPN, both in the resting state (Magnuson et al., 2015) and during task execution (Ullman et al., 2014), is also correlated with WM capacity, consistent with our finding that the reconfiguration of the FPN was significantly correlated with WM performance (RT in both 0‐back and 2‐back; Table 1). The DMN is a well‐accepted spontaneous network, which is not only in charge of internal mental processing in the resting state (Raichle et al., 2001) but also sentinel monitoring of the external environment (Buckner, Andrews‐Hanna, & Schacter, 2008). The DMN is composed of heterogeneous compartments that show active behavior in both the resting state and task execution (Andrews‐Hanna, 2012; Leech & Sharp, 2014), and thus the DMN is considered a coordinator that globally mediates computing resources across the brain (Anticevic et al., 2012). The current findings revealed that, when the brain was confronted with different cognitive demands, the FPN and DMN cooperatively regulated the entire network reconfigurations, but played different roles, as evidenced by their different reconfiguration patterns. Considering the flexibility of the DMN, this network mediates its local activations (by activation or de‐activation) and interactions with other networks (Chai, Ofen, Gabrieli, & Whitfield‐Gabrieli, 2014; Harrison et al., 2008; Nakano, Kato, Morito, Itoi, & Kitazawa, 2013) to rearrange computing resources across the brain. Thus, we postulate that the FPN focuses on task execution, whereas the DMN is resource‐coordinating, similar to the argument made by Ceko and colleagues (2015), who compared normal subjects and chronic pain patients across different cognitive loads. However, they did not establish any significant correlation between the responsiveness of the DMN and WM performance (Ceko et al., 2015), inconsistent with existing reports (Sambataro et al., 2010; Xin & Lei, 2015) and our findings. This contradiction may be due to the different imaging measures and behavioral quantities utilized in these studies. Our results also highlighted the efficacy of the NCD, the brain network property used in this study, in association with behavioral quantification.

4.2. Reconfiguration pattern of core networks

As observed in Figure 5, the core network reconfiguration pattern had several main features. From the resting state to lower demand load (0‐back), the internal connections within the FPN‐group, including those of the visual cortex, increased markedly. This may have been due to the bottom‐up regulation of sensory processing (Felleman & Van Essen, 1991), in which sensory information is transferred to the advanced cortex (e.g., the DAN) through the FPN (Bisley, Krishna, & Goldberg, 2004). From the 0‐back to higher demand load (2‐back), the FPN‐group disintegrated, and the compositional networks were rewired to the DMN. As described from the perspective of the (de‐)activations in the above section, the DMN thus mediates the allocation of brain‐wide computing resources in both the resting and task states (Koshino, Minamoto, Yaoi, Osaka, & Osaka 2014), specifically across cognitive loads (Liang, Zou, He, & Yang, 2016; Scott, Hellyer, Hampshire, & Leech, 2015; Vatansever, Manktelow, Sahakian, Menon, & Stamatakis 2017). From the perspective of functional connectivity, our previous studies indicated that the DMN has active connections with the task positive networks, even in the resting state (Zuo et al., 2016), and that these external connections correlate strongly with WM performance (Liang et al., 2016). The current findings are in line with existing reports that the DAN is actively engaged in cognitively demanding tasks (Liu et al., 2016). The visual cortex also showed a significant transition from the FPN‐group to DMN‐group. This may be due to the dominant role of the DMN in higher cognitive loads (Andrews‐Hanna, 2012; Leech & Sharp, 2014). However, using a similar N‐back WM paradigm, Braun et al. (2015) showed the visual cortex to be one of the most conserved and least flexible modules. This inconsistency could be partially attributable to differences in the location of the visual cortex (Braun et al., 2015), which spans across the occipital and parietal lobes, as defined in Power et al. (2011). Vatansever et al. (2015) asserted that the DMN is one of the most flexible networks. However, previous comparisons across the 10 networks have not exclusively highlighted the flexibility of the DMN (Bola & Borchardt, 2016). This discrepancy is likely due to mixing connection flexibility with strength, an issue that is rooted in the measure of global variability in connectivity (Cole et al., 2013). After extensive study, we developed novel measures based on the participation coefficient (Guimera & Nunes Amaral, 2005) to re‐assess the flexibility of the DMN, and found our results to agree well with the conclusions of Vatansever et al. (2015; see Supporting Information, Figure S6).

The current study confirmed the active engagements of both the task‐negative networks (e.g., the DMN) and task‐positive networks (e.g., the FPN and SN) in WM execution (Liang et al., 2016). We deciphered a brain‐wide reconfiguration map where the function connectivities across the brain rewired to the DMN when the WM loads increased, which is consistent with the behavior of the DMN degrading its activation but increasing its connectivity to other networks across cognitive loads (Čeko et al., 2015; Liang et al., 2016; Vatansever et al., 2017). Furthermore, we showed that the FPN‐group, including the SN and DAN, increased interactions at low level demands (0‐back), thus providing evidence of the executive role of the FPN (Scott et al., 2015), which is generally coordinated by the SN (Seeley et al., 2007). These non‐mono trends in connectivity changes have also been uncovered in different stages of WM tasks (Koshino et al., 2014; Piccoli et al., 2015), and the DMN is consistently found to have an important role in coordinating computing resources (Sambataro et al., 2010; Xin & Lei, 2015).

In this study, we established a significant inverse correlation (p < .05, after FDR correction) between the magnitude of the network reconfigurations measured by NCD and WM performance evaluated by RT. This suggests that individuals with high WM capacity can achieve their goals with less effort, which corroborates the results of Vatansever et al. (2015) and Schultz et al. (2016). By exploring the whole brain network using correlation analyses, we identified the FPN, DMN, and SN to be core networks. Interestingly, these networks dominated the whole brain network reconfiguration and were correlated with WM performance. This confirmed the core network findings and coincided well with the connection‐based (Figure 3) and modularity‐based analyses (Figure 4). In addition, the three core networks (DMN, FPN, and SN) of WM coincided with the triple‐network theory proposed by Menon (2011), where general cognitive disorders include disruptions and dysfunctions of these three networks. Our study signified the importance of the triple‐network in a specific and complex cognitive task, that is, WM. In contrast to existing research specifically investigating individual networks related to WM (Čeko et al., 2015; Sambataro et al., 2010; Xin & Lei, 2015), we presented comprehensive findings for characterizing network reconfiguration across WM loads and provided evidence of a triple‐network model for WM. The significant correlation between core networks and WM scores could be utilized as a novel way to evaluate and predict the capability of a brain performing WM tasks.

4.3. Methodological considerations

The results presented here are based on fully‐functional connections (both positive and negative; Bassett et al., 2011; Vatansever et al., 2015). However, the interpretation of negative connections is still controversial (Bullmore & Sporns, 2009; Murphy et al., 2009). To address this issue, we validated all the main findings by removing the negative functional connectivities (Liu et al., 2016). As seen in the Supporting Information, Figures S4 and S5, the FPN was identified as the least flexible of the brain networks but with the strongest connections across the brain; furthermore, the reconfiguration pattern of the core networks across the WM loads was exactly replicated. In calculating the correlations between the network (Figure 2)/connectivity (Table 1) reconfigurations and behavioral performance, we also replicated the findings by adding sex, age, and head motions as confounding factors (see Section 2 in the Supporting Information). Additionally, due to the undetermined effects of the global signal on functional connectivity (Liu et al., 2017; Wong et al., 2016), we validated our findings separately with and without regressing out the global signal and found our results to coincide well (see Validation section in the Supporting Information,). Collectively, these additional validations demonstrated the robustness of our findings. For more extensive validation of the current study, we released all source code (Matlab) in https://github.com/nmzuo/core_networks.

The current findings characterized in detail the roles of the FPN‐ and DMN‐groups in WM executions and the network reconfiguration patterns across WM loads. These findings were only based on resting, 0‐back, and 2‐back datasets; thus, using more detailed load levels in future studies would be helpful in deciphering the reconfiguration patterns more precisely.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supporting Information

Zuo N, Yang Z, Liu Y, Li J, Jiang T. Core networks and their reconfiguration patterns across cognitive loads. Hum Brain Mapp. 2018;39:3546–3557. 10.1002/hbm.24193