Abstract
Blind source separation (BSS) is commonly used in functional magnetic resonance imaging (fMRI) data analysis. Recently, BSS models based on restricted Boltzmann machine (RBM), one of the building blocks of deep learning models, have been shown to improve brain network identification compared to conventional single matrix factorization models such as independent component analysis (ICA). These models, however, trained RBM on fMRI volumes, and are hence challenged by model complexity and limited training set. In this article, we propose to apply RBM to fMRI time courses instead of volumes for BSS. The proposed method not only interprets fMRI time courses explicitly to take advantages of deep learning models in latent feature learning but also substantially reduces model complexity and increases the scale of training set to improve training efficiency. Our experimental results based on Human Connectome Project (HCP) datasets demonstrated the superiority of the proposed method over ICA and the one that applied RBM to fMRI volumes in identifying task‐related components, resulted in more accurate and specific representations of task‐related activations. Moreover, our method separated out components representing intermixed effects between task events, which could reflect inherent interactions among functionally connected brain regions. Our study demonstrates the value of RBM in mining complex structures embedded in large‐scale fMRI data and its potential as a building block for deeper models in fMRI data analysis.
Keywords: blind source separation, functional magnetic resonance imaging, restricted Boltzmann machine
1. INTRODUCTION
Functional magnetic resonance imaging (fMRI) has played a major role in the study of the human brain function (Friston 2009). The high dimensionality of fMRI data, however, make it challenging to resolve meaningful features embedded in the data. Blind source separation (BSS) is one of the fundamental techniques used to address this problem. It has been instrumental to the understanding of the functional organization of the human brain and its alterations in neuropsychiatric disorders (Biswal et al., 2010; Bullmore and Sporns, 2009; Calhoun and Adali, 2012; Calhoun, Adali, Pearlson, & Pekar, 2001; Damoiseaux et al., 2006; Mckeown and Sejnowski, 1998; Seeley Seeley, Crawford, Juan, Miller, & Greicius, 2009; Smith et al., 2009; van de Ven, Formisano, Prvulovic, Roeder, & Linden, 2004).
BSS aims to identify a set of latent time courses (TCs) and the corresponding spatial maps (SMs) from the observed fMRI data. This process is conventionally modeled as a single matrix factorization (SMF) problem under the assumption that the observed data are produced by a linear combination of latent sources (Calhoun et al., 2001; Mckeown and Sejnowski, 1998). Various approaches have been proposed to solve this SMF problem with different constraints, including principal component analysis (PCA) to enforce orthogonality (Andersen, Gash, & Avison, 1999; Baumgartner et al., 2000; Friston, Frith, Frackowiak, & Turner, 1995), independent components analysis (ICA), and its versatile extensions to group data to optimize independence (Beckmann and Smith, 2005; Bell and Sejnowski, 1995; Calhoun et al., 2001; Damoiseaux et al., 2006; Mckeown and Sejnowski, 1998; van de Ven et al., 2004), as well as sparse PCA (Ulfarsson and Solo, 2007; Zou, Hastie, & Tibshirani, 2012) and sparse representation (Lee, Tak, & Ye, 2011; Lee et al., 2016; Lv et al., 2015a, 2015b; Zhao et al., 2015) to enforce sparsity. Among these SMF models, ICA is the most commonly used method.
The recent emergence of deep learning models has revolutionized latent feature learning and data representation in complex and large‐scale data (Bengio, Courville, & Vincent, 2012; Goodfellow et al., 2014; Graves, Mohamed, & Hinton, 2013; Greff, Srivastava, & Schmidhuber, 2016; He, Zhang, Ren, & Sun, 2016; He, Gkioxari, Dollár, & Girshick, 2017; Hinton, 2002; Hinton, Osindero, & Teh, 2006; Hinton and Salakhutdinov, 2006; Krizhevsky, Sutskever, & Hinton, 2012; LeCun, Bengio, & Hinton, 2015; Lee, Grosse, Ranganath, & Ng, 2009; Simonyan & Zisserman, 2014; Vincent, Larochelle, Lajoie, Bengio, & Manzagol, 2010; Zeiler and Fergus, 2014). Supervised deep learning models have already shown superb performance in image and object recognition (Girshick, Donahue, Darrell, & Malik, 2014; Greff et al., 2016; He et al., 2016, 2017; Jia et al., 2014; Krizhevsky et al., 2012; Lee et al., 2009; Simonyan & Zisserman, 2014; Zeiler & Fergus, 2014) and speech and acoustic modeling (Dahl, Yu, Deng, & Acero, 2012; Deng, Hinton, & Kingsbury, 2013; Graves et al., 2013; Hinton et al., 2012; Mohamed, Dahl, & Hinton, 2012; Sainath, Mohamed, Kingsbury, & Ramabhadran, 2013; Sak, Senior, & Beaufays, 2014). Training supervised deep learning models usually requires large‐scale labelled datasets. Although large‐scale datasets are becoming available in some medical imaging applications such as lesion segmentation (Kamnitsas et al., 2017) and pathology detection (Shin et al., 2016), it is uncommon for fMRI studies. On the other hand, unsupervised deep learning models such as restricted Boltzmann machine (Castro et al., 2016; Hjelm et al., 2014; Plis, Hjelm, Salakhutdinov, & Calhoun, 2013), deep Boltzmann machines (Suk, Lee, Shen, & Initiative, 2014), deep belief networks (Jang, Plis, Calhoun, & Lee, 2016), and stacked auto‐encoders (Kim, Calhoun, Shim, & Lee, 2016; Shin, Orton, Collins, Doran, & Leach, 2013; Suk, Wee, Lee, & Shen, 2016) are less dependent on labeled datasets and have shown great promises for resolving meaningful features in complex neuroimaging data.
As labels (ground truth) are often unavailable in fMRI BSS, neither for the SMs nor the TCs, unsupervised deep learning models are naturally desirable. Schmah et al. compared generative and discriminative training of restricted Boltzmann machines (RBMs) for classification of fMRI images (Schmah, Hinton, Zemel, Small, & Strother, 2008). They showed that training a pair of RBM models generatively rather than discriminatively yielded better discriminative performance. Hjelm et al. (2014) applied a restricted Boltzmann machine (RBM) (Hinton, 2002), one of the building blocks of deep learning models, to fMRI volumes for fMRI BSS. It treated each fMRI volume as a separate element to learn a set of SMs, or intrinsic brain networks, that constitute voxels sharing concurrent signal fluctuations. In contrast to SMF models, RBM is formulated as a density estimation problem. It further avoids potential information loss associated with PCA, a prerequisite for ICA. This fMRI volume‐based RBM approach identified comparable SMs with improved TC extraction as compared to ICA, supporting the application of RBM in fMRI BSS.
This fMRI volume‐based RBM approach, however, has two potential limitations. First, applying RBM to volumes does not interpret time courses explicitly. Alternatively, it re‐interprets the trained RBM as an SMF model and uses the learned SMs as a demixing matrix to infer the corresponding latent TCs (Hjelm et al., 2014). This implicit interpretation, however, cannot fully account for the complexity and heterogeneity embedded in the temporal structures of fMRI signals. FMRI signals of a brain region are not only shaped by its intrinsic activities, but also modulated by its functional interactions with other brain regions; in particularly for heteromodal regions, fMRI signals may contain intermixed effects of divergent neural processes (Duncan, 2010; Jiang et al., 2015; Lv et al., 2015b; Pessoa, 2012). Therefore, an implicit interpretation of fMRI time courses may not take the full advantage of RBMs in latent feature learning. Second, applying an RBM to fMRI volumes is challenging for model training, with extremely high model complexity against a relatively small number of training samples. The training model here is source‐by‐voxel and could be in a very high dimensional space (e.g., millions of voxels), whereas the number of training samples is typically small (e.g., thousands of volumes). Training such a model faces technical difficulties in parameter tuning, model convergence, and data representation.
To address these limitations, we have proposed a BSS method that directly applied RBM to fMRI time courses in our pilot study (Huang et al., 2016). For simplification, hereafter we refer to this method as spatial RBM (sRBM) and the one that applies RBM to fMRI volumes (Hjelm et al., 2014) as temporal RBM (tRBM), to draw a parallel with spatial and temporal ICA. In comparison to tRBM, sRBM provides an explicit interpretation by treating each time course as an input sample. It aims to learn a set of latent factors (TCs) that could best describe the probability distribution of the input time courses so that the inputs can be most effectively represented. Thus, sRBM can potentially improve resolving meaningful latent TCs. Furthermore, when RBM is applied to fMRI time courses, the model under training is source‐by‐time (typically in thousands). Thus, the model complexity is substantially reduced. At the same time, the training set is composed of time courses of all voxels and could be very large (e.g., millions), especially when applied to spatially concatenated group‐wise population‐scale data. As a result, training efficiency can be substantially improved and potentially leads to more accurate BSS. Model simplification through modeling time courses rather than volumes is similar to that in a Diet networks (Romero et al., 2016) for feature mining in high‐dimensional single nucleotide polymorphisms (SNPs) data. We have showed that sRBM outperformed ICA using the Human Connectome Project (HCP) (Van Essen et al., 2012) Motor task fMRI as a test case in our pilot study (Huang et al., 2016). In this work, we provided more technical details and extensive evaluation using the full HCP task fMRI datasets (including Motor, Emotion processing, Gambling, Language, Relational processing, Social cognition, and Working memory tasks). Furthermore, we directly compared the performance of sRBM with tRBM (Hjelm et al., 2014) in BSS and demonstrated that the separation of task‐related components is much improved with our approach. More importantly, our method identified latent components related to intermixed effects, which could represent functional interactions among spatially distributed brain regions. Our results demonstrated the superiority of sRBM over previous BSS models and provided direct evidence of the advantages of using unsupervised deep learning models in fMRI data analysis.
2. METHODS
2.1. Restricted Boltzmann machine
RBM is a probabilistic energy‐based model. It fits a probability distribution model over a set of visible random variables to the observed data (Hinton, 2002; Hinton and Salakhutdinov, 2006). An RBM model can be represented by a bipartite graph (Figure 1). It consists of two layers: the visible layer binding with input and the hidden layer representing latent factors. The units in the two layers are connected by weights. There are no visible–visible nor hidden–hidden connections, introducing the conditional independence between each set of units. Inputs are modeled by RBMs via latent factors expressed through the interaction between hidden and visible variables. RBM defines the probability by the energy of the system, , such that
| (1) |
where is the partition function. For modeling approximately normally distributed real data, is defined in Gaussian–Bernoulli RBM (GB‐RBM) as:
| (2) |
where is the weight between visible variable and hidden variable , and are the bias of visible and hidden variables, respectively. is the standard deviation of a quadratic function for each centered on its bias . Theoretically, needs to be estimated along with the other parameters. However, in practice a faster and effective solution is to normalize the distribution of the data to have zero mean and unit variance (Nair and Hinton, 2010; Melchior, Fischer, & Wiskott, 2016). In RBM, the parameters ( ) are optimized to maximize the log‐likelihood of the data. One common solution to this problem is to find the gradient of the log‐likelihood with respect to the parameters. While the gradient has a closed form, it is intractable due to the derivative of the log partition function . This problem is addressed by an approximation to the gradient through Markov Chain Monte Carlo (MCMC) where contrastive divergence (CD) with truncated Gibbs sampling is applied to improve computational efficiency (Hinton, 2002).
Figure 1.
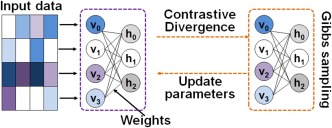
The scheme of an RBM model. An RBM can be represented by a bipartite graph. It consists of two layers: the visible layer binding with input and the hidden layer representing latent factors. The units in the two layers are connected by weights. There are no visible–visible nor hidden–hidden connections [Color figure can be viewed at http://wileyonlinelibrary.com]
Regularizations including L1‐decay on and Kullback‐Leibler (KL) sparsity on the hidden layers are typically employed in RBMs (Hinton, 2002; Hinton and Salakhutdinov, 2006). with L1‐decay that enforces the sparsity of can be updated according to:
| (3) |
where is the learning rate, is a single datapoint, and is for L1‐decay. Taking advantage of parallel and GPU processing, the learning algorithm was implemented to process data in batches, where several datapoints are processed in parallel. For batches of k datapoints, k RBMs are trained in parallel with their contributions to the learning gradient averaged. KL‐sparsity can be formulated as
| (4) |
| (5) |
| (6) |
where J is the KL‐sparsity penalty. controls the tradeoff between and KL‐sparsity penalty, , is target sparsity which indicates the sparsity of simultaneously active hidden units. is the real sparsity of the model during training, and is the activation function. is a sample in a batch, and k is the number of samples in the batch. In the converged model, each hidden unit can be regarded as a latent factor of the inputs, and the inputs can be reconstructed based on the latent factors by one‐step Gibbs sampling (Hinton & Salakhutdinov, 2006). Due to the sparsity constraint in RBMs, the reconstruction of an input sample recruits a limited number of latent factors.
2.2. FMRI blind source separation via RBMs
Applying RBMs for fMRI blind source separation (BSS) cannot be formulated as a single matrix factorization (SMF) problem, however, it shares similar structures in terms of the relationship among the observed fMRI data, latent time courses (TCs), and spatial maps (SMs). After training, RBMs provide a closed‐form representation of the distribution underlying the input fMRI data. The hidden units model the dependencies p(h | v) between the fMRI observations, and can be viewed as non‐linear feature (latent factor) detectors (Fischer and Igel, 2014). When applying RBMs to fMRI volumes (Hjelm et al., 2014), the learned latent factors represent the spatial maps (SMs) of fMRI components. In the model, the visible variables v span the input space as a single fMRI volume. Thus, the number of visible variables, nv, is the number of voxels. The number of hidden variables, nh, is the number of latent sources. The weights from a single hidden unit to all visible units (voxels) represent an SM. In this context, the model parameters are and could be in an extremely high dimensional space while training samples are limited, resulting in difficulties in model training.
When applying RBMs to fMRI time courses as proposed in this study, the learned latent factors represent the TCs of fMRI components. Figure 2 illustrates applying RBMs to fMRI time courses for BSS. FMRI data from multiple subjects are spatially aggregated and used as training samples (Figure 2a). Each visible variable vi corresponds to a temporal observation of a voxel, that is, the number of visible variables is the length of fMRI scans (Figure 2b, e.g., 284 in HCP Motor task). The dimension of the parameter (Figure 2c) under optimization is time‐by‐sources. Thus, the model complexity can be largely reduced. At the same time, large‐scale training samples (the total number of voxels in multiple subjects) are available. The output of the model, F (Figure 2e), is source‐by‐voxel.
Figure 2.
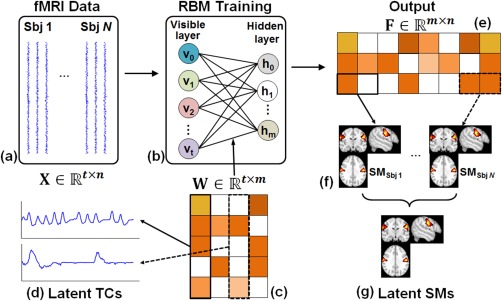
The framework of BSS by applying RBM to the TCs of spatially concatenated fMRI signals of multiple subjects. (a) Spatially concatenated multisubject fMRI data, where N is the number of subjects, t is the number of time points in fMRI sequence, and n is the number of voxels in one subject. (b) RBM training. The number of visible units is t and the number of hidden units is m which specifies the number of latent components. (c) Optimized parameter W. Each column in W is the TC of a latent component (d). (e) The output of RBM model F, representing the parametric representation of inputs based on W. Each row in F represents spatially concatenated SMs of multi‐subjects (f). (g) Groupwise SMs can be derived by group statistical analysis [Color figure can be viewed at http://wileyonlinelibrary.com]
In the perspective of latent feature learning, the weights from a single hidden unit to all visible variables represents a latent factor of the inputs and W serves as a set of bases that optimize the representation of the inputs. Each column in F, ( , Figure 2e), measures the responses of the latent factors to sample j, representing a parametric representation of sample j based on W. Each row in F ( ) measures the responses of latent factor i to the full time courses. In the perspective of fMRI BSS, represents the TC of an intrinsic brain network (Figure 2d), and represents the group of SMs (Figure 2f) associated with an intrinsic brain network i for all the subjects. Group‐wise SMs (Figure 2g) can be derived by a classic group‐wise hypothesis test (Calhoun et al., 2001; Guo & Pagnoni, 2008).
3. COMPARISON STUDIES
We compared sRBM with group ICA and tRBM (Hjelm et al., 2014). We used the HCP Q1 task‐fMRI dataset (Van Essen et al., 2012), including seven well‐established tasks (Motor, Emotion processing, Gambling, Language, Relational processing, Social cognition, and Working memory) (Van Essen et al., 2012). The experiments of these tasks are outlined in a Supporting Information, data description. Intrinsic brain network identification and comparison studies were performed on each task separately. We analyzed the minimally preprocessed data released by HCP, which were motion and spatial distortion corrected (Glasser et al., 2013), and processed with spatial smoothing, temporal prewhitening, slice‐timing correction, and global drift removal using FSL (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012). Voxels outside the brain were removed. The time course of each voxel was normalized to have zero mean and unit variance in each fMRI run independently. Task paradigms and activation detected by GLM implemented in FSL (Jenkinson et al., 2012) are regarded as ground‐truth for TCs and SMs, respectively.
4. EXPERIMENTAL SETTINGS
To match the memory capacity of our local machine, fMRI data of 20 randomly selected subjects were used in our experiments. In sRBM, the fMRI signals of the 20 subjects were aggregated (228,453 voxels in each subject) to form a training set (Fig. 2a), where t is the length of fMRI signal, n is the total number of voxels (228,453 × 20 = 4,569,060). The batch size k was empirically set as 500. The convergence of RBM typically requires multiple epochs of training, where an epoch corresponds to a cycle through the complete training set in batches. We trained RBM with 800,000 batch‐iterations (around 88 epochs) as a fairly conservative strategy—all RBM models converged after far <88 epochs in our experiments. Group‐wise ICA was performed using the GIFT toolbox (http://mialab.mrn.org/software/gift/) (Calhoun et al., 2001). The number of independent components in ICA was automatically estimated using GIFT. In tRBM, each volume was normalized to have zero mean and unit variance. Then all volumes were temporally concatenated into the dataset used for model training. The RMB model was constructed using 228,453 (the number of voxels) visible units and 100 hyperbolic tangent hidden units, and then trained with a batch size of 5. Estimated SMs of components were acquired from the converged RBM model. Then those SMs were used a demixing matrix to obtain corresponding TCs.
5. RESULTS
5.1. Parameter tuning and model convergence
The sRBM model was constructed using 100 sigmoidal hidden units to learn 100 latent fMRI components, keeping the settings consistent with tRBM (Hjelm et al., 2014). The target sparsity specifies the percentage of active hidden units. To separate the components that match the task paradigms the most, we set (one active hidden unit) throughout all HCP tasks. Other hyperparameters including for learning rate and L1 weight decay were tuned empirically to minimize reconstruction error over training ( = 0.005, and L1 = 0.002 in the Motor task). The sRBM model converged approximately after 6 epochs, as indicated by the reconstruction error and model sparsity (Figure 3a for HCP Motor task). An inflection point in the reconstruction error was observed around 4,000 epochs, where the model sparsity was around 0.073. When the reconstruction error was stabilized, the model sparsity approached 0.01 (the target sparsity), relatively decreased by 7.2 times. Thus, the increase of reconstruction error is reasonable as far less components were used to reconstruct the input data. In comparison, the tRBM converged after about 90 epochs (Figure 3b), consistent with the previous report (Hjelm et al., 2014). As model complexity of sRBM is much reduced compared to tRBM, model training was substantially accelerated.
Figure 3.

(a) Convergence of sRBM model in HCP Motor task. The model converged approximately after 6 epochs. For better visualization, we only showed the reconstruction error and sparsity for 60,000 out of the in‐total 800,000 batches. (b) Convergence of tRBM in HCP Motor task. The model converged approximately after 90 epochs [Color figure can be viewed at http://wileyonlinelibrary.com]
5.2. Evaluation of sRBM in fMRI data representation
Next, we assessed the performance of sRBM in modeling the input fMRI data. We calculated the Pearson correlation coefficient between the reconstructed fMRI signal and the original fMRI signal for each voxel. The correlation maps were averaged over the 20 subjects. Most gray matter voxels can be reconstructed well by visual inspection (Figure 4 for HCP Motor task), especially for those voxels that constitute the SMs of task‐related components (as quantified in Table 1). In contrast, white matter voxels were poorly represented, indicating that training samples in white matter were automatically regarded as noise and contributed little to model training. Similar results were observed in the remaining 6 tasks (Table 1 and Supporting Information, Figure 1). These observations demonstrated that the learned latent components could represent well the functional activity patterns embedded in the fMRI data.
Figure 4.
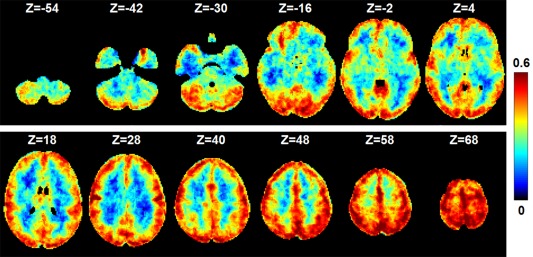
The performance of the trained sRBM model in the representation of input fMRI data. The map shows the Pearson correlation coefficients between the reconstructed and input fMRI signals in HCP Motor task. We calculated the Pearson correlation coefficient between the reconstructed fMRI signal and the original fMRI signal for each voxel. The correlation maps were averaged over the 20 subjects [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 1.
The performance of fMRI signal representation in the voxels that constitute the SMs of task‐related components
| Motor | Language | |||||||
|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | E4 | E5 | E6 | E1 | E2 | |
| R | 0.51 | 0.59 | 0.52 | 0.59 | 0.51 | 0.52 | 0.55 | 0.48 |
| Emotion | Social | Relational | Gambling | |||||
| E1 | E2 | E1 | E2 | E1 | E2 | E1 | E2 | |
| R | 0.55 | 0.54 | 0.66 | 0.65 | 0.53 | 0.59 | 0.59 | 0.57 |
| Working memory | ||||||||
| E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | |
| R | 0.54 | 0.60 | 0.64 | 0.63 | 0.41 | 0.50 | 0.63 | 0.54 |
r is the average Pearson correlation coefficient between the reconstructed fMRI signal and original fMRI signal over all the task‐related voxels.
6. EVALUATION OF sRBM IN BSS
As the sRBM model could successfully represent input fMRI data, we further evaluated its performance in BSS. Again, we focused on the Motor task as the neuroanatomical correlates of motor control are well established in the literature. In particular, this task tests the known lateralization phenomenon, that is, the movement of the left body is predominantly controlled by the right motor cortex while the movement of the right body by the left motor cortex.
6.1. Task‐related components
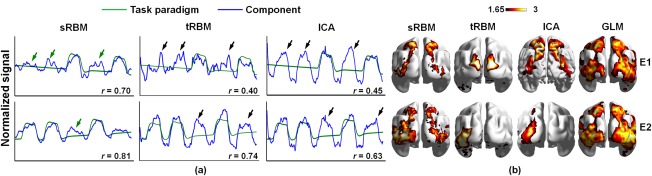
For each event, the task‐related component was identified as the one whose TC correlated best with the corresponding paradigm. The TCs of task‐related components identified by sRBM approach follow the paradigms more consistently than those identified by tRBM and ICA (Fig. 5a). Across all the six events, the TCs of tRBM and ICA components showed much more overshooting than sRBM components. As quantified by the Pearson correlation coefficients between the TCs and task paradigms (r in Figure 5a), the TCs of sRBM components correlated with the paradigms much better in E2‐E5 than the tRBM and ICA components; the correlations in E1 and E6 were similar between the three approaches (Figure 5a). Importantly, sRBM appears to be more accurate and specific than ICA in separating task‐related components. For the two events designed to activate lateralized motor responses, E2 (moving left toes) and E4 (moving right toes), tRBM and ICA failed to reveal any lateralization effect (e.g., ICA identified the same component) (Figure 5a). The corresponding TCs reflect strong intermixed effects across the two events (highlighted by black arrows)—the first and third peaks correspond to E2 activations, whereas the second and forth peaks correspond to E4 activations. In contrast, sRBM successfully identified event‐specific components for E2 and E4, with minimal intermixed effects in the corresponding TCs. In another pair of lateralization tasks, E3 and E5, tRBM and ICA were able to identify different components. Their TCs, however, still suffered from moderate intermixed effects (highlighted by green arrows in Figure 5a). Notably, tRBM was not able to identify task‐related TCs in E3.
Figure 5.
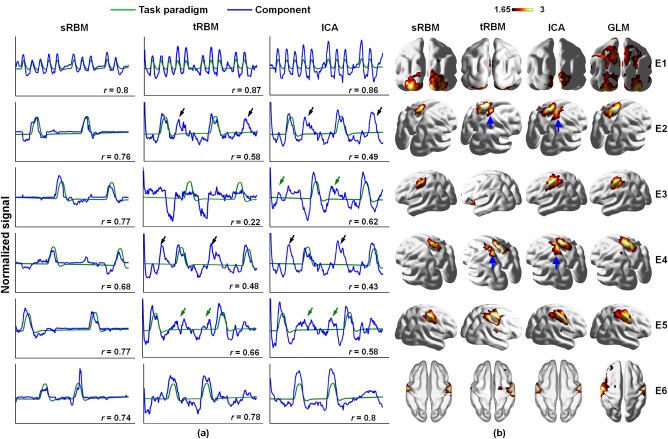
Comparison of TCs (a) and SMs (b) of task‐related components between sRBM, tRBM, and ICA in HCP Motor task. r is the Pearson correlation coefficient between the task‐related TC and the task paradigm in each event. The black and green arrows highlight intermixed effects in TCs. The blue arrows highlight false‐positive activations in SMs in tRBM and ICA [Color figure can be viewed at http://wileyonlinelibrary.com]
The SMs of task‐related components in sRBM also match the GLM activation patterns better than tRBM and ICA components (Figure 5b), as quantified by spatial overlap measures (Table 2). As discussed above, the ICA and tRBM components showed strong intermixed effect in the TCs and false positive activations in the SMs (highlighted by blue arrows in Figure 5b). In contrast, no false positive activation in E2 or E4 was observed in sRBM. As tRBM failed to separate the task‐related TC in E3, the corresponding SM does not reveal the true activations. Overall, sRBM showed improved performance in separating task‐related components compared to ICA and tRBM.
Table 2.
Overlap of the SMs in sRBM, tRBM, and ICA with GLM activations in HCP Motor task
| E1 | E2 | E3 | E4 | E5 | E6 | |
|---|---|---|---|---|---|---|
| sRBM‐GLM | 0.27 | 0.49 | 0.53 | 0.37 | 0.41 | 0.52 |
| tRBM‐GLM | 0.13 | 0.22 | 0.06 | 0.14 | 0.48 | 0.31 |
| ICA‐GLM | 0.19 | 0.33 | 0.35 | 0.27 | 0.31 | 0.51 |
6.2. Components related to intermixed effects
In the previous experiment, we showed that tRBM and ICA are more vulnerable to intermixed effects across task events than sRBM. This difference in BSS performance potentially reflects that the sRBM model could model intermixed effects more effectively. To test this hypothesis, we investigated the contribution of sRBM components in reconstructing the time courses of task‐related voxels, defined as the voxels in the corresponding task‐related sRBM components. While all sRBM components were included in the reconstruction, each voxel recruited only a subset of components due to the sparsity constraint (hyperparameter ρ) in sRBM. We then quantified the contribution of each component by calculating the percentage of the voxels recruiting this component relative to the total task‐related voxels. The results for the 6 components with top probabilities in each event are summarized in Table 3.
Table 3.
Top components contributing to the reconstruction of task‐related fMRI signals in HCP Motor task
| E1 (%) | E2 (%) | E3 (%) | E4 (%) | E5 (%) | E6 (%) |
|---|---|---|---|---|---|
| #47/100 | #56/100 | #41/100 | #21/100 | #30/100 | #63/100 |
| #72/21.2 | #42/40.2 | #78/47.2 | #98/46.1 | #29/6.4 | #3/45.1 |
| #68/4.2 | #98/20.4 | #44/23.7 | #42/22.5 | #33/5.1 | #62/39.5 |
| #16/4.1 | #95/15.8 | #93/18.9 | #13/13.1 | #16/4.7 | #16/35.8 |
| #10/2.6 | #13/15.6 | #20/11.9 | #95/9.80 | #99/4.5 | #85/21.3 |
| #95/2.3 | #59/14.9 | #85/2.5 | #60/8.90 | #15/3.9 | #96/14.4 |
Top six components are shown. For each component, the component index (#) and its probability (%) are listed. The top component is the task‐related component. Concurrent components in E2 and E4 are highlighted by bold.
Strong intermixed effects exist between E2 and E4, as demonstrated by the average time course of task‐related voxels in each event (Figure 6a). Thus, reconstructing the time courses of these voxels is likely to share common sRBM components. Consistently, among the top 6 components in E2 and E4, four were identified concurrently in both events (#13, #42, #95, and #98, bold in Table 3). Figure 6(b–e) show the corresponding TCs and SMs of those concurrent components. For two of the concurrent components (#42 and #98), the TCs and SMs showed shared activations by both E2 and E4 (Figure 6b,c), reflecting intermix effects between the two events. Thus, these concurrent components likely reflect intermixed effects between E2 and E4. Components #13 and #95 did not show significant intermixed effects, and may be related to the visual cue (E1) and global noise (Figure 6d,e). In summary, we showed that the proposed sRBM not only identified task‐related components but also model intermixed effects, resulting in good separation between task‐related and intermixed effects and hence improved performance in representing the fMRI signals.
Figure 6.
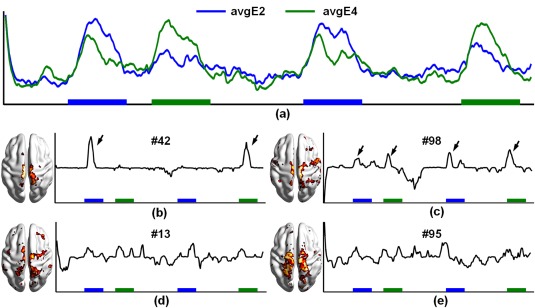
Latent components related to intermixed effects in E2 and E4 in HCP Motor task in sRBM. (a) Average time courses of task‐related voxels in E2 and E4. (b)–(e) TCs and SMs of the common components in E2 and E4. Color boxes indicate the presence of the events [Color figure can be viewed at http://wileyonlinelibrary.com]
7. EVALUATION ON OTHER HCP TASKS
To further validate our approach, we performed similar analyses on the remaining 6 HCP tasks. Consistent with the Motor task, we found that sRBM can separate latent components with improved accuracy and specificity over ICA and tRBM across all the tasks (Supporting Information, Figure 2 and Table 4). The TCs of sRBM components better correlated with the task paradigms (Supporting Information, Figure 2). For example, while ICA and tRBM could not differentiate different events in Working memory and Gambling tasks (Supporting Information, Figure 2b), sRBM successfully separated event‐specific components. The SMs in sRBM showed greater overlaps with GLM activations than ICA and tRBM in most cases (Supporting Information, Figure 2 and Table 4). We next focused on the HCP Social and Language tasks to further illustrate the impact of intermixed effects on BSS performance, as the former was associated with the strongest intermixed effects among all tasks while the latter showed none.
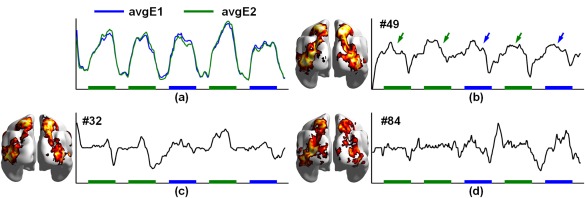
In the Social task, the average time courses of the task‐related voxels in the two events were almost identical (Figure 7a), showing strong intermixed effects across the two events. ICA and tRBM components identified for the two different events (E1 and E2) showed almost identical TCs (Figure 8a), with peak activations corresponding to both events (black arrows). Intermixed effects were also observed in TCs of sRBM components, but at much weaker levels (Figure 8a, green arrows). Quantitatively, sRBM components showed higher temporal correlations (Figure 8a) with task paradigms and greater spatial overlaps with GLM SMs than ICA and tRBM components (Table 4). Similar to the observations in the Motor task, sRBM successfully separated components representing intermixed effects. More specifically, the representation of the fMRI signals in activations for one event recruited the component related to the other event (italic and underlined bold in Supporting Information, Table 1). Three additional common components were identified by sRBM, including components #49, #32, and #84 (italic bold in Supplementary Table 1). In particular, the TCs of component #49 follow the concurrence of the two events well, where peaks are highlighted by blue and green arrows corresponding to E1 and E2, respectively (Figure 7b). Although intermixed effects are inevitable in the TCs of sRBM components in the Social task, the SMs are more meaningful compared with tRBM and ICA.
Figure 7.
Comparison of TCs (a) and SMs (b) of task‐related components between sRBM, tRBM, and ICA in HCP Social task. The arrows highlight intermixed task effects in TCs [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 8.
Latent components related to intermixed effects HCP Social task in sRBM. (a) Average time courses of the task‐related voxels in E1 and E2. (b)–(d) TCs and corresponding SMs of the common components in E1 and E2. Color boxes indicate the presence of the events [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 4.
Overlap of the SMs in sRBM, tRBM, and ICA with GLM activations in other HCP tasks
| Social | Language | Relational | Gambling | Emotion | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E1 | E2 | E1 | E2 | E1 | E2 | E1 | E2 | |
| sRBM‐GLM | 0.30 | 0.30 | 0.24 | 0.41 | 0.27 | 0.38 | 0.41 | 0.36 | 0.47 | 0.23 |
| ICA‐GLM | 0.14 | 0.05 | 0.15 | 0.14 | 0.31 | 0.32 | 0.33 | 0.34 | 0.45 | 0.50 |
| tRBM | <0.01 | 0.21 | 0.013 | 0.027 | 0.18 | 0.32 | 0.11 | 0.21 | 0.21 | 0.02 |
| Working memory | ||||||||||
| E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | |||
| sRBM‐GLM | 0.38 | 0.40 | 0.37 | 0.44 | 0.32 | 0.36 | 0.32 | 0.29 | ||
| ICA‐GLM | 0.02 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | 0.02 | <0.01 | ||
| tRBM | 0.01 | 0.12 | 0.12 | 0.02 | 0.05 | <0.01 | 0.01 | 0.1 | ||
In the Language task, sRBM, tRBM, and ICA achieved comparable performance in identifying task‐related TCs, which followed well the task paradigms without any intermixed effects (Figure 9a). The corresponding SMs, however, were different. The SMs in tRBM and ICA barely overlap with GLM results (underlined in Table 4) with no activations in the superior and middle temporal gyri (Figure 9b). SRBM, on the other hand, produced very similar SMs as to those in GLM (Figure 9b and Table 4). These results showed that sRBM outperforms tRBM and ICA in conditions with little intermixed effects.
Figure 9.
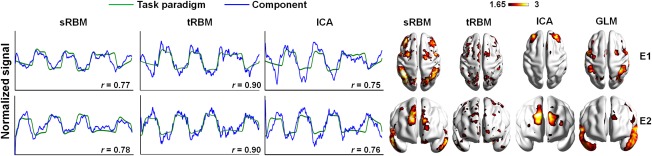
Comparison of TCs (a) and SMs (b) of task‐related components between sRBM, tRBM, and ICA in HCP Language task [Color figure can be viewed at http://wileyonlinelibrary.com]
8. DISCUSSION
In this article, we presented a novel BSS approach that applies RBM, an unsupervised deep learning model to fMRI data analysis. The proposed approach interprets fMRI time courses explicitly to take advantage of deep learning models in latent feature learning, compared to the previous approach that applied RBM to fMRI volumes (Hjelm et al., 2014). Our method substantially improves model training by reducing model complexity and increasing the scale of training samples. To validate our approach, we analyzed seven HCP task‐fMRI datasets, and compared our method with ICA, tRBM, and GLM. Our results demonstrated that the proposed BSS model outperformed ICA and tRBM with better temporal correlation and greater spatial overlap. In addition, the proposed sRBM method could effectively separate latent components related to intermixed effects, resulting in many fewer false activations than ICA and tRBM. Our results demonstrated that sRBM can better capture the complex structures embedded in fMRI data, supporting the use of deep learning models in fMRI data analysis.
The improved performance of sRBM could be related to its ability to model intermixed effects in addition to task‐specific activations. The sRBM components representing intermixed effects followed well the concurrence of multiple events temporally and encompassed the joint‐activations by multiple events spatially (Figures 6b and 7b). This observation indicates that the TCs of these components inherently represent the latent temporal activities of these joint‐activation regions. Given the well‐established resting state connectivity patterns between these regions, it is plausible that these sRBM components represent intrinsic interactions among those brain regions. Therefore, the proposed method not only can separate latent components dedicated to task performance but also may separate the ones related to functional interactions among spatially distributed brain regions. This feature could be particularly desirable for analyzing fMRI data acquired during naturalistic stimulus such as watching videos (Hasson and Honey, 2012), which is likely to engage broad and dynamic functional interactions (Bartels and Zeki, 2005). In addition, the proposed method can potentially decompose the fMRI signal of a single voxel/region into components related to its evoked activities driven by task performance and its intrinsic interactions with other brain regions.
Despite its advantages in latent feature learning and the superb performance in BSS in fMRI demonstrated here, sRBM still faces the challenge of parameter tuning. Parameters are often tuned using cross‐validations over an independent testing dataset with ground truth in supervised deep learning models. However, this is not practical in our study as there is no ground truth in fMRI BSS. Thus, in our model, the parameters were tuned empirically and experimentally to minimize reconstruction error over training. We examined how those trained models performed on an independent test dataset by taking the Motor task as an example. The test dataset consists of HCP Motor task fMRI data of 20 subjects that were not used in the training stage. We then used the trained model to represent the test dataset, and the output is a group of spatial maps in the 20 test subjects. First, we measured how well the test data are represented by the trained model. To do this, we calculated the Pearson correlation coefficient between the reconstructed fMRI signal and the original test fMRI signal for each voxel. The correlation maps were averaged over the 20 test subjects, as shown in Figure 10. The reconstruction performance in the test dataset is comparable with that in the training stage in gray matter, though it is relatively lower in white mater. These results demonstrate that the test dataset can be represented well by the trained model. Second, we derived group‐wise SMs for the test dataset and compared them with the ones in the training stage. The overlap of task‐related SMs in training and testing is summarized in Table 5. The results show that the SMs are highly reproducible in the test dataset. In summary, the results on an independent testing dataset show that parameter tuning in the training stage is reasonable.
Figure 10.
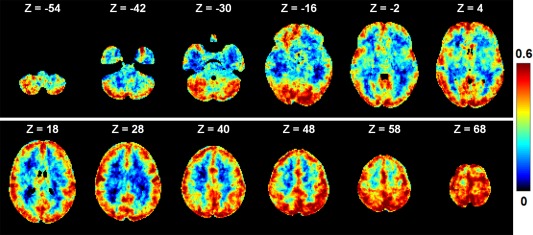
The performance of the trained sRBM model (HCP Motor task) in the representation of an independent test fMRI dataset. The test dataset consists of HCP Motor task fMRI data of 20 subjects that are not used in the training stage. We calculated the Pearson correlation coefficient between the reconstructed fMRI signal and the original fMRI signal for each voxel. The correlation maps were averaged over the 20 test subjects [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 5.
Overlap of task‐related SMs (HCP Motor task) in training and testing
| Overlap | E1 | E2 | E3 | E4 | E5 | E6 |
|---|---|---|---|---|---|---|
| 0.876 | 0.9 | 0.986 | 0.913 | 0.871 | 0.911 |
We found the results of sRBM were robust to the hyperparameters of L2‐decay, learning rate and batch size, and moderately sensitive to the hyperparameters of the target sparsity that specifies the ratio of active hidden units, and the L1‐decay. In our experiments, the target sparsity was fixed at 1% throughout the 7 tasks, and L1‐decay was slightly different across tasks. But we found that the sRBM models worked well when the target sparsity varies within 1%–5%, and the L1‐decay varies within 0.001–0.005. K‐step CD (CD‐k) is a common way to train RBMs. It is a biased estimator of the log‐likelihood gradient relying on Gibbs sampling, where k is one of the factors that bound the magnitude of this bias (Fischer & Igel, 2011). In our experiments, we used one step CD (CD‐1) to train RBMs. Previous studies have shown that CD‐k with larger k (k > 1) can improve RBMs training (Fischer & Igel, 2014). In the future, we will explore how larger k could benefit fMRI BSS based on RBMs. Parameter tuning in RBMs can be time consuming when applied to large‐scale datasets like fMRI. Our approach effectively alleviated this problem with substantially decreased model complexity and accelerated convergence compared to the tRBM. This advantage further enables systematic investigations of the impact of model parameter on BSS performance.
The proposed sRBM BSS model could be sensitive to fMRI time shifts as a temporal offset to a time courses (v) would change the estimation of p(h | v). In our study, this issue was partly addressed by using spatially aggregated multi‐subject data. This strategy trains sRBMs to learn the most common latent factors underlying the large‐scale fMRI time courses and thus provides a certain level of robustness to such time shifts. In addition, as time shits are a common problem in fMRI analysis, previous studies have developed preprocessing strategies to estimate and remove those time shifts (Liao et al., 2002; Saad Saad, Ropella, Cox, & DeYoe, 2001). In the future, we will explore how those preprocessing strategies could benefit our BSS model.
Currently, our approach investigates functional activations in contrast to baselines. However, the main interest sometimes is the contrast between different task events. Theoretically, it is straightforward to apply a second‐level analysis on the subject‐specific SMs of different events to infer event‐contrast activations (e.g., stronger activations in Story in contrast to Math event in HCP Language task). Thus, future work could further investigate whether the learned components directly correlate to event‐contrast activations. In addition, compared to shallow models (like the one‐hidden‐layer RBM used in our study), deeper models have been shown to be more powerful in feature learning (Bengio et al., 2012). It is of great interest in the future to explore how the performance of fMRI BSS can be improved with deeper models, such as deep Boltzmann machines (DBM) and deep belief network (DBN).
CONFLICT OF INTEREST
The authors declare no conflict of interests.
Supporting information
Additional Supporting Information may be found online in the supporting information tab for this article.
Supporting Information
ACKNOWLEDGMENTS
We trained RBMs using the DeepNet package (https://github.com/nitishsrivastava/deepnet). This work was partly supported by National Natural Science Foundation of China (NSFC) 61473234, 61333017, and 61522207, the Fundamental Research Funds for the Central Universities 3102014JCQ01065, NIH Career Award EB006878, NSF Career Award IIS‐1149260, NIH R01 DA033393, NIH R01 AG042599, NSF CBET‐1302089, NSF BCS‐1439051, and NSF DBI‐1564736.
Hu X, Huang H, Peng B, et al. Latent source mining in FMRI via restricted Boltzmann machine. Hum Brain Mapp. 2018;39:2368–2380. 10.1002/hbm.24005
Funding information National Key R&D Program of China, Grant/Award Number: 2017YFB1002201 National Natural Science Foundation of China (NSFC), Grant/Award Numbers: 61473234, 61333017, 61522207; Fundamental Research Funds for the NIH Career Award, Grant/Award Number: EB006878, NSF Career Award, Grant/Award Numbers: IIS‐1149260, NIH R01 DA033393, NIH R01 AG042599, NSF CBET‐1302089, NSF BCS‐1439051, NSF DBI‐1564736
REFERENCES
- Andersen, A. H. , Gash, D. M. , & Avison, M. J. (1999). Principal component analysis of the dynamic response measured by fMRI: A generalized linear systems framework. Magnetic Resonance Imaging, 17(6), 795–815. [DOI] [PubMed] [Google Scholar]
- Bartels, A. , & Zeki, S. (2005). Brain dynamics during natural viewing conditions ‐ a new guide for mapping connectivity in vivo. NeuroImage, 24(2), 339–349. [DOI] [PubMed] [Google Scholar]
- Baumgartner, R. , Ryner, L. , Richter, W. , Summers, R. , Jarmasz, M. , & Somorjai, R. (2000). Comparison of two exploratory data analysis methods for fMRI: Fuzzy clustering vs. principal component analysis. Magnetic Resonance Imaging, 18(1), 89–94. [DOI] [PubMed] [Google Scholar]
- Beckmann, C. F. , & Smith, S. M. (2005). Tensorial extensions of independent component analysis for multisubject FMRI analysis. NeuroImage, 25(1), 294–311. [DOI] [PubMed] [Google Scholar]
- Bell, A. J. , & Sejnowski, T. J. (1995). An information‐maximization approach to blind separation and blind deconvolution. Neural Computation, 7(6), 1129–1159. [DOI] [PubMed] [Google Scholar]
- Bengio, Y. , Courville, A. C. , & Vincent, P. (2012). Unsupervised feature learning and deep learning: A review and new perspectives. CoRR, abs/1206.5538, 1. [Google Scholar]
- Biswal, B. B. , Mennes, M. , Zuo, X.‐N. , Gohel, S. , Kelly, C. , Smith, S. M. , … Milham, M. P. (2010). Toward discovery science of human brain function. Proceedings of the National Academy of Sciences, 107(10), 4734–4739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore, E. , & Sporns, O. (2009). Complex brain networks: Graph theoretical analysis of structural and functional systems. Nature Reviews Neuroscience, 10(3), 186–198. [DOI] [PubMed] [Google Scholar]
- Calhoun, V. D. , & Adali, T. (2012). Multisubject independent component analysis of fMRI: A decade of intrinsic networks, default mode, and neurodiagnostic discovery. IEEE Reviews in Biomedical Engineering, 5, 60–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun, V. D. , Adali, T. , Pearlson, G. D. , & Pekar, J. J. (2001). A method for making group inferences from functional MRI data using independent component analysis. Human Brain Mapping, 14(3), 140–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castro, E. , Hjelm, R. D. , Plis, S. , Dihn, L. , Turner, J. , & Calhoun, V. (2016). Deep independence network analysis of structural brain imaging: Application to schizophrenia. IEEE Transactions on Medical Imaging, PP:1–1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dahl, G. E. , Yu, D. , Deng, L. , & Acero, A. (2012). Context‐dependent pre‐trained deep neural networks for large‐vocabulary speech recognition. IEEE Transactions on Audio, Speech, and Language Processing, 20, 30–42. [Google Scholar]
- Damoiseaux, J. S. , Rombouts, S. A. R. B. , Barkhof, F. , Scheltens, P. , Stam, C. J. , Smith, S. M. , & Beckmann, C. F. (2006). Consistent resting‐state networks across healthy subjects. Proceedings of the National Academy of Sciences, 103(37), 13848–13853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng, L. , Hinton, G. , & Kingsbury, B. (2013). New types of deep neural network learning for speech recognition and related applications: An overview. In IEEE International Conference on Acoustics, Speech and Signal Processing 2013. IEEE. p 8599–8603.
- Duncan, J. (2010). The multiple‐demand (MD) system of the primate brain: Mental programs for intelligent behaviour. Trends in Cognitive Sciences, 14(4), 172–179. [DOI] [PubMed] [Google Scholar]
- Fischer, A. , & Igel, C. (2011). Bounding the bias of contrastive divergence learning. Neural Computation, 23(3), 664–673. ): [DOI] [PubMed] [Google Scholar]
- Fischer, A. , & Igel, C. (2014). Training restricted Boltzmann machines: An introduction. Pattern Recognition, 47(1), 25–39. [Google Scholar]
- Friston, K. J. , Frith, C. D. , Frackowiak, R. S. , & Turner, R. (1995). Characterizing dynamic brain responses with fMRI: A multivariate approach. NeuroImage, 2(2), 166–172. [DOI] [PubMed] [Google Scholar]
- Friston, K. J. (2009). Modalities, modes, and models in functional neuroimaging. Science, 326(5951), 399–403. [DOI] [PubMed] [Google Scholar]
- Girshick, R. , Donahue, J. , Darrell, T. , & Malik, J. (2014). Rich feature hierarchies for accurate object detection and semantic segmentation. In IEEE conference on computer vision and pattern recognition. p 580–587.
- Glasser, M. F. , Sotiropoulos, S. N. , Wilson, J. A. , Coalson, T. S. , Fischl, B. , Andersson, J. L. , … Polimeni, J. R. (2013). The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage, 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodfellow, I. J. , Pougetabadie, J. , Mirza, M. , Xu, B. , Warde‐Farley, D. , Ozair, S. , & Bengio, Y. (2014). Generative adversarial nets. Advances in Neural Information Processing Systems, 2014, 3, 2672–2680. [Google Scholar]
- Graves, A. , Mohamed, A. , & Hinton, G. (2013). Speech recognition with deep recurrent neural networks. IEEE International Conference on Acoustics, Speech and Signal Processing, 2013. 6645–6649. [Google Scholar]
- Greff, K. , Srivastava, R. K. , & Schmidhuber, J. (2016). Highway and residual networks learn unrolled iterative estimation. arXiv preprint arXiv:1612.07771. [Google Scholar]
- Guo, Y. , & Pagnoni, G. (2008). A unified framework for group independent component analysis for multi‐subject fMRI data. NeuroImage, 42(3), 1078–1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasson, U. , & Honey, C. J. (2012). Future trends in neuroimaging: Neural processes as expressed within real‐life contexts. NeuroImage, 62(2), 1272–1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He, K. , Zhang, X. , Ren, S. , & Sun, J. (2016). Deep residual learning for image recognition. In IEEE conference on computer vision and pattern recognition 2016, p. 770–778.
- He, K. , Gkioxari, G. , Dollár, P. , & Girshick, R. (2017). Mask r‐CNN. arXiv preprint arXiv:1703.06870. [DOI] [PubMed] [Google Scholar]
- Hinton, G. , Deng, L. , Yu, D. , Dahl, G. E. , Mohamed, A‐R. , Jaitly, N. , … Sainath, T. N. (2012). Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Processing Magazine, 29(6), 82–97. [Google Scholar]
- Hinton, G. E. (2002). Training products of experts by minimizing contrastive divergence. Neural Computation, 14(8), 1771–1800. [DOI] [PubMed] [Google Scholar]
- Hinton, G. E. , Osindero, S. , & Teh, Y.‐W. (2006). A fast learning algorithm for deep belief nets. Neural Computation, 18(7), 1527–1554. [DOI] [PubMed] [Google Scholar]
- Hinton, G. E. , & Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks. Science, 313(5786), 504–507. [DOI] [PubMed] [Google Scholar]
- Hjelm, R. D. , Calhoun, V. D. , Salakhutdinov, R. , Allen, E. A. , Adali, T. , & Plis, S. M. (2014). Restricted Boltzmann machines for neuroimaging: An application in identifying intrinsic networks. NeuroImage, 96, 245–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, H. , Hu, X. , Han, J. , Lv, J. , Liu, N. , Guo, L. , & Liu, T. (2016). Latent source mining in FMRI data via deep neural network. IEEE 13th International Symposium on Biomedical Imaging (ISBI), p 638–641. [Google Scholar]
- Jang, H. , Plis, S. M. , Calhoun, V. D. , & Lee, J.‐H. (2016). Task‐specific feature extraction and classification of fMRI volumes using a deep neural network initialized with a deep belief network: Evaluation using sensorimotor tasks. NeuroImage, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson, M. , Beckmann, C. F. , Behrens, T. E. , Woolrich, M. W. , & Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. [DOI] [PubMed] [Google Scholar]
- Jia, Y. , Shelhamer, E. , Donahue, J. , Karayev, S. , Long, J. , Girshick, R. , … Darrell, T. (2014). Caffe: Convolutional architecture for fast feature embedding. In the 22nd ACM international conference on Multimedia, ACM. p 675–678.
- Jiang, X. , Li, X. , Lv, J. , Zhang, T. , Zhang, S. , Guo, L. , & Liu, T. (2015). Sparse representation of HCP grayordinate data reveals novel functional architecture of cerebral cortex. Human Brain Mapping, 36(12), 5301–5319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamnitsas, K. , Ledig, C. , Newcombe, V. F. , Simpson, J. P. , Kane, A. D. , Menon, D. K. , … Glocker, B. (2017). Efficient multi‐scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Medical Image Analysis, 36, 61–78. [DOI] [PubMed] [Google Scholar]
- Kim, J. , Calhoun, V. D. , Shim, E. , & Lee, J.‐H. (2016). Deep neural network with weight sparsity control and pre‐training extracts hierarchical features and enhances classification performance: Evidence from whole‐brain resting‐state functional connectivity patterns of schizophrenia. NeuroImage, 124, 127–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krizhevsky, A. , Sutskever, I. , & Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems, 2012. p 1097–1105. [Google Scholar]
- LeCun, Y. , Bengio, Y. , & Hinton, G. E. (2015). Deep learning. Nature, 521(7553), 436–444. [DOI] [PubMed] [Google Scholar]
- Lee, H. , Grosse, R. , Ranganath, R. , & Ng, A. Y. (2009). Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. In the 26th annual international conference on machine learning. p. 609–616.
- Lee, K. , Tak, S. , & Ye, J. C. (2011). A data‐driven sparse GLM for fMRI analysis using sparse dictionary learning with MDL criterion. IEEE Transactions on Medical Imaging, 30, 1076–1089. [DOI] [PubMed] [Google Scholar]
- Lee, Y.‐B. , Lee, J. , Tak, S. , Lee, K. , Na, D. L. , Seo, S. W. , … Initiative, AsDN. (2016). Sparse SPM: Group Sparse‐dictionary learning in SPM framework for resting‐state functional connectivity MRI analysis. NeuroImage, 125, 1032–1045. [DOI] [PubMed] [Google Scholar]
- Liao, C. H. , Worsley, K. J. , Poline, J. B. , Aston, J. A. , Duncan, G. H. , & Evans, A. C. (2002). Estimating the delay of the fMRI response. NeuroImage, 16(3), 593–606. [DOI] [PubMed] [Google Scholar]
- Lv, J. , Jiang, X. , Li, X. , Zhu, D. , Chen, H. , Zhang, T. , … Huang, H. (2015a). Sparse representation of whole‐brain fMRI signals for identification of functional networks. Medical Image Analysis, 20, 112–134. [DOI] [PubMed] [Google Scholar]
- Lv, J. , Jiang, X. , Li, X. , Zhu, D. , Zhang, S. , Zhao, S. , … Han, J. (2015b). Holistic atlases of functional networks and interactions reveal reciprocal organizational architecture of cortical function. IEEE Transactions on Biomedical Engineering, 62, 1120–1131. [DOI] [PubMed] [Google Scholar]
- Mckeown, M. J. , & Sejnowski, T. J. (1998). Independent component analysis of fMRI data: Examining the assumptions. Human Brain Mapping, 6(5–6), 368–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melchior, J. , Fischer, A. , & Wiskott, L. (2016). How to center deep Boltzmann machines. Journal of Machine Learning Research, 17(99), 1–60. [Google Scholar]
- Mohamed, A‐R. , Dahl, G. E. , & Hinton, G. (2012). Acoustic modeling using deep belief networks. IEEE Transactions on Audio, Speech, and Language Processing, 20(1), 14–22. [Google Scholar]
- Nair, V. , & Hinton, G. E. (2010). Rectified linear units improve restricted boltzmann machines. In the 27th International Conference on Machine Learning (ICML‐10), p 807–814.
- Pessoa, L. (2012). Beyond brain regions: Network perspective of cognition–emotion interactions. Behavioral and Brain Sciences, 35(03), 158–159. [DOI] [PubMed] [Google Scholar]
- Plis, S. M. , Hjelm, D. R. , Salakhutdinov, R. , & Calhoun, V. D. (2013). Deep learning for neuroimaging: A validation study. arXiv preprint arXiv:1312.5847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romero, A. , Carrier, P. L. , Erraqabi, A. , Sylvain, T. , Auvolat, A. , Dejoie, E. , & Bengio, Y. (2016). Diet networks: Thin parameters for fat genomic. arXiv preprint arXiv:1611.09340. [Google Scholar]
- Saad, Z. S. , Ropella, K. M. , Cox, R. W. , & DeYoe, E. A. (2001). Analysis and use of FMRI response delays. Human Brain Mapping, 13(2), 74–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sak, H. , Senior, A. , & Beaufays, F. (2014). Long short‐term memory based recurrent neural network architectures for large vocabulary speech recognition. arXiv preprint arXiv:1402.1128. [Google Scholar]
- Sainath, T. , Mohamed, A.‐R. , Kingsbury, B. , & Ramabhadran, B. (2013). Deep convolutional neural networks for LVCSR. In IEEE conference on Acoustics, speech and signal processing, p. 8614–8618.
- Schmah, T. , Hinton, G. E. , Zemel, R. S. , Small, S. L. , & Strother, S. C. (2008). Generative versus discriminative training of RBMs for classification of fMRI images. Advances in Neural Information Processing Systems, 1409–1416. [Google Scholar]
- Seeley, W. W. , Crawford, R. K. , Juan, Z. , Miller, B. L. , & Greicius, M. D. (2009). Neurodegenerative diseases target large‐scale human brain networks. Neuron, 62(1), 42–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin, H.‐C. , Orton, M. R. , Collins, D. J. , Doran, S. J. , & Leach, M. O. (2013). Stacked autoencoders for unsupervised feature learning and multiple organ detection in a pilot study using 4D patient data. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35, 1930–1943. [DOI] [PubMed] [Google Scholar]
- Shin, H. C. , Roberts, K. , Lu, L. , Demner‐Fushman, D. , Yao, J. , & Summers, R. M. (2016). Learning to read chest X‐rays: recurrent neural cascade model for automated image annotation. In IEEE conference on computer vision and pattern recognition, p. 2497–2506.
- Simonyan, K. , & Zisserman, A. (2014). Very deep convolutional networks for large‐scale image recognition. arXiv preprint arXiv:1409.1556. [Google Scholar]
- Smith, S. M. , Fox, P. T. , Miller, K. L. , Glahn, D. C. , Fox, P. M. , Mackay, C. E. , … Beckmann, C. F. (2009). Correspondence of the brain's functional architecture during activation and rest. Proceedings of the National Academy of Sciences of the United States of America, 106(31), 13040–13045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk, H.‐I. , Lee, S.‐W. , Shen, D. , & Initiative, AsDN. (2014). Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. NeuroImage, 101, 569–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk, H.‐I. , Wee, C.‐Y. , Lee, S.‐W. , & Shen, D. (2016). State‐space model with deep learning for functional dynamics estimation in resting‐state fMRI. NeuroImage, 129, 292–307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulfarsson, M. O. , & Solo, V. (2007). Sparse variable principal component analysis with application to fMRI). In IEEE International Symposium on Biomedical Imaging: From Nano to Macro, p 460–463.
- van de Ven, V. G. , Formisano, E. , Prvulovic, D. , Roeder, C. H. , & Linden, D. E. (2004). Functional connectivity as revealed by spatial independent component analysis of fMRI measurements during rest. Human Brain Mapping, 22(3), 165–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen, D. C. , Ugurbil, K. , Auerbach, E. , Barch, D. , Behrens, T. , Bucholz, R. , … Curtiss, S. W. (2012). The Human Connectome Project: A data acquisition perspective. NeuroImage, 62(4), 2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent, P. , Larochelle, H. , Lajoie, I. , Bengio, Y. , & Manzagol, P.‐A. (2010). Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. Journal of Machine Learning Research, 11, 3371–3408. [Google Scholar]
- Zeiler, M. D. , & Fergus, R. (2014). Visualizing and Understanding Convolutional Networks. In European Conference on Computer Vision, p. 818–833.
- Zhao, S. , Han, J. , Lv, J. , Jiang, X. , Hu, X. , Zhao, Y. , … Liu, T. (2015). Supervised dictionary learning for inferring concurrent brain networks. IEEE Transactions on Medical Imaging, 34(10), 2036–2045. [DOI] [PubMed] [Google Scholar]
- Zou, H. , Hastie, T. , & Tibshirani, R. (2012). Sparse principal component analysis. Journal of Computational & Graphical Statistics, 2007, 265–286. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional Supporting Information may be found online in the supporting information tab for this article.
Supporting Information


