Spatio‐temporal dynamics of resting‐state brain networks improve single‐subject prediction of schizophrenia diagnosis

Abstract

Correlation in functional MRI activity between spatially separated brain regions can fluctuate dynamically when an individual is at rest. These dynamics are typically characterized temporally by measuring fluctuations in functional connectivity between brain regions that remain fixed in space over time. Here, dynamics in functional connectivity were characterized in both time and space. Temporal dynamics were mapped with sliding‐window correlation, while spatial dynamics were characterized by enabling network regions to vary in size (shrink/grow) over time according to the functional connectivity profile of their constituent voxels. These temporal and spatial dynamics were evaluated as biomarkers to distinguish schizophrenia patients from controls, and compared to current biomarkers based on static measures of resting‐state functional connectivity. Support vector machine classifiers were trained using: (a) static, (b) dynamic in time, (c) dynamic in space, and (d) dynamic in time and space characterizations of functional connectivity within canonical resting‐state brain networks. Classifiers trained on functional connectivity dynamics mapped over both space and time predicted diagnostic status with accuracy exceeding 91%, whereas utilizing only spatial or temporal dynamics alone yielded lower classification accuracies. Static measures of functional connectivity yielded the lowest accuracy (79.5%). Compared to healthy comparison individuals, schizophrenia patients generally exhibited functional connectivity that was reduced in strength and more variable. Robustness was established with replication in an independent dataset. The utility of biomarkers based on temporal and spatial functional connectivity dynamics suggests that resting‐state dynamics are not trivially attributable to sampling variability and head motion.

1. INTRODUCTION

Over the past two decades, blood oxygenation‐level dependent (BOLD) functional magnetic resonance imaging (fMRI) acquired during rest has emerged as a promising approach to understand complex brain function. Spatially separated brain regions that exhibit correlation in their BOLD activity are said to be functionally connected (Friston 1994; Friston 2011). Functional connectivity (FC) persists even when the brain is at rest and not engaged in an explicit task, giving rise to spatial maps of functionally connected regions called resting state networks (RSNs). These networks are consistently found in healthy individuals, both during rest (Fox et al., 2005) as well as during task performance, with only minimal reconfiguration of network architecture between task and rest (Calhoun, Kiehl, & Pearlson, 2008; Cole, Bassett, Power, Braver, & Petersen, 2014; Sonuga‐Barke & Castellanos, 2007; Smith et al., 2009). RSNs have yielded insight into the brain's functional organization (Fox et al., 2005; Raichle et al., 2001; Raichle 2010), maturation (Doria et al., 2010; Fair et al., 2008), effects of ageing (Damoiseaux et al., 2008), and characterization of many neurological and neuropsychiatric disorders (reviewed in Fox & Greicius 2010; Greicius 2008; Fornito, Zalesky, & Breakspear, 2015).

Using resting‐state fMRI, RSNs can be mapped with seed‐based methods (Biswal, Zerrin Yetkin, Haughton, & Hyde, 1995; Biswal, Kylen, & Hyde, 1997; Cordes et al., 2000; Jiang, He, Zang, & Weng, 2004) or independent component analysis (ICA; Beckmann, DeLuca, Devlin, & Smith, 2005; Calhoun, Adali, Pearlson, & Pekar, 2001; De Luca et al., 2005; van de Ven, Formisano, Prvulovic, Roeder, & Linden, 2004). With the former method, a seed (region of interest, ROI) is defined based on previous studies or atlases and the average time course from this region is correlated with other brain voxels. While these methods rely on prior knowledge about the network architecture, ICA based methods do not require any such information and networks are defined in a data‐driven manner under the assumptions of spatial or temporal independence among voxel time courses. These initial studies assumed functional connections and RSNs to be invariant over time, implying that a single connectivity measure over the whole scan duration provides a sufficient characterization, which we refer to as static FC hereafter. However, it has been demonstrated both empirically and with simulation that resting‐state FC exhibits rich dynamics and temporal structure (Chang & Glover, 2010; Allen et al., 2014; Hutchison, Womelsdorf, Gati, Everling, & Menon, 2013b); giving rise to the currently very active field of dynamic FC (Hutchison et al., 2013a; Tagliazucchi & Laufs, 2015; Preti, Bolton, & Van De Ville, 2016; Karahanoğlu & Van De Ville, 2017). While several studies have sought to identify the neural basis of dynamic FC (Tagliazucchi, von Wegner, Morzelewski, Brodbeck, & Laufs, 2012; Chang, Liu, Chen, Liu, & Duyn, 2013; Thompson et al., 2013), its functional underpinnings (Kucyi & Davis, 2014; Chen, Chen, Xie, & Li, 2011; Zalesky, Fornito, Cocchi, Gollo, & Breakspear, 2014; Yang, Craddock, Margulies, Yan, & Milham, 2014) and aberrant dynamics of FC in disease (Rashid, Damaraju, Pearlson, & Calhoun, 2014; Damaraju et al., 2014; Jones et al., 2012; Liao et al., 2014), the field remains hotly disputed, with suggestions that observed dynamics might be trivially due to nuisance physiological and head motion covariates that have not been adequately removed (Laumann et al., 2016). Additional contention is owing to ambiguity in the core definition of dynamic FC (Liegeois, Laumann, Snyder, Zhou, & Yeo, 2017) and ongoing debate about the utility of sliding‐window analyses and the choice of null model (Hindriks et al., 2016; Zalesky & Breakspear, 2015; Leonardi & Van De Ville, 2015).

Single‐subject prediction of diagnosis, illness outcome and treatment response offers significant potential to influence clinical decision making in neuropsychiatry (Koutsouleris et al., 2009; Koutsouleris & Kambeitz, 2016). To date, single‐subject predictions inferred from fMRI have largely focussed on static FC and other static properties of the BOLD response. In particular, multivariate pattern‐recognition techniques (machine learning) applied to static FC measures have been trained to distinguish psychiatric patients from healthy controls with accuracies ranging between 60% and 80%, depending on the disorder and illness severity (Woo, Chang, Lindquist, & Wager, 2017). To be useful for clinical practice, biomarkers with improved accuracy, reliability and predictive value are essential (Abi‐Dargham & Horga, 2016). Recent evidence suggests that neuropsychiatric disorders are associated with marked abnormalities in dynamic FC and that these dynamic biomarkers can distinguish patients from healthy comparison individuals with greater accuracy than predictions based on static FC alone (Jin et al., 2017; Wee et al., 2012; Price, Wee, Gao, & Shen, 2014). Therefore, the dynamic properties of functional brain networks merit further study in the context of candidate biomarkers for clinically useful predictive models in psychiatric disorders such as schizophrenia.

Studies of dynamic FC have invariably focussed on characterizing the temporal dynamics of FC, with little consideration given to any possible dynamics in the spatial layout of RSNs. The spatial extent of functional networks is typically defined using a parcellation atlas or with ICA, both of which enforce anatomical boundaries that are fixed in space over all time. Here, we aim to establish whether resting‐state FC exhibits meaningful spatial dynamics and whether spatial dynamics can improve single‐subject prediction of schizophrenia diagnosis. While it is known that functional brain networks exhibit spatial dynamics during task performance (Calhoun et al., 2008; Fransson 2006; Sonuga‐Barke & Castellanos, 2007; Kelly, Uddin, Biswal, Castellanos, & Milham, 2008), little is known about whether these spatial dynamics persist in rest or whether they are altered in disease. In addition, neuropsychiatric disorders such as schizophrenia are typically characterized by reductions in gray matter volume and these reductions can remain even after registration to a standard template. Allowing the spatial extent of functional network boundaries to vary between individuals and over time can in principle account for reductions in gray matter volume, since the spatial extent of a functional network is inherently reduced to match the extent of atrophy. While some studies have sought to characterize the spatio‐temporal dynamics of RSNs in healthy subjects (Kiviniemi et al., 2011) and in schizophrenia patients (Ma, Calhoun, Phlypo, & Adalı, 2014), these studies assume spatial independence among networks; further, they have not evaluated the extent to which dynamic FC can improve single‐subject prediction of diagnostic status.

The aim of this study is to evaluate the extent to which biomarkers characterizing both the spatial and temporal dynamics of key RSNs can improve the accuracy of machine‐based single‐subject prediction of schizophrenia diagnosis. We hypothesize that spatio‐temporal dynamics in resting‐state FC is altered in schizophrenia patients and that these dynamics distinguish patients from healthy controls with greater precision compared to static characterizations of RSNs. To address this hypothesis, we developed a novel sliding‐window based method to map both spatial and temporal fluctuations in RSNs defined relative to a seed region. Unlike complementary ICA‐based methods, our method does not enforce temporal or spatial independence between RSNs, meaning that RSNs can potentially overlap and share common regions at any time. Using two independent datasets, we evaluated the accuracy with which schizophrenia patients can be distinguished from healthy comparison individuals with a support vector machine (SVM) classifier trained on: (a) static, (b) dynamic in time, (c) dynamic in space, and (d) dynamic in time and space characterizations of FC in key RSNs.

2. MATERIALS AND METHODS

2.1. Data

2.1.1. Dataset 1

Participants included 41 patients with treatment‐resistant schizophrenia (TRS; mean age 40.9 years, σ = 10.0 years, 28 males) and 41 age‐matched healthy controls (mean age 38.3 years, σ = 10.5 years, 24 males). TRS patients did not respond to at least two different antipsychotics in at least two trials (Suzuki et al., 2012) and were taking clozapine (Kane, Honigfeld, Singer, & Meltzer, 1988; Siskind, McCartney, Goldschlager, & Kisely, 2016). Clinical and demographic characteristics are shown in Table 1. The study was approved by the Melbourne Health Human Research Ethics committee (MHREC ID 2012.069) and all participants provided written informed consent, prior to participation.

Table 1.

Demographic and clinical characteristics of participants (Dataset 1)

	TRS patients (n = 41)	Healthy volunteers (n = 41)	Between group differences
Gender (Male/Female)	28/13	24/17	${\mathrm{\chi }}^2$(1, N = 82) = 0.97, p = .32
Age (years)	40.9 ± 10.0	38.3 ± 10.5	t(82) = 1.1, p = .27
Illness duration (years)	17.9 ± 9.3	–	–
IQ	86.1 ± 18.7	111.2 ± 13.6	t(75) = 6.70, p = .0000*
Education (years)	12.0 ± 0.55	16.4 ± 0.47	t(79) = −6.35, p = .0000*
GAF	45.9 ± 13.0	79.5 ± 10.6	t(79) = −12.79, p = .0000*
SOFAS	46.5 ± 14.8	79.5 ± 11.0	t(80) = −11.49, p = .0000*
Clozapine dosage (mg/day)	393.24 ± 24.6	–	–
Chlorpromazine equivalent dosage (mg/day)	615.4 ± 55.84	–	–
PANSS scores
Positive	15.6 ± 6.58	–	–
Negative	16.4 ± 5.18	–	–
Disorganized	12.4 ± 4.09	–	–
Excited	6.3 ± 2.66	–	–
Depressed	8.3 ± 3.84	–	–
Total	59.1 ± 13.1	–	–

Mean ± SD of each measure is shown. Note that the degrees of freedom are smaller for some measures, as not all information was available for every subject.

Abbreviations: TRS, treatment‐resistant schizophrenia; IQ, intelligence quotient; GAF, the global assessment of functioning; SOFAS, Social and Occupational Functioning Assessment Scale; PANSS, Positive and Negative Syndrome Scale.

*Significant p < .01.

Magnetic resonance images were collected on a Siemens Avanto 3T Magnetom TIM Trio scanner. All participants were instructed to keep their eyes closed and not to fall asleep while scanning. T1 weighted anatomical images were acquired using an optimized Magnetization‐Prepared Rapid acquisition Gradient Echo (MPRAGE) sequence with the following parameters: 176 sagittal slices of 1 mm thickness without gap, field of view (FOV) = 250 × 250 mm², repetition time (TR) = 1980 ms, echo time (TE) = 4.3 ms, flip angle = 15° and resolution = 0.98 × 0.98 × 1.0 mm. Resting‐state fMRI data was acquired for 8 min (234 volumes) using a T2*‐weighted echo‐planar imaging (EPI) sequence with TR = 2 s, TE = 40 ms, voxel dimensions = 3.3 × 3.3 × 3 mm and matrix size 64 × 64.

2.1.2. Dataset 2 (replication cohort)

The replication dataset comprised 15 healthy volunteers (mean age 33.3 years, σ = 9.2 years, 14 male) and 12 patients with chronic schizophrenia (mean age 32.8 years, σ = 9.2 years, 10 male). The two groups were matched for age, pre‐onset IQ and years of education. The patients were diagnosed as per the standard operational criteria in the Diagnostic and Statistical Manual of Mental Disorders IV (the official manual of American Psychiatric Association). All patients were treated with antipsychotic medication; in addition, four patients were receiving psychotropic drugs. To reduce the acute effects of antipsychotic medication on the day of scanning, patients were asked to abstain from their usual medication regime. The study protocol was approved by the Addenbrooke's NHS Trust Local Research Ethics Committee and all subjects provided informed consent in writing before participation.

All scans were acquired using a 1.5 Tesla GE Signa scanner (General Electric, Milwaukee, WI) located at the BUPA Lea Hospital, Cambridge, UK. Resting‐state functional images were acquired using T2*‐weighted EPI sequence, as participants laid quietly in the scanner with eyes closed. Imaging parameters were: TR = 2 s, TE = 40 ms, flip angle = 70°, voxel size = 3.05 × 3.05 × 7 mm, slice gap = 0.7 mm and number of volumes = 512. Further details on the demographics and acquisition of this dataset can be found in a previous study (Zalesky, Fornito, & Bullmore, 2010).

2.2. Data preprocessing

2.2.1. Dataset 1

Scans from individual subjects were preprocessed using FSL (FMRIB software Library, https://fsl.fmrib.ox.ac.uk/fsl/) and SPM8 (http://www.fil.ion.ucl.ac.uk/spm). For every subject, the functional images were slice‐time corrected, realigned to the mean functional volume to correct for head motion and co‐registered to the respective T1‐weighted anatomical image via rigid‐body registration and then spatially normalized to the Montreal Neurological Institute (MNI) 152 template with isotropic 2 mm resolution via non‐linear transformation. Motion parameters (Friston 24‐parameter model; Friston, Williams, Howard, Frackowiak, & Turner, 1996) and signals from the white matter and the ventricles were regressed from each voxel time course, to account for head motion and physiological noise.

The residuals from this regression were spatially smoothed using a Gaussian kernel of full‐width at half‐maximum (FWHM) of 4mm. Any linear trend was removed from each voxel time course and temporal band‐pass filtering (0.01–0.1 Hz) was performed to reduce the effects of low frequency drifts and high frequency physiological noise (Cordes et al., 2001). The resulting time courses were used for further analyses.

Given that the regression of motion parameters is not sufficient to eliminate variance related to head motion (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012; Van Dijk, Sabuncu, & Buckner, 2012; Yan et al., 2013), further motion correction was performed by censoring high‐motion volumes in each individual (Power et al., 2012). Specifically, volumes with a frame‐wise displacement (FD) exceeding 0.5 mm were censored, where FD measures the extent of head movement from one volume to the next, and is calculated as the sum of the absolute values of the differentiated realignment estimates (Power et al., 2012).

2.2.2. Dataset 2

These data were preprocessed as a part of a prior study (Zalesky et al., 2010). The pre‐processing steps were comparable as that described above for Dataset 1, except that these images were normalized to a resampled MNI template with a voxel resolution of 3 × 3 × 7 mm and spatial smoothing was performed using a Gaussian kernel of FWHM = 6 mm; further details can be found in (Zalesky et al., 2010).

2.3. Networks and regions

FC was measured between pairs of regions comprising several canonical RSNs. We considered 14 previously delineated RSNs (Shirer, Ryali, Rykhlevskaia, Menon, & Greicius, 2012). Each RSN comprised multiple spatially contiguous cortical and/or subcortical regions, resulting in a total of 90 regions across the 14 RSNs. While mutual exclusivity among regions was not explicitly enforced, most regions did not share common voxels. The 14 RSNs and their constituent regions are listed in Table 2 and shown in Figure 1. Network regions are shown in green and orange, while the yellow border encapsulating each region represents neighboring voxels. Neighboring voxels include all voxels within a ∼6 mm distance outer to every network region, in all directions. This neighborhood delineates a space in which regions can dynamically shrink/grow as a function of time. Each RSN is associated with a single seed region (green) that was used for conventional seed‐based connectivity analyses (Biswal et al., 1995; Biswal et al., 1997; Cordes et al., 2000; Jiang et al., 2004).

Table 2.

Regions comprising each of the 14 resting‐state networks (RSNs) between which functional connectivity was mapped

Network	Abbreviation	Areas	No. of nodes	Seed region chosen
Anterior salience network	ASN	BA – 9, 46, 48, 47, 24, 32, 8, 6; left lobule VI, right lobule VI, crus I	7	Left middle frontal gyrus
Auditory network	AUD	BA – 22, 48, 38, 42; right thalamus	3	Left superior temporal gyrus
Basal ganglia network	BGN	BA – 45, 48; pons, left thalamus, left caudate, right thalamus, right caudate, putamen	5	Left thalamus
Dorsal default mode network	dDMN	BA – 9, 10, 24, 32, 11, 39, 23, 30, 39, 20, 36; left and right thalamus	9	Posterior cingulate cortex
Higher visual network	hVIS	BA – 17, 18, 19	2	Left middle occipital gyrus
Language network	LAN	BA – 45, 47, 21, 37, 39, 22, 42, 40; left crus I	7	Left inferior frontal gyrus
Left executive control network	LECN	BA – 8, 9, 10, 45, 47, 7, 40, 39, 20, 37; right crus I, left thalamus	6	Left inferior parietal gyrus
Precuneus network	PRE	BA – 7, 19, 23, 40	4	Precuneus
Posterior salience network	PSN	BA – 46, 40, 5, 23, 7, 5, 2, 40, 48; left thalamus, left lobule VI, right thalamus, right lobule VI	12	Right supramarginal gyrus
Primary visual network	pVIS	BA – 17; left thalamus	2	Calcarine sulcus
Right executive control network	RECN	BA – 46, 8, 9, 10, 7, 40, 39, 8; left crus I, left crus II, lobule VI, right caudate	6	Right inferior parietal gyrus
Sensorimotor network	SMN	BA – 3, 4, 6; left thalamus, right thalamus, bilateral lobule IV, V and VI	6	Left precentral gyrus
Ventral default mode network	vDMN	BA – 29, 30, 23, 8, 6, 37, 20, 19, 39, 7, 5, 9; right lobule IX	10	Left middle occipital gyrus
Visuo‐spatial network	VSN	BA – 2, 6, 40, 7, 44, 48, 45, 37; left lobule VIII and VIIb; right lobule VI, VIII and VIIb; right crus I	11	Left superior frontal gyrus

The number of network nodes involved and the seed region chosen to define the network are listed. BA – Broadmann Area. Note that nodes can span multiple BAs and regions; not all voxels comprising a BA or region are necessarily included as part of a node. The fourteen RSNs are shown in Figure 1.

Figure 1.

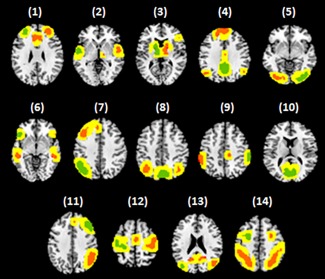
Fourteen resting‐state networks delineated by Shirer et al. (2012). (1) anterior salience, (2) auditory, (3) basal ganglia, (4) dorsal default mode, (5) higher visual, (6) language, (7) left executive control, (8) precuneus, (9) posterior salience, (10) primary visual, (11) right executive control, (12) sensorimotor, (13) ventral default mode and (14) visuospatial. Seed regions are shown in green and other (non‐seed) regions are shown in orange. When characterizing spatial dynamics, the spatial extent of each region can shrink/grow within the confines of the yellow zone, which is a ∼6 mm neighborhood encapsulating each region [Color figure can be viewed at http://wileyonlinelibrary.com]

2.4. Measurement of functional connectivity

Four distinct classes of FC were evaluated: (I) static in time and space; (II) dynamic in time; (III) dynamic in space; and (IV) dynamic in time and space. Class I is the conventional method of measuring FC and results in a temporally and spatially averaged representation of all variations during the acquisition interval. Class II represents the typical definition of dynamic FC as temporal variations in the interactions between spatially separated regions. Class III provides a novel conceptualization involving spatial dynamics in which region size can vary dynamically over time. Finally, Class IV provides a characterization of FC that combines temporal (Class II) and spatial (Class III) dynamics.

Figure 2 shows the salient features that differ between the four classes. In the following, we describe how FC was computed for each of the four classes.

Figure 2.

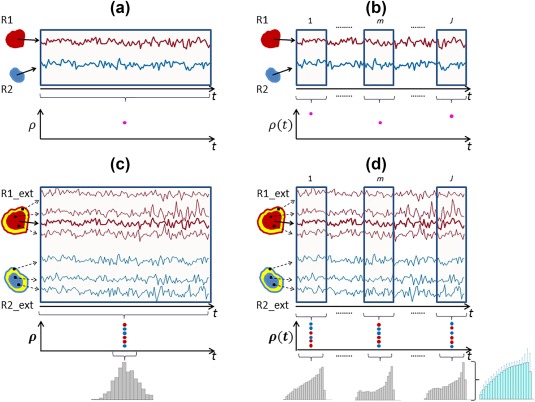
Schematic of four different classes of functional connectivity. R1 and R2 denote two distinct nodes, while R1_ext and R2_ext denote the same two nodes in addition to their spatial neighborhoods (shown in yellow). (a) Class I – Static in both time and space, in which case, regionally‐averaged time courses were correlated to yield a single correlation value. (b) Class II – Static in space, dynamic in time; in this class, correlations were defined between windowed time courses from the two regions. (c) Class III – Dynamic in space, static in time, where a histogram of correlations was obtained by correlating the seed time course with individual voxel time courses from nodes as well as their neighborhood (d) Class IV – Dynamic in both space and time, where a histogram of correlations was defined from each sliding window [Color figure can be viewed at http://wileyonlinelibrary.com]

2.4.1. Class I: Static in time and space

This is the simplest class in which variations in space and time during the acquisition interval are characterized in terms of their averages. The number of pairs of regions considered was varied according to a feature selection heuristic (see Section 2.5). FC was computed independently for each pair of regions. Pairs comprising regions from two distinct RSNs were permitted. The pre‐processed fMRI data was spatially averaged over the voxels comprising each region to yield an average time course for each region. The Pearson cross‐correlation coefficient was then calculated for each pair of regions to yield a measure of static FC. In Class I, a single correlation coefficient thus characterized the FC between a pair of regions for the entire acquisition interval, precluding the representation of any spatial or temporal dynamics. The number of features used for classification was simply the total number of pairs of regions considered, denoted by $M$.

2.4.2. Class II: Dynamic in time and static in space

This class corresponds to the conventional definition of dynamic FC based on temporal variations that remain fixed in space. To study temporal variations, we employed rectangular, overlapping sliding windows of fixed duration. The window was successively progressed in time by the duration of one TR (sampling interval) to yield a series of FC maps spanning the acquisition interval. Previous studies have considered window lengths varying from 13 s up to 4 min (Chang & Glover, 2010; Handwerker, Roopchansingh, Gonzalez‐Castillo, & Bandettini, 2012; Hutchison et al., 2013b; Lee, Zahneisen, Hugger, LeVan, & Hennig, 2013; Leonardi et al., 2013; Allen et al., 2014; Majeed et al., 2011). Here, we evaluated a variety of window lengths, and a length of $W=20$ s (10 TRs) was chosen. The effect of different window lengths was also assessed (see Section 2.6). For a window length of $W$ and an acquisition comprising $T$ time points, the total number of windows was given by $J=T-W+1$.

For each pair of regions, the Pearson correlation coefficient was used to compute FC within each of the $J$ windows to yield a time series of correlation coefficients ${\mathrm{\rho }}_{ij}\left(t\right)$, $t=1,\dots ,J$, where $i$ and $j$ denote regions. The mean and standard deviation of ${\mathrm{\rho }}_{ij}\left(t\right)$ were computed over time,

$${\mathrm{\mu }}_{ij}=\frac{1}{J}\sum _{t=1}^J{\mathrm{\rho }}_{ij}\left(t\right),\hspace{0.17em}{ \mathrm{\sigma }}_{ij}=\sqrt{\frac{1}{J-1}\sum _{t=1}^J{\left({\mathrm{\rho }}_{ij}\left(t\right)-{\mathrm{\mu }}_{ij}\right)}^2},$$

to provide summary statistics of temporal FC dynamics for each pair of regions. It is important to note that ${\mathrm{\mu }}_{ij}$ is not necessarily equal to the static FC between regional pair $\left(i,j\right)$ computed under Class I. Standard deviation provides a simple characterization of dynamics that has been extensively used as a test statistic for dynamic behavior (Lee et al., 2013; Kucyi, Salomons, & Davis, 2013; Kucyi & Davis, 2014; Laufs et al., 2014; Morgan, Abou‐Khalil, & Rogers, 2015; Falahpour et al., 2016). In Class II, the total possible number of features used for classification was $2M$, namely, the mean and standard deviation of ${\mathrm{\rho }}_{ij}\left(t\right)$ for $M$ pairs of regions.

2.4.3. Class III: Static in time and dynamic in space

In this class, rather than computing FC between pairs of regions that are spatially fixed based on a predefined atlas, we used a seed‐based correlation approach to define a distribution of FC that varied in space. Each RSN comprised a set of spatially contiguous regions, otherwise referred to as nodes. The number of regions varied between 2 and 12 across the 14 RSNs. For each RSN, a single region was chosen to serve as the seed region. Seed regions are colored in green in Figure 1 and listed in Table 2. For each RSN, along with the seed region, we defined a mask comprising voxels within a ∼6 mm neighborhood of each region of the RSN (yellow) as well as the voxels within each region (orange). For each voxel comprising the mask, the Pearson correlation coefficient was computed between the seed region and the voxel's pre‐processed fMRI time course, resulting in a spatial connectivity map that varied dynamically across voxels. In this way, FC between the seed region and other regions of each particular RSN varied from voxel to voxel in a spatially dynamic manner. This was repeated independently for each individual and each RSN. Finally, the spatial map for each RSN was converted into a histogram. The histogram was discretised into 20 uniformly spaced bins on the interval $[-\mathrm{1,1}]$ and each seed‐to‐voxel correlation coefficient was assigned to a unique bin. The number of voxels assigned to each histogram bin was used to characterize the spatial distribution of FC for each individual. The total possible number of features used for classification was $20N$, where $N=14$ is the number of RSNs.

2.4.4. Class IV: Dynamic in time and space

In this class, dynamics were characterized in both time and space, representing a combination of Classes II and III. This enabled the regions of each RSN to vary in size (shrink/grow) during the acquisition interval. As with Class III, for each RSN, we defined a seed region and a mask comprising voxels in the other regions of the RSN as well as voxels within a ∼6 mm neighborhood of all regions in the network. The Pearson correlation coefficient was then computed between the seed region and each voxel's pre‐processed fMRI time course, resulting in a spatial connectivity map that varied dynamically across voxels. Unlike Class III, where a single spatial map characterized the entire acquisition interval, we now computed a distinct spatial connectivity map for each time point. In particular, the same temporal sliding window scheme defined in Class II was employed and a spatial map was computed for each window. Each spatial map was converted to a histogram, as described under Class III. For a given RSN, let $h_i\left(t\right)$ be the number voxels assigned to histogram bin $\left[-1+\frac{i-1}{10},-1+\frac{i}{10}\right],\hspace{0.17em}i=1,\dots ,20$ for window $t=1,\dots ,J$. Recall that for a window length of $W$ and an acquisition comprising $T$ time points, the total number of windows is given by $J=T-W+1$. For each histogram bin $i=1,\dots ,20$, the mean and standard deviation of $h_i\left(t\right)$ were computed over time,

$${\mathrm{\mu }}_i^{\ast }=\frac{1}{J}\sum _{t=1}^J{h}_i\left(t\right),\hspace{0.17em}{\mathrm{\sigma }}_i^{\ast }=\sqrt{\frac{1}{J-1}\sum _{t=1}^J{\left(h_i\left(t\right)-{\mathrm{\mu }}_i^{\ast }\right)}^2},$$

to provide summary statistics of temporal variations in the spatially varying FC map for each RSN. The total possible number of features used for classification was $2\hspace{0.17em}\times \hspace{0.17em}20\times N$, namely, 20 means ( ${\mathrm{\mu }}_i^{\ast }$) and 20 standard deviations ( ${\mathrm{\sigma }}_i^{\ast }$) for each of $N$ RSNs. While we did not explicitly quantify region size as a function of time, this could be achieved by counting the number of voxels at each time point with a seed‐to‐voxel correlation coefficient exceeding a given threshold. This kind of binarization with respect to a given threshold squanders the rich spatial variation in FC within regions, and thus we characterized spatial dynamics with a histogram rather than region size.

2.5. Single‐subject prediction of schizophrenia diagnosis

Support vector machine (SVM) classifiers were trained to classify individuals according to diagnostic status (patients or controls) based on four distinct classes of FC. A separate classifier was trained and evaluated for each class. We evaluated the performance of different kernel functions and found that a linear kernel consistently provided the highest classification accuracy. A linear kernel was therefore employed for all experiments. Classification performance was measured in terms of classification accuracy, sensitivity, specificity and area under the receiver operating characteristic curve (AUC). Training and evaluation was undertaken according to the following three cross‐validation (CV) schemes.

2.5.1. Analysis 1: Network selection through exhaustive evaluation

The aim of this analysis was to comprehensively quantify the variation in classification accuracies across different combinations of RSNs. Some RSNs might provide minimal discriminatory power and thus their exclusion may enhance classification accuracy. Note that a total of 14 RSNs was considered, and thus $2^{14}-1\hspace{0.17em}=\hspace{0.17em}\mathrm{16,383}$ combinations of RSNs were evaluated, where each combination consisted of a selected subset of networks. For each combination, ten‐fold cross‐validation was used to evaluate classification accuracy. The mean and standard deviation of accuracy, sensitivity, specificity and AUC was then computed across all combinations. This was repeated independently for each of the four classes of FC to determine which class provided the most accurate classification performance on average across all combinations of RSNs.

In practice, a feature selection heuristic would typically be employed to identify a single combination of RSNs, rather than undertaking an exhaustive search. However, the objective of this analysis was to comprehensively characterize average performance across all possible combinations, without any dependence on a particular feature selection strategy.

Ten‐fold CV: Individuals (patients and controls) were randomly divided into 10 equally‐sized samples. The SVM was then trained using 9 of the 10 samples and the remaining held‐out sample was used to evaluate classification accuracy. This was repeated 10 times, each time holding out a different sample to evaluate accuracy. Classification accuracy, specificity, sensitivity and AUC were averaged across the 10 folds.

For each chosen combination of RSNs, ten‐fold CV was performed 30 times, each time with a different (random) partition of the dataset into 10 folds. Between two separate runs of ten‐fold CV, none of the folds contained exactly the same subjects, avoiding potential sampling bias. This CV procedure was repeated independently for each of the four classes of FC, yielding a distribution of classification accuracy, sensitivity and specificity across combinations of RSNs for each class. For a given class of FC and a chosen network combination, the mean and standard deviation of accuracy, sensitivity and specificity were calculated over 30 runs of ten‐fold CV.

2.5.2. Analysis 2: Ranked feature selection

In this analysis, we firstly implemented a feature selection step to identify the most distinguishing features and these features were then used for classification. The total number of features that were ranked differed between classes: Class I comprised 4005 features corresponding to unique cross‐correlations between 90 regions spanning 14 RSNs; Class II comprised 4005 means and 4005 standard deviations of unique cross‐correlations over sliding windows; Class III comprised 280 features (20 histogram bins from each of 14 RSNs); and Class IV comprised 280 means and 280 SDs of histogram bin heights over sliding windows. Importantly, features were selected based on a training sample. Individuals (patients and controls) were partitioned into two mutually exclusive sets—a training sample comprising 90% of individuals and an evaluation sample comprising the remaining 10% of individuals. Using the training data, a two‐sample t test was computed for each feature to assess the null hypothesis of equality between patients and controls. Features were then ranked in descending order according to the absolute value of each t‐statistic. The classifier was trained using the top‐ranked $K$ features and tested on the evaluation sample, where $K=\mathrm{10,20},\dots ,100$ was considered. This ranking and classification was repeated for 30 different partitions of the dataset.

2.5.3. Analysis 3: Nested CV

To evaluate classifier generalizability, we augmented the exhaustive approach undertaken in Analysis 1 with nested CV. The dataset was partitioned randomly into two groups—60% training sample and 40% test sample. Using the training data, an exhaustive grid search was performed, where a 10‐fold CV was implemented for each of the possible network combinations. The top‐50 network combinations that provided the highest classification accuracy were then selected. For each of these combinations, a classifier was trained using the training data, and the test data was used to evaluate the performance of the trained classifier. The final prediction outcome was decided via majority voting based on predictions from the 50 classification results. This process was repeated 30 times, each time with a different random partition of data into training and test subsets. Thus, in Analysis 3, feature selection and classifier training was performed using training data alone (60%), and the test data (40%) was used only to evaluate the trained classifier. This analysis assessed classifier generalizability and performance on new, unseen data.

2.6. Effect of varying window length, neighborhood, scrubbing, and seed regions

The choice of window length, seed region and neighborhood size are rather subjective, and thus we evaluated the sensitivity of classification performance to variations in these key parameters. For reasons of computational tractability, these sensitivity analyses were performed with respect to Analysis 2. The window length was varied from two TR points (4 s) to 234 TR points (7.8 min, the static case for Dataset 1). A new classifier was trained for each window length using the top‐100 features selected according to the scheme described in Analysis 2 (Section 2.5). Classifier performance was then plotted as a function of window length for both the dynamic‐in‐time classes (Class II and IV). The same process was used to evaluate the impact of variation in neighborhood size, where size varied from 0 mm (no neighboring voxels) to 10 mm. Variation in neighborhood size was only relevant to Classes III and IV, where the spatial extent of each region was permitted to shrink/grow within its neighborhood.

Finally, Analysis 2 was performed with and without high‐motion volumes censored (scrubbing), to evaluate the impact of motion correction on classifier performance. Previously, it has been shown that the networks defined via seed‐based correlation are dependent on the choice of seed location (Cole, Smith, & Beckmann, 2010; Sohn et al., 2015). Hence, we repeated our Analysis 2 with a different set of seed locations chosen from the network templates (Shirer et al., 2012); these regions are reported in Supporting Information Figure S1.

3. RESULTS

Four different classes of static and dynamic FC were inferred from resting‐state fMRI data acquired in schizophrenia patients and healthy controls. We independently trained a SVM for each class of FC to perform single‐subject prediction of diagnostic status. As detailed below, classifiers incorporating both the temporal and spatial dynamics of resting‐state FC consistently achieved substantially higher classification performance than classifiers based on static connectivity characterizations. SVMs were trained using three distinct schemes: Analysis 1 exhaustive evaluation of classification performance across all possible feature combinations; Analysis 2 selection of a single set of discriminatory features, followed by training and evaluation using cross‐validation; and, Analysis 3 nested cross‐validation. Analysis 1 enabled evaluation of average classification performance, independent of a feature selection heuristic, whereas Analyses 2 and 3 quantified classifier generalizability.

3.1. Functional connectivity analyses

Figure 3 shows the distribution of functional connectivity across voxels for two representative subjects (control and patient), in the case of the dorsal default mode network (dDMN). For Class III (Figure 3a,b), functional connectivity measurements across voxels of this network are approximately Gaussian distributed, with truncated left tail, indicating relative scarcity of negative correlation coefficients. In contrast, for Class IV (Figure 3c–f), functional connectivity values are distributed more uniformly (i.e., increased kurtosis, heavier tails), although the distribution remains positively skewed. The distributions are more uniform for Class IV because fewer degrees of freedom (i.e., fewer time samples) were used to compute functional connectivity within each sliding window, resulting in increased dispersion in correlation coefficient estimates. Supporting Information Figure S2 shows the distribution of functional connectivity values for the auditory network, where similar differences appear between Classes III and IV.

Figure 3.

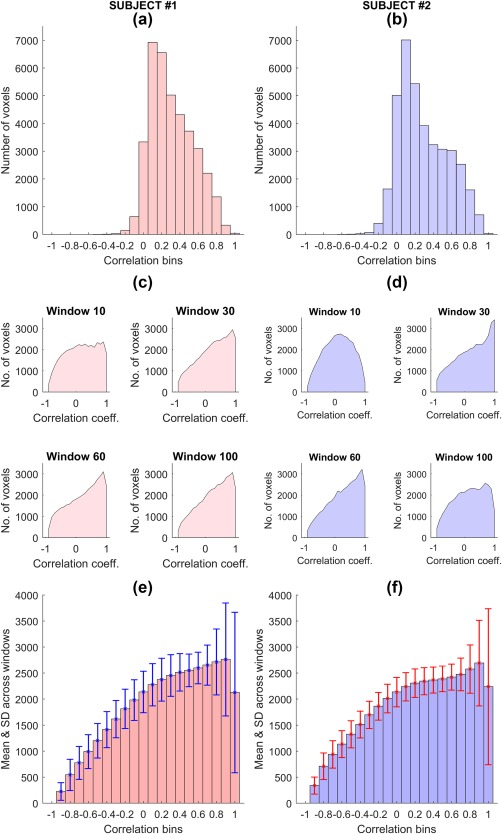
Distribution of correlation coefficients for the dorsal default mode network (dDMN) for two representative subjects (#1 is a control and #2 is a patient). (a and b) – Histograms of correlations corresponding to Class III; (c and d) – Histograms from a few of the sliding windows corresponding to Class IV; (e and f) – Average of histograms across all sliding windows with error bars representing the standard deviations of bin heights. These histograms were calculated via seed‐based correlation; the average seed time course was correlated to every voxel in the network as well as a 6 mm neighborhood and a histogram of these correlations was determined. For Class III (a and b), correlations were defined based on the entire scan duration, whereas for Class IV (c and d), a separate histogram was obtained from each window [Color figure can be viewed at http://wileyonlinelibrary.com]

Supplementary Information includes two videos that characterize the spatio‐temporal dynamics of the dDMN for a representative control subject (Video S1) as well as a patient (Video S2). In these videos, the plot that evolves as a function of time is the number of voxels within each sliding window with a functional connectivity value exceeding 0.3. The topography of the corresponding voxels is also shown for an axial slice. The videos show the contraction/expansion of the spatial extent of regions comprising the dDMN as a function of time. The improvement in single‐subject prediction is achieved by taking into account the dynamics of this regional contraction/expansion, as quantified by the distribution of functional connectivity values across voxels of the network. By comparing these two videos, a qualitative observation can be made that there are fewer correlated voxels in the patient dDMN on average (Video S2), and there are relatively more fluctuations between high and low connected states, compared to that in control subject (Video S1).

3.2. Classification performance

Figure 4 shows the distribution of classification accuracy, sensitivity, specificity and AUC across the $2^{14}-1$ different combinations of RSNs (Analysis 1), evaluated on Dataset 1. A separate boxplot is shown for each class of FC. For Class I, mean classification accuracy (average across all possible network combinations) was 72.5%. For Class II and Class III, mean accuracy was 77.3% and 77.5%, respectively. Class IV yielded the highest mean accuracy (86.3%), providing an improvement of ∼14% compared to Class I. This indicates that dynamic FC analyses (Classes II, III, and IV) provide improved classification accuracy compared to static FC (Class I); in particular, Class IV, which captures dynamics in both spatial and temporal domains, provided the most accurate classification performance.

Figure 4.

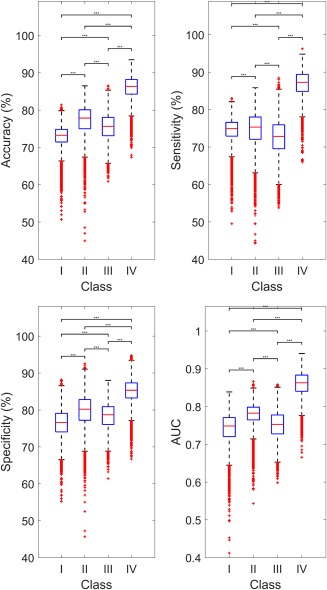
Performance of single‐subject prediction of schizophrenia diagnosis compared across four functional connectivity classes. Accuracy, sensitivity, specificity and area under the receiver operator characteristic curve (AUC) were evaluated for all possible network combinations (Analysis 1). Each box represents the distribution of these performance measures across $2^{14}-1$ different combinations of RSNs. Boxplot legend: upper (lower) box edge = 25th (75th) percentile; central red line = median; dotted whisker lines: 1.5× interquartile length; outliers indicated by red “+”. Classes are: Class I – Static in both time and space, Class II – Dynamic in time and static in space, Class III – Static in time and dynamic in space, Class IV – Dynamic in both time and space. Significant differences between classes are indicated by ***(p < .001) [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 3 shows the combinations of networks that were found with Analysis 1 to provide the maximum predictive power for each of the four different classes. These represent the optimal combinations from a total of 16,383 possible network combinations. Interestingly, the BGN is the only network to feature across all three dynamic classes, but the static functional connectivity of this network was not advantageous to Class I. This suggests that the spatio‐temporal dynamics of the BGN are particularly valuable in improving single‐subject prediction of schizophrenia diagnosis. It can also be seen that visual networks, either pVIS, hVIS or both consistently feature in most of the cases, and thus both static and dynamic connectivity attributes of the visual system appear to be important to single‐subject prediction. Despite prevalent implication of the DMN in schizophrenia pathophysiology (Garrity et al., 2007; Bluhm et al., 2007; Zhou et al., 2007; Whitfield‐Gabrieli et al., 2009; Jang et al., 2011; Fornito et al., 2015), this network only features in two of the four classes, with its spatial dynamics not used in Class III.

Table 3.

Combinations of resting‐state networks providing maximum predictive power

FC Class	Network combination	Number of networks
Class I	AUD, hVIS, LAN, pVIS, SMN, and VSN	6
Class II	AUD, BGN, dDMN, LECN, RECN, SMN, vDMN, and VSN	8
Class III	ASN, BGN, hVIS, LECN, PRE, and SMN	6
Class IV	ASN, BGN, dDMN, hVIS, PSN, and pVIS	6

As part of Analysis 1, the predictive power of every possible network combination (16,383) was evaluated for each of the four classes of FC. For each class, the combination which provided maximum classification accuracy is listed. The abbreviations are as per Table 2.

According to the measures of sensitivity, specificity and AUC (Figure 4), Class IV consistently outperformed the other three classes, while Class I yielded the poorest performance.

Figure 5 shows classification accuracy for the four classes of connectivity when using a feature selection step to identify the features with the strongest discriminatory power based on a training sample (Analysis 2) and then training a single classifier based on the selected features. This is in contrast to Figure 4 (Analysis 1), which shows average performance across all possible combinations of RSNs. In Figure 5, classification performance was evaluated for the top‐ $K$ features, where $K$ is shown between 10 and 100 in increments of 10. Consistent with Figure 4 (Analysis 1), Figure 5 indicates that Class IV consistently yields superior classification performance relative to static FC, as well as the classes that account for either temporal or spatial dynamics.

Figure 5.

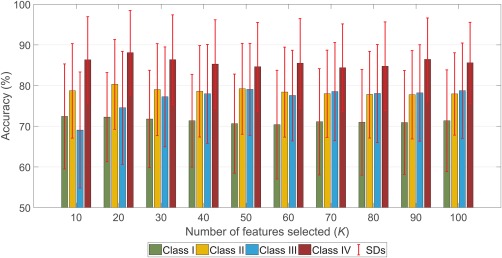
Classification performance evaluated as a function of the number of features selected (Analysis 2). Performance was evaluated independently across four functional connectivity classes. Rather than exhaustively evaluating all network combinations (Analysis 1), a feature selection step was first performed to identify the top‐ $K$ features and then a classifier was independently trained for each class of FC. Feature selection was performed as described in Analysis 2 (Section 2.5). The error bars show the SDs of accuracies across 30 different partitions of the data into training and test samples [Color figure can be viewed at http://wileyonlinelibrary.com]

In Analysis 3, for each partition of the dataset into test and training, the top‐50 network combinations were identified based on ten‐fold CV on the training data. A separate classifier trained for each of these combinations was used to evaluate the performance on the test data and the best performance was noted. This was repeated for 40 different partitions of the dataset and the average of the accuracies and other measures are as shown in Table 4. In agreement with Analyses 1 and 2, here also, Class IV yielded the highest classification accuracy.

Table 4.

Classification performance evaluated using Analysis 3. 60% of data was used to build classifiers, which was then used to classify the remaining data

FC Class	Accuracya (%)	Sensitivitya (%)	Specificitya (%)	AUCa
Class I	79.5 ± 5.5	86.8 ± 8.9	78.6 ± 9.2	0.74 ± 0.06
Class II	84.5 ± 5.4	85.7 ± 7.9	84.0 ± 7.9	0.81 ± 0.08
Class III	86.2 ± 5.3	85.2 ± 8.0	87.5 ± 8.6	0.83 ± 0.07
Class IV	91.1 ± 4.3	90.0 ± 7.4	92.2 ± 6.5	0. 87 ± 0.07

Mean ± SD of performance measures were calculated over classifications using 30 different partitions of dataset.

Abbreviation: AUC, area under the receiver operating characteristic curve.

^aMeasures are significantly different between any two classes of FC compared, with p < .001.

Figure 6 shows the classification performance of each individual RSN, in contrast to the previous results that considered combinations of RSNs. For 13 of the 14 RSNs, it can be seen that incorporating both spatial and temporal dynamics (Class IV) improved classification performance at the level of individual networks.

Figure 6.

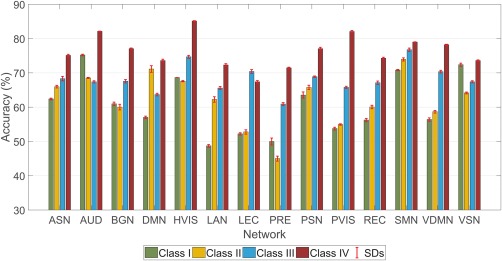
Classification accuracy achieved with individual networks. All 14 networks (as described in Section 2.3) were considered one at a time and with the features from the chosen network, a classifier was trained under 10‐fold CV. The classification accuracies are shown for the four classes (Section 2.4) of FC. Each bar represents the mean of the accuracies obtained from 30 independent runs of 10‐fold CV and the error bar shows the SD [Color figure can be viewed at http://wileyonlinelibrary.com]

3.3. Analysis of features

In Analysis 2, a group‐level comparison was performed to rank features. Features that significantly differed between the two groups are shown in Figures 6 and 7. For Class I, this involves correlation strengths between different nodes, while for Class II, this involves means and standard deviations of the correlations from different windows. Figure 7 shows connections that are significantly different between the two groups after correcting for multiple comparisons using false discovery rate correction (FDR), with an FDR threshold of 0.001. More connections significantly differed between patients and controls in the dynamic class of FC (Class II) compared to the static class (Class II).

Figure 7.

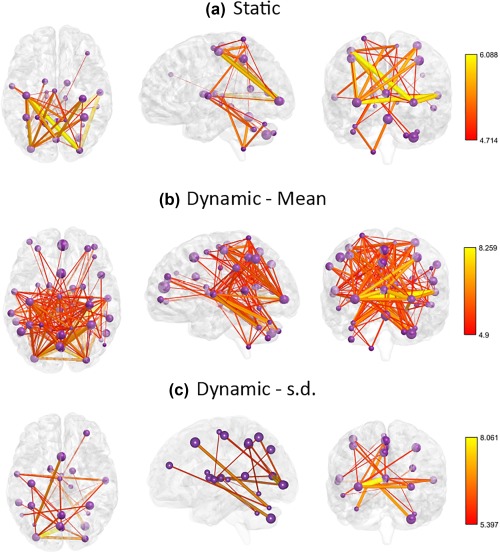
Static and dynamic connections those are significantly different between control and patient groups. (a) Connections that are significantly different for Class I: Static in space and time. (b) Connections for which mean strength is significantly different for Class II: Static in space and dynamic in time. (c) Connections for which variability is significantly different for Class II. Compared to Class I, Class II comprises more connections that are significantly different between the two groups. Purple spheres represent the network nodes, with the size of each sphere scaled according to the spatial volume of the corresponding node. The colour and thickness of each connection represents the t statistic, as per the color bars. s.d. – standard deviation. BrainNet Viewer (Xia, Wang, & He, 2013) was used to visualize these connections [Color figure can be viewed at http://wileyonlinelibrary.com]

For Class III, the features are 20 histogram bins for each of the network. These were compared across the group to identify those bin heights that were significantly different (p < .05) between the groups. For Class IV, both means and standard deviations of histogram bins were compared. These comparisons were performed for every network; Figure 8 demonstrates the specific case of dDMN, where group level averages of each feature are shown. Figure 8a stands for Class III; Figure 8b shows the group averages of means of bins and Figure 8c shows the averages of standard deviations of each bin. For the control group, there were significantly more voxels in many of the positive correlation bins, whereas in patients, negative correlations were more dominant. Again, the dynamic case (Class IV) had a greater number of significantly different bins compared to the static case (Class III). While only the case of dDMN is presented here, a similar trend was observed in the case of other RSNs as well.

Figure 8.

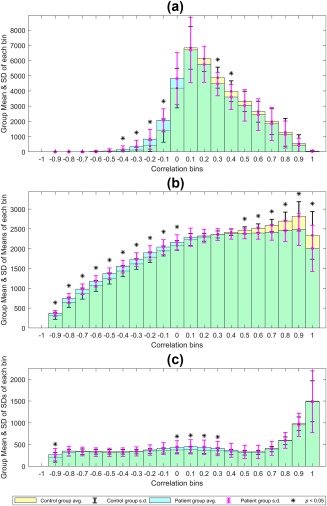
Mean ±  SD histograms at the group level for the dorsal default mode network (dDMN). (a) Class III: Static in time and dynamic in space. (b) Class IV: Dynamic in both time and space, feature = mean. (c) Class IV: feature = standard deviation. Yellow: controls, Cyan: patients. The * indicates bins that are significantly different (p < .05) in height between the two groups (two‐sample t test) [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4. Validation of results

Results from Analysis 1 applied to the validation dataset (Dataset 2) are shown in Figure 9. While classification accuracies for all classes are generally reduced in the validation dataset, it is evident that Class IV once again provides the greatest classification accuracy.

Figure 9.

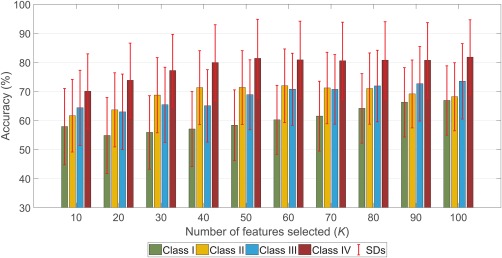
Classification performance replicated using an alternative dataset. Analysis 2 (Ranked feature selection) was performed by ranking features based on training sample and then using the classifier trained on top‐K to classify the test sample. Mean classification accuracy from 30 runs of Analysis 2 is reported with error bars representing standard deviation [Color figure can be viewed at http://wileyonlinelibrary.com]

3.5. Varying window length, neighborhood and seed regions

The effect of varying window length for the cases with dynamic temporal FC (Classes II and IV) in Analysis 2 is depicted in Supporting Information Figure S3. It is observed that for a wide range of window lengths from 10 to 70 TRs (20–140 s), the performance of the classifier is robust, whereas the accuracy decreases for window lengths above and below this range. Supporting Information Figure S4 delineates the effect of varying neighborhood levels on the classifier performance under Analysis 2. Incorporating a neighborhood of 2–6 mm is shown to increase (by ∼6%) the classification accuracy compared to not considering any neighborhood voxels. Varying the extent of the neighborhood to 10 mm did not significantly affect classifier performance.

When scrubbing was performed to correct for head motion, classification accuracies remained largely unchanged for all FC classes (Supporting Information Figure S5, Analysis 2). Scrubbing resulted in an overall slight improvement in classification accuracy, while the relative differences between the four classes were preserved. This suggests that intra‐scan head micro‐movements are unlikely to account for the substantially improved performance achieved with dynamic classes of FC. Repeating Analysis 1 for an alternative set of seed regions indicated that classifier performance was insensitive to seed region choice (Supporting Information Figures S1 and S6).

4. DISCUSSION

Single‐subject prediction of diagnosis, illness outcome and treatment response is important to clinical decision‐making in psychiatry and neurology. While non‐invasive neuroimaging has long been foreshadowed as a technology to enable optimization of individualized care, this potential has yet to be realized in clinical practice, primarily due to the lack of accurate and reliable predictive biomarkers. The development of reliable neuroimaging biomarkers that provide high predictive value at the single‐subject level is therefore crucial to enable the field of psychiatry to progress to an era of precision medicine.

Here, we focussed on developing reliable and accurate machine classifiers to predict the diagnosis of schizophrenia in individuals based on their resting‐state fMRI scan. We demonstrated that the prediction of diagnostic status can be substantially improved by modeling the dynamic properties of FC within key resting‐state networks. In particular, we were able to reliably predict diagnostic status with accuracy exceeding 90% when both temporal and spatial dynamics of FC were taken into account by the machine classifier (Class IV). In contrast, when only static measures of FC were utilized by the classifier, accuracy plummeted to below 80% (Class I).

These findings draw attention to the utility of characterizing both the temporal and spatial dynamics of resting‐state FC in schizophrenia. The dynamics of FC are classically construed and analyzed as statistical dependencies that unfold in time (Hutchison et al., 2013a). A novel contribution of this study is to provide a methodology to enable mapping FC dynamics that unfold in space and time, such that the spatial extent of each region is permitted to shrink/grow within a local neighborhood. It is common practice in FC studies to define regions of interest either using atlases, functional parcellations or in a meta‐analytical manner in which a spherical ROI is defined around the peak activation coordinates, followed by averaging the time courses from all voxels in the ROI to obtain a representative time course for the ROI. Both this approach and alternative ICA based methods impart a fixed spatial layout on the RSNs. In contrast, we developed a simple methodology to accommodate spatial variability in FC.

The importance of characterizing variability in the spatial layout of resting‐state functional networks has been indicated in a few recent studies. In particular, Gopal and colleagues (2015, 2016) report differences in the spatial layout of RSNs between healthy controls and schizophrenia patients, but this study did not characterize spatial dynamics that unfold over time. Furthermore, Kiviniemi and colleagues (2011) used a combination of temporal sliding‐window and ICA in healthy subjects to provide evidence for dynamic variations in the spatial topology of the default mode network. Ma and colleagues (2014) extended this ICA approach to study spatio‐temporal variations in RSNs between healthy individuals and schizophrenia patients. However, none of these studies consider single‐subject prediction of diagnostic status and they mandate an underlying assumption of spatial independence among networks.

Our findings also provide novel evidence against recent claims suggesting that dynamic properties of resting‐state FC are largely attributable to sampling error and/or head motion (Laumann et al., 2016). We calculated the average of FD over time for all subjects and these mean values were then compared between the patient and control groups via two‐sample t‐test; the differences were not significantly different (p > .1). Given this fact, the spatio‐temporal FC dynamics that we have found to improve prediction performance are unlikely to represent a trivial characterization of head motion. In addition, despite rigorous correction for intra‐scan head motion, we found that modeling spatial and temporal dynamics in FC resulted in significant improvements in classification accuracy compared to a static characterization. Indeed, the improvement in classification performance achieved with the inclusion of dynamic properties increased slightly when data scrubbing was employed to correct for head motion. While contention remains about the core definition and neural origins of dynamic FC (Liegeois et al., 2017), our findings provide a practical and clinically relevant demonstration of the utility in modeling spatial and temporal FC dynamics with a simple sliding‐window approach.

Identifying the specific dynamic properties of resting‐state FC that enhanced classification performance is an important line of inquiry. Comparing features between the two groups revealed that the dynamic cases are characterized by a larger number of features that are significantly different. In particular, for Class I, the connections of the frontal lobe regions to other parts of the brain were not significantly different between the patient and control groups (Figure 7a), whereas in Class II, several of these connections appeared to be significantly different (Figure 7b). Similarly, comparisons of Class III and IV reveal that there are more significantly different bins in the dynamic case (Figure 8a,b) and for many of the bins, the variability of bin heights is significantly greater in the patient group (Figure 8c). This indicates lesser integration in networks and more diversity of connections for the patient group. Supporting Information Figures S7 and S8 show the distribution of functional connectivity values across voxels for each network, for Classes III and IV respectively, in the case of a representative subject. Asterisks indicate correlation bins that comprise the top‐10 most predictive features. For Class III, the majority of features comprised the RECN network (5 of top‐10), whereas for Class IV, the majority comprised the hVIS network (6 of top‐10). This suggests that the spatial dynamics of the RECN network are particularly informative, but when spatial and temporal dynamics are considered jointly, the hVIS network provides the greatest predictive power. Interestingly, many of the top‐10 features of Class IV were the standard deviations of bin heights across the sliding windows, implying the significance of the temporal variability in connections. The increased temporal variability in network connections for the patient group (Figure 8c), especially in visual and auditory networks, has previously been reported to be potentially endophenotypic to schizophrenia (Li et al., 2017), due to the lack of sensory gating (Freedman et al., 1987; Mayer et al., 2009).

While the difference in correlation distribution of RSNs is a new observation, it is in line with the theory of “dysconnectivity” among brain regions in schizophrenia (Friston & Frith, 1995; Friston 1999), which has consistently been supported by evidence from studies using multiple imaging modalities (Kim et al., 2003; Calhoun et al., 2006; Zalesky et al., 2011; Ganella et al., 2016). Our observation of more voxels remaining negatively connected in patient group would present as a reduction in FC in the case of fixed region analysis (equivalent to taking average correlation among voxels), as reported in Classes I and II, and in previous studies (Lynall et al., 2010; Nelson, Bassett, Camchong, Bullmore, & Lim, 2017). However, this averaging reduces classification accuracy from 91.1% (Class IV) to 84.5% (Class II, dynamic in time case) and further to 79.5% (Class I, static in time case), as listed in Table 4. In addition, we have provided new insights into aberrant spatio‐temporal FC dynamics in schizophrenia, which build on previous studies that exclusively investigate static FC in the disorder (Liang et al., 2006; Kim et al., 2005; Zhou et al., 2007; Bluhm et al., 2007).

It is worth mentioning that by definition, Classes I and II consider both intra and inter‐network dynamics whereas Classes III and IV incorporate only intra‐network dynamics. Previously, many studies on temporal dynamic FC have analyzed between‐network interactions in schizophrenia. Damaraju et al. (2014) reported hyperconnectivity between thalamic and sensory networks in patients; Su et al. (2016) observed hypoconnectivity among default mode occipital and cingulo‐opercular networks; whereas Rashid et al. (2014) reported both hyper and hypoconnectivities among different RSNs. On the other hand, within‐network dynamics have been studied to a lesser extent; Du et al. (2016) reported reduced interactions among default mode subnetworks in the case of schizophrenia patients. We also have observed the same (Figure 8b,c) in addition to reporting such dynamics in other networks as well.

Due to the inherent differences in class definitions (Sections 2.4 and 2.5), the total number of features differed between classes. Specifically, the maximum possible number of features for Class I–IV was 4005, 8010, 280, and 560, respectively. Despite an augmented feature space that comprised both intra‐ and inter‐network dynamics, Class I and II did not provide superior performance. In general, classifier performance does not necessarily increase with feature space cardinality (Domingos, 2012) and in fact, here we found that the class with the least number of features (Class IV) performed best in all analyses. Furthermore, when the four classes were forced to comprise the same number of features (Analysis 2, top‐K features for all classes), Class IV remained optimal. This suggests that the unique attributes of intra‐network spatio‐temporal FC dynamics underlie the improvement in prediction accuracy, but not the number of features. Performance may potentially be improved by additionally considering the spatial dynamics of inter‐network interactions.

While the relative differences in classification performance between the four FC classes were largely preserved in an independent dataset, performance was overall reduced (Figure 9). This reduction in classifier performance might be due to one or more differences between the two datasets: Dataset 1 comprised more subjects (N = 82), whereas Dataset 2 had only 27 subjects; this may induce truncation errors in performance measures. Also, Dataset 1 was of a higher spatial resolution than Dataset 2 and was acquired at a higher field strength, both of which impact on the signal‐to‐noise ratio of measured time courses. Another consideration is that the datasets comprise schizophrenia patients with distinct clinical characteristics; namely, Dataset 1 comprised only TRS patients, while patients in Dataset 2 were responsive to antipsychotic medication and showed milder positive and negative symptoms. Out of the differences listed above, the only one that can be addressed post‐acquisition is the difference in resolutions of the two datasets. To test the influence of resolution, we down‐sampled images from Dataset 1 to 4 mm isotropic resolution and performed Analysis 1. We found that down‐sampling voxel resolution did not worsen classification performance by more than ∼4%.

While we have developed a new method to evaluate both spatial and temporal dynamics of connectivity and shown that this method provides more disease‐specific information compared to other FC analyses, there are a few methodological limitations that warrant further research. Firstly, we define RSNs based on templates from a previous study (Shirer et al., 2012) and have not investigated other modes of network definition. Secondly, the influence of medication on classifier performance is unknown. All the patients were diagnosed with schizophrenia and medicated for several years, which is a potential confound. Physiological confounds or the effects of antipsychotic medication can potentially impact resting‐state FC dynamics, and thereby impact classifier performance. Thirdly, the possibility of intra‐scan sleep cannot be excluded. As shown previously (Tagliazucchi & Laufs, 2014), sleep can influence resting state dynamics. In the present study, participants were given detailed instructions to stay awake; beyond that, no measures had been employed to identify or control any potential effects of sleep.

Methodologically, we employed a sliding window of fixed duration to assess temporal fluctuations in connection strengths. Interactions among different brain regions can have different durations at different times; therefore the approach of a fixed window length may not be optimal in capturing these variations. Despite the criticism leveled at the sliding window method (Hindriks et al., 2016; Lindquist, Xu, Nebel, & Caffo, 2014), in line with many other studies (Jin et al., 2017; Damaraju et al., 2014; Price et al., 2014), we have shown that this method can be effective in delineating disease states. For Analysis 2, feature selection was performed by ranking features according to t statistic magnitude. This could have resulted in the selection of correlated and thus redundant features. Multivariate feature selection heuristics such as minimum‐redundancy‐maximum‐relevance (MRMR) can alleviate this problem (Ding & Peng, 2005) and potentially improve classification performance.

5. CONCLUSION

We have demonstrated that characterizing the dynamics of resting‐state FC in both time and space can provide substantially improved single‐subject prediction of schizophrenia diagnosis compared to conventional static characterizations of FC. Our novel methodology involves jointly mapping temporal and spatial dynamics in FC and combines sliding‐window and seed‐based correlation analyses. Our findings provide complementary evidence that suggests dynamic fluctuations in resting‐state connectivity are of clinical utility and cannot be trivially ascribed to sampling variability and/or intra‐scan head movement. Rather than employing carefully constructed null models to address the vexed question of whether FC is dynamic and non‐stationary (Hindriks et al., 2016; Laumann et al., 2016; Liegeois et al., 2017), we have explicitly demonstrated that spatio‐temporal dynamics in the resting state can effectively characterize disease pathology in a serious psychiatric disorder. Our work establishes the utility of studying spatio‐temporal dynamics in resting‐state fMRI, at least in psychiatric disorders, irrespective of whether these dynamics satisfy statistical tests of non‐stationarity.

CONFLICTS OF INTEREST

The authors do not have any conflicts of interest to declare.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supporting Information

Supporting Information Video 1

Supporting Information Video 2

Kottaram A, Johnston L, Ganella E, Pantelis C, Kotagiri R, Zalesky A. Spatio‐temporal dynamics of resting‐state brain networks improve single‐subject prediction of schizophrenia diagnosis. Hum Brain Mapp. 2018;39:3663–3681. 10.1002/hbm.24202