SIENA‐XL for improving the assessment of gray and white matter volume changes on brain MRI

Abstract

In this article, SIENA‐XL, a new segmentation‐based longitudinal pipeline is introduced, for: (i) increasing the precision of longitudinal volume change estimation for white (WM) and gray (GM) matter separately, compared with cross‐sectional segmentation methods such as SIENAX; and (ii) avoiding potential biases in registration‐based methods when Jacobians are used, with a smoothing extent larger than spatial scale between tissue‐interfaces, which is where atrophy usually occurs. SIENA‐XL implements a new brain extraction procedure and a multi‐time‐point intensity equalization step before performing the final segmentation that also includes separate segmentation of deep GM structures by using FMRIB's Integrated Registration and Segmentation Tool. The detection of GM and WM volume changes with SIENA‐XL was evaluated using different healthy control (HC) and multiple sclerosis (MS) MRI datasets and compared with the traditional SIENAX and two Jacobian‐based approaches, SPM12 and SIENAX‐JI (a version of SIENAX including Jacobian integration ‐ JI). In scan‐rescan data from HCs, SIENA‐XL showed: (i) a significant decrease in error, of 50–70% when compared with SIENAX; (ii) no significant differences in error when compared with SIENAX‐JI and SPM12 in a scan‐rescan HC dataset that included repositioning. When tested in a HC dataset with scan‐rescan both at baseline and after 1 year of follow‐up, SIENA‐XL showed: (i) significantly higher precision (P < 0.01) than SIENAX; (ii) no significant differences to SIENAX‐JI and SPM12. Finally, in a dataset of 79 MS patients with a 2 years follow‐up, SIENA‐XL showed a substantial reduction of sample size, by comparison with SIENAX, SIENAX‐JI, and SPM12, for detecting treatment effects of 25, 30, and 50%. Hum Brain Mapp 39:1063–1077, 2018. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Magnetic resonance imaging (MRI)‐derived measures of brain volume changes have increasingly gained interest in clinical neurology [Giorgio and De Stefano, 2013]. The assessment of brain volume loss can represent a valid biomarker of clinical progression in many neurological disorders, providing insights into the understanding of physiological and pathological mechanisms leading to brain atrophy [Giorgio and De Stefano, 2013; Pini et al., 2016]. Recently, these measures have been used with success for monitoring treatment efficacy in large clinical trials of patients affected by neurodegenerative disorders [Giorgio and De Stefano, 2013].

While the high accuracy of global brain volume changes as measured, for example, by registration‐based modalities such as SIENA [Smith et al., 2002b] or BBSI [Fox and Freeborough, 1997] has been persistently reported in several studies [Novak et al., 2015; Popescu et al., 2013, Smith et al., 2007], the assessment of volume changes of tissue‐specific measures, such as gray matter (GM) and white matter (WM) volumes, still suffers from important technical limitations leading to significant increases in the measurement error [Sampat et al., 2010]. Among the different limitations, one of the most important is related to difficulty in producing an accurate separation of GM and WM at their interface, which makes the measure of GM and WM volumes relatively unstable. This is particularly evident in longitudinal assessments, due to subtle differences in contrast between images acquired in different MR sessions and in diseased brains, due to inherent brain damage (e.g., focal abnormalities in the WM). Overall, this can cause shifts in the GM/WM intensity distributions and consequent biases in the GM and WM volume estimations [Battaglini et al., 2012; Dwyer et al., 2014; Nakamura and Fisher, 2009]. Furthermore, differences in tissue intensities can produce an additional relevant error, particularly in images from two different MRI sessions, in the separation of brain from nonbrain tissues. This results in regions being erroneously classified as GM or WM and, consequently, in a reduction of the accuracy and robustness of GM and WM volume assessment.

Cross‐sectional methods that evaluate the GM and WM volume changes, which are based on the independent segmentation of each image of the same subject, typically suffer from all the limitations mentioned above. Recently, longitudinal registration‐based methods have been developed to overcome these issues [Guizard et al., 2015]. These methods evaluate the GM and WM volume changes through the calculation of the local Jacobian determinants of nonlinear displacement fields. It is possible to use symmetric diffeomorphic nonlinear registrations with [Ashburner and Ridgway, 2013] or without [Nakamura et al., 2014] temporal regularization. These methods improve the precision of the estimation of GM and WM volume changes, but can suffer from some limitations. In Jacobian integration methods, regardless of whether temporal regularization is applied or not, parameters are chosen to obtain a smooth Jacobian transformation, making the Jacobian potentially insensitive to small spatial scales, such as those associated with the interfaces between tissues, where atrophy usually occurs. Moreover, although the use of temporal regularization reduces the temporal fluctuations due to noise, it could also affect the real, anatomically induced fluctuations of the signal [Guizard et al., 2015].

In this work, we introduce a new segmentation‐based longitudinal pipeline with the aim of increasing the precision of longitudinal volume changes of WM and GM compared with cross‐sectional segmentation‐based methods, avoiding any potential biases related to the regularization parameters used in the registration‐based longitudinal approaches.

More than a decade ago, FSL (http://www.fmrib.ox.ac.uk/fsl) provided a tool (Structural Image Evaluation using Normalization of Atrophy, Cross‐sectional, SIENAX) [Smith et al., 2002b] for a robust, automated measurement of cerebral GM and WM on MRI datasets, which has been extensively used in clinical studies. Despite some recent improvements in accurate brain‐non brain separation [Battaglini et al., 2008; Popescu et al., 2012], in robust longitudinal segmentation [Dwyer et al., 2014] and in reducing bias caused by the presence of hypointense lesions on T1‐weighted (T1‐W) MRI of pathological subjects [Battaglini et al., 2012], the SIENAX approach still provides tissue‐specific volume measurements with an error that is close to 1%, which may be above the expected clinical changes. To overcome, at least in part, some of the above‐mentioned limitations and consequently reduce measurement errors in the separate assessment of GM and WM volumes in healthy and diseased brain, we propose here a new version of SIENAX. This now includes a longitudinal component and is therefore named SIENA‐XL (L for longitudinal).

This paper is organized as follows. First, we describe a new procedure to separate brain from non‐brain and compare it with the traditional FSL procedure (Brain Extraction Tool, BET) [Smith, 2002a] on a dataset of healthy controls (HC) scanned twice on the same day. Second, we use (i) artificial images with different signal‐to‐noise ratio and identical GM and WM volumes (Experiment 1) and (ii) a real dataset of HC with scan‐rescan acquisitions (Experiment 2) to test the error in GM and WM assessments due to partial volume modelling, as implemented in FAST, the FSL segmentation tool used in SIENAX [Zhang et al., 2001]. Third, an intra‐subject intensity equalization of serial images is added before of the MRI segmentation of GM and WM, to reduce biases in the FAST output, as highlighted by experiments 1 and 2 of the previous section. Finally, we describe the new SIENA‐XL procedure for the assessment of GM and WM volume changes, which modifies the traditional SIENAX procedure [Smith et al., 2002b] by implementing, (i) a new approach for brain extraction; (ii) a presegmentation step for equalizing the intensity distributions over multiple MRI sessions of the same subject; (iii) the segmentation of deep GM structures by using FMRIB's Integrated Registration and Segmentation Tool (FIRST) [Patenaude et al., 2011], as this has been shown to substantially decrease the variability in the estimation of GM volume changes [Derakhshan et al., 2010]. This new approach is then evaluated using multiple MRI datasets of HCs and patients with multiple sclerosis (MS) and compared (i) with the traditional SIENAX; (ii) with SIENAX using the Jacobian integration (SIENAX‐JI) that, as mentioned before, is a promising procedure that has recently demonstrated the ability to reduce GM and WM measurement errors [Nakamura et al., 2014] and; (iii) with SPM12, which uses temporal regularization to obtain Jacobian determinants [Ashburner and Ridgway, 2013], and has shown higher robustness and accuracy than other longitudinal methods such as Freesurfer [Guizard et al, 2015].

PART 1. NEW BRAIN EXTRACTION PROCEDURE

Background

If the nonlinear registration between standard space and T1‐weighted (T1‐W) images was perfect, a nonlinear transformation of a standard space brain mask into the native‐space T1‐W image could, in principle, separate brain from nonbrain tissue. However, the nonlinear registration of the standard space brain mask provided by FSL [Jenkinson et al., 2012] to the native T1‐W image at each time‐point has shown a certain degree of variability depending on the dataset analyzed [Dosh et al., 2013]. We therefore propose a method here that uses FSL tools to improve brain extraction and test it on two different sets of 3D T1‐W MRI images.

Method

We first perform a nonlinear registration to MNI space and then transform a dilated MNI space brain mask, provided by FSL, to the T1‐W image, by using the default parameters implemented in the fsl_anat tool of FSL [Jenkinson et al., 2012]. This initial T1‐W brain image is corrected for inhomogeneity using fsl_anat with the weakbias option, and then segmented into three different tissue classes [i.e., GM, WM, and cerebro‐spinal fluid (CSF)] using a separate application of FAST [Zhang et al., 2001]. Subsequently, all voxels with low (< 50%) probability of being CSF are added to a T1‐W brain mask that was obtained by transforming the nondilated MNI space brain mask into the native T1‐W space. A further step is then performed to refine this preliminary brain extraction. The binarized masks of the three tissues are created by taking the maximum partial volume estimation (PVE) for each voxel after transforming them into the standard (MNI) space. In the standard space, the probability that each voxel, of intensity I and coordinate x, is brain tissue is obtained by calculating the Bayesian posterior probability:

$$p\left(C_i|\mathrm{I},\mathbf{x}\right)\alpha p\left(C_i|\mathbf{x}\right)\hspace{0.17em}\ast \hspace{0.17em}p\left(\mathrm{I}|C_i\right)$$

where p(|) are the conditional probabilities and p(C_i|x) is the prior probability that a voxel with coordinate x in standard space belongs to the ith tissue class, C_i. For each class i, the prior probability, p(C_i|x), is provided by the average of PVE maps from 100 3DT1‐W images (TR/TE = 35 ms/10, voxel size = 1 mm³ acquired with a 1.5T magnet) of subjects enrolled in previous studies performed in our laboratory. These images were segmented using FAST and the PVE maps of GM and WM were transformed to the MNI space using a nonlinear registration run with FNIRT [Jenkinson et al., 2012]. Once the posterior probabilities are calculated, a voxel in the brain mask is retained only if the class with the highest p(C_i|I,x) is >0.5. In this way, the use of the prior atlas further reduces the number of false positive (non‐brain) voxels. The final mask, obtained in standard space, is then transformed back into the native space using a trilinear interpolation.

Materials and Analysis

We used 3D T1‐W images of HCs obtained from two different MRI acquisitions. The first set was downloaded from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (http://www.loni.usc.edu/ADNI) and consisted of 192 images from 96 subjects, each scanned twice in the same session. The ADNI was launched in 2003 as a public‐private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial MRI, positron emission tomography, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment and early Alzheimer's disease (AD). The second dataset consisted of 40 high‐resolution 3DT1‐W images (TR = 25 ms, TE = 4.6 ms, voxel size = 1 mm³, acquired with a 3.0T magnet) of 20 healthy subjects. They were recruited locally and each scanned twice on the same day, in two different sessions, in our center.

The new brain extraction procedure was compared with a version of the brain extraction tool of FSL that used an optimized setting (“optimized‐BET”), as previously described [Popescu et al., 2012]. We quantified the similarity of each pair of brain mask images using the DICE measure and the absolute percentage difference of the total brain volumes of the masks. In detail, the DICE was calculated by registering each pair of T1‐W images to the halfway space using siena_flirt, a subroutine in SIENA [Smith et al., 2002b]; then the two masks, mask 1 and mask 2, were linearly transformed into this halfway space, and the DICE measure was obtained with the formula:

$$2\ast n(\text{mask}1\cap \text{mask}2)/\left(n\left(\text{mask}1\right)+n\left(\text{mask}2\right)\right).$$

where n(mask) is the number of voxels in the mask. This gives a measure of the similarity between the brain masks of the two images that is sensitive to excluding different portions of the image, even if the total volumes were similar.

The formula:

$$\Delta V=200\ast \left(V1-V2\right)/\left(V1+V2\right)$$ (1)

was used to obtain the percentage difference in brain volume [Cover et al., 2011].

Comparisons between the median DICE values and between the absolute percentage differences in brain mask volumes were each tested using Wilcoxon rank tests (level of significance P < 0.05).

Results

Brain masks obtained with the new procedure were significantly more similar to each other than those obtained with optimized‐BET (Fig. 1a,b), both in terms of spatial overlap (DICE: 0.987 ±0.0028 vs. 0.977 ± 0.013, P < 0.01) and volumetric differences (absolute differences: 0.15 ± 0.38% vs. 0.27 ± 0.6%, P < 0.001).

Figure 1.

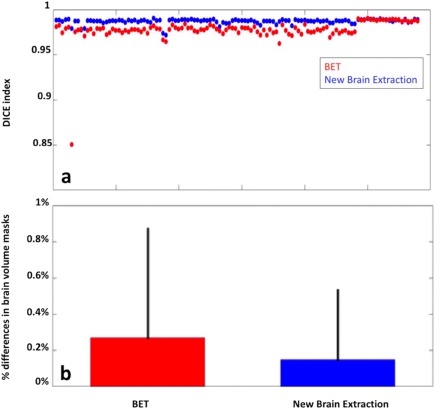
(a) DICE values for scan‐rescan MRI data relative of 116 HCs obtained from the brain masks of the new brain extraction procedure and optimized‐BET. The spatial agreement of the masks obtained with the new procedure is better than that obtained with the optimized‐BET. (b) Differences between the median of the absolute differences in brain mask volume as obtained with the optimized‐BET (red) and with the new procedure (blue). [Color figure can be viewed at http://wileyonlinelibrary.com]

When differences in median DICE between the ADNI group and our local dataset were compared, both our new brain extraction pipeline (ADNI: 0.987 ± 0.0030; local dataset: 0.988 ± 0.0011; P = 0.006) and the optimized‐BET (ADNI: 0.975 ± 0.0133; local dataset: 0.988 ± 0.001; P < 0.0001) showed better spatial overlaps when used in the local dataset.

PART 2. TESTING THE ERROR IN GM AND WM ASSESSMENTS DUE TO PARTIAL VOLUME

Background

Let I be an MR image and I _B the set of N voxels within the brain. Further, let the fractional volumes of the tissues (CSF, GM, and WM) at each of the voxels v_j in I _B be specified by the three numbers {p_i; i = 1,2,3} such that ∑_i p_i = 1 for each voxel. The total volume of a tissue across the brain is then given by V_i = (∑_j^Np_i(v_j))*Vol_v, where Vol_v is the volume of a single voxel.

A simple segmentation model is the hard segmentation model, where each voxel v is only associated with one tissue: in this case one of the p_i values will be equal to one and the other two will be equal to zero. Due to the size of typical voxels and the irregular shape of the interface between brain tissues, a hard segmentation leads to biases and suboptimal precision for volume measurements [Niessen et al., 1999]. Alternatively, several PVE models have been proposed, with the aim of providing more accurate proportions (p_i), reflecting the “real” mixture of tissues in each voxel. Zhang et al. [2001] and Van Leemput et al. [2003] implemented a 2‐stage estimation process, starting with a hard segmentation followed by PVE. These were estimated using the EM algorithm and a Markov Random Field spatial prior model, which incorporates spatial neighborhood information when estimating the p_i values.

A simplified summary of the PVE approach is that it considers a voxel, v, to be made up of M sub‐voxels, v_m, each of them consisting of only one tissue, with the overall intensity modeled by a Gaussian of mean intensity µ_i and standard deviation σ_i. Thus, the hard segmentation gives an initial rough estimate of the initial parameters µ_i and σ_i, and these are then iteratively redefined and used for calculating the triad of p_i values. In this framework, the intensity distributions of the “pure” voxels, (i.e., voxels estimated to only contain one type of tissue), should reflect the unknown intensity distributions of the true pure tissues. These parameters have a complicated relationship with the intensity histogram of I _B, since the intensities in the nonpure tissue voxels (containing mixtures of tissues) distort and blur the histogram. For longitudinal analysis of brain volumes this point is crucial, since differences in intensity contrast between tissues can, on their own, affect the estimation of changes in tissue volume over time.

To test the relationship between the error in volume measurement (as assessed by using FAST) and the partial volume, we performed the following two experiments.

Experiment 1

The first experiment aims at assessing whether, and to what extent, measurement errors of GM and WM, obtained using FAST, are related to changes in the signal‐to‐noise ratio.

Materials and analysis

A set of 50 T1‐W synthetic images was built by varying the “pure” distributions of the GM intensities, but keeping the total GM volume fixed. These images were based on 10 real MRI 3D‐T1W images of HCs and constructed as follows: from each real T1‐W image a brain image was created with optimized‐BET [Popescu et al., 2012] by masking out nonbrain voxels and then this was segmented with FAST to obtain PVE maps for CSF, GM, and WM. For each tissue, the average and the standard deviation of the intensities of those voxels containing only that type of tissue, according to the initial PVE classification, was used to define the simulated ground truth for the pure tissue intensity distributions. Finally, for each real T1‐W image, 5 synthetic images were obtained by filling (i) WM and CSF masks (defined as those voxels where WM or CSF, respectively, was the tissue with the largest PVE) with intensities sampled from the distributions of the respective pure tissues (the simulated ground truth, defined above) and (ii) the GM mask with values from a modified GM distribution. This modified GM distribution was a Gaussian distribution having the same mean as the original pure GM voxel intensities (as estimated above) but with a standard deviation equal to 0.8, 0.9, 1, 1.1, or 1.2 times the standard deviation of the original pure GM voxel intensities (estimated above). For each of the 10 original images a separate image was simulated using a different multiplicative factor for the standard deviation, such that the standard deviation was constant for any one image but varied over the simulated image set; this gave 10 × 5 = 50 simulated images in total. Note that the simulated ground truth voxel labels were the same for all five images derived from a single subject, and that only the intensity distribution of the GM was altered.

All the synthetic images were then segmented with FAST and the volumes of GM and WM were calculated, as well as the number of pure GM and WM voxels. For each synthetic image, percentage changes of total GM and WM volumes and also pure voxel numbers were calculated by comparison with the synthetic image where the multiplicative factor for the GM standard deviation was 1. Averaging across the 10 subjects, the mean of the percentage changes in GM and WM volumes, and the changes in number of pure voxels, were obtained for each separate setting of the GM standard deviation. Finally, Spearman regression analyses were performed between the changes in GM and WM volumes and the standard deviation values, as well as between changes in GM and WM volumes and changes in number of pure GM and WM voxels.

Results and conclusions

Decreases in the standard deviation of the GM in the synthetic images were associated with decreases of GM volume (r = −0.992, P < 0.0001) and increases of WM volume (r = 0.991, P < 0.0001). The mean error of GM and WM in this dataset, defined as the absolute change in volume between synthetic images generated with modified GM standard deviations compared with that of the original standard deviation, was 0.8% for GM and 0.47% for WM. Strong correlations were found between changes in volume and the number of pure voxels of both GM (r = 0.9989, P < 0.001) and WM (r = 0.9995, P < 0.0001).

This first experiment shows that the segmentation of images using FAST, that had the same GM and WM volumes, but with different intensity distributions for pure voxels, provides results that differ by an amount that is comparable with the levels of atrophy that we want to detect. This is without simulating any mixed tissue voxels, and so it demonstrates a fundamental bias in the calculation of volumes that depends on the contrast‐to‐noise ratio.

Experiment 2

Differences in partial voluming and intensity along the GM/WM interface are also likely to have a substantial effect on GM and WM volumes. To investigate this aspect of the FAST outputs, further simulations were conducted using true T1‐W 3D images. More specifically, the second experiment aims at assessing whether, and to what extent, measurement errors of GM and WM volumes, as obtained with FAST on scan‐rescan images, are related to the variability in the number of pure GM and WM voxels.

Materials and analysis

The same dataset of HC was used here as in Part 1 (i.e., 3D T1‐W images obtained from 2 different MRI acquisitions) together with the new procedure for brain extraction (from Part 1). These 3D T1‐W images were then segmented with FAST to obtain PVE maps of CSF, GM, and WM. The total volumes of GM and WM were then obtained by summing the respective PV values. For each tissue class, the number of pure voxels was also measured by counting all the voxels where one of the tissue probabilities was equal to 1.

The percentage error of a given measurement was calculated using Eq. (1). In this formula V can represent volume measurements of GM, WM, (GM + WM) or the number of pure voxels of GM (pGM), WM (pWM), or their sum p(GM + WM). Comparisons between the mean absolute errors in GM, WM and (GM + WM) and between the mean absolute deviations in pGM, pWM, and p(GM + WM) were tested with a Kruskal‐Wallis test, followed by multiple comparison correction using Tukey's honestly significant difference criterion. Correlation between the error of a volume measurement and that of the corresponding number of pure voxels was calculated by a Spearman regression.

Results and conclusions

The results are summarized in Figure 2. The absolute volume error for (GM + WM) (Mean ± SD: 0.3680 ± 0.4771%) was significantly lower (P < 0.05, after multiple comparison correction) than the error of both GM (Mean ± SD: 0.93 ± 1.03%) and WM (Mean ± SD: 1.12 ± 1.07%; Fig. 2‐a1). The absolute deviation of p(GM + WM) (Mean ± SD: 0.56 ± 0.78%) was significantly lower (P < 0.05 after multiple comparison correction) than the deviation of both pGM (Mean ± SD: 1.84 ± 2.02%) and pWM (Mean ± SD:1.05 ± 1.01%; Fig. 2‐a2). A very close correlation was found between the errors in GM and pGM (Spearman's ρ: 0.9418; P < 0.01; Fig. 2‐b1) and between the errors in WM and pWM (Spearman's ρ = 0.9525; P < 0.001; Fig. 2‐b2), but the correlation was only moderate between the errors in (GM + WM) and p(GM + WM; Spearman's ρ = 0.5; P < 0.001; Fig. 1‐b3).

Figure 2.

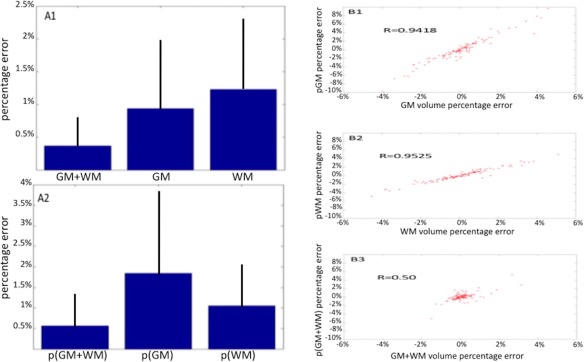
In the left panel, the graphs representing the errors of the (GM + WM), GM, and WM volume measurements (a1) and the errors of the numbers of pure GM (pGM) and pure WM (pWM) voxels and their sum p(GM + WM) (a2). The error of (GM + WM) is significantly lower than the errors of each separate tissue, and the error of p(GM + WM) is always significantly lower than the errors of the number of voxels for each separate tissue. In the right panel, the Spearman correlation between errors in GM and pGM voxels (b1), between WM and pWM voxels (b2) and between of (GM + WM) and p(GM + WM) voxels. In addition, in this case it can be noted that correlation between the (GM + WM) volume measurement and the number of pure voxels of (GM + WM) is significantly lower than the correlations between the volume of each separate tissue and the respective number of pure voxels of that tissue. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 3.

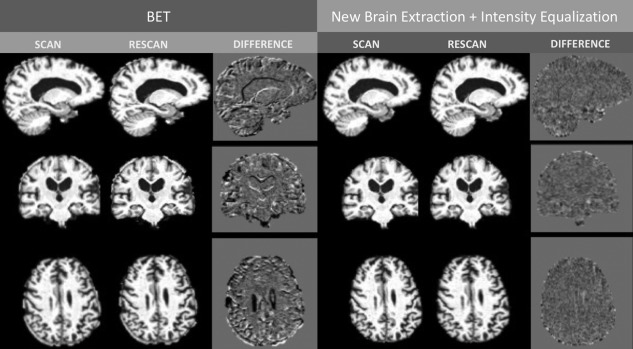
Illustrative example of intensity differences of a scan‐rescan dataset. When the new brain extraction and the joint intensity equalization methods are used (new procedure, on the right) the differences in intensities between images become smaller than when the two images were subctracted using the traditional‐SIENAX method (left panel). Please note the differences in the interface between tissue.

We can conclude here that, as obtained by the FAST PVE model, the number of pure voxels (pGM and pWM) varies substantially and these variations are closely associated with measurement errors in volumes (for GM and WM). However, the variation of their sum, p(GM + WM), is smaller and seems to impact less on the measurement error of (GM + WM) volume.

PART 3. SEGMENTATION PIPELINE

Summarizing the results of Experiment 1 and 2, it can be affirmed that, using FAST, there is a very strong correlation between the measurement error in the GM and WM volumes and the variability in numbers of pure GM and WM voxels. This is true even when the volumes of GM and WM are fixed, as shown by Experiment 1 that used simulated T1‐W images.

We propose a solution to this by performing combined intensity equalization on the set of serially acquired images of the same subject. This is intended to be a preprocessing step that is applied prior to image segmentation, and is described as follows.

Intensity Equalization

Let $I_B^j$ be the jth brain image of a set of serially acquired images from the same subject (this is a generalization that is also valid for more than two images per subject) and ${\mathit{p}}_{\mathit{i}0}^{\mathit{j}}$ be the probability distribution of the intensities of the pure voxels (determined by a preliminary segmentation by FAST of the brain extracted image using the new procedure described above) for the ith tissue; that is, ${\mathit{p}}_{\mathit{i}0}^{\mathit{j}}\left(s\right)$ is the probability of $I_B^j$ (x) = s for a location x that corresponds to the ith pure tissue. The histogram of intensities for the pure voxels is: ${\mathit{H}}_0^j={\sum }_{i=1}^3{{{\mathit{p}}_{i0}^{j}n}_i^j}_{}^{}$ where $n_i^j$ is the number of pure voxels of the ith tissue class and $N_{tot}^j={\sum }_{i=1}^3{n}_i^j$ the total number of pure voxels in the jth image.

Experiments 1 and 2 in the previous section showed that $n_i^j$ depends in a complex way on the MR acquisition conditions (especially the signal‐to‐noise ratio) and on the amount of atrophy. The probability distribution ${\mathit{p}}_{\mathit{i}0}^{\mathit{j}}$, however, should depend only on the MR acquisition if the classification of the pure voxels is reasonably accurate and has little contamination from partial volume voxels. Since atrophy does affect the number of pure voxels, the intensity normalization needs to account for this. Consequently, the probability distribution should not be derived directly from ${\mathit{H}}_0^j$ as this is influenced by $n_i^j$ and hence the unknown amount of atrophy. Therefore, to derive the probability distribution we introduce a quantity, ${n^{\prime }}_i^j$, which represents the value of $n_i^j$ that would have been estimated from a hypothetical image where no atrophy had occurred, but where the MR acquisition had still changed.

To estimate values for ${n^{\prime }}_i^j$ we impose several conditions. The first condition is that $N_{\mathrm{tot}}^1={N^{\prime }}_{\mathrm{tot}}^j$ for j > 1; and the second condition is that:

$$n_{\mathrm{gm}}^1+n_{\mathrm{wm}}^1={n^{\prime }}_{\mathrm{gm}}^j+{n^{\prime }}_{\mathrm{wm}}^j$$ (2)

which is based on the observation, from experiment 2 (Fig. 2), that the sum of the number of GM and WM pure voxels varies very little (a lot less than either one alone).

From these conditions, we obtain:

$$\left\{\begin{array}{c}{n\prime }_{\mathrm{g}\mathrm{m}}^j=n_{\mathrm{g}\mathrm{m}}^1+\hspace{0.17em}{\omega }_j\\ {n\prime }_{\mathrm{w}\mathrm{m}}^j=n_{\mathrm{w}\mathrm{m}}^1+\hspace{0.17em}{\mu }_j\end{array}\right.$$

as we know that the estimated number of pure voxels for the GM and WM do vary with MR acquisition, due to the subtler contrast between them, and so using Eq. (2) we obtain that ${\mu }_j$=‐ ${\omega }_j$ and this gives:

$$\{\begin{array}{l}{n^{\prime }}_{\mathrm{csf}}^j={n^{\prime }}_{\mathrm{csf}}^1\\ {n^{\prime }}_{\mathrm{gm}}^j=n_{\mathrm{gm}}^1-{\mu }_j\\ {n^{\prime }}_{\mathrm{wm}}^j=n_{\mathrm{wm}}^1+{\mu }_j\end{array}$$ (3)

These equations do not uniquely define ${\mu }_j$ and so we will further assume that

$${\mu }_j=\left\{\begin{array}{c}{n}_{\mathrm{g}\mathrm{m}}^j{-n}_{\mathrm{g}\mathrm{m}}^1\hspace{0.17em}if\hspace{0.17em}abs\left(n_{\mathrm{g}\mathrm{m}}^1-n_{\mathrm{g}\mathrm{m}}^j\right)<\hspace{0.17em}abs\left(n_{\mathrm{w}\mathrm{m}}^1-n_{\mathrm{w}\mathrm{m}}^j\right)\\ n_{\mathrm{w}\mathrm{m}}^1-n_{\mathrm{w}\mathrm{m}}^j\hspace{0.17em}if\hspace{0.17em}abs\left(n_{\mathrm{w}\mathrm{m}}^1-n_{\mathrm{w}\mathrm{m}}^j\right)<\hspace{0.17em}abs\left(n_{\mathrm{g}\mathrm{m}}^1-n_{\mathrm{g}\mathrm{m}}^j\right)\end{array}\right.$$ (4)

This is based on the hypothesis that the minimum difference among the pairs of numbers ( $n_{\mathrm{gm}}^1,n_{\mathrm{gm}}^j$) and ( $n_{\mathrm{wm}}^1,n_{\mathrm{wm}}^j$) for the most part depends on differences in acquisition conditions rather than true tissue atrophy. That is, as a result of this calculation, one of the numbers will remain unchanged (e.g., either ${n\prime }_{\mathrm{g}\mathrm{m}}^j=\hspace{0.17em}{n}_{\mathrm{g}\mathrm{m}}^1$ or $\hspace{0.17em}{\hspace{0.17em}n\prime }_{\mathrm{w}\mathrm{m}}^j$ = ${\hspace{0.17em}n}_{\mathrm{w}\mathrm{m}}^1$).

Using the above relationships, we can obtain the probability distributions and from that an intensity transformation that will minimize the differences between the probability distributions ${\mathit{p}}_{i0}^j$ of pure voxels between images, to compensate for changes in MR acquisition with minimal dependence on the amount of atrophy. To do this, we define a hypothetical histogram representing the pure voxels as if no atrophy had occurred. That is:

$${\stackrel{\sim }{\mathit{H}}}_0^j=\sum _{i=1}^3{n\prime }_i^j{\mathit{p}}_{i0}^j$$

where we use the ${n\prime }_i^j$ defined above, and we also define

$${\overline{\mathit{H}}}_0=\frac{1}{M}\hspace{0.17em}\sum _{j=1}^M{\stackrel{\sim }{\mathit{H}}}_0^j$$ (5)

as the average histogram of these hypothetical pure voxel distributions over all the M images of the same subject. The difference in these histograms between different images is:

$${\mathit{D}}_0^j={\stackrel{\sim }{\mathit{H}}}_0^j-\hspace{0.17em}{\overline{\mathit{H}}}_0$$ (6)

and, due to our construction, this primarily depends on differences in MR acquisition conditions, because in each case the histograms are estimates of the hypothetical case where the number of pure voxels is equal for each image of the same subject. Now, we define a new histogram, with the aim to reduce the differences that are due to MR acquisition:

$${\mathit{H}}_{\mathrm{B}\hspace{0.17em}\mathrm{n}\mathrm{e}\mathrm{w}}^j={\mathit{H}}_{\mathrm{B}}^j-{\mathit{D}}_0^j$$

where ${\mathit{H}}_{\mathit{B}}^{\mathit{j}}$ is the histogram of the intensities of all the voxels (not just pure voxels) in the jth brain image.

These two histograms, ${\mathit{H}}_{\mathrm{B}\hspace{0.17em}\mathrm{n}\mathrm{e}\mathrm{w}}^j$ and ${\mathit{H}}_{\mathrm{B}}^j$, are used to create an intensity transformation that acts to normalize, or equalize, the intensities between the different images of the subject. In our implementation, the intensity transformation is defined by using a piecewise mapping between the bins of ${\mathit{H}}_{\mathrm{B}\hspace{0.17em}\mathrm{n}\mathrm{e}\mathrm{w}}^j$ and ${\mathit{H}}_{\mathrm{B}}^j$.

In practice, all histograms are calculated using a set of intensity bins. These bins are defined by the intensity values at their borders, which are denoted as $b_k^j$ for k = 0,…, K for histogram ${\mathit{b}}_B^j$; that is, there are K bins in total, where the first bin spans intensity values between $b_0^j$ and $b_1^j$, the second bins spans intensity values between $b_1^j$ and $b_2^j$ and so on. Given these bins, the histogram is formed directly by determining the number of voxels in the image with intensity values within the bin range; that is, ${\mathit{H}}_B^j\left(k\right)$ is equal to the number of voxels where $b_{k-1}^j$ ≤  $I_B^j$(x) <  $b_k^j$. To create a more continuous intensity mapping, the bin intervals are then more finely sampled by evenly subdividing each bin by the number of elements, L_k, within that bin. That is, the interval $b_{k-1}^j$ to $b_k^j$, which was one bin, now becomes L_k intervals, with borders at m* ( $b_k^j$ – $b_{k-1}^j$)/L_k + $b_k^j$ for m = 0,…, L_k, where L_k =  $H_B^j\left(k\right)$. The new set of intervals (across the whole histogram, and not just one bin) are defined by the set of values $c_v^j$ for v = 0,…, $N_{\mathrm{t}\mathrm{o}\mathrm{t}}^j$, where $N_{\mathrm{t}\mathrm{o}\mathrm{t}}^j$ is the total number of voxels in $I_{\mathrm{B}}^j$; that is, the set of $c_v^j$ values is equal to the set of all values of the form m* ( $b_k^j$ – $b_{k-1}^j$)/L_k + $\hspace{0.17em}{b}_k^j$ for m = 0,…, L_k – 1 for all k (combining across all bins, while avoiding repeated values) plus $b_K^j$, to span the range [ $b_0^j,b_K^j$]. This same process is also performed for $H_{\mathrm{B}\hspace{0.17em}\mathrm{n}\mathrm{e}\mathrm{w}}^j$, creating intervals defined by $c_{v\hspace{0.17em}\mathrm{n}\mathrm{e}\mathrm{w}}^j$. The piecewise mapping function then maps $c_v^j$ to $c_{v\hspace{0.17em}\mathrm{n}\mathrm{e}\mathrm{w}}^j$, with linear interpolation in between. That is, for an intensity value I that is in between $c_v^j$and $c_{v+1}^j$, the transformed intensity value is:

$$I_{\text{new}}=\hspace{0.17em}(I–c_v^j)\ast ((c_{v+1\hspace{0.17em}\text{new}}^j\hspace{0.17em}–c_{v\hspace{0.17em}\text{new}}^j)/(\hspace{0.17em}{c}_{v+1}^j–c_v^j))\hspace{0.17em}+c_{v\hspace{0.17em}\text{new}}^j$$

PART 4. SIENA‐XL

We introduced the above modifications (the new approach for brain extraction and intensity equalization) into a new pipeline to obtain GM and WM volume changes (SIENA‐XL). Figure 3 shows an illustrative example of differences in intensities between a pair of scan‐rescan brain images when the traditional SIENAX compared with when the new SIENA‐XL pipeline is used.

The new pipeline procedure is shown in Figure 4. In comparison to the traditional SIENAX [Smith et al., 2002b], SIENA‐XL works on at least one pair of images and, in addition to the above‐mentioned modifications, introduces the segmentation of deep GM structures by using FIRST [Patenaude et al., 2011].

Figure 4.

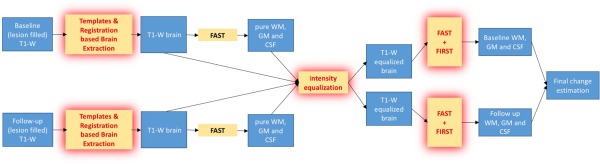
Illustration of the pipeline of SIENA‐XL: after the new brain extraction, the intensities of the T1‐brain images obtained are jointly equalized using the intensity distribution of the pure tissues (see Methods for detail) and finally the segmentation is run, integrating both the FAST and FIRST outputs to obtain the new GM and WM maps, from which the respective volumes are obtained. [Color figure can be viewed at http://wileyonlinelibrary.com]

We assessed this new approach using HC and MS MRI datasets and compared with results obtained by using the traditional SIENAX, SIENAX‐JI [an implementation of the methodology in Nakamura et al., 2014] and SPM12. In MS patients, the lesion‐filling procedure (as provided by FSL) was used in all methods, as it has been shown to substantially decrease the variability in the estimation of GM and WM volume changes [Battaglini et al., 2012].

Materials and Methods

SIENA‐XL was tested on three different datasets:

1. One hundred and sixteen scan‐rescan pairs of 3D T1‐W images of HCs used in Part 1 for testing the new brain extraction procedure. We separately analyzed (i) multicenter ADNI data (96 subjects), where 3D T1‐W images were acquired at 1.5T twice for each subject in the same session (i.e., without removing the subject from the scanner) and (ii) single‐center data of 20 healthy subjects, where high‐resolution 3D T1‐W images were acquired at 3.0T in two different sessions on the same day (i.e., removing the subject from the scanner, or repositioning).

2. One hundred and thirty‐six 3D‐T1‐W images of 34 HCs from the ADNI dataset, each subject having a one‐year follow‐up and scan‐rescan images at each time‐point.

3. One hundred and fifty‐eight 3D‐T1W images from a multicenter dataset of 79 untreated patients with relapsing‐remitting MS and a follow‐up of 2 years.

In all image datasets, the measurements obtained with the proposed method (SIENA‐XL) were compared with those obtained using the traditional SIENAX method, as well as with SIENAX‐JI and SPM12. Furthermore, in the first dataset, the impact of the different steps of the new method was assessed by estimating GM and WM volumes changes using (1) SIENAX with the new brain extraction; (2) SIENAX with the new brain extraction and intensity equalization; (3) SIENAX with the new brain extraction, intensity equalization, and FIRST (i.e., SIENA‐XL).

SIENAX‐JI was performed as previously described [Nakamura et al., 2014], using ANTS [Avants et al., 2011] for the nonlinear, symmetric registration of the second scan to the first scan and then integrating the Jacobian [Leow et al., 2007] of the transformation over the binarised mask of voxels from the first scan, where the probability of being either GM or WM was >0.5. Finally, the SPM12 longitudinal pair‐wise toolbox was used. This is based on a unified model that combines intensity nonuniformity correction, linear registration, and nonlinear registration. This method creates a subject‐specific template and integrates the Jacobian determinants of the deformation map (from the particular visit to the template) over the GM map provided by the segmentation of the template.

The optimized‐BET, as previously described [Popescu et al., 2012], was used in the traditional SIENAX and in SIENAX‐JI. As mentioned before, in the MS dataset, the bias in GM and WM volume assessment due to the presence of hypointense WM lesions in the T1‐W images was reduced by filling each lesion with intensities similar to the surrounding WM, as previously described [Battaglini et al., 2012].

In the tests using the first dataset, the error was quantified using the median of the absolute percentage difference of GM and WM volumes between the scan and rescan images. This was calculated separately for scan‐rescan MRI data without (96 HCs) and with (20 HCs) repositioning. In the tests using the second dataset (one‐year HC follow‐up data), the availability of four different images allowed four measurements of the same underlying volume change over time (from baseline to follow‐up) to be made for each subject and tissue: that is, GMch1 = 100*(GMsc2‐GMsc1)/GMsc1; GMch2 = 100* (GMresc2‐GMsc1)/GMsc1; GMch3 = 100*(GMsc2‐GMresc1)/GMresc1; GMch4 = 100*(GMresc2‐GMresc1)/GMresc1); where sc = scan and resc = rescan at timepoints 1 (baseline) and 2 (follow‐up). Since ideally these four measures should be identical, we used the variance of the four measurements as a quantification of the precision of the volume change assessment. For both the error in the scan‐rescan HC dataset and the precision of the volume changes in the 1‐year HC dataset, a one‐way analysis of variance (ANOVA), followed by a Tukey honest significance difference (Tukey's HSD) post‐hoc test (corrected P < 0.05), was performed to compare the performance between the different methods.

In the MS patient dataset, the sample size required to detect an effect with 90% power, 0.05‐significance level and 25–30‐50% treatment effect for GM was calculated using R [Chow et al., 2008]. The treatment effect was assumed to start immediately and remain constant over 2 years.

Results

3D scan‐rescan dataset of HCs

The results are displayed in Figure 5. Of the 116 HCs, 4 were excluded due to movement artifacts and three more were excluded (one each for SIENAX, SPM12, and SIENAX‐JI) due to highly inconsistent results (i.e., there was a major failure of the analysis pipeline).

Figure 5.

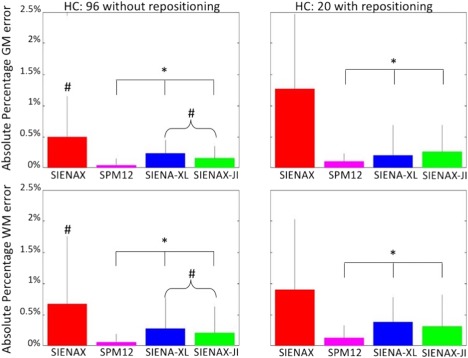
Error of SIENAX (red), SPM12 (magenta), SIENA‐XL (blue), and SIENAX‐JI (green) in scan‐rescan data set for GM (upper row) and WM (bottom row) of the 96 HC scanned twice in the same session (without repositioning) and for the 20 HCs scanned twice in different sessions of the same day (with repositioning). # Significant differences with SPM12; * significant differences with SIENAX (P < 0.05). [Color figure can be viewed at http://wileyonlinelibrary.com]

When the 96 HCs who were acquired twice in the same session without repositioning were analysed, the differences in the results between methods were significant (P < 0.0001 from the one‐way ANOVA) for the GM and WM errors. Comparing the individual methods showed that the measurement errors provided by SIENA‐XL (GM: 0.23 ± 0.21%; WM: 0.28 ± 0.49%) were not significantly different from those of SIENAX‐JI (GM: 0.14 ± 0.21%, P = 0.53; WM: 0.2 ± 0.42%, P = 0.95) but both methods had significantly smaller (P < 0.001) GM and WM errors than SIENAX (GM: 0.5 ± 0.65%; WM: 0.67 ± 1.1%) and significantly larger (P < 0.03) GM and WM errors than SPM12 (GM: 0.05 ± 0.11%; WM: 0.06 ± 0.13%).

When the single‐center data of the 20 HCs, who were acquired twice in different sessions on the same day with repositioning were analyzed separately, differences between methods were significant (P < 0.0001) based on the GM and WM errors. The measurement errors provided by SIENA‐XL (GM: 0.19 ± 0.47%; WM: 0.38 ± 0.4%) were not significantly different from either SIENAX‐JI (GM: 0.26 ± 0.4%, P = 0.98; WM: 0.31 ± 0.5%, P = 0.99) or SPM12 (GM: 0.10 ± 0.14%, P = 0.53; WM: 0.14 ± 0.19%, P = 0.51) but the three the methods had significantly smaller (P < 0.001) GM and WM errors compared with SIENAX (GM: 1.26 ± 1.2%; WM: 0.9 ± 1.13%).

When the separate impact of different steps of the SIENA‐XL pipeline was compared, no differences were seen in GM and WM errors derived from the full SIENA‐XL pipeline (GM: 0.23 ± 0.21%; WM: 0.28 ± 0.49%) and the pipeline with new brain extraction and intensity equalization (GM: 0.23 ± 0.32%, P = 0.9597; WM: 0.31 ± 0.48%, P = 0.9491). However, both of them had a significantly smaller error (P < 0.0001) than the pipeline that only implemented the new brain extraction (GM: 0.53 ± 0.96%; WM: 0.77 ± 1%).

3D dataset with one‐year follow‐up of HCs

Differences between methods were significant (P < 0.0001) overall for the variances of GM and WM volume changes. The variances of the GM and WM volume changes provided by SIENA‐XL (GM: 0.12 ± 0.17; WM: 0.43 ± 0.7) were not significantly different from those of SIENAX‐JI (GM: 0.026 ± 0.034, P = 0.65; WM: 0.24 ± 0.21, P = 0.98) or SPM12 (GM: 0.008 ± 0.02, P = 0.51; WM: 0.01 ± 0.015, P = 0.89) but all of them had significantly smaller variances in GM (P < 0.001) and WM (P < 0.002) volume changes compared with SIENAX (GM: 0.48 ± 0.67; WM:2.24 ± 4.96).

The measured one‐year volume changes in GM and WM for the HCs (mean age: 79 years ± 5) were (i) SIENA‐XL: GM: −1.17 ± 1.2%; WM: −0.25 ± 1.35%; (ii) SIENAX‐JI: GM: −0.6 ± 0.59%; WM: −0.38 ± 1.02%; (iii) SPM12: GM: −0.45 ± 0.83%; WM: −0.46 ± 1%; (iv) traditional SIENAX: GM: −1.55 ± 2.2%; WM: 0.78 ± 2.14%.

3D dataset with two‐year follow‐up of MS patients

In this patient dataset (mean age: 39 years ± 10), the measured two‐year volume changes in GM and WM were (i) SIENA‐XL: GM: −1.12% ± 0.9; WM: −1.37% ± 1.41; (ii) SIENAX‐JI: GM: −0.81% ± 0.77; WM: −0.56% ± 1.4; (iii) SPM12: GM: −0.64% ± 0.78; WM: −0.89% ± 1.02; (iv) traditional SIENAX: GM: −2.62% ± 2.59; WM: −0.63% ± 2.61.

The sample sizes for assessing 25–30‐50% treatment effects for GM volume changes in untreated MS patients with a 1‐year follow‐up were: 219‐152‐56 for SIENA‐XL, 391‐272‐99 for the traditional SIENAX, 305‐212‐77 for SIENAX‐JI, and 501‐348‐126 for SPM12. Results of the sample size calculations are summarized in Table 1.

Table 1.

Sample size versus treatment effect size

Treatment effect size	Sample Size
	SIENA‐XL	SIENAX	SIENAX‐JI	SPM12
25%	219	391	305	501
30%	152	272	212	348
50%	56	99	77	126

The sample size required to detect effect with 80% of power, 0.05‐significance level and 25‐30‐50% treatment effect for GM volume changes for SIENA‐XL, SIENAX, SIENAX‐JI, and SPM12. The treatment effect was assumed to start immediately and remain constant over 2 years.

GENERAL DISCUSSION

In this work, we introduced a new procedure, SIENA‐XL, for assessing longitudinal changes separately in GM and WM volumes. This differs from the traditional SIENAX procedure in the following ways: (i) it introduces a new procedure for separating the brain from non‐brain, (ii) it includes, prior to segmentation, an intensity equalization of serially acquired images by minimizing differences in the intensity histograms of the pure voxels for GM and WM, and (iii) it incorporates FIRST into the segmentation procedure to improve the assessment of deep GM structures. These three new steps, when used together, produced significant decreases in the errors of both the WM and GM volume change measurements.

The new brain extraction has been developed to minimize the differences between intrasubject brain masks, by decreasing the number of voxels erroneously classified as brain in one, but not in the other time point. The results obtained using a scan‐rescan dataset of a relatively large HC population showed that the new procedure was almost two‐fold more precise than the optimized‐BET procedure (error of 0.15 vs. 0.27%), which is also reflected in higher DICE similarity measurements (0.987 ± 0.0027 vs. 0.977 ± 0.013). As one can see by observing the standard deviation of the DICE values for the two procedures, the new brain extraction appears to be less dependent on differences in scanners and centers than the optimized‐BET, suggesting a reduction in the number of voxels that were not mutually classified as parenchyma in the two time‐points. Interestingly, both the new brain extraction procedure and the “optimized BET” method appeared to work better with our local dataset of HCs as compared with the ADNI dataset, even though the HC subjects in the local dataset were repositioned between the two scans. The differences in the DICE values between the two datasets was ten times smaller with our new pipeline (∼0.001) compared with the optimized BET method (∼0.01). Overall, this suggests that the reproducibility of the brain extraction results are related to the contrast between GM and CSF more than to the changes induced in repositioning. The use of this new procedure has relevant consequences for the subsequent intensity equalization step: misclassified voxels that are hyperintense (e.g., eyes ball and fat) or isointense (e.g., dura mater) with respect to the GM may cause an erroneous shifting of histograms, which would affect the GM and WM volume assessment and bias the comparison of GM and WM volumes from the same subject over time. The use of a‐priori information provided by standard space maps of GM, WM and CSF distinguishes this approach from the brain extraction procedure used in the fsl_anat tool of FSL [Jenkinson et al., 2012], but does not represent a novelty by itself, because it is in line with similar recently published software for brain/nonbrain separation [Dosh et al., 2014; Eskildsen et al., 2012].

Another important new step in the SIENA‐XL procedure is the intensity equalization of serially acquired T1‐W images. This intensity equalization method is different from other methods, which aim to standardize intersubject MRI [Nyúl et al., 2000], as this step is an intrasubject MRI equalization, based on the intensities of the pure voxels (i.e., voxels including 100% of one tissue). This new approach was motivated by the analysis of the relationship between the output from FAST and the partial volume, as described in Part 2. These experiments showed that FAST is systematically dependent on the signal‐to‐noise ratio, even when synthetic images without partial volume voxels were analysed (Experiment 1). Furthermore, it was shown that PVE in FAST biases the results of volume measurements of GM and WM, but is significantly more stable when the sum of GM and WM is considered (Experiment 2). Those considerations led to the conception of the new intensity equalization step described in Part 3. This new step has probably the greatest impact on the improvements provided by SIENA‐XL. Assessing errors in GM and WM by using (i) the new brain extraction; (ii) new brain extraction and intensity equalization; (iii) new brain extraction, intensity equalization and FIRST—the largest decrease in error (>50% both for GM and WM) was obtained when the intensity equalization was introduced. The inclusion of FIRST did not substantially improve the precision of the method, but slightly decreased the standard deviation of the error, probably due to a more reproducible segmentation of WM and GM.

In general, the algorithm used for PVE includes: (i) modeling the intensity of each tissue with a Gaussian distribution; (ii) performing an initial segmentation into three pure tissue classes (GM, WM, and CSF); and (iii) enhancing the segmentation of GM, WM, and CSF by adding partial volume classes (e.g., WM/GM, GM/CSF), utilizing the mean and standard deviation of each pure tissue class as provided by the second step [Cardoso et al., 2011; Van Leemput et al., 2003]. In our study, we perform an intensity equalization step with the aim of decreasing the differences in intensity distributions of the pure tissues between different images of the same subject. Once the intensity transformation that equalizes the intensity distributions of pure voxels from serially acquired image is found (see methods in Part 3), this intensity transformation is applied to all the voxels in the set of serial images. Thus we reduce differences in the means and standard deviations of pure voxels as obtained during segmentation, with an indirect effect on the creation of PV classes (WM/GM, GM/CSF). It is worth noting that no information is used from voxels with partial volume content when determining the intensity transformation and that this transformation is also only weakly dependent on the number of pure voxels at each time point. This strategy, although fully segmentation‐based, is longitudinal, as it uses information from different images, acquired at different times, to make the segmentation of each image more robust.

The assessment of the true accuracy of a given brain segmentation strategy is very challenging, due to the great difficulties in creating a realistic gold‐standard where the “true” partial volume content of different tissues at each voxel needs to be appropriately defined. Given this difficulty in measuring the true accuracy of GM and WM volume changes, the use of pairs of scan‐rescan images provides a good compromise by allowing the precision to be estimated. Thus, in this work, the results of SIENA‐XL were quantified in terms of precision and it was shown that this method was significantly more precise in assessing GM and WM volume changes in the scan‐rescan of HCs, and showed a significantly smaller variance of error measured in the longitudinal cohort of HCs, when compared with the traditional SIENAX. Furthermore, it should be noted that the errors obtained from the HC datasets for SIENA‐XL, SIENAX‐JI, and SPM12 did not vary greatly in dataset acquired with or without subject repositioning. This was not true for the traditional SIENAX assessment.

In the cohort of HCs with a one‐year follow‐up, the average GM and WM changes calculated by SIENA‐XL, SIENAX‐JI, and SPM12 were substantially reduced by comparison with those calculated by the traditional SIENAX. In particular, SIENA‐XL reports a WM reduction, which is not usually seen with SIENAX in this work and in other studies. Sometimes, even an increase in WM volume was found [Dwyer et al., 2014] with explanations suggesting that it is related to scanner drift, subject positioning or other acquisition differences. It is possible that the equalization of the intensity distribution of the pure voxels partially corrects for some of these errors, providing a better estimation of the WM and more biologically plausible results.

Overall, no significant differences were found between SIENA‐XL and SIENAX‐JI in the scan‐rescan and longitudinal cohorts of HCs. In contrast, SPM12 significantly outperformed SIENA‐XL and SIENAX‐JI in the HC scan‐rescan dataset without repositioning. SPM12 also showed a general, but not significant, reduction of the GM and WM errors when compared with the other two methods for the dataset with repositioning. These results are similar to those obtained in a recent work [Guizard et al., 2015] where SPM12 had the smallest error (∼0.1%) in detecting whole brain volume changes when compared with other longitudinal approaches. However, it must be stressed here that the interpretation of results might not be straightforward when, as in SPM12 and SIENA‐JI, the Jacobian integration is introduced in the pipeline. This approach attempts to partially circumvent the problems related with the segmentation by using a registration‐segmentation approach, similar to the tensor‐based morphometry method. In brief, the second time‐point image is nonlinearly registered to the first time‐point and the Jacobian, a measure of the local volume change per voxel, is calculated and integrated over the GM mask of the first time‐point, to assess the GM volume change. Given that, with the current segmentation approaches, atrophy is mostly measured at the interface between tissues and these voxels are the most difficult to accurately determine, we need to be particularly accurate when making a reference mask. Any errors in this mask will propagate through all measurements. Interestingly, when we applied the Jacobian integration to GM masks that were obtained with SIENA‐XL we found an error similar to that obtained using SIENAX‐JI (data not shown). However, the GM masks obtained with SIENAX‐JI and SIENA‐XL differed greatly, showing an overlap of only about 75% for the volumes. The 25% difference was mostly driven by voxels in the GM/WM and GM/CSF interfaces. This raises the question as to whether the changes that are detected with Jacobian integration can really be attributed only to changes in the GM tissue volume.

In this work, SIENA‐XL provided sample sizes for 25–30‐50% treatment effects for GM that were much lower than those provided by SPM12, SIENAX, and SIENAX‐JI. Although it may have been expected that the sample sizes measured with both SIENA‐XL and SIENAX‐JI were smaller than that obtained with traditional SIENAX, it is surprising that SIENA‐XL reduces the sample size by ∼50% when compared to SPM12, given the relative performance on the scan‐rescan datasets. In line with this finding, a recent work [Guizard et al., 2015] also showed a poorer performance of SPM12 in calculating the sample size for a patient group when compared with other longitudinal approaches. A plausible explanation for this [Guizard et al., 2015] could be that SPM12 is over‐regularizing the longitudinal deformations and could be smoothing away some of the real volumetric changes. This hypothesis could provide a straightforward explanation of both the strong reduction of the GM and WM errors in the scan‐rescan experiments as well as the increase in sample sizes for detecting treatment effects. Finally, it is worth noting that the results from SIENA‐XL in MS patients had a high rate of GM volume change with a relative small standard deviation, with both of these effects leading to a lower required sample size in comparison to the other methods tested here. Interestingly all the methods showed a larger yearly rate of GM atrophy in HCs (from the longitudinal ADNI cohort) compared to MS patients. This could be explained by differences in age between the two populations (mean age: ADNI: 78 years ± 5; MS cohort: 39 years ± 10) and by differences in the acquisition parameters. It must be stressed, however, that different GM rates obtained with different methods might be not comparable and that values for the rates need to be interpreted with caution.

This work has some limitations. The first is the definition of pure voxels based on a preliminary FAST segmentation: it is hard to predict what might happen in highly pathological brains (e.g., patients with very high lesion loads or with severe brain atrophy), where severe pathological changes are reflected in abnormal tissue intensity contrast in the MR images and could lead to a broad misclassification of GM and WM. However, it is also true that the use of highly pathological brains is very problematic for all segmentation and registration approaches [Djamanakova et al., 2013]. Thus, the normalization of MRI of severely atrophic brain on a template that was built on the MRIs of HCs could fail, biasing the new brain extraction procedure. This could be avoided by building a specific study‐template. Another limitation may lie in the sensitivity of this method to the quality of the images used. The joint intensity equalization step relies on the hypothesis that the intensity distribution of pure voxels is slightly different across the images; whereas if one image has a tissue contrast that is clearly different from the tissue contrast of other images from that subject, this would bias the creation of the average histogram of the pure tissues, expressed in Eq. (5) of Part 3. Furthermore, the method presented here may have difficulties in handling images with diffuse changes in WM intensity due to severe tissue damage, as this might affect the classification of pure voxels and the related histogram. This limitation, however, stands for all segmentation‐ and registration‐based methods and can be avoided only by using multimodal approaches or quantitative imaging. Finally, given the different intensity distributions in deep GM structures compared with the cortical GM, a natural extension of this method could consist of excluding voxels belonging to the deep GM from being included in the intensity equalization step.

CONCLUSIONS

The new SIENA‐XL procedure can provide more precise assessments of GM and WM volume changes over time than the traditional SIENAX, overcoming some of the difficulties in interpretation of volume changes obtained with segmentation‐registration approaches. It has also been shown, in a multicenter dataset of MS patients that SIENA‐XL can provide greater statistical power for discriminating longitudinal changes in GM, reducing the size of patient cohorts needed for testing treatment efficacy.

DISCLAIMER

The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health.

CONFLICTS OF INTEREST

M.B. has nothing to declare.

M.J. has received honoraria from Novartis Pharma AG and royalties from licensing of FSL to non‐academic, commercial parties.

N.D.S has served on scientific advisory boards and steering committees of clinical trials for Merck Serono SA, Novartis Pharma AG and Teva and has received support for congress participation or speaker honoraria from Bayer Schering AG, Biogen Idec, Merck Serono SA, Novartis Pharma AG, Sanofi Aventis and Teva.