Abstract
Neural circuit dysfunction underlies the biological mechanisms of suicidal ideation (SI). However, little is known about how the brain's “dynome” differentiate between depressed patients with and without SI. This study included depressed patients (n = 48) with SI, without SI (NSI), and healthy controls (HC, n = 30). All participants underwent resting‐state functional magnetic resonance imaging. We constructed dynamic and static connectomics on 200 nodes using a sliding window and full‐length time–series correlations, respectively. Specifically, the temporal variability of dynamic connectomic was quantified using the variance of topological properties across sliding window. The overall topological properties of both static and dynamic connectomics further differentiated between SI and NSI, and also predicted the severity of SI. The SI showed decreased overall topological properties of static connectomic relative to the HC. The SI exhibited increases in overall topological properties with regard to the dynamic connectomic when compared with the HC and the NSI. Importantly, combining the overall topological properties of dynamic and static connectomics yielded mean 75% accuracy (all p < .001) with mean 71% sensitivity and mean 75% specificity in differentiating between SI and NSI. Moreover, these features may predict the severity of SI (mean r = .55, all p < .05). The findings revealed that combining static and dynamic connectomics could differentiate between SI and NSI, offering new insight into the physiopathological mechanisms underlying SI. Furthermore, combining the brain's connectome and dynome may be considered a neuromarker for diagnostic and predictive models in the study of SI.
Keywords: diagnostic model, dynamic connectomics, major depression, predictive model, suicidal ideation, topological dissociation
1. INTRODUCTION
Sixteen percent of patients with major depressive disorder (MDD) have attempted suicide at least once during their lifetime (Brådvik, Mattisson, Bogren, & Nettelbladt, 2008). MDD patients with suicidal ideation (SI) are particularly predisposed to suicide attempts or suicidal behaviors (Pfaff & & Almeida, 2004). Thus, SI can be considered as the first step on the pathway to suicide (Klonsky & May, 2014). As such, it is critical to gain a more thorough understanding of the underlying neural circuity to diminish the risks posed by SI.
Multimodal neuroimaging studies revealed brain morphometric and functional abnormalities in MDD with suicide attempts. The accumulated evidence suggested that the fronto‐striato‐limbic circuitry (Johnston et al., 2017; Wagner et al., 2011)—which included the striatum dorsolateral, orbitomedial prefrontal and anterior cingulate cortices, amygdala, and hippocampus—was implicated in the neurobiology of those who attempted suicide (Cox Lippard, Johnston, & Blumberg, 2014; van Heeringen, Bijttebier, & Godfrin, 2011; van Heeringen, Bijttebier, Desmyter, Vervaet, & Baeken, 2014; Zhang, Chen, Jia, & Gong, 2014). However, few studies have focused on MDD with SI. The verbal fluency task‐related functional near‐infrared spectroscopy study suggested that depressed patients with SI showed reduced hemodynamic activation in the prefrontal and temporal cortices compared to healthy controls (Pu et al., 2015). Moreover, depressed patients with SI showed a reduction in the severity of SI following ketamine infusion. Such reductions in SI severity were correlated with decreased regional cerebral glucose metabolism in the infralimbic cortex (Ballard et al., 2015). These neuroimaging findings have recently demonstrated that SI is meidated by neurobiological processes within separate brain regions (Fried & Nesse, 2015). However, the question pertaining to whether MDD with and without SI indicates alterations of topological properties with regard to the underlying functional connectivity and connectomics remains largely unknown (Serafini, Pardini, Pompili, Girardi, & Amore, 2016).
With regard to brain disorders, the evolving domain of human connectomics recently considered the whole brain as a set of an anatomically and/or functionally interconnected network as opposed to distinct units (Fornito, Bullmore, & Zalesky, 2017). MDD patients evidenced alterations in the topological properties of large‐scale brain connectomics (Korgaonkar, Fornito, Williams, & Grieve, 2014; Zhang et al., 2011a). Thus, these disrupted system‐level pathologic networks provide an integrative perspective on the pathophysiological mechanisms and potentially valuable neuromarkers for early detection and risk assessment in cases of depression. Recently, resting‐state (absence of the stimulus) functional magnetic resonance imaging (fMRI) studies have reported that depressed patients with SI exhibited disrupted functional connectivity between the rostral anterior cingulate cortex and orbitomedial prefrontal cortex, that is, brain regions associated with decision‐making and emotional processing in SI (Du et al., 2017). In addition to the aforementioned seed‐based analysis of functional connectivity, recent functional connectomic study suggested that MDD with SI is characterized by decreased functional connectivity in the orbitofrontal‐thalamic circuits (Kim et al., 2017b). Moreover, an anatomical connectomic study suggested that MDD with SI was associated with a reduction of the anatomical connectivity in frontal–subcortical circuits (Myung et al., 2016). Both studies outlined earlier have more recently examined connectivity as fundamental property of brain connectomic. While considering the advantages of brain connectomics in terms of topological properties, the current study utilized system‐level pathological connectomic detection to examine different patterns of functional connectomics, particularly with regard to the topological properties in MDD patients with and without SI.
Conventional functional connectomic assumes that functional connectivity remains stationary throughout the entire duration of the fMRI scan. Moreover, functional connectivity is dynamic and associated with ongoing rhythmic activity, rather than remaining stationary over time (Allen et al., 2014). Emerging methods recognize the dynamics of connectivity and/or the dynamics of networks, which can be investigated by measuring the variability of characteristics including the strength or spatial dynamic properties (Bassett & Sporns, 2017; Hutchison, Womelsdorf, Gati, Everling, & Menon, 2013). Further pathophysiological studies may elaborate upon an understanding of the brain's dynome (Kopell, Gritton, Whittington, & Kramer, 2014). Many psychiatric and neurological diseases—such as MDD (Kaiser et al., 2016), schizophrenia (Braun et al., 2016), and epilepsy (Li et al., 2018; Liao et al., 2014b; Liu et al., 2017)—involve dysfunction of the brain's dynome. Such collective studies offer support for the hypothesis that dynamics of networks are critical to gaining a more thorough understanding of the brain's biological configuration.
With regard to the brain's dynome, the present research proposed that static and dynamic connectomics may generate diagnostic models capable of differentiating between MDD patients with and without SI, and furthermore provide predictive models to indicate the severity of SI. The researchers examined (i) whether the SI and NSI groups exhibit different alterations in topological properties of static and dynamic connectomics relative to healthy controls; (ii) whether these altered overall topological properties constitute potential neuromarkers for diagnostic models regarding the classification of SI and NSI groups; and (iii) whether these altered overall topological properties indicate the severity of SI and offer a predictive model.
2. MATERIALS AND METHODS
2.1. Participants
This study was approved by the Local Medical Ethics Committee of the First Affiliated Hospital of Chongqing Medical University. Written informed consent was obtained from all participants. Patients included a total of 51 drug‐naïve MDD patients with only one depressive episode. The diagnosis of MDD was conducted using a Structured Clinical Interview from the Diagnostic and Statistical Manual of Mental Disorders (SCID‐I/P, Chinese version) with a cutoff score ≥16 on the 17‐item Hamilton Depression Rating Scale (HAMD). Participants were excluded if they had (i) neurological or other psychiatric disorders; (ii) a history of substance, drug or alcohol dependence; (iii) observable brain abnormalities as evidence using MRI; (iv) metal devices such as electronic implants; or (v) excessive head movements during the scan. None of the participants had a history of suicidal, self‐harm behaviors, or suicide attempts during their current depressive episodes.
In addition, healthy controls (HC) comprised 30 participants, matched for age, gender, and education. These participants had no lifetime psychiatric disorder, no history of neurological disorders, and no gross abnormalities as confirmed using MRI. Additionally, participants in the HC group were interviewed to confirm that there was no history of psychiatric illness among their first‐degree relatives. The exclusion criteria also required that participants have no history of substance, drug, or alcohol dependence. Following the exclusion of participants who exhibited excessive head motion, 48 patients and 30 HCs were included in the final analyses.
2.2. Assessment of depression and SI
Depression severity was evaluated using the 17‐item HAMD scale. The severity of SI was determined using the Scale for Suicide Ideation (SSI) (Beck, Kovacs, & Weissman, 1979), a 19‐item clinical research instrument designed to quantify the intensity of current conscious suicidal intent. Item 4 and item 5 were used to estimate participants' current suicidal thoughts and to classify the patients according to those who were currently suicidal (SI group) and those with no suicidal ideation (NSI group) (Du et al., 2017).
2.3. Data acquisition
Functional images were acquired using 3.0 T MRI scanners from GE Medical Systems (Waukesha, WI) at the First Affiliated Hospital of Chongqing Medical University. Functional images were obtained using an echo‐planar imaging sequence with the following parameters: repetition time (TR) = 2,000 ms; echo time = 30 ms; flip angle= 90°; field of view = 240 × 240 mm2; in‐plane matrix = 64 × 64; voxel size = 3.75 × 3.75 × 5 mm3; 33 axial slices without slice gap, and a total of 240 volumes were collected for each participant. All participants were required to keep their eyes closed without thinking of anything in particular, to keep the head still, and not to fall asleep during the resting‐state fMRI scanning.
2.4. Data preprocessing
A schematic of the analyses is shown in Figure 1. Functional images were preprocessed using the DPARSF (V3.2, http://www.restfmri.net) and SPM8 toolkits (http://www.fil.ion.ucl.ac.uk/spm). The first 10 volumes were excluded. Slice‐timing correction and realignment were applied to the remaining volumes. Three out of all 51 participants (i.e., one NSI and two SI) were excluded as head motion exceeded 2.5 mm of translation or >2.5 degrees of rotation during the scan. The mean framewise‐displacement (FD) was then calculated for each participants (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012). Functional images were spatially normalized to the Montreal Neurologic Institute (MNI) space and resampled to 3 × 3 × 3 mm3. To avoid introducing artificial local spatial correlations between voxels, spatial smoothing was not applied, as previously suggested (Ji et al., 2017; Zhang et al., 2011b). Following normalization, several spurious variances—including head motion parameters (Friston 24‐parameter model; Friston, Williams, Howard, Frackowiak, & Turner, 1996), cerebrospinal fluid signals, white matter signals, and global signals—were regressed out using multiple linear regression analysis. Subsequently, linear trends were removed from the time courses. Temporal band‐pass filtering was performed between 0.01 and 0.10 Hz. Finally, as functional connectivity is sensitive to the confounding factor of head motion, scrubbing was performed for motion correction to reduce the negative influence (Power et al., 2012). If the FD exceeded 0.5 mm, the value of the signal at that point was interpolated using piecewise cubic Hermite (Ji et al., 2015).
Figure 1.
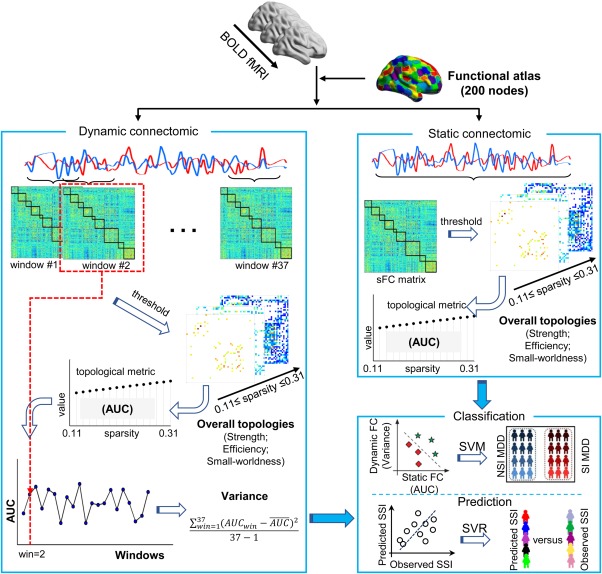
A schematic illustration of the analysis approach. The preprocessed resting‐state BOLD fMRI time series are extracted using a functional atlas with 200 nodes. Static connectomic is constructed using a full‐length time series (230 TRs, 460 s) for each pair of two nodes. The topological properties (i.e., network strength, network efficiency, small‐worldness, and nodal efficiency) are calculated on series sparsity thresholded (0.11 ≤ sparsity ≤ 0.31) weighted matrices for each participant. The area under curve (AUC) of each topological property is computed for subsequent statistical analysis. Dynamic connectomic is constructed using a sliding‐window analysis with sliding‐window length of 50 TRs (100 s), and shifted with a step size of 5 TRs (10 s). The topological properties (i.e., network strength, network efficiency, small‐worldness, and nodal efficiency) are calculated on series sparsity thresholded (0.11 ≤ sparsity ≤ 0.31) weighted matrices in each sliding‐window for each participant. The AUC of each network property is computed for each sliding‐window. The variance of the AUC is then computed across 37 sliding‐windows for temporal variability of dynamic connectomic for subsequent statistical analysis. The overall topologies of both static and dynamic connectomics are used as features to distinguish the SI group from the NSI group using support vector machine (SVM) and to predict the severity of SI group using support vector regression (SVR) [Color figure can be viewed at http://wileyonlinelibrary.com]
2.5. Construction of static and dynamic networks
2.5.1. Node definition
To define the brain nodes, gray matter (including cerebral and cerebellar cortices) parcellation was used to delineate 200 network nodes via a spatially constrained spectral clustering method (Craddock, James, Holtzheimer, Hu, & Mayberg, 2012) (http://www.nitrc.org/projects/cluster_roi/). This approach ensured the same number of voxels in each node, while optimizing within‐cluster similarity and between‐cluster dissimilarity.
2.5.2. Static functional connectomic construction
The time series were calculated by averaging the signal of all voxels within each node. Pearson's correlation coefficients (r) were evaluated using the full‐length time‐series of each pair of two nodes. Subsequently, a 200 × 200 raw matrix was obtained for each participant. Network analysis was processed on the basis of a weighted graph.
where wij expresses the weighted edge between the i th node and the j th node in the graph; rij expresses the raw correlation coefficient between the i th node and the j th node; r thr represents a predefined correlation threshold.
2.5.3. Dynamic functional connectomic construction
The dynamic connectomic were calculated using sliding‐window analysis in the DynamicBC toolbox (Liao et al., 2014a) (V2.0, http://www.restfmri.net/forum/DynamicBC). The “rule of thumb” is that the minimum window length should be no less than 1/f min, as short time segments can introduce spurious fluctuations. According to this rationale, f min was deemed the minimum frequency of the time series (Leonardi & Van De Ville, 2015). Therefore, the final sliding‐window length of 50 TRs (100 s) was selected to optimize the balance between capturing rapidly shifting dynamic relationships (with shorter windows) and achieving reliable estimates of the correlations between regions (with longer windows) (Liao et al., 2014b). The full‐length time‐series was segmented into sliding windows of 50 TRs (100 s) and shifted with a step size of 5 TRs (10 s). This procedure produced 37 windows for each participant. For each sliding window, the Pearson's correlation coefficient (r) matrix was obtained. Subsequently, 37 raw matrices (200 × 200) were obtained for each participant. Network analysis was processed on the basis of a weighted graph that was defined as the same as that for static connectomic.
2.6. Network analysis
2.6.1. Threshold selection
The network comparison needs to be ensured the same number of edges and nodes (Bullmore & Bassett, 2011). To this end, we applied the same sparsity levels to the weighted matrix corresponding to each participant. A sparsity threshold (S) was defined as the ratio of the existing number of edges divided by the maximum possible number of edges in a given network at a . Specifically,
where expresses the existing number of edges generated by thresholding at , and represents the maximum possible number of edges existing in a given network of N nodes (Bullmore & Bassett, 2011). In this case, when , ; when , . At present, there is no formal consensus regarding the selection of a single sparsity threshold. As such, a range of sparsity threshold (S) (0.11 ≤ S ≤ 0.31, interval = 0.01) was preselected as below.
Each participant had one static weighted matrix and 37 dynamic weighted matrices. The minimal S was defined across all participants as follows: (i) the mean degree of a node (the number of connections to the node) over all nodes in thresholded weighted matrices was >2 × log(N); N expresses the number of nodes, N = 200; (ii) the largest component size of thresholded weighted matrices was more than N × 80% = 160, where N expresses the number of nodes, N = 200. The maximal S ensured correlation coefficients p < .05 for all thresholded static and dynamic matrices across all participants.
2.6.2. Topological properties of static and dynamic connectomics
The overall and nodal topological properties of both static and dynamic connectomics were estimated using Gretna software (V1.2.0, http://www.nitrc.org/projects/gretna/) (Wang et al., 2015). The overall topologies included network strength (representing the connectivity capacity of the entire network), network efficiency (measuring the efficiency of information exchanges), and small‐worldness (processing both segregated/specialized and distributed/integrated information). To explore the nodal topologies, we evaluated nodal efficiency, which constituted an important control regarding information flow. These network topologies were computed as follows (Rubinov & Sporns, 2010):
2.6.3. Small‐worldness
where C net of a network expresses the mean weighted correlation coefficient across all nodes; L net of a network represents the mean weighted shortest path length between all possible node pairs; for each participant network, a set of 100 comparable random networks with similar degree sequence and symmetric adjacency matrix were formed; C random and L random were defined as the average weighted clustering coefficient and weighted path length of the comparable random networks.
2.6.4. Network strength
where G expresses a network; N represents the number of nodes; i expresses a node in this network G; and Si constitutes the i th node strength, which was computed using the sum of weighted correlation coefficients between the i th node and its links.
2.6.5. Network efficiency
where G expresses a network; N represents the number of nodes; Li,j expresses the weighted shortest path length between the i th node and the j th node.
2.6.6. Nodal efficiency
where G represents a network; N expresses the number of nodes; Li,j represents the weighted shortest path length between the i th node and the j th node.
For static connectomic, the area under curve (AUC) of each topological property (i.e., network strength, network efficiency, small‐worldness, and nodal efficiency) was calculated in a series of sparsity from 0.11 to 0.31 (interval = 0.01) for each participant. The integrated AUC property was used in subsequent statistical analysis.
For dynamic connectomic, each participant had 37 weighted matrices corresponding to windows. The AUC of each topological property was calculated (i.e., network strength, network efficiency, small‐worldness, and nodal efficiency) in a series of sparsity from 0.11 to 0.31 (interval = 0.01) for each window. The variance of AUC across 37 windows was computed for each participant utilizing the as following formula (Liao et al., 2014a; Liu, Liao, Xia, & He, 2018; Preti, Bolton, & Van De Ville, 2017):
where represents the mean value across 37 windows. Consequently, the variance of the AUC was used to define the temporal variability of both overall topological properties and nodal efficiency in dynamic connectomic unless otherwise specified.
2.7. Classification model
The linear Support Vector Machine (SVM) was selected as the classifier to classify SI and NSI patients using LIBSVM toolbox (V3.22, http://www.csie.ntu.edu.tw/~cjlin/libsvm/). Based on one‐way ANCOVA analysis, we used overall topological properties (AUC of overall topological properties in static connectomic and the variance of AUC of overall topological properties in dynamic connectomic), which showed significant group differences, to determine the classification features. In an effort to produce a robust and reliable model, a six‐fold cross‐validation was adopted (i.e., each fold involved eight participants) to evaluate classification performance (Varoquaux et al., 2017). The dataset was randomly divided into six folds. Among them, one fold was selected as the testing set, and the remaining five folds were used as training sets. As the dataset was imbalanced (28 SI vs 20 NSI), the F1‐score was used as a proxy for classification accuracy to obtain an optimistic estimation (Goutte & Gaussier, 2005). The F1‐score formula was as follows:
where TP expresses the number of true‐positive results; FP expresses the number of false‐positive results; FN expresses the number of false‐negative results.
To assess the statistical significance of accuracy in validation, the null distribution was obtained by conducting nonparametric permutation tests (5,000 times). F1‐scores were obtained across permutations. The p value was computed as the number of times the accuracy obtained from the permuted labels that was equal to or greater than the value of the estimated accuracy obtained from the true labels, then divided by the total number of permutations.
To test which overall topological properties showed high classification power, we computed the classification weight from the model to obtain a weight of each overall topological property (i.e., network strength and network efficiency) for static and dynamic connectomics.
The six‐fold cross‐validation was then performed 50 times to avoid bias introduced by fold randomness. Finally, the mean F1‐scores across 50 times were considered as representative of the final accuracy. Additionally, the mean weights across 50 times for each overall topological property and 50 p values were obtained.
2.8. Prediction model
To investigate the relationship between altered overall topological properties and the SI severity, we performed the prediction of SSI score for each participant in the SI group using linear Support Vector Regression (SVR). Similarly, overall topological properties were considered (the AUC of overall topological properties in static connectomics and the variance of the AUC of overall topological properties in dynamic connectomics), which showed significant group differences and constituted features in prediction model. We utilized six‐fold cross‐validation methods to develop this prediction model. The dataset was randomly divided into six folds. Among them, one fold was selected as the testing set, and the remaining five folds were used as training sets. For each trail of cross‐validation, the predictive SSI score was obtained for each participant in SI group to determine the correlation coefficient between the real SSI score and predicted SSI score. We calculated the predictive weight for each overall topological property (i.e., network strength and network efficiency) for static and dynamic connectomics. Finally, the six‐fold cross‐validation was repeated 50 times, thus enabling the researchers to acquire 50 correlation coefficients and the mean of predictive weights for each overall topological property (i.e., network strength and network efficiency). In addition, a correlation analysis was performed between the SSI score and one of the overall topological properties.
3. STATISTICAL ANALYSIS
3.1. Demographic and clinical characteristics
Demographic and clinical characteristics were evaluated among the three groups. A χ2 test was used to compare the gender among the three groups. Age, education, and mean FD parameters were compared using one‐way ANOVA among the three groups. Illness duration and the 17‐item HAMD were tested using Mann–Whitney U tests (i.e., values were not obtained from a Gaussian distribution) and two‐sample t tests (i.e., values were obtained from a Gaussian distribution) between the SI and NSI group, respectively.
3.2. Edge comparisons
For static connectomic, the weighted connectivity matrix was averaged (following Fisher r to z transformation) across participants in each group (HC, NSI, and SI, separately). For visual inspection, we showed static connectivity matrix (no thresholding) and connectomics (sparsity = 0.11) for the three groups.
For dynamic connectomic, 37 weighted matrices were gathered for each participant. The variance of 37 weighted matrices was computed (following Fisher r to z transformation) across sliding windows to obtain the dynamic matrix corresponding to the participant. Subsequently, the dynamic matrix was averaged for participants in each group (HC, NSI, and SI, separately). For visual inspection, a dynamic matrix (no thresholding) and connectomics was compiled (sparsity = 0.11).
To investigate differences in static and dynamic connectomics among the three groups, a one‐way ANCOVA was performed on the participant's weighted static and dynamic matrices (following Fisher r to z transformation) edge‐by‐edge. Age, gender, education, and mean FD were included as covariates. The significance threshold was set at p < .001. The results were presented on inflated surface maps using BrainNet Viewer (V1.60, http://www.nitrc.org/projects/bnv) (Xia, Wang, & He, 2013).
3.3. Topological properties comparisons
We compared the AUC of overall topological properties of static connectomic and the variance of the AUC of overall topological properties of dynamic connectomic using a one‐way ANCOVA among the three groups. Age, gender, education, and mean FD were included as covariates. The significance threshold was set at a Bonferroni correction of p < .05. Similarly, we compared the AUC of nodal efficiency in static connectomic and the variance of the AUC of nodal efficiency in dynamic connectomic using a one‐way ANCOVA (values obtained from a Gaussian distribution) or nonparametric Kruskal–Wallis test (values were not obtained from a Gaussian distribution) among the three groups (covariates: age, gender, education, and mean FD). We corrected the statistical significance for multiple comparisons using a false‐positive correction (Lynall et al., 2010), which was specific to multiple exploratory analyses at nodal properties (Fornito, Yoon, Zalesky, Bullmore, & Carter, 2011; Ji et al., 2017; Liao et al., 2013). Specifically, the significance threshold was set at p < (1/N), where N = 200 corresponded to the number of comparisons. Post hoc comparisons were then performed using two‐sample t tests (values were obtained from a Gaussian distribution) or nonparametric Mann–Whitney U tests (values were not obtained from a Gaussian distribution) on topological properties. We clarified which nodal efficiency statistic was analyzed with nonparameter statistical tests and the others were parameter statistical tests unless otherwise specified in the results section. The significance threshold was set at p < .05, Bonferroni corrected for three times planned comparisons. Due to the small sample size in each group, effect size (Cohen's d) was calculated to reveal group differences in overall topological properties.
3.4. Validation analysis
To validate our findings, we carried out auxiliary analyses as follows:
Sliding‐window length: Two additional sliding‐window lengths were utilized: 30 TRs (60 s) and 80 TRs (160 s) to estimate the reproducibility of results.
Split‐half: The NSI, SI, and HC groups were divided into two subgroups. The differences within both subgroups were tested to evaluate whether the results were affected by the sample population.
HAMD score regression: Results were reanalyzed by regressing out HAMD scores to test the difference between the SI and NSI groups with respect to the variance of the AUC of overall topological properties (i.e., network strength and network efficiency) in dynamic connectomic.
4. RESULTS
4.1. Demographic and clinical characteristics
The final analysis included data obtained from 48 participants, including 28 SI, 20 NSI, and 30 HCs. No differences in age (p = .27), education (p = .83), gender (p = .26), or head motion (p = .54) were found among the three groups. The results revealed a significant difference in the HAMD score (p = .002; Table 1).
Table 1.
Participant demographic and clinical information
| Demographics | SI | NSI | HC | Statistical | Evaluation |
|---|---|---|---|---|---|
| Group size (n) | 28 | 20 | 30 | NA | NA |
| Handedness (left/right) | 0/28 | 0/20 | 0/30 | NA | NA |
| Gender (male/female) | 7/21 | 4/16 | 12/18 | χ2 = 2.73 | p = .26 |
| Age (years) | 32.5 ± 9.9 | 37.1 ± 10.6 | 35.7 ± 10.2 | F (2,75) = 1.33 | p = .27 |
| Education (years) | 13.3 ± 2.6 | 13.3 ± 2.4 | 12.9 ± 3.2 | F (2,75) = 0.19 | p = .83 |
| Illness duration (months) | 16.6 ± 20.0 | 19.2 ± 20.0 | N.A. | U = 272.0 | p = .87 |
| HAMD score | 26.0 ± 4.0 | 22.2 ±3.8 | 2.8 ± 1.3 | t (46) = 3.38* | p = .002 |
| SSI score | 46.5 ± 9.6 | 0 ± 0 | 0 ± 0 | NA | NA |
| Mean FD | 0.09 ± 0.04 | 0.10 ± 0.06 | 0.10 ± 0.05 | F (2,75) = 0.63 | p = .54 |
Note. Abbreviations: FD = framewise‐displacement; HAMD = 17‐item Hamilton Depression Scale; HC = healthy controls; NA = not available; NSI = major depression disorder patients without suicidal ideation; SI = major depression disorder patients with suicidal ideation; SSI = 19‐item Scale for Suicide Ideation.
Values are mean ± SD.
p, between‐group or among‐group test p value; t (df), between‐group t statistic and degrees of freedom; F (dfn, dfd), one‐way ANOVA test and degrees of freedom numerator and degrees of freedom denominator. *t statistic between SI and NSI.
4.2. Edge comparisons
Static matrices (no thresholding) and connectomics (sparsity = 0.11) were compiled for the three groups (Figure 2a). The significant different edges among the three groups primarily included connectivity between the putamen, temporal, and frontal cortices in static connectomics (Figure 2a, right column). Additionally, dynamic matrices (no thresholding) and connectomics (sparsity = 0.11) were compiled for the three groups (Figure 2b). The different temporal variability of edge among the three groups mainly included connectivity between the caudate nucleus, precuneus, and frontal cortices in dynamic connectomic (Figure 2b, right column).
Figure 2.
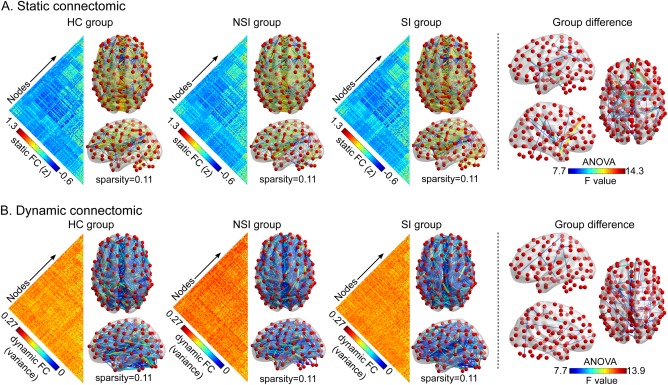
Comparison of raw regional connectivity among groups. (a) Static connectomic results. (b) Dynamic connectomic results. To illustrate, the static matrix (no thresholding) and connectomics (sparsity = 0.11) are depicted for the three groups (the left side of dotted line). The right side illustrates group differences in connectomics among the three groups (HC, NSI, and SI). Abbreviations: HC = healthy controls; NSI = major depressive disorder without suicidal ideation; SI = major depressive disorder with suicidal ideation [Color figure can be viewed at http://wileyonlinelibrary.com]
4.3. Static overall topological alterations
In a series of sparsity range from 0.11 to 0.31, the AUC of network strength (one‐way ANCOVA: F = 4.44, p = .015) and network efficiency (one‐way ANCOVA: F = 4.79, p = .011) in static connectomic showed group differences (Figure 3); while small‐worldness did not (Table 2). Post hoc analysis revealed a significant decrease in network strength (two‐sample t tests, t = −2.63, p = .0109, Bonferroni corrected, Cohen's d = 0.73) and efficiency (two‐sample t tests, t = −2.72, p = .009, Bonferroni corrected, Cohen's d = 0.76) within the SI group compared to the HC group.
Figure 3.
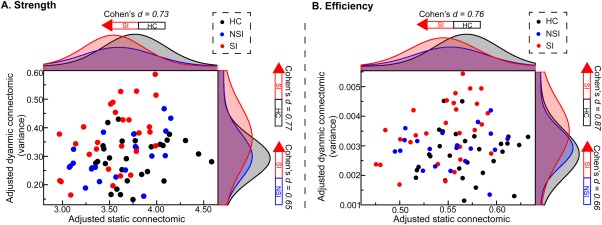
Distribution of topological properties in static and dynamic connectomics. The horizontal and vertical axes represent the overall topological properties of static connectomics and the variability of overall topological properties of dynamic connectomics (adjusted by age, sex, education, and mean FD), respectively. Black, blue, and red dots and lines represent the HC, NSI, and SI groups, respectively. Abbreviations: FD = framewise‐displacement; HC = healthy control; NSI = major depressive disorder without suicidal ideation; SI = major depressive disorder with suicidal ideation [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 2.
Summary of overall topological properties differences among three groups
| Comparisons Overall topologies | ANOVA | SI vs HC | SI vs NSI | NSI vs HC | |
|---|---|---|---|---|---|
| Network strength | Static | √ | ↓ | × | × |
| Dynamic | √ | ↑ | ↑ | × | |
| Network efficiency | Static | √ | ↓ | × | × |
| Dynamic | √ | ↑ | ↑ | × | |
| Small‐worldness | Static | × | × | × | × |
| Dynamic | × | × | × | × | |
Note. Abbreviations: HC = healthy controls; NSI = major depressive disorder without suicidal ideation; SI = major depressive disorder with suicidal ideation.
√ and × denote significant and nonsignificant groups differences, respectively; ↑ and ↓ denote increased and decreased overall topological properties, respectively.
4.4. Dynamic overall topological alterations
In a series of sparsity range from 0.11 to 0.31, the variance of the AUC of network strength (one‐way ANCOVA: F = 5.10, p = .008, Bonferroni corrected) and network efficiency (one‐way ANCOVA: F = 6.28, p = .003, Bonferroni corrected) in dynamic connectomic showed group differences (Figure 3); while small‐worldness did not (Table 2). The results of post hoc analysis showed a significant increase in the variance of the AUC of network strength (two‐sample t tests, t = 2.87, p = .0059, Bonferroni corrected, Cohen's d = 0.77) and efficiency (two‐sample t tests, t = 3.24, p = .0021, Bonferroni corrected, Cohen's d = 0.87) within the SI group compared to the HC group. The SI group also showed an increase in the variance of the AUC of network strength (two‐sample t tests, t = 2.19, p = .0337, uncorrected, Cohen's d = 0.65) and efficiency (two‐sample t tests, t = 2.20, p = .0327, uncorrected, Cohen's d = 0.66) compared to the NSI group.
4.5. Nodal efficiency of static and dynamic connectomics
To evaluate the centers of information flow, the researchers identified brain regions with disrupted nodal efficiency among the three groups. For static connectomic, the results largely revealed transdiagnostic alterations in the SI and NSI groups compared to the HC group. These alterations were found within the bilateral inferior frontal gyrus, triangular (IFGtri), bilateral insula (INS) (Kruskal–Wallis test), left precuneus (PCUN), caudate (CAU), inferior parietal gyrus (IPG), and right superior parietal gyrus (SPG) (Kruskal–Wallis test) (Figure 4a). Post‐hoc analysis revealed that the NSI and SI groups showed a significant decrease in nodal efficiency within the bilateral IFGtri, left CAU, IPG, INS (Mann–Whitney U test), PCUN, and right SPG (Mann–Whitney U tests) compared to the HC group. The SI group showed a decrease in nodal efficiency within the right INS compared with the NSI (Mann–Whitney U test) and HC groups. The results were presented on inflated surface maps using BrainNet Viewer (http://www.nitrc.org/projects/bnv; Xia et al., 2013).
Figure 4.
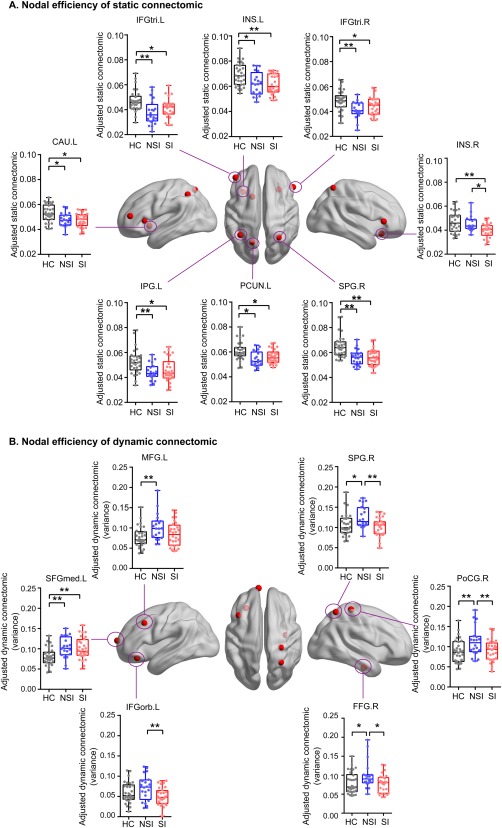
The distribution of brain regions with significant group effects in nodal efficiency of static and dynamic connectomics. (a) Static connectomics results. (b) Dynamic connectomics results. Abbreviations: CAU.L = left caudate; FFG.R = right fusiform gyrus; IFGtri.L = left inferior frontal gyrus, triangular; IFGtri.R = right inferior frontal gyrus, triangular; IFGorb.L = left inferior frontal gyrus, orbital; INS.L = left insula; INS.R = right insula; IPG.L = left inferior parietal gyrus; MFG.L = left middle frontal gyrus; PCUN.L = left precuneus; PoCG.R = right postcentral gyrus; SFGmed.L = left superior frontal gyrus, medial; SPG.R = right superior parietal gyrus. *p < .05 (uncorrected); **p < .05 (Bonferroni corrected) [Color figure can be viewed at http://wileyonlinelibrary.com]
For dynamic connectomic, the results showed alterations in the variance of the AUC of nodal efficiency across the three groups with regard to the left middle frontal gyrus (MFG) (Kruskal‐Wallis test), left inferior frontal gyrus, orbital (IFGorb), left superior frontal gyrus, medial (SFGmed), right postcentral gyrus (PoCG), right SPG (Kruskal–Wallis test), and right fusiform gyrus (FFG) (Kruskal–Wallis test) (Figure 4b). For the NSI and SI groups, post hoc analysis revealed transdiagnostic alterations within the left SFGmed. The NSI group showed specific‐diagnostic alterations within the left MFG (Mann–Whitney U test), left IFGorb, right SPG (Mann–Whitney U test), right PoCG, and right FFG (Mann–Whitney U test) compared to SI and HC groups. The results were presented on inflated surface maps using BrainNet Viewer (http://www.nitrc.org/projects/bnv; Xia et al., 2013).
4.6. Classification and prediction based on overall topological properties
Based on one‐way ANCOVA results, we used the AUC of overall topological properties (i.e., network strength and network efficiency) of static connectomic and the variance of the AUC of overall topological properties (i.e., network strength and network efficiency) of dynamic connectomic as features in the linear SVM and linear SVR.
A six‐fold cross‐validation method was repeated 50 times to obtain classification accuracy (F1‐score) (mean ± SD: 75 ± 1.3%, all p < .001), sensitivity (mean ± SD: 71 ± 3.0%, all p < .001) and specificity (mean ± SD: 75 ± 3.5%, all p < .001). In addition, we demonstrated that these features would distinguish the SI group from HC with classification accuracy (F1‐score) (mean ± SD: 73 ± 1.6%, all p < .01), sensitivity (mean ± SD: 70 ± 4.8%), and specificity (mean ± SD: 80 ± 4.7%), and furthermore differentiate between the NSI group and HC with classification accuracy (F1‐score) (mean ± SD: 62 ± 2.9%, all p < .05), sensitivity (mean ± SD: 62 ± 4.5%), and specificity (mean ± SD: 74 ± 1.5%). The mean classification weight of overall topological properties was expressed as follows: network strength (mean ± SD: 0.11 ± 0.025) and network efficiency (mean ± SD: 0.15 ± 0.032) in static connectomic; while network strength (mean ± SD: 0.30 ± 0.029) and network efficiency (mean ± SD: 0.27 ± 0.083) in dynamic connectomic.
The mean correlation coefficient was obtained following cross‐validation, repeated 50 times, between the observed SSI score and predictive SSI score (mean ± SD: r = .55 ± 0.05, all p < .05). One of the correlations between the observed and predictive SSI score is presented (Figure 5). The mean predictive weight of overall topological properties was expressed as follows: the variability of network strength (mean ± SD: 3.95 ± 1.10) and network efficiency (mean ± SD: 0.01 ± 0.004) in static connectomic; while the variability of network strength (mean ± SD: 4.70 ± 1.39) and network efficiency (mean ± SD: 0.03 ± 0.01) in dynamic connectomic. There were no significant correlation coefficients between the SSI score and one of the overall topological property (i.e., network strength and network efficiency) values for static and dynamic connectomics (Supporting Information, Figure S1).
Figure 5.

Overall topological properties predict the severity of suicidal ideation. Scatter plots show one of the 50 correlations between observed and predicted scale for suicidal ideation (SSI) scores. We combine overall topological properties (i.e., network strength and network efficiency) of static and dynamic connectomics as features, using a support vector regression (SVR) model to obtain the predictive score. Filled circles denote the analyzed points to fit the correlation line; open circles denote outliers. Abbreviation: SSI = Scale for Suicidal Ideation score [Color figure can be viewed at http://wileyonlinelibrary.com]
4.7. Validation results
Having analyzed the reproducibility of the findings, the researchers obtained the following results:
(i) Using different sliding‐window lengths, the results yielded similar findings with regard to network efficiency (Supporting Information, Figure S2).
(ii) The findings of the split‐half analysis showed that the constructed split‐half subgroups were similar in network strength and network efficiency. Differences between subgroups were consistent with previous findings regarding network efficiency and network strength (Supporting Information, Figure S3).
(iii) Regardless of whether or not HAMD scores were regressed out, differences were found between the SI and NSI groups regarding the variance of the AUC of network strength and network efficiency in dynamic connectomic (Supporting Information, Figure S4).
5. DISCUSSION
This study demonstrated that static and dynamic connectomics are capable of generating diagnostic and predictive models. The SI group showed decreased overall topological properties (i.e., network strength and network efficiency) of static connectomic compared to the HC group and increased topological properties (i.e., network strength and network efficiency) of dynamic connectomic compared to the HC and the NSI groups. Importantly, the overall topological properties (i.e., network strength and network efficiency) of dynamic and static connectomics yielded high accuracy when differentiating between SI and NSI participants. Moreover, such features may also predict the severity of SI.
Just one previous static connectomic study has found that MDD with SI reduced functional connectivity in the orbitofrontal‐thalamic network (Kim et al., 2017b). In addition, the nodal properties (i.e., nodal strengths, nodal clustering coefficients, and nodal efficiency) of the left orbital part of the superior frontal and the bilateral thalamus gyrus were significantly correlated with SSI scores (Kim et al., 2017b). Consistent with previous findings on static connectomic, we found that the putamen, temporal, and frontal cortices showed group differences. More broadly, for the first time, this study examined the temporal variability of dynamic connectomic on MDD with SI. At resting state, the brain's dynome reflects underlying temporal changes in topological properties (Liao et al., 2014b; Liao, Cao, Xia, & He, 2017), which are anatomically constrained by white matter connectivity (Liao et al., 2015). It is noteworthy that dynamic connectomic could successfully identify, with high accuracy, healthy individuals and could furthermore significantly predict individual high‐level cognitive behaviors (Liu et al., 2018). In a clinical setting, dynamic connectomic may reflect aspects of the functional capacity of the neural system (Liu et al., 2018), and thus, may serve as a novel physiological neuromarker of brain disease (Kim et al., 2017a).
Relative to the HC group, only the SI group showed a decrease in the overall topological properties (i.e., network strength and network efficiency) of static connectomic. The decreased network strength of static connectomic is consistent with previous connectomic‐level differences (Kim et al., 2017b). Rather unexpectedly, the SI group exhibited an opposite (increased) variability in network strength and efficiency (variance of the AUC as a proxy) in dynamic connectomic relative to the HC and the NSI groups. Increased variability within dynamic functional connectivity potentially facilitates brain information integration and greater flexibility in selectively switching between cognitive processes (Cohen, 2017; Liao et al., 2014a, 2017). Alterations in clinical conditions, excessive variability (increased temporal variance) or excessive stability (decreased temporal variance; Christoff, Irving, Fox, Spreng, & Andrews‐Hanna, 2016) could occur at different times, thereby contributing to alterations in cognitive function and particular pathological states (Preti, Bolton, & Van De Ville, 2016). As such, these findings suggested that the connectivity capacity and efficiency of information exchanges within the entire network were excessively variable in MDD with SI. In light of the discrepancies found with reference to alterations in static and dynamic connectomics in MDD with SI, combining them may assist in differentiating between SI and NSI (see discussion on classification section below).
In addition to examining overall topological properties, this study investigated alterations in nodal efficiency for both static and dynamic connectomics. The differences between the SI and NSI groups with respect to nodal efficiency were found in dynamic (including the SPG, PoCG, FFG, and left IFGorb), and static (the right INS) connectomics. This finding suggested that dynamic connectomic predominantly contributed to detecting diagnosis‐specific (Buckholtz & Meyer‐Lindenberg, 2012) brain alterations. The transdiagnostic alterations (Buckholtz & Meyer‐Lindenberg, 2012) (SI and NSI groups showed common alterations relative to HC group) were found in dynamic (the left SFGmed) and static (the left IFGtri, CAU, and PCUN) connectomics (Figure 4). This finding suggested that static connectomic highly contributed to exploring transdiagnostic features. In combination, static and dynamic connectomics are complementary in differentiating between SI and NSI patients. Moreover, these findings indicate the limitations of using static and dynamic connectomics separately to differentiate SI, particularly as the brain must strike a balance between stability (static connectomics) and variability (dynamic connectomics) (Liu, Chen, Dan, McKeown, & Wang, 2016). As such, a combination of both static and dynamic connectomics has been applied in schizophrenia (Rashid et al., 2016). Nevertheless, the precise means by which to combine static and dynamic connectomics remains an open issue. The coefficient of variation (Gonzalez‐Castillo et al., 2014) used both variation and mean values across sliding‐windows and the joint inference of time‐invariant connections (Liu et al., 2016).
The measurement of static functional connectomic holds great promise for the diagnosis of MDD (Zeng et al., 2012), but requires more reliable measurements for the classification of MDD with and without SI. The current work performed a classification analysis to distinguish between the SI and NSI groups using the overall topological properties of both static and dynamic connectomics. Importantly, using combined overall topological properties of static and dynamic connectomics as classification features has been proven to successfully differentiate between schizophrenia and bipolar patients (Rashid et al., 2016). The classification approach outlined in the present research was based on SVM and evaluated using a six‐fold cross‐validation method. The classification accuracy for distinguishing SI from NSI was 75%, suggesting that utilizing a combination of both static and dynamic connectomics is useful in the identification between SI and NSI. However, the classification features from dynamic connectomics proved more powerful in terms of classification relative to static connectomics, suggesting that the brain's dynome is more sensitive to classification. In addition, the researchers demonstrated that these features would be generalizable in differentiating between SI, NSI, and HC. Future research may examine whether such neuromarkers can differentiate between patients with and without to prevent suicide attempts in MDD patients and establish whether early intervention can diminish the possibility of suicidal thoughts.
The results of this study also suggest that a model based on a combination of static and dynamic connectomics is powerful, as it successfully predicted the SI severity in the SI group. Although previous studies have demonstrated that some neuroimaging features are correlated with the SI severity (Ballard et al., 2015; Myung et al., 2016; Pu et al., 2015), the researchers are not aware of any studies that have demonstrated the use of a connectomic model based on both static and dynamic topological features for utilization in the more accurate prediction of SSI scores for the SI group, as opposed to analyzing these topological features in isolation (Supporting Information, Figure S4). Moreover, the network strength of static and dynamic connectomics showed strong predictive power relative to network efficiency, suggesting that the combination of both static and dynamic network strength is more sensitive for use in predictive models.
There were some methodological limitations. First, there are trends in the differences of network strength (t = −1.70, p = .09) and network efficiency (t = −1.69, p = .09) between the NSI and the HC groups with respect to static connectomic. These results may be attributed to the small size of the NSI group and different brain parcellation schemes which affect brain topological properties (Wang et al., 2009) compared with previous study (Zhang et al., 2011a). In addition, although the group size is relatively small, the power analysis showed a large effect size for abnormal functional brain networks within the SI and NSI groups, suggesting the generalizability of the findings to a large sample size. Moreover, the current work lacked the other independent validation data to test the generality of classification and prediction models. Second, window length is an important parameter to describe dynamic connectomic. The researchers selected the window size according to the filter bandwidth (0.01–0.1 Hz) utilized in a previous study, which recommended that the minimum window length should be not less than 1/f min (1/0.01 = 100 s) (Leonardi & Van De Ville, 2015). Similar, albeit less reliable, results from the utilization of different sliding window lengths suggest that the findings of this study are less influenced by this factor. Third, in this study, in fact, we used a relatively low sampling rate (TR = 2 s). Under this sampling rate, respiratory and cardiac fluctuations may still pose a problem for resting‐state fMRI time series, despite utilization of a band‐pass filter in the range of 0.01–0.08 Hz to counter this. These respiratory and cardiac fluctuations may reduce the specificity of low‐frequency fluctuations to functional connected regions (Murphy, Birn, & Bandettini, 2013). Finally, the researchers did not include follow‐up data as they were unable to examine whether these neuromarkers can predict subsequent SI.
In conclusion, we investigated the dynamic connectomic on MDD with and without SI for the first time. The current findings of overall topological properties highlighted that combining static and dynamic connectomics could differentiate between SI and NSI patients, offering novel insight into the physiopathological mechanisms of SI. Furthermore, the brain's connectome and dynome may be considered as a neuromarker for the utilization and generation of diagnostic and predictive models in cases of SI.
CONFLICT OF INTEREST
The authors declare that they have no conflict of interest.
FUNDING
This work was supported by the National Natural Science Foundation of China (81471653, 61533006, and 61673089), China Postdoctoral Science Foundation (2013M532229), Sichuan Science and Technology Program (2018TJPT0016), and the “111” Project (B12027).
Supporting information
Additional Supporting Information may be found online in the supporting information tab for this article.
Supporting Information
ACKNOWLEDGMENTS
The authors are grateful to all the participants in this study.
Liao W, Li J, Duan X, Cui Q, Chen H, Chen H. Static and dynamic connectomics differentiate between depressed patients with and without suicidal ideation. Hum Brain Mapp. 2018;39:4105–4118. 10.1002/hbm.24235
Funding information National Natural Science Foundation of China, Grant/Award Numbers: 81471653, 61533006, 61673089; China Postdoctoral Science Foundation, Grant/Award Number: 2013M532229; Sichuan Science and Technology Program, Grant/Award Number: 2018TJPT0016; “111” Project, Grant/Award Number: B12027
REFERENCES
- Allen, E. A. , Damaraju, E. , Plis, S. M. , Erhardt, E. B. , Eichele, T. , & Calhoun, V. D. (2014). Tracking whole‐brain connectivity dynamics in the resting state. Cerebral Cortex (New York, N.Y. : 1991), 24(3), 663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballard, E. D. , Lally, N. , Nugent, A. C. , Furey, M. L. , Luckenbaugh, D. A. , & Zarate, C. A. (2015). Neural correlates of suicidal ideation and its reduction in depression. International Journal of Neuropsychopharmacology, 18(1), pyu069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett, D. S. , & Sporns, O. (2017). Network neuroscience. Nature Neuroscience, 20(3), 353–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck, A. T. , Kovacs, M. , & Weissman, A. (1979). Assessment of suicidal intention: The Scale for Suicide Ideation. Journal of Consulting and Clinical Psychology, 47(2), 343–352. [DOI] [PubMed] [Google Scholar]
- Brådvik, L. , Mattisson, C. , Bogren, M. , & Nettelbladt, P. (2008). Long‐term suicide risk of depression in the Lundby cohort 1947–1997–severity and gender. Acta Psychiatrica Scandinavica, 117(3), 185–191. [DOI] [PubMed] [Google Scholar]
- Braun, U. , Schafer, A. , Bassett, D. S. , Rausch, F. , Schweiger, J. I. , Bilek, E. , … Tost, H. (2016). Dynamic brain network reconfiguration as a potential schizophrenia genetic risk mechanism modulated by NMDA receptor function. Proceedings of the National Academy of Sciences of the United States of America, 113(44), 12568–12573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckholtz, J. W. , & Meyer‐Lindenberg, A. (2012). Psychopathology and the human connectome: Toward a transdiagnostic model of risk for mental illness. Neuron, 74(6), 990–1004. [DOI] [PubMed] [Google Scholar]
- Bullmore, E. T. , & Bassett, D. S. (2011). Brain graphs: Graphical models of the human brain connectome. Annual Review of Clinical Psychology, 7, 113–140. [DOI] [PubMed] [Google Scholar]
- Christoff, K. , Irving, Z. C. , Fox, K. C. R. , Spreng, R. N. , & Andrews‐Hanna, J. R. (2016). Mind‐wandering as spontaneous thought: A dynamic framework. Nature Reviews. Neuroscience, 17(11), 718–731. [DOI] [PubMed] [Google Scholar]
- Cohen, J. R. (2017). The behavioral and cognitive relevance of time‐varying, dynamic changes in functional connectivity. NeuroImage. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox Lippard, E. T. , Johnston, J. A. , & Blumberg, H. P. (2014). Neurobiological risk factors for suicide: Insights from brain imaging. American Journal of Preventive Medicine, 47(3 Suppl 2), S152–S162. 1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craddock, R. C. , James, G. A. , Holtzheimer, P. E. , Hu, X. P. , & Mayberg, H. S. (2012). A whole brain fMRI atlas generated via spatially constrained spectral clustering. Human Brain Mapping, 33(8), 1914–1928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du, L. , Zeng, J. , Liu, H. , Tang, D. , Meng, H. , Li, Y. , & Fu, Y. (2017). Fronto‐limbic disconnection in depressed patients with suicidal ideation: A resting‐state functional connectivity study. Journal of Affective Disorders, 215, 213–217. [DOI] [PubMed] [Google Scholar]
- Fornito, A. , Bullmore, E. T. , & Zalesky, A. (2017). Opportunities and challenges for psychiatry in the connectomic era. Biological Psychiatry. Cognitive Neuroscience and Neuroimaging, 2(1), 9–19. [DOI] [PubMed] [Google Scholar]
- Fornito, A. , Yoon, J. , Zalesky, A. , Bullmore, E. T. , & Carter, C. S. (2011). General and specific functional connectivity disturbances in first‐episode schizophrenia during cognitive control performance. Biological Psychiatry, 70(1), 64–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fried, E. I. , & Nesse, R. M. (2015). Depression sum‐scores don't add up: Why analyzing specific depression symptoms is essential. BMC Medicine, 13, 72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston, K. J. , Williams, S. , Howard, R. , Frackowiak, R. S. , & Turner, R. (1996). Movement‐related effects in fMRI time‐series. Magnetic Resonance in Medicine, 35(3), 346–355. [DOI] [PubMed] [Google Scholar]
- Gonzalez‐Castillo, J. , Handwerker, D. A. , Robinson, M. E. , Hoy, C. W. , Buchanan, L. C. , Saad, Z. S. , & Bandettini, P. A. (2014). The spatial structure of resting state connectivity stability on the scale of minutes. Frontiers in Neuroscience, 8, 138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goutte, C. , & Gaussier, E. (2005). A probabilistic interpretation of precision, recall and F‐score, with implication for evaluation In Losada D.E. & FernandezLuna J.M. (Eds.), Advances in information retrieval (pp. 345–359). [Google Scholar]
- Hutchison, R. M. , Womelsdorf, T. , Gati, J. S. , Everling, S. , & Menon, R. S. (2013). Resting‐state networks show dynamic functional connectivity in awake humans and anesthetized macaques. Human Brain Mapping, 34(9), 2154–2177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji, G. J. , Yu, Y. , Miao, H. H. , Wang, Z. J. , Tang, Y. L. , & Liao, W. (2017). Decreased network efficiency in benign epilepsy with centrotemporal spikes. Radiology, 283(1), 186–194. [DOI] [PubMed] [Google Scholar]
- Ji, G. J. , Zhang, Z. , Xu, Q. , Wang, Z. , Wang, J. , Jiao, Q. , … Lu, G. (2015). Identifying corticothalamic network epicenters in patients with idiopathic generalized epilepsy. American Journal of Neuroradiology, 36(8), 1494–1500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston, J. A. Y. , Wang, F. , Liu, J. , Blond, B. N. , Wallace, A. , Liu, J. , … Blumberg, H. P. (2017). Multimodal neuroimaging of frontolimbic structure and function associated with suicide attempts in adolescents and young adults with bipolar disorder. American Journal of Psychiatry, 174(7), 667–675. Am J [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser, R. H. , Whitfield‐Gabrieli, S. , Dillon, D. G. , Goer, F. , Beltzer, M. , Minkel, J. , … Pizzagalli, D. A. (2016). Dynamic resting‐state functional connectivity in major depression. Neuropsychopharmacology, 41(7), 1822–1830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, J. , Criaud, M. , Cho, S. S. , Diez‐Cirarda, M. , Mihaescu, A. , Coakeley, S. , … Strafella, A. P. (2017). Abnormal intrinsic brain functional network dynamics in Parkinson's disease. Brain, 140(11), 2955–2967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, K. , Kim, S. W. , Myung, W. , Han, C. E. , Fava, M. , Mischoulon, D. , … Jeon, H. J. (2017). Reduced orbitofrontal‐thalamic functional connectivity related to suicidal ideation in patients with major depressive disorder. Scientific Reports, 7(1), 15772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klonsky, E. D. , & May, A. M. (2014). Differentiating suicide attempters from suicide ideators: A critical frontier for suicidology research. Suicide &Amp; Life‐Threatening Behavior, 44(1), 1–5. [DOI] [PubMed] [Google Scholar]
- Kopell, N. J. , Gritton, H. J. , Whittington, M. A. , & Kramer, M. A. (2014). Beyond the connectome: The dynome. Neuron, 83(6), 1319–1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korgaonkar, M. S. , Fornito, A. , Williams, L. M. , & Grieve, S. M. (2014). Abnormal structural networks characterize major depressive disorder: A connectome analysis. Biological Psychiatry, 76(7), 567–574. [DOI] [PubMed] [Google Scholar]
- Leonardi, N. , & Van De Ville, D. (2015). On spurious and real fluctuations of dynamic functional connectivity during rest. NeuroImage, 104, 430–436. [DOI] [PubMed] [Google Scholar]
- Li, R. , Liao, W. , Yu, Y. , Chen, H. , Guo, X. , Tang, Y. L. , & Chen, H. (2018). Differential patterns of dynamic functional connectivity variability of striato‐cortical circuitry in children with benign epilepsy with centrotemporal spikes. Human Brain Mapping, 39(3), 1207–1217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao, W. , Wu, G. R. , Xu, Q. , Ji, G. J. , Zhang, Z. , Zang, Y. F. , & Lu, G. (2014). DynamicBC: A MATLAB toolbox for dynamic brain connectome analysis. Brain Connectivity, 4(10), 780–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao, W. , Zhang, Z. , Mantini, D. , Xu, Q. , Ji, G. J. , Zhang, H. , … Lu, G. (2014). Dynamical intrinsic functional architecture of the brain during absence seizures. Brain Structure and Function, 219(6), 2001–2015. [DOI] [PubMed] [Google Scholar]
- Liao, W. , Zhang, Z. , Mantini, D. , Xu, Q. , Wang, Z. , Chen, G. , … Lu, G. (2013). Relationship between large‐scale functional and structural covariance networks in idiopathic generalized epilepsy. Brain Connectivity, 3(3), 240–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao, X. , Cao, M. , Xia, M. , & He, Y. (2017). Individual differences and time‐varying features of modular brain architecture. NeuroImage, 152, 94–107. [DOI] [PubMed] [Google Scholar]
- Liao, X. , Yuan, L. , Zhao, T. , Dai, Z. , Shu, N. , Xia, M. , … He, Y. (2015). Spontaneous functional network dynamics and associated structural substrates in the human brain. Frontiers in Human Neuroscience, 9, 478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, A. P. , Chen, X. , Dan, X. J. , McKeown, M. J. , & Wang, Z. J. (2016). A combined static and dynamic model for resting‐state brain connectivity networks. IEEE Journal of Selected Topics in Signal Processing, 10(7), 1172–1181. [Google Scholar]
- Liu, F. , Wang, Y. F. , Li, M. L. , Wang, W. Q. , Li, R. , Zhang, Z. Q. , … Chen, H. F. (2017). Dynamic functional network connectivity in idiopathic generalized epilepsy with generalized tonic‐clonic seizure. Human Brain Mapping, 38(2), 957–973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, J. , Liao, X. , Xia, M. , & He, Y. (2018). Chronnectome fingerprinting: Identifying individuals and predicting higher cognitive functions using dynamic brain connectivity patterns. Human Brain Mapping, 39(2), 902–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynall, M. E. , Bassett, D. S. , Kerwin, R. , McKenna, P. J. , Kitzbichler, M. , Muller, U. , & Bullmore, E. (2010). Functional connectivity and brain networks in schizophrenia. Journal of Neuroscience, 30(28), 9477–9487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy, K. , Birn, R. M. , & Bandettini, P. A. (2013). Resting‐state fMRI confounds and cleanup. NeuroImage, 80, 349–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myung, W. , Han, C. E. , Fava, M. , Mischoulon, D. , Papakostas, G. I. , Heo, J. Y. , … Jeon, H. J. (2016). Reduced frontal‐subcortical white matter connectivity in association with suicidal ideation in major depressive disorder. Translational Psychiatry, 6(6), e835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfaff, J. J. , & Almeida, O. P. (2004). Identifying suicidal ideation among older adults in a general practice setting. Journal of Affective Disorders, 83(1), 73–77. [DOI] [PubMed] [Google Scholar]
- Power, J. D. , Barnes, K. A. , Snyder, A. Z. , Schlaggar, B. L. , & Petersen, S. E. (2012). Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. NeuroImage, 59(3), 2142–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preti, M. G. , Bolton, T. A. , Van, D. , & Ville, D. (2016). The dynamic functional connectome: State‐of‐the‐art and perspectives. NeuroImage. [DOI] [PubMed] [Google Scholar]
- Preti, M. G. , Bolton, T. A. , & Van De Ville, D. (2017). The dynamic functional connectome: State‐of‐the‐art and perspectives. NeuroImage, 160, 41–54. [DOI] [PubMed] [Google Scholar]
- Pu, S. , Nakagome, K. , Yamada, T. , Yokoyama, K. , Matsumura, H. , Yamada, S. , … Kaneko, K. (2015). Suicidal ideation is associated with reduced prefrontal activation during a verbal fluency task in patients with major depressive disorder. Journal of Affective Disorders, 181, 9–17. [DOI] [PubMed] [Google Scholar]
- Rashid, B. , Arbabshirani, M. R. , Damaraju, E. , Cetin, M. S. , Miller, R. , Pearlson, G. D. , & Calhoun, V. D. (2016). Classification of schizophrenia and bipolar patients using static and dynamic resting‐state fMRI brain connectivity. NeuroImage, 134, 645–657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov, M. , & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069. [DOI] [PubMed] [Google Scholar]
- Serafini, G. , Pardini, M. , Pompili, M. , Girardi, P. , & Amore, M. (2016). Understanding suicidal behavior: The contribution of recent resting‐state fMRI techniques. Frontiers in Psychiatry, 7, 69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Heeringen, C. , Bijttebier, S. , & Godfrin, K. (2011). Suicidal brains: A review of functional and structural brain studies in association with suicidal behaviour. Neuroscience and Biobehavioral Reviews, 35(3), 688–698. [DOI] [PubMed] [Google Scholar]
- van Heeringen, K. , Bijttebier, S. , Desmyter, S. , Vervaet, M. , & Baeken, C. (2014). Is there a neuroanatomical basis of the vulnerability to suicidal behavior? A coordinate‐based meta‐analysis of structural and functional MRI studies. Frontiers in Human Neuroscience, 8, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varoquaux, G. , Raamana, P. R. , Engemann, D. A. , Hoyos‐Idrobo, A. , Schwartz, Y. , & Thirion, B. (2017). Assessing and tuning brain decoders: Cross‐validation, caveats, and guidelines. NeuroImage, 145, 166–179. [DOI] [PubMed] [Google Scholar]
- Wagner, G. , Koch, K. , Schachtzabel, C. , Schultz, C. C. , Sauer, H. , & Schlosser, R. G. (2011). Structural brain alterations in patients with major depressive disorder and high risk for suicide: Evidence for a distinct neurobiological entity? NeuroImage, 54(2), 1607–1614. [DOI] [PubMed] [Google Scholar]
- Wang, J. , Wang, L. , Zang, Y. , Yang, H. , Tang, H. , Gong, Q. , … He, Y. (2009). Parcellation‐dependent small‐world brain functional networks: A resting‐state fMRI study. Human Brain Mapping, 30(5), 1511–1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, J. , Wang, X. , Xia, M. , Liao, X. , Evans, A. , & He, Y. (2015). GRETNA: A graph theoretical network analysis toolbox for imaging connectomics. Frontiers in Human Neuroscience, 9, 386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia, M. , Wang, J. , & He, Y. (2013). BrainNet Viewer: A network visualization tool for human brain connectomics. PLoS One, 8(7), e68910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng, L. L. , Shen, H. , Liu, L. , Wang, L. , Li, B. , Fang, P. , … Hu, D. (2012). Identifying major depression using whole‐brain functional connectivity: A multivariate pattern analysis. Brain, 135(Pt 5), 1498–1507. [DOI] [PubMed] [Google Scholar]
- Zhang, H. W. , Chen, Z. Q. , Jia, Z. Y. , & Gong, Q. Y. (2014). Dysfunction of neural circuitry in depressive patients with suicidal behaviors: A review of structural and functional neuroimaging studies. Progress in Neuro‐Psychopharmacology & Biological Psychiatry, 53, 61–66. [DOI] [PubMed] [Google Scholar]
- Zhang, J. , Wang, J. , Wu, Q. , Kuang, W. , Huang, X. , He, Y. , & Gong, Q. (2011). Disrupted brain connectivity networks in drug‐naive, first‐episode major depressive disorder. Biological Psychiatry, 70(4), 334–342. [DOI] [PubMed] [Google Scholar]
- Zhang, Z. , Liao, W. , Chen, H. , Mantini, D. , Ding, J. R. , Xu, Q. , … Lu, G. (2011). Altered functional‐structural coupling of large‐scale brain networks in idiopathic generalized epilepsy. Brain, 134(10), 2912–2928. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional Supporting Information may be found online in the supporting information tab for this article.
Supporting Information


