ARTIST: A fully automated artifact rejection algorithm for single‐pulse TMS‐EEG data

Abstract

Concurrent single‐pulse TMS‐EEG (spTMS‐EEG) is an emerging noninvasive tool for probing causal brain dynamics in humans. However, in addition to the common artifacts in standard EEG data, spTMS‐EEG data suffer from enormous stimulation‐induced artifacts, posing significant challenges to the extraction of neural information. Typically, neural signals are analyzed after a manual time‐intensive and often subjective process of artifact rejection. Here we describe a fully automated algorithm for spTMS‐EEG artifact rejection. A key step of this algorithm is to decompose the spTMS‐EEG data into statistically independent components (ICs), and then train a pattern classifier to automatically identify artifact components based on knowledge of the spatio‐temporal profile of both neural and artefactual activities. The autocleaned and hand‐cleaned data yield qualitatively similar group evoked potential waveforms. The algorithm achieves a 95% IC classification accuracy referenced to expert artifact rejection performance, and does so across a large number of spTMS‐EEG data sets (n = 90 stimulation sites), retains high accuracy across stimulation sites/subjects/populations/montages, and outperforms current automated algorithms. Moreover, the algorithm was superior to the artifact rejection performance of relatively novice individuals, who would be the likely users of spTMS‐EEG as the technique becomes more broadly disseminated. In summary, our algorithm provides an automated, fast, objective, and accurate method for cleaning spTMS‐EEG data, which can increase the utility of TMS‐EEG in both clinical and basic neuroscience settings.

1. INTRODUCTION

1.1. Importance of spTMS‐EEG and artifact rejection

Neuroimaging has provided tools to noninvasively examine brain regions that are activated during specific cognitive tasks, functionally correlated at rest, and abnormal in neurological and psychiatric disorders. However, these findings provide only an observational view of how brain activity and function are related, and importantly lack the causal inference that is often necessary to dissect circuits and guide therapeutic interventions. Single‐pulse transcranial magnetic stimulation (spTMS) coupled with electroencephalogram (EEG) provides the causal probe and measurement tools, respectively, that can be utilized to study systems‐level causal brain dynamics in both healthy and clinical populations (Ferrarelli et al., 2008; Harquel et al., 2016; Massimini et al., 2005; Morishima et al., 2009; Premoli et al., 2014; Sun et al., 2016). However, in addition to the conventional EEG artifacts (Fisch, & Spehlmann, 1999), spTMS‐EEG suffers from multiple stimulation‐related artifacts including those derived from the stimulation pulse itself (Veniero, Bortoletto, & Miniussi, 2009), scalp muscle activation (Mutanen, Mäki, & Ilmoniemi, 2013), electrode movement or polarization, sensory system activation (Massimini et al., 2005), eye blinks, coil clicks (Nikouline, Ruohonen, & Ilmoniemi, 1999; Ter Braack, de Vos, & van Putten, 2015), and coil recharge (see Figure 1 for examples of main types of artifacts and neural signals) (Ilmoniemi, & Kičić, 2010). These artifacts may directly impact the spatio‐temporal morphology of the TMS‐evoked potentials (TEPs) that are of interest in spTMS‐EEG (e.g., P30, N45, P60, N100, P180, etc.) (Rogasch, Thomson, Daskalakis, & Fitzgerald, 2014). Recent advances in the EEG recording hardware as well as experimental manipulations can help address some of these artifacts. For instance, with direct current (DC)‐coupling, broad measurement ranges and high sampling rates, or with sample‐and‐hold circuits, amplitude saturation caused by the TMS pulse can be prevented. It has also been shown that the TMS pulse artifact as well as the electrode polarization artifact can be largely reduced by reorienting the EEG lead wires perpendicular to the coil handle (Sekiguchi, Takeuchi, Kadota, Kohno, & Nakajima, 2011). In addition, delay of the coil recharge, which is possible with some TMS machines (e.g., MagVenture stimulators, MagVenture, Denmark), can shift the recharge artifact beyond the time periods of interest (Rogasch et al., 2013). However, it is not possible to avoid every stimulation‐related artifact before data analysis. For instance, although the scalp muscle activation can be reduced by stimulating away from regions with dense scalp muscles such as temporalis and frontalis, it is unavoidable when the regions of interest are located in the frontal and temporal cortices. As a result, removing artifacts from the spTMS‐EEG data becomes a laborious endeavor, which is typically performed through manual identification/rejection of artefactual channels and epochs as well as removal of artifact‐associated independent components (ICs) extracted by independent component analysis (ICA) (Rogasch et al., 2016).

Figure 1.

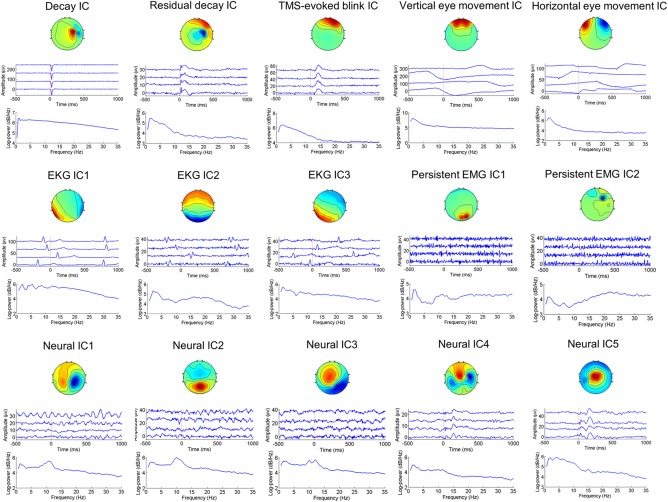
Spatio‐temporal‐spectral patterns of neural and artefactual ICA components. For each IC, the three panels are (from top to bottom) the scalp map, time courses of four exemplary epochs, and mean power spectrum across all epochs. The signs of the scalp maps and time courses are arbitrary due to the scaling ambiguity of ICA. The decay artifact includes the TMS‐evoked muscle artifact, electrode movement artifact, and electrode polarization artifact. The TMS‐evoked blink artifact is time‐locked to the TMS pulse, whereas the vertical eye movement artifact is non‐time‐locked to the TMS pulse. The EKG artifact is highly variable across subjects in its spatial distribution—the activation patterns may be rotational with respect to one another. Unlike the TMS‐evoked muscle artifact, the persistent EMG artifact is higher in frequencies and may appear in any electrodes. Neural ICs typically have dipole‐like scalp maps, and 1/f shape power spectra [Color figure can be viewed at http://wileyonlinelibrary.com]

1.2. Review of current algorithms

Developing an automated algorithm to remove artifacts would standardize preprocessing by reducing bias from human influence (e.g., due to fluctuating changes in judgment or varying levels of artifact rejection skills), decrease processing time, and allow for near real‐time processing for closed‐loop applications. While there has been a recent push to develop automated artifact rejection methods for standard EEG data (Bigdely‐Shamlo, Mullen, Kothe, Su, & Robbins, 2015; Junghöfer, Elbert, Tucker, & Rockstroh, 2000; Mognon, Jovicich, Bruzzone, & Buiatti, 2011; Nolan, Whelan, & Reilly, 2010; Winkler, Debener, Müller, & Tangermann, 2011), to our knowledge only semi‐automated methods for concurrent spTMS‐EEG data have been reported (Rogasch et al., 2016).

Early automated EEG data cleaning methods used statistical thresholding approaches to detect artifacts in channel space (Junghöfer et al., 2000); however, researchers quickly shifted to the use of more advanced techniques, including regression, adaptive filtering, time‐frequency decomposition, and blind source separation (Urigüen, & Garcia‐Zapirain, 2015). Of particular interest is ICA, a blind source separation technique that effectively decomposes the multichannel EEG data into multiple ICs belonging to either artifacts or neural sources, building on the observation that artifact and neural signals possess distinguishable spatio‐temporal patterns (Delorme, Sejnowski, & Makeig, 2007; Frølich, Andersen, & Mørup, 2015; ; Mognon et al., 2011; Nolan et al., 2010; Winkler, Haufe, & Tangermann, 2011). Artifact rejection then becomes a binary pattern classification problem of distinguishing between artefactual and neural ICs. Both unsupervised and supervised methods have been proposed to solve this classification problem. For the unsupervised methods, Viola et al. developed a semi‐automatic algorithm based on user‐defined templates to correct eye blink, horizontal eye movement, and electrocardiogram (EKG) artifacts (Viola et al., 2009). Mognon et al. (2011) introduced the ADJUST (Automatic EEG artifact Detection based on the Joint Use of Spatial and Temporal features) algorithm that uses an expectation‐maximization (EM)‐based approach to automatically threshold the spatio‐temporal features for different artifact types. Nolan et al. (2010) described the FASTER (Fully Automated Statistical Thresholding for EEG artifact Rejection) algorithm that rejects bad channels, epochs, and ICs by statistically thresholding a handful of spatio‐temporal features. For the supervised methods, Winkler et al. (2011) developed the MARA (Multiple Artifact Rejection Algorithm) algorithm in which a sparse linear classifier was trained to automatically classify the ICs. It was found that the use of two spatial, one temporal, and three spectral features could achieve the best classification results. Furthermore, MARA could generalize to a variety of EEG paradigms and might improve the performance of brain–computer interfaces (BCIs) (Winkler et al., 2014).

As spTMS‐EEG data are considered noisier than standard EEG data due to stimulation‐induced artifacts, various additional methods were developed (Atluri et al., 2016; Casula et al., 2017; Hernandez‐Pavon et al., 2012; Herring, Thut, Jensen, & Bergmann, 2015; Korhonen et al., 2011; Mäki, & Ilmoniemi, 2011; Mutanen et al., 2016; Rogasch et al., 2014, 2016). In general, these methods used signal projection techniques to find spatial filters that could suppress the artifacts while leaving the neural signals largely intact. The predominant ones were based on blind source separation that identified artefactual components via time‐consuming and potentially error‐prone visual inspection. In particular, TMSEEG and TESA are two MATLAB toolboxes designed for the ICA‐based artifact rejection and analysis of spTMS‐EEG data (Atluri et al., 2016; Rogasch et al., 2016). While these previous efforts have improved data quality, we still currently lack a fully automated and accurate TMS‐EEG artifact rejection algorithm. Development of such an algorithm would allow a broader application of spTMS‐EEG to both the lab and clinical settings.

Automatic artifact rejection for spTMS‐EEG data is challenging for the following reasons. First, the morphology of the same artifact type may vary across subjects and stimulation sites, requiring that robust and invariant features be identified. Second, there are artifact types unique to spTMS‐EEG data, including TMS‐evoked scalp muscle artifacts and electrode movement/polarization artifacts. These artifacts are time‐locked to the TMS pulse and can overlap with the potentials of interest. Moreover, due to their large amplitude and rapid changes, these artifacts, henceforth referred to collectively as the decay artifacts, can have considerable impact on the signals in the nearby time periods by interacting with the frequency filtering. In addition, the typical spTMS‐EEG time course may contain a series of temporally segregated TMS‐evoked potentials (TEPs) (Ilmoniemi & Kičić, 2010). For automated artifact rejection, new features are required to capture the spatio‐temporal characteristics of these components. Third, spTMS‐EEG has been used to probe the causal brain dynamics by stimulating varying brain regions, subjects, or populations in different studies (Ferrarelli et al, 2008; Harquel et al., 2016; Massimini et al., 2005). It remains unknown whether an automated artifact rejection method can be trained once and successfully applied to new data. In order to address these challenges, here we describe a fully automated ICA‐based artifact rejection algorithm that combines temporal and spectral features to separate artifacts from neural sources. We first describe the basis of the artifact rejection pipeline and subsequently quantify the accuracy of our algorithm benchmarked against manual rejection. Overall, we provide the first evidence of a fully automated artifact rejection algorithm for spTMS‐EEG that is comparable to manual artifact rejection and generalizes across stimulation sites, subjects, and populations.

2. MATERIALS

2.1. Overview

Here, we present an overview of our proposed algorithm, termed Automated aRTIfact rejection for Single‐pulse TMS‐EEG Data (ARTIST), designed to automatically remove a wide variety of artifacts from the spTMS‐EEG data. The workflow of ARTIST can be found in Figure 2. The algorithm consists of three stages, each aimed at removing specific types of artifacts. The first stage removes large‐amplitude TMS‐related artifacts, including the TMS pulse artifact and decay artifacts. The second stage rejects bad epochs and channels. The third stage removes the remaining artifacts, including the residual decay artifacts, ocular artifacts, EKG artifacts, and persistent EMG artifact. The details and rationale of each step of ARTIST are described below.

Figure 2.

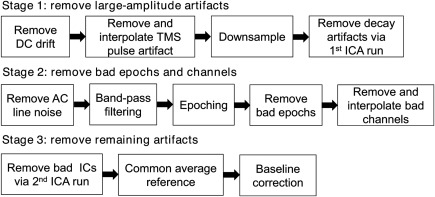
Workflow of the ARTIST algorithm. ARTIST consists of three stages, each aimed at removing certain types of artifacts. The first stage removes large‐amplitude TMS‐related artifacts (TMS pulse artifact and decay artifacts) from the continuous data. The second stage filters the continuous data to remove the AC line noise and high‐frequency noise, and then rejects bad epochs and channels from the epoched data. The third stage removes the remaining artifacts (residual decay artifacts, ocular artifacts, EKG artifact, and persistent EMG artifact) from the epoched data, after which the data are rereferenced to the common average and baseline corrected

2.2. The ARTIST algorithm

2.2.1. Removing large‐amplitude artifacts

Removing the TMS pulse artifact

Each spTMS pulse is followed by a large and transient pulse‐shape artifact in the EEG data, with a magnitude into the millivolt‐to‐volt range depending on the intensity of the stimulation. With low electrode impedance (<5 kΩ) and a high sampling rate (e.g., >5 kHz), the duration of the TMS pulse artifact is typically <10 ms. The enormous strength of the TMS pulse artifact precludes the use of signal processing approaches from removing the artifact while keeping the neural information intact (Ilmoniemi & Kičić, 2010). We thus discard the initial 10 ms post‐TMS data segment and then use the cubic interpolation to replace the discarded segment. To reduce the file size, the EEG data are downsampled to 1 kHz afterward. The cubic interpolation ensures smooth transition edges and therefore avoids the ringing artifact introduced by the anti‐aliasing filter during the downsampling step (Rogasch et al., 2016).

Removing the decay artifacts

Frequency filters are effective tools to remove unwanted components (e.g., DC drift, AC line noise, high‐frequency noise, et al.) that do not spectrally overlap with neural information within the data. Nonetheless, frequency filtering of EEG data containing strong decay artifacts can lead to substantial ringing artifacts in the nearby time period (Widmann & Schröger, 2012), also known as the Gibbs phenomenon in signal processing. More specifically, low‐pass and notch filtering often lead to fast changing ringing artifacts, while high‐pass filtering causes slow drift of the EEG. These artifacts can even appear in the baseline EEG prior to the TMS pulse if zero‐phase filtering in both forward and backward directions is applied (Rogasch et al., 2016). Hence, it is crucial to remove the strong decay artifacts from the EEG before any frequency filtering is performed.

In ARTIST, strong decay artifacts are removed in a first ICA run. The following equation gives the generative model of the ICA:

$$\mathbf{X}=\mathbf{B}\mathbf{Y}$$

where X is the EEG data matrix of C channels (rows) by T time points (columns). B is the mixing matrix of C channels (rows) by K ICs (columns), with each column being the spatial map of an IC. Y is the component signal of K ICs (rows) by T time points (columns), with each row being the time course of an IC (concatenated across epochs for epoched data). In this model, only X is known; both B and Y are unknown. ICA aims to estimate Y from X, based on the assumption that the time courses of the ICs are statistically independent from each other. In ARTIST, the Infomax algorithm (Bell, & Sejnowski, 1995) is used to perform the ICA. To address the scaling ambiguity of the ICA (i.e., a scaling of the columns of B can be offset by applying an inverse scaling of the corresponding rows of Y), each column of the estimated B is normalized to have unit variance.

To remove strong decay artifacts, slow DC drift is first removed from the continuous EEG data by subtracting the mean of each epoch from each time point in the epoch. Next, EEG data are fed into ICA, and ICs with mean magnitude above a certain threshold (30 µv by default) within the first 50 ms after the TMS pulse are rejected. Note that baseline correction is not used for removing the DC drift as it may reduce the reliability of ICA (Groppe, Makeig, & Kutas, 2009).

2.2.2. Rejecting bad epochs and electrodes

Removing the AC line noise and high‐frequency noise via frequency filtering

Following decay artifact removal, continuous EEG recordings are high‐pass filtered (1 Hz cutoff, zero‐phase FIR filter), which facilitates ICA estimation (a) by increasing the mutual independence between sources, as low frequency trends are likely dependent, and (b) by enhancing the dipolarity of the ICs (Winkler et al., 2015). In addition, a 100‐Hz zero‐phase FIR low‐pass filter is employed to attenuate high‐frequency noise, and a 60 Hz zero‐phase FIR notch filter removes 60 Hz AC line noise. The filtered data are then epoched with respect to the TMS pulse (−500 to +1500 ms by default).

Automated rejection of bad epochs

Bad epochs are those contaminated with nonstereotyped artifacts such as those arising from subject motion (e.g., head movement, scalp scratch, jaw clench, talking, swallowing, throat clearing). In general, motion artifact is spatially widespread and may contaminate all channels in an epoch. These artifacts must be pruned prior to IC rejection (Section 2.2.3) as they may introduce nonlinearities into the EEG data, requiring a large number of ICs to capture the variability of all the artefactual contributions and thus reducing the number of ICs available for separating other neural and artifact sources (Delorme et al., 2007).

For bad epoch rejection, we define the z‐score of the magnitude of each epoch (0–50 ms post‐TMS EEG is excluded from the analysis time window to decrease interference from the residual decay artifact) and channel as follows:

$$z_{n,c}=\frac{a_{n,c}-m_c}{s_c}$$

where $a_{n,c}$ is the average magnitude of the n‐th epoch and c‐th channel, $m_c$ is the mean of the average magnitude across epochs for the c‐th channel, and $s_c$ is the standard deviation of the average magnitude across epochs for the c‐th channel. The epoch‐channel combinations where $z_{n,c}$ is greater than a predefined threshold (3 by default) are then determined. Among them, epochs that appear in more than 20% of all channels are rejected in all channels. For epochs appearing in no more than 20% of all channels, the EEG values in these channels are replaced from the adjacent channels by the spherical interpolation approach (Perrin, Pernier, Bertrand, & Echallier, 1989).

Note that it is assumed here that the proportion of bad epochs is low. For data sets with artifacts on a large number of epochs, the average magnitude and standard deviation may be quite high, and an undesirably low number of epochs will be rejected. A warning message will be displayed showing the channels in which the standard deviation of the average magnitude across epochs is above a certain threshold (30 µV by default).

Automated rejection of bad electrodes

Bad electrodes, including faulty, disconnected, and flat electrodes, produce abnormal activity distinct from neighboring electrodes. Therefore, to remove bad electrodes, the maximum correlation coefficient of the EEG at each electrode with the rest of the electrodes is calculated for each epoch (0–50 ms post‐TMS EEG is excluded from the analysis time window to decrease interference from the residual decay artifact). An electrode is labeled as bad if the maximum correlation coefficient is below a predefined threshold (0.4 by default) for more than 2% epochs.

The performance of bad electrode rejection can be affected by the choice of the reference that may alter the EEG spatial correlation structure. Hence, it is crucial to choose a reference that is clean and as inactive as possible. Referencing to a particular electrode runs the risk of contaminating the EEG at all the electrodes if the EEG at the reference electrode is highly noisy, thereby potentially inflating the correlation coefficients between the EEG at different electrodes. To avoid this, the common average reference is a typically used “inactive” reference but it may be highly skewed by an extreme outlier electrode. To address the interaction between referencing and bad electrode rejection, we used a robust referencing algorithm (Bigdely‐Shamlo et al., 2015) that finds the “true” common average reference and detects bad electrodes in an iterative manner. More specifically, the algorithm proceeds as follows:

Initialization: EEG = EEG data, Bad electrode list = [].

1. EEGtemp = EEG − median(EEG), where median(EEG) is the median of the EEG at all the electrodes;

2. Detect bad electrodes from EEGtemp based on the maximum correlation coefficient and add them to the bad electrode list;

3. EEGtemp = EEG − mean(EEGinterp), where EEGinterp is the mean of the EEG with all the bad electrodes interpolated;

4. Repeat steps 2–3 until the bad electrode list does not change.

5. Reject and interpolate the bad electrodes in EEG;

6. EEG = EEG − mean(EEG).

The maximum correlation criterion can only identify single noisy electrodes not resembling any other electrodes. However, in some situations a local cluster of electrodes may become artefactual together in which case electrode correlations will be high within each cluster. To address this issue, the random consensus method (RANSAC) method is employed to detect noisy clusters of electrodes following the maximum correlation criterion (Bigdely‐Shamlo et al., 2015). More specifically, RANSAC uses a random subset (25% by default) of electrodes to predict the EEG of each electrode (excluded from the subset) in each epoch. The prediction is repeated 50 times. The correlation coefficients of the predicted EEGs and the actual EEG of each electrode are then calculated. An electrode is bad if the 50 percentile of the correlation coefficients is less than a threshold (0.75 by default) on more than a certain fraction of epochs (0.4 by default).

The EEG values in the rejected channels are then replaced from the adjacent channels by the spherical interpolation approach.

2.2.3. Removing remaining artifacts

Following bad electrode and epoch rejection, the remainder of EEG artifacts—including the residual decay artifact, ocular artifact, EKG artifact, and persistent EMG artifact—are removed via automated IC rejection in a second ICA run. A summary of automated IC rejection is shown in Figure 3. In particular, based upon the features defined in Winkler et al. (2011) for standard EEG, we proposed a set of features that capture the spatio‐temporal‐spectral patterns of the neural and artefactual sources for spTMS‐EEG. Note that these features are used in conjunction rather than in isolation to determine the label of each IC.

Figure 3.

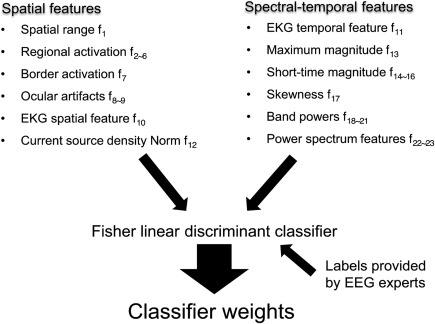
Pattern classification to remove bad components. (a) Spatial and (b) spectral‐temporal features of the training ICs are used to train a Fisher linear discriminant classifier. The IC labels are provided by EEG experts. The outputs of the pattern classifier are a set of weights that are then applied to the ICs of each new data set to reject artefactual components

1. Dynamical range f ₁

   The dynamical range feature is defined as the log absolute difference of the maximum and minimum activation in the scalp map $\mathit{b}$:

   $$f_1=\log \left|\underset{i}{\max }\left(b_i\right)-\underset{i}{\min }{(b}_i)\right|$$

   where $b_i$ denotes the scalp map of the i‐th IC. An artefactual IC oftentimes has a large dynamical range. Note that the logarithmic transform is employed to improve the normality of the feature.

2. Regional activation f _2∼6

   We consider the regional activation to be the absolute value of the average over the activations in the electrodes located within the central, frontal, occipital, and temporal regions of the scalp (Figure 4a):

   $$f_2=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(b_i\right)\right|,\hspace{0.17em}i\hspace{0.17em}\in \mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{l} \mathrm{r}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}$$

   $$f_3=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(b_i\right)\right|,\hspace{0.17em}i\hspace{0.17em}\in \mathrm{f}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{r}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}$$

   $$f_4=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(b_i\right)\right|,\hspace{0.17em}i\hspace{0.17em}\in \mathrm{o}\mathrm{c}\mathrm{c}\mathrm{i}\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{r}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}$$

   $$f_5=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(b_i\right)\right|,\hspace{0.17em}i\hspace{0.17em}\in \mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t} \mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l} \mathrm{r}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}$$

   $$f_6=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(b_i\right)\right|,\hspace{0.17em}i\hspace{0.17em}\in \mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t} \mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l} \mathrm{r}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}$$

   For any electrode montage, these regions can be automatically defined based on the spherical coordinates ( $r,\hspace{0.17em}\mathrm{\theta },\hspace{0.17em}\mathrm{\phi }$) of the electrodes, where $r$ is the radial distance from the center of the head, $\mathrm{\theta }$ is the polar angle from the z‐axis (toward vertex), and $\mathrm{\phi }$ is the azimuthal angle in the x (toward nose)–y (toward left ear) plane. Specifically, the electrodes contained in each region are defined as follows: central ( $\mathrm{\theta }<70°$); frontal ( $\left|\mathrm{\theta }\right|\ge 60°$ and $\left|\mathrm{\phi }\right|\le 60°$); occipital ( $\left|\mathrm{\theta }\right|\ge 70°$ and $155°\le \left|\mathrm{\phi }\right|\le 180°$); left temporal ( $\left|\mathrm{\theta }\right|\ge 70°$ and $30°\le \mathrm{\phi }\le 150°$); left temporal ( $\left|\mathrm{\theta }\right|\ge 70°$ and $\hspace{0.17em}-150°\le \mathrm{\phi }\le -30°$).

3. Border activation f ₇

   The maximum activation of a neural IC's scalp map is unlikely at a border electrode. Therefore, if the maximum activation in the scalp map occurs at a border electrode (Figure 4a), the border activation feature is set to 1, otherwise 0:

   $$f_7=1,\hspace{0.17em}\mathrm{i}\mathrm{f} \arg \underset{i}{\max }\left(\left|b_i\right|\right)\in \mathrm{b}\mathrm{o}\mathrm{r}\mathrm{d}\mathrm{e}\mathrm{r} \mathrm{r}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n}$$

4. Horizontal eye movement f ₈

   The horizontal eye movement artifact has a distinctive scalp map with activations of opposing polarities in the left and right anterior electrodes above the eyes (Fisch et al., 1999; Figure 4c). This allows us to define the corresponding feature as the absolute difference between the mean weight of the electrodes above the left eyes and that of the electrodes above the right eyes:

   $$f_8=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(b_{\mathrm{L}\mathrm{E}}^{\left(i\right)}\right)-\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(b_{\mathrm{R}\mathrm{E}}^{\left(i\right)}\right)\right|$$

   where $b_{\mathrm{L}\mathrm{E}}^{\left(i\right)}$ and $b_{\mathrm{R}\mathrm{E}}^{\left(i\right)}$ deonte the weights of the electrodes above the left and right eyes in the scalp map of the i‐th IC, respectively. The electrodes contained in LE and RE are defined as follows: LE ( $100°\le \mathrm{\theta }\le 130°$ and $40°\le \mathrm{\phi }\le 60°$); RE ( $100°\le \mathrm{\theta }\le 130°$ and $-$ $60°\le \mathrm{\phi }\le -40°$).

5. Blink/vertical eye movement f ₉

   Similarly, the blink/vertical artifact IC has a scalp map with predominantly middle anterior activations (Fisch et al., 1999; Figure 4c). The absolute mean weight of the anterior electrodes in the middle of both eyes:

   $$f_9=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(b_{\mathrm{B}}^{\left(i\right)}\right)\right|$$

   where $b_{\mathrm{B}}^{\left(i\right)}$ denotes the weights of the anterior electrodes in the middle of both eyes in the scalp map of the i‐th IC. The electrodes contained in B are defined as follows: B ( $90°\le \mathrm{\theta }\le 100°$ and $\left|\mathrm{\phi }\right|\le 40°$).

6. EKG spatial feature f ₁₀

   The EKG artifact is a poorly formed QRS complex time‐locked to cardiac contractions that is most prominent when the subject's neck is short and wide (Fisch et al., 1999). Typically, the EKG IC has a scalp map with diffuse activations in the lateral frontal and lateral posterior regions of opposing polarities. However, the specific activation locations vary across subjects, with their scalp maps rotational relative to each other (see the EKG ICs in Figure 1). To achieve rotational invariance, the following detection algorithm is proposed to detect the EKG spatial map:

   1. The two lateral regions of opposing polarities are first identified for each IC. Specifically, each set of outermost electrodes (Figure 4d) that span an azimuthal angle of 60° are determined. The positive lateral region is identified as the set of outermost electrodes with the maximum weight sum, and the negative lateral region is identified as the outermost electrodes with the minimum weight sum.
   2. A template ${\mathit{b}}_K$ is made by setting the weights of the outermost electrodes in the positive lateral region to 1s, the weights of the outermost electrodes in the negative lateral region to −1s, and the weights of the remaining electrodes to 0s.
   3. For each IC, if the absolute correlation coefficient between the scalp map $\mathit{b}$ and the template ${\mathit{b}}_{\mathrm{K}}$ exceeds a preset threshold ԑ (0.6 by default), the binary EKG spatial feature $f_{10}$ is set to 1, otherwise 0:

      $$f_{10}=1,\hspace{0.17em}if\left|\mathrm{r}(\mathit{b},\hspace{0.17em}{\mathit{b}}_K)\right|>ԑ$$

7. EKG temporal feature f ₁₁

   The EKG artifact has a length of ∼50 ms in each QRS complex and a frequency between 1 and 1.67 Hz. Inspired by prior EKG literature (Kadambe, Murray, & Boudreaux‐Bartels, 1999), here we use a robust algorithm based on the maximal overlap discrete wavelet transform (MODWT) (Percival, & Walden, 2006) to detect the QRS complexes in the time course of each IC (Figure 5a). By using a wavelet that resembles the QRS complex in shape, higher specificity of the EKG IC can be achieved by detecting peaks at an appropriate scale in the wavelet subspace than in the original signal space. More specifically, our detection algorithm proceeds as follows:

   1. For the i‐th IC, let ${\mathit{y}}_i$ denote the i‐th row of Y, normalized to have unit variance. Decompose ${\mathit{y}}_i$ using the Daubechies least‐asymmetric wavelet with four vanishing moments ('sym4'). The depth of the decomposition, M, is determined by Fs/2^{M +1} < 1000/50 < Fs/2^M, where Fs is the sampling rate of the EEG data. For instance, when Fs = 1000 Hz, M = 5.
   2. Reconstruct a signal ${\mathit{u}}_i$ using only the scaling coefficients at scale M, which corresponds to Fs/2^{M +1} ‐ Fs/2^M Hz.
   3. Identify the number of peaks in $\left|{\mathit{u}}_i\right|$. The minimum inter peak distance is set to 600 ms to match the frequency of the EKG artifact.
   4. If the number of peaks is greater than a preset threshold J (empirically determined to be 0.8·N·T in ARTIST, where N is the total number of epochs and T is the length of each epoch in second), then set the binary EKG temporal feature $f_{11}$ to 1, otherwise to 0:

      $$f_{11}=1,\hspace{0.17em}\mathrm{i}\mathrm{f}\hspace{0.17em}\#\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{s}>J$$

8. Current source density norm f ₁₂

   Artefactual ICs are often described by sources with complicated patterns and large overall power. The source activity $\mathit{s}$ can be estimated using the weighted minimum norm estimation approach (Hämäläinen, & Ilmoniemi, 1994) on a boundary element head model built from the average structural MRI of 40 subjects (Fischl, Sereno, Tootell, & Dale, 1999). To compensate the bias toward superficial sources, depth weighting that scales the source activity by the L2 norm of the columns of the lead field matrix is performed. The current source density norm feature $f_{12}$ is then defined as the L2 norm of $\mathit{s}$ estimated from $\mathit{b}$:

   $$f_{12}={\mathrm{l}\mathrm{o}\mathrm{g}‖\mathit{s}‖}_2=\log \sqrt{\sum _i{s}_i^2}$$

9. Maximum magnitude f ₁₃

   The maximum magnitude feature $f_{12}$ is defined as the maximum magnitude:

   $$f_{13}=\log \underset{t}{\max }\left|{\mathrm{Y}}_{i,t}\right|$$

10. Short‐time magnitude f _14∼16

    The log mean magnitudes of different time windows are computed to capture the decay artifact and various TEP peaks. The time windows considered in ARTIST are 0–60, 60–140, and 140–220 ms:

    $$f_{14}=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\left|Y_{i,t}\right|\right)\right|,\hspace{0.17em}t\hspace{0.17em}\in \left[0 \mathrm{m}\mathrm{s},\hspace{0.17em}60 \mathrm{m}\mathrm{s}\right]$$

    $$f_{15}=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\left|Y_{i,t}\right|\right)\right|,\hspace{0.17em}t\hspace{0.17em}\in \left[60 \mathrm{m}\mathrm{s},\hspace{0.17em}140 \mathrm{m}\mathrm{s}\right]$$

    $$f_{16}=\mathrm{l}\mathrm{o}\mathrm{g}\left|\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\left|Y_{i,t}\right|\right)\right|,\hspace{0.17em}t\hspace{0.17em}\in \left[140 \mathrm{m}\mathrm{s},\hspace{0.17em}220 \mathrm{m}\mathrm{s}\right]$$

    These are designed to capture TEP peaks that are typically present when different brain areas are stimulated (Harquel et al., 2016; Rosanova et al., 2009), such as n45, p60, n100, and p200 (see neural IC4 and IC5 in Figure 1 for examples). They can also be used to capture the artifacts that are time‐locked to the TMS (e.g., the decay artifact). Computing the mean magnitudes for relatively broad timeframes allows one to quantify the TEP peaks without allowing for spurious fluctuations (which would occur if they have a narrow temporal width) and capture peaks that are significantly earlier or later than typical TMS peaks owing to intersubject or intersite variability.

11. Skewness f ₁₇

    Asymmetric probability distributions are more common in artifacts. The skewness is a high‐order statistics that measures the asymmetry of the probability distribution of the spTMS‐EEG data (Hair, Black, Babin, & Anderson, 2009):

    $$\mathrm{\eta }=E\left[{\left(\frac{Y-\mathrm{\mu }}{\mathrm{\sigma }}\right)}^3\right]$$

    where $\mathrm{\mu }$ is the mean, $\mathrm{\sigma }$ is the standard deviation, and $E$ is the expectation operator. We compute f ₁₇ as the log value of the mean absolute skewness across epochs.

12. Band‐power for EEG rhythms f _18∼21

    To capture the various EEG rhythms, the log band‐power is computed for the theta (4–7 Hz), alpha (8–12 Hz), beta (13–30 Hz), and gamma (31–50 Hz) bands. The gamma band‐power is also useful for detecting persistent EMG artifacts.

13. Spectral features f _22∼23

    Typical EEG power spectra follow the 1/f shape, with the exception of the alpha band, where the alpha rhythm in the EEG data is typically stronger than expected in a 1/f spectrum (Luck, 2014; Figure 5b). We thus extract two spectral features after fitting the following 1/f curve to the power spectrum of each IC, P (between 1 and 35 Hz but excluding the alpha band (8–12 Hz)), by using the nonlinear least squares:

    $$\widehat{P}=\frac{a}{f^b}+c\hspace{0.17em}(b>0)$$

    where $\widehat{P}$ is the fitted power spectrum. The first spectral feature f ₂₂ is the log mean squared fit error between the actual power spectrum of the IC and fitted 1/f spectrum within the alpha band, which is useful for identifying neural signals:

    $$f_{22}=\mathrm{l}\mathrm{o}\mathrm{g}\left({‖P_{\mathrm{\alpha }}-{\widehat{P}}_{\mathrm{\alpha }}‖}^2\right)$$

    where $P_{\mathrm{\alpha }}$ is the power spectrum within the alpha band, and ${\widehat{P}}_{\mathrm{\alpha }}$ is the fitted 1/f spectrum within the alpha band. The second spectral feature f ₂₃ is log(b), which is useful for rejecting persistent EMG artifacts, as they tend to have higher b than neural ICs (Figure 5b).

Figure 4.

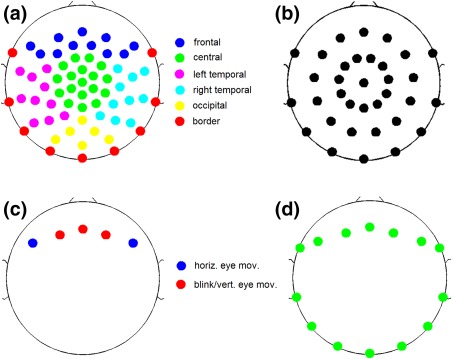
Electrodes used for constructing different spatial features. (a) Electrodes for the regional activation features. The electrode montage follows an equidistant arrangement extending down from the cheekbone back to the inion. (b) A subset of 34 electrodes for assessing the intermontage generalization performance of ARTIST. (c) Electrodes for the horizontal eye movement and blink/vertical eye movement features. (d) Outermost electrodes used to compute the EKG spatial feature [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 5.

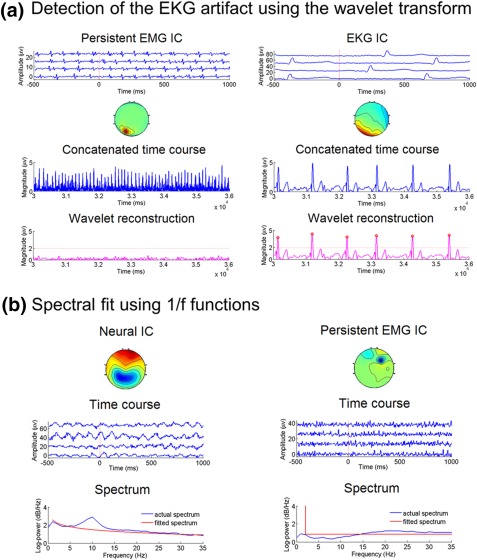
EKG temporal features and power spectrum features. (a) EKG temporal feature. Left: a persistent EMG IC. Right: an EKG IC. For each IC, the third panel shows the magnitude ( $\left|y_i\right|$) of the time course concatenated across epochs. Peak detection on $\left|y_i\right|$ suffers from a high number of false positives. The bottom panel shows the results of peak detection on the wavelet reconstructed signal ( $\left|u_i\right|$). The red circles represent the detected peaks. For the EKG IC, the QRS complexes are accurately detected in the wavelet reconstruction, whereas for the persistent EMG IC, no supra‐threshold peaks are detected in the wavelet reconstruction. (b) Spectral features. Left panel: a neural IC, with the alpha‐band fit error of 1.66 and log(b) = −5.30. Right panel: a persistent EMG IC, with the alpha‐band fit error of −0.36 and log(b) = 8.53 [Color figure can be viewed at http://wileyonlinelibrary.com]

The resulting 23 features are aggregated to form a feature vector that classifies each IC as neural or artefactual. The Fisher linear discriminant analysis (FLDA) classifier (Bishop, 2006) was utilized due to its fast speed, interpretability, and as it is not prone to overfitting (provided the number of the features is comparable with the size of the training set). The ICs labeled as artefactual are rejected by subtracting their summed back‐projections from the spTMS‐EEG data. The artifact‐corrected data are then rereferenced to the common average and baseline corrected (relative to the −300 to −100 ms baseline by default) prior to the subsequent quantitative analyses.

An example of artifact rejection with ARTIST for an actual spTMS‐EEG data set is presented in Figure 6.

Figure 6.

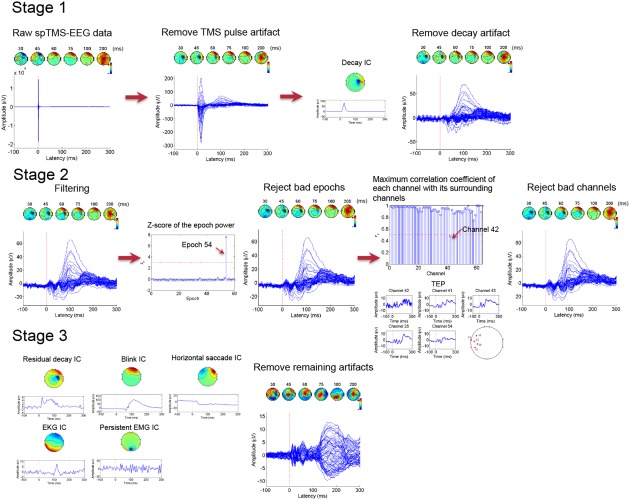
An illustrative example of the ARTIST algorithm. This particular spTMS‐EEG data set was acquired during stimulations at the right posterior DLPFC (see Sections 2.3.2 and 2.3.3 for more details on the recording protocol). Time (in ms) of each scalp map is displayed above. In the first stage, the TMS pulse artifact is removed by cutting off the 10 ms post‐TMS data and replaced by the cubic interpolation. The data is then downsampled to 1 kHz. The decay artifact is removed by automatically rejecting the decay IC during the first ICA run. In the second stage, the data are notched filtered at 60 Hz and bandpass filtered within 1 and 100 Hz. The data are then epoched relative to the TMS pulses. Epochs with z‐scores of the power above 3, and channels with maximum correlation coefficients with their neighbors lower than 0.5, are rejected. In the third stage, the remaining artifacts are removed by automatically rejecting their corresponding ICs during the second ICA run [Color figure can be viewed at http://wileyonlinelibrary.com]

2.3. spTMS‐EEG data collection

2.3.1. Subjects

To determine the robustness of ARTIST, we used spTMS‐EEG data of 12 healthy control (HC) subjects collected from two separated studies (6 HCs in study 1 and 6 HCs in study 2; 7 females, aged 30.11 ± 8.68 year‐old) who gave their informed consent to participating in the studies. The studies were approved by the Institutional Review Board of Stanford University and the Palo Alto VA.

2.3.2. TMS

Following an anatomical MRI (T1‐weghted, 3 T) to determine MRI‐guided spTMS targets, subjects received spTMS using a Cool‐B B65 butterfly coil and a MagPro X100 TMS stimulator (MagVenture, Denmark). Stimulations were delivered to 15 cortical targets, including primary visual cortex (V1), bilateral primary motor cortices (M1), bilateral posterior dorsal lateral prefrontal cortices (pDLPFC), bilateral anterior dorsal lateral prefrontal cortices (aDLPFC), bilateral frontal eye fields (FEF), bilateral inferior parietal lobules (IPL), bilateral intraparietal sulci (IPS), and bilateral angular gyri (ANG). For V1 and M1, the target sites were defined in the standard Montreal Neurological Institute reference. For pDLPFC, aDLPFC, FEF, IPL, IPS, and ANG, the stimulation sites were identified as the peak coordinates in clusters derived from brain networks parcellated from a separate group of subjects' resting‐state fMRI data (Chen et al., 2013; Sridharan, Levitin, & Menon, 2008) using ICA. These targets were then transformed to individual subject native space using non‐linear spatial normalization with FSL (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki) and used for TMS targeting. The resting motor threshold (rMT) was determined as the minimum stimulation intensity that produced visible finger movement of the right hand at least 50% of the times when the subject's left M1 is stimulated. TMS coil placement was guided by Visor2 LT 3D neuronavigation system (ANT Neuro, Netherlands) based on co‐registration of the functionally defined target to each participant's structural MRI (T1 weighted, slice distance 1 mm, slice thickness 1 mm, sagittal orientation, acquisition matrix 256 × 256) acquired with a 3T GE DISCOVERY MR750 scanner. The TMS coil was placed tangentially to the scalp with the handle pointing backwards and laterally at an angle of 45° to the sagittal plane (with the exception of V1, where the handle was pointing downwards along the sagitall plane. Studying the optimal coil angles for different stimulation sites is beyond the scope of this article). Each target site was stimulated with 60 pulses (biphasic TMS pulses, 280 µs pulse width, 120% rMT, 1500 ms recharge delay), interleaved at a random interval of 3 s ± 300 ms. A thin foam pad was attached to the surface of the TMS coil to decrease electrode movement. The subjects were instructed to relax and to fixate at a cross located on the opposing wall while stimulations were administered by a research assistant.

2.3.3. EEG

A total of 64‐channel EEG data were recorded using two 32‐channel TMS‐compatible BrainAmp DC amplifiers (sampling rate: 5 kHz; measurement range: ± 16.384 mv; cutoff frequencies of the analog high‐pass and low‐pass filters: 0 and 1 kHz) and the Easy EEG cap with extra flat, freely rotatable, sintered Ag‐AgCl electrodes designed specifically for TMS applications (BrainProducts GmbH, Germany). The electrode montage followed an equidistant arrangement extending from below the cheekbone back to below the inion (Figure 4a). Electrode impedances were kept below 5 kΩ. An electrode attached to the tip of the nose was used as the reference. DC correction was manually triggered at the end of the stimulations at each site to prevent the saturation of the amplifier due to the DC drift. During the spTMS‐EEG recordings, subjects were seated on a comfortable reclining chair.

All EEG data analyses were performed in MATLAB (R2014b, The Mathworks Inc., MA) using custom scripts built upon the EEGLAB (Delorme, & Makeig, 2004) toolboxes. In ARTIST, following frequency filtering, the EEG data were epoched −500 to +1000 ms relative to the TMS pulse. For the first ICA run, as the primary goal is to remove large amplitude decay artifacts, no dimensionality reduction was performed, (i.e., the number of ICs is equal to the rank of the EEG data matrix). For the second ICA run, dimensionality reduction was performed beforehand via PCA. The dimensionality is determined to be the least number of principal components that can explain higher than 99.9% of the total variance. The decay artifact ICs of the first ICA run and all the ICs of the second ICA run were considered in the following classification assessment. Note that ICs of the second ICA run with negligible variance (<0.2% of the total variance) would not affect reconstruction and were therefore always discarded. After artifact rejection, baseline correction was performed −300 to −100 ms relative to the TMS pulse.

Manual IC classification was developed from both the population #1 HC data (N = 6 subjects, n = 2198 ICs) and the population #2 HC data (N = 6 subjects, n = 2212 ICs). Three EEG experts with extensive experience in spTMS‐EEG manual artifact rejection manually classified each IC to either “nonartifact” or “artifact.” The final label of each IC was determined by consensus, i.e., the category that received the most number of the EEG experts' votes. In order to avoid losing significant neural information, the experts were instructed to keep ICs that appear partly artefactual and partly neural. To determine if ARTIST helps reduce bias from human influence, manual ratings were also performed by two novice EEG users who had received one training session of two hours on TMS‐EEG artifact rejection and practiced on spTMS‐EEG data sets of only two stimulation sites from a single subject.

2.4. Quantification of IC classification accuracy and postprocessing performance

Using the spTMS‐EEG data described above, we benchmarked ARTIST against MARA (Winkler et al., 2011), which is a state‐of‐the‐art supervised IC rejection algorithm developed for cleaning standard EEG data, to determine IC classification accuracy, with manual artifact rejection results by the EEG experts as the gold‐standard. In accordance with (Winkler et al., 2011), the following six features are used in MARA: skewness, log(b), alpha band power, fit error, dynamical range, and current source density. In order to assess their generalization capability across stimulation sites, subjects, and populations, ARTIST and MARA's artifact rejection performance was evaluated using two metrics: (a) IC classification accuracy and (b) correlation coefficient between the group TEPs of auto‐ and hand‐cleaned data.

More specifically, IC classification accuracies were first computed on the population #1 data using split‐half accuracy, intersubject accuracy, and intersite accuracy. To compute split‐half accuracy, ICs were randomized and the FLDA classifier was subsequently trained on half of the randomized ICs and tested on the remaining half. This process was repeated for 20 iterations and averaged to obtain the split‐half accuracy (Kohavi, 1995). The leave‐one‐out strategy was employed to calculate the intersubject/site accuracy. More specifically, in each iteration the FLDA was trained on the ICs of a different set of N − 1 subjects/sites and tested on the ICs of the remaining subject/site. The intersubject/site accuracy is the average of the classification accuracy across N iterations (N = 6 for intersubject accuracy and N = 15 for intersite accuracy).

The classification accuracy measures the performance of ARTIST in IC classification. However, three questions remain unaddressed: (a) How does the algorithm generalize across populations? A fully automated method should perform well when tested on data from a different population that was not used to train the method. (b) How does the algorithm generalize across electrode montages? The classifier trained from the data using one electrode montage should be applicable to the data using a different electrode montage, such that recalibration is not needed. (c) How do the TEPs from the auto‐cleaned data compare to the TEPs of the hand‐cleaned data? To address the first question, we demonstrated the quality of the automated artifact rejection by testing the classifier trained from the population #1 HC spTMS‐EEG data (N = 6) on the population #2 HCs (N = 6). To address the second question, we tested the classifier trained from the population #1 HC spTMS‐EEG data using the full set of 64 electrodes on the population #2 HC data with a subset of 34 electrodes (Figure 4b). For the third question, in addition to calculating the IC classification accuracy, we calculated the within‐subject correlation coefficient between the TEPs and time–frequency power maps of the hand‐cleaned and autocleaned data. The time‐frequency power maps were calculated using the Morlet wavelet transform with a three cycle time window.

3. RESULTS

3.1. Manual classification results

Among all the population #1 HCs' ICs, manual processing by the three EEG experts concluded that 1257 ICs (57.19%) were artefactual and 941 (42.81%) were neural in origin. For population #2, 1285 ICs (58.09%) were artefactual and 927 (41.91%) were neural. The percentage of inter‐rater agreement (i.e., the three experts rated identically) is 93.92%, indicating consistency among experts.

Compared to the gold‐standard IC classification by the EEG experts, classification accuracies by the two EEG novice users were 89.68% and 83.38%, respectively. The sensitivity and specificity were 87.89% and 91.88% for novice user 1, and 98.69% and 64.63% for novice user 2, respectively. The low consistency of the sensitivity and specificity between the novice users highlights the potential for considerable between‐rater variability in IC classification.

3.2. Intrapopulation IC classification results

Compared to IC classification by the EEG experts, intersubject accuracies across the 6 population #1 HCs were 95.93 ± 1.74% (mean ± SD) for ARTIST, and 92.57 ± 4.31% for MARA, significantly higher for ARTIST (p < .05; Wilcoxon signed rank test). The classification accuracies for each subject are listed in Table 1. Intersite accuracy across the 15 sites was calculated to be 95.88 ± 2.41% for ARTIST and 93.14 ± 2.33% for MARA, significantly higher for ARTIST (Figure 7b; n = 15 sites; p < 10⁻⁴; Wilcoxon signed rank test). The classification accuracies for each site are listed in Table 2. The split‐half accuracy over 20 iterations was 96.20 ± 0.33% for ARTIST, and 92.03 ± 0.58% for MARA, significantly higher for ARTIST (Figure 7a; p < 10⁻⁴; Wilcoxon signed rank test). Moreover, for ARTIST, the sensitivity and specificity of the artifact IC detection were 96.83 ± 0.97% and 95.70 ± 0.99%, respectively.

Table 1.

Classification accuracies (%) for each subject in the leave‐one‐subject‐out classification

Methods	Sub A	Sub B	Sub C	Sub D	Sub E	Sub F	Mean ± std
ARTIST	94.89	94.80	94.48	95.12	98.38	97.93	95.93 ± 1.74
MARA	90.42	93.32	94.00	85.12	95.14	97.42	92.57 ± 4.31

Figure 7.

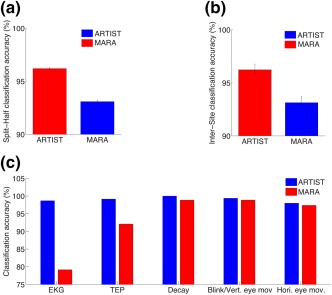
Classification accuracies of ARTIST compared with MARA. (a) Split‐half classification accuracy. (b) Intersite classification accuracy. (c) Split‐half classification accuracy for various types of EEG artifacts for ARTIST and MARA [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 2.

Classification accuracies (%) for each site in the leave‐one‐site‐out classification

Methods	Left M1	Right M1	V1	Left pDLPFC	Right pDLPFC	Left aDLPFC	Right aDLPFC	Left FEF	Right FEF
ARTIST	95.88	90.12	98.77	92.90	95.60	97.18	98.58	97.56	95.80
MARA	94.71	88.89	94.48	90.16	93.71	95.48	95.74	93.29	94.41

Methods	Left IPL	Right IPL	Left IPS	Right IPS	Left ANG	Right ANG	Mean ± std
ARTIST	97.10	92.52	96.27	96.32	95.24	98.28	95.88 ± 2.41
MARA	95.65	90.65	91.79	89.71	95.24	93.10	93.14 ± 2.33

Further breakdown of the split‐half classification accuracy by artifact/neural types demonstrated that ARTIST outperformed MARA for each type by 5.77% on average (Figure 7c). The improvement was particularly noteworthy for the EKG and TEP ICs, for which the accuracies were increased by 19.51% and 7.08%, respectively (all p < 10⁻⁴; Wilcoxon signed rank test).

To assess feature discriminability, we computed the split‐half accuracy and the weighting of each feature (Figure 8a,b). More specifically, each feature was employed to train the FLDA and the classification accuracy was registered. The average classification accuracy over 20 iterations is shown in Figure 8a. The weights of the features shown in Figure 8b are the average weights of each feature over 20 iterations of the split‐half classification using all features. Individually, the dynamical range, b, and fit error features were the most discriminative among all the features. However, high discriminability did not necessarily lead to the high weighting of a feature in the classifier, as many highly discriminative features demonstrated weaker classifier weighting (e.g., the fit error feature f ₂₂; Figure 8a,b).

Figure 8.

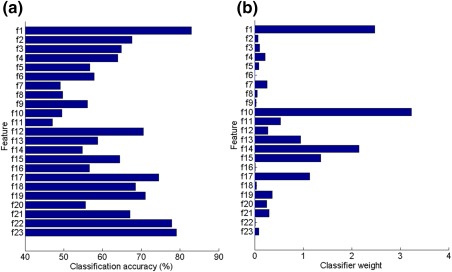
Feature assessment of ARTIST. (a) Feature‐wise classification accuracy. (b) Classifier weight associated with each feature when all the features are used in conjunction. The features from top to bottom are as follows: f ₁, dynamical range; f ₂, central activation; f ₃, frontal activation; f ₄, occipital activation; f ₅, left temporal activation; f ₆, right temporal activation; f ₇, border activation; f ₈, horizontal eye movement; f ₉, blink/vertical eye movement; f ₁₀, EKG spatial feature; f ₁₁, EKG temporal feature; f ₁₂, current source density; f ₁₃, maximum magnitude; f ₁₄, 0–60 ms short‐time magnitude; f ₁₅, 60–140 ms short‐time magnitude; f ₁₆, 140–220 ms short time magnitude; f ₁₇, skewness; f ₁₈, theta‐band power; f ₁₉, alpha‐band power; f ₂₀, beta‐band power; f ₂₁, gamma‐band power; f ₂₂, fit error; f ₂₃, log(b) [Color figure can be viewed at http://wileyonlinelibrary.com]

3.3. Interpopulation IC classification and postprocessing results

Next, following both manual and automated ICA rejection methods, and using the classifiers trained from the population #1 HCs (N = 6), we classified the ICs of the population #2 HCs (N = 6) not used in building the classifier. We also compared the TEP and time–frequency power maps between IC rejection methods.

The interpopulation classification accuracies across the 6 population #2 HCs were 95.10 ± 2.15% for ARTIST and 91.37 ± 2.04% for MARA, significantly higher for ARTIST (p < 0.05; Wilcoxon signed rank test). ARTIST also outperformed both novice users, whose classification accuracies were 88.30 ± 2.70% and 81.96 ± 2.77% (p < 0.05 for both novice user 1 and 2; Wilcoxon signed rank test).

For the postprocessing results, the absolute differences between automated and manual rejection for left pDLPFC and M1 stimulation were computed. Figures 9 and 10 demonstrate the TEP (Figure 9) and time–frequency power map (Figure 10) plots (also see Supporting Information, Figure 1S for the comparison of TEP waveforms). In addition to showing differences at electrodes F3 and C3, which are in close proximity to left DLPFC and M1, respectively, we also showed the global mean‐field power (GMFP) for the TEP, which is a measure that characterizes global EEG activity and is defined as the standard deviation of the TEPs across channels (Lehmann, Skrandies, 1980). For the TEP, the Wilcoxon signed rank test indicated that the absolute differences between ARTIST and manual rejection are significantly smaller than those between MARA and manual rejection at all electrodes (all p <  ${10}^{-6}$, Bonferroni corrected for the number of the stimulation sites and electrodes). For the time–frequency power map, the average absolute differences between automated and manual rejection were assessed separately for each of the following EEG frequency bands: $\mathrm{\alpha }$ (8–12 Hz), $\mathrm{\beta }$ (13–30 Hz), and $\mathrm{\gamma }$ (31–50 Hz). Across all the frequency bands, the Wilcoxon signed rank test indicated that the absolute differences of the time–frequency power between ARTIST and manual rejection are significantly smaller than those between MARA and manual rejection at all electrodes (all p <  ${10}^{-6}$, Bonferroni corrected for the number of the stimulation sites, electrodes, and frequency bands).

Figure 9.

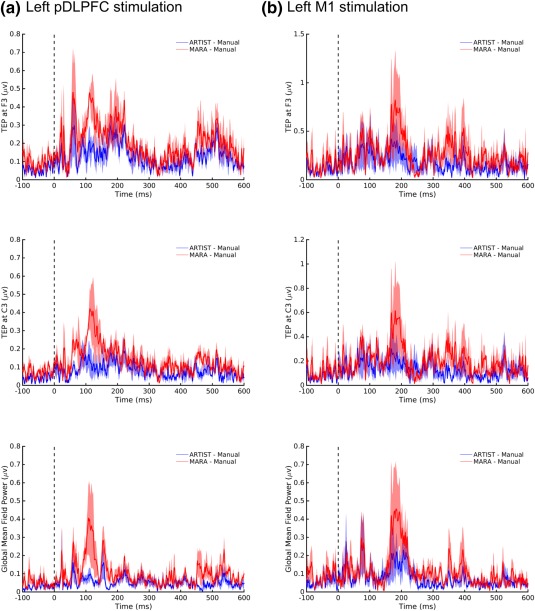
Absolute difference of TMS‐evoked potentials (TEPs) between manual and automated rejection algorithms. Data derived from population #2 subjects (N = 6). The stimulation sites are the (a) left pDLPFC and (b) left M1 [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 10.

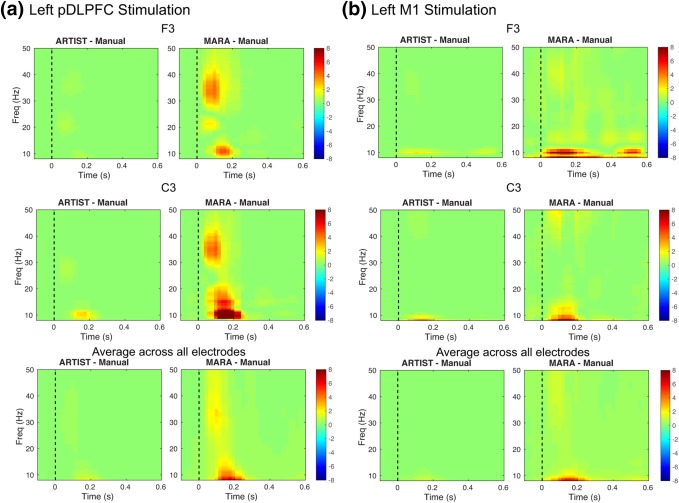
Absolute difference of time–frequency power maps between manual and automated rejection algorithms. Data derived from population #2 subjects (N = 6). The stimulation sites are the (a) left pDLPFC and (b) left M1. The time–frequency power maps are calculated using the Morlet wavelet transform with a three cycle time window and z‐scored with respect to the −300 to −100 ms baseline [Color figure can be viewed at http://wileyonlinelibrary.com]

For ARTIST, the within‐subject correlation coefficient of the TEP time series (averaged over channels) with those from the manual rejection was significantly higher than for MARA (p < 0.005; paired Wilcoxon signed rank test). Moreover, the within‐subject correlation coefficient of the spectral power time series (averaged over channels) with those from the manual rejection was significantly higher than for MARA in each frequency band (all p < 0.01; paired Wilcoxon signed rank test, Bonferroni corrected for number of the frequency bands). The within‐subject correlation coefficient between the log of the GMFP time series from the manual rejection and ARTIST was <0.95 for each site tested (Figure 11a), significantly higher than that between the manual rejection and MARA (p < 10⁻⁴; paired Wilcoxon signed rank test). Finally, for each subject, based on the GMFP time series, the peak magnitude of each TEP component (P45, N100, and P200) was extracted. Each TEP component demonstrated strong GMFP correlation between manual rejection and ARTIST (Figure 11b; R _P200 = .989, R _N100 = .980, R _P45 = .964.), and weaker correlation between manual rejection and MARA (Figure 10b; R _P200 = .960, R _N100 = .944, R _P45 = .879; all p < .01; paired Wilcoxon signed rank test, Bonferroni corrected for the number of the TEP components). The significant performance enhancement in ARTIST compared to MARA for the P45 component may be explained by the fact that the early potentials are more susceptible to the interference from the TMS‐evoked muscle artifact.

Figure 11.

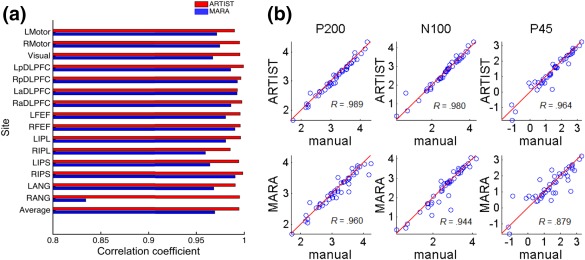
Correlations between GMFP from the manual and automated rejection algorithms in population #2 subjects (N = 6). (a) Within‐subject correlation coefficient for each stimulation site. Each vertical bar represents within‐subject correlation coefficient when each site is stimulated. (b) Scatter plots. From left to right: quantification of GMFPs at p200, n100, and p45 time components. Each circle represents the GMFPs computed from manual rejection (x‐coordinate) versus automated rejection (y‐coordinate), corresponding to one site and subject [Color figure can be viewed at http://wileyonlinelibrary.com]

To demonstrate the generalization across electrode montages, ARTIST classifiers trained from the population #1 HCs (N = 6) using the full set of 64 electrodes were used to classify the ICs extracted from the population #2 HCs (N = 6) using a subset of 34 electrodes (Figure 4b). The three EEG experts again manually rated all the ICs associated with the 34 electrodes for the population #2 HCs (N = 6). The interpopulation classification accuracies across the 6 population #2 HCs were 95.56 ± 1.81%.

4. DISCUSSION

In summary, this article presented a fully automated algorithm ARTIST for TMS‐EEG artifact rejection based on a set of novel features that captured the spatio‐temporal‐spectral profiles of neural and non‐neural sources. ARTIST achieved an IC classification of 95% across a large number of spTMS‐EEG data sets (n = 90 stimulation sites) when compared to manual artifact rejection by EEG experts. This accuracy was retained across stimulation sites, subjects, populations, and electrode montages, demonstrating high generalization performance. Moreover, ARTIST significantly outperformed a state‐of‐the‐art automated algorithm, MARA, by an average of more than 5% across artifact/nonartifact types, and artifact rejection by relatively novice individuals. Finally, reliable postprocessing results were obtained using the ARTIST‐cleaned data, as shown by the strong within‐subject correlations attained for the GMFP and TEP time series between hand‐cleaned and ARTIST‐cleaned data.

4.1. Potential applications and advances

To our knowledge, this work describes the first fully automated artifact rejection algorithm for the analysis of spTMS‐EEG data. Using MATLAB R2014b on a desktop with 3 GHz Intel Core i7 CPU and 16 GB RAM, the average runtime of ARTIST on the spTMS‐EEG data of one stimulation site (60 trials; interstimulus interval of 3 s ± 300 ms) is 1.2 min, compared to the average time of 7 min by the EEG experts using the semi‐automated pipeline that manually classifies the ICs. Therefore, this algorithm will greatly improve the precision and processing time of TMS‐EEG experiments, allowing the analysis of the large‐scale TMS‐EEG connectome data sets to be completed within a short period of time (Harquel et al., 2016). This also opens up the potential for near real‐time processing of data, which could lead to probing of ongoing brain states as well as closed‐loop applications. Furthermore, the high level of IC classification accuracy observed in both populations demonstrates the generalizability of the ARTIST algorithm across populations. Moreover, as TMS‐EEG methods are more broadly disseminated and used by the neuroscience community, likely users will increasingly be relatively novice individuals in terms of manual artifact rejection skills. The clear superiority of the performance of ARTIST when compared to our novice raters (who were themselves inconsistent with each other) demonstrates the capacity of this algorithm to standardize the objective and high‐quality rejection of TMS‐EEG artifacts and support automated processing. The MATLAB code for ARTIST is available at http://etkinlab.stanford.edu/toolboxes/ARTIST/.

4.2. Considerations, limitations, and future directions

The EKG artifact has received little attention in traditional automated EEG artifact rejection approaches. In ARTIST, the EKG spatial feature and temporal feature were proposed for detecting the EKG IC. The EKG spatial feature is robust to the variability of the EKG topography across subjects, and the EKG temporal feature detects the QRS complexes in wavelet subspace, which is less prone to false positives than peak detection in the original subspace (Figure 5a). Together, these two features enable a high classification rate for the EKG IC (98.68%; Figure 7c).

As suggested in Figure 8, high discriminability of a feature did not necessarily yield high classifier weighting of the feature. The reasons are threefold: (a) Redundancy among the features. This is because a certain artifact or non‐artifact type can be captured by multiple features. For instance, the low weighting of the fit error feature may be because it only offers redundant information as compared with the b and alpha band power features. (b) A feature may not be discriminative when used alone but contributes to the classification substantially when combined with other features (e.g., the EKG spatial feature). (c) Imbalances of the sample size in each artifact subtype. For instance, the classification accuracy of the EKG spatial feature is low partly because of the relatively small number of EKG ICs. Note that the EKG spatial feature f ₁₀ is a binary feature, with 0 indicating the absence of the EKG artifact. We have found (data not presented) that using f ₁₀ alone can achieve high classification accuracy (>98.7%) for the EKG artifact (by treating EKG vs other artifacts/neural signals as a binary classification problem). Therefore, the large weight of f ₁₀ reflects the discriminativeness of the feature toward classifying the EKG artifact. For the non‐EKG artifacts or neural signals, as the associated f ₁₀ is 0 in most cases, the large weight of the EKG spatial feature in Figure 8b would not affect their classification.

Our results also reveal that ICs do not weigh equally in their importance for post‐processing (Figure 8b). Some misclassified artefactual ICs may slightly influence postprocessing if they only explain a small amount of variance in the data. By contrast, neural ICs such as the TEP ICs that carry important information, if erroneously classified, may change the postprocessing results dramatically as the corresponding TEP peaks will be missing or considerably distorted. In ARTIST, the detection rate for the TEP ICs is higher than MARA because the short‐time magnitude features are designed for the TEP ICs in ARTIST.

It may be argued that artifacts not time‐locked or phase‐locked to the TMS pulse do not heavily affect postprocessing as they are cancelled out through epoch averaging when the TEP is calculated. However, when one is interested in the spectral content of the TMS‐EEG data, the spectral power of the artifacts is not suppressed by epoch averaging. Hence, it is important that major artifacts are removed prior to spectral analyses of the data. The performance of the ICA‐based artifact rejection depends crucially on ICA's ability to separate artifacts and neural sources into distinct components, which can be distorted by a number of factors. First, it has been shown that large (e.g., thousands of microvolts) TMS‐evoked muscle artifacts could lead to substantial error in the estimation of the IC spatial maps, and several methods were proposed to suppress the muscle artifacts prior to the ICA (Hernandez‐Pavon et al., 2012; Korhonen et al., 2011; Casula et al., 2017). These methods can be combined with ARTIST to further improve its performance. Second, to ensure reliability of the IC estimation, it is important to feed sufficient amount of EEG data into the ICA. As a rule of thumb, the minimum number of data samples required for a reliable ICA is kCN, where C is the number of the ICs, N is the number of the channels, and k is a constant depending on the number of ICs. To decompose a large number of channels, k may need to be at least 20 (Onton, Westerfield, Townsend, & Makeig, 2006). Thus, when N is large, dimensionality reduction approaches should be used to reduce C. In the data analysis presented in this article, we used PCA to reduce the number of ICs in the ICA. The number of ICs can be determined in a more principled manner under more formal statistical frameworks (Beckmann, & Smith, 2004; Wu, Nagarajan, & Chen, 2016). Third, in some cases ICA may produce ICs with strong presence of both neural signals and artifacts that could be classified either way. In the manual rating stage these ICs were classified as neural to prevent the loss of important neurophysiological information. When used for training, ARTIST is able to learn to similarly classify the ambiguous ICs as neural. Fourth, electrode interpolation prior to ICA may introduce nonlinearity into the EEG data, which may lower the performance of ICA. However, we still chose to interpolate the rejected channels to keep the montage consistent across the stimulation sites, subjects, and populations, so that the ICs can be analyzed in a standardized manner (Section 2.2.3). This is also in line with the approach in (Nolan et al., 2010). The influence of electrode interpolation on the performance of ICA is likely small when the number of the rejected channels is low. Assessing the impact of the electrode interpolation on ICA is beyond the scope of this article.

The workflow of ARTIST is similar to the one described in TESA (Rogasch et al., 2016) and TMSEEG (Atluri et al., 2016), but unlike those other packages, here the IC rejection is fully automated. In particular, a semi‐automated algorithm for IC selection was provided in TESA, in which the ICs were classified based on heuristically defined thresholds, as opposed to the thresholds determined in a data‐driven manner as in ARTIST, and the IC classification accuracy was not reported. Moreover, in TESA and TMEEG, the EKG artifact was not considered and the influence of the artifact rejection to the TEPs was not assessed.

Artifact rejection is by no means a substitute for stringent data acquisition protocols. There is no preprocessing trick that will turn low‐quality data into high‐quality results. A set of standard TMS‐EEG acquisition guidelines was provided in (Ilmoniemi & Kičić, 2010; Rosanova et al., 2012) to ensure high‐quality spTMS‐EEG recordings. These include the use of noise‐cancellation earphones with masking white noise to suppress the air‐conducted auditory artifacts due to TMS‐clicks, a thin layer of foam between the coil and EEG cap to reduce the electrode movement and bone‐conducted auditory artifacts, low electrode impedances to shorten the duration of the pulse artifact and minimize electrode polarization artifact, and a high EEG sampling rate to minimize the ringing artifact from the TMS pulse. One limitation of this study is that the masking white noise was not used during the acquisition of the spTMS‐EEG data and the resulting auditory‐evoked potential artifacts were not considered in ARTIST (Rogasch et al., 2014). Somatosensory evoked potentials (SEPs) can also be elicited by TMS via scalp sensations, or peripheral somatosensory feedback from the contracting muscles when the motor cortex is stimulated. It is very difficult to identify the degree of contribution of the SEP to spTMS‐EEG. Despite that ARTIST does not attempt to remove the SEP, several previous studies have used sham stimulations to show that the SEP does not pose a major problem (Nikulin, Kičić, Kähkönen, & Ilmoniemi, 2003).

We highlight several lines of future work related to ARTIST. First, the focus of this paper is artifact rejection for the spTMS‐EEG data, but it also serves as the cornerstone to develop automated artifact rejection algorithms for other types of TMS‐EEG data under similar frameworks, including the concurrent repetitive TMS‐EEG data (Hamidi, Slagter, Tononi, & Postle, 2010) and paired‐pulse TMS‐EEG data (Casula, Pellicciari, Picazio, Caltagirone, & Koch, 2016). The key is to define features that are tailored to the specific time scales of different data types. Second, although we assessed the intersite/subject/population classification performance of ARTIST, it remains to be verified if the algorithm generalizes well across spTMS‐EEG data sets collected in different labs, where the specific experimental protocols, environment, and EEG amplifiers may vary. Third, although the Infomax algorithm was chosen to solve the ICA in ARTIST, other ICA algorithms can also be considered, including FastICA (Hyvarinen, 1999) and TDSEP (Ziehe, & Müller, 1998), which is a computationally efficient algorithm purely based on second‐order statistics. Future work will compare various ICA algorithms and assess how they influence spTMS‐EEG artifact rejection differently. Finally, TMS‐evoked eye blinks that are temporally overlapping with the TEPs may violate the statistical independence assumption of the ICA. To address this issue, new approaches that use different criteria for removing the decay artifacts and TMS‐evoked eye blink artifacts should be developed.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supporting Information

Wu W, Keller CJ, Rogasch NC, et al. ARTIST: A fully automated artifact rejection algorithm for single‐pulse TMS‐EEG data. Hum Brain Mapp. 2018;39:1607–1625. 10.1002/hbm.23938