Functional connectivity predicts gender: Evidence for gender differences in resting brain connectivity

Abstract

Prevalence of certain forms of psychopathology, such as autism and depression, differs between genders and understanding gender differences of the neurotypical brain may provide insights into risk and protective factors. In recent research, resting state functional magnetic resonance imaging (rfMRI) is widely used to map the inherent functional networks of the brain. Although previous studies have reported gender differences in rfMRI, the robustness of gender differences is not well characterized. In this study, we use a large data set to test whether rfMRI functional connectivity (FC) can be used to predict gender and identify FC features that are most predictive of gender. We utilized rfMRI data from 820 healthy controls from the Human Connectome Project. By applying a predefined functional template and partial least squares regression modeling, we achieved a gender prediction accuracy of 87% when multi‐run rfMRI was used. Permutation tests confirmed that gender prediction was reliable ( $p<.001$). Effects of motion, age, handedness, blood pressure, weight, and brain volume on gender prediction are discussed. Further, we found that FC features within the default mode (DMN), fronto‐parietal and sensorimotor networks contributed most to gender prediction. In the DMN, right fusiform gyrus and right ventromedial prefrontal cortex were important contributors. The above regions have been previously implicated in aspects of social functioning and this suggests potential gender differences in social cognition mediated by the DMN. Our findings demonstrate that gender can be reliably predicted using rfMRI data and highlight the importance of controlling for gender in brain imaging studies.

1. INTRODUCTION

Gender differences in cognitive abilities such as spatial perception, memory, and verbal skills have been reported across a wide array of studies (See Miller & Halpern 2014 for review). While overall gender differences in group means have been reported in specific cognitive domains, the underlying neurobiology between genders remains unclear (Del Giudice 2009; Hyde & Plant 1995). Reports of gender differences in cognition have spurred interest in examining structural and functional brain features which may differ between genders and underlie previous reports of cognitive and behavioral differences. Since the prevalence of certain forms of psychopathology differs between genders, such as autism being four times greater in males (Werling & Geschwind 2013) and major depressive disorder twice as common in females (Albert 2015), understanding the neurobiology of gender differences may provide insights into risk and protective factors associated with psychopathology.

A meta‐analysis of structural brain imaging studies reported that males exhibit larger total brain volume and gray and white matter tissue volumes. There are also regional gender differences in areas such as the amygdala, hippocampus, and insula (Ruigrok et al. 2014). When multiple brain regions were examined, recent work concluded that brains can be considered as “mosaics” of male and female structural features with only a few individuals consisting entirely of male or female brain features (Joel et al. 2015). Global trends in structural connectivity have been reported as well. In a DTI study males on average tended to exhibit more intra‐hemispheric connectivity whereas females appeared to exhibit more inter‐hemispheric connectivity (Ingalhalikar et al. 2014). Structural brain features from multiple imaging modalities have also been used to predict gender with high accuracy (Feis et al. 2013).

Functional connectivity (FC) studies report stronger FC in the default mode network (DMN) for females within the posterior cingulate cortex/precuneus and bilateral medial prefrontal cortex (Bluhm et al. 2008). Stronger intra‐network FC in females and stronger inter‐network FC in males (Allen et al. 2011) and a mixture of higher and lower FC in males and females has also been reported in lobar regions (Filippi et al. 2013) in resting networks. Similar to findings using DTI (Ingalhalikar et al. 2014), a study using FC reported that males exhibit greater rightward lateralization of short‐range FC compared to females (Tomasi & Volkow 2012). Moreover, in our previous work (Zhang et al. 2016) we found significant and widespread gender differences of FC in frontal, parietal, and temporal lobes using regression analyses. We also reported graph properties that indicated greater local clustering in males compared to greater global clustering in females.

Despite reports of gender differences in FC, only a few studies have attempted prediction of gender using FC. A great number of gender discriminative FC were found in males in motor, sensory, and association areas, but only achieved a prediction accuracy of 62% (Casanova et al. 2012). Smith et al. (2013) utilized rfMRI for gender prediction and reported a higher prediction accuracy of 87%. In the above studies, the total number of subjects used was small (N < 148). Recent work has found that rfMRI is extremely useful for individual prediction of cognitive, behavioral, and demographic measures. To date, studies have predicted individual brain maturity using resting FC in individuals age 7–30 (Dosenbach et al. 2010) and fluid intelligence in young adults (Finn et al. 2015). Given the lack of previous research, it remains unclear the extent to which rfMRI can accurately predict gender.

Thus, our goal was to implement gender prediction using resting state FC for a large cohort of 820 subjects with four runs of rfMRI. This study attempts to answer the following questions: (a) Can gender be predicted with a high accuracy using rfMRI FC in a large data set? (b) Can prediction accuracy be improved if FC information is combined across multiple runs and what are the different strategies to combine FC across runs? and (c) What FC features are important for predicting gender?

2. MATERIALS AND METHODS

2.1. Data set and preprocessing

This study included 820 healthy adults (Gender: 366 males and 454 females; age: 22–37 years) from the human connectome project (HCP) (Van Essen et al. 2012) S900 release. We use the term “Gender” (instead of “Sex”) following the HCP data dictionary. Subject demographics are shown in Table 1. Age, handedness (Schachter et al. 1987), blood pressure, weight and brain volumes demonstrate significant gender differences. Additionally, the subject motion during rfMRI sessions (average frame displacement across time points and runs, Power et al. 2012) is included. HCP rfMRI data were acquired on a Siemens Skyra 3T scanner housed at Washington University in St. Louis. TR =  $720 ms$, TE =  $33.1 ms$, spatial resolution =  $2\hspace{0.17em}\times \hspace{0.17em}2\times 2 {mm}^3$. More details about HCP data and MR imaging parameters can be found in the S900 release manual available at http://db.humanconnectome.org. Each subject underwent four rfMRI runs of approximately 15 min each, two runs in the first session (Day 1) and two runs in the second session (Day 2). The data consisted of 1,200 volumes for each run and therefore each subject had 4,800 volumes for the four runs. Quality assurance and quality control strategies of HCP rfMRI are described in Marcus et al. (2013).

Table 1.

Subject demographics (N = 820)

			Male–Female
	Male (N = 366) Mean (Std)	Female (N = 454) Mean (Std)	Gender difference (t statistic, p value)
Age (year)	28.0 (3.7)	29.4 (3.6)	−5.4, 1E‐7*
Education (year)	14.8 (1.8)	15.0 (1.8)	−1.6, 0.1
Income**	5.0 (2.2)	5.0 (2.1)	−0.1, 0.9
Handedness***	60.9 (43.1)	69.9 (44.4)	−2.9, 4E‐3*
Blood pressure systolic	129 (13)	120 (13)	9.7, 5E‐21*
Blood pressure diastolic	79 (10)	75 (10)	5.0, 8E‐7*
Weight (pound)	190 (36)	156 (36)	13.5, 8E‐38*
Brain volume (cm3) (Gray matter + White Matter + CSF)	1214 (97)	1063 (82)	24.0, 9E‐97*
Motion: Frame displacement (mm)	0.16 (0.06)	0.17 (0.06)	−0.9, 0.4

*Indicates statistical significance for p < .05.

**Total household income categories: <$10,000 = 1, 10K‐19,999 = 2, 20K‐29,999 = 3, 30K‐39,999 = 4, 40K‐49,999 = 5, 50K‐74,999 = 6, 75K‐99,999 = 7, ≥100,000 = 8.

***Schachter et al. (1987).

Data used in this study were initially preprocessed by the HCP team and included the standard preprocessing steps (such as motion correction and spatial normalization) and ICA denoising to remove non‐neural spatiotemporal components (Griffanti et al. 2014; Salimi‐Khorshidi et al. 2014). In addition, the 24 head motion parameter (Satterthwaite et al. 2013) time series were high‐pass filtered and then regressed out from the rfMRI time series data.

2.2. Region of interest (ROI) and functional connectivity

A functional brain atlas (Dosenbach et al. 2010) was used to reduce rfMRI data of the whole brain to 160 ROIs. These ROIs of 10mm‐diameter spheres were centered around the MNI coordinates of the functional atlas and were functionally defined from a meta‐analysis of five task fMRI studies which encompassed much of the cerebral cortex and cerebellum (Dosenbach et al. 2010). This atlas is a popular brain parcellation scheme and has been integrated into several brain network analysis/visualization tools (Cao et al. 2014; Wang et al. 2015; Xia et al. 2013). For each of the 160 ROIs, an average time series was calculated by averaging the time series of all the voxels that fell within an ROI. This resulted in 160 ROI time series and these 160 time series were used for further analyses. For data presentation and interpretation the 160 ROIs are divided into the following six functional modules: fronto‐parietal, default, cingulo‐opercular, sensorimotor, occipital, and cerebellum (Dosenbach et al. 2010).

For rfMRI of single runs, the FC matrix was calculated as Fisher's z‐transformed Pearson correlation coefficients between time series across the 160 ROIs. After vectorization of the $160\hspace{0.17em}\times \hspace{0.17em}160$ FC matrix and elimination of duplicate FC values, each subject had an FC feature vector of length 12,720. To check for the effect of incorporating FC information across runs on gender prediction performance, we constructed the multi‐run FC features in three different ways. Method 1 (Average FC): First calculate FC for each of the four runs and then average FCs across runs; Method 2 (Concatenate TC): first concatenate time courses of four runs together and then calculate FC; and Method 3 (Concatenate FC): First calculate FC for each run and then concatenate FC features across runs (the length of FC feature vector was $\mathrm{12,720}\hspace{0.17em}\times \hspace{0.17em}4\hspace{0.17em}=\hspace{0.17em}\mathrm{50,880}$). For each of the four individual runs and for the above three methods that combine all four runs, the constructed FC features were fed into subsequent classification analyses.

2.3. Partial least squares regression

Classification algorithms use a number of predictor variables to predict one or more predicted variable(s). Hughes (1968) illustrated that with a fixed number of training samples, the predictive power reduces as the number of predictor variables increases. Therefore, feature selection or dimensionality reduction of the predictors is an essential step in machine learning applications when the number of predictors is large. In this study as gender is predicted from a large number of predictors (at least 12,720 FC) the curse of dimensionality needs to be addressed. Principal component analysis (PCA) is a benchmark dimensionality reduction method that applies a linear projection of the predictors in a manner that best explains the predictor variables. But PCA does not help to find associations between the predictor and predicted variables. Partial least squares (PLS) regression is considered as a supervised version of PCA, and derives linear combinations of the original predictor variables that best predict the predicted variable (Abdi 2010). The PLS method has been demonstrated to be well suited for analyzing associations between measures of brain functional activity and behavior (Krishnan et al. 2011; McIntosh and Lobaugh 2004; Qin et al. 2015; Ziegler et al. 2013). FC features are not linearly independent and PLS regression deals with multi‐collinearity by attempting to find latent variables which model the predictor variable space X (Equation (1)) and simultaneously predict the predicted variable Y (Equation (2))

$$X=T{P}^T$$ (1)

$$\widehat{Y}=TB{C}^T=X\left({P^T}^{+}B{C}^T\right)=X{B}_{PLS}$$ (2)

The values of $p$ predictors from $n$ subjects are collected in a $n\times p$ matrix $X$. The $n$ subjects described by $m$ dependent variables are stored in an $n\times m$ matrix $Y$ ( $m=1$ for the gender prediction case). The $n\times l$ matrix $T$ contains $l$ latent variables ordered according to the amount of variance of $Y$ that they explain. $P$ and $C$ are loadings for $X$ and $Y$, respectively. $B$ is an $l\times l$ diagonal matrix in which the non‐zero entries correspond to the covariance of $X$ and $Y$ for each latent variable. The superscript $T$ indicates the transpose operation to the matrix. ${P^T}^{+}$ is the Moore‐Penrose pseudoinverse of $P^T$. The predicted response variable $\widehat{Y}$ can be considered as a linear combination of either latent variables $(\widehat{Y}=TB{C}^T)$ or the original predictors $\widehat{Y}=X{B}_{PLS}$. In the latter case, linear coefficients are contained in the $p\times m$ matrix $B_{PLS}$. The process of solving PLS regression is described in the supplementary material. Combining the predicted response variable and the true response variable, performance of the prediction can be evaluated and this will be discussed in the next section.

2.4. Cross‐validation of the prediction

Ten‐fold cross validation, which balances the requirements of sufficient training samples to reach a good fit and large test sets to yield stable estimates of predictive accuracy (Varoquaux et al. 2016), was applied to implement gender prediction. In Figure 1a, for each of the 10‐folds, 10% of the subjects were left out as the test set and the remaining served as the training set. For explanatory purposes (to ensure that weights across features were comparable), feature standardization via z‐transforms were implemented before feeding the training data to the PLS regression classifier (i.e., $X_{tr}$ was demeaned and then divided by the standard deviation so that the values of each feature had zero‐mean and unit‐variance). After training was completed, the feature values of test set $X_{ts}$ were standardized by the mean/standard deviation derived from the training set (http://scikit-learn.org/stable/modules/preprocessing.html), and were then combined with the linear coefficient $B_{PLS}$ to generate the predicted continuous response $\widehat{Y_{ts}}$. $Y_{ts}$ and $\widehat{Y_{ts}}$ from 10 folds were combined to construct the receiver operating characteristic (ROC) curve for different classification thresholds. The area under curve (AUC) of the ROC was derived as a summary performance index for the classifier on the 820 subjects studied. Given that the gender variable was labeled as one for male and two for female, classification accuracy was calculated at a threshold of 1.5.

Figure 1.

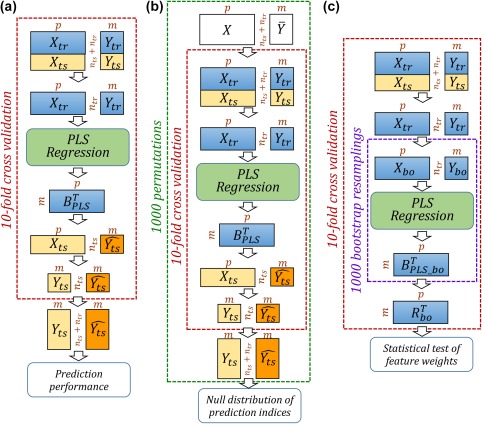
Cross validation of gender prediction, permutation test, and bootstrap resampling. (a) Flow chart of gender prediction. (b) Permutation test applied to evaluate prediction performance. (c) Bootstrap test used to identify important FC features. $X$ contains predictor (FC feature) variables and $Y$ contains the dependent variables (in this case the gender variable, one for male and two for female). Subscripts $tr$ and $ts$ are for training and test sets, respectively. $\widehat{Y}$ contains the predicted gender variable. In b, $\overline{Y}$ represents randomized $Y$. In c, $R_{bo}$ contains the bootstrap ratios of feature weights. Matrix dimensions are indicated by $p \left(=\mathrm{12,720},\hspace{0.17em}total number of FC features\right),\hspace{0.17em}m \left(=1,\hspace{0.17em}number of predicted variables\right),\hspace{0.17em}{n}_{tr} \left(=738,\hspace{0.17em}number of training subjects\right) \mathrm{a}\mathrm{n}\mathrm{d} n_{ts}(=82,\hspace{0.17em}\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{s})$ [Color figure can be viewed at http://wileyonlinelibrary.com]

Two resampling techniques were applied to characterize the statistical significance of the results: the overall prediction performance was assessed by permutation test and the importance of the feature weights were assessed via bootstrap test. In the permutation test (Figure 1b), associations between features and predicted variable (gender) were randomized, that is, the gender values were randomly permuted (from $Y$ to $\overline{Y}$) while the feature matrix was kept intact. 10‐fold cross validation was repeated for each permutation and AUC values from 1000 permutations were used to construct a null distribution of AUC values. In addition, bootstrap was used to derive statistical significance of feature weights (Figure 1c). For each fold in cross validation, subjects in the training set were resampled with replacement (from $X_{tr},Y_{tr}$ to $X_{bo},Y_{bo}$) and the bootstrapped training set was fed into PLS regression to generate a new set of feature weights $B_{PLS\_bo}$. For each feature weight, the bootstrap ratio $R_{bo}$ was calculated as the mean of the 1000 bootstrapped feature weights divided by their standard deviation. The bootstrap ratio is akin to a Student $t$ criterion so if a ratio was large enough (a value of 2 or 3 roughly corresponds to $\mathrm{\alpha }=.05$ or $\mathrm{\alpha }=.003$ for a $t$ test) then the corresponding feature was considered significant for the prediction (Fowler 2013). The statistical strength of each feature was then derived as the absolute value of the average bootstrap ratio across 10 folds (Pereira et al. 2009).

3. RESULTS

3.1. Gender classification results: AUC and accuracy

Results of gender classification for both individual‐run and multi‐run predictions are provided in Table 2. Here the number of components in PLS regression was fixed to be 10. For gender prediction using FC features of single run rfMRI (Run 1 to Run 4), the AUC and classification accuracy are $0.881\hspace{0.17em}\pm \hspace{0.17em}0.006$ and $79.9\%\pm 0.9\%$, respectively. To check the robustness of classification, we also predict gender where the training and test data are from different rfMRI runs. Results of this robustness test are shown in Supporting Information Table 1 and the prediction performance was close to the performance of training and testing within the same rfMRI run. However, as data from multiple rfMRI runs were incorporated, classification performance improved to 0.93 for AUC and 85% for accuracy. There were marginal differences in discrimination capability between the three multi‐run methods. While “Concatenate FC” had the highest AUC value, the classification accuracy at the default threshold of 1.5 was slightly higher for the “Average FC” scheme.

Table 2.

AUC and accuracy for gender classification using PLS regression when number of components was 10

	RUN1	RUN2	RUN3	RUN4	Average FC	Concatenate TC	Concatenate FC
AUC	0.884	0.883	0.873	0.885	0.931	0.930	0.936
Accuracy (%)a	79.2	81.0	79.2	80.2	86.6	85.5	85.7

^aClassification Accuracy for threshold = 1.5 in PLS regression prediction.

Table 3 illustrates the AUC values of gender prediction after regressing out a confound showing significant gender difference in Table 1. Here the number of PLS components was 10 and results for a range of 1–10 components are presented in Supporting Information Tables 2 and 3. The frame displacement is not significantly different between males and females, but was checked as FC can change with motion. The confounding variables were sorted by statistical significance of gender difference. The reduction in gender prediction AUC was found to be associated with the significance of gender difference. Removing a confound that did not show a statistically strong gender difference (e.g., frame displacement, handedness, and age) did not reduce the gender prediction performance. For confounds where the gender difference was highly significant (e.g., blood pressure, weight, and brain volume), gender prediction performance dropped by a larger margin. However, all gender prediction performances remained at AUC > 0.76. The highest performance drop was noted when brain volume was regressed out and as brain volume is strongly correlated to gender, we further investigate the effect of brain volume in a separate section below.

Table 3.

Effect of regressing out potential confounds on the gender prediction performance (the Average FC method)

	Frame displacement	Handedness	Age	Blood pressure	Weight	Brain volume
Male–Female Gender difference (t‐statistic, p‐value)	−0.9, 0.4	−2.9, 4E‐3	−5.4, 1E‐7	Systolic: 9.7, 5E‐21 Diastolic: 5.0, 8E‐7	13.5, 8E‐38	24.0, 9E‐97
Gender prediction AUC	0.93 (0.00)*	0.93 (0.00)	0.92 (−0.01)	0.89 (−0.04)	0.85 (−0.08)	0.76 (−0.17)

*Within parenthesis are the drop in AUC compared to the AUC before regressing out the confound.

The effect of number of components, a hyper‐parameter in the predictive model, was investigated and the results are illustrated in Supporting Information Figure 1. AUC was below 0.7 when only one component of the PLS regression was used. AUC quickly improved as more components were added and plateaued at around five components. Then from 5 to 20 components, AUC remained at around 0.88 and 0.93 for individual‐run and multi‐run predictions, respectively. We also note that for a particular number of components, classification performance for multi‐run methods exceeds that of single run performance.

Statistical significance of overall performance for gender classification was tested by 1,000 permutations. Results for the three multi‐run methods are shown in Figure 2. For all three schemes, as expected, null distributions of the AUC were centered around 0.5, indicating that performance of the classifier was no better than random guessing for the randomly permuted data sets in which the subject labels between predictors and responses were randomized. Not a single AUC value for permuted labels fell beyond the AUC obtained from real labels, and this demonstrates that the statistical significance of gender prediction is high ( $p<.001$).

Figure 2.

Permutation tests of AUC indices when multi‐run functional connectivity features are used for gender prediction. The histograms show the null distributions of AUC when gender labels were randomly permuted and the solid red line indicates the AUC obtained for the true gender labels [Color figure can be viewed at http://wileyonlinelibrary.com]

3.2. Important FC features in gender discrimination

As classification performance was higher for multi‐run methods, we illustrate important FC features only for multi‐run predictions. Distribution of FC with feature weights above a bootstrap ratio of 3 is provided in Figure 3. “Average FC” (Figure 3a) and “Concatenate TC” (Figure 3b) demonstrated both similar patterns and similar numbers of FC features above the threshold. For the “Concatenate FC” method (Figure 3c), because the number of features was $12720\hspace{0.17em}\times \hspace{0.17em}4$ (four for each FC), we averaged the bootstrap ratio of FC across the runs. For weights that are above 3, the number of features is much less for “Concatenate FC” compared to “Average FC” and “Concatenate TC.” Important FC features are widespread across the brain, however, after separating the 160 ROIs into 6 networks (as defined in the original paper of Dosenbach et al. 2010), the block representing intra‐network DMN FC features is prominent for all three methods.

Figure 3.

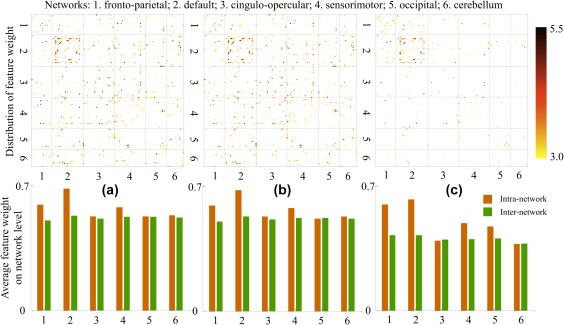
Pattern for feature importance. Top: distribution of FC with feature weights that are larger than 3 for the three multi‐run gender predictions. Numbers of surviving features are: 322 for (a) Average FC, 325 for (b) Concatenate TC, and 128 for (c) Concatenate FC. Black dashed lines in FC matrices separate the 160 ROIs into six functional modules. Bottom: for each network, average of all feature weights for intra‐network FC and inter‐network FC [Color figure can be viewed at http://wileyonlinelibrary.com]

In order to analyze patterns of feature contributions at the network level, and to see which networks contributed most to gender prediction, average intra‐network and inter‐network feature weights without thresholding were calculated for each of the six networks. Patterns from the three multi‐run predictions are very similar and differences between “Average FC” and “Concatenate TC” schemes are minimal. Across all three methods, inter‐network feature weights are close among the six networks and there are no cases where an inter‐network feature has an obviously higher weight than the intra‐network counterpart. Of the networks examined, the DMN has the highest intra‐network feature weight, followed by fronto‐parietal and sensorimotor networks. The other three networks (cingulo‐opercular, occipital, and cerebellum) have comparable weights between intra‐network and inter‐network features. These trends held across all three methods with the exception of the occipital network in “Concatenate FC” method has a higher weight than the cingulo‐opercular network and the cerebellum.

To check the robustness of identified important features across three multi‐run gender prediction methods, FC features for each method were thresholded at a feature weight of three and then binarized and combined across methods. From this we determined the overlap among the three methods. In the top of Figure 4 important FC features and their overlap across methods are identified by the color bars where grey stands for presence in one method, blue, green and purple are for presence in two methods, and red represents presence in all three methods. From Figure 4 few cases of “Average FC + Concatenate FC” and “Concatenate TC + Concatenate FC” were evident. Instead “Average FC + Concatenate TC” (blue, 200 features) and “All three methods” (red, 97 features) dominated, together constituting 79% of all 375 surviving features. 30% of all important features established by the three methods (29 out of 97) reside in the intra‐DMN block, making it a prominent block with red dots. The two lines circled indicate that FC between right fusiform/right vmPFC and other nodes in the DMN regularly have higher contributions in gender classification. Specific pairs of FC with high feature weights in the DMN, observed across all three methods, included connectivity between the right fusiform and inferior temporal and occipital cortex, intraparietal sulcus, posterior cingulate, precuneus, superior frontal, and ventromedial prefrontal cortex and connectivity between the right ventromedial prefrontal cortex, anterior prefrontal cortex, inferior temporal regions, occipital cortex, posterior cingulate, and precuneus. Three views of a brain map displaying the 97 FC features that were common across all three methods are shown in Figure 4. 78% (76 out of 97) of these FC features are between nodes in the first four networks (fronto‐parietal, default, cingulo‐opercular, and sensorimotor), which roughly correspond to the frontal, parietal, and temporal lobes of the brain.

Figure 4.

Robustness of important features. Top: FC features with weights larger than 3 for three multi‐run gender predictions are combined to explore the overlap of the three multi‐run methods. Within the DMN block, the fusiform and the ventromedial prefrontal cortex (vmPFC) demonstrated consistently higher feature weights (these nodes are circled in black). Bottom: Brain maps depicting FC features that are important for gender prediction common across the three multi‐run methods. ROI spheres are color‐coded by network [Color figure can be viewed at http://wileyonlinelibrary.com]

3.3. Gender prediction versus brain volume prediction

Brain volume is one variable demonstrating a significant gender difference. In our study, we also implemented brain volume (gray matter + white matter + cerebrospinal fluid) prediction. Using the same scheme as in predicting gender (10‐fold cross‐validation and 10 components in PLS regression), all three multi‐run methods achieved high correlations between predicted volumes and actual volumes (0.675, 0.678, and 0.675 for 820 subjects). In order to show that gender prediction and brain volume prediction are different (or say that the significant gender difference in brain volume is not dominating in gender prediction), we look at the important features in both gender and brain volume predictions and examine to what extent these features overlap. Figure 5 illustrates the quantitative results for the ratio of overlapping and unique features. At three different levels of threshold, the number of features which are both important for gender and brain volume predictions is small compared to the unique features for either volume or gender prediction. Although the percentage of overlapping features increases as the threshold decreases, it is at most less than 20%.

Figure 5.

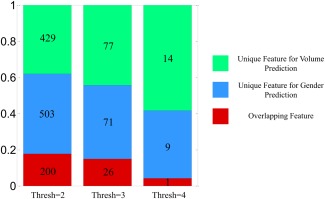
Overlap between important features of gender prediction and brain volume prediction. Important features are defined by combining features with absolute bootstrap ratios above the threshold and across three multi‐run methods. For one specific threshold, those features are divided into three categories: unique feature for volume prediction (green), unique feature for gender prediction (blue), and overlapping feature for both predictions (red). The numbers of corresponding features are labeled in the bar plot and fractions are indicated in the y‐axis. Results for three levels of threshold are shown [Color figure can be viewed at http://wileyonlinelibrary.com]

The distribution of important features for both predictions when the threshold is three is shown in Figure 6. Red dots which represent the overlapping features are scattered across the brain and do not have a clear pattern. The top 20 most important features for gender and brain volume predictions are listed in Table 4. Two common FC features present in both predictions are highlighted.

Figure 6.

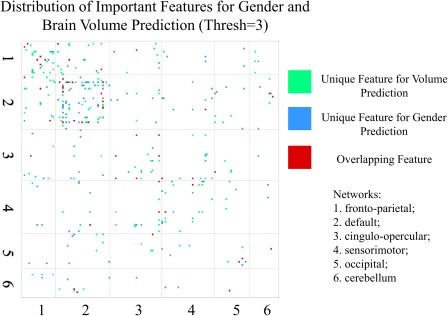
Distribution of important features for gender and brain volume predictions in the $160\hspace{0.17em}\times \hspace{0.17em}160$ square matrix (for the threshold of three, correspond to the middle bar shown in Figure 5). Three types of features are labeled as dots with different colors (154 green dots, 142 blue dots, and 52 red dots). 1–6 represent the six network modules [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 4.

Top 20 FC features (with the highest absolute bootstrap ratios) for gender and brain Volume predictions

For Gender prediction	For Brain volume prediction
Precuneus (DE)—temporal (SE)	Occipital (DE)—med‐cerebellum (CE)
Post‐cingulate (DE)—sup‐frontal (DE)	dlPFC (FP)—vent‐aPFC (FP)
Fusiform (DE)—inf‐temporal (DE)	vFC (CO)—precentral‐gyrus (SE)
Occipital (DE)—thalamus (CO)	Post‐cingulate (DE)—vmPFC (DE)
mFC (CO)—thalamus (CO)	Occipital (OC)—post‐occipital (OC)
IPS (DE)—mPFC (DE)	Angular‐gyrus (DE)—fusiform (DE)
IPL (FP)—mid‐insula (SE)	vPFC (FP)—fusiform (DE)
Occipital (DE)—med‐cerebellum (CE)	Thalamus (CO)—occipital (OC)
vmPFC (DE)—vFC (CO)	Precuneus (DE)—temporal (SE)
Fusiform (DE)—post‐cingulate (DE)	Precuneus (DE)—occipital (OC)
Fusiform (DE)—sup‐frontal (DE)	Thalamus (CO)—thalamus (CO)
Occipital (OC)—inf‐cerebellum (CE)	Post‐cingulate (DE)—med‐cerebellum (CE)
IPS (FP)—inf‐temporal (DE)	Fusiform (DE)—vmPFC (DE)
Post‐cingulate (DE)—vmPFC (DE)	vlPFC (FP)—fusiform (CO)
vmPFC (DE)—post‐occipital (OC)	vFC (CO) — precentral‐gyrus (SE)
vlPFC (DE)—med‐cerebellum (CE)	Angular‐gyrus (DE)—med‐cerebellum (CE)
Angular‐gyrus (DE)—fusiform (DE)	Occipital (DE)—vlPFC (DE)
dFC (SE)—SMA (SE)	Thalamus (CO)—occipital (OC)
Thalamus (CO)—occipital (OC)	Precentral‐gyrus (SE)—SMA (SE)
IPL (FP)—temporal (SE)	dlPFC (FP)—vlPFC (FP)

Note. Each row represents an FC between two ROIs. FC features are ordered (high to low) based on the average absolute bootstrap ratio across three multi‐run methods. FC features that are common between gender prediction and brain volume prediction are highlighted in bold font. The network to which the ROI belongs to is presented in parenthesis.

Network acronym: FP = fronto‐parietal; DE = default; CO = cingulo‐opercular; SE = sensorimotor; OC = occipital; CE = cerebellum

4. DISCUSSIONS

4.1. Gender prediction performance and potential confounds

For the HCP rfMRI data but with a smaller number of subjects, our previous study (Zhang et al. 2016) showed that even for FC with the most significant gender effect the FC values were on a spectrum and there was a large overlap between histograms for males and females. This result indicated that it is difficult to achieve a high gender classification accuracy by looking at a single FC feature. In this study we applied PLS regression to learn the weighting or the contribution of the original FC features and we made a combination of all FC features to derive a new jointly informative FC feature for gender prediction. This multivariate approach allowed for a robust classification of gender using rfMRI. For four individual runs of rfMRI scans, each of which was 15 min in duration, we achieved a consistent classification accuracy of 80% and an AUC of 0.88. Given that the four scans were collected on 2 different days, the consistency of prediction performance reflects the reproducibility of rfMRI data and resulting FC analyses. Experiments with three different ways of combining rfMRI data across four single runs observed an increased AUC from 0.88 to 0.93 and an increased classification accuracy from 80% to 85% for the default threshold (Table 2). Results of permutation tests (Figure 2), in which correspondence between FC features and gender labels were permuted, demonstrate the significant associations between FC and gender and thus enable successful gender prediction. While high prediction accuracies were achieved by single runs of rfMRI, the integration of FC across multiple runs further improved performance. This is explained by the incorporation of an additional “averaging” step, by either averaging FC across runs or calculating FC from concatenated time series of runs, to facilitate noise removal and better characterization of the “true” underlying FC patterns. For the “Concatenate FC” scheme, the number of predictors was quadrupled through the incorporation of four runs into the prediction procedure. Regardless of the method, incorporating multiple runs has been shown to provide more stable connectivity estimates (Glasser et al. 2016). Another recent study (Laumann et al. 2015) reports that highly reliable correlation estimates require considerable data. Therefore, in summary, combination of rfMRI data from multiple runs enables more stable and reliable FC patterns to be characterized. This more precise delineation of individual FC traits, in turn, empowers higher gender classification accuracy.

We explored the potential confounds that may affect the gender prediction performance. In Table 3, for the frame displacement and handedness which demonstrated no or weak gender difference, regressing them out from the FC features had little effect on the gender prediction AUC. However, as the gender difference of a confound became more significant, a higher reduction in the gender prediction performance was noted. This is reasonable and is expected. As the aim of this study is to predict gender, regressing out a confound that is highly correlated with the gender variable from every single FC feature can remove gender specific information from the predictors, and therefore, forcing the prediction performance to be weaker. However, even after regressing out the confounds, a high gender prediction accuracy could still be achieved (80% for regressing out blood pressure, 78% for regressing out weight and 70% for regressing out brain volume), illustrating the robust associations between FC features and gender. For brain volume, which demonstrated the most significant gender difference, we implemented the brain volume prediction algorithm using the same scheme as in gender prediction. Evident correlations were achieved between predicted and actual brain volumes. Different FC feature patterns across gender and brain volume predictions (Figures 5 and 6 and Table 4) demonstrate the distinction between these two predictions, and therefore, reduce the concern of confounding effect of brain volume in gender prediction.

4.2. Effect of implementation schemes on results

The three schemes implemented for multi‐run gender predictions achieved accuracies with only marginal differences. Moreover, two of the methods (“Average FC” and “Concatenate TC”) achieved very similar results with regard to feature weights (Figure 3). These methods represent two ways of deriving FC features utilizing separate scans. For the “Concatenate FC” method, there were four features corresponding to each FC. The effect of one FC was distributed across four similar features and this may explain why it generated less important features (for the same threshold compared to the other two methods). Except for this difference, the three ways of combining rfMRI data from multiple runs demonstrated consistent findings regarding the pattern of FC feature weights. The observation that 79% of important features were either identified by the first two methods or all three methods (Figure 4) demonstrates the robustness of the FC feature importance found in this study.

4.3. Important features for gender discrimination

In this study, we found that components of the DMN exhibited the greatest FC feature weight across all methods (Figure 3). In the top 20 predictive FC features for gender prediction (see Table 4), seven are within the default mode network. Another seven FC features involve a DMN ROI and the other six FC features were distributed between the other five networks. The DMN has been shown to be related to many different functions such as theory of mind (Spreng & Grady 2010), social cognition (Mars et al. 2012), and episodic memory (Sestieri et al. 2011). Previous research has reported conflicting findings regarding gender differences in the DMN with one study reporting females exhibit stronger FC in posterior cingulate and precuneus regions as well as medial prefrontal cortex (Bluhm et al. 2008) and others reporting no gender differences within the DMN (Weissman‐Fogel et al. 2010).

Within the DMN we observed large FC feature weights which were consistent across all three methods (Figure 4) in the right fusiform gyrus and right ventromedial prefrontal cortex (VMPFC). The connectivity pairs in these regions included connectivity between the right fusiform and inferior temporal and occipital cortex, intraparietal sulcus, posterior cingulate, precuneus, superior frontal, and ventromedial prefrontal cortex and connectivity between the right ventromedial prefrontal cortex, anterior prefrontal cortex, inferior temporal regions, occipital cortex, posterior cingulate, and precuneus. The fusiform gyrus is located in the inferior temporal lobe and contains the fusiform face area which is responsible for face processing (Schultz et al. 2003).

Previous work has shown that women and men exhibit differences in their ability to remember faces with women often outperforming men (Herlitz & Lovén 2013). Additionally, the lateralization in this region has also been shown to differ based on gender; men exhibit more rightward lateralized face processing while women exhibit more bilateral function (Proverbio et al. 2006). In the VMPFC it has been reported that men and women exhibit differences in lateralization as well with men exhibiting social, emotional, and decision making deficits following lesions in the right VMPFC but not when the left VMPFC was involved. The opposite finding was found in women (Tranel et al. 2005). Taken together, previous research supports the findings of this article. Connectivity measures with high feature weights in these regions may be important for understanding the aforementioned gender differences in cognition and social cognitive abilities which have been reported previously. Finally, the fusiform gyrus has been implicated in autism spectrum disorder (ASD) (Trontel et al. 2013), which has a 4:1 propensity towards males. Applying the approaches described this article in children and individuals with ASD will help determine if these gender differences are present early in life, prior to puberty, and whether the FC differences, especially in inferior temporal and DMN regions, also extend to those with ASD.

While the DMN demonstrated a prominent role in gender prediction, there were also other networks that reported higher contributions. It is hard to distinguish the brain regions with more important FC features for gender prediction based on the distribution of feature weight plot (Figure 3) as the significant FC features were scattered across the brain. These widespread distribution of FC features were also found in our previous study for those with highly significant gender differences (Zhang et al. 2016). However, the bar plots for the average feature weight on the network level (Figure 3) identified two other sets of intra‐network FC features: frontal‐parietal and sensorimotor. These two networks demonstrated higher feature weights for gender classification. In our previous work Zhang et al. (2016), most FCs within the frontal and parietal lobes were significantly different between males and females. Presence of higher average feature weights in the frontal‐parietal network may demonstrate a gender difference related to aspects of attention such as error adaptation (Dosenbach et al. 2007), working memory (Hill et al. 2014) and attentional control (Scolari et al. 2015). As for the sensorimotor network which is responsible for integrating sensory and motor information, reliable gender difference with increased FC has been previously reported (FC in male > female) (Weis et al. 2017). Well established gender differences in spatial processing and sensorimotor speed (Ingalhalikar et al. 2014; Linn & Petersen 1985) may be associated with the FC differences in the sensorimotor network. Moreover, lower performance in spatial processing in patients with ASD have also been linked to the sensorimotor regions (Silk et al. 2006) and thus gender differences within the sensorimotor network may be associated with gender differences in the prevalence of ASD.

5. LIMITATIONS

In this work, FC between ROIs was computed using Pearson's correlation between the average time series of all voxels that fall within the ROI. Data indicates that time series within an ROI can be heterogeneous and taking the average time series can cancel out important information. Further, the Pearson's correlation is a second‐order statistic and can miss higher‐order interactions. In this work, we have not addressed the issues of heterogeneity and higher‐order interactions and we intend to address this limitation in future work. In this work we show that FC, as defined by Pearson's correlation, a reliable second order statistic, between the average time series of the ROIs can predict gender at a high accuracy.

6. CONCLUSIONS

Utilizing partial least squares regression techniques, gender classification based on rfMRI FC data was implemented with a high classification accuracy around 80% for individual runs. By combining multiple runs of rfMRI the classification accuracy increased to 85%. Further, we report that intra‐network connectivity in the DMN exhibited the greatest importance for gender discrimination. In particular, FC pairs within the DMN containing the right fusiform gyrus and right VMPFC exhibited large FC feature weights. Permutation tests, consistent findings across different implementation schemes, and correspondence between FC feature weights and previous reports of gender differences, demonstrate the reliability of gender prediction using rfMRI FC. These findings hold important implications for future studies. A complete characterization of gender differences is essential to accurately characterize cognitive and behavioral phenotypes and their neural substrates. This study provides further support for the existence of gender differences in brain connectivity and thus points to the need for studies examining brain structure and function to carefully account for gender.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supplementary Figure 1

Supplementary Table 1

Supplementary Table 2

Supplementary Table 3

Supplementary Material

Zhang C, Dougherty CC, Baum SA, White T, Michael AM. Functional connectivity predicts gender: Evidence for gender differences in resting brain connectivity. Hum Brain Mapp. 2018;39:1765–1776. 10.1002/hbm.23950