BrainMap VBM: An environment for structural meta‐analysis

Abstract

The BrainMap database is a community resource that curates peer‐reviewed, coordinate‐based human neuroimaging literature. By pairing the results of neuroimaging studies with their relevant meta‐data, BrainMap facilitates coordinate‐based meta‐analysis (CBMA) of the neuroimaging literature en masse or at the level of experimental paradigm, clinical disease, or anatomic location. Initially dedicated to the functional, task‐activation literature, BrainMap is now expanding to include voxel‐based morphometry (VBM) studies in a separate sector, titled: BrainMap VBM. VBM is a whole‐brain, voxel‐wise method that measures significant structural differences between or within groups which are reported as standardized, peak x–y–z coordinates. Here we describe BrainMap VBM, including the meta‐data structure, current data volume, and automated reverse inference functions (region‐to‐disease profile) of this new community resource. CBMA offers a robust methodology for retaining true‐positive and excluding false‐positive findings across studies in the VBM literature. As with BrainMap's functional database, BrainMap VBM may be synthesized en masse or at the level of clinical disease or anatomic location. As a use‐case scenario for BrainMap VBM, we illustrate a trans‐diagnostic data‐mining procedure wherein we explore the underlying network structure of 2,002 experiments representing over 53,000 subjects through independent components analysis (ICA). To reduce data‐redundancy effects inherent to any database, we demonstrate two data‐filtering approaches that proved helpful to ICA. Finally, we apply hierarchical clustering analysis (HCA) to measure network‐ and disease‐specificity. This procedure distinguished psychiatric from neurological diseases. We invite the neuroscientific community to further exploit BrainMap VBM with other modeling approaches.

1. INTRODUCTION

The BrainMap project (http://www.brainmap.org) began in 1987 and, since its inception, has provided a community accessible environment that allows the x–y–z coordinates and accompanying meta‐data reported in whole‐brain imaging experiments to be compiled and analyzed (Fox & Lancaster, 1994; Gibbons, 1992). Task‐activation experiments using functional magnetic resonance imaging (fMRI) populate most of the database, but other task‐activation modalities include positron emission tomography (PET) and single‐photon emission computed tomography (SPECT). Here, a separate sector of BrainMap is introduced for structural MRI studies that employ voxel‐based morphometry (VBM), titled: BrainMap VBM. VBM is a mass‐univariate, whole‐brain analysis of local grey‐ or white‐matter tissue volume across or within subject groups, where locations of statistical significance are most often reported as x–y–z coordinates (cluster center‐of‐mass or peak voxel) in a standardized coordinate space (Talairach or MNI) (Ashburner & Friston, 2000). To date, VBM has amassed an extensive literature (4,237 publications in PubMed) that can become more scientifically accessible with the resource we present here. In this work, we comprehensively describe BrainMap VBM's novel design, current data volume, quality assurance strategies, and multi‐purpose utility (e.g., region‐to‐disease inference). The unique capacity of this new community resource is then illustrated by employing independent components analysis (ICA)—an exploratory, multivariate strategy that has not previously been applied to VBM coordinates.

Coordinate‐based meta‐analysis (CBMA) has considerably evolved over three decades to provide a powerful family of methods for mining and synthesizing the human neuroscience imaging literature (for review, see Barron & Fox, 2015; Fox, Lancaster, Laird, & Eickhoff, 2014). BrainMap offers a software suite of cross‐platform Java applications for data entry (Scribe), filtered data retrieval (Sleuth) and statistical analysis (GingerALE) (Fox & Lancaster, 2002; Fox et al., 2014). The most common BrainMap application is assessing the convergence of results in conceptually related experiments that evaluate brain function at the level of task paradigm (e.g., Stroop tasks) or that use task‐based activations to contrast clinical patients with healthy controls (e.g., Alzheimer's disease vs. healthy controls assessed using the Stroop task). Numerous univariate methods exist for this purpose, including activation likelihood estimation (ALE; performed with GingerALE software), multi‐level kernel density analysis (MKDA) and signed differential mapping (SDM) (Eickhoff et al., 2016; Radua & Mataix‐Cols, 2012; Turkeltaub, Eden, Jones, & Zeffiro, 2002; Wager, Lindquist, Nichols, Kober, & Van Snellenberg, 2009). Each methodology is similar but conceptually distinct, and data compilation/analysis is assisted with (while not explicitly requiring) BrainMap's database structure. Even though these univariate tools were developed for use in the functional literature, multiple studies have demonstrated their clear applicability with structural MRI studies; ALE, for example, has been redefined as “anatomical likelihood estimation” in this context (Barron, Fox, Laird, Robinson, & Fox, 2013; Fornito, Yücel, Patti, Wood, & Pantelis, 2009; Glahn et al., 2008).

ALE, MKDA, and SDM each address a salient topic in the current neuroimaging environment: reproducibility (Mueller, Lepsien, Möller, & Lohmann, 2017; Poldrack et al., 2017; Roiser et al., 2016). In a highly publicized study, Eklund, Nichols, and Knutsson (2016) demonstrated inflated false‐positive rates in massive null‐fMRI datasets due to faulty cluster‐based thresholding by popular software packages. They concluded that cluster‐based inference is more sensitive to statistical assumptions (e.g., “uniform smoothness,” where local variations in image smoothness are not accounted for) which is corroborated by several VBM studies (Salmond et al., 2002; Scarpazza, Sartori, De Simone, & Mechelli, 2013; Scarpazza, Tognin, Frisciata, Sartori, & Mechelli, 2015; Silver, Montana, & Nichols, 2011). Silver et al. (2011) also reported inflated false‐positives in a VBM null‐dataset when applying lower cluster‐forming thresholds (α_c = 0.01, 0.05) and smaller smoothing kernels (6 mm). Sample size also contributes to varying VBM results, as larger sample sizes introduce more power and higher sensitivity which reduces type‐II error. Fusar Poli et al. (2014) analyzed 324 VBM studies and indeed found a positive, but weak relationship between number of foci reported and sample size. They suggested that reporting biases are more prevalent in smaller studies, which would account for their result. Along with the revaluation of cluster‐based statistical methodology, Eklund et al. (2016) recognized that “meta‐analysis can play an important role in teasing apart false‐positive findings from consistent results.”

Meta‐analytic connectivity has also been examined with the BrainMap functional database through a variety of multivariate approaches. Such applications include meta‐analytic connectivity modeling (MACM), which identifies the co‐activation pattern of an a priori region of interest (ROI; or set of a priori ROIs) by referencing BrainMap's diverse task‐activation collection (Robinson, Laird, Glahn, Lovallo, & Fox, 2010). An extension of this principle has been used for connectivity‐based parcellation (CBP) (Eickhoff, Thirion, Varoquaux, & Bzdok, 2015), where one ROI is clustered into subregions of discrete functional anatomy based on co‐activation networks. Some CBP investigations with BrainMap include the amygdala (Bzdok et al., 2013) and the thalamic pulvinar (Barron, Eickhoff, Clos, & Fox, 2015), which were validated cytoarchitectonically. An unexpected dividend of BrainMap's content and meta‐data structure has been considering the functional database en masse (i.e., with sparse filtrations in analysis regarding predefined experimental categories or spatially confined ROIs). Using graph theory, Crossley et al. (2013) compared the frequency at which each pair of 638 ROIs across the whole‐brain was co‐activated by multiple tasks in BrainMap and found occipital, central, and default‐mode modules that were behaviorally specialized as well as rich clubs that were diversely co‐activated by tasks requiring both action and cognition (van den Heuvel & Sporns, 2011). In a particularly innovative strategy, ICA was extended to the functional sector of the BrainMap database by Smith et al. (2009). Treating each smoothed coordinate (modeled activation; MA) image per experiment as an effective “time‐point” in arbitrary order, they established 10 canonical networks that showed correspondence both during task and resting‐state, and attributed behavioral characteristics to each using BrainMap meta‐data. We expect many of these analytic strategies to translate to BrainMap VBM. Some initial, large‐scale investigations of BrainMap VBM include ALE across six psychiatric disorders (Goodkind et al., 2015) and ALE across more than 25 brain disorders (Crossley et al., 2014).

Structural covariance (SCov), an analog to functional covariance, is a field of research that BrainMap VBM can offer an equivalent potential of meta‐analytic insight. SCov is defined as inter‐individual differences in a regional brain structure (cortical thickness or grey matter density) covarying with inter‐individual differences in other brain regions (Alexander‐Bloch, Giedd, & Bullmore, 2013). Accumulating research demonstrates that lifespan changes to brain structures do not occur independently but follow multi‐regional, coherent patterns that show unique chronological trajectories of integrity and organization (Alexander‐Bloch et al., 2013; Li, Pu, Fan, Niu, Li, & Li, 2013; Váša et al., 2017; Zhu et al., 2012; Zielinski, Gennatas, Zhou, & Seeley, 2010). SCov has proven to be a sensitive method in studying disease, and alterations exist in a range of disorders that are neurodegenerative (Coppen, van der Grond, Hafkemeijer, Rombouts, & Roos, 2016; Minkova et al., 2016), psychiatric (Palaniyappan et al., 2015; Wu et al., 2017; Xu, Groth, Pearlson, Schretlen, & Calhoun, 2009), developmental (Bethlehem, Romero‐Garcia, Mak, Bullmore, & Baron‐Cohen, 2017; Dziobek, Bahnemann, Convit, & Heekeren, 2010), systemic (e.g., cardiovascular risk factors) (Kharabian Masouleh et al., 2017), and even chemotherapy‐related (i.e., cognitive impairment) (Hosseini, Koovakkattu, & Kesler, 2012). A seed‐to‐whole‐brain and seed‐to‐target transdiagnostic SCov application using BrainMap VBM was recently published by Kotkowski, Price, Mickle Fox, Vanasse, and Fox (2018).

As the primary motivation for this work is exhibiting the contents and utility of BrainMap VBM, we chose independent components analysis (ICA) as well‐suited toward this end. ICA is a whole‐brain, voxel‐wise network analysis technique that decomposes spatial maps according to maximal statistical independence (Beckmann & Smith, 2004). Unlike general linear modeling (GLM) and similar methodologies, ICA doesn't require a user‐specified reference function (Mckeown et al., 1998). Here, ICA's exploratory nature is fully leveraged with BrainMap VBM in that many diseases (43) showing grey matter morphology are processed together in a pseudo time‐series for pattern identification. ICA has shown success in identifying SCov components from T1, intersubject covariance data in healthy and diseased populations (Coppen et al., 2016; Eckert, 2010; Hafkemeijer et al., 2014; Kharabian Masouleh et al., 2017; Segall et al., 2012; Xu et al., 2009). In this study, we demonstrate that ICA of BrainMap VBM coordinates—blind to any diagnostic information—can extract spatially independent components of inter‐experiment SCov. In addition, these components comprehensively inform disease specificity through reverse inference (i.e., region‐to‐disease) methodology presented here. While ICA of functional, meta‐analytic coordinates has a strong literature (Laird et al., 2011; Ray et al., 2013; Smith et al., 2009), it has not previously been applied to VBM coordinates.

This study (a) presents the meta‐data structure, existing data volume, automated data‐interpretation functions, and multi‐purpose utility of BrainMap VBM; (b) reports 21 SCov networks computed by applying ICA to coordinates representing 30,218 diagnosed subjects (and 23,007 healthy control subjects) across 43 different diagnoses; (c) assesses an automated and semi‐automated approach to detection and elimination of data‐redundancy; and (d) applies hierarchal clustering analysis (HCA) to investigate the organizational architecture of SCov networks with respect to disease‐ and network‐specificity.

2. METHODS

2.1. BrainMap VBM meta‐data structure and coding

Basic criteria for BrainMap eligibility is whole‐brain analysis (i.e., not region‐of‐interest methods), coordinate results reported in standardized space, and publication in an English‐language journal. The BrainMap VBM hierarchical database design can be separated into Paper‐level, Experiment‐level, and Location‐level tiers. Paper‐level descriptors include—but are not limited to—basic citation information such as the journal, authors, keywords, and institution; an abstract summarizing the paper; each subject‐groups’ size, average age, gender ratio, specific inclusion–exclusion criteria, and relevant diagnosis (or diagnoses) according to the International Classification of Disease Codes (ICD‐10) managed by the World Health Organization per subject‐group; any External Assessments that were used to evaluate subjects (e.g., Clinician Administered PTSD Scale, Body‐Mass Index, etc.); Session information including the number of scans and the time interval apart (e.g., pre‐ vs. post‐treatment, 3 months); the imaging modality used (e.g., 3T MRI) along with software packages, pre‐processing protocol, and standardized space applied (i.e., MNI or Talairach); and a feedback field for any questions or comments for the BrainMap reviewing team.

In BrainMap, an Experiment is defined operationally by the production of a statistical parametric image (SPI) (Fox et al., 2005). A Paper usually reports multiple Experiments. Each Experiment is generated based on criteria defining specific subsets of the subject‐groups, Sessions, External Assessments (e.g., symptom score correlation), or statistical protocol—which Experiment‐level taxonomy accounts for. Once a paper is coded via the Scribe software and submitted, it is verified for quality assurance by a taxonomy expert who has had extensive training. In addition, the user‐interface that is implemented to code papers, Scribe, is regularly evaluated and updated to meet the needs of a burgeoning neuroimaging field. This includes additional meta‐data fields for proper characterization, for example, new software packages for statistical analysis. After Papers are submitted with Scribe, Sleuth is used to search and filter through the BrainMap VBM database via a Workspace, demonstrated in Figure 1.

Figure 1.

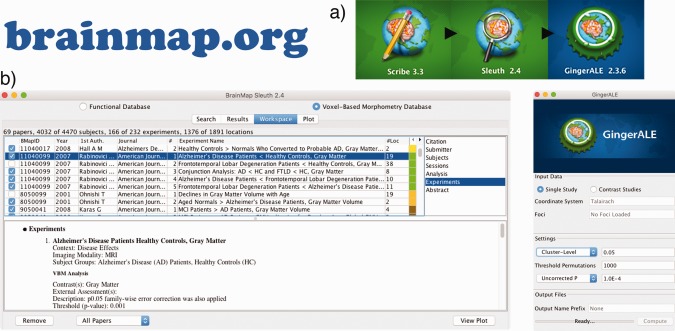
Structure and workflow of BrainMap VBM. (a) BrainMap VBM meta‐analysis workflow of coding papers with Scribe, compiling and filtering a workspace with Sleuth, and performing statistical analysis with GingerALE—each cross‐platform Java application is available at http://www.brainmap.org/software. (b) Screenshots of the Sleuth and GingerALE software are displayed to demonstrate their ease‐of‐use

2.2. Independent component analysis

To investigate transdiagnostic SCov, two filters were applied to the BrainMap VBM database in preparation for ICA; only (a) “Grey Matter” Contrast and (b) “Disease” Context experiments were included (Figure 2). These criteria encompassed most of the VBM database (Table 1). The established method of Independent Component Analysis in BrainMap meta‐data is shown in the Experiment ICA, (Figure 3a) (Laird et al., 2011; Ray et al., 2013; Smith et al., 2009). Peak coordinates in the VBM BrainMap database were smoothed using a Gaussian distribution (FWHM = 12 mm) for “Modeled Activation” (MA) images with 2 × 2 × 2‐mm resolution. ICA was then applied to the 2‐D (vectorized voxel values × Experiment‐ID) dataset using MELODIC (multivariate exploratory linear optimized decomposition into independent components; Beckmann, DeLuca, Devlin, & Smith, 2005) in FSL (FMRIB Software Library; Smith et al., 2004; Woolrich et al., 2009). Due to the ICA algorithm optimizing for non‐Gaussianity in the spatial domain, the temporal domain remains unconstraint (Comon, 1994). Therefore, MA images (which correspond to pseudo time‐points in the present analysis) can be arbitrarily ordered.

Figure 2.

Study selection. Flowchart for selecting studies for transdiagnostic ICA analyses

Table 1.

Data volume of BrainMap VBM

BrainMap context (contrast)	Papers	Experiments	Coordinates
*Disease (grey matter)	763	2,171	15,876
Disease (white matter)	203	448	2,644
Disease (CSF)	10	13	82
Normal mapping	99	243	1,682
Aging	60	129	1,304
Genetic	33	114	643
Gender	22	61	366
Treatment	18	58	449
Learning	9	15	49
Language	4	9	22
Handedness	2	9	81

Note. Data volume of BrainMap VBM sector at time of analysis by distinct Contexts. Contrasts are also designated for the Disease Context. *Only Disease Context/Grey Matter Contrast experiments were included for ICA analysis.

Figure 3.

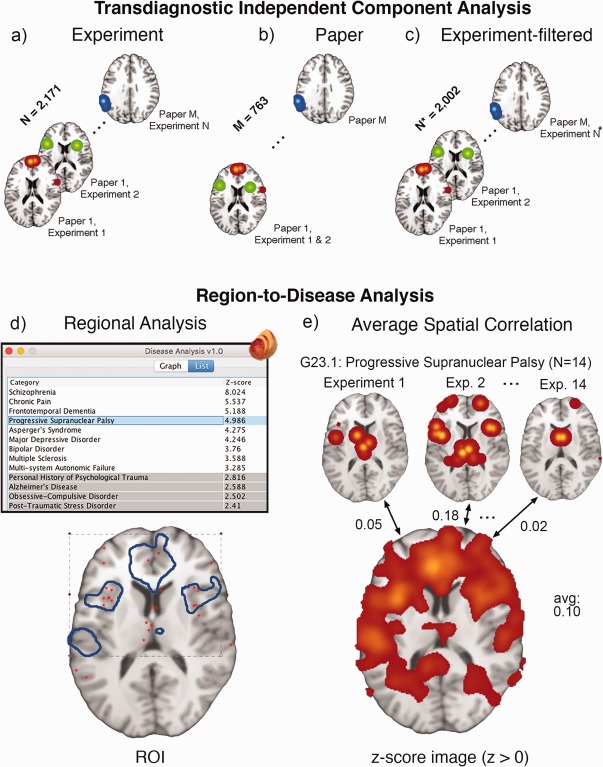
Transdiagnostic ICA and reverse inference. (a) ICA input of BrainMap coordinates per experiment, along with the data‐filtering approaches of (b) Paper ICA and (c) Experiment‐filtered ICA to reduce data‐redundancy influence for large‐scale analysis. Each image shows smoothed VBM coordinates corresponding to an effective “time point” (in arbitrary order) for ICA. The bottom panel refers to separate reverse inference methods of associating an a priori (d) binary mask or (e) positive z‐score image to a disease using BrainMap's extracted coordinate data. G23.1: Progressive Supranuclear Palsy is used as an example—it contains 14 experiments in the database. The Regional Disease Analysis tool is freely available as a plugin at http://www.ric.uthscsa.edu/mango/download

In the current literature of ICA in T1‐weighted data, the dimensionality has ranged considerably across studies. Values chosen include 7 (Eckert, 2010), 9 (Hafkemeijer et al., 2014; Xu et al., 2009), 10 (Coppen et al., 2016), and 75 (Segall et al., 2012). We selected a dimensionality of 20.

Error and artifact naturally occur in massive meta‐analytic datasets like BrainMap, and can stem from experiment mischaracterization, incorrect coordinate documentation, or—of which we address here—within‐group effects. Within‐group effects (i.e., “data‐redundancy”, terms we use here interchangeably) impact the results of ALE and other CBMA methods when groups of subjects with multiple experiments (in a single paper) influence results more than subject groups with only one experiment (Turkeltaub et al., 2011). Incidental findings from the Experiment ICA demonstrated coordinate redundancy in two separate papers (Supporting Information, Figure 1), which spurred two approaches in filtering the database for en masse analysis. The modified Paper ICA was performed by grouping the MA images by Paper‐level to create the 2‐D dataset (vectorized voxel values × Paper‐ID) resulting in M = 763 “time‐points” (Figure 3b). This approach was an expedient solution from a programming perspective. However, collapsing the dataset this way reduced our data volume/statistical power and in some cases combined multiple biologically distinct statistical contrasts. We therefore investigated a separate strategy, the Experiment‐filtered ICA (Figure 3c). This required the removal of experiments that were data‐redundant within a paper. To identify these outlier papers, we queried the database for papers that reported the same x–y–z coordinate in >2 experiments. A total of 28 papers were identified. This represented 4% of publications in the VBM database. Filter criteria in removing experiments are contained in the Supporting Information. In a supplementary analysis, we analyzed the strongest experiment/paper contributors to each component for the three ICA methodologies (Experiment ICA, Experiment‐filtered ICA, and Paper ICA). The MA images that spatially correlated the highest to each component (independent of ICD‐10 category) were ordered (30) and plotted.

2.3. Region‐to‐disease association

Two reverse inference methods were employed to measure the association, that is, weighting, of a given ROI or z‐score image to distinct ICD‐10 Diagnoses, that is, P (Diagnosis | Region). The regional analysis method (Figure 3d), extended from a region‐to‐function study by Lancaster et al. (2012), extracts coordinates for every ICD‐10 Diagnosis separately; the fraction of coordinates falling within the specified ROI was computed and compared with the fraction expected if coordinates of the diagnosis were not clustered, that is, uniformly distributed across the brain. A significant disease association was determined if this discrepancy was large enough, producing a z‐score ≥3.0 when corrected for multiple comparisons. Z‐score calculation is provided below:

$$z=\hspace{0.17em}\frac{p_0-p_{\mathrm{e}}}{{\left(\frac{p_0\left(1-p_0\right)+p_{\mathrm{e}}(1-p_{\mathrm{e}})}{N_{\mathrm{b}}}\right)}^{1/2}}$$

where observed probability (fraction of foci in ROI/outside of ROI) is $p_0$, expected probability (fraction ROI/whole‐brain volume) is $p_{\mathrm{e}}$, and number of total foci (i.e., across the whole‐brain) per distinct ICD‐10 is $N_{\mathrm{b}}$.

In a separate reverse inference method using spatial correlation (Figure 3e), we performed disease association measures using z‐score ICA component images, that is, not ROIs. MA experiment images from each ICD‐10 diagnosis were spatially correlated with z‐score component images and averaged. This averaged correlation value, ranging from −1 to 1, represented the strength of disease association by similar spatial smoothness modeled from coordinates. We confined our interest only in the positive values of the ICA components, masking components at z > 0 for spatial correlation. Because MA images only included positive values (i.e., modeled probabilities), negative z‐scores extracted from ICA only result from mathematical artifacts (Laird et al., 2011). For more information discussing the motivation of two reverse inference strategies, see Supporting Information.

2.4. Hierarchal clustering analysis

Hierarchal clustering analysis (HCA) was performed on the (21 × 43) data matrix of network‐disease loadings to identify clusters of components based on similar disease loading and, conversely, clusters of diseases according to their component loading. R Studio (http://www.r-project.org) was used for heatmap visualization and HCA analysis using the package gplots (v3.0.1). Pearson's correlation (1 − r) was used to calculate the “distance” metric. With the distance matrix, we employed an “average linkage” algorithm that calculated the average distance between elements of each cluster. A similar method was used by Laird et al. (2011) in their analyses of functional BrainMap ICA components. To identify an appropriate number of clusters (k) for HCA in both diseases and components, two separate statistical tests were applied to measure the “distinctness” of cluster groupings for every possible cluster size. These included the silhouette length (Rousseeuw, 1987) and the gap statistic (Tibshirani, Walther, & Hastie, 2001). An in‐depth discussion of both methodologies can be found by Charrad, Ghazzali, Boiteau, and Niknafs (2014).

2.4.1. Age‐related ALE

To better interpret the ICA components and their association with age, we utilized the full scope of BrainMap VBM beyond “Disease” Context. The database was queried for experiments in the “Age” Context. We further excluded positive associations (i.e., hypertrophy) and multiple experiments from the same sample of subjects. The final analysis included 43 experiments representing 3,684 healthy and diseased subjects. Significant clusters in the ALE were identified using a cluster‐level family‐wise error (cFWE) p = .05, and a cluster‐forming p = .001. Additionally, the unthresholded ALE image was spatially compared to the VBM ICA components. A spatial correlation was deemed significant according to the methodology explained by Smith et al. (2009).

2.5. Data and software sharing

All coordinate data used in this meta‐analysis were accessed through the BrainMap VBM database. For large‐scale investigations of BrainMap VBM^®—an electronic compilation and coding taxonomy protected by copyrights held by the University of Texas Board of Regents—a collaboration agreement is required. Because coordinates are not classified as human‐subject data, they are IRB exempt. ICA component visualization and download can be done online via http://www.brainmap.org/icns or http://www.anima.fz-juelich.de (Reid et al., 2016). The Regional Disease Analysis tool (v1.1) is freely available as a Mango plugin at http://www.ric.uthscsa.edu/mango/download. Code used for clustering analyses (Figure 5, Supporting Information, Figures 5 and 6) can be found from TV's github: https://github.com/tvanasse/Hierarchical_Clustering_VBM_ICA.

Figure 5.

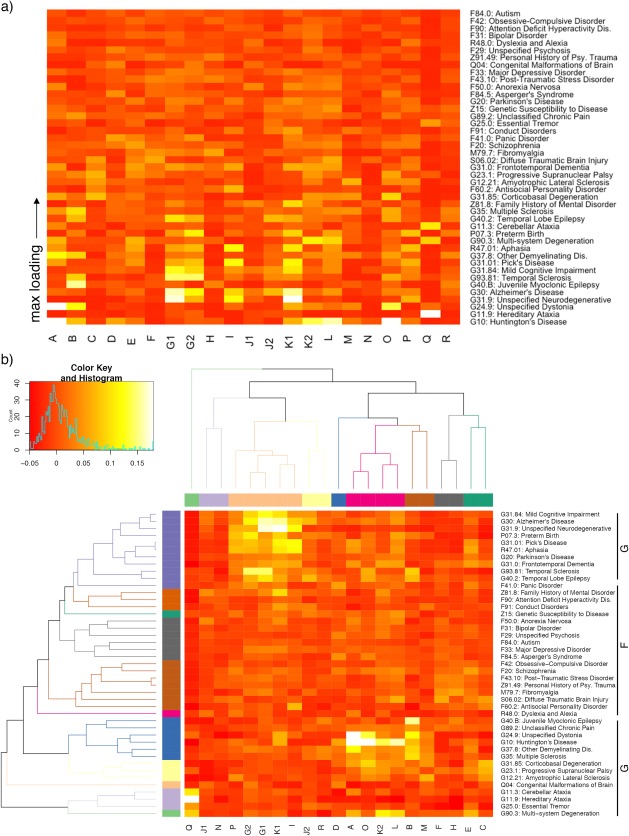
Heatmap of component and disease weighting. (a) Heatmap (before clustering) includes weighting of 43 International Classification of Disease (ICD‐10) codes with ≥10 experiments in BrainMap VBM (average spatial correlation, see Methods). Diseases are ordered bottom‐to‐top by max loading. (b) HCA orders x‐ and y‐axes by similarity between components according to disease weighting, and diseases according to component weighting. The labels “F” and “G” represent psychiatric and neurological ICD‐10 disease codes, respectively, which were clustered by the HCA analysis. Clustering was chosen at k = 9 and k = 11 for components and diseases, respectively

3. RESULTS

3.1. Data volume

The current data volume of the BrainMap VBM database is summarized in Table 1. Papers and experiments are sorted by the Context meta‐data field, and further separated by Contrast within the “Disease” Context only. Some experiments are co‐coded, that is, an experiment is labeled both “Genetic” and “Disease.” Experiments labeled in “Disease” Context comprise most of the database, with “Normal Mapping” and “Aging” also considerably contributing. A PubMed search of (“Voxel‐based Morphometry”) returned 4,237 publications, suggesting that BrainMap contains roughly 20% of the existing VBM literature. The number of experiments varied per ICD‐10 diagnosis (Supporting Information, Figure 4), with a range from 10 to 245 and a median of 20 experiments/ICD‐10 diagnosis. To determine the influence that diseases with more experiments had, a linear regression of experiment count versus average cross correlation was performed. A significant association was found (p < .03), with a slope of 5.375 × 10⁻⁵/experiment.

3.2. Components

The Experiment‐filtered and Paper ICA showed largely similar results, with 14 anatomically matched (r > .4, avg. r = .61) transdiagnostic SCov components. These components are thresholded and displayed in Figure 4A–N, where overlap is colored yellow. In three of these networks the Experiment‐filtered ICA showed fractionation (G, J, K), that is, two components corresponded to one Paper ICA component, and overlap is shown in white. Four networks proved to be unique to their respective method (O – R). Both the Paper ICA and Experiment‐filtered ICA removed two artifacts produced by experiment redundancy caused by two papers (Supporting Information, Figure 1). The Experiment‐filtered ICA thus only extracted one artifact, which contained entirely white matter—an expected result because parts of standard space involving “very few nonzero values in the input data, the combination of demeaning (of what was originally positive or zero data) and the variance normalization of voxels’ time series leads to meaningless components” (Smith et al., 2009). The Paper ICA contained 4 artifact components; each artifact was anatomically diffuse with a low z‐score distribution. The Paper ICA showed the most explained variance at 22%, while the Experiment‐filtered ICA reported 17% explained variance (Supporting Information, Figure 3). Components are individually visualized with layouts in Supporting Information, Figures 7–10. A description of each component and its eight largest anatomical clusters are shown in Table 2. The strongest experiment/paper contributors are visualized as Scree Plots in Supporting Information, Figures 11–13 for every component.

Figure 4.

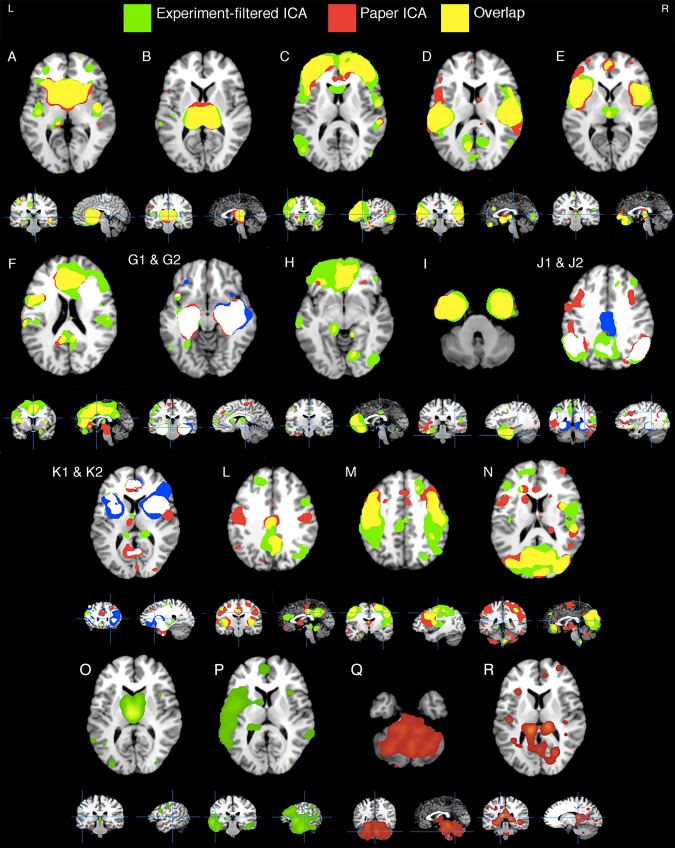
VBM ICA components. Fourteen (A–N) components that showed spatial similarity (r > .4) among the separate Experiment‐filtered ICA (green) and the Paper ICA (red) methodologies. Overlap between thresholded component maps is colored yellow, while white shows overlap between a single Paper ICA component (red) and two Experiment‐filtered ICA components (green and blue). Four nonsimilar components generated from both methods are shown in the bottom (O–R). Artifact components are not displayed

Table 2.

Anatomical clusters of 21 VBM ICA components

Talairach Daemon	Brodmann area	Size (cm3)	Max Z	x	y	z	Talairach Daemon	Brodmann area	Size (cm3)	Max Z	x	y	z
Component A							Component B
Caudate		59.4	35.4	8	12	6	Thalamus		35.3	41.1	8	−22	10
Insula	BA 13	5.0	7.9	42	−8	2	Hippocampus		2.8	7.2	32	−16	−14
Sup temporal gyrus	BA 38	2.7	6.3	32	18	−24	Putamen		1.8	6.0	−24	4	0
Postcentral gyrus	BA 2	2.4	5.9	−42	−26	48	Caudate head		0.9	7.1	12	18	2
Insula	BA 13	1.8	6.2	−44	−16	6	Insula	BA 13	0.8	5.3	−42	−20	12
Cingulate gyrus	BA 31	1.2	6.9	−10	−28	40	Pyramis		0.5	6.0	24	−74	−30
Mid frontal gyrus	BA 10	0.3	4.8	−34	40	18	Caudate		0.3	5.4	12	8	20
Sub‐gyral		0.3	4.6	−30	44	2	Mid temporal gyr	BA 21	0.2	4.6	−46	−2	−18
Component C							Component D
Mid frontal gyrus	BA 10	162.4	25.6	−26	52	20	Postcentral gyrus	BA 40	57.7	24.1	52	−24	18
Mid temporal gyr	BA 39	9.7	6.8	−50	−70	12	Transverse tem gyr	BA 41	37.3	20.4	−48	−20	14
Precentral gyrus	BA 6	6.3	7.7	54	−2	8	Anterior cingulate	BA 25	8.7	11.9	2	4	−6
Subcallosal gyrus	BA 34	3.5	7.5	−16	2	−12	Pos cingulate	BA 30	3.3	8.5	−10	−62	12
Thalamus		2.8	8.3	−14	−28	0	Mid occipital gyr	BA 19	2.7	7.7	−50	−60	−4
Postcentral gyrus	BA 2	1.5	6.6	48	−28	42	Med frontal gyrus	BA 9	2.5	9.0	−6	28	28
Mid temporal gyr	BA 21	1.1	6.5	−52	0	−12	Lingual gyrus	BA 18	2.3	7.4	0	−82	2
Declive		1.0	6.1	−24	−74	−12	Pos cingulate	BA 23	2.0	7.8	10	−58	14
Component E							Component F
Insula	BA 13	39.0	29.9	−40	16	0	Cingulate gyrus	BA 32	135.6	27.6	−4	30	28
Insula	BA 13	37.3	12.7	46	8	4	Inf frontal gyrus	BA 44	6.8	7.6	−48	6	22
Thalamus		2.6	8.5	2	−18	4	Transverse tem gyr	BA 41	6.0	7.3	−50	−20	12
Parahippocampus	BA 34	1.4	7.2	−20	−12	−14	Parahippocampus	BA 34	3.8	8.6	16	−8	−16
Precuneus	BA 7	0.8	5.3	12	−72	40	Postcentral gyrus	BA 40	2.0	6.3	52	−24	18
Precuneus	BA 19	0.5	5.2	−28	−74	34	Insula	BA 13	1.3	6.1	32	14	10
Med frontal gyrus	BA 6	0.2	4.8	−6	−26	58	Thalamus		1.0	5.4	6	−14	10
Parahippocampus	BA 27	0.1	4.7	26	−32	−2	Med frontal gyrus	BA 11	0.9	6.0	0	36	−16
Component G1							Component G2
Hippocampus		27.5	44.1	−26	−16	−14	Hippocampus		66.3	36.3	28	−14	−12
Hippocampus		7.8	15.3	26	−16	−12	Amygdala		5.1	10.1	−24	−12	−12
Inf frontal gyrus	BA 13	2.2	8.2	−34	22	6	Inf frontal gyrus	BA 47	0.7	6.1	−30	32	−6
Caudate		1.7	8.6	−10	12	12	Caudate		0.6	5.2	8	12	10
Thalamus		0.6	5.5	−6	−18	14	Mid occipital gyr	BA 19	0.6	5.1	30	−78	16
Insula	BA 13	0.6	4.8	−54	−32	20	Med frontal gyrus	BA 9	0.4	5.0	8	42	26
Postcentral gyrus	BA 3	0.5	4.7	−40	−20	50	Inf frontal gyrus	BA 47	0.2	4.8	22	28	−8
Inf frontal gyrus	BA 47	0.4	5.4	34	28	−2	Mid frontal gyrus	BA 8	0.2	5.0	36	36	38
Component H							Component I
Med frontal gyrus	BA 10	85.5	21.3	−6	56	6	Uncus	BA 28	97.1	28.3	24	6	−18
Thalamus		6.6	11.6	−14	−32	2	Sup temporal gyr	BA 22	8.0	9.5	−56	−54	6
Insula	BA 13	5.4	9.9	34	20	8	Sup frontal gyrus	BA 9	6.4	10.0	24	44	28
Mid temporal gyr	BA 21	3.5	10.2	−62	−22	−12	Inf temporal gyrus	BA 37	3.5	9.6	56	−60	−10
Inf occipital gyr	BA 19	3.3	8.7	42	−74	−2	Sup temporal gyr	BA 41	2.7	6.5	52	−28	14
Lingual gyrus	BA 18	2.3	7.3	12	−70	−4	Mid frontal gyrus	BA 6	2.3	8.2	22	0	58
Precuneus	BA 19	1.9	6.0	34	−74	36	Thalamus		1.8	8.6	−6	−14	10
Cingulate gyrus	BA 24	1.1	6.1	0	−20	34	Orbital gyrus	BA 11	1.7	6.5	−6	38	−20
Component J1							Component J2
Supramarginal gyr	BA 40	67.6	15.8	−56	−52	28	Hippocampus		43.3	43.4	−26	−36	−2
Mid temporal gyr	BA 39	26.2	14.2	46	−64	30	Cingulate gyrus	BA 24	6.9	6.9	0	−16	34
Inf frontal gyrus	BA 47	3.8	6.9	42	16	−8	Mid frontal gyrus	BA 6	4.2	7.5	−30	16	50
Hippocampus		3.7	8.3	−32	−30	−6	Mid frontal gyrus	BA 47	3.1	6.3	38	36	−2
Med frontal gyrus	BA 6	2.0	6.5	−10	−18	56	Insula	BA 13	2.2	6.2	−48	−38	22
Thalamus		1.9	8.3	6	−2	4	Sub‐gyral	BA 6	2.0	7.2	24	6	56
Inf occipital gyr	BA 19	1.5	6.9	38	−78	−4	Amygdala		1.2	6.5	22	−6	−12
Inf frontal gyrus	BA 47	1.4	6.1	−24	34	−8	Insula	BA 13	0.8	6.2	38	18	8
Component K1							Component K2
Amygdala		49.3	50.8	−22	−2	−14	Insula	BA 13	50.4	23.9	36	10	8
Mid frontal gyrus	BA 46	4.4	8.4	−48	20	24	Claustrum		22.9	17.0	−30	8	6
Thalamus		1.6	6.6	16	−32	6	Anterior cingulate	BA 32	6.8	9.6	2	38	22
Paracentral lobule	BA 31	1.5	7.5	10	−32	40	Hippocampus		1.4	5.7	−32	−26	−8
Cingulate gyrus	BA 31	1.5	6.7	−12	−32	40	Cingulate gyrus	BA 32	1.1	6.6	6	8	42
Med frontal gyrus	BA 9	1.3	5.2	−8	40	16	Declive		1.0	6.3	−44	−56	−20
Mid temporal gyr	BA 21	0.7	6.3	−56	−20	−6	Inf frontal gyrus	BA 47	1.0	6.5	−30	32	−8
Thalamus		0.7	5.6	−14	−34	4	Pos cingulate	BA 23	0.7	5.8	6	−60	16
Component L							Component M
Claustrum		24.7	24.6	−38	0	2	Precentral gyrus	BA 4	62.9	20.0	48	−12	42
Claustrum		23.6	26.0	38	−4	2	Postcentral gyrus	BA 3	49.2	21.3	−46	−18	46
Precuneus	BA 31	13.9	10.4	2	−50	30	Caudate		3.9	7.6	10	10	18
Anterior cingulate	BA 32	4.9	5.7	−6	32	22	Thalamus		3.6	14.3	12	−30	6
Thalamus		1.3	5.8	−16	−32	0	Thalamus		2.5	11.2	−16	−32	2
Culmen		0.7	5.2	8	−48	−8	Cuneus	BA 19	2.1	6.0	26	−84	22
Culmen		0.5	4.8	−6	−42	−18	Cingulate gyrus	BA 31	1.6	5.8	−8	−24	42
Mid frontal gyrus	BA 9	0.5	5.8	48	10	34	Mid frontal gyrus	BA 8	1.5	7.0	20	32	40
Component N							Component O
Cuneus	BA 7	96.2	15.7	12	−72	30	Thalamus		27.5	25.0	−4	−12	10
Anterior cingulate	BA 32	13.3	10.7	−4	36	−4	Mid frontal gyrus	BA 6	4.2	8.9	40	2	38
Sub‐gyral	BA 6	6.2	8.6	28	2	56	Inf frontal gyrus	BA 9	2.6	8.6	−42	8	30
Precentral gyrus	BA 6	5.1	10.5	52	0	8	Amygdala		2.1	6.2	−20	−4	−18
Sup temporal gyr	BA 22	4.3	14.1	−54	0	2	Culmen		1.9	5.8	−6	−38	−20
Fusiform gyrus	BA 37	2.9	6.7	44	−52	−8	Mid temporal gyr	BA 21	1.4	6.0	−58	−50	6
Inf parietal lob	BA 40	2.1	6.3	50	−28	22	Angular gyrus	BA 39	1.3	6.2	44	−66	34
Sup parietal lob	BA 7	1.4	6.7	−20	−54	64	Sup frontal gyrus	BA 9	0.9	5.2	30	34	30
Component P							Component Q
Mid temporal gyr	BA 21	84.9	15.4	−58	−22	−4	Culmen		168.0	13.8	8	−36	−18
Sub‐gyral	BA 20	9.5	9.1	44	−16	−20	Insula	BA 13	4.7	5.5	38	−22	16
Sup frontal gyrus	BA 6	4.5	6.8	−2	6	60	Inf frontal gyrus	BA 47	1.5	5.6	34	30	−4
Thalamus		2.5	6.8	−14	−34	4	Med frontal gyrus	BA 10	1.4	4.9	−6	50	6
Mid frontal gyrus	BA 9	1.7	6.3	46	28	28	Claustrum		1.0	4.5	−28	−22	18
Med frontal gyrus	BA 10	1.1	6.3	−4	50	8	Inf frontal gyrus	BA 47	0.8	5.0	−48	30	2
Thalamus		0.8	5.7	0	−4	−2	Precentral gyrus	BA 9	0.7	4.1	−42	6	32
Sup temporal gyr	BA 22	0.7	5.3	60	−42	14	Precentral gyrus	BA 6	0.5	4.9	52	−8	34
Component R
Thalamus		216.5	19.9	−8	−30	16
*Medulla		10.1	11.3	6	−34	−38
Insula	BA 13	3.7	12.3	−30	22	8
Med frontal gyrus	BA 9	3.1	8.2	8	44	14
Sup frontal gyrus	BA 8	2.4	7.0	−14	28	50
Mid frontal gyrus	BA 10	2.0	7.4	−28	50	20
Mid frontal gyrus	BA 10	1.8	10.8	30	56	8
Substania nigra		1.4	9.4	8	−16	−12

Anatomical clusters (z > 4) were identified in Mango using the “Find Overlay Cluster” tool. The Talairach Daemon Atlas was used for labeling, and x–y–z coordinates are reported in standardized Talairach space. Components are individually displayed with anatomical layouts in Supporting Information, Figures 7–10.

3.3. Region‐to‐disease analyses

A disease‐component heatmap is shown in Figure 5; average spatial cross correlation was employed per network to extract disease loadings. Figure 5 includes 43 ICD‐10 diagnoses across 21 VBM‐ICA components for a total of 903 weights (artifact components—as described in the preceding paragraph—were not included). Figure 5 excludes network weights from ICD‐10 diagnoses with a small sample size (<10 experiments). The regional analysis and average spatial correlation region‐to‐disease methods (Figure 3d,e) showed a significant association in a linear regression (Supporting Information, Figure 2).

3.4. HCA disease and component clusters

Psychiatric diseases (ICD‐10 F codes) were clearly separated from neurological disorders (ICD‐10 G codes) after applying HCA, as is evident in the middle portion of Figure 5b. In the HCA analysis, total cluster numbers were specified at k = 9 for components (each color corresponds to a cluster on the x‐axis in Figure 5) and k = 11 for diagnoses (y‐axis), selected from local maxima in the average silhouette width and gap statistic for each possible cluster size (k = 1, 2, …, k _max) (Supporting Information, Figure 5). Component cluster labels are provided in the silhouette plot (Supporting Information, Figure 7). Three component clusters (Clusters 1, 2, and 5) each showed high within‐cluster similarity having an average silhouette length >0.43 per cluster, that is, they weighted similarly on diseases. We describe these clusters of interest (Clusters 1, 2, and 5) in the following paragraphs; the Talairach Daemon atlas (Lancaster et al., 2000) is used for automated labeling.

Cluster 1 included Components P, I, K1, G2, and G1. Component P, unique to the Experiment‐filtered ICA, was left‐lateralized across the superior/middle temporal gyri and insula. It also incorporated the bilateral middle frontal gyri (BA 9) and medial frontal gyrus (BA 6). Component I peaked in the bilateral inferior frontal gyri (BA 47) and spread inferiorly. G1 and G2 were mostly confined to the left and right anterior hippocampus respectively. Component K1 included the amygdala, thalamus, and cingulate gyri among other regions. Each network heavily weighed on G30: Alzheimer's Disease (min: 0.04, max: 0.16, avg: 0.11), G31.84: Mild Cognitive Impairment (MCI) (min: 0.05, max: 0.13, avg: 0.08), and marginally on G20: Parkinson's Disease (min: 0.02, max: 0.05, avg: 0.03). Excluding Component P, each component loaded on G40.2: Temporal Lobe Epilepsy (avg: 0.07). Component K1 starkly loaded on Z81.8: Family History of Mental Disorder (0.10) and Component I on F60.2: Antisocial Personality Disorder (0.08).

Cluster 2 included components A, O, K2, and L, which shared topological similarity among the thalamus, caudate, and the insula. Component A was most significant in the caudate head and included the posterior insula. Component O was unique to the Experiment‐filtered ICA method, meaning it did not show enough interpaper co‐variance to be identified in the Paper ICA method. It peaked in the medial dorsal nucleus of the thalamus and contained the precentral gyrus (BA 9). Component K2 was most significant in the anterior insula, putamen, and included the anterior cingulate (BA 32). Component L peaked in the posterior insula and included the posterior cingulate/precuneus and anterior cingulate. Each network heavily loaded on G10: Huntington's Disease (avg: 0.22), G37.8: Other Specified Demyelinating Diseases (avg: 0.07), G35: Multiple Sclerosis (avg: 0.06), and G31.85: Corticobasal Degeneration (avg: 0.06). Excluding L, each loaded upon G24.9: Unspecified Dystonia (avg: 0.123). And excluding O, each network loaded upon G90.3: Multi‐system Degeneration (0.09) and G31.0: Frontotemporal Dementia (0.06). Individually, Network O especially loaded upon G31.85: Corticobasal Degeneration (0.09) and Temporal Lobe Epilepsy (0.06).

Cluster 5 contained components F and H. Both networks incorporated different aspects of the frontal lobe. Component F contained a large portion of the medial frontal lobe. Its highest z‐score was in the cingulate (BA 32); it also included the bilateral precentral gyrus, insula and thalamus. Component H peaked in the medial frontal gyrus and the anterior cingulate, and contained the left thalamus/parahippocampus and right occipital gyrus. Both networks weighted most on M79.7: Fibromyalgia (avg: 0.054), F43.10: Post‐traumatic Stress Disorder (avg: 0.037), Z91.49: Personal History of Psychological Trauma (0.033), and moderately on G31.0: Frontotemporal Dementia (avg: 0.023) and G89.2: Unclassified Chronic Pain (avg: 0.022).

The other 10 components—that did not show strong within‐cluster similarity—are anatomically summarized in Table 2, and their network‐disease weights are presented in Figure 5.

3.5. Age‐related ALE

Nine significant clusters of the age‐related ALE are reported in Supporting Information, Table 1. Component M (postcentral gyrus, middle/inferior frontal gyrus), A (caudate, posterior insula), and L (anterior/posterior cingulate, posterior insula) significantly (p < 5 × 10⁻⁴) spatially correlated with the unthresholded ALE—representing different aspects of its topology (Figure 7). Components M, A, and L spatially correlated with the ALE at r = .28, .19, and .18, respectively.

Figure 7.

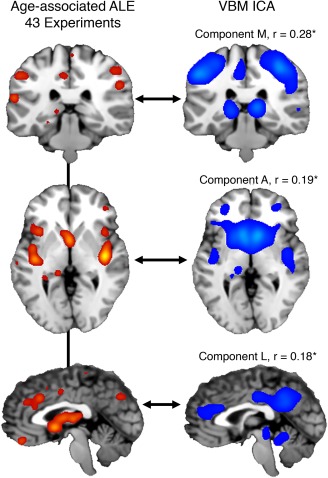
(Left column) An anatomical likelihood estimation (ALE) image was calculated from 43 experiments in healthy and diseased subjects analyzing age‐related, atrophy effects. Different rows are different views of the same ALE image (ALE value > 0.10). (Right column) VBM‐ICA components (z > 3) showing significant, voxel‐wise, whole‐brain spatial correlations corrected for multiple comparisons (p < 5 × 10⁻⁴)

4. DISCUSSION

BrainMap has been extended to include voxel‐based morphometry (VBM) studies in a separate sector, titled: BrainMap VBM. To date, BrainMap VBM contains coordinates from >3,000 experiments with detailed meta‐data descriptors. The database is a community resource and can be utilized with a variety of univariate (e.g., ALE) and multivariate (e.g., MACM) meta‐analytic approaches. As an illustrative use‐case application, we report an independent components analysis (ICA) on BrainMap VBM en masse to extract transdiagnostic, inter‐experiment SCov components. At the time of analysis, BrainMap VBM represented over 53,000 subjects across 43 ICD‐10 diagnostic categories as well as healthy controls. We demonstrate that automated and semi‐automated data‐cleaning approaches appropriately prepared BrainMap VBM for ICA by reducing data‐redundancy effects. In addition, with 43 ICD‐10 disease loadings calculated from 21 networks, hierarchical clustering (HCA) was performed to investigate the brain's structural architecture across disease.

4.1. BrainMap VBM coding & region‐to‐disease inference tools

The BrainMap meta‐data coding scheme is a descriptive system using mostly structured keywords to capture experimental methods and research questions. In designing the functional BrainMap database, Fox et al. (2005) surveyed the neuroimaging literature and designated cogent, hierarchical Behaviors (e.g., Cognition:Working‐Memory, Interoception:Sleep) and Paradigm Classes (e.g., n‐back, Episodic Recall), as well as Conditions to describe the sensory stimulus applied (e.g., visually presented words), the response made (e.g., words spoken aloud), and the instructions for each condition. BrainMap's functional taxonomy was then validated by testing its coherence with data‐filtering choices made by subject‐matter experts carrying out meta‐analyses (Fox et al., 2005). BrainMap VBM's design was intrinsically simpler by nature due to the straightforward experimental methods that encompass most of the VBM literature (i.e., disease vs. control group‐wise contrast). Existing BrainMap data‐fields including Behaviors, Paradigm Classes, and Conditions were necessarily excluded in the VBM database, while International Classification of Disease (ICD‐10) codes were implemented to the facilitate study of distinct brain disorders. A distinguishing feature of this study was the broad inclusion of brain disorders across diagnostic categories. ICA is an ideal exploratory strategy to find multivariate patterns in the data and to exhaustively exhibit its contents. Even at this preliminary analysis stage, our results showcase the breadth of BrainMap VBM's transdiagnostic utility (Figure 5).

“(M)eta‐analysis is itself a study requiring careful planning and execution,” as Jones (1995) calls to attention. To facilitate this practice, the BrainMap workspace structure (Figure 1) is compliant with the Preferred Reporting Items for Systematic Reviews and Meta‐Analysis (PRISMA) (Liberati et al., 2009). PRISMA consists of a 27‐item checklist and a four‐phase flow diagram created by an international team of scientists and methodologists in response to poor reporting of systematic reviews. The meta‐data structure of the VBM database, along with filtered search software (Sleuth), enable inclusion and exclusion criteria to be faithfully applied, reported, and—if the author chooses—shared via a workspace data file. The size of any neuroimaging meta‐analysis varies and depends on the available literature per topic. Eickhoff et al. (2016) performed extensive simulation analyses and recommended a minimum of 20 experiments to achieve sufficient power for moderate effects when using ALE. More information with respect to designing and implementing neuroimaging meta‐analyses can be found by Muller et al. (2017) and Fox, Parsons, and Lancaster (1998).

The Disease Regional Analysis tool presented in this study utilizes the ICD‐10 BrainMap meta‐data. It is a freely‐accessible plugin tool for the Mango GUI that extracts coordinates from the BrainMap VBM database, and assesses the association of a specified ROI across ICD‐10 diagnoses (Figure 3d). The accumulation of coordinates in BrainMap allows the tool to be increasingly powerful, as it is intermittently synchronized to the most recent version of the database. The tool is conceptually straightforward, and provides comprehensive results in a short processing time (∼1 s). Disease Regional Analysis showed a strong association with a separate, more computationally expensive spatial correlation method (Supporting Information, Figure 3).

4.2. Data redundancy

Following the unfiltered experiment‐level ICA (Figure 3, a), two filtering protocols were tested to appropriately handle the observed data‐redundancy artifacts caused by redundant experiments within a single paper (observed across multiple papers, Supporting Information, Figure 1). For example, some papers reported multiple experiments with only varying statistical thresholds. We report these data‐cleaning protocols as it is recommended by the Committee on Best Practices in Data Analysis and Sharing (COBIDAS) following incidental findings (Nichols et al., 2016). Paper ICA, while algorithmically expedient, incorporated less data volume because many experiments of the same paper were combined into one MA image (i.e., pseudo time‐point) to completely avoid coordinate redundancy within a paper. The Experiment‐filtered ICA involved querying the database for papers showing outlier influence (>2 x–y–z coordinate recurrences across experiments in one paper). Once outlier experiments were identified, experimenter review using inclusion–exclusion criterion was used to systematically filter them before ICA (see Supporting Information). This resulted in larger data volume (i.e., more pseudo time‐points) for the Experiment‐filtered ICA input compared to the Paper ICA. We recognize the complimentary nature of both methods in terms of noise artifacts vs. explained variance (Supporting Information, Figure 3), which can be attributed to data input volume (i.e., more to data to model resulted in less explained variance). Each method, while expressing very similar results (Figure 4), gleaned some unique information. Paper ICA produced a cerebellar component (Q) that showed extremely specific weighting on ataxias. Experiment‐filtered ICA generated a left‐hemispheric, temporal component (P) involving language, and predictably weighted on aphasia. These nonredundancy approaches are adaptable to large‐scale CBMA methods beyond ICA and advance the integrity of such analyses.

4.3. HCA clustering and disease specificity

Psychiatric and neurological diseases are categorized in the International Classification of Disease codes (ICD‐10) manual by “F” and “G”, respectively. This distinction was well identified by HCA of network‐disease loadings—an unsupervised learning algorithm that clustered diagnostic categories and independent components into separate dendrograms (Figure 5). As conveyed in the middle portion of Figure 5b, psychiatric diseases did not show robust component association compared to neurological diseases. In a post‐hoc analysis supporting this conclusion, we performed a non‐parametric Wilcoxon rank sum test on network loadings of the psychiatric sample (F code, 13 diseases × 21 networks = 273 sample size) and neurological sample (G code, 21 diseases × 21 networks = 441 sample size). We found a significant difference between samples (p = 0.012); the neurological sample showed a higher mean rank. Neurological diseases indeed induce more atrophy compared to psychiatric disorders, that is, more coordinates (Fusar Poli et al., 2014), but that does not entirely explain the substantially weaker loadings observed. Instead, these findings suggest that psychiatric diseases have a weaker pathognomonic spatial pattern of morphometric change across studies in comparison to neurological diseases. While multiple components showed loading on psychiatric diseases (e.g., Networks F, H, K2), these networks were not disease‐specific.

Figure 6.

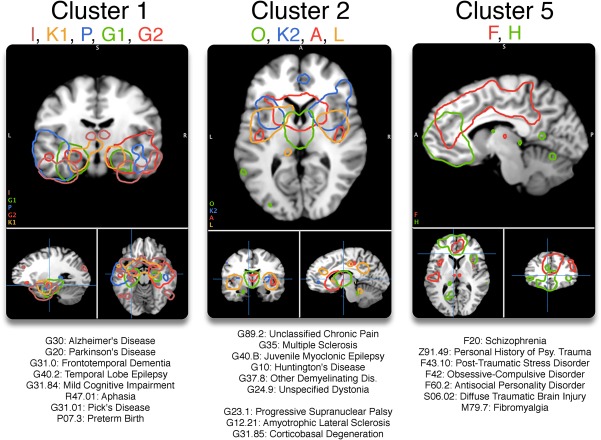
Clusters 1, 2, and 5 each showed high within‐cluster similarity (avg. silhouette > 0.43). Each network is displayed at z > 5, and their strongest associated diseases are displayed at the bottom of the figure

Previous computational approaches toward understanding BrainMap VBM coordinate data en masse compliment the present analysis. An atrophic pattern matching Component K2 (anterior insula and dorsal anterior cingulate) was reported in a VBM meta‐analysis combining schizophrenia, bipolar disorder, depression, addiction, obsessive‐compulsive disorder, and anxiety by Goodkind et al. (2015). They found that decreased gray matter in those regions is associated with worse executive function and sustained attention. Component K2 in the present analysis shared the same topology, and provides more evidence of a shared endophenotype across psychiatric disorders, which Goodkind et al. (2015) points out, “is not currently an explicit component of psychiatric nosology.” Disease nonspecificity was also observed in Component L, which had the highest median disease score (0.022). Component L included the posterior and anterior cingulate, as well as the posterior insula. Consistent with this finding, Crossley et al. (2014) performed ALE of 26 disorders in BrainMap VBM and compared those results with a graph theory analysis of diffusion tensor imaging (DTI) data of healthy subjects. They found that disease lesions most frequently target “hub” regions, that is, grey matter nodes with the highest number of fiber tract connections, which included the posterior cingulate.

4.4. Structural covariance in disease

The transdiagnostic SCov networks reported here reflect other disease‐related SCov networks published. In an ICA of T1‐weighted images of schizophrenia patients and controls combined, Xu et al. (2009) found that the most significant component showing diminished network integrity (i.e., atrophy) included the superior temporal gyri, insula, and medial frontal gyrus. This topology mirrored Component E in this analysis, which weighted highest on schizophrenia. Seeley, Crawford, Zhou, Miller, and Greicius (2009) found that Alzheimer's disease, behavioral variant frontotemporal dementia, semantic dementia, progressive nonfluent aphasia, and corticobasal syndrome each atrophied distinct anatomical regions that reflected seed‐based structural covariance among healthy subjects. The present investigation indeed found SCov networks that revealed those networks in Alzheimer's disease (Component J2), aphasia (Component P), and corticobasal degeneration (Components C and O).

Coppen et al. (2016) combined T1 images from premanifest gene carriers of Huntington's disease, manifest Huntington's disease, and healthy controls to perform structural ICA. Two networks—a caudate nucleus network and a hippocampal network—showed reduced network integrity in both Huntington's disease groups compared to controls. Here we report a network (Component A) with similar topology extending beyond the caudate with extreme loading on Huntington's disease. In a separate study, Wu et al. (2017) investigated SCov in MDD within functional networks involved in emotion regulation. They observed a SCov increase of the right amygdala and right angular gyrus in MDD. Component K1 contained both regions (z > 3), and was MDD's highest network weighting. Considering that Component K1 was associated with many diseases; however, this connection could be non‐specific to MDD.

The mechanisms driving long‐distance SCov are an active area of research (Evans et al., 2013; Romero‐Garcia et al., 2018), and multiple hypotheses have been put forward to understand the network‐based atrophy observed in brain disorders; these include (a) transneuronal spread, (b) nodal stress, (c) trophic failure, and (d) shared vulnerability. (a) The transneuronal spread mechanism begins in an epicenter, often a hub (i.e., the hippocampus, insula, etc.), where alterations spread along axonal pathways in a “prion‐like” manner (Ahmed et al., 2016; Zhou, Gennatas, Kramer, Miller, & Seeley, 2012). (b) The nodal stress mechanism suggests that brain hubs are selectively susceptible to damage from oxidative stress and endothelial damage leading to impairments, such as a leaky blood brain barrier (Crossley et al., 2014). (c) The dysfunction of trophic factors includes brain‐derived neurotrophic factor (BDNF), which is involved in dendritic and axonal branching (Cohen‐Cory, Kidane, Shirkey, & Marshak, 2010). When trophic factor expression and regulation is impaired, trophic failure in the form of poor cellular and synaptic maintenance impairs structural connectivity (Fornito, Zalesky, & Breakspear, 2015). (d) Last, shared vulnerability is a mechanism whereby similar neuronal cell types across the brain are susceptible to disease‐specific changes due to shared genetic and metabolic profiles (Cioli, Abdi, Beaton, Burnod, & Mesmoudi, 2014). Future work can quantitatively compare the transdiagnostic SCov networks reported here to functional networks to investigate the plausibility of these hypotheses. Segall et al. (2012) performed a spatial comparison between structural and functional ICA components in healthy subjects, and proposed further efforts toward understanding how neurodegenerative syndromes play a role in the structural and functional connectome interaction.

4.5. Structural covariance in healthy aging

Healthy, aging subjects have also been studied using structural ICA. Hafkemeijer et al. (2014) performed ICA on 370 T1‐weighted, grey‐matter segmented MRI images in middle‐aged to older adults from 45 to 85 years old. They found strong age‐related atrophy in subcortical, sensorimotor, and posterior/anterior cingulate networks. Upon visual inspection, those SCov networks showed similarity to Components A, M, and L respectively. Segall et al. (2012) also performed structural ICA on 603 healthy subjects, and found the largest age effect on a motor network similar to Component M.

To better interpret VBM ICA components and their shared vulnerability to age, we performed a post‐hoc ALE analyzing coordinates of atrophy related to aging within BrainMap VBM. This ALE image represented a voxel‐wise probability of atrophy with age, and was spatially compared to VBM ICA components. Components M (postcentral gyrus, middle/inferior frontal gyrus), A (caudate, posterior insula), and L (anterior/posterior cingulate, posterior insula)—present in the Hafkemeijer et al. (2014) and Segall et al. (2012) analyses—significantly spatially correlated with the age‐related atrophy ALE image. Each VBM ICA component represented different aspects of the atrophy topology (Figure 7). Component M showed the highest spatial correlation to the age‐associated ALE (r = .28), and included brain regions involved in primary sensorimotor function (BA 2/3/4) and cognitive control (BA 9). Motor deficits in aging adults include coordination difficulty, slowing of movement, and difficulties with balance and gait (Seidler et al., 2010). These results suggest that certain neurodegenerative diseases cause network morphology changes that converge with structural networks that strongly atrophy with age. Hafkemeijer et al. (2014) also reported that age was not significantly associated with gray matter volume in an inferior temporal and three cerebellar networks. These networks matched to Components I and Q respectively, and did not show significant age‐association in this analysis.

While ICA included 17 VBM experiments measuring age effects in diseased populations, we did not find this small sample (0.8% of 2,002 experiments) contributed to the age‐related atrophy convergence observed across multiple SCov components; those experiments did not show meaningful spatial coherence, that is, zero significant clusters in an ALE analysis (cFWE p = .05; cluster‐forming p = .001).

5. LIMITATIONS

The experiments in the BrainMap VBM database varied considerably across the 43 ICD‐10 diagnoses analyzed (Supporting Information, Figure 4). The total number of experiments per disease ranged from 10 to 245 (median: 20). Every experiment was included in the ICA analysis to incorporate as much data as possible for the data‐mining experiment. This limitation was explored with a regression analysis of each weight (in Figure 3) vs. experiment‐count per disease, and a significant (p = .03), but small association was found (slope: 5.375 × 10⁻⁵/experiment). This suggested that diseases with many experiments in the database (e.g., schizophrenia) indeed had more influence than diseases with less experiments (e.g., temporal sclerosis), but only a small effect was observed. As BrainMap VBM gains more traffic, we expect a more representative, and diagnostically homogenous sample of the current literature. An alternative CBMA database, Neurosynth (http://www.neurosynth.org), employs a fully automated coordinate‐/text‐mining approach to populate their database (Yarkoni, Poldrack, Nichols, Van Essen, & Wager, 2011). While this feature allows a quick, massive conglomeration of coordinates, it does not segregate different modalities (e.g., fMRI and VBM) and can conflate diametrically opposed meta‐data categories (e.g., “saccades” and anti‐“saccades”). BrainMap, however, relies on quality review by a managing team for each submission.

One limitation of the present analysis is more fundamental to the CBMA approach, which does not account subsignificant results. Alternatively, Neurovault (http://www.neurovault.org) stores 3‐D unthresholded statistical parametric images (SPI) from each study rather than significant x–y–z coordinates; this methodology is defined as image‐based meta‐analysis (IBMA) (Gorgolewski et al., 2015). While IBMA incorporates data that can prove significant in aggregation, one persistent and fundamental drawback is the sparsity of SPIs shared. Significant, standardized x–y–z coordinates are reliably reported.

In this analysis, we did not explore the effect of ICA dimensionality. Instead, we chose d = 20 because it is familiar to many readers (Smith et al., 2009). The primary purpose of this analysis was to display the massive, transdiagnostic nature of this resource, and draw initial inferences. Future work can investigate varying dimensionality, as was done by Ray et al. (2013) in the functional sector.

6. CONCLUSION

BrainMap VBM is a new, accruing CBMA resource for structural neuroimaging, and can be utilized with univariate methodologies including ALE (via GingerALE software), MKDA, and SDM for convergence analyses to quantitatively summarize the VBM literature. In addition, the entire database can be leveraged en masse with more complex multivariate methodologies. As a use‐case scenario, we extract transdiagnostic, inter‐experiment SCov networks which exhaustively illustrate the content of the database and its region‐to‐disease capability. Some networks reflect previously published inter‐subject ICA SCov components from Alzheimer's, schizophrenia, aphasia, and Huntington's disease, as well in healthy, aging subjects (Coppen et al., 2016; Hafkemeijer et al., 2014; Seeley et al., 2009; Xu et al., 2009). A component showing nonspecific disease weighting compliments previous work suggesting a shared endophenotype across psychiatric diseases (Goodkind et al., 2015). The significantly weaker psychiatric network loading reiterates the need to better distinguish mental disorders according to neurobiological principles (Insel et al., 2010). We hope this resource facilitates reproducibility in the field of structural neuroimaging.

CONFLICTS OF INTEREST

Nothing to report.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supporting Information

Vanasse TJ, Fox PM, Barron DS, et al. BrainMap VBM: An environment for structural meta‐analysis. Hum Brain Mapp. 2018;39:3308–3325. 10.1002/hbm.24078