Identification of Alzheimer's disease and mild cognitive impairment using multimodal sparse hierarchical extreme learning machine

Abstract

Different modalities such as structural MRI, FDG‐PET, and CSF have complementary information, which is likely to be very useful for diagnosis of AD and MCI. Therefore, it is possible to develop a more effective and accurate AD/MCI automatic diagnosis method by integrating complementary information of different modalities. In this paper, we propose multi‐modal sparse hierarchical extreme leaning machine (MSH‐ELM). We used volume and mean intensity extracted from 93 regions of interest (ROIs) as features of MRI and FDG‐PET, respectively, and used p‐tau, t‐tau, and $\mathrm{A}{\mathrm{\beta }}_{42}$ as CSF features. In detail, high‐level representation was individually extracted from each of MRI, FDG‐PET, and CSF using a stacked sparse extreme learning machine auto‐encoder (sELM‐AE). Then, another stacked sELM‐AE was devised to acquire a joint hierarchical feature representation by fusing the high‐level representations obtained from each modality. Finally, we classified joint hierarchical feature representation using a kernel‐based extreme learning machine (KELM). The results of MSH‐ELM were compared with those of conventional ELM, single kernel support vector machine (SK‐SVM), multiple kernel support vector machine (MK‐SVM) and stacked auto‐encoder (SAE). Performance was evaluated through 10‐fold cross‐validation. In the classification of AD vs. HC and MCI vs. HC problem, the proposed MSH‐ELM method showed mean balanced accuracies of 96.10% and 86.46%, respectively, which is much better than those of competing methods. In summary, the proposed algorithm exhibits consistently better performance than SK‐SVM, ELM, MK‐SVM and SAE in the two binary classification problems (AD vs. HC and MCI vs. HC).

1. INTRODUCTION

Alzheimer's disease (AD) is the most common dementia type in the elderly. The number of people suffering from AD is increasing rapidly every year. Because AD is a degenerative disease and progressively attacks memory cells, the development of early diagnostic tools for AD and mild cognitive impairment (MCI) is essential. AD is known to be closely related to structural atrophy, pathological amyloid depositions, and metabolic alterations in the brain (Jack et al., 2010; Nestor, Scheltens, & Hodges, 2004). For this reason, brain atrophy measured by magnetic resonance imaging (MRI), hypometabolism measured by functional imaging, and quantification of specific proteins measured by CSF have been used for AD/MCI diagnosis. In general, features extracted from the hippocampus, entorhinal cortex, parahippocampal gyrus, and cingulate using structural MRIs have been reported to be the most effective in classifying AD/MCI, and these results are consistent with those of previous studies based on group comparison methods (Chételat et al., 2002; Convit et al., 2000; Fox, & Schott, 2004; Jack et al., 1999; Misra, Fan, & Davatzikos, 2009). In addition to structural MRI, another important modality for AD and MCI diagnosis is fluorodeoxyglucose positron emission tomography (FDG‐PET) (Chételat et al., 2003; Foster et al., 2007; Higdon et al., 2004). For example, Diehl et al. (2004) and Drzezga et al. (2003) showed that there is a decrease in glucose metabolism in the parietal, posterior cingulate, and temporal brain regions of AD patients (Diehl et al., 2004; Drzezga et al., 2003). Another modality that is important for diagnosis of AD and MCI is cerebrospinal fluid (CSF). It is generally known that increased CSF total tau (t‐tau), tau hyperphosphorylated (p‐tau), and reduced amyloid β ( $\mathrm{A}{\mathrm{\beta }}_{42}$) at threonine 181 appear in AD patients (Bouwman et al., 2007; Ji et al., 2001; De Leon et al., 2007). Different modalities such as structural MRI, FDG‐PET, and CSF have complementary information, which is likely to be very useful for diagnosis of AD and MCI (Apostolova et al., 2010; Fjell et al., 2010; Foster et al., 2007; Landau et al., 2010; De Leon et al., 2007; Walhovd et al., 2010). For this reason, a number of studies have reportedly integrated multiple modalities such as MRI, PET, and CSF rather than using a single modality to improve the performance of AD/MCI automatic diagnosis (Cui et al., 2011; Fan et al., 2007; Kohannim et al., 2010; Suk & Shen, 2013; Walhovd et al., 2010; Westman, Muehlboeck, & Simmons, 2012; Yuan et al., 2012; Zhang et al., 2011; Zhang, & Shen, 2012). For example, Kohannim et al. (2010) concatenated the features extracted from various modalities into a vector and classified it using support vector machine (SVM) (Kohannim et al., 2010). Walhovd et al. (2010) used multi‐method stepwise logistic regression analysis to integrate multiple modalities. Hinrichs, Singh, Xu, and Johnson (2011), Suk and Shen (2013), and Zhang et al. (2011) used a kernel‐based machine learning method such as multiple kernel SVM (MK‐SVM) to integrate complementary information from multi‐modal data (Hinrichs et al., 2011; Suk & Shen, 2013; Zhang et al., 2011).

Recently, deep learning has become a promising technology in the machine learning field. Deep learning refers to the learning of multiple levels of representation and abstraction. Deep learning has resulted in significant performance improvements in data analysis and classification of images, sounds, and text. In recent years, increasingly more attempts have been made to use deep learning techniques for multi‐modal data analysis and classification. For example, Wang et al. (2014) used stacked auto‐encoders to obtain seamless information from various types of media. Srivastava and Salakhutdinov (2012) proposed a multi‐modal deep belief network to obtain joint representations of image and text data (Srivastava & Salakhutdinov, 2012). Ouyang, Chu, and Wang (2014) developed a multi‐source deep model to obtain information for human pose estimation. Suk and Shen (2013) proposed a method of integrating MRI, PET, and CSF modalities for automatic diagnosis of AD using stacked auto‐encoders.

Learning by most deep learning architectures is based on a back‐propagation algorithm that iteratively adjusts the parameters of all layers. For this reason, conventional neural networks require numerous iterations to obtain good generalization performance (Huang et al., 2004). To overcome this situation, Huang, Zhu, and Siew (2004) proposed an extreme learning machine (ELM) with good generalization performance and computational efficiency by randomly assigning input layer weights and analytically calculating hidden layer weights. However, ELM is fundamentally a shallow network, which makes it difficult to obtain a hierarchical representation of the data (Cao et al., 2012; Cao, & Lin, 2015). To overcome these limitations, the deep ELM (DELM) algorithm was proposed by Kasun, Zhou, Huang, and Vong (2013), with the ELM auto‐encoder (ELM‐AE) as its base building block. Tang et al. (2016) proposed a sparse ELM‐AE, which is an improved version of the existing ELM‐AE, by learning the hidden layer weights sparsely (Tang et al., 2016). Wei, Liu, Yan, and Sun (2016) proposed a multi‐modal deep ELM‐AE (MM‐DELM) framework, an extended version of DELM, for multi‐modal data analysis and classification. MM‐DELM reportedly had successful performance in robotic grasping problems (Wei et al., 2016).

In this article, we propose a multi‐modal sparse hierarchical extreme learning machine (MSH‐ELM) that employs a sparse ELM‐AE as a base building block. Through the MSH‐ELM algorithm, we will extract joint hierarchical representations from three modalities (MRI, PET, and CSF), and finally classify AD and MCI from healthy controls (HC). Volume from MRI, mean intensity from PET, and $\mathrm{A}{\mathrm{\beta }}_{42}$, t‐tau, and p‐tau from CSF were used as the features of classifier. Particularly, the reason for using volume as a feature of MRI is that there are many studies that the volume reflects the brain atrophy induced by AD (Guo et al., 2010; Hirata et al., 2005; Ishii et al., 2005; Karas et al., 2003; Matsuda et al., 2012; Vemuri et al., 2009; Whitwell et al., 2007).

Our experimental results on the Alzheimer's Disease Neuroimaging Initiative (ADNI) dataset prove the utility of the proposed method. To verify the effectiveness of our method, we compared the classification performance with the single kernel support vector machine (SK‐SVM), conventional ELM, multiple kernel support vector machine (MK‐SVM), and stacked auto‐encoder (SAE) (Liu et al., 2014a; Suk & Shen, 2013; Zhang et al., 2011).

Our contributions of this study are as follows:

1. We propose an automated AD/MCI discrimination method based on a deep extreme learning machine framework. Compared to conventional ELM which is shallow network, deep extreme learning machine which is deep neural network and stacked by ELM auto‐encoder (ELM‐AE) can more effectively extract optimal features from the data. This is the first study to introduce a deep extreme learning machine framework for AD and MCI classification.

2. Our proposed framework employs a novel architecture which extracts optimal features from structural MR image, PET, and CSF modalities, simultaneously. Deep extreme learning machine models for multi‐modal data have been rarely studied, and to the best of our knowledge, this is the first multi‐modal deep extreme learning model for medical image classification.

3. The base building block of our proposed framework is sparse ELM auto‐encoder (sELM‐AE). sELM‐AE can generate sparser and more compact features from the data compared to ELM‐AE. This is the first algorithm to apply sELM‐AE as base building block into multi‐modal deep extreme learning machine framework.

4. The proposed algorithm extracts jointly optimized features from multi‐modal data differently from conventional sELM‐AE. The proposed algorithm first obtains high‐level representations individually for each modality. It then computes the joint hierarchical feature representation of the multi‐modal data using the high‐level representation of each modality as input.

5. The classification performance of our framework is expected to be superior to other conventional classification algorithms such as ELM, SVM, and MK‐SVM and so on because of deep neural network structure, sparse, and jointly optimized multi‐modal feature extraction characteristics. This will be addressed in detail through this study.

The remainder of this article is organized as follows: Section 2 describes the information contained in the ADNI database that we used for this study and the preprocessing procedure. Section 2.1 discusses related work, including the fundamental concepts and theories of ELM and the proposed MSH‐ELM framework. Sections 4 and 5 present the results and discussion of the proposed method, respectively. Section 3 presents the concluding remarks.

2. MATERIALS AND IMAGE PROCESSING

2.1. Subjects

The data used in this study were obtained from the ADNI dataset, which is publicly available on the web (http://www.loni.ucla.edu/ADNI). Detailed information on the subjects is presented in Table 1. General criteria for categorizing HC, AD, and MCI are explained on the web (http://adni.loni.ucla.edu). The subjects ranged in age from 55 to 90 years, and independent functioning assessments were evaluated by the study partner. The general inclusion/exclusion criteria were as follows: healthy control (HC) subjects had Mini‐Mental State Examination (MMSE) scores between 24 and 30 (inclusive), a Clinical Dementia Rating (CDR) of 0, and were nondepressed, non‐MCI, and nondemented. MCI patients had MMSE scores between 24 and 30 (inclusive), a memory complaint, objective memory loss measured by education adjusted scores on the Wechsler Memory Scale Logical Memory II, a CDR of 0.5, absence of significant levels of impairment in other cognitive domains, essentially preserved activities of daily living, and an absence of dementia. Mild AD patients had MMSE scores between 20 and 26 (inclusive), a CDR of 0.5 or 1.0, and met National Institute of Neurological and Communicative Disorders and Stroke and the Alzheimer's Disease and Related Disorders Association (NINCDS/ADRDA) criteria for probable AD.

Table 1.

Characteristics of the subjects used in this study

	HC (N = 52)	MCI (N = 99)	AD (N = 51)
Females/males	18/34	32/97	18/33
Age (mean $\pm$ SD)	75.3 $\pm$ 5.2 (62–85)	75.3 $\pm$ 7.0 (55–89)	75.2 $\pm$ 7.4 (59–88)
Education (mean $\pm$ SD)	15.8 $\pm$ 3.2 (8–20)	15.9 $\pm$ 2.9 (8–20)	14.7 $\pm$ 3.6 (4–20)
MMSE (mean $\pm$ SD)	29 $\pm$ 1.2 (25–30)	27.1 $\pm$ 1.7 (24–30)	23.8 $\pm$ 2.0 (20–26)
CDR (mean $\pm$ SD)	0 $\pm$ 0 (0–0)	0.5 $\pm$ 0 (0–0.5)	0.7 $\pm$ 0.3 (0.5–1)

Note. Abbreviations: CDR = clinical dementia rating; MMSE = mini‐mental state examination; N = number of subjects; SD = standard deviation (min – max).

In this study, we only used the baseline MRI, 18‐Fluoro‐DeoxyGlucose PET (FDG‐PET), and CSF data acquired from 51 AD subjects, 99 MCI subjects, and 52 healthy control (HC) subjects, who included all three modalities at baseline. All subject IDs used in this study are provided in Supporting Information.

2.2. MRI, PET, and CSF acquisition

All structural MR scans were collected from 1.5 T scanners. We downloaded MR images in the Neuroimaging Informatics Technology Initiative (NIfTI) format. All MR images were preprocessed for spatial distortion correction owing to gradient nonlinearity and B1 field inhomogeneity.

The FDG‐PET images were collected 30–60 min after injection. The obtained images were averaged, spatially aligned, interpolated to a standard voxel size, normalized in intensity, and smoothed to a common resolution of 8 mm full‐width at half‐maximum.

CSF data were acquired in the morning using a 20‐ or 24‐G spinal needle after overnight fasting. CSF was frozen within 1 h after acquisition, and transported to the ADNI biomarker core laboratory at the University of Pennsylvania Medical Center.

2.3. Image preprocessing

For simplicity of algorithm comparison, we followed the image preprocessing procedure of other studies that classified AD using multi‐modal data. For the same reason, we used the Kabani template as the MRI atlas in this study (Kabani et al., 1998). The Kabani template consists of 93 regions including parahippocampal gyrus, hippocampal formation, and so on. The detailed information about the region is provided in the Supporting Information, S4.

Both MR and PET images were preprocessed using the following procedures. First, in the case of MR images, we applied anterior commissure (AC)–posterior commissure (PC) correction, and the N3 algorithm to correct the intensity inhomogeneity of MR images using MIPAV software. Next, skull stripping and cerebellum removal were performed using both brain surface extractor (BSE) (Shattuck et al., 2001) and brain extraction tool (BET) (Smith, 2002). We manually checked whether skull stripping and cerebellum removal were performed properly. After checking all MR images, we segmented the structural MR images into three tissue types [gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF)] using FAST in the FSL software suite (http://www.fmrib.ox.ac.uk). Finally, the GM, WM, and CSF of MR images were parcellated into 93 regions of interest (ROIs) by warping Kabani et al.'s atlas to each subject's space via the hierarchical attribute matching mechanism for elastic registration (HAMMER) method (Kabani et al., 1998; Shen, & Davatzikos, 2002). As GM is highly related to both AD and MCI, we only considered the volume of GM tissue in each ROI and used it as a feature of structural MRI.

In the case of the PET images, we rigidly aligned them to the corresponding MR images using MIPAV software, and used the mean intensity of each ROI as a feature of FDG‐PET.

In the case of CSF, CSF $\mathrm{A}{\mathrm{\beta }}_{42}$, CSF t‐tau, and CSF p‐tau were used as the features of CSF for discriminating the AD/MCI from HC. Therefore, totals of 93 features from the structural MR image, 93 features from the FDG‐PET image, and 3 features from the CSF data were obtained for each subject.

3. METHODS

Figure 1 illustrates all the techniques and procedures of this study. As shown in Figure 1, GM volume and the mean intensity for each ROI were extracted from preprocessed MR and PET images, respectively, and CSF $\mathrm{A}{\mathrm{\beta }}_{42}$, CSF t‐tau, and CSF p‐tau were utilized as CSF features.

Figure 1.

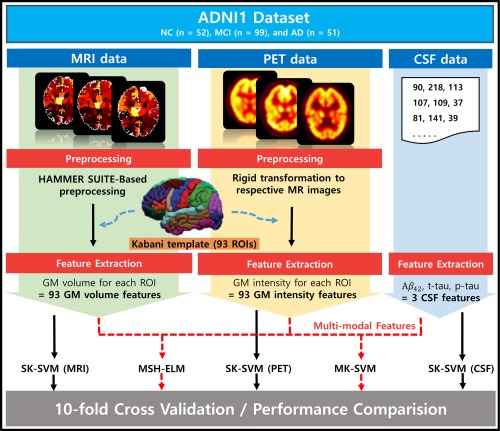
Overall framework proposed in the study. The dataset was collected from the ADNI1, which consists of 51 AD, 99 MCI, and 52 healthy control (HC) subjects including structural MRI, FDG‐PET, and CSF at baseline. MR images were preprocessed using HAMMER SUITE and the gray matter of MR images were parcellated into 93 ROIs by warping Kabani et al.'s atlas via HAMMER registration. FDG‐PET images were rigidly registered to their corresponding MR images. Total of 93 GM volume features, 93 GM intensity features, and 3 CSF features was obtained. The performance of MSH‐ELM was compared with those of four other classifiers using 10‐fold cross‐validation [Color figure can be viewed at http://wileyonlinelibrary.com]

First, high‐level representations of features extracted from each modality were individually computed using the stacked sparse ELM auto‐encoder (sELM‐AE). Then, another stacked sELM‐AE was used to obtain the joint hierarchical feature representation of three modalities (MRI, PET, and CSF), taking the high‐level representations of each modality as the input. Finally, we classified the obtained joint hierarchical feature representation using the kernel‐based extreme learning machine (KELM). We performed this series of processes in an integrated framework called the multi‐modal sparse hierarchical extreme learning machine (MSH‐ELM).

We evaluated the effectiveness of MSH‐ELM by considering two binary classification problems (AD vs. HC and MCI vs. HC) based on the MRI, PET, and CSF biomarkers of 202 baseline subjects in ADNI1 and compared the performance of MSH‐ELM with those of SK‐SVM, conventional ELM, MK‐SVM, and SAE. To estimate the performances of the proposed method and comparative classifiers, 10‐fold cross‐validation was used in this study. Specifically, we split the dataset into 10 subsets at random, with each subset containing 10% of the total data. We used nine sets of 10 subsets for training, and the remaining one was utilized for testing each time. The above process was repeated 10 times. For fair comparison, we compared the proposed method with SK‐SVM, ELM, MK‐SVM, and SAE using the same training and test sets (Liu et al., 2014a; Zhang et al., 2011).

3.1. Extreme learning machine (ELM) and kernel‐based extreme learning machine (KELM)

ELM consists of an input layer, a hidden layer, and an output layer (Huang et al., 2004). Whereas traditional feedforward neural networks require weights and biases for all layers to be adjusted by gradient‐based learning algorithms, ELM arbitrarily assigns input weights and hidden layer biases without iterative adjustment, and computes the output weights by solving a single linear system (Huang et al., 2012). Thus, ELM learns much faster than traditional neural networks and is widely employed in various classification applications as an efficient learning algorithm (Akusok et al., 2015; Cao et al., 2015; Chen, Yao, and Basu, 2016).

Specifically, for N training samples {( ${\mathit{x}}^{\left(j\right)},{\mathit{l}}^{\left(j\right)})\hspace{0.17em}|\hspace{0.17em}{\mathit{x}}^{\left(j\right)}\in {\mathcal{R}}^{\mathrm{p}}$ and ${\mathit{l}}^{\left(j\right)}\in {\mathcal{R}}^{\mathrm{q}}$, and j = 1,2, …, N}, the output in ELM, ${\mathbf{o}}_{\mathrm{j}}$ with $n_h$ hidden neurons can be expressed as follows:

$${\mathbf{o}}_{\mathrm{j}}=\sum _{\mathrm{i}=1}^{n_h}{{\mathbf{\beta }}_i}^{\mathrm{T}}a\left({\mathit{w}}_i^{\mathrm{T}}{\mathit{x}}^{\left(j\right)}+b_i\right)=\sum _{\mathrm{i}=1}^{n_h}{{\mathbf{\beta }}_i}^{\mathrm{T}}{h}_{\mathrm{i}}\left({\mathit{x}}^{\left(j\right)}\right)\hspace{0.17em}={\mathit{h}\left({\mathit{x}}^{\left(j\right)}\right)}^{\mathrm{T}}\mathrm{\beta },$$ (1)

where ${\mathit{x}}^{\left(j\right)}$ and ${\mathit{l}}^{\left(j\right)}$ are the j‐th input and target vectors, respectively. The indices p and q are the dimension of the input and target vector, respectively. And ${\mathbf{o}}_j\in {\mathcal{R}}^{\mathrm{q}}$ indicates the output of ELM for the j‐th training sample, ${\mathit{w}}_i\in {\mathcal{R}}^{\mathrm{p}}$ signifies the input weight that connects the input nodes to the i‐th hidden node, $b_i$ denotes the bias of the i‐th hidden node, and $a(·)$ indicates the activation function for the hidden layer. $\mathrm{\beta }={\left[\begin{array}{ccccc}{\mathrm{\beta }}_1,& ·& ·& ·& {,\mathrm{\beta }}_{n_h}\end{array}\right]}^{\mathrm{T}}$ is the set of output weights between the hidden layer and the output neuron. $\mathit{h}\left({\mathit{x}}^{\left(j\right)}\right)={\left[\begin{array}{ccccc}{h}_1\left({\mathit{x}}^{\left(j\right)}\right),& ·& ·& ·& ,\hspace{0.17em}{h}_{n_h}\left({\mathit{x}}^{\left(j\right)}\right)\end{array}\right]}^{\mathrm{T}}$ is the output vector of the hidden layer with respect to the j‐th training sample ${\mathit{x}}^{\left(j\right)}$. $h_i\left({\mathit{x}}^{\left(j\right)}\right)$ is the output of the i‐th hidden layer for the j‐th training sample.

To find the optimal weights of hidden layer, $\widehat{\mathrm{\beta }}$ with respect to N training samples can be considered to solve the following optimization problem:

$$\underset{\mathrm{\beta }}{\mathrm{min }\mathrm{\lambda }}\Vert {‖\mathbf{H}\mathrm{\beta }-\mathbf{L}\Vert ‖}^2+{\Vert ‖\mathrm{\beta }‖\Vert }^2$$ (2)

where $\mathbf{H}={\left[\begin{array}{ccccc}\mathit{h}\left({\mathit{x}}^{\left(1\right)}\right),& ·& ·& ·& ,\hspace{0.17em}\mathit{h}\left({\mathit{x}}^{\left(N\right)}\right)\end{array}\right]}^{\mathrm{T}}$ and $\mathbf{L}={\left[\begin{array}{ccccc}{\mathit{l}}^{\left(1\right)},& ·& ·& ·& ,{\mathit{l}}^{\left(N\right)}\end{array}\right]}^{\mathrm{T}}$. Equation (2) is a linear optimization problem, and its optimal solution, $\widehat{\mathrm{\beta }},$ can be analytically obtained as follows:

$$\widehat{\mathrm{\beta }}={\mathbf{H}}^{\mathrm{T}}{(\frac{1}{\mathrm{\lambda }}\mathbf{I}+\mathbf{H}{\mathbf{H}}^{\mathrm{T}})}^{-1}\mathbf{L}$$ (3)

where $\mathrm{\lambda }$ is a regularization parameter, and I indicates the identity matrix.

After obtaining the optimal solution $,\hspace{0.17em}\widehat{\mathrm{\beta }}$, the output of the ELM on test data ${\mathit{x}}_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}$ is determined by

$${\mathbf{o}}_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathit{h}\left({\mathit{x}}_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}\right)}^{\mathrm{T}}{\mathbf{H}}^{\mathrm{T}}{(\frac{1}{\mathrm{\lambda }}\mathbf{I}+\mathbf{H}{\mathbf{H}}^{\mathrm{T}})}^{-1}\mathbf{L}$$ (4)

In the case of the output of the kernel‐based extreme learning machine (KELM), $\mathbf{H}{\mathbf{H}}^{\mathrm{T}}$ is transformed to the kernel matrix as follows:

$${\mathbf{o}}_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}=[k\left({\mathit{x}}_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}},{\mathit{x}}^{\left(1\right)}\right),\hspace{0.17em}\dots ,\hspace{0.17em}k\left({\mathit{x}}_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}},{\mathit{x}}^{\left(N\right)}\right)]{\left(\frac{1}{\mathrm{\lambda }}\mathbf{I}+\mathbf{K}\right)}^{-1}\mathbf{L}$$ (5)

where $\mathbf{K}=\mathbf{H}{\mathbf{H}}^{\mathrm{T}}:{\mathrm{\kappa }}_{ij}={\mathit{h}\left({\mathit{x}}^{\left(i\right)}\right)}^{\mathrm{T}}\mathit{h}\left({\mathit{x}}^{\left(j\right)}\right)=k\left({\mathit{x}}^{\left(i\right)},{\mathit{x}}^{\left(j\right)}\right)$ is the kernel matrix of KELM based on Mercer's conditions, and $k\left({\mathit{x}}^{\left(i\right)},{\mathit{x}}^{\left(j\right)}\right)$ is the kernel function of hidden neurons. Instead, the radial basis function (RBF) kernel $k\left({\mathit{x}}^{\left(i\right)},{\mathit{x}}^{\left(j\right)}\right)=\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{\gamma }{‖{\mathit{x}}^{\left(i\right)}-{\mathit{x}}^{\left(j\right)}‖}^2)$ was used in this study.

3.2. Sparse ELM autoencoder (sELM‐AE)

An autoencoder is an artificial neural network that approximates network parameters to make the reconstructed output similar to the input. Thanks to the universal approximation capability of ELM, the ELM‐based auto‐encoder (ELM‐AE) is known to be very effective in many applications (Wei et al., 2016). In this study, we used a sparse ELM auto‐encoder (sELM‐AE) for unsupervised training of the multi‐modal sparse hierarchical extreme learning machine (MSH‐ELM). sELM‐AE adds sparse constraints to the auto‐encoder optimization of ELM‐AE (Tang et al., 2016). In order words, sELM‐AE generates sparser and more compact features from the inputs by conducting $l_1$ optimization for the establishment of the ELM auto‐encoder (Tang et al., 2016). The optimization problem of sELM‐AE can be expressed as follows:

$$O_{\mathrm{\beta }}=\underset{\mathrm{\beta }}{\min }\{\mathrm{\lambda }{‖\Vert |\mathbf{H}\mathrm{\beta }-\mathbf{X}‖\Vert }^2+{‖\Vert \mathrm{\beta }‖\Vert }_{l_1}\}$$ (6)

where $\mathbf{X}={\left[\begin{array}{ccccc}{\mathit{x}}^{\left(1\right)},& ·& ·& ·& {\mathit{x}}^{\left(N\right)}\end{array}\right]}^{\mathrm{T}}$ indicates the input data for N training samples, $\mathbf{H}={\left[\begin{array}{ccccc}\mathit{h}\left({\mathit{x}}^{\left(1\right)}\right),& ·& ·& ·& ,\hspace{0.17em}\mathit{h}\left({\mathit{x}}^{\left(N\right)}\right)\end{array}\right]}^{\mathrm{T}}$ represents the random mapping output, and $\mathrm{\beta }={\left[\begin{array}{ccccc}{\mathrm{\beta }}_1,& ·& ·& ·& {,\mathrm{\beta }}_{n_h}\end{array}\right]}^{\mathrm{T}}$ is the weight matrix for the hidden layer. This optimization problem can be solved by the fast iterative shrinkage‐thresholding algorithm (FISTA) (Tang et al., 2016). In other words, optimal and sparse weight $\widehat{\mathrm{\beta }}$ can be obtained by conducting the iterative procedures of the FISTA algorithm. The detailed procedure employed by FISTA is explained in Beck and Teboulle (2009).

In this study, analogous to other deep learning algorithms such as stacked auto‐encoder adopting auto‐encoder as their basic building block, we adopted sELM‐AE as the basic building block of MSH‐ELM. The weights for each hidden layer were learned by greedy layer‐wise unsupervised training. The detailed procedure for this issue is given in the ensuing section.

3.3. Multimodal sparse hierarchical extreme learning machine (MSH‐ELM)

The approach proposed in this article attempts to extract joint hierarchical representation from three different modalities (MRI, PET, and CSF). The approach employs a proposed hierarchical learning framework, multi‐modal sparse hierarchical extreme learning machine (MSH‐ELM). The training of the proposed multi‐modal architecture consists of three steps: (a) obtain the unsupervised feature representation for each modality individually, (b) compute the feature fusion representation, and (c) apply the supervised feature classification technique based on KELM.

Assuming a training set that consists of N samples $({{\mathit{x}}_1}^{\left(\mathrm{j}\right)},\hspace{0.17em}{{\mathit{x}}_2}^{\left(j\right)},{{\mathit{x}}_3}^{\left(j\right)},{\mathit{l}}^{\left(j\right)})$, where ${{\mathit{x}}_1}^{\left(j\right)}\in {\mathcal{R}}^{p_{\mathrm{M}\mathrm{R}\mathrm{I}}}$, ${{\mathit{x}}_2}^{\left(j\right)}\in {\mathcal{R}}^{p_{\mathrm{P}\mathrm{E}\mathrm{T}}}$, and ${{\mathit{x}}_3}^{\left(j\right)}\in {\mathcal{R}}^{p_{\mathrm{C}\mathrm{S}\mathrm{F}}}$ are the MRI feature vector, the PET feature vector, and the CSF feature vector of the j‐th subject, respectively. ${\mathit{l}}^{\left(j\right)}\in {\mathcal{R}}^q$ is the label vector of the j‐th subject corresponding to the input data $({{\mathit{x}}_1}^{\left(j\right)},\hspace{0.17em}{{\mathit{x}}_2}^{\left(j\right)},{{\mathit{x}}_3}^{\left(j\right)})$. The parameters $p_{\mathrm{M}\mathrm{R}\mathrm{I}}$, $p_{\mathrm{P}\mathrm{E}\mathrm{T}}$, and $p_{\mathrm{C}\mathrm{S}\mathrm{F}}$ are the dimension of MRI feature, PET feature, and CSF feature, respectively. The unsupervised learning procedure of the MSH‐ELM algorithm is summarized in Algorithm 1. In the algorithm, three matrices, ${\mathbf{X}}_1$, ${\mathbf{X}}_2$, and ${\mathbf{X}}_3$ are configured by concatenating an MRI feature set, a PET feature set, and a CSF feature set for N training samples. L is the class label matrix corresponding to the training samples. For example, in Figure 2, three‐layer stacked structures ( $k_1=3)$ are separately constructed for MRI feature ${\mathbf{X}}_1$, PET feature ${\mathbf{X}}_2$, and CSF feature ${\mathbf{X}}_3$ to obtain high‐level representation before they are fused. If the initial input for the first layer is set to ${\mathbf{H}}_{0,m}$ =  ${\mathbf{X}}_m$ (m = 1, 2, 3), the output of the v‐th hidden layer for ${\mathbf{H}}_{0,m}$ can be iteratively computed as

$${\mathbf{H}}_{v,m}\leftarrow a\left({\mathbf{H}}_{v-1,m}{\widehat{\mathbf{\beta }}}_{\mathit{v},m}^{\mathrm{T}}+{\mathbf{B}}_{v,m}\right),\hspace{0.17em}\mathrm{f}\mathrm{o}\mathrm{r} m=1,\hspace{0.17em}2,\hspace{0.17em}3$$ (7)

where $a$(·) represents the activation function, ${\mathbf{H}}_{v,m}$ signifies the feature representation of the v‐th hidden layer for the m‐th modality, and ${\widehat{\mathbf{\beta }}}_{\mathit{v},m}^{\mathrm{T}}$ indicates the optimal weight matrix of the v‐th hidden layer for the m‐th modality. ${\mathbf{B}}_{v,m}$ is the bias matrix for the v‐th hidden layer and the m‐th modality. After obtaining the high‐level representations, ${\mathbf{H}}_{k_1,1}$, ${\mathbf{H}}_{k_1,2}$, and ${\mathbf{H}}_{k_1,3}$, from each modality, they are fused using another three‐layer stacked structure $(k_2=3)$ to estimate the joint hierarchical representation of the three modalities. The combination process is as follows:

$${\mathbf{H}}_{k_1}=[{\mathbf{H}}_{k_1,1},\hspace{0.17em}{\mathbf{H}}_{k_1,2},{\mathbf{H}}_{k_1,3}]$$ (8)

$${\mathbf{H}}_{\mathrm{s}}\leftarrow a({\mathbf{H}}_{s-1}{\widehat{\mathbf{\beta }}}_s^{\mathrm{T}}+{\mathbf{B}}_s),\text{for}\hspace{0.17em}\hspace{0.17em}{k}_1+1\le s\le k_1+k_2$$ (9)

where $k_1$ is the number of hidden layers used to estimate the high‐level representation for each modality, and $k_2$ is the number of hidden layers used to estimate the joint hierarchical representation for the three modalities.

Figure 2.

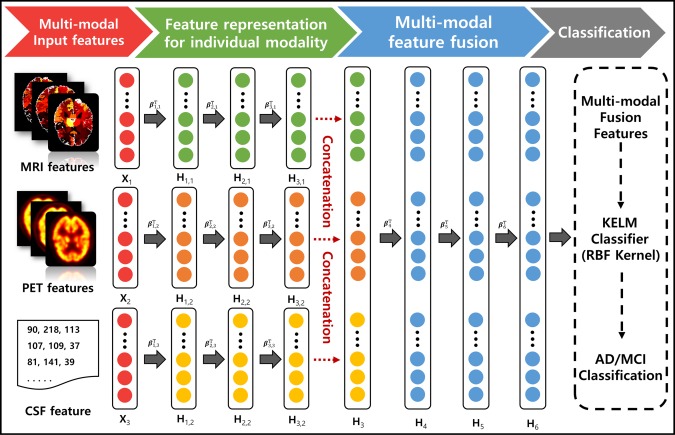
Proposed multi‐modal architecture for fusing MRI, PET, and CSF features. High‐level feature representations extracted from each modality are individually computed using the stacked sparse ELM auto‐encoder (sELM‐AE). Another stacked sELM‐AE is utilized to obtain the joint hierarchical feature representation of MRI, PET, and CSF, taking the high‐level representations of each modality as the input. The obtained joint hierarchical feature representation is classified via the kernel‐based extreme learning machine (KELM) [Color figure can be viewed at http://wileyonlinelibrary.com]

To train the parameters of the network, we used the ELM sparse auto‐encoder (sELM‐AE) described in the previous section. Figure 3 represents the feature learning procedure for the MRI feature ${\mathbf{X}}_1$. It is similar to the feature learning procedure of other modalites and fusion learning. As shown in Figure 3, each hidden layer of MSH‐ELM is a separate sELM‐AE, each of which operates as an individual feature extractor with the target as its input. The high‐level feature representation of the input data can be computed by optimizing Equation (6), and it is utilized as input in the next layer. In Figure 3, sparse optimal weight ${\widehat{\mathrm{\beta }}}_{\mathrm{1,1}}$ for the first layer are computed by optimizing Equation (6) with target matrix ${\mathbf{T}=\mathbf{X}}_1$. Feature representation ${\mathbf{H}}_{\mathrm{1,1}}$ of the first layer corresponding to the input ${\mathbf{X}}_1$ can be calculated by as product of ${\mathbf{X}}_1$ and ${\widehat{\mathrm{\beta }}}_{\mathrm{1,1}}^{\mathrm{T}}$. ${\mathbf{H}}_{\mathrm{1,1}}$ is employed as the input of the sELM‐AE for the next layer.

Figure 3.

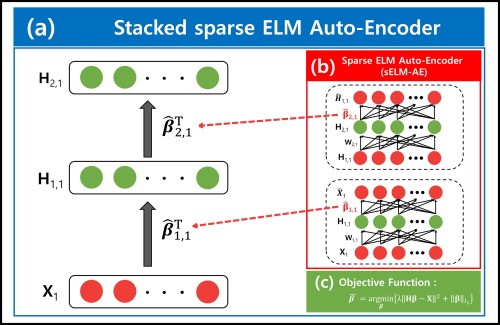
Detailed illustration of the stacked sparse extreme learning machine auto‐encoder (sELM‐AE). (a) Structure of the stacked sELM‐AE for obtaining the hierarchical representation of MR images in MSH‐ELM. It is similar to the feature learning procedure for other modalities and fusion learning in MSH‐ELM. (b) Structure of sELM‐AE. It operates as an individual feature extractor with the target as its input. The weight $\mathrm{\beta }$ of sELM‐AE can be computed by optimizing the objective function denoted in Figure 3c. The calculated weights are utilized as the weights for the hidden layer of stacked sELM‐AE, illustrated in Figure 3a. (c) Objective function for computing the sparse weights of sELM‐AE [Color figure can be viewed at http://wileyonlinelibrary.com]

Finally, the feature representation ${\mathbf{H}}_{{\mathrm{k}}_1+{\mathrm{k}}_2}$ is utilized as the input of KELM to model the mapping between hierarchical joint feature representation and label. In this study, we used RBF $k\left({\mathit{x}}^{\left(i\right)},{\mathit{x}}^{\left(j\right)}\right)=\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{\gamma }{‖{\mathit{x}}^{\left(i\right)}-{\mathit{x}}^{\left(j\right)}‖}^2)$ as the kernel of KELM.

ALGORITHM 1 Multi‐modal sparse hierarchical ELM (MSH‐ELM)

Input : MRI feature matrix ${\mathbf{X}}_1={[{\mathit{x}}_1^{\left(1\right)},\hspace{0.17em}{\mathit{x}}_1^{\left(2\right)},{\mathit{x}}_1^{\left(3\right)},\dots ,{\mathit{x}}_1^{\left(N\right)}]}^T$, PET feature matrix ${\mathbf{X}}_2={[{\mathit{x}}_2^{\left(1\right)},\hspace{0.17em}{\mathit{x}}_2^{\left(2\right)},{\mathit{x}}_2^{\left(3\right)},\dots ,{\mathit{x}}_2^{\left(N\right)}]}^T$, CSF feature matrix ${\mathbf{X}}_3={[{\mathit{x}}_3^{\left(1\right)},\hspace{0.17em}{\mathit{x}}_3^{\left(2\right)},{\mathit{x}}_3^{\left(3\right)},\dots ,{\mathit{x}}_3^{\left(N\right)}]}^T$ and label matrix L =  ${[{\mathit{l}}^{\left(1\right)},{\mathit{l}}^{\left(2\right)},{\mathit{l}}^{\left(3\right)},\dots ,{\mathit{l}}^{\left(N\right)}]}^T$ corresponding to each training instance, ${\mathit{x}}_1^{\left(j\right)}\in {\mathcal{R}}^{p_{MRI}}$, ${\mathit{x}}_2^{\left(j\right)}\in {\mathcal{R}}^{p_{PET}},{\mathit{x}}_3^{\left(j\right)}\in {\mathcal{R}}^{p_{CSF}},{\mathit{l}}^{\left(j\right)}\in {\mathcal{R}}^2$

Output: weight matrixes ${\widehat{\mathbf{\beta }}}_{v,m}$ for $v\in [1,k_1]$, $m\in \left[\mathrm{1,3}\right]$, and ${\widehat{\mathbf{\beta }}}_s$ for $s\in [k_1+1,k_1+k_2]$,

Initialization: Choose separate modality depth $k_1$, fusion learning model depth $k_2$ and the node number $n_h$

for m = 1 to 3 do

${\mathbf{H}}_{0,m}$ =  ${\mathbf{X}}_m$

for v = 1 to $k_1$ do

Randomly generate hidden input weight matrix ${\mathbf{W}}_{v,m}$, bias matrix ${\mathbf{B}}_{v,m}$ ;

Compute hidden layer output ${\mathbf{H}}_{v,m}$ = a( ${\mathbf{W}}_{v,m}{\mathbf{H}}_{v-1,m}$+ ${\mathbf{B}}_{v,m})$ ;

Calculate ${\widehat{\mathbf{\beta }}}_{v,m}$ by solving ${\widehat{\mathbf{\beta }}}_{v,m}=\underset{{\mathbf{\beta }}_{\mathit{v},\mathit{m}}}{\mathrm{argmin}}\left\{\mathrm{\lambda }\Vert {‖{\mathbf{H}}_{v,m}{\mathbf{\beta }}_{v,m}-{\mathbf{H}}_{v-1,m}‖\Vert }^2+{‖{\mathbf{\beta }}_{\mathit{v},m}‖}_{l_1}\right\}$ using fast iterative shrinkage‐thresholding algorithm (FISTA) ;

Update ${\mathbf{H}}_{v,m}$ = a( ${\mathbf{H}}_{v-1,m}{\widehat{\mathbf{\beta }}}_{\mathit{v},m}^{\mathrm{T}}$+ ${\mathbf{B}}_{v,m})$;

end for

end for

${\mathbf{H}}_{k_1}$= $[{\mathbf{H}}_{k_1,1},\hspace{0.17em}{\mathbf{H}}_{k_1,2},{\mathbf{H}}_{k_1,3}]$

for s =  $k_1$+1 to $k_1$+ $k_2$ do

Randomly generate hidden input weight ${\mathbf{W}}_s$, bias matrix ${\mathbf{B}}_s$ ;

Compute hidden layer output ${\mathbf{H}}_s=a({\mathbf{W}}_s{\mathbf{H}}_{s-1}+{\mathbf{B}}_s)$ ;

Calculate ${\widehat{\mathbf{\beta }}}_s$ by solving ${\widehat{\mathbf{\beta }}}_s=\underset{{\mathbf{\beta }}_s}{\mathrm{argmin}}\left\{{\mathrm{\lambda }\Vert ‖{\mathbf{H}}_s{\mathbf{\beta }}_s-{\mathbf{H}}_{s-1}‖\Vert }^2+{‖{\Vert \mathbf{\beta }}_s‖\Vert }_{l_1}\right\}$ using fast iterative shrinkage‐thresholding algorithm (FISTA)

Update ${\mathbf{H}}_s$ = a( ${\mathbf{H}}_{s-1}{\widehat{\mathbf{\beta }}}_s^{\mathrm{T}}$+ ${\mathbf{B}}_s)$ ;

end for

3.4. Experimental setup

We structured a three‐layer stacked sELM‐AE for MRI (MRI‐AE), PET (PET‐AE), and CSF (CSF‐AE), respectively, and another three‐layer stacked sELM‐AE for fusing the high‐level representation of MRI, PET, and CSF (Joint‐AE). We set the number of nodes for MRI‐AE, PET‐AE, CSF‐AE, and Joint‐AE to 200(hidden1)–200(hidden2)–200(hidden3). In the learning of sELM‐AE, we updated the weights with a learning rate of ${10}^{-3}$ for 5,000 iterations. The obtained joint hierarchical feature representation was classified using the KELM classifier, which is the final layer of MSH‐ELM. RBF was utilized as the kernel of KELM. RBF kernel parameter, $\mathrm{\gamma }$ was set to (1/number of features) in this study.

We compared MSH‐ELM to SK‐SVM, ELM, MK‐SVM, and SAE. An LIBSVM toolbox was used to train MK‐SVM and SK‐SVM, and Neural Network Toolbox in MATLAB 2016a was used to train SAE. In case of MK‐SVM, both linear kernel and RBF kernel were applied. We set gamma of kernel function to 1/(number of features) and fixed the trade‐off parameter, C = 100 for RBF kernel as it shows the best classification performance in validation set. The other parameters of MK‐SVM such as weights for the multiple kernels were determined via nested cross‐validation.

In case of SAE, greedy layer‐wise pretraining learning was performed first, and then supervised fine‐tuning was performed to further optimize the network parameters. The parameters computed from the pretraining phase prevent the fine‐tuning optimization from falling into a local optimum (Hinton, 2006). The network structure of SAE that produces the best classification performance was determined via nested cross‐validation only using training dataset.

3.5. Performance evaluation

TP, TN, FP, and FN represent the true positive, true negative, false positive, and false negative, respectively. The accuracy (ACC), sensitivity (SEN), specificity (SPEC), balanced accuracy (BAC), positive predictive value (PPV), and negative predictive value (NPV) can thus be computed as follows:

1. Accuracy (ACC) = (TP + TN)/(TP + TN + FP + FN)

2. Sensitivity (SEN) = TP/(TP + FN)

3. Specificity (SPEC) = TN/(TN + FP)

4. Balanced accuracy (BAC) = (SEN + SPEC)/2

5. Positive predictive value (PPV) = TP/(TP + FP), and

6. Negative predictive value (NPV) = TN/(TN + FN)

4. EXPERIMENTAL RESULTS

Tables 2 and 3 show the performances of the proposed MSH‐ELM and comparative algorithms for the classification of AD from HC and the classification of MCI from HC, respectively. As can be seen in Tables 2 and 3, the proposed multi‐modal classification approach has consistently superior performance to the comparative algorithms for all cases (AD vs. HC and MCI vs. HC). Specifically, in the classification of AD from HC, the proposed MSH‐ELM method shows mean accuracies of 97.12%, sensitivity of 98.08%, a specificity of 94.12%, balanced accuracy of 96.10%, PPV of 94.44%, and NPV of 97.96%, whereas the mean accuracy of MK‐SVM with linear kernel was 93.2%, the mean accuracy of SAE was 88.35% and the best mean accuracy of SK‐SVM among individual modalities was only 86.41% when using PET image.

Table 2.

Summary of the performances for AD versus HC classification

Method	Modality	ACC (%)	SEN (%)	SPEC (%)	BAC (%)	PPV (%)	NPV (%)
SK‐SVM	MRI	83.50	90.38	76.47	83.43	79.66	88.64
	PET	86.41	82.69	90.20	86.44	89.58	83.64
	CSF	85.44	80.77	90.20	85.48	89.36	82.14
	CONCAT	91.26	96.15	86.27	91.21	87.72	95.65
ELM	MRI	83.50	90.38	76.47	83.43	79.66	88.64
	PET	86.41	82.69	90.20	86.44	89.58	83.64
	CSF	85.44	80.77	90.20	85.48	89.36	82.14
	CONCAT	91.26	96.15	86.27	91.21	87.72	95.65
MK‐SVM with linear kernel	MRI + PET + CSF	93.20	98.08	88.24	93.16	89.47	97.83
MK‐SVM with RBF kernel	MRI + PET + CSF	92.23	94.23	90.20	92.21	90.74	93.88
SAE	CONCAT	88.35	88.24	88.46	88.35	88.24	88.46
MHS‐ELM (ELM_RBF)	MRI + PET + CSF	97.12	98.08	94.12	96.10	94.44	97.96

Note. Boldface denotes the best performance in individual metric for each classification task.

Table 3.

Summary of the performances for HC versus MCI classification

Method	Modality	ACC (%)	SEN (%)	SPEC (%)	BAC (%)	PPV (%)	NPV (%)
SK‐SVM	MRI	70.86	40.38	86.87	63.63	61.76	73.50
	PET	82.78	57.69	95.96	76.83	88.24	81.20
	CSF	68.21	50.00	77.78	63.89	54.17	74.76
	CONCAT	85.43	67.31	94.95	81.13	87.50	84.68
ELM	MRI	70.86	40.38	86.87	63.63	61.76	73.50
	PET	82.78	57.69	95.96	76.83	88.24	81.20
	CSF	68.21	50.00	77.78	63.89	54.17	74.76
	CONCAT	85.43	67.31	94.95	81.13	87.50	84.68
MK‐SVM with linear kernel	MRI + PET + CSF	85.43	65.38	95.96	80.67	89.47	84.07
MK‐SVM with RBF kernel	MRI + PET + CSF	84.11	71.15	90.91	81.03	80.43	85.71
SAE	CONCAT	84.77	89.90	75.00	82.45	87.25	79.59
MHS‐ELM (ELM_RBF)	MRI + PET + CSF	87.09	75.00	91.92	83.46	82.98	87.50

Note. Boldface denotes the best performance in individual metric for each classification task.

In classification of MCI from HC patients, our proposed method achieved a classification accuracy of 87.09%, sensitivity of 75.00%, specificity of 91.92%, balanced accuracy of 83.46%, PPV of 82.98%, and an NPV of 87.50%, whereas the mean accuracy of MK‐SVM with linear kernel was 85.43%, the mean accuracy of SAE was 84.77%, and the best mean accuracy of SK‐SVM among individual modalities was only 82.78% when using PET images. Interestingly, the average classification accuracy of MK‐SVM with linear kernel was very close to the classification accuracy of MHS‐ELM. However, in this case, the sensitivity of MK‐SVM with linear kernel was much lower than that of MHS‐ELM. We assume that this result was due to the data imbalance between the classes, that is, MCI (99 subjects) and NC (52 subjects). Balanced accuracy avoids the inflated performance of unbalanced datasets. In terms of balanced accuracy, it is clear that the proposed method outperformed the competition methods in the case of MCI vs. HC.

The performance of MK‐SVM with RBF was slightly lower than that of MK‐SVM with linear kernel for both classification problems (AD vs. HC and MCI vs. HC).

We also investigated the performance of the classifiers after reducing the number of samples in the MCI group by 50% to check the effects of data imbalance problems. Similar to the previous experiment, our proposed method achieved the highest classification performance among other comparative classifiers. Specifically, MSH‐ELM shows a classification accuracy of 86.53%, whereas the mean accuracy of MK‐SVM was 84.62% and the mean accuracy of SAE was 72.12%.

On the basis of the results presented above, the proposed method is clearly superior to MK‐SVM and SK‐SVM in the problem of classifying AD and MCI from HC.

4.1. Comparison with other studies

In Table 4, the classification accuracy of the proposed method is compared with the results of a recently published studies that used multi‐modality data in the classification of AD and MCI from HC. It should be noted that direct comparison of performance between methods is not fair because of the different datasets, preprocessing procedures, and type of features. Nonetheless, it is noteworthy that the proposed method has the highest accuracy among the methods reported in the classification problem of AD and MCI from HC.

Table 4.

Comparison of classification accuracy with state‐of‐the‐art methods

Methods	Dataset (AD/MCI/HC)	AD vs. HC (%)	MCI vs. HC (%)
Kohannim et al.	MRI + PET + CSF (40/83/43)	90.70	75.80
Walhovd et al.	MRI + CSF (38/73/42)	88.80	79.10
Hinriches et al.	MRI + PET + CSF + APOE + Cognitive scores (48/119/66)	92.40	n/a
Westman et al.	MRI + CSF (96/162/111)	91.80	77.60
Zhang and Shen	MRI + PET + CSF (45/91/50)	93.30	83.20
Gray et al.	MRI + PET (51/75/35)	89.00	74.60
Liu et al.	MRI+PET+CSF (51/99/52)	94.37	78.80
Suk et al.	MRI+PET+CSF+ Cognitive scores (51/99/52)	95.90	85.00
Proposed method	MRI+PET+CSF (51/99/52)	97.12	87.09

Note. Numbers in parentheses denote the number of AD/MCI/NC subjects in the dataset used. Boldface denotes the best performance in each classification task.

4.2. Effect of feature selection

In the previous section, we applied the proposed multi‐modal classification method without feature selection for AD and MCI classification. In this section, the proposed method with feature selection is tested and compared with the performance of the proposed method without feature selection. The main objective of this section is to verify whether feature selection is effective for the proposed method. For this reason, we simply applied a feature selection method based on the t test and Least Absolute Shrinkage and Selection Operator (LASSO) which are widely used in this field. We performed a paired t‐test and LASSO on training samples to choose the optimal subset of features. Table 5 shows the list of top 10 brain regions selected by the t‐test‐based feature selection algorithm in AD classification and Figures 4 and 5 present the brain areas detected from MRI and PET in the template MRI space, respectively. The selected regions include the amygdala, hippocampal formation, and uncus, which is known to be highly related to the AD by numerous studies based on the group comparison methods. In particular, the hippocampus, which is found in both Figures 4 and 5, is a brain area that plays an important role in information integration from short‐term memory to long‐term memory and is known as the first brain area to be damaged by Alzheimer's disease (Chételat et al., 2002; Convit et al., 2000; Fox et al., 2004; Jack et al., 1999; Misra et al., 2009). We computed the classification accuracies according to the number of selected features and filled out the result of the feature subset showing the best classification performance in Table 6. Interestingly, there was no significant difference in the results between with feature selection and without feature selection. We assume that these results suggest that MSH‐ELM itself extracts compact and optimal feature subsets that are equal to or greater than the t‐test‐based feature selection method and LASSO based feature selection method.

Table 5.

Top 10 brain regions for AD classification selected by t‐test‐based feature selection method (p value ≪ .001)

	MRI	PET
1	Amygdala right	Precentral gyrus left
2	Amygdala left	Angular gyrus left
3	Hippocampal formation right	Occipital pole right
4	Hippocampal formation left	Medial occipitotemporal gyrus left
5	Uncus left	Temporal lobe WM right
6	Middle temporal gyrus right	Hippocampal formation right
7	Middle temporal gyrus left	Superior parietal lobule right
8	Angular gyrus left	Precentral gyrus right
9	Perirhinal cortex right	Superior parietal lobule left
10	Lateral occipitotemporal gyrus left	Caudate nucleus right

Figure 4.

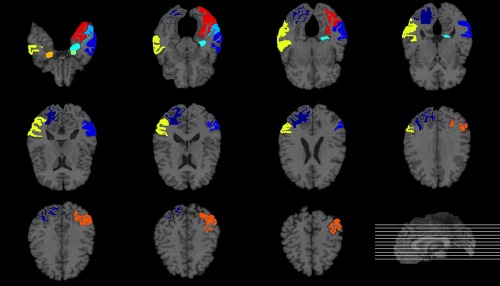
Top ten most frequently selected MRI regions by t‐test‐based feature selection method in AD classification. Different colors represent different brain regions [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 5.

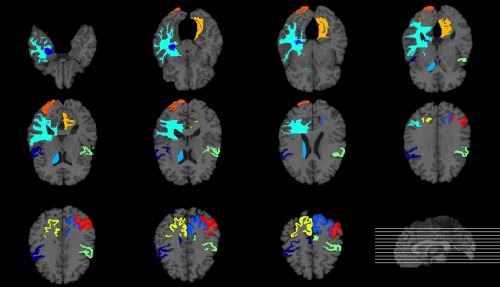
Top ten most frequently selected PET regions by t‐test‐based feature selection method in AD classification. Different colors represent different brain regions [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 6.

Classification performances of the proposed method with feature selection and without feature selection

Method	AD vs. HC			MCI vs. HC
	ACC (%)	SEN (%)	SPEC (%)	ACC (%)	SEN (%)	SPEC (%)
Without feature selection	97.12	98.08	94.12	87.09	75.00	91.92
t‐test‐based feature selection	96.11	98.01	92.12	86.15	75.12	91.95
LASSO‐based feature selection	96.03	97.01	91.13	86.17	75.15	91.96

Note. Feature selection was performed based on a paired t‐test between two groups (AD vs. HC or MCI vs. HC) or LASSO only using training samples.

However, if the advanced method is used instead of the simple feature selection method, the above results may be different. Therefore, further study about the effect of feature selection on the proposed method is needed.

5. DISCUSSION

5.1. Comparative algorithms

We compared the performance of MSH‐ELM to those of SK‐SVM, ELM, MK‐SVM, and SAE. The reasons for choosing SK‐SVM, ELM, MK‐SVM, and SAE as comparative algorithms are as follows: (a) SK‐SVM has been widely used as a reference classifier for performance comparison in AD/MCI classification problem (Cui et al., 2011; Dyrba et al., 2012; Li et al., 2015; Liu, Wee, Chen, and Shen, 2014a; Liu et al., 2014b; Suk and Shen, 2013; Zhang et al., 2011). (b) ELM was selected to prove the effectiveness of multi‐modal feature extraction performance of MSH‐ELM. (c) MK‐SVM is known as one of the most powerful classifier for AD/MCI classification problem (Zhang et al., 2011). Therefore, MK‐SVM has been used as a comparative algorithm in many studies related to AD/MCI classification (Dyrba et al., 2012; Liu et al., 2014b; Suk, Lee, and Shen, 2015; Suk and Shen, 2013). (d) We used SAE as a comparative algorithm because Suk et al. showed that the classification performance of SAE is superior to that of MK‐SVM in AD/MCI classification problem (Suk and Shen, 2013). Another reason to select SAE as comparative algorithm is that SAE is very similar to MSH‐ELM in that SAE is a deep neural network built with many auto‐encoders and trained by greedy layerwise. The major difference between SAE and MSH‐ELM is that ELM‐AE is used as a base building block and multi‐modal feature extraction is performed in MSH‐ELM. We expected to verify the effectiveness of ELM‐AE and multi‐modal feature extraction through comparison of the performances of the two algorithms.

5.2. Performance analysis

The proposed MSH‐ELM shows better AD classification performance than conventional ELM using individual single modality data or simple concatenation feature of multi‐modality data (MRI, PET, and CSF). This means that MSH‐ELM, a deep network, discovered the optimal feature representation for AD classification that was not found in a conventional ELM, shallow network. In addition, MSH‐ELM effectively extracted AD‐related complementary features from multiple modalities which are helpful for discrimination of AD, MCI, and HC. As shown in Tables 2 and 3, the ability of MSH‐ELM to integrate multi‐modal data is superior to that of MK‐SVM, which is widely used in AD classification using multi‐modal data.

Additionally, we compared the classification performance of MSH‐ELM with SAE which is the back propagation‐based multi‐layer perceptron (MLP) learning algorithm. MSH‐ELM showed higher performance than that of SAE in two binary classification problems (AD vs. HC and MCI vs. HC).

Furthermore, the computation load of MSH‐ELM is much lower than SAE as the base building block of MSH‐ELM is ELM‐AE, which randomly assigns the weights for hidden layer. According to Tang et al. (2016), MLP using ELM‐AE as a base building block is more efficient than the latest back propagation‐based MLP (SAE, deep belief network, and deep Boltzmann machine) for MNIST and NORB dataset classification in terms of classification accuracy and computation speed.

Another interesting aspect of the MSH‐ELM is that the MSH‐ELM exhibits excellent classification performance even though the dimension of the hidden neurons was higher than that of input neuron.

We think that this is because the base building block of MSH‐ELM is a sparse ELM auto‐encoder. Imposing the sparsity constraint on the hidden units allows the hidden layers to have larger number of units than the input dimension (Larochelle et al., 2009; Suk and Shen, 2013).

5.3. Limitations and future work

In this study, although the proposed multi‐modal classification framework exhibits utility in binary classification cases (AD vs. HC and MCI vs. HC), it has several limitations.

The first limitation is the lack of the number of data samples (52 AD, 99 MCI, and 51 NC) to learn the proposed algorithm. For this reason, we cannot be certain that the joint hierarchical feature representations extracted from the proposed method are globally optimal. Therefore, additional research is needed such as learning the optimal parameters of the deep network structure from large data samples for practical use in a clinical environment.

Another limitation is that it is difficult to interpret the joint hierarchical feature representation extracted by the MSH‐ELM method and to provide effective clinical information. Thus, further research is required to provide clinicians with useful information such as brain regions that are highly related to AD and MCI.

Next, the training procedure of hierarchical feature extractor and classifier for MSH‐ELM is not performed simultaneously. We expect that the performance of MSH‐ELM would be improved by developing a way to train hierarchical feature extractors and classifiers together. Multiple kernel learning (MKL) which has been recently studied for joint optimal feature fusion might be a suitable way to improve the performance of MSH‐ELM. For example, multiple kernel ELM (MK‐ELM) proposed by Liu et al. shows the improvement of classifier by applying MKL into ELM for Protein, Oxford Flower17, Caltech101 and Alzheimer's disease data sets (Liu et al., 2015). To estimate the possibility of joint optimal feature fusion based on MKL and identify the effectiveness of multi‐modal feature extraction capability of MSH‐ELM, we additionally conducted both simpleMKL and MK‐ELM for automatic diagnosis of AD from NC. We used the SimpleMKL toolbox to implement the simpleMKL method and Multi‐Kernel‐Extreme‐Learning‐Machine toolbox to implement the MK‐ELM method (code is available at http://asi.insa-rouen.fr/enseignants/~arakoto/code/mklindex.html and https://github.com/xinwangliu/Multi-Kernel-Extreme-Learning-Machine) (Rakotomamonjy et al., 2008). We conducted simpleMKL and MK‐ELM using (a) raw feature or (b) joint learned feature from multi‐modal feature extractor of MSH‐ELM as the input of the classifier. We used SVM as a classifier for simpleMKL and fixed the tradeoff parameter, C = 100 as it shows the best classification performance in validation set. Linear kernel and Gaussian kernels with 10 different kernel bandwidths ({ $2^{-3}$, $2^{-2}$,…, $2^6$} multiplied by $\sqrt{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{f}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{s}}$) for each feature representation was applied to simpleMKL and MK‐ELM (Liu et al., 2013). When using the raw features as the input of the classifier, the simpleMKL and MK‐ELM's balanced accuracy were around 0.90 very similarly. When using the joint learned features obtained from the sELM‐AE of the MSH‐ELM, the simpleMKL's balance accuracy was 0.94 and the MK‐ELM's balance accuracy was 0.93. This results show that feature extractor of MSH‐ELM is very robust for multi‐modal feature extraction, and joint learned features of MSH‐ELM are better classified using the single kernel ELM than using multiple kernel methods in our case. It is necessary to develop a better method than existing MKL to improve the performance of AD classification and extract joint multi‐modal optimal feature.

Finally, our multi‐modal classification framework only considers structural MRI, PET, and CSF. However, it is expected that combining as many modalities as possible would be efficient for discrimination of AD and MCI from HC. Accordingly, in further studies, we will build a multi‐modal classification framework that combines the multi‐modal data including medical imaging, genetics, proteomics, and cognition.

6. CONCLUSION

In this article, we proposed a method for obtaining joint hierarchical feature representation from structural MRI, PET, and CSF called MSH‐ELM. The proposed method uses a stacked sELM‐AE to find a high‐level feature representation from individual modalities (MRI, PET, and CSF), and another stacked sELM‐AE to acquire joint hierarchical feature representation. Unlike MK‐SVM, which combines the features extracted from individual modalities in a kernel technique, the proposed MSH‐ELM method extracts the joint hierarchical feature representation through a deep neural network structure. The superior classification performance of our proposed method in terms of various quantitative metrics compared to those of other comparative methods indicates that the proposed MSH‐ELM method effectively integrates the complimentary information from MRI, PET, and CSF.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supporting Information

Kim J, Lee B. Identification of Alzheimer's disease and mild cognitive impairment using multimodal sparse hierarchical extreme learning machine. Hum Brain Mapp. 2018;39:3728–3741. 10.1002/hbm.24207