Abstract
The ability of the cerebral vasculature to regulate vascular diameter, hence resistance and cerebral blood flow (CBF), in response to metabolic demands (neurovascular coupling), and perfusion pressure changes (autoregulation) may be assessed by measuring the CBF response to carbon dioxide (CO2). In healthy individuals, the CBF response to a ramp CO2 stimulus from hypocapnia to hypercapnia is assumed sigmoidal or linear. However, other response patterns commonly occur, especially in individuals with cerebrovascular disease, and these remain unexplained. CBF responses to CO2 in a vascular region are determined by the combined effects of the innate vascular responses to CO2 and the local perfusion pressure; the latter ensuing from pressure‐flow interactions within the cerebral vascular network. We modeled this situation as two vascular beds perfused in parallel from a fixed resistance source. Our premise is that all vascular beds have a sigmoidal reduction of resistance in response to a progressive rise in CO2. Surrogate CBF data to test the model was provided by magnetic resonance imaging of blood oxygen level‐dependent (BOLD) signals. The model successfully generated all the various BOLD‐CO2 response patterns, providing a physiological explanation of CBF distribution as relative differences in the network of vascular bed resistance responses to CO2. Hum Brain Mapp 38:5590–5602, 2017. © 2017 Wiley Periodicals, Inc.
Keywords: cerebral blood flow, carbon dioxide, model, cerebral vascular resistance
INTRODUCTION
Cerebral blood flow (CBF) is regulated to maintain an appropriate blood supply to the diverse regions of the brain. This regulation relies on control of vascular diameter to alter vascular resistance, and parenchymal arterioles, the last smooth muscle‐containing vessels upstream of the capillary bed [Hirsch et al., 2012], account for about 30% of the total resistance [Faraci and Heistad, 1990]. Their role is divided between pressure autoregulation, whereby an appropriate capillary perfusion pressure is maintained under both normal and pathologic alterations in systemic blood pressure [Hill et al., 2006; Lucas et al., 2010; Osol et al., 2002; Tan and Taylor, 2014], and neurovascular coupling, whereby local increases in metabolic demand are satisfied by functional hyperemia [Attwell et al., 2011; Iadecola, 2004; Wells et al., 2015]. Because vascular resistance also changes in response to vasoactive substances like carbon dioxide (CO2), the CBF changes in response to the end‐tidal partial pressures of CO2 (PetCO2) can be used to assess a region's ability to regulate its blood flow [Sobczyk et al., 2015, 2016].
In healthy subjects, the CBF response to PetCO2 in major arteries like the middle cerebral artery is sigmoidal [Battisti‐Charbonney et al., 2011], providing that arterial blood pressure remains constant [Regan et al., 2014]. More detailed regional responses can be seen in studies using magnetic resonance imaging (MRI) where the blood oxygen level‐dependent (BOLD) signal provides a surrogate measure of CBF. In healthy subjects, changes in the BOLD signal are mostly uniform throughout the gray matter (GM) and white matter (WM), again increasing sigmoidally as a function of PetCO2 [Bhogal et al., 2014, 2015; Sobczyk et al., 2014]. However, in some regions, BOLD responses deviate from a sigmoidal or linear relation to PetCO2, especially in patients with cerebrovascular disease, but also in some healthy subjects [Fisher et al., 2017]. These BOLD‐CO2 response patterns are of particular interest in patients because they may be related to the pathophysiology of vascular disease [Sobczyk et al., 2014]. We therefore sought a physiological explanation for these various BOLD‐CO2 response patterns in terms of changes in vascular resistance with PetCO2.
CBF responses to PetCO2 in a vascular region are determined by the combined effects of the innate vascular resistance response to CO2 and the local perfusion pressure. The innate vascular resistance response to CO2 is necessarily of sigmoidal shape, due to the limits of vasodilation and vasoconstriction, with resistance highest in hypocapnia and lowest in hypercapnia. Local perfusion pressure is determined by pressure‐flow interactions within the cerebral vascular network as overall CBF changes in response to CO2. When vessels dilate and CBF increases, the perfusion pressure distal to the major supply arteries decreases, lowering the local perfusion pressure. This aspect is particularly prominent in the cerebral vasculature because of the high resistance of the cerebral arterial supply system–the highest of all body organ vascular supply systems [Faraci and Heistad, 1990]. The net result is that, in brain regions with a robust vasodilatory capacity, increases in blood flow may be accompanied by reductions in regional perfusion pressure. Blood flow may then fall in vascular beds with less robust vasodilatory capacity. The latter situation has been labeled the cerebrovascular steal phenomenon [Conklin et al., 2010; Sobczyk et al., 2014].
To describe the combined effects of the innate vascular resistance responses to CO2 and the network local perfusion pressure changes, we used a simple model of two vascular beds with independent resistance profiles, perfused from the same supply vessel. The resistance model (Fig. 1A) was kept as simple as possible, following the form described by [Sobczyk et al., 2014]. As shown in Figure 2, we suggest that this model, expanded in a fractal pattern of vessels and vessel beds perfused in parallel by a feeding vessel, exists at all scales from individual capillaries up to inter‐hemispheric vascular beds [Lorthois and Cassot, 2010]. To test this model, we used the measured BOLD responses to a ramp change in PetCO2 from hypocapnia to hypercapnia as the flow changes in the model vascular beds, and calculated the changes of resistance with PetCO2. We thought that if the model correctly describes how blood flow is distributed in the brain, then, for all patterns of the BOLD‐CO2 responses to progressive PetCO2, the calculated changes in resistance with PetCO2 should be characterized by sigmoid functions. In turn, these sigmoidal resistance‐CO2 functions, when applied to the model, should correctly generate the various observed BOLD‐CO2 response patterns [Fisher et al., 2017], thus through “changes in vascular resistance,” providing a physiological explanation for them.
Figure 1.

A simple 2‐vascular‐bed model of a cerebral vascular region. (A) A theoretical illustration of two brain vascular territories both supplied in parallel by a major supply artery with resistance. Their vasodilatory responses are shown as shading. (B) A simple resistance circuit model. Reference and examined vascular beds with resistances R1 and R2 are perfused via an arterial flow resistance (Rart) from mean arterial blood pressure (MAP). The pressure perfusing the two branches (Pbranch) and their respective resistances establishes flows through each branch (F1 and F2), that sum to Ftotal. Given F1 and F2 as BOLD measures for the reference and examined voxels, R1 and R2 can be calculated by considering the model as an analog of an electrical circuit.
Figure 2.
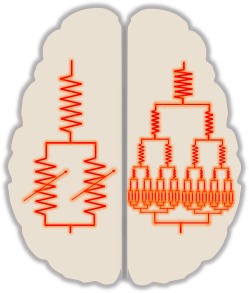
An illustration of the concept that this model, expanded in a fractal pattern of vessels and vessel beds perfused in parallel by a feeding vessel, exists at all scales from individual capillaries up to inter‐hemispheric vascular beds.
METHODS
Resistance Model
Description
The model electrical circuit analog (Fig. 1B) consists of two vascular beds, each with resistance (R1 and R2) and flows (F1 and F2), perfused by a common major arterial vessel of fixed resistance (Rart), so that the local perfusion pressure (Pbranch) changes with the total flow through the two branches (Ftotal). The model assumes a resting state, where metabolic and neural activation is neglected so that the only determinant of vasoactivity is PetCO2. Under conditions where intracranial pressure and venous backpressure are not limiting, the overall cerebral perfusion pressure is determined by the arterial blood pressure (MAP).
F1 and F2 are the BOLD responses to CO2 for a reference voxel, chosen to represent a standard healthy voxel, and any other examined voxel respectively. The standard voxel response acts as a summation of all vascular responses that determine the changes in the local perfusion pressure (Pbranch) experienced by the examined voxel during a CO2 challenge. It should therefore be chosen from a voxel in a region of robust response. While not reproducing the flow that determines the actual local perfusion pressure, which is unknown, the standard voxel response provides a challenge that is the same for all examined voxels. In this way, the resistance response calculated for any examined voxel is relative to that of any other examined voxel so that comparisons can be made between voxels and vascular regions. Thus, despite not measuring absolute vascular resistance, we consider the calculated resistance response patterns to reflect the changes in vascular resistance with PetCO2 that determine the BOLD response patterns that measure cerebrovascular reactivity (CVR).
Solution
Figure 3 illustrates the processing flow for solving the model. As BOLD is not an absolute measure of flow it was scaled to the model as % changes from 100% at resting PetCO2, so that F1 and F2 = 100% and the total flow through Rart is 200%. Assuming the pressure loss in Rart to be 30% of the total perfusion pressure (MAP) at resting PetCO2, [Faraci and Heistad, 1990], then, with MAP as 100 mmHg, Rart = pressure loss divided by total flow = 30/200 = 0.15 (mm Hg/%). The model is analogous to an electrical circuit with the following equations applied at each PetCO2 of the ramp stimulus:
| (1) |
| (2) |
| (3) |
| (4) |
Figure 3.

A diagram showing the data processing flow.
The resistance model solution was automated using a specially written computer program (LabVIEW, National Instruments, TX), which also used the Levenberg–Marquardt algorithm to fit the calculated variations in R1 and R2 with PetCO2 using the following sigmoid function illustrated in Figure 4:
| (5) |
Figure 4.

The sigmoidal relation between resistance and PetCO2 showing the parameters that define it.
Where:
R = resistance (pressure/flow, mmHg/%), a function of PetCO2
a = maximum flow resistance in hypocapnia, Rmax
b = amplitude = minimum – maximum resistance
c = sigmoid midpoint PetCO2 where slope (sensitivity) is maximum (mmHg)
d = PetCO2 range over which resistance is linear (mmHg)
To determine the quality of fit of the resistance sigmoids fitted to the examined voxel we calculated the r 2. The fitted resistance sigmoidal responses to PetCO2 for R1 and R2 were then used to calculate the model flow responses, which should fit the measured BOLD‐CO2 responses, and we recorded the r 2 of the examined voxel BOLD fit.
Experimental Protocol
Subjects
The example data used to illustrate the functioning of the model originated from a 57‐year‐old male patient in our database with left internal carotid occlusion that had undergone a standardized testing protocol as a result of participation in a Research Ethics Board (REB) approved study at our institution. This subject was chosen as typical of those with voxel BOLD responses to a ramp increase in PetCO2 displaying the four types of response pattern seen in an earlier study [Fisher et al., 2017]. The study conformed to the standards set by the latest revision of the Declaration of Helsinki, and was approved by the REB of the University Health Network and Health Canada. All subjects in the database were competent and gave written informed consent.
Data acquisition
For testing, subjects breathe via a face mask, connected to a sequential gas delivery breathing circuit [Somogyi et al., 2005]. The CO2 stimulus sequence consists of clamping PetCO2 at the subject's resting baseline for 1 min, a step increase by 10 mm Hg for 2 min followed by 2 min at baseline. PetCO2 is then slowly reduced by 10 mm Hg over 30 sec, followed by a steady rise in PetCO2 to 15 mm Hg above baseline over 4.3 min, and a return to baseline for 2 min. This stimulus pattern, shown in Figure 5, was programmed into a computer‐controlled gas blender (RespirAct™, Thornhill Research, Toronto, Canada) running a prospective gas targeting algorithm [Slessarev et al., 2007], which has been shown to control the CO2 stimulus such that PetCO2 is equivalent to PaCO2 [Ito et al., 2008; Willie et al., 2012].
Figure 5.
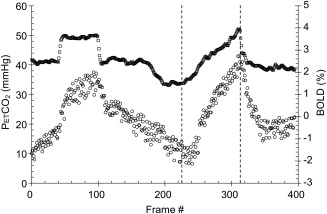
PetCO2 (mm Hg, squares) and mean whole brain BOLD (Δ% from mean, circles) versus time. The step response is used in another analysis for speed of response, and the ramp response used in this study is shown delineated between the dashed lines.
The BOLD acquisitions with echo planar imaging gradient echo (TR/TE = 2,400/30 ms, 3.5 mm voxels, field of view 24 × 24 cm, 39 slices, slice thickness 3.5 mm, matrix size 64 × 64, number of frames = 405, flip angle = 70°) were obtained using a 3.0‐Tesla Signa HDx scanner with an 8‐channel phased‐array receiver coil (GE Healthcare, Milwaukee, Wisconsin). The acquired MRI and PetCO2 data were analyzed using AFNI software [Cox, 1996]. BOLD images were then volume registered and slice‐time corrected and co‐registered to an axial 3‐D T1‐weighted Inversion‐Recovery prepared Fast Spoiled Gradient‐Echo (IR‐FSPGR) volume (TI/TR/TE = 450/8/3 ms, matrix size 256 × 256, field of view 22 × 22 cm, slice thickness = 1 mm, and flip angle = 15°) that was acquired during the same scan session [Saad et al., 2009]. PetCO2 data were re‐sampled at TR, and time‐shifted to the point of coincidence with the mean brain BOLD signal where PetCO2 abruptly decreased at the end of the ramp.
Data analysis
CVR was calculated from the slope of a linear least‐squares fit of the BOLD signal data series to the PetCO2 data series over the range of PetCO2 represented by the ramp portion of the CO2 sequence on a voxel‐by‐voxel basis. The slope of the relation between the BOLD signal and PetCO2 was color‐coded [see Appendix in Poublanc et al., 2015] to a spectrum of colors corresponding to the direction (positive or negative) and the magnitude of the slope to form CVR maps.
As previously described [Fisher et al., 2017], there are four shapes of BOLD‐CO2 response patterns resulting from ramp changes in PetCO2 from hypocapnia to hypercapnia; rising, falling, U‐shaped, and inverted U‐shaped. These pattern shapes are classified according to the signs of the linear slopes of the BOLD versus PetCO2 relations in the hypocapnic and hypercapnic ranges and color coded to form type maps [Fisher et al., 2017] as follows:
Rising, Type A (+/+); BOLD increases in both hypocapnic and hypercapnic ranges of PetCO2.
Inverted U‐shaped, Type B (+/–); BOLD increases in hypocapnia but decreases in hypercapnia.
Falling, Type C (–/–); BOLD decreases in both hypocapnic and hypercapnic ranges of PetCO2.
U‐shaped, Type D (–/+); BOLD decreases in hypocapnia but increases in hypercapnia.
The model was used to calculate resistance‐CO2 responses for all voxels, using their BOLD‐CO2 responses as the examined branch flow F2 and the reference voxel BOLD‐CO2 response, chosen as previously described, as the reference branch flow F1. These calculated resistance‐CO2 responses for the reference voxel R1 and the examined voxel R2 were fitted with sigmoid functions to obtain their sigmoid parameters. In turn, the fitted resistance sigmoids for the examined voxel R1 and reference voxel R2 were then used to derive the reference and examined voxel BOLD‐CO2 responses. Illustrations of these procedures are shown in Figures 6, 7, 8, 9 of the results.
Figure 6.

The reference voxel compared to a type A (+/+) voxel, CVR = 0.508. (A) The CVR map for an axial slice shows the position of the reference voxel (white cursors) and the type A +/+ voxel (purple cursors). (B) Similarly, the type map shows the positions of the chosen voxels. (C) The model flow responses to PetCO2 for the type A +/+ voxel (purple open circles, blue type line fits) and the reference voxel (black open circles). The curves for the type A +/+ (purple line) and reference (black line) voxels were calculated from the model resistance sigmoidal responses. (D) The model resistance‐CO2 responses calculated from the model flow responses for the type A +/+ voxel (purple open circles) and the reference voxel (black open circles). Sigmoid curves (lines) were fitted to the resistance‐CO2 responses for each voxel. (E) The model branch pressure change with PetCO2.
Figure 7.

The reference voxel compared to a type B (+/–) voxel, CVR = 0.241. Explanation as for Figure 6.
Figure 8.
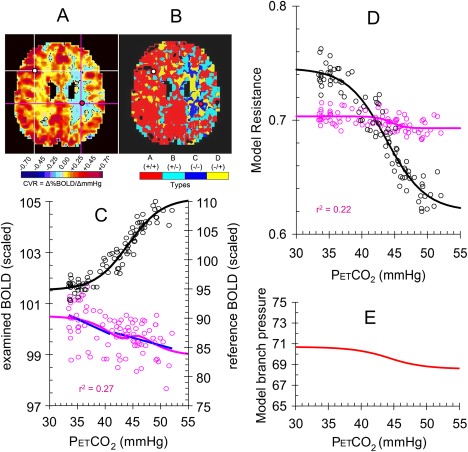
The reference voxel compared to a type C (–/–) voxel, CVR = −0.069. Explanation as for Figure 6.
Figure 9.

The reference voxel compared to a type D (–/+) voxel, CVR = −0.021. Explanation as for Figure 6.
Statistical analyses
The signal/noise ratios (SNR) of the BOLD responses to PetCO2 for each response type were calculated as the ratio of the CVR to the mean square error of the linear fit, with the assumption that CVR was representative of the magnitude of the BOLD response to CO2, and the mean square error of the linear fit was representative of the response noise. The quality of the model fitting for the sigmoidal resistance responses to PetCO2 for examined voxels and the derived fitting of the measured BOLD responses to PetCO2 for examined voxels were assessed as the r 2 of the fits. Comparison of these r 2 values between linear CVR and model fits of the examined voxel BOLD responses to PetCO2 were assessed by signed rank tests for each of the four types of response (SigmaPlot 12.5) as the measures were not normally distributed.
RESULTS
Examples of Model Fitting
Figures 6 to 9 illustrate the use of the model to calculate the sigmoidal resistance‐CO2 responses for voxels with type A +/+, B +/–, C –/–, and D –/+ patterns of BOLD‐CO2 response. The graphs show the reference voxel in black and the examined voxel in purple. The BOLD‐CO2 data were acquired from a 57‐year‐old patient with left internal carotid occlusion. Two more patient examples showing similar figures are included in Supporting Information.
Model Assessment
These individual voxel examples illustrate the sigmoidal nature of the resistance‐CO2 response patterns calculated from the observed BOLD‐CO2 response patterns, no matter which of the four response types is examined. To assess the appropriateness of the sigmoidal fitting of the resistance‐CO2 responses, we calculated the r 2 values for all voxels in this example patient for each pattern type, and Table 1 displays the median values for each type. Using the fitted sigmoidal resistance‐CO2 responses, the BOLD‐CO2 response pattern types can be generated for all voxels, and we calculated these r 2 values to compare with the r 2 values of the linear fit CVR. Table 1 lists the median values of these r 2 fits as well as the median SNR values. Signed rank tests showed that the r 2 values for the model prediction of the BOLD‐CO2 responses are an improvement over the r 2 values for CVR, except for Type C (–/–).
Table 1.
Median values of r 2 fits for the resistance sigmoids, BOLD‐CO2 responses derived from the resistance sigmoids, and the CVR fit to the BOLD‐CO2 responses, and SNR
| Type | Resistance sigmoid | Model BOLD‐CO2 response | CVR | SNR |
|---|---|---|---|---|
| A (+/+) | 0.782 | 0.641 | 0.619 | 0.17 |
| B (+/–) | 0.455 | 0.165 | 0.067 | 0.03 |
| C (–/–) | 0.236 | 0.061 | 0.062 | 0.05 |
| D (–/+) | 0.563 | 0.239 | 0.172 | 0.06 |
Signed rank tests for each type detected significant differences (P < 0.001) between CVR fit r 2 and model BOLD‐CO2 fit r 2 with higher values bolded.
Overall View
To gain an overall view of the resistance‐CO2 response sigmoid patterns for each of the four types of BOLD‐CO2 response pattern types, we used the commonly observed values of the resistance‐CO2 response sigmoid parameters to generate the resistance‐CO2 response sigmoids, and these are shown in Figure 10. As these resistance response patterns show, type A +/+ responses are the most robust and type C –/– the least, with the amplitudes of B +/– and D –/+ types intermediate. The midpoints of all four types tend to the resting PetCO2 of this patient (40 mm Hg), with D –/+ types often slightly above resting PetCO2 and B +/– types often slightly below resting PetCO2 as in Figures 7 and 9. The range of PetCO2 over which the sigmoid is linear is similar for all types, about 5 mm Hg.
Figure 10.
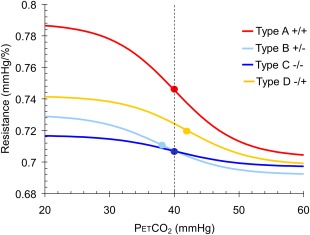
Resistance‐CO2 response sigmoids for the four types of BOLD‐CO2 response pattern based on the values of the sigmoid parameters calculated for all voxels in the example patient. The midpoints are shown as dots and the dashed line shows the resting PetCO2.
DISCUSSION
In this study, we move our investigation of the regional brain vascular regulation cause‐and‐effect cascade upstream; instead of simply observing flow responses to CO2, which are responses to remote, as well as local effects, we calculate the pattern of the underlying local changes in vascular resistance. For our examination of the hypothesized vascular network, where flow interactions between vascular beds result in perfusion pressure changes, we deliberately used the simplest model of a vascular region. It consists of a resistor circuit analogue of two vascular beds perfused in parallel via a fixed resistance; a conceptual model previously described by [Sobczyk et al., 2014]. We suggest that this model can be scaled fractally throughout the brain as illustrated in Figure 2. With this model, we related the differing patterns of BOLD‐CO2 responses observed in different regions, to their underlying physiologic determining factor: relative changes in vascular resistance.
Model Assumptions
A major premise of the model was that the resistance‐CO2 response is sigmoidal. With the effect of CO2 on cerebral vessel smooth muscle to alter vessel diameter, and anatomical limits for changes in vascular diameter with CO2, a sigmoidal relationship results for resistance. Consequently, if local perfusion pressure remains constant, then a sigmoidal resistance‐CO2 response produces a sigmoidal flow response to CO2. Indeed, in healthy subjects the flow response to CO2 for an artery such as the middle cerebral that perfuses a region containing both GM, with highly reactive vessels, as well as WM with less reactive vessels, is sigmoidal [Battisti‐Charbonney et al., 2011]. Moreover, both GM and WM responses of healthy subjects may be fitted with sigmoids, similar to the whole brain response [Bhogal et al., 2014]. These observations support a linkage between sigmoidal resistance‐CO2 responses and resulting sigmoidal flow responses, as in health, the various vascular beds perfused in parallel have balanced changes in resistance resulting in organized and coordinated changes in brain blood flow in response to a global vasoactive stimulus. However, in pathophysiology that balance is disturbed, and manifests as unbalanced distributions of brain blood flow with asymmetric BOLD responses to hypercapnia [Han et al., 2008; Silvestrini et al., 2000; Poublanc et al., 2013].
A second major assumption was that the reference voxel BOLD‐CO2 response acts as a summation of all vascular responses that determine the changes in the local perfusion pressure experienced by the examined voxel during a CO2 challenge. The justification for this assumption lies in the known vascular physiology of blood flow distribution in the complex network of vessels, where regions of high CVR affect regions of low reactivity, so that blood flow distribution is determined by their relative CVR [Sobczyk et al., 2014]; the extreme case being the cerebrovascular steal phenomenon [Conklin et al., 2010]. By choosing a reference voxel flow that interacts with the examined voxel flow to determine the model local perfusion pressure changes with CO2, the model provides a challenge to the examined voxel that represents the vascular network perfusion pressure changes with CO2. While this challenge is not the actual change in perfusion pressure experienced by a voxel, it nevertheless serves to expose the resistance pattern of response. By using a standard reference that is the same for all examined voxels, the resistance responses can be compared between voxels.
The model assumes a constancy of neural activation, cerebral tissue metabolic state and cerebral perfusion pressure during a ramp CO2 challenge. Although subjects are instructed to minimize movement during BOLD‐CO2 response measurements, nevertheless neural activation may occur with changing cognitive and sensory activity, but the degree to which model results would be affected is unknown and assumed to be low. Regardless whether hypercapnia is an isometabolic stimulus or not [Yablonskiy, 2011], the vigorous flow responses to the large hypercapnic stimulus of over 10 mm Hg change in PetCO2 will strongly dominate the BOLD response. Perfusion pressure, conversely, may pose a problem in some subjects as blood pressure may be increased in response to CO2. If so, it is a confounder of the model that cannot be overcome [Regan et al., 2014]. For this reason, it is advisable to monitor blood pressure during testing. Our experience with subjects, supine in MRI tests, is that most maintain MAP within a small, probably physiological range, and the present analysis would be largely unaffected.
The model assumes aggregated parameter resistances for the vascular beds and a fixed supply artery resistance, whereas both are of course in reality spatially distributed. The fixed supply artery resistance can be criticized because although CO2 may be thought to primarily affect the arterioles and precapillary sphincters [Atkinson et al., 1990; Busija and Heistad, 1984; Edvinsson and Krause, 2002], all cerebral vessel smooth muscles are relaxed by CO2 [Willie et al., 2014], with small vessels the most sensitive [Wei et al., 1980], so that in reality the supply artery resistance would decrease somewhat with hypercapnia. Nevertheless, we suggest that none of these model enhancements have a significant effect on the conclusions drawn from its application.
Finally, we offer an alternative interpretation of our modeling; we suggest that the model may be viewed as a BOLD‐CO2 response‐fitting exercise. The model is simply a way of providing a standardized method based on the physiological assumptions of perfusion pressure changes due to vascular network interactions and a sigmoidal change in resistance with CO2.
Model Performance
Sigmoidal patterns of resistance‐CO2 responses are to be expected, not only based on the principle of physical limitations of vasoconstriction and vasodilation but also on the observation of sigmoidal BOLD‐CO2 responses in healthy tissues [Bhogal et al., 2014, 2015; Sobczyk et al., 2014]. Indeed, for all of the four BOLD‐CO2 response patterns we previously catalogued [Fisher et al., 2017], we found that the model calculated resistance responses to CO2 that were well fitted by sigmoids, an observation supported by the high r 2 found for the sigmoidal fits, especially in light of the low SNR of some of the data. That this standardized fitting procedure consistently generates sigmoidal resistance curves for the variety of BOLD‐CO2 response patterns observed, suggests that the sigmoid parameters provide physiological meaning, that is, characterize the relative changes in local vascular resistance with CO2. Further support for the model was evident from higher r 2 values for the model predicted BOLD‐CO2 responses compared to the r 2 of the CVR, in all but type C –/– responses.
Physiological Interpretation
In the following paragraphs, we examine the calculated resistance‐CO2 responses to address the physiological and pathophysiologic implications associated with the four types of BOLD‐CO2 response patterns. We consider the examined voxel resistance sigmoid parameters to characterize the relative ability of the various tissues to control blood flow, and offer the following interpretations.
The resistance sigmoid amplitude value describes the overall ability of the voxel to decrease resistance as PetCO2 increases from hypocapnia to hypercapnia, and as expected, is greatest for type A +/+ vessels where both the examined and standard reference voxels have strong (high amplitude) reductions in resistance. As a result, the BOLD‐CO2 response is sigmoidal, that is, healthy physiology. By contrast, Type C –/– vessel resistance amplitudes are small, reflecting the near loss of ability to vasodilate in response to CO2, so that these vessels are almost completely passive in behavior and become susceptible to steal. Although both Type B +/– and D –/+ vessels are capable of responding to CO2 with similar amplitudes, their amplitudes are intermediate between those of types A +/+ and C –/–, and it is their sigmoid midpoints that characterize them.
The resistance sigmoid midpoints of type A +/+ voxels tend to resting PetCO2, where the maximum sensitivity to CO2 occurs, thereby providing the optimum regulation of flow with respect to PetCO2. For the type C –/– BOLD‐CO2 response pattern pictured in Figure 8, the resistance sigmoid midpoint is similar to that of the reference type A +/+ voxel. We suggest that this similarity is a consequence of the degree to which type C –/– voxel vessels act as passive conduits. In that case, type C –/– voxel flows will then reflect the flow changes of type A +/+ voxels so that the BOLD‐CO2 response patterns are mirror images; the reference type A +/+ voxel steals flow from the type C –/– voxel [Sobczyk et al., 2014].
For the type D –/+ voxel flow response pattern pictured in Figure 9, the resistance sigmoid has a midpoint PetCO2 higher than that of the reference type A +/+ voxel. As a result, the hypocapnic half of the flow response has a negative slope as the reference type A +/+ voxel vessels respond, but the D –/+ type voxel vessels do not, so that steal occurs as PetCO2 increases from hypocapnia to resting. However, in hypercapnia the type D –/+ voxel vessels do respond and vasodilate, while the reference type A +/+ voxel vessels are reaching their maximum vasodilation and no longer steal. With respect to the elevated midpoint of D –/+ type voxel vessels, we note that the speed of response [Blockley et al., 2011; Duffin et al., 2015; Poublanc et al., 2015] could have an effect on the midpoint if the ramp increase in PetCO2 was too fast. The response to a ramp stimulus in a first‐order system remains a ramp but is displaced later in time proportional to the system time constant, and since PetCO2 is proportional to time in a ramp, the response to PetCO2 would be displaced to a higher value. This effect could explain the midpoint increase observed for type D responses if they were very slow: with the initial increase in CO2, a delay in the reduction of resistance results in a redistribution of their blood flow toward vessels with an immediate response. Then, as CO2 increases further, and vessels with fast responses approach their minimal resistance, the slowly responding vessels now reduce their resistance and increase their flow relative to other vessels. Whether this hypothesis accounts for the increased type D –/+ midpoints requires further investigation.
A complementary response pattern describes the type B +/– voxel in Figure 7, where the voxel resistance sigmoid has a midpoint below that of the type A +/+ reference voxel. In the hypocapnic range, the type B +/– voxel vessels vasodilate and are able to increase flow, but in hypercapnia these vessels reach their maximum vasodilation before the reference type A +/+ voxel vessels. Further vasodilation by the type A+/+ vessels diverts flow from the type B +/– voxel vessels.
Limitations
First, it is acknowledged that this model is elementary compared to more comprehensive models [Lorthois et al., 2011; Ursino and Giannessi, 2010], which could be used for the same purpose. However, our model is simpler to understand and the resulting equations are easily solved by applying standard electrical circuit principles, first to convert the BOLD derived flow data to resistance data and then, after fitting the resistance data with sigmoids, converting the fitted resistance data to fitted flow data, enabling modeling of all voxel response patterns. It should be noted that the model is limited in its application, requiring a slow ramp stimulus pattern where it is assumed that the speed of response does not influence the relations between flow distribution and CO2 [Blockley et al., 2011; Duffin et al., 2015; Poublanc et al., 2015].
The response pattern examples used to develop the model are based on BOLD measurements, which were assumed to represent the patterns of CBF‐CO2 responses. While there are methods of assessing CBF other than BOLD such as Doppler arterial velocity measures and arterial spin labeling (ASL) MRI, such methods that are available do not have the temporal or spatial resolution necessary to supply data to our model. Nevertheless, we must stress that the use of BOLD as a surrogate measure of CBF for our model also involves a number of important caveats. First, BOLD deviates from a linear relationship to CBF at very high flows [Hoge et al., 1999] because the concentration of deoxyhemoglobin is diluted with oxyhemoglobin as the oxygen extraction fraction (OEF) falls. Such a nonlinearity could affect the sigmoid fitting at very high PCO2. However, using Doppler ultrasound measurements of middle cerebral artery velocity, sigmoidal relationships were maintained at CO2 tensions in excess of those in our study. In addition, the increases in BOLD we observed were <10%, which is within the linear BOLD–CBF relation according to the Davis [dHb] dilution model [Davis et al., 1998]. Moreover, experimental measurements of brain oxygenation using near infra‐red spectroscopy [Alderliesten et al., 2014], and measurements of CVR using both BOLD and ASL MRI data [Tancredi et al., 2015] acquired using a 2‐dimensional spin‐echo flow‐sensitive alternating inversion recovery sequence, have noted that even in patients with steno‐occlusive disease, the BOLD MRI signal response to hypercapnia predominantly reflects changes in CBF [Mandell et al., 2008].
The second caveat is that BOLD measures are affected by cerebral blood volume (CBV), which also changes with hypercapnia. As the fractional change in CBV relative to baseline can be approximated by the fractional change in CBF relative to baseline raised to the power of 0.2 [Chen and Pike, 2010; Mark and Pike, 2012], we consider this effect to be minor and to have little effect on the sigmoidal responses we measured. BOLD may also reflect changes in cerebral metabolic rate, and changes in oxygen tension [Bulte et al., 2007; Prisman et al., 2008]. As discussed in [Yablonskiy, 2011] and [Yezhuvath et al., 2009], the assumption that hypercapnia does not change cerebral metabolic rate is debateable and must therefore be regarded as a caveat for these experiments. As for changes in oxygen tension, we maintained normoxic isoxia during these tests. Finally, we note that the Δ BOLD–Δ PCO2 relationship depends on the baseline PCO2 [Cohen et al., 2002; Halani et al., 2015; Sobczyk et al., 2014], and so we used the subject's resting PCO2 as baseline with the ramp from hypocapnia to hypercapnia passing through this PCO2.
A further aspect of using BOLD as a surrogate measure of CBF pertains to the fact that the maximum BOLD response in a particular region is set by the amount of deoxyhaemoglobin at rest, which is determined by resting CBF, OEF, and CBV. The only issue is WM voxels, where OEF is similar to GM but CBV is only 1/2 or 1/3, so that the BOLD range is only a fraction of GM BOLD range; that is, WM CBF is a fraction of GM CBF when using BOLD as a proxy for CBF. Therefore, in the model it may be wrong to equate WM and GM CBF at max PCO2. However, the mean BOLD at each voxel is set to 100% at resting PCO2 and the range of CBF over the ramp is such that the range in resistance should correctly describe the response pattern.
In summary, we realize that our translation of BOLD into resistance depends on the assumption that BOLD is a reasonable surrogate for CBF. As better measures of CBF become available, we suggest that the model we present here may be applied equally to these measurements to produce respectively improved measures of resistance
Conclusions
This modeling study demonstrated that the pattern of BOLD‐CO2 responses in an individual voxel resulting from a ramp CO2 challenge can be derived from a simple model of interaction with the BOLD‐CO2 responses of other regions of the brain. It assumes there is a redistribution of flow between vascular beds perfused in parallel from a vessel with a significant resistance, which is brought about via changes in local perfusion pressure with CO2. The model adopts the unifying principle that all vascular bed resistance‐CO2 responses are sigmoidal, a characteristic to be expected based on vascular physiology. The model calculations determine the examined voxel resistance‐CO2 response utilizing a standard BOLD‐CO2 response reference, and so provide a relative estimate of a physiological parameter, resistance, that can be compared between regions. We suggest that the resistance‐CO2 responses provide physiological explanations for the various observed BOLD‐CO2 response patterns. Given that differences in amplitudes and midpoints of the resistance‐CO2 response sigmoids occur under pathological conditions, we speculate that maps of these characteristics would prove of clinical importance, and further development of the ideas proposed in this study could prove fruitful.
Conflict of interest
JAF is Chief Scientist and JD is Senior Scientist at Thornhill Research (TRI), a spin‐off company from the University Health Network that developed the RespirAct™. RespirAct™ is currently a non‐commercial research tool assembled, and made available by TRI to research institutions to enable CVR studies.
Supporting information
Supporting Information
The model equations are as follows:
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
| (A7) |
| (A8) |
Where:
PCO2 = the partial pressure of carbon dioxide affecting the branch resistances
R1 = the resistance of branch 1
R2 = the resistance of branch 2
Re = the equivalent resistance of the combined branches in parallel
Rtotal = the total resistance for the model tissue
Ftotal = the total flow through the model tissue
Pbranch = the branch perfusion pressure
F1 = the flow through branch 1
F2 = the flow through branch 2
R1a and R2a are the maximum resistances in hypocapnia
R1b and R2b are the sigmoid amplitudes
R1c and R2c are the sigmoid midpoints
R1d and R2d are the sigmoid linear ranges
REFERENCES
- Alderliesten T, De Vis JB, Lemmers PM, van BF, Benders MJ, Hendrikse J, Petersen ET (2014): Simultaneous quantitative assessment of cerebral physiology using respiratory‐calibrated MRI and near‐infrared spectroscopy in healthy adults. Neuroimage 85 Pt 1:255–263. [DOI] [PubMed] [Google Scholar]
- Atkinson JLD, Anderson RE, Sundt TM Jr (1990): The effect of carbon dioxide on the diameter of brain capillaries. Brain Res 517:333–340. [DOI] [PubMed] [Google Scholar]
- Attwell D, Buchan AM, Charpak S, Lauritzen M, Macvicar BA, Newman EA (2011): Glial and neuronal control of brain blood flow. Nature 468:232–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battisti‐Charbonney A, Fisher J, Duffin J (2011): The cerebrovascular response to carbon dioxide in humans. J Physiol 589:3039–3048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhogal A, Siero JC, Fisher JA, Froeling M, Luijten P, Philippens M, Hoogduin H (2014): Investigating the non‐linearity of the BOLD cerebrovascular reactivity response to targeted hypo/hypercapnia at 7T. Neuroimage 98:296–305. [DOI] [PubMed] [Google Scholar]
- Bhogal AA, Philippens ME, Siero JC, Fisher JA, Petersen ET, Luijten PR, Hoogduin H (2015): Examining the regional and cerebral depth‐dependent BOLD cerebrovascular reactivity response at 7T. Neuroimage 114:239–248. [DOI] [PubMed] [Google Scholar]
- Blockley NP, Driver ID, Francis ST, Fisher JA, Gowland PA (2011): An improved method for acquiring cerebrovascular reactivity maps. Magn Reson Med 65:1278–1286. [DOI] [PubMed] [Google Scholar]
- Bulte DP, Chiarelli PA, Wise RG, Jezzard P (2007): Cerebral perfusion response to hyperoxia. J Cereb Blood Flow Metab 27:69–75. [DOI] [PubMed] [Google Scholar]
- Busija DW, Heistad DD (1984): Factors involved in the physiological regulation of the cerebral circulation. Rev Physiol Biochem Pharmacol 101:161–211. [DOI] [PubMed] [Google Scholar]
- Chen JJ, Pike GB (2010): MRI measurement of the BOLD‐specific flow‐volume relationship during hypercapnia and hypocapnia in humans. Neuroimage 53:383–391. [DOI] [PubMed] [Google Scholar]
- Cohen ER, Ugurbil K, Kim SG (2002): Effect of basal conditions on the magnitude and dynamics of the blood oxygenation level‐dependent fMRI response. J Cereb Blood Flow Metab 22:1042–1053. [DOI] [PubMed] [Google Scholar]
- Conklin J, Fierstra J, Crawley AP, Han JS, Poublanc J, Mandell DM, Silver FL, Tymianski M, Fisher JA, Mikulis DJ (2010): Impaired cerebrovascular reactivity with steal phenomenon is associated with increased diffusion in white matter of patients with Moyamoya disease. Stroke 41:1610–1616. [DOI] [PubMed] [Google Scholar]
- Cox RW (1996): AFNI: Software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res 29:162–173. [DOI] [PubMed] [Google Scholar]
- Davis TL, Kwong KK, Weisskoff RM, Rosen BR (1998): Calibrated functional MRI: Mapping the dynamics of oxidative metabolism. Proc Natl Acad Sci USA 95:1834–1839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffin J, Sobczyk O, Crawley AP, Poublanc J, Mikulis DJ, Fisher JA (2015): The dynamics of cerebrovascular reactivity shown with transfer function analysis. NeuroImage 114:207–216. [DOI] [PubMed] [Google Scholar]
- Edvinsson L, Krause DN (2002): Cerebral Blood Flow and Metabolism. Philadelphia, PA: Lippincott Williams & Wilkins. [Google Scholar]
- Faraci F, Heistad D (1990): Regulation of large cerebral arteries and cerebral microvascular pressure. Circ Res 66:8–17. [DOI] [PubMed] [Google Scholar]
- Fisher JA, Sobczyk O, Crawley A, Poublanc J, Dufort P, Venkatraghavan L, Sam K, Mikulis D, Duffin J (2017): Assessing cerebrovascular reactivity by the pattern of response to progressive hypercapnia. Hum Brain Mapp 38:3415–3427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halani S, Kwinta JB, Golestani AM, Khatamian YB, Chen JJ (2015): Comparing cerebrovascular reactivity measured using BOLD and cerebral blood flow MRI: The effect of basal vascular tension on vasodilatory and vasoconstrictive reactivity. NeuroImage 110:110–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han JS, Mandell DM, Poublanc J, Mardimae A, Slessarev M, Jaigobin C, Fisher JA, Mikulis DJ (2008): BOLD‐MRI cerebrovascular reactivity findings in cocaine‐induced cerebral vasculitis. Nat Clin Pract Neurol 4:628–632. [DOI] [PubMed] [Google Scholar]
- Hill MA, Davis MJ, Meininger GA, Potocnik SJ, Murphy TV (2006): Arteriolar myogenic signalling mechanisms: Implications for local vascular function. Clin Hemorheol Microcirc 34:67–79. [PubMed] [Google Scholar]
- Hirsch S, Reichold J, Schneider M, Székely G, Weber B (2012): Topology and hemodynamics of the cortical cerebrovascular system. J Cereb Blood Flow Metab 32:952–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoge RD, Atkinson J, Gill B, Crelier GR, Marrett S, Pike GB (1999): Investigation of BOLD signal dependence on cerebral blood flow and oxygen consumption: The deoxyhemoglobin dilution model. Magn Reson.Med 42:849–863. [DOI] [PubMed] [Google Scholar]
- Iadecola C (2004): Neurovascular regulation in the normal brain and in Alzheimer's disease. Nat Rev Neurosci 5:347–360. [DOI] [PubMed] [Google Scholar]
- Ito S, Mardimae A, Han J, Duffin J, Wells G, Fedorko L, Minkovich L, Katznelson R, Meineri M, Arenovich T, Kessler C, Fisher JA (2008): Non‐invasive prospective targeting of arterial PCO2 in subjects at rest. J Physiol 586:3675–3682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorthois S, Cassot F (2010): Fractal analysis of vascular networks: Insights from morphogenesis. J Theor Biol 262:614–633. [DOI] [PubMed] [Google Scholar]
- Lorthois S, Cassot F, Lauwers F (2011): Simulation study of brain blood flow regulation by intra‐cortical arterioles in an anatomically accurate large human vascular network. Part II: Flow variations induced by global or localized modifications of arteriolar diameters. Neuroimage 54:2840–2853. [DOI] [PubMed] [Google Scholar]
- Lucas SJ, Tzeng YC, Galvin SD, Thomas KN, Ogoh S, Ainslie PN (2010): Influence of changes in blood pressure on cerebral perfusion and oxygenation. Hypertension 55:698–705. [DOI] [PubMed] [Google Scholar]
- Mandell DM, Han JS, Poublanc J, Crawley AP, Stainsby JA, Fisher JA, Mikulis DJ (2008): Mapping cerebrovascular reactivity using blood oxygen level‐dependent MRI in Patients with arterial steno‐occlusive disease: Comparison with arterial spin labeling MRI. Stroke 39:2021–2028. [DOI] [PubMed] [Google Scholar]
- Mark CI, Pike GB (2012): Indication of BOLD‐specific venous flow‐volume changes from precisely controlled hyperoxic vs. hypercapnic calibration. J Cereb Blood Flow Metab 32:709–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osol G, Brekke JF, McElroy‐Yaggy K, Gokina NI (2002): Myogenic tone, reactivity, and forced dilatation: A three‐phase model of in vitro arterial myogenic behavior. Am J Physiol Heart Circ Physiol 283:H2260–H2267. [DOI] [PubMed] [Google Scholar]
- Poublanc J, Han JS, Mandell DM, Conklin J, Stainsby JA, Fisher JA, Mikulis DJ, Crawley AP (2013): Vascular steal explains early paradoxical blood oxygen level‐dependent cerebrovascular response in brain regions with delayed arterial transit times. Cerebrovascular diseases extra 3:55–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poublanc J, Crawley AP, Sobczyk O, Montandon G, Sam K, Mandell DM, Dufort P, Venkatraghavan L, Duffin J, Mikulis DJ, Fisher JA (2015): Measuring cerebrovascular reactivity: The dynamic response to a step hypercapnic stimulus. J Cereb Blood Flow Metab 35:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prisman E, Slessarev M, Han J, Poublanc J, Mardimae A, Crawley A, Fisher J, Mikulis D (2008): Comparison of the effects of independently‐controlled end‐tidal PCO(2) and PO(2) on blood oxygen level‐dependent (BOLD) MRI. J Magn Reson Imaging 27:185–191. [DOI] [PubMed] [Google Scholar]
- Regan RE, Fisher JA, Duffin J (2014): Factors affecting the determination of cerebrovascular reactivity. Brain Behav 4:775–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad ZS, Glen DR, Chen G, Beauchamp MS, Desai R, Cox RW (2009): A new method for improving functional‐to‐structural MRI alignment using local Pearson correlation. Neuroimage 44:839–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silvestrini M, Vernieri F, Pasqualetti P, Matteis M, Passarelli F, Troisi E, Caltagirone C (2000): Impaired cerebral vasoreactivity and risk of stroke in patients with asymptomatic carotid artery stenosis. JAMA 283:2122–2127. [DOI] [PubMed] [Google Scholar]
- Slessarev M, Han J, Mardimae A, Prisman E, Preiss D, Volgyesi G, Ansel C, Duffin J, Fisher JA (2007): Prospective targeting and control of end‐tidal CO2 and O2 concentrations. J Physiol 581:1207–1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobczyk O, Battisti‐Charbonney A, Fierstra J, Mandell DM, Poublanc J, Crawley AP, Mikulis DJ, Duffin J, Fisher JA (2014): A conceptual model for CO2‐induced redistribution of cerebral blood flow with experimental confirmation using BOLD MRI. NeuroImage 92:56–68. [DOI] [PubMed] [Google Scholar]
- Sobczyk O, Battisti‐Charbonney A, Poublanc J, Crawley AP, Sam K, Fierstra J, Mandell DM, Mikulis DJ, Duffin J, Fisher JA (2015): Assessing cerebrovascular reactivity abnormality by comparison to a reference atlas. J Cereb Blood Flow Metab 35:213–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobczyk O, Crawley AP, Poublanc J, Sam K, Mandell DM, Mikulis DJ, Duffin J, Fisher JA (2016): Identifying significant changes in cerebrovascular reactivity to carbon dioxide. AJNR Am J Neuroradiol 37:818–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Somogyi RB, Vesely AE, Preiss D, Prisman E, Volgyesi G, Azami T, Iscoe S, Fisher JA, Sasano H (2005): Precise control of end‐tidal carbon dioxide levels using sequential rebreathing circuits. Anaesth Intensive Care 33:726–732. [DOI] [PubMed] [Google Scholar]
- Tan CO, Taylor JA (2014): Integrative physiological and computational approaches to understand autonomic control of cerebral autoregulation. Exptl Physiol 99:3–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tancredi FB, Lajoie I, Hoge RD (2015): Test‐retest reliability of cerebral blood flow and blood oxygenation level‐dependent responses to hypercapnia and hyperoxia using dual‐echo pseudo‐continuous arterial spin labeling and step changes in the fractional composition of inspired gases. J Magn Reson Imaging 42:1144–1157. [DOI] [PubMed] [Google Scholar]
- Ursino M, Giannessi M (2010): A model of cerebrovascular reactivity including the circle of willis and cortical anastomoses. Ann Biomed Eng 38:955–974. [DOI] [PubMed] [Google Scholar]
- Wei EP, Kontos HA, Patterson JL Jr (1980): Dependence of pial arteriolar response to hypercapnia on vessel size. Am J Physiol 238:697–703. [DOI] [PubMed] [Google Scholar]
- Wells JA, Christie IN, Hosford PS, Huckstepp RT, Angelova PR, Vihko P, Cork SC, Abramov AY, Teschemacher AG, Kasparov S, Lythgoe MF, Gourine AV (2015): A critical role for purinergic signalling in the mechanisms underlying generation of BOLD fMRI responses. J Neurosci 35:5284–5292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willie CK, Macleod DB, Shaw AD, Smith KJ, Tzeng YC, Eves ND, Ikeda K, Graham J, Lewis NC, Day TA, Ainslie PN (2012): Regional brain blood flow in man during acute changes in arterial blood gases. J Physiol 590:3261–3275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willie CK, Tzeng YC, Fisher JA, Ainslie PN (2014): Integrative regulation of human brain blood flow. J Physiol 592:841–859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yablonskiy DA (2011): Cerebral metabolic rate in hypercapnia: Controversy continues. J Cereb Blood Flow Metab 31:1502–1503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yezhuvath US, Lewis‐Amezcua K, Varghese R, Xiao G, Lu H (2009): On the assessment of cerebrovascular reactivity using hypercapnia BOLD MRI. NMR Biomed. 22:779–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


