Accumulation of non‐numerical evidence during nonsymbolic number processing in the brain: An fMRI study

Abstract

Behavioral evidence has shown that when performing a nonsymbolic number comparison task (e.g., deciding which of two dot arrays contains more dots), participants' responses are sensitive to affected by both numerical (e.g., number of items) and non‐numerical magnitudes (i.e., area, density, etc.). Thus far it is unclear what brain circuits support this process of accumulating non‐numerical variables during nonsymbolic number processing. To investigate this, 21 adult participants were asked to engage in a dot comparison task. To measure the neural correlates of accumulating numerical and non‐numerical variables, we manipulated the number of the non‐numerical magnitudes that were congruent (correlated with number) or incongruent (anticorrelated with number). In a control task, participants were asked to choose the darker of two gray rectangles (brightness task). The tasks were matched in terms of their difficulty. The results of a whole brain analysis for regions sensitive to the congruity of numerical and non‐numerical magnitudes revealed a region in the right inferior frontal gyrus (rIFG). Activation in this region was found to be correlated with the relative congruency of numerical and non‐numerical magnitudes. In contrast, this region was not modulated by difficulty of the brightness control task. Accordingly in view of these findings, we suggest that the rIFG supports the accumulation of non‐numerical magnitudes that are positively correlated with number. Therefore taken together, this study reveals a brain region whose pattern of activity is influenced by the congruency between numerical and non‐numerical variables during nonsymbolic number judgments. Hum Brain Mapp 38:4908–4921, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Comparing the quantity of items is something we do every day. For example, at the grocery store, we might decide which shopping carts in line contain the fewest items, so that the time we wait in line for the cashier is as short as possible. Which factors guides our decision in such cases? Is it the number of items, their individual sizes, their density, or a combination of all these cues to magnitude? One of the most common tools used to answer this question is the nonsymbolic number comparison task (from hereon, numerosity comparison task). In this task, participants are asked to indicate which of two groups contains a larger number of items. The most common view in the field of numerical cognition suggests that in numerosity comparison tasks, participants are influenced only by the number of the items and not the groups' non‐numerical magnitudes, such as the total area of the items, or their density [Burr and Ross, 2008; Dehaene and Changeux, 1993]. A more recent line of evidence, however, suggests that when making such a comparison, evidence from both number and non‐numerical magnitudes are accumulated to make a decision [Gevers et al., 2016; Henik et al., 2016; Leibovich et al., 2016a, 2016b; Leibovich and Ansari, 2016; Leibovich and Henik, 2013; Mix et al., 2016].

A number of behavioral studies have directly demonstrated the influence of non‐numerical magnitudes on performance in a numerosity comparison task. For example, Leibovich and Henik [2014] asked adult participants to compare the number of dots in two groups. The ratio between the number of dots in these groups was manipulated. Numerical ratio was calculated as the smaller divided by the larger number of dots. For example, the numerical ratio between a group of 5 dots and a group of 10 dots is 5/10 = 0.5, and the ratio between 9 and 10 dots is 0.9. The closer a ratio is to 1, the more similar the to‐be‐compared magnitudes are. In addition, these authors also calculated the ratio between 5 non‐numerical magnitudes of the compared groups of dots. The numerical and non‐numerical ratios were then used as predictors in a multiple regression analysis. The results demonstrated that both the ratio between the numerosities and the ratio between non‐numerical magnitudes predicted performance (i.e., response times (RT) and accuracy). This is in spite the fact that non‐numerical magnitudes were task‐irrelevant, and that in their set of stimuli, none of the non‐numerical magnitudes could have been used as a consistent cue to predict numerosity. These findings therefore suggest that non‐numerical magnitudes influence nonsymbolic numerosity judgements. In this study, we present more direct evidence for the influence of non‐numerical magnitudes on numerosity judgments; here too non‐numerical magnitudes were not relevant to the task, and minimally correlated with number. Hence non‐numerical magnitudes were not able to be used as a predictive cue of numerosity. And still, the effect of congruity level suggests that non‐numerical magnitudes influenced performance.

Is it possible that participants used only non‐numerical magnitudes in their response? While it is possible that in some situations in everyday lives people will use only non‐numerical magnitudes to make magnitude judgments, in the current experimental design this option is less likely. Participants were explicitly asked to choose the group containing more dots. In every trial, some non‐numerical magnitudes positively correlated with number, and some negatively correlated with number. If a participant use only these non‐numerical magnitudes, we would expect accuracy to be influenced by this strategy. Namely, we would expect very low accuracy (below chance level) when 4 out of 5 non‐numerical magnitudes are negatively correlated with number. However, the high accuracy rates even in this condition suggest that participants were relying both on number and non‐numerical magnitudes, as demanded by the task's instructions.

Another line of evidence for the involvement of non‐numerical magnitudes in numerosity comparison comes from nonsymbolic Stroop‐like tasks. In such tasks, non‐numerical magnitudes are either positively correlated (i.e., congruent) or negatively correlated (i.e., incongruent) with numerosity. For example, in congruent trials, the group with the physically larger dots contains more dots; in incongruent trials the group with the physically smaller dots contains more dots. Hurewitz et al. [2006] demonstrated that when asked to choose the group containing more dots, participants were slower in incongruent trials than in congruent trials. This pattern of results was interpreted as an indication for the automatic processing of non‐numerical magnitudes. Namely, the response in incongruent trials is slower because of the need to inhibit processing the irrelevant non‐numerical magnitudes. More recently, Leibovich et al. [2015a, 2015b] have also demonstrated this congruity effect with small (2–4) and large (20–40) numerosities.

The Correlation Between Numerosity and Non‐Numerical Magnitudes

Why do non‐numerical magnitudes influence numerosity comparisons? One explanation might be that there is a natural correlation between numerosity and non‐numerical magnitudes. Namely, in the environment, we usually witness a positive correlation between numerosity and non‐numerical magnitudes (e.g., more items will take more space, will be denser, etc., compared with fewer items). Given the high occurrence of this positive correlation, it can be considered to be adaptive to process non‐numerical magnitudes when making numerical judgments [Cantrell and Smith, 2013; Gebuis and Reynvoet, 2013; Leibovich et al., 2016a; Leibovich and Ansari, 2016; Leibovich and Henik, 2013]. Gebuis and Reynvoet [2012] took the first step to empirically assess the degree to which non‐numerical magnitude influences numerosity discrimination. In their study, participants were asked to compare two groups of dots. The number of non‐numerical magnitudes that are congruent with numerosity was manipulated. For example, in some trials, only one non‐numerical magnitude (e.g., density) was positively correlated with numerosity, and in other trials, three non‐numerical magnitudes (e.g., density, area and total circumference) were positively correlated with numerosity. Critically, the authors found that participants' accuracy increased with the number of non‐numerical magnitudes that were positively correlated (i.e., congruent) with numerosity.

One way to interpret the results of Gebuis and Reynvoet [2012] is by assuming an evidence accumulation mechanism. This mechanism is able to integrate all the available informative visual properties (both numerical and non‐numerical magnitudes), and to use these to make a numerical judgment decision [Gevers et al., 2016].

What might be the neural mechanism that supports this process of accumulation of non‐numerical evidence during numerosity judgments? Here it is helpful to look beyond the numerical domain. In a functional magnetic resonance imaging (fMRI) study, Heekeren et al. [2004] had participants looking at a picture and deciding if the picture contain a house or a face. The pictures were degraded to different degrees. They found that activity in the fusiform face area (FFA) correlated with the clarity of the face image: the area was more active when the picture was clear and hence there was more evidence to accumulate. This pattern of response was selective to pictures of faces, and not pictures of houses. Accordingly, the authors suggested that areas involved in accumulation of evidence should fulfill two criteria: first, the activity in such an area should increase with an increase in the amount of available evidence; second, this response should be selective to the task.

Similar patterns of activation, namely, activity that increases with the amount of available evidence, have also been reported during tactile, auditory and in cross‐modal tasks. In a review article, Heekeren et al. [2008] suggested that perceptual decision making involves a network of complimentary and partially overlapping areas. This network includes (1) sensory areas that are task‐specific (like the FFA) that integrate relevant sensory information, (2) monitoring areas, such as the anterior insula and the inferior frontal gyri (IFG) that detect uncertainty and difficulty level and adjust the activity of attentional networks accordingly, and (3) areas that accumulate and compare sensory evidence to make a decision (dorsolateral prefrontal cortex, DLPFC), along with premotor and motor areas that execute the response, but also take part in the decision process. Importantly, the flow of information between these areas is not linear. Instead, information goes back and forward in this network until a decision is executed (see fig. 2 in Heekeren et al. [2008]).

Figure 2.

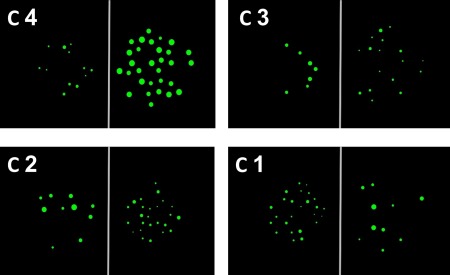
Examples of stimuli in the numerical task. C = congruity level. There were 4 possible levels of congruity. In C 4, only one of the 5 recorded non‐numerical magnitudes was incongruent with number, and 4 non‐numerical magnitudes were congruent with number, providing the possibility to integrate number with 4 non‐numerical magnitudes. In contrast, in C 1, 4 non‐numerical magnitudes are incongruent with number, leaving only one continuous magnitude to integrate with number. [Color figure can be viewed at http://wileyonlinelibrary.com]

According to Heekeren et al.'s model, cognitive‐control related areas monitor evidence accumulation. Such monitoring is important for the accumulation to be task or context‐specific to ensure that only relevant information is accumulated and influences decision making. For example, imagine that you walk to the bus station and notice the bus approaching. You have to decide if running would get you to the bus station on time or if you should wait for the next bus to arrive. In making such a decision, it is adaptive to factor in task‐relevant information, such as your running speed, the bus's speed, and the distance between you, the bus, and the bus stop. Other factors, such as the speed of other cars on the road, for example, should be inhibited because they are irrelevant to the task at hand. Consistent with this, inhibition of irrelevant properties was demonstrated by Noppeney, Ostwald and Werner [2010]. The authors asked participants to decide whether an object depicted in a short video a tool (e.g., a hammer), or a musical instrument (e.g., a violin), or whether the soundtrack of the video contained audio of a tool or a musical instrument. The auditory and visual information were either congruent (seeing and hearing violin) or incongruent (seeing violin but hearing a hammering sound). The visual and auditory information was degraded to different degrees in different trials. The authors reported that accumulation and inhibition of audiovisual information were found to be associated with different prefrontal areas and that these areas are causally related. Namely, separate areas were found to be related to inhibition and accumulation. Moreover, the activity of areas associated with accumulation of evidence increased with an increase in congruent information.

Aims and Predictions

The aim of this study was to investigate, for the first time, the neuronal correlates of the accumulation of numerical and non‐numerical magnitudes in a numerosity comparison task. Therefore, we measured the brain activity during a numerosity comparison task. Critically, we experimentally manipulated the levels of congruity between numerosity and 5 non‐numerical magnitudes: convex hull (the area occupied by the dots and the space between them), density, the total surface area of all the dots, the dots' average diameter, and the total circumference of all the dots. Specifically, the number of non‐numerical magnitudes congruent with numerosity ranged between 1 (only 1 non‐numerical magnitude positively correlated with number, and 4 non‐numerical magnitudes were negatively correlated with number, making this the most difficult and most incongruent condition) and 4 (4 non‐numerical magnitudes positively correlated with number and only 1 non‐numerical magnitude negatively correlated with number, making this the easiest, most congruent, condition).

We hypothesized that if such a magnitude accumulation mechanism exists, we should find evidence for brain areas whose activity is modulated by the amount of congruent non‐numerical magnitudes that could be accumulated, as suggested by Heekeren et al. [2004]. In view of the criteria for accumulation outlined by Heekeren et al., we expect the activity of brain area(s) that are involved in magnitude accumulation to be selectively modulated by the congruity level (i.e., by the number of non‐numerical magnitudes that are positively correlated with numerosity). More specifically, we expect the activity of such area(s) to increase with an increase in congruity level.

Importantly, we predicted that activity of a magnitude accumulation mechanism will be positively correlated with congruity level (Fig. 1b). That is, brain activity in a magnitude‐accumulation area(s) is expected to increase with an increase in congruity level. However, task difficulty should decreases with an increase in congruity level [Fig. 1a; Gebuis and Reynvoet, 2012]. Thus, brain areas that are involved in magnitude accumulation should be distinguishable from brain areas whose activity is influenced by task difficulty. Nevertheless, there are brain areas that are more active when the task is easier and might not be related to evidence accumulation. Hence, to verify that the predicted pattern of activity is not related to task difficulty, but specific to accumulation, we implemented a control task that is not numerical in nature and matches in difficulty to the numerosity comparison task.

Figure 1.

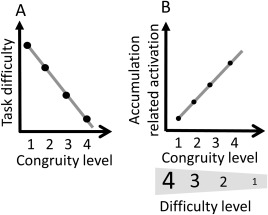
Illustration of predicted results. (A) Task difficulty. We predict that task difficulty will decrease with the number of non‐numerical magnitudes that are congruent with numerosity. (B) Brain activity related to accumulation. We predict that activity in brain regions that are associated with magnitude accumulation will be modulated by the congruity level. Note the opposite expected pattern related to difficulty and to magnitude accumulation.

The control task also enabled us to rule out other explanations for the existence of the pattern of activation mentioned above, such as a comparison process, decision making process, or differences in relative difficulty. In the control task participants were asked to indicate the darker of two gray rectangles (from hereon, the brightness task). This brightness task was selected because it involves comparing magnitudes (i.e., brightness intensity), but not a spatial magnitude. Therefore, accumulation of magnitudes is irrelevant when comparing brightness. Other components, however, such as a comparison process and different difficulty levels, do exist in the brightness task. We also matched performance in the two tasks in behavioral pilot studies to ensure that there would be no interaction of task and congruity for RT, so differences in difficulty levels between the tasks would not be able to confound the results.

At the brain level, we were interested in brain areas revealed by the interaction of task and difficulty. Specifically, we predicted that we would find brain area(s) in which the activity is parametrically modulated by the congruity level. In such regions(s), activity is expected to increase with an increase in congruity level (Fig. 1). In other words, in the numerosity comparison task, activity was hypothesized to decrease with an increase in difficulty. In contrast, in response to the brightness task, activity was expected to either increase with task difficulty or to not be affected by task difficulty at all.

METHODS

Participants

Twenty‐three graduate and undergraduate students from The University of Western Ontario, Canada were recruited to participate in the experiment. The experimental procedures were approved by Western University's Medical Research Ethics Board. All participants were right‐handed, with intact or corrected vision, and no reported learning disabilities or attention deficits. Participants were compensated for their participation in the experiment with a monetary reimbursement ($25). Two participants were excluded from the analysis due to excessive motion during scanning (more than 3mm deviation from the first image collected and/or more than 1 mm deviation between one functional image and the next functional image). For the remaining 21 participants, 11 (8 females) started with the brightness task, and 10 (5 females) started with the numerosity task. The average age of the participants was 21 years (SD = 1 year and 9 months).

Stimuli

Numerosity comparison task

Pairs of dot arrays (green dots on black background, separated by a vertical gray line, presented in the middle of an 800 × 600 pixel screen in an area of 501 × 501 pixels) were generated using the Matlab code provided by Gebuis and Reynvoet, [2012]. This code records the five different non‐numerical magnitudes mentioned above. Each array contained between 5 and 35 dots. It is known that comparing two groups of dots when the numerical ratio is closer to zero (e.g., 15 and 50) is easier than to compare two groups of dots when the numerical ratio is closer to one (e.g., 15 and 20). This phenomenon is known as the ratio effect [e.g., Cantlon et al., 2009; Leibovich et al., 2013; Leibovich and Henik, 2014; Moyer and Landauer, 1967] and is well documented in the literature. Hence, to keep difficulty level similar, the numerical ratio was kept constant between 0.4 and 0.42. The difference between 0.4 and 0.42 is too subtle to affect performance [Leibovich and Henik, 2014]. The number of non‐numerical magnitudes that are congruent with number (i.e., congruity level) was manipulated and ranged from 1 to 4 (Table 1). We ensured that the average ratio between the congruent non‐numerical magnitudes did not differ from the average ratio between the incongruent non‐numerical magnitudes at every congruity level (Table 2). This was necessary because the ratio between the irrelevant non‐numerical magnitudes might also affect performance [e.g., Leibovich and Henik, 2014]. Note that the average ratio of the congruent non‐numerical magnitudes was almost identical to the average ratio of the incongruent non‐numerical magnitudes. The only exception is congruity level 3 where the average ratio of the congruent magnitude was 0.65 and the incongruent magnitude was 0.51. Examples of the stimuli can be seen in Figure 2

Table 1.

Different congruity levels

Congruity level	Convex hull	Density	Total surface	Average diameter	Total circumference
4	C	IC	C	C	C
4	C	C	C	IC	C
3	IC	IC	C	C	C
3	C	IC	C	IC	C
3	C	C	IC	IC	C
2	IC	IC	C	IC	C
1	IC	IC	IC	IC	C

C, congruent with number; IC, incongruent with number.

Table 2.

Average ratio of non‐numerical magnitudes by congruity

congruity level	Congruent magnitudes	Incongruent magnitudes
4	0.45	0.45
3	0.65	0.51
2	0.71	0.73
1	0.74	0.74

The values in the cells are the average non‐numerical ratio magnitude (smaller/larger magnitude) for all the congruent or for all the incongruent magnitudes.

Brightness task

The stimuli were composed of two rectangles (128 × 192 pixels each), presented to the left and to the right of the middle of an 800 × 600 pixels white screen. The shade of gray was manipulated by changing the luminosity value (in “paint” software). Luminosity values range from 0 (the darkest) to 240 (the lightest). We used values from 24 to 188, yielding 4 different ratios of brightness (smaller divided by larger luminosity value): 0.4, 0.5, 0.8 and 0.85 (Fig. 3). These specific ratios were selected in a behavioral pilot study to match as closely as possible to the performance measures (RT and accuracy) of the 4 levels of difficulty of the numerosity task.

Figure 3.

Examples for stimuli in the brightness task. R = ratio between the luminance levels of the two rectangles. Ratio 0.4 is the easiest to discriminate (difficulty level 1) and ratio 0.85 is the most difficulty to discriminate (difficulty level 4).

Tasks

Participants performed two tasks in four separate runs. In the numerosity task, participants were asked to choose the group containing more dots. The numerosity task included two runs. Each run included 20 trials for each congruity level. The side of the larger dot array was counterbalanced for each IC level. In total a run included 80 trials: 4 congruity levels × 10 trials per level × 2 counterbalance response (larger number to the right or to the left), and lasted about 12 minutes. The order of the trials was random. In the brightness task, participants were asked to choose the darker rectangle. The brightness task included two runs. Each run contained 72 stimuli: 4 (ratios) × 9 (different variations for each pair) × 2 counterbalance response (darker rectangle on the right or on the left) and lasted about 10 min. The order of the trials was random.

Procedure

Before starting the scan, participants signed a consent form and were given general instructions about the tasks. An event‐related fMRI design was used to acquire functional imaging data. The experiment was run using OpenSesame [Mathôt et al., 2012] version 2.97 on a Windows 8 operating system.

Each session included an anatomical scan, practice run, and two functional runs per task. Before the first functional run of each task, participants read instructions specific to the task. Then, a 4‐trial practice run started, to verify that the task was clear. If accuracy was higher than 75%, participants continued to the functional runs. If not, the practice was repeated. The feedback for the practice was general for all 4 trials (not per trial). Each functional run started with 10 s of a baseline screen (a black screen in the numerical task and a white screen in the brightness task) and ended with 6 s of a baseline screen, to provide a stable baseline of brain activity.

In the functional runs of the numerosity task, each trial started with a black screen with a vertical gray line in its center. In the middle of the gray line, a red fixation‐dot appeared. The duration of the red fixation‐dot was jittered, namely, displayed for a duration of 4,000–6,000 milliseconds (ms) with an average of 5,000 ms and a uniform distribution (using “advanced delay” plugin of OpenSesame). Following the elimination of the red fixation‐dot, a green fixation‐dot was presented for 250 ms to alert the participants that a target stimulus was soon to appear, allowing them to prepare to respond. After the green fixation‐dot disappeared, a blank screen (black screen with a vertical gray line in the middle) was presented for 700 ms. Thereafter, the target stimulus—two groups of green dots—were presented for 700 ms and finally replaced by a blank screen for 700 ms. Participants were able to respond from the onset of the target stimulus' presentation until a new trial started (i.e., when a red fixation‐dot appeared). The participants were instructed to respond with a button press with the hand corresponding to the side of the presentation of the group containing the larger numerosity. The procedure of the paradigm is depicted in Figure 4a.

Figure 4.

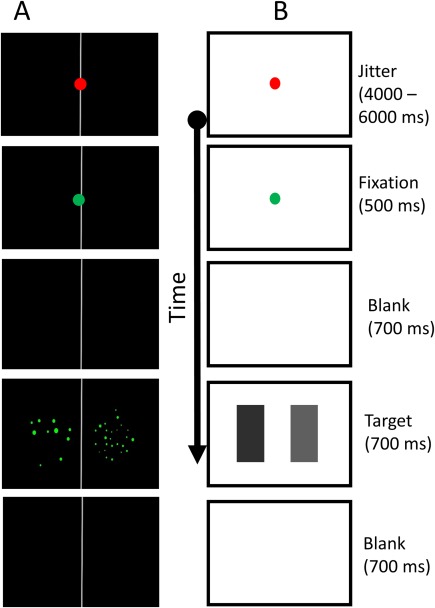
Procedure. A, numerical task. B, brightness task. The durations for each stimulus indicated on the right side were the same for both tasks. In both tasks, participants were able to respond from the onset of the target until the jitter slide appeared. [Color figure can be viewed at http://wileyonlinelibrary.com]

In the functional runs of the brightness task, each trial started with a white screen with a red fixation‐dot in the middle. The red fixation‐dot presentation's duration was jittered as described for the numerosity task (see above), and followed by a green fixation‐dot that was presented for 250 ms. After the green fixation‐dot disappeared, a white screen was presented for 700 ms. Thereafter the target stimulus—two rectangles in different shades of gray—was presented for 700 ms and finally replaced by a white screen for 700 ms. Participants were able to respond from the onset of target stimulus's appearance until a new trial started (i.e., when a red fixation‐dot appeared). The participants were instructed to respond with a button press with the hand corresponding to the side of the presentation of the darker rectangle. The procedure of the paradigm is depicted in Figure 4b.

fMRI data acquisition

A 3 T Siemens PRISMA whole‐body MRI scanner was used to collect the functional and structural data of this study. The brain anatomy of each participant was collected with high‐resolution T1‐weighted images (matrix dimensions: 240 × 256 mm) using an MPRAGE sequence (1 × 1 × 1 mm, TR: 2,300 ms, TE: 4.25 ms, flip angle: 9°). An echo planar (EPI SE) sequence was used to measure BOLD brain signal of the functional run with a 32‐channel Siemens head coil. The order of imaging acquisition was ascending—interleaved, covering the whole brain of participants. The acquisition resulted in 276 whole‐brain images per functional run in the brightness task and 308 per functional run in the numerical task, with a total length of about 10–12 min per run. For each functional volume, 38 slices were collected resulting in a 3 mm isovoxel resolution over a 64 × 64 voxel matrix. The repetition time (TR) was 2,000 ms, the echo time (TE) was 30 ms, and the flip angle was 78°.

Imaging analysis

Brain Voyager QX 2.8 (Brain Innovation, Maastricht, The Netherlands) was used to analyze the functional and structural data sets. Each individual data set was preprocessed according to the following steps: functional imaging data were first corrected for slice scan time acquisition (ascending—interleaved; using a cubic‐spline interpolation algorithm); a high‐pass (GLM—Fourier) frequency filter with a cut‐off value of 2 sines/cosines cycles was applied to remove low‐frequency signals; finally, a Trilinear/sinc interpolation approach was used to remove and to adjust head motion. To be included in the study, participants' movement parameters had to stay within 3 mm of overall movement (maximum deviation from the first volume) and within 1 mm volume‐to‐volume movement (maximum deviation from one collected functional image to the next collected functional image). Five runs (2 of the brightness task and 3 of the number task) were excluded from the analysis due to over 1 mm volume‐to‐volume movement.

An automatic alignment procedure (as implemented in Brain Voyager) was used to spatially align the functional runs of each participant onto the corresponding anatomical scan. The quality of the alignment was checked visually and corrected manually if the automatic procedure did not reveal a sufficient alignment. Subsequently, the co‐aligned images were transformed into Talairach space [Talairach and Tournoux, 1988]. This was achieved in two consecutive steps: first, using the landmarks of the Anterior Commissure (AC) and the Posterior Commissure (PC), the anatomical image of each participant was transformed into ACPC‐plane position; second, the boundaries of the brain tissue were manually selected and transformed into the Talairach grid using a trilinear interpolation algorithm [Talairach and Tournoux, 1988] and smoothed using Gaussian Smoothing Kernel at FWHM of 6 mm.

Individual data sets were entered into a general linear model (GLM) for group‐based analysis. All functional events of the two tasks (i.e., numerosity and brightness) were convolved with a two‐gamma hemodynamic response function (HRF) to assess the fit to the blood oxygen level dependent (BOLD) function [Friston et al., 1998]. Different congruity level trials across the functional runs (for the numerosity task) and different ratios of brightness (for the brightness task) were modeled separately to investigate brain activation differences related to difficulty/congruity level in the two tasks. Incorrect responses were not included in the analysis. The statistical maps derived from brain activation contrasts were thresholded with an uncorrected P value of 0.001 and subsequently cluster corrected to correct for multiple comparisons and to adjust Type I error to a level of P < 0.05. This was achieved by an iterative “Monte Carlo Simulation” (1,000 iterations), which estimates the minimum size of a functional cluster to be significant on the basis of functional data from this study [Forman et al., 1995]. Specifically, an initial uncorrected voxel‐level threshold is estimated. The statistical whole‐brain maps are then submitted to different correction criteria, based on estimates of the map's spatial preprocessing smoothness and on an iterative correction procedure (Monte Carlo simulation) that estimates cluster‐level false‐positive rates across the entire brain. After 1,000 iterations the minimum cluster‐size yielding a cluster‐level false‐positive rate of (α) 0.05 was used to cluster correct the statistical whole‐brain maps.

RESULTS

Behavioral Results

To test the effect of task and difficulty level on performance, a two‐way analysis of variance (ANOVA) was performed with task (numerosity or brightness) and difficulty level (4 different levels) as within‐subject variable. The ANOVA was conducted once for RTs and once for accuracy rates.

For the analysis of accuracy, Greenhouse–Geisser correction was applied as Mauchly's test of sphericity indicated that the assumption of sphericity has been violated (P < 0.05). The analysis revealed that accuracy was generally higher for the numerosity task F (1, 20) = 54.79, P < 0.001, ${\eta }_{{}^{\mathrm{p}}}^2$ = 0.73. Main effect for difficulty suggested that the different conditions differ in their accuracy F (2.3, 46.9) = 16.13, P < 0.001, η ² _p = 0.45. A series of t tests for paired samples was performed to explore the main effect of difficulty level in both tasks. This analysis resulted in 4 paired sample t tests (D1 vs D2; D2 vs D3; D3 vs D4 and mean (D1 + 2) vs mean (D3 + 4)). To correct for multiple comparisons, we divided the alpha by 4, and accepted a P value of below 0.05/4 = 0.0125, to be significant. The results for the numerosity task were as follow: for D1 versus D2: t(20) = 0.087, P = 0.93; D2 versus D3: t(20) = 1.91, P = 0.071; D3 versus D4: t(20) = 0.43, P = 0.67; mean (D1 + 2) versus mean (D3 + 4): t(20) = 3.05, P = 0.006. The results for the brightness task were as follow: for D1 versus D2: t(20) = 1.41, P = 0.17; D2 vs D3: t(20) = 3.39, P = 0.003; D3 vs D4: t(20) = 0.28, P = 0.78; mean (D1 + 2) versus mean (D3 + 4): t(20) = 7, P < 0.0001. Finally, an interaction of task and difficulty was significant F(2.4, 49.6) = 9.16, P < 0.001, η ² _p = 0.31, demonstrating that in the brightness task, the decrease in accuracy with increase in difficulty level was more pronounced than in the numerosity task (Fig. 5a).

Figure 5.

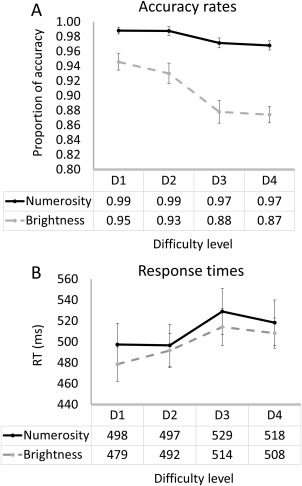
Behavioral results. A, accuracy results. B, response time results. D1 = congruity level 4 (in the numerosity task) and ratio 0.4 (in the brightness task); D2 = congruity level 3 and ratio 0.5; D3 = congruity level 2 and ratio 0.8; D4 = congruity level 1 or ratio 0.85. Note that accuracy was generally high, but higher in the numerosity task.

For the analysis of RT, only the main effect of difficulty was significant F(3, 60) = 17.67, P < 0.001, η ² _p = 0.47. Similar to the accuracy analysis, a series of t tests for paired samples was performed to explore the main effect of difficulty level in both tasks. The results for the numerosity task were as follow: for D1 vs D2: t(20) = 0.12, P = 0.91; D2 versus D3: t(20) = 3.37, p = 0.003; D3 versus D4: t(20) = 1.68, P = 0.109; mean (D1 + 2) versus mean (D3 + 4): t(20) = 3.32, P = 0.003. The results for the brightness task were as follow: for D1 versus D2: t(20) = 2.72, P = 0.013; D2 versus D3: t(20) = 3.89, P = 0.001; D3 versus D4: t(20) = 0.972, P = 0.373; mean (D1 + 2) vs mean (D3 + 4): t(20) = 3.32, P < 0.0001. There was no significant main effect for task (F(1,20) = 0.68, P = 0.42, η ² _p = 0.033) or an interaction between task and congruity (F(3, 60) = 0.84, P = 0.48, η ² _p = 0.04) (Fig. 5b).

fMRI Analysis

We looked for an area where activity increased with an increase in congruity level selectively for the numerosity task. Such a pattern (i.e., activity that is specific to, and positively correlated with, the amount of the to‐be‐accumulated evidence) will suggest an area which is involved in magnitude accumulation [Heekeren et al., 2004, 2008]. To address this, we performed a voxelwise whole‐brain ANOVA with task (numerosity or brightness) and difficulty level (4 levels) as within‐subject variables. The analysis revealed a significant main effect for task, no main effect of difficulty, and a significant interaction between task and difficulty (P < 0.001 cluster corrected for multiple comparisons, P = 0.05).

The main effect of task revealed a bilateral occipital and parietal network of areas that were more active during the numerosity task compared with the brightness task (Table 3 and Fig. 6). The result of the interaction of task and difficulty level revealed one brain area, the right inferior frontal gyrus (rIFG). rIFG activity was found to be modulated by difficulty/congruity level only during the numerosity comparison task (Fig. 7 and Table 3). More specifically, during the numerosity task, activity in the rIFG was positively correlated with the amount of non‐numerical magnitudes that can be accumulated (Fig. 1). In contrast, during the brightness task, activity level was not modulated by difficulty level.

Table 3.

Brain regions found in a voxelwise whole‐brain ANOVA

Brain region	Brodmann area (BA)	Coordinates: x, y, z			F	Cluster size (voxels)
Task: numerosity > brightness
(Cl 1) Right inferior temporal gyrus	37	39	−64	−8	30	3,667
(Cl 2) Right superior temporal lobule/occipital gyrus	7	18	−70	43	45	5,364
(Cl 3) Right lingual gyrus	18	9	−73	−2	29	1,003
(Cl 4) Left lingual gyrus	19	−24	−61	−8	49	1,853
(Cl 5) Left occipital gyrus	39	−24	−70	28	36	8,589
Difficulty NA
Task × difficulty
Right inferior frontal gyrus	44	45	5	19	11	274

CI, cluster.

Figure 6.

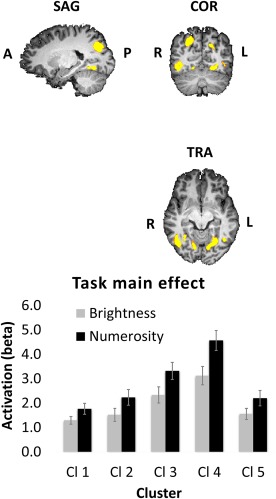
Brain activity related to task. A network of bilateral occipito‐parietal areas found to be more active during numerosity comparisons than during brightness comparisons in a voxelwise whole‐brain ANOVA. Cl 1 = right Inferior temporal gyrus; Cl 2 = right superior parietal lobule/occipital gyrus; Cl 3 = right lingual gyrus; Cl 4 = left lingual gyrus; Cl 5 = left occipital gyrus. Talairach coordinates = −21, −63, −6. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 7.

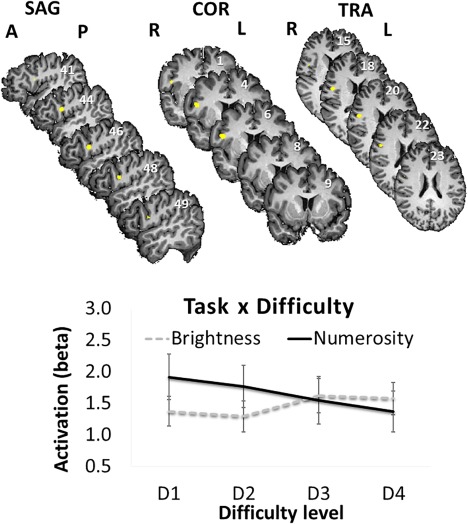
Interaction of task and difficulty in the right inferior frontal gyrus (rIFG). The pattern of results suggests that the activity in the rIFG (label for region determined by using the Mai Atlas [Mai et al., 2008]) decreased with difficulty level only in the numerosity task, but was not significantly influenced by size in the brightness task. The error bars represent standard error (SD/square root of N). Talairach coordinates are mentioned in every section in the figure. In the sagittal sections, the x coordinates; in the coronal sections, the y coordinates; and in the transversal sections, the z coordinates. [Color figure can be viewed at http://wileyonlinelibrary.com]

To verify this pattern, we extracted the beta values of the rIFG for each task and difficulty level and used them as the dependent measure in two separate one‐way ANOVAs with difficulty level as the independent measure, once for the numerosity comparison task and once for the brightness task. These analyses revealed that the influence of difficulty/congruity level on activation was significant during the numerosity comparison task F(3,60) = 4.5, P < 0.01, η ² _p = 0.19, but not during the brightness task F(3,60) = 2.02, P = 0.12.

Post‐Hoc Analysis: Parametric Analysis

Following the request of the reviewers, we used parametric analysis to demonstrate that in the number task, activation level parametrically increased with congruity level. To achieve this, we assigned the following weights before entering the data into a GLM: congruity level 1: 10; congruity level 2: 20; congruity level 3: 30; congruity level 4: 40; brightness ratio 0.4: 40; brightness ratio 0.5: 50; brightness ratio 0.8: 80; brightness ratio 0.85: 85. The resultant GLM included main effect and a parametric effect for each task. These events were processed as described in the “imaging analysis” section.

To look for parametric effects, a whole‐brain contrast between the parametric effect of the numerosity task and the parametric effect of the brightness task was computed. Unlike the results from the ANOVA, the parametric effect in the number task was not found to be significantly greater than the parametric effect of brightness at voxelwise threshold of P < 0.001 corrected for multiple comparisons at the cluster level (P < 0.05). However, this contrast revealed a similar area to the one found by the interaction of task and difficulty (1,168 voxels; peak coordinates: (45, 2, 19)) at a voxel‐wise threshold of P < 0.005, corrected for multiple comparisons at the cluster level (P < 0.05).

DISCUSSION

In behavioral research, it is well established that non‐numerical magnitudes affect performance in numerosity comparison tasks [Gebuis and Reynvoet, 2012; Leibovich et al., 2015a, 2015b; Leibovich and Henik, 2014]. However, the neural mechanism behind this influence is yet to be investigated. In the current work we found, using a whole‐brain analysis, that the activity of the rIFG is modulated by the amount of non‐numerical magnitudes that positively correlated with number. Specifically, the activity in the rIFG increased with the number of non‐numerical magnitudes that were congruent with numerosity. The brightness and the numerosity tasks were carefully matched in RT and accuracy to exclude differences in task difficulties as an alternative explanation to the results. More specifically, as activity in the rIFG was not affected by difficulty in the brightness task, it is less likely that a general “difficulty effect” can explain the activity pattern in this area. Importantly, the rIFG activation observed complies with the two demands set forth by Heekeren et al. [2008] to define an area as an accumulator: (1) selectivity of activation to the task and (2) an activation pattern that is positively correlated with the amount of the to‐be‐accumulated evidence (e.g., the amount of congruent non‐numerical variables). Accordingly, we suggest that the rIFG supports the accumulation of non‐numerical magnitudes that are positively correlated with number during numerosity comparison.

Accumulation of evidence is well established in the field of perceptual decision‐making. Some of the areas that are reported in the context of evidence accumulation are specific to task demands or the modality that is being used, while other areas are more general and could be found across tasks and modalities. The most commonly reported area in perceptual decision‐making across different tasks and modalities is the dorsolateral prefrontal cortex (DLPFC), which includes the inferior frontal gyrus [but see Brass et al., 2005]. For example, Noppeney et al. [2010] suggested that during audio–visual accumulation of evidence, the left inferior frontal sulcus (IFS) presented a pattern of activation that is consistent with an “accumulator” of evidence. In other words, the activity of this region increased with the increase in the amount of the to‐be‐accumulated evidence. Similarly, Heekeren et al. [2008] reviewed a variety of neurophysiological studies with nonhuman primates that revealed that the firing rate of sensory neurons in the DLPFC increased with an increase in the amount of the to‐be accumulated evidence.

In addition to such areas involved in accumulation of evidence across domains, there are also areas whose activity is specific to task and/or modality. For example, as mentioned in the introduction, the FFA, an area that has been associated with face perception, presents an “accumulator” pattern in a task that requires participants to decide if a stimulus is a house or a face.

The rIFG has been found in the context of both perceptual decision‐making and magnitude processing. In the context of perceptual decision‐making, Ploran et al. [2007] gradually presented participants with a picture of an object and asked them to indicate when they recognize the object. BOLD response in the rIFG increased during the presentation of the picture and peaked when the object in the picture was recognized. Similarly, rIFG activity was found to correlate with the rate of evidence accumulation in a stop‐signal task [White et al., 2014]. Recently, Sherman and colleagues [2016] demonstrated, using a visual search task, the involvement of the rIFG in integrating not only visual evidence, but prior beliefs (such as the likelihood of a target to appear) into the decision‐making process.

In the context of magnitude processing, the rIFG has been reported in numerous studies. To mention a few, Kaufmann et al. [2005] reported rIFG activity in a symbolic number comparison task; Chochon et al. [1999] revealed that the rIFG is more active during digit naming, number comparison, multiplication, and subtraction tasks compared to a control task, and Yao et al. [2015] found clusters in the rIFG area that were related to cognitive processing during a symbolic numerical congruity task.

Activation of the rIFG has also been reported in magnitude comparison studies that use nonsymbolic stimuli. Given the evidence reported above, it is possible that the activity of the rIFG in these prior studies is related to accumulation, and not necessarily (or not only) to magnitude processing. For example, Hayashi et al. [2013] employed a time‐numerosity congruity task, where participants sequentially saw two groups of dots for different durations of time and were asked to decide which group of dots appeared for a longer time, or contained more dots. The duration and the number of dots were either congruent (more dots presented for longer time than fewer dots) or incongruent (more dots presented for shorter time). The authors reported that the rIFG was more active during the duration task compared with the number task, consistent with the involvement of the rIFG in time processing (for a review, see Wiener et al. [2010]). Interestingly, the rIFG was also more active during congruent compared with incongruent trials across tasks. Hence, the activity of the rIFG in the experiment by Hayashi et al. could also be interpreted in light of its capacity as an accumulator of evidence; in congruent trials, both number and time could have been used to make a decision (as suggested by the ATOM theory, see Walsh [2003]). Consistent with this interpretation, rIFG activity was greater in congruent compared with incongruent trials (in which time and number are anticorrelated).

The rIFG was also found to play a role in different aspects of cognitive control. Brass et al. [2005], for example, suggested that the rIFG is involved in keeping task‐relevant representations active. Accordingly, in the current task, we should have seen more activation when the incongruity level (i.e., difficulty level) increased, and attending to numerosity becomes more difficult. Similarly, Heekeren et al. [2008] suggested that the IFG detects some perceptual uncertainty or difficulty and signals when more attentional resources are needed. If this is the case, we would have expected activity in the rIFG to increase with difficulty. However, we obtained the opposite pattern (Fig. 7). Accordingly, while it is possible that the rIFG activity is related to a general mechanism of cognitive control, the mechanism itself is less likely to be responding to level of conflict under the specific conditions of our study. Important in this context is that the rIFG itself can be separated into different domains that are involved in different cognitive processes [Liakakis et al., 2011]. Thus, the involvement of rIFG in conflict monitoring might be independent of its role in evidence accumulation.

From the studies above, it seems that there are three possible accounts for the role of the rIFG in magnitude comparison tasks. The first is a domain‐general account, whereby the activity of the rIFG reflects a general accumulation mechanism, such as the one revealed in tasks that do not involve magnitudes. The second is a domain specific account where the role of the rIFG in accumulation is specific to magnitudes, similar to the accumulation‐related activity of the FFA that is specific to face stimuli. The third account is that the rIFG activity is context‐dependent in that the rIFG could be active during magnitude processing, regardless of accumulation, but also active during general accumulation. We argue that this study, together with the literature of perceptual decision‐making cited here, supports the third account. Namely, that the rIFG has a role in both accumulation and processing of magnitudes. Furthermore, the interaction of task and difficulty see Figure 7 suggests that the rIFG was active during the brightness task, but the pattern of activity was not as strongly related to task difficulty.

Importantly, although we found a vast occipito‐parietal network that was more active during the numerosity comparison task than during the brightness task, none of these parietal areas presented an “accumulator pattern.” This implies that while parietal areas are involved in representing and processing numerosities and magnitudes [e.g., Cohen‐Kadosh and Walsh, 2009; Dehaene et al., 2003; Piazza and Eger, 2016; Walsh, 2003], they are not involved in the process of accumulating evidence from non‐numerical magnitudes. This suggestion needs to be taken with a grain of salt, because this is a null effect, and we cannot exclude the possibility of an accumulation‐related activity in parietal areas against the background of the findings reported here. Further studies that will continue this line of research may shed more light on the distinction between magnitude representation and the decision process in magnitude comparison tasks.

In summary, this study tested the hypothesis that when comparing nonsymbolic numerosities (e.g., groups of dots), numerosity and non‐numerical magnitudes are accumulated to make a decision. This hypothesis is at the heart of a recently suggested alternative to the approximate number system (ANS) theory [Gevers et al., 2016; Leibovich et al., 2016b]. The current work is the first to test this hypothesis at the brain level. We found that activity in the rIFG increased with the amount of the to‐be‐accumulated non‐numerical magnitudes, and that this pattern is not likely to be related to task difficulty. With that being said, the interpretation our result should be constrained in view of the general limitations inherent in fMRI studies: due to the low temporal resolution of fMRI, it is impossible to know if activation of the rIFG correlated with difficult levels reflects the actual process of accumulation of evidence. What we can conclude is that activation in this region is correlated with the total congruency of non‐numerical evidence. More research is necessary to determine whether this accumulation is specific to magnitude or whether it reflects a more general accumulation mechanism.