Strategy over operation: neural activation in subtraction and multiplication during fact retrieval and procedural strategy use in children

Abstract

Arithmetic development is characterized by strategy shifts between procedural strategy use and fact retrieval. This study is the first to explicitly investigate children's neural activation associated with the use of these different strategies. Participants were 26 typically developing 4th graders (9‐ to 10‐year‐olds), who, in a behavioral session, were asked to verbally report on a trial‐by‐trial basis how they had solved 100 subtraction and multiplication items. These items were subsequently presented during functional magnetic resonance imaging. An event‐related design allowed us to analyze the brain responses during retrieval and procedural trials, based on the children's verbal reports. During procedural strategy use, and more specifically for the decomposition of operands strategy, activation increases were observed in the inferior and superior parietal lobes (intraparietal sulci), inferior to superior frontal gyri, bilateral areas in the occipital lobe, and insular cortex. For retrieval, in comparison to procedural strategy use, we observed increased activity in the bilateral angular and supramarginal gyri, left middle to inferior temporal gyrus, right superior temporal gyrus, and superior medial frontal gyrus. No neural differences were found between the two operations under study. These results are the first in children to provide direct evidence for alternate neural activation when different arithmetic strategies are used and further unravel that previously found effects of operation on brain activity reflect differences in arithmetic strategy use. Hum Brain Mapp 38:4657–4670, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

To date, relatively little is known about the neural substrate of arithmetic in children, an academic skill of clear importance in everyday life (e.g., we maintain budgets, or work with proportions when cooking). On the other hand, accumulating evidence in adults is suggesting that a frontoparietal network, which includes the superior and inferior parietal lobes, the inferior frontal gyri and the insular cortex, is consistently being activated during arithmetic (for a review, see Arsalidou and Taylor, 2011; Menon, 2015). Most of these studies, however, did not directly take strategy use—arithmetic problems can be solved through fact retrieval or by means of procedural manipulations—into account. This is important as strategy use has been shown to modulate the adult arithmetic brain network (Grabner et al., 2009; Tschentscher and Hauk, 2014). Studies in children have never directly investigated the neural activity during these strategies. This study is therefore the first to investigate neural activation during arithmetic while taking into account individual differences in children's arithmetic strategy use, which is crucial considering the large developmental changes in children's acquisition of arithmetic strategies (Siegler, 1996).

Functional magnetic resonance imaging (fMRI) research in adults has often implicated dorsal parts of the parietal cortex, including the intraparietal sulcus, as a critical hub for the representation and manipulation of numerical quantity (e.g., Ansari, 2008; Cohen Kadosh et al., 2008; Dehaene et al., 2003). These regions make up the magnitude code of the adult Triple Code Model as postulated by Dehaene and Cohen (1997). This model also proposed a visual code, located in bilateral inferior ventral occipitotemporal regions, in which numbers are represented as identified strings of digits. The Triple Code Model also postulated a verbal code, located in left‐hemispheric temporo‐parietal areas, in which numbers are phonologically represented, and which is implicated in accessing arithmetic facts (Dehaene and Cohen, 1997). Although many brain imaging studies in numbers and arithmetic have limited their focus to the parietal cortex, many areas outside the parietal cortex are also involved in arithmetic (Arsalidou and Taylor, 2011; Menon, 2015). Calculation places a demand on various cognitive systems (e.g., working memory or cognitive control), and thus multiple regions, such as the anterior insula and anterior cingulate cortex for directing attention, and the ventro‐ and dorsolateral prefrontal cortex for effortful maintenance and manipulation of information, respectively, are also typically activated during calculation (e.g., Arsalidou and Taylor, 2011; Menon, 2015).

Only a very small number of fMRI studies have investigated the functional properties of the arithmetic network in children (Menon, 2015; Peters and De Smedt, in press, for a review). This network involves a large set of interconnected areas that include frontal (both ventro‐ and dorsolateral prefrontal cortex), parietal (intraparietal sulcus, angular gyrus, and supramarginal gyrus), occipito‐temporal, and medial temporal (including the hippocampus) areas. This network shows some similarities to the network observed in adults, but it is a clearly different network which is recruited by children, particularly during the development of arithmetic facts (Menon, 2015; Peters and De Smedt, in press). For example, adults typically show activation increases in angular and supramarginal gyri during more easy problems, which are likely to be solved by fact retrieval, yet these changes in brain activity have not been consistently observed in children. Moreover, increased activity in the hippocampus has been observed in the early stages of learning arithmetic, more specifically in addition (e.g., De Smedt et al., 2011). It is important to take into account, however, that previous fMRI studies in children used samples with wide age ranges, which may have affected these reported findings. This is particularly relevant, as arithmetic development is characterized by a decreasing engagement of the prefrontal cortex and by an increasing engagement and functional specialization of the inferior and posterior parietal cortex (Kucian et al., 2008; Rivera et al., 2005). Even the short interval from second to third grade is linked to significant task‐related changes in brain activation, such as greater activity in both dorsal stream parietal and ventral visual stream areas (Rosenberg‐Lee et al., 2011), pointing toward a large developmental trajectory in the arithmetic brain network (Menon, 2015). In all, this suggests a need for studies that focus on one particular age range.

As mentioned, arithmetic problems can be solved through different strategies. Furthermore, a well‐validated fact through decades of behavioral research (e.g., Siegler, 1996), is that, over development, changes occur in the strategies that children use, yet this has never been explicitly investigated in children through fMRI. These strategies can be categorized as retrieval (i.e., remembering the solution to a certain problem) or procedure. Such a procedural strategy is used when the solution to a certain problem cannot be directly retrieved from memory, and procedural manipulations, such as counting or the decomposition of operands (e.g., 24 − 7 = 24 − 4 − 3 = 20 − 3 = 17 or 3 × 13 = (3 × 10) + (3 × 3) = 30 + 9 = 39) are needed. When learning to solve arithmetic problems, children initially rely heavily on effortful and time consuming procedures, such as counting. Repeated use of counting, however, will lead to the formation of associations between a problem and its solution, which will in turn lead to the retrieval of the correct answer whenever that problem is presented (Siegler and Shrager, 1984).

Previous studies, particularly neuroimaging work, however, have often made assumptions on strategy use based on reaction time, problem size, or operation, yet it is crucial to emphasize that these approaches are limited (see De Smedt, 2016, for a discussion), as not all problems of a particular size or operation are solved with the same strategy at the same point in development (Siegler, 1987). For example, behavioral studies have shown that, even in adults, single‐digit arithmetic items are sometimes solved by procedures, such as counting (LeFevre et al., 1996). Ignoring the use of different strategies is especially problematic in the context of developmental research, as, with education and practice, the strategies that children use to solve particular types of problems change over time. Therefore, trial‐by‐trial self‐reports, which (in children) have sufficient reliability and validity (Siegler and Stern, 1998), might be more appropriate to capture arithmetic strategy use, as they allow for the estimation of individual differences in the choice of strategy.

Adult fMRI studies have recently started to take arithmetic strategy use into account, and revealed that the choice of strategy modulates brain activity during arithmetic (Grabner et al., 2009; Tschentscher and Hauk, 2014). In an event‐related fMRI study, Grabner et al. (2009) provided the first evidence for alternate neural activation when using different strategies. The study implemented trial‐by‐trial self‐reports in adults immediately after scanning, by asking the participants how they had solved the items during scanning. Their results pointed out that adults show stronger activation of the left angular gyrus when retrieving, while procedural strategy use leads to activation in a more widespread frontoparietal network. Extending these results, Tschentscher and Hauk (2014) also used strategy self‐reports, during addition and multiplication in adults, and mainly found increased activation in the bilateral angular gyrus for fact retrieval. For procedural strategy use, increased activation was observed in the prefrontal cortices, motor areas, posterior superior parietal lobe, and intraparietal sulcus. The results of these studies are thus in line with the idea that the angular gyrus supports retrieval processes in adults, while more activation in the posterior superior parietal lobe and sensory‐motor regions is linked to procedural strategy use. It remains to be determined if a similar pattern of findings can be found in children.

Importantly, Tschentscher and Hauk (2014) did not observe any effect of arithmetic operation on brain activity once arithmetic strategy was taken into account. This suggests that earlier findings on differences in brain activity between arithmetic operations (e.g., Arsalidou and Taylor, 2011; Dehaene and Cohen, 1997; Prado et al., 2011; Zhou et al., 2007) should be interpreted with great caution. In children, such operation effects have also been reported repeatedly (e.g., De Smedt et al., 2011; Prado et al., 2014). More specifically, De Smedt et al. (2011) observed increased activity in the left hippocampus for single‐digit addition in comparison to subtraction, and in a frontoparietal network for subtraction in comparison to addition, while Prado et al. (2014) found grade‐related increases of activity for multiplication, but not for subtraction, in the left temporal cortex, and increases of activity for subtraction, but not for multiplication, in the right parietal cortex. These studies, however, did not take the participants' strategy use into account, and were only able to make implicit assumptions about strategies, as they assumed that the items of the same operation would be solved with the same strategy at the same age. Consequently, it is still unclear how strategy use modulates activation of the arithmetic brain network in children, and whether previously found operation effects in children might be due to differences in arithmetic strategy use.

Interestingly, Cho et al. (2011) assessed children's strategy use through verbal reports with a single‐digit addition task prior to scanning, but categorized their participants into retrievers and counters if they had solved over 60% of the items with a retrieval or procedural strategy, respectively. Subsequently, they compared the brain activity of those two groups during an addition task and observed that the retrievers more strongly activated the left ventrolateral prefrontal cortex. Here as well, brain activity during calculation was not analyzed as a function of the strategy used during problem solving. Furthermore, the study only included one operation (i.e., addition), leaving it open whether these results were transferable to different operations. Research which uses trial‐by‐trial self‐reports, and checks the neural activation patterns for different strategies in different operations, is thus yet to be done in children.

This study is the first to investigate children's neural activation during calculation, as a function of strategy use, determined on a trial‐by‐trial basis. The study follows an approach similar to Grabner et al. (2009) and Tschentscher and Hauk (2014) in adults, who implemented trial‐by‐trial strategy assessment outside of the scanner in order to analyze strategy use for each item separately. Such a trial‐by‐trial approach is even more needed in children, given that children are more likely to implement a variety of strategies, and that, during development, changes in strategy use occur (Siegler, 1996).

We developed an arithmetic task designed to elicit retrieval (single‐digit items) or procedural (double‐digit items) strategies. The task included both subtraction and multiplication, allowing us to investigate potential operation effects. Strategy use was recorded on a trial‐by‐trial basis and the task was administered approximately 3 weeks prior to scanning. During fMRI acquisition, children were presented with a subset of problems of the strategy assessment task, implemented in a 2 × 2 full‐factorial design (strategy: retrieval vs. procedure × operation: subtraction vs. multiplication). We employed an event‐related design that, for each child individually, allowed us to use the trial‐by‐trial strategy data, obtained prior to scanning, to categorize each trial during scanning into retrieval or procedure.

In light of the existing literature, we expected to find increases in activation in the hippocampus (based on the strategy assumptions of developmental literature; De Smedt et al., 2011; Qin et al., 2014) for fact retrieval trials. For procedural trials, we predicted an increase in brain activity in a more widespread frontoparietal network (De Smedt et al., 2011) as has been observed in adults (Grabner et al., 2009; Tschentscher and Hauk, 2014).

As this study used both subtraction and multiplication, we were also able to test differences between operations and possible interaction effects between strategy use and operation. This allowed us to directly verify whether the previously observed operation effects in children (De Smedt et al., 2011; Prado et al., 2014) reflect differences in strategy use. If the latter is the case, then operation effects will disappear when these strategies are taken into account, as has been observed in adults (Tschentscher and Hauk, 2014).

It is important to point out that, different from most of the existing developmental fMRI studies in the field of mathematical cognition, we have focused our study on children with a very narrow age range (i.e., only 4^th graders). This is crucial, as merging data across wide age ranges could lead to missing important neurodevelopmental changes, given that substantial differences in brain activity can already be observed after one year of schooling (Rosenberg‐Lee et al., 2011). By minimizing the variability in age, we reduced the potential effects of the different stages of development and of the received amount of mathematics instruction.

METHODS

Participants

Participants were 26 typically developing Flemish 4^th graders (ages 9–10), with no history of learning difficulties, or neurological or psychiatric disorders. All children were recruited via the elementary school they attended. Data of six children, however, were discarded, five of which due to excessive motion during functional scanning (see details below) and one due to technical acquisition problems. We thus analyzed data of 20 children (M = 9.6, SD = 0.29; 13 boys, 7 girls; 1 left‐handed). In return for participating, all children were given a financial compensation. Written informed consent was obtained from a parent or legal guardian of each participating child. The study was approved by the Medical Ethical Committee of the University of Leuven.

Procedure

All children took part in two test sessions. The first session, during which only behavioral data were collected, always preceded the second one by approximately three weeks (M = 21.92 days, SD = 6.13), and included both standardized and strategy assessment. The second session included the actual acquisition of MRI data.

Standardized assessment

Standardized assessment consisted of the evaluation of arithmetic, reading, and intellectual ability. Arithmetical competence was measured by the Tempo Test Arithmetic (TTA; de Vos, 1992); a standardized test of arithmetical fluency, similar to the Math Fluency subtest of the Woodcock–Johnson III tests of Achievement (Woodcock et al., 2003). The test exists of five columns of arithmetic items, increasing in difficulty (one column per operation and a column with mixed operations); each child gets one minute per column to provide as many correct answers as possible. Reading ability was assessed using a combination of the One‐Minute Test (OMT; Brus and Voeten, 1979) and the Klepel (Van den Bos et al., 1994), which measure the reading of words and pseudowords, respectively; both tests consist of 116 words. For the OMT, the children get 1 min to correctly read aloud as many words as possible; for the Klepel, the time limit is set to 2 min, and the children read aloud pseudowords. Finally, an index of intellectual ability was measured by the WISC‐III‐NL Block Design and Vocabulary subtests, as measures of performance and verbal IQ respectively (Wechsler, 2005). Standardized scores were calculated for all tasks. Figure 1 displays box plots with the descriptive statistics of this cognitive assessment. These results show that the means of our sample were close to the population averages, and show proper variation—especially for the TTA—as is expected in the general population. It is important to note that even though the minimum score for the TTA was low, none of the participating children had been diagnosed with learning disabilities or dyscalculia in particular.

Figure 1.

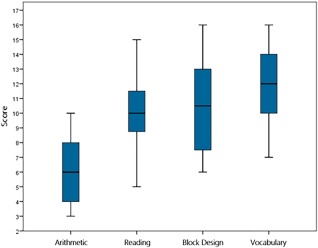
Box plots displaying the performance of the standardized assessment. Note: The scores above are standardized scores. The scores on the arithmetic test are standardized as M = 5, SD = 2, with a maximum of 10. The scores on the other tests are standardized as M = 10, SD = 3, with a maximum of 20. [Color figure can be viewed at http://wileyonlinelibrary.com]

Strategy assessment

Strategy use was assessed by a task in which the children were read aloud 100 arithmetic problems and asked to verbally solve them. They had to report how they had solved each item on a trial‐by‐trial basis; children were allowed and encouraged to use any strategy they wanted. The 100 items were divided into 50 subtraction and 50 multiplication items, each of which in turn were divided into items that were a priori expected to elicit either a retrieval or procedural strategy. The problems were presented in a pseudo‐randomized order (i.e., never more than five consecutive items of the same operation). For each item, the children's accuracy and used strategy was registered.

In subtraction, the retrieval items consisted of two single‐digit operands (e.g., 8–3), which have been indicated to be mainly answered through fact retrieval by previous verbal report data in children of a similar age range and math curriculum (Vanbinst et al., 2012). The procedural items crossed the bridge of either 20 or 30 (i.e., the first operand varied from 21 to 28 or 31 to 38, the second operand varied from 4 to 9, solutions varied from 12 to 19 or 22 to 29; e.g., 25–8). These items were expected to be solved procedurally, as it is unlikely for them to be stored in memory; as the children reported in the verbal reports, multiple steps were needed to find the answer. In multiplication, the retrieval items existed of two single‐digit operands (e.g., 4 × 3), which, by previous verbal report data in a similar sample of children, have also been indicated to be mainly answered through retrieval (Imbo and Vandierendonck, 2008). As all participating children came from Flemish schools, which have a high emphasis on fact retrieval for all single‐digit multiplication items, it was impossible to use a homogenous subset of single‐digit problems to investigate procedural strategy use. Therefore, for the procedural items, one operand varied from 3 to 6 and the other from 12 to 16, leading to solutions between 35 and 100 (e.g., 3 × 14). As multiplication tables beyond 10 are not taught in our curriculum, it is, again, unlikely that, in our sample, these items were stored in memory; as the children reported, multiple steps were needed to find the answer to these problems, making it very likely that these items would be solved by using procedural strategies.

After solving each item, the children were asked how they had solved it; responses were categorized as retrieval (i.e., the participant knew the answer without any sign of overt calculations), procedural (i.e., the participant indicated to have used any form of procedural strategy, such as counting or the decomposition of operands; the type of procedural strategy was also registered), or undefined (i.e., the participant did not know how (s)he had solved the item or used an unclear strategy); this last category was rare as it only occurred in 1.04% of the items.

fMRI experimental design

Each participant was presented with a set of 80 of the 100 problems of the strategy assessment task (i.e., 20 items per operation, per expected strategy). Stimuli were presented with E‐prime 2.0 (Psychological Software Tools, Pittsburgh, PA), via an NEC projector onto a screen behind the participants, made visible through a mirror attached to the head coil. All stimuli were presented in white (Arial, font size 60) on a black background. Problems were presented horizontally in Arabic digits, and after 2 s, two possible answers (a correct and an incorrect one) were simultaneously presented (Fig. 2). The children were asked to indicate the correct answer by pressing the left or right button on the response box for the left or right response alternative, respectively. For the subtraction items, incorrect answers were created by adding or subtracting 1 or 2 from the correct answer. For the multiplication items, incorrect answers were created by adding or subtracting the value of the smallest operand to or from the correct answer; the proposed false answers were thus always a table related product. When choosing the proposed false answers, however, we made sure the equations could not be solved more easily by applying a certain rule, such as the five rule (e.g., in the item 2 × 9, the proposed false answer was 16 instead of 20; in the item 6 × 14, the proposed false answer was 78 instead of 90). The position of the correct answers was balanced.

Figure 2.

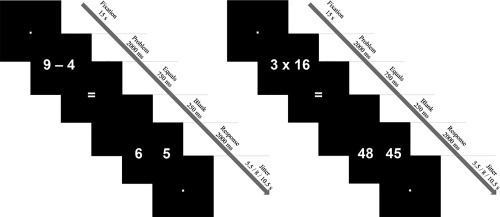
Schematic overview of an expected retrieval (left) and procedural (right) trial.

The task was presented across four functional runs in an event‐related fMRI design (similar to De Smedt et al., 2011 and Grabner et al., 2009). Each run consisted of 15 s of fixation at the start of the run, 20 trials (5 items per operation, per expected strategy), and 15 s of fixation at the end of the run. Every trial included the presentation of a problem (2000 ms), followed by a centered equality sign and a blank screen (750 ms and 250 ms, respectively), followed by the presentation of the response alternatives (2000 ms). In between trials, a jittered intertrial interval of 5.5, 8, or 10.5 s (averaged at 8 s) was randomly added to enable the deconvolution of the hemodynamic response functions (see Fig. 2 for a schematic overview of a trial). The children were asked to answer as accurately and quickly as possible and were allowed to answer during both the presentation of the response alternatives and the intertrial fixation period. Only the first 5000 ms of the trial were used for data analysis. The duration of each run was approximately 5 min.

MRI Data Acquisition and Analysis

Functional and structural images were acquired by a Philips Ingenia 3.0T CX MRI scanner with a SENSE 32‐channel head‐coil, located at the Department of Radiology of the University Hospital in Leuven, Belgium. To minimize head motion, wash cloths were used to stabilize the children's heads. For the fMRI data, 52 slices were recorded in an ascending order, using a T2*‐sequence (2.19 × 2.19 × 2.2 mm voxel size, 2.2 mm slice thickness, 0.3 mm interslice distance, 96 × 95 acquisition matrix, 90° flip angle) and covered the whole brain (field of view: 210 × 210 × 130 mm). Each run consisted of 94 measurements (TR = 3000 ms, TE = 29.8 ms). Anatomical images were acquired with a T1‐weighted sequence (0.98 × 0.98 × 1.2 mm voxel size, 256 × 256 acquisition matrix, 8° flip angle, TE 4.6 ms, 250 × 250 × 218 mm field of view).

All preprocessing was conducted with the Statistical Parametric Mapping software package for Matlab (SPM12, Wellcome Department of Cognitive Neurology, London). Preprocessing included correcting the functional images for slice timing differences, motion correction by realignment to the first functional image, coregistration (alignment to the respective high‐resolution anatomical image), normalization to the standard Montreal Neurological 152‐brain average template, and spatial smoothing with a 10 mm FWHM Gaussian smoothing kernel.

We only included the correctly answered items into our general linear model. In runs that showed excessive motion (i.e., if the movement from one image to the next was greater than the voxel size of 2.2 mm), only the items before the time point of excessive movement were included. This was only the case if at least one item per condition remained in that run; if this was not the case, the entire run was discarded. Data of participants with less than two completely usable runs were discarded entirely. Following these motion criteria, and taking into account the technical acquisition problems for the data collection of one participant, we completely discarded the data of six participants. Of the remaining 20 participants, five runs (i.e., 6.25%) were discarded, and five runs were only partially added to the model.

A general linear model, modeling only the correctly solved items, was calculated per participant. The motion realignment parameters were included as regressors of no interest to control for variation as a result of movement artifacts. A whole‐brain full factorial 2 × 2 ANOVA was performed on the imaging data, with strategy (retrieval vs. procedure) and operation (subtraction vs. multiplication) as within‐subject factors. To provide more information on the direction of any found main effects, t contrasts were calculated between all conditions. All whole‐brain activation maps were corrected for multiple comparisons through a family wise error (FWE) correction with a P < 0.05 threshold.

RESULTS

Behavioral Results

Results of the strategy assessment task are displayed in Table 1. Overall accuracy on this task was very high. Furthermore, the verbal reports indicated that children used a retrieval strategy on most of the items designed to elicit fact retrieval; the same was true for procedural strategy use. It is important to note that the vast majority of the reported procedural items were solved through the decomposition of operands strategy. Other procedural strategies were rare; repeated addition, for example, was only reported in 0.34% of all trials, and a counting strategy was never reported. The consistency of retrieving single‐digit items and the absence of counting for procedural items was expected as, in the Flemish educational system, there is a high emphasis on either fact retrieval or on using the decomposition of operands strategy, while counting, from a very early point on in first grade, is discouraged or even prohibited (De Smedt, 2016, for a discussion). This exclusive focus on the decomposition strategy in teaching arithmetic also resulted in large similarities in the way procedural subtraction and multiplication items were solved. Children always reported a similar decomposition strategy for both operations: e.g., 25 − 8 = 25 − 5 − 3 = 17 for subtraction, and 4 × 13 = (4 × 10) + (4 × 3) = 40 + 12 = 52 for multiplication. As this decomposition strategy was used throughout almost all procedural trials, this study can only discuss this particular strategy and cannot make any claims regarding other procedural strategies, such as counting or repeated addition.

Table 1.

Performance on strategy assessment task

	Accuracy (% correct)		Frequency (%)
Condition	M	SD	M	SD
Retrieval
Multiplication	99.33	1.37	90.83	11.49
Subtraction	100	0	100	0
Procedure
Multiplication	98.50	3.28	99.75	1.12
Subtraction	99.50	2.24	91.50	12.68

The differentiation between retrieval and procedure is based on the self‐reports of the participants.

Behavioral data on the arithmetic task in the scanner are displayed in Figures 3 and 4. We performed a 2 × 2 repeated measures ANOVA with strategy (retrieval vs. procedure; i.e., retrieval vs. decomposition) and operation (multiplication vs. subtraction) as within‐subject factors for both accuracy and reaction time. Note that the reaction times were measured starting from the onset of the presentation of the response alternatives, and of not the problem itself.

Figure 3.

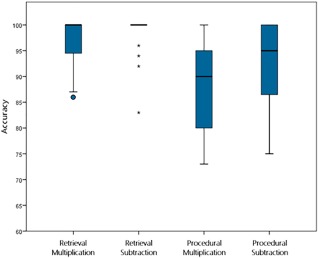
Box plots displaying the accuracy per category on the arithmetic task during fMRI. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 4.

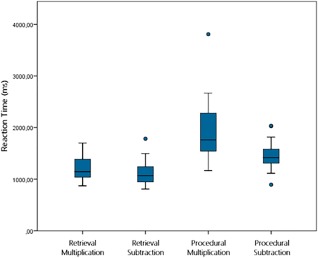
Box plots displaying the reaction time per category on the arithmetic task during fMRI. [Color figure can be viewed at http://wileyonlinelibrary.com]

The analyses of accuracy indicated main effects of both strategy (F(1,19) = 24.59, P < 0.001, η _p ² = 0.56) and operation (F(1,19) = 5.24, P = 0.034, η _p ² = 0.22), showing more accurate performance for retrieval than for the decomposition strategy, and for subtraction than for multiplication. There was no strategy × operation interaction (F(1,19) = 0.68, P = 0.42, η _p ² = 0.04).

With regard to reaction time, similar results were observed, as main effects for strategy (F(1,19) = 49.07, P < 0.001, η _p ² = 0.72) and operation (F(1,19) = 16.94, P = 0.001, η _p ² = 0.47) were found, indicating faster responses for retrieval compared to the decomposition strategy, and for subtraction compared to multiplication. A significant strategy × operation interaction was also found (F(1,19) = 7.69, P = 0.012, η _p ² = 0.29), revealing a larger difference between the use of a decomposition strategy and retrieval in multiplication compared to subtraction.

Imaging Results

Neural differences between both strategies were found, as our whole‐brain analysis revealed a main effect of strategy on brain activation (an overview of all significantly activated clusters can be found in Table 2; a visualization of this main effect is displayed in Fig. 5). Retrieval strategy use was associated with stronger activation in the bilateral angular and supramarginal gyri, the left middle to inferior temporal gyrus, the right superior temporal gyrus, and the bilateral middle orbital and superior medial frontal gyrus. The stronger activation found for the retrieval versus decomposition contrast, however, does not reflect an actual increase in activation, but a lesser amount of deactivation compared to baseline. This was determined by extracting the beta values of each activation cluster for each contrast separately, for which a negative value would imply lower activation in comparison to baseline. The use of a decomposition strategy more strongly activated a large bilateral, mainly frontoparietal, network, which includes the inferior and superior parietal lobes, including the intraparietal sulci, inferior to superior frontal gyri, and also bilateral areas in the occipital lobe, and insular cortex.

Table 2.

Regions, peak coordinates, cluster sizes (k), and t values of the significantly activated clusters (P < 0.05, FWE corrected) for the main effect of strategy

	Peak coordinates
Cluster	x	y	z	k	t
Retrieval > procedural
Bil frontal pole (middle orbital/superior medial frontal G/ACC)	−6	50	−4	943	7.40
L middle/inferior middle temporal G	−52	−4	−32	894	6.41
L inferior parietal lobe (angular/supramarginal G)	−54	−58	36	104	5.86
R superior temporal G to inferior parietal lobe (angular G)	70	−48	8	76	6.33
R inferior parietal lobe (supramarginal G)	66	−44	42	37	5.06
Procedural > retrieval
Bil superior/medial frontal G	−12	16	50	2687	9.09
L superior to inferior parietal lobe (intraparietal sulcus)	−44	−46	52	2273	8.93
R superior to inferior parietal lobe (intraparietal sulcus)	32	−62	54	1917	8.60
L inferior frontal G (Broca's region)/precentral G	−50	6	38	1802	10.22
R occipital lobe (V1/occipital G)	24	−90	−6	1236	8.60
L occipital lobe (V1/occipital G)	−22	−96	4	1234	8.60
R inferior frontal G (Broca's region)	52	10	26	433	7.69
L insula	−34	20	4	294	7.24
R insula	36	20	8	161	6.34
R middle to superior frontal G	32	6	66	111	5.31
L inferior frontal G	−50	46	10	69	5.92

Only clusters of 20 voxels or more are reported.

Abbreviations: L = left hemisphere; R = right hemisphere; Bil = bilateral; G = gyrus; ACC = anterior cingulate cortex; V1 = primary visual cortex.

Figure 5.

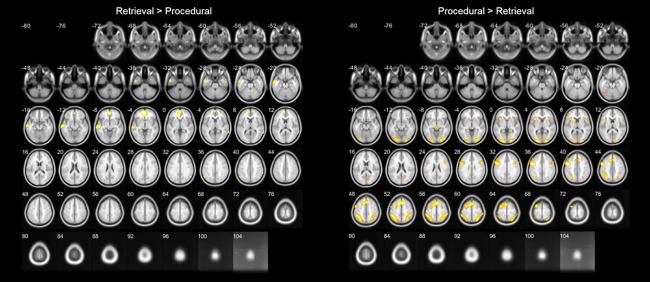
Transverse slices of differences in brain activation between self‐reported retrieval and procedural strategy use (P < 0.05, FWE corrected). [Color figure can be viewed at http://wileyonlinelibrary.com]

Turning to the main effect of operation (Table 3 and Fig. 6), we have only observed differences in the bilateral primary visual cortex, with higher activity during multiplication than for subtraction.

Table 3.

Regions, peak coordinates, cluster sizes (k), and t values of the significantly activated clusters (P < 0.05, FWE corrected) from the main effect of operation

	Peak coordinates
Cluster	x	y	z	k	t
Multiplication > subtraction
R occipital lobe (V1/inferior occipital G/calcarine G)	18	−96	4	243	5.80
L occipital lobe (V1/middle occipital G)	−22	−96	2	128	5.78
Subtraction > multiplication
/	/	/	/	/	/

Only clusters of 20 voxels or more are reported.

Abbreviations: L = left hemisphere; R = right hemisphere; G = gyrus; V1 = primary visual cortex.

Figure 6.

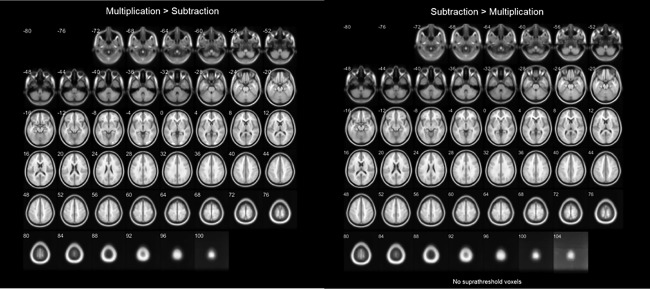
Transverse slices of differences in brain activation between multiplication and subtraction (P < 0.05, FWE corrected).

The strategy × operation interaction revealed no significantly activated clusters, indicating that the effect of strategy was not different for both operations.

Additional Control Analyses

To verify that the observed activation differences were not merely explained by task difficulty effects, we performed an additional control analysis (Table 4 and Fig. 7), in which we compared problems that had a similar level of difficulty, but varied in terms of their strategies. This was done by splitting the trials from both operations into easy and hard items, based on the size of both operands, and comparing the hard retrieval and easy decomposition items (i.e., items of comparable size and difficulty; e.g., hard retrieval: 3 × 8 vs. easy decomposition: 3 × 12). As these analyses were intended as control analyses, and as taking task difficulty into account led to less trials per contrast, and hence a decrease in statistical power, these analyses were performed without a correction for multiple comparisons (P < 0.001).

Table 4.

Regions, peak coordinates, cluster sizes (k), and t values of the significantly activated clusters (P < 0.001, uncorrected) from the control analysis comparing hard retrieval items to easy procedural items

	Peak coordinates
Cluster	x	y	z	k	t
Hard retrieval > easy procedural
R supramarginal G	64	−40	38	295	5.19
Bil ACC	−6	34	0	198	5.02
L middle temporal G	−56	−22	−8	161	4.94
L inferior temporal G	−48	−4	−30	36	4.33
Bil frontal pole (superior medial frontal G)	4	56	2	28	4.07
R inferior parietal lobe	54	−56	38	21	3.81
Easy procedural > hard retrieval
L superior frontal to medial frontal G	−20	4	60	1321	6.31
L precentral G	−48	4	34	1106	6.26
L superior to inferior parietal lobe (intraparietal sulcus)	−48	−40	50	1023	7.20
R superior to inferior parietal lobe (intraparietal sulcus)	28	−56	50	1010	6.03
R middle frontal G/precentral G	24	−4	48	127	4.52
L inferior frontal G	−52	46	12	103	5.33
L middle frontal G	−50	32	40	75	4.08
L insula	−34	18	4	74	4.47
R inferior frontal G	52	10	26	70	4.44
L occipital lobe (middle occipital G)	−28	−94	6	47	4.41
L occipital lobe (inferior occipital G/lingual G)	−22	−90	−12	37	4.22
R cuneus	20	−98	10	36	5.01
R inferior frontal G	58	30	30	30	4.36
R occipital lobe (lingual gyrus/V1)	22	−88	−6	29	4.23

Only clusters of 20 voxels or more are reported.

Abbreviations: L = left hemisphere; R = right hemisphere; G = gyrus; ACC = anterior cingulate cortex; V1 = primary visual cortex..

Figure 7.

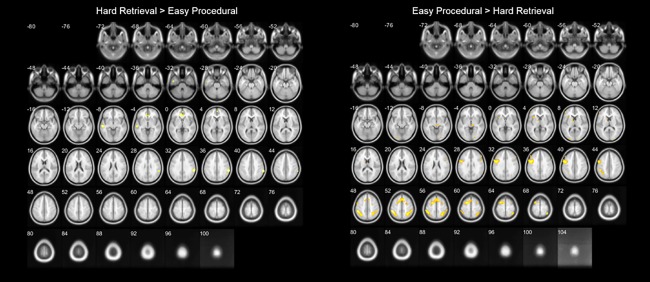
Transverse slices of differences in brain activation between hard retrieval and easy procedural items (P < 0.001, uncorrected). [Color figure can be viewed at http://wileyonlinelibrary.com]

First, for each subject, we compared the difference in accuracy and reaction time between retrieval and decomposition trials vs. the difference in accuracy and reaction time between hard retrieval and easy decomposition items. These differences were significantly smaller in the latter (accuracy: t(19) = 3.474, P = 0.003; reaction time: t(19) = −3.781, P = 0.001), suggesting that the effect of task difficulty is significantly smaller in the hard retrieval versus small decomposition contrast compared to the overall retrieval versus decomposition contrast. If the outcome of the retrieval versus decomposition contrast merely reflected an effect of task difficulty on brain activity, we expected that the contrast with a significantly reduced task difficulty effect (i.e., between hard retrieval vs. easy decomposition items) would show no differences or different activation clusters in comparison to the more general retrieval–decomposition contrasts. This is, however, not what we observed. The neural activation differences between hard retrieval and easy decomposition were very similar to those of the general retrieval–decomposition contrasts (Tables 2 and 4 and Figs. 5 and 7). More specifically, when contrasting the hard retrieval with the easy decomposition items, increased activation was found in the right supramarginal gyrus, left middle to inferior temporal gyrus, and the bilateral frontal pole. The easy decomposition versus hard retrieval contrast, on the other hand, revealed increased activation in a wide frontoparietal network, including the bilateral inferior to superior parietal lobes and inferior frontal gyri, and also bilateral occipital areas. The fact that these networks were very similar to those of the general retrieval–decomposition contrasts further supports the idea that the abovementioned effects of strategy are not merely due to task difficulty effects.

DISCUSSION

To date it is still unclear how children's arithmetic brain network is modulated by the strategies used to solve different problems, as earlier studies were only able to make implicit assumptions on strategy use, based on, for example, operation (De Smedt et al., 2011; Prado et al., 2014). This approach has been criticized for many years in developmental behavioral studies (e.g., Siegler, 1987, 1996), as not all problems of a particular operation are solved with the same strategy. This is especially problematic in the context of developmental research, as the strategies that children use to solve particular types of problems change over time (i.e., with education and practice). Trial‐by‐trial self‐reports offer a valid and reliable way of capturing these differences in (children's) strategy use (Siegler and Stern, 1998), and adult brain imaging studies have already successfully applied this approach to investigate brain activity during different solution strategies (Grabner et al., 2009; Tschentscher and Hauk, 2014). To the best of our knowledge, no such approach had been used in children. Against the background of the previously reported neural activation differences during arithmetic between adults and children, this study set out to investigate the neural differences in children's arithmetic strategy use.

This study was thus the first to explicitly investigate the neural activation underlying different arithmetic strategies during subtraction and multiplication in children of a narrow age range (i.e., 4^th grade). Our data show a clear effect of strategy on brain activity, which is similar in both subtraction and multiplication. These data suggest that previously found effects of operation (subtraction vs. multiplication) on brain activity reflect differences in strategy use, rather than differences in operations.

During retrieval use, we observed increased activation in the supramarginal and angular gyri, middle temporal gyri, and frontal pole. These results concur with previous adult studies that used a similar methodology (Grabner et al., 2009; Tschentscher and Hauk, 2014), as temporoparietal regions (more specifically the angular gyri) have been shown to be related to fact retrieval. Similar to the data of Tschentscher and Hauk (2014), we found bilateral activation in these areas, which is in contrast to earlier observations by Grabner et al. (2009), in which the activity in these areas was left‐lateralized.

The current results further extend previous fMRI studies in children, which could only make implicit assumptions on children's strategy use (Cho et al., 2011; De Smedt et al., 2011; Peters et al., 2016; Prado et al., 2014). For example, we have found stronger activation in the middle temporal gyrus during retrieval, which echoes earlier findings by Prado et al. (2014), who showed that activity in this area increases with age during multiplication, potentially due to increased use of retrieval strategies. This study goes beyond the findings of Prado et al. (2014), as we directly correlated brain activity with participant's strategy use and observed the same effect of strategy use for both multiplication and subtraction. The current data consequently confirm that the earlier reported operation differences reflect the increased use of fact retrieval strategies, and that this activity is independent of the operation that is being performed. Our results also coincide with an fMRI study in children by Peters et al. (2016), who manipulated the presentation format to study differences between retrieval and procedural strategies. Specifically, these authors investigated brain activation during a subtraction task in symbolic (i.e., Arabic digits or number words) and nonsymbolic (i.e., arrays of dots) formats. The symbolic formats, assumed to be solved by fact retrieval, showed increased activity in the bilateral angular and supramarginal gyri, as was also found in this study.

In contrast to our expectations and to previous developmental fMRI studies (i.e., De Smedt et al., 2011; Qin et al., 2014), our analyses did not reveal specific increases in the hippocampus during fact retrieval. However, when applying a less stringent correction for multiple comparisons (i.e., a false discovery rate (FDR) correction with a P < 0.05 threshold), we observed an activated cluster in the left hippocampus (x = −24, y = −16, z = −18, k = 208, t = 4.18), which is in line with the earlier developmental reports. This observation is also in line with a recent adult study on the interference effect in multiplication problems by De Visscher et al. (2015) that also found greater activation in the left hippocampus for fact retrieval, implying that the hippocampus might not only play a role in fact retrieval during the early stages of arithmetic development.

This study also tried to examine neural activation during procedural strategy use, but as the children in our sample almost exclusively implemented a decomposition of operands strategy for all procedural items, only claims can be made on this particular strategy. Furthermore, this decomposition of operands strategy cannot be seen as a procedural strategy in the same way as, for example, counting can, for it—to some extent—also involves fact retrieval. However, it is crucial to emphasize that this decomposition of operands, and consequently the small degree of fact retrieval involved, is not random, as is the case during mere fact retrieval. The decomposition strategy follows a fixed sequence (i.e., in subtraction it starts with subtracting to tens, and in multiplication it includes a multiplication by ten), and, to find the correct solution, both solutions to the newly formed items still need to be subtracted from or added to one another, thus clearly making it a multistep procedural strategy. For the decomposition of operands strategy, we observed increased activation in a frontoparietal network, which includes the bilateral inferior to superior parietal lobes (including the intraparietal sulci), and the inferior to superior frontal gyri, and also bilateral areas in the occipital lobe, and insular cortex. These results converge with previous studies in adults (Grabner et al., 2009; Tschentscher and Hauk, 2014), although the adult data were more left‐lateralized, in contrast to the bilateral network we have found.

These results on the decomposition strategy concur with studies in children who manipulated operation (De Smedt et al., 2011; Prado et al., 2014) or presentation format (Peters et al., 2016) to investigate strategy use. The effect of decomposition on brain activity was also the same across both operations, again indicating that it is the strategy and not the operation that elicits changes in brain activity. The observed increases in frontoparietal activation for the decomposition strategy might point to an increasing demand on working memory and attentional resources, as reflected by increases in frontal activation, especially in the insula and inferior to middle frontal gyrus (Duncan and Owen, 2000; Menon, 2015), and a larger involvement of quantity‐based processes, reflected by the increased parietal activation, specifically in the intraparietal sulci (De Smedt et al., 2011). This study, however, cannot disentangle these different processes; future studies should, therefore, adopt a carefully selected localizer approach to test this.

Besides the decomposition of operands strategy, other types of procedural strategies exist, including repeated addition or counting. The choice of the used (procedural) strategy, however, is highly dependent of the math curriculum under study. The participants in this study all came from schools with a high emphasis on fact retrieval for single‐digit problems and on the use of the decomposition of operands strategy for larger problems (coupled with a limited attention or even prohibition of counting), as is in accordance with the mandatory guidelines of the Flemish education system. Consequently, and as expected, strategies other than the decomposition of one of the operands (e.g., counting or repeated addition) were hardly used. It is noteworthy that different types of procedural strategies (e.g., counting vs. decomposition) might elicit alternate neural activation patters, but unfortunately this could not be tested in the current sample as children were very homogenous in their choice of procedural strategies (i.e., decomposition). In all, it is important to acknowledge potential educational differences between countries. A fact that is often overlooked in educational neuroscience studies that deal with culturally transmitted skills is that the way these skills are taught in school will affect children's performance on an educationally relevant task and will consequently affect brain activity (De Smedt and Grabner, 2015, for a discussion). Future brain imaging studies should therefore take this educational context into account and might consider investigating cross‐curricular differences.

Next, we should also consider to what extent the current differences are driven by task difficulty effects. To investigate this possibility, we ran a control analysis in which we compared problems with a similar level of difficulty, but for which different strategies were needed. Consequently, we split all items into easy and hard items, based on the size of both operands and contrasted the hard retrieval and easy decomposition items, which showed a significantly reduced task difficulty effect (for both accuracy and reaction time) in comparison to the general retrieval‐decomposition contrasts. The results of this control analysis showed similar neural activation networks between the hard retrieval versus easy decomposition contrasts and the general retrieval versus decomposition contrasts. For the hard retrieval versus easy decomposition contrast, we observed increased activation in the right supramarginal gyrus, left middle to inferior temporal gyrus, and the bilateral frontal pole, which is very similar to the retrieval versus procedural contrast. The easy decomposition versus hard retrieval contrast, on the other hand, displayed increased activation in a frontoparietal network, similar to the procedural versus retrieval contrast. The similarities between these findings suggest that the differences between retrieval and decomposition trials are unlikely to be merely driven by task difficulty effects.

Furthermore, it needs to be noted that the stronger activation found for the retrieval condition reflected less deactivation and not increased activation in comparison to baseline (see also, De Smedt et al., 2011; Peters et al., 2016). The regions showing this deactivation are to some extent part of the default mode network (Raichle et al., 2001; Supekar et al., 2010), which decreases in activation as the cognitive demand of a task increases and vice versa. However, the less deactivated regions that were found for the retrieval condition do not fully coincide with the areas active in this resting brain state, as, for example, no activation in the retrosplenial cortex was found (Vann et al., 2009). The regions found to be activated more strongly for the decomposition condition, on the other hand, seem to coincide with those of the so‐called multiple‐demand network (Fedorenko et al., 2013), which, in adults, shows increases of activation for any kind of cognitive demand, independent of the content of the task. These differences between fact retrieval and decomposition and differences in regions that seem to be part of the default mode and multiple‐demand network, respectively, might be explained by the inevitable association between strategy use and the task load of the items at hand. As evidenced by research of Siegler (Siegler, 1996; Siegler and Shrager, 1984; Siegler and Stern, 1998) fact retrieval is an easy, accurate and fast strategy for solving arithmetic problems, which has a smaller cognitive demand than decomposition strategy use. This was also apparent in our data, as the retrieved items were solved more quickly and more accurately, while the decomposition items showed the opposite pattern.

Concurring with the adult data of Tschentscher and Hauk (2014), we did not find any differences in activation between operations. Although such operation differences have been previously observed in children (e.g., De Smedt et al., 2011; Prado et al., 2014), those studies did not directly assess strategy use. The current data show for the first time that such operation differences in children, just as in adults, are explained by the strategy that is used. In other words, it is the strategy and not the operation itself that determines brain activity. One small main effect of operation was observed, however, but only for regions in the primary visual cortex, that were increasingly activated for multiplication in comparison to subtraction. This is due to the inevitable, yet subtle, differences in visual presentation between the subtraction and multiplication items. The response alternatives for multiplication were unavoidably larger in subtraction items; hence, more visual information was displayed during multiplication.

In contrast to the approach of this study, which is based on the distinction between retrieval and procedural strategies, recent studies have suggested that, instead of retrieval, children may use automatized procedural strategies, which over time contrasts the dominant view of an evolution from counting to retrieval strategies, but implies a shift from slow to quick counting procedures (Thevenot et al., 2016). Although this notion cannot strictly be excluded, the current data still point to alternate neural activation between both strategy conditions, and more importantly, provide evidence against the idea that the arithmetic brain network is modulated by the operation of items (Tschentscher and Hauk, 2014). Furthermore, the effects found by Thevenot et al. were only described in small addition problems, and not in subtraction or multiplication. As these small addition problems are consistently solved faster than, for example, subtraction problems, it is uncertain if these automatized counting procedures would also occur in subtraction, let alone in multiplication.

Future developmental imaging studies on mathematical cognition should thus avoid thinking in terms of operations, but instead take strategy use into account. Our results, coupled with those of Tschentscher and Hauk (2014) clearly indicate that arithmetic strategy rather than operation modulates brain activity. Furthermore, behavioral research has implicated large developmental aspects in strategy use, especially in the frequency and efficiency of those strategies (Imbo and Vandierendonck, 2008; Siegler, 1996; Siegler et al., 1996; Vanbinst et al., 2015). Consequently, future brain imaging studies should longitudinally study how the neural networks found in our group of 4^th graders for both retrieval and procedural strategies develop, from an early‐arithmetic stage (e.g., 1^st or 2^nd graders) to a more advanced arithmetic stage. Moreover, as difficulties in arithmetic strategy use are considered the hallmark of children with dyscalculia, who experience persistent deficits in acquiring basic mathematical competencies (American Psychiatric Association, 2013), and as fact‐retrieval deficits have also been observed in children with dyslexia (Evans et al., 2015), future brain imaging studies on strategy use in these atypical populations are also needed.

One limitation of this study lies in the differences in format of the arithmetic task during strategy assessment outside the scanner and during MRI acquisition in the scanner (i.e., a production task with auditory input and verbal output in the strategy assessment session, and a delayed verification task with visual input and manual output during MRI acquisition). This was done to find a balance between ecologically valid strategy assessment (allowing for precise measurement of strategies) and the practical limitations of the scanning environment for the scanning task. In view of the high consistency in the implementation of strategies during the behavioral task, coupled with the use of delayed verification, which limits the possibility of parity checking, five‐checking and other estimation strategies, we contend that children employed the same strategy in the scanner as in the behavioral session. The validity of this verbal protocol is also supported further by the fact that we found a significant main effect for both accuracy and reaction time for the in‐scanner task, pointing to more accurate and faster responses during the retrieval condition, which concurs with previous behavioral findings (e.g., Siegler, 1984). It is also supported by the fact that significantly larger hard‐easy performance differences were found for the decomposition strategy in comparison to fact retrieval, for both accuracy and reaction time (accuracy: t(19) = 2.598, P = 0.018; reaction time: t(19) = −3.748, P = 0.001).

We would like to highlight again that the acquisition and use of arithmetic strategies does not occur in isolation, but depends on the extent to which math curricula emphasize the importance of fact retrieval and automatization, and on the particular strategies these curricula focus on; behavioral studies have clearly shown cross‐cultural differences in retrieval use in adults depending on the emphasis of the math curriculum on fact retrieval and automatization (e.g., Campbell and Xue, 2001). The children of this study came from Flemish elementary schools with a curriculum that puts a high emphasis on automatization processes and fact retrieval on one hand, and on the decomposition of operands as an effective procedural strategy on the other hand, leading to a limited generalization of the current findings to other cultures. Future studies might therefore explore how, for example, differences in the emphasis on fact retrieval or certain procedural strategies in math curricula correlate with strategy‐related brain activity. Such studies have the potential to provide a fruitful contribution to the emerging field of educational neuroscience.

Finally, this study focused on fourth graders, which were capable of both retrieving the answers to multiplication items and solving more difficult items procedurally. As mentioned, we have chosen to focus on a narrow age range, as merging data across wide age ranges, even though statistically controlled for, might lead to misleading conclusions. Accordingly, we would like to emphasize the need for similar studies in children of different ages (e.g., sixth graders or children in secondary school), and for studies with a longitudinal follow‐up throughout development, as such studies are destined to provide meaningful insights in the development of these strategies.