Abstract
During the last 20 years, predictive modeling in epilepsy research has largely been concerned with the prediction of seizure events, whereas the inference of effective brain targets for resective surgery has received surprisingly little attention. In this exploratory pilot study, we describe a distributional clustering framework for the modeling of multivariate time series and use it to predict the effects of brain surgery in epilepsy patients. By analyzing the intracranial EEG, we demonstrate how patients who became seizure free after surgery are clearly distinguished from those who did not. More specifically, for 5 out of 7 patients who obtained seizure freedom (= Engel class I) our method predicts the specific collection of brain areas that got actually resected during surgery to yield a markedly lower posterior probability for the seizure related clusters, when compared to the resection of random or empty collections. Conversely, for 4 out of 5 Engel class III/IV patients who still suffer from postsurgical seizures, performance of the actually resected collection is not significantly better than performances displayed by random or empty collections. As the number of possible collections ranges into billions and more, this is a substantial contribution to a problem that today is still solved by visual EEG inspection. Apart from epilepsy research, our clustering methodology is also of general interest for the analysis of multivariate time series and as a generative model for temporally evolving functional networks in the neurosciences and beyond. Hum Brain Mapp 38:2509–2531, 2017. © 2017 Wiley Periodicals, Inc.
Keywords: epilepsy, quantitative EEG, resective surgery, predictive modeling, Bayesian inference, graphical models, Chow‐Liu tree, Hidden Markov Model, rate distortion theory, distributional clustering
INTRODUCTION
The main goal of epilepsy treatment is the achievement of persistent freedom from seizures. Notwithstanding the wide range of therapies, which in most cases are primarily based on medication, seizure freedom is still not achieved in around 20–30% of all patients [Cascino, 2008]. When a patient is revealed to suffer from a drug‐resistant epilepsy [Kwan et al., 2010] surgical treatment options should be considered. To this end, the “epileptogenic zone” has to be determined, which has been defined as the minimal amount of brain tissue that results in seizure freedom if resected [Lüders, 2006; Rosenow and Lüders, 2001]. However, there is currently no method that is able to directly and unequivocally identify the epileptogenic zone [Höller et al., 2015; Rosenow and Lüders, 2001] and in practice the seizure onset zone (SOZ) is often used as a substitute. Reliable SOZ markers are electrode channels displaying high frequency oscillations (HFO), both ictally and interictally [Malinowska et al., 2015; Modur et al., 2011]. However, even HFOs are neither sufficient for an unambiguous characterization of the SOZ nor is removal of their generating brain areas guaranteed to stop seizures from occurring [Höller et al., 2015]. Hence, there is growing interest in the computational analysis of intracranially recorded EEG (iEEG) time series, in an attempt to find abstract, mathematical quantities as “markers” of ictogenicity. In this study however we follow an alternative machine learning approach, which heads directly for a probabilistic model of iEEG time series and is used to predict the effects of resective surgery. Thus, we attempt to leave the purely descriptive level that is implied by previous “marker‐based” approaches.
In recent years, functional brain networks [Bullmore and Sporns, 2009; Rubinov and Sporns, 2010] have become a standard tool for analyzing epileptiform EEG time series [Bialonski and Lehnertz, 2013; Engel et al., 2013; Kramer et al., 2008, 2010; Ponten et al., 2007; Richardson, 2012; Rummel et al., 2015; Schindler et al., 2008; van Diessen et al., 2013; Wilke et al., 2011; Zubler et al., 2015] (see also [Steimer et al., 2015] for a more detailed review of the related literature). Based on pairwise dependency measures, networks are constructed by establishing (weighted) edges between pairs of signals, which are represented by the nodes of a network. Strength of the edges is either directly derived from the dependency measure or, as an alternative, the measure is thresholded to yield binary values {0, 1}, indicating the absence/presence of an edge. The thus constructed networks may then be analyzed by a variety of graph measures, which either characterize individual nodes (signals) or the network structure as a whole. Functional brain networks have been used extensively to characterize network structures during seizures (see, e.g., [Kramer et al., 2008, 2010; Schindler et al., 2008]), as well as to identify critical nodes as potential targets for surgical interventions [Rummel et al., 2015; Wilke et al., 2011; Zubler et al., 2015]. In [Kramer et al., 2010] for example it was shown that brain networks become more fragmented at seizure onset, such that the network topology decays into a large ensemble of sparsely inter‐ but densely intraconnected subnetworks (modules), which is then followed by only a small number of modules toward seizure end. These findings are also consistent with the U‐profile of global synchronizability during seizure evolution [Schindler et al., 2007, 2008]. On the other hand, Zubler et al. [2015] have shown ictogenic nodes to be more likely to become “hubs” of the network, that is, central nodes that mediate a large number of connection paths between node pairs. A suitable measure of “hubness” may thus highlight the ictogenicity of a given node. Along similar lines Rummel et al. [Rummel et al., 2015] have found nodes of salient strength (i.e., summed edge weights) to be more strongly associated with the set of nodes that got actually surgically removed in patients with favorable postsurgical outcome, when compared to patients with no worthwhile improvement after surgery.
Despite these achievements, a fundamental limitation of the functional networks approach is its inherently descriptive nature; properties of a given time series may be described, but the approach does not allow for predictions if the time series is modified in distinct ways. For example, if some subset of the series are clamped to constant values—or modulated in any other predefined way—it is meaningless to apply node measures to the modulated nodes, as these nodes, due to their constancy, become essentially isolated from the rest of the network. Measures of network structure could be an alternative in this case [Fornito et al., 2015], but we still do not have measures that unambiguously and reliably characterize epileptic brains. Furthermore, even if we were provided by such measures, the lack of modeling temporal dynamics in the standard functional networks approach does not permit predictions for future time points, where no information about the time series is available. Finally, the vast majority of dependency measures that are used to construct networks are based on pairwise dependencies and thus do not capture statistical dependencies of higher order.
In this article, we pursue a radically different approach, the foundations of which have been laid by our previous study [Steimer et al., 2015]. The idea is to derive probabilistic clustering models for multivariate, peri‐ictal iEEG time series, which—after some learning procedure—permit predictions about the ictal (seizure) state under controlled modulation. More concretely, we show how the simulated resection of those brain areas that got actually resected during brain surgery and have thus rendered the patient seizure free (= class I in the Engel classification scheme [Engel et al., 1993]), is predicted to indeed stabilize the preictal and prevent the ictal state. In other words, the ictal state is predicted to become less likely by simulating the resection of the actually resected channels. Likewise, for class III/IV patients who continue to have seizures after surgery our model confirmed the inefficiency of the actually resected channels to stop a developing seizure. While in the literature there have been a few computational studies dealing with the estimation of suitable targets for resective surgery or other seizure abatement strategies [Hutchings et al., 2015; Sinha et al., 2014; Taylor et al., 2015], the present study is the first to our knowledge that uses predictive modeling for that purpose, which provides the possibility to judge a set of virtually resected channels collectively (with respect to the sets potential to stop seizures from occurring), rather than each of the channels separately.
RESULTS
Evaluating the Sets of Truly Resected Electrode Channels by a Distributional Clustering Solution
In this section, we present our main finding, that is, the dynamical behavior of the posterior membership probabilities, when computed under various different resection protocols. We first consider a class I patient according to the Engel classification, that is, a patient who became seizure free after resective surgery. The same analyses are then repeated for a class III/IV patient, who still suffers from postsurgical seizures. The section ends with a population summary across the whole patient database of Table 3.
Table 3.
Information about the 12 patients included in our study
| Patient No. | Engel class | # of electrode channels | # of resected electrode channels | Fraction of resected electrode channels |
|---|---|---|---|---|
| 1 | I | 98 | 11 | 0.10 |
| 2 | I | 42 | 11 | 0.26 |
| 4 | I | 74 | 13 | 0.23 |
| 6 | I | 64 | 13 | 0.20 |
| 7 | I | 60 | 11 | 0.18 |
| 9 | I | 64 | 20 | 0.36 |
| 10 | I | 68 | 13 | 0.19 |
| 5 | III/IV | 59 | 2 | 0.03 |
| 8 | III/IV | 61 | 10 | 0.16 |
| 18 | III/IV | 49 | 8 | 0.16 |
| 21 | III/IV | 62 | 4 | 0.06 |
| NP | III/IV | 36 | 3 | 0.08 |
“Patient No.” refers to the patient number given in table 1 of our previous study [Steimer et al., 2015]. “NP” refers to a new patient that was not included that study. Number of resected electrode channels between Engel class I and III/IV patients was significantly different at the 5% level, whereas number of electrode channels was not (P = 0.001 and P = 0.059 resp., permutation test [Permutation Tests for the Patient Data of Table 3 section]). Fraction of resected electrode channels was significantly different at the 5% level (P = 0.010, two‐sample Kolmogorov‐Smirnov test; P = 0.009, permutation test).
Figure 1 (top panel) shows an iEEG time series of class I Patient 2. The large amplitude part of the beginning seizure starts around 223 s into the seizure and corresponds to the CTSO. This can be seen in the second panel by the corresponding abrupt change in cluster memberships, that is, the abrupt redistribution of posterior probability mass toward the ictal centroids at 223 s. Note that none of the channels has been resected in this case and that the whole seizure data was used as observational input into the Markov chain. Hence, such a redistribution of probability mass toward ictal centroids is to be expected, as we just witness the default development of the seizure. Note also that the model is able to detect the small burst of epileptiform activity in the top panel shortly after n ict—the clinically determined seizure onset (Materials and Methods, Dichotomization of the Centroid Distributions into Preictal and Ictal Subsets section)—as expressed by a corresponding brief “burst” of posterior mass . However, since the preictal centroid indices are reactivated thereafter over fairly long periods, the burst does not signify the CTSO, which thus occurs around 40 s later (see Predictive Modeling Based on a Distributional Clustering Solution section). In a second simulation run, we stopped feeding input into the model after the CTSO and computed the resulting posterior memberships (third panel). Again, an abrupt increase in the membership probability could be observed for future time points , which—contrary to the case of full observation—then declined slowly toward the end of the simulation.
Figure 1.
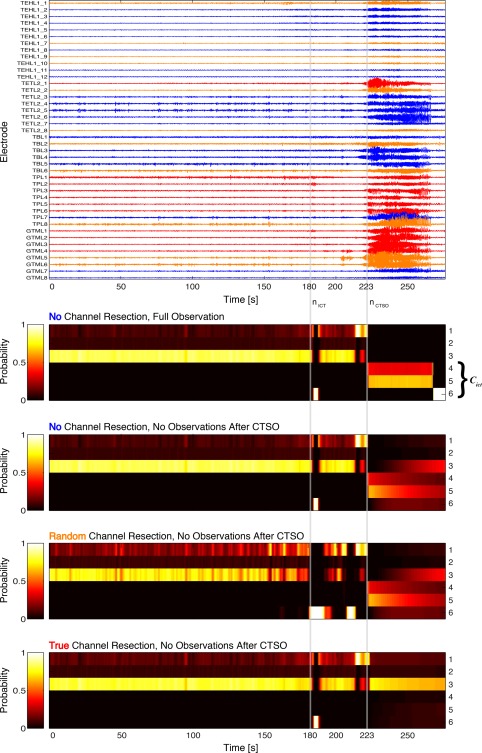
Posterior membership probabilities induced by the empty, a random and the true set of resected channels for a class I patient. Shown are the (color coded) periictal dynamics of the posterior for Patient 2. In case of proper functioning of the model, a distinct redistribution pattern of probability mass is expected after the computational time of seizure onset (CTSO), for each of the considered resection paradigms (empty, random and true). Top panel: Peri‐ictal iEEG time series of patient no. 2. CTSO corresponds to 223 s, seizure end is at 276 s. Truly resected channels are depicted in red, channels belonging to a random set of resected channels are depicted in orange, the remaining channels in blue. Both channel sets are of size 11 and their resection was simulated in separate runs. Second panel: Time course of the posterior membership probabilities after learning of the K = 6 cluster centroids indexed along the y‐axis on the right. The set of ictal centroid vectors is given by . Membership probabilities are displayed for each time window, for which the x‐axis gives the ending time in seconds. Note the redistribution of probability mass toward C ict after n ctso. Third panel: Time course of the membership probabilities . In contrast to the second panel, a discretized version of the data in the top panel was applied only up and until , later time points were computed exclusively from the Markovian dynamics of zn. Note the redistribution of probability mass toward C ict after n ctso. Fourth panel: Time course of the membership probabilities , for a random selection of resected channels. Again, probability mass is redistributed toward C ict after n ctso. Fifth panel: Time course of the membership probabilities , for the set of truly resected channels. This time no redistribution toward C ict takes place. [Color figure can be viewed at http://wileyonlinelibrary.com]
The question is now, what the models predictions are for some random and the true resection protocol. If the model indeed captures some key features of the iEEG time series and as Patient 2 became seizure free after surgery, we expect a decrease in probability mass of the ictal centroids after n ctso in comparison to the no resection protocol. On the other hand, some random resection is not expected to improve much on the situation in this case. Indeed, as panel four shows, the given random resection did not change the picture provided by the no resection protocol, although a more dynamical trading of probability mass within the set of preictal, centroid indices {1, 2, 3} occurred during the preictal period. Also, the burst in was slightly prolonged and an additional such burst could be observed around 210 s. In contrast, when the set of truly resected channels had been chosen (fifth panel), was substantially decreased for and the preictal states C pre were thus stabilized. This latter aspect is appreciated best when concentrating on the posterior mass for centroid 3.
All in all Figure 1 suggests that the distributional clustering model is capable of extracting key features behind epileptic iEEG time series and hence predicts substantially different outcomes for the different resection protocols; on the one hand, the no and random resection protocols are unable to stop the developing seizure, as witnessed by the abruptly increasing probability mass for the ictal centroids after n ctso. The true resection protocol in contrast greatly diminishes this mass and thus stabilizes the preictal state.
To see whether this marked performance discrepancy between a random and the true set of resected channels is a general result, we performed a Monte‐Carlo analysis consisting of 300 trials, where during each such trial a new random set of resected channels was chosen and evaluated in performance (for visual clarity only 300 from 3,000 total trials are illustrated in the following, cf., Materials and Methods, Predictive Modeling Based on a Distributional Clustering Solution section). Figure 2a,b shows the result; for small delays, that is, small intervals between the CTSO and the time when the posterior is evaluated, there is a huge gap in performance between typical random resections and the true resection. For very large delays, this gap is expected to converge to zero, as after the CTSO no observational input is applied to the Markov chain, which thus in the long run becomes stationary and independent of inputs from the distant past. Note also the highly multimodal nature of the data, which can been appreciated by the almost conflated 25% and 75% percentiles, together with the large number of outliers ( ). Importantly however, in none of the random trials the posterior performance was any better than that of the truly resected channels. This result is stable, that is, irrespective of delay.
Figure 2.
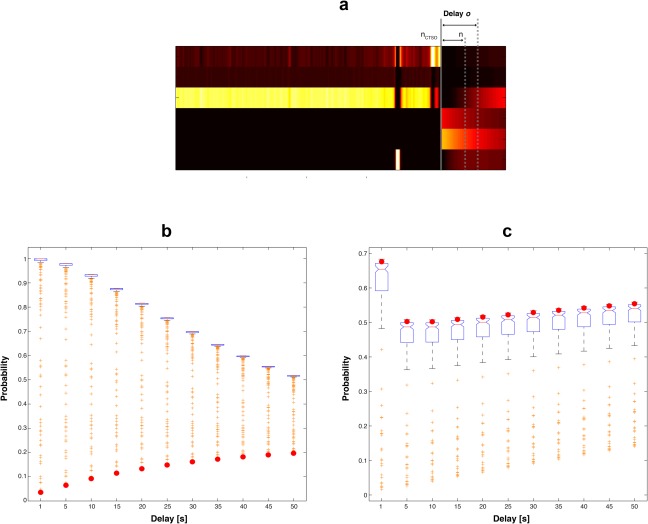
Monte‐Carlo analysis of ictal membership probabilities under repeated random resection for Patients 2 and 5. Shown is, for 300 simulated, random resections, the posterior evaluated at distinct time points (delays) after the CTSO. The single random resection results of Figures 1 and 3 are thus expected to generalize. (a) Definition of delay as the interval between the CTSO and some later time point n, when the posterior ictal membership probability is evaluated (arbitrary illustration example). (b) Boxplots of the posterior ictal membership probabilities obtained from the 300 trials in Patient 2 (class I). x‐axis gives the delay o in seconds and y‐axis the corresponding as boxplots. Orange crosses denote outliers, defined as values larger than , where are the 25% and 75% percentiles. Performances of the truly resected channels are depicted as red dots. For each resection the optimal value for n max was chosen, that is, the n max yielding the smallest posterior ) across the set . Note the superior performance induced by the true resection protocol when compared to random resections. (c) The same as (b) but for class III/IV Patient 5. Note the inferior performance of the true resection protocol. [Color figure can be viewed at http://wileyonlinelibrary.com]
We conclude that, among 300 random resections, the distributional clustering model is indeed capable of singling out the true resection protocol as particularly effective for preventing a developing seizure. Given the vast number of possibilities for randomly selecting 11 out of 42 channels ( ) and the fact that Patient 2 is of class I, this is a remarkable result that shows twofold—the extended experience of the attending epileptologist and the models predictive accuracy.
The exact same procedures underlying Figures 1 and 2b have been repeated for class III/IV Patient 5, the results of which are shown in Figures 2c and 3 respectively. Unlike Patient 2 we here do not expect the true resection protocol to be particularly effective for preventing the seizure, and indeed, our simulations display no signs of improvement for it in comparison to random resections. On the contrary, performance of the truly resected channels resides on the brink of the upper quartile and is thus worse compared to typical random resection performances. These results are in line with the patients self‐report to still suffer from seizures, even after resective surgery had been conducted. Therefore, our expectations for class III/IV are confirmed for Patient 5.
Figure 3.
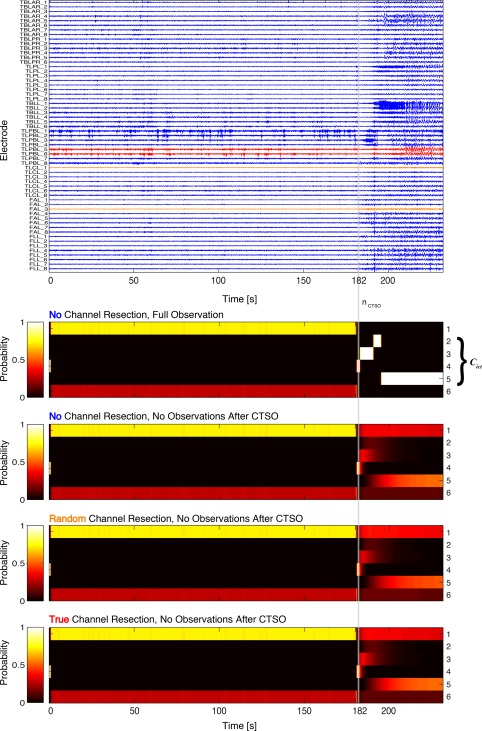
Posterior membership probabilities induced by the empty, a random, and the true set of resected channels for a class III/IV patient. Analogous figure to Figure 1 for Patient 5. See caption of Figure 1 for details. [Color figure can be viewed at http://wileyonlinelibrary.com]
To see if the suggested pattern constitutes indeed a general result, we applied Monte‐Carlo analysis to all of our patients. Figure 4 gives a summary of results for class I based on the full set of random resection trials (Materials and Methods, Predictive Modeling Based on a Distributional Clustering Solution section). However, in contrast to Figure 2 we now evaluate more robust measures for each resection protocol, by reporting its dynamical outcome defined as the averaged, future membership probability
| (2.1) |
which was obtained in two ways, that is, from the best performing and , respectively (see Materials and Methods Predictive Modeling Based on a Distributional Clustering Solution and Assessing Ictal State Transitions from a Distributional Clustering Solution for Defining Latest Observed Time Points sections).
Figure 4.
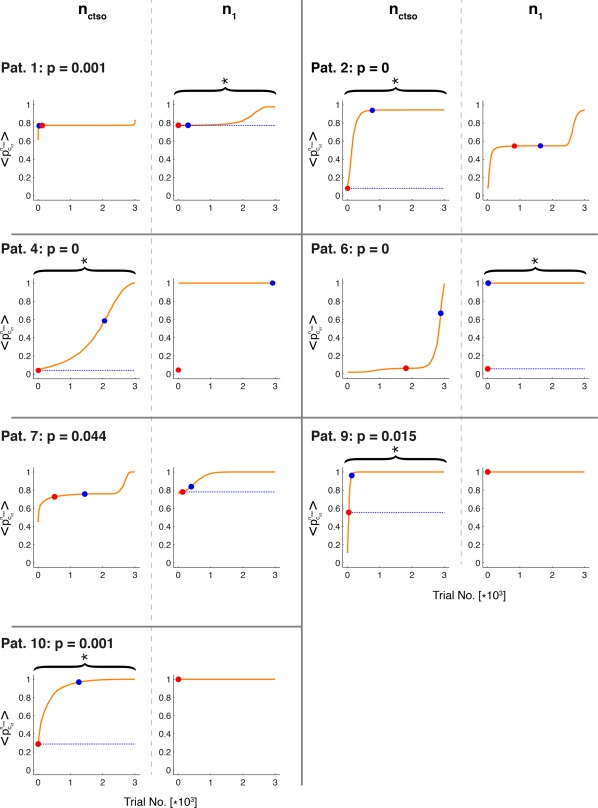
Monte‐Carlo analysis of dynamical outcome under repeated random resections for all class I patients. Shown are the index of the random resection trials (x‐axis) versus the sorted dynamical outcome values (y‐axis) for each class I patient. Sorting is in ascending order. For each resection, the two instantiations were tested (columns separated by gray, dashed lines). Red dots give outcome of the truly resected channels, blue dots outcome in the absence of any resections. Braces and asterisks denote cases, where performance of the truly resected channels is significantly different from performance under random resections (at the 2.5% level, with the indicated p‐value denoting the smaller of the two p‐values at n ctso and n 1, see Statistical Hypothesis Test for Assessing the Chance Level of Actual Resection Protocols section. The degenerated cases of n 1 for Patients 4, 9, and 10 were labeled as insignificant). Horizontal, dashed red/blue lines graphically illustrate these p‐values as the length fraction of red ink versus total length of the line (red sublines are hardly visible in many cases). The red/blue lines were placed in the plots corresponding to the indicated p‐values. [Color figure can be viewed at http://wileyonlinelibrary.com]
If, for each , performance is measured by the largest difference between the dynamical outcome induced by no resection (denoted by ) and the truly resected channels ( ), only Patients 1 and 7 may be deemed misclassified cases, as despite being class I the truly resected channels improve their dynamical outcome only by irrelevant amounts ( and 0.059, respectively, which corresponds to the difference in height between the blue and the red dots). In the remaining five patient cases however these differences range between 0.41 (pat. 9) and 0.95 (pat. 4). If performance is measured in relative terms, that is, with respect to random resections, only Patient 7 is misclassified, by having a dynamical outcome that is smaller than only an insignificant fraction of random resection trials (at the Bonferroni corrected 2.5% significance level, see Materials and Methods Statistical Hypothesis Test for Assessing the Chance Level of Actual Resection Protocols section). In the remaining six cases, dynamical outcomes fell below that level. However, even for Patient 7 the truly resected channels perform better than of the random resection trials.
This stands in marked contrast to the performances displayed by class III/IV patients, as can be appreciated from Figure 5. In this case, the largest differences in dynamical outcome are for patients respectively. Hence, only Patient 8 must be deemed a misclassification, since—as a class III/IV patient‐ his performance lies close to the lower brink of the class I performances and he must thus be placed in the “success” category represented by the class I patients. Measuring performance in relative terms does not change the picture, as Patient 8 has a p‐value of zero and all other class III/IV patients yield highly insignificant performance values.
Figure 5.
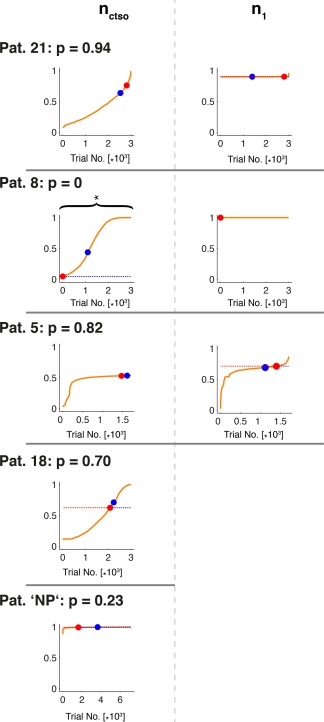
Monte‐Carlo analysis of dynamical outcome under repeated random resections for all class III/IV patients analogous figure to Figure 4 for class III/IV patients. As Patients 18 and NP displayed a single ictal state only, its p‐value was computed only from n ctso. The degenerated case of n 1 for Patient 8 was treated as insignificant. [Color figure can be viewed at http://wileyonlinelibrary.com]
To get an unified picture of the differences between class I and III/IV patients, we pooled the performances of all random resection protocols from all patients of the same class and compared them to the performances of the patients true resection protocols. In total, this amounts to 18,000 and 17,851 random resection trials for class I and III/IV, respectively (see Predictive Modeling Based on a Distributional Clustering Solution section). This way the utility of our distributional clustering method may be judged on a more patient independent population level.
Figure 6 shows a histogram of these data when dynamical outcome performance is normalized to become
| (2.2) |
which quantifies the relative degree of improvement caused by some random ( ) versus the no resection protocol ( ). Unlike our previous figures where the results for n ctso and n 1 were kept separated, we here gave each protocol its best chance to “prove itself” by pooling only the protocols best performance amongst all . It is apparent from the figure that for class I patients the normalized, true resection performances (red dots) are much higher than typical values of either the class I (green histogram) or III/IV (blue histogram) random resection distributions, which both possess a dominant peak at performance values close to zero. Indeed, the true resection performances for class I are highly unlikely to follow any of these distributions ( and P = 0.0015, respectively, for class I and III/IV random resection distributions, 2‐sample Kolmogorov‐Smirnov test). Moreover, as Patient 6 is the only class I example whose performance improves across a wide range of random resections (cf., Fig. 4), he is solely responsible for the slightly increased frequencies at high performance values of the pooled class I resections and may thus bias our population assessment. Hence, we have also pooled the class I resections by leaving out Patient 6 (red histogram), which further decreases the p‐value ( ).
Figure 6.
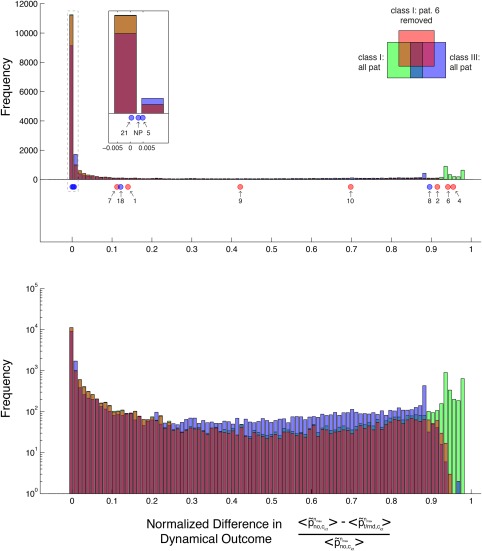
Distribution of normalized dynamical outcome performances for each patient and resection protocol. Top panel: transparent histograms give the number of random resection protocols whose normalized performance falls into the specified bins, when all random trials of all class I patients (green bars), of all class I patients besides no. 6 (red bars) and of all class III/IV patients (blue bars) are pooled. Inset shows a zoom plot of the area framed by the gray, dashed box. Red/blue dots give the normalized performance measure for the truly resected channels of class I and III/IV patients respectively (patient no. as indicated by arrows). Note the marked difference between the distributions induced by random versus true resections. Bottom panel: Same histograms as in top panel but in logarithmic representation. [Color figure can be viewed at http://wileyonlinelibrary.com]
In contrast, true resection performances of the class III/IV patients (blue dots) cluster around the peak at small values of the random resection histogram, with the sole exception of Patient 8 as expected (cf., Fig. 5). Therefore, the null hypothesis of the class III/IV true resection performances to follow any of the two (all patient) random resection distributions is not rejected at the 5% significance level (P = 0.13 and P = 0.41 for the green and blue histogram respectively). These results hold true notwithstanding outlier Patient 8, who displays a remarkably high performance comparable to a class I member. Leaving out the random resections of Patient 6, however, renders the null hypothesis rejected at the 5% level (P = 0.048), but only before Bonferroni correction by a factor of 3 or 6 is applied (note that due to their small p‐values the class I performances remain significant after such correction). All in all, for class I patients the null hypothesis is rejected for all three random resection distributions, neither of which however is rejected for class III/IV patients, when Bonferroni correction is assumed.
To summarize this section, we have shown that our dynamic clustering model is capable of qualitatively reproducing the outcome after true channel resection in 5 or 6 of 7 class I patients. Outcome performance was determined based on the posterior membership probability of the set of ictal centroids, which—for class I patients—should become low in case of true channel resection, when compared to random or no resection at all. Depending on whether performance was measured in absolute or relative terms, a different subset of the class I patients had to be considered as misclassified (either {1, 7} or {7}). That is, our model was unable in these cases to single out the set of truly resected channels as particularly effective for stopping the developing seizure. Conversely, for class III/IV patients the model confirmed in four of five cases (except Patient 8) the insufficiency of the truly resected channels to stop the seizure—both in absolute and relative terms. This picture of separated outcome performances for class I and III/IV patients persisted when the clustering results were considered from a more holistic perspective, that is, after pooling the true and random resection performances across all patients. Note that the inferior performances displayed by the class III/IV patients—both in reality and the model—might in part be explained by systematic differences in electrode setup, as for class III/IV we have found significantly lower values for the fraction of resected channels (see Table 3). Note also that, for the following reason, our findings for class I patients can hardly be explained by chance or overfitting: Imagine a predictive model with random parameterization (i.e., a Markov chain with random transition probabilities together with random distributional centroids) that does not capture any structural information behind a given time series. Given the vast number of possible channel resection protocols, the chances of hitting a model, that still singles out the true resection protocol as particularly effective for suppressing a developing seizure, are extremely low. Therefore, a model which predicts just that is very unlikely to not grasp structural information behind the time series. For class III/IV patients in contrast, interpretation of results is not as conclusive; a failure to single out the true resection protocol could either be a reflection of reality, that is, the inability of the true protocol to stop the seizure, or be due to the models insufficiency to grasp crucial features of the time series.
Improving the Dynamical Outcome of a Class III/IV Patient by a Distributional Clustering Solution
As for class III/IV patients resection of the truly resected channels did not stop seizures from reoccurring, it would be interesting to see if our model identifies any channel sets as better targets for resection. Therefore, we here apply a brute‐force search across all possible channel resections for one feasible class III/IV case. Ideally we would like to obtain dynamical outcome performances for all possible channel resections, however as the number of possible resections increases exponentially with the number of channels and is thus computationally prohibitive, we restrict ourselves to all pairwise channel resections in Patient 5, given that the set of truly resected channels for this patient is also of size two. This way a fair comparison is achieved, between the pair of truly resected channels and all other, possible pairs.
Figure 7a shows the (log)‐histogram of dynamical outcome values for all possible, pairwise resections in Patient 5, after optimization across the set (cf., panel n ctso in Fig. 5). The highly multimodal distribution displays a marked segregation between two performance regimes, separated by a region devoid of any values around . While the majority of resections bring no considerable improvement (right regime, ), the ones in the left regime do. All resections on the left lead to a considerable decrease in dynamical outcome and thus stabilize the preictal states compared to the cases of no and actual resection. When we count for each channel the frequency of occurrence in these of better performing channel combinations, we get the histogram of Figure 7b. Looking at this distribution of channel occurrences, it becomes very clear that the performance of a resection combination mainly depends on the presence of only three channels: 1, 2 and 38. In all but five combinations of the left regime at least one of these three channels was present, whereas in four of the remaining five combinations—which were the worst performing in the left regime—either of the neighboring channels 37 or 39 belonging to the same electrode stripe was present. Combining these three channels in groups of two gives the performances and ranks as displayed in Table 1. Two of these three channels combined (1 and 38) also provide the best performance for this setup.
Figure 7.
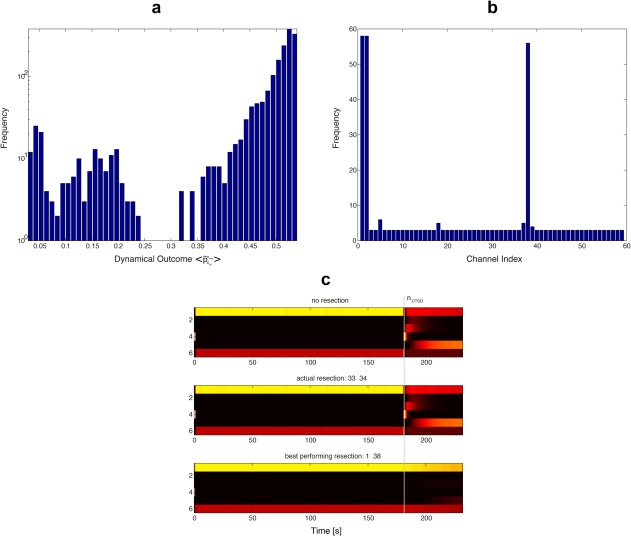
Optimizing the set of resected channels for Patient 5. (a) (Log)‐Histogram of dynamical outcome performances for Patient 5 and the optimal (cf., panel n ctso in Fig. 5). All possible resection protocols (= channel combinations) of set size 2 have been evaluated. Note the two distinct performance regimes separated by a zero‐frequency regime around . (b) Histogram indicating the frequency of occurrence for each of the 59 channels amongst the best performing channel combinations. A combination was labeled “best performing” if its dynamical outcome was smaller than 0.3, corresponding to the left regime in (a). Note the high frequencies for channels 1, 2, and 38. (c) Dynamics of the posterior membership probabilities induced by no resection (top panel), actual resection (middle panel) and the best performing channel resection protocol (bottom panel). [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 1.
Dynamical outcomes of all resections build from pairs of the three most frequent channels in Figure 7b
| Channel A | Channel B |
|
Rank | |
|---|---|---|---|---|
| 1 | 2 | 0.0690 | 63 | |
| 2 | 38 | 0.0325 | 2 | |
| 1 | 38 | 0.0279 | 1 |
gives the dynamical outcome and Rank the rank of the pairs dynamical outcomes within the set of best performing combinations (equivalent to ) Channel A/B define the pair of electrode channels simulated for resection.
To summarize this section, for class III/IV Patient 5 we could reveal by simulation that three distinct channels might be highly effective in rendering the ictal state less likely. Practically all pairwise combinations bringing a considerable improvement in dynamical outcome contained at least one of those crucial channels. In the best performing cases, our model predicts an almost complete stabilization of the preictal states. This opens the question if that patient would really have experienced a reduction in seizure frequency after a corresponding surgery. Interestingly, the three effective channels (1, 2, and 38) would have all been resectable, as they were not located in eloquent regions of cortex. However, two different craniotomies would have been necessary, at least for combinations involving channel 38, which is not adjacent to Channels 1 and 2. Thus, in these cases other techniques than classic resective surgery might be invoked in the future, such as thermocoagulation [Cossu et al., 2015], which is applied using the very same depth electrodes also used for iEEG recordings (and for functional brain mapping if needed).
DISCUSSION AND CONCLUSION
Summary
In this study, we have validated a dynamic, soft clustering approach for multivariate time series that allows for predictive modeling. We have demonstrated this by the models ability to predict the outcomes of (virtual) resection surgeries in epileptic brains. More concretely, the posterior probability of those cluster centroids was assessed, which—prior to resection—had been automatically classified as representatives of the seizure state. Consequently this probability was used as an outcome performance measure (called the dynamical outcome). In total, for 9 out of 12 patients we found a gap in dynamical outcome that was consistent with the patients Engel class, when the outcomes of random or no resection protocols were compared to the outcome of the true resection protocol; class I patients displayed a substantial gap in 5 of 7 cases, whereas such a gap was missing in 4 of 5 class III/IV cases. Table 2 gives a summary of these results. This is a significant result that, at least for class I patients, can hardly be explained by chance or overfitting, given the vast number of possible resections, ranging from (Patient 2) to (Patient 9, cf., Table 3). Moreover, for a specific class III/IV patient we have demonstrated how the presented methodology may be used to improve existing resection protocols.
Table 2.
Patient outcome performance summary outcome performance gap is defined as the difference between the dynamical outcome of the no resection and the true resection protocol
| Patient No. | Engel class | Outcome performance gap | P |
|---|---|---|---|
| 1 | I | 0.136 | 0.001 |
| 2 | I | 0.861 | 0 |
| 4 | I | 0.954 | 0 |
| 6 | I | 0.942 | 0 |
| 7 | I | 0.111 | 0.044 |
| 9 | I | 0.405 | 0.015 |
| 10 | I | 0.677 | 0.001 |
| 5 | III/IV | 0.003 | 0.82 |
| 8 | III/IV | 0.877 | 0 |
| 18 | III/IV | 0.087 | 0.700 |
| 21 | III/IV | 0.024 | 0.940 |
| NP | III/IV | 0.003 | 0.230 |
Relationship to Other Works
Our study is not the first where virtual resection protocols or seizure abatement strategies have been evaluated in silico. In the former context and despite methodological shortcomings (see introduction), virtual resections have been tested based on standard functional networks in a very recent study [Khambhati et al., 2016]. Moreover, two studies combined phenomenological models of neuronal population dynamics with either anatomical [Hutchings et al., 2015] or EEG derived functional network connectivity [Sinha et al., 2014]. Using the anatomical methodology, the effects of seizure abatement through stimulation [Taylor et al., 2015] as well as lesions in a non‐epileptic context [Honey and Sporns, 2008] have also been examined. Note that the incorporation of neuronal population dynamics poses a conceptual departure from the standard functional networks approach, as the former models allow for the assessment of dynamical influences of a given resection protocol.
Several problems, however, are associated with the published methodologies; first, in [Hutchings et al., 2015; Sinha et al., 2014; Taylor et al., 2015] the population models are based on detailed assumptions about the spatio‐temporal dependencies of the modeled set of time series, a problem we have circumvented here by considering the temporal dynamics of the joint amplitude distribution only, which explicitly disregards dynamics within time windows. In particular, the assumed connectivity is static in these models, whereas our model allows for dynamical switchings in functional connectivity as induced by the switching of posterior mass for the individual centroid distributions (cf., [Steimer et al., 2015]). Second, performance of a given resection protocol in the virtual resection approaches of [Hutchings et al., 2015; Sinha et al., 2014] is measured based on the transition (or escape) time of each node from a nonictal to the ictal state. As the model is set up such that these transitions may occur also in healthy controls, it seems to miss some crucial seizure prevention mechanism [Hutchings et al., 2015]. Directly related to this aspect however is the most important shortcoming of these models: their footing on node measures which, for a given resection protocol, deliver performance values only for each node individually and not for the ensemble of resected nodes as a whole. The reason for this is a lack of an undisputed, model‐inherent definition of what constitutes a collective, ictal state—which is distinct from our clustering approach where, for each time window, the distributional centroids judge the joint distribution of all channels (nodes) collectively (based on an automated procedure for classifying markedly different centroids as either ictal and preictal (see Materials and Methods Dichotomization of the Centroid Distributions into Preictal and Ictal Subsets section)). This illustrates a clear advantage provided by trainable, probabilistic models.
While only a limited number of such models has been devised in the context of epileptiform iEEG time series anyway [Direito et al., 2012; Santaniello et al., 2011; Varotto et al., 2012; Wulsin et al., 2013], the approaches by [Direito et al., 2012; Santaniello et al., 2011] are not suited for drawing inferences about specific resection protocols as they were considered in the present study. The works of [Varotto et al., 2012; Wulsin et al., 2013] in contrast may allow for this, however the authors did not consider utilizing their model for simulating the effects of resection. Furthermore, the multivariate autoregressive model used by [Varotto et al., 2012] is restricted to linear interactions between the channels and its model complexity cannot be chosen independently from the sampling rate, as the number of parameters the model uses is proportional to , where D is the number of channels and S the sampling rate. In our model, however, the only effect of an increased sampling rate is a more refined estimate of the underlying empirical distribution, leaving model complexity unaffected. This illustrates again the advantages given by a distributional clustering approach that models only the temporal evolution of dynamical regimes (which are allowed to change for each window), while being oblivious to the dynamics that constitute a regime. To the best of our knowledge, this study is the first, where predictive modeling was used for assessing the collective effects of surgical resection protocols, while avoiding the aforementioned problems.
Apart from epilepsy research, moreover, our proposed clustering methodology is applicable also to EEG analyzes from other domains of science—such as sleep research and psychophysics—and even to general multivariate time series. Note also that the approach is a spatio‐temporal generalization of the mere spatial probabilistic model we have examined before (a single Chow‐Liu tree) and for which we have shown how to derive functional brain networks from it [Steimer et al., 2015]. Thus, in the more general setup considered here, where each cluster centroid corresponds to a specific member of a collection of Chow‐Liu trees, the trees and Markov chain parameters together may serve as a generative model for temporally evolving functional networks, which thus poses a solution to one of the most important challenges in the domain of functional brain networks [Stam et al., 2014].
Model Limitations and Possible Improvements
Despite its capabilities our approach leaves some space for improvement to obtain even more realistic models. For the sake of simplicity and restriction of computational load, we have used for each patient the same settings of (meta)‐parameters during the clustering procedure. More concretely, the number of centroids K, the inverse temperature β and the windowing parameters were identical across all patients (see Distributional Clustering of the Multivariate iEEG Data section). It is well‐known however that parameters such as K and β affect the generalization capability of some clustering model [Buhmann and Held, 2000; Still and Bialek, 2004]. Hence, we are currently in the process of applying recent solutions to this problem to our clustering model, such as approximation set coding [Buhmann, 2010] or the minimum transfer cost principle [Frank et al., 2011], which are expected to yield even more accurate predictions. Likewise one may also consider a more refined class of probabilistic models from which cluster centroids are chosen, although the adequacy of Chow‐Liu trees—which were considered in this study—for modeling epileptiform iEEG time series has been shown recently [Steimer et al., 2015].
Potential Applications of the Model in the Context of Epilepsy Treatment
Having decided on a specific, predictive clustering methodology opens up a wide range of applications in epilepsy prognostication. As we have shown here, clustering can obviously be used to assess the efficacy of distinct and clinically preselected channel resections. However, as our results on brute‐force analysis show, search methods may find interesting channel combinations that, due to the network etiology of epilepsy (see Introduction section), evade the view of even experienced epileptologists. While many epileptologists are successful in searching electrode channels for suspicious patterns—such as spike‐waves or low amplitude, fast oscillations—some forms of epileptic seizures may evade such a simplistic, univariate view and may only be understood in multivariate terms as a complex interaction of many subparts of the epileptic brain [Singh et al., 2015]. In such cases, human iEEG parsing capability is easily stretched to its limits if tens of subparts (channels) are involved in the generation of seizures, while computational methods, such as the clustering procedure presented in this study, may provide a remedy here. On the other hand, computational modeling also offers more efficient search methods than brute‐force, which may thus be used for the automated finding of effective channel resections. Therefore, we have plans to devise search methods—such as genetic algorithms—for this task in the future.
Intimately related to this issue is the problem of finding alternative channel combinations if the area determined for resection is located in the patients eloquent cortex. This is a frequent problem in epilepsy treatment that may also be remedied by our clustering methodology, either presurgically, that is, by providing a whole set of precomputed alternative channel combinations, or by the in situ computation of such alternatives.
Another potential application is concerned with the relief of hardship the patient has to endure during presurgical data acquisition. The time series we have used in this study to train clustering models—and which have also been used for clinical assessment—contained exactly one seizure per patient during presurgical evaluation. Obviously such seizures are debilitating events that affect the patient physically and emotionally. Furthermore, to provoke seizures, anti‐epileptic medication has to be suspended during the presurgical evaluation period, which may distort the actual iEEG dynamics that manifest themselves in the patients postsurgical, daily life, where he is supplied again with medication. For these reasons, it is desirable to avoid seizures, to sustain anti‐epileptic medication and thus to analyze the interictal iEEG during presurgical evaluation, that is, the iEEG data recorded between but not during seizures. Although direct evidence is missing, the proposed clustering methodology might be well suited for this task, which is why its application to interictal data is amongst our immediate next working steps.
MATERIALS AND METHODS
The results presented in Results section were obtained after conducting a variety of preprocessing and analysis methods, whose input/output dependency structure is graphically summarized in Figure 8.
Figure 8.
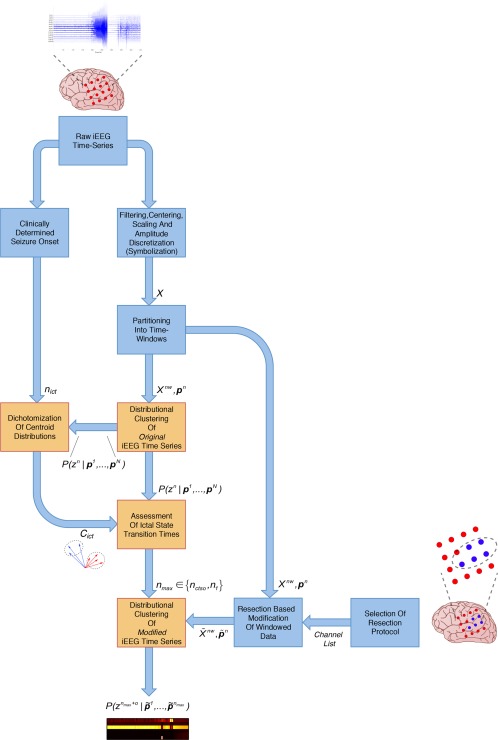
Process flow of preprocessing and analysis methods applied to the raw, periictal iEEG time series. Blue boxes give preprocessing methods applied before subsequent analysis (orange boxes) was performed. Both types of methods are described in the Materials and Methods section. Input/output relationships between the various methods are depicted by blue arrows, with the exchanged quantities indicated next to these arrows. Results presented in the Results section are based on the posterior membership probability obtained at the final output. [Color figure can be viewed at http://wileyonlinelibrary.com]
For 12 pharmacoresistant epilepsy patients (Patient and Periictal iEEG Data section), we examined the effect of distinct resection protocols (= simulated resections of distinct sets of brain areas, where electrode channels were located during presurgical iEEG evaluation) on the predicted dynamical state of the iEEG time series. Prior to analysis these time series were partitioned by a sliding window (Preprocessing of the iEEG Data section), such that changes in dynamical state were assumed to occur only at transitions from one window to the next. Based on the results of a soft distributional clustering technique for Markovian dynamics (Distributional Clustering of the Multivariate iEEG Data section), these states were broadly separated into preictal and ictal states, that is, the states before and during seizures, respectively (Assessing Ictal State Transitions from a Distributional Clustering Solution for Defining Latest Observed Time Points section).
While the cluster vectors (centroids) were given by distributions characterizing the joint EEG signal values within time windows, separation of system states was based on an automated dichotomization of the set of centroids into representatives of the preictal (C pre) and the ictal state (C ict, see Dichotomization of the Centroid Distributions into Preictal and Ictal Subsets section). Therefore, when compared to random or no resections, performance of a given resection protocol was established by its efficiency to reduce the posterior membership probability of the “ictal” centroids , where zn denotes the hidden centroid indicator variable for time window n and the corresponding observed data. To simulate resections, the original time series was modified in a distinct way to reflect the resection protocol and then condensed into a sequence of empirical distributions (or in case of the unmodified time series corresponding to the no resection protocol, see Predictive Modeling Based on a Distributional Clustering Solution section). Subsequently, the sequence was fed into a Markov chain for zn, but only up to a specific time window n max, which marked the beginning of distinct, early state transitions of the developing seizure. Such transitions corresponded either to transitions from the preictal to the ictal period (at n max = n ctso the computational time of seizure onset (CTSO)), or to transitions from the first to the second intraictal state (at ), that is, the first state transition within the seizure (Materials and Methods Assessing Ictal State Transitions from a Distributional Clustering Solution for Defining Latest Observed Time Points section).
Performance was then evaluated based on the averaged posterior of the ictal centroids for future time windows , a quantity that we termed the dynamical outcome of some resection protocol and which is denoted by (see Predictive Modeling Based on a Distributional Clustering Solution section). A high degree of performance for a given resection protocol is thus reflected by a low , which is equivalent to a high, averaged posterior probability of the preictal centroids and hence to a stabilized, preictal state.
Patient and Periictal iEEG Data
In this study, we included 12 periictal, intracranial EEG (iEEG) time‐series of variable length and electrode channel number that were recorded from 12 seizures from pharmacoresistant epilepsy patients with known good or bad clinical outcome after resective surgery (as defined by class I and III/IV respectively in the Engel classification system). While after surgery the class I patients were completely free from seizures and auras, there is no unambiguous separation between class III and IV in the Engel classification system, which is why both were lumped into the same class III/IV. Channels were either located on stripe, grid or depth electrodes. Very few channels ( ) were contaminated by visually detectable artifacts—as judged by an experienced electroencephalographer (K.S.)—and those channels were excluded from analysis. Detailed information about the recoding setup, periictal time series and patients—including the patients sex, age, etiology etc.—can be obtained from our previous study [Steimer et al., 2015], the seizure database of which entails 11 of the 12 patients considered here. More specifically, from the original 25 patients of the previous study, we excluded those whose Engel class was either not known, not equal to I or III/IV, or for whom detailed information regarding the resected channels was missing, leaving patients no. in the database (Table 3 cf. table 1 in [Steimer et al., 2015]). The 12th patient (NP) considered here was excluded from our previous study, as he did not meet our criteria regarding seizure duration ‐an aspect that is of subordinate importance here.
Except for no. 10 only the first seizure after hospitalization was analyzed for each patient of Table 3, as we have found differences between results obtained from the first and all subsequent seizures. More specifically, the first seizure differed w.r.t. the number and duration of ictal state transitions (see Assessing Ictal State Transitions from a Distributional Clustering Solution for Defining Latest Observed Time Points section). This is a clear indication that the dynamical systems underlying the two types of seizure iEEG data are of different nature and thus cannot be explained by the same clustering model (i.e., a Markov chain with the same transition probabilities and centroids, see Distributional Clustering of the Multivariate iEEG Data section). Most likely the differing iEEG properties can be attributed to the withdrawal of sustained medication, which the patients suffer from during presurgical evaluation. As we had to decide for one of the two seizure types and since remnants of medication may still be potent during the early part of evaluation, we assumed the first occurring seizure to be most representative for the postsurgical state, where the patient is supplied again with medication. Moreover, possibly distorting postictal effects are excluded for the first occurring seizure, but not for the following ones. That is, a seemingly preictal period in a subsequent seizure may in fact be influenced by the postictal state of its predecessor. For Patient 10 however, we have analyzed the second seizure, as the first one was found to be corrupted by artifacts.
In contrast to our previous study, we here analyzed, for a given seizure, only its ictal and immediately preceeding 180 s preictal period and thus discarded the postictal period, as we were interested only in the generic parts and dynamics of the seizure. Ictal onset, that is, the beginning of the ictal period, was clinically determined by an experienced epileptologist (KS).
Retrospective data analysis had been approved by the ethics committee of the Canton of Bern/Switzerland. In addition, all patients gave written and informed consent that their data from long‐term video‐EEG recordings might be used for research or teaching purposes.
Preprocessing of the iEEG Data
Preprocessing of the recorded iEEG data was largely identical to our previous study [Steimer et al., 2015] and, for the sake of self‐sufficiency, is only briefly repeated here: After forward/backward bandpass filtering the iEEG time series recorded from individual electrode channels were independently centered and scaled to a mean of zero and a standard deviation of 1. The amplitudes of the thus standardized signals x s were then discretized by seven equidistant bins along the y‐axis, with marking the upper and lower ends of the seventh and first bin, respectively (Fig. 9a,b, signals outside interval were associated with the nearest, that is, either the first or seventh bin). We used σ = 1 for all patients. Thus, for the system of channels the total number of joint states is , where Ne is the number of channels that varies from patient to patient (see Table 3). Discretization of the time series was done because the clustering model we used is based on the Chow‐Liu algorithm [Chow and Liu, 1968; Meila and Jordan, 2001] that is defined for discrete data only.
Figure 9.
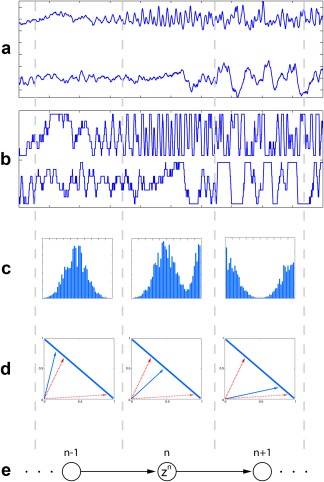
Schematic illustration of iEEG data preprocessing and clustering of the resulting empirical distributions (a) filtered iEEG time series after centering and scaling to mean 0 and standard deviation 1. The series is partitioned into time windows (= vertical, gray lines). (b) The signals in (a) after discretization into seven equidistant bins along the y‐axis. (c) Empirical distributions (histograms) of the subseries extracted from each time window. Each combination of bins from the individual signals (two in example (b)) represents one out of joint system states and contributes one bar to the histogram (histograms are examples only that do not correspond to the actual distribution of joint states in (b)). (d) The sequence of histograms in (c) ‐which correspond to the sequence of time windows indexed by n < N‐ can be considered as a sequence of m‐dimensional probability vectors on the ‐simplex (blue, solid arrows). Drawn here for illustration is the case m = 2. These probability vectors can be clustered by a set of cluster centroid vectors, which also correspond to probability distributions (red, dashed arrows). (e) The cluster membership variable is assumed to evolve according to a Markov chain. Thus, the goal of clustering is to compute the cluster centroids, Markov chain parameters and the posterior membership probabilities . [Color figure can be viewed at http://wileyonlinelibrary.com]
Subsequently, the discretized EEG time series were partitioned by sliding windows, each of length with overlap at a sampling rate of 512 Hz, yielding W = 640 data points per window. The windowed data is referred to as , which denotes the w‐th data point of time window n (with and ). Throughout this article, we interchangeably measure time quantities (such as n and W) either as an integer index or in seconds. If some time window n is referred to in seconds, the seconds correspond to the occurrence time of the first data point contained by the window. Occurrence time in turn is measured w.r.t. to the beginning of the time series based on data point .
Distributional Clustering of the Multivariate iEEG Data
Our goal of clustering in multivariate time series was to find regions (clusters) in phase space, where the system under study typically resides in during different epochs of its temporal evolution. As the systems exact dynamics in phase space may be too complex to model, we here just headed for its coarse description by modeling typical regions in phase space only (note that in our case the phase space is discrete and consists of all m joint configurations of electrode channel states). It was hereby assumed that two data points, whose temporal distance is small, also reside in close proximity to each other in phase space. Thus, it was reasonable to condense all data points from the same temporal “neighborhood” (time window) into a single “data point,” that was given by the m‐dimensional empirical distribution of joint states assumed by the system in phase space. In the literature, this technique is termed “distributional clustering” [Pereira et al., 1993; Puzicha et al., 1999] and Figure 9c,d illustrates it for the time series case.
Having characterized the system as a sequence of empirical distributions our next goal was to cluster them into K clusters and to find a model for the temporal evolution of the cluster membership variable (Fig. 9d,e). Thus, the cluster centroids were themselves distributions and we assumed these distributions to belong to some model class which, for this study, was the set of Chow‐Liu trees [Chow and Liu, 1968; Steimer et al., 2015]. Let
| (4.1) |
| (4.2) |
be the empirical distribution of joint states in time window n.
We considered clustering of the dataset
| (4.3) |
that is, the clustering of a full sequence of distributional observations. Note that is a compound matrix consisting of column vectors (in general we denote vector quantities by bold, lower case letters and matrices by bold capitals). In an analogous fashion we denote by the k‐th centroid distribution (Chow‐Liu tree) and by the corresponding centroid compound matrix:
| (4.4) |
| (4.5) |
where denotes a hidden vector of cluster membership variables , that are each tied to a specific time window n and which collectively are assumed to form a Markov chain (Fig. 9e).
In the case at hand, the goal of clustering is to compute —i.e., the (posterior) cluster membership probability given the observed sequence of distributions—alongside the cluster centroids and the parameters of the Markov chain assumed as probabilistic model for z. Using an efficient message‐passing scheme on this Markov chain, it is also possible to compute from the marginal membership probabilities (see Supporting Information S1 for details). In fact it is these marginal membership probabilities that are the key quantity behind our results in Results section.
The membership probabilities in turn are needed as a necessary prerequisite and are computed by our clustering algorithm. This algorithm is very similar to the learning of Hidden Markov Models by Expectation‐Maximization, but is based on rate distortion theory [Cover and Thomas, 2006] and thus minimizes the following objective (see Supporting Information S1 for a short primer on rate distortion theory and a derivation of the objective)
| (4.6) |
| (4.7) |
| (4.8) |
where is the expected distortion measured by the sum of Kullback‐Leibler divergences . The set
| (4.9) |
is the set of Markov chains on z and β is an inverse temperature parameter which determines the complexity‐accuracy tradeoff that is fundamental in rate distortion theory.
For fixed K and β learning, the cluster centroids and Markov chain parameters consists of an alternating minimization of objective 4.6 w.r.t. and . That is, the three quantities are individually updated in a cyclic manner, while the remaining two quantities are kept unchanged during each such update. This strategy is also known as coordinate descent and is repeated until objective 4.6 has stopped improving (see Supporting Information S1 for how these updates are actually performed). Note however that coordinate descent is prone to converge to local minima of the objective function, which is why we selected the solution corresponding to the minimum objective across six runs of the optimization procedure with random initializations of the cluster centroids and Markov chain parameters. For all patients, we have chosen the uniform values 6 and 0.35 for the (meta)‐parameters K and β, respectively.
Dichotomization of the Centroid Distributions into Preictal and Ictal Subsets
As the iEEG time series consisted of a preictal and an ictal period, our clustering algorithm was expected to produce a dichotomy of distributional centroid vectors, that is, a subset of centroids that belonged to the preictal period, together with its complementary set belonging to the ictal period. To reveal surgical resection protocols that rendered patients seizure free, the strategy pursued in this study was to select the protocol which led to the smallest membership probability of the ictal set of centroids (or equivalently the largest probability of the preictal set). Thus, we were in need of an objective method for labeling centroids as either preictal or ictal, which is described in this section.
Let be some set of indices of putative, ictal centroid vectors after the clustering procedure of Distributional Clustering of the Multivariate iEEG Data section has been conducted and let n ict be the index of the time window that covers the clinically determined seizure onset at (Patient and Periictal iEEG Data section). The complementary subset of C ict is defined as the set of putative, preictal centroid vectors and is denoted by . In an ideal scenario—i.e., when C ict corresponds indeed to the ictal centroid subset and is thus active only during the ictal period—the summed membership probability
| (4.10) |
describes a Heaviside step function, such that for and for . Hence, for each possible subset C ict we characterized the distance between and its ideal profile, the step function, and selected the subset yielding minimal distance. Distances were measured by the ‐norm, that is, by the expression
| (4.11) |
where and is the step function with .
This procedure resulted in ictal subsets C ict that were in perfect agreement with our own, subjective subset selection, which was based on a visual analysis of the membership profiles (see Fig. 10, top panel).
Figure 10.
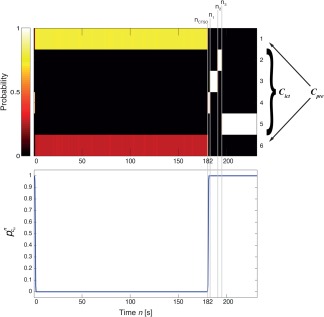
Automatic dichotomization of the centroid set and detection of the ictal state transition times. Top panel: Color‐coded, example posterior membership profile during the preictal and ictal periods (for K = 6 centroids). x‐axis gives the time window n in seconds, y‐axis the centroid index. The procedure described in the main text produces an ictal centroid subset , whose posterior membership probability increases sharply at , that is, 2 s after the clinical seizure onset at (bottom panel, the large value of at is due to the prior probability of the Markov chain for z 0). Within the ictal period individual centroids each become activated with increased membership probability during four distinct states with transition times at . Likewise C ict, the transition times and n 3 are also detected in an automated manner by procedures described in the main text. [Color figure can be viewed at http://wileyonlinelibrary.com]
Predictive Modeling Based on a Distributional Clustering Solution
After having computed the centroid distributions and Markov chain parameters on a given sequence of observed empirical distributions, the results may be used to predict cluster membership probabilities under various different conditions. By making use of an efficient message‐passing scheme (sum‐product belief propagation, see Supporting Information S1), it is possible for example to predict future cluster memberships, that is, to compute for some . We call this type of predictive modeling temporal predictive modeling. Likewise, one may manipulate the observations Xnw within the available time windows to become , recompute the empirical distributions to accordingly and finally update the resulting . We call this strategy spatial predictive modeling, as in this case predictions are indeed made for new observations, but only within the available time frame defined by the training data. In both cases, temporal and spatial predictive modeling, objective 4.6 is recomputed only w.r.t. , the other quantities keep the values they have obtained during the training procedure.
We used spatial predictive modeling to assess the effectiveness of simulated resection protocols for preventing a developing seizure. Distinct combinations of EEG electrode channels were tested in this regard, by setting their discretized signals to a constant value. More concretely, the state of variable —which emerges as the cartesian product of the discretized signals from Ne channels, each with state space —is recomputed to , after having set the states of the channels in the tested combination to value 4 constantly.1 The remaining channels kept their original values. From the thus recomputed values , we updated the empirical distributions to and consequently the input messages of the Markov chain (see Supporting Information S1). This finally allowed us to recompute the cluster membership probabilities . Such spatial aspect of predictive modeling was complemented by a temporal aspect, as we did not utilize the whole sequence of modified observations, but rather only those up and until some time point . Membership probabilities for later time points were then computed analogously to temporal predictive modeling.
Assuming a sensibly defined n max for the moment, in case of class I patients we expect the set of truly resected channels to render the significantly smaller compared to a random or no resection set. For class III/IV patients in contrast we expect a reduced or no such effect. Hence, we will call the or their average across some interval of o the dynamical outcome induced by some specific resection protocol. For all patients, we simulated the dynamical outcome given the (virtual) resection of those channels that got actually resected during surgery, alongside a Monte‐Carlo simulation consisting of 3,000 trials, where during each trial the dynamical outcome induced by a random resection was assessed. The size of these random sets of channels was constrained to the number of actually resected channels, which were prevented from becoming members of the random sets. Apart from these size and membership constraints resection was completely random. However, we have also tried an alternative resection strategy, where correlated channels located on the same stripe, grid, or depth electrode were preferably selected. Our results were only weakly affected by this strategy and are presented in Supporting Information section S2. Preventing the truly resected channels from becoming members of the random sets was necessary in both strategies however, as only then a clean validation of our model w.r.t. its ability to separate class I from IV patients was guaranteed.
Whenever the number of truly resected channels was small enough, that is for patients no. 5 and NP, we simulated the full set of possible resection protocols, which amounted to 1,711 and 7,140 trials for channel sets of size 2 and 3, respectively (see Table 3). For the Monte‐Carlo results of Figures 4, 5, and 6 dynamical outcome was determined by the average
| (4.12) |
for O = 40 time windows. This way a true benchmark was established, which ranked the dynamical outcome of the actually resected channels against those induced by random subsets of their complementary set. For the Monte‐Carlo results of Figure 2 in contrast, dynamical outcome was given by the plain for the indicated values of o.
As providing meaningful values to n max is crucial in this context, we will describe in the next section how such latest observation time points can be defined.
Assessing Ictal State Transitions from a Distributional Clustering Solution for Defining Latest Observed Time Points
As some sensible clustering procedure is very unlikely to associate a fully developed, ictal iEEG state—where most of the channels display strong bursts of activity—with one the preictal centroid vectors in C pre, even if some of the channels were set to constant values, assessing the effectiveness of simulated resection protocols is difficult if the full sequence of N (modified) observations that entail the whole ictal period is used for computing the posterior membership profiles . Thus, we fed observations only up to specific, latest observed time points of the early ictal period into the Markov chain and used sum‐product belief propagation for figuring out future membership profiles (Supporting Information S1). The question remains then, how to define suitable n max for computing the corresponding posterior profiles .
In fact, for all patients we found a highly orchestrated sequence of state transitions during the ictal period that resembled the sequence of song motifs in a musical box. Figure 10 gives a representative example thereof. It turned out that, depending on the patient, different early state transition times were effective in suppressing future ictal membership probabilities . Hence, a procedure for determining these transition times was necessary and is described in the following.
The first relevant state transition is when seizure onset becomes visible in the posterior profile. To specify the time of this transition, we computed the based on the original, unmodified observed data Xnw. For all patients, we thus found a consistent quasi‐step increase in the summed membership probability of the ictal centroid subset, some time after into the time series (Fig. 10 bottom panel, Dichotomization of the Centroid Distributions into Preictal and Ictal Subsets section), which is the time ictal activity was first observed by a trained clinician (see Patient and Periictal iEEG Data section). In some cases, the step was preceded by a short “probability pulse” of during the clinical preictal period. This finding means that after clinical seizure onset different sets of centroid distributions become responsible for the observed data, which is suggestive of a radical and (on a short time scale) irreversible change in system dynamics. Hence, we assumed a set of seizure onset models, each consisting of a Heaviside step function for , with the step occurring at some transition time n ctso. Candidates for n ctso were given by all times when crossed a threshold of 0.995 from below and thus defined members of the model set. The CTSO was then defined as the threshold crossing time corresponding to the candidate model that yielded the smallest ‐norm distance to the actual, binarized profile (that is, the profile obtained by setting values larger than 0.995 to 1 and smaller ones to 0). Note that the thus defined n ctso must not necessarily be equal to n ict.
n ctso corresponds to the 0th state transition that starts the ictal period, whereas later transition times within that period are denoted by and were computed as follows; first, the posterior profiles were binarized separately for each ictal signal (i.e., each value of ), by setting values larger than 0.01 to 1 and smaller values to 0. Then, the downward edges—that is jumps from 1 to 0—were determined and grouped together across signals, such that the jumping times within each group differed by no more than five time steps (windows) and were all larger than n ctso. Each group then defined a separate ictal state, whose time ni of transition to the following state was given by the maximum jumping time across the groups members. Again we found excellent correspondence between the thus computed transition times and our subjective impression (Fig. 10, top panel).
As different resection protocols were maximally effective in suppressing the ictal state at different times n max, we ran—for each protocol—simulations for all n max taken from the set and pooled in Figure 6 only the result for the n max with best dynamical outcome performance (see Predictive Modeling Based on a Distributional Clustering Solution section). This way each resection protocol was given its best chance to “prove itself” as a useful protocol for ictal state suppression. We only considered state transitions n ctso and n 1 as effective in this regard, as for later transitions the ictal waveforms of the unresected channels prevented classification of the resection protocol as seizure suppressing. For the illustrative examples in Figures 1 and 3, we only displayed the case n max = n ctso, whereas their respective Monte‐Carlo results of Figure 2 are based on the best performing . Figures 4 and 5 display separately the best performing n max from the sets and .
Statistical Hypothesis Test for Assessing the Chance Level of Actual Resection Protocols
To assess the difference in posterior membership probability induced by the sets of truly and randomly resected channels, we applied a statistical hypothesis test. Our null hypotheses are that the set of truly resected channels does not lead to a dynamical outcome that is small enough at the two earliest ictal state transitions, such that it cannot be reached by random resections from the complementary set of channels.
To obtain mathematically precise formulations of and let be the dynamical outcome induced by the set of truly resected channels and the corresponding outcome induced by random resection. Then
| (4.13) |
| (4.14) |
We tested and by determining the rank of w.r.t. the obtained from large numbers of random resection trials (see Predictive Modeling Based on a Distributional Clustering Solution section). A corresponding p‐value was computed by dividing this rank through 3,000. Thus, a significant difference between truly and randomly resected channels was given if the p‐value was below the (Bonferroni corrected) significance level of for at least one of the two latest observed time points n ctso and n 1.
Permutation Tests for the Patient Data of Table 3
For the permutation tests of Table 3, the following procedure was conducted: for a given permutation of group labelings (class I or III/IV) of the patient cohorte, we computed the maximum, absolute difference between the cumulative distributions of the (permuted) groups I and III/IV. This quantity then served as a test statistic, the distribution of which was given by the empirical distribution across all permutations. p‐values were then determined in the usual way, that is, by the fraction of permutations yielding a test statistic larger or equal than the one induced by the true labeling.
Supporting information
Supporting Information
ACKNOWLEDGMENTS
We thank Joachim Buhmann for his provision of expertise regarding distributional clustering and Christian Rummel for fruitful discussions about the clinical data. The authors declare no conflict of interest.
Footnotes
To mimic surgical resections, we have chosen a constant channel value, because the EEG state of inanimate objects (e.g., a stone) is arguably constant and is thus also a plausible state for a (virtual) electrode channel placed after surgery above scarred or otherwise unresponsive brain tissue. Value 4 in turn represents best value x s = 0 of the standardized, continuous iEEG signals and consequently also the mean of the uncentered, unscaled iEEG. Note also that setting resected channels to the constant value of zero is equivalent to the removal of nodes in the functional network based approaches used in other virtual resection studies (Hutchings et al., 2015).
REFERENCES
- Bialonski S, Lehnertz K (2013): Assortative mixing in functional brain networks during epileptic seizures. Chaos 23:033139. [DOI] [PubMed] [Google Scholar]
- Buhmann J (2010): Information theoretic model validation for clustering In: Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA: pp 1398–1403. [Google Scholar]
- Buhmann JM, Held M (2000): Model selection in clustering by uniform convergence bounds In: Solla SA, Leen TK, Müller K, editors, Advances in Neural Information Processing Systems, Vol. 12. MIT Press; pp 216–222. [Google Scholar]
- Bullmore E, Sporns O (2009): Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:186–198. [DOI] [PubMed] [Google Scholar]
- Cascino GD (2008): When drugs and surgery don't work. Epilepsia 49(Suppl 9):79–84. [DOI] [PubMed] [Google Scholar]
- Chow C, Liu C (1968): Approximating discrete probability distributions with dependence trees. IEEE Trans Inform Theory IT 14:462–467. [Google Scholar]
- Cossu M, Fuschillo D, Casaceli G, Pelliccia V, Castana L, Mai R, Francione S, Sartori I, Gozzo F, Nobili L, Tassi L, Cardinale F, Russo G (2015): Stereoelectroencephalography‐guided radiofrequency thermocoagulation in the epileptogenic zone: A retrospective study on 89 cases. J Neurosurg 123:1358–1367. [DOI] [PubMed] [Google Scholar]
- Cover T, Thomas J (2006): Elements of Information Theory, 2nd ed. John Wiley & Sons, Hoboken NJ: Wiley. [Google Scholar]
- Direito B, Teixera C, Ribeiro B, Castelo‐Branco M, Sales F (2012): Modeling epileptic brain states using EEG spectral analysis and topographic mapping. J Neurosci Methods 210:220–229. [DOI] [PubMed] [Google Scholar]
- Engel J, van Ness P, Rasmussen T, Ojemann L (1993): Outcome with respect to epileptic seizures. In: Surgical treatment of the epilepsies, 2nd ed. New York, USA: Raven Press. pp 609–621. [Google Scholar]
- Engel J, Thompson PM, Stern JM, Staba RJ, Bragin A, Mody I (2013): Connectomics and epilepsy. Curr Opin Neurol 26:186–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fornito A, Zalesky A, Breakspear M (2015): The connectomics of brain disorders. Nat Rev Neurosci 16:159–172. [DOI] [PubMed] [Google Scholar]
- Frank M, Chehreghani M, Buhmann J (2011): The minimum transfer cost principle for model‐order selection In: Gunopulos D, Hofmann T, Malerba D, Vazirgiannis M, editors. Machine Learning and Knowledge Discovery in Databases, Vol. 6911 of Lecture Notes in Computer Science. Springer Berlin: Heidelberg, pp 423–438. [Google Scholar]
- Höller Y, Kutil R, Klaffenböck L, Thomschewski A, Höller P, Bathke A, Jacobs J, Taylor A, Nardone R, Trinka E (2015): High‐frequency oscillations in epilepsy and surgical outcome. A meta‐analysis. Front Hum Neurosci 9:574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey C, Sporns O (2008): Dynamical consequences of lesions in cortical networks. Hum Brain Mapp 29:802–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchings F, Han C, Keller S, Weber B, Taylor P, Kaiser M (2015): Predicting surgery targets in temporal lobe epilepsy through structural connectome based simulations. PLoS Comput Biol 11:1–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khambhati A, Davis K, Lucas T, Litt B, Bassett D (2016): Virtual cortical resection reveals push‐pull network control preceding seizure evolution. Neuron 91:1170–1182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer MA, Kolaczyk ED, Kirsch HE (2008): Emergent network topology at seizure onset in humans. Epilepsy Res 79:173–186. [DOI] [PubMed] [Google Scholar]
- Kramer MA, Eden UT, Kolaczyk ED, Zepeda R, Eskandar EN, Cash SS (2010): Coalescence and fragmentation of cortical networks during focal seizures. J Neurosci 30:10076–10085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwan P, Arzimanoglou A, Berg A, Brodie M, Hauser WA, Mathern G, Moshé S, Perucca E, Wiebe S, French J (2010): Definition of drug resistant epilepsy: Consensus proposal by the ad hoc Task Force of the ILAE Commission on Therapeutic Strategies. Epilepsia 51:1069–1077. [DOI] [PubMed] [Google Scholar]
- Lüders, H. (2006). The epileptogenic zone: General principles Epileptic Disord. 8(Suppl. 2):S1–S9. [PubMed] [Google Scholar]
- Malinowska U, Bergey G, Harezlak J, Jouny C (2015): Identification of seizure onset zone and preictal state based on characteristics of high frequency oscillations. Clin Neurophysiol 126:1505–1513. [DOI] [PubMed] [Google Scholar]
- Meila M, Jordan M (2001): Learning with mixtures of trees. J Mach Learn Res 1:1–48. [Google Scholar]
- Modur P, Zhang S, Vitaz T (2011): Ictal high‐frequency oscillations in neocortical epilepsy: Implications for seizure localization and surgical resection. Epilepsia 52:1792–1801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira F, Tishby N, Lee L (1993): Distributional clustering of English words. In: Proceedings of the 30th Annual Meeting of the Association for Computational Linguistics, Columbus, OH, USA. pp 183–190. [Google Scholar]
- Ponten SC, Bartolomei F, Stam CJ (2007): Small‐world networks and epilepsy: Graph theoretical analysis of intracerebrally recorded mesial temporal lobe seizures. Clin Neurophysiol 118:918–927. [DOI] [PubMed] [Google Scholar]
- Puzicha J, Hofmann T, Buhmann J (1999): Histogram clustering for unsupervised segmentation and image retrieval. Pattern Recognit Lett 20:899–909. [Google Scholar]
- Richardson MP (2012): Large scale brain models of epilepsy: Dynamics meets connectomics. J Neurol Neurosurg Psychiatry 83:1238–1248. [DOI] [PubMed] [Google Scholar]
- Rosenow F, Lüders H (2001): Presurgical evaluation of epilepsy. Brain 124:1683–1700. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O (2010): Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 52:1059–1069. [DOI] [PubMed] [Google Scholar]
- Rummel C, Abela E, Andrzejak R, Hauf M, Pollo C, Müller M, Weisstanner C, Wiest R, Schindler K (2015): Resected brain tissue, seizure onset zone and quantitative EEG measures: Towards prediction of post‐surgical seizure control. PLoS One 10:e0141023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santaniello S, Sherman D, Mirski M, Thakor N, Sarma S (2011): A Bayesian framework for analyzing iEEG data from a rat model of epilepsy In: Proceedings of the 33rd IEEE EMBS Annual Conference. Boston, MA: IEEE Engineering in Medicine and Biology Society Conference; pp 1435–1438. [DOI] [PubMed] [Google Scholar]
- Schindler K, Leung H, Elger CE, Lehnertz K (2007): Assessing seizure dynamics by analysing the correlation structure of multichannel intracranial EEG. Brain 130(Pt 1):65–77. [DOI] [PubMed] [Google Scholar]
- Schindler K, Bialonski S, Horstmann MT, Elger C, Lehnertz K (2008): Evolving functional network properties and synchronizability during human epileptic seizures. Chaos 18:033119. [DOI] [PubMed] [Google Scholar]
- Singh S, Sandy S, Wiebe S (2015): Ictal onset on intracranial EEG: Do we know it when we see it? State of the evidence. Epilepsia 56:1629–1638. [DOI] [PubMed] [Google Scholar]
- Sinha N, Dauwels J, Wang Y, Cash S, Taylor P (2014): An in silico approach for pre‐surgical evaluation of an epileptic cortex In: Engineering in Medicine and Biology Society (EMBC), 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA: IEEE; pp 4884–4887. [DOI] [PubMed] [Google Scholar]
- Stam C, Tewarie P, van Dellen E, van Straaten EC, Hillebrand A, van Mieghem P (2014): The trees and the forest: Characterization of complex brain networks with minimum spanning trees. Int J Psychophysiol 92:129–138. [DOI] [PubMed] [Google Scholar]
- Steimer A, Zubler F, Schindler K (2015): Chow‐Liu trees are sufficient predictive models for reproducing key features of functional networks of periictal EEG time‐series. NeuroImage 118:520–537. [DOI] [PubMed] [Google Scholar]
- Still S, Bialek W (2004): How many clusters? An information theoretic perspective. Neural Comput 16:2483–2506. [DOI] [PubMed] [Google Scholar]
- Taylor P, Thomas J, Sinha N, Dauwels J, Kaiser M, Thesen T, Ruths J (2015): Optimal control based seizure abatement using patient derived connectivity. Front Neurosci 9:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Diessen E, Diederen S, Braun K, Jansen F, Stam C (2013): Functional and structural brain networks in epilepsy: What have we learned? Epilepsia 54:1855–1865. [DOI] [PubMed] [Google Scholar]
- Varotto G, Tassi L, Franceschetti S, Spreafico R, Panzica F (2012): Epileptogenic networks of type II focal cortical dysplasia: A stereo‐EEG study. NeuroImage 61:591–598. [DOI] [PubMed] [Google Scholar]
- Wilke C, Worrell G, He B (2011): Graph analysis of epileptogenic networks in human partial epilepsy. Epilepsia 52:84–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wulsin D, Fox E, Litt B (2013): Parsing epileptic events using a markov switching process for correlated time series In: Proceedings of the 30th International Conference on Machine Learning, Vol. 28. Atlanta, Georgia, USA: pp 356–364. [Google Scholar]
- Zubler F, Gast H, Abela E, Rummel C, Hauf M, Wiest R, Pollo C, Schindler K (2015): Detecting functional hubs of ictogenic networks. Brain Topogr 28:305–317. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


