Neural mechanisms of motion perceptual learning in noise

Abstract

Practice improves our perceptual ability. However, the neural mechanisms underlying this experience‐dependent plasticity in adult brain remain unclear. Here, we studied the long‐term neural correlates of motion perceptual learning. Subjects’ behavioral performance and BOLD signals were tracked before, immediately after, and 2 weeks after practicing a motion direction discrimination task in noise over six daily sessions. Parallel to the specificity and persistency of the behavioral learning effect, we found that training sharpened the cortical tuning in MT, and enhanced the connectivity strength from MT to the intraparietal sulcus (IPS, a motion decision‐making area). In addition, the decoding accuracy for the trained motion direction was improved in IPS 2 weeks after training. The dual changes in the sensory and the high‐level cortical areas suggest that learning refines the neural representation of the trained stimulus and facilitates the information transmission in the decision process. Our findings are consistent with the functional specialization in the visual cortex, and provide empirical evidence to the reweighting theory of perceptual learning at a large spatial scale. Hum Brain Mapp 38:6029–6042, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Our ability to discriminate or detect sensory stimuli can be enhanced by practice. This phenomenon, known as perceptual learning, is widely used as a model to study experience‐dependent cortical plasticity in adults [Fahle and Poggio, 2002; Sagi, 2011; Watanabe and Sasaki, 2015]. One characteristic of perceptual learning is that the acquired behavioral improvement is usually restricted to the physical properties of the trained stimulus. Such specificity implies that learning is mediated by changes in the early visual processing stage, among neurons with a relative small receptive field and feature‐selective tuning [Poggio et al., 1992]. Electrophysiological and brain imaging studies have revealed learning‐related changes at multiple stages in the visual cortex, from the primary visual cortex V1 [Hua et al., 2010; Jehee et al., 2012; Schoups et al., 2001], extrastriate cortex such as V4 [Adab and Vogels, 2011], to object selective areas in the inferior temporal cortex [Bi et al., 2014; Lim et al., 2015]. An alternative hypothesis, however, assumes that perceptual learning engages the high‐level decision stage. Instead of changes in the tuning properties of sensory encoding neurons, learning can be modeled via adjusting the weights between the early and late areas, so as to optimize the processing of task‐relevant information [Bejjanki et al., 2011; Dosher and Lu, 1999; Law and Gold, 2009].

Compared to the “early” theory regarding the neural locus of perceptual learning, the “late” theory has received limited support from empirical evidence. A closely related issue is how learning‐induced changes in the sensory and decision processes are implemented at a larger spatial scale beyond local visual circuits. When multiple visual areas participate in the information processing for a task, would perceptual learning trigger reweighting at the regional level? Take motion processing for example, MT and V3A are recognized as two key areas in the human brain [Bartels et al., 2008; Orban et al., 2003; Tootell et al., 1997], and their involvement in motion perceptual learning has been demonstrated in several brain imaging studies [Chen et al., 2015, 2016; Shibata et al., 2012, 2016; Tompson et al., 2013; Vaina et al., 1998]. Previously, we found motion direction discrimination training sharpened the cortical tuning for the trained motion direction in area V3A, and enhanced the connectivity from V3A to the motion‐decision making area IPS (intraparietal sulcus) [Chen et al., 2015]. While these results indicate that learning induces retuning in the visual cortex, and reweighting in the high‐level decision process, it remains unclear why there was a lack of learning effect in area MT.

We hypothesized that the neural correlates of perceptual learning are based on the functional specilization of visual cortex. Neuropsychological findings suggest that V3A dominates in local motion processing, whereas MT+ dominates in global motion processing [Cai et al., 2014; Vaina et al., 2005, 2003]. This specilization is consistent with the learning‐related changes in V3A when subjects practiced motion direction discrimination at 100% coherence [Chen et al., 2015, 2016]—as all dots move in the same direction, subjects' ability to discriminate motion directions relied on the improvement in processing the local motion information. Conversely, motion discrimination learning may be mediated by MT/MST when global integration of motion direction is necessary. To test this hypothesis, we introduced external noise in the motion direction discrimination task by reducing the coherence level of the moving dots.

In the present study, we studied the neural mechanisms of motion perceptual learning in noise over a long‐time course. Human subjects were trained to discriminate the global direction of moving dots at 35% coherence over six daily sessions. Subjects' behavioral performance and BOLD signals were measured before, immediately after, and 2 weeks after training. We examined how learning affected the activation pattern of the trained motion direction in V1‐V4, MT, MST, and IPS, using multi‐voxel pattern analysis. In addition, we examined whether learning changed the effective connectivity between the visual motion areas and IPS using dynamic causal modeling (DCM).

MATERIALS AND METHODS

Subjects

Fourteen subjects (nine females) participated in the study. All subjects were right‐handed with reported normal or corrected‐to‐normal vision and had no known neurological or visual disorders. Their ages ranged from 20 to 29 years. They were naïve to the purpose of the study and had never participated in any perceptual learning experiment before. They gave written, informed consent in accordance with the procedures and protocols approved by the human subject review committee of the Center for Cognition and Brain Disorders, Hangzhou Normal University.

Stimuli and Apparatus

Subjects were viewing random dot kinematograms (RDKs) consisting of 400 dark dots (luminance: 3.76 cd/m²; diameter: 0.1°), with a gray background (luminance: 27.5 cd/m²). The dots moved at a velocity of 37°/s within a virtual circular area subtending 9° in diameter (Fig. 1A). In the psychophysical experiments, the stimuli were presented on a NESOJXC FS210A 21‐in monitor (refresh rate: 60 Hz; spatial resolution: 1,024 × 768). Subjects viewed the stimuli at a distance of 60 cm with their head stabilized by a chin and headrest. They were asked to maintain fixation throughout the tests.

Figure 1.

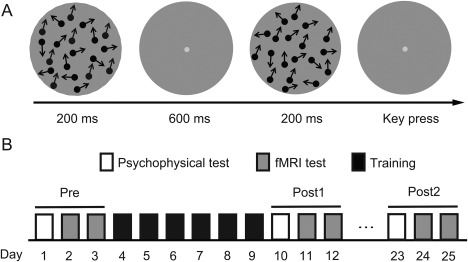
Stimuli and experimental protocol. (A) Schematic description of a two‐alternative forced‐choice (2‐AFC) trial in a QUEST staircase for measuring motion direction discrimination thresholds. (B) Experimental protocol. Subjects underwent eight daily training sessions. The pre‐training test (Pre) and the post‐training test 1 (Post1) and test 2 (Post2) took place on the days before, immediately after, and 2 weeks after training.

DESIGNS

Each subject practiced motion direction discrimination task during six daily sessions. On the day immediately before, after, and 2 weeks after training, they performed pre‐training test (Pre), post‐training test 1 (Post1), and post‐training test 2 (Post2) (Fig. 1B).

Two RDKs were presented successively per trial, with motion directions of θ and θ ± Δθ for 200 ms each and were separated by a 600 ms blank interval (Fig. 1A). The temporal order of these two RDKs was randomized. Subjects judged whether the direction of the second RDK was clockwise or counter‐clockwise relative to the first one via a right‐hand finger press on the response key. After each response, feedback was provided to the subject by brightening (correct response) or dimming (incorrect response) the fixation point. The next trial began 1 s after feedback. Δθ was estimated adaptively from trial to trial with the QUEST staircase, to quantify subjects' discrimination threshold at 75% correct [Watson and Pelli, 1983]. For each subject, the trained direction (θ) was chosen randomly from eight non‐cardinal directions (22.5°, 67.5°, 112.5°, …, and 337.5°), and was fixed for all the training sessions. A daily session (about 1 hour) consisted of 25 QUEST staircases of 40 trials. The discrimination thresholds from these staircases were averaged, and then plotted as a function of training day. The learning curves were fitted with a power function [Jeter et al., 2009].

During each test phase, subject' motion direction discrimination thresholds were measured at four motion directions, 0°, 30°, 60°, and 90° deviated from the trained direction (hereafter referred to as 0°, 30°, 60°, and 90°) in both psychophysical and fMRI tests. Discrimination thresholds from 10 Quest staircases for each direction were averaged as a measure of subjects' discrimination performance. Subjects' performance improvement at each motion direction was calculated as (pre‐training threshold – post‐training threshold)/pre‐training threshold × 100%. The learning effect specific to the trained direction was quantified as Imp (trained) – Imp (untrained), where the improvement for the untrained directions was the average improvement for the 30°, 60°, and 90° directions.

After psychophysical measurements, subjects' BOLD signals responding to the four motion directions in 16 fMRI runs were acquired in two daily sessions (eight runs per session). Similar to the task in psychophysical tests, subjects performed motion direction discrimination during scan. In a trial, two RDKs were each presented for 200 ms and were separated by a 600 ms blank interval, followed by a 1,400 ms blank interval between trials. For the directions of the two RDKs, one was fixed in a block and could be 0°, 30°, 60°, or 90°. The other deviated from the fixed one by ± Δθ, which was the discrimination threshold measured in the corresponding psychophysical test, to make subjects perform equally well at 75% correct across the stimulus conditions and tests. At Pre, we had a fifth condition, in which the RDKs of 0° and 0.5×Δθ were presented. Each stimulus block consisted of five trials. Each run contained 10 stimulus blocks of 12 s, two blocks for one of five stimulus conditions. Stimulus blocks were interleaved with 12 s fixation blocks. Prior to the experiment, subjects practiced 10 staircases for each direction to get familiar with the experimental procedure.

Defining Regions of Interest

Retinotopic mapping of visual areas was performed using standard phase‐encoded methods developed by Sereno et al. [1995] and Engel et al. [1997], in which subjects viewed a rotating wedge or an expanding ring that created traveling waves of neural activity in visual cortex. An independent run was performed to define the regions of interest (ROIs) in areas V1, V2, V3, V3A, V4, MT, MST, and IPS. The run contained eight moving dot blocks of 12 s, interleaved with stationary dot blocks of 12 s. The size and luminance of the RDK stimulus in the motion localizer was identical to that in the main experiment. In motion blocks, each dot moved in a random direction. The dots traveled back and forth, alternating directions once per second. ROIs were identified as cortical areas that responded more strongly to the moving dot blocks than to the stationary dot blocks. Identification of MT and MST were further constrained by the probability maps created by Abdollahi et al. [2014]. IPS was defined as a set of significantly responsive voxels in the medial dorsal intraparietal sulcus, which was referred to as the DIPSM [Orban, 2016].

MRI Data Acquisition

Subjects underwent seven MRI sessions ‐ one for retinotopic mapping, two for Pre, Post1, and Post2, respectively. MRI data were collected using a 3T MR750 General Electrical scanner with a 32‐channel head coil. In the scanner, the stimuli were back‐projected via a video projector (refresh rate: 60 Hz; spatial resolution: 1,024 × 768) onto a translucent screen placed inside the scanner bore. Subjects viewed the stimuli through a mirror located above their eyes. A high‐resolution 3D structural data set (3D MPRAGE; 1 × 1 × 1 mm³ resolution) was collected before functional runs. BOLD signals were measured with an EPI sequence (TE: 30 ms; TR: 2,000 ms; FOV: 192*192 mm²; matrix: 64 × 64; flip angle: 70°; slice thickness: 3 mm; gap: 0 mm; number of slices: 42; slice orientation: axial).

MRI Data Preprocessing

The anatomical volume for each subject at Pre was transformed into the anterior commissure‐posterior commissure (AC‐PC) space [Talairach and Tournoux, 1988]. Functional volumes were preprocessed using BrainVoyager QX, including 3D motion correction, linear trend removal, and high‐pass filtering (0.015 Hz) [Smith et al., 1999]. Head motion within any MRI session was less than 3 mm for any given subject. The functional volumes were then aligned to the anatomical volume and transformed into the AC‐PC space. The first 6 s of BOLD volumes were discarded to minimize transient magnetic saturation effects.

Univariate Analysis

For each ROI, the time course of the BOLD signal per run was first extracted by averaging the signals from all the voxels. Then, beta values for the five stimulus conditions were estimated with a GLM procedure. The BOLD amplitude for each condition was the averaged beta values across 16 runs. To quantify the amplitude difference for the trained direction while subtracting out the difference for the untrained directions, we defined the learning modulation index (LMI) [Op de Beeck et al., 2006] as [Amp (trained, post‐training) – Amp (trained, pre‐training)] – [Amp (untrained, post‐training) – Amp (untrained, pre‐training)]. The amplitude for the untrained condition was defined as the average amplitude for the 30°, 60°, and 90° directions. The LMI measures isolated those effects specific to the trained direction, thus distinguished the perceptual learning effect from general practice effects or common sources of confounds (e.g., day‐to‐day measurement variation). An index significantly above/below zero indicates that training increased/decreased the BOLD signal specific to the trained direction.

Multivariate Decoding Analysis

Decoding analysis was performed to classify the activation patterns evoked by pairs of motion directions. The analysis was based on all the voxels within each ROI. A GLM procedure was first used to estimate beta values for individually responsive voxels in each stimulus block, resulting in 32 patterns per test for each stimulus condition. These patterns were used for training linear support vector machine (SVM) classifiers (http://www.csie.ntu.edu.tw/~cjlin/libsvm) and calculating the average decoding accuracy following a 16‐fold cross‐validation procedure. For each permutation, we trained classifiers on 30 training patterns and tested their accuracy on the remaining two patterns. Similarly, we defined the LMI for decoding accuracy as [Acc(trained, post‐training) – Acc (trained, pre‐training)] – [Acc (untrained, post‐training) – Acc (untrained, pre‐training)], where Acc stands for decoding accuracy. The decoding accuracy for the trained condition was defined as the classification accuracy between 0° and 30°, while the decoding accuracy for untrained condition was defined as the classification accuracy between 60° and 90°.

Tuning functions were constructed based on the performance of all binary classifiers (e.g., 30° vs. 90°) using a 16‐fold cross‐validation procedure. Neural activity patterns induced by each motion direction were predicted by the classifier as one of the four directions, and the classification rate was plotted as a function of the angular difference between the classified direction and viewed direction [Zhang et al., 2010]. For example, the y value at x = 0 indicates the rate of correct classification, when the trained direction was classified as itself; the y value at x = −30 indicates the rate of misclassification, when 30° was classified as the trained direction; the y value at x = 30° indicates the rate of misclassification, when the trained direction was classified as 30°. We then fitted the averaged pattern‐based tuning function using a Gaussian function: $y=A\exp (-x^2/2\sigma ^2))+C$, where A is the scaling parameter, σ is the standard deviation, and C is the baseline.

Dynamic Causal Modeling

DCM, an approach for estimating effective strength of synaptic connections among neuronal populations and their context‐dependent modulation, was performed to examine whether there was any connectivity change between sensory areas and decision‐making areas after training. We estimated the effective connectivities between IPS and two visual areas MT and V3A using DCM in SPM10 [Friston, 2007]. For each area, time series from voxels within a 5‐mm‐radius sphere centered on the most responsive voxel in the localizer run were extracted for the DCM analysis in both hemispheres. The estimated DCM parameters were later averaged using the Bayesian model averaging method [Friston, 2007]. The mean MNI coordinates of these voxels and the SEs across subjects in MT, V3A, and IPS were (41.08 ± 1.1, −71.33 ± 1.7, 4.25 ± 1.2), (24.2 ± 4.1, −86.9 ± 1.2, 16.17 ± 2.0), and (23.6 ± 4.0, −61.2 ± 2.5, 47.5 ± 1.5) for the right hemisphere; (–43.26 ± 1.1, −69.54 ± 2.0, 6.03 ± 1.4), (–25.1 ± 4.6, −87.4 ± 1.0, 12.5 ± 2.2) and (–21.6 ± 4.1, −63.5 ± 2.9, 47.7 ± 1.9) for the left hemisphere.

DCM models neural population dynamics using a bilinear model and a hemodynamic model [Friston et al., 2003]. The model consists of three sets of parameters: extrinsic inputs into one or more regions, intrinsic connectivity among the modeled regions, and parameters encoding the modulation of the specified intrinsic connections by experimental manipulations. FMRI data were modeled with a GLM procedure, including regressors for the trained or the untrained motion direction as the modulatory input from MT/V3A to IPS, as well as a condition comprising all the directions as the extrinsic input to MT/V3A (Fig. 7A). Bidirectional intrinsic connections were hypothesized to exist between IPS and MT/V3A, and the strengths of these connections were modulated by either the trained or the untrained directions. For each subject, we examined the modulatory effects in recurrent, feedforward, and feedback models. Using a hierarchical Bayesian approach, we computed the exceedance probability for each model, that is, the probability to which a given model is more likely than the other two models to have generated data from a randomly selected subject. In the model with the highest exceedance probability, we examined changes in the modulatory effects for either the trained or the untrained directions at Post1 and Post2, relative to Pre.

Figure 7.

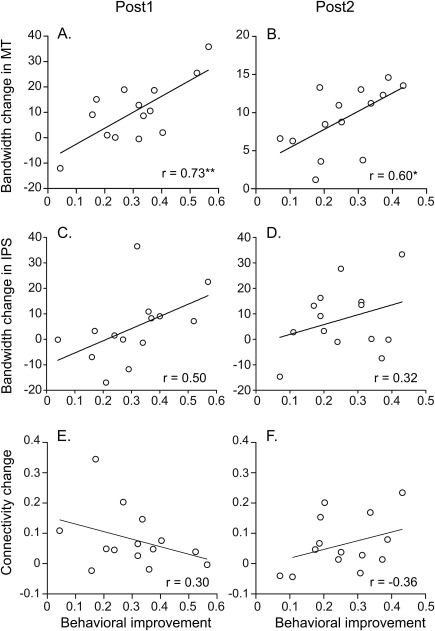
Correlations between the behavioral improvement and neural changes specific to the trained motion direction at Post1 (A, C, E) and Post2 (B, D, F). (A, B) Correlations between the behavioral improvement and the bandwidth change in MT. (C, D) Correlations between the behavioral improvement and the bandwidth change in IPS. (E, F) Correlations between the behavioral improvement and the connectivity change. The asterisk indicates the significance level of the correlation coefficient at Post1 (*P < 0.05, **P < 0.01).

RESULTS

Psychophysical Results

Subjects underwent six daily training sessions (1,000 trials per session) to perform motion direction discrimination around a non‐cardinal direction (Fig. 1A). Throughout the training, subjects' discrimination thresholds gradually decreased and saturated after day 4 (Fig. 2A).

Figure 2.

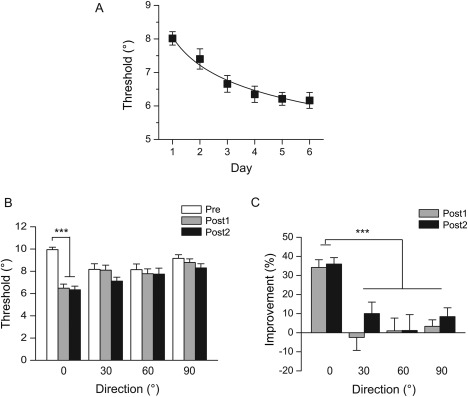
Psychophysical results. (A) Learning curve. Motion direction discrimination thresholds are plotted as a function of training day. (B) Motion direction discrimination thresholds for the trained direction (0°) and the untrained directions (30°, 60°, and 90°) at Pre, Post1, and Post2. Asterisks indicate significant difference between Pre and Post1, Post2 (***P < 0.001). (C) Percent improvement in motion direction discrimination performance for the trained and untrained directions at Post1 and Post2, relative to Pre. The asterisk indicates significant difference between the trained and the untrained directions (***P < 0.001). Error bars denote 1 SEM across subjects.

We compared their discrimination thresholds on the days before (Pre), immediately after (Post1), and 2 weeks after training (Post2) (Fig. 1B). Repeated‐measures ANOVA revealed a significant main effect of test (F(2, 26) = 18.97, P < 0.01) and a significant interaction between test and direction (F(6, 78) = 9.74, P < 0.01) (Fig. 2B). The percent improvements for the trained direction were 34% at Post1 and 36% at Post2, which were significantly higher than those for the untrained directions (<11%) (all t(13) > 4.20, P < 0.01) (Fig. 2C). These results demonstrate that training induced specific and persistent behavioral improvement for the trained motion direction.

Univariate Amplitude Analysis of fMRI Data

FMRI data analyses were focused in eight ROIs, including V1, V2, V3, V3A, V4, MT, MST, and IPS. With the univariate amplitude analysis, we examined whether training could lead to changes in the averaged BOLD amplitude for the trained direction, compared with the untrained directions. We found no significant main effect of test (all F(2, 26) < 1.73, P > 0.19), and no significant interaction between test and direction (all F(2, 26) < 1.08, P > 0.35) in any of the eight ROIs (Fig. 3A).

Figure 3.

Results of the univariate analysis of fMRI data. (A) BOLD amplitudes for the trained and untrained directions. (B) LMIs for BOLD amplitude. Error bars denote 1 SEM across subjects.

The LMI (see Materials and Methods) was defined to isolate the BOLD amplitude change specific to the trained direction. An index significantly above/below zero indicates that training increased/decreased the BOLD signal to the trained direction. Consistent with the ANOVA results above, no significant index was found in any ROI (Fig. 3B). Thus, no learning‐specific effect was observed on the average BOLD amplitudes evoked by the trained and untrained motion directions.

Multivariate Pattern Analysis of fMRI Data

We examined whether training led to specific improvement in the decoding accuracy of the trained condition. Decoding accuracies for 0° versus 30° (trained condition) and 60° versus 90° (untrained condition) were submitted to a repeated‐measures ANOVA. While there was no significant main effect of test in any ROI (all F(2, 26) < 0.79, P > 0.46), we found a significant interaction between test and direction in MT (F(2, 26) = 6.07, P < 0.01) and IPS (F(2, 26) = 4.70, P = 0.02), suggesting specific learning effect on the decoding accuracies for the trained compared to the untrained conditions (Fig. 4A). MT exhibited a significantly positive LMI at both Post1 (t(13) = 2.25, P = 0.04) and Post2 (t(13) = 3.81, P < 0.01) (Fig. 4B), demonstrating that the improved decoding accuracy in MT persisted over the long time course of the perceptual learning. Meanwhile, a higher‐level cortical area IPS, has a significantly positive index at Post2 (t(13) = 2.38, P = 0.03), indicating an improved decoding accuracy in the decision‐related area in the late stage of perpetual learning.

Figure 4.

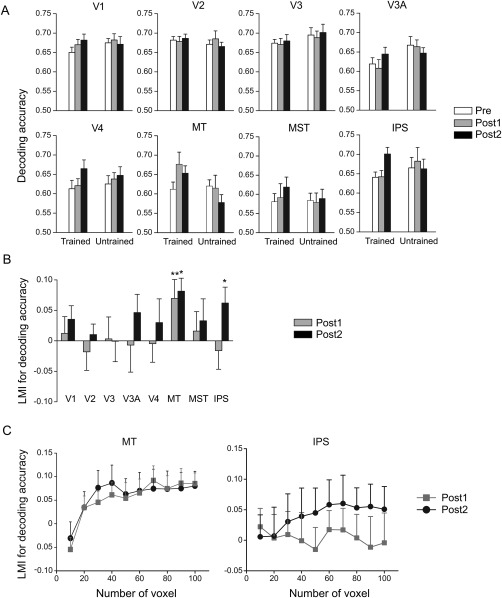
Results of the multivariate pattern analysis of fMRI data. (A) Decoding accuracies for the trained and untrained directions. (B) LMIs for decoding accuracy. Asterisks indicate the index significantly above zero (*P < 0.05, **P < 0.01). (C) LMIs for decoding accuracy as a function of voxel number in MT and IPS. Error bars denote 1 SEM across subjects.

To examine whether the finding depended on the number of selected voxels, the decoding performance was tested on the most responsive voxels with a range from 10 to 100, in MT and IPS (Fig. 4C). The LMI for decoding accuracy in MT was significantly above zero at Post1 and Post2, when at least 80 voxels were selected (all t(13) > 2.19, P < 0.05). The LMI for decoding accuracy in IPS was significantly above zero at Post2 when at least 90 voxels were selected (both t(13) > 2.16, P < 0.05). These results demonstrate that the finding in MT and IPS was robust when a majority of voxels were selected.

Note that to match subjects' discrimination performance, the motion stimuli at Pre, Post1, and Post2 were slightly different. We tested whether the observed fMRI effect was due to this slight change of the threshold Δθ. We found that, in all the ROIs, using a different Δθ acquired at Pre had little effect on the beta value (all t(13) < 1.59, P > 0.14) and decoding accuracy (all t(13) < 2.10, P > 0.05) for the trained condition. It suggests that the observed fMRI effects were not due to the stimulus difference.

To further characterize the learning‐related changes of neural activity patterns in the sensory stage, we plotted pattern‐based similarity functions to reflect the accurate classification for the trained direction as well as the misclassifications between the trained and untrained directions. In MT, the similarity tunings were sharpened after learning. Repeated‐measures ANOVA on the classification proportions under seven angular differences across test sessions revealed a significant interaction between test and direction (Pre vs. Post1: F(6, 78) = 3.53, P < 0.01; Pre vs. Post2: F(6, 78) = 5.16, P < 0.01) (Fig. 5A). We fitted the channel response profiles with a Gaussian function and used σ (the standard deviation) to quantify the tuning width between pre‐ and post‐tests. The bandwidth of the pattern‐based tuning function reduced significantly from Pre (σ = 16.87) to Post1 (σ = 12.21) and Post2 (σ = 12.62) (both t(13) > 4.77, P < 0.01). In IPS, the interaction between test and condition was not significant, both for Pre versus Post1 (F(6,78) = 0.20, P = 0.98), and for Pre versus Post2 (F(6,78) = 2.06, P = 0.07). These results further demonstrate that learning led to a long‐term differentiation in neural representation specific to the trained motion direction in MT.

Figure 5.

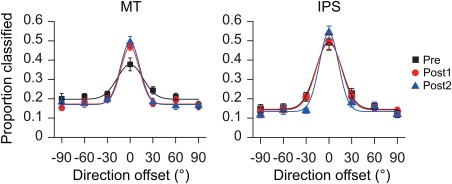
Pattern‐based tuning functions for motion direction in MT and IPS. Symbols indicate average data across subjects; solid lines indicate the best fit of a Gaussian to the averaged data. Error bars denote 1 SEM across subjects. [Color figure can be viewed at http://wileyonlinelibrary.com]

Effective Connectivity Analysis of fMRI Data

As the homologue of monkey LIP [Orban, 2016; Sereno et al., 2001], human IPS plays an important role in motion decision‐making [Heekeren et al., 2008; Kayser et al., 2010; Tosoni et al., 2008]. To test whether learning affected the decision routes above the sensory stage, we performed DCM analysis with hypothesized bidirectional intrinsic connections between MT/V3A and IPS. Given the extrinsic input to MT and V3A, we examined the modulatory effect by the trained and the untrained stimuli at different connections in feedforward, feedback, and recurrent models (Fig. 6A).

Figure 6.

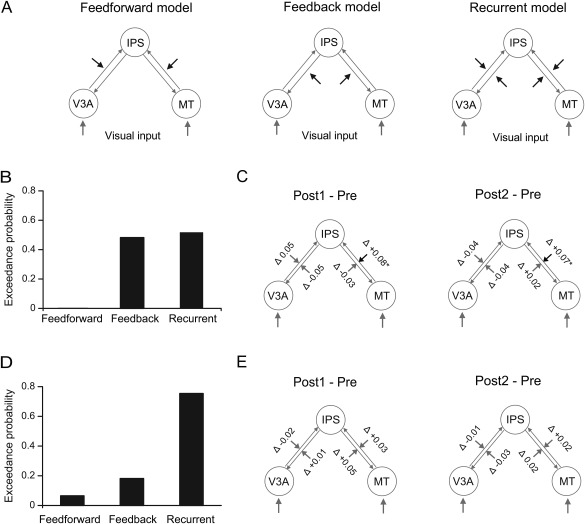
Dynamic causal modeling of connectivities between V3A and IPS and between MT and IPS. (A) Recurrent, feedforward, and feedback models for modeling the modulatory effect by the trained or the untrained directions. (B) Exceedance probabilities for the three models with the trained direction as the modulatory input. (C) Changes in the modulatory effect by the trained direction at Post1 and Post2, relative to Pre. (D) Exceedance probabilities for the three models with the untrained directions as the modulatory input. (E) Changes in the modulatory effect by the untrained directions at Post1 and Post2, relative to Pre.

For the trained condition, we computed the exceedance probability of each model [Friston et al., 2006]. The result showed that the feedforward, feedback, and recurrent models had exceedance probabilities of 0.02%, 48.2%, and 51.8%, respectively, suggesting that the recurrent model was the best one to explain the modulatory effect by the trained direction (Fig. 6B). We further compared the modulatory effects at Pre, Post1, and Post2. The modulatory effect on the forward connection from MT to IPS showed a significant increase at Post1 (t(13) = 3.01, P = 0.01) and a significant increase at Post2 (t(13) = 2.75, P = 0.02), compared to Pre. In contrast, little change was found in the feedback connection from IPS to MT or the connections between V3A and IPS (all t(13) < 1.54, P > 0.14) (Fig. 6C).

For the untrained condition, the exceedance probabilities of the feedforward, feedback, and recurrent models were 6.5%, 18.1%, and 75.4%, respectively, suggesting that the modulatory effect by the untrained directions could also be best explained by the recurrent model (Fig. 6D). However, little change was found in the modulatory effect of the connections between MT/V3A and IPS (all t(13) < 1.55, P > 0.14) (Fig. 6E).

Links Between the Behavioral Improvement and Neural Changes

To evaluate the role of the neural changes revealed in noisy motion perceptual learning, we calculated the correlation coefficients between the behavioral improvement and the neural changes (i.e., changes in the bandwidth of pattern‐based tuning in MT/IPS, and in connectivity strength from MT to IPS) specific to the trained direction across individual subjects. Significant correlations were found between the performance change and the bandwidth change in MT at both Post1 (r = 0.73, P < 0.01) and Post2 (r = 0.60, P = 0.02) (Fig. 7A,B). No significant correlations were found between the performance change and bandwidth change in IPS (Fig. 7C,D), or between the performance change and connectivity change (Fig. 7E,F). These results suggest the sharpening of the pattern‐based tuning functions in MT as the critical neural substrate underlying the behavioral learning effect.

DISCUSSION

We studied the neural mechanisms of perceptual learning, using motion direction discrimination training paradigm with noisy stimuli. Behaviorally, training led to a specific improvement in the trained direction and was well preserved after 2 weeks. We found that motion perceptual learning in noise (1) increased decoding accuracies in MT, (2) sharpened pattern‐based tuning functions in MT, which correlated with subjects' behavioral improvement, and (3) enhanced feedforward connectivity from MT to IPS. In addition, there was an emergence of increased neural decoding accuracy in IPS 2 weeks after training.

Our results lend strong support for the long‐term involvement of MT in motion perceptual learning in noise. Learning‐related changes had been observed in MT/MST in previous electrophysiological and imaging studies [Vaina et al., 1998; Zohary et al., 1994], with a focus on the effect induced within a single session of training. For example, training monkeys to discriminate the direction of motion in a noisy display resulted in enhancement of the neural sensitivity in MT and MST across the first 400 trials within the same training day [Zohary et al., 1994]. The within‐session learning effect in MT+ was also observed in a human fMRI study [Vaina et al., 1998]. However, such “fast” or “warm‐up” learning effects may be different from the typical effect of perceptual learning, which requires intensive training over thousands of trials across multiple days for the behavioral performance to reach an asymptote. The present study demonstrated MT as the neural substrate of the accumulated behavioral effect over six daily training sessions. In addition, the learning‐specific neural change in MT lasted over 2 weeks after training ended, and was correlated with individual behavioral improvement. These persistent changes in MT demonstrate a fundamental role of MT in motion perceptual learning with noise.

It should be noted that the learning‐related changes we observed in MT were not in the average BOLD amplitude, but in the spatial activation pattern evoked by the trained stimuli. Findings from previous studies suggest that changes in the overall neural activation to the trained stimulus may not be an effective indicator of perceptual learning. For example, it has been demonstrated that learning generates changes in the average BOLD amplitude immediately after training. However, after a few weeks, the changes either faded out [Yotsumoto et al., 2008], or failed to predict the persistent behavioral improvement [Bi et al., 2014]. So far, in perceptual learning studies with a near‐threshold discrimination task, the modulation direction in the overall BOLD amplitude are mixed [Jehee et al., 2012; Mukai et al., 2007; Op de Beeck et al., 2006; Schwartz et al., 2002]. Instead of changes in the overall BOLD amplitude, we found a learning‐specific increase in the decoding accuracy in MT, which suggests that training refined the neural representation of the trained stimuli to make it more distinguishable. The increase in decoding accuracy and the reduction of bandwidth in the pattern‐based tuning in MT may reflect the sharpening of direction‐tuned responses at the population level [Bejjanki et al., 2011; Schoups et al., 2001]. The enhanced population coding efficiency was also consistent with the reduction of interneuronal correlation induced by perceptual learning in macaque visual cortex [Gu et al., 2011]. Similar training‐induced changes in the spatial activation patterns in the sensory cortex have also been observed in discrimination training with orientation [Jehee et al., 2012], form [Zhang et al., 2010], or motion [Chen et al., 2015, 2016].

Our findings demonstrate that perceptual learning optimizes the sensory processing based on the functional specialization in the visual cortex. While motion discrimination training at 100% coherence led to improved neural sensitivity in V3A [Chen et al., 2015], motion discrimination training at 35% coherence improved neural sensitivity in MT (see Fig. 8 for a comparison). Neuropsychological evidence suggests that V3A and MT+ play different roles in local and global motion processing [Cai et al., 2014; Vaina et al., 2005, 2003]. The specialization of V3A in coherent motion processing might be due to its greater capacity to process local motion signals, which is underpinned by its relatively small receptive field sizes and narrow tuning curves for motion direction [Lee and Lee, 2012; Wandell and Winawer, 2015]. Conversely, when external noise serves as the fundamental limit, noise exclusion is suggested to be the major mechanism of perceptual learning [Dosher and Lu, 2005]. The specialization of MT in noisy motion processing can be based on its large receptive field size [Albright, 1984]. During the spatial pooling of local motion, neurons in MT operate to average out motion noise to extract the global motion direction. In line with this hypothesis, a recent electrophysiological study showed that motion learning in noise enhanced subjects' spatial integration ability, with a critical contribution of MT [Liu and Pack, 2017]. Compared to learning in a clear display, learning in noise often induces neural changes in a higher‐level cortical area, subserved by its larger receptive field size and broader tuning width. A similar effect has also been observed in orientation learning—while training without noise altered neural activities in V1 [Schoups et al., 2001], training in noise led to changes in V4 [Adab and Vogels, 2011].

Figure 8.

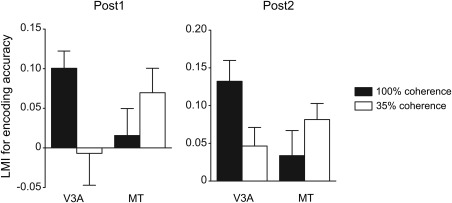
A comparison between the neural changes induced by motion perceptual learning with 100% and 35% coherence RDKs. Two‐way ANOVAs reveal a significant interaction between stimulus coherence and ROI for the LMIs for decoding accuracy at Post1 and Post 2 (both F(1,29) > 5.37, P < 0.03). Motion perceptual learning data at 100% coherence are from Chen et al., NeuroImage, 2015, 115, 17–29, reproduced by permission.

The current study used motion stimuli at a high speed, which may not be optimal for psychophysical performance or MT neurons [Lagae et al., 1993; Orban et al., 1985; Pilly and Seitz, 2009; Seitz et al., 2008]. However, it is still within the effective range of parameters to activate MT [Liu and Newsome, 2003; van Essen and Maunsell, 1983; Rodman and Albright, 1987]. One advantage of using non‐optimal stimuli is that the effect of learning could be more pronounced with non‐optimal stimuli—direction/orientation discrimination learning leads to greater improvement in non‐cardinal than in cardinal directions/orientations [Ball and Sekuler, 1987; Vogels and Orban, 1985]. In addition, motion learning occurred even without motion perception with sub‐threshold motion stimuli [Watanabe et al., 2001]. These results suggest that learning can be triggered by non‐optimal stimuli, at both behavioral and cortical levels.

As the sensory signal of learned motion direction became better represented in MT, the way in which sensory signals were relayed to and weighted by decision‐making areas was also changed. DCM analysis demonstrated an increase in the feedforward connectivity from MT to IPS. Previously, we found that motion direction discrimination training at 100% coherence enhanced feedforward connectivity from V3A to IPS [Chen et al., 2015]. Together with the electrophysiological findings showing the involvement of macaque LIP in motion discrimination training [Law and Gold, 2008], our results support the idea that the learning process could be modeled as a high‐level decision unit refining its pooling from the most relevant sensory neurons through response reweighting [Dosher et al., 2013; Law and Gold, 2009].

The long‐term neural substrate of perceptual learning is another important, yet less addressed issue. Perceptual learning is characterized by its persistency in the behavioral improvement. Once learned, the visual performance can be well maintained over months or years without additional training [Bi et al., 2010; Karni and Sagi, 1993]. In this study, parallel to the behavioral improvement, we found cortical changes immediately after training, in the neural representation in MT and the connectivity from MT to IPS. Two weeks after training, in addition to the existing changes, we discovered an emergence of enhanced decoding accuracy in IPS. This result suggests that the related cortical network may undergo adjustment over a long‐time course, even after training ended. These findings extend our understanding of the learning‐induced temporal dynamics within the sensory cortex [Chen and Fang, 2011; Molina‐Luna et al., 2008; Yotsumoto et al., 2008], indicating that the plasticity in sensory and high‐level stages might be triggered at successive time points during the development of perceptual learning.

In comparison with motion learning in a clear display [Chen et al., 2015], we found that motion perceptual learning in noise led to changes in a different cortical locus along the visual dorsal pathway. These results suggest that learning induces changes in the sensory area based on the functional specialization. Meanwhile, our findings revealed a common neural mechanism underlying motion perceptual learning. First, motion discrimination training with both clear and noisy stimuli induced a refined neural representation in the visual cortex. Second, training enhanced cortico‐cortical communication between the sensory area with a better representation for the trained visual feature and the high‐level decision unit. Third, the neural changes accurately captured the specificity and persistency observed in the behavioral learning effect. These findings indicate that low‐level and high‐level processes work in cohort to optimize the learned visual signal in a long‐time course.