Network component analysis reveals developmental trajectories of structural connectivity and specific alterations in autism spectrum disorder

Abstract

The structural organization of the brain can be characterized as a hierarchical ensemble of segregated modules linked by densely interconnected hub regions that facilitate distributed functional interactions. Disturbances to this network may be an important marker of abnormal development. Recently, several neurodevelopmental disorders, including autism spectrum disorder (ASD), have been framed as disorders of connectivity but the full nature and timing of these disturbances remain unclear. In this study, we use non‐negative matrix factorization, a data‐driven, multivariate approach, to model the structural network architecture of the brain as a set of superposed subnetworks, or network components. In an openly available dataset of 196 subjects scanned between 5 and 85 years we identify a set of robust and reliable subnetworks that develop in tandem with age and reflect both anatomically local and long‐range, network hub connections. In a second experiment, we compare network components in a cohort of 51 high‐functioning ASD adolescents to a group of age‐matched controls. We identify a specific subnetwork representing an increase in local connection strength in the cingulate cortex in ASD (t = 3.44, P < 0.001). This work highlights possible long‐term implications of alterations to the developmental trajectories of specific cortical subnetworks. Hum Brain Mapp 38:4169–4184, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Diffusion MRI allows the non‐invasive inference of white matter pathways in the human brain. At a millimetre‐scale, the structural connections between brain regions can be conceptualized as a complex network and interrogated with graph theoretical approaches [Bullmore and Sporns, 2009]. Graph theory provides a mathematical framework for the analysis of brain networks, with brain regions defined as a set of nodes, connected by a set of edges. From this perspective, a number of metrics exist to define both global and local properties of the brain network: from simple measures of connectivity (or degree), to more complex measures of regional integration, segregation, and influence.

This has led to the broad characterization of the macroscale organization of the mammalian brain as a near‐decomposable system built on multiple, parallel and partially segregated modules [Meunier et al., 2010; Simon, 1962]. Brain networks are organized hierarchically [Bassett et al., 2011] and linked by a set of overarching, densely interconnected hub regions that facilitate distributed interactions across the network [Bullmore and Sporns, 2012; Sporns et al., 2005; van den Heuvel and Sporns, 2011].

This view is supported by evidence that cerebral regions can be clustered together based on the extent of their shared connections into communities [Bullmore and Sporns, 2012; Hilgetag et al., 2000]. Anatomical connectivity between regions reflects a shared functional specialization [Hilgetag et al., 2000; Honey et al., 2009], and connected regions tend to have similar metabolic demands, and gene expression profiles [Collin et al., 2013; French and Pavlidis, 2011; Fulcher and Fornito, 2016; Vaishnavi et al., 2010]. Furthermore, anatomically connected regions tend to mature in tandem across development [Raznahan et al., 2011], resulting in common patterns of cortical growth and functional coordination over the lifespan [Alexander‐Bloch et al., 2013; Hagmann et al., 2010; Zielinski et al., 2010]. Taken together, this evidence suggests that connections within complex brain networks can be decomposed, or clustered, into subnetworks that link modules with distinct roles and developmental trajectories.

Long‐distance cortico‐cortical connections are established during gestation, and complex network architecture is evident at birth [Ball et al., 2014]. The effects of cerebral maturation on increasingly distributed connectivity is marked in the first years of life [Yap et al., 2011], after which the large‐scale topological organization of the structural connectome remains relatively stable [Baker et al., 2015; Dennis et al., 2013]. Over the full lifespan, measures of network efficiency and modularity follow a distinct inverted U trajectory, peaking in the third decade and mirrored by microstructural markers of the underlying white matter [Imperati et al., 2011; Kochunov et al., 2012; Zhao et al., 2015]. In elderly individuals, although network topology remains relatively consistent with younger adults, simulations suggest a preference for local communication compared to long‐range hub‐to‐hub connectivity, correspondent to evidence from functional analyses [Cao et al., 2014; Perry et al., 2015].

The early establishment of structural connectivity and long‐term stability of structural networks suggests that disturbances to network organization may be an important marker of abnormal cerebral development. A number of neurodevelopmental disorders, including autism spectrum disorder (ASD) and attention deficit hyperactivity disorder, have been linked to alterations in the development of structural and functional brain connectivity [Ecker et al., 2015; Konrad and Eickhoff, 2010; Tomasi and Volkow, 2012]. ASD is a complex, multifactorial disorder characterized by social, behavioral, and language impairments evident from an early age. Although the aetiology of ASD remains unknown, neuropathological studies have identified cortical alterations including laminar and columnar disorganization and increased neuronal density in frontal, temporal and cingulate cortices [Bailey et al., 1998; Casanova et al., 2002; Stoner et al., 2014; Uppal et al., 2014]. Early evidence from MRI studies suggested that head growth is accelerated in ASD during infancy but differences appear to dissipate with age [Courchesne et al., 2001; Ecker et al., 2015]. More recently, ASD has been framed as a disorder of connectivity [Belmonte et al., 2004; Vissers et al., 2012], based on accumulating evidence of disruptions to both functional and structural networks in autistic populations [Di Martino et al., 2014; Mueller et al., 2013; Rudie et al., 2012; Supekar et al., 2013]. Although the nature and extent of these alterations remain unclear with a number of conflicting observations, previous studies have described complex patterns of disrupted white matter organization in ASD that appear to be dependent on age and mirrored by evidence of both hypo‐ and hyper‐connectivity between functional networks and differences in electrophysiological recordings [for review, see Vissers et al., 2012].

In this study, we apply an unsupervised and data‐driven approach to model complex networks derived from whole‐brain tractography as a set of components, or subnetworks, that vary together across the population. We first demonstrate that network components can be robustly and reliably identified in a large cohort. We then model component strength across the human lifespan, defining specific developmental trajectories for subnetwork connectivity. Finally, we explore how disruptions to typical development may impact structural connectivity by testing the hypothesis that ASD is associated with alterations in subnetwork component strength. By identifying a set of network components in a group of adolescents with high‐functioning ASD and age‐matched, typically‐developing controls, we find a specific cortical subnetwork with significantly increased connection strength in the autistic population.

METHODS

Data

Preprocessed connectivity data were downloaded from the USC Multimodal Connectivity database (http://umcd.humanconnectomeproject.org) [Brown et al., 2012]. Full MRI acquisition and image processing details are given elsewhere [Brown et al., 2012; Rudie et al., 2012] but are reported in brief below.

NKI‐Rockland lifespan sample

In total, connectivity matrices from 196 healthy participants (114 male; age range: 4–85 years) were available, collected as part of the NKI/Rockland lifespan study [Nooner et al., 2012]. Diffusion MRI was acquired at 3 T with 64 gradient directions and the following parameters: TR, 10,000 ms; TE, 91 ms; voxel size, 2 mm³; b‐value, 1,000 s/mm². After correction for motion and eddy current distortions using linear registration, diffusion tensors were modeled and tractography performed using fiber assignment by continuous tracking with an angular threshold of 45° [Mori et al., 1999].

To construct each connectivity matrix, 188 regions‐of‐interest (ROI) were defined using a group‐based functional MRI (fMRI) parcelation [Craddock et al., 2012], and structural connectivity was calculated as the total number of streamlines connecting any two ROI [Brown et al., 2012]. Prior to analysis, ROI in the brainstem were removed and fiber counts were log‐transformed resulting in a 182 × 182 connectivity matrix for each participant.

UCLA autism sample

Connectivity data from a total of 43 typically developing children and adolescents (36 male; age range: 8.9–17.9 years) and 51 with high‐functioning ASD (45 male; age range: 8.4–18.2 years) were available for analysis [Rudie et al., 2012]. DTI data of 3 T were acquired with: 32 gradient directions; TR, 9,500 ms; TE, 87 ms; voxel size, 2 mm³; b‐value, 1,000 s/mm². Motion and eddy current correction, diffusion tensor modeling, and tractography were performed as above but with an angular threshold of 50°.

ROI were defined as 10 mm radius spheres placed at 264 coordinates in MNI space and transformed to individual diffusion data [Power et al., 2011] and connectivity was defined as streamline count between connected ROI. As above, fiber counts were log‐transformed before analysis, resulting in a 264 × 264 connectivity matrix for each participant.

Non‐Negative Matrix Factorization

Non‐negative matrix factorization (NMF) is an unsupervised, multivariate decomposition technique that models an $n \times m$ data matrix, $V$, as the product of two non‐negative matrices: $W$ and $H$:

$$V\approx WH$$

$$subject to W\ge 0, H\ge 0$$

where $n$ is the number of features and $m$ is the number of samples and $W$ and $H$ have the dimensions $n \times r$ and $r \times m$, respectively, where $r$ is the number of network components or basis images (Fig. 1). The optimal solution is sought by iteratively updating $W$ and $H$ to minimize the (Euclidean) distance between the original and reconstructed matrices, subject to non‐negativity constraints:

$$\underset{W\ge 0,\hspace{0.17em}H\ge 0}{\min }F\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\sum _{ij}{\left[V_{ij}-{\left(WH\right)}_{ij}\right]}^2$$

Figure 1.

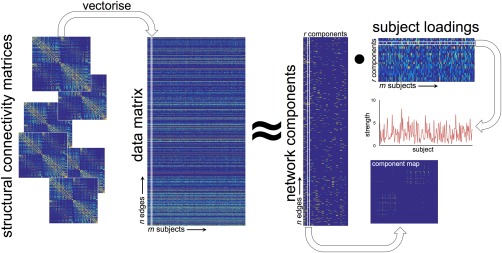
Projective NMF pipeline. Individual connectivity matrices are concatenated into a large data matrix. Projective NMF is used to decompose the data into a set of network components. A map of connections shows the topological organization of each component, or subnetwork, and a subject‐specific weighting estimates the component's contribution each individual's full network. [Color figure can be viewed at http://wileyonlinelibrary.com]

Generally, $r<\min \left(m, n\right)$, thus $WH$ represents a low‐rank approximation of the original data in $V$ [Lee and Seung, 1999]. NMF offers a natural setting for exploration of data that is inherently non‐negative and, as such, is particularly well‐suited to neuroimage analysis allowing an intuitive understanding of image‐derived, non‐negative features including, for example: tissue volume, image intensity, cortical thickness, fractional anisotropy, and structural connectivity [Sotiras et al., 2015].

In a recently introduced variant, projective NMF (PNMF), the subject loading matrix, $H$ is replaced with $W^{T}V$ such that:

$$V\approx W{W}^{T}V$$

PNMF confers a number of benefits over standard NMF including fewer learned parameters, and increased sparsity and orthogonality of the resulting component matrix $W$ [Yang and Oja, 2010].

In terms of a network analysis, PNMF results in a set of highly orthogonal network components, each comprising a sparse set of (topologically) localized connections (i.e., the edge structure of different components does not overlap) and a corresponding subject‐specific weighting (Fig. 1). Together, these elements can then be combined to approximately reconstruct the full connectivity network of any given subject.

In addition, Yang et al. introduced a method to estimate the rank of the factorizing matrix, $W$, using automatic relevance determination (ARD‐PNMF) [Yang et al., 2010]. Here, we use ARD‐PNMF to perform an exploratory analysis of network structure and extract a set of effective network components for further analysis.

Network Decomposition

The analysis pipeline is shown in Figure 1. For each study, the lower triangles of each symmetric structural connectivity network were vectorized and collated into an $n \times m$ matrix before normalizing to $\left[\mathrm{0,1}\right]$. To reduce computation time and remove noisy connections, edges that were present in less than 10% of the study population were removed. ARD‐PNMF was initialized with non‐negative double singular value decomposition (NNDSVD), a procedure that speeds up NMF convergence compared to a random initialization and ensures consistent results across runs [Boutsidis and Gallopoulos, 2008]. We chose an initial rank estimate of 50 and performed a maximum of 20,000 PNMF iterations, or until the algorithm converged.

Network decomposition was performed in Matlab R2015b using PNMF code available at: http://sites.google.com/site/zhirongyangcs/pnmf and NNDSVD code available at: http://www.boutsidis.org/software.html).

Simulations

To demonstrate the application of PNMF to structural connectivity data, we performed a set of simulation experiments. We created a set of 150 “networks,” each comprising a weighted combination of six network components (Fig. 2). Each network component was constructed by adding binary edges between 10 and 20 randomly selected nodes in a 100 $\times$ 100 empty network. The weighted contribution of each component to an individual network was varied according to a set of predefined patterns that varied across the population.

Figure 2.

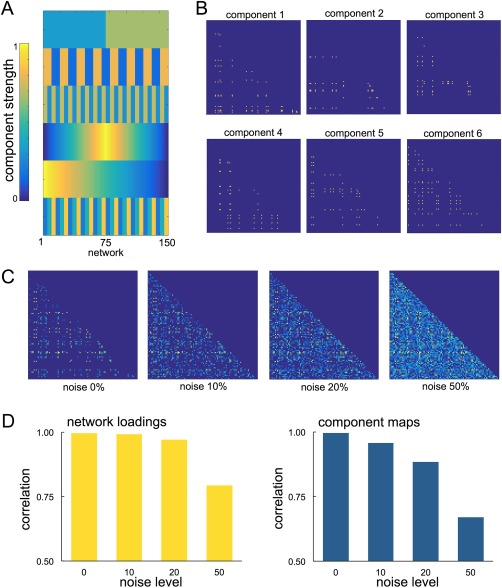
Simulating networks for PNMF decomposition. Component weights (A) and spatial maps (B) for simulating connectivity networks. Each component was weighted according to the corresponding component strength and summed to form a network. Noise was added at four levels to the final network (C). The mean correlation between recovered component loadings and the original network weights is shown in D, alongside the spatial correlation between recovered maps and the original component maps at each noise level. [Color figure can be viewed at http://wileyonlinelibrary.com]

For a given network, each of the six components were multiplied by the corresponding component weight and linearly summed to create the final network. Additionally, noise was added to each network by constructing a symmetric noise matrix with edge density set at 0, 10, 20, or 50%, and edge strength drawn from a normal distribution with mean and variance defined by existing network edge strengths.

The simulated networks (with or without additional noise) were concatenated into data matrix $V$, removing any edges that were empty across all networks. ARD‐PNMF was then initialized using NNSVD with rank 6 and 2,500 iterations.

We found that PNMF was able to recover both the spatial maps and pattern of population variation (network loadings) of all components even under noisy conditions, achieving an average correlation between the original and recovered component maps of 0.996, 0.957, 0.884, and 0.669 (for 0, 10, 20, and 50% noise, respectively) and a correlation between original and recovered component loadings of 0.997, 0.992, 0.971, and 0.794 (Fig. 2).

Split‐Half Reliability

To investigate if the network components can be robustly and reliability identified across population subsamples, we performed a split‐half reliability assessment [Groppe et al., 2009; Groves et al., 2012]. The NKI‐Rockland dataset was split into two, randomly selected and equal size samples and PNMF performed independently on each. The resulting split‐half components were then greedily paired with components obtained from the full dataset. Components were matched based on the correlation between the component loadings of overlapping subject populations in the half and full datasets to produce a triplet, with each original component paired with a single component from each half sample. Reliability of the original components was evaluated by measuring the edgewise (cosine) similarity between correspondent split‐half component maps. Component reliability was compared to a null distribution built by randomly permuting edges in corresponding split‐half pairs before calculating spatial similarity, 1,000 permutations were performed for each pair.

Rich Club Analysis

To further investigate the topological organization of extracted network components, we performed a rich club analysis [van den Heuvel and Sporns, 2011]. Using the group mean structural network, nodes were sorted by degree and low degree nodes incrementally removed in steps. At each step, the density of the remaining network connections was compared to a set of 100 randomized networks of the same size to give a normalized rich club coefficient, $\varphi$. The rich club was defined as nodes with degree >  $k$, where ${\varphi }_k=\mathrm{m}\mathrm{a}\mathrm{x}\left(\varphi \right)$. Following Collin et al., after identifying network nodes comprising the rich club, edges in each network component were defined as either “rich” if they connected two rich club nodes to each other, “local” if they connected two non‐rich club nodes, of “feeder” connections if they connected rich club nodes to non‐rich club nodes [Collin et al., 2013]. The overall “richness” or “locality” of each component was determined by comparing the number of rich or local edges to a set of 1,000 equivalent random networks. Network analysis was performed with the Brain Connectivity Toolbox [Rubinov and Sporns, 2010].

Statistical Analysis

For extracted components in the NKI‐Rockland sample, component strength over the lifespan was modeled using polynomial regression (up to power 3) with age as a covariate and sex as an additional factor. The Akaike Information Criterion (AIC) was used to select the best model for each component (i.e., linear, quadratic, or cubic; with or without sex). Statistical analysis was performed with the $\mathrm{l}\mathrm{m}$ package in R 3.31.

In the UCLA autism cohort, component strength was compared between groups using an independent samples t‐test. Analysis was performed in JASP 0.7.5.6.

Data Visualization

The edge structure of network components were visualized with Circos [Krzywinski et al., 2009], graph nodes were ordered according to cerebral lobe and the x, y, z coordinates of the central voxel of each cerebral ROI supplied with the connectivity matrices.

In addition, to visualize the anatomical location of connected ROI in each network component, we calculated node degree (i.e., the total number of connections of each ROI) and projected the values onto standard space masks of the cortical gray matter, subcortical structures, and cerebellum. Mask voxels were assigned an ROI membership based on Euclidean distance to the nearest ROI center and assigned the corresponding nodal degree value. Node degree images were then smoothed with a Gaussian kernel of FWHM 5mm and projected onto a 3D representation of the smoothed cortical surface using Surf Ice (http://www.nitrc.org/projects/surfice).

RESULTS

Network Components across the Lifespan

Reliability assessment

In total, 22 network components were identified in the NKI‐Rockland dataset (Supporting Information Figure S1). Reliability scores were calculated for each component using a split‐half framework [Groppe et al., 2009]. Network components identified in two independent group samples were matched to the original set of components and the spatial similarity between the respective edge structures compared as a marker of reliability. Both groups were matched in age and sex (group one: mean age = 35.4 years; 55/98 male; group two: 34.5 years; 59/98 male). In total, 19 components were identified in group one and 21 in group two. Of the 19 original components matched with corresponding pairs in the split‐half sample, 15 demonstrated a significantly higher spatial correlation than would be expected between two random matrices with the same number of edges (all P < 0.001, 1,000 permutations; Supporting Information, Figure S2; Table S1). The mean spatial similarity between matched components was 0.49 (range: 0.14–0.96).

Developmental trajectories

The subject loading of each network component (i.e., the contribution of a given component to the individual's full network) was modeled as a function of age using polynomial regression. Of 22 components, 16 demonstrated significant age‐related variation (all P < 0.01; Table 1). Of these, nine components followed nonlinear trajectories over the lifespan best described by quadratic models; six increased linearly with age, and one decreased. The addition of sex as a factor improved the model fit in 4 of the 16 significant components. Table 1 shows the best model selected for each component and Figure 3 highlights some of these trends; networks and modeled trajectories for all components are shown in Supporting Information Figure S1 in order of reliability.

Table 1.

Modeling development trajectories of network components

					Regression coefficients
Component	Best model	AIC	Adjusted R 2	P	–log10(p)	β 1	β 2	β 3
Aa	age + age2 + sex	544.28	0.09	<0.01	3.89	2.13	−3.13	−0.15
Ba	age + age2 + sex	539.04	0.11	<0.01	4.96	−2.28	−2.63	0.29
Ca	age + age2	552.15	0.05	<0.01	2.37	2.71	−1.83	—
Da	age + age2	534.21	0.13	<0.01	6.21	−4.81	−1.93	—
Ea	age + age2	533.10	0.13	<0.01	6.45	4.18	−3.21	—
Fa	age + age2	544.10	0.08	<0.01	4.09	0.47	−4.23	—
Ga	age	520.00	0.19	<0.01	9.75	6.08	—	—
Ha	age	508.38	0.23	<0.01	12.29	6.79	—	—
Ia	age + age2	534.87	0.13	<0.01	6.07	4.61	−2.24	—
Ja	age + age2 + sex	526.97	0.16	<0.01	7.46	5.01	−1.90	−0.17
K	sex	558.34	0.01	0.09	1.04	—	—	−0.12
La	age	545.73	0.07	<0.01	4.04	3.85	—	—
M	age + sex	556.79	0.02	0.04	1.37	1.41	—	−0.15
Na	age	545.37	0.07	<0.01	4.12	−3.89	—	—
Oa	age + sex	515.58	0.21	<0.01	10.19	6.10	—	−0.17
Pa	age	551.21	0.04	<0.01	2.78	3.12	—	—
Qa	age	538.22	0.11	<0.01	5.73	4.65	—	—
R	age + age2	557.08	0.02	0.05	1.31	1.97	−1.46	—
Sa	age + age2	543.80	0.09	<0.01	4.16	4.00	−1.56	—
T	age	555.30	0.02	0.02	1.81	−2.41	—	—
U	intercept only	559.23	0.00	—	—	—	—	—
V	sex	557.16	0.02	0.05	1.34	—	—	−0.14

^aModel significant at P < 0.01.

Figure 3.

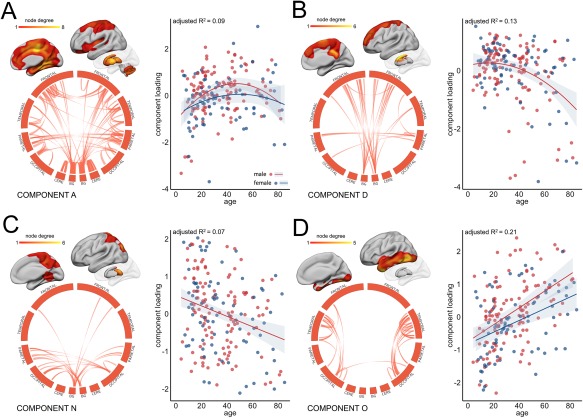
Age‐related variation in component strength. Four network components are highlighted as examples of age‐related variation in subnetwork connectivity (see Supporting Information Figure S1 for all components). For visualization, components maps were thresholded at the 95th percentile and connections are shown in circular format. To show the anatomical location of connected regions, node degree was calculated for each cerebral ROI as the sum of its connections in the thresholded component and projected onto cortical/subcortical surfaces. The relationship between (normalized) component strength and age was modeled using polynomial regression. The best model fit is shown for each component. Separate model fits indicate when sex was included as an additional factor. Red indicates male; blue, female. Cere = cerebellum, BG = basal ganglia and thalamus. [Color figure can be viewed at http://wileyonlinelibrary.com]

In Figure 3, component A comprises a robust (split‐half similarity: 0.96) and relatively dense pattern of connectivity including both local, within‐lobe, and longer, between‐lobe, connections. Inter‐hemispheric connections are apparent between frontal and parietal lobes. Highly connected cerebral regions in this component include the cingulate and paracingulate, insular, medial temporal, and superior parietal cortices, with dense connectivity also evident within the subcortical structures, and between these structures and higher cerebral cortex. Over the lifespan, connectivity between these regions increases rapidly over childhood and adolescence, peaking between 40 and 50 and declining into older age. Component loading is slightly higher in males than in females across the lifespan although follows a steeper decline with old age. Similar trends in connectivity are seen in components E, F and J (Supporting Information Figure S1). Components D and N (Fig. 3B,C) capture bilateral patterns of connectivity between subcortical gray matter structures and frontal and parietal cortices, respectively. Edges in component D predominantly connect the caudate nucleus and superior, medial frontal regions. The strength of this component remains relatively stable until middle age before declining. The strength of component N (Fig. 3C) monotonically decreases with age with edges connecting the thalamus to post‐central cortex and superior parietal regions. In contrast, component O follows a linearly increasing trend with age (Fig. 3D) Connections in this component are primarily local, connecting anatomically adjacent cortical regions within the temporal lobe and temporo‐occipital junction in both hemispheres. A similar pattern can be seen in component L (Supporting Information Figure S1).

Component topology

Qualitative assessment of the patterns of connectivity within components reveals a generally bilateral and symmetric organization across hemispheres. Unilateral components appear to reflect the topology of corresponding components in the opposite hemisphere (e.g., I and S; O and L).

To quantify whether inter‐regional connections within individual network components revealed a preferential support for connectivity between network hubs over topologically local nodes, we performed a rich club analysis. Sixty‐five nodes with degree greater than 100 were defined as the rich club (maximum $\varphi$ = 1.09) and included nodes bilaterally in: frontal pole; cingulate and paracingulate cortex; insula; hippocampus; precuneus and superior parietal lobule; lateral occipital cortex, and subcortical structures (caudate, pallidum, and thalamus).

Component edges were defined as rich, feeder or local connections, and the “richness” or “locality” of each component defined as the number of rich or local connections compared to a set of 1,000 random networks (Table 2). Four components were found to contain significantly more rich‐club connections than expected by chance (A, E, F, and I; all P = 0.001). These components are shown in Figure 4; richness and locality indices for all components are shown in Table 2. All rich components show a similar inverted “U” trajectory with age (Table 1, Supporting Information Figure S1). Edge strength distributions in Figure 4 show that component richness is associated with both an increased number and strength of rich compared to local edges. In contrast, four components were to found to have significantly more local connections than expected by chance (Fig. 5; M, O, L, and J; P = 0.001). These components all had increased number and strength of local compared to rich connections and increased in strength across the lifespan (Table 1, Supporting Information Figure S1).

Table 2.

Rich club analysis of network components

Component	Number of edges	Rich edges	Richness a	P	Local edges	Localitya	P
A	2549	780	1.34	0.001a	658	1.00	0.418
B	788	115	0.64	1.000	223	1.10	0.035
C	530	61	0.50	1.000	152	1.12	0.059
D	605	155	1.12	0.049	134	0.87	0.987
E	1119	434	1.69	0.001a	158	0.55	1.000
F	835	238	1.25	0.001a	169	0.79	1.000
G	1583	396	1.09	0.015	333	0.82	1.000
H	757	160	0.92	0.882	211	1.08	0.071
I	520	155	1.30	0.001a	119	0.89	0.917
J	623	73	0.51	1.000	193	1.21	0.001a
K	1400	293	0.91	0.967	309	0.86	1.000
L	628	86	0.60	1.000	210	1.30	0.001a
M	576	44	0.33	1.000	254	1.71	0.001a
N	535	119	0.97	0.612	103	0.75	1.000
O	761	93	0.53	1.000	316	1.62	0.001a
P	710	161	0.99	0.540	184	1.01	0.446
Q	498	111	0.98	0.599	153	1.19	0.007
R	342	70	0.89	0.830	94	1.07	0.236
S	572	132	1.01	0.425	120	0.82	0.999
T	599	157	1.15	0.019	132	0.86	0.987
U	481	41	0.37	1.000	120	0.97	0.648
V	345	55	0.70	0.999	100	1.13	0.073

^aNumber of edges compared to 1,000 random networks of the same size.

^aSignificant at P = 0.001.

Figure 4.

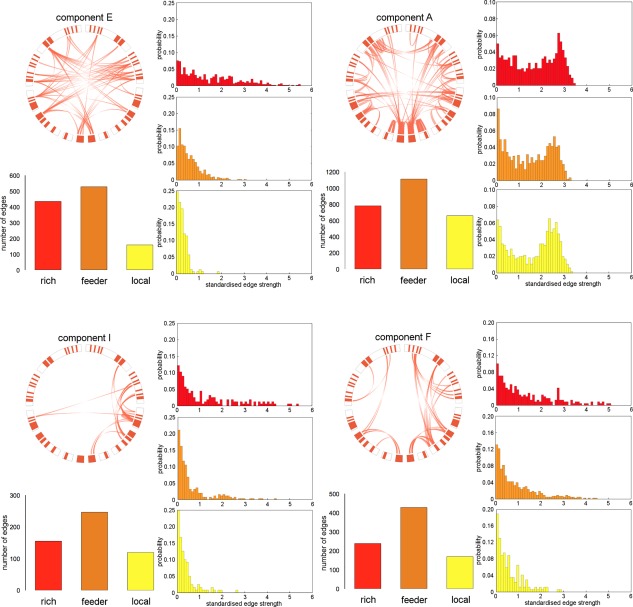
Rich network components. Network components with significantly more rich‐club edges than in a set of 1,000 equivalent random networks are shown. Thresholded connectivity maps are displayed in circular diagrams as in Figure 3, with rich club nodes highlighted in red. The number and probability distribution of rich, feeder, and local edges are displayed for each component. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 5.

Local network components. Network components with significantly more local edges than in a set of 1,000 equivalent random networks are shown. Connectivity maps and edge distributions are shown as in Figure 4. [Color figure can be viewed at http://wileyonlinelibrary.com]

Network Components in Autism Spectrum Disorder

In our second experiment, we applied PNMF to a dataset comprising high‐functioning individuals with ASD and a set of age‐ and sex‐matched controls. In total, 24 components were identified (Table 3). One component was found to have a significantly higher loading in the ASD group compared to typically developing individuals (t _(1,92)=3.161; P = 0.002; P < 0.05 after Bonferroni correction for multiple comparisons). Additionally controlling for age did not alter this relationship (ANCOVA: F _(1,91) = 11.05, P < 0.001). To control for possible gender effects, we repeated the statistical analysis after excluding female participants (n = 7 TD; n = 6 ASD). The difference in component strength remained significant (t _(1,79)=3.44; P < 0.001).

Table 3.

Between‐group comparison of component loadings

Component	t (1,92)	P	Cohen's d
1	1.769	0.080	0.366
2	1.576	0.119	0.326
3	0.809	0.421	0.168
4	0.308	0.759	0.064
5	1.388	0.168	0.287
6	−0.735	0.464	−0.152
7	−0.342	0.733	−0.071
8	−1.180	0.241	−0.244
9	0.698	0.487	0.145
10	3.161	0.002a	0.654
11	0.730	0.467	0.151
12	1.421	0.159	0.294
13	−0.095	0.925	−0.020
14	−0.019	0.985	−0.004
15	1.670	0.098	0.346
16	−0.376	0.708	−0.078
17	0.146	0.884	0.030
18	0.328	0.744	0.068
19	0.283	0.778	0.059
20	0.162	0.872	0.033
21	1.459	0.148	0.302
22	1.162	0.248	0.241
23	0.410	0.683	0.085
24	−0.528	0.599	−0.109

^aSignificant at P < 0.05 after Bonferroni correction for multiple comparisons.

This component is shown in detail in Figure 6 and comprised a bilateral and symmetric pattern of connectivity with edges predominantly linking nodes in the anterior and posterior cingulate cortex, paracingulate cortex, supplemental motor areas, and parietal cortex. Both intra‐ and inter‐hemispheric connections are visible with additional connections between the putamen and parietal cortex in both hemispheres. The mean (±S.D.) component loadings were 2.9 ± 0.69 in the ASD group and 2.5 ± 0.57 in the typically‐developing group (Fig. 6B). Rich club analysis revealed that this component had significantly more local connections than expected by chance (locality: 1.32, P = 0.001).

Figure 6.

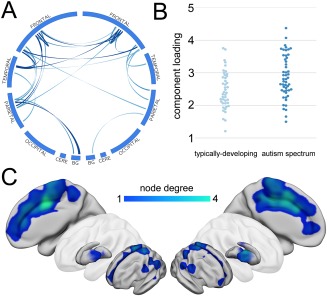
Structural connectivity is significantly increased in ASD. A single subnetwork was found to be significantly stronger in the ASD cohort. The component map is shown in A (thresholded at 95th percentile), and component loadings for both groups compared in B. The anatomical locations of connected regions are visualized as in Figure 3 and shown in C. [Color figure can be viewed at http://wileyonlinelibrary.com]

As noted above, a threshold was applied to the network data before performing PNMF, limiting the analysis to edges shared by at least 10% of participants. We additionally performed PNMF after applying two alternate thresholds: 5% and 20%. At both thresholds, a similar pattern was observed and found to be significantly different between groups (at 5%: t = 2.732, P = 0.008; excluding females: t = 3.16, P = 0.002; at 20%: t = 2.40, P = 0.018; excluding females: t = 2.77, P = 0.007). The spatial patterns associated with this component at each threshold match closely to that described above.

DISCUSSION

In this study, we modeled structural connectivity networks as the combination of separable subnetworks, or network components, using a data‐driven and multivariate approach. We first showed that complex networks could be reliably decomposed into network components using simulated data. We then applied this method to two independent cohorts, demonstrating that network components follow specific developmental trajectories with age and can capture disruptions to neurodevelopment in autism spectrum disorder.

NMF provides a natural setting for the analysis of neuroimaging data due to the inherent non‐negativity common to many imaging‐derived metrics (e.g., tissue volume, fiber count) [Sotiras et al., 2015]. In image analysis, NMF leads to a parts‐based representation of the data, extracting sparse image components with localized spatial support [Lee and Seung, 1999]. In this way, NMF confers a relatively simple interpretation of the data, namely that the complex whole can be approximated by the summation of the localized parts. We show that decomposing structural connectivity networks with NMF results in a soft clustering of connections that co‐vary together across the population forming relatively sparse subnetworks. We also find that these components are biologically relevant, capturing known subsystems (e.g., subcortical‐cortical projections; components C, D, N, and P), local patterns of connectivity between anatomically or functionally homologous regions (e.g., components L, O, and T), and varying with age across the lifespan.

MR studies have found that both white and gray matter tissue volumes follow an inverted U trajectory over the human lifespan, rising rapidly in development, peaking in the second or third decade and declining into older age [Giedd et al., 1999; Westlye et al., 2010; Ziegler et al., 2012]. Markers of microstructural maturation in cerebral white matter also follow similar trends [Lebel et al., 2012; Westlye et al., 2010]. In the NKI‐Rockland cohort, a recent graph theoretical analysis of structural connectivity found several network properties, including efficiency, varied along the similar polynomial trajectories [Zhao et al., 2015]. In contrast, the modularity—or extent to which a network could be segregated into regional communities—remained stable over time.

In this study, using a subsample of the NKI‐Rockland dataset, we found that several network components followed an inverted U‐shaped trajectory. Significant variation in component strength with age was found in 16 of 22 components, of which 9 followed a nonlinear trajectory. When ordered by reliability across subsamples, age variation in 8 of the top 10 most robust components was best described by a polynomial relationship. Of the remaining components, 6 increased linearly with age, and 1 decreased. We found that components linking densely‐connected network hub regions tended to follow a nonlinear trajectory with age, decreasing in strength in later life. In contrast, components that increased in strength with age reflected local connectivity patterns between neighboring regions, or between corresponding regions in the opposite hemisphere (e.g., components H, L, M, O, and Q), compared to more global connectivity patterns (A, E, F, J). This increase in component strength may represent a relative sparing of local connections. It may also reflect age‐related alterations to the underlying microstructural white matter organization. For example, a consequence of regional decreases in the number of crossing fibers in older subjects could be the improved resolution of the predominant fiber direction, resulting in an apparent increase in fiber number in short, local connections.

These observations support evidence of an increasing dependence on local connectivity in the elderly connectome with corresponding decreases in long‐range connection strength between cortical hubs [Betzel et al., 2014; Cao et al., 2014; Perry et al., 2015; Zhao et al., 2015]. Analyses of functional connectivity networks have shown that hub connectivity follows a U shaped trajectory over the human lifespan alongside a decrease in network modularity, suggesting a less segregated network topology in old age [Cao et al., 2014; Chan et al., 2014]. Performing a comparative analysis of both functional and structural networks, Betzel et al. showed structural connectivity of hub regions decreases dramatically with age, while local connectivity is relatively spared. In addition, functional connectivity within resting state networks (RSN) decreased with age whereas connectivity between RSN increased. This increase in between‐network connectivity was subserved by multi‐step structural connections. Similarly, Perry et al. showed that alterations to edge strength in the aging structural connectome likely lead to an increased preference for network communication via multiple, non‐hub, local pathways [Perry et al., 2015]. Taken together, this evidence suggests that the decline of long‐distance, hub‐to‐hub connections with a relative sparing of topologically, local connections results in less efficient network communication in older age, a process that a may underlie progressive cognitive decline [Andrews‐Hanna et al., 2007; O'Sullivan et al., 2001].

Structural connectivity is established early in development [Ball et al., 2014; Kostovic and Jovanov‐Milosevic, 2006], and early disturbances to network organization may be a marker of abnormal neurodevelopment [Ecker et al., 2015]. In our second experiment, we performed a network decomposition in an adolescent cohort and found a single subnetwork with significantly greater connectivity in ASD. This network was composed primarily of multiple, local connections between neighboring regions in the cingulate and paracingulate cortices, both within and between hemispheres, along with connections between supplementary motor areas, parietal cortex and the putamen. The cingulum, and in particular the anterior cingulate cortex, has been linked to ASD due mainly to its role in social interaction and attention [Mundy, 2003]. Indeed, fMRI studies have found that altered anterior cingulate activation in ASD is associated with errors in response inhibition and repetitive behavior [Agam et al., 2010; Kana et al., 2007; Thakkar et al., 2008] and performance during social tasks [Di Martino et al., 2009; Dichter et al., 2009]. Similarly, metabolic [Tebartz van Elst et al., 2014], neuropathological [Simms et al., 2009] and neuroanatomical disturbances [Schumann et al., 2010] have also been reported in the cingulate in ASD. In a comprehensive diffusion tractography study of the white matter tracts of the limbic system, Pugliese et al. found significantly increased tract volume bilaterally in the cingulum bundle (determined by streamline count) of adults with Asperger's syndrome [Pugliese et al., 2009]. This observation is convergent with post‐mortem findings in autistic cases of excessive axonal connectivity between neighboring cortical regions in the cingulate [Zikopoulos and Barbas, 2010]. This is of particular interest, given the putative neurodevelopmental origins of ASD, as the cingulum bundle forms early in gestation, followed by short range cortico‐cortical connections in the third trimester [Takahashi et al., 2012; Vasung et al., 2010] suggesting that any early disruptions to white matter development in utero could have significant long‐term implications on neurodevelopment.

Previous structural network analyses in autistic populations have found significantly increased structural connectivity, inferred from tractography streamline count, among cortical regions including anterior and posterior cingulate cortex, superior frontal, superior parietal, and insula cortex [Ray et al., 2014]. In a subset of the UCLA cohort, Watanabe and Rees found evidence for delayed, or immature, hub connectivity in ASD [Watanabe and Rees, 2015] whereas Ghanbari et al. used a supervised variant of NMF coupled with a graph embedding approach to define discriminative network components and found decreased interhemispheric connection strength in subcortical subnetworks in ASD [Ghanbari et al., 2014]. Similarly, other studies have reported decreases in structural connectivity, dependent on measures of white matter microstructure [Lo et al., 2011; Noriuchi et al., 2010; Thakkar et al., 2008]. These discrepancies may relate, in part, to the uncertain correspondence between different measures of structural connectivity. In the original study of this cohort, Rudie et al. found that streamline count was significantly increased in four times as many connections in ASD subjects compared to controls [Rudie et al., 2012]. However, a concomitant decrease in fractional anisotropy and increase in mean diffusivity was also noted in white matter connections on average in ASD. These differences resulted in an atypical age‐related development of network efficiency in ASD, a factor that related to symptom severity [Rudie et al., 2012].

NMF belongs to a class of multivariate matrix decomposition and dimension reduction techniques that include principal component analysis and independent component analysis (ICA). Recently, exploratory multivariate analysis methods have proven well‐suited to the discovery of complex organizational relationships in the brain [Beckmann and Smith, 2005; Calhoun et al., 2009; McIntosh and Mišić, 2013]. Previous studies have shown the potential of matrix factorization techniques to isolate topological subnetworks from functional and structural connectivity matrices on an individual or group level [Clayden et al., 2013; Ghanbari et al., 2014; Park et al., 2014]. We performed simulations to demonstrate that PNMF is particularly able to retrieve superposed spatial patterns and the corresponding, population‐varying component weights from a set of noisy connectivity networks. In addition, although we were unable to compare network components identified in the UCLA and NKI‐Rockland samples directly, due to the different parcelation schemes used in each study, [Meskaldji et al., 2013;Wijk et al., 2010; Zalesky et al., 2010], a split‐half reliability analysis showed that the majority of structural subnetworks in the NKI cohort could be consistently identified across population subsamples with shared network structure.

Additionally, an important aspect of any dimension reduction task is determining the optimal dimensionality of the solution. In this article, we chose to use an automatic model selection process that iteratively updates model rank, removing components with low spatial variance that do not contribute significantly to the final reconstruction [Yang et al., 2010]. This resulted in around 20 effective components selected in both experimental cohorts. Previous studies have shown that, for ICA‐based decomposition of fMRI data, higher‐dimensional decompositions can reveal nested subsystems within functional networks [Abou Elseoud et al., 2011; Dipasquale et al., 2015; Kiviniemi et al., 2009]. Indeed, in the present study we observed apparently correspondent components that were split between opposite hemispheres (e.g., components I and S), whereas others formed bilateral symmetric patterns (components A, U, and H) suggesting some hierarchical structure within components. We also note that several lateralized components contributed to rich club connectivity. Although there is some evidence for laterality in the human rich club when hemispheric connectivity is analyzed separately, with a stronger rich club present in the right hemisphere [Goulas et al., 2014], it is generally accepted that the rich club is symmetric in organization [van den Heuvel and Sporns, 2011]. Although these components contain rich club edges, they appear to represent a mixture of rich, local and feeder connections that vary together with age. Future exploration of PNMF network decomposition and the relationship between network components derived from PNMF and modules/communities and hierarchies derived from graph theoretical approaches are warranted. Likewise, PNMF network decomposition at multiple dimensionalities would provide a framework to investigate the nested, or hierarchical nature of structural connectivity subnetworks [Betzel et al., 2013; Betzel and Bassett, 2016; Meunier et al., 2010]. Future analyses may also consider the impact of group structure on PNMF decomposition. In this study, we applied PNMF jointly across both typically developing and ASD networks to examine components that were present in all participants. An alternative strategy may be to produce separate decompositions for each group to uncover group‐specific network structures.

STUDY LIMITATIONS

The use of (log‐transformed) streamline counts to estimate structural connectivity could be considered a limitation of this study. Is it important to note that fiber counts do not necessarily reflect true anatomical connectivity, and tractography is prone to mapping false positive connections due to local accumulation of modeling errors [Jones, 2010; Jones et al., 2013]. However, using available open access datasets, we have shown that PNMF is able to extract subnetworks that can provide insight into biological variability, with developmental trajectories that suggest streamline count, in part, can reflect maturational processes in the brain. Importantly, PNMF is generalisable to any inherently non‐negative data. This opens future avenues to explore network components derived from modern, probabilistic tractographic algorithms that better reflect true anatomical connectivity [Pestilli et al., 2014; Smith et al., 2015].

MRI studies in ASD may be at risk of selection bias due to the additional difficulties in scanning non‐compliant, or low‐functioning individuals, who may require sedation [Erbetta et al., 2014]. In this study, only data from high‐functioning ASD participants were available. As such we may underestimate any morphological traits of ASD through the exclusion of low‐functioning participants. Conversely, given the phenotypic heterogeneity of ASD, it may be that specific alterations in brain morphology are not present in all ASD subtypes [Vissers et al., 2012], and as such studies will benefit from identifying endophenotypic variations in specific sub‐populations of the ASD population. We believe this is an exciting avenue for further research.

CONCLUSIONS

In conclusion, we present a multivariate analysis of structural connectivity in two cohorts. We demonstrate that complex networks can be decomposed into robust and reliable subnetworks that vary in strength with age. Furthermore, we identify a specific subnetwork with increased connection strength in autism spectrum disorder. We propose that this form of network component analysis shows good potential for further exploration of the human structural connectome.

Supporting information

Supporting Information